Energetics of twisted DNA topologies

Abstract

Our goal is to review the main theoretical models used to calculate free energy changes associated with common, torsion-induced conformational changes in DNA and provide the resulting equations hoping to facilitate quantitative analysis of both in vitro and in vivo studies. This review begins with a summary of work regarding the energy change of the negative supercoiling-induced B- to L-DNA transition, followed by a discussion of the energetics associated with the transition to Z-form DNA. Finally, it describes the energy changes associated with the formation of DNA curls and plectonemes, which can regulate DNA-protein interactions and promote cross talk between distant DNA elements, respectively. The salient formulas and parameters for each scenario are summarized in table format to facilitate comparison and provide a concise, user-friendly resource.

Our goal is to review the main theoretical models used to calculate free energy changes associated with common, torsion-induced conformational changes in DNA and provide the resulting equations hoping to facilitate quantitative analysis of both in vitro and in vivo studies. This review begins with a summary of work regarding the energy change of the negative supercoiling-induced B- to L-DNA transition, followed by a discussion of the energetics associated with the transition to Z-form DNA. Finally, it describes the energy changes associated with the formation of DNA curls and plectonemes, which can regulate DNA-protein interactions and promote cross talk between distant DNA elements, respectively. The salient formulas and parameters for each scenario are summarized in table format to facilitate comparison and provide a concise, user-friendly resource.

Significance

This review summarizes the theoretical approaches and the applicable equations that have been developed to calculate the energy of torsionally stressed DNA conformations that may form in physiological conditions. The review has a summary of work regarding the energy change of the negative supercoiling-induced B- to L-DNA transition, including a discussion of the energetics of the transition to Z-form DNA. It also describes the energy changes associated with the formation of DNA curls and plectonemes, which can regulate DNA-protein interactions and promote cross talk between distant DNA elements, respectively. Formulas and parameters for each scenario are summarized in table format to facilitate comparison and provide a concise, user-friendly resource.

Introduction

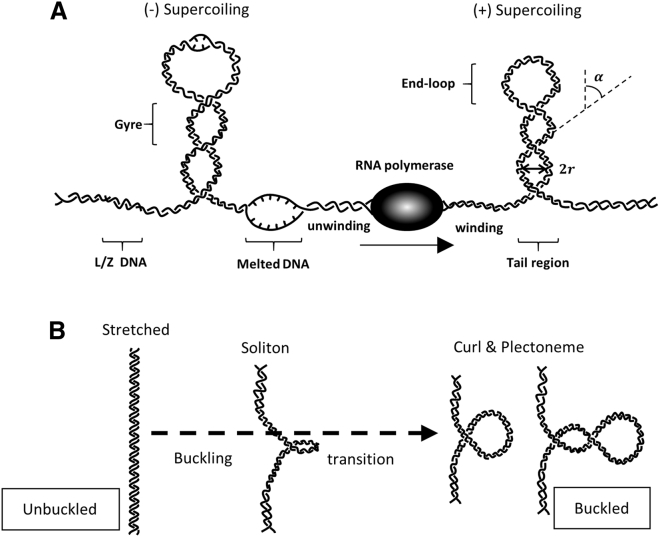
The purpose of this review is to summarize the theoretical approaches and the ensuing equations that have been developed to calculate the energy of torsionally stressed DNA conformations that may form in physiological conditions. Indeed, the right-handed, double-helical B-form DNA with a pitch of ∼10.5 bp/turn characterizes hydrated, torsionally relaxed, and tension-free DNA. However, prokaryotic and eukaryotic genomes are highly remodeled by proteins, tension, and torsion within DNA that generate other conformations. Tension derives mainly from anchorage to intracellular structures, motion in the intracellular milieu, and forces exerted by DNA translocases. Torsion derives from the interaction with proteins that may wrap DNA possibly changing its twist (1) or the activity of DNA-processing enzymes, such as helicases and topoisomerases that wind or unwind DNA. The well-known twin-domain model (2) of transcription is a paradigm of how a DNA-processing enzyme, in this case an RNA polymerase (RNAP), twists DNA (Fig. 1 A).

Figure 1.

Sketches of the twin-domain model and plectoneme formation. (A) During transcription of a template that is torsionally constrained at each end, negative supercoiling accumulates upstream and positive supercoiling accumulates downstream. This RNA-polymerase-generated supercoiling can produce plectonemes, although negative supercoiling may induce DNA melting or transition to the L- or Z-form before plectonemes are formed at the buckling transition. Transcription is not the only supercoil-generating process in the cell, but it is used here as an example. (B) Unwinding DNA may produce a “soliton” in which the DNA curls about the long axis without significantly changing the tether length. Detectable tether length changes result when the curl aligns perpendicular to the direction of extension and subsequently twists to form a plectoneme.

Torsional stress induced by enzymatic activity can significantly change DNA topology at the level of just a few basepairs, as well as over tens of thousands of basepairs. At the basepair level, torsional stress affects sequence-dependent bending, kinking, and reshaping of the grooves that, in turn, determine the specificity of DNA-binding proteins and their readout capabilities (3,4). For example, as twist increases in front of a replication fork, the DNA bending elasticity decreases, and the minor groove becomes narrower. Such conformational changes might influence protein-DNA interactions, especially for those proteins that bend DNA and open the minor groove, such as the lac repressor (5, 6, 7), the integration host factor (IHF) (8,9), or other minor-groove binding architectural proteins such as the male sex determining factor SRY (10). In contrast, reducing the twist (unwinding) increases the bending elasticity of DNA; thus, it stabilizes the binding of proteins, such as histones, that wrap DNA (11). In general, the minor groove in AT-rich regions is narrower, and the negative electrostatic potential higher, than in random sequences. This physical feature can be recognized by arginine (12); thus, a change in the width of the minor groove because of twist can impact greatly the binding of those specific DNA-binding proteins that primarily rely on electrostatic contact by arginine, such as the phage 434 repressor (13), IHF, or high mobility group protein I (10). In fact, twist that modulates the groove widths is likely to be at the basis of the high-specificity binding differences observed among proteins within the same family (14). Furthermore, twist-induced widening or narrowing of the major groove can facilitate or impede the binding of proteins that recognize specific DNA sequences through base readout by changing accessibility (14).

Genome-wide studies (15, 16, 17, 18) have shown that transcription-generated torsion can also extend over thousands of basepairs and, in concert with topoisomerases, dynamically change DNA structure on a large scale. Under low tension (f <̰ 10 pN) in the absence of or below 40 pN·nm positive torque, DNA remains in B-form. Added torsion initially generates a twisted molecule, but when the torsional stress on the DNA exceeds a critical level, at the buckling transition (19), a “curl” forms and the DNA writhes and crosses over itself to form a loop (Fig. 1 B). The aggregate writhe and twist in DNA determine the supercoiling, which can be positive or negative. Further torsion applied to the DNA molecule adds gyres to the stem of this loop to form a plectoneme, which may encompass a long segment of DNA (Fig. 1 B; (20)). Plectonemes are fundamental elements of compacted DNA and facilitate interactions between distant DNA sites (21,22) and their associated proteins (23, 24, 25). The number of plectonemes that form depends on the applied tension and ionic strength (26). They have been observed to diffuse along DNA, as well as to abruptly disappear at one position before reappearing at a another (27), although intrinsically curved DNA sequences, DNA deformability, and DNA-protein complexes can pin plectonemes at a specific site (28, 29, 30, 31, 32, 33).

In addition to plectoneme formation, the DNA helix may change conformation under tensile and torsional stress. Previous experiments have shown that even a small negative torque (when f < 10 pN, τ < 40 pN·nm) may induce stretches of a DNA molecule to transition from B- to a left-handed L-form (L-DNA) (34). L-DNA appears to be a mixture of melted and basepaired DNA with left-handed intertwining of the two strands. AT-rich regions, being less thermodynamically stable than sequences rich in GC, may melt if unwound under tension (35). Thus, in negatively supercoiled plasmids, single-stranded regions may occur (36) as well as Z-DNA, one of the noncanonical, left-handed DNA forms adopted by GC-rich sequences in high salt and believed to be important during transcription (37,38). Only a slight negative torque of ∼−3 pN ⋅ nm can trigger the B-Z transition in GC- or GT-rich regions under 1.4 pN of tension (39) indicating that this transition may be more common than melting in physiological conditions, as the average torque for DNA melting is ∼10 pN·nm. Although it is unlikely that a plasmid will fully convert from B- to L-DNA, certain segments may adopt this form.

In contrast, under high tension (f > 60 pN) and zero torque, B-DNA can be overstretched to form S-DNA (40, 41, 42, 43, 44, 45). Applying large positive torque on DNA under high tension (f > 20 pN, τ > 40 pN·nm) can generate P-DNA (34,46), and the average parameters for the S- and P-DNA forms have been summarized by Marko and Neukirch (34). The energy expressions for B-, melted, intertwined, and Z-DNA will be discussed in this review.

The conformational changes in DNA that result from torsional stress modulate subsequent transactions and are essential for the regulation of DNA biochemistry. The energy changes associated with these torsion-induced conformational changes direct this regulation and are important for understanding cellular energy transactions and balance (47). However, given the different types and length scales of conformational responses to torsion in DNA, it has been challenging to theoretically describe the energetics of torsion-driven, topological, or conformational changes in DNA with a single model.

The goal herein is to review the main theoretical models used to calculate free energy changes associated with common, torsion-induced conformational changes in DNA and provide the resulting equations hoping to facilitate quantitative analysis of both in vitro and in vivo studies. This review begins with a summary of work regarding the energy change of the negative supercoiling-induced B- to L-DNA transition, followed by a discussion of the energetics associated with the transition to Z-form DNA. Finally, it describes the energy changes associated with the formation of DNA curls and plectonemes, which can regulate DNA-protein interactions and promote cross talk between distant DNA elements, respectively. The salient formulas and parameters for each scenario are summarized in table format to facilitate comparison and provide a concise, user-friendly resource.

Free energy of torsion-induced conformational changes in DNA

DNA adopts various conformations and topologies depending on the tension and torque to which it is subjected, and the dominant conformations over a range of tension and torque have been theoretically predicted (34). Here, we will confine our attention to the energy of DNA conformations most relevant in vivo, including B-form, melted, intertwined, Z-form, and plectonemic DNA (Fig. 1). These topological states of a DNA molecule can be described using the linking number, Lk = Tw + Wr, in which twist (Tw) is the number of times the single strands of the DNA helix intertwine and writhe (Wr) is the number of times the main axis of double helix crosses itself. By convention, right-handed intertwining is considered positive. The linking number of relaxed B-DNA with no torsion is calculated with the equation Lk₀ = n₀ (bp)/10.5 (bp/turn), in which n₀ stands for the total number of basepairs in the DNA molecule. When DNA is under torsional stress, the change in linking number is ΔLk = Lk − Lk₀ = ΔTw + ΔWr.

Energies of DNA melting and of the B-Z transition

As B-DNA is progressively unwound, the magnitude of (−) torque increases. The B-L transition is triggered beyond a threshold of negative torque and continues until the entire molecule adopts the L-form. In this transition, if tension is high enough (but still physiological, f < 20 pN) to prevent buckling of a negatively twisted DNA molecule, basepairs will start melting when the torque reaches about −10 pN·nm. With further negative twist, the torque remains constant as B-DNA transitions to L-DNA. Because L-DNA has a much higher twist persistence length (C_L ϵ (10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20) nm) (48) than intertwined, melted DNA (C_melt ≈ 1 nm, Eq. 1), L-DNA is believed to be composed of intertwined, melted DNA and other noncanonical structures like Z-DNA (49). Previous models have shown that less energy is required to denature an A:T basepair than a C:G basepair (ΔG ≈ 1.9 and 2.9 k_BT, respectively (50)), so DNA melting occurs preferentially in AT-rich regions. Conversely, the B-Z transition is most common in DNA regions containing dinucleotide repeats of d(pCpG) or d(pGpT) (51). Both melting and the B-Z transition are highly sensitive to increases of temperature and pH, which destabilize hydrogen bonding in basepairs, and salt concentration, which reduces repulsions between the sugar phosphate backbones to stabilize basepairing. This discussion is limited to the most common experimental conditions, namely room temperature (25°C), pH 7.5–7.7, and salt concentrations from 10 to 400 mM.

Table 1.

Energy expressions for DNA under different conditions of tension and torsion

Common symbols: Ls, stretched DNA contour length; Ceff, effective twist persistence length (twist modulus/kBT); ΔLk, linking number change in stretched B-form DNA; f, tension; τ, torque; ω0, intrinsic twist of DNA, ω0 = $\frac{2\pi }{3.57}$ nm−1; G, twist-bend coupling parameter (G, 30–40 nm (56,57)); g, twist-stretch coupling parameter (unitless) (g, −22 to −17 (54, 55, 56)); A, bend persistence length; C, twist persistence length.
Energy type	Equations	Annotations		Reference	Equation number
Energy of intertwined, strand-separated DNA	EMelted = EtwM + EbpM EtwM, energy of intertwined, melted region: EtwM = 1/2nκmelt${\overline{\theta }}^2=\frac{k_{B}T{C}_{melt}}{2L_{melt}}$(2πΔLkmelted)2 EbpM, energy cost for denatured basepairs in a melted region: EbpM = εini,melt + $\sum _{i=1}^n$εmelt,i	n, number of unpaired basepairs $\overline{\theta }$, average twist angle of each disrupted basepair Length of melted region: Lmelt ≈ n × 0.54 nm/bp (48), 2πΔLkmelted = $n\overline{\theta }$ κmelt, twist modulus of two intertwined strands, ∼2.3 kBT Twist persistence length, Cmelt = $\frac{L_{melt}\times {\kappa }_{melt}}{n{k}_{B}T}$ ≈ 1.2 nm εini,melt: initial energy for melting, 9–11 kBT. $\sum _{i=1}^n$εmelt,i: sum of energy cost for each individual basepair melting, where εmelt,i depends on each basepair and its neighbors; particular values can be found in (50).	Change of linking number that melted region contributes to flanking DNA: ΔLkB − melt = $\frac{n}{10.5}-\frac{n\overline{\theta }}{2\pi }$	(48,50,57, 58, 59, 60, 61, 62)	(1)
Energy of Z-form DNA (fixed two boundaries)	EZ = EtwZ + EbpZ EtwZ, energy of twisting Z-DNA: EtwZ = $\frac{k_{B}T{C}_Z}{2L_Z}$ (2πΔLkZ)2 EbpM, energy cost for B-Z transition: EbpM = 2εwall + $\sum _{i=1}^m$εB-Z,i	LZ, length of Z-form DNA ΔLkZ, twist change in Z-form DNA CZ: twist persistence length, ∼7 nm for d(pCpG)n repeats εwall: domain wall energy, ∼8.4 kBT. m: number of basepairs that undergo B-Z transition, LZ = m × 0.37 nm/bp (65) $\sum _{i=1}^m$εB-Z,i: sum of energy cost for disrupting each additional basepair, following the nucleation of Z-DNA, where εB-Z,i ≈ 1.1 kBT for d(pCpG) repeats and εB-Z,i ≈ 2.4 kBT for d(pCpA) repeats (63,64).	Change of linking number that B-Z transition contributes to flanking DNA: ΔLkB-Z = −am − 2b, a = 2(1/10.5 + 1/12), b = 0.4.	(49,61,63, 64, 65)	(2)
Twist energy of stretched B-form DNA	EtwB = $\frac{k_{B}T{C}_{eff}}{2L_s}$(2πΔLkB)2	1/Ceff = 1/C∗ + 1/(4A∗)$\sqrt{\frac{k_{B}T}{f{A}^{\ast }}}$	TWLC model (G = 0): A∗ = A (≈50 nm), C∗ = C (≈100 nm)	(66)	(3)
			TWLC (G$\ne$0 and very large G) nonperturbation theory: A∗ = κb = $A\frac{1-\frac{{\epsilon }^2}{A^2}-\frac{G^2}{AC}\left(1+\frac{\epsilon }{A}\right)}{1-\frac{G^2}{2AC}};$C∗ = κt = $C\frac{1-\frac{\epsilon }{A}-\frac{G^2}{AC}}{1-\frac{\epsilon }{A}}$; ε, the bending anisotropy.	(52)	(4)
			TWLC (G$\ne$0 and G is small) perturbation theory (f ∈ (0.1 pN, 10 pN): 1/A∗ = 1/A$\left(1+\frac{G^2}{2AC}\right)$, 1/C∗ = 1/C$\left(1+\frac{G^2}{AC}\right)$.	(53)	(5)
Stretched DNA, TWLC model (G = 0)	E(f, ΔLk) = [−f +$\sqrt{\frac{f{k}_{B}T}{A}}+\frac{C_{eff}{k}_{B}T}{2}{\left(\frac{2\pi \text{Δ}Lk}{L_s}\right)}^2$]Ls	For definitions of f, A, Ceff, ΔLk, and Ls, see above.		(66)	(6)
Stretched-twisted DNA, (perturbation theory) (G$\ne$0)	E(f, τ) ≈ $\left(-f+\sqrt{\frac{f{k}_{B}T}{A^{\ast }}}+\text{Γ}\tau -\frac{{\tau }^2}{2k_{B}T{C}_{eff}}\right)$Ls	Torque, $\tau \approx \frac{2\pi k_{B}T{C}_{eff}}{L_s}\Delta Lk$	proportionality constant Γ, Γ = $\frac{G^2}{8A^2{C}^2{\omega }_0}$	(53)	(7)
Stretched-twisted DNA, (CTWLC model)	$\frac{E}{k_{B}T{L}_s}=\frac{1}{A}\sqrt{\frac{Af}{k_{B}T}-\frac{1}{4}{\left(C_{eff}{\omega }_0\sigma +\frac{gf}{K_0}\right)}^2}+\frac{C_{eff}}{2}{\omega }_0^2{\sigma }^2-\frac{f}{k_{B}T}-\frac{k_{B}T}{2K_0}{\left(\frac{f}{k_{B}T}-g{\omega }_0\sigma \right)}^2$	σ: supercoiling levelσ = ΔLk/Lk0	K0, the stretch modulusK0 ≈ 1200 pN	(55,67)	(8)
			For f, A, Ceff, ΔLk, Ls, g, and ω0, see above.
Energy barrier of DNA from unbuckled to soliton state	$E_s=\frac{8k_{B}TA}{l}\text{tanh}(\frac{L}{2l})-2\pi W{r}_s{\left(\tau +\frac{\pi k_{B}T{C}_{eff}W{r}_s}{L}\right)}^2$	L, DNA length in nm,l, soliton length scale: ${\left[{\left(\frac{A}{f}\right)}^{-1}-{\left(\frac{2C_{eff}}{f}\right)}^{-2}\right]}^{-\frac{1}{2}}$	Wrs: writhe in soliton: $\begin{array}{l}\frac{2}{\pi }ta{n}^{-1}\left[\frac{2A}{\tau l}\text{tanh}\left(\frac{L}{2l}\right)\right]\\ \end{array}$	(68,69)	(9)
Curled DNA	Ec = $\left(8-\frac{3.14f{\left(0.8+2.2{\kappa }_D^{-1}\right)}^2}{A{k}_{B}T}\right)\sqrt{k_{B}TAf}$	${\kappa }_D^{-1}$, Debye length; f and A, see above.		(26)	(10)
Plectonemic DNA	Ep = $\frac{2{\pi }^{2}C{k}_{B}T}{L_p+q\text{Γ}}{\left(\text{Δ}L{k}_p-W{r}_p\right)}^2$ + Lp$\left[\frac{A{k}_{B}T{\left(sin\alpha \right)}^4}{2r^2}+U\left(r,\alpha \right)\right]$ + qεp$\sqrt{Af{k}_{B}T}$	q, number of plectonemes along DNA; Lp, plectoneme length; ΔLkp, linking number change of plectoneme, Wrp, total writhe of the plectonemic regions Wrp =$\frac{L_{p}sin2\alpha }{4\pi r}$+ qωp (ωp ≈ 1); U(r, α), electrostatic repulsion and entropic confinement free energy, Γ, length of the end loop and tail region of a plectoneme (Fig. 1); for more details, please refer to (26). The top part of left expression represents the twist energy of plectoneme. The middle term in the sum represents bending energy as well as the electrostatic repulsion and entropic confinement free energy (whole plectonemes except end loop and tail region). The bottom part contains the energy contribution of end loop and tail region.		(26)	(11)

Some variable names have been changed and values/units have been converted from those used in the original reports for uniformity.

The energy necessary to melt B-DNA can be divided into two contributions (E_bpM in Eq. 1, Table 1): 1) the energy required to melt an initial basepair, which depends on the basepair type and averages ε_ini,melt ≈ 9–11 k_BT (52), and 2) the energy associated with melting successive basepairs, which depends on each basepair and its neighbors (50,53,54). After melting, the twist energy of the melted region changes as torsional stress within what was previously double-stranded DNA is sustained by intertwined, but unpaired, single strands and can be expressed as E_twM in Eq. 1 in Table 1. The twist persistence length, C_melt, varies from ∼1 to 3 nm as [Na⁺] drops from 400 to 10 mM (53,54), as expected because the ionic screening of electrostatic repulsions falls with the salt concentration. C_melt for (AAT) repeats can even exceed 15 nm in Tris buffer with no salt, which indicates that like B-form DNA, the twist rigidity of intertwined, melted DNA increases as monovalent cation concentrations decrease. For nonhybridized, intertwined strands, the average twist angle of each disrupted basepair, $\overline{\theta }$, is determined by minimizing the overall energy (55). An intertwined, melted region contributes ΔLk_melted = (n$\overline{\theta }$)/2π to the linking number, where n is the number of denatured basepairs after loss of n/10.5 turns because of melting. If the overall linking number of the molecule is fixed, the linking number change of DNA segments surrounding the melted region will be −ΔLk_melted (55), which can be plugged into Eqs. 3, 4, or 5 in Table 1 (depending on the model used; see Energy of extended, curled, and plectonemic DNA) to calculate the twist energy of the flanking B-DNA.

Similar to melting, the free energy for the B-Z transition can be calculated considering two contributions (E_bpZ in Eq. 2, Table 1). One is the energy of disrupted base stacking including the “domain wall energy,” ε_wall, of ∼8.4 k_BT at each junction between B- and Z-form segments (49,63,64). The other is the energy associated with disrupting each additional basepair after the first one, which depends on the nature of the basepair, for example, ∼1.1 k_BT/bp for d(pCpG) repeats or ∼2.4 k_BT/bp for d(pCpA) repeats (63,64). After a B-Z transition has initiated and considering only d(pCpG) repeats with m basepairs, in a conventional zipper model (64), the change in twist in going from B-form (10.5 bp/turn) to Z-form (−12 bp/turn) is ΔLk_B-Z = −am − 2b, where a is the change in twist for a single GC basepair flipped from B to Z and is given by a = 2 × (1 / 10.5(bp/turn) + 1 / 12(bp/turn)) and b = 0.4 and is the twist at the boundary between the B- and Z-forms. Such a change in twist consequently alters the linking number of flanking DNA and its twist energy as well. The twist energy of Z-DNA is expressed as E_twZ in Eq. 2, Table 1, where the twist persistence length, C_z, is determined to be ∼7 nm in Tris buffer without salt (61).

DNA melting and the B-Z transition alter the DNA conformation over a long range and may affect the DNA-binding energy of proteins. For example, RNA polymerase binds more readily if the DNA is partially melted and there is a lowered energy barrier for strand separation. Similarly, Z-form DNA is the binding target of certain proteins, such as human ADAR1, a prototypic Z-DNA-binding protein, which otherwise must induce Z-form DNA upon binding (70). Knowledge of the energetics of different DNA conformations facilitates a quantitative understanding of how DNA topological changes regulate protein binding and enzyme activity.

Energy of extended, curled, and plectonemic DNA

This section focuses on the buckling transition and the associated energy change. Studies of the buckling transition have often focused on positively supercoiled DNA, in which DNA remains in the B-form under tension up to 10 pN and torsion up to 40 pN·nm (34).

Initially, twisting a DNA molecule under tension produces an extended conformation (Fig. 1 B, left). One of the simplest models for this is the twistable worm-like chain (TWLC) (Eqs. 3 and 6, Table 1), which treats DNA as an inextensible rod with independent flexural and torsional elasticities (71). However, given the intrinsic helicity of DNA, a twist-bend coupling parameter, G, improves the accuracy of theoretical descriptions (72,73).

In the absence of tension, f = 0, and externally applied torsion, τ = 0, when taking into consideration the coupling that must exist between helical DNA bending and the consequent twist, the intrinsic bending stiffness A and twisting stiffness C should be calculated as the renormalized, G-dependent values κ_b and κ_t, respectively (52). Then, κ_b and κ_t can be used to calculate the tension-dependent (f > 0) effective twisting stiffness, C_eff (Eq. 3, Table 1). This was found to be in excellent agreement with the one derived from a coarse-grained model of DNA, which used improved conformational parameters and salt dependence, and in reasonable agreement with experiments, especially at low tension (f <̰ 1 pN) (53). For small values of G, Nomidis et al. (53) proposed a calculation of the free energy of extended DNA under both tension and externally applied torsion based on perturbation theory (Eqs. 4 and 7, Table 1). Their approach identified a very large characteristic force, f₀ ≈ 600 pN, above which C_eff finally approaches the intrinsic value C. For almost all single-molecule measurements on DNA with mechanical properties under physiologically relevant conditions, the forces at play are a lot smaller than f₀, making it justifiable and accurate to use C_eff instead of C.

If the extensibility of DNA is taken into consideration, instead of using the TWLC model, the chiral, extensible worm-like chain (CEWLC) model can be used, which takes into consideration the coupling between twist and stretch, expressed as the coupling parameter g (67). Using this model, the free energy of a DNA molecule under both tension and torsional stress was formulated by Marko (67) (Eq. 8, Table 1) and used to fit experimental data and determine the value of g (54,55). Under low tension, the extension of double-stranded DNA increases upon winding, and a negative g characterizes this behavior. Compared to RNA, DNA has a narrower minor groove but a positive basepair inclination, which leads to a slenderer and more extended double helix (4). Under the same conditions, double-stranded RNA is characterized by a positive g (55,56), with a more compact conformation, a narrower major groove, and reduced helical extension compared with DNA.

Either the TWLC or CEWLC, with G or g, respectively, ≠ 0, are still simplified models of DNA mechanics under torsion, as the bending and twisting stiffness are DNA sequence dependent (74,75). Both the TWLC and CEWLC models have been used to successfully predict the torsional and bending stiffness of DNA (53,67). However, combination of these two models into one that couples G and g would provide a unified model that allows simultaneous consideration of both the asymmetric nature and extensibility of double-stranded DNA. More rigorous constitutive theoretical frameworks have been developed for the short-range mechanical behavior of DNA as a function of sequence (28), defects (30, 31, 32), and distortions (33). These models have proved useful to predict, for example, sequence-dependent local DNA topologies such as the positioning of nucleosomes (76,77) or the position of DNA supercoils (28) based on the energy cost of deforming specific DNA sequences.

When the torque on a DNA molecule exceeds a critical value, τ′, accumulated strain will trigger buckling (19) and plectoneme nucleation, which abruptly shrinks the overall extension. This buckling transition is first characterized by a “soliton” transition state (68,69) with energy given by Eq. 9 in Table 1. After a soliton is formed, a “curled” intermediate state (26,69) is the following step toward the formation of plectonemes (Fig. 1 B). Near the buckling transition, the extension of DNA molecules toggles between two distinct values, the frequencies of which display the probabilities of these states (78). The critical value of linking number at the buckling transition, which corresponds to the torsion that causes the curled and extended DNA states to be equally probable, increases with the applied tension and molecule length (79). The analytical formula is available (26), and the critical torque, τ′, can be easily calculated by using Eq. 7 (Table 1).

Theoretical expressions for the free energy of stretched-twisted DNA (Eq. 6, Table 1), curls (Eq. 10, Table 1), and plectonemic DNA (Eq. 11, Table 1) describe the partitioning of energy associated with a single DNA molecule (26,66). These expressions can be used to calculate the number of curls, plectonemes, the size of plectonemic gyres, the probability of each conformation, and the average extension of DNA as a function of tension, DNA length, and salt concentration.

For salt concentrations lower than 50 mM, the persistence length of DNA increases because of reduced electrostatic screening. This contributes to the electrostatic repulsion energy term, U(r, α) in Eq. 11 of Table 1, and the number of curls and plectonemes along DNA decreases. Even under the most common experimental conditions in which f > 0.25 pN and the monovalent salt concentration is in the range of 100–200 mM, a buckling transition rarely involves more than one plectoneme (26) because of the high energy required to curl the DNA and repulsion between the negatively charged helices. As might be expected because tension opposes bending fluctuations and reduces entropy, the DNA length per plectonemic gyre decreases as tension, f, increases. However, under very low forces (f < 0.25 pN), which negligibly penalize the formation of curls and plectonemic end loops, multiple plectonemes may occur (26).

In vivo, distortions or sequence-dependent architecture of the DNA, as well as protein binding, may favor the formation of multiple plectonemes or curls along DNA. Instead of plectonemes randomly nucleating along DNA, the DNA sequence can favor plectonemes and curls in particular positions because of the intrinsic curvature or deformability of specific DNA sequences, although the AT versus GC content per se is not necessarily a determinant for plectoneme formation (28). In addition, local defects induced by DNA mismatch or damage can also spur the formation and localization of plectonemes, which suggests that plectoneme formation might be a mechanism for locating the site of lesions requiring repair in vivo (32,69). Epigenetically, proteins that bind to and stabilize curls might lower the energy required to induce curls at multiple protein binding sites (26,76,77). In turn, mild torsion generated by motor enzymes may facilitate transcriptional initiation, whereas highly plectonemic regions might stall transcriptional elongation.

The nucleation energy largely determines whether specific DNA sequences with mismatches, kinks, or other deformities pin plectonemes, and various models with which to calculate it have been proposed (28,30,31,33,80). Most begin with the bending or twisting energy of DNA and introduce additional mechanical features. Given that DNA buckling and plectonemes directly affect DNA long-range interactions, it is important to understand how the sequence and tension within a DNA segment, as well as the surrounding salt concentration, affect the free energies of these topologies. This improves our understanding of DNA dynamics and regulation in vivo.

Remarks

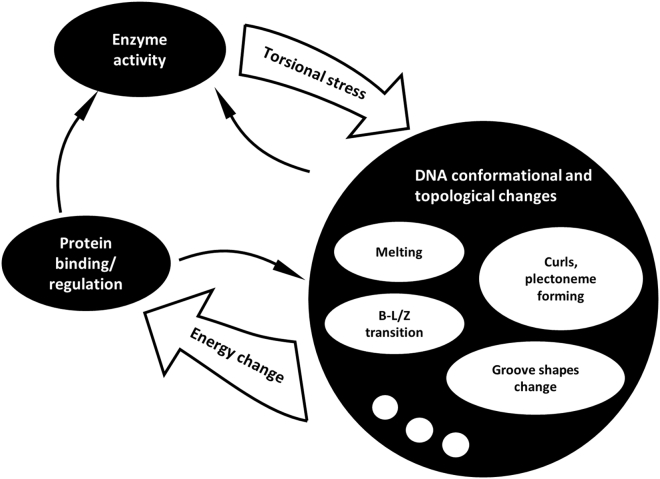
As described in Fig. 2, the interplay between DNA processing, DNA conformational and topological changes, and regulation via protein binding is tuned by a complex network of energy contributions. In vivo, DNA conformations are dynamic because of protein binding and processing by such enzymes as polymerases and helicases, which can generate tension and torque. In turn, different DNA conformations affect protein/enzyme-DNA interactions. Highly supercoiled regions stall transcription, and transcription-generated positive supercoiling destabilizes nucleosomes (81) to facilitate elongation. Previous experiments have shown that elongation by RNAP will stall if the torque in the DNA template exceeds ∼11 pN·nm (82), and topoisomerases are thought to relax excessive torsion to sustain transcription (83, 84, 85). Transcription-coupled DNA supercoiling has also been shown to enable multiple RNAPs moving in the same direction to elongate faster than a single RNAP, as the supercoiling emanating from one reduces the supercoiling produced by others ahead or behind. Likewise, repression of an upstream promoter antagonizes downstream transcription and can cause downstream RNAPs to prematurely dissociate (86,87). Interestingly, the torque at which transcription stalls in negatively supercoiled DNA is similar to the torque that facilitates the separation of duplex DNA into single strands (49). Backtracking on an unwound upstream DNA may be more favorable than on canonical B-form DNA, thereby stalling RNA polymerases. Furthermore, melted regions resulting from unwound upstream DNA may favor the formation of R-loops that might stall transcriptional elongation. For example, in the human c-myc promoter, transcription-induced torsional stress can melt the distant upstream element (FUSE) (15), and elongation from a promoter may recruit additional RNAPs to the same or further upstream promoters (87,88). Negative supercoiling also favors the binding of other transcriptionally relevant proteins such as TATA binding proteins (89).

Figure 2.

Schematic representation of the interplay between torsion-generating DNA transactions, such as transcription, conformational and topological changes in DNA, and protein binding. DNA-enzyme-induced torsional stress causes local and long-range DNA conformational changes that include DNA melting, B to L or Z transition, major and minor groove changes, curls, and plectoneme formation. This affects protein binding. For example, plectonemes facilitate the juxtaposition of binding sites for looping proteins. Also, DNA bending, kinking, melting or B-L or Z transition can affect the energy barrier required for specific DNA-binding proteins or motors to process DNA.

Knowledge of the free energy of different DNA conformations and topologies provides a quantitative basis for understanding the relationship between genomic structure and function. It also provides insight into the likelihood of architectural or topological and conformational rearrangements that, for example, modulate DNA transactions by inducing transitions between B- and Z-form DNA (37,38), by juxtaposing distant sites for regulatory proteins, or by melting DNA to favor the recruitment of enzymes to particular sites.

Discussion and conclusions

Here, we reviewed the expressions with which to estimate energies of different DNA conformations under specific conditions of tension, torque, salt concentration, pH, and temperature. The formation of melted DNA, L- or Z-DNA, or plectonemic domains follows a quite similar pattern: first, nucleation, which requires relatively high energy to overcome a barrier, followed by progressive expansion of denatured basepairs within a bubble, L- or Z-form DNA between B-L or Z junctions, or more gyres in a plectoneme that require relatively less energy. Comparison of the energies associated with nucleation and expansion of these different DNA topologies under different tension, torsion, and salt conditions will give insight into their likelihood in vivo.

Note that these expressions do not include sequence dependence or other DNA defects. However, the mechanical properties of individual basepair steps have been theoretically assessed (90, 91, 92), and they have been used in the calculation of the energy for specific sequences to show that intrinsic curvature lowers the energy required to bend and effectively pin plectonemes (28). Similarly, DNA defects such as mismatches and kinks decrease bending energy, which can be predicted using available models (81, 82, 83, 84). By incorporating sequence-specific parameters into the general energy expressions in Table 1, we might parse the interactions that dictate protein binding and the syntax of gene expression. Knowing the energy of mismatched, kinked, or melted DNA sequences could be an incisive tool to define a sequence or a mismatch to pin a plectoneme. Calibrating these features according to tension in the DNA and salt concentrations will establish the energy required for long-range interactions.

We focused on melted DNA, Z-DNA and plectonemic B-DNA, which are ubiquitous in vivo. Melted DNA plays a critical role in regulating gene expression by recruiting RNA polymerases or altering elongation. Tools with which to predict melting energies may help identify potential promoters (92,93) and indicate DNA melting behind polymerases. Moreover, because melted DNA regions are potential targets for a variety of DNA-binding proteins, learning to control DNA topology with sequence variations would improve our ability to manipulate gene expression.

DNA melting not only makes bases accessible but also relieves torsional stress in the flanking DNA. The transitions to left-handed forms do this as well and appear to be associated with disease. Z-DNA is implicated in diseases of genomic instability and immune responses including cancer and systemic lupus erythematosus (94). Indeed, the level of Z-DNA assayed with Z-DNA antibodies reflected different disease stages of lupus (95). The ability to predict the energies of Z-DNA formation along a sequence might allow specific removal/placement of Z-DNA to treat such diseases. For example, Z-DNA near promoters favors mutagenesis (96), perhaps because of mechanical constraints that interrupt transcription. The mechanical properties of Z-DNA also affect nucleosome organization. Z-DNA is stiffer than B-DNA or melted DNA (48) and does not easily wrap histone octamers, so the ability to predict Z-DNA formation would help identify nucleosomal regions (97).

Of course, we still have much to learn about how DNA topology influences protein binding and function. For example, how (un)winding affects the site-specific protein binding to DNA is unclear, especially at the level of the interactions between protein binding domains and the DNA backbone and basepairs. The suggestion from unconstrained MD simulations (3) that local DNA twist may change the local bendability of DNA and the shape of the major and minor grooves in such a way as to affect protein binding has yet to be experimentally demonstrated. Knowledge of how protein binding changes DNA structure will improve prediction of DNA topology in complex mixtures using the approaches described herein.

In summary, the effect of tension and torsion on DNA conformation has, at this point, been under investigation for about three decades, and several general models exist to estimate the free energy of each of these conformations. These are valuable tools with which to begin to quantitively describe the free energy changes of DNA associated with protein-DNA interactions and predict regulatory behavior. Further computational, theoretical, and experimental work could help improve our understanding of how torsionally induced DNA conformations affect protein binding; determine the likelihood of mismatched, kinked, or melted DNA topologies under different tension, torsion, and salt conditions in vivo, and predict sequences likely to form left-handed conformations including Z-DNA, which appears to be an important epigenetic signal (98).

Author contributions

W.X., D.D., and L.F. reviewed literature and wrote the manuscript. W.X. prepared figures.

Editor: Tamar Schlick.