Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Aug 5;21(16):6748–6755. doi: 10.1021/acs.nanolett.1c00387

Correlation of Yu–Shiba–Rusinov States and Kondo Resonances in Artificial Spin Arrays on an s-Wave Superconductor

Anand Kamlapure †,*, Lasse Cornils †, Rok Žitko ‡,§, Maria Valentyuk †,∥, Roberto Mozara †, Saurabh Pradhan ⊥, Jonas Fransson ⊥, Alexander I Lichtenstein †,∥, Jens Wiebe †,*, Roland Wiesendanger †
PMCID: PMC8392378  PMID: 34351781

Abstract

graphic file with name nl1c00387_0005.jpg

Mutually interacting magnetic atoms coupled to a superconductor have gained enormous interest due to their potential for the realization of topological superconductivity. Individual magnetic impurities produce states within the superconducting energy gap known as Yu–Shiba–Rusinov (YSR) states. Here, using the tip of a scanning tunneling microscope, we artificially craft spin arrays consisting of an Fe adatom interacting with an assembly of interstitial Fe atoms (IFA) on a superconducting oxygen-reconstructed Ta(100) surface and show that the magnetic interaction between the adatom and the IFA assembly can be tuned by adjusting the number of IFAs in the assembly. The YSR state experiences a characteristic crossover in its energetic position and particle–hole spectral weight asymmetry when the Kondo resonance shows spectral depletion around the Fermi energy. By the help of slave-boson mean-field theory (SBMFT) and numerical renormalization group (NRG) calculations we associate the crossover with the transition from decoupled Kondo singlets to an antiferromagnetic ground state of the Fe adatom spin and the IFA assembly effective spin.

Keywords: Scanning tunneling spectroscopy, Yu−Shiba−Rusinov states, Kondo resonance, atom manipulation, artificial spin arrays

Mutually interacting magnetic impurities that are Kondo exchange coupled to the electrons forming the Cooper pairs in a superconducting host constitute building blocks for the realization of a topological superconductor that can potentially host Majorana states on its edges.1,2,11−20,3,21,4−10 While the Kondo exchange coupling JK affects the position of the Yu–Shiba–Rusinov (YSR) states inside the gap of the superconductor (2Δ),22−28 the mutual magnetic interactions J between the impurities dictate how strongly these YSR states split or hybridize into bands29−35 and govern the collective magnetic state of the magnetic impurity cluster. The investigation of the effects of varying JK and J on the YSR states in such systems is, thus, of fundamental interest toward the end of realizing topological superconductivity.

If JK is sufficiently large, the impurity enters the strong-coupling Kondo regime where the impurity spin forms a many-body singlet ground state with the conduction electrons for temperatures below the characteristic Kondo temperature,36TK. For kBTK ≳ Δ, the spectroscopic signature of the Kondo screened spin, the so-called Kondo resonance centered at the Fermi energy and having a width of order kBTK, can coexist with the YSR states.37−39 For normal metallic substrates, the behavior of two Kondo impurities interacting via the same conduction electron system that produces the Kondo screening, the so-called two-impurity Kondo problem,40,41 has been studied in great detail.42−46 For antiferromagnetic (AFM) interimpurity interaction J of increasing strength, the system passes over from two decoupled Kondo singlets (small J) to an AFM dimer (large J), which causes the Kondo resonance to split. However, the analog of this two-impurity Kondo problem for superconducting host systems32,47−49 has not been studied experimentally to a large extent so far,50,51 and it is an interesting question of how the YSR states behave as a function of J.

In this work, we experimentally study artificial Fe clusters consisting of a single Fe adatom magnetically interacting with an assembly of interstitial Fe atoms (IFA) of different shapes and sizes on an oxygen reconstructed superconducting Ta(100) surface. Spectra measured on these clusters show a systematic evolution of the Kondo peak (with kBTK ≫ Δ) seen on the Fe adatoms at high bias voltage, as well as that of the subgap peaks due to YSR states in the low-bias range. We show that with the increasing size of the cluster, the Kondo peak splits at the same time as a change in the asymmetry of the YSR peaks is observed.

The details of the preparation of a (3 × 3) oxygen-reconstructed Ta(100) surface, in the following called TaO, and of the cold-deposition of Fe can be found in refs (4), (52), and (53). We use vertical atom manipulation to build various clusters consisting of a single Fe adatom and an assembly with different numbers of IFAs in close proximity (see Supporting Information). Figure 1a shows a representative STM image of a cluster consisting of an Fe adatom that was placed at the center of the (3 × 3) plaquette and of a single IFA that was positioned between two (3 × 3) plaquettes.4 The corresponding height profile is shown in Figure 1b. Figure 1c shows the result of a geometry optimization of the surface through DFT calculations53 revealing the stable positions of the Fe adatom and the IFA. Within the DFT calculations, we find a finite magnetic moment for both the Fe adatom and the IFA. The DFT calculations also reveal an antiferromagnetic exchange interaction between the Fe adatom and the IFA. [See Supporting Information for the details of our DFT calculations.] The schematic top views and STM images of the other investigated clusters with 0–4 IFAs are shown in Figure 1d (see Supporting Information Figure S4 for other examples of similar clusters). To build such clusters, we initially moved Fe atoms to the interstitial locations to form the assembly and then placed the Fe adatom in close proximity (cases 1–4). We also studied the single Fe adatom without an assembly of IFAs for comparison (case 0).

Figure 1.

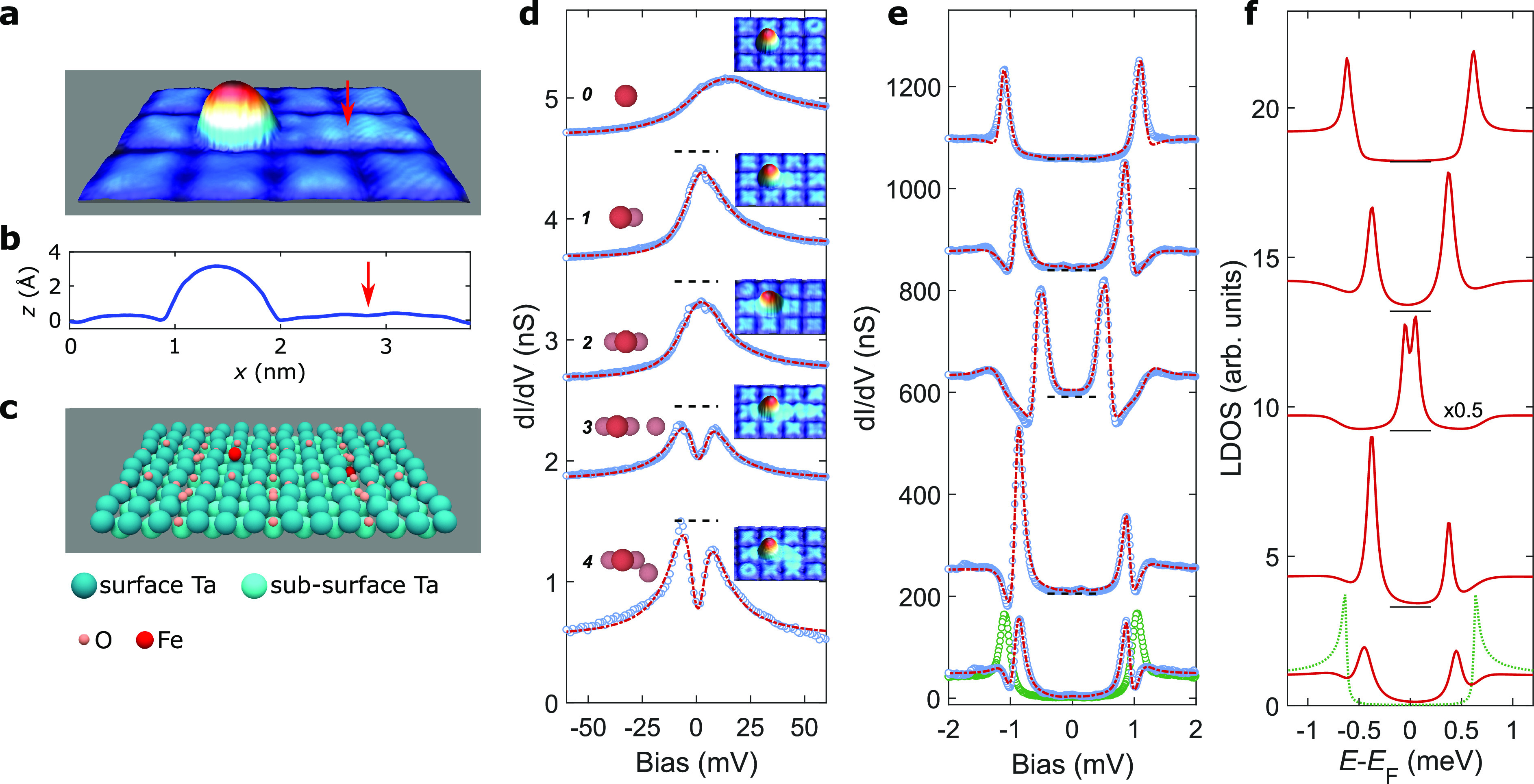
Figure 1

Open in a new tab

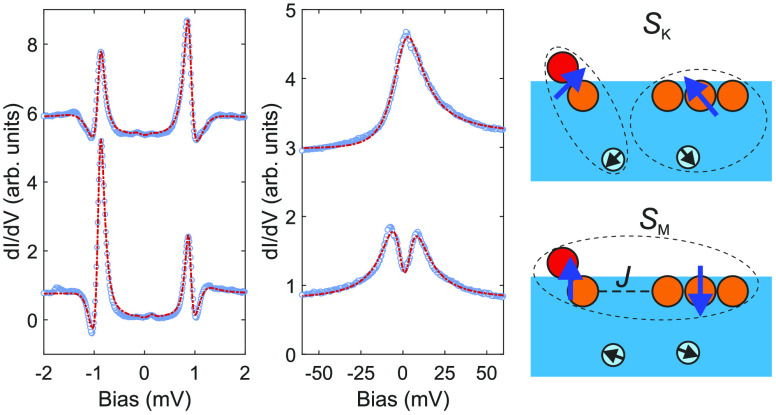
Construction and spectroscopy of Fe clusters at the TaO surface. (a) Constant-current STM image of the TaO surface with an Fe adatom and an interstitial Fe atom (IFA) indicated by the red arrow. (b) Height profile across the IFA and the Fe adatom in (a). (c) Perspective view of the DFT-optimized fully relaxed positions of an Fe adatom, an IFA, and the atoms in the TaO surface. (d) Large-bias dI/dV spectra (open dots) showing the Kondo resonance. The dashed red lines are fits to a Fano function, which is multiplied by a Lorentzian dip for the spectra exhibiting the zero-bias anomaly (ZBA), i.e., the exchange splitting of the Kondo resonance (see Supporting Information). The pictograms and numbers on the left side of the spectra show the corresponding structure of the Fe clusters and numbers of the IFAs in the assemblies. Corresponding STM images are shown in the insets on the right side of the curves (V = 50 mV, I = 100 pA). Spectra are shifted vertically for clarity as indicated by the horizontal dashed zero lines. Stabilization parameters for STS are Vstab = 100 mV, Istab = 100 pA, Vmod = 2–4 mV. (e) Small-bias dI/dV spectra (open dots) showing peaks inside the superconducting gap due to YSR states, together with the substrate spectrum (open green dots). Dashed red lines are fits obtained using a numerical deconvolution method. Spectra are shifted vertically for clarity as indicated by the horizontal dashed zero lines. Stabilization parameters for STS are Vstab = 2.5 mV, Istab = 100 pA, Vmod = 20 μV. The corresponding deconvoluted LDOS is plotted in (f). The green curve in (f) corresponds to the reference substrate density of states.

Spectra measured on these clusters with a superconducting tip in a wide bias range (Figure 1d) show a resonance around the Fermi energy. Here we have used a relatively large amplitude of the modulation voltage such that the superconducting gap and features within it are washed out. For the bare adatom, the resonance is very broad [half-width at half-maximum (HWHM) Γ ∼ 20–25 mV]. The adatom in proximity to one IFA (denoted as “adatom/IFA pair” in the following) shows instead a rather sharp resonance at the Fermi level [Γ ∼ 12 (±1) mV]. The line-shape evokes a Kondo resonance, arising from the effect of the proximal IFA on the Fe adatom, as discussed below. Although we do not observe any change in the lateral adsorption site of the adatom after adding the first closest IFA, we cannot rule out that the adsorption height of the Fe adatom in this assembly is slightly altered with respect to the virgin Fe adatom state, which might explain the initial reduction in the width of the Kondo resonance. Moreover, it is remarkable to see that when further IFAs are added, the resonance peak appears to split, resulting in a zero bias anomaly (ZBA). A careful study of the spectra for adatoms showing ZBAs reveals that during the formation of the gap-like structure at the Fermi level, the overall width of the Kondo resonance actually remains unchanged. More precisely, the asymptotic tails of the peaks in the sequence of 1, 2, 3, 4 IFAs overlap to a good approximation, indicating that JK remains constant, while an increasingly wide gap is forming at the peak center. In order to quantify the width of the zero bias resonance Γ and the gap width ES, we fit each dI/dV spectrum in Figure 1d to a Fano curve54 with an additional multiplicative factor featuring a Lorentzian dip for the spectra with a ZBA (Supporting Information). It is evident from the fits that the details of the spectral shape are very well captured using this functional form. Similar fits performed for a number of other clusters are shown in Supporting Informaiton Figure S4b. The Kondo temperatures TK extracted from the fitted values of Γ are on the order of 25–40 K. It is interesting to note that the Kondo energy scale in our system is very large compared to the superconducting gap4,52 (kBTK ≫ Δ ≈ 0.63 meV) and that the width of the ZBA, ES, is of a similar size as kBTK. We will show below that the ZBA can be interpreted as an exchange-splitting gap due to a strong interaction between the adatom/IFA pair and the assembly of all remaining IFAs.

The dI/dV spectra taken on the same clusters in the low-bias range with small ac modulation (Figure 1e) reveal sharp peaks inside the energy gap of the superconducting substrate due to YSR states.4,52 Since the measurement is performed using a superconducting tip, we extract the corresponding local electron density of states (LDOS) using a standard deconvolution method.4,37 The corresponding curves (Figure 1f) show two sharp peaks, one with larger intensity located at EYSR and one with smaller intensity located at −EYSR. Spatially resolved spectra taken across the Fe adatom and the IFA assembly (Supporting Information Figure S5) reveal that the Kondo and YSR resonances are confined to the location of the adatom, and only a faint YSR signal is still visible on the IFAs. We observe a large variation of EYSR as the Fe cluster size and its configuration changes. In particular, EYSR tends to decrease and reverse its sign when the number of IFAs in the assembly is increased (see, in particular, configurations 1, 2, and 3). This manifests as the reversal of the asymmetry in the intensities of the two peaks on either side of the Fermi level (see Supporting Information Figure S6 for the definition of the asymmetry and data of all clusters).

Next, in order to test if this systematic trend of the Kondo resonance, ZBA, and EYSR continues if we increase the size of the Fe cluster, we created very large Fe clusters consisting of as many as 14 IFAs. Schematic top views and STM images of these very large clusters are shown in Figure 2a. dI/dV spectra measured on these clusters with a nonsuperconducting tip (W tip) in a wide bias range (Figure 2b) show strong splitting of the Kondo resonance with even larger magnitudes (ES = 8.8–10.7 meV). Remarkably, dI/dV spectra measured in the low bias range (Figure 2c) reveal YSR peaks close to the gap edge with a very large asymmetry. In this case, the bias value at which the large YSR peak appears is defined as EYSR.

Figure 2.

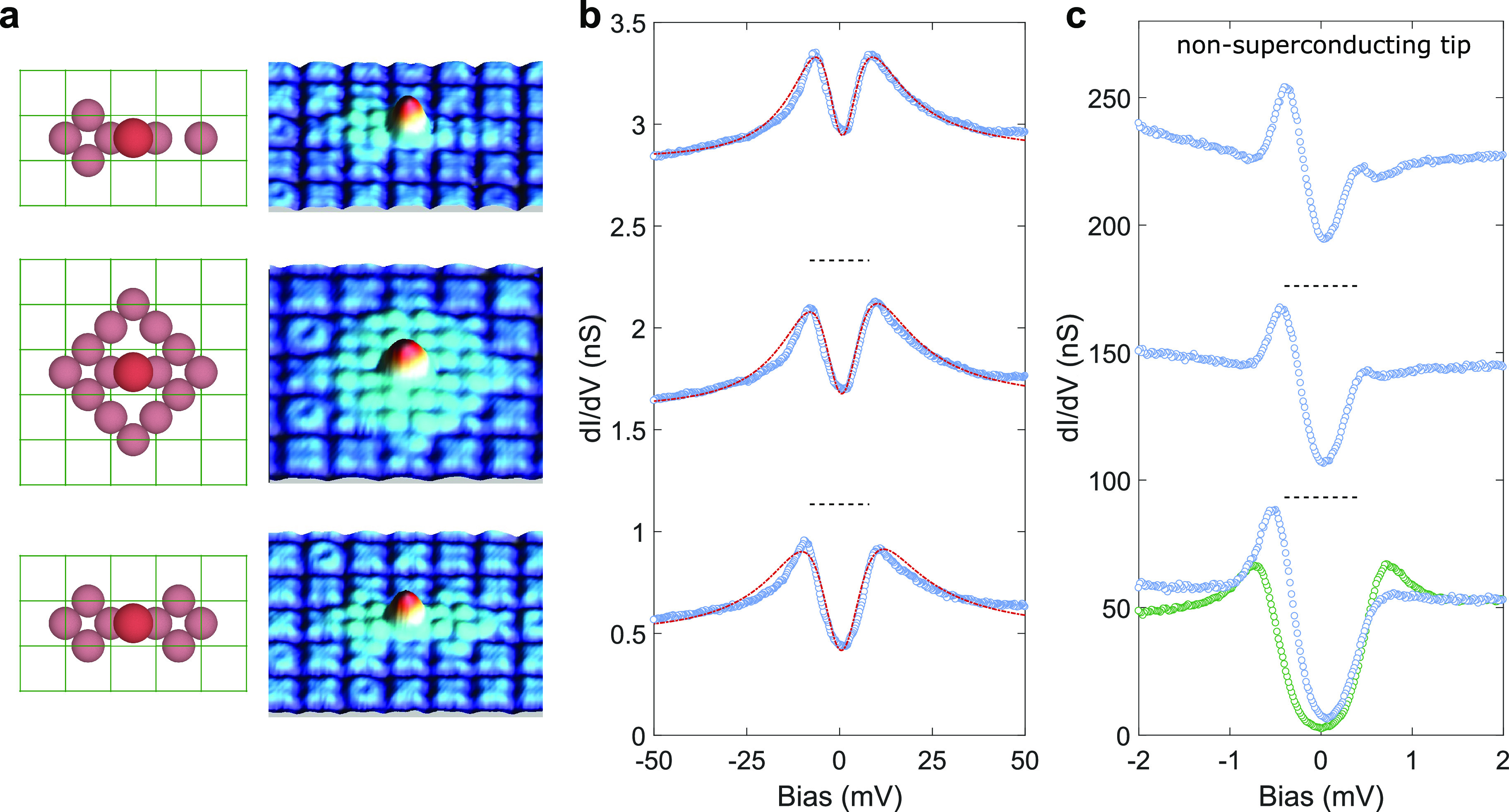
Figure 2

Open in a new tab

Construction and spectroscopy of large Fe clusters. (a) Schematic top-view and the corresponding STM images of an Fe adatom with assemblies of a large number of IFAs (V = 50 mV, I = 50 pA). (b) Large-bias dI/dV spectra (open dots) measured with W tip showing the split Kondo resonance. The dashed red lines are fits to a Fano function, which is multiplied by a Lorentzian dip. Spectra are shifted vertically for clarity as indicated by the dashed horizontal zero lines. Stabilization parameters for STS are Vstab = 50 mV, Istab = 100 pA, Vmod = 2 mV. (c) Corresponding small-bias dI/dV spectra showing peaks inside the superconducting gap due to YSR states, plotted together with substrate spectrum. Spectra are shifted vertically for clarity as indicated by the dashed horizontal zero lines. Stabilization parameters for STS are Vstab = 4 mV, Istab = 200 pA, Vmod = 50 μV.

In order to establish a possible correlation between the YSR states and the shape of the Kondo resonance, we plot EYSR normalized to Δ as a function of the reduced Kondo temperature, kBTK/Δ (Figure 3a) and as a function of ES/Δ (Figure 3b) extracted from the fitting, for all investigated Fe clusters.

Figure 3.

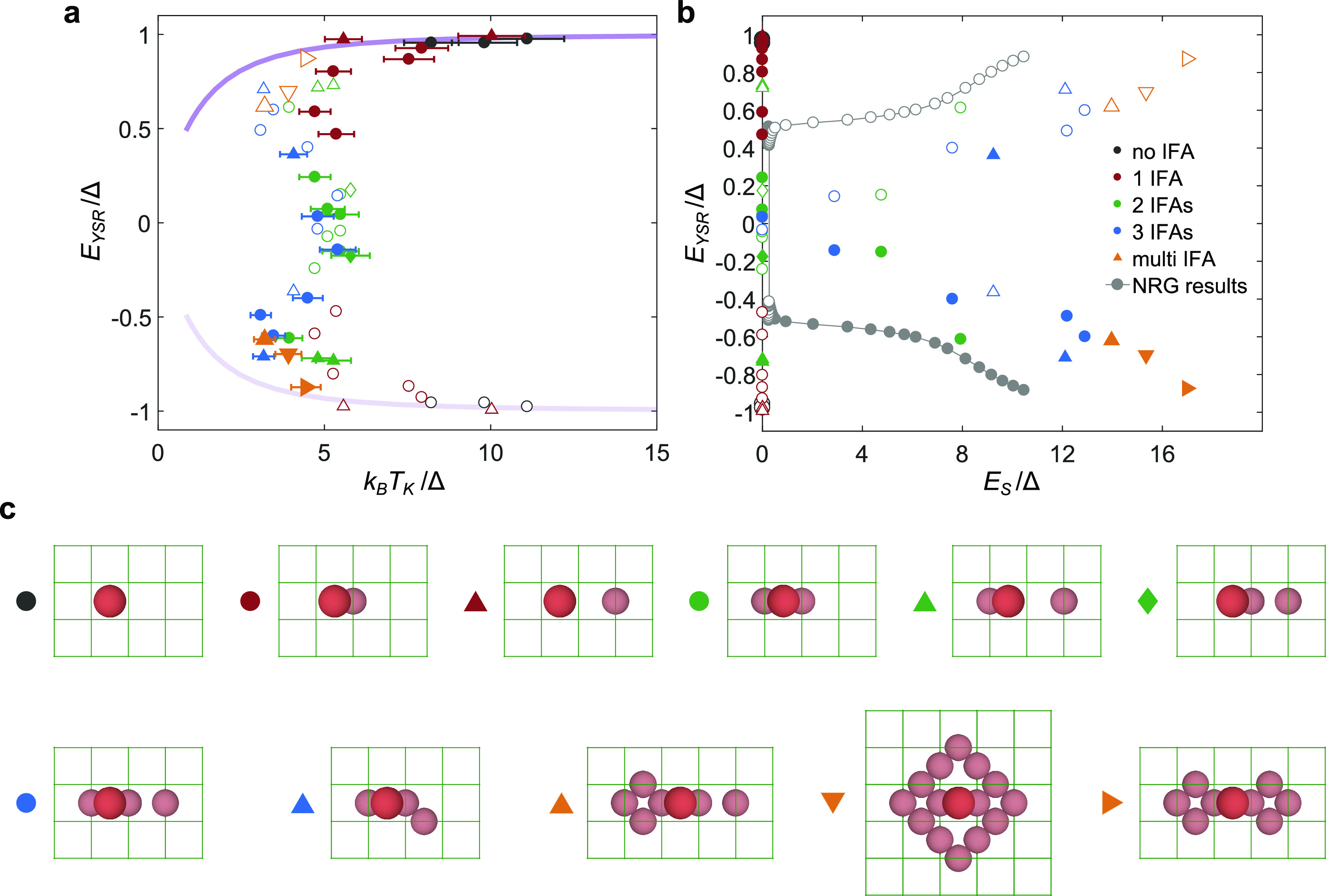
Figure 3

Open in a new tab

Correlation of Kondo temperature, exchange splitting, and YSR state energy. (a) Scatter plot of the energy of the larger YSR peak (filled symbols) versus the Kondo temperature, both extracted from the experimentally investigated Fe adatom with different IFA assemblies. The open symbols give the sign-reversed values of the energies of the corresponding filled symbols. Various types of symbols in the plot represent various types of IFA assemblies as indicated in (c). Horizontal error bars indicate the estimated errors in the fitting of the Kondo-resonance width. The violet curve in (a) represents the slave-boson mean-field theory calculation. (b) Scatter plot of the energy of the larger YSR peak (filled symbols) and its sign-reversed values (open symbols) versus the exchange splitting of the Kondo resonance, both extracted from the experimentally investigated Fe adatom with different IFA assemblies (assignment of the symbols to the different assemblies, see (c)). Results of the NRG calculations, which are plotted as filled and open gray dots, show qualitative agreement with the experiments. All energy scales are normalized to the energy gap (Δ) of the superconducting substrate.

From Figure 3a, it is evident that the resonance width changes by a factor of 1/2 (from ∼10 to 5 in units of Δ) when a single IFA is added to the Fe adatom (forming the “adatom/IFA pair”), but it does not further decrease with the number or configuration of IFAs in the assembly. At the same time, EYSR strongly changes from ∼Δ to −Δ when the number of IFAs in the assembly is increased. Consequently, there is almost no correlation between EYSR and TK. At first glance, this result seems surprising, as similar trends of experimentally observed YSR energies were usually assigned to the quantum phase transition of the system induced by an increasing Kondo coupling.26−28,37−39 On the other hand, from Figure 3b, we observe that EYSR is strongly correlated with the ZBA in the large-bias spectra. In particular, while EYSR is positive for most of the Fe clusters with a small number of IFAs in the assembly which do not show a ZBA in the Kondo resonance (ES = 0), it is negative for those with a large number of IFAs which have a nonzero ES. The correlation between ZBA and EYSR continue even for very large clusters (Figure 2).

In order to check if the Kondo coupling plays major role for the observed changes to EYSR, we simulated spectra within slave-boson mean-field theory (SBMFT), which is ideally suited for the strong-coupling Kondo regime [(kBTK/Δ) ≫ 1] and thus valid for the experimentally investigated system.55−57 We consider a simple model consisting of a single spin-1/2 Anderson impurity coupled to a superconducting substrate [see Supporting Information for the details of our SBMFT calculations]. The SBMFT simulation of EYSR as a function of the Kondo temperature is plotted as a violet line in Figure 3a. The deviation of the experimental data points from the simulation infers that the trend in EYSR in our case is not governed by changes to the Kondo coupling alone. This is also evident from the comparison of our data to experimental data and numerical renormalization group (NRG) calculations for another system38 [Supporting Information Figure S7], where we see that the system of Fe clusters on TaO investigated here always stays on one side of the Kondo-coupling induced quantum phase transition.

The ZBA of the Kondo resonance can naturally be interpreted as an exchange splitting induced by the competition of Kondo screening (TK) and exchange coupling of the Fe adatom with the assembly of IFAs (J) which probably changes by the number of IFAs in the assembly.42,43,46 We qualitatively test our hypothesis by considering the following minimal model. We regard our system as a realization of a Kondo impurity interacting with a complex spin system made of IFAs, where the adatom/proximal IFA pair is represented by a single effective spin-1/2 impurity interacting via exchange interaction J with the assembly of the additional IFAs (see Figure 4e). The physical idea behind such phenomenological model is that an increasingly large IFA assembly exercises an increasingly strong Weiss effective field on the adatom; since the assembly does not order magnetically, this effective degree of freedom is not static but remains fluctuating; hence we represent it with a quantum mechanical spin operator. Within this model, for small J, the two spin systems are independently screened by the conduction electrons (forming two Kondo singlets: SK) resulting in a single peak in the spectral function of the adatom. For large J ≥ Jc, the two spin systems instead undergo a crossover to a local AFM singlet state (antiferromagnetically aligned singlet state: SM).42,43,46,58−60 The spectral manifestation of this phenomenon is the observed splitting of the Kondo peak which for small and moderately large values of J takes the appearance of a “spin-gap” of width ES inside the resonance. The reason behind this particular line-shape is that the Kondo screening proceeds unperturbed at high energy scales until it reaches the scale of J where the residual magnetic moments rapidly bind antiferromagnetically and Kondo screening is inhibited. This matches the evolution of the Kondo peak shape observed in the experiment. The width of the gap ES seen in the spectra with ZBA is, therefore, a direct measure of the effective strength J of the exchange interaction between the adatom/IFA pair and the assembly of the IFAs taken as a whole. Moreover, the order of magnitude of ES of 2–8 meV implies a large AFM interaction between the adatom/IFA pair and the assembly of IFAs. The hierarchy of parameters is thus J ∼ TK ≫ Δ.42,46,58

Figure 4.

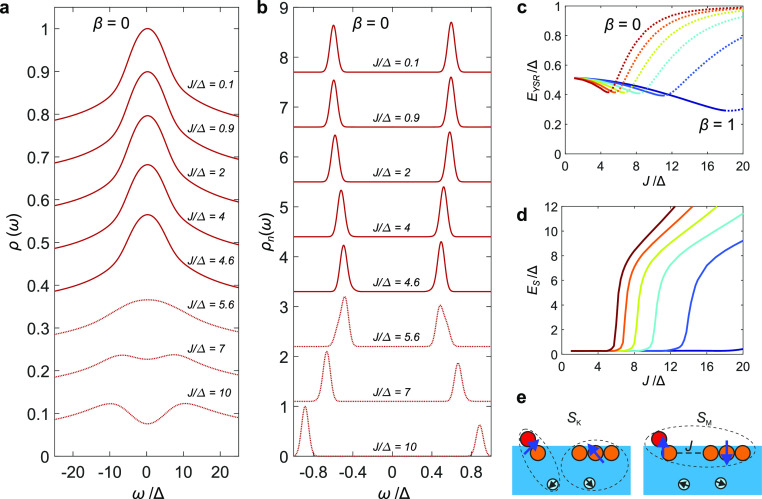
Figure 4

Open in a new tab

Numerical renormalization group calculations. (a) Spectral function of the impurity representing the pair of adatom and closest IFA (see (e)), which is magnetically coupled to a second impurity representing the rest of the IFA assembly, on the energy scale of the Kondo peak for various magnetic interaction strengths J. The superconducting gap is washed out here using a convolution which mimics the experimental lock-in-modulation broadening. The line style indicates the nature of the ground state of the system (solid lines as Kondo vs dotted lines as AFM) controlled by the strength of J. (b) Discrete (subgap) part of the spectral function. A narrow Gaussian kernel is used to broaden the δ peaks. For (a) and (b), the isotropic Heisenberg limit of the model β = 0 has been assumed. (c) Energy of the YSR state as a function of J. (d) Width of the exchange-splitting gap as a function of J. For (c) and (d) the line colors represent different values of β which range from 0 (red, isotropic Heisenberg limit) to 1 (dark blue, anisotropic Ising limit) in steps of 0.2. (e) Schematic illustration of the minimal two-impurity Kondo problem. The Fe (red sphere)/proximal IFA (orange sphere) pair is represented by the first effective spin-1/2 impurity (left blue arrow), and the assembly of additional IFAs (three orange spheres) is represented by the second effective spin-1/2 impurity (right blue arrow). Both impurities Kondo-couple to substrate electrons (smaller spheres). The left and right panels illustrate the two regimes of decoupled Kondo singlets (SK, small J) and AFM singlet (SM, large J).

In order to check whether the competition of Kondo screening (TK) and exchange coupling J within this minimal model can also explain the experimentally observed correlation between the width of the exchange-splitting gap ES and the YSR state binding energy EYSR (Figure 3b), we have performed NRG calculations that produce reliable spectral functions on all energy scales, including the region inside the superconducting gap.61,62 The detailed calculation involving IFAs of different size and shape is beyond the scope of the manuscript. We restrict the NRG calculations to a simple two-impurity Anderson model to extract the essential physics. Within this model, one impurity orbital represents the IFA assembly and one represents the adatom/IFA pair chosen to be particle-hole asymmetric [see Supporting Information for the details of our NRG calculations]. This model can also account for the effects of potential scattering on the adatom/IFA pair. The results show that while the ground state of the system is a spin singlet for all values of exchange coupling (J), its nature smoothly changes from a Kondo singlet to an AFM singlet as indicated, for example, by the increasing magnitude of the spin–spin correlation function. This is reflected by the emergence of the Kondo peak splitting for J ∼ Jc = 5Δ (Jc being the critical exchange interaction) (Figure 4a) and the characteristic evolution of the YSR peaks (Figure 4b). To understand the latter, we remind47 that for two decoupled impurities, the subgap spectrum consists of a singlet (Kondo) ground state S1, two doublet excitations D1,2 (unscreened impurity states of either impurity), as well as a degenerate singlet S2 and triplet T, which correspond to the excited states where both impurities are unscreened. With increasing J, the singlet S2 decreases in energy until it mixes with the Kondo state S1 leading to an anticrossing shape in the energy diagram. For large J, the Kondo state S1 is pushed to higher energies together with the two doublet excitations D1,2, while S2 is the new ground state. This leads to the observed evolution of YSR peaks in Figure 4b, which for small J slightly decrease in energy and then for large J rapidly increase in energy and eventually merge with the continuum (Figure 4c). The change of direction of YSR shifting occurs at J ∼ Jc which is very close to J where the exchange splitting becomes observable in the Kondo peak (compare Figure 4c with Figure 4d). This behavior is in qualitative agreement with the trend observed in the experiment, as shown by the comparison of the plot of EYSR versus ES extracted from the NRG-calculated spectra with the same parameters extracted from the experimental data (see NRG results in Figure 3b). We also observe that the reversal in the asymmetry of the YSR peak intensities occurs across J ∼ Jc, in line with the experiment [Supporting Infromation Figure S6].

The IFA assembly is represented in the above model through a single spin-1/2 degree of freedom representing a collective degree of freedom of the entire cluster, which is expected to become more classical-like in larger assemblies. To consider the possible effects of such an evolution, we also investigated an XXZ anisotropic exchange coupling between the two effective spins introducing an additional parameter β in our model [see Supporting Information]. β ranges from 0 (isotropic Heisenberg limit) to 1 (anisotropic Ising limit). We find (Figure 4c,d) that the coupling anisotropy has only a qualitative effect, while the phenomenology described above remains essentially the same. The qualitative agreement between experiments and NRG calculations is surprising, since the impurities have multiple orbitals, potentially producing high-spin states. Furthermore, it is not a priori expected that multiple IFAs can be conflated into a single effective spin degree of freedom. We speculate that the effective exchange field produced by the IFAs at the position of the adatom/proximal IFA pair is increasing with the size of the IFA cluster because of the increasing tendency toward magnetic order (alignment of IFA spins).

In conclusion, the experimentally observed correlation between the small energy scale position of the YSR state and the large energy scale exchange-splitting gap of the Fe adatom coupled to the assembly of IFAs can be modeled by changes in the effective exchange coupling J between the adatom/IFA pair and the remaining IFA assembly in the regime where J >< TK ≫ Δ. We have shown that the Fe adatom coupled to a single IFA has a reduced Kondo coupling with respect to the isolated Fe adatom, while further addition of IFAs to the assembly only increases J. We compared our experimental results to NRG calculations employing a minimal model that shows how with increasing exchange interaction the system of Fe clusters undergoes a crossover from the regime of an independent Kondo cloud (SK) to a local magnetically aligned state (SM). This crossover results in the opening of a gap in the Kondo peak and in the anticrossing of the subgap YSR states. Our results also indicate that the observation of the crossover is facilitated by the presence of potential scattering, as it leads to a reversal of the particle–hole asymmetry of the YSR peaks across the crossover.

Our work establishes the important role of exchange interaction on the experimentally observed shifts in YSR peaks, which were previously supposed to be prevalently determined by the Kondo coupling of the impurity with the substrate. Our results, therefore, challenge the current understanding of the intimate correlation between Kondo effect and YSR state and motivate further studies. In particular, it is becoming clear that while a phenomenological description in terms of hybridizing classical YSR states is possible and valid, the calculation of its parameters should be based on a microscopic quantum model that needs to properly incorporate exchange coupling. This calls for further development of efficient theoretical tools for solving sizable assemblies of quantum spins in interaction with a superconducting environment.

Acknowledgments

The authors thank Markus Ternes for fruitful discussions. This work was supported by the European Research Council Advanced Grant ADMIRE (Project 786020). R.W. and J.W. acknowledge funding by the Cluster of Excellence “Advanced Imaging of Matter” (EXC 2056, Project 390715994) as well as by the SFB 925-B9 “Light induced dynamics and control of correlated quantum systems” of the Deutsche Forschungsgemeinschaft (DFG). R.Ž. acknowledges support by the Slovenian Research Agency (ARRS) under Program P1-0044. M.V. and R.M. acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) through Projects SFB668-A3 and -A1 and from the European Union’s Horizon 2020 research and innovation program under Grant Agreement 696656—GrapheneCore1. The work of M.V. was additionally funded through 2019 Equal Opportunity Fund of University of Hamburg. The DFT computations were performed with resources provided by the North-German Supercomputing Alliance (HLRN). S.P. and J.F thank Stiftelsen Olle Engqvist Byggmästare and Vetenskapsrådet for financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c00387.

  • Experimental methods, DFT calculations, fitting procedure for the Kondo resonance, slave-boson mean-field theory calculations, and numerical renormalization group calculations (PDF)

Author Contributions

A.K., L.C., and J.W. conceived and designed the experiments. A.K. and L.C. performed the experiments. A.K., J.W,. and R.Ž. analyzed the experimental data. NRG calculations were performed by R.Ž. M.V. and R.M. carried out the DFT calculations. S.P. and J.F. performed SBMFT calculations. A.K. wrote the manuscript. All authors discussed the results and commented on the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl1c00387_si_001.pdf (1.3MB, pdf)

References

  1. Nadj-Perge S.; et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602–607. 10.1126/science.1259327. [DOI] [PubMed] [Google Scholar]
  2. Ruby M.; Heinrich B. W.; Peng Y.; von Oppen F.; Franke K. J. Exploring a Proximity-Coupled Co Chain on Pb(110) as a Possible Majorana Platform. Nano Lett. 2017, 17, 4473–4477. 10.1021/acs.nanolett.7b01728. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kim H.; et al. Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors. Sci. Adv. 2018, 4, eaar5251. 10.1126/sciadv.aar5251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kamlapure A.; Cornils L.; Wiebe J.; Wiesendanger R. Engineering the spin couplings in atomically crafted spin chains on an elemental superconductor. Nat. Commun. 2018, 9, 3253. 10.1038/s41467-018-05701-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Choy T.-P.; Edge J. M.; Akhmerov A. R.; Beenakker C. W. J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 195442. 10.1103/PhysRevB.84.195442. [DOI] [Google Scholar]
  6. Martin I.; Morpurgo A. F. Majorana fermions in superconducting helical magnets. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 144505. 10.1103/PhysRevB.85.144505. [DOI] [Google Scholar]
  7. Braunecker B.; Simon P. Interplay between Classical Magnetic Moments and Superconductivity in Quantum One-Dimensional Conductors: Toward a Self-Sustained Topological Majorana Phase. Phys. Rev. Lett. 2013, 111, 147202. 10.1103/PhysRevLett.111.147202. [DOI] [PubMed] [Google Scholar]
  8. Klinovaja J.; Stano P.; Yazdani A.; Loss D. Topological Superconductivity and Majorana Fermions in RKKY Systems. Phys. Rev. Lett. 2013, 111, 186805. 10.1103/PhysRevLett.111.186805. [DOI] [PubMed] [Google Scholar]
  9. Nadj-Perge S.; Drozdov I. K.; Bernevig B. A.; Yazdani A. Proposal for realizing Majorana fermions in chains of magnetic atoms on a superconductor. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 020407. 10.1103/PhysRevB.88.020407. [DOI] [Google Scholar]
  10. Pientka F.; Glazman L. I.; von Oppen F. Topological superconducting phase in helical Shiba chains. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 155420. 10.1103/PhysRevB.88.155420. [DOI] [Google Scholar]
  11. Vazifeh M. M.; Franz M. Self-Organized Topological State with Majorana Fermions. Phys. Rev. Lett. 2013, 111, 206802. 10.1103/PhysRevLett.111.206802. [DOI] [PubMed] [Google Scholar]
  12. Ruby M.; et al. End States and Subgap Structure in Proximity-Coupled Chains of Magnetic Adatoms. Phys. Rev. Lett. 2015, 115, 197204. 10.1103/PhysRevLett.115.197204. [DOI] [PubMed] [Google Scholar]
  13. Pawlak R.; et al. Probing atomic structure and Majorana wavefunctions in mono-atomic Fe chains on superconducting Pb surface. npj Quantum Inf. 2016, 2, 16035. 10.1038/npjqi.2016.35. [DOI] [Google Scholar]
  14. Schecter M.; Flensberg K.; Christensen M. H.; Andersen B. M.; Paaske J. Self-organized topological superconductivity in a Yu-Shiba-Rusinov chain. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 140503. 10.1103/PhysRevB.93.140503. [DOI] [Google Scholar]
  15. Feldman B. E.; et al. High-resolution studies of the Majorana atomic chain platform. Nat. Phys. 2017, 13, 286–291. 10.1038/nphys3947. [DOI] [Google Scholar]
  16. Jeon S.; et al. Distinguishing a Majorana zero mode using spin-resolved measurements. Science 2017, 358, 772–776. 10.1126/science.aan3670. [DOI] [PubMed] [Google Scholar]
  17. Röntynen J.; Ojanen T. Topological Superconductivity and High Chern Numbers in 2D Ferromagnetic Shiba Lattices. Phys. Rev. Lett. 2015, 114, 236803. 10.1103/PhysRevLett.114.236803. [DOI] [PubMed] [Google Scholar]
  18. Li J.; et al. Two-dimensional chiral topological superconductivity in Shiba lattices. Nat. Commun. 2016, 7, 12297. 10.1038/ncomms12297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Rachel S.; Mascot E.; Cocklin S.; Vojta M.; Morr D. K. Quantized charge transport in chiral Majorana edge modes. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 205131. 10.1103/PhysRevB.96.205131. [DOI] [Google Scholar]
  20. Ménard G. C.; et al. Two-dimensional topological superconductivity in Pb/Co/Si(111). Nat. Commun. 2017, 8, 2040. 10.1038/s41467-017-02192-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Palacio-Morales A.; et al. Atomic-scale interface engineering of Majorana edge modes in a 2D magnet-superconductor hybrid system. Sci. Adv. 2019, 5, eaav6600. 10.1126/sciadv.aav6600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Yu L. Bound State in Superconductors With Paramagnetic Impurities. Acta Phys. Sin. 1965, 21, 75. 10.7498/aps.21.75. [DOI] [Google Scholar]
  23. Shiba H. Classical Spins in Superconductors. Prog. Theor. Phys. 1968, 40, 435–451. 10.1143/PTP.40.435. [DOI] [Google Scholar]
  24. Rusinov A. I. On the Theory of Gapless Superconductivity in Alloys Containing Paramagnetic Impurities. Sov. J. Exp. Theor. Phys. 1969, 29, 1101. [Google Scholar]
  25. Schneider L.; et al. Magnetism and in-gap states of 3d transition metal atoms on superconducting Re. npj Quantum Mater. 2019, 4, 42. 10.1038/s41535-019-0179-7. [DOI] [Google Scholar]
  26. Malavolti L.; et al. Tunable Spin–Superconductor Coupling of Spin 1/2 Vanadyl Phthalocyanine Molecules. Nano Lett. 2018, 18, 7955–7961. 10.1021/acs.nanolett.8b03921. [DOI] [PubMed] [Google Scholar]
  27. Farinacci L.; et al. Tuning the Coupling of an Individual Magnetic Impurity to a Superconductor: Quantum Phase Transition and Transport. Phys. Rev. Lett. 2018, 121, 196803. 10.1103/PhysRevLett.121.196803. [DOI] [PubMed] [Google Scholar]
  28. Liebhaber E.; et al. Yu–Shiba–Rusinov States in the Charge-Density Modulated Superconductor NbSe 2. Nano Lett. 2020, 20, 339–344. 10.1021/acs.nanolett.9b03988. [DOI] [PubMed] [Google Scholar]
  29. Kezilebieke S.; Dvorak M.; Ojanen T.; Liljeroth P. Coupled Yu–Shiba–Rusinov States in Molecular Dimers on NbSe 2. Nano Lett. 2018, 18, 2311–2315. 10.1021/acs.nanolett.7b05050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Flatté M. E.; Reynolds D. E. Local spectrum of a superconductor as a probe of interactions between magnetic impurities. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61, 14810–14814. 10.1103/PhysRevB.61.14810. [DOI] [Google Scholar]
  31. Morr D. K.; Stavropoulos N. A. Quantum interference between impurities: Creating novel many-body states in s -wave superconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 020502. 10.1103/PhysRevB.67.020502. [DOI] [Google Scholar]
  32. Yao N. Y.; et al. Phase diagram and excitations of a Shiba molecule. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 241108. 10.1103/PhysRevB.90.241108. [DOI] [Google Scholar]
  33. Ruby M.; Heinrich B. W.; Peng Y.; von Oppen F.; Franke K. J. Wave-Function Hybridization in Yu-Shiba-Rusinov Dimers. Phys. Rev. Lett. 2018, 120, 156803. 10.1103/PhysRevLett.120.156803. [DOI] [PubMed] [Google Scholar]
  34. Ji S.-H.; et al. High-Resolution Scanning Tunneling Spectroscopy of Magnetic Impurity Induced Bound States in the Superconducting Gap of Pb Thin Films. Phys. Rev. Lett. 2008, 100, 226801. 10.1103/PhysRevLett.100.226801. [DOI] [PubMed] [Google Scholar]
  35. Choi D.-J.; et al. Influence of Magnetic Ordering between Cr Adatoms on the Yu-Shiba-Rusinov States of the β-Bi2Pd Superconductor. Phys. Rev. Lett. 2018, 120, 167001. 10.1103/PhysRevLett.120.167001. [DOI] [PubMed] [Google Scholar]
  36. Hewson A.The Kondo Problem to Heavy Fermions; Cambridge University Press: Cambridge, U.K., 1993. [Google Scholar]
  37. Franke K. J.; Schulze G.; Pascual J. I. Competition of Superconducting Phenomena and Kondo Screening at the Nanoscale. Science 2011, 332, 940–944. 10.1126/science.1202204. [DOI] [PubMed] [Google Scholar]
  38. Bauer J.; Pascual J. I.; Franke K. J. Microscopic resolution of the interplay of Kondo screening and superconducting pairing: Mn-phthalocyanine molecules adsorbed on superconducting Pb(111). Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 075125. 10.1103/PhysRevB.87.075125. [DOI] [Google Scholar]
  39. Hatter N.; Heinrich B. W.; Ruby M.; Pascual J. I.; Franke K. J. Magnetic anisotropy in Shiba bound states across a quantum phase transition. Nat. Commun. 2015, 6, 8988. 10.1038/ncomms9988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Jones B. A.; Varma C. M. Study of two magnetic impurities in a Fermi gas. Phys. Rev. Lett. 1987, 58, 843–846. 10.1103/PhysRevLett.58.843. [DOI] [PubMed] [Google Scholar]
  41. Jones B. A.; Varma C. M.; Wilkins J. W. Low-Temperature Properties of the Two-Impurity Kondo Hamiltonian. Phys. Rev. Lett. 1988, 61, 125–128. 10.1103/PhysRevLett.61.125. [DOI] [PubMed] [Google Scholar]
  42. Wahl P.; et al. Exchange Interaction between Single Magnetic Adatoms. Phys. Rev. Lett. 2007, 98, 056601. 10.1103/PhysRevLett.98.056601. [DOI] [PubMed] [Google Scholar]
  43. Spinelli A.; et al. Exploring the phase diagram of the two-impurity Kondo problem. Nat. Commun. 2015, 6, 10046. 10.1038/ncomms10046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Jayaprakash C.; Krishna-murthy H. R.; Wilkins J. W. Two-Impurity Kondo Problem. Phys. Rev. Lett. 1981, 47, 737–740. 10.1103/PhysRevLett.47.737. [DOI] [Google Scholar]
  45. Prüser H.; et al. Interplay between the Kondo effect and the Ruderman–Kittel–Kasuya–Yosida interaction. Nat. Commun. 2014, 5, 5417. 10.1038/ncomms6417. [DOI] [PubMed] [Google Scholar]
  46. Bork J.; et al. A tunable two-impurity Kondo system in an atomic point contact. Nat. Phys. 2011, 7, 901–906. 10.1038/nphys2076. [DOI] [Google Scholar]
  47. Žitko R. Numerical subgap spectroscopy of double quantum dots coupled to superconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 165116. 10.1103/PhysRevB.91.165116. [DOI] [Google Scholar]
  48. Žitko R.; Bodensiek O.; Pruschke T. Effects of magnetic anisotropy on the subgap excitations induced by quantum impurities in a superconducting host. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 054512. 10.1103/PhysRevB.83.054512. [DOI] [Google Scholar]
  49. Yao N. Y.; Glazman L. I.; Demler E. A.; Lukin M. D.; Sau J. D. Enhanced Antiferromagnetic Exchange between Magnetic Impurities in a Superconducting Host. Phys. Rev. Lett. 2014, 113, 087202. 10.1103/PhysRevLett.113.087202. [DOI] [PubMed] [Google Scholar]
  50. Estrada Saldaña J. C.; et al. Two-impurity Yu-Shiba-Rusinov states in coupled quantum dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 102, 195143. 10.1103/PhysRevB.102.195143. [DOI] [Google Scholar]
  51. Su Z.; et al. Andreev molecules in semiconductor nanowire double quantum dots. Nat. Commun. 2017, 8, 585. 10.1038/s41467-017-00665-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Cornils L.; et al. Spin-Resolved Spectroscopy of the Yu-Shiba-Rusinov States of Individual Atoms. Phys. Rev. Lett. 2017, 119, 197002. 10.1103/PhysRevLett.119.197002. [DOI] [PubMed] [Google Scholar]
  53. Mozara R.; et al. Atomically thin oxide layer on the elemental superconductor Ta(001) surface. Phys. Rev. Mater. 2019, 3, 094801. 10.1103/PhysRevMaterials.3.094801. [DOI] [Google Scholar]
  54. Fano U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. 10.1103/PhysRev.124.1866. [DOI] [Google Scholar]
  55. Coleman P. New approach to the mixed-valence problem. Phys. Rev. B: Condens. Matter Mater. Phys. 1984, 29, 3035–3044. 10.1103/PhysRevB.29.3035. [DOI] [Google Scholar]
  56. Avishai Y.; Golub A.; Zaikin A. D. Superconductor-quantum dot-superconductor junction in the Kondo regime. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 041301. 10.1103/PhysRevB.67.041301. [DOI] [Google Scholar]
  57. Borkowski L. S.; Hirschfeld P. J. Low-temperature properties of anisotropic superconductors with kondo impurities. J. Low Temp. Phys. 1994, 96, 185–206. 10.1007/BF00752405. [DOI] [Google Scholar]
  58. Simon P.; López R.; Oreg Y. Ruderman-Kittel-Kasuya-Yosida and Magnetic-Field Interactions in Coupled Kondo Quantum Dots. Phys. Rev. Lett. 2005, 94, 086602. 10.1103/PhysRevLett.94.086602. [DOI] [PubMed] [Google Scholar]
  59. Heersche H. B.; et al. Kondo Effect in the Presence of Magnetic Impurities. Phys. Rev. Lett. 2006, 96, 017205. 10.1103/PhysRevLett.96.017205. [DOI] [PubMed] [Google Scholar]
  60. Craig N. J.; et al. Tunable nonlocal spin control in a coupled-quantum dot system. Science 2004, 304, 565–7. 10.1126/science.1095452. [DOI] [PubMed] [Google Scholar]
  61. Žitko R.; Pruschke T. Energy resolution and discretization artifacts in the numerical renormalization group. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 085106. 10.1103/PhysRevB.79.085106. [DOI] [Google Scholar]
  62. Bulla R.; Costi T. A.; Pruschke T. Numerical renormalization group method for quantum impurity systems. Rev. Mod. Phys. 2008, 80, 395–450. 10.1103/RevModPhys.80.395. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl1c00387_si_001.pdf (1.3MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES