Significance
Lacking any ability to store glucose, the mammalian brain relies on a constant glucose and oxygen supply via the cerebral vasculature. In the cortex, this supply is maintained by parallel arterioles and venules. Yet, mathematical modeling of both real and idealized cortical networks shows that, far from being perfused uniformly, the cortex is strewn with regions of very low flow. Increasing the number of perfusing vessels increases the number of low-flow spots. Minimizing the influence of low-flow spots sets an optimal arteriole–venule ratio that we find to be closely recapitulated in data from real mammalian cortices. Further, low-flow regions complicate the regulation of metabolite delivery with neuronal activity, leading to unintuitive changes in perfusion when penetrating vessels dilate.
Keywords: microcirculation, sensory cortex, continuum model, low-flow zones, blood flow regulation
Abstract
The energy demands of neurons are met by a constant supply of glucose and oxygen via the cerebral vasculature. The cerebral cortex is perfused by dense, parallel arterioles and venules, consistently in imbalanced ratios. Whether and how arteriole–venule arrangement and ratio affect the efficiency of energy delivery to the cortex has remained an unanswered question. Here, we show by mathematical modeling and analysis of the mapped mouse sensory cortex that the perfusive efficiency of the network is predicted to be limited by low-flow regions produced between pairs of arterioles or pairs of venules. Increasing either arteriole or venule density decreases the size of these low-flow regions, but increases their number, setting an optimal ratio between arterioles and venules that matches closely that observed across mammalian cortical vasculature. Low-flow regions are reshaped in complex ways by changes in vascular conductance, creating geometric challenges for matching cortical perfusion with neuronal activity.
The high energetic cost of neuronal firing creates a fundamental constraint on the number of synaptic circuits that can be simultaneously active (1). Yet, the brain has no capacity to store glucose and must continuously meet its energy needs via the perfusion of oxygen and glucose in the cerebral vasculature (2, 3). The high-gray-matter content of the cerebral cortex means that it has a high metabolic activity and is particularly dependent on vascular supply (4).
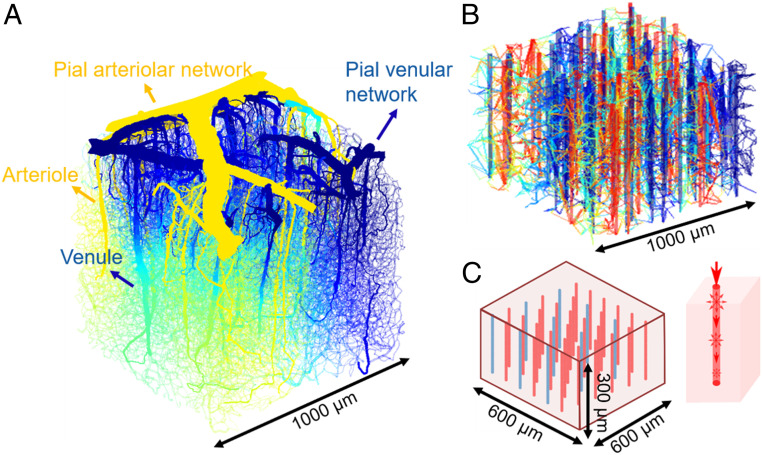
The cerebral cortex is fed by a dense network of nearly parallel penetrating arterioles and venules, which are themselves fed by, and drain into, pial networks of arteries and veins (Fig. 1A). Loops within the pial network ensure robust blood delivery even should a pial artery become occluded (7, 8), and loopiness in general is thought to endow transport networks with the ability to resist damage and to respond to changes in demand (9, 10).
Fig. 1.
Low-flow regions emerge in models with increasing simplification: real mouse sensory cortex vasculature (5), a synthetic hierarchical network, and a continuum model. (A) The hierarchical system of a real mouse brain vasculature. The color indicates the predicted pressure distribution. (B) A synthetic network constructed using the method in ref. 6, but with idealized straight penetrating arterioles and venules. Color indicates pressure from high (red) to low (blue). (C) Exemplary continuum model where penetrating vessels are treated as lines of sources and sinks, and the capillary bed is treated as porous media. (C, Left) Arrangements of straight penetrating arterioles and venules in the model. (C, Right) Schematic of coupling between penetrating vessels and porous medium—source strength on a penetrating vessel is matched to flux decreases along the vessel.
From the pial network, the cortex is perfused by a dense set of penetrating arterioles and venules, along with an interconnecting network of capillaries. The penetrating network is more vulnerable than the pial network to damage; if a penetrating arteriole or venule is blocked, the neurons it supplies may die and form a cyst (5). Small volumes of the dense, multitudinous, penetrating network have been mapped by two-photon automated high-throughput histology (5). Although based on its role as the supply network to an energy-intensive tissue, we would expect the penetrating network to be organized for effective perfusion, it is not clear what physical constraints exist on perfusion and whether and how these constraints shape the network. In particular, we focus on explaining a conserved feature of mammalian cortices: The arterioles and venules are not in a one-to-one ratio, but skew consistently for individual species: ∼2.5:1 (arterioles:venules) for humans (11) and Rhesus monkeys (12) and 0.4:1 for rodents (5).
In the course of our analysis of the penetrating cortical network, we develop mathematical modeling tools that hybridize network- and continuum-level modeling approaches, treating the arterioles and venules as networks embedded in a meshwork of capillaries, modeled here as a (continuum) porous medium, whose conductivity models the density and geometry of capillaries, without needing to represent each capillary explicitly (Fig. 1C). The model provides a general tool for studying perfusion in networks where capillaries are too numerous to be completely mapped (13).
Methods
Observations of Low-Flow Capillaries in Real Mouse Vasculature and a Corresponding Synthetic Network.
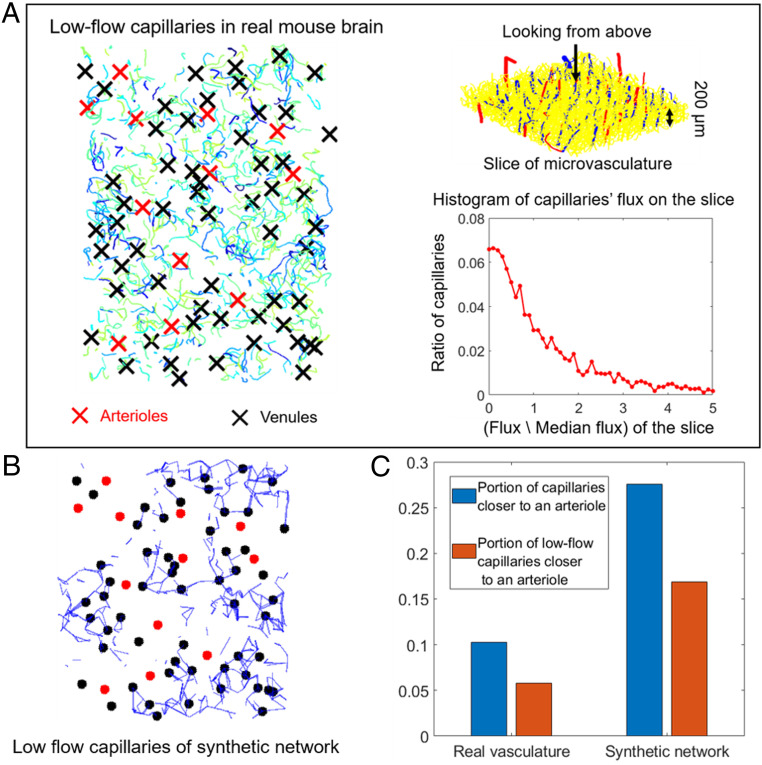
Uniform perfusion—delivery of fluid or metabolites at the same rate to each part of a tissue—underlies the structure of biological transport systems from leaf veins (14) to cardiovascular networks (15). Does the cerebral cortex (Fig. 1A) achieve uniform perfusion? Using mapped networks of penetrating vessels, the capillaries that interconnect them, and inferred pressure distributions within arterioles and venules (5), we analyzed the distribution of flows across all capillaries. We observed that flows were highly heterogeneous across mapped volumes of tissue (Fig. 2A). At depth , fluxes in 24% of capillaries are less than 40% of the median capillary flux. (Median flux changes drastically with depth, but measuring over all depths, we observed 24–29% of capillaries carrying less than 40% of median flux). These low-flow capillaries were spread out over the entire plane, but appeared to be concentrated near venules (Fig. 2A), which in the mapped networks outnumber arterioles among penetrating vessels by a factor of 3:1.
Fig. 2.
Low-flow areas in real mouse sensory cortex and a synthetic network. (A, Left) The low-flow capillaries (vessels with less than 40% of median flux) at depth of the mouse cortical vasculature shown in Fig. 1A. (A, Right) Vessel geometry (Upper) and flux histogram (Lower) in the slice of mouse cortical vasculature. Fluxes are normalized so median . (B) Low-flow capillaries (vessels with less than 40% of median flux) at depth in a synthetic network built to model A with the same penetrating vessel locations. Black dots, venules; red dots, arterioles. The same annotations are used in Fig. 3B as well. (C) In real and synthetic networks, low-flow regions are two times less likely to be found near arterioles than we would expect by chance. Blue bars and red bars, respectively, show the portion of all capillaries or low-flow capillaries that are topologically closer to an arteriole than a venule.
To study whether and why low-flow spots are clustered around venules, and to bridge between real microvascular networks (Fig. 1A) and continuum models (Fig. 1C), we generated synthetic sensory-cortex vasculatures (Fig. 1B). We constrained our model networks to have straight arterioles and venules to make it easier to visualize and measure distances between low-flow capillaries and the penetrating vessels that feed them (Fig. 1B). Our method for generating synthetic vasculatures directly follows (6). Specifically, we started with straight, parallel penetrating vessels in the same domain as (Fig. 1A). We connected these penetrating vessels pairwise at points distributed through the tissue. Then, the points connected to a single penetrating vessel were linked up into a tree with that vessel. The branch-point locations and vessel radii within the tree were numerically optimized to obey Murray’s law (6). Conductances were calculated from radii by using the same modified Hagen–Poiseuille law and pressure boundary conditions ( pressure difference between arterioles and venules) as ref. 5. We scaled synthetic network radii so that synthetic networks had median vessel radii that matched data from mapped networks (5) (respectively, , , and for arteriole, venule, and capillary segments) and chose the number of pairwise connections so that the number of vertices and median flux per edge in the synthetic networks (19,998 and ) approximated a real network (21,895 vertices, median flux ). Just as in the real sensory cortex, model networks contained many low capillaries—in the plane of the computational domain, flows in 26.8% of capillaries were less than 40% of median flux on the plane (Fig. 2B). Again, our results were insensitive to the precise plane on which capillary flow rates were measured.
Low-flow regions appeared to be clustered near venules in both real (Fig. 2A) and synthetic (Fig. 2B) networks. But there were more venules than arterioles in the network, so even a random capillary is more likely to be near a venule than an arteriole. To prove that low-flow capillaries are enriched near venules, we compared the proportion of low-flow capillaries that were closer to an arteriole than to a venule (measuring distances along the network using Dijkstra’s algorithm) with the proportion of randomly chosen capillaries that were closer to an arteriole than a venule (Fig. 2C). In both the real vasculature and synthetic network, low-flow capillaries were around two times less likely to be found near arterioles than we would expect by chance.
Moving from real mouse data to synthetic networks allows us to probe the extent to which arrangements of penetrating vessels control the placement of low-flow regions near venules. We ran replicate simulations in which venules and arterioles were permuted from the arrangement shown in Fig. 2. We found that low-flow capillaries were consistently 1.43 times less likely to be found near arterioles (SI Appendix, Fig. S1).
Although real sensory-cortex and synthetic microvasculatures exhibit regions of capillaries with low flow, mechanistic understanding of what produces low-flow regions requires study of networks that are simplified enough that vessel configurations and arteriole–venule ratios can be effortlessly varied. Accordingly, we built an even simpler continuum model (Fig. 1C) with not only straight arterioles and venules, but in which the capillary network was modeled as a porous medium. The same penetrating vessel arrangements can be simulated both as continua and as hierarchical synthetic networks, allowing us to validate continuum networks using synthetic networks that are known to capture many of the geometric features of the real microvasculature (6).
A continuum model of the capillary bed.
The penetrating arterioles and venules are represented by using a slender-body theory approach (16); i.e., each penetrating vessel is treated as a line of linked sources or sinks that push blood into or draw blood out of a porous medium, representing the capillary network (17). (Similar ideas have been used to simulate the oxygen transport to the tissue in ref. 18 and in ref. 19, where both the tissue and the capillaries are regarded as a porous media.) The source strengths represent the rate at which blood enters the capillary network at each point along an arteriole, while sink strengths represent the rate at which blood is drained from the capillary network into a venule. Sink and source distributions must be solved self-consistently with the flows within the capillary network.
Flows within the capillary network obey Darcy’s law, so that the flow through unit area of capillary bed, is proportional to the gradient of pressure, :
| [1] |
Here, the permeability, , a rank-2 tensor, encodes at a continuum level the density and orientations of capillaries. We assume that the capillary network is isotropic and homogeneous, so , where is a constant and is the identity tensor. is the dynamic viscosity of the blood, and during the computation, we treat as a single parameter and call it the conductivity of the capillary bed. We set to match the average conductivity in real sensory cortex data. We convert from the discrete networks in ref. 5 to an equivalent porous medium by imposing unit pressure gradients throughout the domain sequentially in each of the , , and directions, calculating the mean flux in three directions to obtain a three by three matrix. The off-diagonal entries of this matrix are close to zero, and we identify with the average of the three diagonal entries.
Since Darcy’s Law is linear, we can build up by solving for the pressure field for individual vessels. In the slender-body approximation, vessels are modeled by lines of point sources, so the solution for each vessel is built up, in turn, from the solution for a point source. Consider a single vessel with centerline , where is the arc length along . Conservation of flux implies that the pressure field due to a single source of unit strength at (generally called the Green’s function ) solves:
| [2] |
Our computational domain is the box: , , , with representing the distance from the cortical surface. Because we are simulating only a small part of the cortex, we implement periodic boundary conditions in the x and y directions, effectively stacking the network with replicates of itself in those directions to simulate a wide and thin sheet of penetrating vessels. In the simulations shown in this paper, our model takes and , comparable with the mapped tissue in Fig. 1A. The penetrating vessels have length .
We set no flow boundary conditions on our porous medium, i.e., on the cortical surfaces , , representing the confinement of flow to the modeled layer of tissue. We achieve periodicity in and by Fourier expanding our solution in the x and y directions: , where is obtained from by adding the zero wavenumber component, and we can rewrite Eq. 2 in terms of the functions :
| [3] |
Comparing individual Fourier terms in Eq. 3, we obtain ordinary differential equations for each , which, when combined with the boundary conditions , yield:
| [4] |
where and and are calculated such that the solution is continuous at , but its derivative has a jump of at :
| [5] |
When , the solution of Eq. 3 for a single source or sink diverges. We derive the zero-wavenumber solution for the entire set of sources and sinks by solving directly for the average pressure and an average net flux: , where is the strengh of the sources or sinks. Averaging the mass-conservation law for the entire and domain, we obtain:
| [6] |
which may be integrated to obtain:
| [7] |
for some unknown constant . Written in this form, the solution automatically satisfies no flow at . To satisfy no flow at , we require
| [8] |
in other words, sources and sinks are balanced within the domain. We obtain the overall pressure field by attaching the zero-wavelength solution to our Fourier series.
In a domain containing vessels with center lines , , each parameterized by arc-length and with source or sink distribution , we can derive a pressure field . The source strengths, , are found by requiring consistency with the flows in each penetrating vessel (Fig. 1 C, Right). We may evaluate the pressure on each penetrating vessel:
| [9] |
The strength of the source or sink should be equal to the loss (respectively, gain) of blood along each penetrating vessel (Fig. 1C). The amount of blood leaving (or entering) unit length of a penetrating vessel must be equal to the rate of change of blood flow through the vessel. Hence, if we denote the conductivity of a penetrating vessel by , then:
| [10] |
where is the flow along the vessel at , and we set to match ref. 5.
We assume that pressures are known at the top of each penetrating vessel: (mmHg for arterioles and 50 mmHg for venules), representing their respective connections to the arterial and venous networks, while imposing no flux boundary conditions at their distal ends: . We numerically solve Eqs. 9 and 10 together. If each penetrating vessel is discretized by points, , then we have unknowns, namely: , , and the constant in the zero-wavenumber solution (Eq. 7). Eq. 9 provides linear constraints; Eq. 10 and its boundary conditions, an additional linear constraints; and Eq. 8, the condition of balanced sources and sinks, provides the final linear constraint. Thus, a single matrix solve is sufficient to find all of our unknowns. Once the source strengths are solved for, we can quickly compute the pressure field across the entire domain using fast Fourier transforms. Building and solving the continuum model for a single configuration of penetrating vessels requires ∼4 min on a notebook computer, compared with 70 min to create and solve a synthetic network, and this immense acceleration allows us to use the continuum model to analyze a wide space of vessel ratios and arrangements. We performed numerical convergence studies to determine how many discretization points are needed to model each vessel and how many Fourier modes are necessary to represent the associated Greens functions (SI Appendix, SI Text and Fig. S2).
Modeling Vessel Arrangements.
The degree of randomness in vessel arrangements can affect the size of low-flow regions, so it is essential to our modeling to set the correct level of disorder in vessel placement. We measured the entropy of the number of penetrating vessels within a given distance to any penetrating vessel in the real mouse sensory cortex (SI Appendix, Fig. S4). Real vessel arrangements have higher entropy even than random networks, except at the smallest scales (spacings less than m), presumably because in real networks, vessels are not allowed to be on top of each other, while the random distribution has no such restriction. We model short-range ordering of vessel arrangements by placing all of our penetrating vessels on sites within a lattice, which sets a minimum vessel spacing of 100 m.
Results
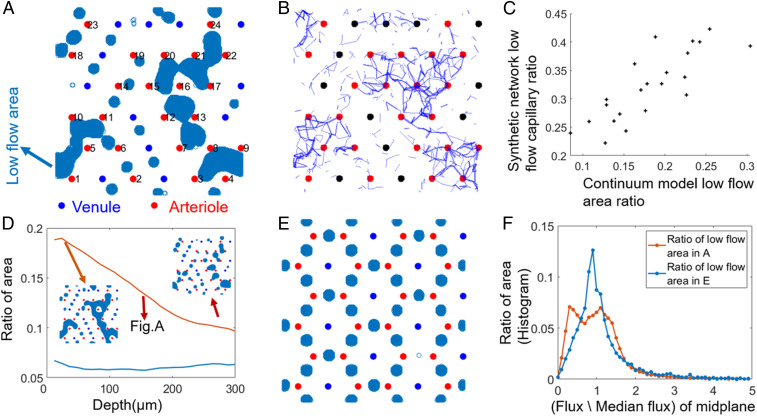
To explore the effect of low-flow regions upon the overall perfusion efficiency of a tissue, we modeled vascular networks in cubical domains containing 12 venules and 24 arterioles (Fig. 1C). We initially considered random configurations of vessels (representative data shown in Fig. 3A). We validated results from the continuum model against synthetic hierarchical networks, finding that continuum and network models agree in the shape and location of low-flow regions (comparing Fig. 3 A and B) and that the resultant fractions of poorly perfused tissue are strongly correlated between models (Fig. 3C).
Fig. 3.
A continuum model predicts the same patterns of low-flow regions as synthetic discrete networks and reveals effects of arteriole–venule arrangements on the effectiveness of perfusion. (A) Low-flow regions (regions with less than 40% of median flux) on midplane are shown in blue for a random distribution of penetrating vessels with a 2–1 arteriole–venule ratio and show a large continuous poorly perfused area surrounded by arterioles. (B) Predicted low-flow regions match closely to a synthetic discrete and hierarchical network model, with the same penetrating vessel placements (shown in blue: capillaries in midplane carrying less than of the median flux). (C) Total low-flow area ratio (x axis) in continuum model predicts the total volume fraction of low perfused capillaries (y axis) in a hierarchical discrete network model with the same vessel arrangements. Each point represents a different random arteriole and venule arrangement. (D) The depth in the modeled tissue where low-flow regions are calculated affects the total low-flow area, but only weakly affects comparisons between different arrangements. Red curve, arrangement A; blue curve, arrangement E. D, Insets show how the low-flow areas in arrangement A change with depth. (E and F) Effect of vessel arrangement. (E): (Ordered) honeycomb arrangement of arterioles and venules with the same 2–1 arteriole–venule ratio as A. Low-flow regions are more numerous, but smaller. (F) The histogram of fluxes for random (A) and ordered (E) arrangements of vessels.
We measured the uniformity of perfusion in the midplane of the domain () from histograms of the flow sampled at every grid point (Fig. 3F). Fluxes in the midplane are nonuniform ( for random vessel arrangement), and a main driver of this nonuniformity is low-flow regions—15.4% of grid points carried less than 40% of the median flow. Similar flow nonuniformity was seen at all depths through the tissue (Fig. 3D): Low-flow regions shrink with depth, but their locations and shapes stay roughly the same (Fig. 3 D, Inset).
In our simulations, low-flow regions emerge between pairs of arterioles or pairs of venules, where source or sink flows cancel (Fig. 3A). Such cancelations are inevitable within a continuum model: In this plane of the sample, the flow of blood is close to planar (in fact, we find that ), and we can approximately count the number of stagnation points—that is, the number of points at which the blood flow goes exactly to zero—using index theory. Because of incompressibility, these stagnation points are all saddle points of the vector field given by . Recall (20) that if is any differentiable closed contour enclosing a region of a two-dimensional vector field that is differentiable except at a finite set of sources or sinks, then if is the angle made between and the x axis:
| [11] |
If we let enclose the entire periodic subdomain: , , then opposite pairs of edges in the integral cancel, sending the left-hand side of Eq. 11 to zero. Accordingly, we find that the number of stagnation points is simply equal to the total number of penetrating vessels of any kind. Since each stagnation point in the vector field must be located in a low-flow region, then under the continuum model, it is impossible to completely eliminate low-flow regions by rearranging vessels.
However, the size of the low-flow regions surrounding stagnation points affects the overall uniformity of perfusion and is sensitive to the vessels’ arrangement. We compared our results for random arrays to ordered arrays (e.g., Fig. 3E). In the shown honeycomb array, small low-flow spots are arranged between every pair of neighboring arterioles (Fig. 3E). Although there still exist 36 low-flow regions (one for each stagnation point), they cover a smaller fraction of the perfused tissue both in the representative plane (7%) and at all other depths (Fig. 3D), and the overall nonuniformity is less (Fig. 3F; ).
Comparing Fig. 3 A and E, we can see why disordered arrangements of vessels have larger low-flow regions. If the vessels are arranged randomly, then since arterioles outnumber venules, we find tissue regions that contain only arterioles in their interior and on their boundary. Arterioles in the interior of such a region are screened by the arterioles on its boundary and supply much less blood, creating a low-flow region.
Adding Arterioles Does Not Increase Tissue Perfusion.
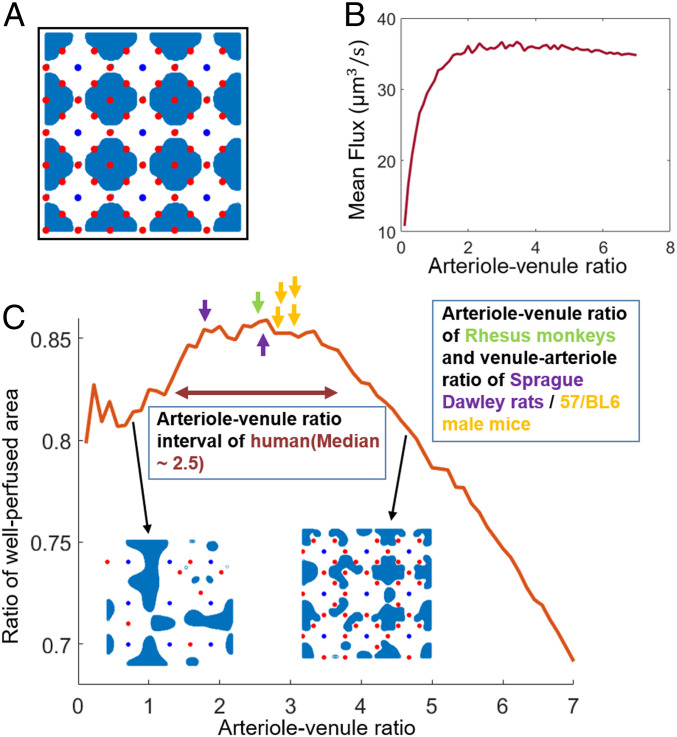
Because low-flow regions emerge in regions of tissue containing only arterioles or venules, increasing the number of penetrating vessels may not improve the overall perfusion of tissue. To test the effect of the number of arterioles on cortex perfusion, we placed venules on a regular grid and then added arterioles randomly, also at grid points to ensure a minimum spacing between vessels (Fig. 4A shows the total set of available sites). We calculated both the total perfusion and the uniformity (fraction of tissue receiving more than 40% of the median flow) in the midplane after each arteriole was added. Results are insensitive to the threshold at which low flow is identified and to the precise configuration of vessels (three other simulated sequences of increasing arteriole–venule ratio, each with different thresholds, are shown in SI Appendix, Fig. S3).
Fig. 4.
Effect of varying arteriole–venule ratio on perfusion. (A) Venules are arranged on a uniform square grid, and arterioles are added randomly one by one at sites marked with red dots. Blue regions show low flow after all red sites have been filled. (B) Change of mean perfusion with the arteriole–venule ratio when the arterioles are set on the grid randomly one by one to vary arteriole–venule ratio. (C) Fraction of tissue with low perfusion, for varying arteriole–venule ratio. Arrows show the measured most numerous–least numerous penetrating vessel ratios for humans (11), Rhesus monkeys (12, 21), Sprague–Dawley rats (22), and C57/BL6 male mice (5). For primate brains, arterioles are more numerous, so the reported ratio is arterioles/venules; for rodent brains, venules are more numerous, and venule/arteriole ratio is reported.
When we first start adding arterioles to the network, the overall uniformity of flow increases with the number of vessels, as adding arterioles initially eliminates the low-flow regions that form between groups of venules (Fig. 4 C, Inset). However, once the ratio of arterioles to venules exceeds three, further increasing the number of venules starts to decrease the perfusion uniformity, as regions of tissue bordered by arterioles begin to emerge. At the same arteriole–venule ratios, the flux into the tissue saturates (Fig. 4B). Fluxes saturate because pressure conditions are imposed on the ends of arterioles, so arterioles that are added within existing low-flow regions do not experience pressure drops large enough to act as significant sources within the porous medium.
The modeled ratio (2.6) at which both fluxes into the tissue saturate and the perfusion uniformity starts to decrease quantitatively match the arteriole–venule ratios measured in real primate cortices: including humans, median 2.5 (interquartile range: 1.75 to 3.7) (11); and Rhesus monkeys, median 2.58 (12). In mouse or rat brains, there are more venules than arterioles. However, in our calculations, the roles of arterioles and venules can be reversed without affecting the size or number of low-flow regions. So another set of optimal configurations exist in which the venule–arteriole ratio should be close to 2.6. Indeed, the normal ratio of the two vessels in mice and rat cortical networks is 2.6 to 3 (5, 21). So in both primates and rodents, the most-numerous to least-numerous ratio is very close to optimal for maximizing uniform perfusion (Fig. 4C). By contrast, when we consider microvasculatures outside of the cortex, such as the cat lung, microvessels are not parallel, and, unsurprisingly, the venule–arteriole ratio (1.25) diverges from the predicted optimum (23).
Why would cortical micronetworks have arteriole–venule ratios that optimize perfusion uniformity? Recent studies of the trunk microvasculature of embryonic zebrafish show that the conductances of intersegmental vessels are optimized to ensure uniform flow between vessels and, hence, achieve uniform perfusion of the trunk (15, 24). Perfusion uniformity implies that every tissue receives the same flux of blood and so may provide a general organizing principle for the arrangement and numbers of vessels in microvascular networks, including in the cortex. Alternatively, arterioles and venules require blood and energy to maintain and deny space to gray matter; the governing tradeoff for arteriole–venule ratios may be the diminishing returns in total blood supply from increasing the number of arterioles.
Throughout this study (and consistent with mapped networks; SI Appendix, Fig. S4), we have assumed a random arrangement of penetrating vessels. Yet, ordered arrangements of vessels may improve perfusion (Fig. 3 D–F). We explored the extent to which nonrandom arrangements outperform random arrangements, by starting with the same lattice of venules and varying the arteriole–venule ratio by placing arterioles sequentially and according to a greedy optimization, in which each new arteriole was added at the grid point with the lowest flow, while maintaining minimum distance from all other vessels in the network. This algorithm places arterioles regularly around the Voronoi boundaries between the venules (SI Appendix, Fig. S5B), avoiding creating any convex regions that contain only arterioles. Under the optimal arrangement, both mean flux and uniformity converge to a limit, rather than selecting for a specific arteriole–venule ratio. Nonetheless, real penetrating vessels have statistically random configurations, at least on large enough length scales (SI Appendix, Fig. S4). Indeed, penetrating vessels form nearly simultaneously (25), so optimal arrangements that arise from steering vessels to existing regions of low perfusion aren’t possible. Yet, the plateauing of total perfusion (SI Appendix, Fig. S5C) and perfusive uniformity (SI Appendix, Fig. S5D) with increasing arteriole–venule ratios means that even under optimal arrangement, if the cost (e.g., from loss of space available to gray matter) of adding additional vessels were included, there would still be an optimal ratio of venules to arterioles.
Penetrating Vessel Conductances Do Not Directly Control Perfusion.
In cortical microvascular networks, conductances of penetrating vessels and capillaries dynamically respond to neuronal activity (26, 27). High neuronal activity requires increased cerebral blood flow (CBF) to meet the tissue’s increased glucose requirements (3, 28) [though oxygen demands may also stimulate blood-flow responses (29)]. Increases in CBF are achieved by the dilation of arteries, arterioles (30, 31), and capillaries (32, 33). Meigel et al. (34) showed theoretically that the hierarchy of vessel radii in the mouse sensory cortex ensures that the glucose delivered by a particular vessel to the surrounding tissue typically increases when that vessel’s conductance increases. However, their analysis did not explore interactions between vessels—specifically, how overall tissue perfusion may be affected by conductance changes. We hypothesized that since increasing vessel conductances can change the location of low-flow spots within the tissue, regions of tissue not immediately perfused by the affected arteriole may lose perfusion.
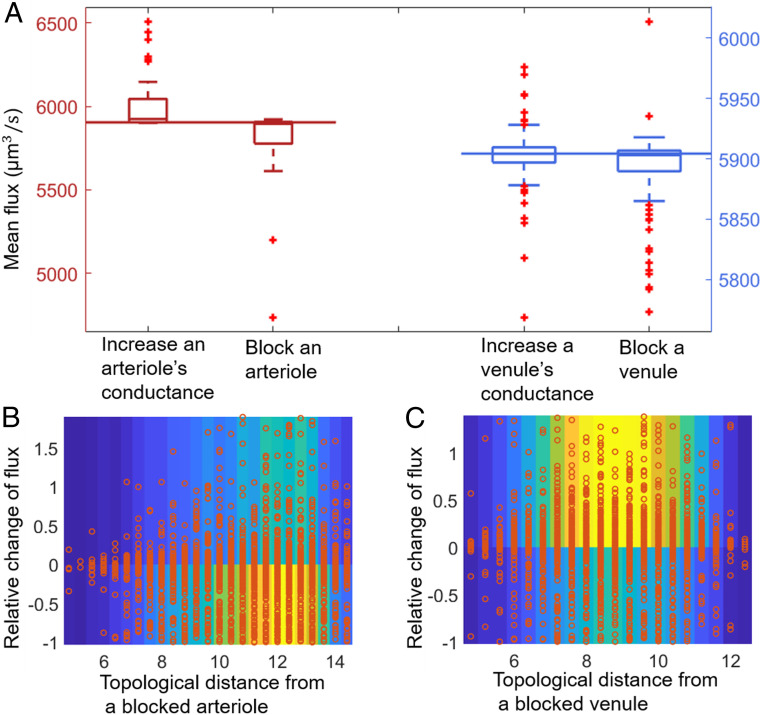
We first performed a perturbation analysis of penetrating vessels using the real mouse vasculature in ref. 5, individually dilating them (increasing their conductances 10-fold) to model vessel dilation or blocking them (setting their conductances to zero) to model ischemic damage within the mapped mouse sensory cortex (venule–arteriole ratio: 2.88). Tenfold conductance increases were chosen because reported arteriole diameters ranged from 5m, comparable to a mouse red blood cell, to 12 m, a regime in which even small changes in vessel diameter can greatly affect conductances (15). However, our results were qualitatively the same under smaller increases in conductance. In the mouse sensory cortex, venules outnumber arterioles, so low-flow regions are typically bounded by venules (Fig. 2). We found then that increasing any arteriole conductance increased flow in the arteriole, consistent with ref. 34, and also increased global perfusion. Similarly, blocking an arteriole consistently reduced global perfusion (Fig. 5A). Conductance changes in the more numerous venules, by contrast, led to unpredictable effects. Surprisingly, increasing venule conductance decreased mean perfusion for 78 (of 127) venules, while blocking the venule increased mean perfusion for 49 venules. For 32 venules, either increasing the conductance or blocking the venule decreased mean flux. Low-flow regions tend to form around whichever vessel is more numerous, and the movement of these regions causes nearby vessels to have less precise control over perfusion. Hence, the less numerous vessels control perfusion more precisely, or, equivalently, fluxes are more robust to changes in conductance, e.g., due to injury, among the more numerous of the penetrating vessels. Similar results were obtained by using other samples of real mouse brain vasculature (SI Appendix, Fig. S6).
Fig. 5.
Changes in penetrating venule conductance, but not changes in arteriole conductance, have unpredictable effects on fluxes in a real mouse sensory cortex microvasculature. (A) The predicted distribution of mean flux on plane when the conductance of a penetrating vessel (red, arteriole; blue, venule) is either increased 10-fold or sent to zero. Horizontal lines represent the mean flux before any change. (B and C) Heterogeneity in capillary responses to block penetrating venules is shown by combined scatterplots (red dots) and heat maps (colors) of the relative change of flux in each capillary versus its topological distance (the number of capillaries on the shortest path) from the conductance-changed arteriole (B) or venule (C). In particular, when a venule is blocked, in around 40% of cases, most capillaries, including nearby ones, experience an increase in flow.
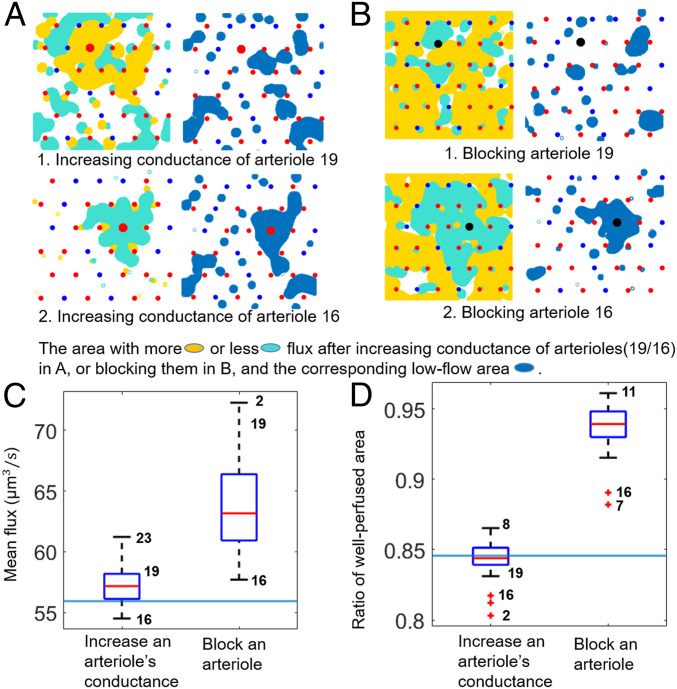
To test our hypothesis that low-flow regions determine the response of perfusion to vessel conductance changes, we perturbed conductances in our continuum models of the cortex. (Mean fluxes in the continuum model [Figs. 4B and 6C] are numerically much smaller than for the network model [Fig. 5A] because they are essentially volume-averaged, i.e., multiplied by the volume fraction occupied by capillaries, ). For representative comparisons, Fig. 6A shows the different effects of individually increasing conductances fivefold in two arterioles (nos. 19 and 16, according to Fig. 3A). When arteriole 19, surrounded by a mix of arterioles and venules, is dilated, capillaries in the pathway from the arteriole to the surrounding venules receive increased flow (Fig. 6 A, Upper Left). Other arterioles perfuse less flux into the tissue because of a global increase in average pressures, but the total perfusion increases (Fig. 6C). Compared to Fig. 3A, the total area of the low-flow region slightly increases, while preserving roughly the same shape (Fig. 6 A, Upper Right). Conversely, when arteriole 16, surrounded by arterioles and in the middle of a low-flow region, is dilated, the flux to surrounding capillaries actually decreases (Fig. 6 A, Lower). In other words, dilating the arteriole in the middle of a low-flow region may have counterintuitive effects upon perfusion. We systematically and individually dilated each of the 24 arterioles in Fig. 3A. For most arterioles, increasing conductance increased mean perfusion (Fig. 6C); however, mean perfusion decreased when 4 of 24 arterioles dilate (arterioles 9, 13, 16, and 21; labeled in Fig. 3A). Although arteriole dilation is usually thought of as a method to achieve a localized increase in perfusion (5, 34), we found that in over half of cases, dilating an arteriole actually created more uniform perfusion, reducing the total low-flow area (Fig. 6D).
Fig. 6.
In a continuum model with more arterioles than venules, changes in arteriole conductance, but not changes in venule conductance, have unintuitive effects upon perfusion. (A and B) Effect of blocking or increasing conductances of arterioles 19 or 16 (the numbering of arterioles follows Fig. 3A). (A and B, Left) Colored regions represent areas where flow increased (yellow) or decreased (cyan) by more than 10%. (A and B, Right) Low-flow spots after conductance change (blue regions). (C) The mean flux distribution after increasing the conductance of individual arterioles fivefold or block them individually. The blue horizontal line represents the mean flux before any conductance change. Mean flux is calculated on the midplane. (D) Fraction of tissue in midplane that is well-perfused (greater than 40% of median flow) when arteriole conductances are individually increased fivefold or arterioles are blocked. The blue horizontal line represents the ratio of well-perfused area before any conductance change.
We then studied the effect on perfusion of blocking the same arterioles, representing ischemic damage to the network, similar to that induced in mouse brains using optically mediated occlusion (35). In separate simulations, we blocked arterioles 19 and 16 from Fig. 3A, setting the conductance of the blocked arteriole to zero. Since arteriole 19 sits on the boundary of a low-flow region, its blocking removed the previous stagnation points between it and the other arterioles, allowing blood in the low-flow region to flow out to surrounding venules (Fig. 6 B, Upper Left). A lower global pressure also ensures that the other arterioles have a larger pressure drop and perfuse more; hence, mean perfusion and overall perfusion uniformity increased (fraction of tissue with more than 40% median blood flow increased from 84.56 to 93.85%) (Fig. 6D). More importantly, there is no large low-flow area formed near the blocked arteriole 19 (Fig. 6 B, Upper Right). Conversely, when arteriole 16, inside a low-flow region, is blocked (Fig. 6 B, Lower), the surrounding arterioles formed new stagnation points and caused a large continuous area of low-flow region around the blocked arteriole. However, the mean perfusion and perfusion uniformity still increased due to the lowered global pressure. Systematically blocking every arteriole in separate simulations, we find that blocking any arteriole increased mean perfusion and perfusion uniformity (Fig. 6 C and D), but that the largest increases in perfusion uniformity occurred when an arteriole on the boundary of a low-flow region was blocked (numbers on plot identify arterioles from which data were taken). Because of the linearity of the underlying equations, dilating or blocking venules would have similarly unpredictable effects in modeled tissues, in which venules outnumber arterioles, as can be seen if we swap arterioles and venules in our model (SI Appendix, Fig. S7).
To expose the limits on flow controllability, we compare the change in mean perfusion from dilating a vessel to the change in mean perfusion from blocking the same vessel. For 20 of the arterioles, mean perfusion increased whether the vessel was dilated or blocked. Similar results were obtained when different arrangements of vessels were perturbed in the same way (SI Appendix, Fig. S8) or when the total inflow into the tissue was plotted instead of the mean perfusion (SI Appendix, Fig. S9).
Discussion
We present a computationally efficient method for representing the perfusion of blood through tissues via continuum-level modeling. Assuming a uniform permeability within the capillary bed, we can use a slender-body approximation, replacing penetrating vessels by lines of sources or sinks that fill or drain a continuum model of the capillary bed. This approximation reduces the partial differential equation (PDE) solution to finding the strengths of sources and sinks along each penetrating vessel. We chose this approach because, in many real situations, complete maps of the microvascular network do not extend below the arteriole level (36), and the structure of the capillary bed between arterioles and venules can only be assumed. In the few networks where comprehensive capillary-level mapping has been performed, such as the mouse sensory cortex, the permeability of the capillary bed has some spatial heterogeneity—we found a coefficient of variation of 0.8423 when we partitioned the domain into boxes of size . Nonetheless, our continuum model agreed in most quantitative respects with synthetic networks that are known to model the conductance hierarchies and connectivities of the real sensory cortex microvasculature. Furthermore, our theory can be extended to model spatially heterogeneous conductances by replacing the known Green’s function for point sources by source terms within the porous medium equations and solving for source strengths self-consistently with fluxes, a problem with a rich set of PDE precedents (37, 38).
With so many sources and sinks distributed through the tissue, it may be unsurprising to see points where flows cancel to produce regions of low flow. Because of the approximately two-dimensional nature of flows in the midplane of our model, we expect, based on index theory, that the number of these points will simply increase with the number of penetrating arterioles. However, regions of low flow tend to be delimited by groups of penetrating vessels of the same type (either all arterioles or all venules), setting the sizes of low-flow regions, and selecting for an optimal ratio () of arterioles to venules or conversely, that is remarkably close to the ratios seen in real cortical microvasculatures.
We have not sought to establish whether or not low-flow areas obstruct the transfer of oxygen and metabolites to the tissue, since both may diffuse some distance [the Krogh length (39)] through the tissue. Indeed, in the mouse sensory cortex, the typical spacing of penetrating arterioles is comparable to twice the Krogh length of oxygen, (39, 40). In our model, tissue and blood flow have already been integrated into a single continuum, so little modification of the model would be needed to include the transport and diffusion of metabolites. Here, however, we have focused only on perfusive flows, including analyzing the complex effect that changing the conductance of a vessel in a low-flow spot has on the nearby flows. The structural constraints that emerge from this analysis may explain why there is no particular association between penetrating vessels and the neuronal columns they supply (5, 12) and why vessel dilation is never restricted to a single penetrating arteriole (41).
Maximizing perfusion or perfusion uniformity selects for an optimal ratio of most numerous penetrating vessels to least numerous; this ratio can be obtained by having more arterioles than venules (as in primates) or conversely (as in rodents). Do physical constraints also determine which vessel type is more abundant? In Fig. 5A and SI Appendix, Fig. S6, we modeled blocking venules and arterioles in two real mouse brain vasculature systems. Since arterioles are the less numerous penetrating vessels, dilating or blocking an arteriole directly changes blood-flow fluxes. By contrast, fluxes are relatively robust to changes in venule conductance. Intriguing hypotheses emerge from this—ischemic damage tends to arise from occlusions within the arterial network, likely due to its vessels being narrower than the venous network or because dislodged plaques or thrombi encounter arteries before they encounter veins (40). In long-lived primates, selection may be for networks that are more robust to microocclusions that affect arteriole conductances (i.e., there is selection for more numerous arterioles), while in mice that do not live long enough to accumulate this damage, more precise control over perfusion (i.e., less numerous arterioles) may be selected for (34). In model tissues with more numerous arterioles, we predict striking robustness of perfusion to occlusion of arterioles, which may link to the variable pathophysiology of ischemic events (42, 43). Conversely, in experiments with rodent brains, blockage of arterioles invariably leads to cyst formation (21, 40), but so does blockage of venules (21), and we must consider how closely our simple model of removing vessels approximates the damage produced when vessels are blocked experimentally. Nonetheless, our models emphasize the importance of the baseline distribution of low-flow regions when evaluating a microvascular network’s tolerance to aging and injury-related damage (44).
Our model predicts perfusion heterogeneities caused by the topology of penetrating vessels and their effects on blood-flow regulation during cerebral functional activities. Past experiments support our prediction of extreme heterogeneity of CBF (45, 46), as well as the shift in heterogeneity during neuronal activation. However, these experimental studies mainly focused on the heterogeneity of blood flow across individual capillaries and either interpreted it as having unclear physiological significance (47) or classified it as a form of capillary dysfunction (48) and provided little data on the spatial patterns of heterogeneity that could reveal the physical inevitability of low-flow regions. Fenstermacher et al. (49) recognized alternating columns of high- and low-flow rates, but speculated that the microvascular flow columns corresponded to cortical neural columns, which was ruled out by ref. 5. As for perfusion regulation, Yaseen et al. (50) found a global redistribution of CBF in penetrating vessels during a localized functional activation and stated ”it is not well understood how CBF redistributes on a microvascular level in response to localized functional activity.” Our theory suggests that these questions may be answered by analyzing spatial patterns of heterogeneity prior to, and CBF redistribution during, neural activity.
Supplementary Material
Acknowledgments
We thank two anonymous reviewers for their many insightful comments and critiques. This work was supported by National Institute of General Medical Sciences Grant 5R01GM126556 .
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. M.P.B. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2021840118/-/DCSupplemental.
Data Availability
Codes have been deposited in Zenodo (10.5281/zenodo.5098086).
References
- 1.Lennie P., The cost of cortical computation. Curr. Biol. 13, 493–497 (2003). [DOI] [PubMed] [Google Scholar]
- 2.Berg J. M., Tymoczko J. L., Stryer L., Biochemistry (W. H. Freeman, New York, ed 5, 2002). [Google Scholar]
- 3.Dienel G. A., Brain glucose metabolism: Integration of energetics with function. Physiol. Rev. 99, 949–1045 (2019). [DOI] [PubMed] [Google Scholar]
- 4.Wang Z., et al., Specific metabolic rates of major organs and tissues across adulthood: Evaluation by mechanistic model of resting energy expenditure. Am. J. Clin. Nutr. 92, 1369–1377 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blinder P., et al., The cortical angiome: An interconnected vascular network with noncolumnar patterns of blood flow. Nat. Neurosci. 16, 889–897 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Linninger A., Hartung G., Badr S., Morley R., Mathematical synthesis of the cortical circulation for the whole mouse brain—Part I. Theory and image integration. Comput. Biol. Med. 110, 265–275 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Schaffer C. B., et al., Two-photon imaging of cortical surface microvessels reveals a robust redistribution in blood flow after vascular occlusion. PLoS Biol. 4, e22 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Blinder P., Shih A. Y., Rafie C., Kleinfeld D., Topological basis for the robust distribution of blood to rodent neocortex. Proc. Natl. Acad. Sci. U.S.A. 107, 12670–12675 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Katifori E., Szöllosi G. J., Magnasco M. O., Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 104, 048704 (2010). [DOI] [PubMed] [Google Scholar]
- 10.Corson F., Fluctuations and redundancy in optimal transport networks. Phys. Rev. Lett. 104, 048703 (2010). [DOI] [PubMed] [Google Scholar]
- 11.El-Bouri W. K., Payne S. J., A statistical model of the penetrating arterioles and venules in the human cerebral cortex. Microcirculation 23, 580–590 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Adams D. L., Piserchia V., Economides J. R., Horton J. C.,Vascular supply of the cerebral cortex is specialized for cell layers but not columns. Cereb. Cortex 25, 3673–3681 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ingham D. B., Pop I., Transport Phenomena in Porous Media (Elsevier, Amsterdam, Netherlands, 1998). [Google Scholar]
- 14.Meigel F. J., Alim K., Flow rate of transport network controls uniform metabolite supply to tissue. J. R. Soc. Interface 15, 20180075 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chang S.-S., et al., Optimal occlusion uniformly partitions red blood cells fluxes within a microvascular network. PLoS Comput. Biol. 13, e1005892 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Batchelor G. K., Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440 (1970). [Google Scholar]
- 17.Keller J. B., Rubinow S. I., Slender-body theory for slow viscous flow. J. Fluid Mech. 75, 705–714 (1976). [Google Scholar]
- 18.Secomb T. W.. A Green’s function method for simulation of time-dependent solute transport and reaction in realistic microvascular geometries. Math. Med. Biol., 33, 475–494, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vidotto E., Koch T., Köppl T., Helmig R., Wohlmuth B., Hybrid models for simulating blood flow in microvascular networks. Multiscale Model. Simul. 17, 1076–1102 (2019). [Google Scholar]
- 20.Jordan D., Smith P., Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers (Oxford Texts in Applied and Engineering Mathematics, Oxford University Press, Oxford, UK, 2007), vol. 10. [Google Scholar]
- 21.Shih A.Y., et al., The smallest stroke: Occlusion of one penetrating vessel leads to infarction and a cognitive deficit. Nat. Neurosci. 16, 55 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nguyen J., Nishimura N., Fetcho R. N., Iadecola C., Schaffer C. B., Occlusion of cortical ascending venules causes blood flow decreases, reversals in flow direction, and vessel dilation in upstream capillaries. J. Cereb. Blood Flow Metab. 31, 2243–2254 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhuang F. Y., Yen M. R. T., Fung Y. C., Sobin S. S., How many pulmonary alveoli are supplied by a single arteriole and drained by a single venule? Microvasc. Res. 29, 18–31 (1985). [DOI] [PubMed] [Google Scholar]
- 24.Chang S.-S., Roper M., Microvascular networks with uniform flow. J. Theor. Biol. 462, 48–64 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Greenberg D. A., Jin K., From angiogenesis to neuropathology. Nature 438, 954–959 (2005). [DOI] [PubMed] [Google Scholar]
- 26.Nielsen A. N., Lauritzen M., Coupling and uncoupling of activity-dependent increases of neuronal activity and blood flow in rat somatosensory cortex. J. Physiol. 533, 773–785 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chaigneau E., et al., The relationship between blood flow and neuronal activity in the rodent olfactory bulb. J. Neurosci. 27, 6452–6460 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mintun M. A., et al., Blood flow and oxygen delivery to human brain during functional activity: Theoretical modeling and experimental data. Proc. Natl. Acad. Sci. U.S.A. 98, 6859–6864 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gagnon L., et al., Modeling of cerebral oxygen transport based on in vivo microscopic imaging of microvascular network structure, blood flow, and oxygenation. Front. Comput. Neurosci. 10, 82 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Drew P. J., Shih A. Y., Kleinfeld D., Fluctuating and sensory-induced vasodynamics in rodent cortex extend arteriole capacity. Proc. Natl. Acad. Sci. U.S.A. 108, 8473–8478 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.O’Herron P., et al., Neural correlates of single-vessel haemodynamic responses in vivo. Nature 534, 378–382 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hall C. N., et al., Capillary pericytes regulate cerebral blood flow in health and disease. Nature 508, 55–60 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cai C., et al., Stimulation-induced increases in cerebral blood flow and local capillary vasoconstriction depend on conducted vascular responses. Proc. Natl. Acad. Sci. U.S.A. 115, E5796–E5804 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Meigel F. J., Cha P., Brenner M. P., Alim K., Robust increase in supply by vessel dilation in globally coupled microvasculature. Phys. Rev. Lett. 123, 228103 (2019). [DOI] [PubMed] [Google Scholar]
- 35.Drew P. J., et al., Chronic optical access through a polished and reinforced thinned skull. Nat. Methods 7, 981–984 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xiong B., et al., Precise cerebral vascular atlas in stereotaxic coordinates of whole mouse brain. Front. Neuroanat. 11, 128 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cortez R., The method of regularized stokeslets. SIAM J. Sci. Comput. 23, 1204–1225 (2001). [Google Scholar]
- 38.Cortez R., Fauci L., Medovikov A., The method of regularized stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 17, 031504 (2005). [Google Scholar]
- 39.Secomb T. W., Hsu R., Beamer N. B., Coull B. M., Theoretical simulation of oxygen transport to brain by networks of microvessels: Effects of oxygen supply and demand on tissue hypoxia. Microcirculation 7, 237–247 (2000). [PubMed] [Google Scholar]
- 40.Nishimura N., Schaffer C. B., Friedman B., Lyden P. D., Kleinfeld D., Penetrating arterioles are a bottleneck in the perfusion of neocortex. Proc. Natl. Acad. Sci. U.S.A. 104, 365–370 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Goense J., Bohraus Y., Logothetis N. K., fMRI at high spatial resolution: Implications for bold-models. Front. Comput. Neurosci. 10, 66 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gabhann F. M., Peirce S. M., Collateral capillary arterialization following arteriolar ligation in murine skeletal muscle. Microcirculation 17, 333–347 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chatterjee S. A., et al., Interpreting prefrontal recruitment during walking after stroke: Influence of individual differences in mobility and cognitive function. Front. Hum. Neurosci. 13, 194 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sweeney M. D., Kisler K., Montagne A., Toga A. W., Zlokovic B. V., The role of brain vasculature in neurodegenerative disorders. Nat. Neurosci. 21, 1318–1331 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Villringer A., Them A., Lindauer U., Einhäupl K., Dirnagl U., Capillary perfusion of the rat brain cortex. An in vivo confocal microscopy study. Circ. Res. 75, 55–62 (1994). [DOI] [PubMed] [Google Scholar]
- 46.Hudetz A. G., Blood flow in the cerebral capillary network: A review emphasizing observations with intravital microscopy. Microcirculation 4, 233–252 (1997). [DOI] [PubMed] [Google Scholar]
- 47.Jespersen S. N., Østergaard L., The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. J. Cereb. Blood Flow Metab. 32, 264–277 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lücker A., Secomb T. W., Weber B., Jenny P., The relation between capillary transit times and hemoglobin saturation heterogeneity. Part 1: Theoretical models. Front. Physiol. 9, 420 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fenstermacher J., et al., Functional variations in parenchymal microvascular systems within the brain. Magn. Reson. Med. 19, 217–220 (1991). [DOI] [PubMed] [Google Scholar]
- 50.Yaseen M. A., et al., Microvascular oxygen tension and flow measurements in rodent cerebral cortex during baseline conditions and functional activation. J. Cereb. Blood Flow Metab. 31, 1051–1063 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Codes have been deposited in Zenodo (10.5281/zenodo.5098086).