Genealogical structure changes as range expansions transition from pushed to pulled

Significance

Spatial dynamics are important for understanding genetic diversity in many contexts, such as cancer and infectious diseases. Coalescent theory offers a powerful framework for interpreting and predicting patterns of genetic diversity in populations, but incorporating spatial structure into the theory has proven difficult. Here, we address this long-standing problem by studying the coalescent in a spatially expanding population. We find the topology of the coalescent depends on the growth dynamics at the front, but not on the functional form of the growth function. Instead, the transition between coalescent topologies is determined by a single dynamical parameter. Our theory makes precise predictions about the effects of population dynamics on genetic diversity at the expansion front, which we confirm in simulations.

Abstract

Range expansions accelerate evolution through multiple mechanisms, including gene surfing and genetic drift. The inference and control of these evolutionary processes ultimately rely on the information contained in genealogical trees. Currently, there are two opposing views on how range expansions shape genealogies. In invasion biology, expansions are typically approximated by a series of population bottlenecks producing genealogies with only pairwise mergers between lineages—a process known as the Kingman coalescent. Conversely, traveling wave models predict a coalescent with multiple mergers, known as the Bolthausen–Sznitman coalescent. Here, we unify these two approaches and show that expansions can generate an entire spectrum of coalescent topologies. Specifically, we show that tree topology is controlled by growth dynamics at the front and exhibits large differences between pulled and pushed expansions. These differences are explained by the fluctuations in the total number of descendants left by the early founders. High growth cooperativity leads to a narrow distribution of reproductive values and the Kingman coalescent. Conversely, low growth cooperativity results in a broad distribution, whose exponent controls the merger sizes in the genealogies. These broad distribution and non-Kingman tree topologies emerge due to the fluctuations in the front shape and position and do not occur in quasi-deterministic simulations. Overall, our results show that range expansions provide a robust mechanism for generating different types of multiple mergers, which could be similar to those observed in populations with strong selection or high fecundity. Thus, caution should be exercised in making inferences about the origin of non-Kingman genealogies.

The genealogy of a population provides a window into its past dynamics and future evolution. By analyzing the relative lengths of different branches in the genealogical tree, we can estimate mutation rates and the strength of genetic drift (1), or infer historical population sizes (2) and patterns of genetic exchange between species (3). At the same time, we can use the structure of genealogies to make predictions about the speed of evolution (4) and even answer important practical questions, such as what the next strain of influenza will be (5).

Typically, the full ancestry is not known, and one has to infer its structure based on DNA samples from the population using theoretical models. The most widely used model is the Kingman coalescent (6, 7). The Kingman coalescent describes the genealogies of a well-mixed population of constant size, in which all mutations are neutral. Because of its simplicity, many statistical properties of the Kingman coalescent can be calculated exactly (7). These mathematical results have formed the basis of many commonly used techniques to infer genealogical trees from DNA sequences. The defining characteristics of the trees generated from the Kingman coalescent are a large number of early mergers and long branches close to the common ancestor. Importantly, the Kingman coalescent contains only pairwise mergers between lineages. However, several studies have attempted to test these predictions directly in real populations and found significant deviations (8–11).

To resolve the inconsistencies between observed genetic diversity and theoretical predictions, numerous extensions of the classic Kingman coalescent have been proposed (12–16). For example, many studies have analyzed the effects of time-dependent population sizes and spatial structure on the coalescent (2, 17). Despite providing better fits to the data, this generalized Kingman coalescent does not capture some of the qualitative features of empirical genealogies—namely, the existence of multiple mergers in the genealogical trees (11, 18).

Mathematically, the genealogies with multiple mergers can be described by a more general coalescent model known as the $\mathrm{\Lambda }$-coalescent (19–21). Several mechanisms that give rise to such coalescents have also been proposed. Theoretical studies have shown that highly fecund populations have multiple mergers in their genealogies (21, 22). Likewise, selective sweeps can lead to fat-tailed distributions in the number of offspring, which generate genealogies with multiple mergers. However, these mechanisms have limited applicability—most species have few offspring and, excluding microbes, typical population sizes and selective pressures are unlikely to have a large effect on genealogies (23–25). Here, we show that a ubiquitous demographic mechanism generates genealogical trees with a wide range of topologies, including topologies with exclusively pairwise mergers as well as topologies with multiple mergers. This mechanism relies on unusually large genetic drift at the leading edge of expanding population fronts. Such expansions can occur in a variety of contexts, such as range expansions (26), range shifts due to climate change (27), or the growth of bacterial colonies (28, 29) and tumors (30, 31).

Despite their importance, very little is known about the genealogies of spatially expanding populations. Two approaches have been used previously to study this problem, often leading to very different conclusions (32–34). The most common approach is to approximate spatial expansions by a series of discrete bottlenecks at the front (23, 32, 35). This is known as the serial bottleneck approximation, and it implicitly assumes that genealogies along the expansion are described by a series of replacement events (as illustrated in Fig. 1 A and B), while those at the leading edge are described by the Kingman coalescent, with a potentially time-dependent population size (33, 36). The Kingman structure of genealogies has also been recently proven for a certain class of range expansions with negative growth rates at the leading edge (37). An alternative approach, introduced in ref. 34, is based on an analogy between spatial expansions and traveling waves describing the increase in fitness in a population of constant size under strong selection (38–40). Using heuristic arguments, supported by extensive numerical simulations, Brunet et al. (34) conjectured that expansions under the Fisher–Kolmogorov–Petrovsky–Piskunov (FKPP) universality class are described by a different type of coalescent, known as the Bolthausen–Sznitman coalescent.* Unlike the standard Kingman coalescent, in which only pairwise mergers between branches are allowed, the Bolthausen–Sznitman coalescent is characterized by large merger events, during which a substantial fraction of branches can coalesce simultaneously (42, 43). Despite subsequent investigations, reconciling these two diametrically opposed points of view is still an open problem (33, 36, 40).

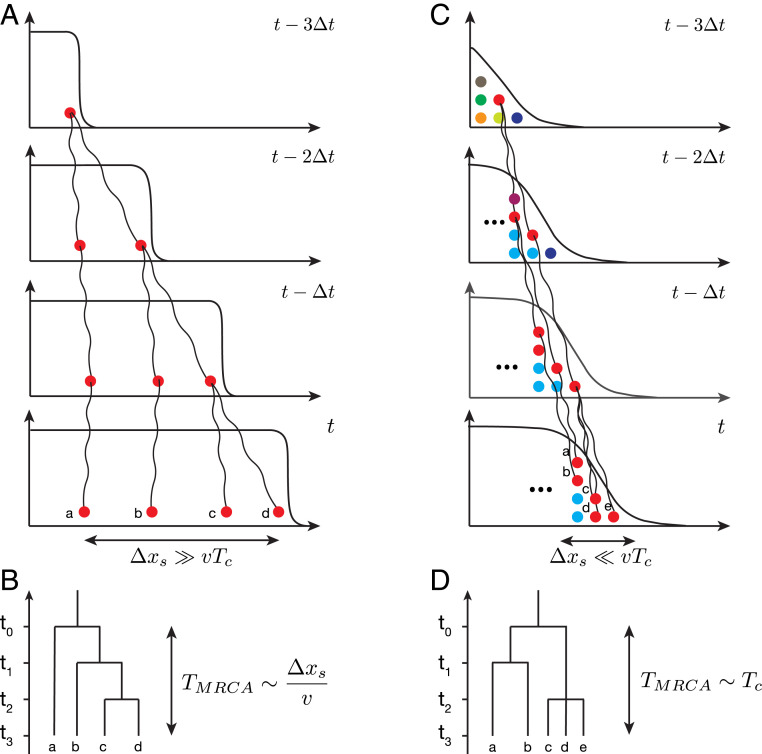
Fig. 1.

Shape of genealogies in expanding populations depends on spatial location of sampled individuals. The genealogies in two limiting sampling regimes are shown schematically. (A) When sampling is done over large distances along the expansion, the coalescence time is mainly determined by the motion of the front. (B) In this regime, the lineage coalescence depends on spatial locations, and genealogies correspond to a series of replacement events. (C) When sampling is done at the front, lineage coalescence is independent of spatial location, and the motion of the front does not play an important role. (D) In this regime, a characteristic coalescence time $T_c$ emerges which is determined by the topology of the genealogical tree.

Recent studies by the authors point to a potential resolution of the above-mentioned contradiction (44, 45). Specifically, we examined whether population dynamics at the front could lead to differences in the rate of diversity loss during range expansions. Surprisingly, we found that a dependence of the growth or migration rates on population density has large effects on genetic diversity. These effects can be grouped into three distinct regimes. When density dependence is positive and large—such as when growth and migration are highly cooperative, for example—the time scale over which diversity is lost scales linearly with the carrying capacity. This is the scaling expected from the Kingman coalescent and is consistent with the serial bottlenecks view. However, when cooperation is reduced, large fluctuations in density at the front tip lead to sublinear scaling, as would be expected if multiple mergers were present in the genealogies (ref. 7, section 3.2). Finally, when cooperation is absent, the time scale of diversity loss scales logarithmically with the carrying capacity, as would be expected from a population described by the Bolthausen–Sznitman coalescent (see section 3.2 of ref. 7 and references therein). These results lead to a natural hypothesis, that these changes in the rate of diversity loss are a result of changes in the underlying genealogies, driven by large fluctuations in the low-density region of the front.

In this paper, we elucidate the connection between population dynamics and genealogies during expansion. We focus on understanding the topology of genealogies in the well-mixed region close to the front of the expansion (Fig. 1 C and D). Using simulations, we obtain genealogical trees and examine how they change as growth dynamics vary. We indeed find that changes in growth cooperativity lead to a transition from the Kingman to a non-Kingman coalescent with multiple mergers. The fluctuations in the position and shape of the expansion front are crucial to these results because we observe that artificially suppressing fluctuations leads to large changes in the structure of the genealogies.

To explain our findings, we developed an effective model of the expansion front using analytical arguments. We showed that the front can be treated as a well-mixed population with a broad distribution of number of offspring (reproductive values). The tail of the distribution follows a power law with an exponent that depends only on the ratio of the expansion velocity and the geometric mean of the growth and dispersal rates at low population densities. The topology of the genealogies is described by a $\mathrm{\Lambda }$-coalescent and is, in turn, determined by the exponent (20–22). Thus, the distribution of merger sizes in the genealogies of expanding populations is dependent on the growth dynamics.

Simulation Results

Expansion Model.

We simulated a population expansion using a setup similar to the classic stepping stone model (46). Specifically, we consider a one-dimensional landscape of demes (patches). For computational efficiency, we use a simulation box of $L=300$ demes, which moves with the expansion front such that the box is approximately half-filled at all times. Each generation, individuals migrate between neighboring demes with probability $m/2$ and reproduce. The number of descendants is determined by the growth function that depends on the local population density (see Materials and Methods for details). On average, the population density increases to a maximum value set by the carrying capacity $N$. All individuals are resampled every generation, so demes that are at carrying capacity still experience genetic drift. As a result, the model reduces to a Wright–Fisher process in the bulk and a branching process with Poisson distributed number of offspring at the front. All simulations are initiated from a random configuration generated after a “burn-in” time of 1,000 generations starting from a half-filled box. In order to efficiently simulate the allele frequency distributions shown later (see Fig. 5) and in SI Appendix, Fig. S3, we use a simpler model in which the front comprises two identical but distinctly labeled subpopulations, as in refs. 44 and 45. After the initial burn-in time, the population in each deme is assigned from a binomial distribution with sample size $n_k$ and success probability 0.5, where $n_k$ is the population size in deme $k$ after the burn-in time.

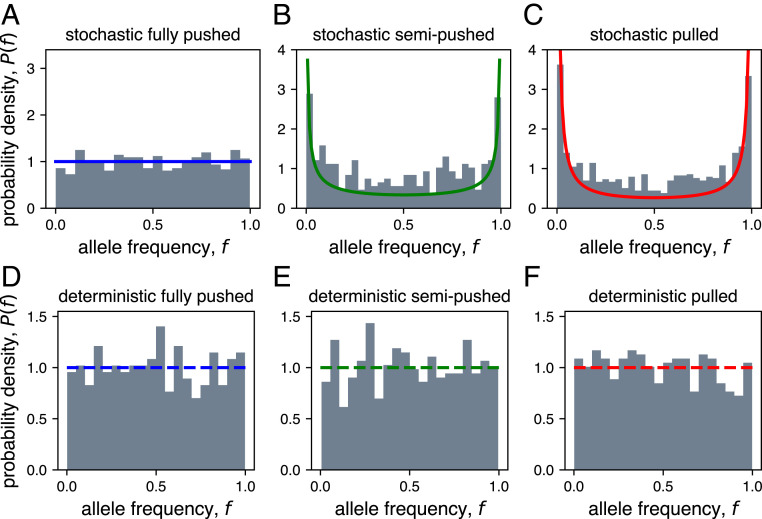
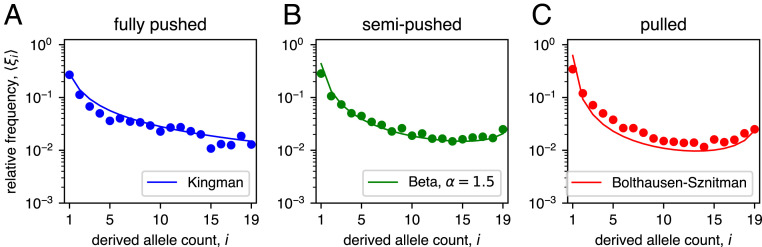
Fig. 5.

Deterministic front approximation fails to capture full range of coalescent topologies. (A–C) Long-time distribution of the frequency of one allele in stochastic two-allele simulations for each expansion type. Histogram of allele frequencies are shown in gray, and the theoretical predictions assuming the (A) Kingman (blue), (B) Beta- (green), and (C) Bolthausen–Sznitman (red) coalescents are shown with solid lines. (D–F) Same as above, but for simulations with a deterministic front. The dashed lines show the theoretical prediction from the Kingman coalescent, for comparison. For each panel, we ran $10^3$ simulations and report the distribution of allele frequencies at a fixed time after the distribution becomes quasi-stationary.

Spatial Self-Averaging.

Range expansions are inherently heterogeneous in time and space. Therefore, ancestral relationships can, in general, depend on the times and locations of samples from the population. Consider two extreme sampling scenarios of either sampling individuals uniformly from the colonized range (Fig. 1A) or sampling all individuals from the front (Fig. 1C). In both cases, coalescent events primarily occur when ancestral lineages are at the front, because genetic drift in the population bulk is much weaker. When two samples are taken from distant spatial locations, their lineages need to “wait” until both are at the front. Viewed backward in time, this occurs when the front recedes past the left-most lineage (Fig. 1 A and B). Thus, in this sampling protocol, the shape of the genealogical tree explicitly depends on the spatial separation between the sampling locations. In contrast, there is no position dependence when all individuals are sampled at the front, because all lineages start merging at the same time (Fig. 1 C and D). Here, we focus exclusively on the second regime and leave the characterization of the first regime and the transition region between them as topics for future research.

Previous work suggests that, over long time scales, lineages sampled at the front can be viewed as if they are part of a well-mixed population, comoving with the front (44, 47). For this approximation to be valid, the time necessary for the front to become well mixed, ${\tau }_m$, must be shorter than the coalescence time (see also SI Appendix, section 1 for the precise definition of ${\tau }_m$). In other words, we require a separation of time scales between mixing and coalescence at the front.

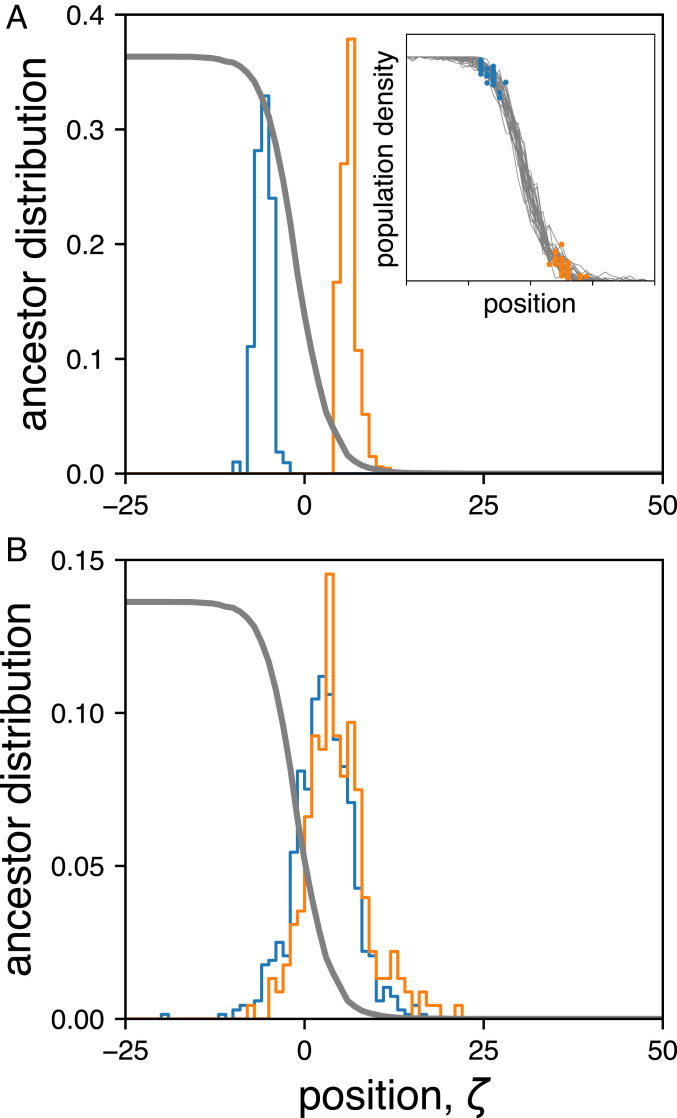
To test whether the mixing time ${\tau }_m$ is indeed much shorter than the coalescence time, we tracked the spatial distribution of ancestors of individuals at the front. Specifically, we performed 30 independent simulations and sampled individuals from two spatial locations, one closer to the front and the other closer to the bulk. The two sampling locations are shown in Fig. 2A, Inset (blue and orange dots) together with the final front (gray line) for each run. The main panels show the distribution of ancestors of individuals from the two sampling locations shortly after the sampling time (Fig. 2A), and at a time close to ${\tau }_m$ (Fig. 2B). Importantly, we found that the time necessary for the ancestor distributions to become independent of sampling location was much shorter than the time to reach the common ancestor for the whole front. For example, from Fig. 2B, we estimated ${\tau }_m\approx 10^2$ generations, compared to $T_c\approx 10^3$. These results show that the sampling positions do not affect genealogies, and, therefore, the lineages can be considered exchangeable, which is a key requirement for describing them using the coalescent theory.

Fig. 2.

Genetic processes in spatially expanding populations are effectively well mixed on time scales larger than the mixing time of the front. (A) The distribution of initial locations from which the ancestor position was tracked backward in time. Due to the stochastic nature of the front, the distribution of sampling locations has a finite width with respect to the average front profile shown in gray. (Inset) The final front from 30 independent runs used to generate histograms in A. For each run, two subpopulations were chosen, one close to the bulk (blue) and another close to the edge of the front (orange), and the locations of their ancestors were recorded at different times in the past (see SI Appendix, section 5 for exact sampling procedure). (B) Distribution of locations of ancestors of individuals shown in A from 100 generations in the past.

Structure of Genealogies.

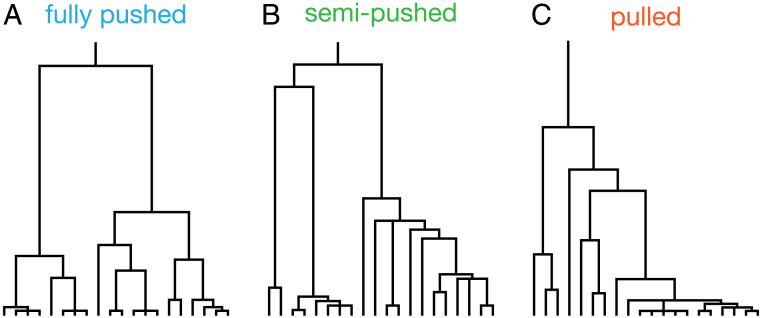
We performed simulations using three levels of cooperativity that are expected to lead to qualitative differences in the genealogies because they correspond to pulled, semi-pushed, and fully pushed expansions (44). The genealogy of the population was obtained using the procedure described in Materials and Methods. The examples of these genealogies shown in Fig. 3 have the qualitative features predicted by the theory. In fully pushed expansions, genealogies have only pairwise mergers, whereas semi-pushed and pulled expansions show several examples of multiple mergers. Moreover, the genealogies in pulled expansions appear highly skewed, with most mergers occurring on one side of the tree, while, in fully pushed expansions, branching is more symmetric. These features are consistent with our hypothesis that cooperativity drives the transition from the Bolthausen–Sznitman to the Kingman coalescent.

Fig. 3.

The genealogical tree of spatially expanding populations changes as the expansion transitions from pulled to pushed. Sample genealogies from (A) fully pushed, (B) semipushed, and (C) pulled expansions are shown. These trees were generated by randomly sampling 20 individuals from the first 15 occupied demes from the front, after fixation. For illustration purposes, we chose representative trees from our simulations that provided good visual clarity.

To get a more quantitative measure of the changes in topology of the genealogies during expansion, we calculated two summary statistics that can distinguish between coalescents: the site frequency spectrum (SFS), and the two-site frequency spectrum (2-SFS) (48, 49).^† We found that both SFS and 2-SFS supported our hypothesis that genealogies change from the Kingman to a non-Kingman coalescent at the transition between fully pushed and semi-pushed expansions. Because it is simpler to quantitatively test the SFS against the theoretical predictions, we report these results here and refer the interested reader to SI Appendix, section 3 for the analysis of the 2-SFS.

The SFS provides a histogram of the number of sites in the genome that have a given frequency of mutations in the sample. Assuming mutation rates are constant throughout the genome, the expected SFS is given by the length of branches with a given number of terminal nodes (leaves) (7, 52). We are particularly interested in the shape of the SFS for high-frequency mutations (allele frequencies $f\approx 1$), because the SFS is qualitatively different between the Kingman and the Bolthausen–Sznitman coalescent in this regime.

High-frequency mutations occur on internal branches that have a large number of leaves. Genealogies with such mutations are highly skewed because one branch can contain the majority of leaves. Skewed trees are unlikely in the Kingman coalescent because each pairwise merger joins lineages randomly, independent of the number of their leaves. Thus SFS monotonically decays with the mutant frequency. In contrast, SFS for the Bolthausen–Sznitman coalescent is expected to have an uptick at high $f$, related to a significant probability that nearly all lineages coalesce in a single merger. Consistent with our hypothesis, we indeed find a monotonic SFS for fully pushed expansions (Fig. 4A), while semipushed and pulled expansions display the uptick at high allele counts characteristic of coalescents with multiple mergers (Fig. 4 B and C). Moreover, both fully pushed and semipushed expansion SFS agree quantitatively with the predictions from the Kingman coalescent and the Beta-coalescent, respectively (see SI Appendix, section 3 for details). In the case of pulled expansions, we find the quantitative agreement is less good, which we believe is due to the very long relaxation times required to reach steady state in the pulled regime (see SI Appendix, section 2). Nevertheless, taken together, these results clearly establish that the genealogies of the three expansion classes have distinct topologies.

Fig. 4.

The SFS of genealogies reveals differences between pulled and pushed waves. Approximately 100 trees were recorded from simulations of (A) fully pushed, (B) semipushed, and (C) pulled expansions. Each full genealogy was sampled 10 times using a sample size of 20 individuals chosen from the front (see SI Appendix, section 5 for sampling procedure). The resulting SFS, averaged over samples and simulations, is shown with colored dots. The solid line shows the exact predictions for the SFS in each regime (see SI Appendix, section 5 for details).

Theoretical Results

Descendant Distribution in Stochastic Fronts.

To develop an intuitive understanding of how genealogies emerge in range expansions, we developed a theoretical framework based on continuous reaction−diffusion equations. In this framework, it is easier to examine the dynamics of clones forward in time and relate the expansion of these clones to mergers in the genealogy. Previous work has shown that the frequency of a subpopulation $f_i\left(t,\zeta \right)$ within the front changes according to the following equation (44, 47):

$$\frac{\partial f_i}{\partial t}=D\frac{{\partial }^2{f}_i}{\partial {\zeta }^2}+\left[v+2D\frac{\partial \ln n}{\partial \zeta }\right]\frac{\partial f_i}{\partial \zeta },$$ [1]

where $D$ is the effective diffusion constant which describes the migration of individuals, $v$ is the velocity of the front, $n\left(\zeta \right)$ is the population density, and $\zeta =x-vt$ is the position along the front in the comoving reference frame.

From Eq. 1, we can calculate the fraction of the population descended from a single individual at some position ${\zeta }_0$ as $t\to \infty$. In SI Appendix, section 1, we show that $f_i\left(t,\zeta \right)=\text{const}.$ after some time $O\left({\tau }_m\right)$. To quantify the reproductive success of an individual initially located at ${\zeta }_0$, we define the reproductive value $u\left({\zeta }_0\right)$ which is equal to the limit as $t\to \infty$ of $f_i\left(t,\zeta \right)$.^‡ This result also provides a mathematical definition of the mixing time ${\tau }_m$ which we introduced in Simulation Results. On time scales longer than ${\tau }_m$, the distribution of surviving clones $f_i\left(t,\zeta \right)$ loses all spatial information, and $u\left({\zeta }_0\right)$ is simply the fraction of individuals in the population descended from an ancestor located at ${\zeta }_0$.

Because $u$ varies strongly with ${\zeta }_0$, individuals from different locations can have wildly different numbers of descendants. When coarse grained over the mixing time, the initial spatial dependence of $u$ gives rise to a distribution of reproductive values in the effectively well-mixed population at the front. We calculate this distribution in SI Appendix, section 1 and show that it has a power law tail of the form

$$P\left(u\right)\sim u^{-2-\alpha }.$$ [2]

The Origin of Different Topologies.

The exponent $\alpha$ is calculated exactly and depends only on $v/v_F$, the ratio between the actual expansion velocity and the velocity of the corresponding FKPP equation $v_F=2\sqrt{r_{0}D}$, that would occur in the absence of positive feedback,

$$\alpha =\frac{2\sqrt{1-v_F^2/v^2}}{1-\sqrt{1-v_F^2/v^2}}.$$ [3]

Note that the specific form of the density dependence in the growth and dispersal rates does not enter Eq. 3. In fact, all of our analyses have been carried out for an arbitrary model with short-range dispersal. Thus, the tails of $P\left(u\right)$, and all of the properties of the genealogies derived from them, only depend on a single, easy-to-measure parameter (55).

For high cooperativity, when $v/v_F$ is greater than a critical value ${\nu }_c=3/2\sqrt{2}$, the exponent $\alpha$ is greater than one, and the variance of $u$ is finite.^§ Therefore, the clone frequencies only change by small amounts each generation, and genealogies are described by the Kingman coalescent (56). For intermediate values of cooperativity, defined by $1<v/v_F<{\nu }_c$, the exponent $\alpha$ is less than one, and the variance of $P\left(u\right)$ diverges. This leads to occasional large jumps in clone frequencies and the appearance of multiple mergers in the coalescent (21). Finally, when $v/v_F=1$, we have $\alpha =0$ and $P\left(u\right)\sim u^{-2}$, which leads to a Bolthausen–Sznitman coalescent when the process is viewed backward in time (21, 57).

To verify the change in descendant distribution predicted by theory, we measured clone sizes during range expansions in simulations. Direct measurements of $P\left(u\right)$ are challenging because the distribution emerges only over a time scale of $O\left({\tau }_m\right)$, which we cannot determine precisely. However, we can circumvent this problem in two limits: on short time scales, on the order of a few multiples of ${\tau }_m$, and, on long time scales, when the population comprises two clones. In the first limit, we can consider all individuals at the front at some initial time as clones of size one. As the front expands, some clones go extinct while others increase in size. For short time scales (comparable to ${\tau }_m$), clone sizes are small, and each can be modeled as an independent branching process. In the second limit, we can track the dynamics of a population with only two clones—which we can think of as two alleles. As both alleles are neutral, the dynamics can be described by the frequency of one of them, which can be derived from the more general $\mathrm{\Lambda }$-Fleming−Viot process (57, 58).

The branching process calculation makes two testable predictions about the clone size distributions.^¶ First, the average size of a surviving clone increases as $t^{1/\alpha }$. Second, the probability $1-F\left(s\right)$ to observe a clone $\mathrm{s}$ times larger than the average clone decays as $e^{-s}$ for $P\left(u\right)$ with a finite variance and as $s^{-1-\alpha }$ when $\alpha <1$. In SI Appendix, we show that the results of simulations for fully pushed expansions agree well with these predictions (SI Appendix, Fig. S4). Outside of the fully pushed regime, we see a broadening in the clone size distribution which is inconsistent with the exponential prediction for a short-tailed descendant distribution (SI Appendix, Fig. S4). However, due to the large carrying capacities required to allow for the relaxation of the transient dynamics in the semipushed and pulled regimes, we were not able to quantitatively verify the expected power law for $1-F\left(s\right)$.

The forward-in-time simulations of a population with just two genotypes were more efficient and allowed us to demonstrate a quantitative agreement with our theoretical predictions. Specifically, we started forward-in-time simulations with two clones of equal abundance and monitored the frequency $f$ of one of the clones (see Expansion Model for details). Conditioned on having both clones present, the probability $P\left(f\right)df$ of observing a clone frequency between $f$ and $f+df$ approaches a steady state in simulations and can also be computed analytically. In simulations, the conditioning on both clones being present simply amounts to discarding from the analysis simulations in which $f=0$ or $f=1$ at the time of observation. The distributions can then be compared to the theoretical predictions: a uniform distribution on the interval $\left(\mathrm{0,1}\right)$ for the Kingman coalescent (61), and $P\left(f\right)\propto 1/f\left(1-f\right)$ for the Bolthausen–Sznitman coalescent. Our simulations match both of these predictions quantitatively (Fig. 5 A–C).^#

The Role of Fluctuations in Population Density at the Front.

All of our results so far explicitly account for demographic fluctuations at the front. However, most studies of range expansions have ignored demographic fluctuations, either because of the mathematical difficulties they introduce or because their effects were thought to be small (32, 62, 63). To understand to what extent density fluctuations influence the dynamics at the front, we performed simulations in which the total population density was updated deterministically, while still allowing for genetic drift by stochastically sampling the front composition (SI Appendix, section 4). These simulations behaved as if they are described by the Kingman coalescent for both pulled and pushed fronts (Fig. 5 D–F).

While the previous result may appear surprising, it can be explained by considering the effect of deterministic population dynamics on the descendant distribution at the front. In Materials and Methods, we show that the deterministic approximation leads to a cutoff in $P\left(u\right)$ at a value $u_c$ that goes to zero as $N$ becomes very large (see SI Appendix, section 1). This implies that the fraction of lineages which can merge in one event in the limit of large $N$ goes to zero. The suppression of large merger events leads to the flat allele frequency distribution we observe in simulations, but more work is needed to establish whether the genealogies converge to the standard Kingman coalescent (see Discussion). Nevertheless, these results clearly demonstrate that demographic fluctuations play a crucial role in the emergence of non-Kingman coalescents at the front.

Discussion

Many species, from microbes (64, 65) to humans (23), have undergone expansions in their history, and many others are currently expanding due to globalization (66, 67) and climate change (27, 68). Previous work has demonstrated that range expansions reduce the amount of genetic diversity in the population (32, 62, 69, 70) and allow for some alleles to become dominant, through a process known as gene surfing (47, 63, 71). However, underneath the overall decrease in diversity, many patterns can be found which are still not well understood.

Evolutionary dynamics during range expansions vary greatly depending on how much demographic fluctuations and genetic drift at the leading edge influence future generations (44). The dependence is captured by a single dynamical parameter, $v/v_F$. This ratio between the actual expansion velocity and the velocity that would occur without density dependence quantifies the degree of cooperativity (or positive feedback) in growth and dispersal. When this parameter is large, the front makes a small contribution to the rate of expansion, and allele frequencies change slowly. When $v/v_F$ is close to one, expansion proceeds primarily via a highly stochastic advancement of the population edge.

We showed that these differences in evolutionary dynamics are captured by a simple and intuitive model, which describes the front as an effective well-mixed population with broad distribution of reproductive values. As $v/v_F$ decreases, the distribution becomes broader until, at a critical value, the variance diverges—this signals the transition from the Kingman to a non-Kingman coalescent. In this intermediate regime, the distribution has the form of a power law with exponent between $-2$ and $-3$, which is known to lead to a Beta-coalescent (21). As $v/v_F$ decreases further, the distribution broadens until a Bolthausen–Sznitman coalescent is reached.

Density fluctuations are essential for all of our results. When these fluctuations are artificially suppressed, the structure of the genealogical tree is strongly perturbed, leading to a large change in the shape of the allele frequency distribution. Prior studies attempted to capture the effects of demographic fluctuations by setting the growth rate to zero at low population densities, specifically, when $n\left(\zeta \right)<1$ (72). Such a cutoff is similar to the one we used for deterministic fronts, but it does not capture large fluctuations at the leading edge, which can result in sites being temporarily occupied in the region where the deterministic density is below one (40, 73). Recently, it was discovered that, in semi-pushed and fully pushed expansions, these stochastic effects can be captured by a different cutoff, that explicitly depends on $v/v_F$ (44). There, quantitative changes in the rate of diversity loss were found when the wrong cutoff was used. Here, we found the choice of cutoff leads to qualitative changes in the genealogies. Thus, any theory that aims to predict or characterize genetic changes during range expansions needs to account for fluctuations in the position and shape of the front.

Throughout our analysis, we have made several simplifying assumptions whose effect on our results could provide interesting directions for future work. Here, we focused exclusively on models with positive growth rate—equivalent to a weak Allee effect in ecology. Other types of growth functions are, of course, possible, including cases with a strong Allee effect in which growth rates are negative at low densities. Such growth models have been extensively studied in many organisms (74–76). However, it is important to note that our derivation of the distribution of reproductive values does not make any assumptions about the shape of the growth function. This leads us to conjecture that all one-dimensional expansions with short-ranged dispersal fall into one of the three classes described here, with their corresponding coalescents. In the case of strong Allee effect, this suggests genealogies are always described by the Kingman coalescent, for which there is already very good supporting evidence in addition to the results presented here. Namely, analytical calculations confirmed by numerical simulations show that the coalescence time scales linearly with $N$ for all expansions with a strong Allee effect, as expected if their genealogies follow the Kingman coalescent (44). In addition, a rigorous proof that expansions with strong Allee effect are described by the Kingman coalescent was established in ref. 37 using a specific form of the growth function. Taken together, we believe these results provide strong evidence that the coalescent structures presented here describe a wide class of expansion models.

Another interesting topic for future study is the nature of the coalescent in deterministic semipushed and pulled fronts. In SI Appendix, we show that the deterministic cutoff leads to a maximum reproductive value at the front $u_c$, which corresponds to a maximum fraction of lineages that can coalesce within a generation. This maximum goes to zero as $N$ goes to infinity, which explains the large difference we saw in the shape of the allele frequency distribution between stochastic and deterministic fronts (Fig. 5). However, we have previously shown that the coalescence time in deterministic fronts, while different from those of stochastic fronts, still scales as a sublinear power law and logarithmically with $N$ in semi-pushed and pulled fronts, respectively (44). This unusual scaling is in sharp contrast to the linear increase with $N$ found in most models described by the Kingman coalescent (7). It would be interesting to explore the origin of this scaling and determine whether it signifies some subtle changes in the genealogies compared to the standard Kingman coalescent. On time scales much shorter than the coalescence time, we certainly expect transient dynamics that differ from the predictions of classical neutral models, because the distribution of reproductive values still has a broad power law tail. In fact, we expect that Kingman-like dynamics emerge only for clones with frequencies sufficiently high to sample the offspring distribution near $u_c$. While we are not aware of any direct applications of deterministic front models, the genealogies that they produce might emerge in other contexts and therefore deserve further study (77–79).

Moving beyond our framework, one of the most important avenues for future research is to consider expansions in higher dimensions. The two-dimensional case is especially relevant for most expansions on land (23, 76), but also for marine populations living close to the ocean surface (80). In addition, other effects such as environmental noise or the inclusion of nonneutral mutations could have a large impact on the structure of genealogies in natural populations (81–83).

Our results provide a framework to link genetic diversity at the front to ecological dynamics. This framework can be used to infer the importance of density feedback in growth and dispersal or to predict evolution during range expansions. Furthermore, our work provides a generic explanation for the skewed genealogies observed in empirical studies (11, 84). Previously, such genealogies were attributed to either very strong selection or sweepstakes reproduction, both of which could be less common than range expansions. The complete theory of skewed genealogies would, of course, require an integration of these different mechanisms, which could act simultaneously in natural populations.

Materials and Methods

The detailed implementation of the sampling of descendants can be found in SI Appendix, section 4. For our purposes here, the change in the local population size $n_k$ can be represented by a growth function $r\left(n_k\right)$, given by the following expression:

$$r\left(n_k\right)=r_0\left(1-n_k/N\right)\left(1+B{n}_k/N\right),$$ [4]

where $k$ is the deme index and $r_0$ is the growth rate at zero density. For convenience, we set the generation time to one and omit it from future expressions. The parameter $B$ in Eq. 4 sets the growth cooperativity in the population. For $B=0$, Eq. 4 is the widely used logistic growth function (85, 86), which has the maximum growth rate $r\left(n_k\right)=r_0$ at $n_k=0$. For $B>1$, the position of the maximum shifts to $n_k>0$, and $r\left(n_k\right)$ becomes larger as $B$ increases. We showed previously that $B$ in Eq. 4 controls the scaling between the carrying capacity $N$ and the effective population size of the front $N_e$, which we define as the time scale over which genetic diversity is lost. This dependence of $N_e$ on $N$ changes from a linear function for $B\ge 4$ to a power law for $2<B<4$, and then to ${\ln }^{3}N$ for $B<2$ (44); we refer to the three expansion classes as fully pushed, semipushed, and pulled, respectively (44, 45). This terminology reflects the fact that growth in pulled expansions occurs mainly at the edge of the front, while, in semipushed and fully pushed expansions, it is in the bulk. We performed simulations with one value of $B$ for each regime: $B=10$ for fully pushed expansions, $B=3.33$ for semipushed expansions, and $B=0$ for pulled expansions. Although our simulations are based on the specific growth and migration model detailed above, our theoretical results are model independent (see SI Appendix, section 1). Therefore, we do not expect any of our conclusions to change if different growth or migration models are used.

Genealogies can be obtained by storing all ancestral relationships. This approach, however, would severely constrain the population size and duration of our simulations. Instead, we keep track of genealogies by periodically assigning a unique label to every individual in the population. After assignment, the size of surviving clones—defined as a group of individuals with the same label—increases, while other clones become extinct. After a fixed number of generations, $\mathrm{\Delta }t$, we relabel all individuals and store their previous labels. One can then trace the ancestry backward in time with temporal resolution $\mathrm{\Delta }t$. As long as $\mathrm{\Delta }t$ is not too large compared to the generation time, and the maximum clone size is small compared to the total population size, this procedure introduces only minor information losses in the genealogies for sample sizes much smaller than the carrying capacity.

Descendant Distribution in Deterministic Fronts.

Without demographic fluctuations, the front profile $n_d\left(\zeta \right)$ assumes a steady-state solution with a cutoff in the density determined by $n_d\left({\zeta }_c\right)=1$, since the number of individuals cannot be less than one. Thus, for values of $\zeta >{\zeta }_c$, the population density is zero. This density cutoff implies a maximum reproductive value $u_c$, which can be calculated as discussed in SI Appendix, section 1.^∥Viewed backward in time, $u_c$ is the maximum fraction of lineages that can merge at the same time. We find that $u_c\to 0$ in the limit of large $N$ (SI Appendix, section 1). Hence, large multiple mergers become increasingly rare as $N$ increases.

Data Availability

The results presented in this manuscript are purely theoretical and there are no data associated with it. The scripts and simulation results used to generated the figures in the main text and the SI Appendix have been deposited to GitHub (https://github.com/gbirzu/range_expansion_coalescent).