Abstract
Light-sheet fluorescence microscopy (LSFM) is a minimally invasive and high throughput imaging technique ideal for capturing large volumes of tissue with sub-cellular resolution. A fundamental requirement for LSFM is a seamless overlap of the light-sheet that excites a selective plane in the specimen, with the focal plane of the objective lens. However, spatial heterogeneity in the refractive index of the specimen often results in violation of this requirement when imaging deep in the tissue. To address this issue, autofocus methods are commonly used to refocus the focal plane of the objective-lens on the light-sheet. Yet, autofocus techniques are slow since they require capturing a stack of images and tend to fail in the presence of spherical aberrations that dominate volume imaging. To address these issues, we present a deep learning-based autofocus framework that can estimate the position of the objective-lens focal plane relative to the light-sheet, based on two defocused images. This approach outperforms or provides comparable results with the best traditional autofocus method on small and large image patches respectively. When the trained network is integrated with a custom-built LSFM, a certainty measure is used to further refine the network’s prediction. The network performance is demonstrated in real-time on cleared genetically labeled mouse forebrain and pig cochleae samples. Our study provides a framework that could improve light-sheet microscopy and its application toward imaging large 3D specimens with high spatial resolution.
1. Introduction
Imaging intact specimens and their complex three-dimensional (3D) structure has provided invaluable insights and discoveries in the life science community [1–5]. Among the 3D optical imaging modalities, light-sheet fluorescence microscopy (LSFM) is a powerful technique for imaging biological specimens at high spatial and temporal resolutions. Key to this success is LSFM’s capacity to balance the trade-off between speed and optical sectioning [2,6–9]. Combined with recently developed tissue clearing techniques that allow for rendering the tissue transparent [10–14], LSFM is capable of imaging thick tissues or even entire organs with sub-cellular resolution at all depths [15–20].
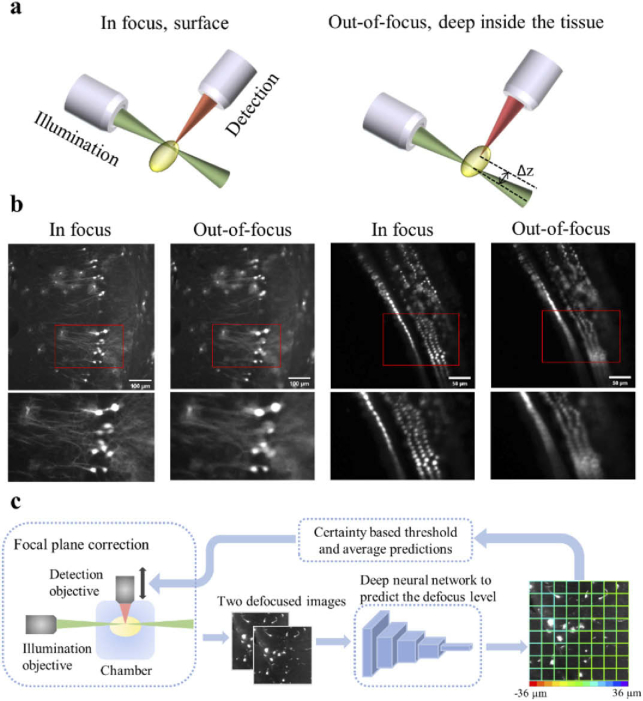
The working principle for LSFM is to generate a thin layer of illumination (a light-sheet) to excite the fluorophores in a selective plane of the prepared sample (Fig. 1(a)), while detecting the emitted signals using an orthogonal detection path [7,21]. This unique and orthogonal excitation-detection scheme makes the LSFM fast and non-destructive but also dictates a strict requirement: the thin sheet of excitation light needs to overlap with the focal plane of the objective lens. Any deviation from this requirement severely degrades the LSFM image quality and resolution (Fig. 1(b)). However, this restriction is often violated when imaging deep within cleared tissues due to the specimen’s structure and composition. The heterogeneous composition of tissues often leads to refractive index (RI) mismatches that cause: (i) spherical aberrations, and (ii) minute changes in the objective lens focal plane distance [22]. Consequently, the relative position of the light-sheet and the objective focal plane (Δz) constantly shifts in volume imaging, and in our implementation, the detection objective often needs to be translated to compensate for this shift.
Fig. 1.
A schematic of the light-sheet excitation-detection module and the proposed deep neural network-based autofocus workflow. (a) An illustration of the geometry of light-sheet fluorescence microscopy (LSFM), and the drift in the relative position of the light-sheet and the focal plane of the detection objective (Δz), when imaging deep into the tissue. (b) Fluorescence images of in focus and out-of-focus neurons (left) and hair cells (right). The images were captured from a whole mouse brain and a pig cochlea that were tissue cleared for 3D volume imaging. The red boxes mark the locations of the zoom-in images at the bottom. The degradation in the quality of out-of-focus images can be observed. (c) Overview of the integration of the deep learning-based autofocus method with a custom-built LSFM. During image acquisition, two defocused images will be collected and sent to a classification network to estimate the defocus level. The color of the borders of each individual patch in the right image indicates the predicted defocus distance. In the color bar, the red and purple colors represent the extreme cases, in which the defocus distance is −36 µm and 36 µm respectively. The borders’ dominant color is green, which indicates that this image is in focus.
Determining the best position of the objective lens that overlaps with the light-sheet to provide superior image quality can be accomplished by eye. However, this is highly time-consuming and laborious, especially in high throughput platforms that image large numbers of specimens. To solve this problem, autofocus methods have been implemented whereby the microscope captures a stack of images (10 - 20) at different defocus positions. Each image in the stack is then evaluated based on image quality measures, and the position that corresponds to the highest score is considered the in-focus position [23]. Previous studies have extensively evaluated the performance of image quality measures, and for LSFM, the Shannon entropy of the normalized discrete cosine transform (DCTS) shows superior results [5,24]. Nevertheless, the requirement to capture 10–20 images slows the acquisition process and can lead to photo-bleaching in sensitive samples. Additionally, the occurrence of spherical aberrations is more likely in tissue clearing applications, since they use a diverse range of immersion media (RI 1.38–1.58). In the presence of spherical aberrations, the performance of traditional image quality measures is degraded [25], however, even in this case DCTS still shows superior results (see Fig. S1).
Deep learning has recently been used to solve numerous computer vision problems (e.g., segmentation and classification) [26–28] and enhance the quality of biomedical images [29–34]. Several studies have used deep learning to perform autofocus, mostly on histopathology slides that were acquired by a bright field microscope and using a single frame [35–37]. Yang et al. proposed using a classification network to perform autofocus in thin fluorescence samples using a single shot, and their results outperformed traditional image metrics [33]. A certainty measure was also introduced to determine whether the viewed patch contains an object of interest or background. However, this approach remains to be extended to challenging 3D samples acquired using LSFM, which are dominated by aberrations, making them challenging for traditional autofocus measures.
Here, based on previous work on a custom-built LSFM design [11,13], we introduce a deep learning-based autofocus algorithm that uses two defocused images to improve image quality in acquisition (Fig. 1(c)). The use of multiple images accelerates the network’s training and provides results that are more accurate. We tested the effectiveness of our integrated framework using cleared whole mouse brain, pig cochlea, and lung samples. We show that our real-time autofocus framework performs well in thick cleared tissues with inherent scattering and spherical aberration that are difficult to solve using traditional autofocus methods.
2. Methods
2.1. Sample preparation
In this study, three wild-type (WT) pig cochleae samples were tissue cleared and labeled using a modified BoneClear protocol [13,38], while the one WT lung and three mouse brains were labeled using iDISCO protocol [39–41]. The cochleae samples were labeled using Myosin VIIa (CY3 as secondary), while the brain samples were labeled using GFP (Alexa Fluor 647 as secondary) and RFP (CY3 as secondary). The mice for the brain samples were generated using Mosaic Analysis with Double Markers chromosome 11 (MADM), which were previously described in [42–45]. All the animals were harvested under the regulation and approval of the Institutional Animal Care and Use Committee (IACUC) at North Carolina State University.
2.2. Image acquisition
Samples were imaged using a custom-built LSFM [13]. After tissue clearing, specimens were placed in an imaging chamber made from aluminum and filled with 100% dibenzyl-ether (DBE). Samples were mounted to a compact 4D stage (ASI; stage-4D-50), which incorporated three linear translation stages and a motorized rotating stage. The stage scanned the sample across the static light-sheet to acquire a 3D image. The light sheet was generated by a 561 nm laser beam (Coherent OBIS LS 561-50; FWHM = 8.5 µm) that was dithered at a high frequency (600 Hz) by an arbitrary function generator (Tektronix; AFG31022A) to create a virtual light-sheet. The detection objective lens (10×/numerical aperture (NA) 0.6, Olympus; XLPLN10XSVMP-2) was placed on a motorized linear translation stage (Newport; CONEX-TRB12CC with SMC100CC motion controller), which provides 12 mm travel range with ±0.75µm bi-directional repeatability.
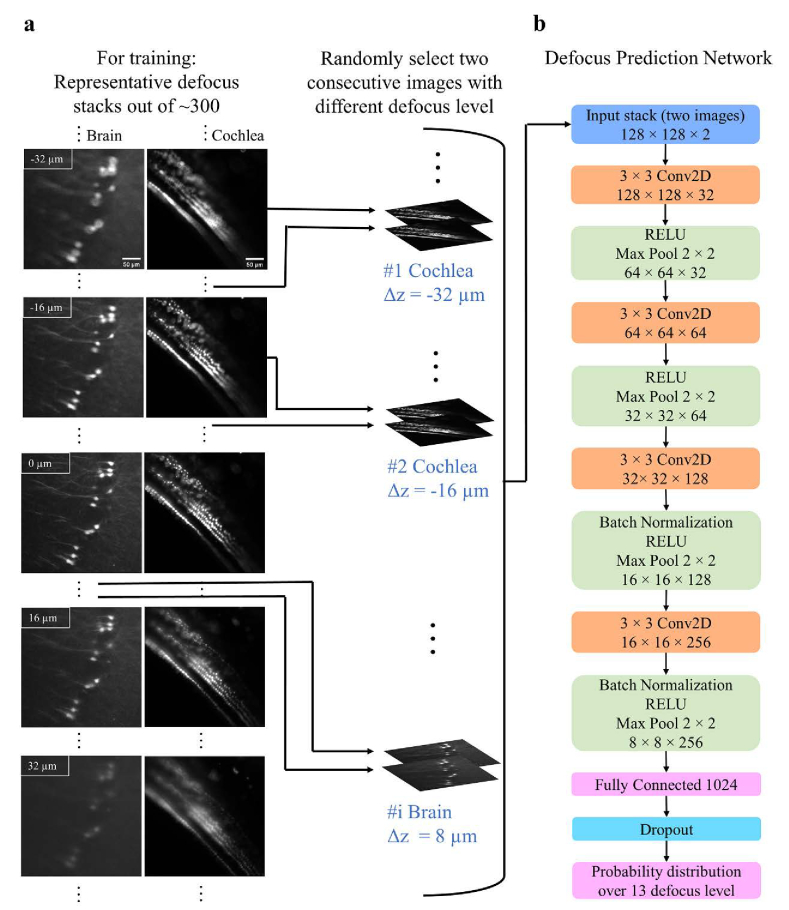
For every defocused image stack that was used in the training and testing stages (∼420 stacks), first, the objective lens was translated (CONEX-TRB12CC motor) by the user to find the optimal focal plane. Once the optimal position was found by eye, the control software automatically collected a stack of 51 defocused images with 2 µm spacing between consecutive images. The optimal focal point, which was determined by the microscope’s operator, was in the middle of the stack. All the stacks were acquired at random depths and spatial locations along the specimens, with a pixel size of 0.65 × 0.65 µm2, and 10 ms exposure time. Figure 2(a) shows representative defocused stacks that were used for the network’s training. From Fig. 2(a), we observed that images that were taken above and below the focal plane have distinct features i.e., asymmetrical point spread function (PSF), which suggested that the network could determine if Δz was negative or positive.
Fig. 2.
The training pipeline and the structure of the network. (a) Representative defocus stacks captured from tissue cleared whole mouse brains (first column) or intact cochleae (second column). In each stack, the distance between slices was 2 µm. From top to bottom we show representative images . Spherical aberrations lead to asymmetrical point spread function (PSF) for defocused images above (Δz > 0) and below (Δz < 0) the focal plane. The network uses this PSF asymmetry to estimate whether is positive or negative. In the training process, two defocused images with a constant distance between them and a known Δz are randomly selected from the stacks. The images are then randomly cropped into smaller image patches (128 × 128) and these patches are fed into the network. (b) The architecture of the network. The output of the network is a probability distribution function over N = 13 different values of with constant bin size , which equals 6 µm. The value for N was determined empirically.
2.3. Architecture of the network and its training process
The classification network’s architecture is presented in Fig. 2(b). The aim of the network was to classify an unseen image into one of 13 classes. Each class represented a different range of Δz, for instance: if the bin size (Δb) was equal to 6 µm, the in-focus class corresponded to Δz values in –3 to 3 µm range, and the classes center points had the values of −36, −30, −24, −18, −12, −6, 0, 6, 12, 18, 24, 30 and 36 µm. The network’s architecture was previously presented by [33]. Here, we modified the network to accept multiple defocused images as an input, instead of solely one image. To train the network, 421 defocused image stacks were acquired: 337, 42, and 42 datasets were dedicated for training, validation, and testing respectively. The network was implemented in Python 3.6 with PyTorch-1.4.0 Deep-Learning Library. The network was trained on an Nvidia Tesla V100-32GB GPU on Amazon Web Services for about ∼35 hours. The cross-entropy loss function was selected, the learning rate was 1e-5, and an Adam optimizer was used. Data augmentation techniques including normalization, saturation, random crop, horizontal and vertical flip were applied during the training process.
Figure 2(a) illustrates the network’s training process. Two defocused images with Δs spacing (e.g., Δs = 6 µm) and known defocus distance Δz were randomly selected from the defocused stack (IΔz and IΔz + Δs). Then a random region of interest (128 × 128 pixels) was selected and cropped from the two images. The two cropped image patches were fed into the network for training, while the known defocus distance Δz, served as the ground truth. The output of the model was a probability distribution {pi, i = 1, 2…N} over N = 13 classes (or defocus levels), and the predicted defocus level was the one with the highest probability. The spacing (Δb) between the classes (or defocus levels) in the output of the network was given by: . Please note that the number of defocused levels (N) was determined empirically, and it determined how fine the correction was. A larger number of N (e.g., N = 19 and Δb = 4 µm) could theoretically provide a better overlap between the objective focal plane and the light sheet. Nevertheless, in our case, it was difficult to observe big differences in image quality between two images that were separated by a distance smaller than 6 µm (Fig. S2). Therefore, Δb smaller than 6 µm would not necessarily provide better image quality after the correction. This was the case since as long as the objective focal plane was approximately within the light sheet full width half maximum (FWHM; on average ∼14 µm across the entire field of view) the image remained sharp.
2.4. Measure of certainty
A valuable measure to calculate from the probability distributions was the measure of certainty (cert), with the range of [0, 1]. Cert was calculated as follows [33,46]:
A low value of cert corresponded to a probability distribution which was similar to an equal distribution, which translated to low confidence in . Therefore, predictions with cert below 0.35 were discarded. In contrast, a high cert value, corresponded to the case where the network was more certain in its prediction, for example, when the maximum was much higher than the remaining probabilities.
2.5. Integration with a custom-built light-sheet microscopy
The control software and graphical user interface (GUI) of the LSFM were implemented in MATLAB R2019b environment. The MATLAB environment can integrate with a deep learning model, which was trained with Python. The graphical user interface was also written in MATLAB.
3. Results
3.1. Performance of the network with various input configurations
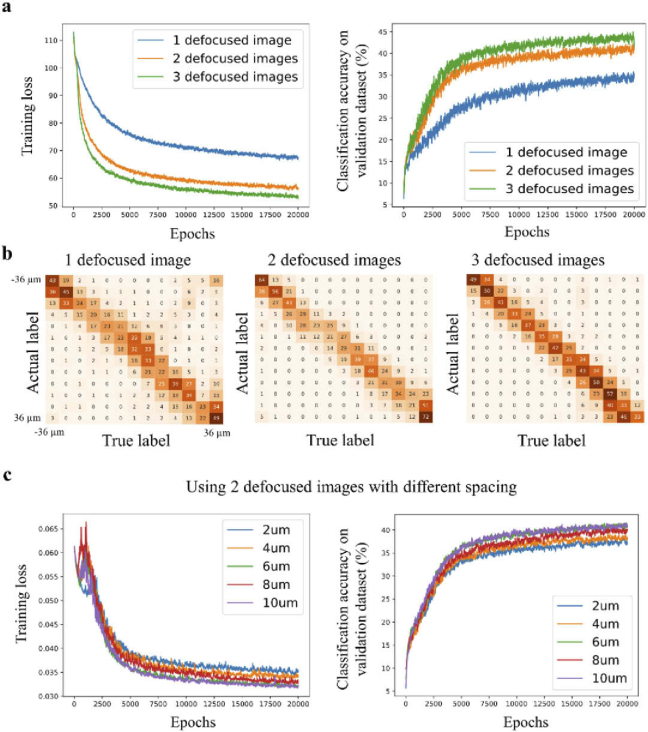
We investigated various training configurations and their influence on the network’s performance. First, we tested how the number of defocused images, which were fed into the deep neural network (DNN), influenced the classification accuracy (Fig. 3(a)). Figure 3(a) shows the training loss and the classification accuracy as the function of epochs for 1, 2, and 3 defocused images (blue, yellow, and green graphs respectively). In these experiments, the DNN output was a probability distribution over 13 classes (defocus levels) with various values ranging from −36 µm to 36 µm, with Δb = 6 µm, and Δs = 6 µm (see Methods section). We found that when the DNN received two or three defocused images as input, it performed better in terms of classification accuracy than using only one defocused image (Fig. 3(a)). The resulting confusion matrices of the three models, which were trained on 1, 2, and 3 defocused images, are shown in Fig. 3(b). When observing the confusion matrix for a single defocused image, we observed the following: (i) The distribution around the diagonal (upper left to bottom right) was not as tight as the other two confusion matrices, which was consistent with its low classification accuracy. (ii) The values on the second diagonal (upper right to bottom left) were higher in comparison with the two other confusion matrices. This observation indicated that the predicted was correct, but not the sign. To balance the tradeoff between the network’s performance and acquisition time of the additional defocused images, we decided to proceed with 2 defocused images rather than 3, although the DNN trained with 3 defocused images showed slightly higher classification accuracy.
Fig. 3.
Training configurations that influence the classification accuracy. (a) The graphs show the training loss and classification accuracy as a function of the number of epochs. For comparison, the network is trained with one\two\three defocused images that are provided to the network as an input (N = 13, Δs = 6 μm). The graphs show that two (IΔz and ) and three (, , and ) defocus images yield higher classification accuracy than a single defocused image . (b) Confusion matrices for a different number of defocused images that are provided to the network as input. Training with only one defocused stack shows inferior performance. (c) Training loss and classification accuracy as a function of the number of epochs using 2 defocused images as an input, but with variable spacing between the images. The highest classification accuracy corresponds to values of 6 and 10 μm.
Next, we tested the performance of the network with different values (2, 4, 6, 8, and 10 µm). Figure 3(c) shows the training loss and classification accuracy as a function of epochs (N = 13, and Δb = 6 µm). The graphs show that when equals 6 or 10 µm, the classification accuracy was higher in comparison to other values of . Therefore, was set to 6 µm henceforward.
3.2. DNN performs better or comparable to traditional autofocus quality measures
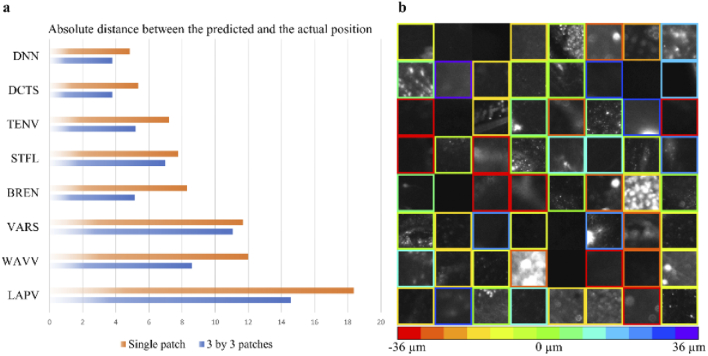
To determine the prediction accuracy of the proposed model, the model was compared with traditional autofocus methods (Fig. 4(a); 2 defocused images, Δs = Δb = 6 µm). For the test cases, image patches with a size of 83 × 83 µm2 (single patch) and 250 × 250 µm2 (3 by 3 patches) were randomly cropped from 42 defocus stacks, which were dedicated to testing. While the DNN used only two defocused images, the full defocused stack i.e., 13 images were provided to the traditional autofocus measures that included the following: Shannon entropy of the normalized discrete cosine transform (DCTS), Tenengrad variance (TENV), Steerable filters (STFL), Brenner’s measure (BREN), Variance of Wavelet coefficients (WAVV), image variance (VARS), and Variance of Laplacian (LAPV). The average absolute distance between and the ground truth was calculated to compare the DNN and traditional metrics. Please note, for the larger patches, was calculated based on the average result of 9 (3 by 3) patches with a predefined threshold on the certainty of 0.35, i.e., any tile with a certainty score below 0.35 is discarded from the average.
Fig. 4.
Performance evaluation. (a) Performance comparison between Deep Neural Network (DNN), and traditional autofocus measures across 420 test cases. While only 2 defocused images are provided to the DNN, the traditional autofocus methods receive as an input 13 images. In both cases, the spacing between two consecutive images is 6 µm. On a single image patch with a size of ∼83 × 83 µm2 the DNN outperforms traditional autofocus measures, while on larger image patches (250 × 250 µm2) the DNN and DCTS achieve comparable results. Please note that for the larger image patch the DNN performs its calculation on nine (83 × 83 µm2) patches, and results with certainty (cert) above 0.35 are averaged to achieve the final prediction. (b) Representative examples of defocus level prediction by the DNN on the test dataset (single patch). Each box shows an individual and independent image patch, and the color of the border indicates the value. If the certainty of an image patch is lower than 0.35, the colored border is deleted, and this patch is discarded.
For a single patch, the DNN and DCTS, which was the best of traditional methods, achieved an average distance error of 4.84 and 5.36 µm on the test dataset, respectively (Fig. 4(a)). When larger images (250 × 250 µm2) were tested, the DNN and DCTS achieved an average distance error of 3.80 and 3.80 µm, respectively. Our DNN model presented better or comparable results over the tested autofocus metrics and only required two images, whereas the other metrics required a full stack of images. Table S1 compares the performance of DNN and DCTS with various conditions such as providing the DCTS 9 (3 by 3) smaller patches and averaging the results with or without certainty. Overall, the DNN performed better or comparable under all conditions. Figure 4(b) shows representative single patches from the test set, and their values are indicated with a color-coded border. If the certainty was smaller than the threshold (0.35), the prediction was discarded, and the border was not presented. The inference time for a single patch on our modest computer (Intel Xeon W-2102 CPU 2.90GHz), which operated MATLAB was ∼0.18 sec.
3.3. Real-time integration of the deep learning-based autofocus method with LSFM
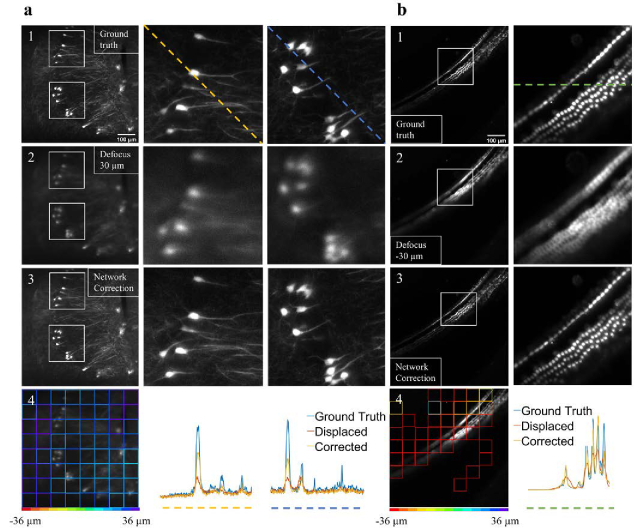
Based on the performance of the defocus prediction model, we decided to integrate the model with our custom-built LSFM. To test the model, we performed perturbation experiments on tissue cleared mouse brain (Fig. 5(a)) and cochlea (Fig. 5(b)). In the experiments, the objective lens was displaced by 30 and −30 µm for the brain and cochlea, respectively. Then, two defocused images were captured and fed into the trained model. In these real-time cases the network used 64 (8 by 8) patches per image, and the average was calculated as followed: . Where Δz1 and Δz2 were the two most abundant classes in the whole image, and S1 and S2 were the corresponding number of patches with the predicted label of Δz1 and Δz2, respectively. This approach removed outliners. The model’s values per patch are presented in Fig. 5(a4 and b4), and the corresponding averaged values were 26.9 and −35.3 µm for the brain and cochlea, respectively. According to the value of the averaged , the detection focal plane was adjusted. Figure 5(a3 and b3) show the improvement in image quality after the applied corrections. The color-coded line profiles in Fig. 5(a4 and b4) demonstrate the improved image quality. Additional examples are shown in Fig. S3.
Fig. 5.
Real-time perturbation experiments in light-sheet fluorescence microscopy. (a1 and b1) The in-focus images of neurons and hair cells, respectively. (a2 and b2) Images that show the same field of view as in a1 and b1 after the objective lens is displaced by 30 µm and −30 µm, respectively. (a3 and b3) Images of the same field of view after the objective is moved according to the network defocus evaluation as shown in a4 and b4. The improved image quality in a3 and b3 indicates that the network can estimate the defocus level and adjust the detection focal plane to improve image quality. In a and b, the white boxes mark the location of the zoom-in images, and the color-coded line profiles in a4 and b4 represent image intensities along the dashed lines in a and b.
3.4. Performance of the deep learning model on unseen tissue
Finally, to evaluate the deep learning model’s ability to generalize to other unseen tissue types, we used the same deep learning model on a mouse lung sample that was tissue cleared. By and large, the lungs exhibited different morphology than the brain and cochlea samples that the model was trained on. The lung’s tissue structure can be seen in Fig. 6(a and b). We performed again the real-time perturbation experiment, and the objective lens was translated by −30 and −20 in Fig. 6(a2 and b2), respectively. The model’s values per patch are presented in Fig. 6(a4 and b4), and the averaged values were −34.2 and −33.57 µm, respectively. We corrected the position of the objective based on the averaged values as seen in Fig. 6(a3 and b3). Although several patches in Fig. 6(b4) had questionable predictions, the overall image quality was improved after the network’s correction.
Fig. 6.
Real-time perturbation experiments on unseen tissue type. (a1 and b1) The in-focus auto-fluorescence images of tissue cleared mouse lung samples, which are highly scattering. These samples exhibit different morphology than the brain and the cochlea, and the network is not trained on such samples/morphology. (a2 and b2) Images that show the same field of view as in a1 and b1 after the objective lens is displaced by −30 µm and −20 µm, respectively. (a3 and b3) Images of the same field of view after the objective is moved according to the network correction as shown in a4 and b4. The improved image quality in a3 and b3 indicates that the network can correctly estimate the defocus level and adjust the detection focal plane to improve image quality. Although further refinement might be required, the network can still generalize to unseen tissue types. Please note, in tissue cleared lung samples the auto-fluorescence is easily photo-bleached therefore making it especially suitable for autofocus methods that require as few defocused images as possible.
4. Discussion and conclusion
Here, we build upon previous work on thin 2D slides that used DNN to measure image focus quality using a single frame [33]. We expand the use of the DNN to 3D samples, and we demonstrate the advantages of using two or three defocused images rather than a single image: First, the network performs better in terms of classification accuracy and convergence speed (Fig. 3(a)). Second, the network minimizes sign errors i.e., the DNN can determine whether the light-sheet is above or below the objective focal plane. Using two defocused images and after optimizing the spacing between them, we find that on small image patches (∼83 × 83 µm2) the network outperforms DCTS, which requires a full stack of defocused images (∼13 images). Therefore, using only two images can significantly increase imaging speed and reduce photo-bleaching in a sensitive sample (e.g., single-molecule fluorescence in-situ hybridization). On large image patches (∼250 × 250 µm2), the network provides comparable results to DCTS. Another advantage of the proposed method is that it inherently provides a measure of certainty in its prediction. Consequently, one can exclude image patches that may contain background or low contrast objects. In fact, when we exclude low certainty cases, we improve our accuracy (Table S1).
As a proof-of-concept experiment, the network is integrated with a custom-built LSFM. We demonstrate that the network performs reasonably well not only on tissue cleared mouse brain and cochlea but also on unseen tissue. The proposed approach can facilitate the effort to characterize large volumes of tissue in 3D, without a tedious and manual calibration stage that is performed by the user prior to imaging the sample.
A major limitation of the presented approach is the drop in its performance for unseen samples (specimen types that are outside the training set). This limitation is expected as new specimens likely exhibit unique morphologies and distinct features such as the lung samples in Fig. 6. There are several approaches to mitigate this challenge: (i) given that acquiring and labeling the dataset is relatively straightforward, one can train a network per specimen type. This approach is reasonable for experiments that require imaging many instances of the same specimen. (ii) Diversifying the training set with a plethora of specimens, and under multiple imaging conditions, such as multiple exposure levels. (iii) To synthesize data for the training set instead of physically capture it. This could be achieved by using publicly available 3D confocal microscopy datasets that do not require synchronization between the light-sheet and the objective focal plane. Then, from the confocal datasets, defocused images could be synthesized either by employing a physical model to defocus the image [47], or by utilizing generative adversarial networks (GAN). Utilizing GAN for data augmentation would allow to learn the LSFM distortion and synthesize artificial training sets [48,49].
Acknowledgments
The authors would like to thank Dr. Jorge Piedrahita and the NCSU Central Procedure Lab for their help with tissue collection.
Funding
Life Sciences Research Foundation10.13039/100009559; National Institutes of Health10.13039/100000002 (R01NS089795, R01NS098370).
Disclosures
The authors declare no conflicts of interest.
Data availability
The source code of training deep learning model in this paper is available at GitHub [50]. Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (1.6MB, pdf) for supporting content.
References
- 1.Ahrens M. B., Orger M. B., Robson D. N., Li J. M., Keller P. J., “Whole-brain functional imaging at cellular resolution using light-sheet microscopy,” Nat. Methods 10(5), 413–420 (2013). 10.1038/nmeth.2434 [DOI] [PubMed] [Google Scholar]
- 2.Royer L. A., Lemon W. C., Chhetri R. K., Keller P. J., “A practical guide to adaptive light-sheet microscopy,” Nat. Protoc. 13(11), 2462–2500 (2018). 10.1038/s41596-018-0043-4 [DOI] [PubMed] [Google Scholar]
- 3.Hillman E. M. C., Voleti V., Li W., Yu H., “Light-sheet microscopy in neuroscience,” Annu. Rev. Neurosci. 42(1), 295–313 (2019). 10.1146/annurev-neuro-070918-050357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weber M., Huisken J., “Light sheet microscopy for real-time developmental biology,” Curr. Opin. Genet. Dev. 21(5), 566–572 (2011). 10.1016/j.gde.2011.09.009 [DOI] [PubMed] [Google Scholar]
- 5.Royer L. A., Lemon W. C., Chhetri R. K., Wan Y., Coleman M., Myers E. W., Keller P. J., “Adaptive light-sheet microscopy for long-term, high-resolution imaging in living organisms,” Nat. Biotechnol. 34(12), 1267–1278 (2016). 10.1038/nbt.3708 [DOI] [PubMed] [Google Scholar]
- 6.Chen B. C., Legant W. R., Wang K., Shao L., Milkie D., Davidson M. W., Janetopoulous C. J.,“Lattice light-sheet microscopy: Imaging molecules to embryos at high spatiotemporal resolution,” Science 346, 1257998 (2014). 10.1126/science.1257998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Santi P. A., “Light sheet fluorescence microscopy: a review,” J Histochem Cytochem. 59(2), 129–138 (2011). 10.1369/0022155410394857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bouchard M. B., Voleti V., Mendes C. S., Lacefield C., Grueber W. B., Mann R. S., Bruno R. M., Hillman E. M. C., “Swept confocally-aligned planar excitation (SCAPE) microscopy for high-speed volumetric imaging of behaving organisms,” Nat. Photonics 9(2), 113–119 (2015). 10.1038/nphoton.2014.323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ryan D. P., Gould E. A., Seedorf G. J., Masihzadeh O., Abman S. H., Vijayaraghavan S., Macklin W. B., Restrepo D., Shepherd D. P., “Automatic and adaptive heterogeneous refractive index compensation for light-sheet microscopy,” Nat. Commun. 8(1), 612 (2017). 10.1038/s41467-017-00514-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ariel P., “A beginner’s guide to tissue clearing,” Int. J. Biochem. Cell Biol. 84, 35–39 (2017). 10.1016/j.biocel.2016.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Greenbaum A., Chan K. Y., Dobreva T., Brown D., Balani D. H., Boyce R., Kronenberg H. M., McBride H. J., Gradinaru V., “Bone CLARITY: clearing, imaging, and computational analysis of osteoprogenitors within intact bone marrow,” Sci. Transl. Med. 9(387), eaah6518 (2017). 10.1126/scitranslmed.aah6518 [DOI] [PubMed] [Google Scholar]
- 12.Ueda H. R., Ertürk A., Chung K., Gradinaru V., Chédotal A., Tomancak P., Keller P. J., “Tissue clearing and its applications in neuroscience,” Nat. Rev. Neurosci. 21(2), 61–79 (2020). 10.1038/s41583-019-0250-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Moatti A., Moatti A., Cai Y., Cai Y., Li C., Li C., Sattler T., Sattler T., Edwards L., Edwards L., Piedrahita J., Piedrahita J., Ligler F. S., Ligler F. S., Greenbaum A., Greenbaum A., Greenbaum A., “Three-dimensional imaging of intact porcine cochlea using tissue clearing and custom-built light-sheet microscopy,” Biomed. Opt. Express 11(11), 6181–6196 (2020). 10.1364/BOE.402991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ertürk A., Becker K., Jährling N., Mauch C. P., Hojer C. D., Egen J. G., Hellal F., Bradke F., Sheng M., Dodt H.-U., “Three-dimensional imaging of solvent-cleared organs using 3DISCO,” Nat. Protoc. 7(11), 1983–1995 (2012). 10.1038/nprot.2012.119 [DOI] [PubMed] [Google Scholar]
- 15.Chakraborty T., Driscoll M. K., Jeffery E., Murphy M. M., Roudot P., Chang B.-J., Vora S., Wong W. M., Nielson C. D., Zhang H., Zhemkov V., Hiremath C., De La Cruz E. D., Yating Y., Bezprozvanny I., Zhao H., Tomer R., Heintzmann R., Meeks J. P., Marciano D. K., Morrison S. J., Danuser G., Dean K. M., Fiolka R., “Light-sheet microscopy of cleared tissues with isotropic, subcellular resolution,” Nat. Methods 16(11), 1109–1113 (2019). 10.1038/s41592-019-0615-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fu Q., Martin B. L., Matus D. Q., Gao L., “Imaging multicellular specimens with real-time optimized tiling light-sheet selective plane illumination microscopy,” Nat. Commun. 7(1), 11088 (2016). 10.1038/ncomms11088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wan Y., McDole K., Keller P. J., “Light-sheet microscopy and its potential for understanding developmental processes,” Annu. Rev. Cell Dev. Biol. 35(1), 655–681 (2019). 10.1146/annurev-cellbio-100818-125311 [DOI] [PubMed] [Google Scholar]
- 18.Huang Z., Gu P., Kuang D., Mi P., Feng X., “Dynamic imaging of zebrafish heart with multi-planar light sheet microscopy,” J. Biophotonics 14, e202000466 (2021). 10.1002/jbio.202000466 [DOI] [PubMed] [Google Scholar]
- 19.Vladimirov N., Mu Y., Kawashima T., Bennett D. V., Yang C.-T., Looger L. L., Keller P. J., Freeman J., Ahrens M. B., “Light-sheet functional imaging in fictively behaving zebrafish,” Nat. Methods 11(9), 883–884 (2014). 10.1038/nmeth.3040 [DOI] [PubMed] [Google Scholar]
- 20.Singh J. N., Nowlin T. M., Seedorf G. J., Abman S. H., Shepherd D. P., “Quantifying three-dimensional rodent retina vascular development using optical tissue clearing and light-sheet microscopy,” J. Biomed. Opt. 22(07), 1 (2017). 10.1117/1.JBO.22.7.076011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Keller P. J., Dodt H.-U., “Light sheet microscopy of living or cleared specimens,” Curr. Opin. Neurobiol. 22(1), 138–143 (2012). 10.1016/j.conb.2011.08.003 [DOI] [PubMed] [Google Scholar]
- 22.Tomer R., Lovett-Barron M., Kauvar I., Andalman A., Burns V. M., Sankaran S., Grosenick L., Broxton M., Yang S., Deisseroth K., “SPED light sheet microscopy: fast mapping of biological system structure and function,” Cell 163(7), 1796–1806 (2015). 10.1016/j.cell.2015.11.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Silvestri L., Müllenbroich M. C., Costantini I., Giovanna A. P. D., Sacconi L., Pavone F. S., “RAPID: Real-time image-based autofocus for all wide-field optical microscopy systems,” bioRxiv 170555 (2017).
- 24.Bray M.-A., Fraser A. N., Hasaka T. P., Carpenter A. E., “Workflow and metrics for image quality control in large-scale high-content screens,” J. Biomol. Screening 17(2), 266–274 (2012). 10.1177/1087057111420292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tian Y., Shieh K., Wildsoet C. F., “Performance of focus measures in the presence of nondefocus aberrations,” J. Opt. Soc. Am. A 24(12), B165–B173 (2007). 10.1364/JOSAA.24.00B165 [DOI] [PubMed] [Google Scholar]
- 26.Yadav S. S., Jadhav S. M., “Deep convolutional neural network based medical image classification for disease diagnosis,” J Big Data 6(1), 113 (2019). 10.1186/s40537-019-0276-2 [DOI] [Google Scholar]
- 27.Ronneberger O., Fischer P., Brox T., “U-net: convolutional networks for biomedical image segmentation,” in International Conference on Medical image Computing and Computer-assisted Intervention (Springer, 2015), pp. 234–241. [Google Scholar]
- 28.Jaeger P. F., Kohl S. A., Bickelhaupt S., Isensee F., Kuder T. A., Schlemmer H.-P., Maier-Hein K. H., “Retina u-net: Embarrassingly simple exploitation of segmentation supervision for medical object detection,” in Machine Learning for Health Workshop, (PMLR, 2020>), pp. 171–183. [Google Scholar]
- 29.Sharma A., Pramanik M., “Convolutional neural network for resolution enhancement and noise reduction in acoustic resolution photoacoustic microscopy,” Biomed. Opt. Express 11(12), 6826–6839 (2020). 10.1364/BOE.411257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pitkäaho T., Manninen A., Naughton T. J., “Performance of autofocus capability of deep convolutional neural networks in digital holographic microscopy,” in Digital Holography and Three-Dimensional Imaging (2017), Paper W2A.5 (Optical Society of America, 2017), p. W2A.5. [Google Scholar]
- 31.Rivenson Y., Göröcs Z., Günaydin H., Zhang Y., Wang H., Ozcan A., “Deep learning microscopy,” Optica 4(11), 1437–1443 (2017). 10.1364/OPTICA.4.001437 [DOI] [Google Scholar]
- 32.Belthangady C., Royer L. A., “Applications, promises, and pitfalls of deep learning for fluorescence image reconstruction,” Nat. Methods 16(12), 1215–1225 (2019). 10.1038/s41592-019-0458-z [DOI] [PubMed] [Google Scholar]
- 33.Yang S. J., Berndl M., Michael Ando D., Barch M., Narayanaswamy A., Christiansen E., Hoyer S., Roat C., Hung J., Rueden C. T., Shankar A., Finkbeiner S., Nelson P., “Assessing microscope image focus quality with deep learning,” BMC Bioinformatics 19(1), 77 (2018). 10.1186/s12859-018-2087-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ivanov T., Kumar A., Sharoukhov D., Ortega F., Putman M., “DeepFocus: a deep learning model for focusing microscope systems,” in Applications of Machine Learning 2020 (International Society for Optics and Photonics, 2020), 11511, p. 1151103. [Google Scholar]
- 35.Pinkard H., Phillips Z., Babakhani A., Fletcher D. A., Waller L., “Deep learning for single-shot autofocus microscopy,” Optica 6(6), 794–797 (2019). 10.1364/OPTICA.6.000794 [DOI] [Google Scholar]
- 36.Luo Y., Huang L., Rivenson Y., Ozcan A., “Single-shot autofocusing of microscopy images using deep learning,” ACS Photonics 8(2), 625–638 (2021). 10.1021/acsphotonics.0c01774 [DOI] [Google Scholar]
- 37.Jiang S., Liao J., Bian Z., Guo K., Zhang Y., Zheng G., “Transform- and multi-domain deep learning for single-frame rapid autofocusing in whole slide imaging,” Biomed. Opt. Express 9(4), 1601–1612 (2018). 10.1364/BOE.9.001601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jensen K. H. R., Berg R. W., “Advances and perspectives in tissue clearing using CLARITY,” J. Chem. Neuroanat. 86, 19–34 (2017). 10.1016/j.jchemneu.2017.07.005 [DOI] [PubMed] [Google Scholar]
- 39.Renier N., Wu Z., Simon D. J., Yang J., Ariel P., Tessier-Lavigne M., “iDISCO: a simple, rapid method to immunolabel large tissue samples for volume imaging,” Cell 159(4), 896–910 (2014). 10.1016/j.cell.2014.10.010 [DOI] [PubMed] [Google Scholar]
- 40.Liebmann T., Renier N., Bettayeb K., Greengard P., Tessier-Lavigne M., Flajolet M., “Three-dimensional study of Alzheimer’s disease hallmarks using the iDISCO clearing method,” Cell Rep. 16(4), 1138–1152 (2016). 10.1016/j.celrep.2016.06.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mzinza D. T., Fleige H., Laarmann K., Willenzon S., Ristenpart J., Spanier J., Sutter G., Kalinke U., Valentin-Weigand P., Förster R., “Application of light sheet microscopy for qualitative and quantitative analysis of bronchus-associated lymphoid tissue in mice,” Cell. Mol. Immunol. 15(10), 875–887 (2018). 10.1038/cmi.2017.150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang X., Mennicke C. V., Xiao G., Beattie R., Haider M. A., Hippenmeyer S., Ghashghaei H. T., “Clonal analysis of gliogenesis in the cerebral cortex reveals stochastic expansion of glia and cell autonomous responses to Egfr dosage,” Cells 9(12), 2662 (2020). 10.3390/cells9122662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Johnson C. A., Ghashghaei H. T., “Sp2 regulates late neurogenic but not early expansive divisions of neural stem cells underlying population growth in the mouse cortex,” Dev. Camb. Engl. 147(4), dev186056 (2020). 10.1242/dev.186056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hippenmeyer S., Youn Y. H., Moon H. M., Miyamichi K., Zong H., Wynshaw-Boris A., Luo L., “Genetic mosaic dissection of Lis1 and Ndel1 in neuronal migration,” Neuron 68(4), 695–709 (2010). 10.1016/j.neuron.2010.09.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liang H., Xiao G., Yin H., Hippenmeyer S., Horowitz J. M., Ghashghaei H. T., “Neural development is dependent on the function of specificity protein 2 in cell cycle progression,” Dev. Camb. Engl. 140(3), 552–561 (2013). 10.1242/dev.085621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shannon C. E., “A mathematical theory of communication,” Bell Syst. Tech. J. 27(3), 379–423 (1948). 10.1002/j.1538-7305.1948.tb01338.x [DOI] [Google Scholar]
- 47.Chaudhuri S., Rajagopalan A., Depth From Defocus: A Real Aperture Imaging Approach (Springer, 1999). [Google Scholar]
- 48.Frid-Adar M., Diamant I., Klang E., Amitai M., Goldberger J., Greenspan H., “GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification,” Neurocomputing 321, 321–331 (2018). 10.1016/j.neucom.2018.09.013 [DOI] [Google Scholar]
- 49.Hollandi R., Szkalisity A., Toth T., Tasnadi E., Molnar C., Mathe B., Grexa I., Molnar J., Balind A., Gorbe M., Kovacs M., Migh E., Goodman A., Balassa T., Koos K., Wang W., Caicedo J. C., Bara N., Kovacs F., Paavolainen L., Danka T., Kriston A., Carpenter A. E., Smith K., Horvath P., “nucleAIzer: a parameter-free deep learning framework for nucleus segmentation using image style transfer,” Cell Syst. 10(5), 453–458.e6 (2020). 10.1016/j.cels.2020.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li C., “Python code for autofocus using deep learning,” Github 2021, https://github.com/Chenli235/Defocus_train/
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The source code of training deep learning model in this paper is available at GitHub [50]. Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.