Using response surface models to analyze drug combinations

Abstract

Quantitative evaluation of how drugs combine to elicit a biological response is crucial for drug development. Evaluations of drug combinations are often performed using index-based methods, which are known to be biased and unstable. We examine how these methods can produce misleadingly structured patterns of bias, leading to erroneous judgments of synergy or antagonism. By contrast, response surface models are less prone to these defects and can be applied to a wide range of data that have appeared in recent literature, including the measurement of combination therapeutic windows and the analysis of discrete experimental measures, three-way drug combinations, and atypical response behaviors.

Introduction

The importance of combination therapy to modern medicine is well established. The strategy of combining therapeutic agents affords greater efficacy with a potential reduction in toxicity and drug resistance [1], and is widely used in cancer [2–4] and infectious diseases [5–10]. Analysis of combined behavior can also be used to illuminate compound mechanisms and off-target effects [11].

Robust quantification of combined action is essential to the development of combination therapies. The most widely used methods for such evaluations are index-based, meaning that they distill the combination experiment down to a single metric that describes the interaction between drugs as either synergistic, antagonistic, or additive. Examples of these methods include those involving volumetric deviations from Bliss independent [12], Loewe additive [13], and highest-single agent surfaces [14], as well as potency shift methods such as the Combination Index (Cl) [15]. However, numerous authors have noted that these methods are unstable, unpredictable, and biased [11, 16–19], creating an analytical blind spot that represents a critical weakness of combination therapy development — one that is rapidly becoming more apparent because of three recent trends. First, improvements in high-throughput screening have spawned the rise of large-scale drug combination databases [20–25], as well as expansive combination data portals [26, 27] and online tools for combination analysis [11, 28]. Second, advances in nucleic acid sequencing technology have enabled facile genomic and transcriptomic characterization of disease targets, leading to biology-driven tools for comprehending compound interactions [29–31]. Third, the application of machine learning to molecular data has provided a framework for linking compound structure to disease biology, spurring a host of computational methods for learning and predicting combination interactions [32–35]. Taken together, these three advances carry the potential to robustly predict the combined behavior of drugs in silico, freeing combination therapeutic research from the curse of dimensionality. This goal cannot be achieved, however, without a reliable, robust means of quantifying the interaction between drugs – an issue that many assume to be well understood.

Fortunately, more robust, unbiased, statistically grounded evaluations of combination experiments are achievable with a sufficiently flexible parametric response surface model (RSM) such as the universal response surface approach (URSA) [36], GRS [37], BRAID [17], and MuSyC [38]. These models, though arguably more complex to use, afford greater stability and insight into combined action. They allow the analysis to move beyond simple designations of synergy and antagonism by providing a complete representation of the behavior of a combination at all doses through a parametric mathematical function of each drug’s concentration. Here, we demonstrate examples of the structured bias produced by two widely used index methods, Bliss volume (Bliss) and Cl, and statistically compare response surface methods to a wide battery of index methods in a real-world large-scale combination dataset. We then use the BRAID model to demonstrate how RSMs can be extended to new arenas of combination evaluation.

The meaning of drug synergy

The term synergy is used quite liberally in the literature, and has different connotations depending on the research context. Formally, a synergistic interaction is one in which compounds produce a larger effect in combination than one would expect from their behavior in isolation [19]. Critically, synergy does not mean that the combined effect is merely larger than the sum of the individual effects. Figure 1A shows an example in which two drugs are combined to produce a ‘super-additive’ or ‘sub-additive’ effect, but in this case, it makes little sense to call these combinations synergetic and antagonistic because they were simply derived by combining a single compound with itself at different concentrations (Figure 1B). Synergy represents a deviation from what is expected when doses are combined: to assess such a deviation, one needs a model of non-interaction that can account for the non-linear relationship between dose and effect. Although several null interaction models have been proposed [12–14, 38], Loewe additivity is widely regarded as the gold standard, in large part because it assumes an additive interaction when a compound is combined with itself [19].

Figure 1. Patterns of bias in synergy analysis methods.

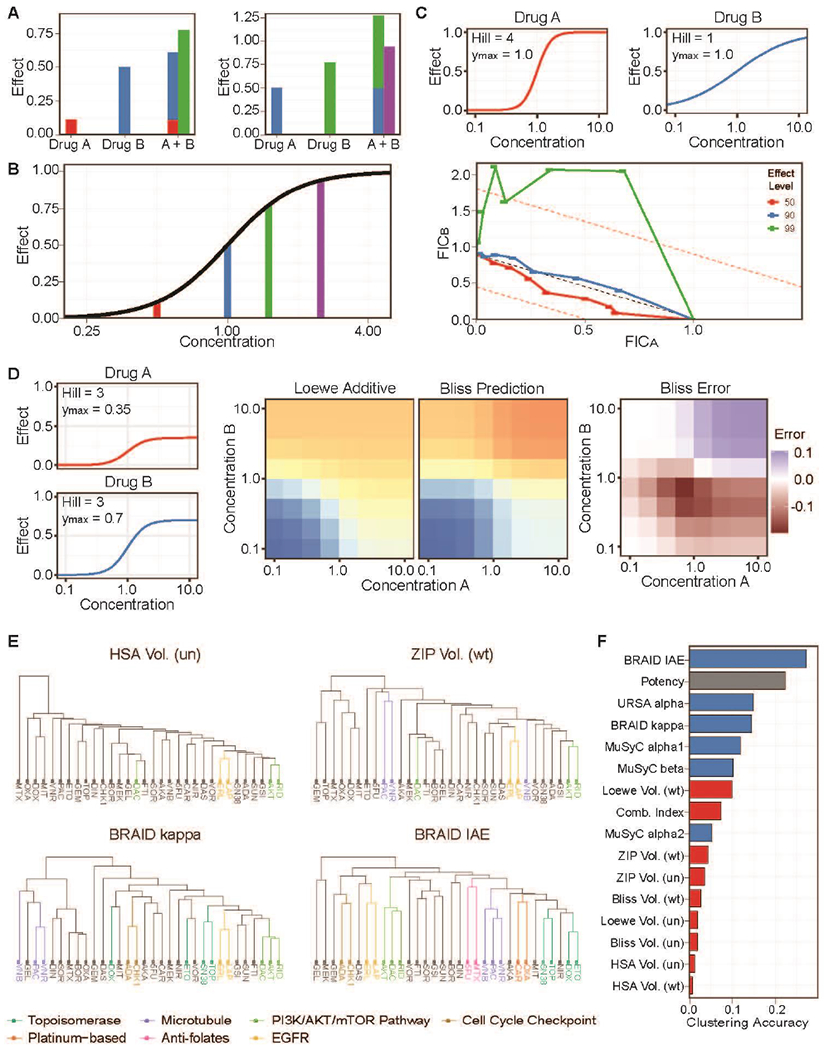
(a) Examples of drug combinations producing a super-additive and a sub-additive effect. (b) Each treatment from (a) is a different concentration of a single drug. (c) Fractional inhibitory coefficient curves depicting the combination index for a simulated additive combination at differing effect levels. A combination of drugs with differing Hill slopes produces a false conclusion of extreme antagonism. (d) A combination of drugs in which Drug A has a lower maximum efficacy (0.35) than Drug B (0.70) (left) produces different predictions under Loewe additivity and Bliss independence (center). This results in a false landscape of Bliss synergy and antagonism (right). (e) Examples of the clustering of OncoPolyPharmacology Screen (OPPS) compounds based on four interaction metrics, with fully or partially identified mechanistic classes highlighted. Volume metrics estimated with a uniform average of all 4-by-4 deviations in each response surface are marked (un), whereas metrics estimated with a weighted average placing more weight on central concentrations are marked (wt). (f) Ranking of clusterings based on all RSMs (blue) and index-based methods (red) by their agreement with the stated mechanistic classification of the 32 compounds. EGFR, epidermal growth factor receptor; FIC, fractional inhibitory coefficient; HSA, Highest single agent; IAE, index of achievable efficacy; MuSyC, multi-dimensional synergy of combinations; PI3K/AKT/mTOR, phosphatidylinositol 3-kinase/AKT/mammalian target of rapamycin; URSA, universal response surface approach.

Formal synergy analysis also requires knowledge of the individual dose–response behavior of each compound. This requirement makes combination evaluation difficult or impractical in situations which resources are limited or experimental design is constrained by logistical or ethical considerations, for example, in vivo efficacy studies or clinical trials. The designation of ‘synergy’ in such research contexts often means that the observed response was greater than what could be practically achieved by the use of single agents alone — and this connotation is distinct from the definition of synergy as understood in pharmacology.

Examples of bias in methods that are commonly used to analyze drug combinations

The two index-based methods for the analysis of drug combinations, Cl and Bliss, are ubiquitous in the drug discovery literature and have together been cited over 8000 times, including over 1000 citations in the past three years alone. The deviations that arise from index calculations often present as structured patterns of synergy and antagonism that give a false impression of the underlying interaction. To visualize these patterns, we simulated several dose–response curves with the same EC₅₀ but varying with respect to Hill slope and maximum efficacy, combined them to be Loewe additive, and then analyzed the results using Cl and Bliss (Supplementary data).

Patterned bias in the Cl

Figure 1C depicts simulated single agent dose–response curves and fractional inhibitory coefficient (FIC) curves for an additive simulated combination experiment. Drug A and Drug B differ only in the value of their Hill slopes. FIC curves are a common method for visualizing the Cl across multiple dose ratios: deviations below and above the diagonal (FIC_A + FIC_B = 1) indicate synergy or antagonism, respectively. In this case, the FIC plot shows synergy at the 50% effect level, but additivity and antagonism were observed at the 90% and 99% effect levels, respectively. The presence of synergy for combinations involving these two curve shapes was not consistently present, but the observed antagonism occurred in every simulated experiment (Supplementary figure S1). Likewise, combining two drugs that differ in their maximum efficacies resulted in the conclusion of synergy in every case (Supplementary figure S2). These patterns of bias result from a false assumption about the behavior of constant ratio combinations in Loewe additive surfaces.

Patterned bias in Bliss

Bliss independence does not adhere to the principles of Loewe additivity, and therefore, Bliss-based methods such as Bliss volume and ZIP volume will often yield divergent conclusions about synergy or antagonism when compared to Loewe volume, Cl, and additivity-based RSMs [11,18,19]. Notably, the predicted Bliss surface will deviate from the Loewe additive surface in reproducible patterns as a result of varying the Hill slope and the maximum efficacy of the single agent dose–response curves. For example, Figure 1D depicts a simulation in which the maximum efficacies of Drugs A and B are 0.35 and 0.7, respectively. Bliss independence predicts that at high concentrations of both drugs, the combined effect will be even higher (0.815), which yields a divergent judgment of antagonism at these doses. Conversely, Bliss underestimates the total effect when half of the EC₅₀ of one drug is combined with half of the EC₅₀ of the other drug and concludes synergy. Bliss also predicts the lower doses of Drug B to have little or no effect on the higher doses of Drug A, which strongly disagrees with the additive surface. The result is a structured pattern of interaction that reflects only the disagreements between the two non-interaction models. Additional examples of reproducible patterns of deviation between Loewe additivity and Bliss independence are shown in Supplementary figure S3. These simulations underscore the fact that differences in the underlying assumptions of index methods can lead to divergent judgments of synergy and antagonism that are not driven by true mechanistic interactions but merely by changes in the shape of the single agent dose–response curves.

Mechanism of action as a ground truth of synergy

In discussions of interaction measure bias, it is impossible to avoid a sense of circularity: Bliss methods are biased because they do not agree with Loewe additivity, and Loewe methods are unbiased because they do agree with Loewe additivity. At the core of these issues is the reality that synergy lacks a general ground truth: there is no widely applicable means to determine whether a drug combination is truly synergistic. In previous work, we addressed this epistemological gap by postulating that a valid measure of synergy should be driven by, and hence carry information about, mechanism of action [11]. In essence, compounds that operate through the same mechanism of action should induce similar patterns of interaction when combined with compounds operating by different mechanisms. Therefore, the accuracy of the output from a method of analyzing drug combinations can be quantified by determining how well that metric clusters compounds according to their mechanism of action.

Here, we expand on that analysis to include a broader range of index methods, including the four volume-based methods examined by Vlot et al. [18] (Highest single agent (HSA), Bliss [12], Loewe [13] and zero interaction potency (ZIP) [39]), and the interaction measures of the RSMs URSA [36] and MuSyC [38]. These methods were applied to more than 22,000 combinations from 38 drugs tested in 39 cancer cell lines reported in the Merck OncoPolyPharmacology Screen (OPPS) [23] and were used as the basis for similarity clustering of 32 compounds in the dataset (Figure 1E; Supplementary table S1). The resulting clusters were compared with the known mechanism of action of each compound and ranked by their agreement with that classification (Figure 1F). The RSM metrics, except for the MuSyC alpha2 parameter, outperformed the index-based methods, indicating that they were better at capturing the type of interaction present in these drug combinations. Furthermore, the pattern of potencies exhibited by a drug in multiple biological contexts is another means for determining a compound’s mechanism of action, as exemplified by the NCI COMPARE algorithm [40]. Because RSMs model the observed drug combination response surface, they incorporate information from both potency and interaction type. As part of its analysis, the BRAID method reports the index of achievable efficacy (IAE) metric, which is essentially a surface integral over the fitted response surface. Gratifyingly, BRAID IAE outperformed all methods, including potency alone, in the OPPS clustering experiment, identifying seven mechanistic classes within the 32 compounds evaluated.

Using RSMs to assess therapeutic window

Although drug combination analysis has paid significant attention to discerning the type of interaction (additive, synergistic, or antagonistic), such information is not as critical for therapeutic evaluation as the degree to which these interactions impact the therapeutic window of the combination – the range of effective, yet safe, doses. As noted earlier, RSMs fit the observed drug combination response surface to a parametric model, so the combined effect at any concentration of the component drugs can be estimated and compared to other drug combinations, or to the same combination across different models. Weinstein et al. [25] elegantly demonstrated how combination evaluation in two highly divergent strains of yeast could be used to gauge the selectivity of a drug combination, producing a combined therapeutic window driven by the potency and interaction of the drugs in both organisms. In one example, not only were pentamidine (PEN) and staurosporine (STA) more potent in Candida albicans, but a significantly stronger synergy in that species produced an elevated selectivity over Saccharomyces cerevisiae (Figure 2A). By contrast, rapamycin (RAP) and methyl methanesulfonate (MMS) were less active and more antagonistic in C. albicans, thereby enhancing the selectivity of those two drugs for S. cerevisiae (Figure 2B).

Figure 2. Response surface quantification of a two-drug therapeutic window.

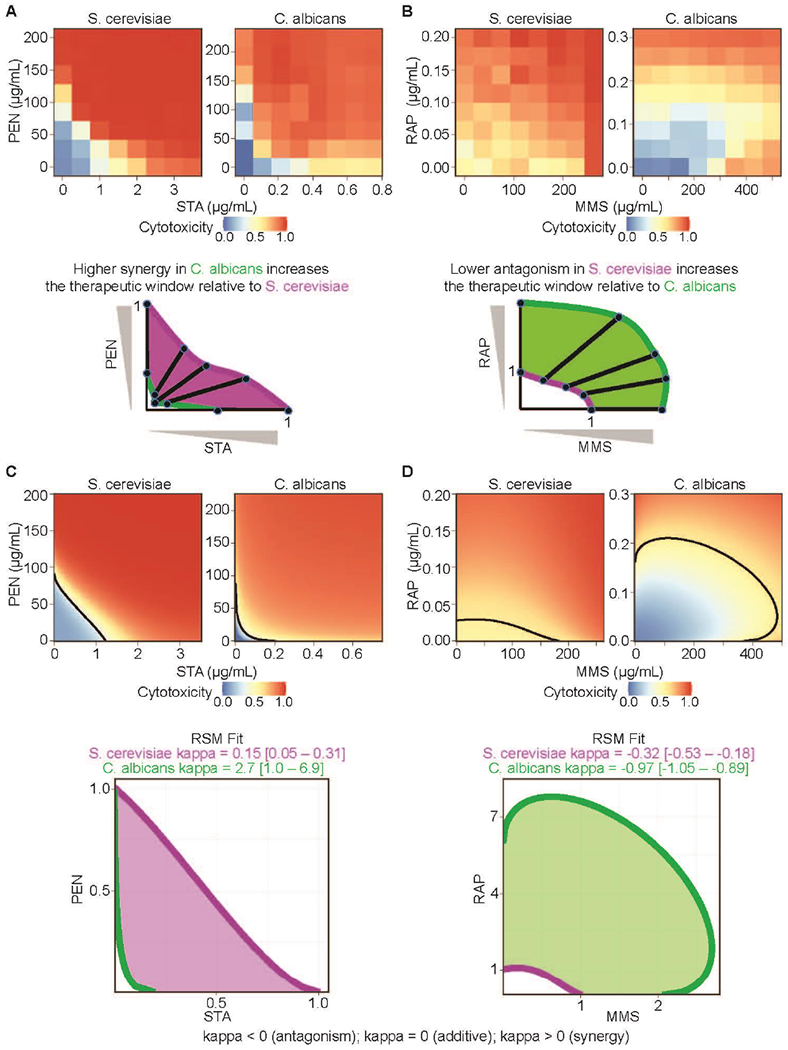
(a) Measured cytotoxicity of staurosporine (STA) and pentamidine (PEN) in Saccharomyces cerevisiae and Candida albicans. Examination of interpolated isoboles shows that the elevated apparent synergy in C. albicans (green) increases the selectivity of the compounds for that strain over S. cerevisiae (magenta). (b) A similar examination shows that a smaller apparent antagonism in S. cerevisiae (magenta) increases the selectivity of the combination of methyl methanesulfonate (MMS) and rapamycin (RAP) for that strain over C. albicans (green). (c, d) Best fitting BRAID response surfaces for all four combination experiments. (c) BRAID fits confirm that STA and PEN exhibit greater synergy in C. albicans than in S. cerevisiae, whereas (d) MMS and RAP exhibit less antagonism in S. cerevisiae than in C. albicans. The fitted response surface effect contours (bottom) agree with the qualitative results from (a) and (b).

To quantify these therapeutic windows, the authors used linear interpolation between raw measurements. Consequently, a linearly spaced checkboard sampling of two drug combinations was required, and this constrained the experiment to a narrow range of dose levels. Furthermore, robust goodness-of-fit statistics could not be applied to assess variability and confidence in the estimated values. Fortunately, the ideas presented by Weinstein et al. [25] can be extended and expanded through the use of an RSM. Figures 2C, D show how the BRAID model fits for the four combination experiments can recapitulate the non-parametric results in richer, more robust detail using a defined mathematical function that avoids over-fitting. The heightened synergy between PEN and STA and antagonism between RAP and MMS in C. albicans is clearly statistically significant. Furthermore, the therapeutic dose-pair windows obtained from RSM analysis can be interpolated and extrapolated to new dose regimes, quantified using such metrics as the BRAID IAE and used for comparison with other combinations, and evaluated statistically using bootstrapped confidence intervals.

RSMs are amenable to alternate assay endpoints

Though many combination experiments quantify the effect of a given combined dose as a continuously varying measure such as fluorescence or image intensity, a wide range of assays that may be relevant to combination evaluation do not produce endpoints that can be analyzed so cleanly. For example, discrete endpoints such as binary measures or integer counts lend themselves poorly to index methods, as comparison of a discrete value to a continuous reference surface can produce unexpected results. Several ways in which continuous response surface methods can be applied to such alternate endpoints are described below.

Binary output

Some assays, such as the determination of minimum inhibitory coefficient (MIC), do not apply a continuously varying measure to a given dose, but instead separate doses into one of two classes (above or below the MIC). Application of an index method such as CI to such data would be meaningless, as there are an infinite range of doses producing both possible endpoint values. However, if the output is treated as a probabilistic variable, it can be modeled as being sampled from a Bernoulli distribution, with the expected value of the distribution varying as a function of dose. The same logic can be applied to two-drug combination data: if a two-drug response surface is used to model the varying likelihood of lying above the MIC, the likelihood of the observed data can be maximized to fit the best response surface. Figure 3A demonstrates this approach applied to the combination of micafungin and posaconazole in Candida auris isolated from a fungal infection [41]. Each tested dose pair was classified as lying above the MIC or below in one or more replicates, and the probability of lying above the MIC was fitted as a BRAID response surface. The resulting fit indicates statistically significant synergy between the two compounds.

Figure 3. Alternate assay endpoints and three-way combinations,

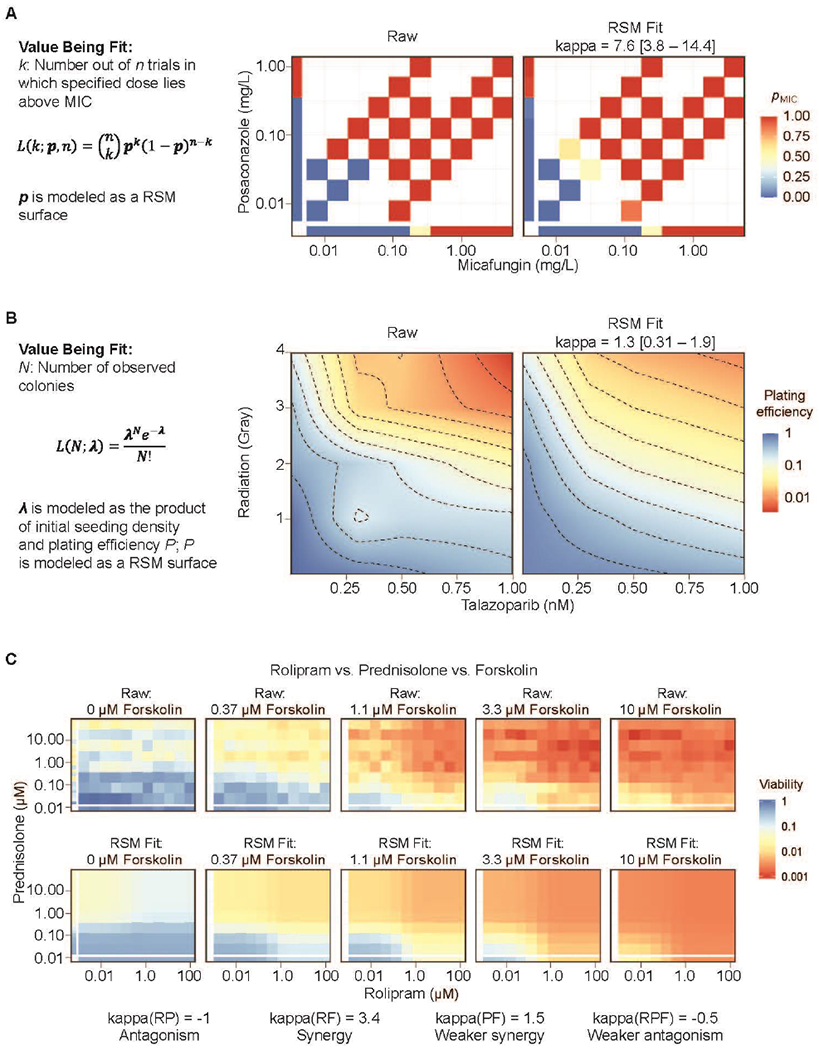
(a) A BRAID response surface model (RSM) fit to the proportion of replicates in which a particular dose or dose-pair lies above the measured minimum inhibitory concentration (MIC). The high kappa value of 7.6 indicates synergy between micafungin and posaconazole. (b) A BRAID response surface fit to the plating efficiency in a clonogenic experiment, optimized by maximizing the likelihood of discrete colony counts according to a Poisson distribution. A kappa value of 1.3 indicates synergy between talazoparib and ionizing radiation, (c) Relative viability of the cancer cell line 697 in response to rolipram, prednisolone, and forskolin, along with the three-drug BRAID response volume fit. The best fit indicates antagonism between rolipram and prednisolone [kappa(RP) = −1], synergy between rolipram and forskolin [kappa(RF) = 3.4], weaker synergy between prednisolone and forskolin [kappa(PF) = 1.5], and weaker antagonism for the three two-drug interactions [kappa(RPF) = −0.5].

Natural number outputs

Colony-forming assays, a gold standard for the evaluation of radio-sensitization [42], are increasingly used in combination evaluation to evaluate a therapy’s growth inhibitory potential directly [43–46]. The endpoint of the assay is a count of the number of colonies formed, which can be particularly challenging to fit, as more effective treatments often reduce the number of colonies down to zero. To address this challenge, the effect of the combined doses can be treated as a response surface, which can be optimized by maximizing the likelihood of the observed colony counts given a varying-rate Poisson distribution. Figure 3B demonstrates such an application, in which the expected plating efficiency (the expected average number of colonies as a proportion of the initially seeded cells) was described by a BRAID surface, which was then fitted to the measured colony counts as a maximum likelihood estimate. The resulting fit showed a clear synergy between the poly ADP ribose polymerase (PARP) inhibitor talazoparib and radiation in the desmoplastic small round cell tumor cell line JN-DSRCT-1.

Extending RSMs to triplet combinations

Paired compounds have received the lion’s share of the attention in the in vitro testing literature, but clinically important drug combinations often involve three or more components. A method that has no means of representing or analyzing three-drug combinations is severely limited in its application to translational research. The logistical challenges of collecting three-drug combination data with sufficient sampling are often the factor limiting the in vitro testing of triplet combinations, but the extension of analysis methods, particularly two-drug response surface methods, to such data is hardly a trivial question. Fortunately, nearly all response surface methods, including URSA, MuSyC, and BRAID, can be naturally extended to three-drug combinations. For example, both URSA and BRAID can be expressed as implicit equations of the form:

$$f_E\left(E\right)=f_A\left(E,D_A\right)+f_B\left(E,D_B\right)+\theta I\left(E,D_A,D_B\right)$$

where Θ is an interaction parameter indicating synergy or antagonism (α in URSA, κ in BRAID). Extending this equation to three dimensions involves adding a third single-drug term, two additional two-drug interaction terms, and a possible triplex interaction term:

$$f_E\left(E\right)=f_A\left(E,D_A\right)+f_B\left(E,D_B\right)+f_C\left(E,D_C\right)+{\theta }_{AB}{I}_{AB}\left(E,D_A,D_B\right)+{\theta }_{AC}{I}_{AC}\left(E,D_A,D_C\right)+{\theta }_{BC}{I}_{BC}\left(E,D_B,D_C\right)+{\theta }_3{I}_3\left(E,D_A,D_B,D_C\right)$$

Figure 3C depicts the growth-inhibitory effect of a three-drug combination in the acute lymphoblastic leukemia cell line 697, along with the best-fitting three-drug BRAID response volume. In this instance, the fit indicated potential antagonism between rolipram and prednisolone, clear synergy between rolipram and forskolin, weaker synergy between prednisolone and forskolin, and weaker antagonism for the three-drug interaction. These simultaneous interactions can be successfully extracted given robust, densely sampled data and a well-defined response volume model, whereas index methods offer no way of distinguishing between the different types of interaction.

Using RSMs to analyze atypical responses to drug combinations

Despite the breadth of work in the field, nearly all methods that analyze drug combinations make certain assumptions about the behavior of compounds when combined. A prototypical combined action behavior, illustrated in Figure 4A, is one in which both compounds produce a clear, non-zero effect of the same sign, with one effect potentially of smaller magnitude. Moreover, it is often posited that the combined effect will be at least as great as the smaller of the two maximal effects for each drug. Traditional analyses of synergy and antagonism assume that the response surface falls into this framework. However, it is far from obvious that all combination behaviors should follow this pattern. Here, we show how the mathematical transformation of atypical response surfaces can make them behave like prototypical surfaces, and thus, make it possible to leverage the computational and logistical advantages of RSM approaches to examine a much wider range of combined actions.

Figure 4. Non-traditional response surfaces,

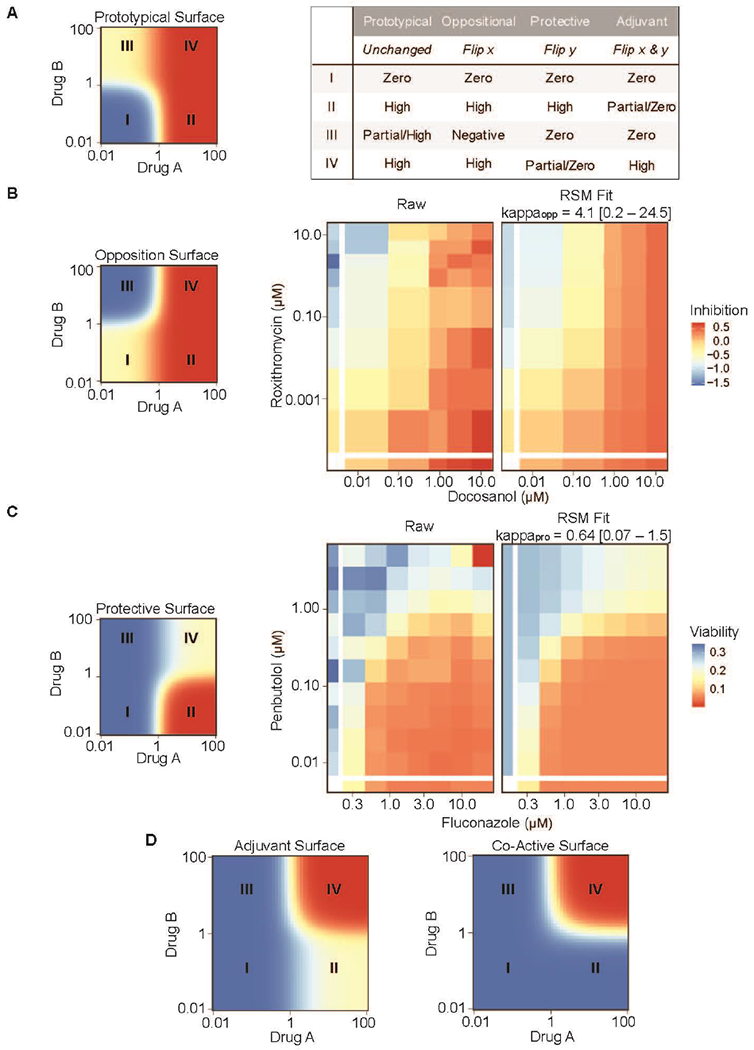
(a) The prototypical response surface model (RSM) produces high effects when either drug is present at high doses, with one of the drugs potentially producing only a partial effect. However, manipulations to this surface can produce atypical surfaces that have qualitatively different behaviors, as described in the table. (b) Reflecting the prototypical surface along the x-axis produces an oppositional response surface (left) that resembles the inhibited HIV expression response surface induced by doconasol and roxithromycin (center). The best-fit BRAID surface is shown on the right. White bars on the left and bottom indicate single-agent dose responses, (c) Reflecting the prototypical surface along the y-axis and then inverting the effect sign produces a protective surface (left) that resembles the observed C. albicans viability response to the combination of fluconazole and penbutolol (center). The best-fit BRAID surface is shown on the right. White bars on the left and at the bottom indicate single-agent dose responses. (d) Flipping the prototypical surface along both the x and y axes and then inverting the effect sign produces the ‘Adjuvant’ surface, in which high effects occur only when both drugs are present at high concentrations (left). An extreme form of this surface, ‘Co-Active’, occurs when both drugs are completely inactive on their own, but induce high activity when both drugs are present (right).

The oppositional surface

When viewed in a log-log space, the prototypical response surface carves dose space into four quadrants (Figure 4a). In the case where Drug B has an incomplete response, these four quadrants behave as follows: (I) when both drugs are low, the effect is near zero (blue); (II) when Drug A is high and Drug B is low, the effect is high (red); (III) when Drug B is high and Drug A is low, a partial or high effect is observed (yellow); and (IV) when both drugs are high, the effect is high (red). If this surface is flipped along the x-axis (Figure 4b), a new surface is generated, which behaves as follows: (I) when both drugs are low, the effect is near zero (yellow); (II) when Drug A is high and Drug B is low, the effect is still high (red); (III) when Drug B is high and Drug A is low, the effect is in the opposite direction (below zero) from Drug A (blue); and (IV) when both drugs are high, the effect of Drug A dominates, and is therefore still high (red). The oppositional surface resembled a drug response surface formed by the combination of doconasol and roxithromycin which was reported in a cell-based screen for inhibitors of HIV replication [21]. After inverting the concentration of roxithromycin, the BRAID RSM successfully fit the observed data (Supplementary data) and could then be analyzed to identify the effects of different dose regimes, determine therapeutic windows, estimate potentiation or suppression, and quantify confidence intervals for statistical comparisons.

The protective surface

Flipping the prototypical response surface along the y-axis and then inverting the effect sign (so that a low effect becomes high and vice versa) produces another new surface (Figure 4c), which behaves as follows: (I) when both drugs are low, the effect is near zero (blue); (II) when Drug A is high, and Drug B is low, the effect is high (red); (III) when Drug B is high, and Drug A is low, the effect is near zero (blue); and (IV) when both drugs are high, the effect is below that of Drug A (yellow) because Drug B ‘protects’ against the effects of Drug A. This drug response surface was similar that formed by the combination of fluconazole and penbutolol in C. albicans [47]. After inverting the concentration of fluconazole (Supplementary data), the BRAID RSM successfully fit the observed data.

The adjuvant surface

Naturally, one straightforward manipulation remains: if the prototypical response surface is inverted along both the x-axis and the y-axis, and once again the effect sign is inverted, then the response surface in Figure 4d is produced: (I) when both drugs are low, the effect is zero (blue); (II) when Drug A is high and Drug B is low, the effect is partial (yellow); (III) when Drug B is high and Drug A is low, the effect is zero (blue); and (IV) when both drugs are high, the effect is high (red) because Drug B acts like an adjuvant and enhances or activates the effect of Drug A. Furthermore, one can imagine that if the single-agent effects of both Drug A and Drug B are both zero, then the ‘Co-Active’ surface would be observed. This response surface represents the ‘purest’ form of synergy because the drugs produce a response only in the context of the combination. Although both surfaces are amenable to RSM analysis, we have not encountered either one in our work to date.

In summary, transformation of the prototypical response surface leads to atypical responses that are amenable to analysis using RSMs. It should be noted that the application of traditional index methods to any of these non-traditional surfaces would be of little value. Such methods would reach a conclusion of extreme synergy when applied to oppositional or adjuvant surfaces, and extreme antagonism when applied to protective surfaces. Yet these judgments will tell us nothing about the details of these combinations, about how similar combinations behave in different contexts, or about how various combinations can be leveraged to produce a desired effect.

Concluding remarks

The need for reliable methods to analyze drug combinations is more critical than ever due to the burgeoning of large drug combination data sets from high-throughput screening efforts. Despite their popularity, index methods such as Cl and Bliss are unstable and/or biased on the basis of the shape of the individual responses of the drugs in the combination. RSMs offer a flexible means to model compound interaction that is not only robust to noise and unbiased, but capable of providing a more complete, holistic combination representation than that afforded by mere classifications of synergy or antagonism.

Highlights:

• Index methods for identifying synergy produce structured patterns of bias.

• Response surface methods (RSMs) more reliably identify synergy and antagonism.

• RSMs can quantify two-drug therapeutic windows.

• Discrete and probabilistic endpoints can be evaluated using RSMs.

• RSMs can be extended to triplet combinations and atypical drug combination responses.