Abstract
Natural compounds that either increase or decrease polymerization of actin into filaments have become indispensable tools for cell biology. However, to date, it was not possible to use them as therapeutics due to their overall cytotoxicity and their unfavorable pharmacokinetics. Furthermore, their synthesis is in general quite complicated. In an attempt to find simplified analogues of miuraenamide, an actin nucleating compound, we identified derivatives with a paradoxical inversion of the mode of action: instead of increased nucleation, they caused an inhibition. Using an extensive computational approach, we propose a binding mode and a mode of action for one of these derivatives. Based on our findings, it becomes feasible to tune actin-binding compounds to one or the other direction and to generate new synthetic actin binders with increased functional selectivity.
Introduction
Actin is the most abundant protein in eukaryotic cells.1 The discovery of actin-binding natural compounds (cytochalasin D, latrunculin, jasplakinolide2−4) has enabled the identification of the central roles actin plays in many cellular processes (e.g., cell migration, cell division, and intracellular transport). Small actin-binding molecules can roughly be divided into two groups: destabilizers (like, e.g., latrunculin or cytochalasin D) and stabilizers (like, e.g., phalloidin or jasplakinolide). Miuraenamide A, a myxobacterial compound that has been identified and chemically characterized some years ago,5,6 belongs to the group of nucleators and is quite well synthetically accessible.7−9 Consequently, this compound has previously been used by us for derivatization to define a structure–activity relationship.10 Using an extensive computational approach, we have previously proposed a binding mode of miuraenamide, which explains its biological activity:11 miuraenamide binding ensures a tighter and stronger packing of the actin monomers compared to the apo F-actin by shifting the DNase-I binding loop (D-loop), which is indispensable for F-actin stabilization, thus promoting nucleation of actin monomers. Astoundingly, some of the derivatives we created showed a paradoxical effect in a bulk actin polymerization assay (pyrene assay).10 In the present study, we characterize these surprising derivatives biologically and present a structural explanation for the stunning difference in their mode of action. Considering the experimental findings, we hypothesize that, in contrast to miuraenamide, LK701 binds to the actin monomer, but not to any already formed oligomeric structures, thus keeping single LK701-bound actin subunits from accumulating into nuclei by blocking crucial intersubunit interaction sites. Thus, intriguingly, it is possible to tune not only the potency but also the mode of action of derivatives of miuraenamide, making this natural compound an interesting scaffold for further studies. Interestingly, it has very recently been shown in a different kind of protein–protein interaction (PPI) that the exchange of just one atom can be enough to revert an SOS1 activator into an SOS1 inhibitor.12
Results and Discussion
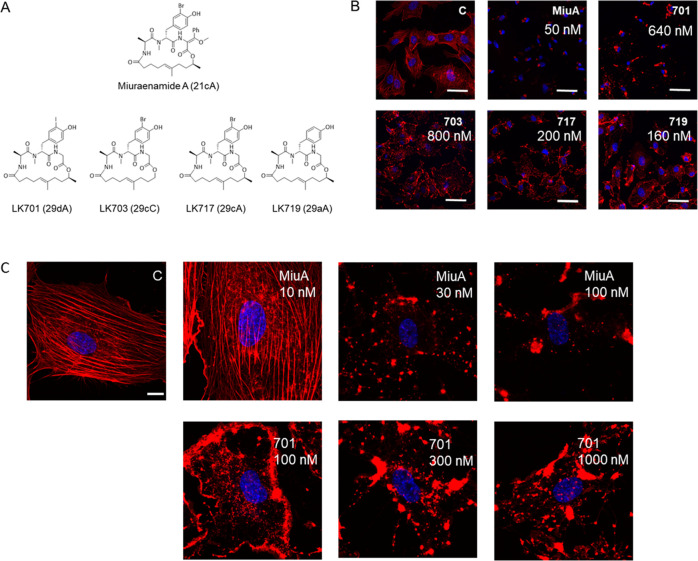
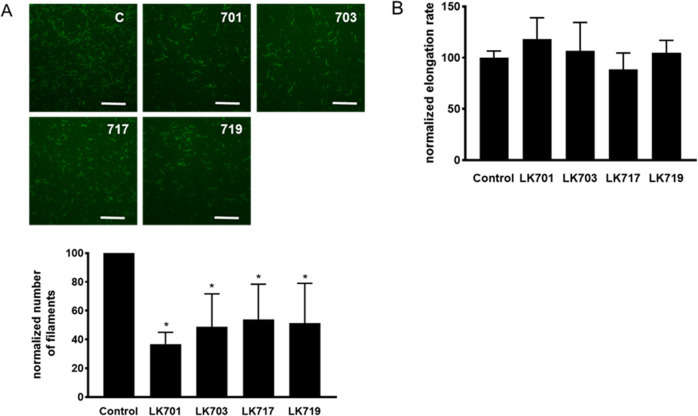
Five derivatives with paradoxical behavior in a bulk actin polymerization assay from a previous study10 were selected (Figure 1A) and tested for their effects on the cellular actin architecture. All compounds led to a complete breakdown of the F-actin cytoskeleton (Figure 1B); however, the morphology differed clearly between the derivatives and the mother compound miuraenamide A: instead of a single perinuclear actin aggregate, a multitude of aggregates dispersed over the cytoplasm and especially along the cell borders was formed (Figure 1B). In high-resolution images of single cells treated with Miuraenamide A or LK701, respectively (Figure 1C), it is clearly visible that Miuraenamide does not cause a localization of F-actin at cell borders like LK701 even at a low concentration, while even a high concentration of LK701 does not cause the pronounced perinuclear aggregation of F-actin, which can be observed with Miuraenamide A (Figure 1C). The quantitative analysis of polymerization dynamics by TIRF microscopy revealed that all of the compounds significantly reduced the number of filaments, i.e., the process of nucleation (Figure 2A), while none of them changed the elongation rate of the filaments (Figure 2B).
Figure 1.
(A) Structures of the original natural compound miuraenamide A and the derivatives. The nomenclature from ref (7) is set in parentheses. (B) Miuraenamide A causes a clear perinuclear accumulation of F-actin and complete loss of the F-actin network compared to untreated controls. The derivatives LK701, LK703, LK717, and LK719 change morphology of F-actin in a completely different way with accumulations along the cell borders, indicating a different mode of action. Scale bar: 30 μm. (C) High-resolution images of single cells treated with different concentrations of Miuraenamide A or LK701. Scale bar: 10 μm. In (B) and (C), the respective concentrations of the compounds are indicated. In (B), the concentrations have been adapted to 5 times the EC50 value in previous studies to guarantee comparability of the compounds. Blue: nuclear staining with Hoechst; red: actin fibers stained with rhodamine-phalloidine. (C) indicates untreated control.
Figure 2.
(A) Top: representative images of in vitro formed actin filaments (TIRF microscopy). Scale bar: 5 μm. Bottom: Quantitative analysis of the number of filaments (normalized to control). All derivatives inhibit formation of filaments at a concentration of 500 nM. (B) Calculated elongation rate of actin filaments normalized to control. Mean +/– SD, *p < 0.05.
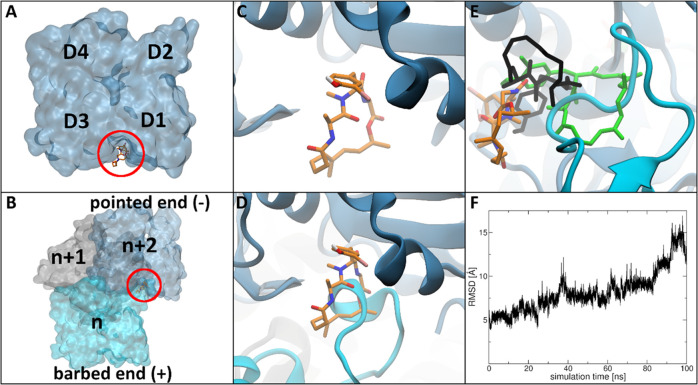
To investigate this putative effect on nucleation on a structural basis, we exemplarily investigated the binding mode of LK701 in the actin monomer as well as its trimeric structure by combined molecular docking and molecular dynamics simulations. Thus, we first performed molecular docking calculations with the program DynaDock13 for LK701 in the known binding site of miuraenamide A (i.e., the macrolide binding cleft) (Figure 3A) in the actin monomer structure followed by molecular dynamics (MD) simulations for proper equilibration of the complex (LK701mono).
Figure 3.
LK701 molecular docking and MD simulation results. The ligand is shown in stick, and the protein in cartoon and surface representation. Ligand atom color code: dark blue (nitrogen), red (oxygen), white (hydrogen), pink (iodine), orange (carbon). Nonpolar hydrogens are not shown for clarity. (A) Surface representation of the actin monomer highlighting the macrolide binding cleft (red), the subdomains D1–D4 are shown for orientation. (B) Surface representation of the actin trimer structure; the three subunits were color-coded and labeled n (cyan), n + 1 (gray), and n + 2 (light blue) from the barbed to the pointed end of the nucleus and the intersubunit binding cleft is highlighted by a red circle. (C) Macrolide binding cleft with equilibrated bound conformation of LK701 in the actin monomer LK701mono. (D) Superposition of LK701mono on subunit n + 2 of the stable actin apo nucleus showing a clash between LK701 and the D-loop of subunit n. (E) Most prominent structure of LK701 in the actin trimer LK701tri during MD (orange). Docked position in black, position of the LK701mono in green for reference. (F) Root-mean-square deviation (RMSD) of the position of LK701 relative to the bound position in the actin monomer LK701mono as obtained during the MD simulation for the LK701–actin trimer complex.
As the macrolide binding cleft is located close to the surface of actin and thus highly solvent-exposed, multiple potential binding poses were generated during docking. After clustering all final docking poses, MD simulations were performed for each of the best ranked poses of the three highest populated clusters (see the Experimental Section), as MD simulations are a common tool for the investigation of the stability of protein conformations obtained by molecular docking calculations (Figure S1). During the simulations, a stable protein–ligand complex was only obtained for one pose, which subsequently was chosen as the predicted binding pose of LK701 in the actin monomer: LK701mono (Figures 3C and S1A). A more detailed analysis of the MD simulations of the three selected poses can be found in Supplementary Text 1.
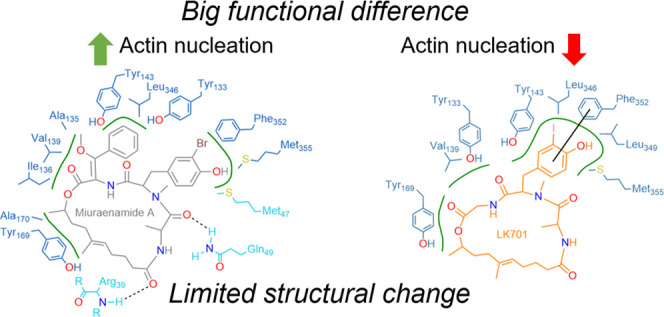
We compared the position of LK701mono with the predicted binding pose of miuraenamide from our previous study11 and found that LK701 fills the macrolide binding cleft more precisely. Missing a second phenyl side extension, LK701 is sterically less hindered and therefore able to slide deeper into the macrolide binding cleft and to form more favorable hydrophobic interactions deep inside the cleft compared to miuraenamide (see Supplementary Text 1 and Figure S3).
Next, we investigated if LK701 could bind to the already formed trimeric actin nucleus. For this, first, an actin trimer structure was built based on the monomer structure11 and afterward MD simulations were performed to obtain an equilibrated, structurally relaxed apo-trimer structure, which was used as model for the actin nucleus in this study. Afterward, docking calculations were performed for LK701 in the macrolide binding cleft of subunit n + 2 at the pointed end of the nucleus (Figure 3B), which is interacting with the D-loop of subunit n at the barbed end, followed by MD simulations, applying the same protocols as in the LK701–actin monomer investigations.
As stated above, first, an unbound actin trimer structure was thoroughly equilibrated to serve as the starting structure for the planned docking simulations. During these MD simulations, it could be observed that the residues of the D-loop of subunit n moved into the macrolide binding cleft of subunit n + 2 (cyan in Figure 3D) in which it binds in an extended conformation, thereby forming a stable trimeric structure. This marked an important characteristic of the equilibrated nucleus model and is in agreement with crucial longitudinal interactions during filament formation reported before.14−17Figure 3D shows the superposition of the predicted LK701mono binding pose on subunit n + 2 of the equilibrated apo-trimer. It can be clearly observed that the rearranged D-loop of subunit n clashes with the position of the ligand in the actin monomer. This indicates that formation of this nucleus-stabilizing D-loop conformation might not be possible in the presence of LK701, further suggesting that LK701 inhibits actin nucleation by blocking this important interaction site on the monomer level. Furthermore, it indicates that an already formed trimer structure is not able to bind LK701 in the macrolide binding cleft of the interacting subunits anymore, since the ligand and the D-loop compete for the same binding site as discussed above. To investigate the latter assumption, we performed docking calculations for LK701 into the macrolide binding cleft of subunit n + 2 of the equilibrated apo nucleus, i.e., with the D-loop located inside the cleft, clustered all generated poses, and chose three docking poses (the best ranked pose of the highest populated cluster and the two docked poses closest to the predicted reference position of LK701 in the monomer) for further investigation by MD simulations. For the molecular docking calculations, the DynaDock algorithm was specifically applied as it allows for ligand-binding-induced adaption of binding site loops and residues during docking. However, in this case, no successful adaption of the D-loop of the adjacent actin subunit was possible if LK701 was placed fully inside the binding cleft. Thus, all final docking poses were located at least partially outside of the macrolide binding cleft and accumulated to either side of the D-loop (as shown in black in Figure S2A,D,G), suggesting that the above alternative binding hypothesis might be true. Thus, through the following MD simulations of the three selected docking poses, we investigated not the stability of the docked poses (as for the actin monomer complexes), but the ligand’s ability to move deeper into the binding site from its half-solvent-exposed docked position while pushing the D-loop away, as such longer-time-scale effects cannot be seen during docking. However, as shown in Figure S2C,F,I (black line showing the root-mean-square deviation (RMSD) of the position of the ligand with respect to the bound position in LK701mono), in all three cases, the ligand either remained close to its docked position half-outside the binding cleft during the MD simulations or moved even further into the solvent. The latter was interestingly the case for the pose, originally docked closest to LK701mono and the binding cleft (Figure 3E,F and S2D–F). These results further confirm the above hypothesis that the ligand cannot move into the binding site once the D-loop of the adjacent actin subunit has formed its nucleus-stabilizing conformation inside the macrolide binding cleft. Based on the MD simulations above, we performed a DSSP analysis (provided in Figure S2) of the bound D-loop conformation to analyze its general stability/flexibility. This analysis showed that a very stable bend conformation is formed by the D-loop, which is conserved throughout the whole simulation time. Thus, although some movement of the D-loop can be observed during the simulations, it retains its overall stable conformation and stays bound inside the macrolide binding cleft, prohibiting the ligand from entering. A more detailed analysis of all three selected docking poses in the actin nucleus can be found in Supplementary Text 1.
Conclusions
Actin does not only bind to other actin molecules, but is one of the proteins with the highest number of interacting proteins.1 The biological function of actin is defined—and subcellularly localized—by its interaction with specific subsets of actin-binding proteins. It has previously been speculated that, in a process termed “biomolecular mimicry”,18,19 small molecules might compete with actin-binding molecules for their binding to actin. Thus, the knowledge how to “tune” an actin nucleating compound into a nucleation inhibitor might be the basis for the rational design of novel actin modulating compounds, which might enable a higher functional selectivity—especially in the light of the fact that actin-binding compounds did not find their way into clinical use yet due to functional selectivity issues.
Experimental Section
Compounds
Miuraenamide A and the derivatives were synthesized as previously described.10,20
Cell Culture
Human umbilical vein endothelial cells were purchased from Promocell (Heidelberg, Germany) and cultured as previously described.11 For the experiments, the cells were used in passage 4 in a subconfluent state. For microscopy, the cells were fixed in 4% paraformaldehyde for 10 min, permeabilized with 0.1% Triton X-100 for 1 min, and subsequently stained with rhodamine–phalloidin (1:400, R 415, Molecular Probes, Life technologies) and bis-benzimide (H33342 trihydrochloride, B2261 Sigma-Aldrich) as a nuclear counterstain as previously described.11 Representative images were obtained with a Leica confocal microscope (SP8 SMD). The cells were treated with the respective compound for 1 h at 5 times the EC50 calculated previously.10
TIRF Microscopy
The TIRF assays were conducted as described previously.11 In brief, Atto488-actin and actin (unlabeled) from rabbit skeletal muscle were purchased from Hypermol (Bielefeld, Germany) and mixed in a 1:1 ratio. α-Actinin from turkey gizzard smooth muscle (Hypermol, Bielefeld, Germany) was used as tethering protein for actin filaments. Images of freshly nucleated and elongating filaments were obtained on a TIRF setup (Leica, Mannheim, Germany) equipped with a 100× oil immersion lens. Quantitative image analysis was performed as previously described,11 using programs custom-written in MATLAB (The MathWorks, Natick, MA) R2017a for nucleation, and Image J software (version 1.49) for calculating the elongation rate.
Structure Preparation
LK701 was built and minimized in Avogadro.21 The actin monomer consisted of the actin protein, an ATP molecule, and a calcium ion, and was taken from the crystal structure PDB:3EKS.22 After docking LK701 in the actin monomer structure, an actin trimer structure was built by aligning three monomers on three adjacent subunits in the middle of the filamentous scaffold of PDB:3J8A,23 similar to our previous study.11 The ligand was subsequently removed, and the thus-generated nucleus structure was thoroughly equilibrated (see the Molecular Dynamics Simulations section) to obtain a proper apo nucleus model.
Parameterization
Throughout this study, the Amber Force Field ff14SB24 and the General Amber Force Field GAFF25 parameters were used on protein and ligand atoms, respectively. Furthermore, for water molecules and atomic ions, the TIP3P26 force field, and for ATP, the parameters of Carlson27 and colleagues were employed. Additionally, for LK701, the following point charge derivation procedure was applied: first, initial point charges were calculated on AM1-BCC level using antechamber of AmberTools17. The ligand was then minimized, heated up to 300 K (see the Molecular Dynamics Simulations section), and equilibrated in gas phase for 4 μs. The trajectory was clustered in dihedral space with cpptraj28 considering the four most flexible macrocyclic ring torsions, and the centroid structures of the 10 highest populated clusters were extracted. Each conformer was optimized with the Gaussian0929 program on the HF/6-31G(d) (LanL2DZ for iodine) level of theory. After fitting the atomic charges to the electrostatic potential according to the Merz–Singh–Kollman30 scheme, the final atomic point charges were derived applying a multiconfigurational RESP procedure.
Molecular Dynamics Simulations
All MD simulations were performed with the Amber16/AmberTools1731 program package applying the following settings, if not stated otherwise. A truncated octahedron (cuboid box) was chosen as a simulation box for actin monomer (trimer) complexes employing periodic boundary conditions and a maximum distance of 18.0 Å from the solute. Sodium ions for neutralization and explicit water molecules as solvent were added. Electrostatic interactions were calculated according to the particle mesh Ewald method,32 and a 12.0 Å cutoff was used for all nonbonded interactions. The SHAKE algorithm33 was used to restrict bonds involving hydrogen atoms and a timestep of 1 fs was applied. The density of the water shell was adjusted iteratively by minimizing the system with positional restraints on all nonsolvent atoms using a force constant of 3.0 kcal/(mol Å2) while gradually changing the box size until a density of 1.0 g/cm3 was reached. A final unconstrained conjugate-gradient minimization for 20 000 steps was performed afterward. All minimization steps were performed with the sander module of Amber16. A stepwise heat-up procedure heated each system to a target temperature of 300 K over a simulation time of 1.5 ns. Starting from a fully restrained system until 20 K, the positional restraints were removed from solvent atoms up to 200 K. The fully unrestrained system was further heated up to 300 K. All heat-up steps were performed with the NVT ensemble, while all following simulations used the NPT ensemble employing the pmemd.cuda engine and mixed-precision mode on graphics processing units.34−36 For temperature control, the Langevin thermostat37 with a collision frequency of 4.0 ps–1 and for pressure regulation, the Berendsen barostat38 were employed.
For MD simulations of the actin nucleus without LK701 (see the Structure Preparation section), three individual replica were simulated for 300 ns each. The replica trajectories were combined, aligned on the protein backbone, and clustered hierarchically with cpptraj using an epsilon cutoff of 2.0 and the average linkage method considering all protein backbone heavy atoms. The centroid structure of the highest populated cluster was used as our nucleus model in this study. For the production runs of the docked monomer (Amono, Bmono, Cmono) and trimer (Atri, Btri, Ctri) complexes, see the Molecular Docking section.
Molecular Docking
Conformational Sampling of LK701
LK701 was simulated separately at elevated temperature to generate a diverse set of macrocyclic ring conformers, which was used as starting structures for molecular docking calculations to compensate the lack of flexibility of ring torsions during pose generation. Therefore, an MD protocol specifically designed for macrocyclic ligands was used, which was successfully applied in our previous macrocycle docking studies.11,39−41 LK701 was placed inside a truncated octahedron box with 18.0 Å distance from the ligand, which was filled with explicit water molecules. Three individual replica simulations were used starting from different ligand conformations and velocities, applying the same simulation conditions as introduced above. The heat-up procedure was extended by two steps to reach a target temperature of 600 K. Every replicon was simulated at 600 K for 1 μs using the NVT ensemble. All replica simulations were combined and clustered in dihedral space considering the four most flexible torsions of the macrocycle. The centroid structures of the five highest populated clusters were used as starting conformers for the molecular docking calculations inside the actin monomer as well as the actin nucleus.
Molecular Docking with the Presampled Macrocyclic Ring Conformations
DynaDock,13 an MD-based docking program, was used for all molecular docking calculations. The algorithm consists of a broad sampling step, in which random ligand poses are generated, allowing for a certain atomic overlap with the protein. Subsequently, this overlap is removed in the following refinement step, in which short optimized potential MD (OPMD) simulations were performed. This way, a fully flexible docking procedure is applied since the protein is able to adapt its conformation to the presence of the ligand while resolving the initial overlap. However, the conformation of the macrocycle of LK701 is kept rigid during broad sampling since torsional degrees of freedom within rings cannot be changed independently. To compensate this, a conformational sampling step was performed (described above) before the actual docking calculations to generate a subset of diverse ring conformations. This way, five different conformers of LK701 were obtained, which were used as starting conformations for the broad sampling.
For docking calculations inside the actin monomer, each selected LK701 conformer was manually aligned on the position of miuaraenamide A determined in our previous study11 and 500 initial docking poses were generated during broad sampling. For this, LK701 was randomly displaced inside the binding site with a maximum translation distance of 10.0 Å. Since the binding site is located at the surface of actin, a maximum distance of 4.0 Å between the center of LK701 and any protein atom was applied to avoid accumulation of docking poses in the solvent outside the binding site. Overall random rotation of the ligand and additionally random rotational modifications of nonterminal aliphatic single-bond torsions outside of ring systems (i.e., all aliphatic side chains) were applied. During pose generation, 80% overlap of van der Waals radii between protein and ligand atoms and 60% overlap within the ligand were tolerated. 5 × 500 Initial docking poses generated in that way were refined with 50 ps OPMD at 300 K employing a 1 fs timestep using soft-core potentials for nonbonded interactions between ligand and protein atoms, thereby removing atomic overlap created during broad sampling. After successful refinement (i.e., after all atomic overlap has been resolved), a 25 ps simulation without soft-core potentials was performed for short equilibration of all refined poses. Protein backbone atoms 20.0 Å and further from any ligand atom were restrained with a force constant of 1000 kJ/(mol nm2), and hydrogen atoms were constrained using the SHAKE algorithm. All refined ligand poses were clustered hierarchically considering all ligand heavy atoms with cpptraj, employing an epsilon cutoff of 2.0. All structures of the three highest populated clusters were ranked according to the interaction score implemented in DynaDock. The best scored poses of the first, second, and third clusters were selected and labeled poses Amono, Bmono, and Cmono (black in Figure S1A,C,E), respectively, for which long-term MD simulations were performed afterward. For that, each selected pose of the docked LK701–actin monomer complex was solvated, minimized, and heated to a target temperature of 300 K as described above. For each system, three individual replica simulations were conducted for 200 ns each. The replica simulations were combined, aligned on the protein backbone, clustered hierarchically considering all protein backbone heavy atoms and the centroid structure of the highest populated cluster were taken as the final equilibrated poses of Amono, Bmono, and Cmono and correspond to those shown in orange in Figure S1A,C,E, respectively. As our structural analysis suggests (see main text), only pose Amono was able to form a stable protein–ligand complex during these simulations. Therefore, the final equilibrated pose Amono was appointed the predicted binding position of LK701 in the actin monomer (LK701mono, Figures 3C and S1A).
Correspondingly, the five LK701 conformers extracted from the conformational sampling step were docked into the equilibrated actin nucleus with similar settings as introduced above, starting from the final predicted binding position in the monomer LK701mono aligned on subunit n + 2 of the nucleus structure. This way, LK701 was docked into the macrolide binding cleft of actin subunit n + 2 in the presence of the interacting D-loop of the adjacent subunit n. During broad sampling, 200 initial docking poses were generated for each conformation of LK701. Due to the large size of the actin nucleus, 5 × 200 broad sampling poses were refined for 15 ps with OPMD. After any atomic overlap was resolved, each pose was simulated for 5 ps without soft-core potentials. All protein atoms 15.0 Å and more from the ligand were positionally restrained. Successfully refined ligand poses were clustered hierarchically employing an epsilon cutoff of 5.0. All structures of the highest populated cluster were ranked according to the interaction score of DynaDock, and the best ranked docking pose was labeled Atri (black in Figure S2A). Additionally, the root-mean-square deviation (RMSD) of the position of all ligand heavy atoms was calculated relative to the predicted binding position in LK701mono. The two docked poses closest to that reference were labeled Btri (black in Figures 3E and S2D) and Ctri (black in Figure S2G), respectively. The three selected docking poses Atri, Btri, and Ctri were solvated, minimized, heated to 300 K, and equilibrated for 100 ns. Each trajectory was aligned on the protein backbone, clustered in a hierarchical manner using an epsilon cutoff of 2.0, and the representative structure of the highest populated cluster was used as the final equilibrated poses of Atri (orange in Figure S2A), Btri (orange in Figures 3E and S2D), and Ctri (orange in Figure S2G), respectively. Although none of the selected poses could penetrate into the binding site (see main text) and thus no stable protein–ligand complex could be formed for the nucleus, for comparison with corresponding calculations in the monomer structure, the docked pose that came closest to the predicted binding position of LK701mono during the simulation (Btri) was chosen to represent the equilibrated “holo” nucleus structure LK701tri.
Analysis of Protein–Ligand Interactions with PoseView
To compare the binding mode of miuraenamide A to that of LK701 in more detail, the protein–ligand interactions were calculated using PoseView version 1.1.42 The results displayed in Figure S3 were generated using a hydrophobic atom distance of 2.8 Å, a hydrogen bond atom center distance of 2.4 Å, a hydrogen bond cone angle of 120°, and a π–π center distance of 5.0 Å.
Acknowledgments
The authors acknowledge the expert technical assistance by Jana Pelsikova.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02838.
Molecular dynamics simulations for LK701–actin monomer and LK701–actin nucleus; comparison between the actin-binding modes of LK701 and miuraenamide A (PDF)
Author Contributions
S.W., L.Y., L.Z., and M.M. performed experiments and acquired data. S.K. and U.K. synthesized compounds. A.V., I.A., and S.Z. conceived the study and wrote the manuscript.
S.W. was funded by the Chinese Scholarship Council. I.A. was funded by the Deutsche Forschungsgemeinschaft (DFG): SFB1035. and S.Z. was funded by the Doktor Robert Pfleger-Stiftung.
The authors declare no competing financial interest.
Author Status
⊥ S.W. and M.M. are co-first authors.
Supplementary Material
References
- Dominguez R. Actin-binding proteins--a unifying hypothesis. Trends Biochem. Sci. 2004, 29, 572–578. 10.1016/j.tibs.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Bubb M. R.; Senderowicz A. M.; Sausville E. A.; Duncan K. L.; Korn E. D. Jasplakinolide, a cytotoxic natural product, induces actin polymerization and competitively inhibits the binding of phalloidin to F-actin. J. Biol. Chem. 1994, 269, 14869–14871. 10.1016/S0021-9258(17)36545-6. [DOI] [PubMed] [Google Scholar]
- Katagiri K.; Matsuura S. Antitumor activity of cytochalasin D. J. Antibiot. 1971, 24, 722–3. 10.7164/antibiotics.24.722. [DOI] [PubMed] [Google Scholar]
- Spector I.; Shochet N. R.; Kashman Y.; Groweiss A. Latrunculins: novel marine toxins that disrupt microfilament organization in cultured cells. Science 1983, 219, 493–495. 10.1126/science.6681676. [DOI] [PubMed] [Google Scholar]
- Iizuka T.; Fudou R.; Jojima Y.; Ogawa S.; Yamanaka S.; Inukai Y.; Ojika M. Miuraenamides A and B, novel antimicrobial cyclic depsipeptides from a new slightly halophilic myxobacterium: taxonomy, production, and biological properties. J. Antibiot. 2006, 59, 385–91. 10.1038/ja.2006.55. [DOI] [PubMed] [Google Scholar]
- Ojika M.; Inukai Y.; Kito Y.; Hirata M.; Iizuka T.; Fudou R. Miuraenamides: antimicrobial cyclic depsipeptides isolated from a rare and slightly halophilic myxobacterium. Chem. - Asian J. 2008, 3, 126–33. 10.1002/asia.200700233. [DOI] [PubMed] [Google Scholar]
- Kappler S.; Siebert A.; Kazmaier U. Synthesis of New Cyclopeptide Analogues of the Miuraenamides. Curr. Org. Synth. 2021, 18, 418–424. 10.2174/1570179418666210113161550. [DOI] [PubMed] [Google Scholar]
- Karmann L.; Schultz K.; Herrmann J.; Muller R.; Kazmaier U. Total syntheses and biological evaluation of miuraenamides. Angew. Chem., Int. Ed. 2015, 54, 4502–7. 10.1002/anie.201411212. [DOI] [PubMed] [Google Scholar]
- Ojima D.; Yasui A.; Tohyama K.; Tokuzumi K.; Toriihara E.; Ito K.; Iwasaki A.; Tomura T.; Ojika M.; Suenaga K. Total Synthesis of Miuraenamides A and D. J. Org. Chem. 2016, 81, 9886–9894. 10.1021/acs.joc.6b02061. [DOI] [PubMed] [Google Scholar]
- Kappler S.; Karmann L.; Prudel C.; Herrmann J.; Caddeu G.; Muller R.; Vollmar A. M.; Zahler S.; Kazmaier U. Synthesis and Biological Evaluation of Modified Miuraenamides. Eur. J. Org. Chem. 2018, 2018, 6952–6965. 10.1002/ejoc.201801391. [DOI] [Google Scholar]
- Wang S.; Crevenna A. H.; Ugur I.; Marion A.; Antes I.; Kazmaier U.; Hoyer M.; Lamb D. C.; Gegenfurtner F.; Kliesmete Z.; et al. Actin stabilizing compounds show specific biological effects due to their binding mode. Sci. Rep. 2019, 9, 9731 10.1038/s41598-019-46282-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramharter J.; Kessler D.; Ettmayer P.; Hofmann M. H.; Gerstberger T.; Gmachl M.; Wunberg T.; Kofink C.; Sanderson M.; Arnhof H.; Bader G.; Rumpel K.; Zophel A.; Schnitzer R.; Bottcher J.; O’Connell J. C.; Mendes R. L.; Richard D.; Pototschnig N.; Weiner I.; Hela W.; Hauer K.; Haering D.; Lamarre L.; Wolkerstorfer B.; Salamon C.; Werni P.; Munico-Martinez S.; Meyer R.; Kennedy M. D.; Kraut N.; McConnell D. B. One Atom Makes All the Difference: Getting a Foot in the Door between SOS1 and KRAS. J. Med. Chem. 2021, 64, 6569–6580. 10.1021/acs.jmedchem.0c01949. [DOI] [PubMed] [Google Scholar]
- Antes I. DynaDock: A new molecular dynamics-based algorithm for protein–peptide docking including receptor flexibility. Proteins: Struct., Funct., Bioinf. 2010, 78, 1084–1104. 10.1002/prot.22629. [DOI] [PubMed] [Google Scholar]
- Dominguez R.; Holmes K. C. Actin structure and function. Annu. Rev. Biophys. 2011, 40, 169. 10.1146/annurev-biophys-042910-155359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou S. Z.; Pollard T. D. Mechanism of actin polymerization revealed by cryo-EM structures of actin filaments with three different bound nucleotides. Proc. Natl. Acad. Sci. USA 2019, 116, 4265–4274. 10.1073/pnas.1807028115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujii T.; Iwane A. H.; Yanagida T.; Namba K. Direct visualization of secondary structures of F-actin by electron cryomicroscopy. Nature 2010, 467, 724–728. 10.1038/nature09372. [DOI] [PubMed] [Google Scholar]
- Chu J.-W.; Voth G. A. Allostery of actin filaments: molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA 2005, 102, 13111–13116. 10.1073/pnas.0503732102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klenchin V. A.; Allingham J. S.; King R.; Tanaka J.; Marriott G.; Rayment I. Trisoxazole macrolide toxins mimic the binding of actin-capping proteins to actin. Nat. Struct. Mol. Biol. 2003, 10, 1058–63. 10.1038/nsb1006. [DOI] [PubMed] [Google Scholar]
- Tanaka J.; Yan Y.; Choi J.; Bai J.; Klenchin V. A.; Rayment I.; Marriott G. Biomolecular mimicry in the actin cytoskeleton: mechanisms underlying the cytotoxicity of kabiramide C and related macrolides. Proc. Natl. Acad. Sci. USA 2003, 100, 13851–6. 10.1073/pnas.2233339100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karmann L.; Schultz K.; Herrmann J.; Müller R.; Kazmaier U. Total syntheses and biological evaluation of miuraenamides. Angew. Chem., Int. Ed. 2015, 54, 4502–4507. 10.1002/anie.201411212. [DOI] [PubMed] [Google Scholar]
- Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 2012, 4, 17 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair U. B.; Joel P. B.; Wan Q.; Lowey S.; Rould M. A.; Trybus K. M. Crystal structures of monomeric actin bound to cytochalasin D. J. Mol. Biol. 2008, 384, 848–864. 10.1016/j.jmb.2008.09.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von der Ecken J.; Müller M.; Lehman W.; Manstein D. J.; Penczek P. A.; Raunser S. Structure of the F-actin–tropomyosin complex. Nature 2015, 519, 114–117. 10.1038/nature14033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Meagher K. L.; Redman L. T.; Carlson H. A. Development of polyphosphate parameters for use with the AMBER force field. J. Comput. Chem. 2003, 24, 1016–1025. 10.1002/jcc.10262. [DOI] [PubMed] [Google Scholar]
- Roe D. R.; Cheatham T. E. III PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Mennucci B.; Petersson G.. Gaussian 09; Gaussian Inc.: Wallingford, CT, 2009.
- Singh U. C.; Kollman P. A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. 10.1002/jcc.540050204. [DOI] [Google Scholar]
- Case D.; Betz R.; Cerutti D.; Cheatham I.; Darden T.; Duke R.; Giese T.; Gohlke H.; Goetz A.; Homeyer N.. AMBER 2016; University of California: San Francisco, 2016.
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N· log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Le Grand S.; Götz A. W.; Walker R. C. SPFP: Speed without compromise—A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013, 184, 374–380. 10.1016/j.cpc.2012.09.022. [DOI] [Google Scholar]
- Salomon-Ferrer R.; Götz A. W.; Poole D.; Le Grand S.; Walker R. C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- Gotz A. W.; Williamson M. J.; Xu D.; Poole D.; Le Grand S.; Walker R. C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized born. J. Chem. Theory Comput. 2012, 8, 1542–1555. 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gunsteren W. F.; Berendsen H. J. Computer simulation of molecular dynamics: Methodology, applications, and perspectives in chemistry. Angew. Chem., Int. Ed. 1990, 29, 992–1023. 10.1002/anie.199009921. [DOI] [Google Scholar]
- Berendsen H. J.; Postma Jv.; van Gunsteren W. F.; DiNola A.; Haak J. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Eyermann B.; Meixner M.; Brötz-Oesterhelt H.; Antes I.; Sieber S. A. Acyldepsipeptide probes facilitate specific detection of caseinolytic protease P independent of its oligomeric and activity state. ChemBioChem 2020, 21, 235–240. 10.1002/cbic.201900477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütz R.; Meixner M.; Antes I.; Bracher F. A modular approach to the bisbenzylisoquinoline alkaloids tetrandrine and isotetrandrine. Org. Biomol. Chem. 2020, 18, 3047–3068. 10.1039/D0OB00078G. [DOI] [PubMed] [Google Scholar]
- Ugur I.; Schroft M.; Marion A.; Glaser M.; Antes I. Predicting the bioactive conformations of macrocycles: a molecular dynamics-based docking procedure with DynaDock. J. Mol. Model. 2019, 25, 197 10.1007/s00894-019-4077-5. [DOI] [PubMed] [Google Scholar]
- Stierand K.; Maaß P. C.; Rarey M. Molecular complexes at a glance: automated generation of two-dimensional complex diagrams. Bioinformatics 2006, 22, 1710–1716. 10.1093/bioinformatics/btl150. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.