Constrained Mixture Models of Soft Tissue Growth and Remodeling – Twenty Years After

Abstract

Soft biological tissues compromise diverse cell types and extracellular matrix constituents, each of which can possess individual natural configurations, material properties, and rates of turnover. For this reason, mixture-based models of growth (changes in mass) and remodeling (change in microstructure) are well-suited for studying tissue adaptations, disease progression, and responses to injury or clinical intervention. Such approaches also can be used to design improved tissue engineered constructs to repair, replace, or regenerate tissues. Focusing on blood vessels as archetypes of soft tissues, this paper reviews a constrained mixture theory introduced twenty years ago and explores its usage since by contrasting simulations of diverse vascular conditions. The discussion is framed within the concept of mechanical homeostasis, with consideration of solid-fluid interactions, inflammation, and cell signaling highlighting both past accomplishments and future opportunities as we seek to understand better the evolving composition, geometry, and material behaviors of soft tissues under complex conditions.

1. INTRODUCTION

Many point to the mid-1960s as the beginning of the modern field of biomechanics [1]. Notwithstanding early work on the mechanics of tissue growth [2] and seminal work on adaptive elasticity in bone [3], it was the 1981 paper by R. Skalak that provided critical insight into methods for studying and modeling the growth of soft tissues using methods of nonlinear elasticity [4]. This work eventually led, in particular, to the widely used theory of finite volumetric growth [5]. It was twenty years after Skalak’s seminal work that we introduced (submitted August 2001) a theory of constrained mixtures [6] as an alternate approach for modeling together growth (changes in mass) and remodeling (changes in microstructure). Our approach was motivated by Y.C. Fung’s call for “mass-stress” constitutive relations [7], but more so by observations that soft tissues comprise diverse structurally significant constituents that have individual natural configurations, material properties, and rates of turnover.

The goal of this paper is to review and illustrate constrained mixture models (CMMs) for describing growth and remodeling (G&R) of blood vessels, which serve as an archetype for soft tissues, particularly given that they exhibit nonlinearly anisotropic material behaviors under finite deformations that depend on both a passive extracellular matrix and contractile capacity; blood vessels also experience complex fluid-solid interactions, with multiple interacting cell types dictating the evolving immunomechanics in many cases. The importance of G&R simulations is revealed further by the many different forms of G&R that drive or are driven by diverse vascular adaptations, diseases, and injuries as well as the success in modeling the in vivo development of tissue engineered vascular grafts, which are now in clinical trials. The goal of this review is to note some of the fundamental concepts and highlight progressive advances while providing insights into opportunities for further development and use of the theory of constrained mixtures in soft tissue mechanics.

2. MECHANOBIOLOGY and HOMEOSTASIS

Mechanobiology can be defined as the study of biological responses to mechanical stimuli. It has long been appreciated that the structure and function of biological tissues depend in large part on the mechanical loads to which they are exposed, with early recognition dating back at least to Galileo Galilei (1564-1642) and fundamental concepts advanced by Henry Gassett Davis (1807-1896), Julius Wolf (1836-1902), Wilhem Roux (1850-1924), and D’Arcy Thompson (1860-1948), among others. Nevertheless, it was not until the mid-1970s that cell culture studies revealed that multiple cell types respond directly to changes in mechanical loading via changes in gene expression, which in turn result in gene products that range from chemokines, cytokines, growth factors, proteases, and vasoactive molecules to structural constituents such as glycoproteins, glycosaminoglycans,and proteins, including the fibrillar collagens that endow most soft tissues with their tensile stiffness and strength. Importantly, many such responses stem from a mechanical homeostasis that exists at sub-cellular, cellular, and tissue levels, as revealed well in blood vessels [8].

The concept of homeostasis was advanced by Walter Cannon in the 1920s; it states that many biological and physiological processes tend to maintain key regulated variables within a defined range via negative feedback. Clearly, Cannon was careful in his choice of the prefix “homeo,” meaning similar to, rather than “homo,” meaning the same. In this way he emphasized that, when key variables are perturbed from homeostatic targets, or set-points, homeostasis tends to restore the regulated value toward, not necessarily to, the set-point. Hence, homeostasis tends to regulate quantities via proportional control, modulated by associated gains. Any theory of soft tissue G&R should seek to capture such homeostasis.

3. A CONSTRAINED MIXTURE THEORY

3.1. Guiding Remarks.

The first attempt to model the evolving mechanical behavior of a soft tissue by considering a constrained mixture with matrix deposition and degradation necessarily focused on a simple boundary value problem and simple conditions [9]. Foundations for a general CMM were proposed later [6], at which time we put forth six guiding statements that surprisingly ring true twenty years after:

1. Mathematically modeling growth and remodeling requires that one track local balances or imbalances in the continual production and removal of individual constituents, the thermomechanical state in which the constituents are formed, and how these constituents are organized.

2. Rates of production and removal of individual constituents are likely coupled to those of other constituents. Not only do these rates change from their normal/baseline values in response to changes in the mechanical environment, the baseline values may change during development and aging or due to functional adaptation.

3. Normal growth and remodeling tend to be a stable dynamical process, one that seeks to optimize structure and function with respect to yet unidentified parameters. In comparison to processes during development, there appear to be genetic and perhaps epigenetic constraints on this process during maturity.

4. New constituents are likely deposited under stress, but this stress need not equal the stress in the neighboring, pre-existing constituents. As this “deposition-stress” has yet to be identified, it must be hypothesized, the validation of which may be found via an examination of the associated natural configurations.

5. Within the continuum assumption, each neighborhood can have a different natural configuration κ_n. If all sufficiently small neighborhoods have the same natural configuration, the body will be stress-free when traction-free; if not, the traction-free body will be stressed provided that the gradients in the mappings that take particles from the abstract body and place them in the gross natural configuration ${\mathcal{B}}_n$ do not equal the identity tensor or result from rigid body motions.

6. As each constituent within a neighborhood (about a point) can have a different natural configuration, soft tissues are materially nonuniform in general although on a macro-scale they may be considered to be homogenous. Since each of these natural configurations can evolve in response to changes in the mechanical environment, the non-uniformity, material symmetry, and material stiffness are expected to evolve in general.

These remarks were motivated by myriad observations in the literature on mechanobiology and they inspired the theoretical framework suggested, which admitted for the first time evolving natural configurations for individual structurally significant constituents that are deposited within extant matrix at individual pre-stresses and thereafter begin to degrade at different rates.

3.2. Wall Properties, Wall Mechanics.

It is emphasized, however, that CMMs need not be used only to quantify G&R. Rather they also prove useful in studying soft tissue mechanics in the traditional manner. Regarding Remark 4, for example, we used a CMM of the common carotid artery to account for the different properties of the primary structurally significant constituents of the medial layer (consisting mainly of elastic fibers, smooth muscle cells, and reticular collagens) and adventitial layer (consisting mainly of fibrillar type I collagen and fibroblasts). We found advantages of selecting the current, rather than traction-free or stress-free, configuration as a computational reference, and that appropriate choices of constituent-specific pre-stresses (or associated pre-stretches) yield good descriptions of the experimentally measured bulk mechanical behavior as well as good predictions of the traction-free and nearly stress-free configurations [10]. Hence, supporting Remarks 5 and 6, it is the different natural configurations of individual constituents that give rise to residual stresses in the materially non-uniform artery. This interpretation is consistent with experimental findings through development [11] and avoids the need to prescribe residual stress-related opening angles a priori [12], which are never available from in vivo observation. It similarly avoids the need to conceptualize incompatible growth of neighborhoods within a materially uniform body through successive fictitious stress-free states as in the theory of finite volumetric growth.

3.3. Mass Balance.

Remark 1 strongly suggests that a theory of soft tissue G&R should be founded on a continuum theory of mixtures statement of mass balance, which can be written in spatial form as

$$\frac{\partial {\rho }^{\alpha }}{\partial s}+div\left({\rho }^{\alpha }{\mathbf{v}}^{\alpha }\right)={\overline{m}}^{\alpha }\forall \alpha =1,2,\dots ,N,$$ (1)

where ρ^α are apparent mass densities (mass of constituent α per current mixture volume), v^α are velocities (no sum on α), and ${\overline{m}}^{\alpha }$ are so-called mass exchange terms, interpreted here as net rates of change of mass density, each for up to N different structurally significant constituents α (e.g., collagen fibers, elastin, and glycosaminoglycans). Importantly, ${\overline{m}}^{\alpha }$ can have any signed value, negative (as in atrophy), zero (as in maintenance), or positive (as in growth). Regardless, it must be prescribed constitutively. Based on mechanobiological observations, ${\overline{m}}^{\alpha }$ should depend on changes in the mechanical state from homeostatic, among other factors. It proves convenient to account for this net rate of change in one of two ways. First, one can let ${\overline{m}}^{\alpha }(s)=m^{\alpha }(s)-r^{\alpha }(s)$, where m^α > 0 is the true rate of mass density production and r^α > 0 is the true rate of removal; this approach is useful when formulating a rate-based approach. Second, one can pursue a heredity integral-based formulation.

As in the original formulation, the focus herein is on the heredity integral-based approach, which stems from the three key assumptions of CMMs. Assumption 1: Let the motion of each structurally significant constituent α be constrained to equal that of the mixture, that is, let x^α = x despite differences in natural configurations and thus original positions (i.e., X^α ≠ X). For this reason, velocities of the individual constituents similarly equal that of the mixture (v^α = v) while the constituent-specific deformation gradient tensors necessarily differ (i.e., ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)\ne \mathbf{F}\left(s\right),$ where n(τ) denotes a possibly evolving natural configuration ${\kappa }_n^{\alpha }(\tau )$ for constituent α that is produced at G&R time τ and survives at current G&R time s). Importantly, relative to time scales associated with mechanical loading, including that due to the cardiac cycle, G&R tend to occur continually, but slowly; it is thus reasonable to neglect v^α in most cases. We thus find that equation 1 can be integrated directly in spatial or referential form, leading to Assumption 2: Account for mass exchanges in heredity integral form by considering a true rate of production function m^α(τ) > 0 and a non-dimensional survival function q^α(s, τ) ∈ [0,1], both of which are to be prescribed constitutively. Hence, equation 1 yields [13]

$${\rho }^{\alpha }\left(s\right)={\rho }^{\alpha }\left(0\right)Q^{\alpha }\left(s\right)+{\int }_0^s{m}^{\alpha }\left(\tau \right)q^{\alpha }\left(s,\tau \right)d\tau \forall \alpha =1,2,\dots ,N,$$ (2)

where Q^α(s) ∈ [0,1] is another survival function, with Q^α(0) = 1. This form of mass balance arises when integrating from the distant past (at which time it is assumed that mass density was zero) to the current G&R time s well into maturity, with G&R time τ = 0 marking a time of interest in maturity at which the tissue is perturbed from its homeostatic state. Note, too, that the mixture mass density is ρ(s) = ∑ρ^α(s). Assumption 3: The mass density of many soft tissues does not change appreciably during most cases of G&R, hence let ρ(s) = ρ(0), which is to say that G&R related changes in mass are proportional to changes in volume.

3.4. Linear momentum balance.

Although the classical continuum theory of mixtures similarly provides a relation in terms of constituent stresses and a momentum exchange, prescribing such exchanges can be problematic in soft tissues as they grow and remodel. For this reason, we adopt a rule-of-mixtures relation for the stresses and satisfy the classical linear momentum balance, typically in the absence of body forces. Consistent with the aforementioned assumption that G&R tend to be slow processes that can be studied quasi-statically at all G&R times s, let

$$div\left(\mathbf{t}\right)=\rho \mathbf{a}\to div\left(\mathbf{t}\right)=\mathbf{0},$$ (3)

where t is the Cauchy stress tensor, also to be prescribed constitutively. Consequently, the G&R problem can be solved in strong or weak form using methods of finite elasticity, consistent with the original ideas of R. Skalak and Y.C. Fung.

3.5. Constitutive Relations.

As in all cases in nonlinear continuum mechanics, one of the greatest challenges is identification of appropriate constitutive relations. In heredity integral-based CMMs, there is need for three classes of relations: one for the true rate of mass density production (i.e., m^α(τ) > 0 for each constituent), one for mass removal (i.e., survival q^α(s, τ) ∈ [0,1] of each constituent), and one for Cauchy stress (for a rule-of-mixtures). In finite elasticity, the continuum-level Cauchy stress can be determined given a stored energy function W, defined per unit reference mixture volume, namely

$$\mathbf{t}\left(\text{s}\right)=\frac{2}{\mathit{det}\mathbf{F}\left(\text{s}\right)}\mathbf{F}\left(\text{s}\right)\frac{\partial W\left(s\right)}{\partial \mathbf{C}\left(\text{s}\right)}{\mathbf{F}}^T\left(s\right),$$ (4)

where F(s) is the deformation gradient tensor for the mixture at G&R time s and C(s) = F^T(s)F(s) is the associated right Cauchy-Green tensor; detF is constant only during transient loading at a fixed G&R time since mass and volume can both evolve in general. Conceptually, in a simple rule-of-mixtures one can write W = ∑ϕ^α W^α, where ϕ^α are constituent-specific mass fractions. Yet, consistent with Remark 6 above, the constituent-specific mass fractions and stored energies can evolve in response to diverse stimuli; there was a need for more generality.

Constitutive relations can be identified in one of three ways: theoretically, experimentally, or simply postulated. Although theoretically determined relations are the best in principle, few such relations have proven useful; although experimentally determined relations are robust, there exist few situations wherein response functions can be identified directly from data. Consistent with these caveats, we postulated constituent-specific stored energy functions of the form [e.g., 13–15]

$$\rho W^{\alpha }\left(s\right)={\rho }^{\alpha }\left(0\right)Q^{\alpha }\left(s\right){\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(0\right)}^{\alpha }\left(s\right)\right)+{\int }_0^s{m}^{\alpha }\left(\tau \right)q^{\alpha }\left(s,\tau \right){\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(\mathrm{\tau }\right)}^{\alpha }\left(s\right)\right)d\tau ,$$ (5)

for each constituent α = 1,2, …, N, where ρ is the mass density of the tissue (mixture) per current volume and ${\widehat{W}}^{\alpha }$ are constituent-specific stored energy functions, per reference volume of the mixture, that depend on constituent-specific deformation gradients ${\mathbf{F}}_{n(\tau )}^{\alpha }(s)$, with τ ∈ [0, s] the G&R time at which that constituent was deposited in maturity, typically after a perturbation to the homeostatic state. It can be shown [13] that ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)=\mathbf{F}\left(s\right){\mathbf{F}}^{-1}\left(\tau \right){\mathbf{G}}^{\alpha }\left(\tau \right),$ where F(s) and F(τ) are tissue-level deformation gradients and, consistent with the aforementioned Remark 4, G^α(τ) is a “deposition stretch” at which the new constituent was deposited within extant matrix at G&R time τ (Figure 1). Note the special case at G&R time τ = s, at which ${\mathbf{F}}_{n(s)}^{\alpha }(s)={\mathbf{G}}^{\alpha }\mathbf{\left(}s\mathbf{\right)},$ consistent with G^α being a deposition stretch tensor (with R = I in the polar decomposition theorem at that time).

Figure 1.

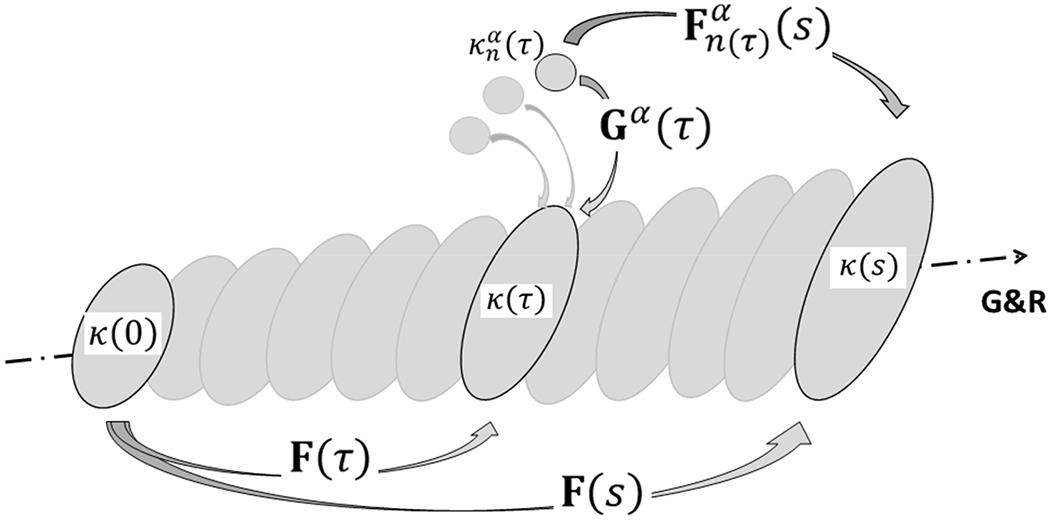
Schema of finite deformations associated with growth and remodeling (G&R) of a soft tissue in maturity using a constrained mixture model. Individual constituents α = 1,2, …, N are assumed to be deposited within extant matrix at preferred deposition stretches G^α(τ) at G&R time τ ∈ [0, s], each relative to individual evolving natural (stress-free) configurations ${\kappa }_n^{\alpha }(\tau )$. Thereafter, these constituents may deform further because they are constrained to move with the tissue, the in vivo configuration of which evolves from κ(τ) at time τ to κ(s) at time s. Note that the reference configuration κ(0) for the tissue need not be stress-free or traction-free; indeed an in vivo configuration such as that near mean arterial pressure is often convenient in vascular mechanics. Finally, it is the constituent-specific deformation ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)=\mathbf{F}\left(s\right){\mathbf{F}}^{-1}\left(\tau \right){\mathbf{G}}^{\alpha }\left(\tau \right)$ that is most important because the associated constituent-specific stored energy function depends on this deformation alone. Of course, at the time of deposition, ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(\tau \right)\equiv {\mathbf{G}}^{\alpha }\left(\tau \right)$.

This constitutive postulate (equation 5) is best appreciated by considering two special cases [14]. First, at s = 0, the time in maturity just prior to a perturbation, we find

$$\rho W^{\alpha }\left(0\right)={\rho }^{\alpha }\left(0\right)Q^{\alpha }\left(0\right){\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(0\right)}^{\alpha }\left(0\right)\right)\to W^{\alpha }\left(0\right)=\frac{{\rho }^{\alpha }\left(0\right)}{\rho \left(0\right)}{\widehat{W}}^{\alpha }\left(0\right)={\varphi }^{\alpha }\left(0\right){\widehat{W}}^{\alpha }\left(0\right),$$ (6)

which recovers the desired rule-of-mixtures relation with $W\left(0\right)=\sum W^{\alpha }\left(0\right)=\sum {\varphi }^{\alpha }\left(0\right){\widehat{W}}^{\alpha }\left(0\right)$. Second, consistent with Remarks 1 and 4, consider a situation wherein tissue turns over in an unchanging (homeostatic) configuration whereby ${\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)={\mathbf{F}}_{n\left(0\right)}^{\alpha }\left(s\right)$, which is to say that neither the constituent-specific deformation nor the associated stored energy function depends on G&R time τ. As a result, equation 5 can be written (using equation 2)

$$\rho W^{\alpha }\left(s\right)=\left({\rho }^{\alpha }(0)Q^{\alpha }(s)+{\int }_0^s{m}^{\alpha }(\tau )q^{\alpha }(s,\tau )d\tau \right){\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n(0)}^{\alpha }(s)\right)={\rho }^{\alpha }(s){\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n(0)}^{\alpha }(s)\right),$$ (7)₁

whereby

$$W^{\alpha }\left(s\right)=\frac{{\rho }^{\alpha }\left(s\right)}{\rho \left(s\right)}{\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(0\right)}^{\alpha }\left(s\right)\right)={\varphi }^{\alpha }\left(s\right){\widehat{W}}^{\alpha }\left(s\right),$$ (7)₂

which, again recovers the desired rule-of-mixtures relation at each G&R time s with $W\left(s\right)=\sum {\varphi }^{\alpha }\left(s\right){\widehat{W}}^{\alpha }\left(s\right)$. The most important validation of the utility of any postulated constitutive relation is, however, the experimental test, examples of which are discussed below. First, however, note that various forms of equation 5 can be postulated similarly when letting ${\widehat{W}}^{\alpha }$ be defined per mixture volume (strain energy function), per mixture mass (Helmholtz function), per constituent volume, or per constituent mass. Equivalencies can be realized via use of the Jacobian of the deformation gradient and/or the true constituent mass density (constituent mass defined per constituent volume, not mixture volume). From a practical perspective, differences in these many definitions manifest primarily as differences in the values of the dimensioned material parameters in the energy function, which are determined via best-fits to appropriate data. We are thus reminded that, albeit structurally motivated, the current CMM framework is yet phenomenological because experimental details on many microstructural features (e.g., different types of cross-links, physical entanglements, secondary bonds) remain lacking.

Next, consider possible functional forms for the three key constitutive relations: production m^α(τ), removal q^α(s, τ), and mechanical properties of that which persists ${\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)\right)$, subject to useful guiding principles such as determinism, material frame indifference, and so forth. Recalling Remark 1, many cells and structurally significant constituents are continually produced and removed in the vasculature, with cells involved in matrix turnover including smooth muscle cells, fibroblasts, and resident macrophages. This continual, albeit typically slow, turnover is intuitive since all biological materials – cells and extracellular matrix – have a finite half-life and typically are replaced unless there is a physiological constraint against such (cf. Remark 3). One such constraint in the vasculature is that functional elastin appears to be produced, organized, and cross-linked early in life; that is, there is a biological constraint against such production later in life. Fortunately, the normal half-life of elastin is on the order of 50+ years, hence endowing the wall with the requisite resilience for long periods except in cases of particular mutations or disease states [16].

Copious experimental studies reveal baseline rates of production of structurally significant constituents (e.g., fibrillar collagens I and III as well as glycosaminoglycans) in maturity, denoted here as $m_0^{\alpha }$ with subscript o denoting an original, homeostatic, value. Consistent with Remark 2, one can allow $m_0^{\alpha }$ to evolve in cases such as development or aging, though it is typically constant under normal conditions in maturity. Many studies report increases in production in maturity, as a function of biochemical or biomechanical stimuli, as evolving (non-dimensional) fold-changes, as, for example, $m^{\alpha }(\tau )/m_0^{\alpha }$ at G&R time τ. These fold-changes often appear to follow sigmoidal relations (Figure 2), saturating as the mechano-stimulus increases or decreases. Two of the primary hemodynamically induced stresses in the vasculature can be represented by the mean flow-induced wall shear stress τ_w and the mean pressure-induced circumferential stress σ_θ, thus to first approximation consider the fold-changes in production to scale linearly with differences in mean values of these intramural and shear Cauchy stresses relative to original homeostatic target values, as, for example,

$$m^{\alpha }\left(\tau \right)=m_0^{\alpha }\left(1+K_{\sigma }^{\alpha }\Delta \sigma \left(\tau \right)-K_{{\tau }_w}^{\alpha }\Delta {\tau }_w\left(\tau \right)\right),$$ (8)

where the parameters $K_i^{\alpha }$ are constituent-specific gains that capture the sensitivity of the proportional response. Note that increases in intramural stress above baseline tend to increase rates of matrix production due in part to local production of the cytokine transforming growth factor-beta; conversely, increases in flow-induced wall shear stress tend to decrease these rates due to endothelial production of the biomolecule nitric oxide (NO) whereas decreases in wall shear stress tend to increase these rates due to endothelial production of endothelin-1 (ET-1). That is, NO is both a potent paracrine vasodilator and attenuator of matrix production; ET-1 has opposite effects [8,12]. It is for these reasons that the negative sign precedes the shear stress term.

Figure 2.

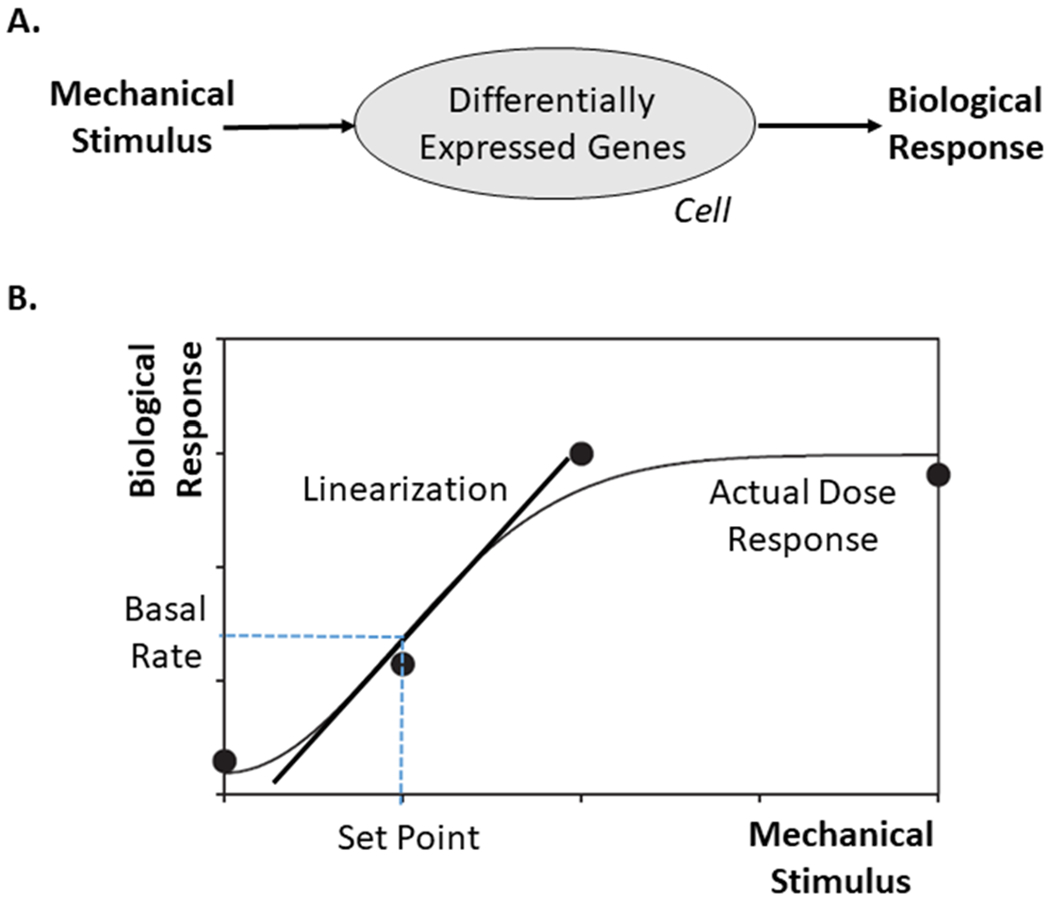
A. Schema of a mechanobiological response: a mechanical stimulus drives differential gene expression, leading to different gene products that define the biological response. B. Typical sigmoidal biological response to a mechanical stimulus, as, for example, production of eNOS by endothelial cells in response to increased wall shear stress or production of collagen by smooth muscle cells or fibroblasts in response to increased intramural stress. Importantly, this nonlinear, saturating response can be approximated linearly for changes about the homeostatic set-point, which is often sufficient if the biological response is fast enough to prevent stresses from deviating too much from homeostatic.

It proves convenient to consider normalized stress differences in equation 8 by dividing the actual differences by the original homeostatic values because of the orders of magnitude differences in these two stresses. Wall shear stresses are on the order of 1.5 Pa and intramural (circumferential and axial) stresses on the order of 150 kPa (though values differ across species, including ~6.5 Pa and 250 kPa, respectively, in the mouse). It also proves convenient to use a coordinate invariant measure of the multiaxial intramural stress, as, for example, the first invariant of the Cauchy stress. Yet, given that the (compressive) radial stress is significantly lower (~ −6 kPa) than both of the in-plane (tensile) components (~ 150 kPa), it is often neglected. Hence, consider the following stress-differences at the time of deposition τ of the form,

$$\Delta \sigma \left(\tau \right)=\frac{\left(1-\delta \right)\left({\sigma }_{\theta }\left(\tau \right)+{\sigma }_z\left(\tau \right)\right)-\left({\sigma }_{\theta }^0+{\sigma }_z^0\right)}{\left({\sigma }_{\theta }^0+{\sigma }_z^0\right)},\Delta {\tau }_w\left(\tau \right)=\frac{\left(1-\xi \right){\tau }_w\left(\tau \right)-{\tau }_w^0}{{\tau }_w^0},$$ (9)

where quantities with a superscript o represent original (homeostatic) values, or set-points in the parlance of homeostasis. The parameters δ and ξ remind us that, from the perspective of mechanobiology, it is actually not the value of the stress that is important but rather the value of stress that is perceived (i.e., sensed) by the cell. Here, δ = 0 and ξ = 0 for perfect mechanosensing (e.g., by intramural and endothelial cells, respectively, in blood vessels); δ ∈ (0,1] and ξ ∈ (0,1] for compromised mechanosensing. Whereas specific values of the non-dimensional gain parameters $K_i^{\alpha }$ in equation 8 are determined from experimental data, one must enforce the condition that the true mass density production m^α(τ) > 0. This condition is satisfied by $K_{\sigma }^{\alpha }=K_{{\tau }_w}^{\alpha }=0$ as long as $m_0^{\alpha }>0$, but then there is no mechano-regulation. We previously showed that lack of mechano-regulation results in an inability of a numerical vessel to adapt to even modest perturbations in flow or pressure [14], consistent with empirical observations that vascular cells are highly sensitive to changes in mechanical stimuli. Hence, these gains must be strictly positive. Conversely, note that the stress differences in equation 9 go to zero when current stresses equal the homeostatic values, thus returning rates of production to baseline values via equation 8 as they should. Following the great adage of A. Einstein that “Everything should be made as simple as possible, but no simpler,” recall that the typical sigmoidal dose response curves (Figure 2) are only approximated by equation 8 near the homeostatic values and the stresses in equation 9 are mean, not pointwise, values. Both assumptions can be relaxed, yet that this simple relation surprisingly captures many actual vascular responses, as noted more below.

Next, consider the survival function q^α(s, τ) ∈ [0,1]. Again, recall that all biological materials have a finite half-life, often with natural death (apoptosis) of cells and degradation (proteolysis) of matrix following a first-order type of kinetics. Hence, consider

$$q^{\alpha }\left(s,\tau \right)=\exp \left(-{\int }_{\tau }^s{k}^{\alpha }\left(t\right)dt\right),$$ (10)

where k^α(t) is a possibly evolving constituent-specific rate parameter (not constant) having units of inverse time. In the special case where k^α(t) is constant for constituent α, say $k_0^{\alpha }$, we see that $q^{\alpha }\left(s-\tau \right)=\exp \left(-k_0^{\alpha }\left(s-\tau \right)\right)$, thus yielding the desired first order decay, with q^α(τ − τ) = q^α(0) = 1 as it should, meaning that all material produced at any G&R time τ yet survives at time τ. In general, however, these rate parameters depend on various biochemical and biomechanical stimuli. Consider a simple case of the effect of intramural stress alone. Experiments reveal that degradation / death rates can increase both for increases (due to damage) and decreases (due to teleologically favorable atrophy) in stress. Hence, let

$$k^{\alpha }\left(t\right)=k_0^{\alpha }\left(1+{\omega }^{\alpha }\Delta \sigma {\left(t\right)}^2\right)$$ (11)

where ω^α is a non-dimensional weight parameter, often set to unity for simplicity and lack of sufficient data to determine its value. Again, this relation recovers the homeostatic rate $k_0^{\alpha }$ parameter when the stress difference is driven to zero.

At this point it is useful to consider further the special case wherein the stress differences are zero, that is, when cells and tissues turnover at constant rates within an unchanging homeostatic state. In this case the rates of production and removal reduce to their homeostatic values, and equation 2 can be written,

$${\rho }^{\alpha }\left(s\right)={\rho }^{\alpha }\left(0\right)e^{-k_0^{\alpha }s}+\frac{m_0^{\alpha }}{k_0^{\alpha }}{e}^{-k_0^{\alpha }s}{\int }_0^s{e}^{k_0^{\alpha }\tau }{k}_0^{\alpha }d\tau =\frac{m_0^{\alpha }}{k_0^{\alpha }}+\left({\rho }^{\alpha }\left(0\right)-\frac{m_0^{\alpha }}{k_0^{\alpha }}\right)e^{-k_0^{\alpha }s}\forall s,$$ (12)

with the constraint that ρ^α(s) ≡ ρ^α(0) because apparent mass densities remain the same within an persistent homeostatic state. Hence, ${\rho }^{\alpha }\left(s\right)\equiv m_0^{\alpha }/k_0^{\alpha }$ in this state, which is to say that tissue maintenance requires balanced rates of production and removal, here related via the original constituent-specific apparent mass density. This finding is particularly useful because rates of degradation (half-lives) can be easier to determine experimentally than rates of production. Table 1 summarizes various functional forms for production and removal, illustrating how they have evolved over the years and how they can be specialized for different vascular conditions.

Table 1.

The full (heredity integral based) constrained mixture theory requires three classes of constitutive relations for each structurally significant constituent α = 1, 2, 3, …, N to capture the evolving composition and material properties of a mature tissue for all G&R times τ ∈ [0, s]: constitutive-specific rates of mass density production m^α(τ) > 0, mass survival functions q^α(s − τ) ∈ [0,1], and stored energy functions ${\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)\right)>0,$ the latter of which include information on the deposition stretch and orientation. Although the basic framework has persisted over the past 20 years, notation has evolved to increase clarity: for example, G&R time t changed to time s, subscript or superscript h for homeostatic changed to o for original homeostatic (to accommodate possible adaptive homeostasis), constituent index k changed to α, the rate parameter $K_q^{\alpha }$ changed to k^α, and dimensional rate-gain parameters $K_g^{\alpha }$ changed to non-dimensional gain parameters $K_j^{\alpha }$, which can be subscripted to denote j = stress related or inflammation related. Of course, because these functions are constitutive, they necessarily differ for different problems, depending on 2D versus 3D formulations as well as, in some cases, on particular stresses of concern (constituent-specific versus tissue level), the presence of blood clots, damage to or healing of the functional cells, and the presence of inflammation. Listed here are a few of the key forms for the production and removal functions; the stored energy functions tend to follow standard forms, as, for example, neoHooken or Fung exponential. To facilitate comparisons here, some notations have been changed as appropriate for consistency with current conventions.

Year/Ref	Production Functions	Survival Functions
2005/2006 [13,26]	$m^{\alpha }(\tau )=\frac{\rho (\tau )}{\rho (0)}{m}_0^{\alpha }(1+K_g({\sigma }^{\alpha }(\tau )-{\sigma }_o))$	$q^{\alpha }\left(\tilde{\tau }\right)=\{\begin{array}{ll}1& 0\le \tilde{\tau }<t_1\\ 0.5\left(\cos \left(\frac{\pi \left(\tilde{\tau }-t_1\right)}{t_2-t_1}\right)+1\right)& t_1\le \tilde{\tau }\le t_2\\ 0& t_2<\tilde{\tau }\end{array}$
--	General Form          $m^{\alpha }(\tau )=m_0^{\alpha }{f}^{\alpha }(\tau )$ with	General Form    $q^{\alpha }\left(s,\tau \right)=\exp \left(-{\int }_{\tau }^s{k}_0^{\alpha }{g}^{\alpha }\left(t\right)dt\right)$ with
2007 [42]	$f^{\alpha }(\tau )=\frac{{\rho }^{\alpha }(\tau )}{{\rho }^{\alpha }(0)}(1+K_{\sigma }^{\alpha }\Delta {\sigma }^{\alpha }+K_C^{\alpha }\Delta C)$	$g^{\alpha }\left(t\right)=1+\omega {\left(<T^{\alpha }\left(t\right)-T_c^{\alpha }>\right)}^2$
2009,2009 [14,103]	$f^{\alpha }(\tau )=1+K_{\sigma }^{\alpha }\Delta \sigma +K_{\sigma }^{\alpha }\Delta C$	gα(t) = 1 + (ΔTα(t))2
2012,2013 [28,29]	$f^{\alpha }(\tau )=\frac{{\rho }^{\alpha }(\tau )}{{\rho }^{\alpha }(0)}(1+K_{\sigma }^{\alpha }\Delta {\sigma }^{\alpha })$	gα(t) = 1 + ω(ΔTα(t))2
2014,2015 [73,76]	$f^{\alpha }\left(\tau \right)=\left(1-e^{-\tau }\right)\left(1+K_{\sigma }^{\alpha }\Delta \sigma +K_{\phi }^{\alpha }\beta \tau e^{-\beta \tau }\right)$	gα(t) = 1 (stress driven) or gα(t) = ω (inflammation)
2015,2017 [48,49]	$f^{\alpha }\left(\tau \right)=\frac{{\rho }^{\alpha }\left(\tau \right)}{{\rho }^{\alpha }\left(0\right)}\left(1+K_{\sigma }^{\alpha }\Delta \sigma -K_{\sigma }^{\alpha }\Delta {\tau }_w\right)$	gα(t) = 1 + (ΔTα(t))2
2018,2020 [75,78]	$f^{\alpha }\left(\tau \right)=\left(1-e^{-\tau }\right)\left(1+K_{\sigma }^{\alpha }\Delta \sigma -K_{\sigma }^{\alpha }\Delta {\tau }_w+K_{\phi }^{\alpha }{\delta }^{\beta }{\tau }^{\beta -1}{e}^{-\delta \tau }\right)$	$g^{\alpha }\left(t\right)=1+k_D^{\alpha }$ (stress) or $g^{\alpha }\left(t\right)=1+k_D^{\phi }$ (inflam)
2019 [69]	$f^{\alpha }\left(\tau \right)=1+K_{\sigma }^{\alpha }\Delta \sigma -K_{\sigma }^{\alpha }\Delta {\tau }_w+K_{\sigma }^{\alpha }\Delta {\rho }_{\phi },$ with $m_0^{\alpha }\to {\rho }^{\alpha }\left(\tau \right)k^{\alpha }\left(\tau \right)$	gα(t) = 1 + (Δσ)2
2020 [70]	$f^{\alpha }\left(\tau \right)=1+{\mathcal{F}}_{\sigma }^{\alpha }\left(\Delta \sigma \right)-{\mathcal{F}}_{{\tau }_w}^{\alpha }\left(\Delta {\tau }_w\right)+{\mathcal{F}}_{\phi }^{\alpha }\left(\Delta {\rho }_{\phi }\right),$ with $m_0^{\alpha }\to {\rho }^{\alpha }\left(\tau \right)k^{\alpha }\left(\tau \right)$	$g^{\alpha }\left(t\right)={\mathcal{H}}^{\alpha }\left(\Delta {\rho }_{\phi }\right)\left(1+{\left(\Delta \sigma \right)}^2\right)$

Note that ρ here represents a mass density having units of mass per reference or current volume (or area), depending on context, $m_0^{\alpha }$ is a constant basal production rate having units of mass per volume (or area, again reference or current) per time, and $k_0^{\alpha }$ is a constant basal removal rate having units of inverse time. Hence, f^α and g^α are nondimensional functions of time that vary spatially depending on that which they depend on – stress, thrombus, inflammation, etc. Moreover, Δσ ≡ Δσ(τ) and Δτ_w ≡ Δτ_w(τ) are normalized differences in scalar measures (e.g., magnitude or first invariant) of Cauchy stress from their homeostatic values, either intramural or wall shear, respectively, while ΔC ≡ ΔC(τ) is a difference in the ratio of vasoconstrictors to vasodilators (including shear stress dependence) and Δρ_φ is a normalized measure of inflammation. T^α is a fiber tension.

Finally, we note that functional forms for the constituent-specific stored energy functions are more straightforward to postulate, as, for example, neo-Hookean type forms for vascular elastin and Fung-Exponential forms for fibrillar collagens. We thus refer the reader to the original papers for these forms. It is important to note, however, that these constituent-specific relations depend on the constituent-specific deformation gradient (or more precisely the right Cauchy-Green tensor), thus the deposition stretch becomes a constitutive parameter (cf. Remark 4 above). That is, ${\widehat{W}}^{\alpha }\left({\mathbf{F}}_{n\left(\tau \right)}^{\alpha }\left(s\right)\right)={\widehat{W}}^{\alpha }\left(\mathbf{F}\left(s\right){\mathbf{F}}^{-1}\left(\tau \right)G^{\alpha }\left(\tau \right)\right)$.

Figure 3 illustrates the overall G&R formulation described here for blood vessels, with the regulated variables in the homeostatic system often being hemodynamically induced intramural and wall shear stresses, which are determined computationally in strong or weak form given information on the evolving geometry, material properties, and applied loads, and which then dictate subsequent changes (if appropriate) in mass production via the constituent-specific gain parameters K^α. Note that the constituents incorporated within the extant matrix at particular deposition stretches G^α, and in some cases particular orientations α^α, will begin to degrade via first order type kinetics according to the associated rate parameters k^α. Such turnover can, of course, evolve the material composition, and thus geometry and properties, which then feedback to alter the stress stimulus, which in a homeostatic process will be returned toward normal thus ensuring a stable system.

Figure 3.

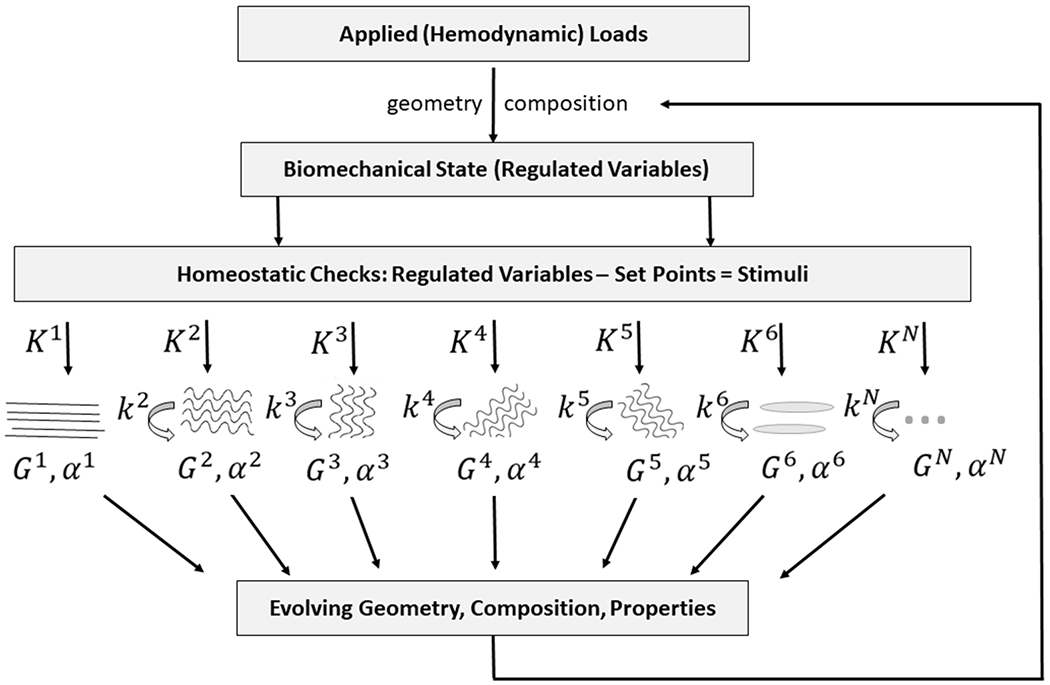
Schema of negative feedback characteristic of mechanical homeostasis in blood vessels and associated modeling via a constrained mixture model of N constituents. For illustrative purposes, constituent N=1 is assumed to not degrade during the G&R period of interest, as, for example elastic fibers under normal conditions in maturity. Importantly, the other constituents are deposited at a rate modulated by gain K^α > 0 and they degrade at rate k^α > 0, noting that deposition is at a homeostatic prestretch G^α >1 and particular orientation defined by angle α^α.

4. VASCULAR APPLICATIONS

At the time that we were finalizing our ideas on a CMM for soft tissue G&R (summer of 2001), I was similarly finalizing a manuscript for a book to be published by Springer on Cardiovascular Solid Mechanics [12]. In it, I noted many different manifestations of vascular G&R (Figure 9.34 therein) with the hope that a common framework would be able to describe and eventually predict such diverse situations. Only from a common approach did I feel that we could achieve general understanding. Here, I briefly review multiple papers that have appeared over the past twenty years, which show that CMMs provide such a framework when enriched with problem-specific constitutive relations (Figure 4).

Figure 4.

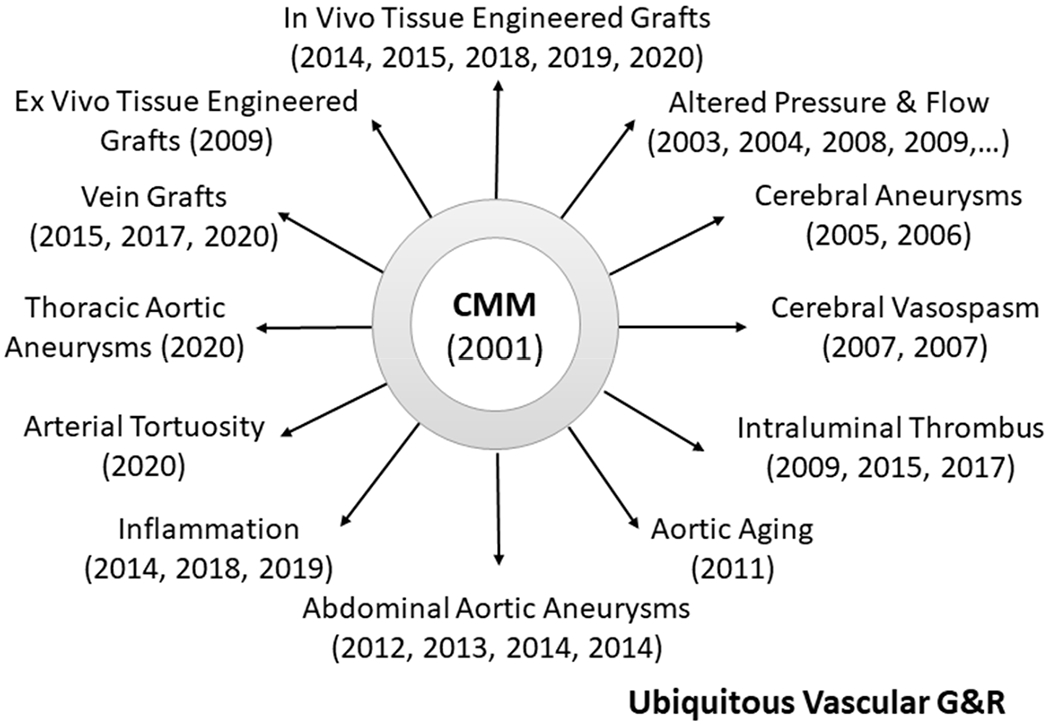
Chronological summary of implementations of the same constrained mixture model (CMM) by one group to study vascular adaptations, diseases, and interventions. That one basic theoretical framework, enriched with condition-specific constitutive relations for mass production, removal, and constituent properties, can describe such diverse situations provides some confidence in the general utility of the approach.

4.1. Adaptations – Axial Extension, Flow, Pressure.

Arteries exhibit a remarkable ability to adapt to modest sustained alterations in blood flow Q and blood pressure P, the former by adjusting luminal radius a and the latter mainly by adjusting wall thickness h [17,18]. Indeed, given simple relations for mean stresses, both flow-induced wall shear τ_w = 4μQ/πa³ (with μ the viscosity) and pressure-induced circumferential stress σ_θ = Pa/h, it is easy to show that ${\tau }_w\to {\tau }_w^0$ and ${\sigma }_{\theta }\to {\sigma }_{\theta }^0$ require a mechanoadaptation whereby a → ε^1/3a₀ and h → γε^1/3h₀ if ε = Q/Q₀ and γ = P/P₀ denote fold-changes in flow and pressure, respectively. The key question, however, is how do the cells effect such changes? This question can only be answered with an understanding of the mechanobiology and a theory of G&R. Early on we used a simplified version of the CMM given the assumption that there were only two states, original homeostatic and that associated with a constant sustained alteration in hemodynamics [19,20], which was particularly appropriate for bioreactor applications. This work revealed the importance of the physiologic constraint that functional elastin cannot be produced in maturity; that is, responses to altered flow and pressure cannot be perfect in maturity because elastin does not turnover, though in the spirit of mechanical homeostasis the adaptations tend to drive stresses back toward homeostatic values. We also used a heredity integral-based formulation to account for the continuous turnover of matrix in evolving states while introducing the concept of deposition stretches [21] consistent with the postulate of Fung [7] that “At homeostasis, all collagen fibers have the same stress, all elastin fibers have another stress…”. Whereas we initially assumed that mass density production could be described by the form $m^{\alpha }=m_0^{\alpha }+m_n^{\alpha }\Delta {\sigma }_{\theta }$, with $m_n^{\alpha }$ potentially depending on wall shear stress, we subsequently adopted the form in equation 8, or equivalently in terms of ratios of vasoconstrictors-to-vasodilators [14]. Importantly, we confirmed numerically the importance of Rodbard’s [22] observation that “Deviations of drag [wall shear stress] from this set-point initiate negative feedback mechanisms that return the magnitude of the drag to its set-point. In blood vessels, these effects appear to operate through two related mechanisms: an immediate physiological adjustment in vascular tone induced by the change in flow, and a delayed anatomical change that develops when the flow rate persists.” In other words, changes in smooth muscle cell tone and turnover of matrix in vaso-altered mechanical states are fundamental to effective mechanoadaptations (cf. Remark 1). Similarly, we confirmed numerically the essential role of mechano-sensing and mechano-regulation of matrix; the gains need to be strictly positive and deposition stretches need to be greater than unity to ensure physiologically meaningful predictions [14].

4.2. Aneurysms – Intracranial and Aortic.

Aneurysms are local dilatations of the arterial wall. The three most prevalent sites are the cerebral circulation (mainly saccular lesions) and aorta (fusiform lesions), both thoracic and abdominal [23–25]. Although lesions in these three sites share some histo-mechanical characteristics, particularly loss of elastic fiber integrity, loss of smooth muscle cells or at least their contractile function, and collagen remodeling, the etiologies and biomechanics are distinct. Initial studies of intracranial saccular aneurysms confirmed the importance of these three key histo-mechanical characteristics, but also the importance of the magnitude of the gains that model the mechano-sensitivity – simulated lesions had unbounded behaviors for small gains but stable bounded behaviors for larger gains [26]. Because of the severity of the insult that leads to rapidly enlarging aneurysms, the basal production rate was pre-multiplied by a term accounting for increasing numbers of synthetic cells. This work used a prescribed nonlinear survival function (Table 1), but demonstrated that the heredity integral-based CMM was amenable to nonlinear finite element implementation, albeit for axisymmetric membranes in this case. Also shown was the importance of the orientation of the newly deposited fibrillar collagen in controlling the rate of aneurysmal expansion [13].

A rate-based mixture model of G&R was first published by a group at Glasgow studying G&R of abdominal aortic aneurysms (AAAs), which were predicted to have an unbounded enlargement [27]. We subsequently showed that data from human AAAs could be captured well with a heredity integral-based CMM, with mass production depending on constituent-specific stress differences and inclusion of evolving anisotropy. Rates of enlargement depended in part on the age of onset, which is to say the initial degree of damage to the elastic fibers [28,29]. We showed further that AAA enlargement could be bounded and stable, particularly with increases in the rate of production of fibrillar collagen [30]. Importantly, the computational prediction that increased rates of collagen deposition can slow and bound lesion expansion preceded an experimental finding in a mouse model [31] that used a microRNA antagonist (antago-miR29b, which increases matrix synthesis), thus demonstrating utility of G&R models in generating and testing hypotheses. Importantly this work motivated studies of mechanobiological stability [32], which is discussed more below.

Thoracic aortic aneurysms (TAAs) are distinct in that they have a strong genetic predisposition and they appear to initiate independent of inflammation. Rather, multiple mutations that predispose to TAAs, including defects in the actomyosin apparatus or in microfibrils that connect the smooth muscle cells to the elastic laminae, suggest that dysfunctional mechano-sensing or mechano-regulation of matrix help drive the aneurysmal enlargement [33,34]. We used a new 3D finite element implementation (see below) of the CMM to contrast competing hypotheses regarding rates of enlargement of these lesions if any of the following were compromised: elastic fibers, collagen cross-links, smooth muscle contractility, mechano-sensing, or mechano-regulation [35]. Whereas compromised mechano-sensing can be modeled easily by the parameters δ or ξ in equation 9, compromised mechano-regulation can be modeled, in part, via altered deposition stretches G^α, which is to say that compromised cells may not be able to endow the newly deposited matrix with appropriate pre-stress. Importantly, the model confirmed that compromised mechano-sensing can have as devastating consequences on overall lesion enlargement as loss of elastic fiber integrity; by contrast, loss of vessel-level smooth muscle contractility had less severe consequences.

4.3. Thrombus – Extravascular and Intramural.

Thrombus is responsible for significant morbidity and mortality, including via myocardial infarction, ischemic and hemorrhagic stroke, and pulmonary embolism, among other conditions. Thrombus develops via a complicated series of chemical reactions, but phenomenological simulations provide some insight. Importantly, in addition to the rapid formation of a thrombus, there is a complex longer term process of resolution or maturation, the latter of which is part of normal wound healing wherein the fibrin-based thrombus transitions into collagen-based tissue [36]. The CMM is ideally suited to consider such evolution involving multiple constituents. We initially considered a generic case of thrombus maturation as observed in vitro [37], but later modeled in vivo data from a mouse model of venous occlusion by a maturing thrombus [38]. In these cases, it was seen that the standard CMM coupled easily with descriptions of the kinetics of chemical reactions (reaction-diffusion) involving non-structurally significant constituents as well as with modest fluid transport within a thrombus with evolving permeability. Methods of considering reactive constrained mixtures have been developed much further by others [39,40].

We also modeled two different cases whereby thrombus affects the underlying wall mechanics: extravascular thrombus in cerebral vasospasm and intraluminal thrombus in AAAs. Extravascular blood from a ruptured cerebral aneurysm or arteriovenous malformation enters the cerebrospinal fluid whereby it can contact adventitial collagen of nearby normal arteries, thus initiating and forming an extravascular clot. Myriad substances are released by such a clot, including vasoconstrictors such as thromboxane, serotonin, and thrombin, which together cause both local smooth muscle contraction and accelerated matrix turnover in evolving vasoconstricted states, thus entrenching the vessel at progressively smaller lumens that are unresponsive to exogenous vasodilators. The CMM framework allows one to model early clot-dominated effects on the wall followed by normal mechano-dominated effects once the clot resolves (with mass density production depending on differences in both wall stress and vasoconstrictors from homeostatic baseline values). Moreover, these studies showed how a CMM of evolving wall mechanics can be coupled easily to the hemodynamics, though based on a simple network pipe-flow analysis. Predictions reflected well the actual short time-course of inward remodeling in cerebral vasospasm and its resolution if the clot resolved [41,42].

Over 80% of AAAs contain a significant intraluminal thrombus (ILT), which can evolve into a complex layered structure having diverse effects on the underlying wall – stress shielding of intramural cells, reduced oxygen transport within the wall, and release of cytokines, growth factors, proteases, and vasoconstrictors, all of which can affect wall structure and function [24,43]. One can use computational fluid dynamics to predict where and to what extent such ILTs form [44,45], but a key question relates to the evolving biochemomechanical effects of the ILT on the wall, which may enlarge, arrest, or rupture. Again, the CMM approach proved useful for accounting for lesion G&R in the presence of an ILT [46,47]. In this particular application, the mass density production term depended on changes in the magnitude of the constituent-specific stress while separate production equations were postulated to account for growth of the ILT (including, embedded platelets, red blood cells, thrombin, plasmin, and fibrin) as the aneurysm expanded. As expected, effects ILT can be dramatic and must be considered.

4.4. Vein Grafts.

Atherosclerosis remains a leading cause of morbidity and mortality, particularly as a contributor to coronary and peripheral artery disease. Notwithstanding the widespread use of vascular stents, coronary artery bypass grafts using autologous veins remains a mainstay in clinical care. Yet, many venous bypass grafts fail, up to 50% within 10 years for coronary artery bypass grafts. Such failures result in large part from maladaptive G&R by the veins when placed in an arterial environment, which subjects these veins to marked step increases in both blood pressure (from venous values of 3-5 mmHg to arterial values of 120/80 mmHg or more) and blood flow. We used a CMM to study vein graft (mal)adaptation, with basic relations for mass production and removal functionally similar to those for arteries, though with different parameter values. These values were determined, in part, using formal methods of optimization [48,49], which had previously been shown to be well-suited for parameter estimations for CMMs [50]. Importantly, the numerical solutions suggested that the veins maladapt due in part to the sudden, step increase in pressure and flow, whereas more gradual loading could lessen the adverse G&R. A follow-up study showed that gradual loading, and thus more favorable adaptation, could be achieved in a vein graft by using a biodegradable external support that could initially off-load some of the hemodynamically induced loads of the arterial circulation and thus allow the cells to respond to gradual increases in stress [51].

4.5. Aging and Tortuosity.

Vascular aging is a dominant risk factor for diverse cardiovascular, renovascular, and neurovascular diseases and thus all-cause mortality. Effects of aging on arteries are many, including diffuse decreases in elastic fiber integrity, progressive endothelial dysfunction, attenuated or lost smooth muscle function, and collagen remodeling, often with increased cross-linking via non-enzymatic advanced glycation. Each of these effects are easily captured within a CMM, as shown previously [52]. This model confirmed the detrimental effects of compromised elastic fiber integrity and smooth muscle function, but suggested that increased collagen stiffening can actually help offset the hemodynamic loads and reduce diffuse enlargement, which is common in aging. Such locally favorable mechanobiological responses can yet adversely affect global hemodynamics, in this case with increased structural stiffness increasing the speed at which the pulse pressure wave travels, leading to wave reflections earlier in the cardiac cycle with possible central pulse pressure augmentation [53]. Such positive feedback loops must be identified and better addressed.

It has long been known that myriad conditions give rise to persistent abnormal bends, twists, turns, and kinks within arteries that are referred to as tortuosity. These include vascular aging as well as arterial tortuosity syndrome, genetic conditions that give rise to thoracic aortopathies, and hypertension, among others [54,55]. Recent interest in tortuosity has increased since it may be a biomarker for additional conditions. Regardless, most studies of tortuosity have been motivated by the common in vitro observation that a cylindrical segment of an artery can bend when pressurized, depending on the length of the specimen, the degree of fixed axial extension, and the pressure applied. This acute pressure-induced bending can be understood as an elastic buckling instability [56], which has been suggested by many to contribute to or underlie tortuosity, a persistent deviation from a normal straight geometry. Numerical studies using a CMM suggest, however, that tortuosity appears to arise from maladaptive G&R in the presence of local imperfections or irregularities in wall geometry, properties, or perivascular support [57]. Importantly, these simulations suggested further that multiple insults must coexist to drive tortuosity, which is to say that arteries are otherwise surprisingly fault tolerant.

4.6. Inflammation – Homeostatic and Pathologic.

Inflammation plays fundamental roles in many vascular diseases, including atherosclerosis [58], aortic and intracranial aneurysms [59,60], pulmonary and systemic hypertension [62,62], and vascular aging [63]. Similarly detrimental inflammatory effects on the aorta arise in obesity [64], diabetes [65], rheumatoid arthritis [66], and cystic fibrosis [67]. Notwithstanding the importance of each of these conditions, it is also becoming evident that inflammation can play key roles in hypertension, which increasingly affects more and more people. In this regard, it is important to note that immune processes evolved to protect against life-threatening insults, particularly viral and bacterial, and thus are prioritized [68]. It is becoming increasingly clear that prioritized processes can over-ride homeostatic processes, including mechanical, by changing the biological response by re-setting homeostatic set-points, gains, and rates (cf. Figure 3). Indeed, we discovered using a CMM that it was possible to describe the evolving geometry and properties of the thoracic aorta in an angiotensin II-induced model of hypertension in normal wild-type (C57BL/6) mice using standard relations for arterial G&R enhanced with inflammation-dependent stimuli [69], but not in angiotensin II-induced hypertension in atheroprone (Apoe^−/− on a C57BL/6 background) mice. In the latter, we needed to adjust gains and rate parameters [70] consistent with the over-riding role of exuberant inflammatory cell infiltration. Indeed, it was the model that first suggested this need, which was justified based on independent findings in the immunobiology literature [71]. Although we have not studied atherosclerosis using CMMs, it would be expected that mechanical effects could help explain the Glagov phenomena but that inflammatory stimuli likely dominate since the development of an occluding lesion is not mechanobiologically favorable.

4.7. Tissue Engineered Vascular Grafts (TEVGs).

Tissue engineering seeks to develop living constructs for replacing, repairing, or regenerating diseased or injured tissues. Many different approaches have emerged, with different TEVGs now in clinical trials. Importantly, there are two basic strategies for developing such grafts. First, one can seed vascular cells on a biodegradable scaffold ex vivo within a bioreactor environment and allow the cells to produce matrix to replace the degrading polymer. Second, one can implant a similar biodegradable scaffold in the body and allow the transition from polymeric scaffold to native tissue to occur in vivo. An advantage of the former is that grafts can be made in large numbers and have off-the-shelf availability, though they must be decellularized to prevent immuno-rejection if the synthetic cells were not autologous. An advantage of the latter is that it is the patient’s own cells that personalize the graft under normal hemodynamic conditions, though implantation of a biodegradable scaffold elicits a foreign body (inflammatory) response. In both cases, there are myriad design parameters, and G&R modeling can play important roles in designing these grafts and understanding their evolution, the latter with clear clinical benefit. We first modeled the ex vivo situation, finding that the previously used periods of development should be extended, hence revealing another key role for in silico studies [72]. It is important to note, of course, that a mixture-based approach can easily handle the evolution of both the degrading polymeric scaffold via Q^α(s) and accumulating neotissue via m^α(τ)q^α(s, τ), whether ex vivo or in vivo. We showed further that in vivo TEVG development could be described [73] and predicted [74], demonstrating that early development is immuno-driven while later development is mechano-mediated [75]. In particular, the mass production term needed to account for these two phases, as, for example,

$$m^{\alpha }\left(\tau \right)=\left(1-e^{-\tau }\right)m_0^{\alpha }\left(1+m_{\mathit{inflam}}^{\alpha }+m_{\mathit{stress}}^{\alpha }\right),$$ (13)

where the first term on the right hand side accounts for the fact that tissue cannot begin to be produced until synthetic cells infiltrate the scaffold. Note, too, that the inflammatory contribution (inflam) was prescribed via a gamma function (based on experimental data), capturing a rapid increase in response to the foreign body that progressively diminished as the polymer degraded and the inflammation waned.

Finally, note that such G&R models can be used via parametric sensitivity studies to begin to explore how scaffold design will affect the cell-mediated in vivo development of neotissue [76] or coupled with formal methods of optimization to begin to identify improved design parameters for the scaffolds (e.g., select optimal fiber diameters and pore sizes) based on simulations [77]. Regardless, these CMMs predicted an unexpected natural history of implanted TEVGs, namely, that an early narrowing (due to inflammation) would resolve spontaneously (in part due to mechano-mediated turnover of matrix by stress-shielded cells), which motivated a pre-clinical study and eventually led to FDA-approval of the use of a particular TEVG in children born with congenital heart defects [78]. Again we refer to Table 1, but the reader is encouraged to consult the original papers for more details.

5. ADDITIONAL ADVANCES, CONTINUING NEEDS

5.1. Fluid-Solid-Growth (FSG).

Blood vessels are exposed to persistent hemodynamic loads and it can be critical to account for solid-fluid interactions. In particular, changes in the hemodynamics can drive changes in wall geometry and properties, which in turn can drive changes in the hemodynamics, and so forth. As noted above, our first FSG model used a simple pipe-flow analysis of the blood in a model of the circle of Willis in the brain to simulate cerebral vasospasm [42]. More formally, however, FSG models can be built using full 3D Navier-Stokes solutions for the hemodynamics [79]; indeed, a theory of “small deformations superimposed on large” can facilitate such solid-fluid coupling [80]. FSG models have been used, for example, to study evolving AAAs, with loose coupling between the hemodynamics and wall mechanics in part because of the very differing time scales – one second for a cardiac cycle and days-to-months for wall G&R [81,82]. Such coupled models provide increased understanding of vascular G&R and must be pursued with greater vigor. Theoretical advances will be needed, however, to ensure computational efficiency within complex multiphysics models.

5.2. Multiscale Models.

Mechanisms that drive adaptations and disease progression necessarily arise at molecular and cellular levels, yet manifest clinically at tissue and organ levels. There is, therefore, a pressing need to develop models that couple mechanism and manifestation across spatial and temporal scales. Much remains to be accomplished in this regard, but prior efforts provide confidence to move forward. Among others, we previously showed that agent based models (ABMs, often rule-based at the cellular level) and CMMs (continuum-based at the tissue level) can be coupled efficiently [83]. Importantly, this work emphasized that different types of models can be parameterized using the same data from either cells or tissues, both in vitro and in vivo. Of course, one has much greater control over in vitro studies on cells, though the results necessarily have less in vivo relevance. Conversely, one has much less control over in vivo studies at the tissue level (e.g., one may be able to control pressure, though not individual sympathetic or hormonal influences), but increased in vivo relevance. Hence, no data are without limitations and no model informed by a particular type of data will be without limitations. Yet, when the same data can be used to inform models at multiple scales there is a unique opportunity to seek congruency across scales, namely to achieve consistency via parameter estimation. This was shown when coupling ABMs and CMMs. More recently, we showed further that logic-based cell signaling models and CMMs can be coupled similarly, thus enabling models from transcript to tissue [84]. In particular, whereas CMMs focus on phenomenological relations for the production of particular structurally significant constituents, cell signaling models can estimate such production directly as a result of the signaling that leads to transcriptional activity for particular gene products, including structurally significant ones such as the collagens. Much more attention should be directed towards such coupling. Of course, one should similarly seek to couple CMMs of cell mechanics (e.g., [85,86]) with those at the tissue or organ level.

5.3. Computational Efficiency.

The heredity integral-based CMM has proven useful in describing and predicting many different vascular adaptations, disease processes, and tissue engineered constructs (Figure 4). Yet, such simulations can be computationally expensive, particularly for problems having complex 3D geometry. For this reason early modeling focused on 2D or membrane descriptions of the wall (e.g., [13,14,81]). Although direct 3D implementations have been advanced [87,88], there have also been attempts to identify simplifications that afford greater computational efficiency. First, temporal homogenization was introduced to combine advantages of the CMM and the theory of finite volumetric growth [89,90]. Briefly, the basic idea is to perform a temporal homogenization over all mass deposition for a single constituent and to decompose the overall deformation into an elastic part and a G&R part, considering separately that for changes in mass and changes in organization. It was found that this rate-type approach can recover prior simulations using the full heredity integral-based approach at a fraction of the computational time.

Second, a concept of mechanobiological equilibrium was exploited to generate a rate-independent approximation, one that again recovers well the full CMM predictions in multiple cases [15]. Recall that mechanical homeostasis requires that $m_{\alpha }(s)\to m_0^{\alpha }$ at the time s when the adaptation is complete, which in terms of the constitutive assumption of equation 8 requires that the combined stress differences $K_{\sigma }^{\alpha }\Delta \sigma -K_{{\tau }_w}^{\alpha }\Delta {\tau }_w\to 0$ at that time (with Δσ → 0 and Δτ_w → 0 separately if the adaptation is ideal). A more stringent requirement, however, is that $m_{\alpha }(s)=m_0^{\alpha }$ at all times s during the adaptation, which in terms of equation 8 requires that $K_{\sigma }^{\alpha }\Delta \sigma =K_{{\tau }_w}^{\alpha }\Delta {\tau }_w\forall s$, which can be shown to be reasonable if a time-scale for the stimulation is greater than a characteristic internal time-scale of G&R; that is, if the actual “slow” adaptation is otherwise “fast” in relative terms. In this case, the heredity integrals can be pre-integrated to yield evolving rule-of-mixture relations, resulting in a rate-independent equivalent that holds provided that the time scales admit this assumption of quasi-mechanobiological equilibrium. An associated finite element implementation thus becomes as computationally efficient as standard solvers for nonlinear finite elasticity [91]. Full CMMs remain preferred when details of the time-course of mass production and removal are critical, particularly when degradation rates depend strongly on the cell phenotype or extracellular milieu at the time the neotissue was originally incorporated within the extant matrix. These, and future, approximations nonetheless promise considerable advantages, especially when used in FSG simulations or formal methods of optimization given their associated computational expense.

5.4. Mechanobiological Stability.

Consistent with Remark 3 above, many cases of vascular G&R stem from homeostatic mechanisms, thus suggesting negative feedback that seeks to maintain stable, optimal responses. We suggested that mechanical homeostasis can be considered via formal stability analyses of G&R models [92], which motivated similar work by others [93]. Briefly, as in classical mechanics, stability suggests robust, recoverable responses to perturbations, in this case for those that affect cell and matrix turnover. In our first study, we showed that deposition stresses are critical for promoting mechanobiological stability, consistent with Remarks 1 and 4, with higher tissue stiffness and higher rates of mass production similarly promoting stability. Recalling the prior findings on aneurysmal enlargement, particularly the different findings in [27] and [29], it may be appropriate to think of unbounded aneurysmal enlargement as a mechanobiological instability [32], though fortunately with guidance from the theory as to how to stabilize such lesions. Importantly, this initial study of mechanobiological stability in 2014 suggested that such stability was typically neutral, namely, that adaptivity against perturbations is a natural response by such tissues. This finding is consistent with the concept of adaptive homeostasis [94] as well as the possibility that inflammation can over-ride homeostasis, resulting in some cases in new (possibly adaptive) homeostatic states [95].

More recently, we reformulated the mechanobiological stability framework using a rate-dependent CMM and found that neutral stability is indeed possible, but so too asymptotic stability [96]. Again, increased material stiffness and increased rates of production promote such stability, but now with static and dynamic stabilities delineated similar to that in arterial mechanics without G&R [12]. Importantly, particular to aneurysm research, we found that a critical value of elastin degradation could induce an unbounded G&R response, consistent with findings using our earlier approach [32].

5.5. Frontiers.

There remains a need for increased theoretical understanding of soft tissue G&R, particularly with respect to constraints imposed by Clausius-Duhem type descriptions of the entropy inequality, and continued development of improved computational methods, particularly for coupled problems, both FSG and multiscale. With regard to vascular biology, there remains a pressing need to understand vascular development and maturation, which will require significantly more data but also conceptual advances. There have been a few initial studies along these lines, using volumetric growth [97] and simplified CMMs [98], but much remains unknown. Understanding vascular development is critical for advancing many fields, including tissue engineering, designing interventions for congenital heart defects, and understanding early onset and genetically triggered diseases, among others.

A general problem that demands increased study is the overall genotype-to-phenotype relationship. As increasingly more information becomes available via advancing biological assays, including bulk and single cell RNA sequencing, there will be increasing need to model G&R from transcript to tissue. Related to this, most prior studies of vascular G&R have focused on but a few of the key extracellular matrix constituents – elastic fibers, collagen fibers, and perhaps bulk glycosaminoglycans. Yet, we know that the vascular wall contains on the order of 100 different proteins, glycoproteins, and glycosaminoglycans and increasing evidence reveals how mutations therein can have dramatic consequences on wall composition, geometry, properties, and responses to altered loading. For example, mutations in the gene that encodes the glycoprotein fibrillin-1 promote thoracic aneurysms; mutations in the gene that encodes the protein collagen III promotes dissections. Similarly, mutations in genes that encode cytokines such as TGFβ, or its receptors, lead to dramatic aortopathies; mutations in genes that encode intracellular signaling molecules such as Smad3 result in similar aortopathies. Mutations to the gene that encodes the nuclear envelop protein lamin-A lead to rapid, unprecedented vascular aging. These and many, many examples like them remind us that we must begin to include in our models the many different extracellular and intracellular constituents that affect G&R, with due consideration to the role of matrix homeostasis [99]. Only in this way will we truly understand many diseases, with hopes of identifying new targeted methods of treatment, especially in the spirit of personalized medicine.

6. CLOSURE

Can it really be twenty years after? Yes, and fortunately much has been learned and much has been accomplished (Figure 4). Personally, I am particularly encouraged by our recent CMM predictions that led to a 1.5 year confirmatory pre-clinical study and associated restart of a clinical trial with promise to improve outcomes in children born with congenital heart defects [78]. Indeed, a similar study of tissue engineered heart valves by a European group shows equal promise [100]. There is, therefore, considerable reason for optimism; we must continue the work.

I focused herein on a single approach (CMM) and area of application (vascular) by one group for two primary reasons: first, this focus allows a direct comparison of constitutive equations that enabled diverse situations to be addressed within a single framework (Table 1) and, second, it enabled a simpler historical perspective that I hope will be motivational to those who seek to model the breadth of soft tissue G&R, particularly for non-vascular tissues. In hindsight, it was interesting to realize that the constrained mixture theory was initiated twenty years after R. Skalak’s seminal paper of 1981, and sobering that it is now twenty years after our first submission (Figure 5). There are, of course, many other applications of CMMs by others covering broader topics, including [82,85,86,101–121]. Moreover, there are other approaches for modeling G&R, some mixture-based [39,40,122–124] but many based on the theory of finite volumetric growth [5] and extensions thereof. Regarding the latter, the reader is referred to a few key reviews [125–131], but especially the recent books by Goriely [132] and Taber [133].

Figure 5.

Simple timeline showing some key advances in modeling G&R, emphasizing in particular the seminal paper of Skalak in 1981, the introduction of a general constrained mixture theory twenty years after (submitted 2001, published 2002), and yet unimagined opportunities (?) again twenty years thereafter. Notwithstanding the importance of the theory of finite volumetric growth – formalized by Rodriguez and colleagues in 1994 and quickly shown to be useful by Taber, Rachev, and others – consistent with the review herein this timeline focuses primarily on key advances for the constrained mixture model (CMM), including the first finite element implementations in 2005/2006, fluid-solid-growth modeling first used in 2007 but advanced generally in 2009, the utility of such models in describing tissue engineered constructs (introduced in 2009, advanced in 2014, shown to be useful for scaffold design in 2015, and used to guide a clinical trial in 2020), the concept of mechanobiological stability introduced in 2014 and extended in 2019, and finally the computational efficiency engendered by the assumption of quasi-static mechanobiological equilibria shown in 2020 as well as the importance of coupling across scales, including with cell signaling models to appear in 2021. Note, too, some of the key reviews and books that address broader approaches to G&R.

In closing, although much has been accomplished, much remains to be done. In the near term, there remains a need for continued study of the immuno-mechanical mechanisms by which soft tissues grow and remodel and how to capture these mechanisms within multiphysics (solid-fluid) and multiscale (molecular-cellular-tissue) models. There is a continuing need for improved understanding of the theoretical foundations and limitations as well as need for improved computational implementations. Finally, and most importantly, there is a pressing need to address new frontiers, including the genotype-phenotype connection, and to address more clinical scenarios, for it is only in this way that modeling will truly have the impact that it should. The future is bright and one must now wonder what will be achieved in another twenty years after.