On the robustness of latent class models for diagnostic testing with no gold standard

Abstract

It is difficult to estimate sensitivity and specificity of diagnostic tests when there is no gold standard. Latent class models have been proposed as a potential solution as they provide estimates without the need for a gold standard. Using a motivating example of the evaluation of point of care tests for leptospirosis in Tanzania, we show how a realistic violation of assumptions underpinning the latent class model can lead directly to substantial bias in the estimates of the parameters of interest. In particular, we consider the robustness of estimates of sensitivity, specificity, and prevalence, to the presence of additional latent states when fitting a two-state latent class model. The violation is minor in the sense that it cannot be routinely detected with goodness-of-fit procedures, but is major with regard to the resulting bias.

1 |. INTRODUCTION

Diagnostic tests are a critical component of effective clinical management and disease surveillance. Useful tests need to be simple, affordable and timely, and must accurately discriminate individuals with and without the disease in question. For many infectious diseases, the standard “best” available tests are either expensive, require specialist expertise, or involve considerable delay, for example, tests based on culture or requiring acute and convalescent samples.¹ Recent advances in biology and technology have lead to a proliferation of new, rapid, point of care tests for infectious diseases. While these novel tests are often simple, affordable and timely, their diagnostic accuracy requires evaluation. Traditional approaches have estimated the sensitivity and specificity of novel assays by comparing them to a reference standard. For many diseases, however, the reference test has imperfect sensitivity or specificity. This has, in turn, hampered evaluation of the novel tests.

Two main approaches are used to overcome the deficiencies of an imperfect reference test: (i) defining a composite reference standard (CRS)² and (ii) use of a latent class model (LCM).^3,4 With the CRS approach, a combination of tests are used to develop rules for the determination of presence or absence of disease; a new test is then compared against this reference standard. Finding an agreed CRS that leads to minimal bias is difficult, if not impossible.

Latent class models have been widely used in many areas of research. Essentially, the models specify a probabilistic relationship between a set of measured variables and a hypothesized unmeasured latent class variable. In diagnostic testing, the measured variables are the outcomes from two or more diagnostic tests. The simplest LCM used is a two class model, with the two classes treated as “disease” and “disease free,” with the various tests assumed to be independent conditional on the disease status. Model parameters are interpreted as sensitivity, specificity, and disease prevalence. For simplicity, we use these labels for the remainder of the manuscript, while recognizing that use of these labels without a gold standard reference test can be problematic.⁵

In the last decade, there has been steady growth in the use of latent class analysis to evaluate new diagnostic tests, particularly in the area of infectious diseases.⁴ Three concerns with LCMs have been outlined in the statistics literature. First, the LCM is geometrically complex, and identifiability is not guaranteed even when the degrees of freedom are greater than the number of parameters.^6,7 Second, parameter estimates can be biased if the dependence relationship between tests is misspecified.^2,8 It is possible to have two or more dependence models that fit the data equally as well but lead to different conclusions regarding sensitivity and specificity.⁸ The importance of the assumed dependence relationship was highlighted by Pepe and Janes who provided explicit maximum likelihood estimators for the case of three conditionally independent tests with two classes.⁹ They showed that the estimated sensitivities and specificities rely on observed associations between the tests. The third concern is the validity of the interpretation of the latent classes. The classes are inferred in order to provide an optimal fit to the data. There is no reason why these inferred classes need to represent disease status, or in fact any realistic variable.² In discussing latent variable models Agresti,¹⁰ pg 544, states

A danger with latent variable models … is the temptation to interpret latent variables too literally… One should realize the tentative nature of the latent variable. Be careful not to make the error of reification – treating an abstract construction as if it has actual existance.

With this in mind, the remainder of the manuscript explores the robustness of LCMs to a particular violation of assumptions. This was motivated by a study of leptospirosis in northern Tanzania in which 225 patients presenting to hospital with fever were tested for leptospirosis using a standard test and three new point of care tests.¹¹ We fit a Bayesian two-state latent class model to explore the properties of the new tests; the results obtained did not conform with our understanding about the scientific basis of the tests in question. We present full details of the model in Section 2 and the motivating example in Section 2.3. It is possible that our expectations were incorrect and the latent class model has provided insight into the performance of these tests that would be otherwise hidden. Another possibility is that unidentified model misspecification has led to substantial bias in the estimates of sensitivity and specificity. We explore one such model misspecification in Section 3 that even for the simplest LCM can lead to substantial bias and is difficult to detect in practice. The remainder of the manuscript explores the implications of this form of misspecification.

2 |. BACKGROUND

2.1 |. Data description

The data are denoted by the N × T matrix y, where N is the number of individuals in the study and T is the number of tests. The entry y_ij denotes the result of the jth test for the ith individual. The value y_ij = 1 indicates a positive test, with y_ij = 0 a negative test. These data can be summarized by counting the number of times each possible combination of test results was seen. The S = 2^T possible combinations of test results are specified in the S × T matrix x, with the number of times each combination of test results was seen recorded in the S-vector n. The ith entry of n is the number of individuals who have the combination of test results given in the ith row of x. An example of y, x and n for a hypothetical T = 2 study with N = 6 is

$$y=\left(\begin{array}{cc}1& 1\\ 1& 1\\ 1& 1\\ 1& 0\\ 0& 0\\ 0& 0\end{array}\right)\text{can be summarized as}x=\left(\begin{array}{cc}1& 1\\ 1& 0\\ 0& 1\\ 0& 0\end{array}\right)n=\left(\begin{array}{c}3\\ 1\\ 0\\ 2\end{array}\right).$$

The data (x and n) for our motivating example is shown in Table 1, where T = 4 and N = 225.

TABLE 1.

Summary of the observed data among patients with fever, Northern Tanzania, 2007-2008 and 2012-2014

MAT	Leptorapide	Leptocheck	Test-It	Count
1	1	1	1	3
1	1	1	0	0
1	1	0	1	0
1	1	0	0	1
1	0	1	1	3
1	0	1	0	4
1	0	0	1	0
1	0	0	0	12
0	1	1	1	6
0	1	1	0	3
0	1	0	1	0
0	1	0	0	25
0	0	1	1	11
0	0	1	0	17
0	0	0	1	9
0	0	0	0	131

Note: The indicator 1 represents that the patient tested positive for the given test and 0 that the patient tested negative. The counts give the number of participants with each combination of test results.

2.2 |. Latent class model

We outline an M-state LCM where all tests are assumed independent. The LCM consists of two components. The first allocates a class (or state) c to each individual,

$$\begin{array}{ccc}{c}_i\stackrel{iid}{\sim }Cat\left({\pi }_1,\dots ,{\pi }_M\right),& \sum _h{\pi }_h=1,& i=1,\dots ,N,\end{array}$$ (1)

where π_j gives the probability of an individual being in class j, iid denotes an independent and identically distributed random variable and Cat(b₁, … , b_p) represents a categorical distribution with support 1, … , p and parameters b₁, … , b_p. Throughout, we use the terms class and state interchangeably.

The second model component describes the distribution of the observed data conditional on the class

$$\begin{array}{ccc}{y}_{ij}|c_i,\stackrel{ind}{\sim }Bern\left(p_{j{c}_i}\right),& i=1,\dots ,N,& j=1,\dots ,T,\end{array}$$ (2)

where p_jc gives the probability that test j is positive for an individual in class c, ind denotes an independent random variable and Bern(b) represents a Bernoulli distribution with probability b.

When fitting in a Bayesian context, model specification is completed with prior distributions on π = (π₁, … , π_M) and p = (P₁₁, … , P_TM).

We can use (1) and (2) as a complete data model that requires the inclusion of the latent variable c = (c₁, … , c_N) directly in the model. Despite being intuitive, this approach is slow to fit when using Markov chain Monte Carlo (MCMC) as each entry in c needs to be updated. A more computationally efficient strategy is to explicitly sum over c. The resulting marginal model is

$$\mathit{n}\sim MN\left(N,\mathit{q}\right),$$ (3)

where MN(a, b) represents a multinomial distribution with index a and vector of probabilities b, and q = (q₁, … , q_s), with

$$\begin{array}{cc}{q}_k=\sum _{c=1}^M{\pi }_c\prod _{j=1}^T{p}_{jc}^{x_{kj}}{\left(1-p_{jc}\right)}^{1-x_{kj}},& k=1,\dots \end{array},S.$$ (4)

2.3 |. Motivating example: Leptospirosis in Tanzania

Leptospiriosis is a zoonotic disease, and is transmitted from animals to humans through contact with infected animal urine, blood or other bodily fluids, or through contaminated water or soil. Leptospirosis is a leading cause of morbidity and mortality among zoonotic diseases, particularly in resource-poor countries.¹² Humans present with symptoms common to many infectious diseases, so laboratory testing is required for diagnosis.¹³

The best available diagnostic test for leptospirosis is a serological test, the microscopic agglutination test (MAT). In the MAT live antigens representing different serovars are reacted with patient serum samples to measure immunoglobulin M (IgM) and immunoglobulin G (IgG) antibody levels. Because antibodies can remain detectable for months after an acute infection, a second MAT test identifying either seroconversion or a rise in antibody titres is required to determine current infection. The specificity of the MAT is thought to be near perfect, but sensitivity has been estimated as approximately 0.8 with at least 11 days after the onset of illness among patients with positive blood cultures.¹⁴ The diminished sensitivity is thought due to an incomplete panel of serovars, a subjective degree of agglutination used as the cut-off for interpretation, and some patients failing to mount an antibody response to Leptospira infection.

As outcome following leptospirosis infection is improved by early treatment with antibiotics,¹³ there is a need for a diagnostic test which provides a quick, accurate result early in the illness. A number of point-of-care tests for acute leptospirosis disease have been developed which aim to detect anti-Leptospira IgM. The three tests carried out in our study were Test-It Leptospira IgM Lateral Flow Assay (Lifeassay Diagnostics (Pty) Ltd. Cape Town, South Africa), Leptocheck-WB (Zephyr Biomedicals, Goa, India) and Leptorapide (Linnodee Ltd., Doagh, Northern Ireland). Test-It Leptospira and Leptocheck WB are similar in that they both use lateral flow technology and antigen from whole-cell boiled Leptospira biflexa serovar Patoc. In our systematic review of lateral flow assays we found sensitivity ranged from 53% to 95%, but noted the variation may reflect different reference tests or different stages of the illness.¹⁵ As all assays detect antibodies, which take between one and four weeks after illness onset to develop, lateral flow assays performed on serum taken from early in the illness were expected to have lower sensitivity than MAT performed on serum from 4-6 weeks after the onset of illness.¹⁴

Participants were enrolled from August 2007 through September 2008 and from February 2012 through May 2014 as part of febrile illness surveillance studies at Kilimanjaro Christian Medical Centre (KCMC) and Mawenzi Regional Referral Hospital (MRRH) in Moshi, Tanzania. Blood samples were taken on the date of enrolment, and participants were requested to return 4-6 weeks later for a convalescent sample. The MAT test returned a positive leptospirosis diagnosis if a patient returned a single reciprocal titer ≥800, or a ≥4 fold rise in antibody titer between enrolment and convalescent samples.^11,16 The analysis presented here included all patients enrolled who had results for all 4 tests (n = 225).

Ethical approval for the study was granted by the Kilimanjaro Christian Medical Centre Research Ethics Committee (# 295), the Tanzania National Institutes for Medical Research National Ethics Coordinating Committee (NIMR1HQ/R.8cNo1. 11/283), Duke UniversityMedical Center Institutional Review Board (IRB# Pro00016134), and the University of Otago Human Ethics Committee (Health) (H15/055).

The data are presented in Table 1. We fit a two-state Bayesian LCM as outlined in (3) and (4) in JAGS.¹⁷ We ran three Markov chains for 10 000 iterations following a burn-in/adaptive phase of 5000 iterations.

We assumed uniform prior distributions for π and p. We used the algorithm of Stephens^18,19 to correct for label switching (see the supplementary materials for more information). We take the inferred state that has the lowest prevalence to be state 1, and refer to this as the “disease” group. The sensitivities are given by p₁₁, … , p_T1 and the specificities are given by 1 – p₁₂, … ,1 – p_T2.

Posterior summaries of the sensitivities and specificities are plotted in Figure 1. The posterior median for π₁, the prevalence of disease, was 0.14. The results obtained did not conform to our expectations regarding the properties of the tests (Figure 1). In particular, the estimated sensitivity for Test-It Leptospira and Leptocheck were both considerably higher than that for the MAT (posterior medians 0.77 and 0.93 versus 0.27). If we extend the model in (2) to allow two-way dependence between Test-It Leptospira and Leptocheck WB, the estimate of the MAT test sensitivity remains lower than that for Test-It Leptospira and Leptocheck WB, however, there is increased posterior uncertainty. Details of the dependence model implemented are provided in the Supplementary Materials.

FIGURE 1.

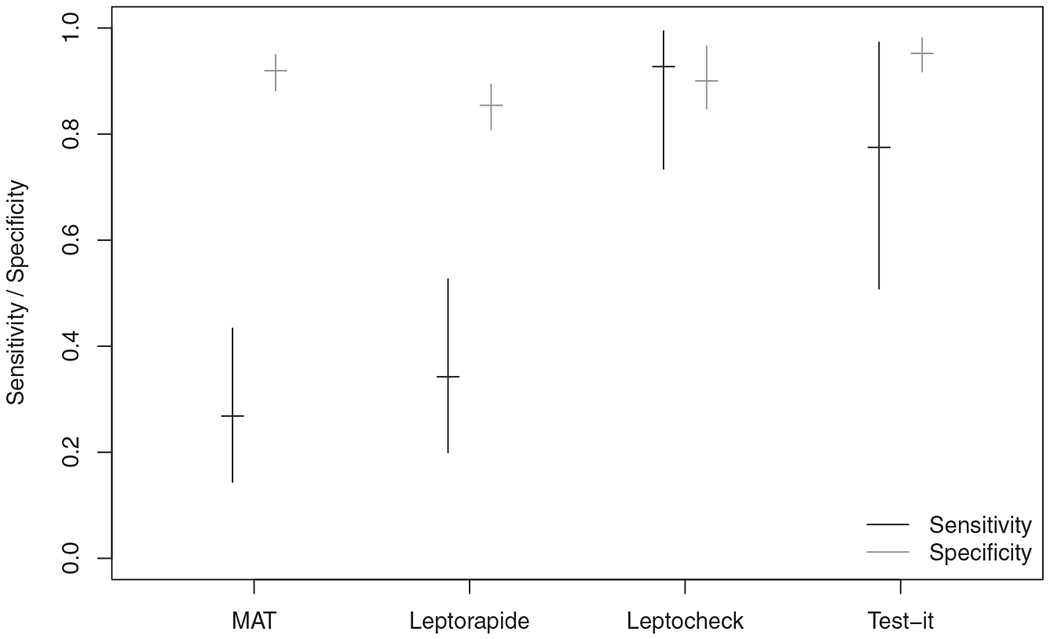
The vertical lines represent the central 90% credible intervals for sensitivity (black) and specificity (gray) for each of the four tests for the Tanzania data using a two-state latent class model, where are tests are conditionally independent. The horizontal line represents the median of the posterior distribution

To assess goodness-of-fit in the latent class model we use posterior predictive assessment.²⁰ We graphically compare the posterior predictive distribution for each of the S combinations of test results with the observed counts (Figure 2). In the Supplementary Materials, we also consider posterior predictive checks of the pairwise counts in the spirit of Qu et al.²¹ In both cases, the observed counts are consistent with draws from the posterior predictive distribution indicating that there is no evidence of substantive lack-of-fit in the model. If it were not for the results being the opposite of our expectations, there would be little cause for concern.

FIGURE 2.

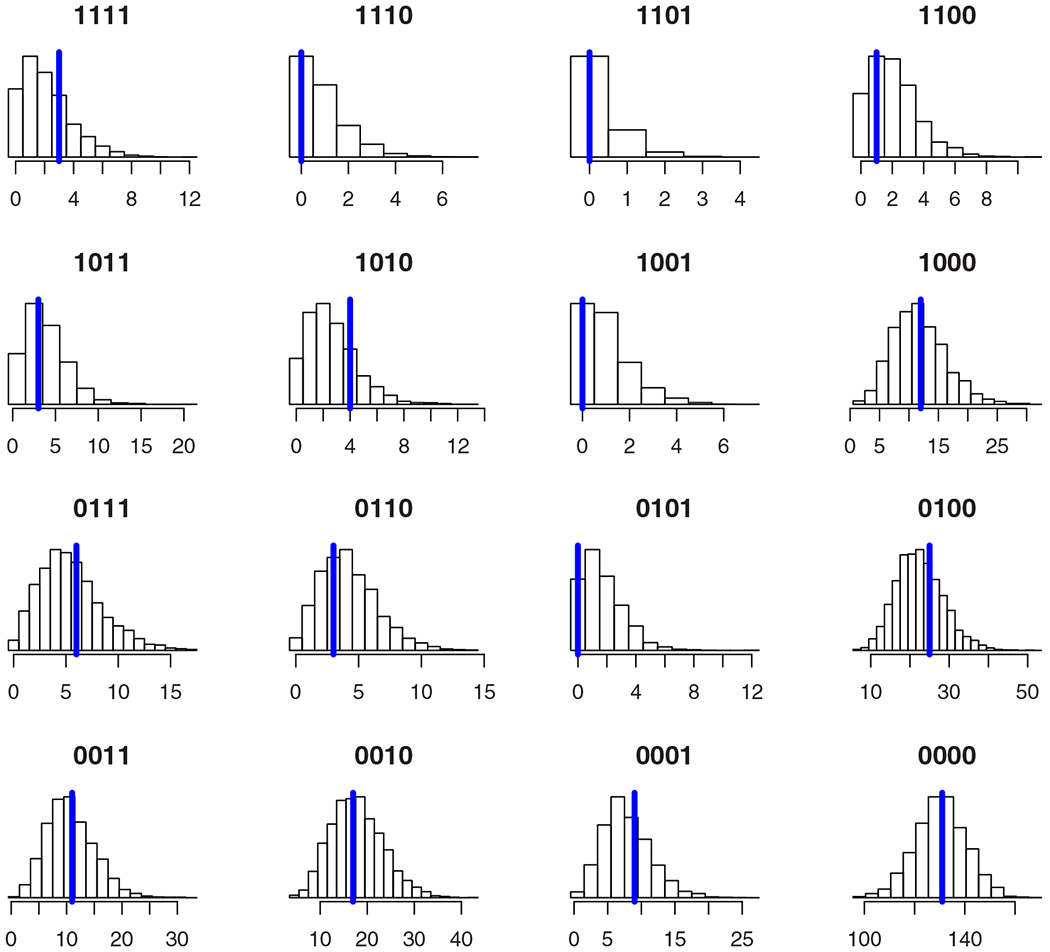
Posterior predictive distributions for the counts n. Each entry in n is referenced by the corresponding combination of test results given in the plot title. The vertical blue line gives the observed count [Colour figure can be viewed at wileyonlinelibrary.com]

Our results are more extreme than those of Limmathurotsakul et al²² who estimated a sensitivity for the MAT test of approximately 50%, although we note that they assessed different tests and implement LCMs that differ from those we have used. The key finding of their article was that the true sensitivity of the MAT is low (pg. 328), making the MAT inappropriate for use as a gold standard. In our case, the estimated sensitivity is so low that we believe it to be implausible. Instead, we believe the results are due to model misspecification that is difficult to detect with standard goodness-of-fit assessment, yet has led to considerable bias in the estimates of interest.

3 |. MODEL VIOLATION

To assess the robustness of the LCM to underlying assumptions, we consider the possibility that there is a third state in the LCM. We replicate the motivating example with four tests (test 1 through test 4) and consider two situations.

In the first situation, the data generating process is a two-state LCM (M = 2). The two states correspond to diseased and non-diseased individuals. This provides a baseline where the generating and fitting model are the same.

In the second situation, we allow the data generating process to be a three-state LCM (M = 3). This provides a scenario where the data generating process is no longer the same as the fitting model. There are numerous possible definitions that we could assume for the three states. One such possibility that we refer to as the “alternate disease” definition is where we take the first two states to be the disease of interest and non-diseased individuals as in the M = 2 model. We allow the third state to represent individuals that have an alternate disease that can trigger a test response at rates in excess of those with no disease. Another possibility that we refer to as the “mixed disease” definition is where state 2 refers to non-diseased individuals, and states 1 and 3 reflect different biological aspects of the disease of interest.

Either of these situations are biologically plausible for our motivating leptospirosis example. One example where the alternate disease situation would be appropriate is if there is moderate prevalence of other diseases that can trigger an IgM response. IgM is a relatively non-specific immunoglobulin that is produced rapidly in response to illness. While its rapid response can be leveraged for testing purposes, the downside is that we may detect diseases other than that we are targeting. One example where the mixed disease situation would be appropriate is where tests detect one biological process (eg, IgG response) at a different rate from another process (eg, IgM response). We restrict our attention to three-state models, but note that the actual process is likely to be more complex.

The input values for the simulation were determined so that the expected counts for M = 2 and M = 3 are (i) similar to each other, and (ii) similar to the observed leptospirosis data (Tables 2 and 3).

TABLE 2.

True parameter values for two-state (M = 2) simulation and the three-state (M = 3) simulation

Parameter	M = 2	M = 3
p 11	0.27	0.88
p 21	0.33	0.10
p 31	0.94	0.22
p 41	0.67	0.05
p 12	0.08	0.01
p 22	0.14	0.15
p 32	0.08	0.10
p 42	0.05	0.05
p 13	—	0.25
p 23	—	0.36
p 33	—	0.93
p 43	—	0.81
π 1	0.15	0.08
π 2	0.85	0.80
π 3	—	0.12

Note: The first two classes represent the disease of interest and no disease, respectively. The third class represents individuals with an alternate disease that triggers a response in some or all of the tests. The value p_jc represents the probability of testing positive for test j when in class c and π_c is the probability of being in class c.

TABLE 3.

The expected counts for the two true simulation models when N = 225

Test 1	Test 2	Test 3	Test 4	Expected count
				M = 2	M = 3
1	1	1	1	1.9	1.8
1	1	1	0	1.1	0.8
1	1	0	1	0.2	0.2
1	1	0	0	1.9	1.4
1	0	1	1	3.9	3.4
1	0	1	0	2.9	3.9
1	0	0	1	0.9	0.9
1	0	0	0	11.6	11.9
0	1	1	1	5.2	5.6
0	1	1	0	4.4	3.9
0	1	0	1	1.5	1.6
0	1	0	0	21.7	23.1
0	0	1	1	11.0	10.5
0	0	1	0	16.6	17.1
0	0	0	1	7.6	7.6
0	0	0	0	132.6	131.1

Note: The expected counts are similar between the two-state (M = 2) and three-state (M = 3) models.

The true sensitivities for the two-state model are given by p₁₁, … ,p₄₁ in Table 2, while the true specificities are given by 1 – p₁₂, … , 1 – p₄₂. The sensitivities and specificities for the three-state model depend on the definition that we have made regarding the three states. Initially we interpret the results assuming the “alternate disease” definition. In this situation, group 1 refers to disease and the true sensitivities are given by p₁₁, … ,p₄₁ in Table 2. As there are two groups that do not have the disease of interest, we combine the two classes “no disease” and “other disease” so that the true specificity for test i is

$$\begin{array}{cc}1-\frac{{\pi }_2{p}_{i2}+{\pi }_3{p}_{i3}}{{\pi }_2+{\pi }_3},& i=1,\dots ,4,\end{array}$$

where p_ij and π_j are given in Table 2. We consider the interpretation of the results using the “mixed disease” definition in Section 3.3.

3.1 |. Goodness-of-fit assessment

To assess model fit, we use posterior predictive model assessment with a Pearson-type test statistic

$$T\left(\mathit{n},\mathit{p},\mathit{\pi }\right)=\sum _{k=1}^S\frac{{\left(n_k-N{q}_k\right)}^2}{N{q}_k},$$

where n_k is the observed count for combination of test results k, and Nq_k is the expected count for combination of test results k, with q_k given in (4).

In iteration t, we use the posterior sample (p^(t), π^(t)), t = 1, … , l to generate replicate data ${\mathit{n}}_{\mathit{rep}}^{\left(t\right)}$ ~ MN(N, q^(t)), where q^(t) = (q^(t)₁, … ,q^(t)_S). The Bayesian p-value, denoted P_B is proportion of posterior samples in which the test statistic evaluated using the replicated data T(${\mathit{n}}_{\mathit{rep}}^{\left(t\right)}$, p^(t), π^(t)) exceeds the test statistic calculated using the observed data T(n, p^(t), π^(t)).

The use of Bayesian P-values for model assessment is often conservative.²³ Under the true model, the distribution of P_B is underdispersed relative to a uniform distribution for many choices of test statistic T. To overcome this, we use a calibrated Bayesian P-value,²⁴ denoted $P_B^{*}$. The calibrated value $P_B^{*}$ adjusts P_B according to an estimate of its empirical distribution when the model is correct. Conveniently, we can estimate this distribution using values of P_B from our baseline simulations with M = 2 as we are simulating and fitting under the true model. For a given simulation with Bayesian p-value of P_B = X, we calculate the $P_B^{*}$ value as the proportion of P_B values from the baseline simulation that were smaller than X.

3.2 |. Simulation results

We simulated 1000 datasets under each the following four scenarios:

1. True model has two-states; sample size is N = 225.

2. True model has two-states; sample size is N = 1000.

3. True model has three-states; sample size is N = 225.

4. True model has three-states; sample size is N = 1000.

The sample size of N = 225 corresponds to that observed in the motivating example. A sample size of N = 1000 allows us to assess the impact of a larger sample size on the properties of the model and estimation.

For each scenario, we fit a two-state latent class model in JAGS with three parallel Markov chains. The starting values for each of the chains are drawn at random from the prior distribution. In each chain we discard 5000 iterations for burn-in, before obtaining a posterior sample of 10 000 iterations, that is thinned by 10. This gives a posterior sample of 3000 across all chains. We then run the algorithm of Stephens¹⁸ to resolve label switching. The use of thinning is to mitigate the computational demands of the label switching algorithm in a simulation setting. We assess convergence using the Ȓ statistic.²⁵ In each simulation we find the maximum Ȓ value across all parameters in the model. The maximum $\widehat{R}<$ 1.02 in more than 99% of the simulations across all four scenarios (3984 simulations of 4000). We discard all simulations where $\widehat{R}>$ 1.02.

For each simulated dataset, we obtain point and interval estimates for the sensitivity and specificity of each test in terms of the posterior median, and central 90% credible interval, respectively. We also find the values P_B and $P_B^{*}$ to assess lack-of-fit.

For each simulation scenario we summarize the estimation of sensitivity and specifity for each of the four tests. In particular, we find (i) the bias of the point estimates (Figure 3 and Table 4); (ii) the coverage of the interval estimates (Table 4); and (iii) the proportion of models that were assessed as ill-fitting (Table 5).

FIGURE 3.

The difference between the true sensitivity/specificity and estimated sensitivity/specificity in each of the 1000 simulations when the true model had two-states (M = 2) and three-states (M = 3)

TABLE 4.

The bias and coverage of sensitivity and specificity for each of the four tests across the various simulation strategies

	M = 2				M = 3
	Bias		Coverage		Bias		Coverage
	N = 225	N = 1000	N = 225	N = 1000	N = 225	N = 1000	N = 225	N = 1000
sens1	0.005	−0.004	0.92	0.90	−0.613	−0.617	0.00	0.00
sens2	0.007	−0.002	0.92	0.92	0.235	0.227	0.06	0.00
sens3	−0.092	−0.041	0.94	0.92	0.623	0.677	0.00	0.00
sens4	0.011	0.006	0.98	0.91	0.628	0.629	0.00	0.00
spec1	−0.001	−0.000	0.89	0.90	−0.042	−0.040	0.31	0.01
spec2	0.000	−0.000	0.90	0.89	0.034	0.033	0.68	0.17
spec3	−0.007	0.000	0.97	0.92	0.118	0.123	0.03	0.00
spec4	0.005	0.005	0.95	0.91	0.106	0.103	0.00	0.00
π 1	0.012	0.009	0.97	0.92	0.082	0.076	0.26	0.01

Note: The value of M denotes the number of states in the true model. The labels sens_i and spec_i represent the sensitivity and specificity of test i, respectively. The posterior median was used for estimation and the coverage is based off a 90% central credible interval.

TABLE 5.

The probability of rejecting the Bayesian p-value (P_B) as well as the calibrated Bayesian p-value $\left(P_B^{*}\right)$ in the simulation

M	N	Pr(PB < 0.05)	Pr$\left(P_B^{*}<0.05\right)$
2	225	0.00	0.05
2	1000	0.00	0.06
3	225	0.00	0.07
3	1000	0.04	0.23

Note: The true model is indexed based on the number of latent states (M) and the sample size is given by N.

The estimates are close to unbiased and coverage near nominal when data are simulated and fitted under a two-state latent class model (Figure 3 and Table 4). The properties of the model are as expected when a two-state LCM is the true data generating process.

In contrast, many of the sensitivities and specificities are biased with very low coverage when data are simulated under the three-state model (Figure 3 and Table 4). The extent of the bias is concerning. In the three state model, test 1 has a true sensitivity of 0.88. The bias (when N = 1000) is −0.62 completely changing our interpretation. What is a highly sensitive test is estimated as only correctly identifying around one in four individuals who truly have the disease. Things are equally as worrying regarding the effect on the estimated sensitivity of test 3. What is in truth a poor test is estimated as having high sensitivity due to a bias of 0.68 (N = 1000).

It is common for statistical models to be biased when assumptions are violated. This need not be a concern if we can identify the model violation and adjust our model and/or interpretation accordingly. The model violation we implement cannot be easily identified with standard goodness-of-fit assessment (Table 5). When the sample size is N = 225 we identify lack-of-fit at the nominal (α = 0.05) rate. Even when the sample size is N = 1000 individuals, we only identify lack-of-fit in little more than 1 in 5 of the cases.

We note that similar results (and identical conclusions) are obtained if we fit the models using maximum likelihood instead of Bayesian inference. We have opted for Bayesian inference here for two reasons. The first is that Bayesian inference appears to be the preferred method of inference for those applying LCMs to diagnostic testing.^22,26 The second is that using Bayesian inference avoids the need to rely on asymptotic approximations and combining cells when performing goodness-of-fit testing.

3.3 |. Interpretation of latent variable

The results above are interpreted assuming the “alternate disease” definition where state 1 refers to disease, and states 2 and 3 refer to no disease. If instead, we consider the “mixed disease” definition, then states 1 and 3 refer to disease and the true sensitivity of test i becomes

$$\begin{array}{cc}\frac{{\pi }_1{p}_{i1}+{\pi }_3{p}_{i3}}{{\pi }_1+{\pi }_3},& i=1,\dots ,4,\end{array}$$

while the specificities are given by 1 – p₁₂, … ,1 – p₄₂.

We can consider this definition using the same simulation results as above; only the definition of “disease” differs when assessing bias and coverage. For this definition, the bias of the sensitivities and specificities are non-negligible and the coverage rates poor (Figure 4 and Table 6). When N = 1000, none of the coverage rates for sensitivity are over 55% and for two tests the coverage is no more than 2%. The inferred latent variable does not appear to correspond to either of the two definitions that we have considered (“alternate disease” or “mixed disease”).

FIGURE 4.

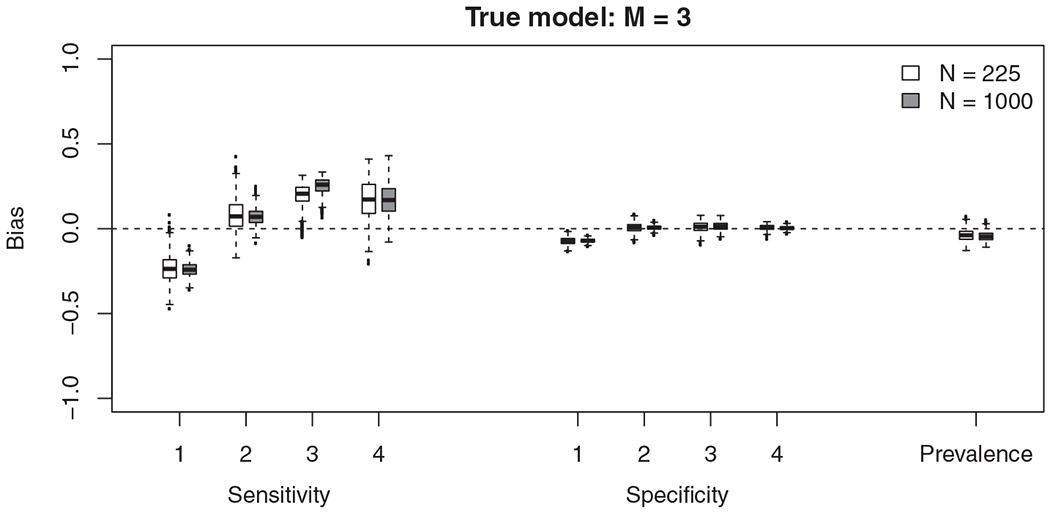
The difference between the true sensitivity/specificity and estimated sensitivity/specificity of the 1000 simulations when the true model has three-states (M = 3). We assess the sensitivity of the test to diagnose any disease (either state 1 or state 3)

TABLE 6.

The bias and coverage of sensitivity and specificity when assessing the sensitivity of the test to diagnose any disease (either state 1 or state 3) when the three state model is true

	Bias			Coverage
	N = 225	N = 1000	N = 225	N = 1000
sens1	−0.235	−0.239	0.21	0.00
sens2	0.079	0.071	0.77	0.54
sens3	0.197	0.251	0.53	0.02
sens4	0.172	0.173	0.74	0.41
spec1	−0.073	−0.071	0.01	0.00
spec2	0.006	0.006	0.89	0.87
spec3	0.010	0.015	0.94	0.84
spec4	0.007	0.004	0.95	0.92
π 1	−0.038	−0.044	0.91	0.61

Note: The labels sens_i and spec_i represent the sensitivity and specificity of test i, respectively. The posterior median was used for estimation and the coverage is based off a 90% central credible interval.

3.4 |. Further simulations

In the Supplementary Materials, we present a second simulation study with different input values. The broad conclusions are the same as the simulation above, that is, many of the estimates are biased, coverage is poor, and we are unable to detect lack-of-fit in the majority of simulations.

4 |. DISCUSSION

Our work was motivated by a real example where the tests detect disease at various times through different biological characteristics. For the best available diagnostic test (MAT), a two state LCM gave estimated sensitivity well below what was expected. Our simulations show that one possible explanation is that there was undetected misspecification in the two-state LCM. We considered two definitions for a three state model (“alternate disease” and “mixed disease”). The inferred latent “disease” state does not appear to correspond to either definition, with simulation results showing that the sensitivity and specificity estimated using the two-state model is heavily biased with poor coverage. This is a reminder that we must be careful with interpretation of latent variables, as they exist only in the hypothetical model in which we have defined them and they need not relate to any realistic quantity.

In our simulation studies, there was little power to detect lack-of-fit when the model was incorrect even when N = 1000. This is similar to the lack-of-power observed in LCMs when distinguishing between models for dependence.⁸ Evaluations of novel diagnostic tests often have far fewer than 1000 participants as data are challenging and expensive to collect. A requirement of thousands or tens of thousands of samples for the evaluation of diagnostic tests would challenge standard practice.

Our results show that model misspecification, even when it cannot be detected by lack-of-fit assessment, may result in the latent class variables no longer representing disease status. This can lead to substantial bias in estimates of sensitivity, specificity and prevalence. As such, we advise caution with the use of latent class models for evaluating novel diagnostic tests in the absence of a gold standard. Care is needed in determining both the number of latent states and what they represent. As it is the latent classes themselves that are of interest, it is critical that the assumptions underlying LCMs be justified when they are used for evaluating diagnostic tests. Such justification should be made by a cross-disciplinary team and account for biological underpinnings of the various tests and diseases under consideration.^27,28 In some situations, gold standard tests (those with perfect sensitivity and specificity), or silver standard tests²⁹ (those with perfect specificity) may be available but expensive or difficult to perform. If this is the case, we advise that such tests be used on a subset of patients.^29–31 Having some form of ground truth for a subset of observations is advantageous; not only are the latent variables more likely to represent disease status, but the presence of known disease status individuals can aid lack-of-fit assessment.

The model violation we have considered could be overcome through extensions to the statistical model. In principle, we could fit a three-state LCM so that the data generating and fitting models once again coincide. We do not consider that here because our goal was to evaluate the performance of two-state LCMs, as they are highly used for evaluating diagnostic tests with no gold standard. Moreover, there was no evidence of lack-of-fit when fitting the two-state model to the motivating data, nor the majority of simulations, therefore no obvious remedial measures were required. We also note that fitting a three-state model need not solve the underlying problems. Fitting and interpreting three-state models is challenging. The three state model is not identifiable with only four tests.⁶ Moreover, the interpretation of a three state model is as difficult, if not more so, than the two-state models we focus on here. While more flexible, a three-state model is still unlikely to incorporate all aspects of the complexity of the underlying biological process, including that different tests may vary in the time at which they can detect the disease. Model misspecfication remains a potential issue for more complex models.

Latent variables models have become an essential tool in applied statistical modelling. We think they have tremendous value in uncovering hidden processes that cannot be directly observed. Often the application of latent variable models can generate hypotheses about scientific processes that can be tested using external data, leading to gains in scientific knowledge that might otherwise be impossible. Our objection is not to the use of latent variable models themselves, but to the way in which they are often used and interpreted. Care needs to be taken when the goal is to estimate parameters or to confirm hypotheses that depend on direct interpretation of the hidden process.

DATA AVAILABILITY STATEMENT

The motivating data used in manuscript are available in Table 1. R code to replicate the simulations are available upon request from the lead author.