Topological magnon insulators in two-dimensional van der Waals ferromagnets CrSiTe₃ and CrGeTe₃: Toward intrinsic gap-tunability

A new family of topological magnon insulators with intrinsic gap-tunability is realized in 2D van der Waals ferromagnets.

Abstract

The bosonic analogs of topological insulators have been proposed in numerous theoretical works, but their experimental realization is still very rare, especially for spin systems. Recently, two-dimensional (2D) honeycomb van der Waals ferromagnets have emerged as a new platform for topological spin excitations. Here, via a comprehensive inelastic neutron scattering study and theoretical analysis of the spin-wave excitations, we report the realization of topological magnon insulators in CrXTe₃ (X = Si, Ge) compounds. The nontrivial nature and intrinsic tunability of the gap opening at the magnon band-crossing Dirac points are confirmed, while the emergence of the corresponding in-gap topological edge states is demonstrated theoretically. The realization of topological magnon insulators with intrinsic gap-unability in this class of remarkable 2D materials will undoubtedly lead to new and fascinating technological applications in the domain of magnonics and topological spintronics.

INTRODUCTION

Recent theoretical predictions and experimental realizations of exotic quasiparticles and topological excitations in condensed matter have led to a tremendous research interest in topological quantum materials (1–5). The topology of the electronic band structure is closely linked to the Berry curvature in the k-space (6, 7), for which the spin-orbit coupling (SOC) plays a key role. In principle, it is also possible to realize nontrivial topology in a bosonic system, such as a system of magnonic excitations (8–18), since the band topology can be treated independently from the statistical nature of the particles. Such topological excitations and the corresponding nontrivial in-gap edge states are chiral and robust against disorder; it is thus believed that the emergence and manipulation of the topological magnonic states bare a tremendous promise for future applications in magnonics and topological spintronics, such as, e.g., quantized pumping of magnons (19), spin-wave beam splitter (10), magnon waveguides (20), chiral traveling-wave magnon amplifiers (21), and magnon-driven orbitronics (22).

However, in contrast to the case of fermionic systems, the topological excitations have been realized only in very few bosonic systems. This is largely owing to the lack of suitable candidate materials as well as to the tremendous challenges in experimental probes of uncharged bosonic topological excitations and, in particular, in a direct detection of in-gap surface/edge states. For instance, inelastic neutron scattering may be the method of choice, e.g., for disentangling topological excitation gaps, but, to directly probe the in-gap edge excitation mode is unfortunately beyond its reach even with the most powerful neutron instruments available nowadays. Nevertheless, since topological magnon edge states contribute to the transverse thermal Hall conductivity, it has recently been demonstrated that the nontrivial topological nature of the magnonic bands can be manifested experimentally by the thermal Hall effect even in a charge-neutral spin system (23–26).

Following the pioneering study of the magnon thermal Hall effect in the pyrochlore ferromagnet Lu₂V₂O₇ (23, 24), the evidence for the gapped magnonic topological insulating phase was reported in the Ising-like kagome ferromagnet Cu[1,3-bdc] under applied magnetic field via inelastic neutron scattering (8). The search for topological excitations in various spin systems has been intensified since then. Recently, Dirac magnons that exhibit symmetry-protected band crossings have been observed in a three-dimensional (3D) Heisenberg antiferromagnet Cu₃TeO₆ (15, 16) and in a 3D quantum XY magnet CoTiO₃ (17). Meanwhile, 2D honeycomb van der Waals (vdW) magnets (27–29), such as the 2D ferromagnets CrGeTe₃ and Fe₃GeTe₂ as well as the Kitaev material α-RuCl₃, have attracted tremendous research interest owing to their fascinating physical properties. Since the recent observation of the gapped topological excitations in ferromagnetic CrI₃ (11), 2D vdW honeycomb-lattice magnets start to emerge as a unique platform for the exploration of the topological magnonics (9, 12, 14). In this class of materials, as schematically shown in Fig. 1A, a topological gap can be opened at the magnon band-crossing Dirac points when a sufficiently large SOC is present. Pronounced SOC would, in turn, give rise to antisymmetric or anisotropic exchange interactions, such as the Dzyaloshinskii-Moriya (DM) (30) and Kitaev interactions, which can drive nontrivial magnonic topology.

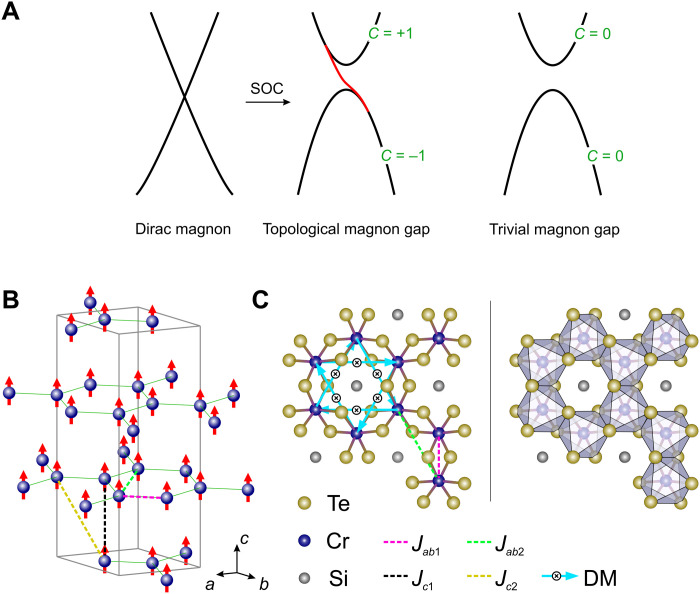
Fig. 1. Schematic of the trivial and topological magnon bands and of the magnetic and atomic structures of CrXTe₃.

(A) Schematic of the band dispersion for a Dirac magnon, a topological magnon, and a trivial magnon. (B) Magnetic structure of CrSiTe₃. In the ab plane, the Cr atoms form a honeycomb lattice represented by the dark blue spheres and green solid lines. The magnetic moments are represented by red arrows. The first and second NN exchange interactions in intra- and interplanes are represented by purple, green, black, and yellow dashed lines, respectively. (C) View perpendicular to the ab plane showing the honeycomb network of CrSiTe₃. The honeycomb network is caged by the edge-sharing octahedra composed of Te atoms and Si─Si dimers located at the center. The light blue arrows represent the bond directions of the DM interactions between the second NN Cr atoms, and all the DM vectors share a common sign along the c axis.

While the current research focus of the community falls primarily on few-layer vdW heterostructures and Morié superlattices, a variety of recently found quantum phenomena in bulk vdW materials—e.g., the half-integer thermal quantum Hall effect and fractionalized Majorana fermions in α-RuCl₃ (29) or topological magnetic textures in Fe₃GeTe₂ (28)—clearly indicate the potential of bulk, quasi-2D vdW magnetic materials as a rich playground in topological quantum matter research. A thorough understanding of intrinsic magnetic interactions and emergent topological properties in single-crystal bulk samples will undoubtedly stimulate further research on monolayer, few-layer, and Morié-based counterparts. In this context, 2D vdW CrXTe₃ compounds emerge as one of the very promising representatives in this class. One would expect the existence of topological magnons in CrXTe₃ similarly to CrI₃ (9, 18, 26), as long as SOC and the antisymmetric exchange interactions are strong enough in this ferromagnetic honeycomb system. Furthermore, because of high versatility in terms of chemical composition, a range of topological magnon insulators with intrinsic gap-tunability may be realized in the CrXTe₃ family. Hence, the intrinsic control of topological magnon properties, for instance, via the engineering of DM interaction, may lead to novel applications in magnonic spintronics and quantum technology.

In this work, we present a comprehensive inelastic neutron scattering study of the spin-wave excitations in single-crystal CrSiTe₃ and CrGeTe₃, which belong to a family of 2D vdW honeycomb ferromagnets. Our inelastic neutron scattering experiments performed at low temperatures show clear dispersive magnonic bands and a well-resolved bandgap opening at the high-symmetry K points in the Brillouin zone (BZ). By fitting to experimental data within the linear spin wave theory (LSWT), the magnitude of exchange interactions in studied materials has been determined. Moreover, the observed bandgap opening was ascribed to the antisymmetric exchange interactions, namely, the DM interaction, and a spin Hamiltonian model including the second nearest-neighbor (2nd-NN) DM interaction could provide a very good description of the magnonic dispersion in CrXTe₃. In line with expectations, the size of the topological gap was found to be strongly dependent on the strength of the DM interaction that intrinsically originates from SOC in this system. Furthermore, the Chern numbers of the magnonic bands were found to be nonzero, thus indicating that the bandgap opening is indeed topologically nontrivial and corresponding edge states could emerge inside the gap. By theoretically assessing the magnitude of the thermal Hall effect, we find that the topologically nontrivial features could be detected in thermal transport measurements in two considered systems. On the basis of the compelling evidence obtained in our inelastic neutron scattering experiments and theoretical calculations, we thus conclude that the exotic topological magnon insulator, which is intrinsically gap tunable, can be ideally realized in the family of 2D vdW honeycomb ferromagnets CrXTe₃.

RESULTS AND DISCUSSION

High-quality single crystals of CrXTe₃ (X = Si, Ge) were grown by the flux method and were carefully examined by x-ray Laue, single-crystal x-ray, and neutron diffraction. The Cr³⁺ ions with S = 3/2 in CrXTe₃ (X = Si, Ge) occupy an ABC stacked honeycomb lattice, as shown in Fig. 1B. Despite the presence of the Si/Ge atoms, each layer shares a similar atomic structure to that of the chromium trihalides CrI₃ (31) and CrBr₃ at low temperature. All the Cr³⁺ ions are located in the center of the edge-shared trigonal distorted octahedra (D_3d symmetry) composed of Te atoms, as shown in Fig. 1C. Below T_c, both materials exhibit ferromagnetic order with the magnetic moments aligned along the c axis. As shown in fig. S1, the magnetic susceptibilities measured with fields applied along the a and c axes clearly show ferromagnetic phase transitions occurring at ∼33 and ∼63 K for CrSiTe₃ and CrGeTe₃, respectively, with the easy axis along the c axis. As the isothermal magnetization curves shown in fig. S1, their magnetic moments can be easily aligned and saturated along both the a and c axes by an application of a small magnetic field, which indicates a small magnetic anisotropy energy in these two materials, consistent with the previous magnetization measurements (32–35). In addition, the ferromagnetic transitions are further confirmed by neutron diffraction, and the transition temperatures T_c are extracted from the fitting of the temperature-dependent intensity of the (1,1,0) magnetic Bragg peak. Among them, the magnetic moment direction of CrGeTe₃ in the ferromagnetic phase is determined along the c axis by polarized neutron diffraction, as shown in fig. S2.

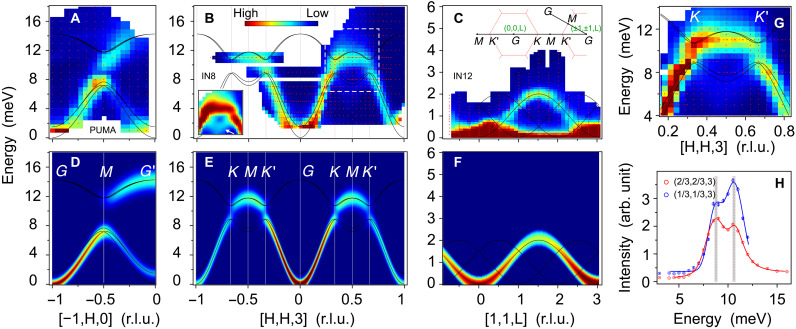
In Fig. 2, we show the magnon spectra of CrSiTe₃ along the high-symmetry directions [−1,H,0] and [H,H,3] in the (H,K,0) reciprocal plane as well as along the [1,1,L] direction in the (H,H,L) reciprocal plane. The measured momentum transfer Q positions in reciprocal space are shown as the black solid lines in the inset of Fig. 2C. The measured magnon bands lie below 16 meV and show clear dispersion along all directions. As shown in Fig. 2A, the low-energy magnon mode (referred to as “acoustic” magnon mode) emerges from the BZ center Γ point and reaches its maximum energy with a gap opening at the M point of the in-plane BZ boundary, consistently with its ferromagnetic nature. Along the [H,H,3] direction, in the vicinity of the K points, as shown in Fig. 2B, a small spin gap is faintly visible at E ≈ 9 meV. Besides, as highlighted by the white arrow in the inset of Fig. 2B, a new branch connected to the acoustic magnon mode was observed along the BZ boundary K-M-K′ direction although its intensity is rather weak. From a zoom-in plot in Fig. 2G, the high-energy branch (referred to as “optical” magnon mode) is found to be less dispersive as compared to the acoustic magnon mode, and it also seems disconnected from the acoustic branch at K points. To further confirm whether a magnon gap is opened at the K point, the line profiles of the constant-Q scans at two different K points are shown in Fig. 2H, where a gap opening of about 2 meV can be clearly resolved. Subsequently, the maximum of the acoustic and the minimum of the optical magnon mode at the K point are determined as 8.6(1) meV and 10.7(1) meV by the multipeak fitting, respectively. Given that the magnitude of the gap is quite large and no clear phonon modes are observed, we conclude that the magnon-phonon hybridization is unlikely to be the origin of the observed gap opening. Instead, introducing an antisymmetric exchange interaction, such as the DM interaction, into the spin Hamiltonian could potentially induce such a considerable gap at the K point. As for the [1,1,L] direction, the acoustic magnon mode only extends up to 2 meV, which is much smaller than that in the Γ-M and Γ-K directions, indicating that the coupling between vdW layers is notably weak and that the magnon spectra are mainly dictated by the intralayer exchange interactions.

Fig. 2. Spin-wave excitations in CrSiTe₃.

(A to C) Energy- and momentum-resolved neutron scattering intensity maps of magnons in CrSiTe₃ along the high-symmetry directions measured at the thermal neutron triple-axis spectrometer PUMA and IN8 and at the cold neutron triple-axis spectrometer IN12, respectively. The black solid lines are the calculated magnon dispersion curves based on the parameters of Heisenberg-DM model presented in this paper. The inset in (B) is a contrast-adjusted plot for the dashed rectangle part to make the acoustic branch easy to see. The inset in (C) shows the exact scan paths in the reciprocal space. (D to F) Calculated magnon spectra intensity maps for (A) to (C), respectively. The calculated spectra are convolved with an energy resolution of 1 meV to compare with the experimental data. (G) Zoom-in plot of the magnon spectra from (B) near the K points. (H) Energy scans of magnon density of states at the K points. The solid lines are the two-peak Gauss fitting results, and the fitted peak positions and error bars are indicated by the vertical dashed lines with gray shadow. r.l.u, reciprocal lattice unit.

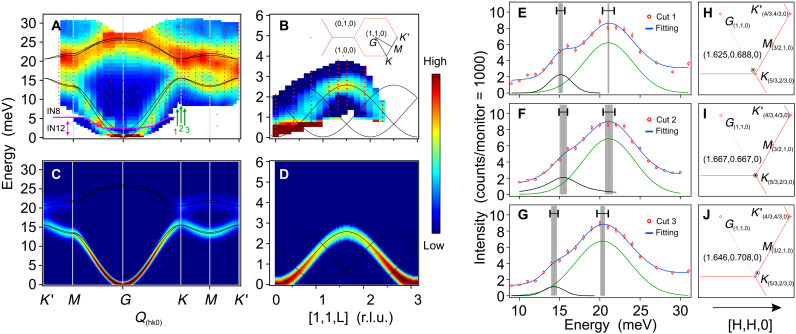
As for the analogous CrGeTe₃, whose transition temperature T_c is nearly doubled as compared to that of CrSiTe₃, we also measured its spin waves along all high-symmetry directions, and the black solid lines in the inset of Fig. 3B show the corresponding Q positions for the measurements. The magnon modes in the (H,K,0) reciprocal plane are shown in Fig. 3A, where two branches, namely, the acoustic and optical modes, can be easily distinguished, and the magnon modes along [1,1,L] directions, dictated by the interlayer exchange interactions, are shown in Fig. 3B. As expected, the acoustic mode has a stronger dispersion than the optical mode and also emerges from the magnetic BZ center Γ point at low energy. Except for the scale of the energy transfers, the overall feature of the magnon modes of CrGeTe₃ appears very similar to that of CrSiTe₃ including the gap opening at the K point. The acoustic magnon mode in the (H,K,0) plane reaches its energy maximum at around 15 meV, which is nearly two times that of CrSiTe₃, but, along the out-of-plane direction, the magnon mode only extends to 2.5 meV, basically the same as in CrSiTe₃. It indicates that replacing the Si atoms by heavier Ge atoms in CrXTe₃ will notably enhance the intralayer exchange interactions and, meanwhile, will have little influence on the interlayer exchange interactions. This suggests that the exchange interactions can be tuned by nonmagnetic atoms without destroying the magnetic network and that the strength of SOC of nonmagnetic atoms may also play an important role in the superexchange interactions in this vdW honeycomb ferromagnet family.

Fig. 3. Spin-wave excitations in CrGeTe₃.

(A and B) Energy- and momentum-resolved neutron scattering intensity maps of magnon in CrGeTe₃ along the high-symmetry directions measured at IN8 and IN12, respectively. Black solid lines are the calculated magnon dispersion curves. Inset in (B) shows the projected BZ with high-symmetry points and the scan paths in the experiments. (C and D) The corresponding calculated magnon spectra intensity maps for (A) and (B) by using the 2nd-NN DM interaction model. The calculated spectra are convolved with an energy resolution of 1 meV to compare with experimental data. (E to G) The line profiles of constant-Q energy scan at the positions of 1,2,3 marked by the green arrows in (A) near the K point Q = (5/3,2/3,0). The solid lines are the multipeak Gauss fitting results. The peak positions and the errors are indicated, respectively, by the dashed lines and the gray shadows; the corresponding energy resolutions are represented by the black horizontal bar with caps. (H to J) The actual Q positions of the cut 1, 2, and 3 are marked by black circles with center dots in the reciprocal space. The red solid lines are the BZ boundaries.

Furthermore, one can notice that the optical mode of CrGeTe₃ is rather broad in energy even after taking into consideration the instrument resolution of ∼2 meV at such energy transfer, and is quite intense, in contrast to the situation of CrSiTe₃. We find that the intensity of this optical magnon branch at the K point is about four times higher than the prediction of our LSWT calculation.

Given that the optical phonon mode of CrGeTe₃ has a similar energy scale (36) and that the evidence for the spin-lattice coupling in CrGeTe₃ has already been reported in previous Raman experiments (37, 38), we tend to believe that both the broadening in energy and the intensity enhancement could be a result of possible magnon-phonon interactions. The phonon modes around 25 meV are indeed mainly contributed by the magnetic atoms Cr (39); the coexistence of the phonon and magnon modes in the same energy range may allow for a possible spectral weight transfer between them, thus leading to the observed unusual intensity enhancement. Generally, a dynamic spin-lattice coupling can create hybridization gaps or broadening in the magnon spectra at the intersection points of the coupled magnon and phonon modes.

Regardless of the unusual broadening of the optical branches, a gap opening at the K point is still resolvable. In Fig. 3 (E to G), three line profiles of energy scans are extracted from the vicinity of the K point and fitted by two Gauss peaks to accurately determine the size of the opened gap, and the corresponding positions of momentum transfer in reciprocal space in the measurements are marked by the black circles in Fig. 3 (H to J). From Fig. 3F, a weak but clear shoulder can be seen around 15 meV, which denotes the band maximum of the acoustic mode, and subsequently, the size of the opened gap at the K point can be determined as ∼5 meV from the fitting results. We conclude that such a large gap is unlikely to arise as a result of possible magnon-phonon coupling, since the magnon-phonon coupling–induced gap always occurs at the intersection between the magnon and phonon bands and it does not extend over the entire BZ. It is thus expected that the gap in CrGeTe₃ shares the same origin as in CrSiTe₃, namely, the antisymmetric exchange interaction, e.g., similar to the SOC-mediated DM interaction. Hence, it appears natural that a larger gap opening in CrGeTe₃ must arise from the larger SOC in the latter material when Si is replaced by heavier Ge.

To determine the nature of magnon bands and the underlying magnetic exchange interactions in CrXTe₃ systems, we carry out LSWT calculations based on a generalized Heisenberg spin Hamiltonian including DM interaction and single-ion magnetic anisotropy (40)

$$\begin{array}{cc}\hfill H=& -{\displaystyle \sum _{i<j}}{J}_{\mathit{ij}}({\mathbf{S}}_i·{\mathbf{S}}_j)-A_{\mathit{zz}}{\displaystyle \sum _i}{(S_i^z)}^2\hfill \\ & -{\displaystyle \sum _{i<j}}{\mathbf{D}}_{\mathit{ij}}·({\mathbf{S}}_i\times {\mathbf{S}}_j)\hfill \end{array}$$ (1)

where J_ij is the Heisenberg exchange constant between spins S_i and S_j, D_ij represents the vector of the DM interaction between two magnetic ions when the inversion symmetry is broken, and A_zz is the easy-axis anisotropy along the c axis. Note that we take S = 3/2 given that the measured moment of Cr ions is extracted as ∼3 μ_B from the isotherm magnetization curve shown in fig. S1. As illustrated in Fig. 1B, we consider the 1st- and 2nd-NN Heisenberg exchange couplings in every honeycomb plane labeled as J_ab1 and J_ab2, and the 1st- and 2nd-NN exchange couplings between layers labeled as J_c1 and J_c2. From the symmetry analysis, there will be no DM interaction between the nearest neighbors (NNs) because of the space inversion. However, the space inversion symmetry is broken between the second NNs, which can lead to a nonzero 2nd-NN DM interaction.

After a proper fitting process of the experimentally observed magnon spectra along the high-symmetry directions, the best-fit values for the exchange parameters of CrSiTe₃ and CrGeTe₃ were extracted. As shown in Table 1, we find that the intralayer interactions in CrXTe₃ are mainly dominated by the NN exchange couplings J_ab1, which are one order of magnitude larger than the interlayer exchange. Given the presence of sizeable interlayer exchange interactions, it is worth noting that CrXTe₃, strictly speaking, should be classified as quasi-2D spin systems. While the direct exchange coupling between Cr ions is expected to be antiferromagnetic due to the formation of Cr─Te─Cr bonds with a bond angle of nearly 90°, the NN exchange couplings among Cr ions become ferromagnetic (J > 0) according to the Goodenough-Kanamori-Anderson rules (41). Although the fitting values of the interlayer couplings J_c1 and J_c2 are quite comparable, the magnon dispersion along the [0,0,L] direction is likely much more sensitive to the 2nd-NN interlayer coupling J_c2 because each Cr³⁺ spin has nine 2nd-NNs but only one 1st-NN. Besides, the strength of the DM interactions is fitted as ∣D_ij ∣ = 0.12 meV for CrSiTe₃ and ∣D_ij ∣ = 0.32 meV for CrGeTe₃, which results in a ∼2- and ∼5-meV gap opening at the K points, respectively. We remark that the magnitude of the DM interaction in CrXTe₃ constitutes about 10% of J_ab1, and it is quite comparable to the value of exchange J_ab2 between 2nd-NN Cr ions. From the isothermal magnetization curve at 2 K (fig. S1), we can extract the magnetocrystalline anisotropy energy per Cr³⁺, which is only 0.09 meV for CrSiTe₃ and 0.02 meV for CrGeTe₃, indicating a small single-ion anisotropy in the CrXTe₃ system. In terms of the small single-ion anisotropy, as expected, we failed to determine the size of the gap at the Γ point from our energy scan data directly, and we used instead the quadratic fitting result 0.01 meV (shown in figs. S5 and S6) for the anisotropy term A in the Heisenberg-DM model.

Table 1. Spin Hamiltonian parameters.

The values of exchange interactions including the DM interactions are listed together for both CrSiTe₃ and CrGeTe₃. The value of the 2nd-NN DM vector was chosen to reproduce the experimental spin-wave dispersion. The unit of the parameters indicated here is milli–electron volts. The single-ion anisotropy is fixed to 0.01 meV.

Unit (meV)	J ab1	J ab2	J c1	J c2	Dij
CrSiTe3	1.49	0.15	0.07	0.06	(0,0,0.12)
CrGeTe3	2.73	0.33	0.10	0.08	(0,0,0.32)

As shown in Fig. 2 (D to F) and Fig. 3 (C and D), the magnon bands of CrXTe₃ calculated from the Heisenberg-DM model are consistent with our experimentally observed spectra, taking into account a finite energy resolution. Especially in the vicinity of the K points, the opened gap is also well described by the model. In addition, a range of constant energy slices near the BZ boundary are found to be in an excellent agreement with the simulation results, as shown in fig. S4. Moreover, the calculated spectra also reproduce the characteristic weak/strong intensity of the magnon bands in different BZs, except that the optical modes of CrGeTe₃ are notably enhanced by the possible hybridization with the phonon modes, as discussed above.

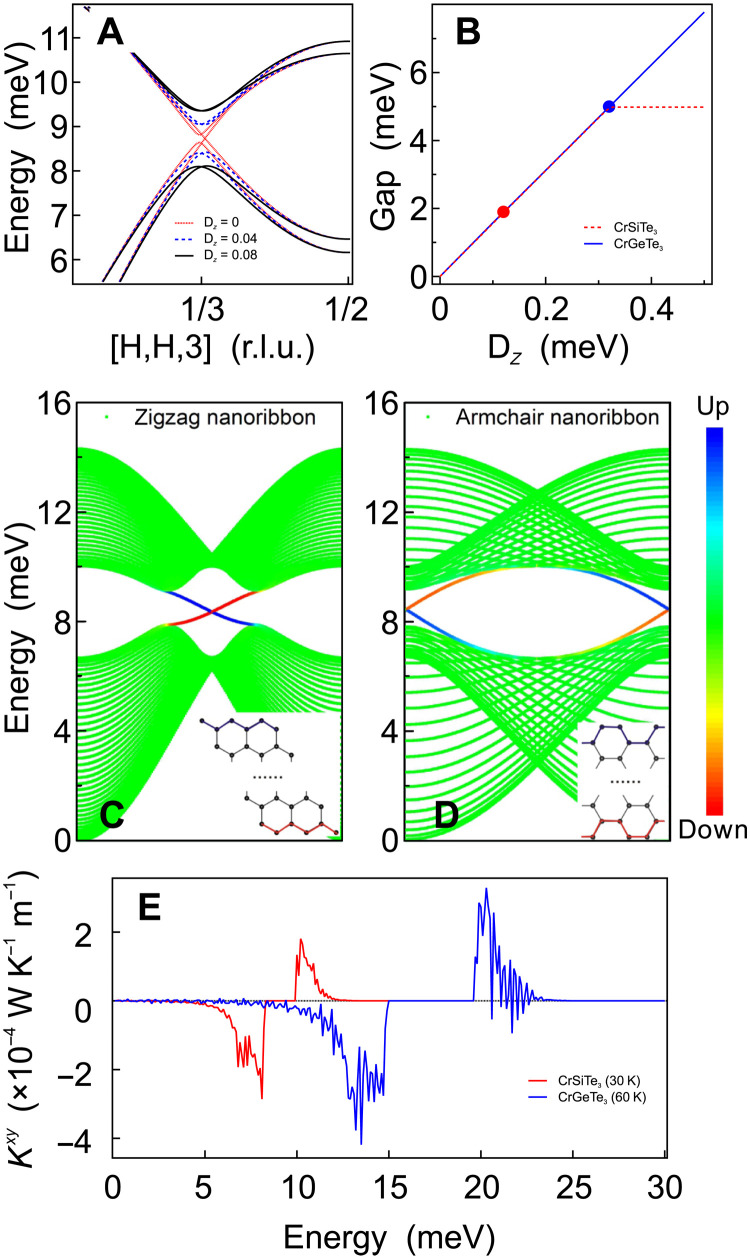
The overall band dispersion is mainly determined by the ferromagnetic NN Heisenberg exchange couplings, and the gap opening at the K points cannot be reproduced by simply adding exchange couplings with further neighbors in the model, until an anisotropic exchange coupling term such as the DM interaction is taken into consideration. It is known that the DM interaction acts as an effective gauge potential for magnonic states and it can open topologically nontrivial bandgaps in a magnonic system (9, 42). Without the DM interaction, a crossing point located in the vicinity of K point would be present (Fig. 4A), while the gap is opened immediately as the DM interaction is introduced, with the bandgap size increasing almost linearly with the strength of the DM interaction (Fig. 4B). Overall, the constructed Heisenberg-DM model reproduces spin waves in CrXTe₃ very nicely, with one key point being that the DM interaction in our case is not only dependent on the SOC strength of Te atoms along the Cr─Te─Cr paths but also influenced by Si/Ge atoms. The large difference of the gap size in CrXTe₃ thus translates into a possibility to tune the DM interaction by the substitution of the atoms with different SOC strength in the honeycomb center.

Fig. 4. The impact of the DM interaction on the magnon dispersion.

The magnon dispersions of CrSiTe₃ with different DM interaction strength are compared in (A). (B) The relationships between the opened global bandgap and the strength of the DM interaction; the red and blue filled circles correspond to the values extracted from the magnon bands. (C and D) The edge states of the monolayer CrSiTe₃ for the respective zigzag and armchair nanoribbon. The color scale represents the weight of the magnonic wave function along the slab. (E) Temperature dependence of the topological thermal Hall conductivity of CrSiTe₃ and of CrGeTe₃ in the ferromagnetic ordered phases.

In addition to the Heisenberg-DM model, introducing the Kitaev interactions can also produce similar spin-wave spectra and induce a gap opening at the K points. If we exclude X atoms, the rest of CrXTe₃ shares a common atomic structure with the well-studied Kitaev spin liquid candidate α-RuCl₃ (43), and three kinds of diamond-shaped planes, composed of the NN Cr─Te─Cr bonds, are nearly orthogonal to each other. In terms of the structure symmetry, it is possible to have an anisotropic exchange interaction between NN, for instance, an anisotropic Ising interaction in the local basis that consists of the normal vectors of three Cr─Te─Cr planes, as shown in fig. S7. The presence of the additional anisotropy can make it possible to construct the Heisenberg-Kitaev Hamiltonian. Unexpectedly, to match the magnetic excitations in CrXTe₃, we found that the Kitaev exchange needs to be one order of magnitude larger than the NN Heisenberg term, as shown in table S1. In the latter case, the fitted Kitaev exchange parameters of CrGeTe₃ are almost two times those of CrSiTe₃, which is quite interesting, since CrSiTe₃ and CrGeTe₃ share a similar local environment including the bond distance for NN Cr atoms. One possible explanation would be that the sp3 hybridized orbitals of Si/Ge atoms in the honeycomb center are strongly coupled with the p orbitals of Te atoms and subsequently strongly influence the strength of the Cr─Te─Cr superexchange interaction. Similar orbital hybridization effect is not rare since the superexchange interaction mediated by nonmagnetic ions is also proposed in inverse-trirutile compound (44) and double perovskites (45). In any case, if CrXTe₃ is dominated by the Kitaev interaction, then a strong in-plane anisotropy should be easily evident in the magnetization measurements, which has never been reported. We thus conclude that the Heisenberg-Kitaev model is not a proper model for CrXTe₃. More details concerning the discussion of Heisenberg-Kitaev model are given in the Supplementary Materials.

Having determined the microscopic spin Hamiltonians for CrXTe₃, we turn to the analysis of the topological nature of the magnonic bands and reveal theoretically the presence of a large thermal Hall effect, an unambiguous experimental signature of topologically nontrivial in-gap edge states. Our numerical calculations confirm a nonzero Berry curvature at the K points and also a nonzero Chern number, indicating nontrivial topology of these magnon bands. For bulk CrXTe₃, the total Chern number is determined to be −3 and +3 for the acoustic and optical magnon bands, respectively, which means that there is one topological edge state at the boundary of each honeycomb layer. The sign of the Chern number depends on the magnetization direction, which, in our case, is the z axis. The sign of the Chern number can be changed by reversing the magnetization direction, which can be naturally achieved at the magnetic domain walls in CrXTe₃, acting as perfect waveguides for the topological edge states. In addition to the bulk system, we also investigated the topological properties of the monolayer system, where we observe an almost identical BZ Berry curvature distribution and predict only one acoustic branch with Chern number −1 and one optical branch with Chern number +1 for the magnon bands. Because of the lack of any interlayer interactions, the magnon bands in the monolayer are not split as in the bulk, but the topological properties are sustained as long as the intralayer DM interaction exists. To simplify the calculation, we use the monolayer system to study the edge states. The edge states of zigzag and armchair nanoribbons with the projections of the bulk states are shown together in Fig. 4 (C and D), where one can observe that the edges on the two sides of a nanoribbon hold their own exclusive edge states but with opposite propagation direction. The role of the DM interaction here is similar to that of strong SOC in graphene-like systems that turns them into a quantum spin Hall insulator (2), and so, CrXTe₃ can also be considered as a bosonic version of the well-known topological insulator state. Correspondingly, the presence of nontrivial edge states can contribute to the transverse thermal Hall conductivity to yield the topological thermal Hall effect when a longitudinal temperature gradient and out-of-plane magnetic field are applied. As shown in Fig. 4E, our numerical estimates indicate that the thermal Hall conductivity generated by the edge states can reach the order of 10⁻⁴ W K⁻¹m⁻¹, which is large enough to be observed in experiment. This motivates the future confirmation of topological thermal Hall effect in CrXTe₃ from thermal transport experiments.

In summary, we carried out a very comprehensive inelastic neutron scattering study of the spin-wave excitations on the ferromagnetic honeycomb magnets CrXTe₃. Our data show a clear gap opening in the magnon bands at the K points, with the gap size of about 2 and 5 meV for CrSiTe₃ and CrGeTe₃, respectively. The magnon band dispersion in CrXTe₃ can be described very well by either the Heisenberg-DM model or the Heisenberg-Kitaev model. The gap opening can be ascribed to the asymmetric DM interaction with an out-of-plane DM vector or Kitaev interactions. However, because of the very small magnetic anisotropy observed in CrXTe₃, the Heisenberg-DM model, in which the isotropic Heisenberg exchange dominates, is perceived as the proper model for these materials. The magnon spectra of CrXTe₃ are successfully reproduced by using the LSWT calculations. The gap size was found to be proportional to the strength of the DM interaction. The strength of the DM interaction is also strongly dependent on the SOC of the nonmagnetic Si/Ge atoms that are located at the honeycomb center. Furthermore, our numerical calculations predict the nontrivial topological nature of the magnon bands gap at the K points and also reveal the existence of topological edge states at the sample boundaries and domain walls. In addition, we also calculated the reference values for the expected thermal Hall conductivity that may arise from the topological magnon edge states, which can be measured in future thermal transport experiments. On the basis of our experimental and theoretical results, we propose that CrSiTe₃ and CrGeTe₃ present an ideal platform to realize topological magnon insulators, in which the nontrivial magnon gaps can be intrinsically tuned by varying the SOC of nonmagnetic ions. In contrast to CrI₃, the substitution of Si/Ge in the CrXTe₃ system using a wide range of nonmagnetic ions such as C, Si, Ge, Sn, Pb, and Ga (46–50) can, in principle, change the balance of the exchange interactions and, thus, enable the manipulation of the topological magnon gap size, leading to novel magnetic properties rooting in complex magnonic topology.

MATERIALS AND METHODS

High-quality single crystals of CrXTe₃ (X = Si, Ge) were grown by the flux method at the sample preparation laboratory of Jülich Centre for Neutron Science (JCNS) at Heinz Maier-Leibnitz Zentrum (MLZ) in Garching. Starting materials of Cr, X, and Te were mixed in an Ar-filled glove box at a molar ratio of Cr:X:Te = 1:1:10. The mixture was placed in an alumina crucible, which was then sealed in an evacuated quartz tube. The tube was heated up to 930°C (X = Ge) or 1030°C (X = Si) in 4 hours and sustained there for 10 hours. Then, the tube was slowly cooled down to 600°C with a cooling speed of 3°C/hour followed by separating the crystals from the Te flux by centrifuging. Shiny and sizable crystals with hexagonal natural edges were obtained.

Single-crystal x-ray diffraction was performed at room temperature with an incident wavelength of 1.54 Å (Cu-K_α) on a Bruker D2 PHASER x-ray diffractometer. By using a MPMS SQUID magnetometer (Quantum Design), the temperature and field dependence of the magnetization of CrSiTe₃ and CrGeTe₃ were measured along both the a and c axes, respectively. The magnetic susceptibility was measured from 2 to 300 K with both zero-field-cooling and field-cooling conditions for some selected single crystals. The isothermal magnetization (M-H) curves were also measured in a sweeping field from −50 to 50 kOe at 2 K.

The polarized neutron diffraction measurement on single-crystal CrGeTe₃ was carried out at the cold-neutron polarized spectrometer DNS at MLZ (with λ_i = 4.2 Å) at T = 4 K. 2D Q maps in the (H,K,0) and (H,H,L) planes of reciprocal space at three different polarization modes were measured at 4 K. For the measurements of spin-wave excitations, we coaligned two pieces of large single crystals with a total mass of 1.3 g for CrSiTe₃ and more than 100 pieces with a total mass of about 1.4 g for CrGeTe₃. All the inelastic neutron scattering experiments were performed by using a range of thermal and cold neutron triple-axis spectrometers, including PUMA at MLZ, FLEXX (51) at HZB, and IN12, IN8, and IN22 at the Institut Laue-Langevin (ILL). Both the (H,H,L)- and (H,K,0)-oriented samples were prepared for each of CrSiTe₃ and CrGeTe₃. The low-energy magnon dispersion along [0,0,L] was measured at the cold neutron triple axis at IN12 (with a fixed k_f = 1.7 and 2.8 Å⁻¹) and at FLEXX (with k_f = 1.55 Å⁻¹). The magnon dispersions along [H,H,0] and [H,0,0] were measured at the thermal neutron triple-axis spectrometers IN8 and PUMA (both with a fixed k_f = 2.662 Å⁻¹). All the magnon dispersion data were collected at the base temperature of T = 2 K.

Supplementary Materials

This PDF file includes:

Sections S1 to S3

Figs. S1 to S11