Explaining Groups of Points in Low-Dimensional Representations

Abstract

A common workflow in data exploration is to learn a low-dimensional representation of the data, identify groups of points in that representation, and examine the differences between the groups to determine what they represent. We treat this workflow as an interpretable machine learning problem by leveraging the model that learned the low-dimensional representation to help identify the key differences between the groups. To solve this problem, we introduce a new type of explanation, a Global Counterfactual Explanation (GCE), and our algorithm, Transitive Global Translations (TGT), for computing GCEs. TGT identifies the differences between each pair of groups using compressed sensing but constrains those pairwise differences to be consistent among all of the groups. Empirically, we demonstrate that TGT is able to identify explanations that accurately explain the model while being relatively sparse, and that these explanations match real patterns in the data.

1. Introduction

A common workflow in data exploration is to: 1) learn a low-dimensional representation of the data, 2) identify groups of points (i.e., clusters) that are similar to each other in that representation, and 3) examine the differences between the groups to determine what they represent. We focus on the third step of this process: answering the question “What are the key differences between the groups?”

For data exploration, this is an interesting question because the groups often correspond to an unobserved concept of interest and, by identifying which features differentiate the groups, we can learn something about that concept of interest. For example, consider single-cell RNA analysis. These datasets measure the expression levels of many genes for sampled cells. Usually the cell-type of each of those cells is unknown. Because gene expression and cell-type are closely related, the groups of points that can be seen in a low-dimensional representation of the dataset often correspond to different cell-types (Figure 1). By determining which gene expressions differentiate the groups, we can learn something about the connection between gene expression and cell-type.

Figure 1:

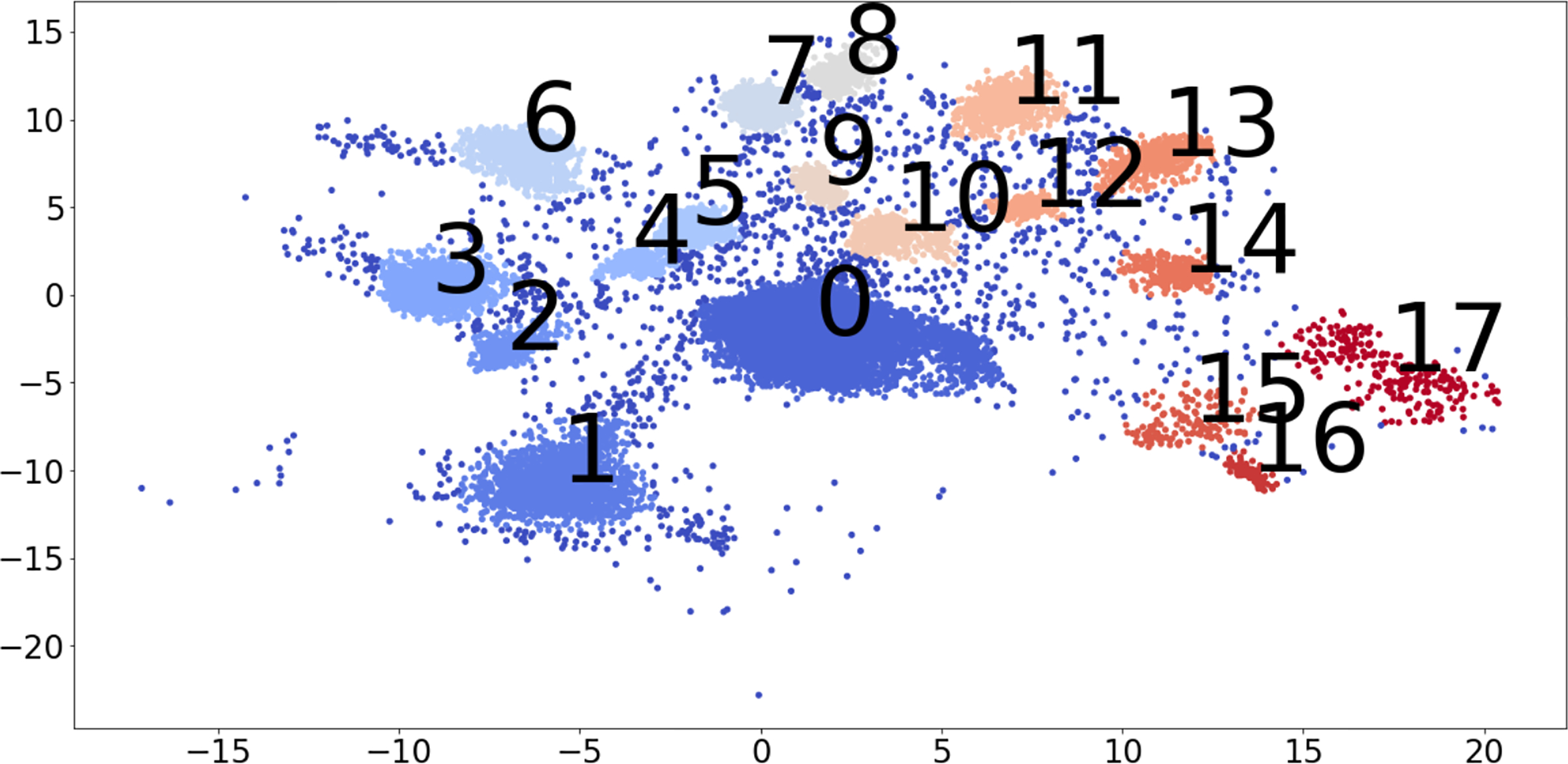
A representation learned for a single-cell RNA sequence dataset using the model from (Ding et al., 2018). Previous work on this dataset showed that these groups of cells correspond to different cell-types (Shekhar et al., 2016). The goal of a GCE is to use this representation to identify the changes in gene expression that are associated with a change of cell type.

One common approach for answering this question is manual interpretation. One simple way to do this, that we will use as a naive baseline, is to calculate the Difference Between the Mean (DBM) value of each feature in the original input space between a pair of groups. For example, consider using DBM to explain the differences between the cells in Group 3 and Group 17 from Figure 1. In this case, DBM’s explanation contains many hundreds of non-zero elements, which is far too many to be understood by a person (Figure 2). If we make DBM’s explanation sparse by thresholding it to include only the k largest changes, it is no longer an effective explanation because it no longer reliably maps points from Group 3 to Group 17 (Figure 3). More generally, manual interpretation can be time-consuming and typically ad-hoc, requiring the analyst to make arbitrary decisions that may not be supported by the data.

Figure 2:

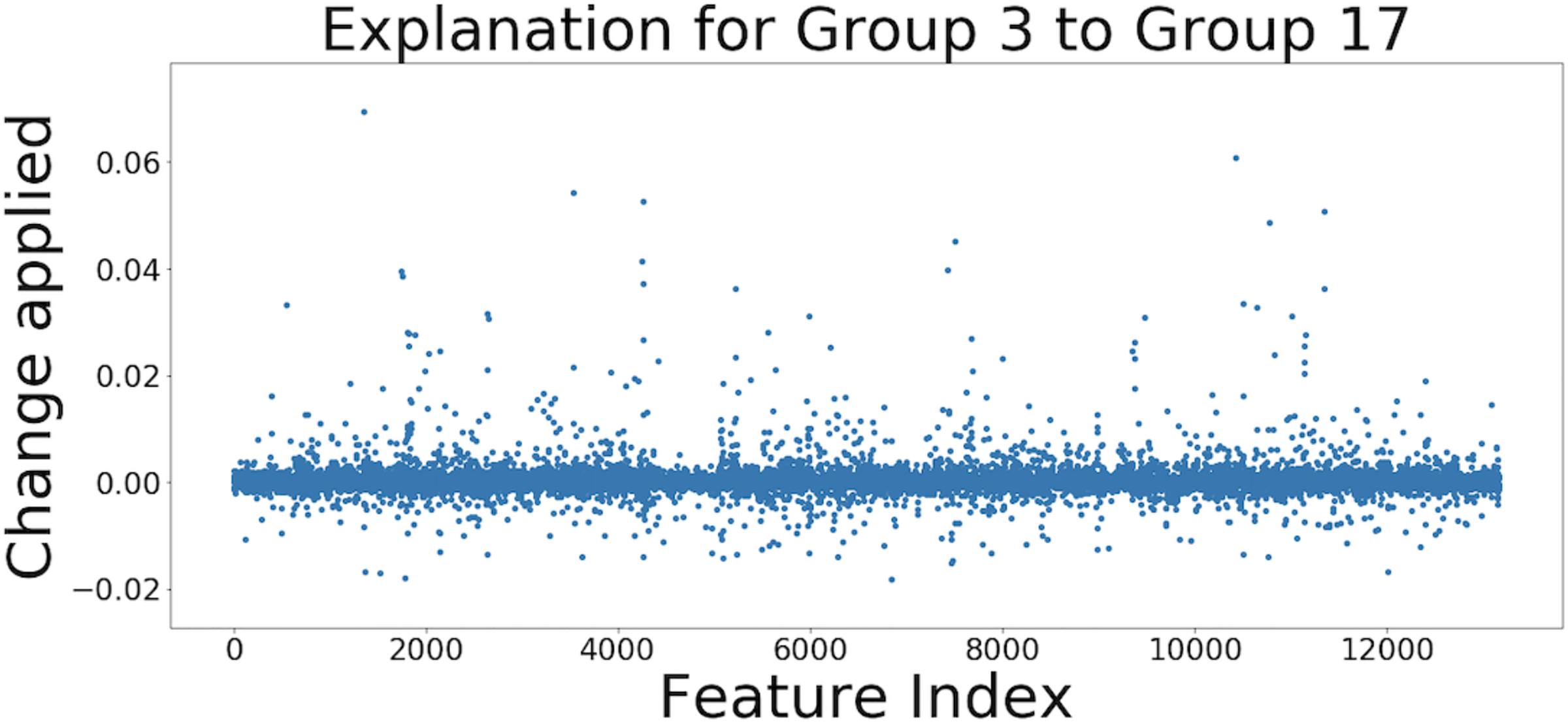
DBM’s explanation for the difference in gene expression between the cells in Group 3 and Group 17. The x-axis shows which feature index (gene expression) is being changed and the y-axis shows by how much. Because it is very high dimensional and not sparse, it is difficult to use DBM to determine what the key differences actually are between this pair of groups (i.e., which genes differentiate these cell-types).

Figure 3:

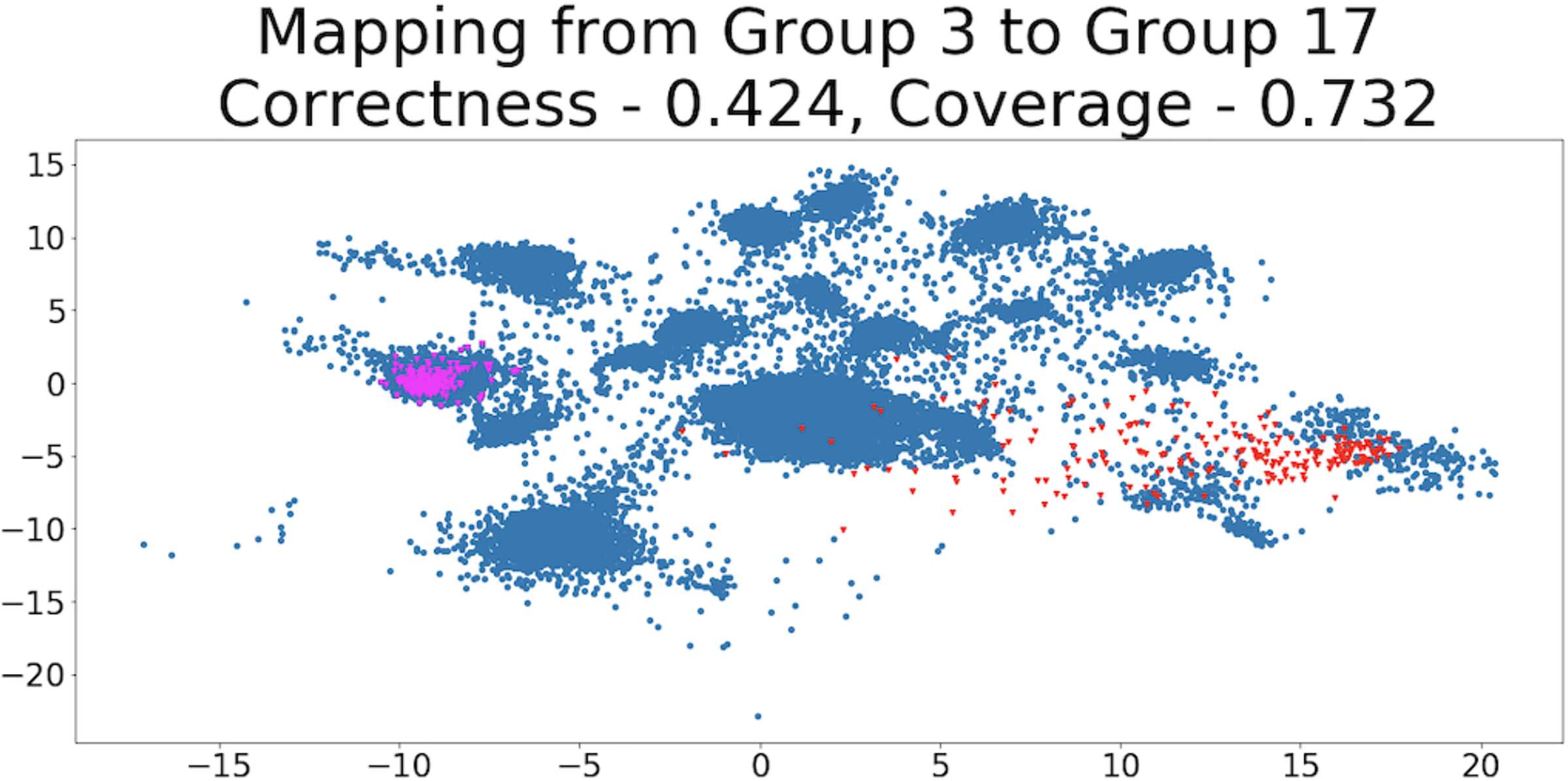
By thresholding DBM’s explanation for the differences between Group 3 and Group 17 to include only the k largest changes (250 in this case), we can make it sparse enough to be human interpretable. However, this simplified explanation is no longer an effective explanation. We show this visually: the magenta points are the representations of points sampled randomly from Group 3 and the red points are the representations of those points after the explanation was applied to them. We can see that the red points are usually not in Group 17 (poor correctness) and that they do not cover much of Group 17 (poor coverage). These metrics will be defined in Section 3.

Another, more principled, method is statistical hypothesis testing for the differences between features across groups (Shaffer, 1995). However, the trade-off between the power of these tests and their false positive rate becomes problematic in high-dimensional settings.

Both manual interpretation and statistical testing have an additional key shortcoming: they do not make use of the model that learned the low dimensional representation that was used to define the groups in the first place. Intuitively, we would expect that, by inspecting this model directly, we should be able to gain additional insight into the patterns that define the groups. With this perspective, answering our question of interest becomes an interpretable machine learning problem. Although there are a wide variety of methods developed in this area (Ribeiro et al., 2016; Lundberg & Lee, 2017; Wang & Rudin, 2015; Caruana et al., 2015; Ribeiro et al., 2018; Zhang et al., 2018), none of them are designed to answer our question of interest. See Section 2 for further discussion.

To answer our question of interest, we want a counterfactual explanation because our goal is to identify the key differences between Group A and Group B using the low-dimensional representation and the most natural way to do this is to find a transformation that causes the model to assign transformed points from Group A to Group B. Additionally, we want a global explanation because we want to find a explanation that works for all of the points in Group A and because we want the complete set of explanations to be consistent (i.e., symmetrical and transitive) among all the groups. See Section 3.2 for further discussion of our definition of consistency in this context. Hence, our goal is to find a Global Counterfactual Explanation (GCE). Although the space of possible transformations is very large, we consider translations in this work because their interpretability can be easily measured using sparsity.

Contributions:

To the best of our knowledge, this is the first work that explores GCEs. Motivated by the desire to generate a simple (i.e., sparse) explanation between each pair of groups, we derive an algorithm to find these explanations that is motivated by compressed sensing (Tsaig & Donoho, 2006; Candès et al., 2006). However, the solutions from compressed sensing are only able to explain the differences between one pair of groups. As a result, we generalize the compressed sensing solution to find a set of consistent explanations among all groups simultaneously. We call this algorithm Transitive Global Translations (TGT).

We demonstrate the usefulness of TGT with a series of experiments on synthetic, UCI, and single-cell RNA datasets. In our experiments, we measure the effectiveness of explanations using correctness and coverage, with sparsity as a proxy metric for interpretability, and we compare the patterns the explanations find to those we expect to be in the data. We find the TGT clearly outperforms DBM at producing sparse explanations of the model and that its explanations match domain knowledge. ¹

2. Related Work

Most of the literature on cluster analysis focuses on defining the clusters; the interpretation methods discussed in that literature are primarily manual inspection/visualization or statistical testing (Jiang et al., 2004). Consequently, the focus of our related work will be on interpretable machine learning. Although interpretability is often loosely defined and context specific (Lipton, 2016), we categorize existing methods along two axes in order to demonstrate how a GCE differs from them. Those axes are the explanation’s level and its form.

The first axis used to categorize explanations is their level: local or global. A local explanation explains a single prediction made by the model (Ribeiro et al., 2016; Lundberg & Lee, 2017; Plumb et al., 2018). Kauffmann et al. (2019) studies a problem closely related to ours of explaining why a point was assigned to its cluster/group. A global explanation will explain multiple predictions or the entire model at once (Wang & Rudin, 2015; Caruana et al., 2015; Ribeiro et al., 2018).

The second axis we use to categorize explanations is their form: feature attribution, approximation, or counterfactual. A feature attribution explanation assigns a value measuring how each feature contributed to the model’s prediction(s) (Lundberg & Lee, 2017; Sundararajan et al., 2017). Importantly, it is necessary to define a baseline value for the features in order to compute these explanations. An approximation explanation approximates the model being explained using a function that is simple enough to be considered directly interpretable (e.g., a sparse linear model or a small decision tree) across some neighborhood, which could be centered around a point or could be the entire input space (Ribeiro et al., 2016; Plumb et al., 2018; Wang & Rudin, 2015; Caruana et al., 2015; Ribeiro et al., 2018). A counterfactual explanation finds a transformation of the input(s) such that the transformed version of the input is treated in a specific way by the model (Zhang et al., 2018; Dhurandhar et al., 2018; Goyal et al., 2019; Dhurandhar et al., 2019).

For various reasons, it would be challenging to use other types of explanations to construct a GCE. Local explanations would have to be aggregated in order to produce an explanation that applies to a group of points and it would be nontrivial to ensure that the resulting “aggregated group explanations” are consistent (i.e., symmetrical and transitive). For feature attribution and local approximation explanations, it is difficult to guarantee that the baseline value or neighborhood they consider is defined broadly enough to find the transformation we want. For global approximation explanations, we might not be able to approximate a complex model well enough to find the transformation we want because of the accuracy-interpretability trade-off that stems from the complexity constraint on the explanation model (Lipton, 2016). For a concrete example of these difficulties, see the Appendix A.1. This example uses Integrated Gradients (Sundararajan et al., 2017) which is a local feature attribution method that produces symmetrical and transitive explanations with respect to a single class.

3. Global Counterfactual Explanations

We will start by introducing our notation, more formally stating the goal of a GCE, and defining the metrics that we will use to measure the quality of GCEs. We do this under the simplifying assumption that we have only two groups of points that we are interested in. Then, in Section 3.1, we will demonstrate the connection between finding a GCE and compressed sensing. We use that connection to derive a loss function we can minimize to find a GCE between a single pair of groups of points. Finally, in Section 3.2, we will remove our simplifying assumption and introduce our algorithm, TGT, for finding a set of consistent GCEs among multiple groups of points.

Notation:

Let $r:{ℝ}^d\to {ℝ}^m$ denote the function that maps the points in the feature space into a lower-dimensional representation space. The only restriction that we place on r is that it is differentiable (see the Appendix A.2 for more discussion on r). Suppose that we have two regions of interest in this representation: R_initial, $R_{target}\subset {ℝ}^m$. Let X_initial and X_target denote their pre-images. Then, our goal is to find the key differences between X_initial and X_target in ${ℝ}^d$ and, unlike manual interpretation or statistical testing, we will treat this as an interpretable machine learning problem by using r to help find those key differences.

Defining the Goal of GCEs:

At a high level, the goal of a GCE is to find a transformation that takes the points in X_initial and transforms them so that they are mapped to R_target by r; in other words, r treats the transformed points from X_initial as if they were points from X_target. Formally, the goal is to find a transformation function $t:{ℝ}^d\to {ℝ}^d$ such that:

$$r(t(x))\in R_{target}\forall x\in X_{initial}$$ (1)

Because we are using t as an explanation, it should be as simple as possible. Since they are very simple and their complexity can be readily measured by their sparsity, we limit t to a translation:

$$t(x)=x+\delta$$ (2)

Measuring the Quality of GCEs:

To measure the quality of a GCE we use two metrics: correctness and coverage. Correctness measures the fraction of points mapped from X_initial into R_target. Coverage measures the fraction of points in R_target that transformed points from X_initial are similar to. Mathematically, we define correctness as:

$$cr(t)=\frac{1}{\left|X_{initial}\right|}\sum _{x\in X_{initial}}\mathbb{1}\left[\exists x^{\prime }\in X_{target}\mid {\Vert r(t(x))-r\left(x^{\prime }\right)\Vert }_2^2\le ϵ\right]$$ (3)

And coverage as:

$$cv(t)=\frac{\mathbb{1}}{\left|X_{target}\right|}\sum _{x\in X_{target}}1\left[\exists x^{\prime }\in X_{initial}\mid {\Vert r(x)-r\left(t\left(x^{\prime }\right)\right)\Vert }_2^2\le ϵ\right]$$ (4)

Clearly, correctness is a necessary property because an explanation with poor correctness has failed to map points from X_initial into R_target (Equation 1). However, coverage is also a desirable property because, intuitively, an explanation with good coverage has captured all of the differences between the groups.

Defining these metrics requires that we pick a value of ϵ.² Observe that, if X_initial = X_target and t(x) = x, then cr(t) = cυ(t) and we have a measure of how similar a group of points is to itself. After r has been learned, we increase ϵ until this self-similarity metric for each group of points in the learned representation is between 0.95 and 1.

A Simple Illustration:

We will now conclude our introduction to GCEs with a simple example to visualize the transformation function and the metrics. In Figures 4, 5, and 6, the data is generated from two Gaussian distributions with different means and r(x) = x. We use DBM between Group 1 and Group 0 to define the translation/explanation. In Figure 4, the two distributions have an equal variance and, as a result, the translation is an effective explanation with good correctness and coverage. In Figures 5 and 6, Group 0 has a smaller variance than Group 1. Because a simple translation cannot capture that information³, the translation has poor coverage from Group 0 to Group 1 while its negative has poor correctness from Group 1 to Group 0. This illustrates the connection between correctness and coverage that we will discuss more in Section 3.2.

Figure 4:

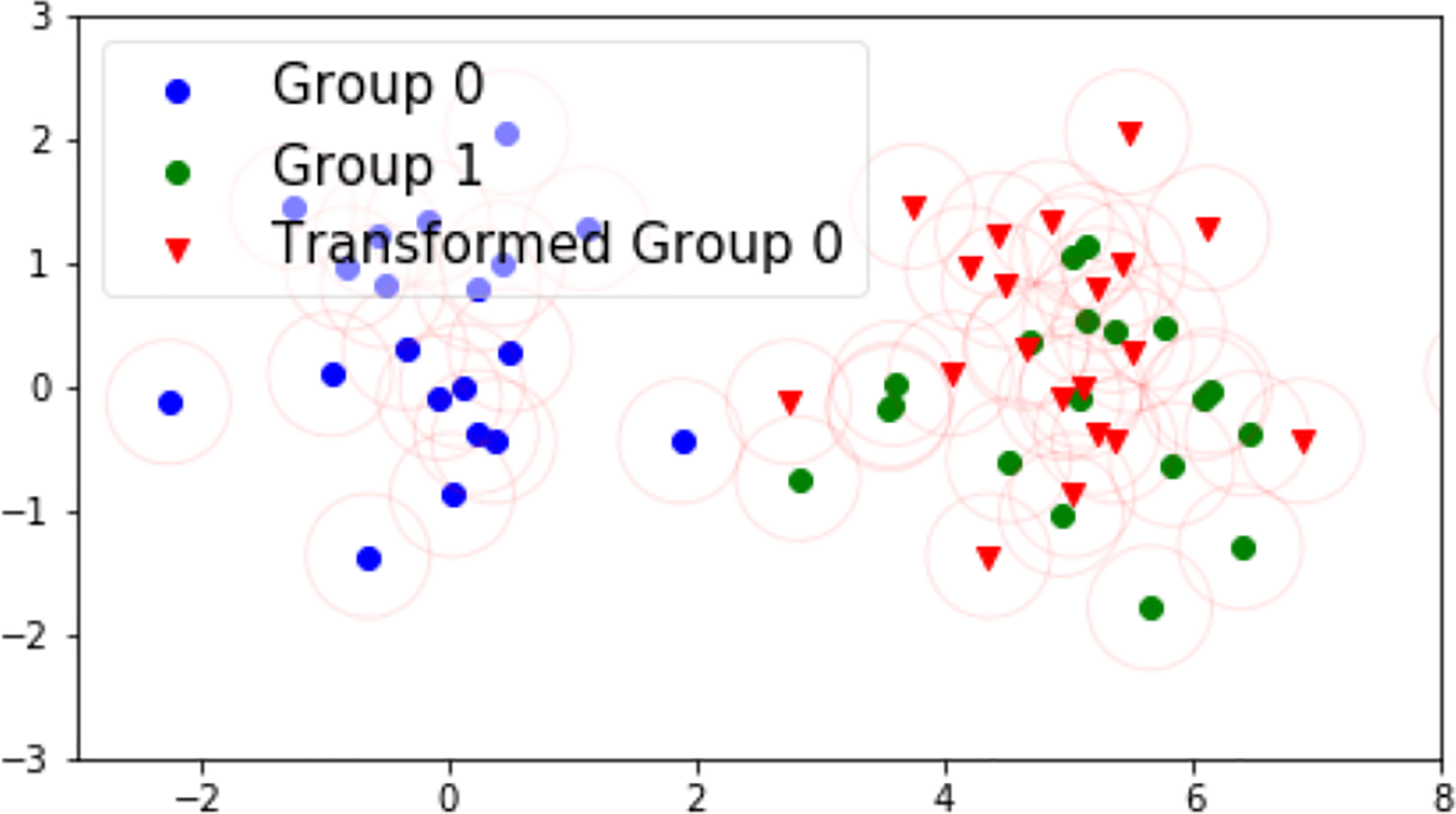
Two groups of points and the transformed version of Group 0. The red circles indicate the balls of radius ϵ used to calculated the metrics. Observe that the translation has both good correctness and coverage.

Figure 5:

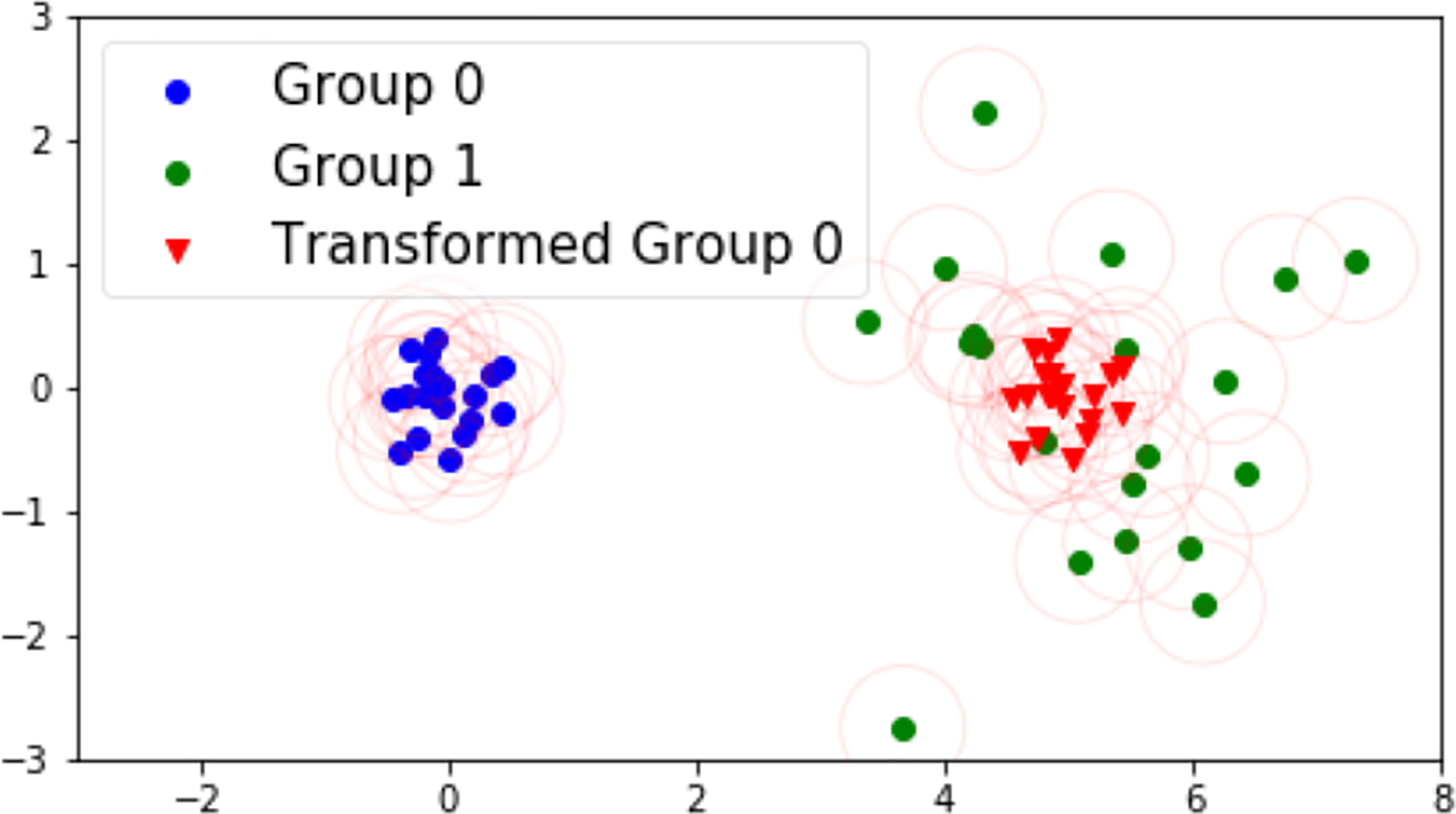
The same idea as Figure 4, but now Group 0 has a smaller variance than Group 1. Observe that the translation has good correctness but poor coverage.

Figure 6:

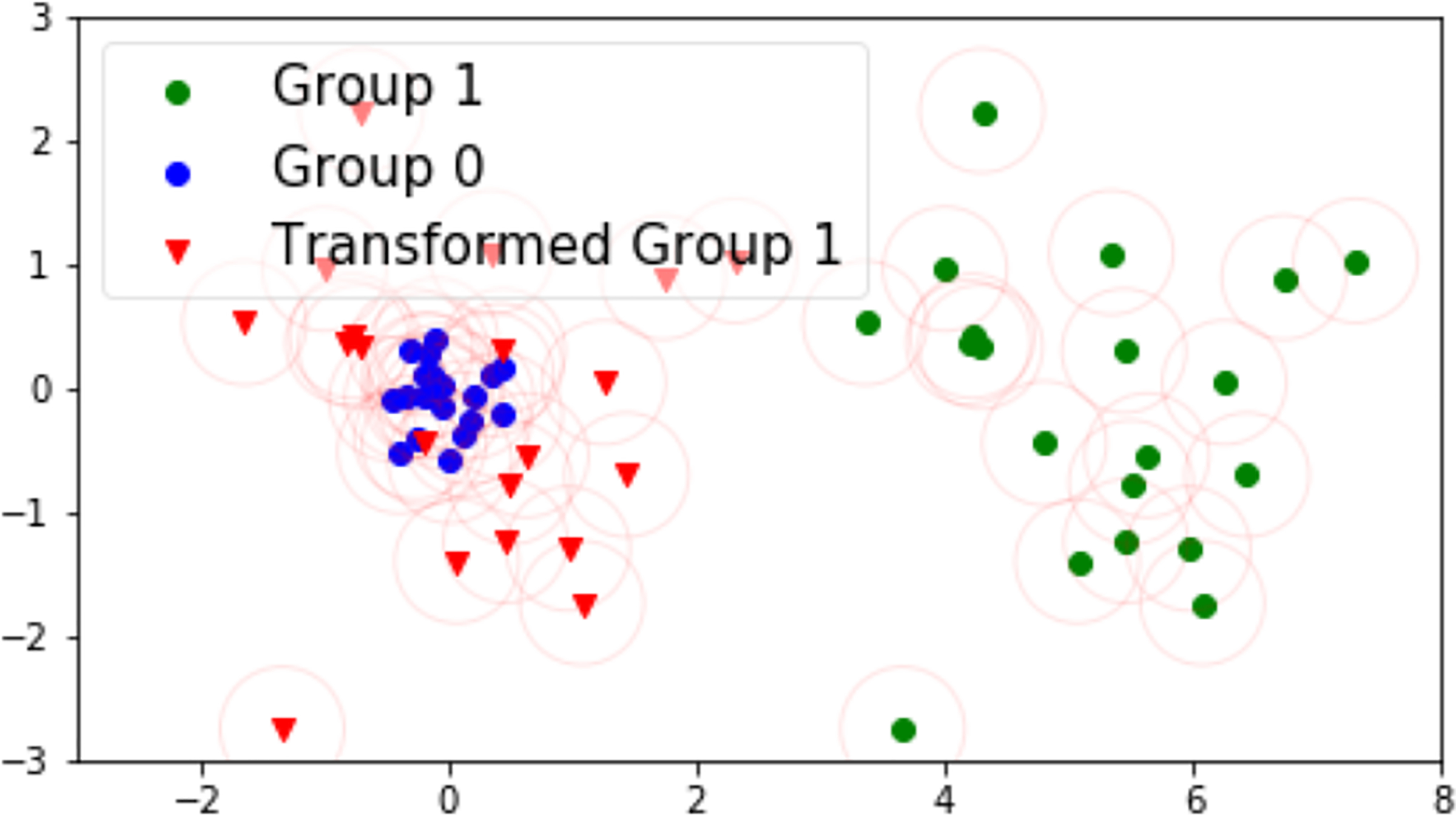
The same setup as in Figure 5, but showing what happens when the negative of the translation is applied to Group 1. Observe that it has good coverage but poor correctness.

3.1. Relating GCEs and Compressed Sensing

We will now demonstrate how the problem of finding a GCE between a pair of groups is connected to compressed sensing. We start with an “ideal” loss function that is too difficult to optimize and then make several relaxations to it.

In principle, Equations 1, 3, or 4 define objective functions that we could optimize, but they are discontinuous and hence difficult to optimize. To progress towards a tractable objective, first consider a continuous approximation of correctness (Equation 3):

$$los{s}_{min}(t)=\frac{1}{\left|X_{initial}\right|}\sum _{x\in X_{initial}}\underset{x^{\prime }\in X_{target}}{\min }{\Vert r(t(x))-r\left(x^{\prime }\right)\Vert }_2^2$$ (5)

This loss could be optimized by gradient descent using auto-differentiation software, although doing so might be difficult because of the min operation. Consequently, we consider a simplified version of it:

$$los{s}_{mean}(t)=\frac{1}{\left|X_{initial}\right|}\sum _{x\in X_{initial}}{\Vert r(t(x))-{\overline{r}}_{target}\Vert }_2^2$$ (6)

where ${\overline{r}}_i=\frac{1}{\left|X_i\right|}\sum _{x\in X_i}r(x)$. ⁴

Next, we are going to make use of our restriction of t to a translation, δ, and assume, for now, that r is a linear mapping: r(x) = Ax for $A\in {ℝ}^{m\times d}$. Although this assumption about r will not be true in general, it allows us to connect a GCE to the classical compressed sensing formulation. Under these constraints, we have that:

$$los{s}_{mean+linear}(\delta )=\frac{1}{\left|X_{initial}\right|}\sum _{x\in X_{initial}}{\Vert A(x+\delta )-{\overline{r}}_{target}\Vert }_2^2$$ (7)

By setting its derivative to zero, we find that solving $A\delta ={\overline{r}}_{target}-{\overline{r}}_{initial}$ yields an optimal solution to Equation 7. Observe that this is an undetermined linear system, because m < d, and so we can always find such a δ.

Recall that, in general, we want to find a sparse δ. This is partially because we need the explanation to be simple enough to be understood by a person, but also because the explanation is hopefully modeling real world phenomena and these phenomena often have nice structure (e.g., sparsity). Then, because we are finding a GCE by solving $A\delta ={\overline{r}}_{target}-{\overline{r}}_{initial}$⁵, we can see that ${\overline{r}}_{target}-{\overline{r}}_{initial}$ is the model’s low-dimensional measurement that we are trying to reconstruct using the high-dimensional but sparse underlying signal, δ. This is exactly the classical compressed sensing problem formulation. As a result, we will add l₁ regularization to δ as an additional component to the loss function as is done in both linear and non-linear compressed sensing (Blumensath, 2013).

Consequently, we could consider finding a GCE by minimizing the linear compressed sensing loss:

$$los{s}_{cs}(\delta )={\Vert A\left({\overline{x}}_{initial}+\delta \right)-{\overline{r}}_{target}\Vert }_2^2+\lambda \Vert \delta {\Vert }_1$$ (8)

where ${\overline{x}}_i=\frac{1}{\left|X_i\right|}\sum _{x\in X_i}x$. Or, by removing the assumption that r(x) = Ax, minimizing the more general version that we use for our experiments:

$$loss(\delta )={\Vert r\left({\overline{x}}_{initial}+\delta \right)-{\overline{r}}_{target}\Vert }_2^2+\lambda \Vert \delta {\Vert }_1$$ (9)

3.2. Computing GCEs

We have thus far limited ourselves to explaining the differences between l = 2 groups of points labeled as X₀ (“initial”) and X₁ (“target”), and focused on learning an explanation t_0→1 from X₀ to X₁. However, this is not a realistic setting because this labeling was arbitrary and because we usually have l > 2.

Unfortunately, the naive solution of using compressed sensing to independently produce explanations for all O(l²) pairs of groups will fail to satisfy two desirable properties related to the internal consistency of the explanations. For instance, we would like t_0→1 to agree with t_1→0, a property we call symmetry. Additionally, we would like t_0→2 to agree with the combined explanations t_0→1 and t_1→2; we call this transitivity. Formally, symmetry requires that $t_{i\to j}=t_{j\to i}^{-1}$ and transitivity requires that $t_{i\to k}=t_{j\to k}\circ t_{i\to j}$ for any j.

Our approach to finding a consistent (i.e., symmetrical and transitive) set of explanations is to enforce the consistency constraints by-design. We do this by computing a set of explanations relative to a reference group. We assume that X₀ is the reference group and find a set of basis explanations t₁, . . . , t_l−1, where t_i = t_0→i. We then use this set of basis explanations to construct the explanation between any pair of the groups of points.⁶ Algorithm 2 describes how t_i→j can be constructed from t₁, . . . , t_l−1.

Algorithm 1.

TGT: Calculating GCEs with a Reference Group. Note that, because λ is applied to all of the explanations, we cannot tune it to guarantee that each explanation is exactly k-sparse.

Input: Model: r

Group Means: ${\overline{x}}_i$(feature space) and ${\overline{r}}_i$(representation space) for i = 0, . . . , l − 1

l1 Regularization Weight: λ

Learning Rate: α

Initialize: δ1, . . . , δl−1 to vectors of 0

while not converged do

Sample i ≠ j from {0, . . . , l − 1}

Construct ti→j (δi→j) using Algorithm 2

Calculate objective: υ = loss(δi→j) using Equation 9

Update the components of δi→j using Algorithm 3

end while

Return: δ1, . . . , δl−1

Algorithm 2.

How to construct any explanation between an arbitrary pair of groups, t_i→j, using the set of basis explanations relative to the reference group, t₁, . . . , t_l−1

Input: i, j

if i == 1 then

Return: tj

else if j == 1 then

Return: $t_i^{-1}$

else

Return: $t_j\circ t_i^{-1}$

end if

Algorithm 3.

How to update the basis explanations, δ₁, . . . , δ_l−1, based on the performance of δ_i→j. This splits the signal from the gradient between the basis explanations used to construct δ_i→j. Note that it does not maintain any fixed level of sparsity.

Input: i, j, α (learning rate), ∇υ (gradient of the loss function)

if i == 1 then

δj = δj − α∇υ

else if j == 1 then

δi = δi + α∇υ

else

δj = δj − 0.5α∇υ

δi = δi + 0.5α∇υ

end if

Overview of TGT.

We now have all of the pieces necessary to actually compute a GCE: a differentiable loss function to measure the quality of t_i→j, l₁ regularization to help us find the simplest possible explanation between X_i and X_j, and a problem setup to ensure that our explanations are consistent across X₀, . . . ,X_l−1. At a high level, TGT will proceed to sample random “initial” and “target” groups from the set of all groups, construct that explanation from the set of basis explanations (Algorithm 2), and then use Equation 9 as a loss function to use to update the explanation using gradient descent (Algorithm 3). Pseudo-code for this process is in Algorithm 1.⁷ The main hyper-parameter that requires tuning is the strength of the l₁ regularization, λ.

Why can we prioritize correctness in Equation 9?

In the previous subsection, we noted that the Equation 9 prioritizes correctness over coverage. Because Algorithm 1 randomly chooses the “initial” and “target” groups many times, it updates the basis explanations based on both cr(δ_i→j) and cr(δ_j→i). When t is a translation and the explanations are symmetrical, we can see that cr(δ_j→i) is closely related to cυ(δ_i→j). This is because they only differ in whether they add δ_j→i to a point in X_j or subtract δ_j→i from a point in X_i in their respective indicator functions. Further, if we consider r(x) = Ax, then they are identical metrics (this is consistent with the example from Figure 5). Collectively, this means that Algorithm 1 implicitly considers both cr(δ_i→j) and cυ(δ_i→j) while computing the explanations.

3.3. Controlling the Level of Sparsity

Because neither TGT nor DBM is guaranteed to produce a k-sparse explanation, we will threshold each of the explanations to include only the k most important features (i.e., the k features with the largest absolute value) for our experiments. This is done after they have been calculated but before their quality has been evaluated. Importantly, TGT has a hyper-parameter, λ, which roughly controls the sparsity of its explanations; as a result, we will tune λ to maximize correctness for each value of k.

The fact that λ is tuned for each value of k raises an interesting question: “Does TGT use a subset of the features from its k₂-sparse explanation for its k₁-sparse explanation when k₁ < k₂?”. Naturally, we would like for the answer to be “yes” because, for example, it does not seem like a desirable outcome if a 2-sparse explanation uses Features A and B but a 1-sparse explanation uses Feature C.

Suppose we have two explanations between Group i and Group j: e₁ which is k₁-sparse and e₂ which is k₂-sparse with k₁ < k₂. To address this question, we define the similarity of e₁ and e₂ as:

$$similarity\left(e_1,e_2\right)=\frac{\sum \left|e_1[i]\right|\mathbb{1}\left[e_2[i]\ne 0\right]}{{\Vert e_1\Vert }_1}$$ (10)

This metric captures how much of e₁’s explanation uses features that were also chosen by e₂.⁸ So a score of 1 indicates that e₁ uses a subset of the features of e₂ and a score of 0 indicates that it uses entirely different features. Because DBM does not solve a different optimization problem to achieve each level of sparsity, its similarity measure is always 1. When we run experiments with a list of sparsity levels k₁, . . . ,k_m, we will plot similarity(e₁, e₂), . . . , similarity(e_m−1, e_m) to measure how similar TGT’s explanations are as the level of sparsity increases.

4. Experimental Results

Our experimental results are divided into two sections. In the first section, we demonstrate that TGT is better at explaining the model than DBM is when we restrict the explanations to varying degrees of sparsity. In the second section, we move beyond assessing whether or not TGT explains the model and demonstrate that it also appears to capture real signals in the data.

4.1. TGT’s Efficacy at Explaining the Model

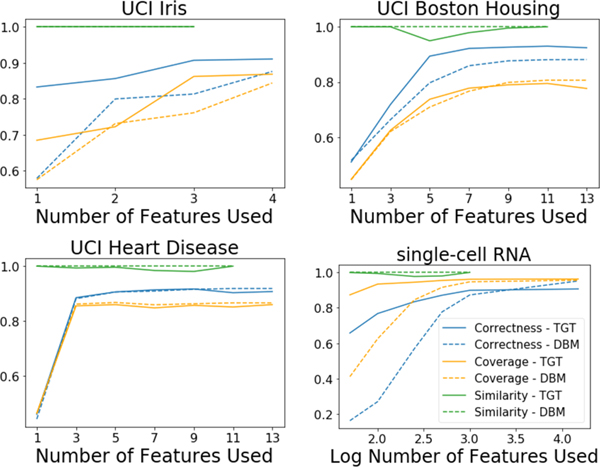
From an interpretable machine learning perspective, our goal is help practitioners understand the dimensionality-reduction models they use in the data exploration process. We measure the quality of GCEs using correctness (Equation 3) and coverage (Equation 4) at varying degrees of sparsity (Figure 7).

Figure 7:

A comparison of the effectiveness of TGT to DBM at explaining the model (measured by correctness and coverage) at a range of sparsity levels. Note that TGT performs at least as well as DBM and usually does better. Looking at the similarity metric, we see that TGT is fairly consistent at picking a subset of the current features when asked to find an even sparser solution.

We use the model from (Ding et al., 2018)⁹ on the UCI Iris, Boston Housing, and Heart Disease datasets (Dua & Graff, 2017) and a single-cell RNA dataset (Shekhar et al., 2016) and use its a visualization of its two-dimensional representation to define the groups of points. Figure 1 shows this representation and grouping for the single-cell RNA dataset; similar plots for all of the datasets are in the Appendix A.3. This model learns a non-linear embedding using a neural network architecture which is trained to be a parametric version of t-SNE (Maaten & Hinton, 2008) that also preserves the global structure in the data (Kobak & Berens, 2018).

Next, because the acceptable level of complexity depends on both the application and the person using the explanation, we measure the effectiveness of the explanations produced by TGT and DBM at explaining the model across a range of sparsity levels.

Explanation effectiveness at different levels of sparsity.

Figure 7 shows the results of this comparison. We can see that TGT performed at least as well as DBM and usually did better. Further, we can see that TGT’s explanations are quite similar to each other as we ask for sparser explanations. Note that all of these metrics are defined for a single pair of groups and so these plots report the average across all pairs of groups.

Exploring a Specific Level of Sparsity.

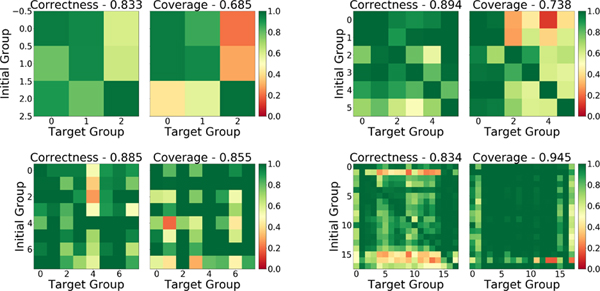
Figure 7 shows that TGT’s performance: is almost as good when k = 1 as when k = 4 on Iris, drops off sharply for k < 5 on Boston Housing, and drops off sharply for k < 3 on Heart Disease. Further, on the single-cell RNA dataset, it shows that TGT significantly outperforms DBM when k = 250 (Appendix A.4 Figure 16) and that this comparison becomes more favorable for TGT for smaller k. The level of sparsity where the metrics drop off indicates the minimum explanation complexity required for these methods to explain the model. See Figure 8 for an example of the pairwise correctness and coverage metrics for these levels of sparsity.

Figure 8:

The pairwise explanation metrics for TGT with: Top Left) 1-sparse explanations on Iris, Top Right) 5-sparse explanations on Boston Housing, Bottom Left) 3-sparse explanations on Heart Disease, and Bottom Right) 250-sparse explanations on single-cell RNA.

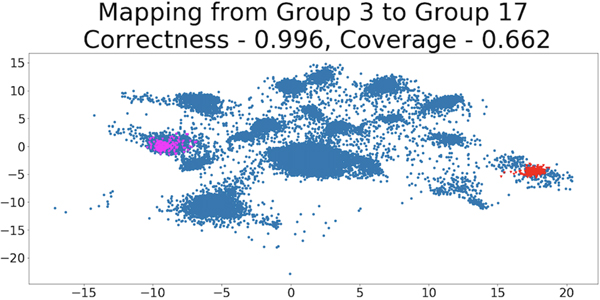
Figure 3 shows that DBM does not produce a good 250-sparse explanation for the difference between Group 3 and Group 17 from Figure 1. For the sake of an easy comparison, Figure 9 shows a similar plot that uses TGT’s 250-sparse explanation; it is clearly a much better explanation.

Figure 9:

Unlike DBM, TGT is able to produce an effective 250-sparse explanation for the difference between Group 3 and Group 17 on the single-cell RNA dataset. This can be seen both visually and with the correctness and coverage metrics.

4.2. TGT’s Efficacy at Capturing Real Signals in the Data

In the previous section, we demonstrated that TGT provides accurate explanations of the model that learned the low-dimensional representation. However, in practice, there could be a mismatch between what the model itself learns and the true underlying structure in the data. In this section, we evaluate empirically whether or not TGT provides explanations that match underlying patterns in the data.

We begin with an experiment on a synthetic dataset with a known causal structure and demonstrate that TGT correctly identifies this structure. This also serves as an intuitive example of why a sparser explanation can be as effective as a less-sparse explanation. Next, we leverage the labels that come with the UCI datasets to compare TGT’s explanations to some basic domain knowledge. Finally, we modify the UCI datasets and demonstrate that TGT is able to identify those modifications. Together, these results indicate that TGT is identifying real patterns in the data.

Synthetic Data with a Known Causal Structure.

By specifying the causal structure of the data, we can know which differences are necessary in the explanation, since they are the casual differences, and which differences are unnecessary, since they are explained by the causal differences. We find that TGT correctly identifies the causal structure of this dataset and that DBM does not.

We use the following procedure to generate each point in our synthetic dataset:$x_1,x_2~Bern(0.5)+\mathcal{N}(0,0.2)$, $x_3~\mathcal{N}(0,0.5)$, and $x_4~x_1+\mathcal{N}(0,0.05)$. The causal structure of this dataset is simple. x₁ and x₂ jointly cause 4 different groups of points. The explanation for the differences between these groups must include these variables. x₃ is a noise variable that is unrelated to these groups and, as a result, should not be included in any explanation. x₄ is a variable that is correlated with those groups, since it is caused by x₁, but does not cause those groups. As a result, it is not necessary to include it in any explanation.

We generate a dataset consisting of 400 points created using this process and train an autoencoder (Kramer, 1991) to learn a two dimensional representation of the dataset. A visualization of this learned representation is in the Appendix A.3 Figure 14; as expected, there are four distinct groups of points in it. Then, we use TGT and DBM to calculate the GCEs between these groups. The pairwise and average correctness and coverage metrics for these solutions are in the Appendix A.4 Figures 17 and 18; observe that the two methods are equally effective at explaining the model.

When we inspect the explanations ()Table 1), we see that both TGT and DBM use x₁ and x₂, neither use x₃, and that DBM uses x₄ while TGT does not. This shows that, even in a very simple setting, there is good reason to believe that an explanation that is simpler (i.e., sparser) than the DBM explanation exists and that TGT might be able to find it.

Table 1:

A comparison of the explanations from TGT and from DBM. Note that they are similar except that TGT does not use x₄, which is the variable that is not causaly related to the groups.

Explanation	Method	x 1	x 2	x 3	x 4
0→1	TGT	−1.09	0.01	0.03	0.00
	DBM	−1.02	0.04	0.01	−1.03
0→2	TGT	0.00	0.88	0.00	0.00
	DBM	−0.01	0.97	0.06	−0.03
0→3	TGT	−0.99	0.71	0.00	0.00
	DBM	−1.02	1.03	−0.01	−1.03

Qualitative Analysis of the UCI Datasets using the Labels.

Qualitatively, we find that TGT’s explanations agree with domain knowledge about these datasets. Specifically: On the Iris dataset, its explanations agree with a simple decision tree because they both rely mostly on the Petal Width to separate the groups. On the Boston Housing dataset, it identifies the differences between a set of inexpensive urban houses vs expensive suburban houses as well as equally priced groups of houses that differ mainly in whether or not they are on the Charles River. Finally on the Heart Disease dataset, it finds that the difference between a moderate and a low risk group of subjects was that the low-risk group’s symptoms are explained by something other than heart disease and the difference between the moderate and high risk group of subjects is that the former is made up of men and the later of women. For full details, see the Appendix A.5.

Quantitative Analysis of Modified Versions of the UCI Datasets.

In order to perform a more quantitative analysis, we artificially add a known signal to the dataset by choosing one of the groups of points, creating a modified copy of it by translating it, and adding those new points back into the dataset. We then ask two important questions about TGT’s behavior. First, does TGT correctly identify the modifications we made to the original dataset? Second, do TGT’s explanations between the original groups change when the modified group is added to the dataset? Details of how we setup these experiments and their results are in the Appendix A.6.

We find that TGT does identify the modifications we made and that, in doing so, it does not significantly change the explanations between the original groups. Importantly, this result remains true even if we retrain the learned representation on the modified dataset.

These results are a strong indicator that TGT finds real patterns in the data because it recovers both the original signal and the artificial signal even when the algorithm is rerun or the representation is retrained.

5. Conclusion

In this work, we introduced a new type of explanation, a GCE, which is a counterfactual explanation that applies to an entire group of points rather than a single point. Next, we defined reasonable metrics to measure the quality of GCEs (i.e., correctness and coverage) and introduced the concept of consistency (i.e., symmetry and transitivity), which is an important additional criteria that GCEs must satisfy. Given that, we defined an algorithm for finding consistent GCEs, TGT, that treats each pairwise explanation as a compressed sensing problem. Our first experiments empirically demonstrated that TGT is better able to explain the model than DBM across a range of levels of sparsity. Our next experiments showed that TGT captures real patterns in the data. This was done using a synthetic dataset with a known causal structure and by comparing TGT’s explanations to background knowledge about the UCI datasets. As an additional test, we then added a synthetic signal to the UCI datasets and demonstrated that TGT can recover that signal without changing its explanations between the real groups. Importantly, this result remains true even when the representation is retrained.

Although we focused on data exploration in this work, similar groups arise naturally whenever the model being trained uses an encoder-decoder structure. This technique is ubiquitous in most areas where deep learning is common (e.g., semi-supervised learning, image classification, natural language processing, reinforcement learning). In these settings, identifying the key differences between the groups is an interesting question because we can observe that “The model treats points in Group A the same/differently as points in Group B”, determine that “The key differences between Group A and Group B are X”, and then conclude that “The model does not/does use pattern X to make its decisions”. We believe that exploring these applications is an important direction of future work that will require more sophisticated transformation functions, optimization procedures, and definitions of the groups of points of interest.