Abstract
Imaging systems with miniaturized device footprint, real-time processing speed and high resolution three-dimensional (3D) visualization are critical to broad biomedical applications such as endoscopy. Most of existing imaging systems rely on bulky lenses and mechanically refocusing to perform 3D imaging. Here, we demonstrate GEOMScope, a lensless single-shot 3D microscope that forms image through a single layer of thin microlens array and reconstructs objects through an innovative algorithm combining geometrical-optics-based pixel back projection and background suppressions. We verify the effectiveness of GEOMScope on resolution target, fluorescent particles and volumetric objects. Comparing to other widefield lensless imaging devices, we significantly reduce the required computational resource and increase the reconstruction speed by orders of magnitude. This enables us to image and recover large volume 3D object in high resolution with near real-time processing speed. Such a low computational complexity is attributed to the joint design of imaging optics and reconstruction algorithms, and a joint application of geometrical optics and machine learning in the 3D reconstruction. More broadly, the excellent performance of GEOMScope in imaging resolution, volume, and reconstruction speed implicates that geometrical optics could greatly benefit and play an important role in computational imaging.
Keywords: 3D imaging, 3D microscopy, computational imaging, lensless imaging, light field, microlens array, geometrical optics
Graphical Abstract
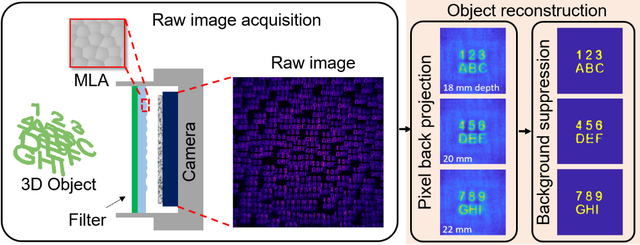
A lensless single-shot 3D microscope which forms image through a single layer of thin microlens array is demonstrated. The imager reconstructs objects by an innovative hybrid algorithm developed through a joint application of geometrical optics and machine learning. The algorithm requires minimal computational resources and enables real-time 3D high-resolution imaging over a large field of view.
1. Introduction
Three-dimensional (3D) imaging over large volume with high resolution, real-time processing speed and compact device footprint is important for many biological applications. Widefield microscopes are standard tools in biological imaging [1–3]. The limitations of conventional microscopes are their inability on imaging 3D volumetric objects. Besides, the objective lenses with large magnification typically have a small depth of field and can only image a very small field of view. Mechanical refocusing with the bulky optics is required to image samples at different depths. All these prevent fast and efficient 3D imaging over a large field of view.
Light field imagers [4, 5] can capture 3D object information through single exposure. They encode the object into a 4D light field, and then use ray tracing to digitally refocus object at different depths. However, this often comes with a degraded resolution, as recording 4D light field trades camera resolution for depth information. Moreover, conventional ray tracing methods have challenges in processing microscopy images where there is high extent of crosstalk between microlens units in the light field. Modified light field microscopes adopt iterative optimizations with a more precise forward model and point-spread function (PSF) than geometrical optics, but a large benchtop system is still required [6–9].
Lensless imaging devices [10–21] replace the bulk lenses in conventional imaging systems by a thin amplitude or phase mask [10–18], and enable compact 3D imaging through single exposure. However, they face challenges on the expensive computational cost in object reconstruction and tradeoffs among reconstruction quality, speed and volume. Lensless imagers reconstruct objects globally by solving the inverse problem of imaging through convex optimizations [10, 12–20] or deep neural networks [22–24]. Both require a large amount of computational resource that scales with both image size and object size. This limitation stems from that the entire object space has to be reconstructed altogether. The extremely high demand of computation not only slows the reconstruction speed but also limits the total number of object voxels that can be reconstructed [6, 25–27].
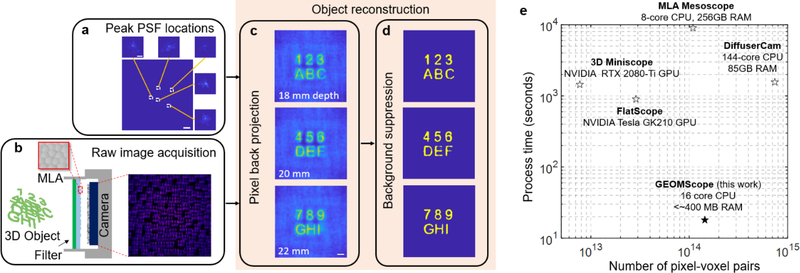
Here we report a widefield fluorescence microscope using a single layer of random microlens array and an innovative hybrid 3D reconstruction algorithm, which can achieve high resolution over a large volume with near real-time processing speed and reduce the computational resource by orders of magnitude. The hybrid reconstruction combines a pixel back projection algorithm and a background suppression algorithm (Figure 1a–d). We term our microscope to be “GEOMScope” as we heavily utilize geometrical optics for object reconstruction. Compared with the prevailingly used iterative optimization techniques that reconstruct the object globally, our approach solves object information locally and independently through small amounts of image pixels. This results in orders of magnitude less computational memory and orders of magnitude faster processing speed (Figure 1e, Supporting Table S1).
Figure 1. Architecture of GEOMScope.
(a) Experimental PSF measurement from single point source. Scale bar: 2 mm; inset, 200 μm. (b) Schematic of GEOMScope. Raw image is simulated through ray tracing in OpticStudio. MLA, microlens array. (c) Initial reconstruction at different depths through pixel back projection. (d) Resolved objects with background suppression through a trained neural network. (e) Comparison between GEOMScope and other lensless imagers (FlatScope [11], DiffuserCam [10], 3D Miniscope [14], MLA Mesoscope [16]) on the number of camera pixel and object voxel pair versus computation time (with the processor type and required RAM) in reconstruction. The number of object voxel is either the reported value or the derived value as the ratio of imaged volume and 3D resolution.
We emphasize that our reconstruction through geometrical optics does not degrade the resolution, and we can achieve similar resolution as the iterative optimization techniques. In conventional wisdom, reconstruction through geometrical optics often results in a lower resolution than iterative optimization process, particularly in microscopic imaging, due to its inability to model complex PSF [6, 9, 28]. Here, we engineer GEOMScope such that the PSF is sparse and can be considered as a Dirac comb function. As a result, geometrical optics can leverage a precise image formation model, resulting in a resolution on par with iterative optimization.
Another feature of our reconstruction algorithm is that it can well handle volumetric objects with dense features, thought it requires low computational resources. This is attributed to the background suppression step after the pixel back projection. Our geometrical optics approach can reconstruct objects at different depths, as if they were imaged sequentially by mechanically adjusting the distance between the object and the lens in a conventional imaging system (Figure 1c). The reconstruction contains defocused light as the background. We sharpen the object features through the subsequent background suppression algorithms (Figure 1d). Such a hybrid approach enables faithful reconstructions of volumetric objects.
Thanks to the high efficiency and high resolution reconstruction, GEOMScope enables a large field-of-view imaging in high resolution, with a near real-time reconstruction speed. Using a single layer of microlens array (20×20 mm2), GEOMScope is capable of single-shot 3D imaging across a large volume of ~23×23×5 mm3 with a lateral resolution of ~40 μm and an axial resolution of ~300 μm. A total of ~5.5×106 resolvable points can be reconstructed in 10s of second scale, which was not possible using existing approaches. We experimentally validated the 3D microscope through volumetric imaging of fluorescence beads and objects across a large volume. GEOMScope is particularly promising for biomedical applications that require real-time high resolution 3D visualization through miniaturized and implantable imaging devices.
2. Design of GEOMScope
2.1. Image formation
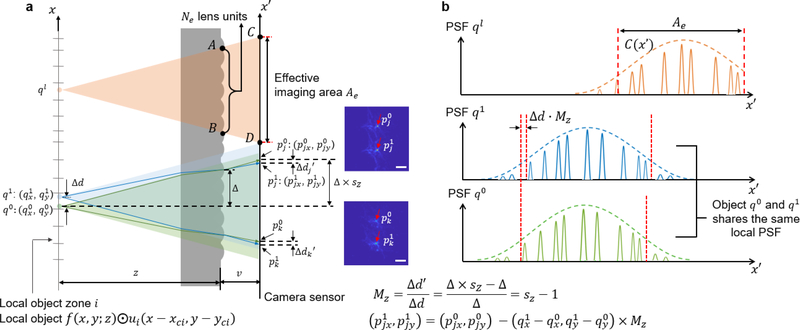
The system architecture of GEOMScope contains the microlens array with a filling factor of ~1, fluorescence emission filter, and the image sensor (Figure 2a). The microlens array and the image sensor has a similar size in the lateral dimension (on the orders of 10s mm), and they are located in close proximity (with a distance of v on the orders of a few mm), so the overall geometry of the integrated imager is flat. Each lens unit is randomly positioned in the microlens array (Figure 1b, Supporting Figure S1a). Compared with the periodically arranged microlens array, the randomly arranged microlens array has non-periodic PSF (Figure 1a), which not only facilitates the suppression of lens unit crosstalk and thus background in the object reconstruction, but also provides a more balanced frequency support among different spatial frequency (Supporting Figure S1). We segment the object domain into a grid of small zones matching the spatial segmentation profile of individual lens units in the microlens array (Figure 2). As the dimension of each object zone is much smaller than the nominal working distance z, within individual object zone the PSF is spatial invariant in the lateral direction and scales linearly with the object depth. The reference object plane is segmented into N zones, with (xci, yci) being the centroid of each zone, where i=1,2…N and N is the number of microlens units. Defining f(x,y;z) as the object intensity, ui as a 2D circular boundary operator to select the objects in the ith zone, and ⨀ as an element-wise multiplication, the local object falling into the ith zone can be written as f(x,y;z)⨀ui(x−xci,y−yci) (Figure 2a).
Figure 2. Image formation and object reconstruction.
(a) Each point source is effectively imaged by Ne lens units, and forms images across an area Ae on the image sensor. For each object point q to be reconstructed, all the imaged points p on the image sensor are found within the effective imaging area Ae through the local PSF and the lateral magnification Mz. The two insets show the experimentally measured PSF of two adjacent object points q0 and q1 imaged by two lens units. The centroids of the PSF are indicated by red arrows, which will be used in the pixel back projection algorithm. Scale bar, 60 μm for ∆d=952 μm. (b) Local PSF for the individual point sources. The intensity falloff is characterized by the envelop function C(x',y'), attributed to the angular distribution of the point source intensity and the geometric aberration of the lens units. As q0 and q1 are two object points in the same local zone, they share the same local PSF.
The PSF can be derived from the arrangement of the microlens units. We define on the image plane, where is the centroid of each microlens unit. In our imaging configuration, has the same value as (xci, yci). Any object point can only be effectively imaged by a certain amount of lens units Ne (across in Figure 2a), onto an effective area Ae (across in Figure 2a) on the image sensor, due to the Lambert’s cosine law [29] of light intensity distribution falloff and geometric aberration of the lens unit. Therefore, we can use an envelope function C(x',y') to model the overall envelope of the PSFs (Figure 2b). The local PSF for the ith object zone can then be expressed as , where PSFo(x',y') is the PSF of an individual lens unit, * represents convolution, and is a local scaling operator to scale the coordinates (with a factor of sz) to obtain the local PSF for different object depth z. sz can be expressed as
| (1) |
The image on the image sensor b(x',y') can be expressed as the summation of local image from all zones and object depths. The local image in a certain zone and object depth is the convolution between the local objects and local PSFs, with an appropriate lateral magnification Mz of the microlens unit:
| (2) |
2.2. Object reconstruction
So far, nearly all the lensless imagers employ iterative optimization approach with sparsity constrains to reconstruct the objects. To overcome the challenge of high demand of computational resource, we developed a pixel back projection algorithm followed by background suppression. The required computational resource is greatly reduced, and scales linearly with the number of reconstruction voxel in the object.
The pixel back projection algorithm uses geometrical optics approach to solve the inverse process of Equation 2 and reconstruct the object at different depths (Figure 2a). As each object point projects to multiple points on the camera sensor through different lens units, our goal is to collect these points on the camera to recover the object points. While each lens unit could image a point source into multiple pixels on the camera sensor (defined by PSF0), to simplify the process, we only pick up the centroid pixel, as the others are typically much weaker (Figure 2a). We start with a calibration process of , by finding the scaling factor sz between the local PSF for object depth z and the microlens arrangement pattern h0(x',y') (Equation 1). The magnification Mz of each lens unit can be approximated through the scaling factor sz (Figure 2a):
| (3) |
Once we have and Mz, we can locate all the pixels for a voxel of interest at depth z. The reconstructed voxel value is the sum of all mapped pixel values across the effective image area Ae, which can be determined based on the field of view of the single lens unit (Materials and Methods). Such a reconstruction strategy avoids considering all pixels in the image sensor to reconstruct a single object voxel, which is the key difference from the global iterative optimization approach. It is this local reconstruction strategy that significantly reduces the required computational resource.
The reconstructed results in each depth from pixel back projection contain both the in-focus objects and artifacts, which includes the defocused light from objects locating at other depths and possible ghost objects. The ghost objects originate from the “one-to-many mapping” nature of the microlens array so a single pixel on the camera could come from multiple object points. All these contribute to the background and becomes more severe when the object is less sparse. The second step of our reconstruction process is to suppress these backgrounds, by either a particle clustering algorithm [30] or a U-net based convolutional neural network [31] (Supporting Figure S2).
For sparse, discrete and isolated point objects in 3D, we developed a particle clustering algorithm to remove the ghost object points and the defocused light in the 3D stack reconstructed from the pixel back projection algorithm (Materials and Methods, Supporting Section S1, Figure S2–3). The clustering algorithm is based on graph connectivity. For less sparse 3D objects which contains continuously connected features, we developed a convolutional neural network to suppress the background (Materials and Methods, Supporting Section S2, Figure S2, S4). It slices overlapped objects in depth and picks out focused objects from background light. The output image from the neural network contains sharper contrast and the defocused features are largely removed.
2.3. Design of microlens array
We designed the microlens array in GEOMScope so it can image dense fluorescent objects (~520 nm central wavelength) across a large volume (~23×23 mm2 field of view and ~5 mm depth of field) with a lateral resolution ~40 μm. The microlens array and the image sensor both have a size ~20×20 mm2, matching the field of view. To reduce the thickness of the microscope, we minimize the distance between the microlens array and the image sensor to be v<5 mm. For a convenient placement of samples, we set the nominal working distance z as 20~30 mm. Based on this performance metrics, we can optimize the design parameters of the microlens array (Materials and Methods, Supporting Section S3, Figure S5–7). For a single lens unit, our major optimization interests are depth of field, lateral resolutions and aberrations. For the performance of the entire lens array, our optimization focuses on balancing 3D resolving ability and image reconstruction speed. We summarize the design parameters and performance metrics in Table 1.
Table 1.
Design parameters and the derived/simulated performance of GEOMScope.
| Design parameters | Performance metrics | ||||
|---|---|---|---|---|---|
| Working distance z | 18~30 mm | MLA-camera distance v | ~4 mm | Lateral resolution | ~40 μm |
| Lens array area | 20×20 mm2 | Number of lenses | 213 | Axial resolution | ~300 μm |
| Average pitch size | 1.23 mm | Lens focal length f | ~4.65 mm | Field of view | ~23×23 mm2 |
| Lens refractive index | 1.43 | Lens radius of curvature | 2 mm | Depth of field | ~5 mm |
| Effective imaging lens number for single point object Ne | 15~20 | Diameter of the effective field of view of single lens unit | ~ 6 mm | Magnification Mz | 0.1–0.15 |
| Camera pixel size dp | 4.5×4.5 μm2 | Emission wavelength | 500–530 nm | Sensor occupancy parameter | ~0.4 |
3. Simulation results
To verify the design of GEOMScope, we first simulated its ability to image a single point source. We used ray tracing algorithm (OpticsStudio) to form an image of a single point source (Figure S8). Reconstruction of the object shows a FWHM ~40 μm and ~300 μm in the lateral and axial direction respectively (Figure S8a–b). We then simulated its ability to resolve two point sources separated laterally by 40 μm at a depth of 20 mm. The two point sources could be clearly distinguished in the reconstructed object (Figure S8c), where the intensity drops below ~85% of the peak object intensity in between the two reconstructed points. Similarly, two points sources that are separated by 300 μm along the same axial axis could be distinguished in the reconstruction (Figure S8d). These simulation results agree with our design.
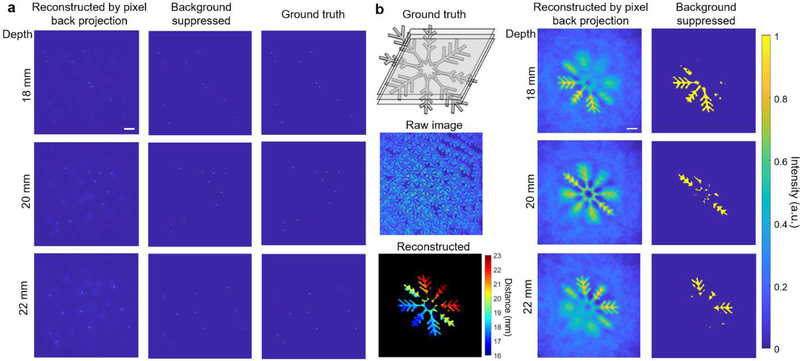
We then simulated the image formation and object reconstruction for 3D distributed fluorescent point sources (Figure 3a) and a 3D volumetric objects (Figure 3b), which are placed at a distance of 18~22 mm from the front surface of lens array. The images are again formed by ray tracing algorithm. The pixel back projection algorithm reconstructs the objects at different depths. These reconstructed object stacks are then fed to the particle clustering algorithm (Figure 3a) or convolutional neural network (Figure 3b) for background suppression. The objects in 3D can then be faithfully reconstructed.
Figure 3. Simulated image formation and reconstruction of fluorescent objects in 3D.
(a) Imaging and reconstruction of 3D distributed fluorescent particles, for a depth of 18 mm, 20 mm, 22 mm. Left column: reconstructed objects through pixel back projection only; middle, final reconstructed objects after background suppression through particle clustering algorithm; right, ground truth object. The point objects are smoothed on intensity profile to make their positions more visible. Scale bar, 2 mm. (b) Imaging and reconstruction of a 3D snowflake fluorescent object, for a depth of 18 mm, 20 mm, 22 mm. Left column: top, 3D ground truth object; middle, raw image; bottom, reconstructed depth-resolved volumetric object. Middle column, reconstructed objects through pixel back projection only; right column, final reconstructed objects after background suppression through convolutional neural network. Scale bar: 2 mm.
4. Experimental results
4.1. Imaging of point source and resolution target
We fabricated the microlens array using optical transparent polydimethylsiloxane (PDMS) with a negative 3D printed mold (Materials and Methods, Figure S10a). To quantify the image quality of GEOMScope across the 3D volume, we measured the FWHM of the lateral and axial reconstruction profile of a point source (created by illuminating a 10 μm pinhole) located at different positions in the object space. Here, we removed the filter so the imaging wavelength is ~457±25 nm. The lateral and axial reconstruction profile of the point source maintains stable for a depth range over ~5 mm when it is placed ~20 mm from the lens array (Figure S9), in an overall good agreement with the design (Supporting Section S4).
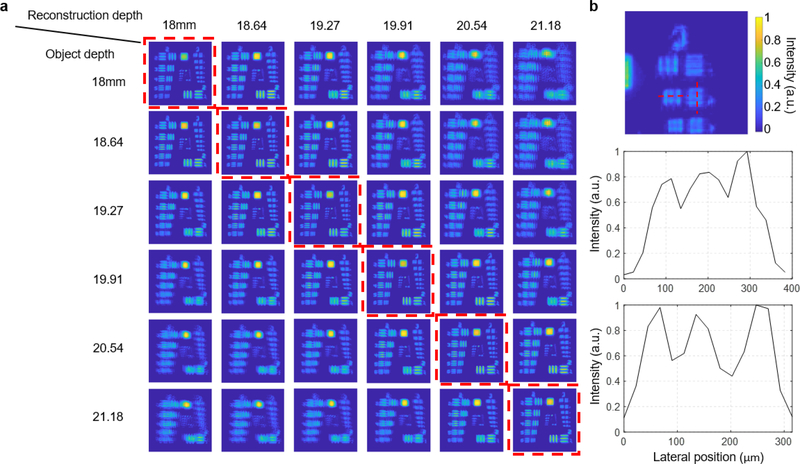
To further quantify the imaging resolution, we imaged a negative 1951 USAF resolution target. We inserted a diffuser (600 Grit) between the LED and the resolution target to increase the angular spread of light passing through the target, so that the target acted like an isotropic source as a fluorescence sample. We placed the target at different depth, captured single-shot images, and performed image reconstruction in 3D for each case (Figure 4). For 2D objects, the pixel back projection step alone can already achieve a high quality reconstruction, so no background suppression algorithm is used. The reconstruction at different depths clearly demonstrated the effectiveness of our algorithm: the objects reconstructed at the correct focal plane show the highest sharpness. We can clearly resolve group 3 element 2, which has a line space of 55 μm (Figure 4b). This is in a good agreement with the simulated two-point resolution.
Figure 4. Imaging and reconstruction of 1951 USAF resolution target for group 2 and 3.
(a) Object reconstruction at various depths, when the target was positioned at a depth of 18 mm, 18.64 mm, 19.27 mm, 19.91 mm, 20.54 mm, and 21.18 mm. The best reconstruction corresponding to the actual target depth is labeled by a red dashed boundary. No background suppression was employed for this 2D sample. (b) Zoom-in view of the best reconstruction of target at 18 mm depth, and the line profiles of the horizontal line pairs and vertical line pairs of group 3, element 2.
4.2. Imaging of 3D fluorescence and phosphorescent samples
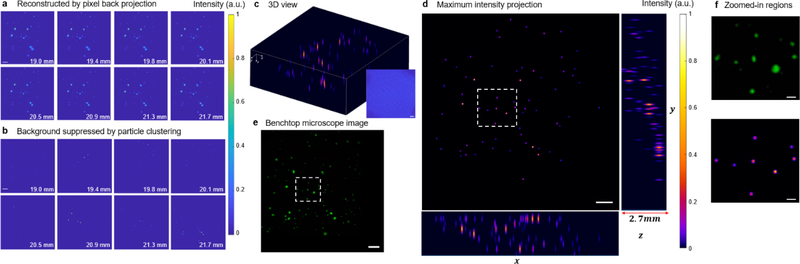
We fabricated a 3D fluorescent sample by embedding fluorescent beads [Firefli Fluorescent Green (468/508 nm), 5.0 μm, Thermo Scientific] into PDMS. The sample is 35 mm in diameter and ~2.5 mm thick, where clusters of fluorescent beads were randomly distributed. We captured the fluorescence image through GEOMScope, and a benchtop inverted microscope with a 1x objective lens as a control (Figure 5). The 1x objective lens provides a large field of view, but at a tradeoff of a poor axial resolution in the benchtop microscope. Nonetheless, it requires multiple exposures and subsequent image stitching to cover the entire field of view (23 mm×23 mm). The depth information is lost due to the poor axial resolution. In comparison, only a single exposure is needed in GEOMScope to cover the entire field of view, and the bead clusters at different depths can be resolved. This clearly demonstrates the strength of GEOMScope: the ability to capture 3D images across a large field of view. We note that for fluorescent particles with a wide intensity range, signal from very weak particles might be covered by background light or ghost images of particles that are much larger and brighter. In this scenario, those object points with very weak intensity could be rejected in the background suppression algorithm, and thus may not be resolved (Figure 5f). We note that this is a general challenge in solving inverse problems, including the commonly used iterative optimization approaches.
Figure 5. Imaging of 3D distributed fluorescent particles.
(a) Reconstruction from pixel back projection algorithm for different depth. (b) Background suppression of (a) through the particle clustering algorithm. Different particle clusters are separated at different depths. The clustered particles are intentionally blurred for a clearer visualization. (c) 3D volumetric view of the reconstructed volume. Each point has a fixed axial span, the same as the depth interval between adjacent slice in the reconstruction. Inset: raw captured image. (d) Maximum intensity projection view of the reconstructed particle clusters in 3D at xy, xz and yz plane. (e) Images captured by a benchtop microscope and stitched for same field of view as (c-d). (f) zoomed-in view of the same selected regions identified by the dashed line in (d) and (e). Scale bar for (a-e): 2 mm; (f): 500 μm.
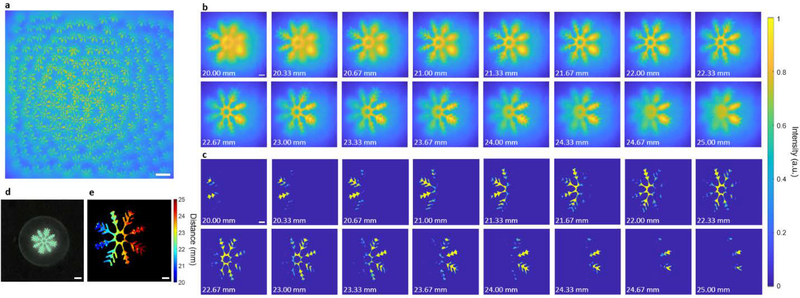
We next tested the GEOMScope on resolving large scale 3D volumetric object, which is not sparse in spatial domain (Figure 6). We 3D printed a snowflake mold with feature thickness of 0.25 mm on a clear substrate. Glowing powders in green color was mixed with PDMS and spread onto the mold to form phosphorescent features. The target was tilted with respect to the lens array surface and spanned a depth range of 20~25 mm from microlens array. While the object was relatively dense so different sub-images overlapped (Figure 6a), the reconstruction algorithm successfully recovered the 3D information (Figure 6b–c, e). There are a total number of ~5×106 voxels and ~1014 pixel-voxels pairs in this 3D reconstruction. The processing time is ~18 second in total using a workstation (8 threads parallelization).
Figure 6. 3D imaging of large scale phosphorescent objects.
(a) Raw image. (b) Reconstruction from pixel back projection algorithm for different depth. (c) Background suppression of (b) through a convolutional neural network. (d) Macroscopic photo of the phosphorescent object. (e) Reconstructed depth-resolved volumetric object. Scale bar for (a-c), (e): 2 mm; (d): 5 mm.
5. Object reconstruction speed of GEOMScope and comparison with iterative optimization algorithms
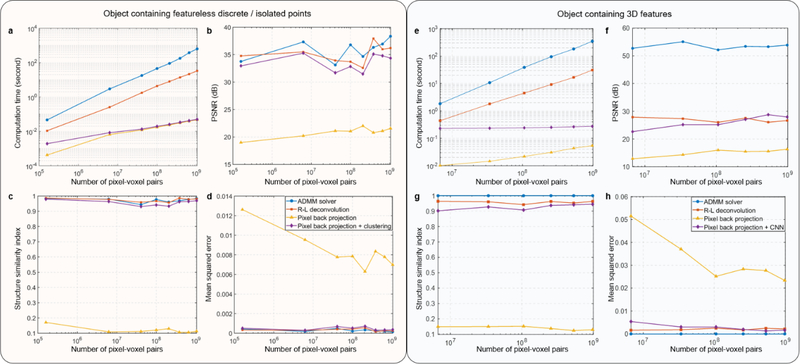
A key advantage of GEOMScope is that its object reconstruction has a much lower computational cost and achieves a much faster reconstruction than existing algorithms. To quantitatively validate this assessment, we compared the object reconstruction time using pixel back projection and the iterative optimization algorithms such as ADMM or Richardson–Lucy (R-L) deconvolution, for small data scales with pixel (camera)-voxel (object) pair number from ~106 to ~109 on a workstation (Figure 7, see also Supporting Table S1). We conducted the comparison for both featureless discrete/isolated point objects (Figure 7a–d, Supporting Figure S11) and 3D objects with continuous features (Figure 7e–h, Supporting Figure S12). In each set of comparison, we kept the same pixel-voxel ratio for different pixel-voxel pair numbers. For data size within the physical RAM limit, the computation time increases very fast with the number of pixel-voxel pairs when using optimization solvers and R-L deconvolutions, while pixel back projection method has a stable computation time on the order of tens of milliseconds (Figure 7a, e). The ADMM solver exceeds physical RAM limit when the number of pairs reach ~109, resulting in a rapidly increased computing time. The process time of both R-L deconvolution and ADMM solvers increase linearly with the number of pixel-voxel pair. This is expected as the number of elements in the system matrix in image formation (and thus the number of scalar multiplication in matrix operation) equals to (scales with) the number of pixel-voxel pair. In pixel back projection, for each voxel, we only pick one pixel in one sub-image of the lens unit within the effective image area, so the computation time only scales with the number of reconstructed voxel, resulting in a sublinear relationship with the pixel-voxel pair number. We note that the increase of pixel number in the image could increase the resolution and thus the object complexity that the reconstruction algorithm can handle. However, it will not increase the processing time, which is one advantage of our algorithm. In terms of RAM usage, deconvolution and optimization solver requires additional RAM to store the entire system matrix and operate the matrix algebra, while our method only requires a minimum amount of RAM as only one pixel-voxel pair is traced at each step. Our method using geometrical optical prior from microlens arrangement is thus much more suitable to solve large scale image reconstruction problems, though it suffers from a poorer reconstruction quality resulted from ghost objects. The reconstruction quality is greatly improved with the background suppression algorithm and becomes similar as those using ADMM solver or Richardson-Lucy deconvolution for both the featureless discrete/isolated point objects using particle clustering for background suppression (Figure 7b–d, Supporting Section S5, Supporting Figure S11), and 3D objects with continuous features using convolutional neural network for background suppression (Figure 7f–h, Supporting Section S5, Supporting Figure S12). We note that particle clustering algorithm is highly computational efficient, and only slightly increases the computation time compared with pixel back projection itself. Convolutional neural network requires more computational resources, but it is still greatly reduced compared with the iterative optimization algorithms.
Figure 7. Comparison between hybrid reconstruction method (pixel back projection followed by background suppression) and iterative-optimization-based methods on computational cost and reconstruction quality merit.
(a-d) Comparison for object containing featureless discrete / isolated points, where particle clustering was used for background suppression. The computation was conducted on a workstation (Intel Xeon E5–2686 v4, 128 GB system RAM, MATLAB 2019b). (a) Computational cost. (b) Peak signal-to-noise ratio (PSNR) of the reconstruction. (c) Structure similarity index (SSIM) of the reconstruction. (d) Mean squared error of the reconstruction. (b)-(d) is compared to ground truth. (e-h) Same as (a-d), but for comparison for 3D object containing continuous features, where a convolutional neural network was used for background suppression. The computation was conducted on a workstation (2x Intel Xeon E5–2667 v3, 384 GB system RAM, MATLAB 2019b). The computational cost of the two optimization-based methods, ADMM and Richard-Lucy deconvolution increases rapidly with data scale, while it only increases modestly in our hybrid reconstruction method. When paired with background suppression algorithms, the pixel back projection method has a greatly improved reconstruction quality, similar as those from the two iterative-optimization-based methods.
Benefited from its local reconstruction nature, the speed of the pixel back projection algorithm can be further increased by parallelizing the pixel-voxel ray matching in reconstruction. Multi-thread processing can be applied to resolve objects in each local region across different depths while maintaining the overall reconstruction rate. In our tests, the effectiveness of parallel computing is significant when the data size or number of voxel-pixel pairs is larger than 2×107. Compared with parallelized optimization process using gradient descent, our multi-threading method is straightforward and simple to conduct. For 16 depths reconstruction in our method (~1014 voxel-pixel pairs), parallel computing with 4 threads on a desktop or 8 threads on a workstation yields a speed increase of 230% with 30 sec total computing time or 380% with 18 sec total computing time respectively. Through further optimization on data structure and more threads, we expect reconstruction of large 3D volume with speed close to video frame rate.
6. Summary and Discussion
We demonstrated a lensless integrated microscope that can perform 3D imaging across a large field of view with high resolution and fast object reconstruction speed (Figure 1). The pixel back projection algorithm, in combination with efficient background suppression algorithm, significantly reduces the computational cost and increases the object reconstruction speed, while preserving a good resolution. It enables large field-of-view microscopic imaging with mega pixel reconstruction of the object, which would consume an unrealistic amount of computational resource and processing time using the prevailing iterative optimization algorithms or the more recently proposed deep neural network. We designed our microlens array based on the performance metrics of individual lens unit as well as lens array in both geometrical and wave optics aspects. We demonstrated the performance of our methods in theoretical modeling (Table. 1), numerical simulation (Figure 3, S8) and experiment (Figure 4–6, S9), and showed excellent results across different types of samples ranging from point source (Figure S9), resolution target (Figure 4), fluorescent particles (Figure 5) and volumetric objects (Figure 6). We also verified the efficiency of our reconstruction algorithm by a quantitative comparison on the reconstruction speed with the iterative optimization approaches (Figure 7). This work presents a promising approach of applying miniaturized lensless imaging device for high speed, high throughput imaging.
Compared to conventional cameras and microscopes where there is a one-to-one pixel mapping between the object plane and the sensor through the bulk lenses, lensless imagers map a single voxel in 3D objects to multiple pixels on a 2D camera through a thin piece of optics [10, 11, 13–17, 32–34]. Depending on the imaging optics, which fundamentally determines the measurement matrix from object to image, there have been two major classes of lensless cameras reported (Supporting Table S1). The first class is amplitude mask [11, 15, 35–37]. In Ref. [11, 15], the amplitude mask was designed such that the measurement matrix could be broken down to two small matrices, which greatly reduces the required memory and improves speed in object reconstruction. Its major drawback is the low light throughput and high sensitivity to alignment between the mask and the camera. The second class, which employs a phase mask such as a diffuser [10, 17, 38] or a microlens array [13, 14, 16, 39, 40], increases the light throughput. Diffusers have a dense PSF requiring large spatial support, and it is not suitable for pixel back projection. When using a microlens array, the PSF is relatively sparse. This could increase the signal-to-background ratio in the images and thus relax the general requirement of sparse objects in lensless imaging. We thus choose a random layer of microlens array as the imaging optics. The random position of lens units reduces the ambiguous crosstalk between lenses, which facilities the pixel back projection algorithm.
Our method solves the general challenges of lensless imagers where there is a high demand of computational resources for object reconstruction. In the prevailing iterative optimization algorithms, the object is solved by mapping the entire object world to the camera sensor and performing a global optimization with appropriate regularizations. While this could typically achieve a reconstruction result in high fidelity, the global mapping could contain high redundancy when an object feature is only effectively imaged by a local part of phase mask. In addition, it requires complex operation on a large matrix with the number of matrix elements being the product of camera pixel count and object voxel count, leading to a very high computational cost. This restrains the application in high resolution large field of view imaging. In GEOMScope, the random microlens array has a relatively sparse PSF and a near identity transformation matrix between the object and each sub-image. This allows us to use the pixel back projection algorithm, which reconstructs each object voxel by summing the corresponding camera pixels according to the geometry of the microlens array. This essentially turns the global optimization into local reconstruction, where different voxel reconstruction can run independently. Such approach shows excellent scalability with the data size. The field of view can be increased by increasing the number of lens unit, without increasing the reconstruction complexity of each object voxel. In GEOMScope, we pair the large-area microlens array with a high-pixel-count large-sensor-area camera. This enables a high resolution large field of view imaging with a fast reconstruction speed, which would otherwise consume a very expensive computational resource using global optimization algorithm. Furthermore, the local reconstruction nature of our algorithm works very well with parallelized processing. Our computation imaging strategy combining a sparse PSF design and localized reconstruction through pixel back projection is thus an effective way for large field of view lensless microscopic imaging.
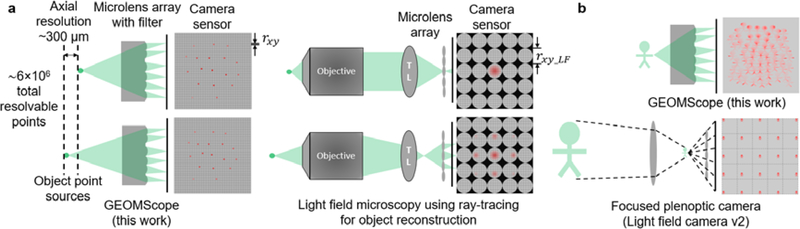
We note that GEOMScope has a high reconstruction resolution through geometrical optics. The PSF of each lens unit is well confined within the 3D resolving range, and this ensures a high efficacy of reconstruction using geometrical optics. We achieve a resolution close to that determined by wave optics (Materials and Methods). This is very different from the early generation of light field camera [41] or light field microscopy [4] (Figure 8a). There, the PSF is not locally sparse, so reconstruction through geometrical optics suffers from a large uncertainty, bounded by the size of the microlens unit [4, 41, 42]. In GEOMScope, we configure the microlens units and the system magnification such that the PSF behaves as a Dirac comb function. This results in a highly precise image formation modeled by geometrical optics, and thus a high resolution reconstruction without using iterative optimization approach.
Figure 8. Comparison between GEOMScope and light field cameras.
(a) Comparison between GEOMScope (left) and traditional light-field microscope using ray-tracing for object reconstruction (right). The resolution in traditional light-field microscope (rxy_LF) is limited by the size of microlenses. TL, tube lens. (b) Comparison between GEOMScope (top) and focused plenotpic camera (i.e. light field camera v2, bottom). Existing geometrical optics based reconstruction algorithm in focused plenoptic camera only works when the magnification is small (i.e. macroscopic imaging in photography setting) and there is no substantial overlap between sub-images from each microlens unit.
GEOMScope shares some similarity with focused plenoptic camera [5] as the PSFs in both are well confined. Though both of their reconstruction algorithms are based on geometrical optics, they are fundamentally different (Figure 8b). The reconstruction algorithm in the focused plenoptic camera is designed for photography application in macroscale, and would fail for microscopy application. There, the object is reconstructed by selecting sub-images from each microlens and stitching them together [5]. Each region of the reconstructed object only uses one patch from a single sub-image. For microscopic imaging, the system magnification becomes much larger, leading to a substantial crosstalk between the sub-images of microlens units. Using image-patches to fill up the reconstruction space will thus generate a lot of artifacts. In contrast, the pixel back projection algorithm used in GEOMScope reconstructs each voxel by collecting a single image pixel from each sub-image and summing them across multiple sub-images. Such strategy makes it highly effective to handle crosstalk and generate high quality reconstruction.
Another feature of our work is the innovative implementation of background suppression after the pixel back projection algorithm. Unlike global optimization approach, background such as the out-of-focus light or ghost object is inevitable in pixel back projection as it performs local reconstruction without consideration of other object source points. An additional background suppression step is thus critical to enhance the overall reconstruction performance. It greatly improves the signal-to-background ratio, and brings the reconstruction quality similar to those of iterative optimization algorithms. We note that this extra step only minimally increases the computation time, particularly for the particle clustering algorithm. The convolutional neural network requires a bit more computational resource (~40 ms inference time for each object slice, Intel Xeon CPU @2.30GHz, NVIDIA Tesla T4 GPU), but still significantly lower than the iterative optimization algorithms or the deep neural network directly mapping the images to the objects. For sparse samples with featureless characteristics (i.e. discrete / isolated points), we adopt particle clustering algorithm because of its simplicity and fast processing time. For 3D object with continuous connected features, convolutional neural network is used as it has a better scalability to dense and overlapped objects, and better generalization to object shapes and sizes, compared to other object detection methods such as circle detection through Hough transform [43] and bag of words feature recognition [44]. While the current convolution neural network is highly effective to suppress the background, it may occasionally mispredict some features. This could be due to the subtle inaccuracy of the out-of-focus background model in generating the training data (Materials and Methods, Supporting Section S2, Figure S4). In the future work, we aim to enhance the performance of neural network by using real images as training data, adapting more advanced network structures, and including the physical mechanism of pixel back projection to form trainable inversion module of the network.
In current work, we aim for a large field of view imaging and thus choose a camera with large sensor area. The working distance and system magnification are restricted by mechanical casting of off-the-shelf camera, which determine the upper limits of resolution and thus the number of resolved voxels (Materials and Methods). Nevertheless, we achieve a resolution close to that dictated by wave optics. By implementing board level camera and further optimizing the microlens design, GEOMScope could achieve a higher resolution and more resolved voxels.
7. Materials and Methods
7.1. Design consideration of the GEOMScope
We choose the design parameters of GEOMScope, including the pitch, focal length, total size of the microlens array, as well as object-microlens-array distance, and microlens-array-camera distance, based on the performance metrics.
7.1.1. Lateral resolution
The lateral resolution of GEOMScope depends on the Abbe diffraction limit of a single lens unit. At light wavelength λ, the minimum resolvable distance of image spots on sensor is λ/(2NA), where NA represents the numerical aperture of a single lens unit. The theoretical diffraction limited lateral resolution rxy0 can be expressed as
| (4) |
Considering the finite pixel size dp on the camera sensor, the final lateral resolution is expressed as
| (5) |
7.1.2. Axial resolution
The object movement in the axial direction results in a lateral shift of its images on the sensor. We can thus model the axial resolution rz as the distance change of an object point that leads to a shift of the image point at the boundary of the effective sensing area Ae in a distinguishable value rxy (Figure S5):
| (6) |
where is the radius of effective imaging area on sensor. Here, we assume the axial movement is small compared to the object distance, thus the variation of lateral resolution can be ignored.
7.1.3. Depth of field
For small object-lens distance z and low numerical aperture, the depth of field is determined by the confusion circle of each lens. When the object moves away from the focal plane, the imaged spot on the camera sensor will spread out in the lateral direction, forming a confusion circle. We set the diameter of the confusion circle to be two-pixel size on the sensor, and the corresponding depth of field DOF can be calculated following the geometrical optics [45] (Supporting Section S3, Figure S6):
| (7) |
| (8) |
where c is the dimeter of the confusion circle, and F#=f/D is the f-number of the individual lens unit, f and D being the focal length and diameter of the lens units respectively.
7.1.4. Field of view
The field of view is measured as the lateral range of objects within the depth of field distance range that can be effectively imaged onto the camera sensor. Unlike the conventional microscope where the field of view is much smaller than the imaging optics, GEOMScope can have a field of view in a similar size as the microlens array.
One related concept is the field of view of an individual lens. A larger field of view of a single lens unit is equivalent to a larger Ne, i.e. more lens unit could image a single object point, thus increasing the accuracy of reconstruction through pixel back projection. The field of view of a single lens unit can be evaluated when the Strehl ratio of the PSF falls below a threshold. The Strehl ratio Strehl can be approximated through the RMS wavefront error Δw from coma (Δwc), and spherical aberration (Δws+Δwd) [46]:
| (9) |
| (10) |
In general, a smaller lens diameter D and a larger focal length f would reduce the aberration and thus result in a larger field of view of a single lens unit.
7.1.5. Consideration of object sparsity
As one object point source is imaged by Ne microlens units, some level of sparsity is required on the object so as to reconstruct objects effectively without regularization. If there is a substantial overlap between the sub image from each lens unit, the reconstruction becomes ill-posed. From the perspective of pixel projection, we define an occupancy parameter V to describe the percentage of the camera sensor area being illuminated when an object occupies the entire field of view at a single depth:
| (11) |
In general, a small V allows denser objects to be imaged and reconstructed.
7.1.6. Design of the microlens array
We aim to design GEOMScope such that it can image fluorescent objects (~520 nm central wavelength) across a large volume ~23×23×5 mm3 with a lateral resolution ~40 μm. The distance between the microlens array and the image sensor is <5 mm whereas the nominal working distance is 20~30 mm. We choose an off-the-shelf camera (DALSA Genie Nano-CL M5100 NIR, Teledyne) equipped with PYTHON25K CMOS image sensor (ON Semiconductor) as it has a large sensor area (23×23 mm2), pixel count (5120×5120), and a small pixel size of 4.5×4.5 μm2, suitable for large field-of-view high resolution imaging.
The working distance and the object-microlens-array distance determines the magnification Mz~0.15 for each lens unit. To resolve objects 20~30 mm away from the microlens array with ~5 mm depth of field (radius of confusion circle ~2dp), the numerical aperture of the individual lens unit should be less than NAmax≅0.20 (Eq. 7~8) when we set a ~4 mm focal length. A larger numerical aperture is allowed when we reduce the focal length. Meanwhile, the lateral resolution and the magnification sets a lower limit of the numerical aperture NAmin≅0.045 (Eq. 5). The number of lens on the lens array could impact the computational cost in object reconstruction (pixel back projection), the occupancy parameter (Eq. 11), and the 3D resolving capability. On the one hand, to reduce the computational cost in object reconstruction and the occupancy parameter, the total number of lens should be small. On the other hand, more lens units to image an object point could provide more angular information of the light rays and thus improve the 3D resolving ability. Considering all the above factors, we set the diameter D and the focal length f of an individual lens unit as 2 mm and 4.65 mm respectively. A total of 213 lens units are randomly positioned across the 20×20 mm2 lens array area, with a fill factor ~1. The partial overlap between the lenses results in a reduced pitch size to ~1.23 mm on average, leading to an effective NA of ~0.13 for each lens. We simulate the aberration of the lens unit (Supporting Section S4, Figure S7). Setting a Strehl ratio above half of its peak value, we determine that the diameter of the effective field of view of each lens unit is ~6 mm, and one object point can be imaged by Ne~20 lens units (corresponding to an effective image area ~9π mm2). With Mz~0.15, we have the ratio between total area of sub images and sensor area ~0.4 (Eq. 11). This allows imaging dense 3D objects. The design parameters and the calculated performance metrics are summarized in Table 1.
7.2. Fabrication of microlens array and setup of GEOMScope
Based on the design parameters, we generated a 3D layout of the microlens array where individual lens units are randomly distributed across a 20×20 mm2 area. We ensured a relatively uniform lens density across the array, with a near unity fill factor and a desired distance range between lenses (mean 1.23 mm, standard deviation 0.09 mm). A negative mold of the microlens array was manufactured through 3D optics microfabrication (Luximprint). We then transferred the pattern into a lens array with 1 mm thick substrate using optical transparent PDMS (SYLGARD® 184, refractive index ~ 1.43) (Figure S10a). We use a blue LED with a 457/50 nm bandpass filter as an illumination source to the object. A fluorescent emission bandpass filter (525/45 nm) is attached to the microlens array, which is then positioned in front of the camera sensor (with an adjustable distance) (Figure S10b).
7.3. Background suppression through a particle clustering algorithm
Particle clustering algorithm is developed to suppress the background after the pixel back projection, and is suitable for sparse, featureless objects (i.e. discrete / isolated points) (Figure S2b and S3). It is based on graph connectivity. We first separate and cluster the 3D volumetric object into isolated groups through a combined operation of thresholding and clustering. The thresholding could remove the ghost objects and the system noise (e.g. stray light, camera readout noise), as they typically have much lower intensity than both the focused light and defocused light from the real object. This essentially cleans up the background between groups of object points isolated from each other. Different groups of object points are then clustered based on their pixel connectivity. For each object group, we reiterate the above process with multiple threshold values so as to remove the defocused light and separate the group into smaller clusters that contain the focused light. For each cluster, we then find the voxel that has peak intensity to represent the position of the object point in focus. Results from different thresholds are unionized to maximize the possibility of separating agminated object points. The clustering method does not require training nor down sampling of large size of image stacks, thus allowing high reconstruction resolution. While this resolution could be arbitrarily small, it is ultimately determined by the meaningful reconstruction voxel size, which depends on system magnification and 3D resolving ability. See more details in Supporting Section S1.
7.4. Background suppression through a convolutional neural network
For less sparse 3D objects with continuous features, we developed a convolutional neural network to suppress the background (Figure S2c). It slices overlapped objects in depth and picks out focused objects from background light. The network contains five levels of down sampling and up sampling. To train the network, we generate polygon shapes with random intensity and they are randomly distributed in different depths. We stack ten such slices together to form one set of training data, and in each slice we superimpose the features in current slice and the Gaussian blurred features from its nearby slices (Supporting Section S2, Figure S4). The slices have a lower weight when they become farther away. We also add 5% of additive noise on the image. The network is trained with single slice each time with RMSprop optimizer [47] and we use mean squared error as the loss function. The output image from the neural network contains sharper contrast and the defocused features are largely removed.
Supplementary Material
Acknowledgments
We acknowledge support from National Eye Institute (R21EY029472) and Burroughs Wellcome Fund (Career Award at the Scientific Interface 1015761).
Footnotes
Conflict of Interest
The authors declare no conflict of interest.
Supporting Information
Supporting Information is available from the Wiley Online Library or from the author.
References
- 1.Yuste R, ed., Imaging: A Laboratory Manual (Cold Spring Harbor Laboratory Press, 2011). [Google Scholar]
- 2.Lanni F, and Keller HE, “Microscope Principles and Optical Systems,” in Imaging: A Laboratory Manual, Yuste R, ed. (Cold Spring Harbor Laboratory Press, 2011), pp. 1–56. [Google Scholar]
- 3.Mertz J, Introduction to optical microscopy (Cambridge University Press, 2019). [Google Scholar]
- 4.Levoy M, Ng R, Adams A, Footer M, and Horowitz M, “Light field microscopy,” Acm T Graphic 25, 924–934 (2006). [Google Scholar]
- 5.Lumsdaine A, and Georgiev T, “The focused plenoptic camera,” in 2009 IEEE International Conference on Computational Photography (ICCP)(2009), pp. 1–8. [Google Scholar]
- 6.Broxton M, Grosenick L, Yang S, Cohen N, Andalman A, Deisseroth K, and Levoy M, “Wave optics theory and 3-D deconvolution for the light field microscope,” Opt Express 21, 25418–25439 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pegard NC, Liu HY, Antipa N, Gerlock M, Adesnik H, and Waller L, “Compressive light-field microscopy for 3D neural activity recording,” Optica 3, 517–524 (2016). [Google Scholar]
- 8.Guo CL, Liu WH, Hua XW, Li HY, and Jia S, “Fourier light-field microscopy,” Opt Express 27, 25573–25594 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li H, Guo C, Kim-Holzapfel D, Li W, Altshuller Y, Schroeder B, Liu W, Meng Y, French JB, Takamaru K-I, Frohman MA, and Jia S, “Fast, volumetric live-cell imaging using high-resolution light-field microscopy,” Biomedical Optics Express 10, 29–49 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Antipa N, Kuo G, Heckel R, Mildenhall B, Bostan E, Ng R, and Waller L, “DiffuserCam: lensless single-exposure 3D imaging,” Optica 5, 1–9 (2018). [Google Scholar]
- 11.Adams JK, Boominathan V, Avants BW, Vercosa DG, Ye F, Baraniuk RG, Robinson JT, and Veeraraghavan A, “Single-frame 3D fluorescence microscopy with ultraminiature lensless FlatScope,” Sci Adv 3 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mait JN, Euliss GW, and Athale RA, “Computational imaging,” Adv Opt Photonics 10, 409–483 (2018). [Google Scholar]
- 13.Kuo G, Liu FL, Grossrubatscher I, Ng R, and Waller L, “On-chip fluorescence microscopy with a random microlens diffuser,” Opt Express 28, 8384–8399 (2020). [DOI] [PubMed] [Google Scholar]
- 14.Yanny K, Antipa N, Liberti W, Dehaeck S, Monakhova K, Liu FL, Shen KL, Ng R, and Waller L, “Miniscope3D: optimized single-shot miniature 3D fluorescence microscopy,” Light-Sci Appl 9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Asif MS, Ayremlou A, Sankaranarayanan A, Veeraraghavan A, and Baraniuk RG, “FlatCam: Thin, Lensless Cameras Using Coded Aperture and Computation,” Ieee T Comput Imag 3, 384–397 (2017). [Google Scholar]
- 16.Xue Y, Davison IG, Boas DA, and Tian L, “Single-shot 3D wide-field fluorescence imaging with a Computational Miniature Mesoscope,” Sci Adv 6 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cai ZW, Chen JW, Pedrini G, Osten WG, Liu XL, and Peng X, “Lensless light-field imaging through diffuser encoding,” Light-Sci Appl 9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ozcan A, and McLeod E, “Lensless Imaging and Sensing,” Annu Rev Biomed Eng 18, 77–102 (2016). [DOI] [PubMed] [Google Scholar]
- 19.Coskun AF, Sencan I, Su TW, and Ozcan A, “Lensless wide-field fluorescent imaging on a chip using compressive decoding of sparse objects,” Opt Express 18, 10510–10523 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Greenbaum A, Luo W, Su TW, Gorocs Z, Xue L, Isikman SO, Coskun AF, Mudanyali O, and Ozcan A, “Imaging without lenses: achievements and remaining challenges of wide-field on-chip microscopy,” Nat Methods 9, 889–895 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cui XQ, Lee LM, Heng X, Zhong WW, Sternberg PW, Psaltis D, and Yang CH, “Lensless high-resolution on-chip optofluidic microscopes for Caenorhabditis elegans and cell imaging,” P Natl Acad Sci USA 105, 10670–10675 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Monakhova K, Yurtsever J, Kuo G, Antipa N, Yanny K, and Waller L, “Learned reconstructions for practical mask-based lensless imaging,” Opt Express 27, 28075–28090 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Khan SS, Adarsh VR, Boominathan V, Tan J, Veeraraghavan A, and Mitra K, “Towards Photorealistic Reconstruction of Highly Multiplexed Lensless Images,” Ieee I Conf Comp Vis, 7859–7868 (2019). [Google Scholar]
- 24.Khan SS, Sundar V, Boominathan V, Veeraraghavan A, and Mitra K, “FlatNet: Towards Photorealistic Scene Reconstruction from Lensless Measurements,” IEEE Trans Pattern Anal Mach Intell PP (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Boyd SP, Distributed optimization and statistical learning via the alternating direction method of multipliers (Now Publishers Inc., 2011). [Google Scholar]
- 26.Boyd SP, and Vandenberghe L, Convex optimization (Cambridge University Press, 2004). [Google Scholar]
- 27.Almeida MSC, and Figueiredo MAT, “Deconvolving Images With Unknown Boundaries Using the Alternating Direction Method of Multipliers,” Ieee T Image Process 22, 3074–3086 (2013). [DOI] [PubMed] [Google Scholar]
- 28.Chen Y, Xiong B, Xue Y, Jin X, Greene J, and Tian L, “Design of a high-resolution light field miniscope for volumetric imaging in scattering tissue,” Biomed. Opt. Express 11, 1662–1678 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lambert, Lamberts Photometrie (W. Engelmann, 1892). [Google Scholar]
- 30.Hartuv E, and Shamir R, “A clustering algorithm based on graph connectivity,” Information Processing Letters 76, 175–181 (2000). [Google Scholar]
- 31.Ronneberger O, Fischer P, and Brox T, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, Navab N, Hornegger J, Wells WM, and Frangi AF, eds. (Springer International Publishing, Cham, 2015), pp. 234–241. [Google Scholar]
- 32.Boominathan V, Adams JK, Asif MS, Avants BW, Robinson JT, Baraniuk RG, Sankaranarayanan AC, and Veeraraghavan A, “Lensless Imaging A computational renaissance,” Ieee Signal Proc Mag 33, 23–35 (2016). [Google Scholar]
- 33.Tanida J, Kumagai T, Yamada K, Miyatake S, Ishida K, Morimoto T, Kondou N, Miyazaki D, and Ichioka Y, “Thin observation module by bound optics (TOMBO): concept and experimental verification,” Appl Optics 40, 1806–1813 (2001). [DOI] [PubMed] [Google Scholar]
- 34.Varjo S, Hannuksela J, and Silven O, “Direct Imaging With Printed Microlens Arrays,” Int C Patt Recog, 1355–1358 (2012). [Google Scholar]
- 35.Fenimore EE, and Cannon TM, “Coded Aperture Imaging with Uniformly Redundant Arrays,” Appl Optics 17, 337–347 (1978). [DOI] [PubMed] [Google Scholar]
- 36.Huang G, Jiang H, Matthews K, and Wilford P, “Lensless Imaging by Compressive Sensing,” Ieee Image Proc, 2101–2105 (2013). [Google Scholar]
- 37.Zomet A, and Nayar SK, “Lensless Imaging with a Controllable Aperture,” in 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06)(2006), pp. 339–346. [Google Scholar]
- 38.Boominathan V, Adams JK, Robinson JT, and Veeraraghavan A, “PhlatCam: Designed Phase-Mask Based Thin Lensless Camera,” Ieee T Pattern Anal 42, 1618–1629 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tian F, Hu J, and Yang W, “Three-dimensional Imaging with a Single Layer of Random Microlens Array,” in Conference on Lasers and Electro-Optics(Optical Society of America, Washington, DC, 2020), p. STh3M.3. [Google Scholar]
- 40.Linda Liu F, Kuo G, Antipa N, Yanny K, and Waller L, “Fourier DiffuserScope: single-shot 3D Fourier light field microscopy with a diffuser,” Opt Express 28, 28969–28986 (2020). [DOI] [PubMed] [Google Scholar]
- 41.Ng R, “Digital light field photography,” (Stanford University, 2006). [Google Scholar]
- 42.Martinez-Corral M, and Javidi B, “Fundamentals of 3D imaging and displays: a tutorial on integral imaging, light-field, and plenoptic systems,” Adv Opt Photonics 10, 512–566 (2018). [Google Scholar]
- 43.Tappert C, “Computer vision: algorithms and applications,” Choice: Current Reviews for Academic Libraries 48, 1733–1734 (2011). [Google Scholar]
- 44.Csurka G, Dance CR, Fan L, Willamowski J, and Bray C, “Visual categorization with bags of keypoints.,” ECCV International Workshop on Statistical Learning in Computer Vision (2004). [Google Scholar]
- 45.Merklinger HM, The INs and OUTs of FOCUS: An Alternative Way to Estimate Depth-of-Field and Sharpness in the Photographic Image (1992). [Google Scholar]
- 46.Mahajan VN, “Strehl Ratio for Primary Aberrations in Terms of Their Aberration Variance,” J Opt Soc Am 73, 860–861 (1983). [Google Scholar]
- 47.Ruder S, “An overview of gradient descent optimization algorithms,” arXiv e-prints, arXiv:1609.04747 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.