Abstract
Introduction: COVID-19 has disrupted daily life and societal flow globally since December 2019; it introduced measures such as lockdown and suspension of all non-essential movements. As a result, driving activity was also significantly affected. Still, to-date, a quantitative assessment of the effect of COVID-19 on driving behavior during the lockdown is yet to be provided. This gap forms the motivation for this paper, which aims at comparing observed values concerning three indicators (average speed, speeding, and harsh braking), with forecasts based on their corresponding observations before the lockdown in Greece. Method: Time series of the three indicators were extracted using a specially developed smartphone application and transmitted to a back-end platform between 01/01/2020 and 09/05/2020, a time period containing normal operations, COVID-19 spreading, and the full lockdown period in Greece. Based on the collected data, XGBoost was employed to identify the most influential COVID-19 indicators, and Seasonal AutoRegressive Integrated Moving Average (SARIMA) models were developed for obtaining forecasts on driving behavior. Results: Results revealed the intensity of the impact of COVID-19 on driving, especially on average speed, speeding, and harsh braking per 100 km. More specifically, speeds were found to increase by 2.27 km/h on average compared to the forecasted evolution, while harsh braking/100 km increased to almost 1.51 on average. On the bright side, road crashes in Greece were reduced by 49% during the months of COVID-19 compared to the non-COVID-19 period.
Keywords: COVID-19, Driving behavior, Time-series forecasting, SARIMA, XGBoost
1. Introduction
The first cases of COVID-19 (also reported as SARS-CoV-2 or simply Coronavirus) were reported in the city of Wuhan in China in December 2019 (Cheng and Shan, 2020, Lau et al., 2020, Wu et al., 2020). After a significant rise in the new cases across the globe, it was declared a pandemic in March 2020 (WHO, 2020). At present, confirmed cases of COVID-19 are more than 93.1 million, while COVID-19-induced casualties are more than 1.98 million (WHO, 2020).
In an effort to restrict the spread of the virus among susceptible population groups, a “lockdown” restricting all non-essential activities was imposed by the majority of governments worldwide. Citizens were also instructed to practice “social distancing” by means of keeping at least 2 meters away from each other. Confinement and “social distancing” aimed to slow down the spread of the disease. Moreover, in combination with the aforementioned measures, schools, theaters, cinemas, restaurants, fitness centers, and shops were closed to avoid crowding. As a result, financial, environmental, and social impacts were observed (Anderson et al., 2020, Hendrickson and Rilett, 2020, Zhang et al., 2020a, Zhang et al., 2020b).
Driving behavior also changed radically. Road traffic volume, public transport users, and overall mobility activity reduced significantly (Apple, 2020, Google LLC, 2020, Moovit, 2020). For example, a study in the city of Santander, Spain, analyzed the impact of COVID-19 confinement and demonstrated that overall activity decreased by 67% and public transport use decreased by 93% (Aloi et al., 2020), while forecasts on travel demand revealed less traffic, public transport usage, and congestion or flow levels (Aloi et al., 2020, De Vos, 2020). In the same context, nearly 80% of people in the Netherlands reduced their activities outdoors, and subsequently elderly people had a greater decrease (de Haas et al., 2020). A behavioral change in mobility as a result of COVID-19 could also be on track, as according to de Haas et al. (2020) 27% of Dutch people stated that they will work from home more frequently, while 20% expressed the willingness to cycle and walk more in the future. Road traffic crashes were found to be reduced as road traffic and pedestrian volume decreased (Aloi et al., 2020). Furthermore, data provided by TomTom showed that traffic volumes decreased by 70–85% in the majority of European cities (ETSC, 2020, TomTom., 2020). Despite a dramatic decline in traffic volumes due to COVID-19 restrictions, in urban areas there was a 35% increase in speeding and an almost 200% increase in stunt driving offences in the March 15–31, 2020 timeframe, compared to the same period last year (City of Toronto, 2020).
Nevertheless, to date, the impact of COVID-19 on transportation can only be assessed through individual reports (e.g., Molloy, 2020) or web applications of data companies such as Google (Google LLC, 2020), Apple (2020), and TomTom (2020), which have recorded mobility activities during the lockdown phase. Τhe impact on driving behavior still remains relatively unknown. This fact is the motivation for the current paper, which aims at quantifying the effect of the COVID-19 lockdown on driving behavior through a naturalistic driving dataset captured through a novel mobile phone application. More specifically data on driving speed, speeding, and harsh braking/100 km are recorded before, during, and slightly after the imposition of a lockdown state in Greece. Time series forecasts of driving indicators based on the normal (pre-lockdown) phase are used to compare observed driving behavior with a normal evolution of itself, so as to quantify the change during lockdown.
A variety of published studies and reports were examined concerning road collisions, injuries, and fatalities. Road crashes were reduced in the majority of countries as road traffic and pedestrian volume decreased (Aloi et al., 2020). Road crashes in Germany decreased by approximately 23% during a quarantine month, injured people by 27%, and fatalities by 32% compared to the same period last year (DW, 2020). The same impact was observed in the Netherlands, where 50% less collisions were reported. Italy, France, and Spain displayed a drop in road deaths of 40–70%, however, in Australia the reported deaths had not declined despite the overall reduced traffic (ETSC, 2020). Barnes et al. (2020) revealed that the total number of crashes decreased; but unfortunately, crashes involved individuals (especially males) from age 25 to 64. Lin et al. (2020) highlighted that, although the number of nonfatal crashes reduced, the severe and fatal cases of road crashes were not changed during the pandemic. The overall number of road crashes as well as crash fatalities reported across United States was also reduced (Wagner et al., 2020). Although the number of road crashes was in general positively correlated with the amount of traffic volumes, the number of fatalities, surprisingly, was observed to experience an increase at some states during COVID-19 period (Vingilis et al., 2020).
This study is structured as follows: (a) an introduction to the subject of the paper (see above); (b) a brief literature review on driving behavior in relation with the effect of COVID-19 or other pandemics on transportation; (c) a description of the methodological approach and the utilized data; (d) XGBoost analyses, which are used to explore the importance of contributor variables, are then conducted; (e) the main part of the paper is dedicated to time-series forecasting and the comparison between observed driving behavior indicators and the forecasted ones; and (f) conclusions on the impact of COVID-19 on driving behavior are drawn and a discussion on how policy-makers and researchers should take advantage of the analysis is provided.
2. Literature review
The literature research aimed to link driving behavior, mobility, and transportation with the COVID-19 pandemic. The literature search was conducted in popular scientific databases such as Scopus, Science Direct and Google Scholar. The Boolean terms used to search these databases were “COVID-19” or “Corona Virus” or “SARS Cov 2” and “road” or “traffic” or “safety” or “accidents” or “collisions” or “mobility” or “transport” or “transportation” or “behavior” or “behavior.” The searches were limited to engineering and social sciences, and the results included approximately 18,500 studies (at present: 5/1/2021). These studies were screened concerning their titles and abstracts, and the most relevant papers to the investigating topic are included in this review.
Initially, De Vos (2020) analyzed the effect of COVID-19 in terms of the impact of social distancing on travel behavior, while Budd and Ison (2020) introduced a new theoretical concept of responsible transport that tries to reconsider transport policy due to behavioral change of passenger during the pandemic. Moreover, Vingilis et al. (2020) investigated the COVID-19 disease and its effects on road safety and it was revealed that travel decreased and drivers were exposed to a lower risk of collisions. Inada et al. (2020) indicated that empty roads triggered some speed-related traffic law violations among drivers, such as speeding, failing to stop at a stop sign, red light running, and failing to yield to pedestrians. In addition, Neuburger and Egger (2020) revealed an increase in risk perception of COVID-19, travel risk perception, and travel behavior over a short period of time. However, the aforementioned studies were limited to discussions over the impact of COVID-19 and did not provide quantifiable results on the impact of the pandemic on driving behavior.
Apart from studies discussing the impact of COVID-19 on travel behavior, particular emphasis was given on descriptive statistics regarding average speed, speeding, harsh events, mobile phone use, and driving distance per trip during the pandemic. For example, Aloi et al. (2020) conducted an empirical study and concentrated exclusively on urban mobility and COVID-19. Only descriptive results were included in that study and the authors demonstrated the change of mode choice, purpose of trip, number of trips, macroscopic traffic flow, public transport trips travel time and demands, and general trip features during lockdown. It was also revealed that, in Tokyo, speeding increased by 52% in March 2020 compared to March 2019, while the police officially enhanced enforcement of fines and penalties for speeding during the following months (Inada et al., 2020). Similarly, Katrakazas et al. (2020) provided descriptive evidence from Greece and Saudi Arabia on the deterioration of road safety levels during the period of the lockdown. In particular, it was shown that reduced traffic volumes due to lockdown led to a slight increase in average driving speed by 6–11%, but more importantly, to more frequent harsh accelerations and harsh braking per 100 km (up to 12%). Additionally, during March and April 2020, which were the months where COVID-19 spread was at its peak, mobile phone use while driving increased by 42%, while driving within the risky hours (00:00am–05:00am) dropped by up to 81%. Furthermore, spatial patterns of speeding pre (2019) and post (2020) the COVID-19 outbreak were visualized and compared in order to examine if the spatial extent of speeding increased (Lee et al., 2020).
Regarding studies employing questionnaires, a large-scale sample survey was conducted by de Haas et al. (2020) with questions concentrating mostly on mobility behavior, population, or demographic characteristics. Their findings concern the mobility behavior change since the COVID-19 outbreak. They investigated the change concerning the purpose of traveling, number of trips travel modes, stated opinion for future outdoors activities, remotely working, or education aspects. In the same context, Mogaji (2020) conducted an online survey to evaluate the impact of COVID-19 on transportation. More explicitly, the examined variables were mode choice, public transportation choice, and reduction of social, religious, and economic activities during the COVID-19.
To date, only a few studies have conducted statistical analyses on the effect of COVID-19 on driving behavior. One of them is Stavrinos et al. (2020), which utilized multi-level modelling to investigate driving behavior of adolescents in the United States before and during the pandemic period. Their results indicated that after the appearance of COVID-19 pandemic and its corresponding restrictions, driving days per week decreased by 37%, while vehicle miles driven dropped by 35. Nevertheless, the data used were concerned with self-reported driving behavior, and as a result a bias existed. Within-subjects general linear models were used in Roe et al. (2020) to investigate driving behavior of older adults during COVID-19. Indicators used included mean length in miles, the average speed in miles per hour of each trip, along with the mean number of three types of aggressive behaviors (i.e., harsh braking, harsh accelerations, and speeding) per mile per trip. It was clearly highlighted that participants reduced the proportion of days driven during the pandemic compared with the same period the year before. At the same time, trips per day showed a similar decline. Participants also took shorter trips, drove slower, had fewer speeding incidents, and had different trip destinations.
As can be understood from the previous paragraph, no study has statistically analyzed the impact of the COVID-19 pandemic on driving behavior and road safety, nor has any study taken into account time patterns in corresponding data. As a result, a gap in the literature exists that the current paper hopes to fill by performing time-series analysis in driving behavior data during the COVID-19 pandemic. In order to quantify the daily impact of COVID-19 on driving behavior, time-series analysis is deemed the most appropriate method and, as a result, a review of the literature was also conducted on methodological issues. Several published papers have used the corresponding variables to estimate the driving behavior.
3. Methodology
In order to quantify the daily impact of the COVID-19 pandemic on driving behavior indicators, a statistical relationship between COVID-19 and observed driving indicators had to be established. Therefore, a feature importance algorithm was used to evaluate the significance of variables on forecasting speed, speeding and harsh braking/100 km. After the initial explanatory analysis, in order to assess how driving behavior changed over time during the pandemic, time-series forecasting was exploited. For each of the three indicators (i.e., speed, speeding, harsh braking/100 km), the daily time-series was extracted as well as the time-series describing the evolution of COVID-19 cases and casualties. For the time-series analysis using ARIMA models, the following steps were followed according to Bisgaard and Kulahci, 2011, Box and Jenkins, 1976, Essi, 2018:
-
•
Seasonal decomposition to identify the trend, seasonality and residual variance
-
•
Stationarity check using the augmented Dickey-Fuller test (Dickey & Fuller, 1979)
-
•
Consideration of a general ARIMA Model
-
•
Autocorrelation and Partial Autocorrelation plots to explore the relationship between time point and individual lags and find a tentative model
-
•
Determination of the model using a parameter search
-
•
Split into training and test dataset
-
•
Forecasting and evaluation of the predictions
The aforementioned methods and steps are further elaborated in the following paragraphs.
3.1. XGBoost algorithms
As a preliminary step, Extreme Gradient Boosting (XGBoost) algorithms were implemented so that the importance of the collected variables, including the COVID-19 related variables, could be assessed and quantified in regards to the examined driving behavior indicators (i.e., speed, speeding, and harsh braking/100 km). XGBoost is a potent machine learning (ML) technique, encompassing multiple Classification And Regression Trees (CART), also known as tree ensemble. Additionally, XGBoost belongs to the family of supervised ML techniques, meaning that it uses labeled training data, the structure of which is defined by the researcher. In practice, this means that the independent/dependent variable division is known and present in the examined variables, and the outcome is a mapping function to the effect of y = f(x).
XGBoost algorithms apply the gradient boosting decision tree algorithm, also known as multiple additive regression trees, stochastic gradient boosting, or gradient boosting machines. The learning process of the algorithm is iterative and includes correction of previous errors in future iterations of the algorithm. A detailed presentation of the algorithm is described in the seminal study by Chen and Guestrin (2016). XGBoost has been demonstrated to outclass other ML methods such as Random Forests and Support Vector Machines in performance both in road safety (Ting et al., 2020) and in other fields (Nielsen, 2016).
Furthermore, XGBoost algorithms have functions that can calculate the importance of each predictor variable. This is known as Gini feature importance, or, equivalently, Mean Decrease in Impurity (MDI), and was proposed in a seminal study by Breiman (2001). One definition for Gini Importance for tree-based algorithms is the following: Gini Importance is the value obtained as the sum over the number of splits that include the feature across all trees, optionally divided by the number of samples it splits. This allows for powerful and accurate models to be created by utilizing only the most important predictor variables from a given dataset.
In XGBoost, three particular variable importance metrics are observed (XGBoost developer team, 2019):
-
•
Gain, describing the improvement in accuracy added by a feature to the branches it is on.
-
•
Cover, describing the relative quantity of observations (or number of samples) concerned by a feature.
-
•
Frequency, describing the number of times a feature is used in all generated trees.
These variable importance metrics used by the XGBoost algorithms were calculated in the analysis and examined to reveal that variables are informative to describe the examined driving behavior indicators.
3.2. Time-series forecasting
Autoregressive Integrated Moving Average (ARIMA) type models are considered the most popular time-series models, and are extensively used in the transportation research field. Their popularity can be explained due to their well-defined theoretical background and their quite straightforward calculations (Karlaftis & Vlahogianni, 2009). Thus, ARIMA models were deemed the most appropriate to model the impact of COVID-19 on daily driving behavior. An ARIMA model is a generalization of an Autoregressive Moving Average (ARMA) model and are generally denoted as:
| (1) |
where: p denotes the autoregressive order (i.e., number of time lags), d denotes the differencing (i.e., the number of differencing transformations required by the time series in order to become stationary.), q denotes the non-seasonal moving average order (i.e., the lag of the error component, which is the part of the time series not explained by trend or seasonality).
Then, the model can be written more formally as (Wang et al., 2020):
| (2) |
where: Φ∈ p is a vector of coefficients for the AR terms, θ∈ q is a vector of coefficients for the MA terms, y t is the outcome variable measured at time t, B is a vector used equivalently to indicate the lag operator, ∊t is random error (white noise, residual) associated with measurement t with ∊t∼N(0,σ2)
On the other hand, Seasonal ARIMA models are used when the time series exhibits seasonality. These models are similar to ARIMA models and they are usually denoted as:
| (3) |
where: p denotes the non-seasonal autoregressive order, d denotes the non-seasonal differencing, q denotes the non-seasonal moving average order, P denotes the seasonal autoregressive order, D denotes seasonal differencing, Q denotes seasonal moving average order, m is the number of periods in each season and the seasonal ARIMA model can be generalized as:
| (4) |
where: p denotes the non-seasonal autoregressive order, S is the period at which the seasonal trend occurs, B is a vector used equivalently to indicate the lag operator, Φ is a vector of coefficients for the AR terms, d denotes the non-seasonal differencing and y t is the outcome variable measured at time t.
3.2.1. Seasonal decomposition and stationarity
In cases of evident seasonality, ARIMA models can be extended to seasonal ARIMA (SARIMA) models. SARIMA models are considered as a straightforward extension of the non-seasonal ARIMA (Hipel & McLeod, 1994). With regards to SARIMA models, related studies were found to perform better than models of random walk (Clark et al., 2003; Ghosh et al., 2005, Williams, 2003), support vector regression (SVR) (Lippi et al., 2013), historical average (Chung and Rosalion, 2001, Williams, 2003) as well as regular ARIMA (Lippi et al., 2013; Clark et al. in Williams, 2003). Another study reported that the seasonal ARIMA models predicted more accurately, compared to the best performing k-NN (k-nearest neighbors algorithm) forecast models (Smith et al., 2002 in Kumar & Vanajakshi, 2015).
As a first step for the model identification and the interpretation of time-series data, the decomposition of the time series of the observed variable was required in order to identify its fundamental (and unobserved) parts: trend, seasonality, and residuals. A time series decomposition was used to measure the strength of trend and seasonality in a time series (Wang et al., 2006). The manner in which the decomposition is performed depends on whether time-series data are multiplicative or additive (Hyndman & Athanasopoulos, 2018). The decomposition can be written as:
| (5) |
where: is the outcome variable measured at time t, is the smoothed trend component, is the seasonal component, is a remainder component.
It was also essential to make sure that the utilized time series were stationary (Hyndman & Athanasopoulos, 2018). In order to make a time series stationary, a transformation was applied to the data, using the method of differencing. The latter removed the changes in the level of a time series, eliminating trend and seasonality and consequently stabilizing the mean of the time series. In order to check a time series for stationarity the Augmented Dickey-Fuller test was utilized (Dickey & Fuller, 1979). The Augmented Dickey-Fuller (ADF) test is checking if in models of the form:
| (6) |
where: is the observed time series data, is a constant, is the coefficient of the time trend, is a zero-mean error term. Using the ADF test, if = 0, then a unit root does not exist for the observed time series and the time series is non-stationary. In the different case that < 0, the time series is stationary.
3.2.2. Autocorrelation and partial autocorrelation
In order to identify an initial ARIMA model, the plots of the Autocorrelation (ACF) and Partial Autocorrelation functions (PACF) were used.
Correlation between two random variables and can be defined as (Dettling, 2018):
| (7) |
where: is the correlation between the two variables, is the covariance of the two variables, and are their individual variances.
For stationary time series, autocorrelation (i.e., the correlation of a specific variable with its earlier iteration) can be defined as a function of the lag k (Dettling, 2018):
| (8) |
where: is the measurement at time t and is the measurement at lag k. It can be understood that the ACF defines the correlation of an observation with previous measurements of the same variable.
Similarly, partial autocorrelation at lag k can be defined as:
| (9) |
which denotes the association between and , given that the linear dependence between and is removed.
By plotting both ACF and PACF it was easier to identify the correlation between more recent observations of the variable and simultaneously the existence of either actual lagged autocorrelations or autocorrelations caused by other measurements.
3.2.3. Model identification
In order to decide the parameters p, d, q for the ARIMA model as mentioned in equation (3) and the corresponding parameters for a potential SARIMA model, an automatic search of the best parameters according to the Akaike information criterion (AIC) or Bayesian Information Criterion (BIC) was used. The automatic search was based on popular packages in R and Python programming languages (Hyndman and Khandakar, 2007, Smith, et al., 2017), which have been found to be implemented successfully in recent publications (Ma et al., 2018, Ma et al., 2020). The best fitting model was selected based on the smallest AIC and BIC.
The Ljung-Box test (Ljung & Box, 1978) a popular diagnostic tool to test model fitness was also utilized. The Ljung-Box test is defined as:
-
•
The model does not exhibit lack of fit
-
•
The model exhibits lack of fit
given the test statistic:
| (10) |
where: is the length of the time series, is the estimated autocorrelation of the time series at lag and is the number of lags being tested.
The test rejects the null hypothesis if:
| (11) |
where: is the chi-square distribution table value with degrees of freedom and signicance level . The degrees of freedoms should be equal to , where is the number of residual autocorrelations that need to be checked, and are the autoregressive and moving average ARIMA parameters, respectively.
3.2.4. Choosing the training and testing samples
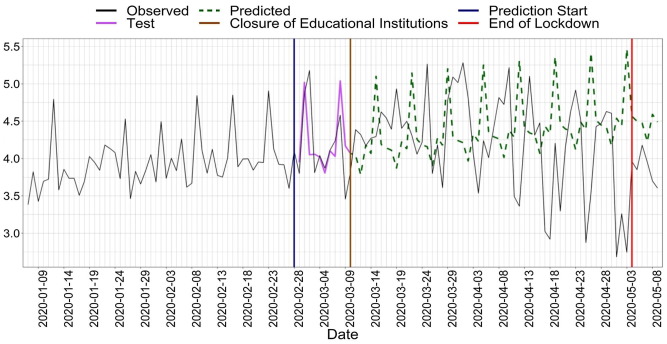
As the purpose of this paper was to quantify the effect of COVID-19 on three driving behavior indicators (i.e., driving speed, speeding, and harsh braking/100 km), the ARIMA models were trained using a representative dataset of normal operations (i.e., prior to COVID-19) and tested on the early stages of COVID-19 spread in Greece when no countermeasures were taken. Following the development of training and testing procedures for the algorithm, then forecasts of these normal operations-based models during the lockdown time period would give a picture of how these traffic indicators would normally evolve and could enable comparisons between the actual observations during the lockdown phase and the forecasted ones. In order to assist comparisons, time series models were trained using data from the months of January and February (i.e., when no COVID-19 case was reported in Greece), were tested on the period before the lockdown and were validated on the time period concerning mid-March until early May when the lockdown status was lifted. It should be noted that the training, test, and validation set was the same for all the examined variables (i.e., average speed, speeding, harsh braking/100 km). Fig. 1 depicts an example of training, test, and validation set.
Fig. 1.
An overview of training, test and validation sets.
3.2.5. Evaluation of predictions
After developing the ARIMA models on the testing and validation sets, forecasts were evaluated using popular forecasting evaluation metrics such as:
-
•
Mean Error (ME), which gives the mean of the forecasting error:
| (12) |
-
•
Mean Absolute Error (MAE), which gives the mean of the absolute forecasting error:
| (13) |
-
•
Mean Percentage Error (MPE), which gives the mean of the forecasting error in percentage:
| (14) |
-
•
Mean Absolute Percentage Error (MAPE), which depicts the mean error in percentage terms:
| (15) |
-
•
Root Mean Squared Error (RMSE), which is the square root of the average squared error:
| (16) |
where: N is the number of forecasted points, and is the error (i.e. )
Finally, statistical significance of the non-seasonal and seasonal components of the ARIMA models was checked.
4. Data overview
For the purposes of this study, a large naturalistic dataset of daily driving trips was used. The datasets correspond to a complete 5-month timeframe spanning from 01/01/2020 to 09/05/2020 in Greece. The timeframe was chosen so that sufficient periods are available both before the spread of COVID-19 to represent normal operations and during the COVID-19 pandemic to quantify the effect of the lockdown measures.
The first case of COVID-19 in Greece was diagnosed on 26/02/2020. The first reactive measure that was enforced in Greece, after the initial diagnosis of coronavirus, was the nationwide suspension of the operation of educational institutions of all levels on 10/03/2020. This was followed by the decision to close down all cafes, restaurants, bars, shopping centers, sports facilities, museums, and all services in the areas of religious worship of any religion and finally, a restriction on all non-essential movement was put in place on the 23/03/2020. The lockdown was lifted on the 04/05/2020 after 42 days.
For the purpose of the analyses, microscopic trip data and a representative subset of 122,275 trips was provided by OSeven Telematics. It should be noted that the microscopic trip data used referred to the users of OSeven smartphone application and not the entire population of Greece. Both male and female drivers aged 18–65 participated and a large database of thousands of trips was obtained through the OSeven application. The sample utilized in this research was also counterbalanced regarding age group and gender, in order to be as representative as possible. The raw driving behavior data from the mobile phone sensors (i.e., GPS, accelerometers, or gyroscope) was collected through driving behavioral analytics platforms, state-of-the-art technologies and smart algorithms, reliable metrics and novel gamification schemes, developed by OSeven. Several published studies have used naturalistic driving data from smartphone sensors provided by OSeven Telematics for investigating driving parameters such as driving behavior (Papadimitriou et al., 2019, Stavrakaki et al., 2020, Tselentis et al., 2019). Regarding data collection, data from smartphone sensors have been shown to allow for continuous and rapid data collection and seamless storage and analysis. Since smartphones are programmable, flexible implementation possibilities become available. However, there are increased demands in data storage and analysis, and considerable upfront costs during development of the data handling infrastructure, with much lower costs as time progresses and participant numbers increase (Ziakopoulos et al., 2020).
It should be mentioned that as privacy and security consist two of the platform’s main design principles, all data are stored and specific measures are taken to protect them based on encryption standards for data in transit and at rest. The above procedure is done using the latest technologies that comply with the national regulation in EU as well as with the General Data Protection Regulation (GDPR). As a result, all data has been provided by OSeven Telematics in a completely anonymized format. Readers are also referred to the studies provided in section 2.1 for a more detailed description of the OSeven application and platform in the scientific literature.
The collected trip data contained information on driving performance regarding average driving speed, average total speed, average speed limit exceedance (speeding), harsh events (i.e., harsh accelerations, harsh braking), other trip characteristics (i.e., total distance and total duration), as well as mobile phone use or driving during risky hours (00:00am–05:00am). The descriptive statistics of the aforementioned indicators during the collection period (i.e., between 01/01/2020 and 09/05/2020) are depicted in Table 1 .
Table 1.
Driving performance indicators along with their corresponding description (Source: OSeven, Data processing: NTUA).
| Variables | Unit | Description |
|---|---|---|
| Average speed | km/h | Average speed during driving with stops excluded from the duration of the trip |
| Average total speed | km/h | Average speed during the total duration of the trip |
| Speeding | km/h | Average speed over the speed limit |
| Duration of speeding | sec | Total duration of speeding in a trip |
| Harsh accelerations/100 km | – | Number of harsh acceleration events per distance (100 km) |
| Harsh braking/100 km | – | Number of harsh braking events per distance (100 km) |
| Total distance | km | Total trip distance |
| Total duration | sec | Total trip duration |
| Driving duration | sec | Total duration of driving, i.e. duration of stops has been excluded |
| Risky hours driving | km | Distance driven during risky hours (00:00–05:00) |
| Duration of mobile phone use | sec | Total duration of mobile usage |
| GR-Total Cases | – | Total number of confirmed cases due to COVID-19 pandemic in Greece |
Within this paper, three variables were selected and analyzed in detail:
-
•
average speed (km/h)
-
•
speeding (km/h); namely average excess speed over the limit
-
•
harsh braking per distance (100 km)
Furthermore, the enforcement of quarantine measures during the critical period for Greece is treated as a binary quantity: the value 1 is assigned for trips during the period from 23/03/2020 to 05/05/2020, and the value 0 is assigned for all other examined trips.
Table 2 illustrates descriptive statistics (i.e., mean, standard deviation, maximum value, minimum value) with regards to the examined variables for the complete subset of trips (122,275 trips), while Table 3 depicts descriptive statistics for the examined variables for the months of COVID-19 in Greece (46,614 trips). It should be also noted that the sample size for each variable in Table 2 is N = 130, while for the examined variables for the months of COVID-19, the sample size is denoted by n = 56 values.
Table 2.
Descriptive statistics for the examined variables for the complete subset of trips in Greece (from 01/01/2020 to 09/05/2020).
| Variable | Mean | Standard deviation | Maximum value | Minimum value |
|---|---|---|---|---|
| Average speed (km/h) | 43.16 | 2.65 | 49.68 | 38.82 |
| Speeding (km/h) | 4.09 | 0.53 | 5.28 | 2.68 |
| Harsh braking/100 km | 13.07 | 1.91 | 20.33 | 7.06 |
| Total trips | 122,275 | |||
| Sample size of each variable (N) | 130 |
Table 3.
Descriptive statistics for the examined variables for the months of COVID-19 in Greece (from 26/02/2020 to 09/05/2020).
| Variable | Mean | Standard deviation | Maximum value | Minimum value |
|---|---|---|---|---|
| Average speed (km/h) | 44.34 | 2.68 | 49.68 | 38.82 |
| Speeding (km/h) | 4.17 | 0.61 | 5.28 | 2.68 |
| Harsh braking/100 km | 13.26 | 2.08 | 20.33 | 7.70 |
| Total trips | 46,614 | |||
| Sample size of each variable (n) | 56 |
5. Exploratory feature analysis with XGBoost
An initial exploration of feature importance as yielded by the implementation of XGBoost methodology is conducted in this section. All variables are positive continuous variables, and are therefore examined with a regression with squared loss function. In order to calibrate the XGBoost tree ensemble, a uniform split was applied in the described data: 75% was randomly designated as the training subset, while the remaining 25% was randomly designated as the test subset. Furthermore, a number of hyperparameters can be optimized for each XGBoost ensemble, such as learning rate (eta), gamma, maximum tree depth, minimum child weight, number of rounds and mean squared error. The selection of the optimal values is conducted by examining large numbers of hyperparameter combinations, as described by Bischl et al. (2016); in this research, a grid search of 5000 hyperparameter combinations was conducted for each analysis. All XGBoost analyses were conducted in R-studio (R Core Team, 2019).
5.1. Average speed (km/h)
The examined range and obtained parameters from the XGBoost tuning for average speed are provided in Table 4 .
Table 4.
Examined and optimized hyperparameters for average speed XGBoost algorithms.
| Hyperparameter | Examined range | Optimized Value |
|---|---|---|
| Learning rate | 0.000–1.000 | 0.38 |
| Gamma | 0–100 | 4.17 |
| Maximum tree depth | 1–50 | 9 |
| Minimum child weight | 1–10 | 2 |
| Number of rounds | 1–1000 | 42 |
| Mean Squared Error | as low as possible | 1.256 |
The predictive power was provided by the application of the XGBoost tree ensemble on the test subset, and yielded RMSE = 1.106 and MAPE = 0.024. The respective obtained feature importance is provided in Table 5 .
Table 5.
Feature importance of average speed XGBoost algorithms.
| Feature | Gain | Cover | Frequency | |
|---|---|---|---|---|
| 1 | GR-Total Cases | 0.574 | 0.306 | 0.308 |
| 2 | Total distance | 0.387 | 0.489 | 0.500 |
| 3 | Trip duration | 0.035 | 0.154 | 0.154 |
| 4 | Risky hours | 0.005 | 0.051 | 0.038 |
5.2. Speeding (km/h)
The examined range and obtained parameters from the XGBoost tuning for speeding is provided in Table 6 .
Table 6.
Examined and optimized hyperparameters for speeding XGBoost algorithms.
| Hyperparameter | Examined range | Optimized Value |
|---|---|---|
| Learning rate | 0.000–1.000 | 0.06 |
| Gamma | 0–100 | 0.34 |
| Maximum tree depth | 1–50 | 2 |
| Minimum child weight | 1–10 | 4 |
| Number of rounds | 1–1000 | 250 |
| Mean Squared Error | as low as possible | 0.177 |
The predictive power was provided by the application of the XGBoost tree ensemble on the test subset, and yielded RMSE = 0.318 and MAPE = 0.062. The respective obtained feature importance is provided in Table 7 .
Table 7.
Feature importance of speeding XGBoost algorithms.
| Feature | Gain | Cover | Frequency | |
|---|---|---|---|---|
| 1 | Total distance | 0.551 | 0.558 | 0.467 |
| 2 | GR-Total Cases | 0.212 | 0.224 | 0.228 |
| 3 | Trip duration | 0.130 | 0.142 | 0.152 |
| 4 | Duration of mobile use | 0.054 | 0.053 | 0.076 |
| 5 | Quarantine | 0.027 | 0.018 | 0.033 |
| 6 | Risky hours | 0.026 | 0.006 | 0.043 |
5.3. Harsh braking/100 km
The examined range and obtained parameters from the XGBoost tuning for harsh braking/100 km is provided in Table 8 .
Table 8.
Examined and optimized hyperparameters for harsh braking/100 km XGBoost algorithms.
| Hyperparameter | Examined range | Optimized Value |
|---|---|---|
| Learning rate | 0.001–0.6 | 0.374 |
| Gamma | 0.001–10 | 1.37 |
| Maximum tree depth | 2–10 | 6 |
| Minimum child weight | 1–10 | 1 |
| Number of rounds | 1–250 | 242 |
| Mean Squared Error | as low as possible | 0.018 |
The predictive power was provided by the application of the XGBoost tree ensemble on the test subset, and yielded RMSE = 1.279 and MAPE = 0.08. The respective obtained feature importance is provided on Table 9 .
Table 9.
Feature importance of harsh braking/100 km XGBoost algorithms.
| Feature | Gain | Cover | Frequency | |
|---|---|---|---|---|
| 1 | Duration | 0.541 | 0.396 | 0.327 |
| 2 | Totaldist | 0.278 | 0.211 | 0.173 |
| 3 | GRTotalCases | 0.075 | 0.043 | 0.135 |
| 4 | Risky_hours | 0.058 | 0.206 | 0.192 |
| 5 | Time_mobile_usage | 0.049 | 0.144 | 0.173 |
In summary, the COVID-19-related parameter of total cases in Greece seems to exert a considerable influence in allowing the prediction of average speed, speeding, and harsh braking/100 km, as expressed by the gain scores of each XGBoost tree ensemble. This applies for the presence and enforcement of quarantine measures for average speeding as well. It is apparent that the exposure variables of total trip distance and duration also affect all examined quantities, and a small contribution is also provided by driving during risky night-time hours.
6. Time-series modelling assessment
6.1. Model specification
Following the identification of the influence of COVID-19-related parameters on driving behavior indicators, Seasonal Autoregressive Integrated Moving Average (SARIMA) modelling was followed to quantify the impact of the pandemic. The three components (i.e., trend, seasonality, and residuals) for the time-series of the considered indicators were analyzed. It was observed that the seasonal component for all three indicators changed over time, and similar patterns were observed for consecutive months. However, later observations displayed greater difference. With regards to average speed and speeding, there was an overall increasing trend through the months, which means that there was a significant rise in average speed and speeding during the period of COVID-19 pandemic. Taking into consideration harsh braking/100 km, a smaller seasonal trend was evident. With regards to the non-seasonal trend, values reached a maximum during mid-March, but started to decrease thereafter. Lastly, the contribution of random noise was negligible for all the examined variables.
As described in the methodology, the next step in the time series pipeline was to check for stationarity. For that purpose, the ADF test was performed for the 1st difference (Yt-Yt-1) of average speed, speeding, and harsh braking/100 km. In order to eliminate the seasonal effect from the time series observations, a seasonal first differencing was utilized for all considered time-series. The first difference was used because all the original time series were not stationary. Such a transformation also assisted to consolidate the variance of a time series. Moreover, differencing can help stabilize the mean of a time series by removing changes in the level of a time series, and therefore eliminating, or reducing, trend and seasonality.
Table 10 illustrates the ADF test for the original variables, while Table 11 depicts the ADF test for the 1st difference of each variable. In addition, Table 12 illustrates the Box-Ljung Test (white noise check) for the examined variables, which was performed on the 1st difference of average speed, speeding and harsh braking/100 km.
Table 10.
Augmented Dickey-Fuller Test for the considered variables.
| Augmented Dickey-Fuller Test |
|||
|---|---|---|---|
| Original | Test statistics | Lag order | p-value |
| Average speed | −2.49 | 5 | 0.37 |
| Speeding | −3.59 | 5 | 0.04 |
| Harsh braking/100 km | −3.53 | 5 | 0.04 |
Table 11.
Augmented Dickey-Fuller Test for the 1st difference of each variable.
| Augmented Dickey-Fuller Test |
|||
|---|---|---|---|
| Variable | Test statistics | Lag order | p-value |
| diff(Average speed) | −8.94 | 5 | 0.01 |
| diff(Speeding) | −10.09 | 5 | 0.01 |
| diff(Harsh braking/100 km) | −8.39 | 5 | 0.01 |
Table 12.
Box-Ljung Test for the 1st difference of each variable.
| Box-Ljung Test |
|||
|---|---|---|---|
| Variable | X2 | df | p-value |
| diff(Average speed) | 78.1 | 24 | 1.218e-07 |
| diff(Speeding) | 55.64 | 24 | 2.563 e-04 |
| diff(Harsh braking/100 km) | 44.75 | 24 | 6.22 e-03 |
ACF and PACF plots for the 1st difference of driver behavior indicators (i.e., average speed, speeding and harsh braking/100 km) were performed that indicated the levels at which the autocorrelation is significant and determined the order of the autoregressive term. It was found that both ACF and PACF dropped to zero relatively quickly. For all the candidate SARIMA models, p-values of the autoregressive and seasonal autoregressive terms were found to be less or equal to 0.05, which indicates their statistical significance. Table 13 shows the final selected candidate models along with their corresponding ARIMA terms. The specifications of the best model per driving behavior indicator with regards to AIC and BIC are also demonstrated.
Table 13.
Summary of estimated candidate SARIMA models for the 1st difference of each variable.
| Variable | Candidate model | Estimate | Std. Error | z value | Pr(>|z|) | AIC | BIC |
|---|---|---|---|---|---|---|---|
| diff(Average speed) | ma1 | −0.95 | 0.13 | −7.12 | 1.07e-12 *** | 116.94 | 122.36 |
| sma1 | −0.74 | 0.36 | −2.01 | 0.042 * | |||
| diff(Speeding) | ar1 | −0.60 | 0.12 | −4.99 | 6.15e-07 *** | 25.11 | 30.53 |
| sar1 | −0.49 | 0.14 | −3.65 | 2.61e-04 *** | |||
| diff(Harsh braking/100 km) | ma1 | −0.45 | 0.13 | −3.43 | 6.09e-04 *** | 194.11 | 205.70 |
| ma2 | −0.34 | 0.14 | −2.49 | 0.013 * | |||
| sar1 | 0.66 | 0.22 | 2.93 | 3.337e-03 ** | |||
| sma1 | −0.92 | 0.31 | −2.95 | 3.174e-03 ** | |||
| sma2 | 0.69 | 0.37 | 1.87 | 0.061 . |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1.
Following the observation of the ACF and PACF plots, the best models were obtained through the forecast package in R (Hyndman et al., 2020), as described in Table 14 . The number in brackets (i.e. [7]) represents the exponential decay in weekly lags. As described in section 3.2, the corresponding values for the best SARIMA models denote the non-seasonal and seasonal autoregressive order, differencing as well as moving average order, respectively.
Table 14.
SARIMA models for the 1st difference of each variable.
| Variable | SARIMA Model |
|---|---|
| diff(Average speed) | (0,1,1)x(0,1,1)[7] |
| diff(Speeding) | (1,1,0)x(1,1,0)[7] |
| diff(Harsh braking/100 km) | (0,1,2)x(1,0,2)[7] |
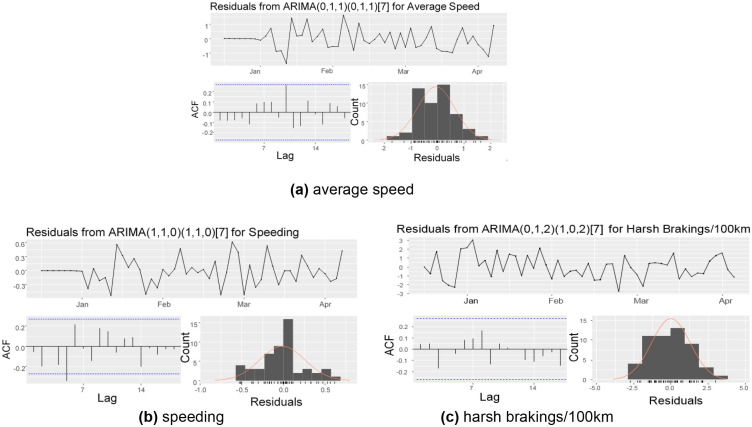
In order to further validate the models, their residuals were also checked. As depicted in Fig. 2 , the residuals appear to be randomly scattered, and no evidence of the error terms being correlated with each other exists. Consequently, the residuals or errors can be conceived as independently and identically distributed (i.i.d.) sequences with a constant variance and a zero mean. Therefore, the developed SARIMA models appeared to be well-fitted and were chosen to be used for prediction.
Fig. 2.
Residual Plots for the 1st difference of each variable: (a) average speed, (b) speeding, (c) harsh braking/100 km.
Table 15 illustrates the results of the estimated SARIMA models for each of the three variables. With regards to the error terms of RMSE and MAE, the values of RMSE were proven to be larger, which means that all the errors are not of the same magnitude; actually, the greater difference between them, the greater the variance in the individual errors.
Table 15.
Performance metrics for the estimated SARIMA model on the test set.
| Variable | ME | RMSE | MAE | MPE | MAPE | ACF1 |
|---|---|---|---|---|---|---|
| diff(Average speed) | 0.19 | 2.23 | 1.51 | 0.23 | 3.46 | 0.17 |
| diff(Speeding) | −0.05 | 0.45 | 0.31 | −1.98 | 7.25 | −0.01 |
| diff(Harsh braking/100 km) | −0.33 | 1.98 | 1.61 | −5.60 | 15.04 | 0.34 |
Regarding RMSE, the best performance is observed for speeding with 0.45, while the worst performance is observed using the average speed time series. Looking, however, at the MAPE indicator, it is distinguishable that the speed time series resulted in the best forecasting performance, with only 3.46% difference from the observed measurements. This is further resembled in the MPE indicator with speed having a 0.23% difference from the observed values. Lastly, with regards to the first-order autocorrelation coefficient (ACF1), all three SARIMA models perform well, with the speeding time series having the best performance. It should be noted that as the autocorrelation function can provide the correlation among different points separated by various time lags, ACF1 is a measure of how much is the current value influenced by the previous values in a time series.
6.2. Forecasting
After validating the performance of the developed model, focus was given on the forecasting performance. The results of the models with regards to the COVID-19 lockdown period is described in the following sections.
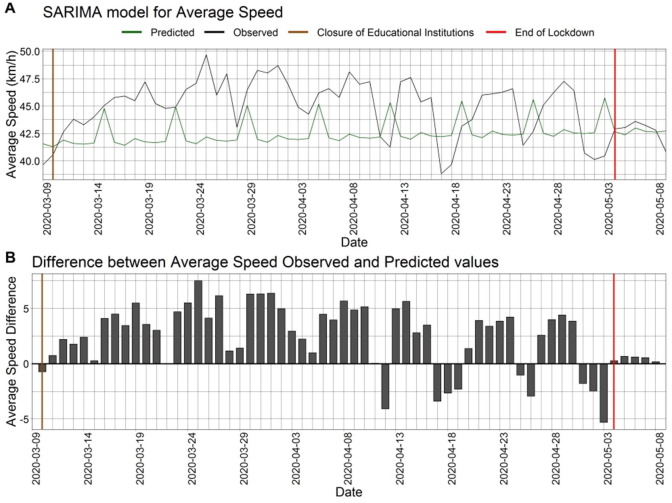
6.2.1. Average speed (km/h)
With regards to average speed, the forecasted values were based on the (0,1,1)x(0,1,1) SARIMA model. It can be observed that speed significantly increased over the COVID-19 lockdown with large fluctuations, while in normal conditions speed would not increase above 46 km/h. To further illustrate the effect of COVID-19 lockdown on average speed, the differences between forecasted and observed values, as well as the RMSE, MAPE and ACF1 were estimated. Fig. 3 depicts the SARIMA model for average speed for the prediction time along with the differences between average speed observed and predicted values.
Fig. 3.
SARIMA model forecasts for average speed and Differences between observed and predicted average speed values.
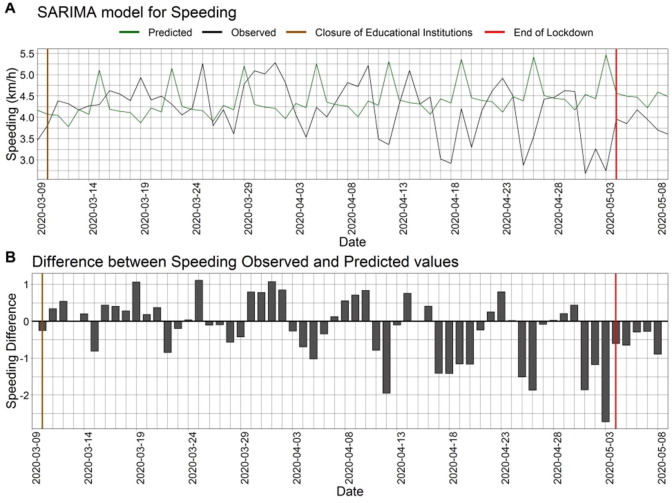
6.2.2. Speeding (km/h)
Concerning speeding, the forecasts were based on the (1,1,0)x(1,1,0) best-fit SARIMA model. It is evident that speeding was forecasted to be increased during the months of March and April, but actually demonstrated a downwards trend during the pandemic. Regarding the difference between the observed and forecasted values, Fig. 4 illustrates that in the beginning of March and until the beginning of April, the actual values for speeding were higher than the potential normal forecasted values, while within April speeding gradually decreased.
Fig. 4.
SARIMA model forecasts for speeding and differences between observed and predicted speeding values.
6.2.3. Harsh braking/100 km
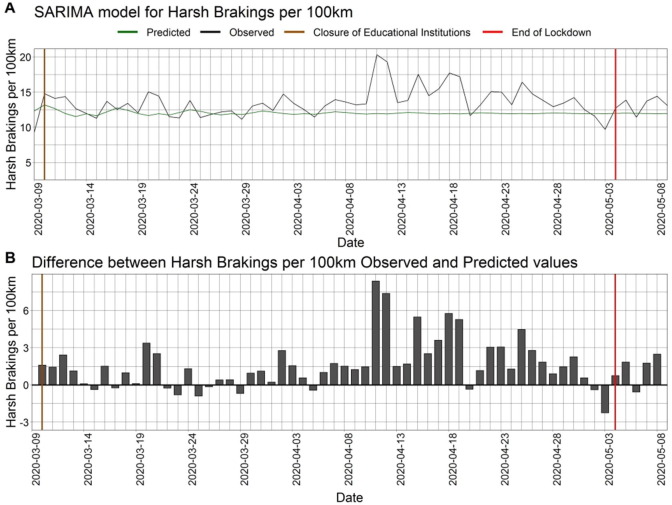
It was found that observed values differ a lot from the forecasts. In more detail, harsh braking/100 km was forecasted to have a frequency of around 12 and 13 events/100 km, but observed values are largely higher than the forecasts, reaching a maximum of 21 and minimum of 9 harsh braking/100 km. From Fig. 5 , it is further validated that during the COVID-19 pandemic, values for harsh braking/100 km were much higher than the forecasted values.
Fig. 5.
SARIMA model for harsh brakings /100 km and differences between observed and predicted harsh braking values.
6.2.4. Overall evaluation
In order to have an overall picture of the difference between forecasted and observed values, the MAPE, RMSE, ACF1 errors as well as the minimum and maximum and average of the three indicators were obtained and are described in Table 16 .
Table 16.
MAPE, RMSE, ACF1, min, max, average difference for observed and forecasted values.
| Variables | MAPE | RMSE | ACF1 | Minimum Difference (Date of occurrence) | Maximum Difference (Date of occurrence) | Average |
|---|---|---|---|---|---|---|
| Average speed | 7.12 | 3.76 | 0.50 | −5.30 (3/5/2020) | 7.51 (25/3/2020) | 2.27 |
| Speeding | 17.76 | 0.87 | 0.44 | −2.72 (3/5/2020) | 1.11 (25/3/2020) | −0.22 |
| Harsh brakings/100 km | 12.27 | 2.51 | 0.43 | −3.06 (9/3/2020) | 8.37 (11/4/2020) | 1.51 |
From Table 16, it can be observed that in terms of RMSE, speed is performing worse than the rest of the three indicators, but better in terms of MAPE. As a result, forecasts for speed tend to be more accurate than forecasts for speeding and harsh braking/100 km. With regards to the average difference between observed and forecasted values, similar to RMSE speed provided larger errors but this is due to the fact that speed units (i.e. km/h) are larger than the measurement units of speeding or harsh braking per distance. Finally, observing the dates for minimum and maximum values of forecasts, the minimum difference between observed and forecasted values was identified on the 3rd of May, the last day of the lockdown, for speed and speeding, while the minimum difference for harsh braking/100 km was found on the 9th of March. In addition, the maximum difference for the average speed and speeding time series was observed on the 25th of March, a traditional Greek holiday (i.e., Greek Independence Day), and with regards to harsh braking/100 km, the maximum difference was identified in the 11th of April.
7. Discussion
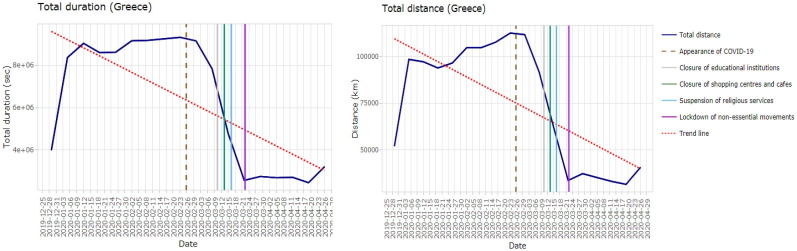
This study aimed to quantify the effect of the COVID-19 pandemic on driving behavior by forecasting the evolution of time-series data based on values before the pandemic and comparing forecasts with actual values during the COVID-19 lockdown in Greece. Initially, the importance of COVID-19 indications (e.g., cases, casualties, lockdown countermeasures) was investigated using the feature importance extracted from XGBoost algorithms. The number of total cases was one of the two most important factors for three out of the three examined indicators (i.e. speed, speeding, and harsh braking/100 km). As a result, it can be derived that the spread of the virus had a significant effect on driving behavior. Total distance and trip duration were also among the most influential factors for all examined indicators. This can be explained by the significant decrease in trip duration and distance driven during the lockdown phase as seen in Fig. 6 .
Fig. 6.
Total duration and distance of trips during the COVID-19 period in Greece.
The effect of the lockdown initiation was not found to have a significant effect on driving behavior indicators, as was indicated in section 5 of the current paper. This is probably explained by the fact that Greek drivers did not change their behavior due to the lockdown but rather because of the spread of the virus that led them to minimize trips and car driving.
The authors recognize that there is no immediate causal connection between total COVID-19 cases and/or quarantine presence and road safety, in the form of an established road safety risk factor or measure. The findings of the exploratory analysis through XGBoost, however, suggest a correlational value of the parameter of number of cases at least temporally. Therefore, they provided additional incentive for the time-series modelling and examination of trends that impact the three examined road safety indicators, as the pandemic progresses.
Τhe effect of COVID-19 on driving behavior in terms of average speed, speeding, harsh braking/100 km both during the COVID-19 pandemic and the time period before the first case of the disease in Greece was quantified through seasonal time series modeling approach. With regards to the forecasting of the “normal evolution” (i.e., the potential evolution if COVID-19 had not spread and no lockdown measures were applied) it was observed that the best model was obtained for average speed with only 3.46% of MAPE. In general, no large errors were observed with harsh braking/100 km (i.e., the variable with the larger MAPE) being able to forecast with 84.96% accuracy on the test dataset. Βy applying the developed models on the validation dataset that described the lockdown period in Greece and looking at the difference between observed and forecasted values, the effect of COVID-19 could be evaluated for all three indicators.
With respect to average speed, it was revealed that the observed values were higher than the forecasted ones, which means that a significant increase in average speed was identified during the COVID-19 lockdown. Τhe maximum difference (7.51) between observed and predicted values of average speed was identified in 25/03/2020, during the lockdown period due to COVID-19, which seems reasonable as the 25th of March is a public holiday. Conversely, the minimum difference (-5.30) between actual and forecasted values of average speed was found in 03/05/2020, a day before the gradually lift restrictions in Greece, when drivers started to restart their business activity and return to their daily routines. On average, it was demonstrated that observed speeds are 2.27 km/h higher than the forecasted ones, but as seen from the maximum and minimum values a lot of variance existed. This finding can be explained by the fact, that with emptier streets and much lower volumes, average vehicle speed tends to be increased. This finding can be supported by Inada et al. (2020) who indicated that the empty roads possibly triggered speed-related violations among drivers.
Speeding was forecasted to be increased during the months of March and April; however, a downward trend during the pandemic was demonstrated, but the models failed to predict it. Especially in March, it was demonstrated that actual values for speeding were higher than forecasted, while within April speeding gradually decreased, with an overall average difference of 0.22 fewer events between observed and predicted values. The demonstrated average reduction is contradicting with the increase of speed that was observed, but can be explained by the fact that the forecasting model for speeding was the worst in terms of RMSE and MAPE. As a result, the forecasting ability of the model cannot capture successfully the evolution of speeding occurrence and results should be interpreted with caution.
The forecasting results on harsh braking/100 km demonstrated that if no lockdown was imposed, the average number of harsh brakings/100 km would be lower for the majority of the lockdown days. Increases of harsh braking/100 km with lower traffic and higher speeds are compliant with recent research using similar data (i.e., from smartphones), where it is stated that with higher speeds more harsh braking events occur (Petraki et al., 2020).
Lastly, a more comprehensive picture of the effects of COVID-19 pandemic on road safety can be drawn from the high quality data on total number of road crashes along with the corresponding fatalities, severe and slight injuries. Table 17 illustrates the difference in the total number of road crashes and persons injured from January to April 2020 in Greece. In particular, a 49% reduction in the total number of road crashes was observed during March-April 2020 (i.e., months of COVID-19) compared to January–February 2020 (i.e., when no COVID-19 case was reported in Greece). Furthermore, during March–April 2020, the total number of fatalities decreased by 53%, severe injuries were reduced by 39%, while slight injuries were reduced by 53% compared to January–February 2020.
Table 17.
Road crashes and persons injured from January to April 2020 in Greece (Hellenic Statistical Authority (2021)).
| January | February | March | April | Change (March–April) – (January–February) | |
|---|---|---|---|---|---|
| Road crashes | 788 | 858 | 507 | 326 | −49% |
| Fatalities | 49 | 47 | 24 | 21 | −53% |
| Severe injuries | 46 | 31 | 26 | 21 | −39% |
| Slightly injuries | 909 | 965 | 545 | 332 | −53% |
Despite the fact that provisional data for road crashes occurred in 2020 (Hellenic Statistical Authority, 2021) showed that there was a decrease in absolute numbers of crashes, fatalities, and injuries, driving performance was found to be more careless and more risky overall during the lockdown period. This finding can be supported by previous studies in which it was found that less vehicle traffic volumes and empty roads led to higher speeds and harsh events (Carter, 2020). Results from the current research are also consistent with findings reported by Wagner et al. (2020), who analyzed U.S. data from the second quarter of 2020 compared to the first quarter. It was revealed that the total number of road crashes and fatalities reported across states was reduced, while drivers were more willing to take risks that included speeding, driving while impaired, and not using their seat belts. These drivers, along with a potential reduction in law enforcement and safety messaging, were identified as possible factors that created an environment favoring risky driving. The same finding was recently reported by Brodeur et al. (2020) who used difference-in-differences in order to evaluate the impact of Stay-at-Home orders on road crashes for five states in the United States and a 50% reduction in road crashes was identified. However, some of the conclusions delivered from Lin et al. (2020) were found to be different compared to the present ones. In particular, the impact of COVID-19 on road traffic safety in Los Angeles and New York was examined. Results indicated that the pandemic has disproportionately affected certain age groups and that nonfatal road crashes decreased, while the number of fatal crash cases remained the same during the pandemic (Lin et al., 2020).
8. Conclusions
This paper presented an investigative approach to quantify the impact of the COVID-19 pandemic on driving behavior using naturalistic driving data obtained from smartphone sensors and time series forecasting in Greece. The evaluation of the impact of COVID-19 was based on the comparison between observed values for three driving indicators (i.e., speed, speeding, and harsh braking) and forecasts based on the period before the coronavirus spread. Methodologically, the influence of COVID-19 was initially evaluated with explanatory XGBoost feature importance and was primarily modelled using seasonal ARIMA models, which have been a popular choice for transportation-related forecasting.
Results demonstrated the magnitude of the impact due to the COVID-19 lockdown, as it was observed that the “natural evolution” of the three aforementioned indicators was forecasted with major differences compared to the actual observations. Measurements regarding speed were the ones demonstrating the larger difference. The most reliable forecasting model for speed demonstrated that speeds increased by 2.27 km/h on average and up to 7.5 km/h on a national holiday day during the lockdown. Furthermore, the increase in speeds also assisted in manifesting an increase in harsh braking/100 km, which is supported by recent literature. The number of road crashes and road traffic fatalities and injuries decreased during the COVID-19 period (i.e., from March to April 2020), compared to non-COVID-19 period (i.e., from January to February 2020).
Nevertheless, this paper is not without shortcomings. The developed models for speeding have limitations and do not seem to capture the trend and seasonality of the original time series effectively. More sophisticated models, such as deep neural networks (e.g., Convolutional Neural Networks (CNNs) or Long Short-Term Memory Networks (LSTMs)) could have a better fit on the time series data and provide better forecasts. Furthermore, rates for harsh acceleration events per km were not found statistically significant in this work, but the aforementioned sophisticated models could succeed in forecasting using these variables as well.
Future research should initially concentrate on comparing COVID-19 driving indicators from different countries so as to compare and contrast different effects. Furthermore, the development of more sophisticated models (as those mentioned in the previous paragraph), as well as multivariate forecasting models using Vector AutoRegression (VAR) in order to capture the interdependencies between time series should provide more insights on the impact of COVID-19 on driving behavior. Finally, more driving behavior indicator time series, such as the use of mobile phone during driving or aggressiveness levels, would also assist in quantifying the effects of lockdown on driving.
Acknowledgements
The authors would like to thank OSeven Telematics, London, UK for providing all necessary data exploited to accomplish this study.
Biographies
Dr. Christos Katrakazas is a Research Associate at the Department of Transportation Planning and Engineering at the School of Civil Engineering of the National Technical University of Athens (NTUA). He holds a Civil Engineering Diploma from NTUA majoring in Transportation Engineering (2013) and a Ph.D. in safety of autonomous vehicles from Loughborough University (2017). After finishing his doctoral studies, he worked as a Research Associate at Loughborough University, and the Chair of Transportation Systems Engineering at the Technical University of Munich (TUM), Germany. He has more than 6 years of experience in several aspects of transport safety and engineering.
Ms. Eva Michelaraki is a Civil Engineer, PhD Candidate and Researcher at the Department of Transportation Planning and Engineering at the School of Civil Engineering of the National Technical University of Athens (NTUA). Since 2019, she holds a Civil Engineering Diploma from NTUA majoring in Transportation Engineering. She is pursuing her Doctoral Thesis, entitled: “Road accident risk factors and big data“. She has more than 1 year of experience in several aspects of traffic engineering and road safety. The current focus of her work lies on driver behaviour, crash and statistical analysis and modeling. She has participated in 2 research projects and has published two (2) scientific papers (one (1) in scientific journal and one (1) in scientific conference proceedings after peer review).
Mr. Marios Sekadakis is a Civil – Transportation Engineer and Research Associate at the Department of Transportation Planning and Engineering at the School of Civil Engineering of the National Technical University of Athens (NTUA). Since 2020, he holds a Civil Engineering Diploma from NTUA, majoring in Transportation Engineering.
Dr. Apostolos Ziakopoulos, PhD, MSc DIC is a Research Associate at the Department of Transportation Planning and Engineering at the School of Civil Engineering of the National Technical University of Athens (NTUA). He holds a Civil Engineering Diploma from NTUA majoring in Transportation Engineering (2013). He also holds a Master of Science – DIC in Transport from Imperial College London and University College London (2014). His Ph.D. dissertation was in spatial analysis of road safety and traffic behavior from NTUA (2020). He has worked as a researcher for the University of Sheffield through the I.A.E.S.T.E. scheme. His main research interests involve road crash analyses, statistical and spatial modelling and traffic engineering. He has participated in 7 research and engineering projects and studies and has published 39 papers in scientific journals, textbooks and conferences.
Ms. Armira Kontaxi is a Ph.D. Candidate and Researcher at the Department of Transportation Planning and Engineering at the School of Civil Engineering of National Technical University of Athens. Since 2017, she holds a Civil Engineering Diploma from NTUA, majored in Transportation Engineering. She is pursuing her Doctoral Thesis, entitled: “Integrated support of driver traffic behaviour and safety by smartphone data”. Her research primarily involves data analysis and statistical modelling in the field of traffic behaviour and safety.
Prof. George Yannis is a Professor in Traffic Safety and Management with particular focus on data management and analysis and currently Director of the Department of Transportation Planning and Engineering of the School of Civil Engineering at the NTUA. He has contributed extensively in more than 245 research and engineering projects and studies and in several scientific committees of the European Commission and other International Organizations (UN/ECE, OECD, WHO, World Bank, EIB, CEDR, ERF, UITP, ETSC, ECTRI, WCTR, TRB). He has published more than 560 scientific papers (169 in scientific journals) widely cited worldwide.
References
- Aloi A., Alonso B., Benavente J., Cordera R., Echániz E., González F., et al. Effects of the COVID-19 lockdown on urban mobility: Empirical evidence from the City of Santander (Spain) Sustainability. 2020;12(9):3870. doi: 10.3390/su12093870. [DOI] [Google Scholar]
- Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apple. (2020). COVID‑19 - Mobility Trends Reports - Apple [WWW Document]. Accessed 11/06/20. https://www.apple.com/covid19/mobility.
- Barnes, S. R., Beland, L. P., Huh, J., & Kim, D. (2020). The effect of COVID-19 lockdown on mobility and traffic accidents: Evidence from Louisiana (No. 616). GLO Discussion Paper.
- Bischl B., Lang M., Kotthoff L., Schiffner J., Richter J., Studerus E., et al. mlr: Machine Learning in R. The Journal of Machine Learning Research. 2016;17(1):5938–5942. [Google Scholar]
- Bisgaard S., Kulahci M. Wiley & Sons; 2011. Time series analysis and forecasting by example. [Google Scholar]
- Box, G. E., & Jenkins, G. M. (1976). Time series analysis: Forecasting and control San Francisco. 1970, 1989.
- Breiman L. Random forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]
- Brodeur, A., Cook, N., & Wright, T. (2020). On the effects of COVID-19 safer-at-home policies on social distancing, Car Crashes and Pollution. [DOI] [PMC free article] [PubMed]
- Budd L., Ison S. Responsible transport: A post-COVID agenda for transport policy and practice. Transportation Research Interdisciplinary Perspectives. 2020;6:100151. doi: 10.1016/j.trip.2020.100151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter, D. (2020) Effects of COVID-19 shutdown on crashes and travel in North Carolina. North Carolina Department of Transportation. Transportation Research Board: Traffic Trends and Safety in a COVID-19 World webinar: https://vimeo. com/425250264 Accessed 05/01/21.
- Chen, T., & Guestrin, C. (2016, August). Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785-794).
- Cheng Z.J., Shan J. 2019 Novel coronavirus: Where we are and what we know. Infection. 2020;48(2):155–163. doi: 10.1007/s15010-020-01401-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung, E., & Rosalion, N. (2001). Short term traffic flow prediction. Proceedings of the 24th Australian Transportation Research Forum, Hobart, Tasmania.
- City of Toronto, 2020. City of Toronto Urges Drivers to Obey Rules of the Road. 2020 November 3, https://www.toronto.ca/news/city-of-toronto-urges-drivers-to-obey-rules-of-the-road/.
- de Haas M., Faber R., Hamersma M. How COVID-19 and the Dutch ‘intelligent lockdown’ change activities, work and travel behaviour: Evidence from longitudinal data in the Netherlands. Transportation Research Interdisciplinary Perspectives. 2020;6:100150. doi: 10.1016/j.trip.2020.100150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Vos J. The effect of COVID-19 and subsequent social distancing on travel behaviour. Transportation Research Interdisciplinary Perspectives. 2020;5 doi: 10.1016/j.trip.2020.100121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dettling, M. (2018). Applied Time Series Analysis - Lecture notes SS 2018.
- Dickey D.A., Fuller W.A. Distribution of the estimators for autoregressive time series with a Unit Root. Journal of the American Statistical Association. 1979;74(366a):427–431. doi: 10.1080/01621459.1979.10482531. [DOI] [Google Scholar]
- DW. (2020). Germany: Traffic deaths fall to lowest point since reunification. https://www.dw.com/en/germany-traffic-deaths-fall-to-lowest-point-since-reunification/a-53556709.
- Essi, I. D. (2018). Seasonal autoregressive integrated moving average (SARIMA) modelling and forecasting of inflation rates in Nigerian (2003-2016). 4(1), 1–14.
- ETSC. (2020). COVID-19: Huge drop in traffic in Europe, but impact on road deaths unclear. https://etsc.eu/covid-19-huge-drop-in-traffic-in-europe-but-impact-on-road-deaths-unclear/.
- Ghosh, B., Basu, B., & O’Mahony, M. (2005). Time-series modelling for forecasting vehicular traffic flow in Dublin. 85th Annual Meeting of the …, 12(00353), 1–22. https://doi.org/10.1109/JPHOTOV.2015.2434597.
- Google LLC. (2020). Google COVID-19 Community Mobility Reports [WWW Document]. Accessed 11/06/20. https://www.google.com/covid19/mobility/.
- Hellenic Statistical Authority Road traffic accidents - Monthly/October 2020. 2021. https://www.statistics.gr/en/statistics/-/publication/SDT03/- Accessed 05/01/21. Retrieved from.
- Hendrickson C., Rilett L.R. The COVID-19 pandemic and transportation engineering. Journal of Transportation Engineering Part A: Systems. 2020;146(7):1–2. doi: 10.1061/JTEPBS.0000418. [DOI] [Google Scholar]
- Hipel, K., & McLeod, A. (1994). Chapter 12 seasonal autoregressive integrated moving average models. Developments in Water Science, 45.
- Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
- Hyndman, R. J., & Khandakar, Y. (2007). Automatic time series forecasting : the forecast package for R Automatic time series forecasting : the forecast package for R. June.
- Hyndman, R. J., Athanasopoulos, G., Bergmeir, C., Caceres, G., Chhay, L., O'Hara-Wild, M., & Wang, E. (2020). Package ‘forecast’. Online] https://cran. r-project. org/web/packages/forecast/forecast. pdf.
- Inada H., Ashraf L., Campbell S. COVID-19 lockdown and fatal motor vehicle collisions due to speed-related traffic violations in Japan: A time-series study. Injury Prevention. 2020;27(1):98–100. doi: 10.1136/injuryprev-2020-043947. [DOI] [PubMed] [Google Scholar]
- Karlaftis, M. G., & Vlahogianni, E. I. (2009). Memory properties and fractional integration in transportation time-series. 17, 444–453. https://doi.org/10.1016/j.trc.2009.03.001.
- Katrakazas C., Michelaraki E., Sekadakis M., Yannis G. A descriptive analysis of the effect of the COVID-19 pandemic on driving behavior and road safety. Transportation Research Interdisciplinary Perspectives. 2020;7:100186. doi: 10.1016/j.trip.2020.100186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S.V., Vanajakshi L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. European Transport Research Review. 2015;7(3):1–9. doi: 10.1007/s12544-015-0170-8. [DOI] [Google Scholar]
- Lau H., Khosrawipour V., Kocbach P., Mikolajczyk A., Schubert J., Bania J., et al. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. Journal of Travel Medicine. 2020;March:1–7. doi: 10.1093/jtm/taaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, J., Porr, A., & Miller, H. (2020). Evidence of Increased Vehicle Speeding in Ohio’s Major Cities during the COVID-19 Pandemic.
- Lin, L., Shi, F., & Li, W. (2020). Assessing road traffic safety under COVID-19: Inequality, irregularity, and severity. arXiv preprint arXiv:2011.02289. [DOI] [PMC free article] [PubMed]
- Lippi M., Bertini M., Frasconi P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Transactions on Intelligent Transportation Systems. 2013;14(2):871–882. doi: 10.1109/TITS.2013.2247040. [DOI] [Google Scholar]
- Ljung G.M., Box G.E.P. On a measure of lack of fit in time series models. Biometrika. 1978;65(2):297–303. doi: 10.1093/biomet/65.2.297. [DOI] [Google Scholar]
- Ma T., Antoniou C., Toledo T. Hybrid machine learning algorithm and statistical time series model for network-wide traffic forecast. Transportation Research Part C: Emerging Technologies. 2020;111(January):352–372. doi: 10.1016/j.trc.2019.12.022. [DOI] [Google Scholar]
- Ma, T., Zhou, Z., & Antoniou, C. (2018). Dynamic factor model for network traffic state forecast. 118, 281–317. https://doi.org/10.1016/j.trb.2018.10.018.
- Mogaji E. Impact of COVID-19 on transportation in Lagos, Nigeria. Transportation Research Interdisciplinary Perspectives. 2020;6:100154. doi: 10.1016/j.trip.2020.100154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molloy, J. (2020). MOBIS Covid19 Mobility Report.
- Moovit. (2020). Impact of coronavirus (COVID-19) on public transit usage. Accessed 11/06/20. https://moovitapp.com/insights/en/Moovit_Insights_Public_Transit_Index-countries.
- Neuburger L., Egger R. Travel risk perception and travel behaviour during the COVID-19 pandemic 2020: A case study of the DACH region. Current Issues in Tourism. 2020:1–14. [Google Scholar]
- Nielsen, D. (2016). Tree boosting with xgboost-why does xgboost win“ every” machine learning competition? (Master's thesis, NTNU).
- Papadimitriou E., Argyropoulou A., Tselentis D.I., Yannis G. Analysis of driver behaviour through smartphone data: The case of mobile phone use while driving. Safety Science. 2019;119(May):91–97. doi: 10.1016/j.ssci.2019.05.059. [DOI] [Google Scholar]
- Petraki, V., Ziakopoulos, A., & Yannis, G. (2020). Combined impact of road and traffic characteristic on driver behaviour using smartphone sensor data. Accident Analysis & Prevention, 144(November 2019), 105657. https://doi.org/10.1016/j.aap.2020.105657. [DOI] [PubMed]
- R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2019. R: A language and environment for statistical computing. URL: https://www.R-project.org/ [Google Scholar]
- Roe C.M., Rosnick C.B., Colletta A., Babulal G.M. Reaction to a pandemic: Social distancing and driving among older adults during COVID-19. Journal of Applied Gerontology. 2020 doi: 10.1177/0733464820966516. 0733464820966516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, T. G. et al. (2017). ARIMA estimators for Python. Http://Www.Alkaline-Ml.Com/Pmdarima.
- Stavrakaki A.M., Tselentis D.I., Barmpounakis E., Vlahogianni E.I., Yannis G. Estimating the necessary amount of driving data for assessing driving behaviour. Sensors (Switzerland) 2020;20(9) doi: 10.3390/s20092600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stavrinos D., McManus B., Mrug S., He H., Gresham B., Albright M.G., et al. Adolescent driving behavior before and during restrictions related to COVID-19. Accident Analysis & Prevention. 2020;144:105686. doi: 10.1016/j.aap.2020.105686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting, C. Y., Tan, N. Y. Z., Hashim, H. H., Ho, C. C., & Shabadin, A. (2020). Malaysian road accident severity: Variables and predictive models. In Computational science and technology (pp. 699-708). Springer, Singapore.
- TomTom. (2020). COVID-19 response | TomTom [WWW Document]. https://www.tomtom.com/covid-19/.
- Tselentis, D. I., Vlahogianni, E. I., & Yannis, G. (2019). Driving safety efficiency benchmarking using smartphone data. Transportation Research Part C: Emerging Technologies, 109(June 2018), 343–357. https://doi.org/10.1016/j.trc.2019.11.006.
- Vingilis E., Beirness D., Boase P., Byrne P., Johnson J., Jonah B., et al. Coronavirus disease 2019: What could be the effects on road safety? Accident Analysis & Prevention. 2020;144:105687. doi: 10.1016/j.aap.2020.105687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, W., Baumann, M., & Jiang, X. (Eds.). (2020). Green, smart and connected transportation systems: Proceedings of the 9th international conference on green intelligent transportation systems and safety (Vol. 617). Springer Nature.
- Wang X., Smith K., Hyndman R. Characteristic-based clustering for time series data. Data Mining and Knowledge Discovery. 2006;13(3):335–364. [Google Scholar]
- Wagner, E., Atkins, R. G., Berning, A., Robbins, A., Watson, C., & Anderle, J. (2020). Examination of the traffic safety environment during the second quarter of 2020: Special Report (No. DOT HS 813 011). United States. National Highway Traffic Safety Administration. Office of Behavioral Safety Research.
- World Health Organization. (2020). Corona Virus 2019. https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
- Williams B.M. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results article. Journal of Transportation Engineering. 2003;129(6) [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. The Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- XGBoost developer team (2019). XGBoost Documentation. Official website. Available from: https://xgboost.readthedocs.io/en/latest/index.html [Accessed 20/06/2020].
- Zhang, D., Hu, M., & Ji, Q. (2020). Financial markets under the global pandemic of COVID-19. Finance Research Letters, April, 101528. https://doi.org/10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed]
- Zhang, L., Ghader, S., Pack, M. L., Xiong, C., Darzi, A., Yang, M., & Hu, S. (2020). An interactive COVID-19 mobility impact and social distancing analysis platform. medRxiv. [DOI] [PMC free article] [PubMed]
- Ziakopoulos A., Tselentis D., Kontaxi A., Yannis G. A critical overview of driver recording tools. Journal of Safety Research. 2020;72:203–212. doi: 10.1016/j.jsr.2019.12.021. [DOI] [PubMed] [Google Scholar]