Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Sep 1;13(36):43615–43621. doi: 10.1021/acsami.1c11245

Boosted Solar Light Absorbance in PdS2/PtS2 Vertical Heterostructures for Ultrathin Photovoltaic Devices

Lorenzo Bastonero †,⊥, Giancarlo Cicero ‡, Maurizia Palummo §, Michele Re Fiorentin ∥,*
PMCID: PMC8447185  PMID: 34468121

Abstract

graphic file with name am1c11245_0007.jpg

Transition-metal dichalcogenides (TMDs) represent a class of materials whose archetypes, such as MoS2 and WS2, possess exceptional electronic and optical properties and have been massively exploited in optoelectronic applications. The layered structure allows for their exfoliation to two-dimensional samples with atomic thickness (≲ 1 nm), promising for ultrathin, ultralight devices. In this work, by means of state-of-the-art ab initio many-body perturbation theory techniques, we focus on single-layer PdS2 and PtS2 and propose a novel van der Waals heterostructure with outstanding light absorbance, reaching up to 50% in the visible spectrum and yielding a maximum short-circuit current of 7.2 mA/cm2 under solar irradiation. The computed excitonic landscape predicts a partial charge separation between the two layers and the momentum-forbidden lowest-energy state increases the carrier diffusion length. Our results show that the employment of vertical heterostructures with less conventional TMDs, such as PdS2/PtS2, can greatly boost light absorbance and favor the development of more efficient, atomic-thin photovoltaic devices.

Keywords: photovoltaics, TMDs, van der Waals heterostructures, 2D materials, excitons

1. Introduction

Two-dimensional (2D) materials have elicited great attention over the last few decades thanks to their unique electronic and optical properties induced by their atomic-scale thickness.1−3 A plethora of materials are currently under investigation, and particular interest has been focused on transition-metal dichalcogenides (TMDs) in their monolayer form. TMDs can be easily exfoliated to single layers and allow for largely tunable optoelectronic properties,4,5 thanks to the plentiful possible combinations of transition metal and chalcogen species. For instance, band gaps of monolayer TMDs range from 0.5 to 7.0 eV6 and can be both direct and indirect. This wide range of electronic properties can be further enriched by devising vertical van der Waals heterostructures (vdWHs)7,8 between a monolayer TMD and another 2D material, such as graphene,9,10 black or blue phosphorene,11,12 hexagonal boron nitride,13,14 or a different TMD monolayer.15,16 vdWHs make it possible to realize devices that allow for the separation of the optically excited electrons and holes thanks to the valence and conduction band discontinuities of the two composing layers. Together with nanometer thickness and suitable band gaps, this feature makes TMD vdWHs appealing for the design of ultrathin, ultralight photovoltaic devices.17 In this respect, it is therefore necessary that the composing layers show significant light absorbance within the solar spectrum. For photon energies varying between 1.5 and 3 eV, widely studied TMDs show absorbance values that roughly range from 5 to 25% for MoS218 to 20% for MoSe2 or 17% for WSe2 and WS2.19 Their vdWHs exhibit similar behaviors, for instance, reaching peak values of 10% in MoS2/WS220 and in MoSe2/WSe2 or 15% in MoS2/WSe2.21 In combination with the incident AM1.5G solar flux Φs(ω),22 the absorbance Abs(ω) determines the maximum short-circuit current that can be extracted from the solar cell as

1. 1

assuming that all photogenerated charge carriers are collected. Common amorphous Si–H and GaAs solar cells in a single-pass configuration show Jscmax values which lie around 25 and 35 mA/cm2, for sample thicknesses above 1 μm, and quickly drop much below 1 mA/cm2 when their thickness is decreased to around 1 nm.23 In contrast, it has been predicted that a 1 nm-thick MoS2/WS2 vdWH displays a Jsc ≃ 3.5 mA/cm2,20 the same value obtained in Si–H or GaAs cells about 1 order of magnitude thicker. The nanoscale thickness of the heterostructure allows for the design of ultralight devices with high power densities,24 even though the Jscmax remains low on an absolute scale. Higher short-circuit currents can be obtained by suitable arrangements of multiple heterostructures, albeit at the expense of the overall device thinness. Increasing the absorbance of the heterostructure, while keeping its thickness within ∼1 nm, is then of key importance for the development of new nanoscale photovoltaic devices that can introduce a paradigm shift in solar energy harvesting.

In this work, we focus on two less-studied single-layer TMDs which hold great potential, both as distinct monolayers and as part of a vdWH: PdS2 and PtS2. Single-layer PtS2 has been experimentally obtained from bulk PtS225,26via exfoliation27,28 and reported to be in the 1T phase, Figure 1b. Monolayer PdS2 has been investigated in its 1T phase,29Figure 1a, and its exfoliation process from bulk crystals has been suggested.30 The lattice parameters and electronic properties of 1T-PtS2 and 1T-PdS2, as reported in the literature,6 suggest the possibility of realizing a low-strain vdWH with type-II band alignment. We therefore propose and investigate a novel 1T-PdS2/1T-PtS2 vdWH by employing state-of-the-art ab initio simulations, based on density functional theory (DFT) for geometry optimization and the GW-Bethe Salpeter31,32 approach for the study of optoelectronic properties.

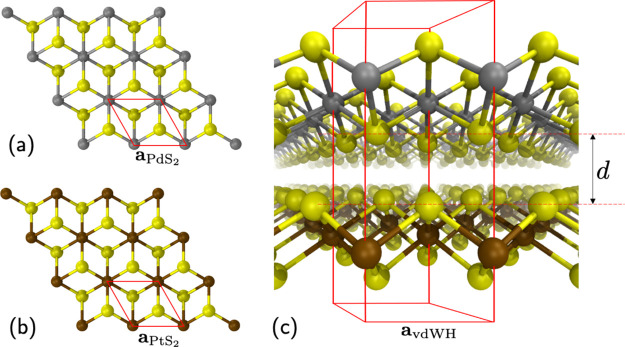
Figure 1.

Figure 1

Open in a new tab

Monolayer PdS2 (a) and PtS2 (b) in the 1T phase. (c) Perspective view of the PdS2/PtS2 heterostructure with marked unit cell and lattice parameter avdW and layer separation d.

2. Methods

2.1. DFT Calculations

All the DFT calculations reported in this work were performed using the Quantum ESPRESSO suite.33−35 For all systems, we employed the Perdew–Burke–Ernzerhof functional36 and fully relativistic, norm-conserving pseudopotentials37 on a uniform 4 × 4 × 1 Monkhorst–Pack k-point mesh.38 A kinetic energy cutoff of 70 Ry was adopted. We introduced a 20 Å vacuum region along z, the direction perpendicular to the layer planes, to ensure the decoupling of the periodic replicas. In the studied systems, spin–orbit coupling effects can be sizeable and were accounted for in all calculations by means of a fully spinorial treatment.39,40 Dispersion forces between the layers of the heterostructure were reproduced within the DFT-D3 semiempirical model.41 Structure relaxation was assumed at convergence when the maximum component of the residual forces on the ions was smaller than 10–4 Ry/Bohr.

2.2. Many-Body Perturbation Theory Calculations

The optimized structures were studied by means of many-body perturbation theory methods as implemented in the YAMBO code.42,43 The quasiparticle (QP) electronic structure was obtained within the non-self-consistent G0W0 approximation. A box cutoff along z was applied on the bare Coulomb potential. The inverse dielectric matrix, εGG′–1, was obtained within the Godby-Needs plasmon-pole approximation model.44,45 As a convergence parameter, we adopted the QP band gap value at the Γ point and deemed satisfactory a convergence of this value within 50 meV. Convergence of the G0W0 calculations with respect to the simulation parameters is shown in Figure S1 in Supporting Information. Following the chosen convergence criterion, we chose a 20 × 20 × 1 k-point mesh for all structures.

For both PdS2 and PtS2, 2000 bands were included in the calculation of the dielectric function εGG′–1 and a 20 Ry cutoff was set on the G vectors in ε–1.

Following ref6, we obtain the correction to the band gap due to the number of bands included in the correlation self-energy Σc by extrapolation to the limit of infinite bands, cf. Supporting Information, Figure S1c. For PdS2 and PtS2 monolayers, the calculations can then be performed with 1000 bands explicitly included in the sum and then corrected by the application of a rigid scissor operator of −0.12 eV. For the vdWH, we employ 4000 bands and 20 Ry in the calculation of the dielectric matrix and 1000 bands in Σc, thanks to the adoption of Bruneval–Gonze terminators.46

Convergence of the BSE calculations with respect to the simulation parameters is shown in Figure S2 in Supporting Information. For PdS2 and PtS2, convergence is reached on a 30 × 30 × 1 grid, with 200 bands and a 2 Ry cutoff on the static screening and 6 valence +6 conduction bands in the BSE kernel. In the case of the vdWH, the number of included bands is doubled.

3. Results and Discussion

From our DFT calculations, we compute the equilibrium lattice parameters of the isolated monolayers to be aPdS2 = 3.53 Å for 1T-PdS2 and aPtS2 = 3.56 Å for 1T-PtS2, in excellent agreement with the literature.47 By vertically stacking the two monolayers in the AA configuration,48 we obtain the vdWH geometry represented in Figure 1c, whose equilibrium lattice parameter results in avdWH = 3.57 Å and interlayer distance in d = 2.4 Å. The increase in the lattice parameter in the heterostructure can be traced back to the interaction between the layers and the reduced screening, as happens for multilayers of both PdS2 and PtS2.49,50 The resulting strain can be estimated as εi = (avdWH – ai)/ai with i = PtS2 and PdS2. The highest value of ε is obtained for the PdS2 layer, which is subject to about 1.1% tensile strain with respect to its equilibrium geometry. Hence, the monolayers undergo a very mild strain, which does not significantly affect the electronic properties of the system (c.f. Figure S3a in Supporting Information). The equilibrium geometries of the isolated monolayers and the vdWH are used to compute the electronic band structure at the G0W0 level, as reported in Figure 2. On top of the G0W0 quasiparticle energies, we solve the Bethe–Salpeter equation to obtain the light absorption spectrum and excitonic properties, Figure 3. 1T-PdS2, Figure 2a, presents a top valence band (tVB) with a flattened parabolic structure around the Γ point and a conduction band minimum (CBm) at a k-point intermediate between M and Γ, resulting in an indirect band gap 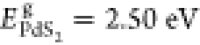Inline graphic and a direct gap 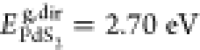Inline graphic in correspondence with the CBm. The optical absorbance Abs(ω) is shown in Figure 3a, together with the lowest-energy exciton (blue) and the two brightest states (red and green) contributing to the absorption peak. Their energies and binding energies are reported in Table 1. The shaded areas in Figure 2a mark the excitonic weights of excitons B (blue), G (green), and R (red), projected on the QP band structure. From the shaded regions in Figure 2a, it is possible to notice that the strongest transitions contributing to the excitons, rather than occurring at high symmetry points, take place at k-points at which the valence and conduction bands present a similar slope along the k-path, giving rise to the band-nesting phenomenon.51 This feature is responsible for large divergencies in the joint density of states (jDOS) which, in turn, influences the material dielectric function, enhancing light absorption. We notice that the absorption peak of monolayer 1T-PdS2 falls around 2 eV and, remarkably, its absorbance reaches up to 55% in that range.

Figure 2.

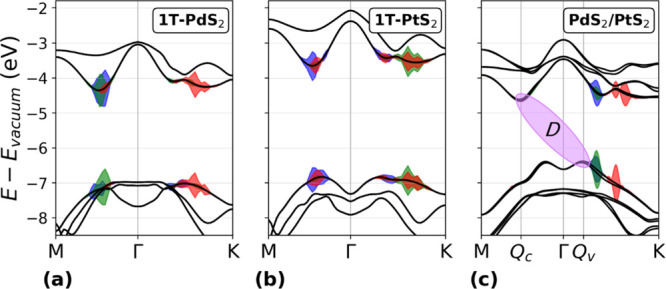
Figure 2

Open in a new tab

G0W0 band structures of (a) 1T-PdS2, (b) 1T-PtS2, and (c) PdS2/PtS2 vdWH aligned to the vacuum level. The shaded areas in red, green, and blue mark the excitonic weights of the R, G, and B states, respectively (see Figure 3). The violet ellipse in (c) indicates the indirect exciton D with finite momentum qD.

Figure 3.

Figure 3

Open in a new tab

Absorbance Abs(ω) of (a) 1T-PdS2, (b) 1T-PtS2, and (c) PdS2/PtS2 vdWH. The vertical bars mark the position and relative intensities of the R, G, and B excitons, respectively. In (c), the AM1.5G solar spectrum Φs(ω) is reported in light yellow.

Table 1. Transition Energies Eλ [eV] and Exciton Binding Energies Eb [eV] of the Analyzed Excitons (B = Blue; R = Red; and G = Green).

  1T-PdS2
 1T-PtS2
 1T-PdS2/1T-PtS2
  B G R B G R B G R
Eλ 1.91 1.95 2.04 2.20 2.48 2.49 1.49 1.53 2.11
Eb 0.8 0.8 0.7 0.9 0.6 0.6 0.7 0.6 0.1
Open in a new tab

1T-PtS2, Figure 2b, shows a peculiar Mexican-hat-shaped tVB, with a valence band maximum (VBM) and CBm midway between M and Γ. Although VBM and CBm are closer in k-space, the resulting band gap is nonetheless indirect, 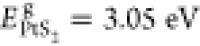Inline graphic, while the direct gap is 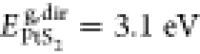Inline graphic. The absorbance spectrum, Figure 3b, is blue-shifted with respect to 1T-PdS2: the absorption peak is due to two excitons (green and red), at around 2.5 eV, and a dark exciton (blue) is the lowest-energy state, about 30 meV below. The peak in absorbance of PtS2 is lower than the one of PdS2 and reaches about 30%. Such a difference in absorbance can be traced back to the different orbital character of the electronic states in the tVB and bCB of the two monolayers. In PdS2, we observe a sizeable participation of sulfur p orbitals in the tVB states, in contrast to PtS2, where S p and Pt d orbitals are almost equally contributing to the topmost valence band (c.f. Supporting Information Figures S4 and S5). The difference in the orbital character results in a stronger band-nesting for PdS2 which, consequently, increases the jDOS, as shown in Figure S6a,b. Moreover, we determined that the independent-particle electric dipole matrix elements dcvk of the transitions v → c at k, contributing to the absorption peak, are larger in PdS2 than in PtS2, c.f. Figure S6c. The larger jDOS and the stronger dipole elements thus cooperate to enhance the optical absorption of PdS2 with respect to PtS2.

In Figure 3b, at around 2.8 eV, it is also possible to notice a broader peak in the absorbance spectrum, originating from states, close in energy, whose main dipole transitions involve the bCB and tVB-1.

Although less pronounced than in PdS2, the contribution from the p-orbitals of the outer S layers to the tVB of PtS2 is non-negligible, Figure S4. Therefore, in a vdWH, the tVB of each monolayer is significantly affected by the presence of the facing one, resulting in a vdWH tVB which shows sizeable contributions from both PdS2 and PtS2 valence band states. In Figure 4, we show the k-resolved density of states (DOS) of the 1T-PdS2/1T-PtS2 heterostructure, projected on the orbitals of the atoms composing the two layers. The bands along the k-path are colored according to the difference between the DOS contributions from the two layers, allowing us to identify on which layer the electronic states at various k-points are spatially localized. As mentioned, the vdWH tVB shows some degree of delocalization on both layers, while the bCB, being mostly composed of inner metal d-orbitals, is less affected by the interlayer interactions and clearly localized on 1T-PdS2. The G0W0-corrected band structure, aligned to the vacuum level, is reported in Figure 2c. In contrast to the isolated monolayers, in the vdWH case, the inversion symmetry is broken; hence, its band structure shows spin–orbit splitting. The band gap is indirect, EvdWHg = 1.72 eV, between k-points Qc and Qv, and notably smaller than each monolayer’s. The direct band gap is found to be EvdWH = 2.17 eV in correspondence with Qv. The electronic band gap reduction is an expected feature linked to the type-II alignment of the single TMD band structures, cf. Figure 2a,b, and the interaction between the two layers, which determines an upshift of the top valence band, and the increased electronic screening. This similarly entails a reduction in the optical band gap, as shown in Figure 3c. The absorption onset red-shifts to about 1.5 eV and stems from a bright exciton (labeled “green”, G) at 1.53 eV, c.f. Table 1. This exciton is almost degenerate in energy with the lowest-energy, dark state (blue, B), whose constituting transitions take place at the same k-points as the green exciton but connect states with the opposite spin.

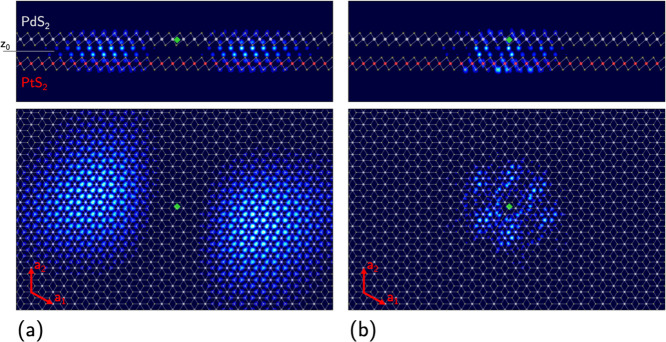
Figure 4.

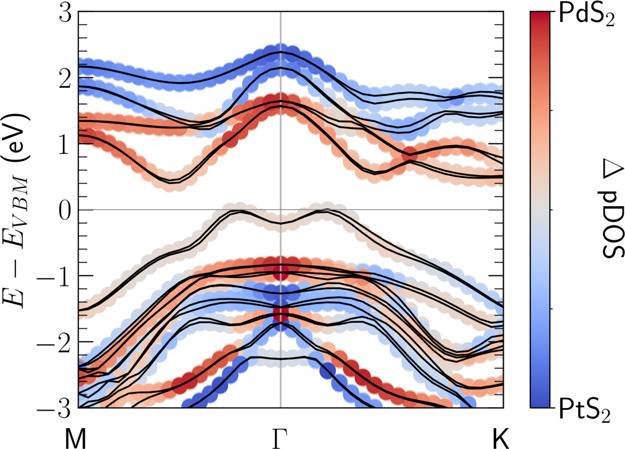
Figure 4

Open in a new tab

1T-PdS2/1T-PtS2 vdWH k-resolved projected density of states superimposed to the DFT band structure. Each state is colored according to the size of the contributions from PdS2 (red) and PtS2 (blue) orbitals.

By means of eq 1 and the absorbance spectra in Figure 3, we can compute the maximum short-circuit currents that can be extracted from the monolayers and from the vdWH, in the idealized situation of total carrier collection at the electrodes. 1T-PtS2 has a higher-energy absorption edge and a moderate absorption, resulting in Jscmax = 1.9 mA/cm2, while 1T-PdS2 shows a lower absorption onset and outstanding absorbance values so that its maximum short-circuit current reaches 5.4 mA/cm2. The vdWH shows less pronounced absorbance peaks than 1T-PdS2; however, the optical gap falls at lower energy, optimizing sunlight absorption in the visible range. Hence, the short-circuit current of the heterostructure reaches 7.2 mA/cm2, slightly lower than the sum of the Jsc of the isolated monolayers. The predicted value of maximum short-circuit current is exceptionally high and can largely boost the efficiency of a device made with such a vdWH. As a comparison, the obtained maximum short-circuit current is twice the predicted value in MoS2/WS2 vdWH20 and can be obtained with amorphous Si–H samples about 2 orders of magnitude thicker.

The brightest excitons, red and green, which induce the peaks in the absorption spectrum of the vdWH, vertically excite electrons and holes at k-points away from the CBm and VBM, respectively. In mono- and few-layer TMDs, intraband relaxation is very fast (≲500 fs);52,53 therefore, we can expect a rapid relaxation of the optically active excitons to the dark, indirect exciton D, involving states at the CBm and VBM, violet ellipse in Figure 2c. The relaxation to this exciton, with finite momentum qD = Qc – Qv, is energetically favorable, since ED = 1.15 eV, smaller than the dark direct exciton B. Being momentum-forbidden, the radiative recombination of state D is suppressed and, consequently, its lifetime is largely enhanced with respect to bright excitons.54 Electron–hole recombination is therefore slowed down, and the carrier diffusion length increased. Hence, due to the indirect gap in the 1T-PdS2/1T-PdS2 heterostructure, we expect carrier diffusion lengths longer than 20 μm, as recently measured in the direct-gap WS2/WSe2 vdWH.55 The expected sizeable diffusion length will then contribute to enhance the actual short-circuit current of the real device, by increasing the collection probability, thus positively impacting on the efficiency of the cell. These efficiency boosting factors, that is, very large absorbance and increased diffusion length, can then counterbalance the limited charge separation due to the mixed PdS2–PtS2 states in the tVB, c.f. Figure 4, that could also act as recombination centers. Indeed, the optically excited electrons will populate states which are well spatially localized on the PdS2 layer, while the holes will still present a sizeable delocalization on both monolayers. In Figure 5a, we show the square modulus of the D exciton wave function as a function of the hole position |ΨD(rh|re = r′)|2, when the electron is fixed at r′ on the PdS2 layer, in a region with maximum probability density. The electron is marked by the green diamond on the PdS2 layer. The electron and hole show a peculiar in-plane spatial separation, due to the electronic orbitals involved in D. As a comparison, in Figure 5b, we report the square modulus of the bright, G exciton wave function, with fixed electron in the same position. It is evident that the G and D excitons are not spatially indirect between the two layers, and their wave functions involve both PdS2 and PtS2. From Figure 5a, it is possible to notice that the hole is fairly delocalized on both layers and it is possible to obtain the probability of finding the hole on the PtS2 layer as ∫zh<z0drh|ΨD(rh|re = r′)|2 ≃ 50%, where z0 defines the intermediate plane between the two monolayers. This provides us with an estimate of the charge separation probability, given that the hole distribution varies little when the electron position is moved in the region of sizeable probability density, concentrated on PdS2. The estimated charge separation is not complete, however, its magnitude, combined with the encouraging properties previously highlighted, can be nonetheless adequate for viable applications of the proposed vdWH. Moreover, it has been proven that spatially indirect excitons inducing interlayer charge separation can be enhanced by applying strain56,57 to the heterostructure or controlled through electric fields,58 thus conceivably leaving room for further efficiency improvements.

Figure 5.

Figure 5

Open in a new tab

Side (upper panels) and top (lower panels) views of the square modulus excitonic wave function |Ψλ(rh|re = r′)|2 for states λ = D (a) and λ = G (b). In both (a,b), the electron is marked by the green diamond and kept fixed on PdS2.

4. Conclusions

The field of nanoscale photovoltaic devices is still in open development and appears alluring for its potential to compete with conventional systems. The intrinsic advantages of ultrathin, ultralight devices urge the research activities toward improved efficiency and design. The employment of monolayer TMDs in heterostructures has been proposed and investigated, with most attention paid to group-VI TMDs, such as MoS2 and WS2, which have provided encouraging results. A key factor for choosing TMDs for this type of application resides in their large light-electron coupling, which results in sizeable light absorbance. Our work unveiled the remarkable properties of two, less common, TMDs, PdS2 and PtS2, which can be positively employed in the domain of photovoltaics. In particular, the uncommon absorbance of 1T-PdS2 is inherited by the low-strain vdWH with PtS2, which also shows a very favorable optical gap at around 1.5 eV. This translates into exceptionally high maximum short-circuit currents, Jscmax = 7.2 mA/cm2, about twice the values previously reported for MoS2/WS2 vdWH. Although the predicted charge separation is partial, the high absorbance, together with the extended carrier diffusion length, due to the indirect electronic band gap, can turn out very advantageous for improving the efficiency of nanometer-thick photovoltaic devices.

Acknowledgments

We acknowledge CINECA for the availability of high-performance computing resources under the Iscra-B initiative, and the computational facilities and support provided by HPC@POLITO.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.1c11245.

  • G0W0 and BSE convergence tests, details on PdS2 and PtS2 monolayer optical absorbance, and selected wave functions (PDF)

The authors declare no competing financial interest.

Supplementary Material

am1c11245_si_001.pdf (5.3MB, pdf)

References

  1. Bhimanapati G. R.; Lin Z.; Meunier V.; Jung Y.; Cha J.; Das S.; Xiao D.; Son Y.; Strano M. S.; Cooper V. R.; Liang L.; Louie S. G.; Ringe E.; Zhou W.; Kim S. S.; Naik R. R.; Sumpter B. G.; Terrones H.; Xia F.; Wang Y.; Zhu J.; Akinwande D.; Alem N.; Schuller J. A.; Schaak R. E.; Terrones M.; Robinson J. A. Recent Advances in Two-Dimensional Materials Beyond Graphene. ACS Nano 2015, 9, 11509–11539. 10.1021/acsnano.5b05556. [DOI] [PubMed] [Google Scholar]
  2. Tan T.; Jiang X.; Wang C.; Yao B.; Zhang H. 2D Material Optoelectronics for Information Functional Device Applications: Status and Challenges. Adv. Sci. 2020, 7, 2000058. 10.1002/advs.202000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kang S.; Lee D.; Kim J.; Capasso A.; Kang H. S.; Park J.-W.; Lee C.-H.; Lee G.-H. 2D Semiconducting Materials for Electronic and Optoelectronic Applications: Potential and Challenge. 2D Materials 2020, 7, 022003. 10.1088/2053-1583/ab6267. [DOI] [Google Scholar]
  4. Huang H. H.; Fan X.; Singh D. J.; Zheng W. T. Recent Progress of TMD Nanomaterials: Phase Transitions and Applications. Nanoscale 2020, 12, 1247–1268. 10.1039/c9nr08313h. [DOI] [PubMed] [Google Scholar]
  5. Manzeli S.; Ovchinnikov D.; Pasquier D.; Yazyev O. V.; Kis A. 2D Transition Metal Dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. 10.1038/natrevmats.2017.33. [DOI] [Google Scholar]
  6. Rasmussen F. A.; Thygesen K. S. Computational 2D Materials Database: Electronic Structure of Transition-Metal Dichalcogenides and Oxides. J. Phys. Chem. C 2015, 119, 13169–13183. 10.1021/acs.jpcc.5b02950. [DOI] [Google Scholar]
  7. Liu Y.; Weiss N. O.; Duan X.; Cheng H.-C.; Huang Y.; Duan X. Van Der Waals Heterostructures and Devices. Nat. Rev. Mater. 2016, 1, 16042. 10.1038/natrevmats.2016.42. [DOI] [Google Scholar]
  8. Geim A. K.; Grigorieva I. V. Van Der Waals Heterostructures. Nature 2013, 499, 419–425. 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
  9. Li C.; Cao Q.; Wang F.; Xiao Y.; Li Y.; Delaunay J.-J.; Zhu H. Engineering Graphene and TMDs Based Van Der Waals Heterostructures for Photovoltaic and Photoelectrochemical Solar Energy Conversion. Chem. Soc. Rev. 2018, 47, 4981–5037. 10.1039/c8cs00067k. [DOI] [PubMed] [Google Scholar]
  10. Azadmanjiri J.; Srivastava V. K.; Kumar P.; Sofer Z.; Min J.; Gong J. Graphene-Supported 2D Transition Metal Dichalcogenide Van Der Waals Heterostructures. Appl. Mater. Today 2020, 19, 100600. 10.1016/j.apmt.2020.100600. [DOI] [Google Scholar]
  11. Peng Q.; Wang Z.; Sa B.; Wu B.; Sun Z. Electronic Structures and Enhanced Optical Properties of Blue Phosphorene/Transition Metal Dichalcogenides Van Der Waals Heterostructures. Sci. Rep. 2016, 6, 31994. 10.1038/srep31994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Maniyar A.; Choudhary S. Visible Region Absorption in TMDs/phosphorene Heterostructures for Use in Solar Energy Conversion Applications. RSC Adv. 2020, 10, 31730–31739. 10.1039/d0ra05810f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Latini S.; Winther K. T.; Olsen T.; Thygesen K. S. Interlayer Excitons and Band Alignment in MoS2/hBN/WSe2 Van Der Waals Heterostructures. Nano Lett. 2017, 17, 938–945. 10.1021/acs.nanolett.6b04275. [DOI] [PubMed] [Google Scholar]
  14. Jadczak J.; Kutrowska-Girzycka J.; Bieniek M.; Kazimierczuk T.; Kossacki P.; Schindler J. J.; Debus J.; Watanabe K.; Taniguchi T.; Ho C. H.; Wójs A.; Hawrylak P.; Bryja L. Probing Negatively Charged and Neutral Excitons in MoS2/hBN and hBN/MoS2/hBN Van Der Waals Heterostructures. Nanotechnology 2021, 32, 145717. 10.1088/1361-6528/abd507. [DOI] [PubMed] [Google Scholar]
  15. Huo N.; Yang Y.; Li J. Optoelectronics Based on 2D TMDs and Heterostructures. J. Semiconduct. 2017, 38, 031002. 10.1088/1674-4926/38/3/031002. [DOI] [Google Scholar]
  16. Saha D.; Varghese A.; Lodha S. Atomistic Modeling of Van Der Waals Heterostructures With Group-6 and Group-7 Monolayer Transition Metal Dichalcogenides for Near Infrared/Short-Wave Infrared Photodetection. ACS Appl. Nano Mater. 2020, 3, 820–829. 10.1021/acsanm.9b02342. [DOI] [Google Scholar]
  17. Furchi M. M.; Höller F.; Dobusch L.; Polyushkin D. K.; Schuler S.; Mueller T. Device Physics of Van Der Waals Heterojunction Solar Cells. npj 2D Mater. Appl. 2018, 2, 3. 10.1038/s41699-018-0049-3. [DOI] [Google Scholar]
  18. Li Y.; Chernikov A.; Zhang X.; Rigosi A.; Hill H. M.; van der Zande A. M.; Chenet D. A.; Shih E.-M.; Hone J.; Heinz T. F. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides:MoS2,MoSe2,WS2, andWSe2. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 205422. 10.1103/physrevb.90.205422. [DOI] [Google Scholar]
  19. Wurstbauer U.; Miller B.; Parzinger E.; Holleitner A. W. Light-matter interaction in transition metal dichalcogenides and their heterostructures. J. Phys. D: Appl. Phys. 2017, 50, 173001. 10.1088/1361-6463/aa5f81. [DOI] [Google Scholar]
  20. Bernardi M.; Palummo M.; Grossman J. C. Extraordinary Sunlight Absorption and One Nanometer Thick Photovoltaics Using Two-Dimensional Monolayer Materials. Nano Lett. 2013, 13, 3664–3670. 10.1021/nl401544y. [DOI] [PubMed] [Google Scholar]
  21. Flöry N.; Jain A.; Bharadwaj P.; Parzefall M.; Taniguchi T.; Watanabe K.; Novotny L. A WSe2/MoSe2 Heterostructure Photovoltaic Device. Appl. Phys. Lett. 2015, 107, 123106. 10.1063/1.4931621. [DOI] [Google Scholar]
  22. National Renewable Energy Laboratory . Solar Spectra. http://rredc.nrel.gov/solar/spectra/am1.5/ (accessed 30 March 2021).
  23. Andreani L. C.; Bozzola A.; Kowalczewski P.; Liscidini M.; Redorici L. Silicon Solar Cells: Toward the Efficiency Limits. Adv. Phys.: X 2019, 4, 1548305. 10.1080/23746149.2018.1548305. [DOI] [Google Scholar]
  24. Jariwala D.; Davoyan A. R.; Wong J.; Atwater H. A. Van Der Waals Materials for Atomically-Thin Photovoltaics: Promise and Outlook. ACS Photonics 2017, 4, 2962–2970. 10.1021/acsphotonics.7b01103. [DOI] [Google Scholar]
  25. Furuseth S.; Selte K.; Kjekshus A.; Gronowitz S.; Hoffman R. A.; Westerdahl A. Redetermined Crystal Structures of NiTe2, PdTe2, PtS2, PtSe2, and PtTe2. Acta Chem. Scand. 1965, 19, 257–258. 10.3891/acta.chem.scand.19-0257. [DOI] [Google Scholar]
  26. Hulliger F. Electrical Properties of Some Nickel-Group Chalcogenides. J. Phys. Chem. Solids 1965, 26, 639–645. 10.1016/0022-3697(65)90140-x. [DOI] [Google Scholar]
  27. Zhao Y.; Qiao J.; Yu P.; Hu Z.; Lin Z.; Lau S. P.; Liu Z.; Ji W.; Chai Y. Extraordinarily Strong Interlayer Interaction in 2D Layered PtS2. Adv. Mater. 2016, 28, 2399–2407. 10.1002/adma.201504572. [DOI] [PubMed] [Google Scholar]
  28. Tang C. Y.; Cheng P. K.; Wang X. Y.; Ma S.; Long H.; Tsang Y. H. Size-Dependent Nonlinear Optical Properties of Atomically Thin PtS2 Nanosheet. Opt. Mater. 2020, 101, 109694. 10.1016/j.optmat.2020.109694. [DOI] [Google Scholar]
  29. Miró P.; Ghorbani-Asl M.; Heine T. Two Dimensional Materials Beyond MoS2: Noble-Transition-Metal Dichalcogenides. Angew. Chem., Int. Ed. 2014, 53, 3015–3018. 10.1002/anie.201309280. [DOI] [PubMed] [Google Scholar]
  30. Wang Y.; Li Y.; Chen Z. Not your familiar two dimensional transition metal disulfide: structural and electronic properties of the PdS2monolayer. J. Mater. Chem. C 2015, 3, 9603. 10.1039/c5tc01345c. [DOI] [Google Scholar]
  31. Onida G.; Reining L.; Rubio A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. 10.1103/revmodphys.74.601. [DOI] [Google Scholar]
  32. Martin R.; Reining L.; Ceperley D.. Interacting Electrons: Theory and Computational Approaches; Cambridge University Press, 2016. [Google Scholar]
  33. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  34. Giannozzi P.; Andreussi O.; Brumme T.; Bunau O.; Buongiorno Nardelli M.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Cococcioni M.; Colonna N.; Carnimeo I.; Dal Corso A.; de Gironcoli S.; Delugas P.; DiStasio R. A.; Ferretti A.; Floris A.; Fratesi G.; Fugallo G.; Gebauer R.; Gerstmann U.; Giustino F.; Gorni T.; Jia J.; Kawamura M.; Ko H.-Y.; Kokalj A.; Küçükbenli E.; Lazzeri M.; Marsili M.; Marzari N.; Mauri F.; Nguyen N. L.; Nguyen H.-V.; Otero-de-la-Roza A.; Paulatto L.; Poncé S.; Rocca D.; Sabatini R.; Santra B.; Schlipf M.; Seitsonen A. P.; Smogunov A.; Timrov I.; Thonhauser T.; Umari P.; Vast N.; Wu X.; Baroni S. Advanced Capabilities for Materials Modelling With Quantum ESPRESSO. J. Phys.: Condens. Matter 2017, 29, 465901. 10.1088/1361-648x/aa8f79. [DOI] [PubMed] [Google Scholar]
  35. Giannozzi P.; Baseggio O.; Bonfà P.; Brunato D.; Car R.; Carnimeo I.; Cavazzoni C.; de Gironcoli S.; Delugas P.; Ferrari Ruffino F.; Ferretti A.; Marzari N.; Timrov I.; Urru A.; Baroni S. QuantumESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. 10.1063/5.0005082. [DOI] [PubMed] [Google Scholar]
  36. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  37. Hamann D. Optimized Norm-Conserving Vanderbilt Pseudopotentials. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 085117. 10.1103/physrevb.88.085117. [DOI] [Google Scholar]
  38. Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 1976, 13, 5188–5192. 10.1103/physrevb.13.5188. [DOI] [Google Scholar]
  39. Corso A. D.; Conte A. M. Spin-Orbit Coupling With Ultrasoft Pseudopotentials: Application to Au and Pt. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 115106. 10.1103/physrevb.71.115106. [DOI] [Google Scholar]
  40. Marsili M.; Molina-Sánchez A.; Palummo M.; Sangalli D.; Marini A. Spinorial formulation of the GW -BSE equations and spin properties of excitons in two-dimensional transition metal dichalcogenides. Phys. Rev. B 2021, 103, 155152. 10.1103/physrevb.103.155152. [DOI] [Google Scholar]
  41. Grimme S. Semiempirical GGA-type Density Functional Constructed With a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  42. Marini A.; Hogan C.; Grüning M.; Varsano D. Yambo: An Ab Initio Tool for Excited State Calculations. Comput. Phys. Commun. 2009, 180, 1392. 10.1016/j.cpc.2009.02.003. [DOI] [Google Scholar]
  43. Sangalli D.; Ferretti A.; Miranda H.; Attaccalite C.; Marri I.; Cannuccia E.; Melo P.; Marsili M.; Paleari F.; Marrazzo A.; Prandini G.; Bonfà P.; Atambo M. O.; Affinito F.; Palummo M.; Molina-Sánchez A.; Hogan C.; Grüning M.; Varsano D.; Marini A. Many-Body Perturbation Theory Calculations Using the Yambo Code. J. Phys.: Condens. Matter 2019, 31, 325902. 10.1088/1361-648x/ab15d0. [DOI] [PubMed] [Google Scholar]
  44. Godby R. W.; Needs R. J. Metal-Insulator Transition in Kohn-Sham Theory and Quasiparticle Theory. Phys. Rev. Lett. 1989, 62, 1169–1172. 10.1103/physrevlett.62.1169. [DOI] [PubMed] [Google Scholar]
  45. Rojas H. N.; Godby R. W.; Needs R. J. Space-Time Method forAb InitioCalculations of Self-Energies and Dielectric Response Functions of Solids. Phys. Rev. Lett. 1995, 74, 1827–1830. 10.1103/physrevlett.74.1827. [DOI] [PubMed] [Google Scholar]
  46. Bruneval F.; Gonze X. Accurate GW Self-Energies in a Plane-Wave Basis Using Only a Few Empty States: Towards Large Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 085125. 10.1103/physrevb.78.085125. [DOI] [Google Scholar]
  47. Sajjad M.; Singh N.; Schwingenschlögl U. Strongly Bound Excitons in Monolayer PtS2 and PtSe2. Appl. Phys. Lett. 2018, 112, 043101. 10.1063/1.5010881. [DOI] [Google Scholar]
  48. By directly checking the stability of different stacking patterns, we identified the AA structure to be the most stable.
  49. Villaos R. A. B.; Crisostomo C. P.; Huang Z.-Q.; Huang S.-M.; Padama A. A. B.; Albao M. A.; Lin H.; Chuang F.-C. Thickness Dependent Electronic Properties of Pt Dichalcogenides. npj 2D Mater. Appl. 2019, 3, 2. 10.1038/s41699-018-0085-z. [DOI] [Google Scholar]
  50. Ahmad S. Strain and Electric Field Dependent Variation in Electronic and Thermoelectric Properties of PtS2. Results Phys. 2020, 17, 103088. 10.1016/j.rinp.2020.103088. [DOI] [Google Scholar]
  51. Carvalho A.; Ribeiro R. M.; Castro Neto A. H. Band Nesting and the Optical Response of Two-Dimensional Semiconducting Transition Metal Dichalcogenides. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 115205. 10.1103/physrevb.88.115205. [DOI] [Google Scholar]
  52. Shi H.; Yan R.; Bertolazzi S.; Brivio J.; Gao B.; Kis A.; Jena D.; Xing H. G.; Huang L. Exciton Dynamics in Suspended Monolayer and Few-Layer MoS22D Crystals. ACS Nano 2013, 7, 1072–1080. 10.1021/nn303973r. [DOI] [PubMed] [Google Scholar]
  53. Sohier T.; Campi D.; Marzari N.; Gibertini M. Mobility of Two-Dimensional Materials From First Principles in an Accurate and Automated Framework. Phys. Rev. Mater. 2018, 2, 114010. 10.1103/physrevmaterials.2.114010. [DOI] [Google Scholar]
  54. Kuroda T.; Hoshi Y.; Masubuchi S.; Okada M.; Kitaura R.; Watanabe K.; Taniguchi T.; Machida T. Dark-state impact on the exciton recombination of WS2 monolayers as revealed by multi-timescale pump-probe spectroscopy. Phys. Rev. B 2020, 102, 195407. 10.1103/physrevb.102.195407. [DOI] [Google Scholar]
  55. Jin C.; Kim J.; Utama M. I. B.; Regan E. C.; Kleemann H.; Cai H.; Shen Y.; Shinner M. J.; Sengupta A.; Watanabe K.; Taniguchi T.; Tongay S.; Zettl A.; Wang F. Imaging of pure spin-valley diffusion current in WS2-WSe2heterostructures. Science 2018, 360, 893–896. 10.1126/science.aao3503. [DOI] [PubMed] [Google Scholar]
  56. Mueller T.; Malic E. Exciton Physics and Device Application of Two-Dimensional Transition Metal Dichalcogenide Semiconductors. npj 2D Mater. Appl. 2018, 2, 29. 10.1038/s41699-018-0074-2. [DOI] [Google Scholar]
  57. Re Fiorentin M.; Cicero G.; Palummo M. Spatially Indirect Excitons in Black and Blue Phosphorene Double Layers. Phys. Rev. Mater. 2020, 4, 074009. 10.1103/physrevmaterials.4.074009. [DOI] [Google Scholar]
  58. Jauregui L. A.; Joe A. Y.; Pistunova K.; Wild D. S.; High A. A.; Zhou Y.; Scuri G.; De Greve K.; Sushko A.; Yu C.-H.; Taniguchi T.; Watanabe K.; Needleman D. J.; Lukin M. D.; Park H.; Kim P. Electrical Control of Interlayer Exciton Dynamics in Atomically Thin Heterostructures. Science 2019, 366, 870–875. 10.1126/science.aaw4194. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am1c11245_si_001.pdf (5.3MB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES