Glioblastoma and primary central nervous system lymphoma: differentiation using MRI derived first-order texture analysis – a machine learning study

Abstract

Objectives

To evaluate the diagnostic performance of multiple machine learning classifier models derived from first-order histogram texture parameters extracted from T1-weighted contrast-enhanced images in differentiating glioblastoma and primary central nervous system lymphoma.

Methods

Retrospective study with 97 glioblastoma and 46 primary central nervous system lymphoma patients. Thirty-six different combinations of classifier models and feature selection techniques were evaluated. Five-fold nested cross-validation was performed. Model performance was assessed for whole tumour and largest single slice using receiver operating characteristic curve.

Results

The cross-validated model performance was relatively similar for the top performing models for both whole tumour and largest single slice (area under the curve 0.909–0.924). However, there was a considerable difference between the worst performing model (logistic regression with full feature set, area under the curve 0.737) and the highest performing model for whole tumour (least absolute shrinkage and selection operator model with correlation filter, area under the curve 0.924). For single slice, the multilayer perceptron model with correlation filter had the highest performance (area under the curve 0.914). No significant difference was seen between the diagnostic performance of the top performing model for both whole tumour and largest single slice.

Conclusions

T1 contrast-enhanced derived first-order texture analysis can differentiate between glioblastoma and primary central nervous system lymphoma with good diagnostic performance. The machine learning performance can vary significantly depending on the model and feature selection methods. Largest single slice and whole tumour analysis show comparable diagnostic performance.

Introduction

Glioblastoma is the most aggressive primary malignant brain tumour in adults. Primary central nervous system lymphoma (PCNSL) has a reported incidence of 3–4% among newly diagnosed brain tumours.¹ Typically, glioblastoma manifests on imaging as an enhancing mass with variable necrosis, while the appearance of PCNSL is variable, depending on the underlying immune status of the patient. However, the imaging features may overlap, making it challenging to differentiate the two entities.² The distinction is, however, critical because the therapeutic options are entirely different. Glioblastoma is managed by maximum safe surgical resection and chemoradiation, whereas methotrexate-based chemotherapy with or without radiation is the mainstay for PCNSL.³

Multiple prior studies aimed to distinguish between glioblastoma and PCNSL by utilising advanced magnetic resonance imaging (MRI) (arterial spin labelling, diffusion tensor imaging (DTI) and perfusion imaging).^3–7 However, these advanced sequences require additional expertise and expense, are time-consuming and as such are not performed routinely. Thus, conventional MRI sequences are still the mainstay in brain tumour imaging in routine clinical practice. More recently, magnetic resonance texture analysis (MRTA) is being increasingly utilised in neuro-oncology for tumour classification, assessing treatment response and prognostication.^8,9 MRTA includes extraction of first, second or higher order texture, and shape features from medical images. These are thought to reflect underlying tumour micro-environment and heterogeneity.¹⁰

Filtration-based MRTA is a technique that involves the initial application of a Laplacian of Gaussian (LoG) filter to remove image noise followed by extraction and enhancement of image features at different sizes based on the applied filter. A total of six histogram-based first-order texture parameters are subsequently derived from each filter level. As there is a total of six filtration levels, this yields a total of 36 texture features for evaluation.

Prior studies have previously utilised filtration-based first-order histogram features for evaluating tumour grade, genotyping, treatment response and survival.^11–14 However, the effectiveness of this technique to differentiate between glioblastoma and PCNSL has not been studied before. We aimed to determine the diagnostic performance of texture features extracted from T1 contrast-enhanced (CE) sequence in differentiating glioblastoma from PCNSL. For this, we investigated multiple machine learning classifier models and feature reduction strategies for texture-based glioblastoma and PCNSL classification. A secondary aim was to determine if the texture analysis of a largest single tumour slice can provide comparable diagnostic accuracy compared with the texture features derived from the entire tumour.

Materials and methods

Data collection

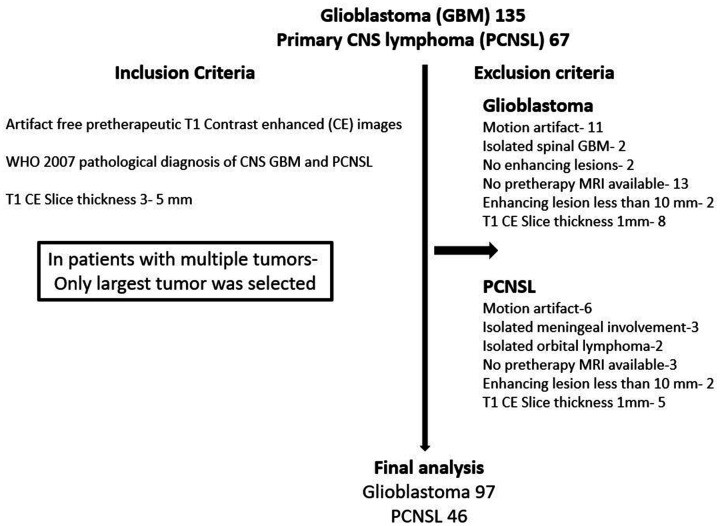
The retrospective study was approved by the institutional review board (IRB) of the University of Iowa Hospital and the requirement for informed consent was waived. Between 2005 and 2016, patients with pathologically confirmed glioblastoma (n = 135) or PCNSL (n = 67) were identified. Eligibility criteria included untreated patients and the availability of artifact-free preoperative T1-weighted CE MRI images with slice thickness 3–5 mm and the presence of a CE tumour greater than 10 mm. Patients with motion artefacts or absence of preoperative CE imaging, and a history of treatment (surgery or chemoradiation) prior to initial imaging or recurrent tumours were excluded. This yielded a total of 97 patients with glioblastoma and 46 with PCNSL (Figure 1). All patients with PCNSL were immunocompetent.

Figure 1.

Patient selection.

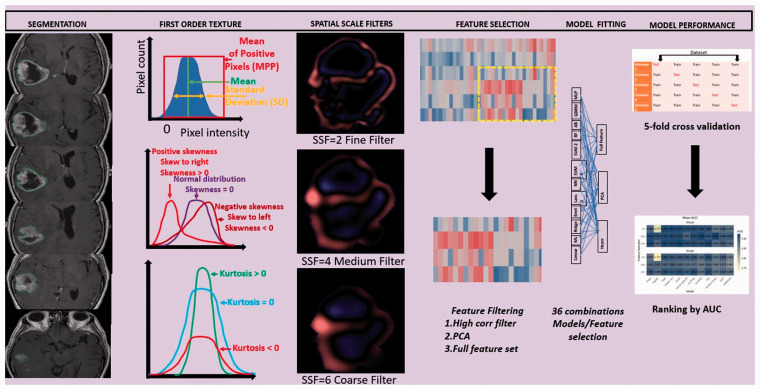
Figure 2.

Overall study workflow showing segmentation, feature selection, model building and validation.

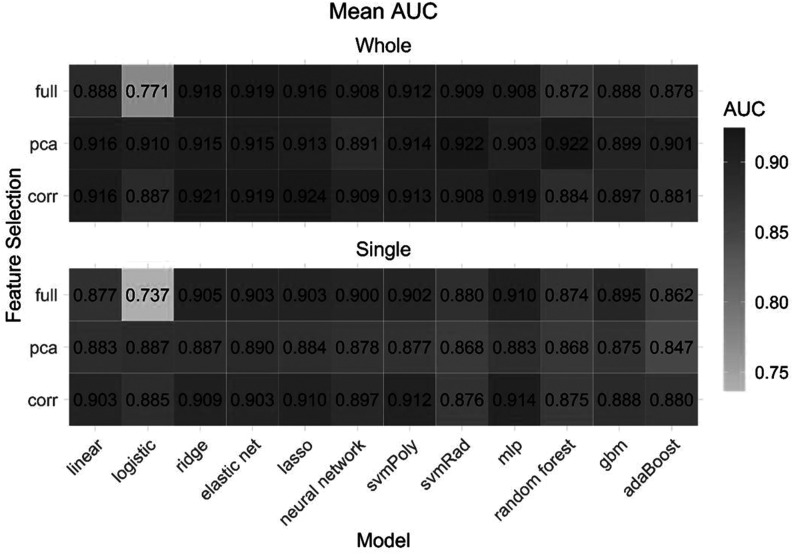
Figure 3.

Mean cross-validated area under the curve for each model and feature selection method on each feature set.

Image acquisition

All patients had preoperative imaging on a 1.5 T MRI system (Siemens, Erlangen, Germany). The acquisition protocol for brain tumour evaluation at our hospital includes pre-contrast axial T1-weighted, T2-weighted, fluid-attenuated inversion recovery (FLAIR), diffusion-weighted imaging (DWI) with ADC maps, gradient echo and T1-weighted CE images. The typical imaging parameters were: T1-weighted (TR/TE/TI: 1950/10/840; NEX: 2; slice thickness: 5 mm; matrix: 320 × 256; field of view (FOV) 240 mm; pixel size 0.75 mm); T2-weighted (TR/TE: 4000/90; NEX: 2; slice thickness: 5 mm; matrix: 512 × 408; FOV 240 mm; pixel size 0.5 mm); and FLAIR (TR/TE/TI: 9000/105/2500; NEX: 1; slice thickness: 5 mm; matrix: 384 × 308; FOV 240 mm; pixel size 0.6 mm). T1-weighted CE images were acquired after administration of gadobenate dimeglumine (Multihance; Bayer Healthcare Pharma, Berlin, Germany) or gadobutrol (Gadovist; Bayer Healthcare Pharma, Berlin, Germany) injected at the rate of 0.1 ml/kg body weight.

Tumour segmentation/region of interest delineation

Tumour segmentation was performed on axial T1 CE images by a medical researcher under supervision of a fellowship-trained neuroradiologist. Manual segmentation was performed using a commercial research software (TexRAD version 3.3, TexRAD Ltd., part of Feedback Plc, Cambridge, UK) by employing a polygon drawing tool. Total tumour volume segmentation was performed by contouring all axial two-dimensional (2D) slices containing the tumour. The region of interest (ROI) encompassed both the necrotic and solid enhancing regions of the tumour with the exclusion of oedema (Figure 2). The averaged sum of all texture features from all tumour slices was used for the whole tumour subgroup while the ROI with the largest pixel count was selected for single slice analysis.

Texture analysis

MRTA was performed using the same software. The software employs a filtration histogram technique with application of LoG band-pass filter. The filtration step extracts and enhances image features of variable size and intensity corresponding to spatial scaling filter (SSF) values. Different SSF values extract information for different filter sizes, ranging from fine filter (SSF 2), medium (SSF 3–5) and coarse filter (SSF 6) (Figure 2). SSF 0 corresponds to an unfiltered image. In the filtration approach, image noise was reduced by the Gaussian component of the filter, while feature enhancement (image heterogeneity) was performed by the Laplacian component. Additional details regarding post-processing have previously been described in detail.^15,16 Image texture of the filtered and unfiltered pixels was further quantified by measurement of the histogram, and six statistical parameters for each SSF were calculated in both groups of patients followed by mathematical interpolation of slice data. Thus, a total of 36 statistical parameters are obtained for each tumour (six parameters for each SSF). These included mean (average value of the grey-level intensities); standard deviation (SD; dispersion from the mean); entropy (irregularity or randomness of the grey-level distribution); skewness (asymmetry of histogram); kurtosis (pointedness of histogram) and mean of positive pixels (MPP) for each filtration level, giving a total of 36 texture features.^13,16

Feature selection and reduction

Two feature sets were considered for the model fitting. The first included features extracted from the whole tumour and the second included features extracted from the single largest slice. Each feature set consisted of 36 features.

Three different feature selection strategies were used. In the ‘full feature’ strategy, the optimal features were determined by the model itself, based on penalised or non-penalised inbuilt classifier. The other two feature selection methods involved a high correlation filter and principal components analysis (PCA). The high correlation filter removes variables from the feature set which have a large absolute correlation. A user-specified threshold was given to determine the largest allowable absolute correlation. This threshold was set at 0.95 to remove highly correlated variables. The PCA transformation calculates new variables from orthogonal linear combinations of the observed features. The number of components retained in the PCA transformation was determined by specifying the fraction of the total variance that should be covered by the components. This cut-off was set to 95% to allow for much of the information in the features to be retained while still addressing the multicollinearity.

Model building

Twelve different machine learning classifiers were considered. These models can be categorised into three broad groups: linear classifiers, non-linear classifiers and ensemble classifiers. The linear classifiers used were linear, multinomial logistic, ridge, elastic net and least absolute shrinkage and selection operator (LASSO) regression. The non-linear classifiers used were neural network, support vector machine (SVM) with a polynomial kernel, SVM with a radial kernel and the multilayer perceptron (MLP). Finally, the ensemble classifiers used were random forest, generalised boosted regression model (GBRM) and boosting of classification trees with AdaBoost. The penalised regression approaches of the LASSO and elastic net, as well as the tree-based approaches used in the GBRM, AdaBoost and random forest models all allow for additional embedded feature selection. For approaches that do not allow for embedded feature selection, they simply use the number of features remaining after the filter. For each feature set, all 12 classifiers were fit using all features as well as with the two filtering methods. This led to 36 possible model/feature selection combinations on each of the two feature sets (whole tumour and largest single slice, respectively) (Figure 2). All variables were standardised prior to filtering and model fitting. Optimal feature subset and variable (feature) importance was also evaluated.

Statistical analysis

The predictive performance of each model was evaluated using five-fold repeated cross-validation with five repeats. For models with tuning parameters, important parameters were tuned using nested cross-validation to avoid bias. The feature selection techniques were carried out within each cross-validated split of the data, so as not to bias the estimate of predictive performance. Feature selection methods were implemented using the recipes package in R version 4.0.2. Model fitting and cross-validated predictive performance was implemented using the MachineShop package and RSNNS package in R version 4.0.2. Predictive performance was measured with the area under the receiver operating characteristic curve (AUC). As models were formulated to predict lymphoma, AUC estimates the probability that a randomly selected subject with PCNSL will have a greater predicted value than a randomly selected subject that had glioblastoma.

The two-sample t-test was used to test for a significant difference in the mean age between the groups and the chi-square test was used to test for a significant association between sex and group.

Results

Patient characteristics

Table 1 provides summary statistics of the clinical characteristics age and sex by group and for the entire sample. There were no significant differences in the age and gender distribution between the two tumour classes (P > 0.05).

Table 1.

Summary statistics for clinical characteristics and P values for comparisons between tumour classes.

	Glioblastoma (n = 97)	Lymph (n = 46)	Overall	P value
Age, mean (SD)	61.38 (12.35)	63.87 (12.47)	62.18 (12.40)	0.2668
Sex, male, n (%)	53 (54.6%)	25 (54.3%)	78 (54.5%)	0.9739
Necrosis
Yes	92	10	102	–
No	5	36	41

SD: standard deviation.

Comparison of model performance

The combination of the LASSO model with high correlation filter selection strategy had highest diagnostic performance for whole tumour (cross-validated mean AUC of 0.924, accuracy 88%). For single slice analysis, the combination of the MLP (multilayer perceptron network) model with high correlation filter achieved highest performance (AUC 0.914, accuracy 86%). Table 2 displays the diagnostic performance of the top five models based on feature numbers with the highest average cross-validated AUC on both feature sets. Figure 3 displays the mean AUC for all model/feature selection combinations. The LASSO model fit using high correlation filter was the best model for whole tumour and was built using eight optimal features. For the single slice, MLP was the highest performing model again fit using high correlation filter and was built using 20 optimal features. For whole tumour, the random forest model utilised a minimum of seven features whereas for single slice, the LASSO model utilised a minimum of six features with both showing comparable performance to top performing models (Table 2). Detailed summaries of the performance metrics for the best performing model for the whole tumour and single slice are given in Table 3 and Table 4, respectively.

Table 2.

Top five models on each feature set and mean (SD) of AUC.

Rank	Whole tumour			Single largest slice
	Model	AUC	Optimal feature subset	Model	AUC	Optimal feature subset
1	lasso_corr	0.924 (0.049)	8	mlp_corr	0.914 (0.059)	20
2	svmRad_pca	0.922 (0.046)	8	svmPoly_corr	0.912 (0.065)	20
3	rf_pca	0.922 (0.044)	7	mlp_full	0.910 (0.053)	36
4	ridge_corr	0.921 (0.051)	19	lasso_corr	0.910 (0.065)	6
5	mlp_corr	0.919 (0.053)	19	ridge_corr	0.909 (0.068)	20

lasso: least absolute shrinkage and selection operator; svmRad: support vector machine with a radial kernel; rf: random forest; ridge: ridge regression; mlp: multilayer perceptron; svmpoly: support vector machine with a polynomial kernel; corr: high correlation filter; PCA: principal components analysis; SD: standard deviation; AUC: area under the curve.

Table 3.

Performance metrics for the best overall model, LASSO with the high correlation filter fit using features from the whole tumour.

Metric	Mean	SD	Min	Max
Accuracy	0.884	0.055	0.786	0.967
AUC	0.924	0.049	0.836	0.994
Sensitivity	0.804	0.130	0.556	1.000
Specificity	0.921	0.048	0.842	1.000

AUC: area under the curve; LASSO: least absolute shrinkage and selection operator; SD: standard deviation.

Table 4.

Performance metrics for the best model using the single largest slice, MLP with the high correlation filter.

Metric	Mean	SD	Min	Max
Accuracy	0.858	0.061	0.733	0.964
AUC	0.914	0.059	0.785	0.989
Sensitivity	0.780	0.111	0.500	1.000
Specificity	0.895	0.066	0.737	1.000

AUC: area under the curve; MLP: multilayer perceptron; SD: standard deviation.

Single slice versus whole tumour analysis

The paired t-test was used to test for significant differences in AUC for the top model on each feature set. Comparing the mean AUC between the top models fit using features from the whole tumour (LASSO_Cor) and the single largest slice (MLP_Corr) the P value was 0.1112, indicating no significant different in their predictive performance.

Feature importance

The list of the total number of features used in the modelling process when fit to the full dataset is provided in Supplemental Table 1. As variable importance is not defined for the MLP and SVM models, the next high performing model (LASSO) was used to define variable importance for single slice. Skewness was the most important feature for both whole tumour (at SSF 6) and for single slice (at SSF 0). Table 5 provides the details of the optimal features used to build the best model on the whole tumour and single slice.

Table 5.

Relative importance of features used for model building (LASSO) for whole tumour and single slice.

Whole tumour		Single slice
Feature	Relative importance	Feature	Relative importance
Skewness (SSF 6)	100	Skewness (SSF 0)	100
SD (SSF 2)	61.97877	Mean (SSF 6)	68.4919
Skewness (SSF 0)	60.16302	SD (SSF 2)	61.35226
Kurtosis (SSF 3)	29.48633	Skewness (SSF 6)	43.51694
Mean (SSF 2)	27.38745	Entropy (SSF 2)	17.33853
Kurtosis (SSF 6)	20.33263	Kurtosis (SSF 2)	11.05598
MPP (SSF 6)	19.11105	–	–
Kurtosis (SSF 0)	8.136731	–	–

SD: standard deviation; MPP: mean of positive pixels; SSF: spatial scale filter; LASSO: least absolute shrinkage and selection operator.

Discussion

Our study evaluated the diagnostic performance of multiple classifier models and feature selection methods to differentiate glioblastoma from PCNSL using filtration-based first-order texture features derived from T1 CE images. We found highest diagnostic performance for the combined LASSO model and high correlation filter method. High correlation filter was the best feature reduction method with high performance in the majority of the classifier models. In addition, the diagnostic performance for tumour classification was comparable for both the whole tumour and largest single slice derived texture features, more so among the top performing models.

Our study also showed that the model performance is variable and depends on the selected machine learning technique and feature selection combination. Although the top five models in our study had high performance with AUC of 0.909–0.924, there was still a minor difference in their performance. Models also varied according to the number of optimal features utilised for model building (Table 2). Both the LASSO (whole tumour) and MLP model (single slice) resulted in higher performance than other classifiers. LASSO regression works by finding the most relevant features and turns all the irrelevant feature coefficients to zero and tunes the model by user-specified k-fold cross-validation. LASSO is commonly used to reduce data collinearity when the number of features exceed the sample size.¹⁷ Correlation filter is a type of feature selection method in which feature selection is independent of the model construction process. The filter removes highly correlated features that may only provide redundant information. In addition, by applying five-fold nested cross-validation, the process of data overfitting can be avoided as in our case.¹⁸ Similarly, the MLP model is a type of feed-forward artificial neural network model that has an input and output layer connected by a hidden layer. MLP evaluates non-linear relationships and helps in classification when linear separation of data is not possible.¹⁹ Yun et al. also found high performance of the MLP model in their study of glioblastoma and PCNSL classification, with MLP performing even better than unsupervised deep-learning-based convolutional neural network. They also proposed that MLP-based feature selection may avoid data overfitting, especially if models are trained and tested from the same institute.²⁰ While some of the non-linear classifiers were among the best models (MLP, SVM), we also observed similar or better performance using linear classifiers, indicating that these simpler approaches may be sufficient for this classification problem. In addition, linear classifiers are less computationally extensive.²¹

We found comparable diagnostic performance for models built using limited or a slightly higher number of features for both whole tumour and single slice. However, presuming that a model using fewer features is a good strategy against overfitting may be an oversimplification. It is theoretically possible that the model using many fewer variables will be prone to poor performance if the feature used is not robust to repeat measurements or shows variation in the external dataset.

Only a few prior studies have evaluated the performance of multiple classifier models as in our study to differentiate glioblastoma and PCNSL. The majority of studies only included single or a few classifier models. Kang et al.²² evaluated eight classifier models and found the random forest model with recursive feature elimination feature selection as the highest performer (AUC 0.944) on radiomics extracted from ADC maps. Kim et al.²³ evaluated three classifier models, random forest, logistic regression and SVM with minimum redundancy maximum relevance feature selection algorithm. They found logistic regression as the highest performer (AUC 0.956) classifier model. Of note, both random forest and ridge regression models were among the top five models in our study as well, albeit with different feature selection techniques. A pertinent methodological difference between our study and the afore-mentioned studies is that we only used first-order texture features unlike prior studies which also included higher order texture features. Our findings overall support that the performance of classifier models is dependent on the available data and can be influenced by the selected combination of feature reduction and classifier model. As such, the diagnostic role of multiple machine learning models and feature selection strategies in classifying glioblastoma and PCNSL should be evaluated in future studies.

The other important observation from our study was that both the largest single slice and whole tumour texture analysis had comparable diagnostic performance in tumour classification. This is critical as performing texture analysis on the largest single slice is less resource intensive, time-efficient and may be relatively easy to incorporate in the clinical workflow. Wang et al.²⁴ also evaluated single slice analysis performance on T2-weighted imaging in 81 patients with glioblastoma and 28 patients with PCNSL but reported modest performance (AUC 0.752). The low performance in their study was likely tpo be due to the inclusion of only enhancing regions in the analysis. We, however, included both the necrotic and enhancing components with higher performance. Necrosis is a key component of glioblastoma and its inclusion may lead to an improvement in texture performance. In contrast, Nakagawa et al.²⁵ reported higher diagnostic performance using a multivariate (xGBoost) regression model with an AUC of 0.980. They, however, extracted features from multiple sequences (T2-weighted, ADC, T1 CE) and perfusion MRI sequence. Our results were also comparable to other prior studies that also evaluated the utility of texture analysis to differentiate glioblastoma from PCNSL (Supplemental Table 2).^2,20,22–31

The higher performance of Kim et al.²³ (AUC 0.956) and Nakagawa et al.²⁵ (AUC 0.980) may be secondary to texture feature extraction from multiparametric images including three-dimensional (3D) T1 CE sequence, T2-weighted and diffusion-weighted images. In contrast, we performed texture analysis on a routinely acquired 2D T1 CE sequence which is performed universally. Advanced sequences such as perfusion MRI are also not widely available. Although 3D T1 CE have high spatial resolution that can affect texture features;¹⁰ 3D T1 CE are more time consuming and as such are not performed routinely. The extraction of radiomics features from multiple sequences may provide additional information; however, this needs to be further investigated. This is pertinent because unlike these studies, our technique requires minimal pre-processing and would therefore be easier to implement in a busy clinical setting.

Besides the retrospective nature, our study is also limited by the absence of an external validation set. We also did not evaluate the performance of MRTA on other routinely performed sequences such as FLAIR and ADC, which could have potentially improved model performance further.³² Our rationale for utilising T1-weighted CE images was based on the observation from prior studies that found T1 CE as the single best sequence and comparable in performance to multiparametric imaging in predicting glioma grading and survival.¹⁰ The other limitation includes unclear knowledge of biological correlates of these texture features. In addition, due to the inherent limitation of the software, we could not compare the diagnostic performance of first-order and higher order texture features (software used in the current study only provides first-order parameters).

Despite these limitations, our study had many strengths as well. We showed that using only first-order features for differentiating between PCNSL and glioblastoma can achieve excellent model performance comparable to multiple other studies using higher order texture features. Secondly, our findings suggest that using texture features derived only from a single slice can provide comparable diagnostic performance to whole tumour texture analysis. Finally, our extensive evaluation of different machine learning models provides a benchmark of the variable performances of different machine learning models for this problem. Unlike multiple prior studies in which different models were used on different imaging data, making the assessment of best machine learning models difficult, we provide a metric of variable model performance on the same data.

Conclusion

Our findings suggest that first-order texture-based machine learning models built from T1 CE imaging can discriminate between glioblastoma and PCNSL non-invasively and with excellent diagnostic accuracy. In addition, the diagnostic performance of whole tumour versus single largest slice derived features is comparable.