Cell patterning by secretion-induced plasma membrane flows

Exocytosis causes bulk membrane flows that drag associated proteins and form a negative feedback restricting the exocytic site.

Abstract

Cells self-organize using reaction-diffusion and fluid-flow principles. Whether bulk membrane flows contribute to cell patterning has not been established. Here, using mathematical modeling, optogenetics, and synthetic probes, we show that polarized exocytosis causes lateral membrane flows away from regions of membrane insertion. Plasma membrane–associated proteins with sufficiently low diffusion and/or detachment rates couple to the flows and deplete from areas of exocytosis. In rod-shaped fission yeast cells, zones of Cdc42 GTPase activity driving polarized exocytosis are limited by GTPase activating proteins (GAPs). We show that membrane flows pattern the GAP Rga4 distribution and that coupling of a synthetic GAP to membrane flows is sufficient to establish the rod shape. Thus, membrane flows induced by Cdc42-dependent exocytosis form a negative feedback restricting the zone of Cdc42 activity.

INTRODUCTION

Cells are highly polarized entities that exhibit one (or several) front with distinct lipid and protein plasma membrane (PM) composition. Reaction-diffusion systems have come a long way in explaining polarity establishment through positive and negative feedback regulations. For instance, in yeast cells, scaffold-mediated positive amplification of Cdc42 guanosine triphosphatase (GTPase) activity underlies the formation of one (or two) cell front (1, 2), with negative feedback promoting oscillations (3, 4). Biochemical reactions are also modulated by physical processes such as fluid flows, which may happen in the cytosol and at the membrane. In large metazoan cells, cytoskeletal-driven cortical and cytosolic fluid flows, causing advective protein movements, play important roles in cell polarization (5) and can, in principle, promote polarity establishment (6). Membrane flows are predicted to occur and equilibrate membrane tension between spatially segregated zones of exo- and endocytosis, such as in tip growth of walled pollen tubes (7, 8) or in cell migration, as initially proposed in (9). However, although membrane flows have been observed in migrating amoebae, apicomplexans, amoeboid macrophages, and neuronal growth cones (10–13), their role in cell patterning has not been explored.

In contrast to metazoan cells, fungal cells are not thought to harbor an actin cortex that may contribute to cortical flow forces. In fission yeast cells, which are rod shaped and grow by tip extension at one or both cell poles, Cdc42 GTPase activity promotes local exocytosis for polarized cell growth. Membrane is retrieved through endocytosis, which also occurs mainly at cell poles. The width of the cell correlates with the size of the Cdc42–guanosine triphosphate (GTP) zones at cell poles, which is regulated by GTPase activating proteins (GAPs) inhibiting Cdc42 activity (14). In particular, Cdc42 GAPs that localize to the sides of rod-shaped fission yeast cells through unknown mechanisms are thought to control cell width by restricting the size of the Cdc42 active zone (14–16).

We recently described the use of the CRY2-CIB1 (cryptochrome 2–cryptochrome-interacting basic helix-loop-helix) optogenetic system in fission yeast cells (2). In our CRY2-CIB1 setup, blue light activates the cytosolic photosensor domain CRY2PHR (CRY2) to bind its ligand N terminus (CIBN), which is linked to the PM-interacting domain of the mammalian protein Rit1 (RitC). RitC, which is a disordered peptide that reversibly associates with the membrane through hydrophobic and charge interactions (17), specifically associates with the PM but not with secretory vesicles or other endomembranes (18, 19). Blue light also promotes CRY2 oligomerization (20). Here, we describe our serendipitous discovery of membrane flows away from sites of secretion, revealed by the behavior of the CRY2-CIB1 system. We show that PM-associated proteins with sufficiently low diffusion and/or detachment rates, including the Cdc42 GAP Rga4, are displaced from sites of exocytosis. We further reveal that coupling of a synthetic GAP to membrane flows is sufficient to establish the rod cell shape. Thus, secretion-induced membrane flows underlie a negative feedback that shapes the cell by restricting the size of the secretion zone.

RESULTS

Whereas CIBN-RitC is nearly uniform at the PM in the dark and blue light initially caused uniform CRY2 recruitment, we unexpectedly observed that both proteins cleared from most interphase cell poles within 5 min (Fig. 1A and movie S1). Similarly, in predivisional cells, CRY2 and CIBN cleared from mid-cell, where exocytosis is targeted, but reappeared at nongrowing cell poles (fig. S1A and movie S2). CRY2 depletion at cell poles after 5 min correlated with local levels of Cdc42-GTP, marked by CRIB-3GFP (Cdc42/Rac interactive binding-green fluorescent protein) (Fig. 1, A and B), the secretory vesicle associated Rab11-like GTPase Ypt3 (Fig. 1B and fig. S1B), and exocyst subunits Exo70 and Exo84 (fig. S1, C and D), and with fast depletion rates (fig. S1E). Thus, light-induced changes in CRY2-CIBN interactions provoke their clearance from zones of exocytosis.

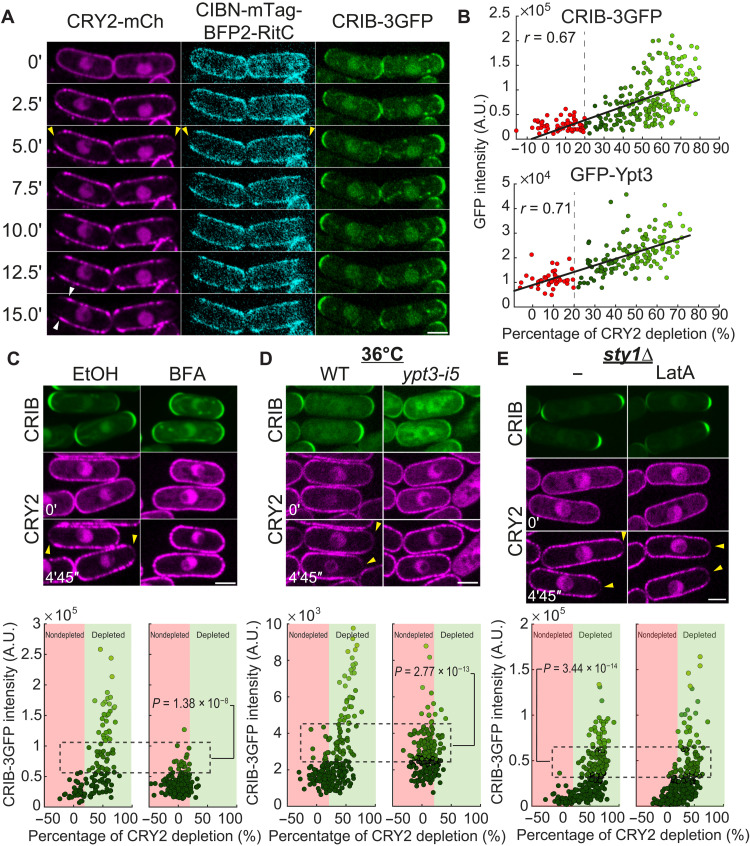
Fig. 1. Depletion of membrane-associated CRY2 around sites of secretion.

(A) Spinning disk imaging time-lapse of CRY2-mCherry, CIBN-mTag-BFP2 (blue fluorescent protein 2)-RitC, and CRIB-3GFP cells grown in the dark. Time 0 is the first time point after illumination. Yellow arrowheads indicate depletion zones. White arrowheads point to lateral peaks. (B) Correlation plot of CRY2 depletion after 5 min and pole GFP intensity of CRIB-3GFP and GFP-Ypt3. Depletion cutoff is indicated by red to green color change. A.U., arbitrary units. (C) Cells as in (A) treated with 300 μM BFA or solvent [ethanol (EtOH)]. (D) Cells as in (A) carrying or not carrying the ypt3-i5 temperature-sensitive allele and grown at 36°C for 30 min to inactivate secretion. The control at the permissive temperature of 25°C is shown in fig. S1H. WT, wild type. (E) Cells as in (A) carrying a sty1 deletion (sty1∆) treated or not treated with 50 μM Latrunculin A (LatA) to prevent endocytosis. The control for LatA treatment is shown in fig. S1I. In (C to E), the GFP channel is a 5-min temporal sum projection. mCherry shows individual time points. Yellow arrowheads indicate depletion zones. Bottom graphs show CRIB-3GFP fluorescence plotted against CRY2 depletion at cell tips, as in (B). Data points are colored with different shades of green according to CRIB-3GFP fluorescence. The indicated Kruskal-Wallis test P value compares CRY2 depletion values between cells of equivalent CRIB-3GFP intensities. Scale bars, 3 μm (in all figures).

CRY2 was not depleted from cell poles upon brefeldin A (BFA) treatment, which completely stops secretion (21, 22), with some cell poles even gaining in CRY2 signal (Fig. 1C and fig. S1, F and G). CRY2 was also not depleted upon secretion inactivation in the ypt3-i5 mutant (Fig. 1D and fig. S1H). We note that both conditions also caused reduction in CRIB-3GFP, perhaps due to loss of positive feedback between growth and polarity (23). GFP-Ypt3 intensity was also slightly reduced in BFA-treated cells (fig. S1G). Nevertheless, comparison of cell poles with similar GFP intensity clearly showed that CRY2 does not deplete upon secretion block. Thus, polarized secretion is essential for CRY2 depletion from cell poles.

Cell poles are also sites of endocytosis, which is strictly dependent on actin patch assembly by the actin-related protein-2/3 (Arp2/3) complex. To test the role of endocytosis, we disrupted all actin structures with Latrunculin A (LatA). Because LatA treatment elicits activation of the mitogen-activated protein kinase (MAPK) stress signaling pathway, which leads to loss of cell polarity, we performed these experiments in cells lacking the MAPK Sty1, in which this stress response is abrogated and cell polarity is retained (24). In LatA-treated sty1∆ cells, actin patches were lost, but CRY2 still depleted from cell poles (Fig. 1E and fig. S1I). As LatA also depolymerizes actin cables, we can conclude that cytoplasmic actin cable retrograde flow is not driving depletion. We note however that the extent of depletion was reduced relative to untreated samples. We hypothesize that this reduction is due to reduced rates of exocytosis in LatA-treated cells both due to the absence of actin cable–mediated vesicle transport and to accommodate the absence of endocytosis, but we cannot exclude a possible direct contribution of endocytosis in CRY2 depletion from cell poles. We conclude that endocytosis may partially contribute but is not essential for CRY2 depletion from cell poles.

Simulations of membrane flow-dependent depletion

How may CIBN-RitC and CRY2 become depleted from sites of polarized growth? Because they are not native to Schizosaccharomyces pombe cells, their localization is unlikely to be directly regulated by endogenous yeast proteins. A reaction-diffusion mechanism would require a source of energy to maintain the pattern and potentially nonlinear interactions through activation/deactivation, which is not likely for CRY2-CIBN. We have also shown above that endocytosis could not solely explain the depletion. We thus hypothesized that deposition and retrieval of membrane material through exo- and endocytic events at sites of growth locally perturbs the distribution of peripherally associated membrane proteins, such as CIBN-RitC, through bulk membrane flows causing associated protein movement toward cell sides.

We performed computer simulations to test the hypothesis that exo- and endocytic events generate flows strong enough to deplete membrane-associated proteins at growth sites. We modeled proteins as particles with association/dissociation rate constants k_on and k_off, diffusing on a sphere approximating the cell tip, and displaced by exo/endocytotic events over zones of width σ_exo and σ_endo (Fig. 2A and movie S3; see Material and Methods for details). Particles are displaced radially by up to a distance of R_cutoff around the site of each vesicle delivery/internalization (Fig. 2B and Eqs. 2 and 3), as an approximation for how proteins in a fluid membrane move, adjusting their position to accommodate the change of membrane area on a background of membrane tension. A minimum value R_cutoff ~ 1 μm was required to observe substantial depletion in subsequent analysis (see fig. S9E). To calibrate the model, we measured rates of fission yeast endocytosis (Table 1). We also measured cell growth to estimate the net rate of new membrane addition (Table 1). Rates of exocytosis were derived from the sum of new membrane required to both compensate endocytosis and provide net growth.

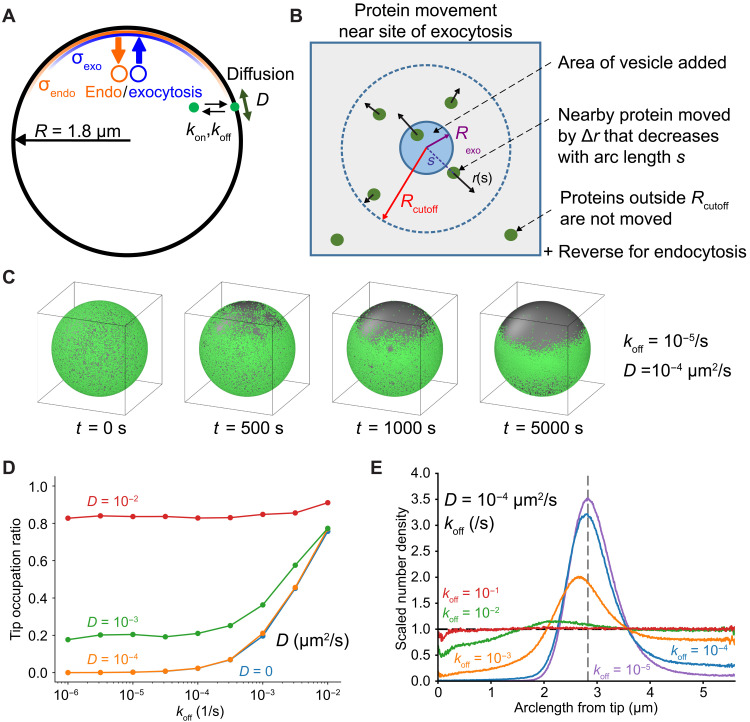
Fig. 2. Simulations of membrane flow–induced concentration gradients.

(A) Particles representing proteins (green particle) have diffusion coefficient D on a spherical cell and exchange with a uniform internal pool with rates k_off and k_on. Exocytosis (endocytosis) events occur with a distribution of width σ_exo (σ_endo) around a point representing cell tip. The green particle represents any protein that reversibly associates with the PM. (B) Particle displacement away/toward site of exocytosis/endocytosis by a distance ∆r up to a maximum distance of R_cutoff. (C) Depletion of particles starting from uniform distribution occurs for σ_exo < σ_endo, under static conditions (exocytosis rate is equal to measured endocytosis rate). (D) Tip occupation ratio versus k_off and D, same conditions as (C). Points are an average taken from t = 15,000 to 20,000 s after the start of the simulation. (E) Scaled number density versus arclength shows depletion and lateral peak near sphere equator at low k_off values, same conditions as (C). Dashed vertical gray line represents equator; dashed horizontal black line represents isotropic density value. Lines are time averaged from 10,000 to 20,000 s.

Table 1. Reference parameter values used in simulations.

Variable	Value	Description
R	1.8 μm	Radius of model sphere, approximation to S. pombe radius
R cutoff	2 μm	Cutoff range for exocytosis/endocytosis effect on sphere surface
α	0.5	Mobile membrane fraction
γ	1	Ratio of lipid to protein velocity
R exo	50 nm	Radius of individual exocytotic vesicles (57, 58, 76)
A exo	3.14 × 10−2 μm2	Surface area of individual exocytotic vesicles
R endo	22.6 nm	Radius of individual endocytotic vesicles based on measurements in S. cerevisiae (60)
A endo	6.42 × 10−3 μm2	Surface area of individual endocytotic vesicles
r endo	2.44/s	Rate of endocytosis events (this work)
r exo, growth	0.68/s	Rate of exocytosis events under growth conditions (20.7 μm2/hour) (this work)
r exo, static	0.50/s	Static rate of exocytosis events (no net added area)
σexo	0.848 μm	SD of exocytosis distribution (this work)
σendo	1.838 μm	SD of endocytosis distribution (this work)

We first considered conditions where overall membrane delivery by exocytosis balances internalization by endocytosis and assumed that neither exocytic nor endocytic vesicles carry membrane-associated proteins. This assumption is based on prior work showing that RitC does not associate with endomembranes (18, 19) and on our findings that endocytosis is not necessary for depletion. In these conditions, we found tip depletion when exocytosis is narrower than endocytosis, σ_exo < σ_endo (Fig. 2C and fig. S2A). This is a condition that we verified in cells (fig. S3 and Materials and Methods). When σ_exo = σ_endo, the active diffusion generated by the randomness of endo- and exocytic events was not by itself sufficient to drive substantial concentration gradients (fig. S2, A and C). Under net growth conditions, where exocytosis exceeds endocytosis by the amount of extra membrane needed for cell growth, depletion was stronger and faster and occurred even when σ_exo = σ_endo (fig. S2, A to C). Net growth conditions in the absence of endocytosis also led to depletion, even if the rate of exocytosis was concomitantly reduced to retain the same net membrane area addition (fig. S2E). This latter situation, which may best mimic growth upon LatA treatment, showed somewhat reduced depletion, similar to our experimental observations in LatA-treated cells. Thus, an area-change model of membrane flow can reproduce the observed depletion from cell poles.

Using the measured endocytosis and exocytosis profiles in our model, we plotted the tip occupation ratio, a measure of depletion, as a function of k_off and diffusion coefficient D (Fig. 2D). The model makes two key, testable predictions: First, substantial tip depletion requires both parameters to be sufficiently small—this is the limit where particle movement and exchange are too slow to counteract flow away from the tip (movies S3 and S4). Second, membrane material flowing away from the cell tip accumulates in a region of enhanced density near the end of the depletion area (Fig. 2E). Lateral peak formation requires slow diffusion rates (fig. S2D). Both tip depletion and lateral buildup were stronger in conditions of net growth (fig. S2B).

Evidence of membrane flow in vivo

The finding that depletion is only observed for proteins with slow dynamics (low k_off or D) provides an explanation for the acute change in CIBN localization upon light-induced CRY2 interaction. Light activation promotes not only CIBN-CRY2 binding but also formation of CRY2 oligomers through a distinct binding interface (20, 25). CRY2 oligomers form bright foci (see Fig. 1A), predicted to reduce dynamics through clustering of membrane anchors. Using FRAP (fluorescence recovery after photobleaching) to estimate D and k_off (fig. S4 and Supplementary Materials), we found that CRY2 interaction causes a >10-fold decrease in CIBN-RitC D and k_off, to values consistent with tip depletion in the simulations (Fig. 3A). CRY2-CIBN tip depletion was more marked in experiments than predicted by the measured D and k_off values, which we reasoned is due to CRY2 oligomerization not only decreasing membrane-unbinding dynamics but also biasing CRY2 binding from the cytosol. This can be accounted for in the model by increasing the rate of particle dimerization on the membrane, which leads to exacerbated tip depletion (fig. S5). We propose that tip depletion events revealed by optogenetics are due to acute clustering-mediated changes in membrane-binding properties.

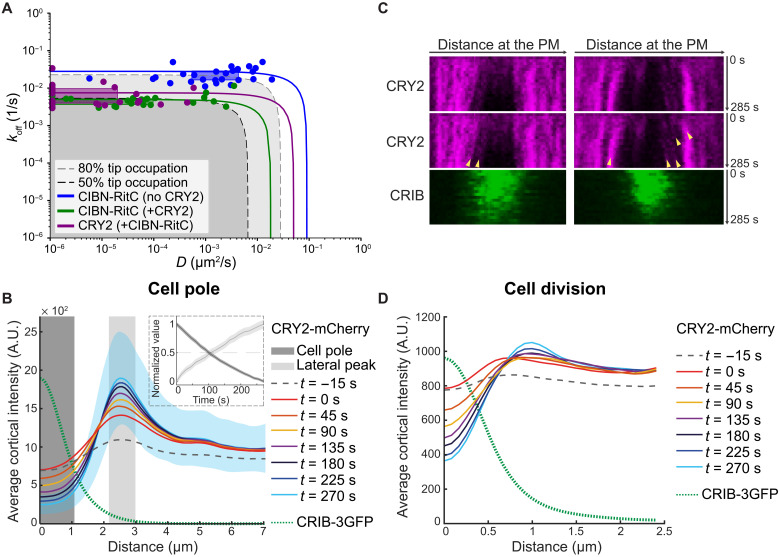
Fig. 3. Experimental validation of membrane flows with the optogenetic CRY2-CIBN system.

(A) D and k_off of CIBN-RitC and CRY2 with or without CRY2 coexpression, derived from FRAP measurements. Points are best D and k_off fits for individual cells. Boxes are data point lower and upper quartiles. Lines show D and k_off combinations resulting in same overall FRAP recovery (from ridge of averaged R² data fits; fig. S4). Curved corner region corresponds to comparable contributions of D and k_off; outer limits to recovery dominated by diffusion or exchange. Gray shaded regions have predicted tip occupation below indicated levels (from growth condition simulations). (B) CRY2 cortical profiles around cell poles in time-lapse imaging as in Fig. 1A. Time 0 is the first post-illumination image. Please compare to Fig. 2E. The green dashed line shows the average CRIB distribution. The inset shows the average fluorescence value over time in the shaded areas. Blue shaded area is the SD for time point t = 270 s. (C) Kymographs of the cell pole in cells as in Fig. 1A. Arrowheads mark clusters of CRY2 that move away from the center of the CRIB-labeled region, suggestive of flow-driven displacement. (D) CRY2 cortical profiles around division sites in time-lapse imaging as in fig. S1A. Traces represent average values of cells at different times of the cell division process. Time 0 is the first post-illumination image. The green dashed line shows the average CRIB distribution.

Simulations of protein removal by endocytic vesicles neglecting membrane flows, which were previously shown to maintain the polarization of slow-diffusing transmembrane proteins delivered by secretory vesicles (26), generate tip depletion for similar, low values of k_off and D. However, in contrast to simulations with flow displacement, they do not produce a lateral accumulation peak (fig. S2, F and G). Depletion and lateral accumulation peaks occur in a model with combined endocytic removal and displacement by flow (fig. S2, H and I). Thus, protein accumulation on the edges of the depletion zone is a characteristic feature of the model with protein displacement by membrane flow. As for tip depletion, protein accumulation on the edges of the depletion zone was dependent on k_off and D and was strongly enhanced by oligomerization (fig. S5D). Concordant with the flow displacement model, a lateral CRY2 peak corresponding to the edge of the CRIB-labeled depletion zone increased over time (Figs. 3B and 1A, white arrowheads). The rates of CRY2 level decrease from cell pole and increase at edges were indistinguishable, suggesting that they reflect the same molecular process (Fig. 3B). Kymographs of CRY2 oligomers at cell tips also directly showed events of flow away from the cell pole (Fig. 3C). We observed similar lateral CRY2 peaks on the edges of the depletion zone at the division site (Fig. 3D). These observations support the existence of bulk membrane flows carrying associated proteins away from sites of polarized secretion.

Protein dynamics condition tip depletion

To test the role of membrane binding in flow-mediated protein patterning without the amplifying effect of oligomerization, we constructed a series of one, two, or three tandem copies of the membrane anchor RitC tagged with sfGFP (Fig. 4A). As RitC binds the membrane peripherally and can exchange between membrane and cytosolic pools, our hypothesis was that tandem copies would lead to increased residence time at the PM. Estimated k_off and D rates extracted from FRAP experiments were higher for 1xRitC than 2xRitC and 3xRitC (Fig. 4B). A control 3xsfGFP-1xRitC construct showed only slightly reduced k_off compared to sfGFP-1xRitC but more reduced lateral diffusion, suggesting a possible effect of protein size or perhaps weak sfGFP-mediated oligomerization. The measured dynamic parameters of 2xRitC and 3xRitC, but not 1xRitC and 3xsfGFP-1xRitC, fall within the range predicted in the model to cause local depletion (Fig. 4B). Cell pole depletion was observed for 2xRitC and, more prominently, 3xRitC, but not 1xRitC constructs (Fig. 4C). This is particularly visible in comparison with the uniform localization mCherry-1xRitC coexpressed in these cells (Fig. 4A). Signal depletion at cell poles correlated with Cdc42-GTP levels (fig. S6A). In time-lapse experiments, 3xRitC was observed to dynamically deplete from sites marked by CRIB at both growing cell poles and division sites and repopulate cell poles during cell division when growth stops and CRIB disappears (Fig. 4D and movie S5). Thus, slowing down the dynamics of a peripherally membrane-associated protein suffices to displace it from sites of active secretion.

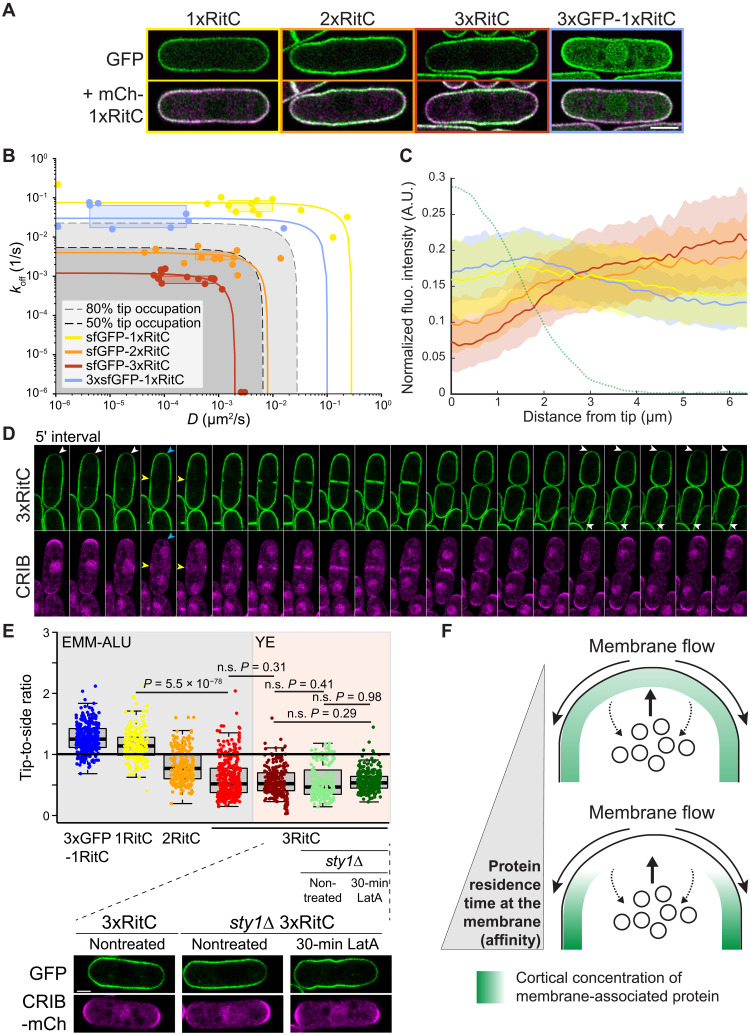
Fig. 4. The lateral diffusion and detachment rates of peripheral membrane proteins condition their cortical distribution by coupling to bulk membrane flows.

(A) Airyscan imaging localization of indicated sfGFP-tagged RitC constructs in cells coexpressing mCherry-1xRitC. Color-coded boxes match color coding in (B), (C), and (E). (B) D and k_off of indicated RitC constructs derived from FRAP measurements (points, boxes, and lines) and compared to predicted tip occupation levels (gray shaded), similar to Fig. 3A. (C) Distribution of sfGFP-RitC constructs at the cortex and CRIB signal distribution (green dashed line) (from cells as in fig. S6). (D) Time-lapse of 3xRitC coexpressed with CRIB-3xmCherry at 5-min interval. White arrowheads point to depletion at growth sites; the blue arrowhead indicates tip repopulation event when growth stops during cell division, and yellow arrowheads point to depletion at the future division site also marked by CRIB. (E) Ratios of tip-to-side signal measured for the indicated constructs and growth conditions. LatA treatment experiments were performed in sty1∆ cells on cells grown on lectin-coated plates in rich media (YE) as reported (24). The bottom panel shows corresponding images. P values are from Student’s t test with unequal variance. n.s., not significant. (F) Scheme of secretion-induced membrane flow and influence on the distribution of peripheral membrane–associated proteins. Local secretion associated with endocytosis over a wider zone leads to bulk membrane flows away from the secretion site. Membrane-associated proteins (green) with sufficiently long membrane residence time (high affinity) couple to the flows and are depleted from the secretion zone.

We further confirmed that 3xRitC depletion from cell poles was independent of endocytosis by probing its distribution in LatA-treated cells, again using the sty1∆ mutant background to alleviate the LatA-triggered stress response. Depletion from cell poles is reflected in a <1 fluorescence ratio between cell tips and cell sides: 0.8 for 2xRitC and 0.5 for 3xRitC (Fig. 4E). In sty1∆ cells, the tip-to-side ratio of 3xRitC was 0.5 as in wild-type cells and was unchanged upon LatA treatment, indicating that 3xRitC depletion from cell poles does not depend on endocytosis.

Collectively, these data demonstrate that the membrane residence time of peripheral membrane–associated proteins, which is defined by both membrane dissociation and lateral diffusion rates, is a strong predictor of protein distribution around sites of polarized exocytosis–induced membrane flows (Fig. 4F). The dependence of protein distribution on membrane affinity should invite careful consideration of this parameter when designing probes to evaluate lipid distribution.

Rga4 GAP localization is consistent with membrane flow coupling

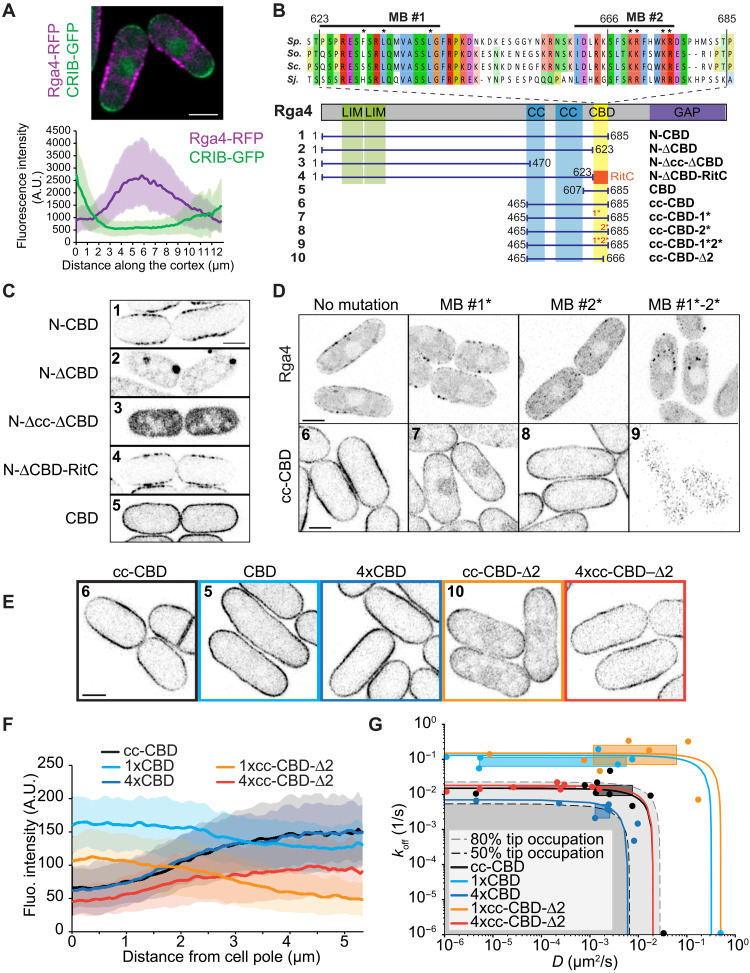
To probe the role of membrane flows in cell patterning, we focused on the Cdc42 GAP Rga4, which is excluded from cell poles and forms membrane-associated clusters previously described to form a “corset” pattern around the site of growth (15). Quantitative profiles around the cell cortex indeed showed that Rga4 is depleted from the CRIB-labeled cell poles, and its distribution is skewed toward the cell tip with higher CRIB intensity (Fig. 5A) (15, 27).

Fig. 5. Structure-function analysis of the Cdc42 GAP Rga4 defining membrane-binding and oligomerization motifs coupling to membrane flows.

(A) Maximum projection image of Rga4-RFP (red fluorescent protein) and CRIB-3GFP over a medial 4-μm cell section. The graph shows average Rga4 distribution in sum projections along the cell cortex in 70 cells from three experiments. Profiles were aligned from the cell tip with higher CRIB intensity (green line). Shaded areas indicate SD. (B) Scheme of Rga4 and truncation fragments. The sequence alignment shows the CBD across Schizosaccharomyces species (Sp., S. pombe; So., Schizosaccharomyces octosporus; Sc., Schizosaccharomyces cryophilus; Sj., Schizosaccharomyces japonicus). Fragments are numbered to help guidance through panels (C to E). (C) Localization of indicated Rga4 truncations, showing role of CBD in membrane localization and role of coiled coils (cc) in cluster formation. (D) Localization of full-length Rga4 and the cc-CBD minimal Rga4 with or without mutations in membrane-binding (MB) motifs #1 and #2. For full-length Rga4, maximum projections of 10 time points at 2-s interval are shown. (E) Localization of the minimal cc-CBD Rga4 fragment and single or 4x tandem CBD and cc-CBD-∆2 constructs. Color-coded boxes match color coding in (F) and (G). (F) Average cortical distribution of indicated constructs. Shaded areas show SD. (G) D and k_off of Rga4 fragments as in (E) derived from FRAP measurements (points, boxes, and lines) and compared to predicted tip occupation levels (gray shaded), similar to Fig. 3A.

Through structure-function analysis of GFP-tagged Rga4 fragments, we defined determinants of membrane association and cluster formation. Consistent with previous observations (27), a cortex-binding domain (CBD; amino acids 623 to 685) was both necessary and sufficient for membrane association (Fig. 5, B and C). This region could be replaced by RitC to target Rga4 N terminus to the cortex. CBD sequence analysis revealed two conserved sequences: a weak amphipathic helix prediction (membrane-binding motif #1) and a region rich in basic residues, predicted by a high basic and hydrophobic (BH) score (membrane-binding motif #2; fig. S7A) (28). Mutations of key residues in these two motifs did not individually block cortical binding but together resulted in cytosolic localization. This was the case whether the mutations were introduced in a short Rga4 fragment containing coiled coils and the CBD (cc-CBD), or whether they were introduced in the full-length Rga4 expressed from the native genomic locus (Fig. 5D). Full-length Rga4 containing mutations in both membrane-association motifs, which was cytosolic, was nonfunctional, as shown by the round shape of cells also lacking the other two Cdc42 GAPs Rga3 and Rga6 (fig. S7B) (29). Thus, these data identify two membrane-binding motifs in the CBD, which are together essential for Rga4 localization at the PM.

The N-terminal fragment lacking the CBD and full-length Rga4 with a nonfunctional CBD formed cytosolic condensates, as previously observed upon overexpression of a cytosolic form of Rga4 (Fig. 5, C and D) (14). These condensates disappeared upon exposure to high temperature (37°C for 6 hours) or 5% 1,6-hexanediol, thought to interfere with weak hydrophobic interactions (fig. S7, C and D), suggesting phase-separation properties. In the N-terminal fragment, condensates were absent upon further truncation of the coiled coils (Fig. 5C; compare fragments 2 and 3). The Rga4 N terminus containing the LIM domains likely also contributes to condensate formation, as we did not observe condensates in cytosolic fragments lacking this region (Fig. 5D, fragment 9). We conclude that Rga4 forms larger molecular assemblies for which the coiled coils and perhaps other determinants are necessary.

A minimal Rga4 fragment containing both coiled coils and CBD (cc-CBD) recapitulated the main features of Rga4 localization, as it formed membrane-associated clusters that were partly depleted from cell poles (Fig. 5, E and F). We used this fragment to probe how a simplified endogenous protein may be affected by membrane flows. Truncating the coiled coils led to faster membrane-binding dynamics and repopulation of the cell poles (CBD fragment; Fig. 5, E to G). Tandem multimerization of the CBD (4xCBD) increased membrane affinity and restored depletion from cell poles (Fig. 5, E to G), as did artificial CBD oligomerization by fusion with CRY2 (fig. S8A). Truncating one of the membrane-binding motifs (cc-CBD-∆2) to reduce membrane affinity led to faster protein dynamics, as confirmed by FRAP analysis (Fig. 5G) and total internal reflection fluorescence (TIRF) microscopy (fig. S8, B and C, and movies S6 and S7). This truncation caused enrichment at cell poles (Fig. 5, E to G), indicating affinity of the coiled coil region for cell tips. Similar enrichment at cell poles was observed upon mutations in either membrane-binding motifs #1 or #2 to reduce membrane binding affinity (Fig. 5D, fragments 7 and 8). Conversely, increasing membrane affinity by multimerization (4xcc-CBD-∆2) restored tip depletion and enrichment to cell sides (Fig. 5, E to G). The estimated k_off and D of all protein fragments largely covaried, falling in parameter space regions consistent with their observed distribution. We conclude that, even with a preferential association at cell poles, the oligomerization and two membrane-binding motifs of Rga4 ensure a sufficiently long membrane residence time that couples Rga4 to membrane flows toward cell sides.

Flow-driven negative feedback shapes the cell

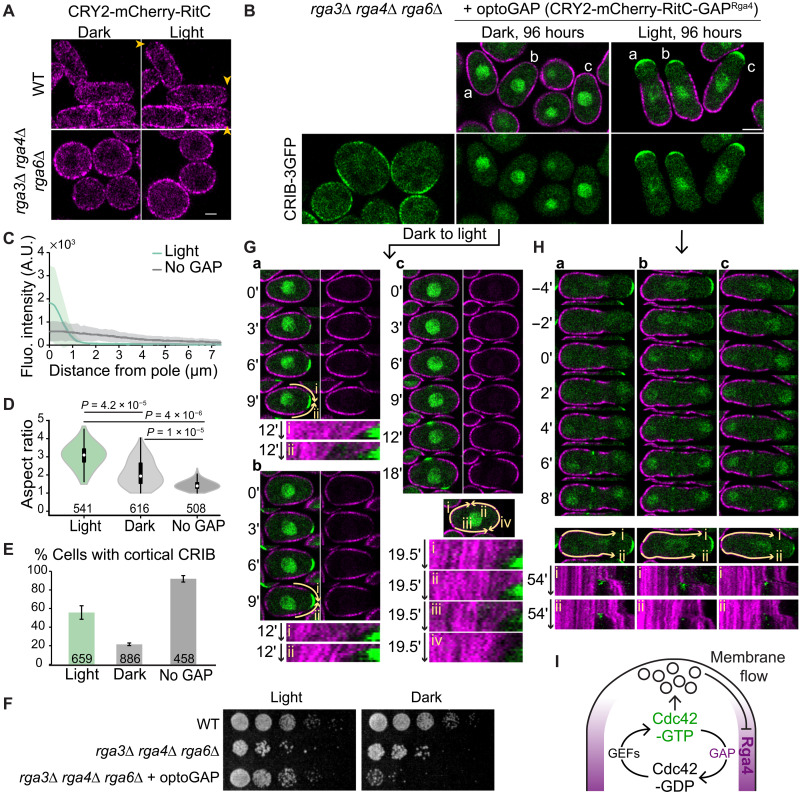
To directly test the importance of the GAP lateral localization, we constructed a synthetic GAP (optoGAP) consisting of CRY2, the membrane-binding RitC, and the Rga4 GAP domain. RitC targets optoGAP to the PM. In the dark, the distribution is predicted to be uniform including at cell poles because RitC unbinding and lateral diffusion dynamics are fast enough (as measured in Fig. 4B). In the light, oligomerization of CRY2 is predicted to increase membrane residence time by clustering several RitC molecules and thus couple the optoGAP probe to membrane flows, leading to depletion from cell poles. A control CRY2-RitC construct lacking the GAP domain was uniformly distributed in wild-type cells in the dark but was depleted from cell tips within 7 min of light exposure (Fig. 6A). In contrast, in cells lacking all endogenous Cdc42 GAPs, which display very large zones of Cdc42 activity leading to the absence of polarized exocytosis, round morphology, and poor growth (29), CRY2-RitC distribution was uniform in both dark and light conditions. Expression of optoGAP in these mutant cells in the light led to a strong reduction in the size of Cdc42-GTP zones, with concomitant local depletion of optoGAP (Fig. 6, B and C), restoring viability and the rod cell shape (Fig. 6, D and F). By contrast, upon growth in the dark, optoGAP was present around the cell periphery (Fig. 6B) and was toxic to the cells (Fig. 6F), which retained a round morphology (Fig. 6D). The round shape and toxicity are likely due to uniform GAP activity suppressing Cdc42-GTP, as the majority of dark-grown cells showed no cortical CRIB (Fig. 6E). These data agree with the conclusion that lateral localization of the Cdc42 optoGAP is critical to constrain the zone of Cdc42-GTP activity and build the rod cell shape.

Fig. 6. Bulk membrane flow–induced Cdc42 GAP depletion forms a negative feedback restricting the secretion zone.

(A) Localization of CRY2-mCherry-RitC probe in light versus dark conditions in wild-type and rga3∆ rga4∆ rga6∆ cells. Arrowheads point to depletion zones in light conditions. (B) rga3∆ rga4∆ rga6∆ CRIB-3GFP cells expressing or not expressing optoGAP continuously grown in the light or dark for 96 hours. (C) CRIB-GFP cortical profiles in light-grown optoGAP cells versus cells not expressing optoGAP as in (B). (D) Aspect ratio of cells as in (B). P values calculated from Student’s t test with equal variances. (E) Percentage of cells as in (B) with CRIB cortical signal. (F) Serial dilution of indicated cells on rich medium. (G) Cells indicated as a, b, and c in (B) (dark conditions), grown in the dark and shifted to light at time 0. Kymographs at the bottom were constructed over segmented lines of invariant length marked by the yellow arrows (i to iv). OptoGAP clusters show directional movement away from the newly forming polarity site but are almost static at lateral positions. (H) Cells indicated as a, b, and c in (B) (light conditions) grown in the light. Time 0 is set at the first time point with CRIB-3GFP signal at the division site. Kymographs at the bottom were constructed over segmented lines of invariant length marked by the yellow arrows (i and ii). During cell division, optoGAP clusters display extensive directional movement away from the division site toward the previously growing cell end. Note that in the 12-min time-lapse shown, the cells are not growing. (I) A double-negative feedback regulates the size of the Cdc42-GTP zone. Cdc42-GTP promotes secretion, which induces membrane-associated flow of Rga4 GAP to cell sides where it restricts Cdc42 activation, thus constraining the Cdc42-GTP zone. GEFs, guanine nucleotide exchange factors.

To further probe the mode of optoGAP exclusion from sites of growth, we imaged cells during the dark-to-light transition, which acutely increases the optoGAP membrane residence time. Light exposure provoked strong local optoGAP depletion coinciding with establishment of a zone of Cdc42 activity, followed by outgrowth of a tube of restricted width (Fig. 6G and movies S8 and S9). During depletion, which occurred before tube outgrowth, clusters of optoGAP exhibited lateral flow movements away from the CRIB-labeled zone, captured in kymographs of the cell periphery. These movements are consistent with the view that optoGAP couples to membrane flows. We note that upon longer growth in the light, optoGAP did not form visible lateral peaks on the edges of the CRIB zone and instead appeared depleted from proximal regions of the growing cell pole, although small amounts were present along the shaft of the tube. We suspect that the large pools of optoGAP present in the back of the cell titrate the majority of optoGAP through strong CRY2-mediated oligomerization. We conclude that coupling of Cdc42 inhibition to membrane flows, which are themselves induced by Cdc42 activity, forms a spatial negative feedback sufficient to restrict zones of Cdc42 activity and define cell width (Fig. 6I).

We also observed strong, directional movements of optoGAP away from the division site in cells grown continuously in the light. Most optoGAP cells are monopolar, growing at only one cell pole. At cell division, the optoGAP cleared from the division site, concurrent with the arrival of CRIB marking Cdc42-GTP. OptoGAP clusters displayed long-distance (several micrometers) unidirectional movement toward the cell pole that was growing in the preceding interphase (Fig. 6H and movie S10). While further work will be required to establish the cause of these movements with certainty, these observations agree with the idea of long-distance membrane flows at the PM caused by targeted secretion at the division site and endocytosis still present at the previously growing half of the cell.

DISCUSSION

Eukaryotic cell membranes are in constant flux, with exocytosis and endocytosis universally controlling PM homeostasis. Serendipitous observations of an optogenetic system in fission yeast cells led to our discovery that membrane-associated proteins can be depleted from sites of exocytosis. Our complementary simulations and experiments indicate that this depletion is best explained by bulk membrane flow away from the secretion site, where membrane-associated proteins are displaced in a fountain-flow manner away from zones of polarized secretion, due to membrane area addition in the center of a wider subtraction area. Not all membrane-associated proteins are depleted from secretion sites: Only those with sufficiently long residence time at the membrane are. Because membrane flows are a consequence of polarized secretion, they are likely to be prevalent in cells and pattern membrane-associated proteins, coordinating with the cytoskeleton that can independently tune membrane rheology (30, 31).

The observation that non-native proteins (CRY2 and RitC multimers) are displaced from sites of secretion raises the question of whether secretion site–derived bulk membrane flows also pattern the localization of native proteins. We have focused here on the Cdc42 GAP Rga4, showing that a short fragment containing elements of oligomerization (coiled coils) and membrane binding (CBD) displays localization consistent with flow coupling. Thus, membrane flows are likely to be an important factor to pattern the native Rga4 protein. Additional factors may influence Rga4 localization. For instance, previous work proposed that the lateral localization of Rga4 is due to an exclusion mechanism controlled by the Pom1 kinase (27). The documented interaction of Rga4 with Pom1, which accumulates at cell poles, may indeed provide an explanation for the cell pole enrichment of cc-CBD fragments with low membrane affinity (27, 32). However, we note that membrane flows can be sufficient to explain Rga4 exclusion from growing cell ends, without invoking a Pom1-dependent exclusion mechanism.

Our experiments with the artificial Cdc42 optoGAP demonstrate that bulk membrane flows can be harnessed to pattern and shape the cell. These experiments provide a notable example of cell shape regulation by a simple change in protein localization. The optoGAP is constitutively active whether cells are grown in dark or light conditions, as shown by its effect on the localization of the Cdc42-GTP CRIB reporter, but its localization is markedly different. In the dark, optoGAP localizes indiscriminately to the entire PM, preventing Cdc42 activity, leading to sick, round cells. In the light, CRY2 oligomerization leads to increased membrane residence time, coupling optoGAP to membrane flows, which displace it from sites of secretion. This creates a local depletion of Cdc42 inhibition, allowing enhancement of activity and establishment of polarized growth. We note that strong oligomerization of immobile optoGAP in the nongrowing part of the cell likely titrates a large fraction of optoGAP, explaining the very low signals along the newly grown cell portion. Because Cdc42 activity promotes secretion, which creates flows that displace the Cdc42 inhibitor to lateral regions, this results in the formation of Cdc42 activity zones of defined dimension (Fig. 6I). Thus, membrane flows underlie a negative feedback that shapes the cell.

Membrane flows may pattern a variety of membrane-associated factors. Besides Rga4, membrane flows may promote the lateral localization of other proteins that organize the yeast cell shape and division and explain their exclusion from both cell poles in wild-type cells, as well as from the only growing pole in monopolar mutants (for instance Rga6, Mid1, Blt1, Cdr2, and Skb1 (16, 27, 33–37)). Establishment of daughter cell identity in Saccharomyces cerevisiae through exocytosis-mediated septin ring formation is likely to belong to the same class of morphogenetic processes (38). Membrane flows may also help couple endocytosis around sites of exocytosis, which also promote polarity establishment (39, 40). Other proteins localize to secretion sites despite membrane flows, thanks to fast membrane unbinding, directed cytoskeletal transport, or preferred affinity to static components. For instance, pole-enriched Pom1 shows association to microtubule-transported factors and very fast membrane unbinding dynamics (32, 41). The Cdc42 GTPase also has to resist dilution from secretion-derived membrane addition, through rapid turnover at the membrane and likely other mechanisms (42).

Protein patterning via membrane lipid flow is likely to take place in all eukaryotic cells, in parallel to other patterning processes, such as actin cortex–dependent transport in animal cells. In yeast cells, membrane flow away from cell tips occurs because the membrane secreted by polarized exocytosis associated with net growth far exceeds that needed for growth and is recovered by endocytosis over a broader zone. The excess membrane delivery is about four- to fivefold according to our estimates (Table 1) and other measurements made in a recent study (43). This is likely also the case in tip-growing fungi and pollen tubes (44). More broadly, long-range membrane flow should be a general phenomenon occurring even in cells maintaining their size, whenever regions of exocytosis and endocytosis are spatially segregated or when they overlap but have unequal widths. They may thus accompany cellular processes ranging from the formation of neuronal connections, cilia, and immunological synapses (45, 46) to cell migration and cytokinesis (47, 48).

Our simulations and experiments clearly demonstrate how the dynamic properties of membrane-associated proteins are the determining factor for membrane flow patterning. Membrane proteins that couple to lipid flow will spatially segregate if they remain associated on the membrane for a sufficiently long time and their diffusion is sufficiently slow relative to the flow rate and length scale involved, such that transport dominates diffusive spreading. We thus found that protein depletion at tips of yeast cells only occurs for proteins with slow enough membrane detachment and diffusion rates. More generally, for flows with velocity v over length scale L, diffusion and detachment rates leading to depletion can be estimated as D/v < L < v/k_off (see Materials and Methods). Animal and plant cells, like yeast cells, likely harbor membrane-associated proteins that couple to flows and are displaced from sites of secretion. While transmembrane proteins in yeast cells are well known to exhibit particularly slow diffusion rates [perhaps due to interaction with the static cell wall (26), which may also hinder their movement along with lipid flow], the lateral diffusion of proteins associated with the inner leaflet (for instance, Rho/Ras-family proteins) is only about two- to fourfold slower in yeast than animal cells (18, 49–51). Some membrane proteins in animal cells can have lateral diffusion coefficients significantly reduced upon tandem linkage or oligomerization (52, 53), compatible with flow coupling. Because protein localization can be altered by a simple change in membrane unbinding rates, as shown, for instance, by the acute localization change of CRY2 complexes, similar changes may occur in physiological conditions through posttranslational modifications that modulate membrane affinity and/or oligomerization.

MATERIALS AND METHODS

Model methods

Simulations of effects of exocytosis and endocytosis on protein distributions

To investigate conditions that lead to depletion of proteins from a growing cell tip, we simulate the motion of non-interacting particles moving along a surface representing the PM under the effects of membrane binding/unbinding, diffusion, and membrane delivery/removal by exocytosis/endocytosis. The biophysical assumptions of our model are presented together with the model implementation below. For simplicity, the particles in these simulations are restricted to the surface of a sphere with a radius of 1.8 μm with a fixed point on the sphere surface specified to be the growing tip. All arclengths are measured with respect to this fixed point.

Time step

The simulation was evolved through time primarily by using the Gillespie algorithm (54). An event is chosen from the list of possible events that include particle association and dissociation from the membrane, endocytosis, and exocytosis (excluding diffusion). The probability of a specific event occurring is given by the ratio of the event rate to the sum of the rates of all possible events (i.e., P_i = r_i/∑ r_j, where r_i is the rate of event i). The time until the selected event occurs is calculated as Δt = −ln (u′)/∑ r_j, where u′ is a uniform random number between 0 and 1.

Diffusion

Particle diffusion, with diffusion coefficient D, is implemented with Brownian dynamics. The magnitude of the displacement due to diffusion over time ∆t is calculated as $\sqrt{2D\text{∆}t}\mathrm{\xi }(t)$ independently in both directions in the plane tangent to the sphere, and ξ(t) is a random Gaussian distributed variable with zero mean and unit variance. After calculating the displacement in the tangent plane, the positions of each particle are then projected down to the sphere surface while keeping the distance conserved to correctly describe diffusion on a spherical surface (55). Since particles are assumed to diffuse independently of each other, we only calculated the displacement due to diffusion before endocytosis or exocytosis events or before saving the data (except for a model with particle dimerization described below). We ensured that this implementation of diffusion on the sphere surface reproduced the correct scaling behavior for the angular diffusion (55) by measuring the change in the polar angle, 〈θ(t)²〉, as a function of time up to a time step of 1000 s as shown in fig. S9A.

Membrane binding and unbinding

Particles on the sphere undergo an unbinding event with rate k_off where they are removed from the sphere surface and placed in an internal pool representing the cytoplasm. Particles in this internal pool are placed back on the surface anywhere with uniform probability with rate k_on. This process assumes a sufficiently fast cytoplasmic diffusion to ensure uniform cytoplasmic concentration. We fix k_on = 0.01 s⁻¹ since, within our independent particle approximation, this rate should only affect the average number of particles on the surface but not the relative level of tip depletion at steady state. To calculate smooth concentration profiles, there are, on average, approximately 50,000 particles on the surface at steady state in the simulations.

Particle movement by exocytosis and endocytosis

We assume that exocytosis and endocytosis near cell tips create a local flow that displaces lipids and proteins around the site of the vesicle event (42, 56). Our assumption is supported by the appearance of a flat PM in electron micrographs of fission yeast cell at cell sides and tips, except at sites of vesicle traffic or around eisosomes (57–59), similar to S. cerevisiae (59, 60). This observation indicates the presence of a membrane tension, which, combined with turgor pressure, can flatten the vesicle membrane delivered by exocytosis (61, 62), causing lateral flow. Similarly, flow of lipids toward endocytic vesicles must occur over a sufficiently wide area, preventing membrane strains larger than a few percent that would otherwise lead to formation of membrane pores (63).

We simulate the movement associated with exocytosis as occurring instantaneously (i.e., no diffusion or membrane binding/unbinding occurs during the movement of the particles for either exocytosis or endocytosis). Our simulations are technically an area-change model, as they do not explicitly include hydrodynamics, considered in many prior membrane models, such as in (64). Our rationale for this choice is that unlike single-component membranes, cellular membrane hydrodynamics remain unresolved (65), likely resembling those of a two-dimensional (2D) multiphase fluid in the presence of obstacles, such as immobile transmembrane proteins connected to the cell wall (66). We thus judged that these complexities would not justify the assumptions and additional computational complexity of a full hydrodynamic model.

We do however consider a few key hydrodynamic parameters. First, similar to animal cells, we anticipate a fraction of the membrane, as high as 50%, to be immobile, with the fluid component undergoing Darcy-type flow (64, 65, 67). The fraction α of the fluid component of the membrane (that could be heterogeneous, containing lipids and proteins with different diffusion coefficients) is a parameter that we vary in the model. Peripherally associated membrane proteins whose viscous drag is determined by the lipid membrane are assumed to be physically and hydrodynamically coupled to this lipid flow. To account for proteins whose drag and diffusion coefficient is influenced by interactions with structures that remain stationary or less mobile with respect to lipid flow, such as in the cell wall or in the cytoplasm, we introduce a parameter γ measuring the ratio of lipid to protein velocity (with γ ≥ 1). Unless otherwise indicated, we assume γ = 1.To simulate the effect of slow equilibration of membrane tension over long distances (31), we also introduce a cutoff distance to the flow induced by individual exocytosis and endocytosis events. As we show below, our results on tip depletion are robust with respect to the precise values of the mobile fraction α, velocity ratio γ, and cutoff distance.

In the simulation, exocytosis and endocytosis events take place on the surface of the sphere and affect the positions of nearby particles. The location of these events is selected randomly from an experimentally determined distribution (see below). Lipids on the surface at arclength distance s from the event are assumed to be pushed away radially from the center of exocytosis as shown in Fig. 2B by arclength distance ∆r(s). It is assumed that the difference between the spherical cap surface area corresponding to mobile lipids, A_cap, measured at the final and initial arclength positions of the particle from the center of exocytosis equals the surface area of the exocytotic vesicle A_exo

$$\begin{array}{c}{\mathit{A}}_{\text{cap}}(\mathit{s}+∆\mathit{r}(\mathit{s}))-{\mathit{A}}_{\text{cap}}(\mathit{s})={\mathit{A}}_{\text{exo}},\\ {\mathit{A}}_{\text{cap}}(\mathit{s})=\mathrm{\alpha } 2\mathrm{\pi }{\mathit{R}}^2[1-\text{cos}(\frac{\mathit{s}}{\mathit{R}}\left)\right]\end{array}$$ (1)

where s is the arclength distance, R is the radius of the sphere, and parameter α describes the fraction of mobile proteins and lipids between 0 (no mobility) and 1 (all mobile). This gives for the displacement of membrane proteins

$$\begin{array}{c}∆{\mathit{r}}_{\text{exo}}(\mathit{s})=\frac{1}{\mathrm{\gamma }}\{\mathit{R}\prime \mathrm{a}\text{cos}[1-{\left(\frac{\mathit{R}}{\mathit{R}\prime }\right)}^2 [1-\text{cos}(\frac{\mathit{s}}{\mathit{R}}\left)\right]-\frac{{\mathit{A}}_{\text{exo}}}{2\mathrm{\pi }{\mathit{R}}^{\prime 2}\mathrm{\alpha }}]-\mathit{s}\},\\ \mathit{R}\prime =\sqrt{{\mathit{R}}^2+{\mathit{A}}_{\text{exo}}/4\mathrm{\pi }}\end{array}$$ (2)

where R′ is the radius that the sphere would have to accommodate the membrane area contributed by the exocytotic vesicle. The parameter γ describes the coupling between the proteins and the flowing membrane with higher values correlating with weaker coupling. The displacement is only applied to particles up to an upper arclength distance, s < R_cutoff, beyond which we assume that the effects of membrane delivery are not felt immediately. The small difference between R and R′ was introduced to avoid artificial accumulation of particles at the opposite sphere end in the absence of a cutoff R_cutoff but is otherwise insignificant for the simulations with a cutoff distance smaller than the arclength corresponding to the half sphere. For an endocytosis event, particles within the cutoff distance R_cutoff are moved radially toward the endocytic point, similar to the calculation for exocytosis, with displacement magnitude

$$\begin{array}{c}∆r_{\text{endo}}(s)=\frac{1}{\mathrm{\gamma }}\{-R\prime \mathrm{a}\text{cos}[1-{\left(\frac{R}{R\prime }\right)}^2[1-\text{cos}(\frac{s}{R}\left)\right]+\frac{A_{\text{endo}}}{2\mathrm{\pi }{R}^{\prime 2}\mathrm{\alpha }}]+s\},\\ R\prime =\sqrt{R^2-A_{\text{endo}}/4\mathrm{\pi }}\end{array}$$ (3)

where A_endo is the surface area of the endocytic vesicle. When the displacement magnitude ∆r_endo(s) calculated by Eq. 3 is larger than s, particles are moved to the endocytosis event point for the simulations where endocytosis does not contribute to internalization; for the model with endocytic removal, they are internalized into the internal pool of particles.

The dependence of the model on parameters α and γ occurs approximately through their product, αγ, as the distance proteins are displaced by exocytosis is ∆r_exo ≈ A_exo/[αγ2πR∣sin (s/R)∣] and similarly for endocytosis, as long as s > 0.25 μm and α > 0.1 for the reference parameters of Table 1.

Distribution of exocytosis and endocytosis

The distribution for exocytosis/endocytosis is based on the experimental distribution as a function of arclength distance from the cell tip, P_exp(s), measured by imaging the profile along a medial confocal plane. The distribution P_exp(s) can be well described by a Gaussian of SD σ_exo and σ_endo for exocytosis and endocytosis, respectively. To convert this 2D distribution to a 3D one, we assume that the experimentally observed profiles account for events within a slab of width on the order of the microscope’s resolution along the axis perpendicular to the glass slide (b = 0.71 μm) (fig. S9B). Thus, assuming cylindrical symmetry, the distribution of an event at arclength s from the position defined as cell tip used in simulations is calculated as

$$\begin{array}{cc}\hfill \mathit{P}(\mathit{s})& =\mathit{C} {\mathit{P}}_{\text{exp}}(\mathit{s})\mathit{f}(\mathit{s}),\text{where}\mathit{f}(\mathit{s})\hfill \\ & =\{\begin{array}{cc}1,& \mathit{s}\le \mathit{R} \mathit{a}\text{sin}\left(\frac{\mathit{b}}{2\mathit{R}}\right)\\ \mathrm{\pi }/[2 \mathit{a}\text{sin}(\frac{\mathit{b}}{2\mathit{R}\text{sin}(\mathit{s}/\mathit{R})}\left)\right],& \mathit{R} \mathit{a}\text{sin}\left(\frac{\mathit{b}}{2\mathit{R}}\right)<\mathit{s}\le \frac{\mathrm{\pi }\mathit{R}}{2}\\ \mathrm{\pi }\text{sin}\left(\frac{\mathit{s}}{\mathit{R}}\right)/[2 \mathit{a}\text{sin}(\frac{\mathit{b}}{2\mathit{R}}\left)\right],& \mathit{s}>\frac{\mathrm{\pi }\mathit{R}}{2}\end{array}\hfill \end{array}$$ (4)

where P_exp(s) is the experimental 2D probability distribution, P(s) is the adjusted 3D probability distribution used in simulations, C is a normalization constant, and f(s) is the fraction of the circumference of the circle at a given value of s outside the slab region (i.e., thin line region of the circle circumference divided by the thick line region in fig. S9B). The expression for f(s) initially assumes that for s > πR/2, the shape is that of a spherocylinder (as this is the shape of the actual cell), which is then mapped back onto a sphere by keeping the density of events constant by multiplying by sin(s/R). Agreement between experimental and simulated P(s) considering only the slab region is shown in fig. S9C. The azimuthal angle for the exocytotic or endocytic event is picked from a uniform distribution.

Rates of membrane area delivery by endocytosis and exocytosis

We calibrated the model based on measurements performed as described in Supplementary Methods. First, the measured average rate of old end tip growth was 0.0305 ± 0.0151 μm/min (n = 75 cells; average ± SD), which, multiplying by 2πR, corresponds to net membrane area added of 0.345 μm²/min = 20.7 μm²/hour.

Second, we measured the rates of endocytosis at growing old end tips by counting the number of Fim1 patches in a medial section and extrapolating to the whole cell tip area. Please see experimental details in the Supplementary Materials. Since the Gaussian profile of the endocytosis distribution extends beyond the hemispherical tip region, we considered separately the medial section rates at the hemispherical region (arclength from tip 0 to πR/2, with 24.35 ± 10.56 events/min) and cylindrical segment (arclength πR/2 to πR, with 5.26 ± 3.85 events/min counting both sides). The fraction of events in a medial section of the hemispherical region would be ${\displaystyle {\int }_0^{\mathrm{\pi }\mathit{R}/2}}{\mathit{P}}_{\text{exp}}(\mathit{s})\mathit{ds}/{\displaystyle {\int }_0^{\mathrm{\pi }\mathit{R}/2}}\mathit{f}(\mathit{s}){\mathit{P}}_{\text{exp}}(\mathit{s})\mathit{ds}$. This ratio is 0.233 using the measured σ_endo, leading to 104.53 endocytosis events/min for the whole hemispherical region. The fraction of cylindrical area imaged in a medial section is b/(πR) = 0.126, leading to 41.62 endocytosis events/min in the cylindrical region around the cell tip. Summing the numbers for hemispherical and cylindrical regions provides a rate of r_endo = 146.2/min = 2.44/s as listed on Table 1. This corresponds to endocytosed membrane area of 0.939 μm²/min, using the estimate of endocytic vesicle radius in Table 1.

Third, we estimated the rates of exocytosis by assuming that the rate of membrane area delivered by exocytosis is equal to the sum of net area added because of growth plus the membrane area endocytosed (sum = 1.28 μm²/ min ). Using the estimate of exocytic vesicle radius in Table 1 leads to r_exo = 40.9/min = 0.68/s as listed on Table 1.

Measurement of tip occupancy ratio and reference parameters

The tip occupancy ratio is calculated by dividing the density of particles at an arclength of πR/4 = 1.41 μm (a quarter of half sphere total tip arclength) away from the top tip of the sphere by the density of particles in the remaining area of the sphere. The reference parameter values are listed in Table 1.

Effect of parameters k_on, cutoff distance R_cutoff, mobile fraction α, and velocity ratio γ

Results presented in the main figures and fig. S2 used values of k_on = 0.01 s⁻¹, α = 0.5, and R_cutoff = 2 μm. We also examined the effect of varying these parameters. As expected, the steady state reached is independent of k_on (fig. S9D). Decreasing the value of R_cutoff to 1.0 μm decreases overall depletion and lateral peak magnitude, shifting the peak toward the left, while increasing R_cutoff to 2.5 μm reverses the trend (fig. S9E). We find that decreasing α to a value of 0.1 (low mobile fraction) results in larger depletion and higher lateral peak, while increasing α to a value of 1.0 (highest mobile fraction) reverses the trend (fig. S9F). This trend reflects that with increasing α, the mobile PM and associated proteins are displaced by a smaller distance to accommodate the area of exocytic or endocytic vesicles. Increasing the value of γ to 10.0 (10-fold lower protein flow compared to lipid flow) results in decreased lateral peak and a decreased tip exclusion compared to same conditions with γ = 1.0 (fig. S9F).

Requirements for tip depletion: Dimensional analysis

We can rationalize the requirements for k_off and D to be sufficiently for tip depletion using dimensional analysis. Consider that membrane flow develops over length scale L, i.e., the approximate arclength distance along the cell tip spanning the region between the peak of exocytosis rate at the cell tip and the tail end of endocytosis close to the start of the cell’s cylindrical segment. First, for proteins to remain bound to the membrane during their transport via membrane flows with velocity v over distance L, they require L < v/k_off. Second, diffusion will cover a smaller distance compared to such transport when D/v < L. Conditions for tip depletion can thus be summarized as D/v < L < v/k_off. Considering that, in our system, L ≈ 2 μm and estimating $\mathit{v}\approx {\mathit{A}}_{\text{exo}}{\mathit{r}}_{\text{exo}}/(4\mathrm{\pi }\overline{\mathit{s}})\approx 3 \text{nm}/\mathrm{s}$ at an average exocytic arclength position $\overline{\mathit{s}}$ = 0.57 μm (where approximately half of all exocytic vesicles push the membrane radially away from the tip and assuming α ≈ γ ≈ 1) give D < 0.006 μm²/s and k_off < 0.0015/s, on the same order as the threshold values in Fig. 2.

Dimerization simulations

To investigate the effect that oligomerization has on the extent of tip depletion and lateral peak height, we performed additional simulations in which we allow surface particles representing proteins to bind together to form dimers (fig. S5A). We did not explicitly include the effects of oligomerization in our main simulations (Fig. 2), where the values of D and k_off measured from FRAP can be thought to reflect average behavior from individual particle to aggregate. Here, we show that the binding of particles together into multimers further enhances the depletion and lateral peak, even without a change in the diffusion coefficient or membrane dissociation rate from the multimer. To avoid artificial concentration gradients as a result of implicit energy input to the system, we implemented a scheme designed to satisfy detailed balance in equilibrium in the absence of exocytosis and endocytosis. In addition to association and dissociation of particles between cytoplasm and surface representing the PM (reaction 1 in fig. S5A with rate constants k_on and k_off), dimers can be formed in two ways: Either two surface particles can bind reversibly to form a dimer (reaction 2 in fig. S5A with rate constants k₊ and k₋), or a particle from the bulk cytoplasm and a surface particle can bind reversibly to form a dimer (reaction 3 in fig. S5A with rate constants k_on,2 and k_off,2). While two particles are bound in the dimer state, they have the same position and they move together under diffusion, exocytosis, and endocytosis. To distinguish between the effects of oligomerization versus diffusion, as well as for simplicity, we used the same diffusion coefficient for surface monomers and dimers.

With rate constants in units of inverse time, detailed balance in the absence of exocytosis and endocytosis requires ${\mathit{k}}_{\text{on}}{\mathit{N}}_{\mathit{b}}={\mathit{k}}_{\text{off}}{\mathit{N}}_{\mathit{sm}},{\mathit{k}}_{+}{\mathit{N}}_{\mathit{sm}}^2={\mathit{k}}_{-}{\mathit{N}}_{\mathit{sd}},{\mathit{k}}_{\text{on},2}{\mathit{N}}_{\mathit{b}}{\mathit{N}}_{\mathit{sm}}={\mathit{k}}_{\text{off},2}{\mathit{N}}_{\mathit{sd}},$ where N_b is the number of bulk particles in the cytoplasm, N_sm is the number of surface bound particles as monomers, and N_sd is the number of surface particles in dimers. We also have N_b + N_sm + N_sd = N_tot, where N_tot is the total number of particles that is constant throughout the simulation. Simultaneously solving these four equations results in expressions for the number of particles in each state in equilibrium—N_b,eq, N_sm,eq, and N_sd,eq—and a fourth equation, the detailed balance condition, for the reaction rate constants, which can be written as k₊ = k_on,2k₋ k_off/(k_off,2 k_on). In these simulations, we kept k_on = 0.01 s⁻¹.

To investigate the effect of dimerization on tip depletion, we then turned on exocytosis and endocytosis. We define a parameter describing the effect of cooperativity, which is the ratio of equilibrium rate of particle association to the surface through dimer formation (reaction 3) versus the equilibrium rate of bulk cytoplasm particle attaching to the surface as monomer (reaction 1): p = k_on,2N_b,eqN_sm,eq/(k_onN_b,eq) = k_on,2N_sm,eq/k_on. The value of p thus implicitly defines the value of rate constant k_on,2, as well as that of k₊ through detailed balance when k_off, k_off,2, and k₋ are given.

All reactions, except dimer formation through surface monomers, were handled with the Gillespie algorithm, similar to the case without dimerization described earlier. When a cytoplasmic particle binds to the surface to form a dimer, it is placed at the same position as a randomly picked surface monomer particle. In the reverse reaction, one of the two particles in the dimer is selected to become a cytoplasmic particle while the other maintains its original position.

To handle the reaction of two surface particles binding together to form a dimer, we used the method implemented in Smoldyn (68), where particles associate when separated by a distance less than a binding radius, σ_b, and are placed at an unbinding radius, σ_u, upon unbinding into two surface monomers, using σ_b = σ_u. To determine σ_b, we followed the 3D reaction scheme of Smoldyn as a guide (where σ_b is determined on the basis of the time step, diffusion coefficient, and k₊); however, as reactions in 2D involve additional complexities (69, 70), we adjusted σ_b by explicitly checking that detailed balance is satisfied in simulations without endocytosis or exocytosis. Values of σ_b ranged from 5·10⁻⁵ to 0.05 μm as p was varied. The association reactions were checked over a fixed time interval Δt_fixed = 0.01 s. Diffusion of surface particles was implemented every Δt_fixed and before any endocytosis or exocytosis event. Dimerization between a pair of particles occurs if they are at a distance less than or equal to σ_b at the end of such a timestep. The unbinding reaction of a dimer into two surface particles is handled by the Gillespie algorithm and the rate constant k₋ where the particles are placed a distance of σ_u away from each other with random orientation. Because of the additional computational costs associated with calculating distances between particle pairs, we reduced the total number of particles to N_tot = 5000 and simulations were run for 10,000 s.

We find that as p increases (keeping k_off = k₋ = k_off,2), the number of dimers at steady state increases at the expense of monomers on the surface and cytoplasm particles (fig. S5B). The tip depletion and height of lateral peak also increases as a function of p for fixed values of D and k_off, when these were taken to be close to those of CRY2 + CIBN-RitC (fig. S5, C to E). This result shows that dimerization, and more generally oligomerization, can lead to an enhancement of tip depletion and lateral peak. A decrease of the dimer dissociation rates k₋ = k_off,2 compared to the monomer k_off further enhances this effect (fig. S5, F to H).

Determination of membrane diffusion and dissociation rates by FRAP

Diffusion coefficients and membrane dissociation constants were determined by fitting FRAP recovery profiles to a 1D model (fig. S4). The method relies on the different effects of diffusion and association/dissociation on the recovery, with diffusion providing smoothing of profile over time (71) and association/dissociation contributing to uniform recovery. Detailed methods are described in the Supplementary Materials.

Experimental materials and methods

Media and growth conditions

For microscopy experiments, cells were grown to exponential phase in Edinburgh minimal medium (EMM) supplemented with amino acids as required, unless indicated otherwise. For experiments in Figs. 1 and 3 and figs. S1 and S3, cells were first precultured in 3 ml of EMM in dark conditions at 30°C for 6 to 8 hours; exponentially growing precultures were diluted [optical density at 600 nm (OD_600nm) = 0.02] in 10 ml of EMM and incubated in dark conditions overnight at 30°C, except for ypt3-i5 and control strains that were cultured at 25°C in yeast extract (YE). To allow proper aeration of the culture, 50-ml Erlenmeyer flasks were used. For experiments in Figs. 4 to 6 and figs. S4 and S6 to S8, S. pombe cells were grown at 25°C. All live-cell imaging were performed on EMM-ALU (adenine-leucine-uracil supplement) agarose pads, except for the experiment shown in Figs. 1E and 4E, for which lectin-coated 96-well plates were used.

The control CRY2-mCherry-RitC was transformed in the triple mutant background (rga3Δ rga4Δ rga6Δ) and in wild-type cells (Fig. 6A). For the triple mutant, the strain was cultured either continuously in light or in dark conditions for 72 hours before imaging. In the wild-type background, the strain was cultured under dark conditions and light exposure was performed at the microscope using a 488-nm laser over three Z-stack planes to trigger CRY2 oligomerization over a 15-min time period. The optoGAP strain (Fig. 6) was generated and grown continuously in light conditions (details on strain generation below). To compare cell morphologies in light and dark conditions (Fig. 6, B to E), the strains were grown on YE plates over 2 days at 30°C in the presence of light. Cultures in EMM-ALU were then prepared and split in incubators with or without light and diluted over 4 days to maintain exponential growth until imaged. The strains grown in the dark were not exposed to any light source until the moment of imaging. From these cultures, half of the cell material was used for Airyscan imaging and half was used for Calcofluor imaging. To study the dark-to-light transition (Fig. 6G), cultures grown in the dark as above were shifted to light conditions at the microscope during live-cell imaging performed on EMM-ALU 2% agar pads using blue light exposure at five focal planes through the cell depth every 2 min. For the drop-test assay (Fig. 6F), cultures were grown in the light as above, adjusted to OD₆₀₀ = 0.3 and subjected to 5× serial dilutions, and 5 μl of each dilution was spotted on YE plates and grown at 30°C under light or dark conditions.

Strain construction

Strains used in this study are listed in table S1. Standard genetic manipulation methods for S. pombe transformation and tetrad dissection were used. Gene tagging was performed at endogenous genomic locus at the 3′ end, yielding C-terminally tagged proteins, as described (72). GFP-Ypt3 protein was ectopically expressed in addition to the endogenous gene by transforming a wild-type strain with Pme I–linearized pBSII(KS⁺)-based single integration vector (pSM2366-3′UTR^ade6-GFP-Ypt3-hphMX-5′UTR^ade6) targeting the ade6 locus (73). Gene tagging, gene deletion, and plasmid integration were confirmed by diagnostic polymerase chain reaction (PCR) for both sides of the insertion. The construction of plasmids and strains expressing the CRY2-CIB1 optogenetic system was done as described in (2).

To generate the RitC strain series, a synthetic gBlocks DNA fragment was ordered (Integrated DNA Technologies Inc.) containing four RitC repeats separated by linker sequences with restriction sites for the generation of 1x, 2x, and 3xRitC constructs. For all ordered synthetic gBlocks with repeat sequences, codon usage was modified between repeats to allow successful synthesis. The RitC constructs are N-terminally tagged with sfGFP through subcloning in the stable integration vector (S.I.V.) backbone pAV0327 for ura4 integration under expression from act1 promoter and with tdh1 terminator (Addgene ID: 133488) (73). Plasmid numbers and descriptions are in table S2. Plasmids maps are available upon request. 1xRitC was additionally tagged N-terminally with mCherry in the S.I.V. pAV607 for ade6 locus integration (Addgene ID: 133504) (73). The 3xsfGFP-1xRitC tagging was performed on pAV327 backbone carrying one sfGFP sequence and subcloning of a synthetic gBlock with two additional sfGFP sequences and the RitC sequence. Plasmids were integrated as described (73). Strains with either mCherry-1xRitC or CRIB-3xmCherry along with the respective sfGFP-tagged RitC construct were generated through mating and tetrad dissection.

For the structure-function analysis of Rga4, fragments were amplified from the full-length gene originally amplified from cDNA using primers listed in table S3 and first cloned in pSM621 (pREP41-GFP) for C-terminal tagging with GFP. All tagged fragments were subsequently amplified and introduced in S.I.V. for ura4 single integration pAV327 in S. pombe with act1 promoter–driven expression and tdh1 terminator (Fig. 5, C to E, and fig. S7C). The cc-CBD and cc-CBD-Δ2 fragments were additionally also expressed under a pom1 promoter at the ura4 locus to allow resolution of single clusters by TIRF imaging (fig. S8, B and C). All integrations of Afe I–linearized plasmids were performed in a rga4Δ::kanMX strain (YSM3826). Synthetic gBlocks DNA fragments were ordered for the generation of the multimerized 4xCBD and 4xcc-CBD-Δ2 constructs and introduced in S.I.V.s by In-Fusion cloning (Takara Bio Inc.) (Fig. 5E). The CRY2-mCherry-CBD construct was also generated on a S.I.V. backbone for ura4 integration and driven by act1 promoter pAV0328 (Addgene ID: 133489; fig. S8A) (73). Immediately after transformation, this strain was grown and stored only in dark conditions in the absence of any light source until the moment of imaging. Point mutations in Rga4 membrane binding domains 1 and 2 were generated through several rounds of side-directed mutagenesis with primers listed in table S3 for both fragments and full-length Rga4. The mutagenized fragments were introduced in S.I.V.s and transformed at ura4 locus as described above. The mutagenesis of the full-length Rga4 was performed on a plasmid carrying the open reading frame and 112 base pairs of up- and downstream sequence. The entire sequence was excised (Bam HI/Sal I) and transformed in rga4Δ::ura4⁺ background for integration at the endogenous locus, selected by growth on 5-fluoroorotic acid (5-FOA) and verified by the absence of growth on EMM-AL medium. The strains were genotyped and verified by sequencing for the presence of mutations. Each mutagenized allele was subsequently tagged with GFP-natMX via standard PCR-based WACH approach (72) and additionally introduced in rga3Δ::hphMX rga6Δ::kanMX background through the standard S. pombe mating protocol and tetrad dissection.

The optoGAP was generated on a S.I.V. for ade6 locus integration (pAV0356; Addgene ID: 133468) (73) with act1 promoter driving the expression of CRY2-mCherry-RitC-rga4(aa665-933). Fragments were assembled by standard cloning. CRY2-mCherry-RitC control was generated by Asc I/Sac I digestion of the optoGAP backbone vector and reintroduction of RitC through standard cloning. The Pme I–linearized plasmids were transformed in a rga3Δ::hphMX rga4Δ::ura4+ rga6Δ::kanMX strain (YSM3136) (29) and in wild-type background for the CRY2-mCherry-RitC control. The optoGAP strain was continuously grown in the presence of light at 30°C, unless otherwise indicated. We note that attempted transformation of these cells in the dark resulted in the absence of colonies, suggesting toxicity as subsequently shown in the serial dilution assay (Fig. 6F). This growth defect was absent for the CRY2-mCherry-RitC control. Both CRY2-RitC and the optoGAP strain (rga3Δ::hphMX rga4Δ::ura4⁺ rga6Δ::kanMX ade6::pact1-CRY2-mCherry-RitC-rga4(aa665-933)::ade6⁺) were then transformed with pAV046 for CRIB-3xGFP-kanMX integration at leu32 locus in light conditions. BH-search prediction was performed at https://hpcwebapps.cit.nih.gov/bhsearch/ with window size for residue averaging of 15 amino acids and values for amino acids set to standard BH parameters.

Microscopy

Spinning disk microscopy

Images in Figs. 1 and 3 and figs. S1 and S3 were acquired using a spinning disk confocal microscope, essentially as described (74, 75). Image acquisition was performed on a Leica DMI6000SD inverted microscope equipped with an HCX PL APO 100×/1.46 numerical aperture oil objective and a PerkinElmer confocal system. This system uses a Yokogawa CSU22 real-time confocal scanning head, solid-state laser lines, and a cooled 14-bit frame transfer electron-multiplying charge-coupled device (EMCCD) C9100-50 camera (Hamamatsu) and is run by Volocity (PerkinElmer). When imaging strains expressing the CRY2-CIB1 optogenetic system, an additional long-pass color filter (550 nm; Thorlabs, Newton, NJ, USA) was used for bright-field image acquisition to avoid precocious photoactivation caused by the white light. In ypt3-i5 experiments, an objective heater (Bioptechs, Butler, PA, USA) was used for temperature control. Experiments in Figs. 1 and 3 and fig. S1 were carried out using cell mixtures. Cell mixtures were composed of one sample strain of interest (the sample optogenetic strain coexpressing the indicated GFP-tagged protein) and up to two control strains, namely, (i) RFP (red fluorescent protein) control, an RFP bleaching correction strain expressing cytosolic CRY2PHR-mCherry and (ii) drug performance control, a strain expressing specific GFP or RFP markers tagging molecular components targeted by the drug used in the specific experiment [see fig. S1 (F and I)].

Strains were handled in dark conditions throughout. Red light-emitting diode light was used in the room to manipulate strains to prepare the agarose pads and lectin-coated 96-well plates. Strains were cultured separately. For experiments using agarose pads, exponentially growing cells (OD_600nm = 0.4 to 0.6) were mixed in 2:1:1 (strain of interest, RFP control, and drug performance control) ratio and harvested by soft centrifugation (2 min at 1600 rpm). The cell mixture slurry (1 μl) was placed on a 2% EMM-ALU agarose pad, covered with a #1.5-thick coverslip, and sealed with Vaseline, lanolin, and paraffin (VALAP). Samples were imaged after 5 to 10 min of rest in dark conditions. For experiments using lectin-coated 96-well plates, wells were first coated using 100 μl of soy bean lectin (L1395, Sigma-Aldrich) overnight. Coated wells were washed three times using 200 μl of H₂O and dried for 4 hours at room temperature. Exponentially growing cells (YE liquid media, OD_600nm = 0.4 to 0.6) were mixed in 2:1:1 (strain of interest, RFP control, and drug performance control) ratio to a final OD_600nm = 0.1. The cell mixture slurry (200 μl) was placed in lectin-coated wells and left for 45 min in the dark to allow cell-lectin attachment. Last, cells were washed three times with 200 μl of YE, and 200 μl of fresh YE liquid medium was added for imaging.

CRY2PHR signal depletion at the cell tips and cell middle

Spinning disk time-lapse images shown in Fig. 1A, fig. S1A, and movies S1 and S2 correspond to middle section focal planes. Images were acquired every 30 s for GFP, RFP, and bright-field channels. Ultraviolet (UV) channel was acquired every 1.5 min to avoid phototoxicity caused by UV light. Lasers were set to 100%; shutters were set to sample protection, and in all instances, the GFP channel was imaged first (for CRY2 photoactivation) and then the additional channels. RFP exposure time was set to 200 ms, whereas the GFP exposure was set to 1 s. Cells were monitored in these conditions for 20 min.

CRY2PHR tip depletion dynamic and cell-side accumulation dynamic analyses

Strains coexpressing CRIB, Ypt3, Exo84 or Exo70 GFP-tagged proteins, and the CRY2-CIB1 system were monitored to assess tip depletion dynamics. In these experiments, an RFP control strain was added to the cell mixtures. Results of these experiments are shown in Figs. 1B and 3 (B and C) and fig. S1 (B to E). Lasers were set to 100%; shutters were set to sample protection, and in all instances, the GFP channel was imaged first and then the RFP channel. RFP exposure time was always set to 200 ms, whereas the GFP exposure time varied depending on the monitored protein. Cells were monitored in these conditions for 285 s, and images were acquired every 15 s.

Tip depletion dynamics upon disrupting exocytosis using BFA

For BFA (B6542, Sigma-Aldrich) experiments shown in Fig. 1C and fig. S1 (F and G), cells coexpressing CRIB-3GFP or GFP-Ypt3 and the CRY2-CIB1 system were imaged. An RFP control strain and a strain expressing Anp1-GFP were mixed in this experiment. Anp1-GFP is a Golgi marker that, in normal conditions, forms prominent puncta (fig. S1F, left). Upon blocking of endomembrane trafficking due to BFA treatment, Anp1 puncta disappear and the protein relocalizes to the endoplasmic reticulum (fig. S1F, right). BFA (diluted in ethanol; final concentration, 300 μM) was added to the cell mixture slurry. Cells were placed on top of 2% EMM-ALU + 300 μM BFA agarose pads to be imaged. Lasers were set to 100%; shutters were set to sample protection, and in all instances, the GFP channel was imaged first and then the RFP channel. RFP exposure time was always set to 200 ms, whereas the GFP exposure time varied depending on the monitored protein. Cells were monitored in these conditions for 285 s, and images were acquired every 15 s.

Tip depletion dynamics upon disrupting exocytosis using ypt3-i5 ts allele.

For ypt3-i5 experiments shown in Fig. 1D and fig. S1H, ypt3-i5 and ypt3⁺ cells coexpressing CRIB-3GFP and the CRY2-CIB1 system were imaged. In these experiments, an RFP control strain was added to the cell mixtures. Cells were cultured at 25°C throughout the experiment and placed on 2% EMM-ALU agarose pad sealed with VALAP. Two sets of pads were prepared, one to be imaged at 25°C and another one to be imaged at 36°C. Before imaging, pads were incubated for 30 min either at 25° or 36°C and imaged at the respective temperatures by setting the objective heater accordingly. Lasers were set to 100%; shutters were set to sample protection, and in all instances, the GFP channel was imaged first and then the RFP channel. RFP exposure time was always set to 200 ms, whereas the GFP exposure was set to 1 s. Cells were monitored in these conditions for 285 s, and images were acquired every 15 s.

Tip depletion dynamics upon disrupting endocytosis using LatA

For LatA (BML-T119-0500, Enzo Life Sciences) experiments shown in Fig. 1E and fig. S1 (H and I), sty1∆ cells coexpressing CRIB-3GFP and the CRY2-CIB1 system were imaged on lectin-coated 96-well plates. An RFP control strain and a strain coexpressing Exo70-GFP and Fim1-mCherry were mixed in this experiment. The Fim1-mCherry actin patch marker serves to verify actin depolymerization due to LatA treatment (fig. S1I). LatA [diluted in dimethyl sulfoxide (DMSO); final concentration, 50 μM] was added to 200 μl of YE liquid media. Lasers were set to 100%; shutters were set to sample protection, and in all instances, the GFP channel was imaged first and then the RFP channel. RFP exposure time was always set to 200 ms, whereas the GFP exposure was set to 1 s. Cells were monitored in these conditions for 285 s, and images were acquired every 15 s.

Cortical distribution profiles of exocytosis (Exo70-GFP) and endocytosis (Fim1-mCherry) and counting endocytic events at the cell cortex.

A strain expressing endogenous tagged Exo70-GFP and Fim1-mCherry was monitored to assess their cortical distribution at the cell tips. Results of these experiments are shown in fig. S3. Lasers were set to 100%, and shutters were set to sample protection. Cells were monitored in these conditions for 300 s, and images were acquired every 15 s (21 time points).

Airyscan imaging

All images in Figs. 4 to 6 and figs. S4 and S6 to S8 (except figs. S7B and S8B) were acquired on a Zeiss LSM 980 system with Plan-Apochromat 63×/1.40 oil differential interference contrast objective and acquired by the ZEN Blue software (Zeiss). Imaging was set in superresolution mode with frame bidirectional maximum speed scanning. Laser power was kept at <0.4%, with pixel time around 6.6 μs and frame acquisition time <2 s per channel. All other settings were optimized as recommended by the ZEN Blue software.

For the LatA (BML-T119-0500, Enzo Life Sciences) experiment shown in Fig. 4E, sty1∆ cells coexpressing sfGFP-3xRitC and CRIB-3xmCherry were imaged using lectin-coated 96-well plates. Cells were grown in YE at 25°C, and LatA (diluted in DMSO; final concentration, 50 μM) was added to 200 μl of YE liquid media. Cells were imaged after 30 min of treatment. LifeAct-GFP–expressing strain was used as a control for LatA depolymerization.

In Fig. 5A, z-stacks were set at optimal interval with 0.16-μm spacing over a total of 4 μm from the medial plane of the cell. All other imaging shows medial focal planes. Frames for movie S5 and Fig. 4D were acquired with 488- and 561-nm lasers every 5 min; frames for movies S8 and S9 and Fig. 6G were acquired with 488- and 561-nm lasers every 1 min and 30 s, and frames for movie S10 and Fig. 6H were acquired every 2 min.

FRAP was performed on cells on a microscope slide (maximum imaging time of 5 min) by finding the focal plane closest to the coverslip and defining a rectangular region of interest in the middle of the visible signal (see fig. S4A). Two snapshots were taken before bleaching, which was done using 20% laser power and a five-time repeat of the bleach zone. To determine the depth of the bleached signal immediately after bleaching, z-stacks optimally spaced at 0.16-μm interval were acquired across the entire depth of the cell, which allowed us to calculate that bleaching occurs over a depth of 2.0 to 2.5 μm. For 2xRitC and 3xRitC, recovery was imaged for 5 min, every 10 s; 1xRitC and Rga4 fragments were imaged at maximum speed every 729 ms for 1 min. For FRAP of CRY2-CIBN in the light-activated state, cells were first found in focus using the 561-nm laser, after which they were illuminated with transmitted white light for 45 s and a snapshot of CRY2 to CIBN recruitment at the mid-plane of the cell was taken. The FRAP was then performed as described above at the focal plane closest to the coverslip over a 5-min recovery time, acquired every 10 s; at each time point, acquisition was performed first with a 561-nm laser, followed by a 488-nm laser for a total frame acquisition time of 900 ms. The recovery for the FRAP of CIBN-GFP alone was recorded over 1 min, every 700-ms maximum speed imaging. All Airyscan images were processed in Zeiss Zen Blue software.

Other imaging

For cell length measurements (Fig. 6D) and cell morphology imaging (fig. S7D), cells were stained with Calcofluor (final concentration, 2 μg/ml; Fluorescent Brightener 28; F3543, Sigma-Aldrich) and imaged with a Leica epifluorescence microscope (×63 magnification). TIRF microscopy (fig. S8, B and C) was performed on a DeltaVision OMX SR imaging system, equipped with a 60× 1.49 numerical aperture TIRF oil objective (oil, 1.514), an illumination pathway for ring-TIRF and a front illuminated scientific complementary metal-oxide semiconductor (sCMOS) camera size 2560 × 2160 pixel (manufacturer PCO AG). Imaging settings were as follows: 512 × 512 pixel field of view, 100-ms exposure time, and laser power of 20% with TIRF angle 488 nm at 86.7°. Samples were placed on a 0.17 ± 0.01–mm–thick glass slide and imaged within 15 min. Imaging was performed every second over a 60-s imaging period.

Image analysis of concentration profile

All image processing analyses were performed with ImageJ software (http://rsb.info.nih.gov/ij/). Image and time-lapse recordings were imported to the software using the Bio-Formats plugin (http://loci.wisc.edu/software/bio-formats). Time-lapse recordings were aligned using the StackReg plugin (https://sites.imagej.net/BIG-EPFL/) using the rigid body method. All optogenetic data analyses were performed using MATLAB (R2019a), with scripts developed in-house. Figures were assembled with Adobe Photoshop CC2019 and Adobe Illustrator 2020. Details of image quantification procedures are available in the Supplementary Materials.

Statistical analysis

The Kruskal-Wallis test was used for comparison of CRY2 depletion for identical values of CRIB intensity in Fig. 1 and fig. S1. The Student’s t test with unequal variance was used in Fig. 4E to compare tip-to-side ratios of GFP signal and in fig. S8C. In Fig. 6D, the Student’s t test with equal variance was used. Experiments were conducted in triplicates, except where indicated. For the exact number of cells in each experiment, please refer to the experimental details.

Supplementary Materials

This PDF file includes:

Supplementary Methods

Tables S1 to S3

Figs. S1 to S9

Legends for movies S1 to S10

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S10

View/request a protocol for this paper from Bio-protocol.