Significance
Healthcare-associated infections caused by antimicrobial-resistant agents are hard to eliminate in hospitals partly because of the existence of asymptomatic spreaders who unwittingly transmit these pathogens to others. In practice, identifying asymptomatic patients colonized with antimicrobial-resistant agents is challenging, as only a limited number of carriers are typically observed. Here, we develop an efficient, individual-level inference method capable of estimating the colonization probability for each individual in a hospital network. Using real-world patient-to-patient contact networks and sparse observations of colonization, the proposed method identifies carriers of methicillin-resistant Staphylococcus aureus, a prevalent antimicrobial-resistant pathogen, more accurately than competing approaches informed by hospitalization history and contact tracing. In in silica control experiments, the individual-level inference supports improved, targeted interventions against healthcare-associated infections.
Keywords: antimicrobial resistance, asymptomatic colonization, healthcare-associated infections, infection control, mathematical model
Abstract
Antimicrobial-resistant organisms (AMROs) can colonize people without symptoms for long periods of time, during which these agents can spread unnoticed to other patients in healthcare systems. The accurate identification of asymptomatic spreaders of AMRO in hospital settings is essential for supporting the design of interventions against healthcare-associated infections (HAIs). However, this task remains challenging because of limited observations of colonization and the complicated transmission dynamics occurring within hospitals and the broader community. Here, we study the transmission of methicillin-resistant Staphylococcus aureus (MRSA), a prevalent AMRO, in 66 Swedish hospitals and healthcare facilities with inpatients using a data-driven, agent-based model informed by deidentified real-world hospitalization records. Combining the transmission model, patient-to-patient contact networks, and sparse observations of colonization, we develop and validate an individual-level inference approach that estimates the colonization probability of individual hospitalized patients. For both model-simulated and historical outbreaks, the proposed method supports the more accurate identification of asymptomatic MRSA carriers than other traditional approaches. In addition, in silica control experiments indicate that interventions targeted to inpatients with a high-colonization probability outperform heuristic strategies informed by hospitalization history and contact tracing.
Antimicrobial-resistant (AMR) organisms (AMROs) remain a leading cause of healthcare-associated infections (HAIs) (1–4). Because of a lack of effective treatment and high-mortality rates, the prevalence of existing and emerging drug-resistant agents continues to impose a heavy burden on healthcare systems globally (5). The World Health Organization declared antimicrobial resistance is one of the top 10 global public health threats facing humanity (6). In the United States alone, more than 2.8 million AMR infections occur each year, resulting in over 35,000 deaths (7). In Europe, among participating countries in the European Antimicrobial Resistance Surveillance Network (EARS-Net), 29 of 30 countries reported the occurrence of antimicrobial resistance among all eight bacterial species tracked by the EARS-Net during 2019 (8). The burden of AMR infections is even higher in low- and middle-income countries (9). Currently, five AMROs (carbapenem-resistant Acinetobacter, Candida auris, and Clostridioides difficile; carbapenem-resistant Enterobacteriaceae; and drug-resistant Neisseria gonorrhoeae) are highlighted as urgent threats by the US Centers for Disease Control and Prevention (CDC) (2), with a dozen other agents listed as serious threats, including methicillin-resistant Staphylococcus aureus (MRSA) (10–12).
In hospital settings, AMR infections are difficult to eliminate because of the existence of asymptomatic colonization (13–19). While most colonized patients do not experience infections, they can transmit AMROs to other patients and contaminate the environment in healthcare facilities (20). For instance, in two hospitals in the United Kingdom, undetected MRSA carriers were estimated to be the source of 75% of total transmission events in general wards (21). As a result, successful HAI control relies on the accurate and timely identification of asymptomatic AMRO spreaders (22, 23). In practice, however, sparse observations of colonization due to insufficient testing limit our ability to track transmission events, which are typically unobserved. In addition, community importation (24–26) and multiple modes of transmission in hospital [e.g., direct contact transmission (2) and environmental contamination (27, 28)] further complicate the detection of AMRO carriers. Although AMRO colonization in clinical settings has been linked to a number of risk factors, such as recent hospitalization and antibiotic use (29, 30), colonized patients without these risk factors may still be under detected and shed AMROs (31). Without improved identification methods, the asymptomatic carriage of AMROs constitutes a major barrier to effective containment of HAIs.
Mathematical modeling has been widely used to investigate and understand the transmission dynamics of AMROs (32–37) and guide the development of intervention measures against HAIs in healthcare systems (22, 23, 38–42). A number of approaches have been developed to estimate population-level transmission characteristics, including nosocomial transmissibility and importation rates from the community (43–46). In addition, several studies have used individual-level observations to infer the origin of a simulated outbreak using a susceptible, infected, and recovered model in a contact network (47–49). Despite these advances, it remains challenging to efficiently estimate patient AMRO colonization probabilities at the individual level using personal diagnostic information on colonization.
In this study, we develop and validate an individual-level inference method that supports the improved identification of AMRO carriers and apply this method to an outbreak of MRSA in 66 Swedish hospitals and healthcare facilities with inpatients, henceforth “Swedish healthcare facilities” (Materials and Methods). Using deidentified real-world hospitalization records, we construct an agent-based model in a time-varying patient-to-patient contact network to simulate MRSA transmission within hospitals. To better represent realistic transmission processes, we incorporate components of direct contact transmission, environmental contamination, and community importation into the model dynamics. The inference method propagates information from limited observations of colonized patients across the contact network and provides the estimates of colonization probability for each individual. For both model-generated and historical outbreaks, the proposed method more accurately identifies MRSA colonization than traditional approaches informed by hospitalization history and contract tracing. Additionally, interventions targeted to the inferred, high-probability MRSA carriers yield the greater identification of colonized patients and better control of the transmission in control simulation experiments.
Results
Modeling MRSA Transmission.
We use a data-driven, agent-based model informed by real-world patient movements to simulate outbreaks of MRSA. For the model, we construct a time-varying contact network using the hospitalization records from 66 Swedish healthcare facilities (46, 50). Patients staying in the same ward simultaneously are connected in the network, as shared healthcare workers (HCWs) within the ward may facilitate transmission between patients. This patient-to-patient contact network is updated on a daily basis, following the flow of new admissions, discharges, and patient transfers within the hospital network.
To represent actual transmission processes within the healthcare setting, several factors must be considered: transmission due to person-to-person contact, environmental contamination of the healthcare facility, and importation from outside the healthcare facility. In the agent-based model, we incorporate all three processes (Fig. 1A). Specifically, patients in hospital are either susceptible individuals who are free of MRSA (S) or colonized individuals who carry the bacterium (C). Each new admission from the community is colonized with a given probability. Within hospitals, a susceptible patient can be colonized through direct contact with an MRSA carrier, indirect contact mediated by HCWs, or through a contaminated environment (e.g., surfaces, objects, and medical instruments) in the ward where the patient stays. We treat the ward environment as a vector of MRSA transmission: Each colonized patient in a ward contributes to the environmental force of infection in that ward, which decays over time. Colonized patients return to the susceptible state at a spontaneous decolonization rate, or they are tested and observed with an observation rate. We present details of the model structure in Materials and Methods and provide model description using a modified Overview, Design concepts, and Details framework (51) in SI Appendix.
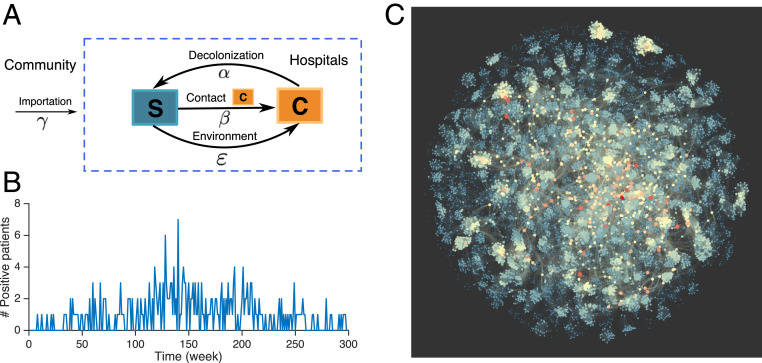
Fig. 1.
Structure of the agent-based model and MRSA outbreak in 66 Swedish healthcare facilities. (A) Schematic of the transition dynamics between the susceptible (S) and colonized (C) states for each individual in the agent-based model. The parameters , , , and are the importation rate, transmission rate, environmental force of infection, and patient decolonization rate. (B) Weekly incidence of patients testing positive with UK EMRSA-15. (C) An example of the patient-to-patient contact network in Swedish healthcare facilities during 1 wk. Nodes represent individual patients in the hospital who are connected in the contact network when residing in the same room on the same day. Node color represents the number of connections for each individual. Blue indicates a node that has a small number of connections, whereas red indicates a node has a large number of connections.
Each node of the time-evolving network is a patient. In stochastic agent-based model simulations, the patient state is binary (i.e., either S or C); however, for the transmission dynamics represented here, we instead quantify the evolution of the probability of each individual currently being in each state. Here, and represent the probability of individual being susceptible and colonized on day . If the states of neighbors in the contact network are independent, the evolution of and can be described by the following mean-field equations (see details in SI Appendix):
| [1] |
| [2] |
| [3] |
Here, is the patient decolonization rate, is the baseline transmission rate, is the ward in which patient resides, is the occupancy of ward , is the environmental force of infection in ward , is the baseline environmental contamination coefficient, is the mean environmental decolonization period, and is the set of patients in contact with patient on day . For networks without loops, the colonization probability computed using Eqs. 1–3 is in agreement with the result obtained through a large number of model simulations. For real-world contact networks with short loops, clustering is unlikely to significantly affect the accuracy of Eqs. 1–3 (52, 53). To initialize the system, new admitted patients are colonized with an importation rate . We use the above equations to track the evolution of patient colonization probability at the individual level within the time-evolving network. Each day, colonized patients in the hospital are observed with observation rate . Note that in both the agent-based model and the mean-field equations, we assume a common infectiousness for all colonized patients and a common initial probability of colonization for all new admitted patients.
In this study, we focus on the transmission of the most prevalent MRSA strain, UK EMRSA-15, in the network of Swedish healthcare facilities during a 6-y period (46). During this time, 289 patients tested positive for this strain (Fig. 1B). The hospitalization records for all patients are available, from which we construct the real-world patient-to-patient contact network. Individuals in the contact network have highly variable numbers of connections, which results in a highly heterogeneous network structure (Fig. 1C). The hospitalization history for confirmed MRSA carriers is shown in SI Appendix, Fig. S1.
Identifying Asymptomatic Carriers.
The identification of asymptomatic carriers is important for the containment of MRSA. In a previous study, we demonstrated that, by using parameters estimated from incidence numbers aggregated across all patients, an agent-based model can reproduce observed population-level, epidemic curves in free simulations (46). However, to obtain a more precise colonization probability for each patient, an inference system that utilizes individual-level, diagnostic information is needed. This task is particularly challenging, as observations of colonization are highly sparse, relative to the total number of patients in hospital.
To address this challenge, we develop a sequential, individual-level inference (SILI) algorithm to estimate model states. With this algorithm, in order to supplement the sparse data and thus better constrain the model, we use a backward temporal propagation process that augments the limited, observed information by inferring the colonization probability of confirmed carriers prior to their diagnoses. Using this augmented information, we can estimate the colonization probability for each individual in hospital. We begin at the start of the observed record and sequentially update the model states using the augmented data. During this process, information from past and future observations propagates in the contact network and reaches individuals with no observations. This expanded information is used to constrain the states and of unobserved individuals. An illustration of the inference framework is shown in SI Appendix, Fig. S2. Details and the pseudocode of the SILI algorithm are reported in Materials and Methods and SI Appendix.
Validation of Inference Using Synthetic Outbreaks.
We first validate the SILI inference using model-generated outbreaks, for which all colonized patients are known. Specifically, we generated a 52-wk outbreak using the stochastic, agent-based model with a prescribed set of parameters (SI Appendix, Table S1) and binary state conditions, and the output observed colonized individuals and the time of diagnosis. In total, only 91 cases were observed in the hospital during this simulation. All three modes (i.e., importation, contact transmission, and environmental transmission) contribute to the emergence of colonization, with contact transmission playing a major role (SI Appendix, Fig. S3).
We next used the synthetic observations and a two-step procedure to infer the colonization probability of each patient in hospital. First, we used population-level case numbers aggregated every 4 wk to estimate model parameters. We employed an iterated filtering (IF) method developed for agent-based models, which estimates parameters in a series of iterations (46) (Materials and Methods). With each iteration, model parameters are updated toward the actual values used in generating the synthetic outbreak (Fig. 2A). Certain estimates (e.g., , the mean environmental decolonization period) have a small bias, as the model dynamics are less sensitive to those parameters. However, as we show later, performance of the inference is robust to such estimation bias. Second, we used the estimated parameters and individual-level observations in the SILI algorithm to infer the colonization probabilities of all patients. We ranked patients present in the hospital in week 52, according to their estimated colonization probability, and compare the performance of the SILI algorithm in identifying asymptomatic spreaders with several other approaches: 1) free model simulation using inferred parameters without individual-level information; 2) length of stay in hospital; 3) number of total person–day contacts; 4) contact tracing to identify patients who have had direct contact with observed cases; and 5) a multivariate logistic regression model that uses the length of stay, number of total contacts, and number of contacts with observed cases as predictors (SI Appendix).
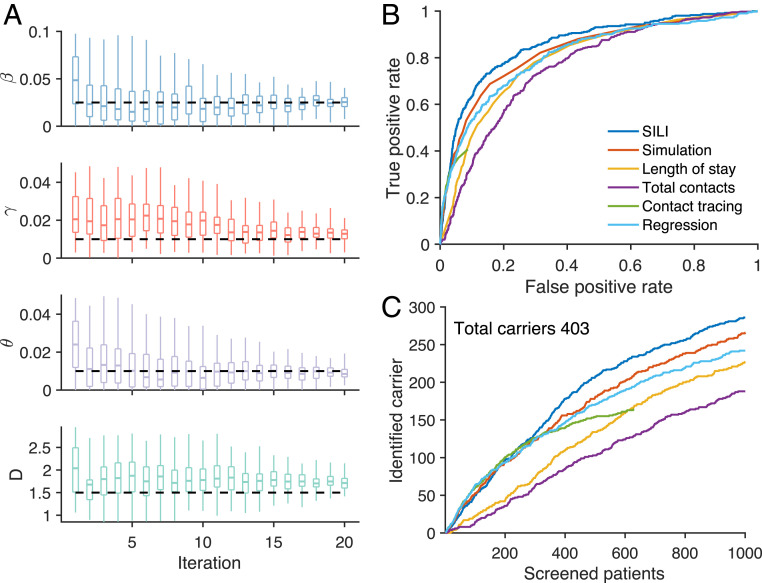
Fig. 2.
Inference of MRSA carriers in a model-simulated outbreak. (A) Inferred distributions of key epidemiological parameters (boxes and whiskers, interquartile, and 95% CI) and the actual values (horizontal dash lines) used in generating the synthetic outbreak. Distributions are presented for 20 iterations of the parameter inference using iterated filtering. The parameters , , , and are the baseline transmission rate, importation rate, baseline environmental contamination coefficient, and the mean environmental decolonization period. (B) The ROC curves for the identification of MRSA carriers using different methods at week 52. The ROC curve for contact tracing is incomplete, as it can only reach a subset of patients who have had contact with observed cases. (C) The number of MRSA carriers identified by screening a given number of patients using different approaches at week 52. The total number of carriers in the hospital is 403. The inference was performed for a simulated outbreak, with the majority of cases colonized within hospital because of person-to-person contacts. Results for a synthetic outbreak with most cases being imported, similar to the situation in real-world Swedish healthcare facilities, are provided in SI Appendix, Fig. S5.
We use the receiver operating characteristic (ROC) curve to compare identification accuracy. Methods that more accurately identify MRSA carriers have a larger area under the ROC curve. The SILI algorithm outperforms the other competing methods (Fig. 2B). Contact tracing is effective for patients who have interactions with observed cases but can only identify about 600 patients. The logistic regression model outperforms the other factors individually but still underperforms the SILI algorithm. Unlike the logistic regression model, the SILI algorithm incorporates the transmission dynamics depicted by the agent-based model, which likely improves its inference performance. We further compare the number of identified carriers by screening a given number of patients selected by different approaches (Fig. 2C). The SILI algorithm performs substantially better than other methods by identifying over 70% of carriers (286 out of 403) in the hospital during week 52 by screening 10% of patients (1,000 out of 9,812). We also demonstrate a consistent, superior identification of colonized patients by the SILI algorithm throughout the 52-wk period (SI Appendix, Fig. S4). Analyses for two other synthetic outbreaks, each with a different dominate mode of colonization, yield similar results (SI Appendix, Figs. S5 and S6). Note that, for the outbreak primarily driven by importation (SI Appendix, Fig. S5), the performance of all methods is degraded as the majority of colonized patients are admitted randomly from the community. Such highly stochastic dynamics limits the ability to infer asymptomatic carriers.
We further performed inference using a synthetic outbreak with both positive and negative observations (SI Appendix). The inference framework allows the incorporation of positive and negative test results, as well as test sensitivity and specificity, if this information is available (SI Appendix). The SILI algorithm again outperforms other ranking approaches when the information of negative tests is included (SI Appendix, Fig. S7).
MRSA Outbreak in Swedish Healthcare Facilities.
We apply the SILI inference to the real-world MRSA outbreak in 66 Swedish healthcare facilities spanning 320 wk. Unlike the synthetic outbreaks, the actual colonization states of the unobserved patients are unknown. To circumvent this difficulty, we took an indirect approach. For each week (, we use hospitalization records and observations within a sliding time window from week to week to estimate model parameters and infer colonization probabilities for all patients in week using the SILI algorithm. We then integrate Eqs. 1–3 to week and compute the colonization probability for each hospitalized patient during week . If the inference method is accurate, the observed cases should have a higher colonization probability than most of other patients present in hospital. Note that colonization probability is obtained using only information prior to the confirmation of observed cases. We additionally ranked the colonization risk for all patients each week using five other competing methods (free simulation, length of stay, number of contacts, contact tracing, and multivariate logistic regression), informed by hospitalization history during the same time window (SI Appendix).
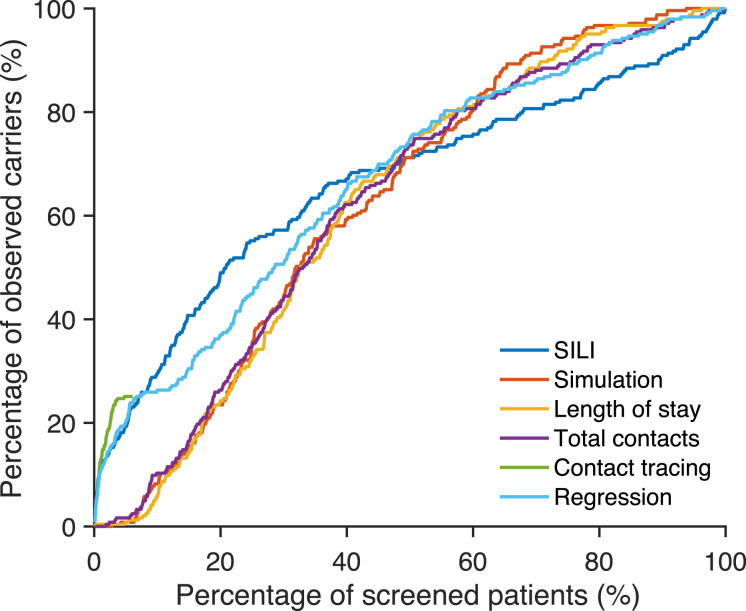
To examine whether the inference algorithm can better identify confirmed cases, we screened top-ranked patients selected by each approach and calculated the percentage of identified carriers among all ascertained cases. In Fig. 3, we compare the cumulative percentage of identified, positive cases among high-risk patients ranked by different approaches. As estimated in a previous study (46), the majority of confirmed cases in Swedish healthcare facilities were imported. Indeed, a substantial proportion of MRSA cases in Sweden were imported from abroad because of travel and healthcare contact in foreign countries (54, 55). As a result, only a small proportion of confirmed cases can be tracked by any of the inference methods. The SILI algorithm is the most accurate: 30% of positive cases can be identified by screening the 10% of patients ranked at highest risk. Simulation, length of stay, number of contacts, and the multivariate logistic regression are less accurate, but the majority of positive cases are still ranked within top 50%. This is in line with previous findings showing that long-term hospitalization is associated with the increased risk of colonization and infection with AMROs (29, 30). Contact tracing can identify only 25% of positive cases, as many observed cases have no direct contact with other observed cases. However, contact tracing outperforms the SILI algorithm for patients who had contacts with an identified case. This superior performance of contact tracing is possibly due to the biased observation process (i.e., in healthcare systems testing is often preferentially performed on close contacts of identified cases). As a result, the ascertained, colonized patients (i.e., the “ground truth” in Fig. 3) are likely biased to individuals who have had contacts with colonized patients, which circularly advantages the contact-tracing approach.
Fig. 3.
Percentage of observed carriers identified by screening high-risk patients selected using different methods. For each observed MRSA carrier, we use different approaches to estimate the colonization risk of all patients present in hospital during the week of confirmation and rank patients according to the estimated colonization risk (from high to low). We screen the top-ranked patients selected by each approach and calculate the percentage of identified carriers among all confirmed cases. Results are compared for the SILI algorithm, free simulation, length of stay, total number of contacts, contact tracing, and multivariate logistic regression. Only 25% of confirmed cases can be reached through contact tracing, as others have no direct contact with other observed cases.
The performance of the SILI algorithm degrades for patients ranked below 50%, possibly because of imported cases that cannot be effectively identified by inference. An ensemble approach drawing on multiple predictors, including the SILI algorithm, contacts with identified cases, and other risk factors, could potentially further improve identification; we leave such analysis for future study.
Targeted Control Experiment.
Given the individual-level heterogeneity in colonization risk, control measures targeted to inpatients with a higher chance to be asymptomatic spreaders could more effectively reduce MRSA-related HAIs. To evaluate whether the SILI algorithm can support improved control, we ran a set of control experiments using the agent-based model and compared targeted interventions informed by different approaches, specifically, the SILI algorithm, length of stay, total number of contacts, contact tracing, free model simulation, and logistic regression. The alternate methods use information that is widely available in electronic healthcare records and have been used in clinical settings to evaluate patient colonization risk.
To mimic a realistic MRSA outbreak, we calibrated the model parameters to the real-world incidence numbers every 4 wk. For each consecutive 4-wk interval after week 52, we used case numbers in the sliding time window of the prior 52 wk to estimate the latest parameters (SI Appendix, Fig. S8). Those posterior parameter estimates were then used to simulate the 4-wk interval. The 52-wk time window was then slid forward 4 wk, and the process was repeated. The simulated outbreak reproduces observed MRSA incidence (Fig. 4A).
Fig. 4.
Retrospective control experiment in 66 Swedish healthcare facilities. (A) Observed incidence every 4 wk (red crosses) and corresponding distributions generated from simulated outbreaks using the inferred parameters (boxes and whiskers, interquartile, and 95% CI). The calibrated model reproduces the observed incidence in Swedish healthcare facilities during a 6-y period. Results are obtained from 300 simulations. (B and C) Distributions of the observed incidence and total colonization by isolating 1% of patients in the hospital, selected by different methods every 4 wk. Results are obtained from 100 independent control experiments. Asterisks indicate statistical significance that the SILI algorithm outperforms other approaches, obtained from the Mann–Whitney U test (*** , ** , and * ). (D and E) Results for isolating 5% of patients in the hospital, selected by different methods every 4 wk.
For the control experiments, we implemented targeted interventions informed by the SILI algorithm and other competing methods to reduce transmission in the simulated outbreak. Every 4 wk, after each sliding 52-wk window, we selected 1% of patients present in the hospital (around 100) with the highest-colonization risk, ranked by the different approaches. The selected, high-risk individuals were screened and put into isolation in the following 4 wk if they remained hospitalized. During isolation, the targeted individuals will neither be colonized nor transmit MRSA to other patients. We track the numbers of observed incidence and all colonized patients during the 320-wk period under each control strategy and compare them with the outcomes without any control.
We performed 100 realizations for each control experiment and display the distributions of observed incidences and total colonization in Fig. 4 B and C. The SILI algorithm informs the most effective, targeted control and significantly outperforms the other approaches (Mann–Whitney U test). By isolating just 1% of patients in hospital every 4 wk, incidence and colonization are reduced 40 and 12%, respectively, compared with the no-control scenario. In contrast, interventions based on the length of stay, total number of contacts, contact tracing, model simulation, and regression reduced incidence by 19, 7, 1, 33, and 13% and colonization by 6, 3, 0, 10, and 4%. Note that, as a considerable number of colonized patients were discharged shortly after hospitalization, they are less likely to be diagnosed in hospital. As a consequence, the reduction of colonized patients is less pronounced than observed cases. The effect of contact tracing is rather limited because of the existence of a large number of undetected, asymptomatic carriers.
Another set of control experiments screening 5% of hospitalized patients every 4 wk (around 500) yielded similar results (Fig. 4 D and E). By targeting more individuals, the benefits of the interventions based on length of stay, number of contacts, and free simulation are substantially improved. While these approaches are less accurate in locating asymptomatic carriers, they can identify patients who suffer a higher risk of colonization. The isolation of such patients could disrupt the contact network and block potential transmission pathways. However, this improvement requires four more times of testing, which could impose a heavy strain on healthcare resources. The marginal benefit of screening more patients (5%) for the SILI algorithm is more limited—the remaining, unidentified carriers are possibly imported randomly from the community and cannot be accurately located unless a universal screening at admission is implemented. However, the SILI algorithm still significantly outperforms the alternate intervention approaches. We further tested the performance of weekly targeted control and found that the strategy informed by the SILI algorithm again outperforms other methods (SI Appendix, Fig. S9).
Discussion
In this study, we demonstrate that the accurate identification of asymptomatic carriers of MRSA can inform more cost-effective control measures in the hospital. We develop and validate an individual-level inference system for agent-based models using sparse observations of MRSA carriers. Unlike intervention approaches based on length of stay, total number of contacts, and contact tracing, the inference system additionally represents transmission dynamics among patients and interactions with the community and hospital environment. This fuller representation of the disease transmission process appears to support the more accurate estimation of colonization probabilities. The contributions of this study are multiple. First, by combining electronic healthcare records and data-driven, mathematical modeling, we address the pressing need to control HAIs caused by MRSA in hospital settings and develop a more cost-effective, better-targeted intervention strategy. Second, we develop an efficient, individual-level inference method that is applicable to large-scale, agent-based models with limited observations. This methodological advance could expand capabilities for studying disease transmission and other individual-level systems. With proper modifications, the inference framework can be generalized to other AMROs and infectious diseases and, more broadly, to other systems using agent-based models. Undocumented infections play a substantial role in the spread of a range of infectious diseases, including COVID-19 (56), influenza (57), and other respiratory diseases (58). The inference framework developed here does not depend on specific model dynamics and thus can be flexibly adapted for use with other infectious diseases. In addition, the algorithm is computationally efficient and can be scaled up for the estimation of unobserved spreaders in large populations.
Here, we have tested an inference methodology in silica and compared its accuracy with alternative approaches. Ultimately, the algorithm could be operationalized for use in real-world clinical settings. Such application will require formal evaluation, as the inference method needs further refinement and validation in real-world hospital settings, through the active sampling of identified high-risk patients. However, the implementation of the algorithm and full-model inference system is feasible. The method is computationally efficient and uses only hospitalization records and laboratory test results for AMROs, which are readily available from electronic healthcare records.
Several limitations exist in this modeling study. First, we did not differentiate the relative transmission rates among different types of wards (23, 59), whose information is not available in the Swedish hospital dataset. Were such information available, we could define separate transmission rates by ward, based on relative infection risk. In addition, we also did not allow certain parameters, such as infectiousness and importation rate, to vary among patients. Second, personal risk factors associated with increased colonization risk (e.g., medical procedures, antibiotic use, etc.) were not provided with the dataset (29, 30). Such factors could inform the prior colonization probability for each individual and potentially further improve the accuracy of inference. Lastly, we used the same model to generate outbreaks in control experiments and perform inference. As a result, the effects of the inference-guided intervention could be overestimated. However, given the superior performance of the SILI algorithm for real-world data (Fig. 3), the agent-based model should not be heavily misspecified.
In this study, we did not consider the effects of test sensitivity and specificity due to a lack of information on the testing platforms utilized. However, evidence shows that tests for MRSA generally have high specificity but moderate sensitivity (85 to 90%) (60, 61), indicating that 10 to 15% of carriers would yield false-negative outcomes. As these missed positives are undetected spreaders who could facilitate onward transmission, including test performance in the inference system will be crucial. Particularly, for the SILI algorithm, false negatives compromise inference accuracy by erroneously assigning low-colonization probability to undetected spreaders. This error can propagate to their close contacts and other patients, undermining inference accuracy for a large number of individuals.
The complex transmission dynamics and ecology of AMROs complicate the design of optimal control measures. Our results using synthetic outbreaks indicate that outbreaks dominated by different modes of colonization may need distinct control strategies. For instance, if the majority of colonization occurs via person-to-person contact in the hospital, the inference algorithm can effectively identify transmission sources (Fig. 2 B and C). However, with more colonized patients imported from the community, our ability to locate sources of infection within the hospital is compromised (SI Appendix, Fig. S5). Under this condition, screening at admission plus the protection of high-risk patients would support better control outcomes. A framework to systematically evaluate and select the optimal combination of interventions is needed.
Materials and Methods
Data.
The MRSA dataset contains 2,041,531 deidentified hospitalization records (admission, discharge, and location) for 743,599 distinct patients from 66 healthcare facilities in Stockholm County, Sweden. Data were collected during 3,500 continuous days from 2000 to 2010. For patient privacy protection, the exact dates were not reported. Individual diagnostic records for patients who tested positive for MRSA are also available, which provide the relative date of confirmation and strain of MRSA. Diagnosis was performed on patients with symptomatic infections, as well as asymptomatic patients in contact with positive cases. In this study, we focus on the most prevalent strain, UK EMRSA-15 (289 cases). We limit our analysis to a period of 320 wk with reported United Kingdom EMRSA-15 incidence.
Transmission Model.
The contact network within a collection of hospitals is represented by a time-varying graph constructed using the actual hospitalization records. In this contact network, nodes represent uniquely labeled patients, connected by undirected links among individuals sharing the same ward. HCW-mediated contacts between patients facilitate the transmission of MRSA. We model HCW-mediated transmission indirectly by assuming that MRSA can spread between all pairs of patients staying in the same ward at the same time. The colonization of patients may spillover to contaminate the environment, resulting in the indirect transmission to patients admitted to the same ward at a later time. Nosocomial transmission interacts with the community through the admission and discharge of colonized patients.
Individuals are classified into two categories: susceptible (S) and colonized (C). Within hospital, transitions between these states are governed by model transmission dynamics. 1) Contact transmission: A susceptible individual can be colonized, with probability per day, upon contact with a colonized person who is directly linked to in the contact network. Here, is the capacity of the room in which patient resides. We use a frequency-dependent transmission model (62) as the chance of person-to-person contact decreases in larger rooms (with the denominator set to in order to exclude the focal patient). 2) Environmental contamination: Each colonized patient in a given room contributes a daily increment to the environmental force of infection . Meanwhile, decays to of its prior value per day. A susceptible individual in room becomes colonized with probability because of environmental contamination. 3) Community importation: For new admissions, patients are colonized with a probability . Colonized patients become susceptible, with a decolonization rate . Each day, colonized patients in the hospital may be observed with a probability . In reality, some model parameters may differ from person to person. To account for this variability, parameters and , for each individual, are randomly drawn from uniform ranges obtained from prior literature (SI Appendix, Table S1). We varied the parameters (the baseline transmission rate), (the importation rate), (the baseline environmental contamination coefficient), and (the mean environmental decolonization rate) to adjust MRSA transmission dynamics. Transmission, importation, and decolonization are all run stochastically, according to predefined probabilities.
Inference Algorithm.
In the SILI algorithm, an ensemble of system states, which represent the distribution of probabilities and for all patients, are sequentially adjusted using individual-level, diagnostic information. This adjustment, developed based on the Bayes’ rule, is applied weekly following model initialization. Each week , three procedures are used to constrain the model state. 1) Backward temporal propagation: For each patient tested for MRSA carriage at some later week, we infer his/her colonization probability at week . Using Eqs. 1–3, we calculate the likelihood of observing the reported cases at some later week given that patient is colonized at week . Together, with the prior probability for patient being colonized at week , the posterior colonization probability for patient at week is computed. 2) Covariability adjustment: Using the inferred colonization probability, we adjust the states of observed carriers’ neighbors based on the covariability between their colonization probabilities, which arises from dynamical coupling before week . 3) Forward propagation: We integrate the model to week using the updated states. This sequence of procedures uses inference and dynamic simulation to augment the sparse observations back in time and propagates information to individuals without observations. An illustration of the SILI algorithm is shown in SI Appendix, Fig. S2. The pseudocode is provided in SI Appendix. In this study, 100 ensemble members were used in the SILI algorithm.
Parameter Estimation.
We used a statistical filtering technique to infer epidemiological parameters within the agent-based model using aggregated incidence numbers (46). Using an equation-free approach (63), the algorithm repeatedly applies an efficient data assimilation method, the ensemble adjustment Kalman filter (EAKF) (64), within an IF framework (65–67), such that the system parameters are gradually adjusted toward their true values. The EAKF algorithm is an efficient data assimilation technique that has recently been used in infectious disease forecasting and inference (68, 69). Specifically, it is applicable to high-dimensional, infectious disease models (70–72). The IF framework proceeds as follows: An ensemble of system states, which represent the distribution of parameters, are repeatedly adjusted using the EAKF in a series of iterations, during which the variance of the parameters is gradually tuned down. In the process, the distribution of parameters is iteratively optimized per observations and narrowed down to values that achieve maximum likelihood. This IF-EAKF framework has been used to infer epidemiological parameters for MRSA outbreaks in Swedish healthcare facilities (46) and COVID-19 transmission in China (56). In our implementation, because of the limited number of observations, we calibrated model parameters to incidence numbers summed every 4 wk. We used 300 ensemble members and ran the EAKF for 20 iterations. Details can be found in ref. 46.
Supplementary Material
Acknowledgments
This study was supported by NIH Grant GM110748 and CDC Grant CK000592, as well as a gift from the Morris-Singer Foundation. We also thank Columbia University Mailman School of Public Health for high-performance computing resources.
Footnotes
Competing interest statement: J.S. and Columbia University disclose partial ownership of SK Analytics. J.S. discloses consulting for Business Network International.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2111190118/-/DCSupplemental.
Data Availability
Public sharing of the hospitalization records and MRSA diagnostic data is not permitted by its owner, Stockholm County Council. However, for reproducing the synthetic analysis, we have deposited the code and an example contact network at GitHub, https://github.com/SenPei-CU/MRSA_inference. All other study data are included in the article and/or SI Appendix.
References
- 1.Magill S. S.et al.; Emerging Infections Program Healthcare-Associated Infections and Antimicrobial Use Prevalence Survey Team , Multistate point-prevalence survey of health care-associated infections. N. Engl. J. Med. 370, 1198–1208 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Centers for Disease Control and Prevention , Antibiotic Resistance Threats in the United States, 2019 (Centers for Disease Control and Prevention, 2019). https://www.cdc.gov/drugresistance/pdf/threats-report/2019-ar-threats-report-508.pdf. Accessed 24 February 2021. [Google Scholar]
- 3.Weiner L. M., et al., Antimicrobial-resistant pathogens associated with healthcare-associated infections: Summary of data reported to the national healthcare safety network at the Centers for Disease Control and Prevention, 2011-2014. Infect. Control Hosp. Epidemiol. 37, 1288–1301 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weiner L. M., et al., Vital signs: Preventing antibiotic-resistant infections in hospitals - United States, 2014. Am. J. Transplant. 16, 2224–2230 (2016). [DOI] [PubMed] [Google Scholar]
- 5.Prestinaci F., Pezzotti P., Pantosti A., Antimicrobial resistance: A global multifaceted phenomenon. Pathog. Glob. Health 109, 309–318 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.World Health Organization , Antimicrobial Resistance Fact Sheet (2020). https://www.who.int/news-room/fact-sheets/detail/antimicrobial-resistance. Accessed 24 February 2021.
- 7.Centers for Disease Control and Prevention , What Exactly is Antibiotic Resistance? (Centers for Disease Control and Prevention, 2020). [Google Scholar]
- 8.European Centre for Disease Prevention and Control , Antimicrobial resistance in the EU/EEA (EARS-Net) - Annual Epidemiological Report for 2019 (ECDC, Stockholm, 2020). https://www.ecdc.europa.eu/sites/default/files/documents/surveillance-antimicrobial-resistance-Europe-2019.pdf. Accessed 24 February 2021.
- 9.Pokharel S., Raut S., Adhikari B., Tackling antimicrobial resistance in low-income and middle-income countries. BMJ Glob. Health 4, e002104 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lowy F. D., Staphylococcus aureus infections. N. Engl. J. Med. 339, 520–532 (1998). [DOI] [PubMed] [Google Scholar]
- 11.Dantes R., National burden of invasive methicillin-resistant Staphylococcus aureus infections, United States, 2011. JAMA Intern. Med. 173, 1970–1978 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Klein E., Smith D. L., Laxminarayan R., Hospitalizations and deaths caused by methicillin-resistant Staphylococcus aureus, United States, 1999-2005. Emerg. Infect. Dis. 13, 1840–1846 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.MacKinnon M. M., Allen K. D., Long-term MRSA carriage in hospital patients. J. Hosp. Infect. 46, 216–221 (2000). [DOI] [PubMed] [Google Scholar]
- 14.Eyre D. W., et al., Asymptomatic Clostridium difficile colonisation and onward transmission. PLoS One 8, e78445 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schechner V., et al., Asymptomatic rectal carriage of blaKPC producing carbapenem-resistant Enterobacteriaceae: Who is prone to become clinically infected? Clin. Microbiol. Infect. 19, 451–456 (2013). [DOI] [PubMed] [Google Scholar]
- 16.Agodi A., et al., Pseudomonas aeruginosa carriage, colonization, and infection in ICU patients. Intensive Care Med. 33, 1155–1161 (2007). [DOI] [PubMed] [Google Scholar]
- 17.Zimmerman F. S., et al., Duration of carriage of carbapenem-resistant Enterobacteriaceae following hospital discharge. Am. J. Infect. Control 41, 190–194 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Wiener-Well Y., et al., Carriage rate of carbapenem-resistant Klebsiella pneumoniae in hospitalised patients during a national outbreak. J. Hosp. Infect. 74, 344–349 (2010). [DOI] [PubMed] [Google Scholar]
- 19.Scanvic A., et al., Duration of colonization by methicillin-resistant Staphylococcus aureus after hospital discharge and risk factors for prolonged carriage. Clin. Infect. Dis. 32, 1393–1398 (2001). [DOI] [PubMed] [Google Scholar]
- 20.Smith D. L., Dushoff J., Perencevich E. N., Harris A. D., Levin S. A., Persistent colonization and the spread of antibiotic resistance in nosocomial pathogens: Resistance is a regional problem. Proc. Natl. Acad. Sci. U.S.A. 101, 3709–3714 (2004). Correction in: Proc. Natl. Acad. Sci. U.S.A. 101, 5696 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Worby C. J., et al., Estimating the effectiveness of isolation and decolonization measures in reducing transmission of methicillin-resistant Staphylococcus aureus in hospital general wards. Am. J. Epidemiol. 177, 1306–1313 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cooper B. S., et al., Methicillin-resistant Staphylococcus aureus in hospitals and the community: Stealth dynamics and control catastrophes. Proc. Natl. Acad. Sci. U.S.A. 101, 10223–10228 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bootsma M. C. J., Diekmann O., Bonten M. J. M., Controlling methicillin-resistant Staphylococcus aureus: Quantifying the effects of interventions and rapid diagnostic testing. Proc. Natl. Acad. Sci. U.S.A. 103, 5620–5625 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Otter J. A., French G. L., Nosocomial transmission of community-associated methicillin-resistant Staphylococcus aureus: An emerging threat. Lancet Infect. Dis. 6, 753–755 (2006). [DOI] [PubMed] [Google Scholar]
- 25.D’Agata E. M. C., Webb G. F., Horn M. A., Moellering R. C. Jr, Ruan S., Modeling the invasion of community-acquired methicillin-resistant Staphylococcus aureus into hospitals. Clin. Infect. Dis. 48, 274–284 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Klein E. Y., Sun L., Smith D. L., Laxminarayan R., The changing epidemiology of methicillin-resistant Staphylococcus aureus in the United States: A national observational study. Am. J. Epidemiol. 177, 666–674 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Boyce J. M., Environmental contamination makes an important contribution to hospital infection. J. Hosp. Infect. 65 (suppl. 2), 50–54 (2007). [DOI] [PubMed] [Google Scholar]
- 28.Kumar J., et al., Environmental contamination with Candida species in multiple hospitals including a tertiary care hospital with a Candida auris outbreak. Pathog. Immun. 4, 260–270 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hidron A. I., et al., Risk factors for colonization with methicillin-resistant Staphylococcus aureus (MRSA) in patients admitted to an urban hospital: Emergence of community-associated MRSA nasal carriage. Clin. Infect. Dis. 41, 159–166 (2005). [DOI] [PubMed] [Google Scholar]
- 30.Girou E., Pujade G., Legrand P., Cizeau F., Brun-Buisson C., Selective screening of carriers for control of methicillin-resistant Staphylococcus aureus (MRSA) in high-risk hospital areas with a high level of endemic MRSA. Clin. Infect. Dis. 27, 543–550 (1998). [DOI] [PubMed] [Google Scholar]
- 31.Harbarth S., et al., Evaluating the probability of previously unknown carriage of MRSA at hospital admission. Am. J. Med. 119, 275.e15–275.e23 (2006). [DOI] [PubMed] [Google Scholar]
- 32.Grundmann H., Hellriegel B., Mathematical modelling: A tool for hospital infection control. Lancet Infect. Dis. 6, 39–45 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Weinstein R. A., Bonten M. J., Austin D. J., Lipsitch M., Understanding the spread of antibiotic resistant pathogens in hospitals: Mathematical models as tools for control. Clin. Infect. Dis. 33, 1739–1746 (2001). [DOI] [PubMed] [Google Scholar]
- 34.van Kleef E., Robotham J. V., Jit M., Deeny S. R., Edmunds W. J., Modelling the transmission of healthcare associated infections: A systematic review. BMC Infect. Dis. 13, 294 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Doan T. N., Kong D. C. M., Kirkpatrick C. M. J., McBryde E. S., Optimizing hospital infection control: The role of mathematical modeling. Infect. Control Hosp. Epidemiol. 35, 1521–1530 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Kajita E., Okano J. T., Bodine E. N., Layne S. P., Blower S., Modelling an outbreak of an emerging pathogen. Nat. Rev. Microbiol. 5, 700–709 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Lee B. Y., et al., Modeling the spread of methicillin-resistant Staphylococcus aureus (MRSA) outbreaks throughout the hospitals in Orange County, California. Infect. Control Hosp. Epidemiol. 32, 562–572 (2011). Correction in: Infect. Control Hosp. Epidemiol. 32, 938 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paul P., Slayton R. B., Kallen A. J., Walters M. S., Jernigan J. A., Modeling regional transmission and containment of a healthcare-associated multidrug-resistant organism. Clin. Infect. Dis. 70, 388–394 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Slayton R. B., et al., Vital signs: Estimated effects of a coordinated approach for action to reduce antibiotic-resistant infections in health care facilities - United States. MMWR Morb. Mortal. Wkly. Rep. 64, 826–831 (2015). [PMC free article] [PubMed] [Google Scholar]
- 40.Toth D. J. A., et al., The potential for interventions in a long-term acute care hospital to reduce transmission of carbapenem-resistant Enterobacteriaceae in affiliated healthcare facilities. Clin. Infect. Dis. 65, 581–587 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Smith D. L., Levin S. A., Laxminarayan R., Strategic interactions in multi-institutional epidemics of antibiotic resistance. Proc. Natl. Acad. Sci. U.S.A. 102, 3153–3158 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rubin M. A., et al., A simulation-based assessment of strategies to control Clostridium difficile transmission and infection. PLoS One 8, e80671 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cooper B. S., Medley G. F., Bradley S. J., Scott G. M., An augmented data method for the analysis of nosocomial infection data. Am. J. Epidemiol. 168, 548–557 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thomas A., et al., Efficient parameter estimation for models of healthcare-associated pathogen transmission in discrete and continuous time. Math. Med. Biol. 32, 79–98 (2015). [DOI] [PubMed] [Google Scholar]
- 45.Thomas A., et al., Extended models for nosocomial infection: Parameter estimation and model selection. Math. Med. Biol. 35 (suppl. 1), 29–49 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pei S., Morone F., Liljeros F., Makse H., Shaman J. L., Inference and control of the nosocomial transmission of methicillin-resistant Staphylococcus aureus. eLife 7, e40977 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Altarelli F., Braunstein A., Dall’Asta L., Lage-Castellanos A., Zecchina R., Bayesian inference of epidemics on networks via belief propagation. Phys. Rev. Lett. 112, 118701 (2014). [DOI] [PubMed] [Google Scholar]
- 48.Pinto P. C., Thiran P., Vetterli M., Locating the source of diffusion in large-scale networks. Phys. Rev. Lett. 109, 068702 (2012). [DOI] [PubMed] [Google Scholar]
- 49.Lokhov A. Y., Mézard M., Ohta H., Zdeborová L., Inferring the origin of an epidemic with a dynamic message-passing algorithm. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 90, 012801 (2014). [DOI] [PubMed] [Google Scholar]
- 50.Rocha L. E. C., et al., Dynamic contact networks of patients and MRSA spread in hospitals. Sci. Rep. 10, 9336 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Grimm V., et al., The ODD protocol: A review and first update. Ecol. Modell. 221, 2760–2768 (2010). [Google Scholar]
- 52.Gleeson J. P., Melnik S., Ward J. A., Porter M. A., Mucha P. J., Accuracy of mean-field theory for dynamics on real-world networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 85, 026106 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Melnik S., Hackett A., Porter M. A., Mucha P. J., Gleeson J. P., The unreasonable effectiveness of tree-based theory for networks with clustering. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 036112 (2011). [DOI] [PubMed] [Google Scholar]
- 54.Stenhem M.et al.; Swedish Study Group on MRSA Epidemiology , Epidemiology of methicillin-resistant Staphylococcus aureus (MRSA) in Sweden 2000-2003, increasing incidence and regional differences. BMC Infect. Dis. 6, 30 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Stenhem M., et al., Imported methicillin-resistant Staphylococcus aureus, Sweden. Emerg. Infect. Dis. 16, 189–196 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Li R., et al., Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 368, 489–493 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Cohen C.et al.; PHIRST group , Asymptomatic transmission and high community burden of seasonal influenza in an urban and a rural community in South Africa, 2017-18 (PHIRST): A population cohort study. Lancet Glob. Health 9, e863–e874 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Galanti M., et al., Rates of asymptomatic respiratory virus infection across age groups. Epidemiol. Infect. 147, e176 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Forrester M. L., Pettitt A. N., Gibson G. J., Bayesian inference of hospital-acquired infectious diseases and control measures given imperfect surveillance data. Biostatistics 8, 383–401 (2007). [DOI] [PubMed] [Google Scholar]
- 60.Luteijn J. M., Hubben G. A. A., Pechlivanoglou P., Bonten M. J., Postma M. J., Diagnostic accuracy of culture-based and PCR-based detection tests for methicillin-resistant Staphylococcus aureus: A meta-analysis. Clin. Microbiol. Infect. 17, 146–154 (2011). [DOI] [PubMed] [Google Scholar]
- 61.Andersen B. M., et al., Rapid MRSA test in exposed persons: Costs and savings in hospitals. J. Infect. 60, 293–299 (2010). [DOI] [PubMed] [Google Scholar]
- 62.Begon M., et al., A clarification of transmission terms in host-microparasite models: Numbers, densities and areas. Epidemiol. Infect. 129, 147–153 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kevrekidis I. G., et al., Equation-free, coarse-grained multiscale computation: Enabling mocroscopic simulators to perform system-level analysis. Commun. Math. Sci. 1, 715–762 (2003). [Google Scholar]
- 64.Anderson J. L., An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 129, 2884–2903 (2001). [Google Scholar]
- 65.Ionides E. L., Bretó C., King A. A., Inference for nonlinear dynamical systems. Proc. Natl. Acad. Sci. U.S.A. 103, 18438–18443 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.He D., Ionides E. L., King A. A., Plug-and-play inference for disease dynamics: Measles in large and small populations as a case study. J. R. Soc. Interface 7, 271–283 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.King A. A., Ionides E. L., Pascual M., Bouma M. J., Inapparent infections and cholera dynamics. Nature 454, 877–880 (2008). [DOI] [PubMed] [Google Scholar]
- 68.Shaman J., Karspeck A., Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. U.S.A. 109, 20425–20430 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pei S., Shaman J., Counteracting structural errors in ensemble forecast of influenza outbreaks. Nat. Commun. 8, 925 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Pei S., Kandula S., Yang W., Shaman J., Forecasting the spatial transmission of influenza in the United States. Proc. Natl. Acad. Sci. U.S.A. 115, 2752–2757 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pei S., Kandula S., Shaman J., Differential effects of intervention timing on COVID-19 spread in the United States. Sci. Adv. 6, eabd6370 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pei S., Teng X., Lewis P., Shaman J., Optimizing respiratory virus surveillance networks using uncertainty propagation. Nat. Commun. 12, 222 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Public sharing of the hospitalization records and MRSA diagnostic data is not permitted by its owner, Stockholm County Council. However, for reproducing the synthetic analysis, we have deposited the code and an example contact network at GitHub, https://github.com/SenPei-CU/MRSA_inference. All other study data are included in the article and/or SI Appendix.