Prediction of arrhythmia susceptibility through mathematical modeling and machine learning

Significance

Despite our understanding of the many factors that promote ventricular arrhythmias, it remains difficult to predict which specific individuals within a population will be especially susceptible to these events. We present a computational framework that combines supervised machine learning algorithms with population-based cellular mathematical modeling. Using this approach, we identify electrophysiological signatures that classify how myocytes respond to three arrhythmic triggers. Our predictors significantly outperform the standard myocyte-level metrics, and we show that the approach provides insight into the complex mechanisms that differentiate susceptible from resistant cells. Overall, our pipeline improves on current methods and suggests a proof of concept at the cellular level that can be translated to the clinical level.

Abstract

At present, the QT interval on the electrocardiographic (ECG) waveform is the most common metric for assessing an individual’s susceptibility to ventricular arrhythmias, with a long QT, or, at the cellular level, a long action potential duration (APD) considered high risk. However, the limitations of this simple approach have long been recognized. Here, we sought to improve prediction of arrhythmia susceptibility by combining mechanistic mathematical modeling with machine learning (ML). Simulations with a model of the ventricular myocyte were performed to develop a large heterogenous population of cardiomyocytes (n = 10,586), and we tested each variant’s ability to withstand three arrhythmogenic triggers: 1) block of the rapid delayed rectifier potassium current (I_Kr Block), 2) augmentation of the L-type calcium current (I_CaL Increase), and 3) injection of inward current (Current Injection). Eight ML algorithms were trained to predict, based on simulated AP features in preperturbed cells, whether each cell would develop arrhythmic dynamics in response to each trigger. We found that APD can accurately predict how cells respond to the simple Current Injection trigger but cannot effectively predict the response to I_Kr Block or I_CaL Increase. ML predictive performance could be improved by incorporating additional AP features and simulations of additional experimental protocols. Importantly, we discovered that the most relevant features and experimental protocols were trigger specific, which shed light on the mechanisms that promoted arrhythmia formation in response to the triggers. Overall, our quantitative approach provides a means to understand and predict differences between individuals in arrhythmia susceptibility.

Predicting individual susceptibility to ventricular arrhythmias is a long-standing issue in the field of cardiac electrophysiology. Many factors can contribute to ventricular arrhythmia risk, including variants in a wide variety of genes, structural heart disease, and drugs that block important cardiac ion channels (1–3). However, even in patients who are clearly at high risk of developing ventricular arrhythmias, these are uncommon events. Moreover, two patients can experience dramatically different arrhythmia burdens, even if their genetic profiles or cardiac function might suggest a similar level of risk (4). These observations have led to the notion that arrhythmias arise due to an inherent susceptibility combined with a temporary, triggering factor such as an electrolyte imbalance, a change in autonomic tone, or a circulating medication (1, 5–7). There is therefore a great need to identify the individuals who are most at risk for developing arrhythmias for proper management of their lifestyles and clinical care.

Due to the role played by drugs in triggering some ventricular arrhythmias, prediction of proarrhythmia is a major issue in drug development. In this context, the electrocardiographic QT interval has played a central role (8). Drug-induced prolongation of the QT interval, corresponding at the cellular level to prolongation of the action potential duration (APD), is assessed in preclinical and clinical assays, and a positive signal can doom an otherwise-promising drug development project (8). Similarly, when examining differences between individuals, those with the longest QT intervals are generally considered to be at greatest risk (9–11). Although useful, this QT-centric approach also has obvious limitations. First, the baseline QT interval in patients does not correlate with the degree of QT prolongation produced by drugs, indicating that other factors contribute (12, 13). Second, both a long baseline QT and drug-induced QT prolongation are only imperfect predictors of arrhythmia risk (14–16). Noninvasive methods to determine the individuals most at risk for arrhythmia could therefore be of great benefit in clinical care.

Improved prediction of arrhythmia risk could potentially be achieved by combining two complementary computational techniques: 1) supervised machine learning (ML) algorithms and 2) simulations with mechanistic mathematical models. ML, which has proven to be useful for discovering hidden patterns in data (17, 18), can be used for classification problems such as separating high-risk and low-risk patients. However, ML requires large sample sizes to be effective, and it is difficult to apply directly to clinical data due to heterogeneity in standards of data collection. In this regard, simulations with mechanistic models can play an important role, as this strategy allows for the generation of large sets of pseudodata, all produced under controlled and repeatable conditions (19–22). A rigorous ML study of arrhythmia susceptibility based on simulated data would provide an important proof of concept to inform later studies that analyzed clinical recordings.

A few recent publications have combined modeling and ML by applying either unsupervised or supervised ML to data sets generated through simulation (23–26). Here, we extended this strategy to address a more challenging question: can measurable features from cellular APs, obtained in the absence of an arrhythmogenic perturbation, predict how cells will respond in the future to such a perturbation? Using simulation results from a controllable, understandable cellular system, we show that ML can successfully be applied to answer this question, offering the possibility that measurements made in normal sinus rhythm can predict arrhythmia risk. Moreover, the results demonstrate how the combination of the two computational techniques can be used to prioritize experiments and to understand mechanistic differences in how ventricular myocytes respond to different proarrhythmic triggers. Overall, the study provides a road map for the application of ML to assess arrhythmia susceptibility.

Results

Arrhythmogenic Triggers Produce Variable Responses across a Population of Myocytes.

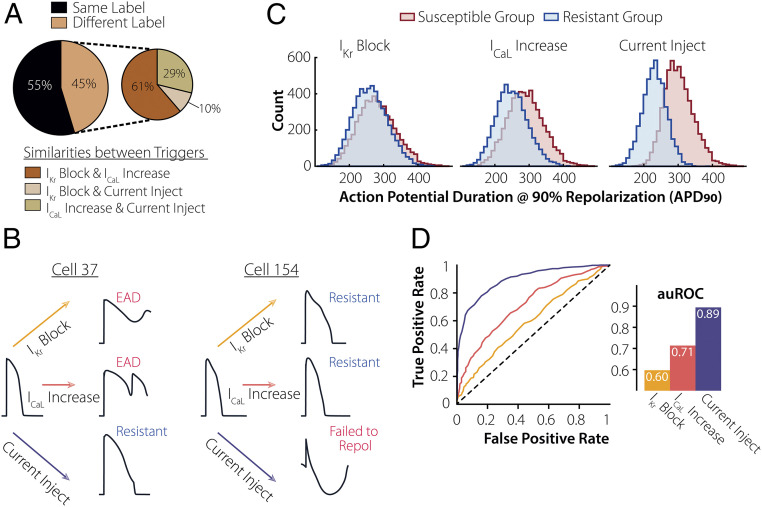
We investigated individual arrhythmia susceptibility in a population of cardiomyocytes. Using the O’Hara et al. ventricular myocyte model as a baseline (27), we created a virtual population of 10,586 myocytes by randomly varying model parameters (19, 28, 29). Arrhythmia susceptibility was assessed by subjecting each cell in the population to three different triggers: 1) block of delayed rectifier potassium channel (I_Kr Block); 2) augmentation of the L-type Ca²⁺ current (I_CaL Increase); and 3) injection of inward current (Current Injection). After applying each trigger, we split our population into resistant and susceptible groups based on whether the triggers caused arrhythmogenic behavior (Fig. 1), which was characterized as either a repolarization failure or an appearance of an early afterdepolarization (EAD). We found that 48%, 52%, and 55% of the population was susceptible to I_Kr Block, I_CaL Increase, and Current Injection, respectively. Across all myocytes, we found that 55% of cells exhibited the same arrhythmogenic response (appearance or lack thereof an arrhythmia) to all three triggers, while the remaining 45% showed differences (Fig. 2A). Of the 45% for which differences were observed, 61% exhibited the same response to I_Kr Block and I_CaL increase and a different response to Current Injection. The alternative possibilities were encountered less frequently. As an example, Fig. 2B shows two cells with similar pretrigger APs, in which one was resistant to Current Injection and susceptible to I_Kr Block and I_CaL Increase, while the other was resistant to the latter two triggers but susceptible to Current Injection.

Fig. 1.

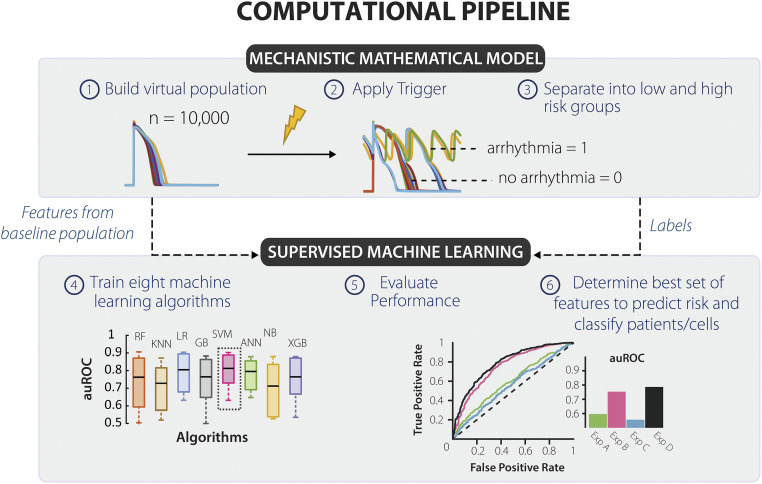
Computational pipeline devised to predict how physiological waveforms under normal sinus rhythm might indicate susceptibility to a future trigger. Our computational pipeline combines population-based cardiac modeling with supervised ML to predict arrhythmia susceptibility. (1) We began by creating a virtual population of myocytes by varying model parameters that correspond to channel conductance and kinetic properties. (2) Next, we applied three individual triggers: I_Kr Block, I_CaL Increase, and Current Injection on the population. (3) This allowed us to create two groups, high- and low-risk cells (cells that were susceptible or resistant to the perturbation, respectively). Susceptible cells were described as myocytes that formed a repolarization failure or EADs. (4) We took features from baseline (pretrigger) state of the cells along with the risk classification labels and fed them to 8-ML classifiers. (5) We evaluated performance of each classifier by computing the area under the receiver operator characteristic curve and kept the results of the superior algorithm. (6) We analyzed the results to define a unique set of features/experiments that can predict an individual's susceptibility to each trigger.

Fig. 2.

APD₉₀ cannot predict susceptibility to every arrhythmogenic trigger. (A) Upon applying three individual perturbations on the virtual population, 55% had similar arrhythmogenic responses. Within the population where the responses varied, I_Kr Block and I_CaL Increase had the greatest number of common labels (61%). (B) Examples of cells from the population, both with an APD₉₀ = 330 ms, demonstrate varied responses to the three triggers. (C) Distribution of APD₉₀ for the resistant (blue) and susceptible (red) subgroups for each arrhythmogenic trigger. (D) APD₉₀ used to predict susceptibility to each trigger. Based on the resulting ROC and corresponding auROC, APD₉₀ is a strong predictor of susceptibility to current injection (purple) but a mediocre one for I_CaL Increase (pink) and I_Kr Block (yellow).

APD Only Predicts Susceptibly to Current Injection.

Once we had established a population that exhibited variable susceptibility to arrhythmic perturbations, we used ML to predict susceptibility. The goal of this analysis was to predict whether a cell would be susceptible to a trigger based on AP characteristics measured in the absence of the trigger (Fig. 1). Since APD at 90% repolarization (APD₉₀) is commonly considered to correlate with arrhythmia risk (30), we first examined how well this single metric could predict susceptibility (Fig. 2C). To evaluate performance, we plotted the receiver operator characteristic (ROC) curve and calculated the area under it (auROC). We found that APD₉₀ is an excellent predictor of susceptibility to current injection (auROC = 0.89) but a mediocre predictor for I_Kr Block and I_CaL Increase (auROC = 0.60 and 0.71, respectively) (Fig. 2D). Thus, APD₉₀ alone is not sufficient to predict cellular susceptibility to every arrhythmogenic trigger.

Measuring Additional Metrics of the AP Waveform Improves Risk Prediction.

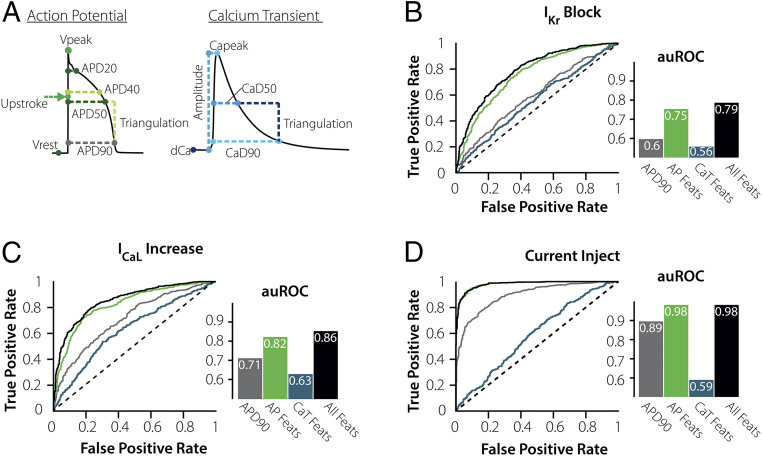
Next, we aimed to determine whether susceptibility prediction could be improved by considering additional features of the AP and calcium transient (CaT) waveforms. We calculated eight features from the AP and six features from the CaT, extracted from waveforms obtained during steady-state pacing at 1 Hz, before triggers were applied (Fig. 3A and SI Appendix, Supplementary Methods). These features were then used as predictors to train a series of ML classifiers, as described in Materials and Methods, and classifiers were compared by plotting ROC curves. For instance, with the classifiers that predicted susceptibility to I_Kr Block (Fig. 3B), inclusion of more AP features increased classifier performance from auROC = 0.60 to auROC = 0.75. In contrast, features calculated from CaTs were not effective at predicting susceptibility to this trigger (auROC = 0.56). Similar results were observed for the I_CaL increase (Fig. 3C) and Current Injection (Fig. 3D) triggers: inclusion of AP features improved classifier performance, whereas CaT features did not. Thus, for prediction of arrhythmia susceptibility, APs appear to provide considerably greater information than CaTs. Although this is not surprising given the complex membrane potential dynamics involved in EADs, results such as these can nonetheless be useful when making decisions about experimental protocols.

Fig. 3.

Measuring the AP waveform under steady-state conditions greatly improves risk prediction. (A) Additional features describing the AP and CaT waveforms were added to the ML algorithms to test their impact on the predictive performance. (B–D) ROCs and computed auROC plots compare the ML performance for predicting susceptibility using APD₉₀ (gray), eight AP Waveform features (green), six CaT Waveform features (blue), and 14 combined AP + CaT Waveform features (black). Predicting risk with just the AP Features improves the overall results for I_CaL Increase and I_Kr Block and is superior for Current Injection. However, adding the CaT waveform features has no significant impact for any trigger.

It is evident in Fig. 3D that quantifying features from an AP measured during steady-state pacing is sufficient to predict how a cell will respond to Current Injection (auROC = 0.98, green bar). After further investigating these eight AP features, we found that triangulation of the AP (TriAP) is most important for predicting the response to this perturbation (SI Appendix, Fig. S1). Cells with triangulated APs tend to be much more susceptible to Current Injection than those with normal APs.

ML Performance Changes Based on the Parameters that Are Varied in the Mathematical Model.

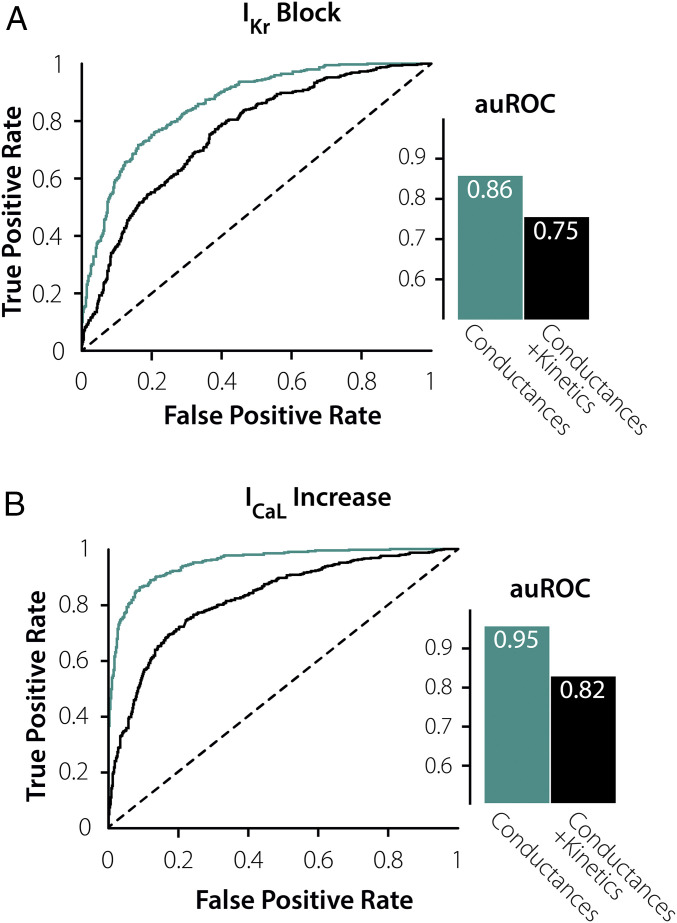
Our population of 10,586 myocytes was generated by varying both ionic current maximal conductances and parameters controlling ion channel gating (29, 31, 32). Because several previous studies have produced model populations by only varying conductances (20, 33, 34), we tested whether this difference influenced ML classifier performance by creating a population (n = 8,200 cells) in which only conductances varied between myocytes. These cells were subjected to I_Kr Block and I_CaL Increase, and ML classifiers were developed to determine how well features of the preperturbed APs could predict susceptibility. For both perturbations, ML performance was substantially better when only conductances were varied compared with the population in which both categories of parameters were varied (Fig. 4). These results imply that differences in kinetic parameters, in addition to differences in conductances, are important in determining arrhythmia susceptibility. Moreover, the results show that the features of the AP waveform during steady-state 1 Hz pacing are insufficient to infer critical kinetic parameters. Thus, we hypothesized that studying the cell under additional conditions could improve ML performance by providing information about these parameters.

Fig. 4.

ML performance changes based on the parameters that are varied in the mechanistic mathematical model. (A) Plots of ROCs and corresponding auROCs comparing how the 8 AP Features at steady-state predict susceptibility to I_Kr Block when varying just channel conductances (turquoise) and combined channel conductances and current kinetics (black). (B) Plots of ROCs and corresponding auROCs comparing how the 8 AP Features at steady state predict susceptibility to I_CaL Increase when varying just channel conductances (turquoise) and combined channel conductances and current kinetics (black). This highlights the inability for steady-state features to infer critical kinetic parameters.

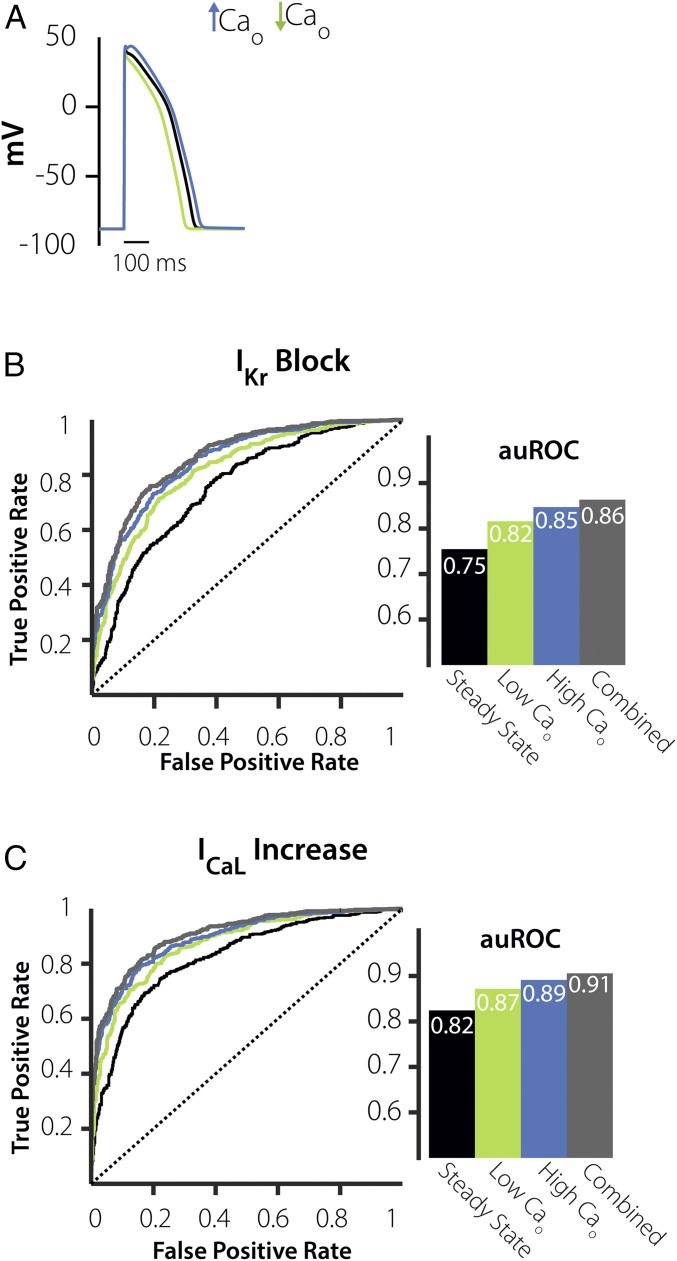
Prediction of Cellular Response to an Increase in I_CaL Can Be Improved by Examining Cells under Hypocalcemic and Hypercalcemic Conditions.

To attempt to improve ML performance, we considered alterations to experimental conditions that are easily achievable in a standard cellular electrophysiology laboratory. For instance, because changes in pacing rate and extracellular solutions can be readily performed, we simulated the population of myocytes at fast and slow pacing rates (2.5 Hz and 0.2 Hz) and under hypercalcemic and hypocalcemic conditions (3.6 mM and 0.9 mM extracellular [Ca²⁺], respectively). We then evaluated ML performance after adding AP features calculated under these conditions to those obtained under standard conditions of 1 Hz pacing, 1.8 mM [Ca²⁺]. Inclusion of either set of features improved ML performance, with somewhat better results seen with the hypercalcemia/hypocalcemia experiment (Fig. 5) compared with the pacing rate experiment (SI Appendix, Figs. S2 and S3). For example, auROC for prediction of the response to the I_CaL Increase trigger improved from 0.82 with eight AP features only to 0.87 with inclusion of the pacing protocol but improved to 0.91 by simulating hypercalcemic and hypocalcemic conditions. Similar results were seen for prediction of the I_Kr Block trigger (auROC = 0.75 with eight AP features, 0.84 when adding pacing rates, and 0.86 when adding hyper/hypo-calcemia). The comparison between the two protocols is useful for experimental prioritization, and the improvement in ML performance implies that these experiments can help to infer model parameters that control arrhythmia susceptibility.

Fig. 5.

I_CaL Increase prediction is augmented when adding features from a high-extracellular Ca²⁺ (Ca_o) experiment. (A) APs simulated under 2× extracellular Ca²⁺ (blue), 0.5× extracellular Ca²⁺ (green), and steady-state conditions (black). (B) Plots of ROCs and corresponding auROCs comparing how the eight AP features, steady-state + low extracellular Ca²⁺ (green), and steady-state + high extracellular Ca²⁺ (blue), and all three combined protocols (gray), predict susceptibility to I_Kr Block. (C) Plots of ROCs and auROCs comparing how the AP Features at steady state + low extracellular Ca²⁺ (green), steady state + high extracellular Ca²⁺, and combined all three experimental protocols (gray) predict I_CaL Increase.

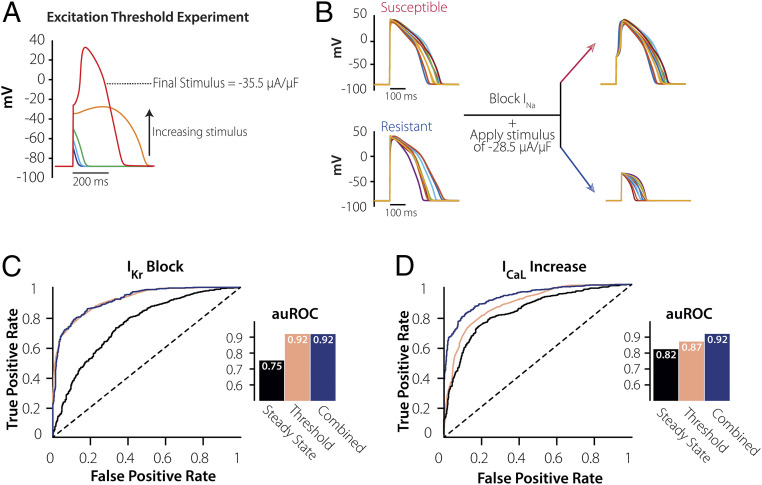
An Excitation Threshold Experiment Greatly Improves Prediction of Cellular Response to I_Kr Block.

Although the hypocalcemia and hypercalcemia experiments successfully improved ML performance, the susceptibility prediction for I_Kr Block was inferior to the prediction for I_CaL increase (auROC = 0.86 versus 0.91). We hypothesized that this difference occurred because the AP features from these simulated protocols were insufficient to infer one or more biological parameters that determine susceptibility to I_Kr Block. Because cellular arrhythmias often occur via EADs and these events result from reactivation of I_CaL, we reasoned that better inferences of parameters related to this current’s kinetics could improve ML prediction (35, 36). We therefore simulated, in our virtual population, an excitation threshold experiment performed under conditions in which I_Na is inhibited and AP upstrokes must be carried by I_CaL (Fig. 6A, red trace). Example cells from the population, shown in Fig. 6B, suggest that this experiment may be useful for distinguishing between resistant and susceptible cells that have similar APs during 1-Hz pacing, and ML analysis confirms a dramatic improvement to the I_Kr Block prediction (Fig. 6C). Indeed, the excitation threshold produced excellent classification either by itself or when combined with eight AP features measured during 1-Hz pacing (auROC = 0.92 in either case). Interestingly, while the excitation threshold also improved ML prediction of the I_CaL Increase perturbation (Fig. 6D), in this case, the threshold needed to be combined with additional features, such as those recorded during steady-state 1 Hz pacing (auROC = 0.87 for threshold alone, 0.92 when combined).

Fig. 6.

Excitation threshold experiment greatly improves the performance of predicting susceptibility to I_Kr Block. (A) Simulating an excitation threshold experiment in an individual cell. The I_Na channel is blocked, and then increasing levels of current are injected till an AP forms (red). (B) Demonstration of excitation threshold experiment in resistant and susceptible subgroups. When I_Na is blocked and a single stimulus of −28.5 µA/µF is applied on cells from the susceptible and resistant groups (with similar APD₉₀), the susceptible cells are able to stimulate an AP, whereas the resistant group requires a much higher stimulus to perform the same. (C) Plots of ROCs and corresponding auROCs comparing how the 8 AP Features at 1 Hz (black), Threshold Experiment (pink), and Combined Protocols (blue) predict susceptibility to I_Kr Block, here knowing the threshold alone would be enough to predict susceptibility to arrhythmia. (D) Plots of ROCs and corresponding auROCs comparing how the 8 AP Features at 1 Hz (black), Threshold Experiment (pink), and Combined Protocols (blue) predict susceptibility to I_CaL Increase. Compared with I_Kr Block, I_CaL Increase requires both the steady-state AP features and the Threshold to achieve the same level of performance.

Multiple Biological Parameters Are Required to Understand Susceptibility to I_CaL Increase.

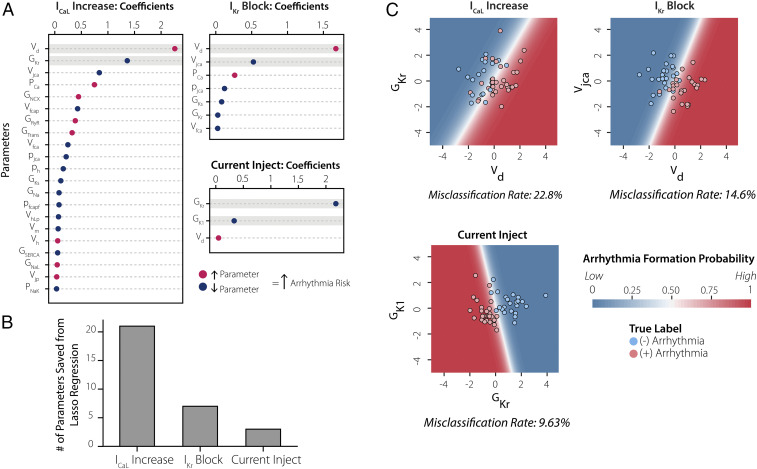
The results presented thus far show that ML classifiers can successfully predict, based on features measured in the absence of a perturbation, how cells will respond to any of the three perturbations tested (auROC > 0.9 in all cases). However, these analyses also indicate that Current Injection and I_Kr Block can be predicted with well-chosen individual metrics (TriAP and excitation threshold, respectively), whereas prediction of the response to I_CaL Increase requires that data from multiple experiments be combined. We hypothesized that this occurred because a greater number of biological parameters influence susceptibility to I_CaL Increase compared with the other two perturbations. To test this idea, we performed Least Absolute Shrinkage and Selection Operator (LASSO) logistic regression (37) on the results using the biological parameters as the independent variables and susceptibility as the dependent variable (Fig. 7A). This approach allowed us to iteratively eliminate parameters until a particular performance was reached, thereby quantifying the number of biological parameters needed for the prediction. Consistent with our hypothesis, the analysis showed that Current Injection, I_Kr Block, and I_CaL increase required 3, 7, and 21 parameters, respectively (Fig. 7B).

Fig. 7.

Multiple biological parameters are required to understand susceptibility to I_CaL increase. (A) β coefficients extracted from LASSO regression analysis performed on mechanistic model parameters for each of the triggers with an auROC = 0.95. (B) Bar graph counts the number of β coefficients extracted from LASSO regression analysis in A, indicating that I_CaL Increase requires knowledge of many more model parameters to reach a 0.95 auROC. (C) Plotting the results using the top two parameters, highlighted in gray in A, to predict risk. The dots indicate the color-coded arrhythmic risk for each cell (red, susceptible; blue, resistant). The contour maps in the background represent model predictions using only the top two parameters to predict arrhythmogenic risk. It is evident that I_CaL Increase has the highest misclassification rate, demonstrating that this trigger depends on multiple additional parameters to reach a high predictive performance.

This idea is further illustrated in Fig. 7C, in which we examine for each trigger how well the two most important parameters can separate resistant and susceptible cells. The individual dots represent 100 cells from the population and are colored based on susceptibility (red = susceptible, blue = resistant). The background contour map represents the LASSO model prediction calculated only from the top two parameters, in which the more lightly shaded areas indicate the region of uncertainty. It is evident both from the regions of uncertainty and the misclassification rates that prediction is weakest for I_CaL Increase, better for I_Kr Block, and best for Current Injection (Fig. 7C). Thus, the I_CaL Increase trigger required more electrophysiological features to achieve strong prediction because many more biological parameters determine susceptibility to this trigger.

Discussion

In this study, we developed a computational pipeline that combines mechanistic modeling with ML analyses, and we applied this to examine individualized arrhythmia susceptibility. Mechanistic simulations were used to generate a heterogeneous population of thousands of cardiomyocytes, and several ML algorithms were applied to predict how the members of this population would respond to triggers that induced arrhythmic behavior in some cells. Importantly, ML was not employed to detect the arrhythmic dynamics, a task that can often be performed by visual inspection, but to predict how physiological waveforms under normal sinus rhythm might indicate susceptibility to a hypothetical future trigger. The ML analyses indicated that it is more difficult to predict the cellular responses to certain triggers than to other triggers. Following from this result, we determined which pretrigger experimental protocols were effective at improving the performance of the ML classifiers. The results indicate the value of combining mechanistic simulations with ML and provide insight into the factors that may determine susceptibility to particular proarrhythmic triggers.

The electrocardiographic QT interval has been the most common metric employed for the prediction of individual susceptibility to ventricular arrhythmias (10), and the QT interval continues to be used in clinical decision-making, for instance, when choosing treatments early in the COVID-19 pandemic (38). Over time, however, many alternative approaches have been proposed, sometimes grouped together under the acronym TRIaD (Triangulation, Reverse use dependence, Instability of the AP, and Dispersion). Over a decade ago, a series of important studies from Hondeghem and colleagues established the utility of TRIaD for prediction of drug-induced arrhythmia (9, 15). More recently, mathematical modeling studies have proposed various quantities derived from simulation results, such as qNet, which calculates the total charge flowing through a specific set of ionic currents (39), or the electromechanical window, which looks at how drugs may differentially affect AP and CaT waveforms (40). Most of these efforts, however, have focused on predicting drug-induced arrhythmias, and conclusions have often been reached by comparing how different metrics perform across a series of drugs. Considerably less research has been performed to address which individuals are especially susceptible to arrhythmias, and critical questions remain unresolved, such as: 1) Will an individual who is susceptible to one arrhythmic trigger be equally susceptible to similar triggers? 2) Can information captured during experimental perturbations complement recordings made during normal sinus rhythm to improve predictions? Here, we addressed such questions by combining mechanistic simulations with ML analyses.

Broadly speaking, ML can be considered a statistical analysis that is more comprehensive and unbiased than a traditional, user-driven approach (17). It therefore represents an appealing strategy for determining the best predictors of an individual’s arrhythmia susceptibility. In principle, ML could be applied directly to clinical data to produce a straightforward, “black box” predictor. For example, convolutional neural networks have been applied to electrocardiographic (ECG) traces from tens of thousands of patients to build classifiers that differentiate between different types of arrhythmias (41, 42). At least two challenges, however, make it difficult to apply a direct strategy to predict arrhythmia susceptibility from clinical data obtained during normal sinus rhythm. One is the question of interpretability; black box ML classifiers often provide practical utility without offering new insight into biological mechanisms (43). A second, more important issue is the heterogeneous and often inconsistent structure of clinical data. ML is straightforward to implement when the same calculations and transformations can be performed on each sample. It can become extremely challenging, however, when data are missing, because patients receive different tests, they are seen at irregular intervals, and arrhythmias are infrequent events. By developing our ML classifiers using synthetic data generated with a mechanistic model, we could perform ML on results with a consistent structure that were produced under identical, well-controlled conditions.

The combination of mechanistic modeling and ML employed in this study provided at least two benefits. The first was an improved mechanistic understanding of the factors that control arrhythmia risk in response to different arrhythmic triggers. The ML analyses showed that it was relatively easy to predict how cells respond to injection of constant current, more challenging to predict the response to block of I_Kr, and most difficult to predict how cells respond to an increase in I_CaL. These surprising results inspired further analyses, which demonstrated important differences between the triggers in terms of which model parameters and how many model parameters determine susceptibility (Fig. 7). For example, the voltage dependence of I_CaL activation, the parameter V_d, greatly affects susceptibility to I_Kr block (Fig. 7A). However, because AP upstrokes carried by I_Na rapidly drive membrane potential past the normal range of I_CaL activation (roughly −30 to 0 mV), small changes in V_d have only a minimal effect on APs recorded during steady-state conditions. This explains why the eight AP features recorded during 1-Hz pacing are ineffective for susceptibility prediction (Fig. 3B), while the excitation threshold under blocked I_Na conditions, which correlates with V_d (SI Appendix, Fig. S5), improves ML performance dramatically. For the current injection trigger, in contrast, V_d has little effect on susceptibility (Fig. 7A). Here, TriAP correlates well with the important model parameters (SI Appendix, Fig. S5), which explains why this single metric is sufficient for strong ML classification performance (SI Appendix, Fig. S1). These mechanistic insights, as well as similar insights into susceptibility to I_CaL Increase (SI Appendix, Fig. S5), illustrate important differences between the triggers.

A second benefit from combining the two approaches is the potential for experimental prioritization. We initially examined cells under conditions that mimicked an individual at rest (steady-state, 1-Hz pacing), then we added predictors to our ML classifiers by simulating additional experimental protocols. The results, which showed that some protocols improved ML performance more than others, can be used to guide decisions when resources are limited and not every experiment can be performed. For prediction of the response to I_Kr Block, for instance, we found that a single experiment measuring excitation threshold could provide as much information as recording APs under multiple experimental conditions (Fig. 6). Similarly, analyses showed that prediction of the response to I_CaL Increase was improved more by including AP waveforms simulated under hypocalcemic and hypercalcemic conditions than by recording at multiple pacing rates. Thus, if the goal of a cellular physiology experiment is to determine the arrhythmia susceptibility of each cell, the results suggest that the simple interventions of altering extracellular [Ca²⁺] and measuring excitation threshold, which are straightforward in most laboratories, provide extremely informative results. We note, however, that these conclusions are specific to the conditions we have considered, namely, EADs caused by reactivation of I_CaL. Different experimental protocols are likely to prove most valuable when different arrhythmia mechanisms are involved.

This experimental prioritization is likely to be important when adapting ML to predict arrhythmia susceptibility in patients. Although cellular APs, which were used to build the classifiers in this study, are not routinely measured in the clinic, features derived from the ECG waveform contain similar information and may also prove useful for building ML classifiers using clinical data. In this context, the additional experimental protocols we simulated here would be analogous to, for instance, monitoring a patient’s ECG during a treadmill test, at multiple times of the day, or during a Valsalva maneuver. Based on the results presented, in which not all protocols were equally valuable, we suggest that classifiers built on simulated results can be used to guide and prioritize protocols for clinical classifiers.

Several limitations of this work suggest future studies to advance the prediction of arrhythmia susceptibility. First, the classifiers were built from simulated results rather than from experimental data. The results, however, have generated predictions that can readily be tested experimentally, especially since these interventions can be implemented in most cellular electrophysiology laboratories. A second limitation is that although we tested eight different ML algorithms, most of these are relatively standard methods rather than state-of-the-art approaches currently referred to as “deep learning.” In this initial study, we opted for ML algorithms that did not require extensive parameter tuning, but in future work, we intend to determine whether more complex ML approaches can improve the predictive power.

In summary, we have demonstrated that a combination of mechanistic mathematical modeling and ML analysis can be applied to predict arrhythmia susceptibility. This combined approach allowed for experimental prioritization and provided mechanistic insight into how ventricular myocytes respond to different proarrhythmic triggers. The work offers a methodology to understand and predict differences between individuals in the susceptibility to dangerous ventricular arrhythmias.

Materials and Methods

The code used to run the simulations in this manuscript have been uploaded to the following repository https://github.com/meeravarshneya1234/ArrhythmiaPredictionProject.git.

Mathematical Model.

We used a mathematical model that describes the electrophysiology of a single human endocardial ventricular myocyte (27). This model consists of 41 ordinary differential equations that capture changes over time in membrane voltage, intracellular ion concentrations, and ion channel gating. This system of equations reproduces two important physiological waveforms—the cardiac AP and the CaT. We ran the model at 1-Hz pacing and extracted features from both the AP and CaT. Refer to SI Appendix, Supplementary Methods for more details on the stimulation protocol and the features calculated from the waveforms.

Heterogeneous Population Development.

Beginning with the baseline ventricular myocyte model (27), we built a large heterogeneous population by applying random variation to two categories of parameter, namely, those that control: 1) ion channel densities (G, for conductances) and 2) kinetic properties that include time constants (p) and voltage dependences (V) of channel gating. Scaling factors for G and p model parameters were taken from a lognormal distribution with median m = 1 and shape parameter σ = 0.3, whereas V parameters were taken from a normal distribution with mean µ = 0 and SD σ = 4 mV (29, 31, 32). A complete list of the 66 model parameters is included in SI Appendix, Tables S1 and S2. We chose shape factors and SDs of these distributions based on the experimental data, from human ventricular myocytes, against which the model (27) was originally calibrated (44–46). For example, time constants reported in those papers had relative variability (coefficients of variation) ranging from 0.13 to 0.58 and voltage dependences of activation and inactivation had SDs ranging from 3 to 10.8 mV. The values we have used are therefore somewhat conservative compared with previously reported variability.

We initially created a population of 25,000 model variants, then calibrated the population by excluding model variants that produced AP or CaT waveforms that were inconsistent with experimental data, as previously described by Passini et al. (34) This experimental data from healthy ventricular cardiomyocytes depicts appropriate ranges for morphological features describing the AP and CaT, which include APD₂₀, APD₅₀, APD₉₀, CaT amplitude, CaD₅₀ (CaT duration at 50% return to baseline), and CaD₉₀ (CaT duration at 90% return to baseline). SI Appendix, Fig. S4 illustrates our simulated distributions along with the calibration ranges. The final calibrated population consisted of 10,586 model variants. A second population was created by varying only ionic channel conductances and not the other categories of parameters. Calibration resulted in a population of 8,200 cells.

Simulating Multiple Experimental Protocols.

We simulated multiple additional experimental protocols in the population, including the following: 1) altered pacing rate; 2) hypercalcemia/hypocalcemia; and 3) excitation threshold. For the pacing rate experiment, each cell was stimulated at least 200 times at 0.2 Hz and 2.5 Hz, and features from the steady-state cellular waveforms were calculated (Fig. 3A and SI Appendix, Supplementary Methods). For hypercalcemia/hypocalcemia, we changed extracellular [Ca²⁺] to 3.6 mM and 0.9 mM, respectively, stimulated each cell at least 200 times at 1 Hz, and calculated features from the steady-state waveforms. In the mechanistic model, this required altering the variable Cao, which controls extracellular [Ca²⁺]. For excitation threshold, we set Na⁺ current in each cell equal to zero so that AP upstrokes had to be carried by I_CaL and determined the threshold stimulus current required to produce an AP.

Arrhythmogenic Triggers.

To test our pipeline’s ability to predict arrhythmogenic risk, we studied three triggers, 1) block of the rapid delayed rectifier potassium current (I_Kr Block), 2) augmentation of the L-type calcium current (I_CaL Increase), and 3) injection of inward current (Current Injection). I_Kr Block mimics the actions of many potent Class III anti-arrhythmics that have proven to be arrhythmogenic. I_CaL increase simulates the period at the beginning of β-adrenergic stimulation, when a temporal mismatch between phosphorylation of I_CaL and I_Ks may temporarily create proarrhythmic conditions (47). Although the current injection trigger simulates artificial conditions created in the laboratory rather than a trigger encountered in vivo, this metric has been used in prior work as a quantitative representation of repolarization reserve (48).

Both I_Kr Block and I_CaL Increase were simulated by scaling the conductance values for each channel, G_Kr and G_CaL, respectively, while Current Injection was performed by injecting a constant inward current at all times that the membrane voltage exceeded −60 mV. For each perturbation, we determined an arrhythmia threshold in the baseline ventricular myocyte by gradually increasing the magnitude of the perturbation until arrhythmic behavior was observed at any time during the last 10 beats of simulation. The final threshold for each trigger was 94% block of I_Kr, a 15.13-fold increase in I_CaL, and injection of −0.7 μA/μF current. When these triggers were applied to each cell in the virtual population, roughly half of the cells exhibited arrhythmic behavior, defined as either repolarization failure, or an EAD, any change in the voltage derivative from negative to positive occurring more than 100 ms after the AP initiation. Under these conditions, EADs were initiated by reactivation of I_CaL rather than spontaneous Ca²⁺ release or reactivation of I_Na.

Supervised ML.

For each perturbation, every cell in the population was classified as either susceptible or resistant. To perform this classification task, we employed supervised ML. ML algorithms learn from data to identify patterns that relate a set of features to a binary predictor. Here, we used features computed from simulated AP and CaT waveforms, before a trigger was applied, to predict whether individual cells would exhibit arrhythmic dynamics in response to the trigger. Since we were unsure which ML classifier would be best suited for our dataset, we constructed a robust pipeline that tested each task in eight parameter-tuned classifiers. These algorithms include Support Vector Machine (SVM), Multi-Layer Perceptron (MLP), Random Forest, Naïve Bayes, Gradient Boosting, XGBoost, Logistic Regression, and K-Nearest Neighbors. We consistently found that SVM and MLP exhibited the best classification performance (SI Appendix, Fig. S6). We ran these algorithms in Python 3.7.4, using the ML package scikit-learn version 0.21.3 (49), and for each classification task, we display results from the best-performing classifier (50–52).

To train the algorithms, we split the population into 90% training and 10% testing stratified by the target class. We normalized the input features using MinMaxScaler for MLP and StandardScaler for the remaining. The MinMaxScaler normalized the features to a range of 0 and 1, while the StandardScaler normalized by removing the mean and scaling to the unit variance. To fine-tune the hyperparameters for each classifier, we applied the function GridSearchCV on the training set. This allowed us to effectively loop through a series of different parameter sets using threefold cross validation. The best parameters were then used to assess the performance of the algorithms on the test set.

To evaluate classifier performance, the primary metric we employed was the auROC. Our pipeline calculated a series of additional metrics including accuracy, positive and negative predictive value, and specificity and sensitivity, reported on our github. However, since the datasets were balanced, all metrics displayed similar trends, and only auROC is reported in the main figures for simplicity.

LASSO Regression.

To quantify the number of biological parameters needed to predict arrhythmia susceptibility for each trigger, we utilized LASSO regression (37). The random-scale factors (for G and p parameters) or offset voltages (for V parameters) were collected into an X matrix of independent variables (dimensions 10,586 × 66), and labels (resistant or susceptible) were collected into a Y vector of dependent variables (dimensions 10,586 × 1). This method outputs a β coefficient matrix that defines the relative contribution of each parameter to arrhythmia susceptibility. With LASSO regression, the penalty term iteratively sets the coefficients of insignificant parameters β to zero, thus providing a means of assessing which parameters are truly necessary to reach a particular prediction accuracy. We implemented this in Python using the LogisticRegression function in the scikit-learn package and specifying the l1 penalty. To compare the results among the three triggers, we took the number of β coefficients required to achieve an auROC of 0.95.

Data Availability

Anonymized code data have been deposited in Github (https://github.com/meeravarshneya1234/ArrhythmiaPredictionProject.git). Some study data available.