Generative models and abstractions for large-scale neuroanatomy datasets

Abstract

Neural datasets are increasing rapidly in both resolution and volume. In neuroanatomy, this trend has been accelerated by innovations in imaging technology. As full datasets are impractical and unnecessary for many applications, it is important to identify abstractions that distill useful features of neural structure, organization, and anatomy. In this review article, we discuss several such abstractions and highlight recent algorithmic advances in working with these models. In particular, we discuss the use of generative models in neuroanatomy; such models may be considered “meta-abstractions” that capture distributions over other abstractions.

Introduction

As the scale of neuroanatomy data has grown, algorithms and abstractions have been developed to distill high-dimensional data into usable forms. Such approaches have allowed us to address questions such as: What is the density of synapses in a specific region of the brain? What is the connectivity between an area of interest and the rest of the brain? What is the best way to divide a brain area into subregions? As the number of data points grows yet further, however, it is possible to ask a different kind of question about variation across different samples or different individuals. These questions can be thought of as “how” instead of “what”: How does neuroprotective treatment alter the density of synapses? How does learning affect the sparseness of connections in a network? How does the modularity of brain networks vary across subjects?

The goal of this article is to discuss how generative approaches in machine learning can be used to address such questions in large-scale neuroanatomy. A generative model captures the variability between samples in a dataset, or between entire datasets, by generating artificial examples with similar statistics to the real data. For example, a generative modeling approach can be used to sketch artificial neurons that are structurally similar to genuine ones, or to simulate a connectome for which the network properties match those observed from microscope data. Generally, the model itself incorporates randomness in order to simulate the true probability distribution over data. A perfect generative model would parameterize the underlying data distribution exactly, allowing the entire dataset to be recreated algorithmically.

We start by describing three main classes of abstractions widely used in neuroanatomy: counts or densities to model the spatial distribution of discrete objects like cells or synapses, connectomes to model the connectivity between either cells or brain areas, and modular or hierarchical models that describe how data are organized into groups. We then describe generative models that are matched to these various abstractions. For example, Poisson models can generate count data of objects such as cells or synapses [1], stochastic block models can be used to build graphs [2], and hidden Markov models can be used to generate the dendritic trees of neurons [3]. In each case, we describe both the algorithmic approach and the conclusions that can be drawn from these abstractions.

After providing an overview of generative models that are built on top of these popular abstractions, we outline generative models that are not built upon any lower-level abstraction. Instead, models such as generative adversarial networks (GANs) [4], [5] and variational autoencoders (VAEs) [6] can generate very high-dimensional data, including entire images. Such models can be used to analyze the sources of variability in observed images [7], to augment observed data, or to interpolate between different imaging modalities [8].

Abstractions

In this section, we highlight key classes of abstractions used in neuroanatomy and describe approaches to estimate these models from high-dimensional and complex brain data (see Figure 1). Each of these abstractions can be considered in terms of (i) what data sources it is commonly derived from, (ii) what questions it can be used to answer, (iii) what information it retains and what it discards from the full-dimensional data, and (iv) algorithms used to derive the abstraction.

Figure 1: Abstractions and Generative Models for Neuroanatomy.

(1) COUNTS & DISTRIBUTIONS: From left to right, we show a (left) retinal dataset before and after cell detection [9], (middle) a depiction of how count data can be represented as a density function, and (right) a Poisson model for generating new count data. (2) CONNECTOMES: From left to right, we show (left) an electron microscope image of a thin slice of cortical brain tissue before and after dense segmentation to build a connectome, (middle) a depiction of a connectome as a graph, and (right) an example of the random overlapping communities model for sparse graphs with three communities displayed as different colors [10]. (3) Modular and Hierarchical Representations: From left to right, we show (left) a light microscope image with a biocytin filled neuron in two views before and after tracing (from the Allen Institute for Brain Science’s Cell Types Atlas [11]), (middle) a hierarchical representation of a dendrite, and (right) example neuronal morphologies generated after an iterative sampling procedure [3], where the iteration number is displayed over each generated morphology.

Counts and Densities.

In neuroanatomy, quantification of brain structure often starts by counting cells, synapses, spines, or other objects in the brain. Counts, or the number of discrete objects in a interval/bin of fixed size, provide the data necessary to compute density estimates from many samples. A large body of work in neuroanatomy involves modeling changes in densities across multiple samples or conditions.

• Example data sources: Cellular densities can be resolved in Nissl- or DAPI-stained brain images [12] and retinal datasets (Figure 1a) [13], as well as X-ray microCT [14]. Synapses can be resolved in electron microscopy (EM) [15], [16] and array tomography [17] datasets. Individual mRNAs can now be resolved in brain tissue with spatial transcriptomics (mFISH) [18], multiplexed error-correcting FISH (merFISH) [19], and expansion microscopy-based FISH [20].

• Type of conclusion drawn: The spatial distribution and patterns of discrete objects like cells or synapses. Micro and macroscale architecture can also be detected by analyzing spatial patterns in the data. Counts can also be used to track changes to the nervous system in development [21], disease [22], or aging [23].

• Information included: The spatial position of objects is included but the connectivity between these objects is not modeled. In some cases, each count can also be associated with additional metadata or ‘marks’ like the object’s size.

• Algorithms used to create abstraction: Segmentation and density-based methods have been developed to quantify the spatial organization and distributions of cells [14], [24] (Figure 1c), synapses [25]–[28], neuronal arbors [29], organelles [30], and spines [31].

Connectomes.

Graphs are some of the most widely used abstractions for neuroanatomical data. They are typically used to convey observed physical connectivity between individual neurons or neuronal assemblages. Such graphs are commonly referred to as “structural” connectomes (in contradistinction to “functional” connectomes, which capture correlations between observed activity of neurons). At the microscale, cellular connectomes have nodes for neurons and (weighted) edges for synapses. In meso- or macro-scale connectomes, nodes represent local or global brain areas, while edges represent projections between the areas. Such graphs are also referred to as “projectomes”.

• Example data sources: At the microscale, connectomes can be extracted from EM [16] (Figure 1) and expansion microscopy (ExM) [32] datasets. Projectome mapping methods have made use of viral tracing methods and whole-brain serial two-photon microscopy (STP) and MOST [33]–[36] to reveal long-range connections. Projectome data has also been obtained from humans using magnetic resonance imaging (MRI) [37]–[40], mainly through the use of diffusion tensor imaging.

• Type of conclusion drawn: Connectomes and projectomes can be used to understand learning and plasticity, as well as constrain models of neural information processing.

• Information included: The connectivity between neurons or brain areas is included in these models. In some cases, the strength of connections can also be estimated and included to produce a weighted graph. The spatial position of each node is often excluded in a graphical representation of the data.

• Algorithms used to create abstraction: There has been extensive recent work on automatic labeling of EM and ExM images to segment neurons [41]–[49] and synapses [26], [50]. On the computational side, Majka et al. [51] demonstrate tools for coregistering projectomes to create a common map of primate (marmoset) cortex, while other algorithms have been developed to infer higher resolution completions of partial connectivity data [52], [53].

Modular and Hierarchical Models.

Finally, we consider modular and hierarchical abstractions which divide data into groups based upon which examples/segments have similar characteristics. One example is representing a large brain volume as a collection of brain regions, modules, or spatially-defined regions of interest [54], [55]. This principle can be iterated by expressing data examples in terms of a hierarchical model, where discrete groups are divided into subgroups at many scales. For example, the morphology of a neuron can be described with a hierarchical format, with a coarse division into soma, axon, and dendrite which is further broken down into individual branches.

• Example data sources: Serial two-photon and fMOST for whole-brain imaging have been used to obtain parcellations of the brain [34]. Morphological reconstructions for modeling the components of neurons can be extracted from light microscopy datasets [56].

• Type of conclusion drawn: The high-level organization of the data and which parts of the signal are similar and thus belong to the same group. A hierarchical format for data can be advantageous in representing similarities in data across multiple spatial or evolutionary divisions/scales.

• Information included: Modular representations group the structure of many nearby segments of a neuron (parts) or nearby parts of a brain region into one bulk class. The membership of data to a class is preserved and perhaps the average (centroid) of the class is also maintained. Hierarchical models further provide information about the distance between different groups as relative to their multi-scale dependencies.

• Algorithms used to create abstraction: To obtain an informative parcellation and simplification of the data, clustering algorithms [57] such as k-means and spectral clustering methods [58] can be used to group spatial loci that have similar statistics in terms of their measured anatomical signal. Semi-automated approaches have recently been shown to provide new insights into structurally and functionally distinct areas in whole human brains with multi-modal measurements [59].

Generative Models for Abstractions

In this section, we describe different generative models that are built on top of the previously discussed abstractions. Each generative model represents a design choice about what features of the true data are most important to capture, based upon the questions under consideration.

Generative models for count-valued data

A generative model for count-valued data (i.e., how many objects are in a region of interest) creates a synthetic dataset where objects are placed across space according to the underlying statistics of real data. Which statistics are important represent a design choice. For example, a model might be designed so that the density functions of real and synthetic data match or so as to preserve nearest-neighbor properties of the counts (e.g., the Ripley k-function [60]).

The simplest generative model used for count-valued data is a Poisson process. Here, we assume that the number of objects observed in a bin/interval is a Poisson-distributed random variable with mean given by an intensity (density) function, and where the numbers of objects in different bins are conditionally independent. Thus, given the potentially spatially-varying intensity of the process, samples can be generated to create a simulated dataset. To extend the independence assumption of Poisson models to ensure that objects are separated by a minimum distance, random sequential adsorption (RSA) processes have been used to model synapses throughout all cortical layers [27]. Point process models can also be constrained to generate counts along a graph structure, for instance in the modeling of spines along a neurite [61].

See [1] for a review of spatial point process models and their applications in neuroanatomy.

To model more complex spatial properties of the data, the underlying intensity function can be approximated by a sparse combination of simpler functions. LaGrow et al. [9], [62] show that by using a basis that can capture change points in the density, this enables the efficient estimation of mesoscopic properties of the density, like the layering structure in the cortex.

Generative models for connectomes

To create a realistic generative model for graphs, we need to first specify the property of the graph we wish to capture. One such property is the average degree of all nodes. Random graph theory provides a wealth of resources for generating graphs that have certain edge and high-level properties [63]. A more complex generative model could ask that graph metrics like clustering and modularity match between real and synthesized data. Such generative models can be introduced by building on random graph models like the widely used Erdős-Renyi random graph model [64], in which each pair of nodes is assigned an edge with some fixed probability p. The random overlapping communities (ROC) model is a good example of a generative model that can generate overlapping communities as observed in neural circuits, and has provable convergence in terms of its desired properties [10]. In this model, many subsets of the overall graph are chosen at random, and dense Erdős-Renyi random graphs are constructed on these (possibly overlapping) subsets. Additionally, stochastic block models (SBMs) are a class of generative models for synthesizing graphs [65], which have been used to model hierarchical modules within a connectome. In an SBM, the nodes of the graph are divided into several blocks, and the probability of connection between two nodes depends only on the blocks in which they lie. Jonas and Kording [66] introduce a variant of SBMs to model connectivity between neurons, where the blocks of the model correspond to cell types, and where distances also affect the probability of connection. They use Markov Chain Monte Carlo (MCMC) methods to fit the parameters of the model, thereby automatically inferring cell types from connectomics data.

Hidden Markov model (HMMs) have also been applied successfully to the graph structures representing the branching of individual neurons. HMMs model the growth of a graph or other data structure over time using a Markov chain that depends on hidden variables that can be statistically inferred but are not observed directly. For example, the hidden state of a neuron as it grows might include biochemical factors that are not directly observable, even though they lead to observable data such as the morphology of the neuron. In Farhoodi et al. [67], the branching patterns of different types of neurons are learned and incorporated into a generative model by analyzing single-neuron morphological data compiled by neuromorpho.org [68]. The HMM inferred by Farhoodi et al. suggests that the probability of branching within a neuron depends on the distance to the soma, whether whether the branching occurs in a main branch or a side branch, and what the type of neuron is. The model thus yields both insights into the underlying factors that may be at play in neural branching and also a procedure for generative artificial neuronal morphologies. See also Farhoodi and Kording [3] for a generative approach to neuron morphologies based on Markov chain Monte Carlo (MCMC) sampling.

Modular and hierarchical generative models

Generative models built on top of hierarchical abstractions, typically will generate a sequence of items wherein the probabilistic model depends upon what was generated at previous generate samples. To ensure that our generative model matches the distribution of data, the sequence of steps must generate an output that matches the same sequence generation of real data.

SBMs (defined in the preceding section) are well-suited to dissecting graphical data into hierarchically organized modules. Lyzinski et al. [2] combine SBMs with clustering algorithms to decompose a partial Drosophila connectome into blocks, which are then clustered into similar subnetworks (motifs). The process is then repeated to generate a hierarchy of motifs. Priebe et al. [69] apply another generalization of SBMs to the Drosophila connectome to explain variation in cells that is fit poorly by simple clusters.

Generative Models for Image Data

Whereas the generative models highlighted in the previous section require (often intensive) pre-processing steps to first build an abstraction from image data, modern machine learning methods make it possible to learn a generative model from images directly. Learning models from images directly could potentially allow us to by-pass the initial steps of building an abstraction (e.g., segmenting or finding objects in images). Rather than specifying what to look for in an image, the generative model would be able to automatically pull out features from the image data that are important for building realistic representations of neural structure and capturing variability across examples. In this section, we highlight matrix factorization and deep learning approaches for learning generative models from collections of images, and discuss their applications in neuroanatomy.

Latent variable models

Learning to model the distribution of high-dimensional image data is extremely challenging. A first step is often to form a low-dimensional representation that is easier to model. A simple and widely used linear approach for learning latent factors from data is principal component analysis (PCA); PCA fits a k-dimensional linear approximation to a dataset with many examples, such as a collection of many brain images. Other dimensionality reduction techniques such as non-negative matrix factorization [70], probabilistic PCA [71], and sparse PCA [72] can all be used to form a low-dimensional representation of collection of data (see [73] for a comprehensive review of dimensionality reduction techniques and their applications in analyzing measurements of neural activity).

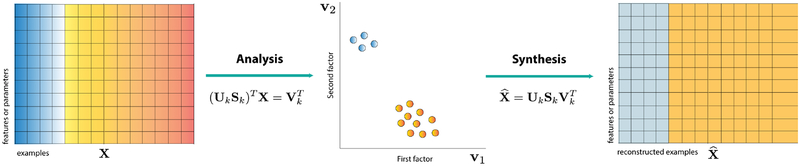
After distilling data into a low-dimensional space, image data can be reconstructed by inverting the low-dimensional model learned in the analysis step (Figure 2, left). This synthesis operation is visualized in Fig. 2 for a linear system learned in PCA. In this case, a new image is created by either: reconstructing an input (pass in a noisy signal and the output is a clean version) or generating a new sample in the low-dimensional space and then using the decoder to synthesize a new image as output. This interpretation of linear matrix factorization (PCA) as a generative model provides a simple strategy for creating high-dimensional images when the data lie near a linear subspace.

Figure 2: Linear matrix factorization methods like PCA and their interpretation as a generative modeling procedure.

From left to right, we show the decomposition of a data matrix consisting of examples along its columns, into a low-dimensional format. In the middle, we depict the low-d representation of the data in two dimensions. On the right, we show a reconstructed or synthesized data matrix that uses the inverse mapping to expand the low-d data back into a high-dimensional space again.

Autoencoders

Generative models that rely on PCA and other matrix factorization approaches use linear transformations of data. It is also possible to find nonlinear low-dimensional representations of data. Autoencoders are now routinely used for this task [74]. Autoencoders can be constructed through different neural network architectures, encompassing models such as stacked convolutional autoencoders [75] and variational autoencoders [6]. Essentially, an autoencoder functions by passing high-dimensional input through a sequence of layers, including a low-dimensional “bottleneck” layer, then reconstructing the full-dimensional input again in the output layer (see Figure 3, left). The bottleneck layer thus learns a low-dimensional latent representation of the data. The first part (up to the bottleneck) is the encoder and the remainder (reconstructing the input) is the decoder. Thus, the encoder compresses the data to the latent representation, and the decoder is a generative model that recreates data from this latent representation. Thus autoencoders provide an analogous architecture for generative modeling for the nonlinear case as that depicted for the linear case in Figure 2.

Figure 3: Generative models for synthesizing structural brain images.

On the left, we depict an autoencoder consisting of an input layer, a low-dimensional hidden layer (latent space), and output layer. In the training phase, a low-dimensional model for data is learned and in the synthesis phase, a sample from this model is generated and used to generate a new image. This architecture is applied to auto-fluorescence images of 1,700 different brains (25 micron resolution) to synthesize new images: on the right, a synthetically generated image (top), example of a real image used to train the network (bottom), and a denoised (reconstructed) version of the image displayed on the bottom.

Generative adversarial networks

Within deep learning, generative adversarial networks (GANs) have recently been developed to learn from an unlabeled training dataset to generate artificial data resembling examples from the dataset. Like autoencoders, GANs learn a nonlinear generative process for data via an artificial neural network. However, unlike autoencoders, which learn both an “encoding” step and a “decoding” (generative) step, GANs learn by pitting two network algorithms against each other, with one (the generator) attempting to generate plausible examples from a dataset, while the other (the discriminator) tries to tell the difference between real and fake examples, thus forcing the generator to improve. While extensive applications to neuroanatomy have yet to be developed, GANs have already been used to simulate neuron morphologies [76] and spike trains [77]. A similar approach (using deep learning methods distinct from GANs) uses the output of one imaging modality to simulate the result of another imaging modality [78].

It is tempting to consider using the output of a GAN to augment real data in fitting additional algorithms. However, there is so far no magical algorithm that replaces the power of large real datasets. For example, while a GAN might be used to learn from a thousand images and then create a million more similar-seeming images, the artificial images would likely either fail in subtle ways to be truly realistic or would fail to capture the full diversity of real-world data. We therefore believe the function of generative algorithms in neuroanatomy should be, for the moment, more in modeling than in augmenting data for training.

Conclusions

As neuroanatomy datasets become more numerous and higher-dimensional, there is increasing need for generative models that capture variability across data samples and subjects. Where traditional abstractions such as connectomes compress data, generative “meta-abstractions” compress distributions over data or over abstractions. We believe that an understanding of the breadth of available abstractions and concomitant generative models, each suited to different questions and data modalities, is essential to present-day neuroanatomy.

Many of the generative models we have described make strong assumptions about the structure of the data-for example, that it is well-approximated by a density function or succinctly described by a Markov chain. By contrast, generative algorithms from deep learning typically have no such prior assumptions, and the models they learn are often “black boxes” that are hard to interpret. Interpretation becomes increasingly difficult as we move to full images and raw data because it is not always clear what properties of the data are being modeled and how. New approaches for ‘disentangling representations’ [79] aim to mitigate these issues and build architectures that reveal more interpretable factors. An important line of research is to build deep learning architectures that are interpretable and can be used to draw inferences about disease, inter-subject variability, and other changes to neural structure.

Traditionally, neuroscience has provided views of the structure of the nervous system that resolve or model one aspect of the anatomy at a time. Neuroscience methods are, however, increasingly moving towards resolving multiple types of structures simultaneously to provide multi-modal and multi-scale structural information for large volumes, in some cases up to whole brains [12], [34]. With increasing access to multi-modal information, it is critical to develop abstractions and generative models that distill the data into a usable simplification that leverages the multi-modal data provided. Because traditional methods for modeling neuroanatomy have focused on modeling a single attribute of the data (a graph, or a density), in some cases it is not clear how best to integrate data formats and models across different modalities of information. It is exceedingly likely that different aspects of anatomy (change in density of synapses or cells, or strengthening of connections in a specific region of the brain) co-vary in complex and nonlinear ways and multi-modal datasets will be necessary to reveal these relationships.

Generative models are now being used to learn increasingly complex attributes of a wide range of datasets. We believe that they will be a useful tool moving forward for modeling variability in large-scale neuroanatomy datasets.

Highlights.

1. Modern neuroscience has now entered the age of big data. Low-dimensional models and abstractions are needed to distill high-dimensional neuroanatomical data into a simpler format.

2. Generative models provide a powerful strategy for modeling large-scale neuroscience datasets. Such approaches aim to synthesize new data, rather than analyzing data.

3. Deep learning-based generative modeling frameworks like generative adversarial networks and autoencoders are still difficult to interpret; however, they have the potential to reveal hidden factors that control variability across complex large-scale neuroanatomy datasets.