SUMMARY
The curse of dimensionality plagues models of reinforcement learning and decision-making. The process of abstraction solves this by constructing variables describing features shared by different instances, reducing dimensionality and enabling generalization in novel situations. Here we characterized neural representations in monkeys performing a task described by different hidden and explicit variables. Abstraction was defined operationally using the generalization performance of neural decoders across task conditions not used for training, which requires a particular geometry of neural representations. Neural ensembles in prefrontal cortex, hippocampus, and simulated neural networks simultaneously represented multiple variables in a geometry reflecting abstraction but that still allowed a linear classifier to decode a large number of other variables (high shattering dimensionality). Furthermore, this geometry changed in relation to task events and performance. These findings elucidate how the brain and artificial systems represent variables in an abstract format while preserving the advantages conferred by high shattering dimensionality.
Keywords: Abstraction, factorized representations, disentangled representations, prefrontal cortex, hippocampus, anterior cingulate cortex, dimensionality, artificial neural networks, representational geometry
Graphical Abstract
ETOC
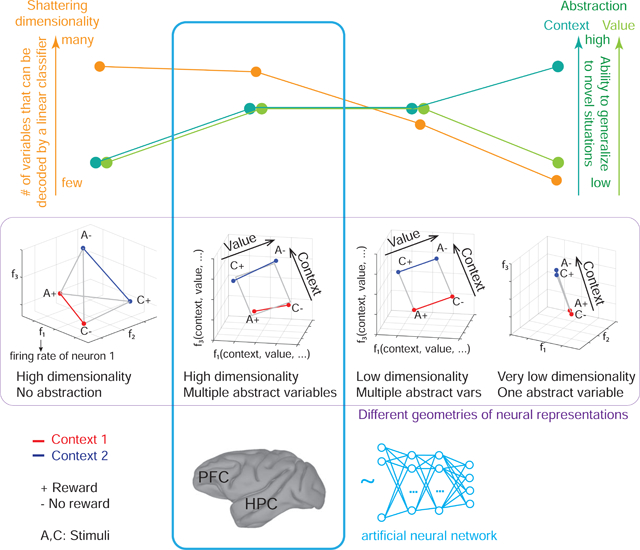
Different types of cognitive, emotional and behavioral flexibility – generalization in novel situations and the ability to generate many different responses to complex patterns of inputs -place different demands on neural representations. This paper shows how the geometry of neural representations can be critical for elucidating how the brain supports these forms of flexible behavior.
INTRODUCTION
When encountering a new situation, the ability to determine right away what to do is a hallmark example of cognitive flexibility. This ability relies on the fact that the world is structured and new situations often share features with previously experienced ones. These shared features provide a compact representation that uses a small number of variables to describe the environment. This representation can be constructed using a process of dimensionality reduction, which obviates the need to observe all possible combinations of values of all features appearing in the environment, overcoming the ‘curse of dimensionality’. The variables describing features shared by multiple instances can be represented in an “abstract” format in the brain, a format that can enable generalization in novel situations.
An account of how the brain may represent these variables has remained elusive. Motivated by the fact that the process of abstraction enables generalization, we developed analytic methods for determining when the geometry of neural representations encodes variables in an abstract format. We operationally defined a neural representation of a variable as being in an abstract format (an “abstract variable”) when a linear neural decoder trained to report the value of the variable can generalize to situations not experienced by the decoder during training. Previously unseen combinations of the values of other variables describe these situations. In experiments, these situations correspond to task conditions not used for training the linear decoder. We call the performance of this decoder “cross-condition generalization performance” (CCGP), because it reflects the ability of a decoder to generalize to task conditions not used for training. CCGP is distinct from the type of generalization normally referred to when a variable is decoded by training on some samples from all experimental conditions and testing on held-out samples from the same types of conditions. Techniques similar to CCGP have previously been employed to examine the representation of one variable at a time and/or to identify a common neural substrate that might underlie 2 or more cognitive operations (Horikawa et al. 2013; Zabicki et al. 2017; Parkinson et al. 2014; King & Dehaene 2014; Saez et al. 2015; Munuera et al. 2018; Isik et al. 2013, 2017).
Representations of variables in an abstract format, as identified by CCGP, are typically low dimensional (their dimensionality equals the number of encoded variables). The machine learning community often refers to them as “disentangled”, or factorized (e.g. (Higgins et al. 2017)). A disentangled representation can encode multiple variables in an abstract format simultaneously. However, since a perfectly factorized representation is low dimensional, it places severe limits on the number of different potential responses that a simple linear readout can generate(Rigotti et al. 2013; Fusi et al. 2016). To quantify this limitation we used another measure that characterizes the geometry of representations, the shattering dimensionality (SD) (see also (Rigotti et al. 2013)). The SD is the number of different ways that points corresponding to the firing rates of one or more neurons in different (experimental) conditions can be separated (shattered) by a linear decoder. Typically when SD increases, CCGP decreases. However, this trade-off between CCGP and SD is not necessary and there are geometries that allow for a surprisingly good compromise in which both SD and CCGP are high. These geometries enable good generalization in novel situations and retain properties that confer the flexibility to respond in many different ways to complex combinations of inputs.
We used CCGP and SD to examine the geometry of neural representations recorded from monkeys as they performed a serial reversal-learning task in which they switch back and forth between 2 un-cued contexts. A distinct stimulus-response-outcome (SRO) mapping described each trial, and sets of SRO mappings defined contexts (“task sets”). Some variables were observable (related to sensory input or motor output), while context, a hidden variable, was defined by the temporal statistics of events and could not be directly inferred by the value of any observable variable. Therefore, if a neural ensemble represents the variable context in an abstract format, it would reflect a process of dimensionality reduction (i.e. abstraction) that consistently captures the relational properties of the states of the external world across time(Eichenbaum 2017; Behrens et al. 2018; Recanatesi et al. 2019; Whittington et al. 2019; Benna & Fusi 2019).
Neurophysiological recordings were targeted to the hippocampus (HPC) and two parts of the pre-frontal cortex (PFC), the dorsolateral pre-frontal cortex (DLPFC) and anterior cingulate cortex (ACC). The HPC has long been implicated in generating episodic associative memories that could play a central role in creating and maintaining representations of variables in an abstract format (Milner et al. 1998; Eichenbaum 2004; Wirth et al. 2003; Schapiro et al. 2016; Kumaran et al. 2009). Neurons in ACC and DLPFC have been shown to encode rules and other cognitive information (Wallis et al. 2001; Miller et al. 2003; Buckley et al. 2009; Antzoulatos & Miller 2011; Wutz et al. 2018; Saez et al. 2015), but testing whether a neural ensemble of single units represents one or more variables in a format that can support CCGP has generally not been examined (but see (Saez et al. 2015)). Our data reveal that neural ensembles in all 3 brain areas, and ensembles of units in simulated multi-layer networks, simultaneously represent hidden and explicit variables in an abstract format, as defined by high CCGP, yet also possess high SD. Our results highlight the importance of characterizing the geometry of a neural representation - not just what information is represented - in order to understand a brain region’s potential contribution to different types of flexible cognitive behavior.
RESULTS
In the ensuing sections of the Results, we first present behavioral data and the theoretical framework and analytic methodology developed to characterize geometry. Then we characterize the geometry of neural representations in the HPC, DLPFC, and ACC, and in simulated neural networks.
Monkeys use inference to adjust behavior.
Monkeys performed a serial-reversal learning task in which each of 2 blocks of trials contained 4 types of trials (conditions). Three variables described each condition: a stimulus, and its operant and reinforcement contingencies (SRO mapping). Un-cued switches occurred between the blocks of trials in which SRO mappings changed simultaneously for all 4 conditions. Thus each block was a context defined by its set of 4 SRO mappings (‘task sets’), a hidden variable.
Correct performance for 2 stimuli in each context required releasing a button after stimulus disappearance; for the other 2 stimuli, the correct operant response was to continue to hold the button (Figure 1a,b; see Methods). For 2 stimuli, correct performance resulted in reward delivery; for the other 2 stimuli, correct performance did not result in reward, but it avoided a time-out and repetition of the same unrewarded trial (Figure 1b). Without warning, randomly after 50–70 trials, context switched, and many switches happen within an experiment.
Figure 1: Task and behavior.
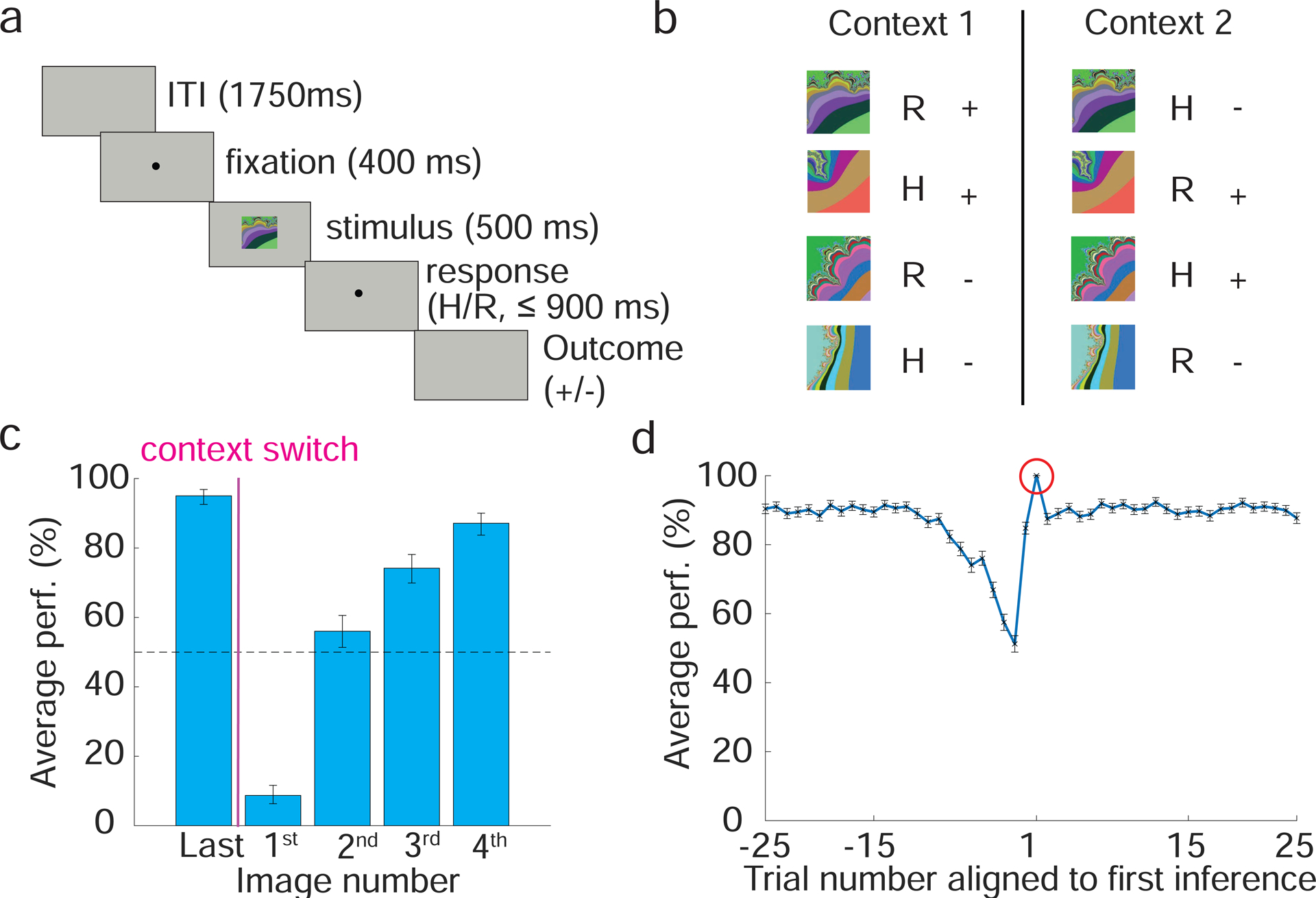
a. Sequence of events within a trial. A monkey holds down a button, then fixates and views one of 4 familiar fractal images. A delay interval ensues, during which the operant response must be indicated (release or continue to hold the button, H and R). After a trace period, a liquid reward is delivered for correct responses for 2 of the 4 stimuli. Correct responses to the other 2 stimuli result in no reward, but avoids a timeout and trial repetition. b. Task scheme, SRO mappings for conditions in the 2 contexts. A-D, stimuli. +/−, reward/no reward for correct choices. Operant and reinforcement contingencies are orthogonal. After 50–70 trials in one context, context switches; experiments contain many context switches. c. Monkeys utilize inference to adjust behavior. Average percent correct plotted for the first presentation of the last image appearing before a context switch (”Last”) and for the first instance of each image after a context switch (1–4). For image numbers 2–4, monkeys adjusted performed at above chance despite not having experienced these trials in the current context (inference). Binomial parameter estimate, bars are 95% Clopper-Pearson confidence intervals d. Average percent correct performance plotted vs. trial number aligned on the first correct trial where the monkey used inference (red circle, defined as the first correct trial among the first presentations of the 2nd, 3rd or 4th image type appearing after a context switch). So if Image 1 is the first image after a context switch, and the first presentation of image 2 is performed correctly, it is the first correct inference trial. If it is performed incorrectly, the first correct inference trial could occur on the first presentation of image 3 or 4.
Not surprisingly since context switches were un-cued, monkeys’ performance dropped to significantly below chance immediately after a context switch (image 1 in Fig. 1c). In principle, after this incorrect choice, monkeys could re-learn the correct SR associations for each image independently. Instead, behavioral evidence shows that monkeys perform inference such that after a context switch. After experiencing changed contingencies for one or more stimuli, average performance is significantly above chance for the stimulus conditions not yet experienced (image numbers 2–4, Fig. 1c). Once monkeys exhibit evidence of inference, performance remains asymptotic for the remainder of trials in that context (~ 90 % correct, Fig. 1d). Note that the temporal statistics of events (trials) define the variable context. The only feature that trials of Context 1 have in common is that they are frequently followed or preceded by other trials of Context 1; the same applies to Context 2 trials. Monkeys’ behavior suggests that they exploit knowledge of these temporal statistics.
The geometry of neural representations that encode abstract variables.
A neural ensemble can represent variables in many different ways. We now consider different representations that have distinct generalization properties. We use these properties to define when a variable is represented in an abstract format. Consider the hidden variable context. Some representations encode context but do not reflect a process of abstraction. For example, assume that the average firing rate of each neuron is random for each experimental condition (i.e. for each SRO mapping). Figure 2a depicts in the firing rate space an example of this representation. Each coordinate axis is the firing rate of one neuron. Each point in Figure 2a represents a vector containing the average activity of 3 neurons for each condition within a specified time window. The geometry of the representation is defined by the arrangement of all the points corresponding to the different experimental conditions.
Figure 2: The geometry of abstraction.
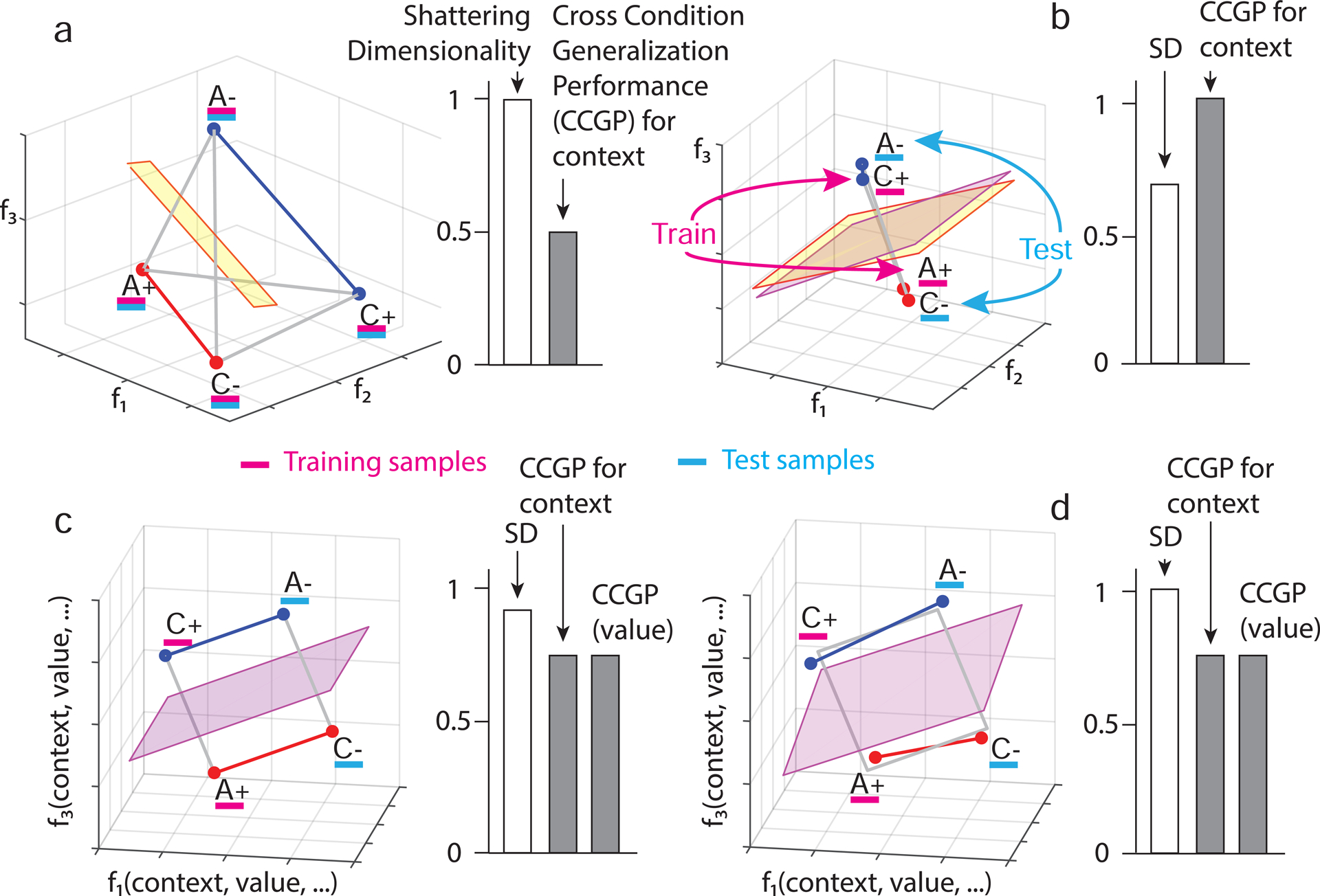
Different representations of context can have distinct geometries, each with different generalization properties. Each panel depicts in the firing rate space points that represent the average firing rate of 3 neurons in only 4 of the 8 conditions from experiments. The 4 conditions are labeled according to stimulus identity (A,C) and reward value (+,−). a. A random representation (points are at random locations in the firing rate space), which allows for decoding of context. The yellow plane represents a linear decoder that separates the 2 points of context 1 (red) from the 2 points of context 2 (blue). The decoder is trained on a subset of trials from all conditions (purple) and tested on held out trials from the same conditions (cyan) (see Figure S1a for more details). All other variables corresponding to different dichotomies of the 4 points can also be decoded using a linear classifier; hence the shattering dimensionality (SD) is maximal, but CCGP is at chance (right histogram). b. Abstraction by clustering: points are clustered according to context. A linear classifier is trained to discriminate context on rewarded conditions (purple). Its generalization performance (CCGP) is tested on unrewarded conditions not used for training (cyan). The separating plane when trained on rewarded conditions (purple) is different from the one obtained when all conditions are used for training (yellow), but for this clustered geometry, both planes are very similar. With clustered geometry, CCGP is maximal for context, but context is also the only variable encoded. Hence, SD is close to chance (right histogram). (See Methods S2 Clustering index as a measure of abstraction). Notice that the form of generalization CCGP involves is different from traditional decoding generalization to held out trials (see Methods S3 Relation between CCGP and decoding performance in classification tasks). c. Multiple abstract variables: factorized/disentangled representations. The 4 points are arranged on a square. Context is encoded along the direction parallel to the two colored segments, and value is in the orthogonal direction. In this arrangement, CCGP for both context and value are high; the SD is high but not maximal because the combinations of points that correspond to an exclusive OR (XOR) are not separable. Individual neurons exhibit linear mixed selectivity (see Methods S6 Selectivity and abstraction in a general linear model of neuronal responses). d. Distorted square: a sufficiently large perturbation of the points makes the representation higher dimensional (points no longer lie on a plane); a linear decoder can now separate all possible dichotomies, leading to maximal SD, but at the same time CCGP remains high for both value and context. See Methods S5 The trade off between dimensionality and our measures of abstraction and Fig. S2 that constructs geometries that have high SD and CCGP at the same time.
In the random case under consideration, if the number of neurons is sufficiently large, the pattern of activity corresponding to each condition will be unique. If trial-by-trial variability in firing rate (i.e. noise) is not too large, even a simple linear classifier can decode context, as the 2 points of one context can be separated from the 2 points of the other context (Figure 2a). Notice that in this geometry any arbitrarily selected 2 points can be separated from the others. Each way of grouping the points (i.e. each dichotomy) corresponds to a different variable, and when 2 groups of points are linearly separable the corresponding variable is decodable. One way to characterize the geometry of representations is to determine how many dichotomies can be decoded by a linear classifer. We call this quantity shattering dimensionality (SD). SD is defined as the performance of a linear decoder averaged over all possible balanced dichotomies. A high SD means that a linear readout can generate a large number of input-output functions. SD is similar to the measure of dimensionality used in (Rigotti et al. 2013). The representation in Figure 2a has maximal SD, as all dichotomies can be decoded.
The random representations just described allow for a form of generalization, as a decoder trained on a subset of trials from all conditions can generalize to held-out trials. This form of generalization is clearly insufficient to characterize a variable that is in an abstract format because the representations are random and hence they do not reflect the links between the different instances (SRO mappings) of the contexts. Therefore, despite encoding context, this type of representation cannot be considered to represent context in an abstract format.
A neural representation of context in an abstract format needs to incorporate into the geometry information about the links between different instances of the same context. One way to accomplish this is to cluster together patterns of activity that correspond to conditions in the same context (see Figure 2b). Clustering is a geometric arrangement that permits an important and distinct form of generalization that we use to define when a neural ensemble represents a variable in an abstract format. We propose that this format can support a fundamental aspect of cognitive flexibility, the ability to generalize to novel situations. To identify in our experiments when a variable is represented in a format that could support this type of generalization, we determined if one could decode a variable in experimental conditions not used for training the decoder. This type of generalization is illustrated in Figure 2b. A linear decoder is trained to decode context on the rewarded conditions of the 2 contexts. Then the decoder is tested on trials not rewarded. The clustered geometric arrangements of the points ensures that the decoder successfully generalizes to the conditions not used for training.
In marked contrast to clustered geometric arrangements, random responses to trial conditions do not allow for this form of generalization. In the case of random responses (e.g. Figure 2a), if only rewarded conditions are used to train the decoder to classify context, then the separating plane will be very different from the one where the decoder is trained on a subset of trials from all conditions. Now the 2 test points corresponding to unrewarded conditions will have the same probability of being on either side of the separating plane derived from the decoder trained on rewarded conditions only. We designate the performance of decoders in classifying variables when testing and training on different types of conditions as cross-condition generalization performance (CCGP) (see also (Saez et al. 2015)). We use the average CCGP across all possible ways of choosing training and testing conditions as a metric of the degree to which a variable is represented in an abstract format. A variable is defined as being represented in an abstract format when CCGP is significantly different from one in which the points from the same conditions would be at random locations (see Methods).
The geometry of multiple abstract variables.
The clustering geometry allows a single variable to be encoded in an abstract format. In the case in which the differences within each cluster are only due to noise, the single variable encoded in an abstract format is the only decodable variable, and SD would be low. How can neural ensembles represent multiple variables in an abstract format at the same time? One way would be if different neurons exhibit pure selectivity for different variables (e.g. one neuron specialized to encode context, and another specialized to encode value). This factorized or disentangled geometry allows for high CCGP for both context and value. However, in our dataset neurons that respond to a single variable are rarely observed, a finding consistent with many studies showing that neurons more commonly exhibit mixed selectivity for multiple variables (Rigotti et al. 2013; Fusi et al. 2016) (see Methods S7 Recorded neurons are not highly specialized). Nonetheless, the generalization properties of factorized representations are preserved when all the points are rotated in the firing rate space, as in Figure 2c. Here the 4 data points lie on the corner of a square, with neurons exhibiting linear mixed selectivity(Rigotti et al. 2013). Under the assumption that a decoder is linear, CCGP will not change if a linear operation like rotation is performed on the data points. Using a similar construction, it is therefore possible to represent as many variables in an abstract format as the number of neurons.
For the representation depicted in Figure 2c, SD is high but not maximal because the combinations of points that correspond to an exclusive OR (XOR) are not separable (i.e. a linear classifier cannot separate the visual stimuli A and C). Although in this simple example SD is still relatively high, it can decrease exponentially with the total number of conditions. However, a sufficiently large distortion of the representation in Figure 2c can lead to a representation that allows for maximal SD and, at the same time, high CCGP for both context and value (Figure 2d). Simulations show that there is a surprisingly wide range of distortions in which the representations can have both high SD and high CCGP for multiple variables (see Figure S2).
Measuring abstraction.
The serial reversal-learning task contains 8 types of trials (SRO combinations). There exist 35 different ways of dividing the 8 types of trials into 2 groups of 4 conditions (i.e. 35 dichotomies). Each dichotomy corresponds to a variable that could be in an abstract format. Three of these variables describe the context, reward value and correct action associated with each stimulus in each of the 2 contexts. We took an unbiased approach to determine which dichotomy is decodable and which is in an abstract format. To assess which variables were in an abstract format and to further characterize the geometry of the recorded neural representations, we used two quantitative measures, CCGP and the Parallelism Score (PS).
As described in reference to Figure 2b–d, CCGP can be computed by training a linear decoder to classify any dichotomy on a subset of conditions, and testing classification performance on conditions not used for training. Since there are multiple ways of choosing the subset of conditions used for training, we report the average CCGP across all possible ways of choosing the training and testing conditions (see Methods and Figure S1a). The parallelism score (PS) is related to CCGP, but it focuses on specific aspects of the geometry. In particular, the PS quantifies the degree to which coding directions are parallel when training a decoder to classify a variable for different sets of conditions. Consider the case depicted in Figure S1b,c. Two different lines (which would be hyperplanes in a higher dimensional plot) are obtained when a decoder is trained to classify context using the two points on the left (rewarded conditions, magenta) or the two points on the right (unrewarded conditions, dark purple). The two lines representing the hyperplanes are almost parallel, indicating that this geometry will allow for high CCGP. The extent to which these lines (hyperplanes) are aligned can be quantified by calculating the coding directions (arrows in Figure S1b,c) that are orthogonal to the lines. The PS is the degree to which these coding vectors are parallel. Analogous to CCGP, there are multiple ways of pairing points that correspond to two different values of a dichotomy. We compute the PS for all of them and report the maximum observed PS. For random representations, which do not represent variables in an abstract format, the representations of individual conditions will be approximately orthogonal if the number of neurons is large. In this case, however, the coding directions will be randomly oriented, and hence orthogonal to each other. Therefore small PS values would be observed in the case of random representations. PS can be used an an alternative measure of abstraction: a variable would be abstract when its PS is significantly larger than the PS of a random representation. High PS usually predicts high CCGP (see Methods).
HPC, DLPFC, and ACC represent variables in an abstract format.
We recorded the activity of 1378 individual neurons in two monkeys while they performed the serial reversal learning task. Of these, 629 cells were recorded in HPC, (407 and 222 from each of the 2 monkeys, respectively), 335 cells were recorded in ACC (238 and 97 from each of the 2 monkeys), and 414 cells were recorded in DLFPC (226 and 188 from the 2 monkeys). Our initial analysis of neural data focused on the time epoch immediately preceding a response to a stimulus. If monkeys employ a strategy in which context information is mixed with stimulus identity information to form a decision, then context information could be stored right before responses to stimuli begin. Furthermore, information about recently received rewards and performed actions may also be present during this interval, as knowing whether the last trial was performed correctly is useful (see Discussion).
In a 900 ms time epoch ending 100 ms after stimulus onset on the current trial (visual response latencies are greater than 100 ms in the recorded brain areas), individual neurons in all 3 brain areas exhibited mixed selectivity with respect to the task conditions on the prior trial, with diverse patterns of responses observed (see Fig. S3a). Information about the current trial is not yet available during this time epoch. We then determined which variables (among the 35 dichotomies) were represented in each brain area and which variables were in an abstract format. The traditional application of a linear neural decoder revealed that most of the 35 variables could be decoded from neural ensembles in all brain areas, including the context, value and action of the previous trial (Fig. 3a). However, very few variables were represented in an abstract format at above chance levels, as quantified by CCGP. Variables with the highest CCGP were those corresponding to context and value in all 3 brain areas, as well as action in DLPFC and ACC. Action was not in an abstract format in HPC despite being decodable using traditional methods. The representation of variables in an abstract format did not preferentially rely on the contribution of neurons with selectivity for only one variable, indicating that neurons with mixed selectivity for multiple variables likely play a key role in generating representations of variables in abstract format (see Section S7). Consistent with the CCGP analyses, the highest PSs observed in DLPFC and ACC corresponded to the 3 variables for context, value, and action. In HPC, the two highest PSs were for context and value, with action having a PS not significantly different than chance. The geometric architecture revealed by CCGP and the PS can be visualized by projecting the data into a 3D space using multidimensional scaling (MDS), see Fig. S4. Figure 3c,d shows how the geometry that represents the variables context, value and action evolves over time prior to a visual response; the degree to which context is represented in an abstract format increases during this time interval.
Figure 3: Decoding accuracy, CCGP and parallelism score (PS) in the 3 recorded brain areas.
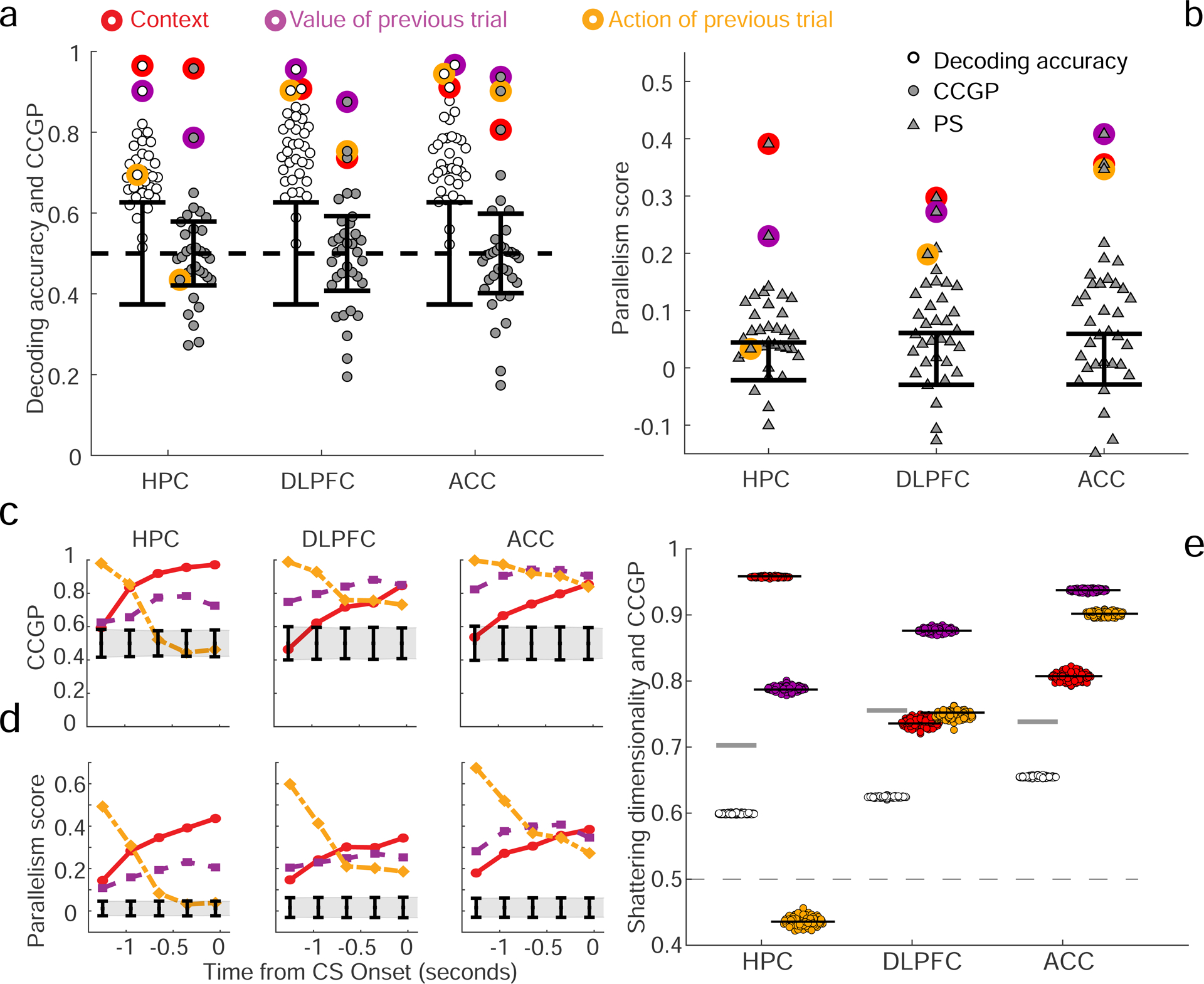
A-b. CCGP, decoding accuracy and PS for the variables that correspond to all 35 dichotomies shown separately for each brain area in a 900 ms time epoch beginning 800 ms before image presentation. The points corresponding to the context, value and action of the previous trial are highlighted with circles of different colors. Table T2 contains the values of CCGP and PS for all dichotomies. Context and value are represented in an abstract format in all 3 brain areas, but action is abstract only in PFC (although it can be decoded in HPC (see also Fig. S4 to visualize the arrangement of the points in the firing rate space). Almost all dichotomies can be accurately decoded, and the SD is high: HPC, 0.70; DLPFC, 0.75; ACC, 0.74 (see also Methods S4 PCA Dimensionality of the neural representations, which describes other measures of dimensionality). Error bars are ± two standard deviations around chance level as obtained from a geometric random model (CCGP) or from a shuffle of the data (decoding accuracy and PS). Results were qualitatively similar in the 2 monkeys (see Figure S5). c-d. CCGP (c) and the PS (d) plotted as a function of time for the variables context, action and value in the 3 brain areas (900 ms window stepped in 300 ms increments; last window ends at 100 ms after stimulus onset, before a visual response occurs). e. Measured SD in each brain area is significantly greater than the SD of a perfectly factorized representation. To determine if a perfectly factorized representation, which typically has high CCGP, is consistent with the high SD observed in experimental data, a perfectly factorized null model is constructed by placing the centroids of the noise clouds that represent the 8 different experimental conditions at the vertices of a cuboid. The lengths of the sides of the cuboid are tuned to reproduce (on average) the CCGP values observed in the experiment for the variables context, value, and action. From this artificially generated data corresponding to a perfectly factorized model, SD and CCGP are calculated, with the procedure repeated 100 times for each brain area. SD (empty circles) and CCGP for the variables context, value and action (colored circles) plotted for each realization of the random model. Gray horizontal lines, SD from the experiments; black horizontal lines, CCGP for context, value and action, mimicking experimental data shown in a. The factorized models re-capitulate the recorded CCGP values, but the SD values measured in all 3 brain areas are significantly higher than in any realization of the factorized model. The difference between the experimentally measured SD and the average SD of the factorized model is more than an order of magnitude larger than the standard deviation of the model SD distribution in all cases, indicating that the experimental data is not consistent with such a factorized geometry.
Notice that the hidden variable context was represented in an abstract format in all 3 brain areas just before neural responses to stimuli on the current trial occur. An analysis that only assesses whether the geometry in the firing rate space resembles clustering, similar to what has been proposed in (Schapiro et al. 2016), would lead to the incorrect conclusion that context is abstract only in HPC (see Fig. S4c–e). The representation of context in an abstract format in ACC and DLPFC relies on a geometry revealed both by CCGP and the PS, but missed if only considering clustering. The data also show that CCGP and the PS identify when multiple variables are represented in an abstract format simultaneously.
We next wondered whether the observed geometry is consistent with a perfectly factorized representation. In such a representation multiple variables could exhibit high CCGP, but the SD would be relatively low. However, as shown in Figure 3, nearly all dichotomies could be decoded in each brain area, and thus SD was greater than 0.7 in every case. These SD values are significantly greater than the SD expected in the case of a perfectly factorized representation tuned to replicate the observed CCGP values for context, action and value (Figure 3e). Thus the geometry of recorded representations has properties inconsistent with a perfectly factorized representation.
The dynamics of the geometry of neural representations during task performance.
The different task events in the serial-reversal learning task engage a series of cognitive operations, including perception of the visual stimulus, formation of a decision about whether to release the button and reward expectation. These task events modulated the geometry of the neural representations. Shortly after stimulus appearance, decoding performance for stimulus identity, expected reinforcement outcome and the to-be-performed action on the current trial rises rapidly from chance levels to asymptotic levels in all 3 brain areas (Figure 4). The very short temporal gap between the rise in decoding for stimulus identity and the rises in expected outcome and operant action suggest a rapid decision process upon stimulus appearance. Decoding performance for value and action rises the most slowly in HPC, suggesting that the signals reflecting decisions are not first represented there.
Figure 4: Decoding accuracy for stimulus, value and action.
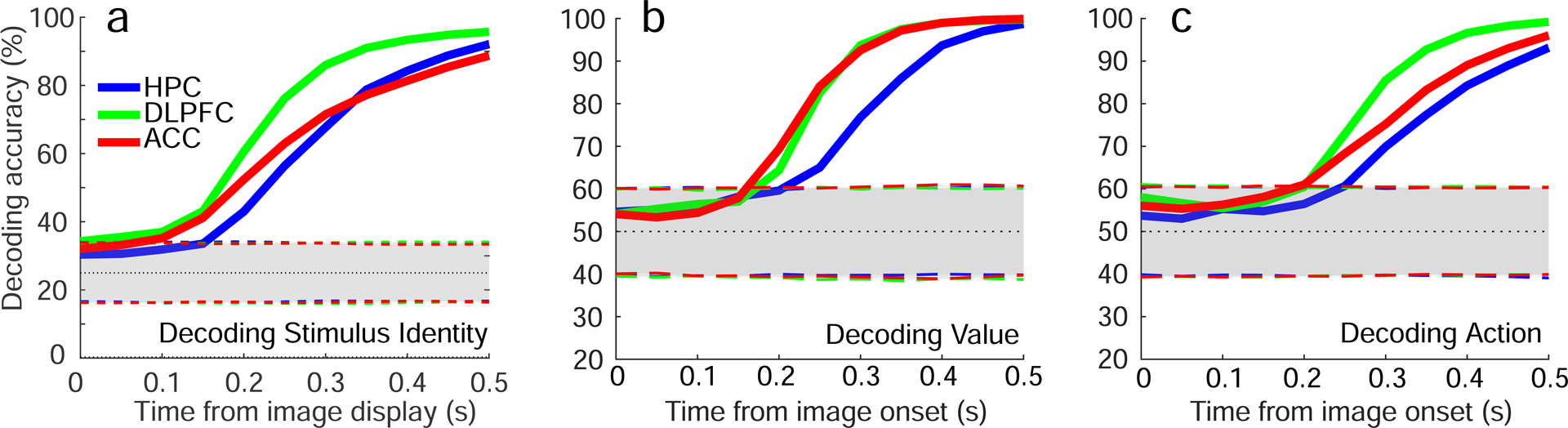
Decoding accuracy for stimulus identity, value and action plotted as a function of time in the 3 brain areas. Decoding of stimulus identity employs a 4-way classifier, so chance is 0.25. The use of a linear decoder was employed because neural responses are highly heterogeneous, exhibiting mixed selectivity (see Fig. S3a) and are rarely specialized (see Fig. S6). Dotted line, chance. Shaded areas, two-sided 95%-confidence intervals calculated with a permutation test (randomly shuffling trials, 1,000 repetitions). See Figure S3 for decoding of task relevant variables across a longer timescale).
We next analyzed the geometry of neural representations during the time interval in which the planned action and expected trial outcome first become decodable, focusing on a 900 ms window beginning 100 ms after stimulus onset. We again took an unbiased approach, and considered all 35 dichotomies. Nearly all dichotomies were decodable using a traditional decoding approach (Figure 5a). The SD was accordingly high in all 3 brain areas (> 0.88) and significantly larger than the SD computed for a factorized representation (Figure 5e). Despite the high SD, multiple variables were simultaneously represented in an abstract format (Figure 5a,b). Strikingly, context was not represented in an abstract format in DLPFC, despite being decodable well above chance levels; in ACC, CCGP indicated that context was only very weakly abstract. These data demonstrate that high decoding performance using traditional cross-validated decoding does not necessarily predict CCGP above chance. For example, decoding performance is ~ 0.9 for context in DLPFC in the 900 ms window beginning 100 ms after image presentation, and for context in ACC prior in the interval ending 100 ms after image presentation. Yet, in DLPFC, CCGP is at chance (Figure 5a), similar to the example in Figure 2a), but in ACC during the earlier time interval, CCGP is ~ 0.8, well above chance (Figure 3a). Of course, the converse is not true, and high CCGP is always accompanied by high decoding performance.
Figure 5: Decoding accuracy, CCGP and the PS after stimulus onset in the 3 brain areas.
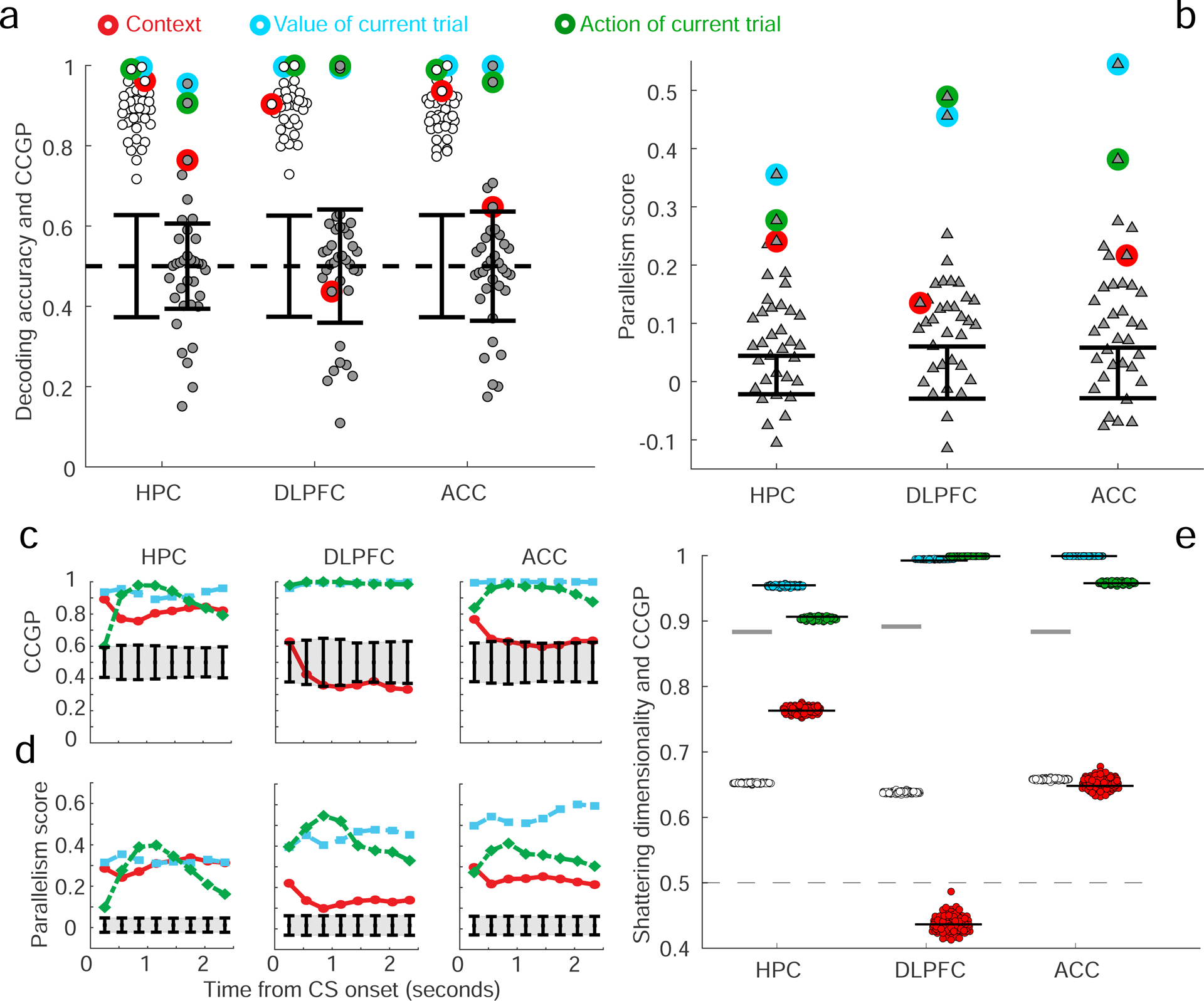
a,b. CCGP, decoding accuracy and PS for all 35 dichotomies in the time interval from 100ms to 1000ms after stimulus onset. See Table T2 for the values of CCGP and PS for all dichotomies. Error bars, ± 2 standard deviations around chance as obtained from a geometric random model (CCGP) or from a shuffle of the data (decoding accuracy and PS). The SD is higher in this interval than in the earlier time epoch: HPC 0.88, DLPFC 0.89 and ACC 0.88. Results were qualitatively similar in the two monkeys (see Figs. S5). C-d. CCGP (c) and the PS (d) plotted as a function of time for the variables context, action and value in the 3 brain areas (900 ms window beginning 100 ms after stimulus onset, 300 ms steps). e. The SD observed in each brain area is significantly greater than the SD of a perfectly factorized representation. Same analysis as in Figure 3e but for this later time interval.
CCGP for context is not significantly different from chance in DLPFC and ACC for a sustained period of time after image presentation. During this time, value and action are represented in an abstract format in all 3 brain areas (Figure 5c,d). Recall, however, that the geometry of the representation of context in DLPFC and ACC evolves prior to the presentation of the stimulus on the next trial, as context is in an abstract format in DLPFC and ACC during this time interval (Fig. 3a,b). In HPC, context was maintained more strongly in an abstract format after stimulus appearance, as well as prior to stimulus appearance on the next trial. Overall, the CCGP results were largely correlated with the PS. Together these findings indicate that task events both engage a series of different cognitive operations to support performance and modulate the geometry of neural representations. The analytic approach reveals a fundamental difference in how the hidden variable context is represented in HPC compared to PFC brain areas during and after decision-making on this task.
Correlation between level of abstraction (CCGP) and behavior
We next sought evidence that the geometry of neural representations was related to behavioral performance of the task. We focused on the representation of the variable context during the 900 ms time interval beginning 800 ms before image onset. The maintenance of information about context during this time interval is potentially useful, because it may be utilized once a stimulus response occurs. Decisions may be made by combining information about context and stimulus identity. We note that the analysis of the geometry of representations in relation to behavioral performance was not feasible in the time interval where the decision itself occurs. This is because the variables for the selected action and expected reinforcement become represented extremely rapidly after stimulus identity is decodable (Figure 4), and this time interval is too short for CCGP analysis to be possible.
In all 3 brain areas, there was a statistically significant decrease in CCGP for context on error compared to correct trials (Figure 6a). By contrast, using a traditional linear decoder, the decoding of context in all the brain areas was not significantly related to behavioral performance (Figure 6b). Context is a variable that monkeys could not have known about prior to their gaining experience on this particular task with these specific stimuli. Yet, a representation of the variable context within these brain areas conforms to a particular geometry, a geometry that must have been created de novo and that specifically relates to task performance.
Figure 6: The relationship between CCGP for context and behavioral performance.
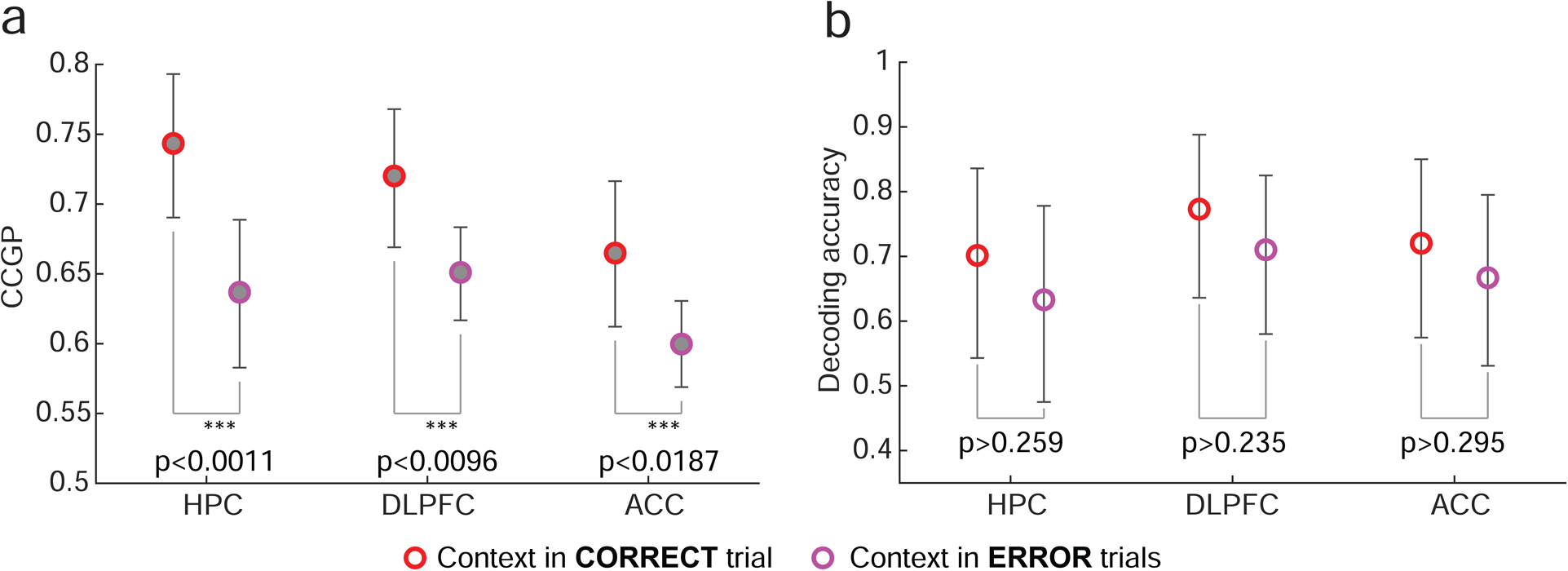
a. CCGP for context, measured in the 900 ms time interval ending 100 ms after stimulus onset, is significantly lower on error trials than on correct trials in all 3 brain areas. Average decreases (± one standard deviation) in CCGP on error trials are: 0.107 ± 0.038 (p<0.0011) in HPC, 0.0691±0.0303 (p<0.0096) in DLPFC, and 0.0651±0.0309 (p<0.0187) in ACC (average, standard deviation and p-values computed over 10,000 repetitions of bootstrap re-sampling trials using a sub-population of 180 neurons per area; error bars, 95th percentiles of the bootstrap distributions). Since errors occurred in a relatively small fraction of all trials, neurons were selected according to a different criterion than other analyses, resulting in fewer neurons being included in this analysis (see Methods). Results in this figure and Figure 3 are thus not directly comparable. b. Decoding accuracy for context is not significantly different for correct and error trials. Average drops (± one standard deviation) of decoding accuracy between correct and error trials: 0.069±0.108 (p≥0.259) in HPC, 0.0627±0.0903 (p≥0.235) in DLPFC, and 0.0532±0.0984 (p<0.295) in ACC (averages, standard deviations, p-values and error bars obtained analogously as in (a) on the same neurons). See Methods and Table T1 for details.
Abstraction in multi-layer neural networks trained with back-propagation.
We wondered whether neural representations observed in a neural network model trained with back-propagation have similar geometric features as those observed experimentally. We designed our simulations such that the 8 classes of inputs contained no structure reflecting a particular dichotomy. The network had to output two arbitrarily selected variables corresponding to two specific dichotomies. We hypothesized that forcing the network to output these two variables would break the symmetry between all dichotomies,leading to the creation of representations of the output variables in an abstract format, as defined by CCGP. Other variables (other dichotomies) would not be expected to be in an abstract format. If our hypothesis is confirmed, it would demonstrate a way of generating representations of selected variables in an abstract format which in turn could be used to benchmark our analytic methods.
We trained a two layer network using back-propagation (Figure 7a) to read an input representing a handwritten digit between 1 and 8 (MNIST dataset) and to output whether the input digit is odd or even, and, at the same time, whether the input digit is large (>4) or small (≤4) (Figure 7b). Parity and magnitude are the two variables that we hypothesized could be represented in an abstract format. Training the network to perform this task resulted in changes in the geometry of the representations in each stage of processing, as revealed by 2-dimensional MDS plots of a subset of the images in the input space, and in the first and second layers (Figure 7e–g). We tested whether the learning process led to high CCGP and PS for parity and magnitude in the last hidden layer of the network. If these variables are in an abstract format, then the abstraction process would be similar to the one studied in the experiment in the sense that it involves aggregating together inputs that are visually dissimilar (e.g. the digits ‘1’ and ‘3’, or ‘2’ and ‘4’). Analogously, in the experiment very different sequences of events (different conditions defined by SRO mappings) are grouped together into what defines the contexts.
Figure 7: Simulations of a multi-layer neural network replicate experimentally observed geometry.
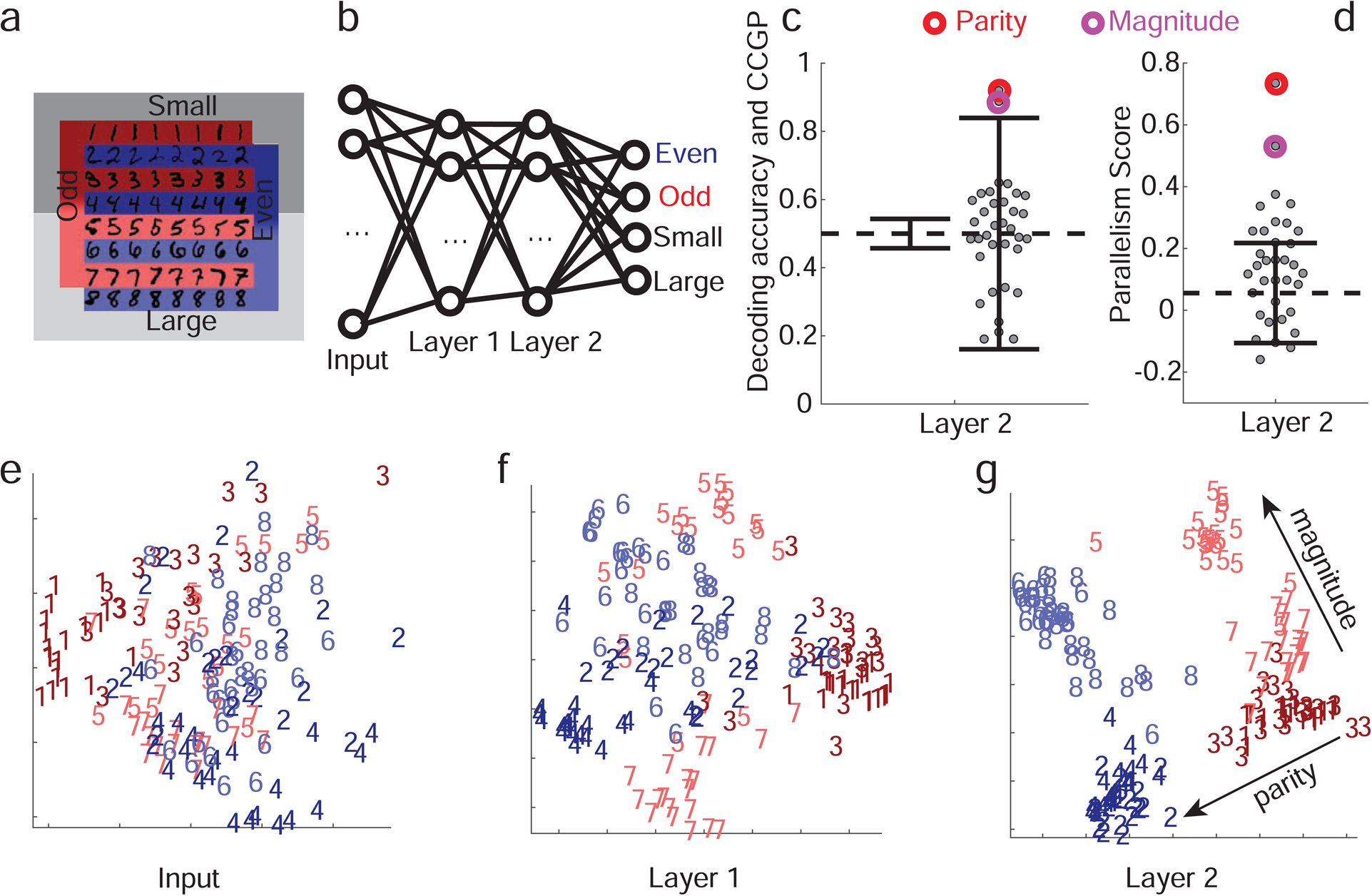
a. Schematic of the two discrimination tasks using the MNIST dataset and color code for panels e,f,g. The colors indicate parity, and shading indicates the magnitude of the digits (darker for smaller ones). b. Diagram of the network architecture. The input layer receives images of MNIST handwritten digits 1–8. The two hidden layers have 100 units each, and in the final layer there are 2 pairs of output units corresponding to 2 binary variables. The network is trained using back-propagation to simultaneously classify inputs according to whether they depict even/odd and large/small digits. c. CCGP and decoding accuracy for variables corresponding to all 35 balanced dichotomies when the second hidden layer is read out. Only the 2 dichotomies corresponding to parity and magnitude are significantly different from a geometric random model (chance level: 0.5; the two solid black lines indicate ±2standard deviations). Decoding performance is high for all dichotomies, and hence inadequate to identify the variables stored in an abstract format. d. Same as b, but for the PS, with error bars (±2 standard deviations) obtained from a shuffle of the data. Both CCGP and the PS allow us to identify the output variables used to train the network. e-g. Two-dimensional MDS plots of the representations of a subset of images in the input (pixel) space (e), as well as in the first (f) and second hidden layers (g). In the input layer there is no structure apart from the accidental similarities between the pixel images of certain digits (e.g. ones and sevens). In the first, and even more so in the second, layer, a clear separation between digits of different parities and magnitudes emerges in a geometry with consistent and approximately orthogonal coding directions for the two variables. For neural network simulations of the task performed by the monkeys, See Methods S1 Simulations of the parity/magnitude task: dependence on hyperparameters for more details. See also Methods S8 Deep neural network models of task performance, Figure S7 for a reinforcement learning model, and Figure S8 for a supervised learning model.
We computed both CCGP and the PS for all possible dichotomies of the 8 digits. Figure 7c,d shows decoding accuracy, CCGP and the PS for all dichotomies. The two largest CCGP and PS values are significantly different from those of the random model and correspond to the parity and the magnitude dichotomies. No other dichotomies have a statistically significant CCGP value, but all dichotomies can be decoded. CCGP and the PS therefore identify in the last hidden layer variables that correspond to the dichotomies encoded in the output. Note that the geometry of the representations in the last layer actually allow the network to perform classification of any dichotomy, as decoding accuracy is close to 1 for every dichotomy. Thus SD is very close to 1 (0.96). Abstraction therefore is not necessary for the network to perform tasks that require outputs corresponding to any of the 35 dichotomies.
A neural network was then trained to perform a simulated version of our experimental task, and a similar geometry was observed as in experiments (see Methods S8 Deep neural network models of task performance). We used a reinforcement learning algorithm (Deep Q-Learning) to train the network. This technique uses a deep neural network representation of the state-action value function of an agent trained with a combination of temporal-difference learning and back-propagation refined and popularized by (Mnih et al. 2015). As commonly observed, neural representations displayed significant variability across runs of the learning procedure. However, in a considerable fraction of runs, the neural representations during a modeled time interval preceding stimulus presentation recapitulate the main geometric features that we observed in the experiment. In particular, after learning, the hidden variable context is represented in an abstract format in the last layer, despite not being explicitly represented in the input, nor in the output. The representations also encode value and action in an abstract format, consistent with the observation that hidden and explicit variables are represented in an abstract format in the corresponding time interval in the experiment.
DISCUSSION
In this paper, we developed analytic approaches for characterizing the geometry of neural representations to understand how one or more variables may be represented in an abstract format simultaneously. Electrophysiological recordings of neural ensembles in DLPFC, ACC and HPC reveal that all 3 areas represent multiple variables in an abstract format, as revealed by CCGP, while still retaining high SD. Artificial multi-layer networks trained with back-propagation exhibited a similar geometry. Thus geometries exist in which variables are represented in an abstract format to support generalization in novel situations while retaining properties that enable a linear classifier to generate many different responses to complex combinations of inputs.
The relationship between neural representations and behavior.
CCGP measures how well a decoder generalizes to conditions held out from training. Admittedly and by construction, these conditions need not be new to an experimental subject. In our experiments, all conditions indeed were experienced by monkeys repeatedly. Nevertheless, we assume that generalization across conditions ”new to the decoder” is a good proxy for generalization across genuinely novel conditions. This assumption may not be valid in all situations, but it is reasonable to suppose that it holds if new conditions are ecologically and behaviorally not too dissimilar from familiar ones.
In our data, high CCGP for context indicates that the 4 conditions defining each context have been grouped together with a particular geometry that can enable generalization in novel situations. Consider a subject that can already perform the serial-reversal learning task. Suppose that for each already-learned context, a distinct novel contextual cue is presented in association with 3 of the conditions. If the geometry of the representation of context is sufficiently preserved during learning of these new associations, then it is likely that the remaining condition from each context will also be associated with its respective novel contextual cue. In this case, the subject can exhibit behavioral generalization the first time the remaining condition appears with a novel contextual cue. This is made possible by the fact that the links between conditions in the same context have already been learned and are reflected in the geometry of representations. In principle, one can use CCGP for all possible groupings (or variables) to predict whether behavioral generalization will be observed for an exponential number of novel situations. Testing whether these predictions are correct will require new and very challenging studies that generate a sufficiently large number of novel situations during experimental sessions.
In our experiments, the degree to which context is represented in an abstract format decreases significantly in all 3 brain areas when monkeys make mistakes even though objectively novel conditions were not part of the design. Information about context could be useful to monkeys as they utilize inference to adjust behavior after experiencing at least one trial upon a context switch. However, context need not be represented in an abstract format to support inference. Inference could also result from a strategy that creates a large look-up table of all possible sequences of trials; here no explicit knowledge of context is required to support inference. Nonetheless, the fact that the geometry of the representation of context relates to task performance suggests that at some stage of learning to perform the task, a geometry that confers generalization properties may have been created to support monkeys’ strategy. One possibility is that this geometry is created early in the learning process, when stimuli are first being experienced. This possibility will need to be explored by recording from neurons during initial learning when stimuli are novel.
Information about the value and action of the previous trial are also represented in all 3 brain areas just before stimulus onset. When context switches, the reward received on the previous trial is the only feedback from the external world that indicates context has changed, suggesting that representing this information is beneficial. Consistent with this, simulations reveal that value becomes progressively more abstract as the frequency of context switches increases (see Figure S8g and Methods S8 Deep neural network models of task performance). In addition, monkeys occasionally make mistakes that are not due to a context change. To discriminate between these errors and those due to a context change, information about value is not sufficient and information about the previously performed action can help select the correct response on the next trial. Conceivably, the abstract representations of reward and action may also afford the animal more flexibility in learning and performing other tasks.
Abstraction and linear mixed selectivity.
Our analytic approach emphasizes the importance of studying the geometry of neural representations at the level of the patterns of activity of a neural ensemble. In principle, one could analyze single neurons to detect low dimensional structure that relates to abstraction. In perfectly factorized representations, which represent variables in an abstract format as defined by CCGP, individual neurons exhibit either pure selectivity to a factor or linear mixed selectivity to 2 or more factors. Linear mixed selectivity neurons have been observed in previous work (see e.g. (Raposo et al. 2014; Parthasarathy et al. 2017; Chang & Tsao 2017; Dang et al. 2020)). However, examination only of single neuron coding properties may fail to reveal important properties of a representation considered at the level of an ensemble. This is because at the level of individual neurons, the linear component of responses dominates in many situations (Rigotti et al. 2013; Lindsay et al. 2017; Fusi et al. 2016), and it is easy to miss the fact that non-linear components of multiple neurons make representations high dimensional at the level of an ensemble. More importantly, an analysis of single neurons ignores the correlations between non-linear components across neurons; these correlations can strongly affect the generalization properties of representations.
Dimensionality and abstraction in neural representations.
Dimensionality reduction is widely employed in machine learning applications and data analyses because it leads to better generalization. The recorded neural representations here are high dimensional, as assessed by SD, in line with previous studies on monkey PFC(Rigotti et al. 2013). This observation might seem at odds with the idea that high CCGP requires low dimensonality. However, SD is only one method for measuring dimensionality; it focuses on the ability of a linear classifier to decode a large number of dichotomies. SD is correlated but not identical to other measures of dimensionality based on the number of large principal components (see e.g. (Stringer et al. 2018; Machens et al. 2010; Mazzucato et al. 2016)). A representation may be well described by a small number of components or dimensions, but still have a large SD if the noise is not too large, especially along dimensions relevant for decoding the different dichotomies. Our data confirm that a PCA-based measure of dimensionality can be low when SD is high. This discrepancy is particularly evident in the interval that precedes stimulus onset. When the stimulus appears, both PCA dimensionality and SD increase (see Figure S3c and Methods S4 PCA Dimensionality of the neural representations).
The observed increase in dimensionality upon stimulus appearance is probably due to the fact that stimulus identity and context need to be mixed non-linearly to make a correct decision on our task. Any non-linear mixing leads to higher dimensional representations (Rigotti et al. 2013; Fusi et al. 2016). The decision on this task is likely made in the time between when stimulus identity becomes decodable and when expected reinforcement value and selected action become decodable. Representations of stimulus identity, planned action and expected reward emerge rapidly in DLPFC and ACC, faster than in HPC, suggesting that they play a more prominent role in the decision process. The time interval between when stimulus identity and value and action become decodable is extremely short (Figure 4). We lack sufficient data to estimate dimensionality in this interval. As a result, we analyze a larger time window that also includes time bins in which the decision is already made; time bins after the decision have been shown to exhibit lower PCA dimensionality and SD (Rigotti et al. 2013). Nonetheless, the variable context is not represented in an abstract format in DLPFC in this longer time interval, and it is only weakly abstract in ACC. Future studies will require a larger number of recorded neurons to reveal if the increase in dimensionality and the decrease in CCGP for context, observed in DLPFC and ACC, may be accounted for by non-linear mixing of information about context and stimulus identity.
The role of abstraction in reinforcement learning (RL).
Abstraction provides a solution for the notorious “curse of dimensionality”, the exponential growth of the solution space required to encode all states of the environment (Bellman 1957). Most abstraction techniques in RL can be divided into 2 main categories: ‘temporal abstraction’ and ‘state abstraction’. Temporal abstraction is the workhorse of Hierarchical RL (Dietterich 2000; Precup 2000; Barto & Mahadevan 2003). It is based on the notion of temporally extended actions (or options), can can be thought of as an attempt to reduce the dimensionality of the space of action sequences. Instead of composing policies in terms of long action sequences, an agent can select options that automatically extend for several time steps.
State abstraction methods most closely relate to our work. State abstraction hides or removes information about the environment not critical for maximizing the reward function. This technique typically involves information hiding, clustering of states, and other forms of domain aggregation and reduction (Ponsen et al. 2009). Our use of neural networks as function approximators to represent a decision policy constitutes a state abstraction method (see S8). The inductive bias of neural networks induces generalization across inputs sharing a feature, mitigating the curse of dimensionality. The modeling demonstrates that neural networks create similar geometry to that observed in data, suggesting that our analysis techniques could be useful to elucidate the geometric properties underlying the success of Deep Q-learning neural networks trained to play 49 different Atari video games with super-human performance (Mnih et al. 2015). Future work will consider models that explicitly incorporate structures designed to encode the spatio-temporal statistics of sensory stimuli, motor responses and reward history. This relational structure has been proposed to be supported by the hippocampus (Behrens et al. 2018; Whittington et al. 2019; Recanatesi et al. 2019; Benna & Fusi 2019).
Other forms of abstraction in the computational literature.
The principles delineated for representing variables in abstract format are reminiscent of recent work in computational linguistics. This work suggests that difficult lexical semantic tasks can be solved by word embeddings, which are vector representations whose geometric properties reflect the meaning of linguistic tokens (Mikolov, Yih & Zweig 2013; Mikolov, Sutskever, Chen, Corrado & Dean 2013). Recent forms of word embeddings exhibit linear compositionality that makes the solution of analogy relationships possible via linear algebra (Mikolov, Yih & Zweig 2013; Mikolov, Sutskever, Chen, Corrado & Dean 2013). For example, shallow neural networks trained in an unsupervised way on a large corpus of documents organize vector representations of common words such that the difference of the vectors representing ‘king’ and ‘queen’ is the same as the difference of vectors for ‘man’ and ‘woman’(Mikolov, Yih & Zweig 2013). These word embeddings, which can be translated along parallel directions to consistently change one feature (e.g. gender, as in the previous example), share common coding principles with the geometry of abstraction we describe. This type of vector representation predicts fMRI BOLD signals measured while subjects are presented with semantically meaningful stimuli (Mitchell et al. 2008).
A different approach to extracting compositional features in an unsupervised way relies on variational Bayesian inference to learn to infer interpretable factorized representations (usually called ‘disentangled’ representations) of some inputs (Chen et al. 2016; Higgins et al. 2017; Chen et al. 2018; Kim & Mnih 2018; Behrens et al. 2018). These methods can disentangle independent factors of variations of a variety of real-world datasets. Our analytical methods can help to gain insight into the functioning of these algorithms.
The capacity to represent variables in an abstract format is also critical for many other cognitive functions. For example, in vision, the creation of neural representations of objects invariant with respect to position, size and orientation in the visual field is a typical abstraction process studied in machine learning (see e.g. (Riesenhuber & Poggio 1999; LeCun et al. 2015)) and in the brain ((Freedman et al. 2001; Rust & Dicarlo 2010)). This form of abstraction is sometimes referred to as ‘untangling’ because the retinal representations of objects correspond to manifolds with a relatively low intrinsic dimensionality but are highly curved and tangled together before becoming ”untangled” in visual cortex ((DiCarlo & Cox 2007; DiCarlo et al. 2012); untangled representations are not the same as disentangled representations). Untangling typically requires transformations that either increase the dimensionality of representations by projecting into a higher dimensional space, or decrease dimensionality by extracting relevant features.
In studies in vision, the final representation is typically required to be linearly separable for only one classification (e.g. car vs. non-car (DiCarlo & Cox 2007; DiCarlo et al. 2012)). The geometry of the representation of ”nuisance” variables that describe features of the visual input not relevant for the classification is typically not studied systematically. By contrast, the variables in our experiment are simple binary variables, allowing us to study systematically all possible dichotomies.
Conclusion.
Our data demonstrate that geometries of representations exist that support high CCGP for multiple variables, yet retain high SD. Thus the same representation can in principle support 2 forms of flexibility, one characterized by generalization in novel situations, and the other by the ability to generate many responses to complex combinations of inputs.
STAR METHODS
Resource Availability
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, C. Daniel Salzman (cds2005@cumc.columbia.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
The datasets and analysis code supporting the current study are available from the lead contact on request.
Experimental Model and Subject Details
Monkeys
Two male rhesus monkeys (Macaca mulatta; two males, 10 years old, 8kg: 11 years old, 13 kg respectively) were used in these experiments. Experiments were performed in an AAALAC approved facility at New York State Psychiatric Institute which provided for paired housing of non-human primates as well as regular access to play cages and a robust environmental enrichment program. All experimental procedures were performed in accordance with the National Institutes of Health guide for the care and use of laboratory animals and the Animal Care and Use Committees at New York State Psychiatric Institute and Columbia University.
Method Details
Task and Behavior
Monkeys performed a serial-reversal learning task in which they were presented one of four visual stimuli (fractal patterns). Stimuli were consistent across contexts and sessions, presented in random order. Each trial began with the animal holding down a button and fixating for 400 ms (Fig. 1a). If those conditions were satisfied, one of the four stimuli was displayed on a screen for 500 ms. In each context, correct performance for two of the stimuli required releasing the button within 900 ms of stimulus disappearance; for the other two, the correct operant action was to continue to hold the button. For 2 of the 4 stimuli, correct performance resulted in reward delivery; for the other 2, correct performance did not result in reward. If the monkey performed the correct action, a trace interval of 500 ms ensued followed by the liquid reward or by a new trial in the case of non-rewarded stimuli. If the monkey made a mistake, a 500 ms time out was followed by the repetition of the same trial type if the stimulus was a non-rewarded one. In the case of incorrect responses to rewarded stimuli, the time-out was not followed by trial repetition and the monkey simply lost his reward. After a random number of trials between 50 and 70, the context switched without warning. Upon a context switch, operant contingencies switched for all images, but for two stimuli the reinforcement contingencies did not change, in order to maintain orthogonality between operant and reinforcement contingencies. A different colored frame (red or blue) for each context appears on the edges of the monitor on 10 percent of the trials, randomly selected, and only on specific stimulus types (stimulus C for context 1 and stimulus D for context 2). This frame never appeared in the first five trials following a context switch. All trials with a contextual frame were excluded from all analyses presented.
Electrophysiological Recordings
Recordings began only after the monkeys were fully proficient in the task and performance was stable. Recordings were conducted with multi-contact vertical arrays electrodes (v-probes, Plexon Inc., Dallas, TX) with 16 contacts spaced at 100 μm intervals in ACC and DLPFC, and 24 contacts in HPC, using the Omniplex system (Plexon Inc.). In each session, we individually advanced the arrays into the three brain areas using a motorized multi-electrode drive (NAN Instruments). Analog signals were amplified, band-pass filtered (250 Hz - 8 kHz), and digitized (40 kHz) using a Plexon Omniplex system (Plexon, Inc.). Single units were isolated offline using Plexon Offline Sorter (Plexon, Inc.). To address the possibility that overlapping neural activity was recorded on adjacent contacts, or that two different clusters visible on PCA belonged to the same neuron, we compared the zero-shift cross-correlation in the spike trains with a 0.2 ms bin width of each neuron identified in the same area in the same session. If 10 percent of spikes co-occurred, the clusters were considered duplicated and one was eliminated. If 1–10 percent of spikes co-occurred, the cluster was flagged and isolation was checked for a possible third contaminant cell. Recording sites in DLPFC were located in Brodmann areas 8, 9 and 46. Recording sites in ACC were in the ventral bank of the ACC sulcus (area 24c). HPC recordings were largely in the anterior third, spanning across CA1-CA2-CA3 and DG.
Quantification and Statistical Analysis
Selection of trials/neurons, and decoding analysis:
The neural population decoding algorithm was based on a linear classifier (see e.g. (Saez et al. 2015)) trained on pseudo-simultaneous population response vectors composed of the spike counts of the recorded neurons within specified time bins and in specific trials (Meyers et al. 2008). The trials used in decoding analyses are only those in which the animal responded correctly (both for the current trial and the directly preceding one), in which no context frame was shown (neither during the current nor the preceding trial), and which occurred at least five trials after the most recent context switch. We retain all neurons for which we have recorded at least 15 trials satisfying these requirements for each of the eight experimental conditions (i.e., combinations of context, value and action). Every decoding analysis is averaged across many repetitions to estimate trial-to-trial variability (as explained more in detail below). For every repetition, we randomly split off five trials per condition from among all selected trials to serve as our test set, and used the remaining trials (at least ten per condition) as our training set. For every neuron and every time bin, we normalized the distribution of spike counts across all trials in all conditions with means and standard deviations computed on the trials in the training set. Specifically, given an experimental condition c (i.e., a combination of context, value and action) in a time bin t under consideration, we generated the pseudo-simultaneous population response vectors by sampling, for every neuron i, the z-scored spike count in a randomly selected trial in condition c, which we indicate by . This resulted in a single-trial population response vector , where N corresponds to the number of recorded neurons in an area under consideration. This single-trial response vector can be thought of as a noisy measurement of an underlying mean firing rate vector , such that , with indicating a noise vector modeling the trial-to-trial variability of spike counts. Assuming that the trial-to-trial noise is centered at zero, we estimate the mean firing rate vectors taking the sample average: , where the angular brackets indicate averaging across trials. We then either trained maximum margin (SVM) linear classifiers on the estimated mean firing rate vectors for the eight conditions in the training set (this is the approach adopted to train the decoders used to compute the CCGP, see below), or we trained such classifiers on the single-trial population response vectors generated from the training set of trials (this is what we used in all the figures that report the ”decoding accuracy”).
In the latter case, in order to obtain a number of trials that is large compared to the number of neurons, we re-sampled the noise by randomly picking noisy firing rates (i.e, spike counts) from among all the training trials of a given experimental condition for each neuron independently. Specifically, in this case, we re-sampled 10,000 trials per condition from the training set. While this neglected correlations between different neurons within conditions, we only had little information about these correlations in the first place, since only a relatively small numbers of neurons were recorded simultaneously. Regardless of whether we trained on estimated mean firing rate vectors or on re-sampled single-trial population response vectors, the decoding performance was measured in a cross-validated manner on 1,000 re-sampled single-trial population response vectors generated from the test set of trials. For every decoding analysis training and testing were then repeated 1,000 times over different random partitions of the trials into training and test trials. The decoding accuracies that we report were computed as the average results across repetitions.
Statistical significance of the decoding accuracy was assessed using a permutation test for classification(Golland et al. 2005). Specifically, we repeated the same procedure just described, but at the beginning of every repetition of a decoding analysis, trials were shuffled, i.e., associated to a random condition. This is a way of estimating the probability that the population decoders that we used would have given the same results that we obtained by chance, i.e., when applied on data that contain no information regarding the experimental conditions.
In Fig. S3b we show the cross-validated decoding accuracy as a function of time throughout the trial (for a sliding 500 ms time window) for maximum margin classifiers trained only on the mean neural activities for each condition. Figs. 3a and 5a show similar results for linear classifiers trained on the mean firing rates in the neural data within time windows from −800 ms to 100 ms and from 100 ms to 1000 ms relative to stimulus onset, respectively.
For all analyses, data were combined across monkeys, because all key features of the data set were consistent across the two monkeys.
The cross-condition generalization performance (CCGP):
The hallmark feature of neural representations of variables in abstract format (“abstract variables”) is their ability to support generalization in novel situations. When several abstract (in our case binary) variables are encoded simultaneously, generalization must be possible for all the abstract variables. We quantify a strong form of generalization using a measure we call the cross-condition generalization performance (CCGP.) We use this measure as a quantitative definition of the degree to which a variable is represented in abstract format. CCGP is distinct from traditional cross-validated decoding performance commonly employed to determine if a neural ensemble represents a variable. In traditional cross-validated decoding, the data is split up randomly such that trials from all conditions will be present in both the training and test sets. For CCGP, trials are split instead according to their condition labels, such that the training set consists entirely of trials from one group of conditions, while the test set consists only of trials from a disjoint group of conditions (see the scheme in Figure S1). In computing CCGP, we train a linear classifier for a certain dichotomy that discriminates the conditions in the training set according to some label (one of the variables), and then ask whether this discrimination generalizes to the test set by measuring the classification performance on the data from entirely different conditions, i.e., conditions not used for training the decoder. Since the conditions used for testing were not used for training, they are analagous to novel situations (conditions the trained decoder has never experienced). We always report the average CCGP across all possible ways of choosing training and testing conditions (see below); thus CCGP provides a continuous measure which quantifies the degree of abstraction.
Given our experimental design with eight different conditions (distinguished by context, value and action of a trial), we can investigate variables corresponding to different balanced (four versus four condition) dichotomies, and choose one, two or three conditions from each side of a dichotomy to form our training set. We use the remaining conditions (three, two or one from either side, respectively) for testing, with larger training sets typically leading to better generalization performance. For different choices of training conditions we will in general obtain different values of the classification performance on the test conditions, and we define CCGP as its average over all possible sets of training conditions (of a given size). In Figs. 3a and 5a we show the CCGP (on the held out fourth condition) when training on three conditions from either side of the 35 balanced dichotomies (with dichotomies corresponding to context, value and action highlighted). Note that traditional decoding will always have a performance level as high or higher than CCGP, but high traditional decoding does not ensure that CCGP will be different from chance.
We emphasize that in order to achieve high CCGP, it is not sufficient to merely generalize over the noise associated with trial-to-trial fluctuations of the neural activity around the mean firing rates corresponding to individual conditions. Instead, the classifier has to generalize also across different conditions on the same side of a dichotomy, i.e., across those conditions that belong to the same category according to the variable under consideration.
For the CCGP analysis, the selection of trials used is the same as for the decoding analysis, except that here we retain all neurons that have at least ten trials for each experimental condition that meet our selection criteria (since the split into training and test sets is determined by the labels of the eight conditions themselves, so that for a training condition we don’t need to hold out additional test trials). We pre-process the data by z-scoring each neuron’s spike count distribution separately. Again, we can either train a maximum margin linear classifier only on the cluster centers, or on the full training set with trial-to-trial fluctuations (noise), in which case we re-sample 10,000 trials per condition, with Figs. 3a and 5a showing results using the latter method.
For all analyses, data were combined across monkeys, because all key features of the data set were consistent across the two monkeys.
CCGP and decoding performance of context in error trials:
In order to measure CCGP and decoding performance of context in error trials we had to address the issue that, due to the high behavioral performance of the monkeys, error trials are scarce compared to correct trials. We therefore adapted our approach for computing CCGP and traditional decoding performance in two ways. First, we performed all training procedures only on correct trials, reserving held-out error trials for testing, which could be compared to testing on held-out correct trials. As a result, our analyses of the geometry of representations in relation to behavioral performance asks specifically about the difference between correct and error trials in terms of the cross-validation performance of CCGP and traditional decoding. Note also that we only considered error trials that occurred more than 5 trials after the context switch in this analysis, similar to that done for analyses of correct trials. Second, we recognized that decoding performance on trials for a specific trial condition can be cross-validated irrespective of any other type of trial condition. This means that a neuron can participate in the population response vector for a given condition if it has been recorded for a sufficient number of error trials for that condition, even if there are not enough recorded trials with errors for other conditions. We therefore built held-out (error trial) population response vectors for each condition independently, including for each such condition only neurons that have enough error trials for that condition. For each condition, on the training set of trials we trained decoders only on the neurons that also participate in the held-out response vectors for error trials (see Table T1). This approach allows us to include many more neurons in the analysis, which was critical for gaining statistical power. This combination of techniques resulted in our being able to include in our analysis 440, 233 and 223 neurons in HPC, DLPFC and ACC, respectively, with at least 2 trials per held-out condition for a CCGP analysis on error trials, and 385, 198 and 184 neurons with at least 3 trials per held-out condition for the traditional decoding analysis on error trials. We also required 18 trials for training, which is performed on correct trials for both CCGP and decoding. All analyses are then performed 10000 times (to estimate confidence intervals with bootstrap resampling), each time sampling 180 neurons from each area and subsampling cross-validation trials so as to equalize the number of held-out correct and error trials. Subsampling 180 neurons from each brain area ensures that comparison across brain areas is not skewed by the numbers of neurons used in the analyses. For each iteration, the same set of 180 sub-sampled neurons is used to decode correct and error trials whether using CCGP or traditional decoding. The results of the CCGP analysis on error vs correct trials, and the corresponding traditional decoding analysis is presented in Fig. 6.
The parallelism score (PS):
We developed a measure based on angles of coding directions to characterize the geometry of neural representations of variables in the firing rate space. Consider a pair of conditions, one from each side of a dichotomy, such as the two conditions that correspond to the presentation of stimulus A in the two contexts (here context is the dichotomy under consideration). A linear classifier trained on this pair of conditions defines a separating hyperplane. The weight vector orthogonal to this hyperplane aligns with the vector connecting the two points that correspond to the mean firing rates for the two training conditions if we assume isotropic noise around both of them. This corresponds to the coding direction for the variable under consideration (context in the example). Other coding directions for the same variable can be obtained by choosing a different pair of training conditions (e.g. the conditions that correspond to the presentation of stimulus B in the two context). The separating hyperplane associated with one pair of training conditions is more likely to correctly generalize to another pair of conditions if the associated coding directions are parallel (as illustrated in Fig. S1). The parallelism score (PS) that we developed directly quantifies the alignment of these coding directions.
If we had only four conditions as shown in Fig. S1, there would be only two coding directions for a given variable (from the two pairs of training conditions), and we would simply calculate the cosine of the angle between them (i.e., the normalized overlap of the two weight vectors). In our experiments, there were 8 conditions whose mean firing rates we denote by f(c), with c = 1,2,…,8 A balanced dichotomy corresponds to splitting up these eight conditions into two disjoint groups of four, corresponding to the conditions to be classified as positive and negative, respectively, e.g. Gpos = [1,2,4,7] versus Gneg = [3,5,6,8]. To compute four unit coding vectors for i=1,2,3,4 (corresponding to four pairs of potential training conditions) for the variable associated with this dichotomy, we have to match each condition in the positive group with a unique condition in the negative group (without repetitions). We parametrize these pairings by considering all possible permutations of the condition indices in the negative group. For a particular choice of such a permutation the resulting set of coding vectors is given by
Note that we have defined the vi as normalized coding vectors, since we want our parallelism score to depend only on their direction (but not on the magnitude of the un-normalized coding vectors). To compute the parallelism score from these unit coding vectors, we consider the cosines of the angles between any two of them and we average these cosines over all six of these angles (corresponding to all possible choices of two different coding vectors).
In general there are multiple ways of pairing up conditions corresponding to the two values of the variable under consideration. We don’t want to assume a priori that we know the ‘correct’ way of pairing up conditions. For example, it is not obvious that the two conditions corresponding to the same stimuli in two contexts are those that maximize the cosine between the coding vectors. It could be that cosine is larger when the conditions corresponding to a certain value are paired. In other words, to perform the analysis in an unbiased way, we should ignore the labels of the variables that define the conditions within each dichotomy (in the case of context we should just consider all conditions corresponding to context 1 and pair them in all possible ways to all conditions in context 2). So we consider all possible ways of matching up the conditions on the two sides of the dichotomy one-to-one, corresponding to all possible permutations , and then define the PS as the maximum of the average cosine across all possible pairings/permutations. There are two such pairings in the case of four conditions, and 24 for eight conditions. In general there are (m/2)! pairings for m conditions, so if m was large there would be a combinatorial explosion in the obvious generalization of this definition to arbitrary m, which would also require averaging the cosines of (m/2)(m/2−1)/2 angles.
The parallelism score for a given balanced dichotomy in our case of eight conditions is defined as
Note that this quantity depends only on the normalized coding directions (for the best possible pairing of conditions), which are simply the unit vectors pointing from one cluster center (mean firing rate for a given condition) towards another. Therefore, finding the PS doesn’t require training any classifiers, which makes it a very simple, fast computation (unless m is large). However, because it depends only on the locations of the cluster centers, the parallelism score ignores the shape of the noise (within condition trial-to-trial fluctuations).
The parallelism scores of all 35 dichotomies in our data (with the context, value and action dichotomies highlighted) are plotted in Figs. 3b and 5b. The selection of trials used in this analysis is the same as for the decoding and cross-condition generalization analyses, retaining all neurons that have at least ten trials for each experimental condition that meet our selection criteria, and z-scoring each neuron’s spike count distribution individually.
Note that a high parallelism score for one variable/dichotomy doesn’t necessarily imply high cross-condition generalization. Even if the coding vectors for a given variable are approximately parallel, the test conditions might be much closer together than the training conditions. In this case generalization would likely be poor.
In addition, for the simple example of only four conditions the orthogonal dichotomy would have a low parallelism score in such a situation (corresponding to a trapezoidal geometry).
We also emphasize that high parallelism scores for multiple variables do not guarantee good generalization (large CCGP) of one dichotomy across another one. When training a linear classifier on noisy data, the shape of the noise clouds could skew the weight vector of a maximum margin classifier away from the vector connecting the cluster centers of the training conditions. Moreover, even if this is not the case (e.g. if the noise is isotropic), generalization might still fail because of a lack of orthogonality of the coding directions for different variables. (For example, the four conditions might be arranged at the corners of a parallelogram instead of a rectangle, or in the shape of a parallelepiped instead of a cuboid for eight conditions).
In summary, while the parallelism score is not equivalent to CCGP, high scores for a number of dichotomies with orthogonal labels characterize a family of (approximately factorizable) geometries that can lead to good generalization properties if the noise is sufficiently well behaved (consider e.g. the case of the principal axes of the noise distributions being aligned with the coding vectors). For the simple case of isotropic noise, if the coding directions for different variables are approximately orthogonal to each other, CCGP will also be high.
For all analyses, data were combined across monkeys, because all key features of the data set were consistent across the two monkeys.
Random models
In order to assess the statistical significance of the above analyses we need to compare our results (for the decoding performance, abstraction index, cross-condition generalization performance, and parallelism score, which we collectively refer to as scores here) to the distribution of values expected from an appropriately defined random control model. There are various sensible choices for such random models, each corresponding to a somewhat different null hypothesis we might want to reject. We consider two different classes of random models, and for each of our abstraction analyses we choose the more conservative one of the two to compute error bars around the chance levels of the scores (i.e., we only show the one that leads to the larger standard deviation). We note that although we examined all 35 dichotomies in the same way, we had pre-registered interest in the 3 binary variables context, value and action.
Shuffle of the data:
One simple random model we consider is a shuffle of the data, in which we assign a new, random condition label to each trial for each neuron independently (in a manner that preserves the total number of trials for each condition). In other words, we randomly permute the condition labels (with values from 1 to 8) across all trials, and repeat this procedure separately for every neuron. When re-sampling artificial, noisy trials, we shuffle first, and then re-sample in a manner that respects the new, random condition labels as described above. This procedure destroys almost all structure in the data, except the marginal distributions of the firing rates of individual neurons. The error bars around chance level for the decoding performance in Figs. 3, 5 and S5, and for the parallelism score in Figs. 3, 5 and 7 are based on this shuffle control (showing plus/minus two standard deviations). These chance levels and error bars around them are estimated by performing the exact same decoding/PS analyses detailed in the preceding sections on the shuffled data, and repeating the whole shuffle analysis a sufficient number of times to obtain good estimates of the means and standard deviations of the resulting distributions of decoding performances/parallelism scores (e.g. for the PS we perform 1,000 shuffles).
Geometric random model:
Another class of control models is more explicitly related to neural representations described by random geometries, and can be used to rule out a different type of null hypothesis. For the analyses that depend only on the cluster centers of the eight conditions (i.e., their mean firing rates, as e.g. for the PS), we can construct a random geometry by moving the cluster of points that correspond to different conditions to new random locations that are sampled from an isotropic Gaussian distribution. We then rescale all the vectors to keep the total variance across all conditions (the signal variance, or variance of the centroids of the clusters). Such a random arrangement of the mean firing rates (cluster centers) is a very useful control to compare against, since such geometries do not constitute abstract neural representations, but nevertheless typically allow relevant variables to be decoded (see also Figure 2). For analyses that depend also on the structure of the within condition trial-to-trial fluctuations (in particular, CCGP and decoding with re-sampled trials), our random model in addition requires some assumptions about the noise distributions. We could simply choose identical isotropic noise distributions around each cluster center, but training a linear classifier on trials sampled from such a model would essentially be equivalent to training a maximum margin classifier only on the cluster centers themselves. Instead, we choose to preserve some of the noise structure of the data by moving the (re-sampled) noise clouds to the new random position of the corresponding cluster and performing a discrete rotation around it by permuting the axes separately for each condition. We basically shuffled the neuron labels in a different way for each condition. This shuffling corresponds to a discrete rotation of each noise cloud (i.e. the cloud of points that represents the set of all trials for one specific condition). The rotations are random and independent for each condition. While the structure of the signal is completely destroyed by generating a random set of cluster centers for the eight conditions, the within condition noise structure (but not the correlations across conditions) is retained in these models. If our scores are significantly different from those obtained using this random model, we can reject the null hypothesis that the data were generated by sampling a random isotropic geometry with the same total signal variance (i.e., the variance across the different cloud centers) and similarly shaped noise clouds as in the data. The error bars around chance level for the CCGP in Figs. 3, 5 and 7 are derived from this geometric random control model by constructing many such random geometries and estimating the standard deviation of the resulting CCGPs.
Random models and the analysis of different dichotomies:
One might be tempted to consider the scores for the 35 different dichotomies as a set of score values that defines a random model. Indeed, this could be described as a type of permutation of the condition labels, but only between groups of trials belonging to the same condition (thus preserving the eight groups of trials corresponding to separate conditions), as opposed to the random permutation across all trials performed in the shuffle detailed above. However, there are clearly correlations between the scores of different dichotomies (e.g. because the labels may be partially overlapping, i.e., not orthogonal). Therefore, we should not think of the set of scores for different dichotomies as resulting from a random model used to assess the probability of obtaining certain scores from less structured data. After all, the different dichotomies are simply different binary functions to be computed on the same neural representations, without changing any of their essential geometric properties. Instead, the set of scores for the 35 dichotomies allows us to make statements about the relative magnitude of the scores compared to those of other variables that may also be decodable from the data and possibly abstract, as shown in the form of bee-swarm plots in Figs. 3, 5 and 7.
Expected SD for a perfectly factorized representation
As we showed in Figures 3 and 5, the measured SD in each brain area is significantly greater than the SD of a perfectly factorized representation. A perfectly factorized null model is constructed by placing the centroids of the noise clouds that represent the 8 different experimental conditions at the vertices of a cuboid. The cuboid is randomly rotated and embedded in an N-dimensional firing rate space, where N equals the number of neurons that pass the selection criteria for the decoding analysis of the experimental data. The lengths of the sides of the cuboid are tuned to reproduce (on average) the CCGP values observed in the experiment for the variables context, value, and action. We then sample 10,000 trials for each condition from a Gaussian distribution with unit covariance matrix (centered on the vertex corresponding to that condition) in this firing rate space. From this data set - artificially generated from a perfectly factorized model - we calculate the SD and CCGP, just as in the analyses of experimental data. This procedure is repeated 100 times for each of the 3 brain areas and 2 time intervals, with results for the early time interval shown in Fig. 3e, and those for the late time interval shown in Fig. 5e.
Simulations of the multi-layer network:
The two hidden layer network depicted in Figure 7 contains 768 neurons in the input layer, 100 in each hidden layer and four neurons in the output layer. We used eight digits (1–8) of the full MNIST data set to match the number of conditions we considered in the analysis of the experiment. The training set contained 48128 images and the test set contained 8011 digits. The network was trained to output the parity and the magnitude of each digit and to report it using four output units: one for odd, one for even, one for small (i.e., a digit smaller than 5) and one for large (a digit larger than 4). We trained the network using the back-propagation algorithm ‘train’ of matlab (with the neural networks package). We used a tan-sigmoidal transfer function (‘tansig’ in matlab), the mean squared normalized error (‘mse’) as the cost function, and the maximum number of training epochs was set to 400. After training, we performed the analysis of the neural representations using the same analytical tools that we used for the experimental data, except that we did not z-score the neural activities, since they were simultaneously observed in the simulations.
The description of the methods to model our task using a reinforcement learning algorithm (Deep Q-learning) appears below in Methods S8 Deep neural network models of task performance.
Multi Dimensional Scaling (MDS) plots
All MDS plots (Figure 7e–g, and Figure S4) are obtained as follows. Within a chosen time bin the activity of each neuron across all conditions is z-scored. It is then averaged across trials within each condition to obtain the firing rate patterns for each condition. These patterns are then used to construct an nc×nc dissimilarity matrix (where nc is the number of conditions), which simply tabulates the Euclidean distance between firing rate patterns for each pair of conditions. This dissimilarity matrix is then centered, diagonalized, and projected along the first 3 eigenvectors rescaled by the squared root of the corresponding eigenvalues, in accordance with the Classical Multidimensional Scaling algorithm (Borg & Groenen 2003).
Supplementary Material
Highlights.
The geometry of abstraction supports generalization
Hippocampal and PFC representations are simultaneously abstract and high-dimensional
Multiple task-relevant variables are represented in an abstract format
Representations in simulated neural networks are similar to recorded ones
Acknowledgements
We are grateful to L.F. Abbott and R. Axel for many useful comments on the manuscript. This project is supported by the Simons Foundation, and by NIMH (1K08MH115365, R01MH082017). SF and MKB are also supported by the Gatsby Charitable Foundation, the Swartz Foundation, the Kavli foundation and the NSF’s NeuroNex program award DBI-1707398. JM is supported by the Fyssen Foundation. SB received support from NIMH (1K08MH115365, T32MH015144 and R25MH086466), and from the American Psychiatric Association and Brain & Behavior Research Foundation young investigator fellowships.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interest
The authors declare no competing interests.
References
- Antzoulatos EG & Miller EK (2011), ‘Differences between neural activity in prefrontal cortex and striatum during learning of novel abstract categories’, Neuron 71(2), 243–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barak O, Rigotti M & Fusi S (2013), ‘The sparseness of mixed selectivity neurons controls the generalization-discrimination trade-off.’, The Journal of neuroscience : the official journal of the Society for Neuroscience 33, 3844–3856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barto AG & Mahadevan S (2003), ‘Recent advances in hierarchical reinforcement learning’, Discrete Event Dynamic Systems 13(4), 341–379. [Google Scholar]
- Behrens TE, Muller TH, Whittington JC, Mark S, Baram AB, Stachenfeld KL & Kurth-Nelson Z (2018), ‘What is a cognitive map? organizing knowledge for flexible behavior’, Neuron 100(2), 490–509. [DOI] [PubMed] [Google Scholar]
- Bellman RE (1957), Dynamic Programming., Princeton University Press. [Google Scholar]
- Benna MK & Fusi S (2019), ‘Are place cells just memory cells? memory compression leads to spatial tuning and history dependence’, bioRxiv p. 624239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borg I & Groenen P (2003), ‘Modern multidimensional scaling: Theory and applications’, Journal of Educational Measurement 40(3), 277–280. [Google Scholar]
- Buckley MJ, Mansouri FA, Hoda H, Mahboubi M, Browning PGF, Kwok SC, Phillips A & Tanaka K (2009), ‘Dissociable components of rule-guided behavior depend on distinct medial and prefrontal regions..’, Science 325(5936), 52–58. [DOI] [PubMed] [Google Scholar]
- Chang L & Tsao DY (2017), ‘The code for facial identity in the primate brain’, Cell 169(6), 1013–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TQ, Li X, Grosse RB & Duvenaud DK (2018), Isolating sources of disentanglement in variational autoencoders, in ‘Advances in Neural Information Processing Systems’, pp. 2610–2620. [Google Scholar]
- Chen X (2008), ‘Confidence interval for the mean of a bounded random variable and its applications in point estimation’, arXiv preprint arXiv:0802.3458 . [Google Scholar]
- Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I & Abbeel P (2016), Infogan: Interpretable representation learning by information maximizing generative adversarial nets, in ‘Advances in neural information processing systems’, pp. 2172–2180. [Google Scholar]
- Dang W, Jaffe RJ, Qi X-L & Constantinidis C (2020), ‘Emergence of non-linear mixed selectivity in prefrontal cortex after training’, bioRxiv . https://www.biorxiv.org/content/early/2020/08/02/2020.08.02.233247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiCarlo JJ & Cox DD (2007), ‘Untangling invariant object recognition’, Trends in cognitive sciences 11(8), 333–341. [DOI] [PubMed] [Google Scholar]
- DiCarlo JJ, Zoccolan D & Rust NC (2012), ‘How does the brain solve visual object recognition?’, Neuron 73(3), 415–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietterich TG (2000), ‘Hierarchical reinforcement learning with the maxq value function decomposition’, Journal of Artificial Intelligence Research 13, 227–303. [Google Scholar]
- Eichenbaum H (2004), ‘Hippocampus: Cognitive processes and neural representations that underlie declarative memory.’, Neuron 2004, 109–120. [DOI] [PubMed] [Google Scholar]
- Eichenbaum H (2017), ‘On the integration of space, time, and memory’, Neuron 95(5), 1007–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T & Miller EK (2001), ‘Categorical representation of visual stimuli in the primate prefrontal cortex’, Science 291(5502), 312–316. [DOI] [PubMed] [Google Scholar]
- Fusi S, Miller EK & Rigotti M (2016), ‘Why neurons mix: high dimensionality for higher cognition’, Current opinion in neurobiology 37, 66–74. [DOI] [PubMed] [Google Scholar]
- Golland P, Liang F, Mukherjee S & Panchenko D (2005), Permutation tests for classification, in ‘International Conference on Computational Learning Theory’, Springer, pp. 501–515. [Google Scholar]
- Higgins I, Matthey L, Pal A, Burgess C, Glorot X, Botvinick M, Mohamed S & Lerchner A (2017), β-VAE: Learning basic visual concepts with a constrained variational framework, in ‘ICLR’. [Google Scholar]
- Horikawa T, Tamaki M, Miyawaki Y & Kamitani Y (2013), ‘Neural decoding of visual imagery during sleep’, Science 340(6132), 639–642. [DOI] [PubMed] [Google Scholar]
- Isik L, Meyers EM, Leibo JZ & Poggio T (2013), ‘The dynamics of invariant object recognition in the human visual system’, Journal of neurophysiology 111(1), 91–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isik L, Tacchetti A & Poggio T (2017), ‘A fast, invariant representation for human action in the visual system’, Journal of neurophysiology 119(2), 631–640. [DOI] [PubMed] [Google Scholar]
- Kim H & Mnih A (2018), ‘Disentangling by factorising’, arXiv preprint arXiv:1802.05983 . [Google Scholar]
- King J-R & Dehaene S (2014), ‘Characterizing the dynamics of mental representations: the temporal generalization method’, Trends in cognitive sciences 18(4), 203–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP & Ba J (2014), ‘Adam: A method for stochastic optimization’, arXiv preprint arXiv:1412.6980 . [Google Scholar]
- Kumaran D, Summerfield J, Hassabis D & Maguire E (2009), ‘Tracking the emergence of conceptual knowledge during human decision making’, Neuron 63, 889–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeCun Y, Bengio J & Hinton G (2015), ‘Deep learning.’, Nature 521, 436–444. [DOI] [PubMed] [Google Scholar]
- Lindsay GW, Rigotti M, Warden MR, Miller EK & Fusi S (2017), ‘Hebbian learning in a random network captures selectivity properties of the prefrontal cortex.’, The Journal of neuroscience : the official journal of the Society for Neuroscience 37, 11021–11036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machens CK, Romo R & Brody CD (2010), ‘Functional, but not anatomical, separation of ”what” and ”when” in prefrontal cortex.’, J Neurosci 30(1), 350–360. 10.1523/JNEUROSCI.3276-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A & La Camera G (2016), ‘Stimuli reduce the dimensionality of cortical activity’, Frontiers in systems neuroscience 10, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyers EM, Freedman DJ, Kreiman G, Miller EK & Poggio T (2008), ‘Dynamic population coding of category information in inferior temporal and prefrontal cortex’, Journal of neurophysiology 100(3), 1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikolov T, Sutskever I, Chen K, Corrado GS & Dean J (2013), Distributed representations of words and phrases and their compositionality, in ‘Advances in neural information processing systems’, pp. 3111–3119. [Google Scholar]
- Mikolov T, Yih W. t. & Zweig G (2013), Linguistic regularities in continuous space word representations, in ‘Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies’, pp. 746–751. [Google Scholar]
- Miller EK, Nieder A, Freedman DJ & Wallis JD (2003), ‘Neural correlates of categories and concepts’, Current opinion in neurobiology 13(2), 198–203. [DOI] [PubMed] [Google Scholar]
- Milner B, Squire L & Kandell E (1998), ‘Cognitive neuroscience and the study of memory..’, Neuron 1998, 445–468. [DOI] [PubMed] [Google Scholar]
- Mitchell TM, Shinkareva SV, Carlson A, Chang K-M, Malave VL, Mason RA & Just MA (2008), ‘Predicting human brain activity associated with the meanings of nouns’, science 320(5880), 1191–1195. [DOI] [PubMed] [Google Scholar]
- Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, Graves A, Riedmiller M, Fidjeland AK, Ostrovski G et al. (2015), ‘Human-level control through deep reinforcement learning’, Nature 518(7540), 529. [DOI] [PubMed] [Google Scholar]
- Morcos AS, Barrett DG, Rabinowitz NC & Botvinick M (2018), ‘On the importance of single directions for generalization’, arXiv preprint arXiv:1803.06959 . [Google Scholar]
- Munuera J, Rigotti M & Salzman CD (2018), ‘Shared neural coding for social hierarchy and reward value in primate amygdala’, Nature neuroscience 21(3), 415–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkinson C, Liu S & Wheatley T (2014), ‘A common cortical metric for spatial, temporal, and social distance’, Journal of Neuroscience 34(5), 1979–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parthasarathy A, Herikstad R, Bong JH, Medina FS, Libedinsky C & Yen S-C (2017), ‘Mixed selectivity morphs population codes in prefrontal cortex’, Nature neuroscience 20(12), 1770–1779. [DOI] [PubMed] [Google Scholar]
- Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, Lin Z, Desmaison A, Antiga L & Lerer A (2017), Automatic differentiation in pytorch, in ‘NIPS 2017 Autodiff Workshop’. [Google Scholar]
- Ponsen M, Taylor ME & Tuyls K (2009), Abstraction and generalization in reinforcement learning: A summary and framework, in ‘International Workshop on Adaptive and Learning Agents’, Springer, pp. 1–32. [Google Scholar]
- Precup D (2000), Temporal abstraction in reinforcement learning, PhD thesis, University of Massachusetts; Amherst. [Google Scholar]
- Raposo D, Kaufman MT & Churchland AK (2014), ‘A category-free neural population supports evolving demands during decision-making’, Nature neuroscience 17(12), 1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanatesi S, Farrell M, Lajoie G, Deneve S, Rigotti M & Shea-Brown E (2019), ‘Predictive learning extracts latent space representations from sensory observations’, bioRxiv p. 471987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesenhuber M & Poggio T (1999), ‘Hierarchical models of object recognition in cortex’, Nature neuroscience 2(11), 1019. [DOI] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK & Fusi S (2013), ‘The importance of mixed selectivity in complex cognitive tasks’, Nature 497(7451), 585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Ben Dayan Rubin D, Wang X-J & Fusi S (2010), ‘Internal representation of task rules by recurrent dynamics: the importance of the diversity of neural responses’, Frontiers in Computational Neuroscience 4, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust N & Dicarlo J (2010), ‘Selectivity and tolerance (”invariance”) both increase as visual information propagates from cortical area v4 to it.’, J Neurosci 30(39), 12978–12995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saez A, Rigotti M, Ostojic S, Fusi S & Salzman C (2015), ‘Abstract context representations in primate amygdala and prefrontal cortex’, Neuron 87(4), 869–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schapiro AC, Turk-Browne NB, Norman KA & Botvinick MM (2016), ‘Statistical learning of temporal community structure in the hippocampus’, Hippocampus 26(1), 3–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanini F, Kushnir L, Jimenez JC, Jennings JH, Woods NI, Stuber GD, Kheirbek MA, Hen R & Fusi S (2020), ‘A distributed neural code in the dentate gyrus and in ca1’, Neuron . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Carandini M & Harris KD (2018), ‘High-dimensional geometry of population responses in visual cortex’, bioRxiv p. 374090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallis JD, Anderson KC & Miller EK (2001), ‘Single neurons in prefrontal cortex encode abstract rules’, Nature 411(6840), 953. [DOI] [PubMed] [Google Scholar]
- Whittington JC, Muller TH, Mark S, Chen G, Barry C, Burgess N & Behrens TE (2019), ‘The tolman-eichenbaum machine: Unifying space and relational memory through generalisation in the hippocampal formation’, bioRxiv p. 770495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirth S, Yanike M, Frank L, Smith A, Brown E & Suzuki W (2003), ‘Single neurons in the monkey hippocampus and learning of new associations.’, Science 300, 1578–1581. [DOI] [PubMed] [Google Scholar]
- Wutz A, Loonis R, Roy JE, Donoghue JA & Miller EK (2018), ‘Different levels of category abstraction by different dynamics in different prefrontal areas.’, Neuron 97(3), 716–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zabicki A, de Haas B, Zentgraf K, Stark R, Munzert J & Krüger B (2017), ‘Imagined and executed actions in the human motor system: testing neural similarity between execution and imagery of actions with a multivariate approach’, Cerebral Cortex 27(9), 4523–4536. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets and analysis code supporting the current study are available from the lead contact on request.


