Deep-LIBRA: An artificial-intelligence method for robust quantification of breast density with independent validation in breast cancer risk assessment

Abstract

Breast density is an important risk factor for breast cancer that also affects the specificity and sensitivity of screening mammography. Current federal legislation mandates reporting of breast density for all women undergoing breast cancer screening. Clinically, breast density is assessed visually using the American College of Radiology Breast Imaging Reporting And Data System (BI-RADS) scale. Here, we introduce an artificial intelligence (AI) method to estimate breast density from digital mammograms. Our method leverages deep learning using two convolutional neural network architectures to accurately segment the breast area. An AI algorithm combining superpixel generation and radiomic machine learning is then applied to differentiate dense from non-dense tissue regions within the breast, from which breast density is estimated. Our method was trained and validated on a multi-racial, multi-institutional dataset of 15,661 images (4,437 women), and then tested on an independent matched case-control dataset of 6,368 Breast Cancer risk digital mammograms (414 cases; 1,178 controls) for both breast density estimation and case-control discrimination. On the independent dataset, breast percent density (PD) estimates from Deep-LIBRA and an expert reader were strongly correlated (Spearman correlation coefficient = 0.90). Moreover, in a model adjusted for age and BMI, Deep-LIBRA yielded a higher case-control discrimination performance (area under the ROC curve, AUC = 0.612 [95% confidence interval (CI): 0.584, 0.640]) compared to four other widely-used research and commercial breast density assessment methods (AUCs = 0.528 to 0.599). Our results suggest a strong agreement of breast density estimates between Deep-LIBRA and gold-standard assessment by an expert reader, as well as improved performance in breast cancer risk assessment over state-of-the-art open-source and commercial methods.

Graphical Abstract

1. Introduction

Studies have shown that breast density, the extent of fibroglandular tissue within the breast, not only limits the sensitivity of screening mammography but is also an independent breast cancer risk factor Engmann et al. (2017); Freer (2015); Brentnall et al. (2018). Breast density can be estimated from full-field digital mammography (FFDM) images and is most commonly assessed in the clinic by visual grading into one of the four categories defined by the American College of Radiology BI-RADS Dorsi et al. (2003). However, BI-RADS density assessment is highly subjective and does not provide a quantitative, continuous measure of breast density, which would allow for more refined risk stratification and assessment of breast density changes Irshad et al. (2016); Sprague et al. (2016).

Automated quantitative measurement of breast density from FFDM can be performed through commercially available software Hartman et al. (2008); Regini et al. (2014) and research-based tools Keller et al. (2012); Mustra et al. (2016); Li et al. (2013); Shi et al. (2018); Anitha et al. (2017); Ferrari et al. (2004); Kwok et al. (2004); Mustra and Grgic (2013); Nagi et al. (2010); Taghanaki et al. (2017); Rampun et al. (2017); Czaplicka and Włodarczyk (2011); Dembrower et al. (2020). Although these tools are useful, important limitations persist. Most commercially available packages, such as Quantra and Volpara Hartman et al. (2008); Regini et al. (2014) calculate breast density based on x-ray beam interaction models. These packages make assumptions based on specific metadata to simplify various estimates, including identifying the fatty tissue. Therefore, these assumptions can lead to inaccurate estimates, especially when the required metadata is missing. Moreover, commercial tools do not provide the corresponding spatial maps of dense tissue segmentation, while they are also costly, and therefore inaccessible for general use. On the other hand, with a few exceptions, such as the publicly available LIBRA software Keller et al. (2012); Gastounioti et al. (2020), research-based methods are not freely available, making it challenging to adopt such tools broadly and rigorously compare their performances. Most research-based tools have also been developed using small, single-institution datasets, and lack independent validation Keller et al. (2012); Li et al. (2013); Shi et al. (2018); Anitha et al. (2017).

In general, the key computational steps for automated breast density quantification from FFDM are image background removal; identification of the pectoralis muscle; and segmentation of the dense tissue areas within the breast region. Background removal consists of identifying the air and extraneous objects (paddles, markers, rings, etc.) to accurately delineate the breast region and remove extraneous objects from density calculations. Similarly, the pectoralis muscle must be removed from the area to be processed, which can be challenging due to anatomic variation of the pectoralis muscle and the extension of dense glandular tissue which often superimposes over the pectoralis muscle in the axillary tail. To simplify its delineation, the pectoralis muscle has typically been modeled as a straight line Keller et al. (2012); Mustra et al. (2016); Kwok et al. (2004); Ferrari et al. (2004) or a curve Mustra and Grgic (2013)), which can lead to inaccurate breast density estimation. Most crucial to breast density evaluation is the segmentation of dense versus non-dense tissue. Most methods for this task to date Keller et al. (2012); Zhou et al. (2001); Anitha et al. (2017) are relatively simplistic, leading to over- or underestimating the amount of dense tissue.

Artificial intelligence (AI), including deep learning, has shown great potential in breast imaging applications, substantially improving image segmentation, risk assessment and cancer detection Rodríguez-Ruiz et al. (2018); Kontos and Conant (2019); Kooi et al. (2017); Wang et al. (2016); Becker et al. (2017); Lehman et al. (2018); Yala et al. (2019); Mohamed et al. (2018); Hamidinekoo et al. (2018); Ronneberger et al. (2015); Mortazi and Bagci (2018); Kaul et al. (2019); Murugesan et al. (2019). Combining conventional image processing methods and machine learning with deep learning techniques can further boost the performance of AI methods in mammographic tasks Kooi et al. (2017). Here, we introduce Deep-LIBRA, an AI method for breast density estimation, which combines the U-Net deep learning architecture with image processing and radiomic machine learning techniques to estimate breast density from FFDM. Like LIBRA, but unlike other techniques, Deep-LIBRA employs radiomic machine learning in densetissue segmentation, but, unlike the earlier tool, incorporates this information into an AI approach. Moreover, Deep-LIBRA was developed using a large racially diverse, multi-institutional train-validation set totaling 15,661 FFDM images from 4,437 women. Further, it was independently evaluated on 6,478 case-control FFDM images from 1,702 women to assess its accuracy both in breast density estimation and in breast cancer risk assessment. Deep-LIBRA has been implemented as open-source software using Python packages and has been made publicly available through GitHub (files will be moved to GitHub upon publication).

2. Methods

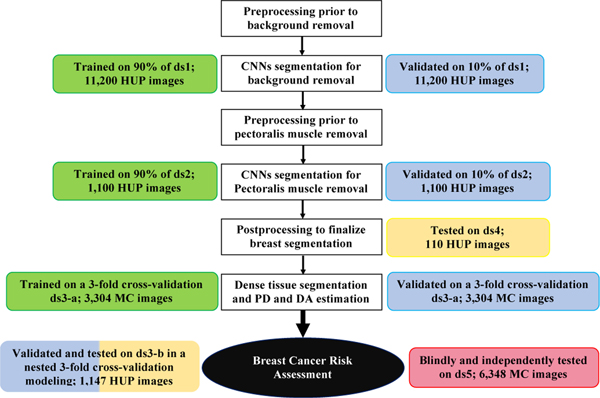
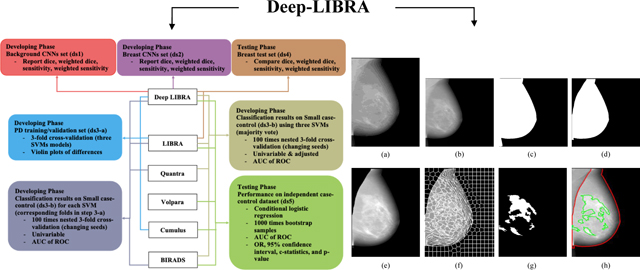
Deep-LIBRA is a pipeline of AI modules sequentially performing all three key computational steps involved in automated breast density quantification from FFDM. Through these steps, Deep-LIBRA provides estimates of the total dense tissue area (DA), as well as the relative amount of dense tissue within the breast, also known as breast percent density (PD). This section describes the study datasets and the experiments used to develop and evaluate each AI module of Deep-LIBRA (Table 1, Figure 1 and Supplementary Figure 1).

Table 1:

General characteristics of the six study datasets. For each dataset, this table shows the institution where images were collected, the number of images and individual women, the range of screening dates, the racial distribution, and information about the dataset usage in this study. The case-control datasets (ds3-b and ds5) include any available cancer case from the HUP and MC screening cohorts as long as a negative FFDM exam acquired prior to breast cancer diagnosis was available for analysis.

	ds 1	ds 2	ds 3-a	ds 3-b	ds 4	ds 5
Institution	HUP	HUP	MC	HUP	HUP	MC
Number of Images	11,200	1,100	3,314	1,147	110	6,368
Number of Women	2,200	1,100	1,662	575	110	1,592
Screening start date	2010	2010	2008	2010	2010	2013
Screening end date	2012	2012	2012	2014	2012	2015
Caucasian/White(%)	45	45	98	47	45	97
African American/Black (%)	45	45	_	53	45	_
Other (%)	10	10	2	-	10	3
Used in development	Yes	Yes	Yes	Yes	No	No
Cross-validation or Bootstrap	No	No	Yes	Yes	No	Yes
Training (%)	90	90	67	67	-	_
Validation (%)	10	10	33	33	-	_
Testing (%)	-	-	-	-	100	100
Accuracy in breast density assessment	No	No	Yes	No	No	Yes
Case-control classification based on breast density	No	No	No	Yes	No	Yes

Fig. 1:

Development and evaluation experiments. White boxes: workflow of the Deep-LIBRA algorithm. Green, blue, yellow, and red boxes: training, validation, independent testing, and blinded independent testing, respectively. HUP: Hospital of the University of Pennsylvania; MC: Mayo Clinic.

2.1. Study datasets

A total of six non-overlapping datasets were compiled from retrospectively collected negative FFDM screening exams acquired in two large breast cancer screening practices: the Hospital of the University of Pennsylvania (HUP), Philadelphia, PA, and the Mayo Clinic (MC), Rochester, MN (Table 1). For all datasets, our study used raw (i.e., “FOR PROCESSING”) FFDM images acquired with Selenia or Selenia DimensionsTM units (Hologic Inc, Bedford, MA, USA).

2.1.1. Training and validation datasets

• Dataset to develop the background removal module (ds1): This dataset consisted of 11,200 bilateral images from 2,200 women randomly selected from the HUP screening cohort. The images were evenly split among left and right breast lateralities, and craniocaudal (CC) and mediolateral oblique (MLO) breast views, and represented the racially diverse screening population at HUP McCarthy et al. (2016).

• Dataset to develop the pectoralis muscle removal module (ds2): Since the pectoralis muscle is almost always visible only in the MLO view, the MLO-view images of ds1 were used as the basis of this dataset. Due to the time required for manual delineation of the pectoralis muscle (5 to 10 minutes per image), 1,100 MLO-view images were randomly selected from ds1, maintaining the corresponding racial and breast laterality distributions.

• Dataset to develop the breast density estimation module (ds3): One portion of this dataset (ds3-a) was used to guide the development of this module in terms of accuracy in breast density estimation, and another (ds3-b) to account for the performance of breast density in breast cancer risk assessment.

  1. Dataset to train and validate the breast density estimation module (ds3-a): This subset consisted of 3,314 bilateral CC-view images from 1,662 women from the MC dataset, for which “gold-standard” human-rater Cumulus PD values were available by a single reader with over twenty years of experience estimating density with Cumulus (FFW). Automated density scores extracted with LIBRA were also available for these images. This dataset has been previously published Brandt et al. (2016); Gastounioti et al. (2020).
  2. Case-control dataset to evaluate the breast density estimation module in breast cancer risk-assessment (ds3b): We used 1,147 bilateral MLO-view images from 115 women who developed breast cancer at least one year later and 460 age- and ethnicity-matched controls, acquired at HUP. Clinical BI-RADS density assessments, as well as automated density scores extracted with LIBRA and Quantra, were also ascertained for these images. This case-control dataset has been previously published Gastounioti et al. (2018) and is described in detail in Supplementary Table 1.

2.1.2. Independent test datasets

The following two datasets were used to independently evaluate Deep-LIBRA after development was complete. There was no overlap with images nor women used in training and validation.

• Dataset to evaluate breast segmentation performance (ds4): This dataset consisted of 110 MLO-view images from 110 women randomly selected from the HUP screening cohort, with a racial distribution representative of the diverse screening population at HUP McCarthy et al. (2016).

• Dataset to evaluate breast cancer risk assessment performance (ds5): This dataset consisted of 6,368 bilateral CC and MLO images from 414 women who developed breast cancer an average of 4.7 years [interquartile range (IQR): 4.1, 5.1] later and 1,178 matched controls, acquired at MC. Approximately three controls without prior breast cancer were matched to each case on age (5-year caliper matching), race, state of residence, FFDM screening exam date, and FFDM machine. Automated breast density scores extracted with LIBRA and Volpara, as well as semi-automated Cumulus breast density scores and clinical BI-RADS density assessments, were also ascertained for these images. This dataset is described in detail in Supplementary Table 2.

2.2. Algorithm operation

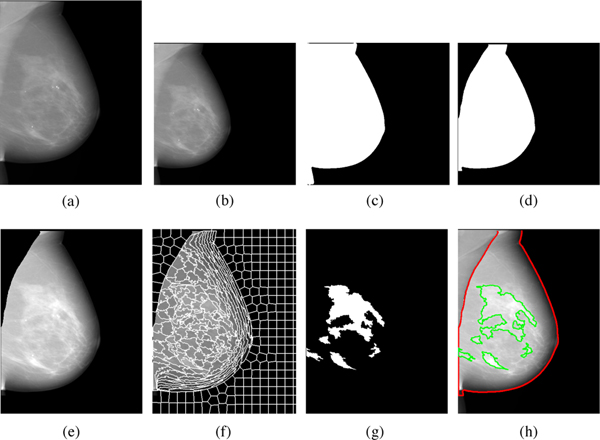
The core of Deep-LIBRA are three AI modules for (1) removal of the FFDM image background, (2) removal of the pectoralis muscle, and (3) segmentation of the dense versus fatty tissue and subsequent breast density estimation (Figure 2). The first two modules of Deep-LIBRA are based on deep learning; radiomic machine learning forms the basis of the third module. Before applying these modules, standard pre-processing steps for raw FFDM images are applied Keller et al. (2012), in which image intensity is logtransformed, inverted, and squared, and image orientation is standardized.

Fig. 2:

Detailed illustration of the Deep-LIBRA algorithm operation. Panel (a) shows the original FFDM image in 16-bit resolution, and panel (b) is the zero-padded image in an 8-bit intensity resolution. The zero-padded image is used by the background segmentation U-Net, which generates the image shown in panel (c). Panel (d) is the output of the module of pectoralis muscle removal using the second U-Net resulting to the final breast segmentation shown in panel (e). The image from panel (e) is used to generate superpixels as shown in panel (f) and perform radiomic feature analysis. Finally, the SVM classifies the superpixels based on the extracted features, resulting in dense tissue segmentation, as shown in panel (g). The panel (h) shows the final dense tissue segmentation overlaid on the original image. Note: The image sizes are different in this figure because the panels (a), (e)-(h) show images in the original image resolution, while the panels (b)-(d) are downsampled images of size 512 × 512 pixels used in U-Net segmentation.

2.2.1. Background removal

This module performed binary segmentation of the background versus non-background image regions, where the background consisted of both air and extraneous objects. This module was implemented as a binary segmentation convolutional neural network (CNN) based on the widely used U-Net architecture, slightly modified by replacing the simple convolutional layers of the encoder with ResNet encoder modules to extract more in-depth information Szegedy et al. (2017); Maghsoudi et al. (2020). The U-Net was developed using the dataset ds1 and a 90%10% split-sample approach for training and validation. To further improve the U-Net performance, data augmentation Ronneberger et al. (2015) was applied: for each training epoch, each image was randomly altered by combinations of rotation (−22.5 to +22.5 degrees); horizontal shift (−20% to +20% of image width); vertical shift (−20% to +20% of image height); zoom (−20% to +20%); and horizontal flip. The background region segmented by the U-Net was further refined by removing any regions not connected to any of the four image boundaries. Figure 2 (c) shows the outcome from this step.

Reference background segmentation masks were generated using the publicly available LIBRA software Keller et al. (2012) and were further reviewed and manually corrected using the ImageJ software Rueden et al. (2017) by a research scientist (OHM, two years of experience) under the guidance of a fellowship-trained, board-certified, breast imaging radiologist (EFC, more than 25 years of experience). The loss function for training was the inverse weighted Dice measure, calculated as 1 - weighted dice Chang et al. (2009), to reduce the effect of unbalanced regions in training (definition available in the Supplementary Material).

2.2.2. Pectoralis muscle removal

This module segmented the breast from the image remaining after background removal (Figure 2 (c, d)). As with the background removal module, this module was implemented as a binary segmentation CNN based on the U-Net architecture. Training used the ds2 dataset, again using a 90%10% split-sample approach for training and validation, and the inverse weighted dice measure as the loss function. Data augmentation was applied, with alterations of rotation (−22.5 to +22.5 degrees); horizontal shift (−15% to +15% of image width); vertical shift (−15% to +15% of image height); and zoom (−15% to +15%). The zoom and shift ranges were bounded at 15%, rather than 20% used in background removal because the pectoralis muscle occupies an appreciably smaller portion of an image than the background. Any abdominal tissue remaining in the image was removed. The paddle compression effect, a bump of abdominal tissue below the breast caused by paddle compression, was also removed, based on the gradient of the breast contour coordinates (see also Supplementary Material). Reference delineations of the pectoralis muscle were manually obtained using the ImageJ software by OHM under the guidance of EFC.

2.2.3. Dense tissue segmentation and breast density calculation

The breast density calculation module involved three major steps: 1) Partitioning the breast into superpixels using image intensity information. 2) Calculating global and superpixel-wise radiomic features. 3) Using these radiomic features as inputs to machine learning models to classify superpixels as either dense or non-dense, and calculate breast density (Figure 2 (e)-(h)).

A superpixel is a contiguous subregion of the breast image. By defining superpixels using gray-level intensity values and spatial information, we can generate meaningful localized clusters Achanta et al. (2012). To aggregate neighboring pixels into superpixels, we used simple linear iterative clustering (SLIC), a spatially localized version of k-means clustering, which is fast, adheres to local boundaries, and generates superpixels of similar sizes (making the superpixels suitable for representation of scale-variant features such as texture features) Achanta et al. (2012). Based on the image size, we partitioned each image into 512 superpixels.

Then, we generated a reference classification of each superpixel as dense versus non-dense, using the image-wise “gold-standard” PD scores available for ds3-a. Specifically, an average intensity was calculated for each superpixel. For a given intensity cutoff, an overall (across all images) PD score was calculated. Similarly, the “gold-standard” PD values were combined into an overall PD. The intensity cutoff that minimized the difference between the overall PD and the “gold-standard” PD values was selected and was used to assign each superpixel a reference value of dense versus non-dense region.

For each image, the module then computed a total of 101 radiomic features from the entire image, and an additional 50 radiomic features on each superpixel (Supplementary List 1). Radiomic features were extracted using the PyRadiomics library Van Griethuysen et al. (2017) and additional Python packages (a detailed list of packages can be found on GitHub).

To reduce feature dimensionality, two steps were applied. First, for highly-correlated groups of radiomic features (i.e., absolute Pearson’s correlation r > 0.95), a single feature from each group was retained (100 features remained from the total of 151 features) which had a maximum interquartile range. Second, a random-forest classifier was applied to all superpixels with the remaining radiomic features as predictors and the reference dense versus non-dense classification as the supervised classification labels. This two-step procedure determined the 80 most-predictive features to retain.

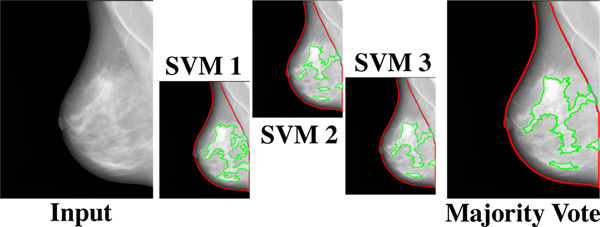
In this module’s final step, we trained a support vector machine (SVM) on ds3-a, classifying superpixels as dense versus non-dense with the retained texture features as predictors. Three-fold cross-validation was used, resulting in three trained SVM models. To reduce the effect of data partitioning in the SVM performance (Table 2) and to alleviate potential overfitting, an ensemble model based on the majority vote of the three SVMs was used as the final model assigning dense versus non-dense labels to superpixels (Figure 3), based on which Deep-LIBRA provided estimates of DA and PD.

Table 2:

Case-control discrimination performance on the dataset ds3-b for breast percent density (PD) values generated by Deep-LIBRA and LIBRA, area-based (A Quantra) and volumetric (V Quantra) PD values by Quantra, and clinical BI-RADS density assessments. Results correspond to mean AUCs and 95% CIs in parentheses. Folds 1, 2 and 3 are the held-out folds used for the evaluation of the corresponding Deep-LIBRA SVM. Unadj. and adj. indicate unadjusted logistic regression models and logistic regression models adjusted for age and BMI, respectively.

	1 LIBRA	V_Quantra	A_Quantra	BI-RADS	Deep_LIBRA
Fold l unadj.	0.469 (0.465, 0.472)	0.578 (0.578, 0.579)	0.560 (0.559, 0.560)	0.541 (0.540, 0.541)	0.532 (0.528, 0.536)
Fold 2 unadj.	0.460 (0.455, 0.465)	0.579 (0.578, 0.579)	0.560 (0.559, 0.560)	0.541 (0.540, 0.541)	0.594 (0.593, 0.594)
Fold 3 unadj.	0.467 (0.463, 0.471)	0.578 (0.578, 0.579)	0.561 (0.559, 0.561)	0.541 (0.541,0.541)	0.561 (0.560,0.561)
All unadj.	0.467 (0.464, 0.471)	0.579 (0.579, 0.580)	0.561 (0.560, 0.561)	0.540 (0.539, 0.542)	0.578 (0.577, 0.578)
All adj.	0.498 (0.494, 0.502)	0.586 (0.584, 0.587)	0.568 (0.567, 0.570)	0.550 (0.548, 0.552)	0.582 (0.581,0.583)

Fig. 3:

The majority voting approach. The majority voting approach uses the outcome of three SVM models, each trained on two folds of ds3-a, to make the final dense tissue segmentation. The majority voting scheme assigns the dense or non-dense label to each superpixel based on at least two SVM models agreeing on the label.

2.3. Algorithm evaluation

2.3.1. Evaluation on development datasets

• Background and pectoralis muscle removal: Images in the ds1 and ds2 datasets were used to train and validate the CNNs for background and pectoralis muscle removal, respectively. The segmentation performance of the trained CNNs was measured using four parameters: 1) dice Chang et al. (2009), 2) weighted dice, 3) sensitivity Chang et al. (2009), and 4) weighted sensitivity. Detailed definitions of the performance evaluation measures are available in the Supplementary Material.

• Breast density estimation: Deep-LIBRA training resulted in three SVMs, each trained on two of three folds of ds3-a. For unbiased evaluation of its performance in breast density estimation, we measured each SVM’s performance separately on the corresponding held-out fold via Spearman correlation coefficients and absolute differences between Deep-LIBRA and gold-standard Cumulus PD values. We also compared the performance of Deep-LIBRA with the performance of the LIBRA software on the images of each fold.

• Breast cancer risk assessment based on breast density: Using ds3-b, we evaluated the case-control discriminatory ability of Deep-LIBRA PD and DA measures, while also comparing with LIBRA PD and DA, Quantra area-based (A-Quantra) and volumetric (V-Quantra) density measures, and clinical BI-RADS density assessments. For each breast density measure, the case-control status was modeled as the outcome in each of two conditional logistic regression models Breslow et al. (1978): an unadjusted model consisting of the breast density measure alone, and an adjusted model including also age and body-mass index (BMI). Case-control discriminatory ability was assessed via the mean area under curve (AUC) of the receiver operation curve (ROC) across 100 bootstrap samples where case-control matching was maintained, with confidence intervals (CIs) derived from those 100 repetitions. Additionally, we examined differences in breast density distributions between cases and controls using the Wilcoxon rank sum test.

2.3.2. Evaluation on independent testing datasets

• • Breast segmentation: The images of the ds4 dataset were used to independently evaluate the total segmented breast area by Deep-LIBRA. The Dice, weighted Dice, sensitivity and weighted sensitivity were used as the evaluation measures, while also comparing with the breast segmentation performance of LIBRA via two-sided t-tests.

• • Breast cancer risk assessment based on breast density: A blinded evaluation of the associations of Deep-LIBRA PD and DA with breast cancer was independently performed by an analyst at MC on the dataset ds5, with the Deep-LIBRA developing team being blinded to the case-control status of the images. LIBRA density measures, area-based and volumetric Volpara density metrics, gold-standard Cumulus density metrics, and clinical BI-RADS density assessments were also analyzed for comparison purposes. Unadjusted and adjusted conditional logistic regression analysis was performed for each density measure with case-control status as the outcome. Model discriminatory ability was assessed via AUCs, and effect sizes as odds ratios (ORs) per one standard deviation of breast density. P-values, for both AUCs and ORs, versus the null hypothesis of no difference from the AUC or OR derived from Deep-LIBRA, were estimated from testing across 1,000 bootstrap samples where case-control matching was maintained.

Moreover, we investigated the effect of simultaneously using Deep-LIBRA density measures with measures from other breast density estimation approaches in case-control discrimination performance. To this end, we evaluated Deep-LIBRA density measures in combination with density measures from LIBRA, Volpara, and Cumulus, as well as with clinical BI-RADS density assessments.

Last, for each density measure, we tested for breast density distribution differences between cases and controls using Wilcoxon rank sum tests. We also evaluated the correlations of different breast density measures using the Spearman correlation coefficient. SAS version 9.4 (Cary, NC) was used for all statistical analyses, and p-values were considered statistically significant at the 0.05 cutoff.

3. Results

3.1. Evaluation on development datasets

3.1.1. Background and pectoralis muscle removal

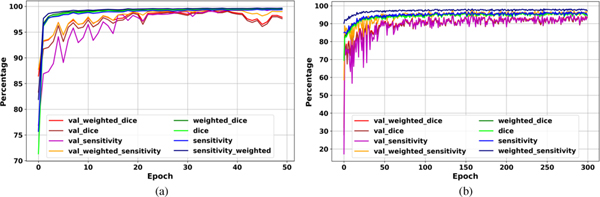
The evaluation curves in the development phase of Deep-LIBRA show sufficient training and high performance in breast segmentation (Figure 4). The highest weighted dice score achieved by the background removal module on the validation set was 99.4% after 35 epochs, with a value of 99.5% on the training set at the same epoch (Figure 4 (a)). The pectoralis muscle removal module achieved the highest weighted dice of 95.0% on the validation set after 158 epochs, with a value of 96.3% on the training set at the same epoch (Figure 4 (b)).

Fig. 4:

Deep-LIBRA evaluation curves in the development phase. Panels (a) and (b) show the training and validation (noted as as “val_”) results for background and pectoral muscle segmentation CNNs, respectively. As the panel (b) shows, there is no sign of overfitting for pectoralis muscle segmentation while panel (a) indicates some possible signs of overfitting after epoch 40 shown by a wider fluctuation on the validation set.

3.1.2. Breast density estimation

Deep-LIBRA breast density evaluation on ds3-a showed high agreement with “gold-standard” Cumulus values. Mean PD differences between Deep-LIBRA and Cumulus, measured with each of the three Deep-LIBRA SVMs on the corresponding held-out fold, were 4.91 [95% CI: 4.48, 5.34], 4.64 [95% CI: 4.31, 4.99], and 4.22 [95% CI: 3.95, 4.49]; mean PD differences between LIBRA and Cumulus on the same folds were 5.28 [95% CI: 4.95, 5.60], 5.24 [95% CI: 4.96, 5.52], and 5.39 [95% CI: 5.08, 5.70]. For two of the three folds, PD differences between Deep-LIBRA and Cumulus were significantly lower than those between LIBRA and Cumulus (paired two-sided t-test p-values: 0.179, 0.008 and 0.001, respectively). The correlations between Deep-LIBRA and Cumulus PD (0.80, 0.79, and 0.84) were also higher than those between LIBRA and Cumulus (0.70, 0.70, and 0.69) for all three folds.

3.1.3. Breast cancer risk assessment based on breast density

Using the dataset ds3-b and unadjusted logistic regression models, PD values generated by the three Deep-LIBRA SVMs yielded mean AUCs of 0.532, 0.594, and 0.561 on the corresponding held-out folds (Table 2). Similar performance was observed for Quantra and clinical BI-RADS density measures.

The PD generated by the ensemble SVM model gave a mean AUC of 0.578 and 0.582 in the unadjusted and adjusted logistic regression models, respectively (Table 2). In both cases, the performance of Deep-LIBRA PD was comparable to volumetric PD evaluation with Quantra, and substantially improved compared to LIBRA PD and clinical BI-RADS density assessments.

3.2. Evaluation on independent testing datasets

3.2.1. Breast segmentation

Using the images of ds4, Deep-LIBRA gave a mean dice score of 92.5% for breast segmentation, which was also statistically significantly lower (p<0.001) than LIBRA (mean dice 83.4%) (Supplementary Table 3 and Supplementary Figure 2).

3.2.2. Breast cancer risk assessment based on breast density

Deep-LIBRA PD and DA measures were positively associated with breast cancer regardless of the breast views considered in density calculations (Table 3 and Supplementary Tables 4–6). The ORs for Deep-LIBRA PD ranged from 1.33 to 1.40 in unadjusted models (Supplementary Table 4) and from 1.46 to 1.61 for models adjusted for age and BMI (Table 3). Similarly, the ORs for Deep-LIBRA DA ranged from 1.46 to 1.58 in unadjusted models (Supplementary Table 6) and from 1.50 to 1.64 for models adjusted for age and BMI (Supplementary Table 5). Best case-control discriminatory performance for Deep-LIBRA was achieved for PD (AUC = 0.612 [95% CI: 0.583, 0.640]) and DA (AUC = 0.642 [95% CI: 0.615, 0.669]) estimates averaged over the four breast views (i.e. left and right CC and MLO views). The performance of Deep-LIBRA was comparable to Cumulus and volumetric Volpara density measures, and significantly improved compared to area-based LIBRA and Volpara density metrics (Table 3).

Table 3:

Associations of percent density (PD) measures with breast cancer and case-control discriminatory performance on ds5, using logistic regression models adjusted for age and BMI. P-values for both AUCs and ORs were obtained from 1,000 bootstrap samples to test for the null hypothesis of no difference from the AUC or OR derived from Deep-LIBRA using the same breast views.

Density score	OR (95% CI)	p-value	AUC (95% CI)	p-value
Deep-LIBRA PD (4 views)	1.61 (1.37,1.88)	-	0.612 (0.584, 0.640)	-
Deep-LIBRA PD (CC)	1.64(1.40,1.91)	-	0.611 (0.583, 0.639)	-
Deep-LIBRA PD (MLO)	1.46(1.26,1.69)	-	0.596 (0.568, 0.624)	-
Cumulus PD (CC)	1.64(1.39,1.93)	0.99	0.619 (0.592, 0.647)	0.85
LIBRA PD (4 views)	1.26(1.09,1.46)	<.001	0.564 (0.535, 0.592)	0.01
LIBRA PD (CC)	1.19 (1.04,1.36)	<.001	0.557 (0.528, 0.585)	0.01
LIBRA PD (MLO)	1.26(1.10,1.46)	0.07	0.561 (0.533, 0.589)	0.04
Volumetric Volpara PD (4 views)	1.55 (1.31,1.82)	0.43	0.599 (0.572, 0.627)	0.37
Volumetric Volpara PD (CC)	1.45 (1.24,1.71)	0.02	0.588 (0.559, 0.616)	0.09
Volumetric Volpara PD (MLO)	1.62(1.37,1.92)	0.10	0.598 (0.570, 0.626)	0.88
Area Volpara PD (4 views)	1.48 (1.25,1.74)	0.10	0.578 (0.551, 0.607)	0.04
Area Volpara PD (CC)	1.38 (1.18,1.61)	<.001	0.567 (0.539, 0.596)	0.01
Area Volpara PD (MLO)	1.62(1.28,1.79)	0.53	0.591 (0.563, 0.619)	0.49
BI-RADS density	1.54(1.30,1.81)	0.45	0.596 (0.568, 0.624)	0.35

When Deep-LIBRA PD averaged over the four breast views was evaluated in combination with other density measures, Deep-LIBRA PD was the only PD measure that maintained significant associations with breast cancer (Supplenentary Table 8). Moreover, the AUC was only minimally modified by the addition of other density measures to Deep-LIBRA PD. Similar observations were found for Deep-LIBRA DA when evaluated in combination with absolute density measures from other density estimation approaches (Supplenentary Table 9). However, besides Deep-LIBRA DA, Cumulus DA and absolute volumetric density by Volpara also maintained significant associations with breast cancer.

Deep-LIBRA PD averaged over the four breast views was significantly lower in controls (median PD = 11.5% [IQR: 5.7, 19.9]) compared to cases (median PD = 14.1% [IQR: 7.7, 23.9]) (Table 4). Significant differences between cases and controls were also found for other breast density estimation approaches, with slightly narrower PD ranges for LIBRA and volumetric Volpara density metrics (Table 4). Deep-LIBRA PD was also strongly correlated with Cumulus PD (r = 0.90), as well as with LIBRA (r = 0.76) and Volpara (r = 0.89) PD measures and clinical BI-RADS density assessments (r = 0.80) (Supplementary Figure 3). However, moderate to strong correlations were found between Deep-LIBRA DA and Cumulus (r = 0.79), LIBRA (r = 0.44), Volpara (r = 0.52–0.71), and clinical BI-RADS density assessments (r = 0.71) (Supplementary Figure 4).

Table 4:

Breast density distributions on ds5. Except for BI-RADS density, data corresponds to median and interquartile range in parentheses. For BI-RADS density, data corresponds to number of women and percentage in parentheses. *P-values from Wilcoxon Rank-sum tests for continuous density measures and from Pearson chi-squared test for BI-RADS density.

Breast density measure	Controls (N=1178)	Cases (N=414)	*p-Value
Deep-LIBRA PD (4 views)	11.5 (5.7, 19.9)	14.1 (7.7,23.9)	<.001
Deep-LIBRA PD (CC)	12.0(6.6, 20.6)	15.7 (8.6,25.7)	<.001
Deep-LIBRA PD (MLO)	10.3 (4.4, 19.8)	13.4 (6.1,22.1)	<.001
Cumulus Proc PD (CC)	12.4 (6.6, 21.6)	15.5 (8.8,25.3)	<.001
LIBRA PD (4 views)	10.8 (7.6, 16.0)	11.2(7.6, 16.9)	0.004
LIBRA PD (CC)	10.5 (7.1, 15.6)	11.5 (7.6, 18.7)	0.006
LIBRA PD (MLO)	11.2 (7.6, 16.9)	12.3 (8.0, 19.4)	0.005
Volumetric Volpara PD (4 views)	6.0 (4.4, 10.0)	6.7 (4.6, 12.0)	<.001
Volumetric Volpara PD (CC)	6.0 (4.4, 9.9)	6.7 (4.6, 11.7)	<.001
Volumetric Volpara PD (MLO)	5.9 (4.3, 9.7)	6.8 (4.7, 12.7)	<.001
Area Volpara PD (4 views)	48 (28.9,68.3)	53.8(32.9,76.7)	<.001
BI-RADS density, n (%)			<.001
A	255 (22%)	61 (15%)
B	487 (41%)	149 (36%)
C	364 (31%)	170 (41%)
D	71 (6%)	34 (8%)

4. Discussion

This study introduced Deep-LIBRA, an open-source AI tool for fully automated breast density evaluation from raw FFDM images. Deep-LIBRA’s promising performance in breast density estimation and density-based risk assessment suggests the effectiveness of combining deep learning with conventional radiomic machine learning methodologies towards developing a useful computational tool for accurately estimating mammographic density, a critical imaging biomarker in breast cancer screening.

We acknowledge that AI could be used for direct risk prediction from FFDM images Dembrower et al. (2020); Yala et al. (2019). However, accurate estimation of breast density is of utmost importance for several reasons. First, breast density measurements have been shown to be useful in several tasks beyond predicting a womans risk for breast cancer, from evaluating the risk of decreased mammographic sensitivity due to masking of tumors by dense breast tissue Mandelson et al. (2000); Boyd et al. (2007) to assessing effects of aspirin use and bariatric surgery on breast parenchymal patterns Williams et al. (2017); Wood et al. (2017). Second, spatial dense tissue segmentation maps such as the ones provided by Deep-LIBRA can provide valuable insights about breast regions associated with tumor masking, potentially also driving breast cancer risk. Most importantly, in 2019, federal legislation mandated that women be notified of their breast density in all 50 states and US Territories as part of routine breast cancer screening letters Are-You-Dense-Advocacy (2019). Therefore, an automated tool that can accurately evaluate a womans actual breast density value can have a substantial clinical impact.

To segment the breast region, Deep-LIBRA employs two binary segmentation U-Nets, one for background and one for pectoral muscle removal instead of a single multi-class network. We found that this design could better address intensity variations in the input images as well as remove unpredictable artifacts, such as paddles and rings, that can substantially affect breast segmentation. To segment the dense tissue area within the breast, Deep-LIBRA is based on a ensemble of radiomic machine learning models. This design was motivated by the observed effect of data partitioning in the performance of machine learning models. To alleviate this effect, an ensemble model based on the majority vote of the three SVMs is used as the final model assigning dense versus non-dense labels to superpixels, based on which Deep-LIBRA provides estimates of breast density measures.

Deep-LIBRA was trained and validated on a unique multi-racial dataset of 15,661 FFDM images (4,437 women) from two different clinical sites, and then tested on an independent matched case-control dataset of 6,368 digital mammograms for both breast density estimation and case-control discrimination. Our results suggest a strong agreement of breast density estimates between Deep-LIBRA and gold-standard assessment by an expert reader, as well as improved performance in breast cancer risk assessment over state-of-the-art open-source and commercial methods. Interestingly, Deep-LIBRA DA had a stronger association with breast cancer risk than Deep-LIBRA PD, while adjusting for BMI increased the strength of associations for both density measures. While an interplay between breast density, BMI, and race has been found in previous studies McCarthy et al. (2016), our results potentially indicate the need to better understand the associations of absolute versus percent density measures with breast cancer risk, especially across different BMI levels and in diverse populations.

The limitations of our study must also be noted. At this point, Deep-LIBRA has only been trained on “FOR PROCESSING” FFDM images from a single manufacturer (Hologic). Motivated by the promising Deep-LIBRA performance reported in this study, our immediate next step will be training and reevaluating Deep-LIBRA for “FOR PRESENTATION” vendor-processed FFDM images, while utilizing multi-vendor datasets. As such, we will also be able to compare and potentially integrate Deep-LIBRA density measures with other AI methods for BI-RADS density estimation and risk assessment which have been developed for vendor-processed FFDM images Dembrower et al. (2020); Lehman et al. (2018); Yala et al. (2019). Moreover, we trained Deep-LIBRA for breast density estimation using semi-automated PD scores as a reference. In reality, actual ground-truth density estimations could be obtained only via breast excisions. To overcome this limitation, and acknowledging the inter-reader variation in semi-automated breast density scores, we used “gold standard” Cumulus PD estimates by a single reader with over twenty years of experience estimating density with Cumulus (F.F.W.). In our future work, we will explore the use of reference PD estimates from multiple readers and their effect of Deep-LIBRA training.

Moreover, we realize that evaluating Deep-LIBRA density measures in predicting breast cancer masking will be another important step to help determine its value in precision breast cancer screening. Although our study had limited power for this analysis due to the small number of interval cancers in our case-control datasets (15%), we anticipate that this study will provide instrumental evidence for Deep-LIBRA to facilitate larger, multi-site studies to validate Deep-LIBRA density measures in predicting risk of masking. With Deep-LIBRA being an open-source software, we aim to encourage a widespread utilization of Deep-LIBRA in various studies of mammographic breast density and risk towards an extensive validation of Deep-LIBRA in multi-site and multi-racial populations.

Highlights.

• Mammographic breast density is a well-established breast cancer risk factor

• Deep-LIBRA Our results on a large multi-ethnic population from two di_fferent sites demonstrate high accuracy

• It improved density-based discrimination of breast cancer over state-of-the art research and commercial methods

• Deep-LIBRA provides researchers across the world a reliable, reproducible and robust breast density measure with spatial segmentation maps for various studies

• Deep-LIBRA is an important advancement towards personalized breast cancer risk calculations in the clinical setting