Abstract
Motivation
Methods for analyzing microbiome data generally fall into one of two groups: tests of the global hypothesis of any microbiome effect, which do not provide any information on the contribution of individual operational taxonomic units (OTUs); and tests for individual OTUs, which do not typically provide a global test of microbiome effect. Without a unified approach, the findings of a global test may be hard to resolve with the findings at the individual OTU level. Further, many tests of individual OTU effects do not preserve the false discovery rate (FDR).
Results
We introduce the linear decomposition model (LDM), that provides a single analysis path that includes global tests of any effect of the microbiome, tests of the effects of individual OTUs while accounting for multiple testing by controlling the FDR, and a connection to distance-based ordination. The LDM accommodates both continuous and discrete variables (e.g. clinical outcomes, environmental factors) as well as interaction terms to be tested either singly or in combination, allows for adjustment of confounding covariates, and uses permutation-based P-values that can control for sample correlation. The LDM can also be applied to transformed data, and an ‘omnibus’ test can easily combine results from analyses conducted on different transformation scales. We also provide a new implementation of PERMANOVA based on our approach. For global testing, our simulations indicate the LDM provided correct type I error and can have comparable power to existing distance-based methods. For testing individual OTUs, our simulations indicate the LDM controlled the FDR well. In contrast, DESeq2 often had inflated FDR; MetagenomeSeq generally had the lowest sensitivity. The flexibility of the LDM for a variety of microbiome studies is illustrated by the analysis of data from two microbiome studies. We also show that our implementation of PERMANOVA can outperform existing implementations.
Availability and implementation
The R package LDM is available on GitHub at https://github.com/yijuanhu/LDM in formats appropriate for Macintosh or Windows.
Contact
yijuan.hu@emory.edu
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Data from studies of the microbiome are accumulating at a rapid rate. The relative ease of conducting a census of bacteria by sequencing the 16S rRNA gene (or, for fungi, the 18S rRNA gene) has led to many studies that examine the association between microbiome and health states or outcomes. Many microbiome studies have complex design features (e.g. paired, clustered or longitudinal data) or complexities that frequently arise in medical studies (e.g. the presence of confounding covariates). While a number of new methods for analyzing microbiome data have been recently proposed, there is still a need for methods that can account for the special features of microbiome data and the complex study designs in common use while preserving size or controlling the false discovery rate (FDR).
Statistical methods for analyzing microbiome data seem to fall into one of two camps. One camp comprises methods that test the global effect of the microbiome, such as PERMANOVA (Anderson, 2001; McArdle and Anderson, 2001), MiRKAT (Zhao et al., 2015), aMiSPU (Wu et al., 2016) and pairNM (Shi and Li, 2017), which can be used to test the hypothesis that variables of interest (e.g. case–control status) are significantly associated with overall microbial compositions. However, these methods do not provide convenient tests of the effects or contributions of individual operational taxonomic units (OTUs), should a global microbiome effect be found (here we use ‘OTU’ generically to refer to any feature such as amplicon sequence variants or any other taxonomic or functional grouping of bacterial sequences). The other camp is comprised of OTU-by-OTU tests, often directly using a method developed for RNA-Seq data such as DESeq2 (Love et al., 2014) and edgeR (Robinson et al., 2010) or a modification thereof such as MetagenomeSeq (Paulson et al., 2013); some other methods in this camp have adopted a compositional data approach [such as ANCOM (Kaul et al., 2017; Mandal et al., 2015) and ALDEx2 (Fernandes et al., 2014)] were developed for longitudinal data [such as ZIBR (Chen and Li, 2016)], or employed a multi-stage strategy [such as massMap (Hu et al., 2018)]. While some of these approaches have been widely applied, they generally do not give a single test of the global null hypothesis. Although test statistics or P-values from OTU-specific tests can of course be combined to give a global test, the performance of this kind of global test is often poor since many of the OTU-specific tests only contribute noise.
We introduce here the linear decomposition model (LDM) for analyzing microbial count or relative abundance data that are obtained in a 16S rRNA study or a shotgun metagenomics sequencing study. The LDM gives a unified approach that allows both global testing of the overall effect of the microbiome on arbitrary traits of interest, while also providing OTU-specific tests that correspond to the contribution of individual OTUs to the global test results. It allows for complex fixed-effects models such as models that include multiple variables of interest (both continuous and categorical), their interactions, as well as confounding covariates. It is permutation-based, and so can accommodate clustered data and maintain validity for small sample sizes and when data are subject to overdispersion. Because the permutations are based on the Freedman–Lane approach (Freedman and Lane, 1983), we can construct powerful type III or ‘last variable added’ tests like those used in most linear regression packages (Kleinbaum et al., 2007; Muller and Fetterman, 2012). We also provide a new version of the PERMANOVA test based on our approach that we show outperforms the functions adonis and adonis2 in the R package vegan, the most commonly used implementations of PERMANOVA. Recent simulation studies suggest that many microbiome analysis methods fail to control the FDR when applied to overdispersed data (Hawinkel et al., 2019). We show that the LDM controls FDR in exactly the kind of situations where other methods fail.
We describe the LDM in detail in Section 2. In Section 3, we describe the simulation studies and the two real datasets that we use to assess the performance of the LDM, and compare it to results obtained by PERMANOVA, MiRKAT, aMiSPU, DESeq2, edgeR, MetagenomeSeq, the Wilcoxon rank-sum test, ANCOM and ALDEx2. We conclude with Section 4. Some technical details are relegated to Supplementary Materials.
2 Materials and methods
Data from a microbiome study are usually summarized in a table of read counts, here referred to as the OTU table and denoted by Y. The OTU table is the n × J data matrix whose element is the number of times OTU j is observed in sample i. The total counts in each sample (the library size) can vary widely between samples and this variability must be accounted for. Here, we accomplish this by converting counts to frequencies (i.e. relative abundances) by dividing the raw counts in each sample by the library size of that sample, although other normalizations can be used with the LDM if desired. Our simulation studies showed that the LDM performs well when counts are scaled to frequencies, even with highly overdispersed data. Although the LDM accounts for the compositionality of the frequency data by using an appropriate permutation scheme, a compositional analysis in the sense of Aitchison (1986) can also be conducted by applying the LDM to appropriately transformed (e.g. centered log-ratio) data.
2.1 The LDM as a linear model
Many reasonable models of the relationship between data in an OTU table and covariates that describe traits or characteristics of individual samples can be expressed as a linear model. Because the large number of OTUs is a problem for models in which OTU frequencies predict traits or covariates when the goal is inference, we consider models in which traits and covariates are used as predictors of OTU frequencies. Thus, we consider the model
| (1) |
where X is an n × r design matrix containing r covariates (including traits and confounders), β is an r × J matrix that we must estimate and ϵ is an n × J matrix of error terms with . Considered as J models for the columns of Y, the j-th column of β are the regression coefficients for the j-th regression model. In order to provide a clean decomposition of the sum of squares of Y, we first make the columns of X orthonormal using the Gram–Schmidt process. This also aids in the interpretation of some hypothesis tests, particularly terms that represent interactions with main effect terms that are also being tested. A motivating example for (1) is when X contains only an intercept and an indicator for a binary trait such as case–control status; then the first row of β is proportional to the means of the OTU frequencies while the second row of β is proportional to the differences in the OTU frequencies between case and control participants.
The least-squares estimators for the matrix β can be obtained by minimizing with respect to β (holding X and Y fixed), where is the Frobenius (matrix) norm of matrix A and is the trace operator. Satten et al. (2017) showed that the resulting estimators are , which are also the estimators obtained by fitting the regression model column by column. If we write where is a diagonal matrix with elements given by the norms of the rows of , so that the columns of are normalized rows of , then we may rewrite (1) as
| (2) |
where is the residual matrix. Equation (2) is the basic form of the LDM. It is similar to the singular value decomposition (SVD) in that a matrix Y is decomposed into the product of an orthogonal matrix X, a diagonal matrix D with positive elements and a third matrix V, but differs from the SVD because X may be chosen in any convenient way as long as it has orthonormal columns, and because the columns of V are not orthogonal.
In some situations, we may wish to partition covariates into K groups, which we call ‘submodels’. For example, we may wish to group several measures of smoking history into a single smoking ‘submodel’. In this case, we partition X as (), and rewrite (1) and (2) as
| (3) |
where the least-squares estimators of βk are given by for each k. We will refer to the number of linearly independent columns in Xk as the number of components in the submodel.
The LDM (3) can be used to describe the amount of the total sum of squares that is explained by each submodel Xk or the full model X by noting that where for . In analogy with Satten et al. (2017) we can express Sk in one of two ways:
| (4) |
or
| (5) |
where is the j-th column of and is the Euclidean norm of vector b. The first representation indicates that, as with a standard SVD, the sum of squares for the k-th submodel is given by the sum of squares of the corresponding singular values (diagonal elements of ). The second representation partitions Sk into contributions from each OTU. Note these results only require X has orthonormal columns, not .
2.2 Testing hypotheses using the LDM
The LDM uses the decomposition of the sum of squares in (4) and (5) to test global and OTU-specific null hypotheses about the effect of individual covariates or sets of covariates grouped into submodels. To test hypotheses about the contribution of the j-th OTU to the sum of squares for the k-th submodel, we use its contribution to the model sum of squares given in (5), normalized as an F-statistic, to give the test statistic
| (6) |
where is the j-th column of Y and we have dropped the constant of proportionality found in a typical F test as we intend to use permutation to assess significance.
To test the global hypothesis, we consider the total sum of squares for the k-th submodel given in (4), again normalized as a F-statistic. This statistic can either be constructed directly, or by summing the numerator and denominator of the OTU-specific statistics (5) separately, i.e.
| (7) |
The presence of all submodels in the denominator indicates that this is a type III or ‘last variable added’ test statistic. As before, the usual constant of proportionality in a F-statistic is dropped because significance will be assessed using permutation. Note that OTU-specific and global tests are linked through (6) and (7) in a natural way. If Y is centered, the sums-of-squares in (4) and (5) are proportional to the variance explained (VE) by a submodel or an individual OTU in a submodel; for this reason, we sometimes refer to the F-tests in the LDM as tests of the VE.
2.3 The LDM as a decomposition
The LDM in Equation (3) can also lead to an exact decomposition of the OTU table Y, if we augment X with extra columns Xr so that the full set of columns span the column space of Y. The ‘extra’ columns Xr are used to decompose the residual matrix r. If we further write , where is a diagonal matrix with entries given by the norms of the rows of , so that the columns of are normalized, then we can rewrite (3) as
| (8) |
where and . Thus, the LDM, like the SVD, can give a full-rank decomposition of Y.
We can establish a connection between the LDM and distance-based methods such as PERMANOVA by choosing Xr to be the eigenvectors of a (residual) distance matrix that have non-zero eigenvalues, where is the hat matrix of X. Note these eigenvectors are always orthogonal to the columns of X. This choice allows direct comparison of the variability explained by covariates to the variability explained by the principal components of a (residual) distance matrix, in analogy with PERMANOVA. A scree plot based on values of in (8) can visually indicate whether that values of are ‘large’ relative to the residual error. To help ensure that the rank of and Δ agree, if Y has been column-centered, then we also center Δ as recommended by Gower (1966). Then, the columns of both and Y are orthogonal to the vector 1. Some caution is necessary for submodels having more than one component; although Sk in (4) is invariant to the choice of basis for Xk, the individual diagonal elements of depend on the choice of basis. Thus, we recommend these elements be replaced by . Note that the individual diagonal elements of are uniquely defined, as the columns of Xr are the eigenvectors of Δr. The scree plot obtained in this way is a quick and easy way to see which submodels explain a reasonable fraction of the variability we would expect to see in an ordination using distance Δ. Additionally, the residual distance matrix Δr can also be used for ordination if we wish visualize the observations after removing the (linear) effects of covariates from a distance matrix Δ.
A further connection to PERMANOVA can be made by noting that, as long as Δ is not rank-deficient (i.e. as long as Xk is in the range of Δ), the column vectors Xk span the range of for any Δ. In fact, when constructing X, the columns Xk could be replaced by the eigenvectors of Δk having non-zero eigenvalues (denoted, say, by ); note this would not change the sums-of-squares test statistics since Xk and are each orthonormal and span the same space, and are hence related by an orthogonal transformation. In either case, has columns that span the model matrices (the Δks) and the residual (Δr) matrix of a PERMANOVA analysis. Of course, if Xk is comprised of a single column, then Xk automatically corresponds to the single eigenvector of Δk having non-zero eigenvalue.
Even if we choose for the columns of , note that the diagonal elements of in the LDM are not eigenvalues of the distance matrix Δ, but rather represent the amount of variability in the OTU table Y that is explained by the (Euclidean) projection of the columns of Y on Xk. Thus, the diagonal elements of only correspond to the eigenvalues in a PERMANOVA analysis if the distance matrix Δ is the Euclidean distance. In some cases, it is possible to convert a distance matrix Δ into the Euclidean distance matrix by data transformation; in these cases, the LDM can also be considered distance-based. However, choosing when constructing does have an advantage when constructing the scree plot, as it gives an unambiguous meaning to the individual diagonal elements of for submodels with more than one component.
2.4 Assessing significance by permutation
We assess the significance of our test statistics, Fkj and , using a variant of a permutation scheme described by Freedman and Lane (1983). The original Freedman–Lane procedure permutes residuals. To preserve the correlation structure among OTUs, we use the same permutation scheme for each OTU (i.e. permuting the residual matrix by row). We show in Supplementary Text S1 that this is equivalent to a permutation procedure in which the residuals are held fixed but the covariates (i.e. the rows of X) are permuted.
To describe our permutation approach, define Yk, the residual matrix obtained after fitting a reduced model to Y that excludes the k-th submodel term Xk, to be and note that, because of the orthogonality of the columns of X, we can write as . As a result, Fkj in (6) can be rewritten as
| (9) |
where is the j-th column of Yk. The analogous result for the global test statistic is obtained by summing numerator and denominator over j. In Supplementary Text S1, we show that if is a permutation matrix corresponding to π, a permutation of the integers , then the Freedman–Lane procedure is equivalent to forming the test statistics
| (10) |
where is a row-permuted version of Xk. The test statistic for the global test is obtained by (separately) summing the numerator and denominator of (10) over OTUs and can be written as
| (11) |
Although Freedman and Lane (1983) only considered residuals from independent observations, some simple but important cases involving correlated data from clustered samples can be tested using the Freedman–Lane approach. Considering permutation of covariates rather than residuals, the main requirement for a valid permutation replicate dataset is that the dataset preserve the correlation found in the original data. Thus, variables that vary within clusters (sometimes called ‘plots’ in the Ecology literature) can be permuted within each cluster; here, we only consider the case of clustered data in which residuals within each cluster can be considered as exchangeable. For example, if each cluster consists of a ‘before treatment’ observation and an ‘after treatment’ observation from the same individual, the effect of treatment can be tested by randomly permuting the ‘before’ and ‘after’ assignment within each cluster (individual). Note that, in this situation, the cluster sizes need not be balanced (i.e. have equal size). If all variables in an analysis are constant for all cluster members (i.e. are assigned at or ‘above’ the cluster level), only permutation replicates that assign the same value to each cluster member are allowed; here, exchangeability is not required. For example, in a rodent study of the effect of diet on the gut microbiome, rodents housed in the same cage should be treated as a cluster, as rodents are coprophagic. Thus, when permuting diet, rodents in the same cage should always be assigned the same diet. Note that for datasets with variables assigned at or above the cluster level, the cluster sizes must all be equal or the data must be stratified by cluster size with all permutations taking place within strata. Our implementation of the LDM uses the same permutation options available in the R package vegan, through the R package permute.
Our software implementation of the LDM uses sequential stopping rules to increase computational efficiency. When only the global test is of interest, we adopt the sequential stopping rule of Besag and Clifford (1991) for calculating the P-value of the global test. This algorithm terminates when either a pre-determined number of rejections (i.e. the permutation statistic exceeded the observed statistic) has been reached or a pre-determined maximum number of permutations has been generated. When the OTU-specific results are desired, we use the algorithm proposed by Sandve et al. (2011), which adds an FDR-based sequential stopping criterion to the Besag et al. algorithm. Note that the Sandve et al. algorithm limits the total number of needed permutations to , which is 200 times the number of OTUs J when the nominal FDR and . When testing multiple hypotheses (e.g. both the global and OTU-specific hypotheses, or hypotheses corresponding to multiple submodels), we generate permutations until all hypotheses reach their stopping point.
2.5 A Freedman–Lane PERMANOVA test (PERMANOVA-FL)
The operations that lead to the F-statistics for the LDM can also be used to develop an improved PERMANOVA test statistic. We first consider a Euclidean distance Δ. Following McArdle and Anderson (2001), we note that any Euclidean distance Δ can be written as for some matrix Z; we then write a linear model of the form (3) in which Z replaces Y. Here, the only tests of interest are the global tests; the analogs of the OTU-specific tests are tests of the effect of covariates on the j-th component (column) of Z and are only used as intermediate steps. After replacing Y with Z in (7) and using the invariance of the trace to cyclic permutations, the statistic can be rewritten as
| (12) |
which is the usual form of the PERMANOVA F-statistic; note that Δ here can be generalized to any (non-Euclidean) distance Δ. The same argument leading to (9) yields
where
Thus, for a replicate dataset having covariates , the Freedman–Lane PERMANOVA test statistic can be obtained by replacing Y by Z in (11):
| (13) |
We refer to this test as PERMANOVA-FL. The same kinds of restricted permutations as in our implementation of the LDM are available in PERMANOVA-FL.
The permutation scheme implemented in adonis is similar to (13) except that the s are all replaced by Δ. We further note that our proposed permutation replicates in (13) have the same advantages as the PERMANOVA replications implemented in adonis, in that they only require functions of the distance matrix Δ (which, in our approach, are the projected distance matrices ). As a result, our approach, like other implementations of PERMANOVA, can be computed even if the distance matrix is non-Euclidean. Further, the distance matrices do not need to be recalculated for each replicate.
2.6 The arcsin-root transformation
The LDM can also be applied to transformed data. Because we consider frequency data, we show we achieve good results using the arcsin-root transformation, which is variance-stabilizing for Multinomial and Dirichlet-Multinomial (DM) counts. Thus, we write where Yij are the raw counts and Ni are the library sizes. We can additionally center the data matrix Θ={Θij}, replacing it by if we also plan to center Δ. We can now replace Y by Θ in (1) or (3) and proceed as before. This approach is related to an approach of Berkson (1944) for fitting logistic models to bioassay data. We also had considered a logit-based model using Haldane’s (Haldane, 1956) unbiased logit by forming but found that the arcsin-root transform performed better in all cases we examined. We expect the LDM applied to (untransformed) frequency data will work best when the associated OTUs are abundant, while we expect the LDM applied to arcsin-root-transformed frequencies to work best when the associated OTUs are less abundant. Since we do not know the association mechanism a priori, we also consider an omnibus strategy that simultaneously applies LDM on both data scales. For the omnibus tests, we use the minimum of the P-value obtained from the frequency and arcsin-root-transformed data as the final test statistic and use the corresponding minima from the permuted data to simulate the null distribution (Westfall and Young, 1993). As demonstrated by our simulation studies, the omnibus test achieves the best overall performance compared to the LDM applied to either data scale and is recommended for use in real data analysis.
3 Results
3.1 Simulation studies
We conducted several simulation studies to evaluate the performance of the LDM and compare it to competing methods. To evaluate the global test, we compared our results to those obtained using our own implementation of PERMANOVA and the PERMANOVA implemented in adonis2. We also calculated OTU-specific tests using the LDM, which we compared to results from DESeq2. We only performed limited comparisons to aMiSPU, edgeR, MetagenomeSeq, Wilcoxon rank-sum test (applied to OTU frequencies), ANCOM and ALDEx2, because aMiSPU does not allow for clustered data, edgeR generally has highly inflated FDR (Hawinkel et al., 2019), and the others do not allow for confounding covariates.
To generate our simulation data, we used the same motivating dataset as Zhao et al. (2015), specifically data on the upper-respiratory-tract (URT) microbiome first described by Charlson et al. (2010). To simulate read count data for the 856 OTUs reported in this study, we adopted a DM model using the empirical frequencies calculated from the study data; we set the overdispersion parameter to the estimate 0.02 obtained from these data, which is also the median value we observed in an admittedly brief survey of the literature (Chen and Li, 2013; La Rosa et al., 2012; Morgan et al., 2015). While the original microbiome dataset was generated from 454 pyrosequencing with mean library size ∼1500, we increased the mean library size to 10 000 to reflect Illumina MiSeq sequencing which is currently in common usage. For each simulation, we generated data for 100 samples unless otherwise noted. We also conducted sensitivity analysis with a wide range of library sizes, overdispersion parameters and sample sizes, and by replacing the DM model with a Poisson log-normal model (PLNM) or negative-binomial (NB) model to generate the read count data (the PLNM and NB model are described in Supplementary Text S2 and S3, respectively).
We focused on two complementary scenarios. The first scenario (S1) assumed that a large number of moderately abundant and rare OTUs were differentially abundant between cases and controls, and the second scenario (S2) assumed the top 10 most abundant OTUs were differentially abundant. Both scenarios have a one-way, case–control design with a confounder and independent samples. Later we varied these scenarios to simulate a continuous trait, a two-way design, or clustered data.
In both scenarios S1 and S2, we let U denote case–control status and assumed an equal number of cases (U = 1) and controls (U = 0). We simulated a confounder, , where ϵ was drawn from a uniform distribution on . In S1, we uniformly and independently sampled two (overlapping) sets of 428 OTUs (half of all OTUs), the first set associated with U and the second set associated with C; the set for U was sampled after excluding the top three most abundant OTUs to focus on less abundant OTUs. In S2, we assumed the 10 most abundant OTUs were associated with U and the next 40 most abundant OTUs were associated with C. These OTU sets were held fixed across replicates of data. We denoted the OTU frequencies estimated from the real data by the vector π1 and formed vectors π2 and π3 by first setting π2 and π3 equal to π1 and then randomly permuting those frequencies in π2 and π3 that belong to the selected set of OTUs associated with U and C, respectively. Note that the frequencies for OTUs not selected to be associated with U (or C) remain the same in π1 and π2 (or π3). We then defined a sample-specific frequency vector as , where . In this model, β and βC are the effect sizes of U and C on the overall community compositions, respectively; here we set βC to 0.3 except for simulations with no confounding, for which we set βC to zero. At the OTU level, the strengths and directions of the effects of U (or C) are heterogeneous because the resulting frequencies at each OTU are characterized not just by β (or βC), but also by the differences between π1 and π2 (or π1 and π3), which vary in magnitude and sign at different OTUs. We then generated the OTU count data for each sample using the DM model with , overdispersion parameter of 0.02, and library size sampled from and left-truncated at 500. By mixing π1, π2 and π3 in a way that depends on the values of U and C, we induced associations between the selected OTUs and U and C. Note that π1 serves as the ‘reference’ OTU frequencies that characterizes samples for which U and C are both zero. In addition, the correlations among U, C and OTU frequencies establish C as a confounder of the association between U and the OTUs. Finally, note that when β = 0, does not depend on U, so that the null hypothesis of no association between U and OTU frequencies holds. The simulations of clustered data, data with a two-way design and data with a quantitative trait are described in Supplementary Text S4.
We evaluated type I error and power for testing the global hypothesis at nominal significance level 0.05, and we assessed empirical sensitivity (proportion of truly associated OTUs that are detected) and empirical FDR for testing individual OTUs at nominal FDR 10%. Results for type I error were based on 10 000 replicates; all other results are based on 1000. In all simulations with confounders, we treated C and U as separate submodels, when fitting the LDM. For the two-way simulations, U1 and U2 were considered as separate submodels.
3.1.1 Results for testing global hypotheses with independent samples in the one-way case–control design
For testing the global hypothesis of no association between microbiome composition and U, we applied the LDM on the frequency and arcsin-root scales and also calculated the omnibus test; these results are presented as VE-freq, VE-arcsin and VE-omni, respectively, where VE denotes variance explained. We also applied our own implementation of PERMANOVA as well as the adonis2 implementation; we refer to them as PERMANOVA-FL and adonis2, respectively.
Table 1 (top panel) shows our results for type I error. All methods, after adjusting for confounders, had correct type I error; with the small sample size 20, the type I error rates of PERMANOVA-FL and LDM methods were slightly conservative, which is consistent with the findings of Anderson and Legendre (1999). There was substantial inflation of type I error for S1 and modest inflation for S2 when the confounder was not accounted for, demonstrating that our methods are effective in accounting for confounders, with either modest or substantial confounding. The type I error rates were also close to 0.05 when the PLNM was adopted for count data simulation (Supplementary Table S1).
Table 1.
Type I error for testing the global hypothesis at level 0.05
| Scenario | n | P-FL | adonis2 | VE-freq | VE-arcsin | VE-omni | |
|---|---|---|---|---|---|---|---|
| Independent samples, one-way case–control design | |||||||
| Adjusting for confounder | S1 | 20 | 0.040 | 0.052 | 0.045 | 0.031 | 0.038 |
| 100 | 0.053 | 0.052 | 0.050 | 0.054 | 0.053 | ||
| S2 | 20 | 0.039 | 0.054 | 0.043 | 0.026 | 0.034 | |
| 100 | 0.050 | 0.050 | 0.052 | 0.047 | 0.053 | ||
| Not adjusting for confounder | S1 | 20 | 0.299 | 0.296 | 0.215 | 0.408 | 0.362 |
| 100 | 0.987 | 0.987 | 0.913 | 0.998 | 0.997 | ||
| S2 | 20 | 0.065 | 0.064 | 0.056 | 0.076 | 0.067 | |
| 100 | 0.151 | 0.151 | 0.083 | 0.245 | 0.194 | ||
| Independent samples, two-way design | |||||||
| Testing for U1 | S1 | 100 | 0.046 | 0.013 | 0.048 | 0.048 | 0.050 |
| S2 | 100 | 0.049 | 0.048 | 0.051 | 0.051 | 0.050 | |
| Testing for U2 | S1 | 100 | 0.049 | 0.036 | 0.049 | 0.046 | 0.049 |
| S2 | 100 | 0.053 | 0.048 | 0.053 | 0.054 | 0.054 | |
| Clustered samples, one-way case–control design | |||||||
| Accounting for clustering | S1 | 100 | 0.050 | 0.050 | 0.048 | 0.051 | 0.053 |
| S2 | 100 | 0.044 | 0.047 | 0.047 | 0.044 | 0.045 | |
| Not accounting for clustering | S1 | 100 | 1 | 1 | 1 | 1 | 1 |
| S2 | 100 | 1 | 1 | 0.999 | 1 | 1 | |
| Independent samples, continuous trait | |||||||
| Adjusting for confounder | 100 | 0.049 | 0.051 | 0.055 | 0.049 | 0.051 | |
| Not adjusting for confounder | 100 | 0.095 | 0.095 | 0.090 | 0.093 | 0.091 | |
Note: P-FL, PERMANOVA-FL. Results for PERMANOVA-FL and adonis2 are based on the Bray–Curtis distance. n is the number of samples. When testing U1, we set ; when testing U2, we set . All analyses of clustered data adjust for the confounder.
Figure 1 (top panel) displays our results for power. We can see that VE-arcsin is more powerful than VE-freq under S1 and vice versa under S2; this is presumably because the variance stabilization of the arcsin-root transformation gives greater power to detect association with the rare OTUs that carry association in S1, while the untransformed data give increased power to detect the common-OTU associations that characterize S2. In both cases, VE-omni achieved almost the same power as the most powerful test, without having to know whether common or rare OTUs were most important. PERMANOVA-FL has varying power depending on the choice of distance measure: the power is lowest with the weighted-UniFrac distance, since the association was induced without reference to any phylogenetic tree, and the power is highest with the Hellinger distance in S1 and Bray–Curtis in S2. In both S1 and S2, our best-performing method has comparable power as the best-performing PERMANOVA-FL. aMiSPU has a comparable power to VE-omni under S1 but has the least power under S2. Our sensitivity analysis showed that the relative performance of these methods persists for a wide range of library sizes, overdispersion parameters and sample sizes (Supplementary Fig. S1), as well as with the PLNM (Supplementary Fig. S2). For this set of studies, PERMANOVA-FL and adonis2 yielded very similar power.
Fig. 1.
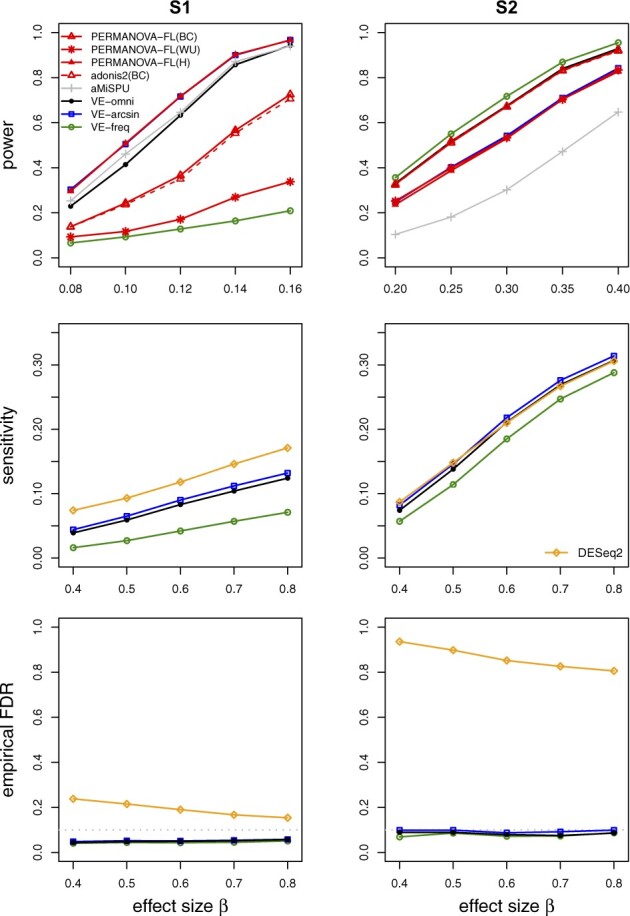
Simulation results for one-way, case–control studies with independent samples. The gray dotted lines represent FDR = 0.1. BC, Bray–Curtis; WU, weighted-UniFrac; H, Hellinger
3.1.2 Results for testing individual OTUs with independent samples in the one-way case–control design
Because PERMANOVA-FL and adonis2 does not provide OTU-specific results, we compared our results on testing individual OTUs to DESeq2. When applying DESeq2, we replaced the default normalization by GMPR normalization (Chen et al., 2018), which was specifically developed for zero-inflated microbiome data.
Figure 1 middle and bottom panels display results on empirical sensitivity and empirical FDR, respectively. The LDM-based methods controlled FDR at 10% in all cases; their empirical FDRs are conservative (and the sensitivity values are low) in S1 because this scenario permuted frequencies among 428 OTUs selected for U, majority of which are rare, and thus generated many weakly associated OTUs that are essentially null OTUs. The sensitivity of VE-omni tracks the method between VE-freq and VE-arcsin that performs better. Note that VE-arcsin has a higher sensitivity than VE-freq in both S1 and S2, but the order can be reversed in the scenario with a continuous trait (Supplementary Fig. S6). In contrast, the empirical FDRs for DESeq2 are modestly inflated under S1 and highly inflated under S2. Even when the read count data were simulated from the NB model (for which DESeq2 was designed), the empirical FDRs of DESeq2 are still inflated (Supplementary Fig. S3), likely due to the large number of zero counts.
Because MetagenomeSeq, the Wilcoxon rank-sum test, ANCOM, and ALDEx2 do not allow for adjustment of confounding covariates, we have not included results from these methods in Figure 1. To compare with these methods, we set for both scenarios S1 and S2 to remove confounders and displayed the results in Supplementary Figure S4. MetagenomeSeq always controlled FDR but was extremely conservative (FDR < 2% for nominal FDR of 10% and sample size 100) in detecting associated OTUs for the simulations we conducted. The Wilcoxon test controlled FDR and achieved good sensitivity when the DM model was used for generating the read count data; when the PLNM was used (with no confounders), the data appeared less overdispersed and Wilcoxon had consistently lower sensitivity than VE-omni (Supplementary Fig. S2). ANCOM cannot control FDR under S2. While ALDEx2 controlled FDR under S1 and S2, its sensitivity is consistently lower than the LDM-based methods. We have also included edgeR in this study, whose highly inflated FDR corroborated the finding in Hawinkel et al. (2019). Finally, DESeq2 failed to control FDR even in the absence of any confounders.
3.1.3 Results for the two-way design
We set and to ascertain the type I error of the test of U1, and and to ascertain the type I error of the test of U2, which results were summarized in Table 1. Both the LDM and PERMANOVA-FL yielded correct type I error for testing each factor, whereas adonis2 had conservative type I error in scenario S1. The type I error using adonis2 was about a factor of 3 smaller for testing U1 than for testing U2 because the sampled OTUs for association with U2 (or C) included the top two most abundant OTUs and, as a result, U2 had a stronger global effect on the OTUs than U1. Consistent with the conservative type I error, adonis2 had lower power than PERMANOVA-FL (Fig. 2). LDM (VE-omni) continued to maintain good power relative to PERMANOVA-FL for either factor (Fig. 2). Further, LDM controlled FDR for OTUs that was detected to be associated with either factor (Fig. 2).
Fig. 2.
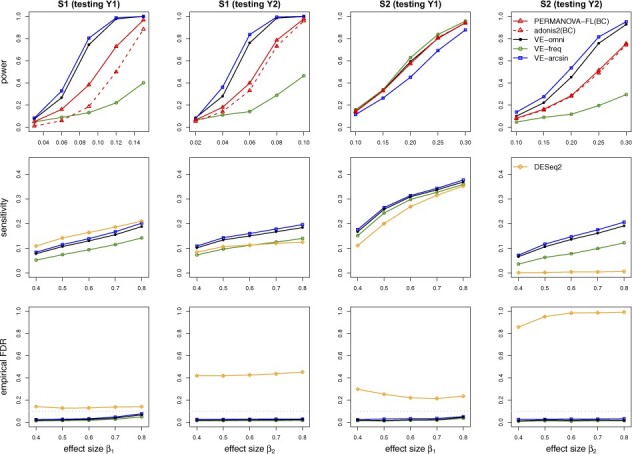
Simulation results for studies with the two-way design and independent samples. BC, Bray–Curtis. When testing U1, we set ; when testing U2, we set
3.1.4 Results for clustered data
In Table 1, we can see that permuting the case–control status over clusters rather than observations yields the correct type I error for all methods. We also calculated the type I error we would have obtained if we had incorrectly ignored the clustering structure when performing the permutations. Note that failure to account for the clustering structure result in a type I error of 100%. In Supplementary Figure S5, we see the LDM controlled FDR for these data, although the power and sensitivity are lower than was observed with the same number of samples which were unclustered (Fig. 1). This is reasonable, as data with within-individual correlation is typically not as informative as data from an equivalent number of independent samples.
3.1.5 Results for continuous trait
From Table 1, we again see that all methods (adjusting for the confounder) have the correct type I error for data with a continuous trait; there was inflation of type I error when the confounder was not accounted for. In Supplementary Figure S6, we see that the power of most methods is about the same. Although the sensitivity remains low as the effect size β increases, this appears to be related to the sample size, as we also show that the sensitivity increases rapidly as the sample size increases (at fixed β = 3). The LDM continues to control FDR as the sample size and sensitivity increase, while the empirical FDR for DESeq2 is never <40% for the range of sample sizes we considered.
3.2 Analysis of two microbiome datasets
To show the performance of the LDM in real microbiome data, we reanalyzed two datasets that were previously analyzed using MiRKAT and MMiRKAT (Zhan et al., 2017) (a variant of MiRKAT for testing association between multiple continuous covariates and microbiome composition). The first is from a study of the association between the URT microbiome and smoking, and the second is from a study of the association between the prepouch-ileum (PPI) microbiome and host gene expression in patients with inflammatory bowel disease (IBD). We compared the performance of our global test (VE-omni) with PERMANOVA-FL, MiRKAT and MMiRKAT; we also compared our OTU-specific results with results from DESeq2.
3.2.1 URT microbiome and smoking association study
The data for our first example were generated as part of a study to examine the effect of cigarette smoking on the orpharyngeal and nospharyngeal microbiome (Charlson et al., 2010). The 16S sequence data are summarized in an OTU table consisting of data from 60 samples and 856 OTUs with mean library size 1500; metadata on smoking status (28 smokers and 32 non-smokers) and two additional covariates (gender and antibiotic use within the last 3 months) was also available. An imbalance in the proportion of male subjects by smoking status (75% in smokers, 56% in non-smokers) indicates potential for confounding. Zhao et al. (2015) analyzed these data using MiRKAT, finding a significant global association between microbiome composition and smoking status after adjusting for gender and antibiotic use. We used the Bray–Curtis distance for our analysis because it led to the smallest P-values compared to other distances in Zhao et al. (2015). We combined gender and antibiotic use into a single submodel and treated smoking status as another submodel when fitting the LDM.
We first constructed the ordination plots in Figure 3 using the Bray–Curtis distance after removing the effects of gender and antibiotic use (i.e. using as the distance matrix); these plots demonstrate a clear shift in smokers compared with non-smokers even after removing the effect of potential confounders. The accompanying scree plots (Fig. 3) on both frequency and arcsin-root scales further suggest that smoking explains an important faction of the variability in the OTU table. The residual (non-model) components are plotted in decreasing order of the size of the eigenvalue of the component in the spectral decomposition of (after removing the effect of confounders and smoking); the high correlation between the order of values Dk from the LDM and the order of eigenvalues of is noteworthy. We filtered out OTUs with presence in <5 samples, retaining 233 OTUs for analysis. The results of the LDM global tests, along with results from PERMANOVA-FL and MiRKAT, are presented in top-left panel of Table 2. VE-omni gave a smaller P-value than MiRKAT or PERMANOVA-FL based on the Bray–Curtis distance. In the top-right panel of Table 2, we show the results of our OTU-specific tests. VE-omni detected 5 OTUs (which include the 4 OTUs detected by VE-freq and constitute 5 of the 14 OTUs detected by VE-arcsin) whereas DESeq2 detected none. The inefficiency of DESeq2 is consistent with our simulation studies when the mean library size was 1500 (results not shown).
Fig. 3.
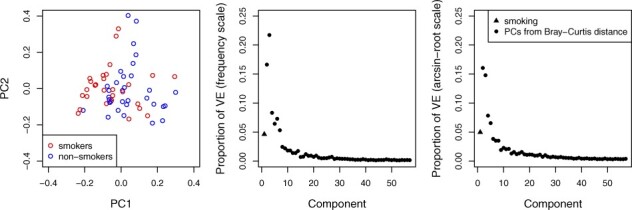
Exploratory analysis of the URT microbiome data based on the Bray–Curtis distance. Left plot: ordination plot after removing the effects of confounders gender and antibiotic use, colored by smoking status. Center and right plots: proportions of VE by smoking and the PCs of the (residual) distance measure after removing the effects of gender and antibiotic use. The center plot is based on frequency data and the right plot is based on arcsin-root-transformed data. The PCs are ordered by the magnitude of their corresponding eigenvalue in a spectral decomposition of (the distance matrix after removing the effect of the confounders and smoking)
Table 2.
Results in analysis of the two real datasets
| Testing the global hypothesis |
Testing individual OTUs |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trait | MiRKAT | P-FL | VE-freq | VE-arcsin | VE-omni | VE-freq | VE-arcsin | VE-omni | DESeq2 |
| URT microbiome data | |||||||||
| Smoking | 0.0019 | 0.0018 | 0.0070 | 0.0006 | 0.001 | 4 | 14 | 5 | 0 |
| PPI microbiome data | |||||||||
| gPC1 | 0.22 | 0.19 | 0.13 | 0.47 | 0.19 | 0 | 0 | 0 | 14 |
| gPC2 | 0.36 | 0.19 | 0.19 | 0.19 | 0.26 | 0 | 0 | 0 | 49 |
| gPC3 | 0.24 | 0.31 | 0.30 | 0.21 | 0.29 | 0 | 0 | 0 | 29 |
| gPC4 | 0.16 | 0.088 | 0.013 | 0.080 | 0.021 | 0 | 1 | 0 | 13 |
| gPC5 | 0.0094 | 0.015 | 0.034 | 0.010 | 0.015 | 0 | 3 | 3 | 48 |
| gPC6 | 0.19 | 0.41 | 0.43 | 0.49 | 0.53 | 0 | 1 | 1 | 23 |
| gPC7 | 0.15 | 0.21 | 0.76 | 0.16 | 0.22 | 0 | 0 | 0 | 59 |
| gPC8 | 0.21 | 0.33 | 0.64 | 0.36 | 0.47 | 1 | 0 | 0 | 4 |
| gPC9 | 0.15 | 0.12 | 0.10 | 0.12 | 0.15 | 0 | 0 | 0 | 20 |
Note: P-FL, PERMANOVA-FL. For the global hypotheses, reported results are P-values. For the individual OTU tests, results reported are the number of OTUs detected at FDR = 10%. MiRKAT and PERMANOVA-FL results are based on the Bray–Curtis distance. In analysis of the URT microbiome data, MiRKAT and PERMANOVA-FL yielded P-values 0.005 and 0.0042, respectively, when the weighted-Unifrac distance was used, and 0.00078 and 0.0006 when the Hellinger distance was used.
3.2.2 PPI microbiome and host gene expression association study
The data for our second example were generated in a study of the association between the mucosal microbiome in the PPI and host gene expression among patients with IBD (Morgan et al., 2015). The PPI microbiome data are summarized in an OTU table with data from 196 IBD patients and 7000 OTUs; gene expression data at 33 297 host transcripts, as well as clinical metadata such as antibiotic use (yes/no), inflammation score (0–13) and disease type (familial adenomatous polyposis/FAP and non-FAP) were also available. The data also included nine gene principal components (gPCs) that together explain 50% of the total variance in host gene expression. Zhan et al. (2017) gave a joint test of all nine gPCs for association with microbiome composition, using MMiRKAT based on the Bray–Curtis distance measure and adjusting for antibiotic use, inflammation score and disease type (FAP/non-FAP). Here, we performed the same joint test using the LDM by putting the confounders in one submodel and then including all nine gPCs in another submodel; however, we followed Morgan et al. (2015) in only analyzing the original 196 PPI samples, not an additional 59 pouch samples from some of the same individuals included in the analysis of Zhan et al. (2017). We filtered out OTUs found in fewer than 5% of samples, retaining 2096 OTUs for analysis. VE-freq, VE-arcsin and VE-omni yielded P-values 0.023, 0.0084 and 0.015, respectively, and detected 0, 4 and 3 OTUs (the 3 OTUs detected by VE-omni are included in the 4 OTUs detected by VE-arcsin) that significantly accounted for the global association at a nominal FDR rate of 10%. PERMANOVA-FL had P-value 0.0076 and MMiRKAT 0.0049, both based on the Bray–Curtis distance.
We also followed Zhan et al. (2017) to conduct individual tests of each of the nine gPCs. We treated each gPCs as a separate submodel in a single LDM, with the first submodel accounting for the same confounders as in the joint test. Note that the gPCs are orthogonal. Scree plots for frequency and arcsin-root-transformed data are shown in Supplementary Figure S7, and indicate that gPC4 and gPC5 are most likely to be associated with microbial composition although any association is likely to be marginal. In fact, Table 2 confirms that gPC4 and gPC5 showed significant associations (at the 0.05 significance level) with the overall microbiome composition by the global tests; no other gPCs were found to be associated. Both VE-omni and VE-arcsin detected (the same) 3 associated OTUs for gPC5, while VE-arcsin additionally found one OTU associated with gPC4. Both VE-omni and VE-arcsin also detected (the same) 1 OTU for gPC6, which was not significantly associated with the microbiome in a global test by any method. In contrast to the results obtained by the LDM, DESeq2 detected between 4 and 59 OTUs for each of the nine gPCs, which seems implausible given the results of the global tests. These findings may be related to the failure of DESeq2 to control FDR in the presence of confounders in our simulation studies.
4 Discussion
We have presented the LDM, a linear model for testing association hypotheses for microbiome data that can account for the complex designs found in microbiome studies. We have shown that the LDM has good power for global tests of association between variables of interest and the microbiome when compared to existing methods such as PERMANOVA and MiRKAT (the simulation results of MiRKAT were similar to those of PERMANOVA and thus not shown), but also provides OTU-specific tests. This is true even when confounding covariates are present, or when the study design results in correlated data. We have additionally shown that the OTUs identified by the LDM preserve FDR, while those identified by RNA-Seq-based approaches such as DESeq2 typically do not; further, since global and OTU-specific tests are unified, our analysis of the PPI microbiome data show that the LDM is less likely to identify ‘significant’ OTUs for variables that are not globally significant. In the analyses we show here, there was only one instance where the LDM discovered OTUs that were significantly associated with a variable but the LDM global test for that variable was non-significant (gPC6 in the PPI data); in our simulations there were no such cases, although that may be because we only evaluated sensitivity for effect sizes that were large enough that the global test was always positive. While some analysts may choose to only calculate OTU-specific tests in the presence of a significant global test, this restriction is not required to control FDR at the OTU level. We have evaluated our approach using simulated data with realistic amounts of overdispersion, confounding covariates and clustered data, and have shown how it can be applied to two real datasets.
We have implemented our approach in the R package LDM, which is scalable to large sample sizes. Using a single thread of a MacBook Pro laptop (2.9 GHz Intel Core i7, 16 GB memory) and the default value , it took 8, 19, 833 s to perform integrated global and OTU tests with a simulated dataset that consists of 20, 100 and 1000 samples. In our applications to real data, we used to ensure stability of results which are based on Monte Carlo sampling. It took 23 s (and stopped after 29 400 permutations) to perform global and OTU tests with the URT data, and 5 h (and stopped after 1 273 000 permutations) to perform global and OTU tests of nine gPCs separately with the PPI data. Because the LDM has dual goals of testing both the global and OTU-specific hypotheses, and because it is based on permutation, it generally takes more run time than tests that only test the global hypotheses, such as PERMANOVA, or OTU-specific tests that are based on analytical P-values, such as DESeq2. However, because our R package LDM uses a sequential stopping rule, the computational time is still manageable. In particular, LDM is much faster than ANCOM and comparable to ALDEx2.
The LDM has features in common with redundancy analysis (RA), a multivariate technique to describe how much variability in one matrix (say, an OTU table Y) can be described by variables in a second matrix (say, a design matrix X); see more details in Supplementary Text S5. The LDM differs from RA most importantly in its ability to simultaneously obtain results for several submodels. To fit more than one submodel using RA, it is necessary to fit RA to each submodel, using data for which the previous submodels have been projected off. This precludes use of type III (last variable added) tests, which are known to be the most powerful (Muller and Fetterman, 2012). Our use of the Freedman–Lane approach also gives superior performance; in simulations, our PERMANOVA-FL had higher power than the adonis and adonis2 functions in the R package vegan, even though adonis2 is based on some form of permutation of residuals (according to adonis2 output).
Although the LDM is primarily based on the Euclidean distance in its focus on sums-of-squares, variability explained and F-like tests, we have shown how information on an arbitrary distance can be incorporated in exploratory analyses, and how a distance matrix can be used to choose analysis directions when submodels contain multiple components. Although the Euclidean distance has been criticized when used for ecological analysis, Chao and Chiu (2016) have recently suggested the problems associated with use of the Euclidean distance as a measure of beta diversity are related to normalization, rather than any intrinsic failure of the Euclidean distance. Finally, while distance-based RA (Legendre and Anderson, 1999) does incorporate distance information, like PERMANOVA, it removes information on the effects of individual OTUs, and so was not included in our discussion.
In our examples here, we have put all confounders into the first submodel X1. This conforms with practice in epidemiology in which confounders are not tested for inclusion into a model, but rather are included based on subject-area knowledge (VanderWeele and Shpitser, 2011). With this in mind, our implementation of the LDM does not provide P-values for the set of variables that are designated as confounders, which makes the code run faster. However, for those who want to estimate and test the individual effects of confounders, each confounder can be treated as separate submodel, and the LDM will calculate a P-value for each confounder. The results obtained in this way for the remaining variables are identical.
Among OTU-specific tests in absence of confounders, we found that MetagenomeSeq controlled FDR in the simulations we conducted, while Hawinkel et al. (2019) claimed that MetagenomeSeq failed to control FDR. We noticed that Hawinkel et al. (2019) adopted the zero-inflated Gaussian mixture distribution (i.e. the fitZig function), whereas we adopted the zero-inflated log-normal mixture model (i.e. the fitFeatureModel function) as recommended by the MetagenomeSeq R package. We also found that the Wilcoxon rank-sum test is a robust and powerful choice for detecting differentially abundant OTUs when testing a single binary covariate. A recently developed version of the rank-sum test (Satten et al., 2018) that uses inverse-probability-of-treatment weights could provide an interesting extension for categorical testing when adjustment for confounding covariates is required. However, OTU-specific tests based on the rank-sum test do not provide coherent results with any global test.
The question of whether rare OTUs should be removed before analyzing microbiome data is unresolved. In our simulations, we did not filter out any OTUs to show the validity of the LDM even in the most challenging situation where these rare OTUs are retained. We applied filters in the real data analysis to reduce the multiple-comparison penalty and increase the chance of finding OTU-level associations. Retaining only those OTUs found in at least five samples, or in at least 5% of samples, are both commonly used filters in the literature, and we used one for each data analysis. Filtering out the very rare OTUs will only minimally affect the performance of our global test because these OTUs explain a negligible proportion of the variability in either the frequency-scale or arcsin-root-transformed data.
Disclaimer
The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention.
Funding
This work was supported by the National Institutes of Health awards R01GM116065 (Hu).
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Yi-Juan Hu, Department of Biostatistics and Bioinformatics, Emory University, Atlanta, GA 30322.
Glen A Satten, Centers for Disease Control and Prevention, Atlanta, GA 30333, USA.
References
- Aitchison J. (1986) The Statistical Analysis of Compositional Data. Chapman and Hall, London, New York, USA. [Google Scholar]
- Anderson M.J. (2001) A new method for non-parametric multivariate analysis of variance. Aust. Ecol., 26, 32–46. [Google Scholar]
- Anderson M.J., Legendre P. (1999) An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. J. Stat. Comput. Simul., 62, 271–303. [Google Scholar]
- Berkson J. (1944) Application of the logistic function to bio-assay. J. Am. Stat. Assoc., 39, 357–365. [Google Scholar]
- Besag J., Clifford P. (1991) Sequential Monte Carlo p-values. Biometrika, 78, 301–304. [Google Scholar]
- Chao A., Chiu C.-H. (2016) Bridging the variance and diversity decomposition approaches to beta diversity vis similarity and differentiation measures. Methods Ecol. Evol., 7, 919–928. [Google Scholar]
- Charlson E.S. et al. (2010) Disordered microbial communities in the upper respiratory tract of cigarette smokers. PLoS One, 5, e15216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L. et al. (2018) GMPR: A robust normalization method for zero-inflated count data with application to microbiome sequencing data. PeerJ, 6, e4600. doi: 10.7717/peerj.4600. [DOI] [PMC free article] [PubMed]
- Chen J., Li H. (2013) Variable selection for sparse Dirichlet-multinomial regression with an application to microbiome data analysis. Ann. Appl. Stat., 7, 418–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen E.Z., Li H. (2016) A two-part mixed-effects model for analyzing longitudinal microbiome compositional data. Bioinformatics, 32, 2611–2617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman D., Lane D. (1983) A nonstochastic interpretation of reported significance levels. J. Bus. Econ. Stat., 1, 292–298. [Google Scholar]
- Fernandes A.D. et al. (2014) Unifying the analysis of high-throughput sequencing datasets: characterizing RNA-seq, 16S rRNA gene sequencing and selective growth experiments by compositional data analysis. Microbiome, 2, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gower J.C. (1966) Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika, 53, 325–338. [Google Scholar]
- Haldane J. (1956) The estimation and significance of the logarithm of a ratio of frequencies. Ann. Hum. Genet., 20, 309–311. [DOI] [PubMed] [Google Scholar]
- Hawinkel S. et al. (2019) A broken promise: microbiome differential abundance methods do not control the false discovery rate. Brief. Bioinform., 20, 210–221. [DOI] [PubMed] [Google Scholar]
- Hu J. et al. (2018) A two-stage microbial association mapping framework with advanced FDR control. Microbiome, 6, 131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaul A. et al. (2017) Analysis of microbiome data in the presence of excess zeros. Front. Microbiol., 8, 2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinbaum D.G. et al. (2007) Applied Regression Analysis and Other Multivariable Methods. Cengage Learning, USA. [Google Scholar]
- La Rosa P.S. et al. (2012) Hypothesis testing and power calculations for taxonomic-based human microbiome data. PLoS One, 7, e52078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legendre P., Anderson M.J. (1999) Distance-based redundancy analysis: testing multispecies responses in multifactorial ecological experiments. Ecol. Monogr., 69, 1–24. [Google Scholar]
- Love M.I. et al. (2014) Moderated estimation of fold change and dispersion for RNA-seq data with deseq2. Genome Biol., 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandal S. et al. (2015) Analysis of composition of microbiomes: a novel method for studying microbial composition. Microb. Ecol. Health Dis., 26, 27663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle B.H., Anderson M.J. (2001) Fitting multivariate models to community data: a comment on distance-based redundancy analysis. Ecology, 82, 290–297. [Google Scholar]
- Morgan X.C. et al. (2015) Associations between host gene expression, the mucosal microbiome, and clinical outcome in the pelvic pouch of patients with inflammatory bowel disease. Genome Biol., 16, 67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller K.E., Fetterman B.A. (2012) Regression and ANOVA: An Integrated Approach Using SAS Software. SAS Institute, USA. [Google Scholar]
- Paulson J.N. et al. (2013) Differential abundance analysis for microbial marker-gene surveys. Nat. Methods, 10, 1200–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D. et al. (2010) edger: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics, 26, 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandve G.K. et al. (2011) Sequential Monte Carlo multiple testing. Bioinformatics, 27, 3235–3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satten G.A. et al. (2017) Restoring the duality between principal components of a distance matrix and linear combinations of predictors, with application to studies of the microbiome. PLoS One, 12, e0168131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satten G.A. et al. (2018) Multisample adjusted u-statistics that account for confounding covariates. Stat. Med., 37, 3357–3372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi P., Li H. (2017) A model for paired-multinomial data and its application to analysis of data on a taxonomic tree. Biometrics, 73, 1266–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T.J., Shpitser I. (2011) A new criterion for confounder selection. Biometrics, 67, 1406–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westfall P.H., Young S.S. (1993) Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment. John Wiley & Sons, USA. [Google Scholar]
- Wu C. et al. (2016) An adaptive association test for microbiome data. Genome Med., 8, 56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X. et al. (2017) A small-sample multivariate kernel machine test for microbiome association studies. Genet. Epidemiol., 41, 210–220. [DOI] [PubMed] [Google Scholar]
- Zhao N. et al. (2015) Testing in microbiome-profiling studies with MiRKAT, the microbiome regression-based kernel association test. Am. J. Hum. Genet., 96, 797–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


