Abstract
Interest in analyzing X chromosome single nucleotide polymorphisms (SNPs) is growing and several approaches have been proposed. Prior studies have compared power of different approaches, but bias and interpretation of coefficients have received less attention. We performed simulations to demonstrate the impact of X chromosome model assumptions on effect estimates. We investigated the coefficient biases of SNP and sex effects with commonly used models for X chromosome SNPs, including models with and without assumptions of X chromosome inactivation (XCI), and with and without SNP–sex interaction terms. Sex and SNP coefficient biases were observed when assumptions made about XCI and sex differences in SNP effect in the analysis model were inconsistent with the data‐generating model. However, including a SNP–sex interaction term often eliminated these biases. To illustrate these findings, estimates under different genetic model assumptions are compared and interpreted in a real data example. Models to analyze X chromosome SNPs make assumptions beyond those made in autosomal variant analysis. Assumptions made about X chromosome SNP effects should be stated clearly when reporting and interpreting X chromosome associations. Fitting models with SNP × Sex interaction terms can avoid reliance on assumptions, eliminating coefficient bias even in the absence of sex differences in SNP effect.
Keywords: bias, model assumptions, sex coefficient, SNP coefficient, X chromosome variants
1. INTRODUCTION
X chromosome inactivation (XCI) is an epigenetic process that leads to inactivation of one of the two X chromosomes in females (Ross et al., 2005). It prevents females from having twice as much X chromosome gene expression as males, who only have one X chromosome. Generally, XCI is believed to be random, but research has shown that XCI can be skewed in some individuals, meaning that one chromosome is more likely to be silenced than the other (Heard & Disteche, 2006). Also, approximately 9%–14% of X‐linked genes escape from XCI and both copies are expressed (Carrel & Willard, 1999). These complexities have implications for modeling X chromosome variant effects on phenotypes and have resulted in the X chromosome often being excluded from genome‐wide association study (GWAS) analyses (Wise et al., 2013).
Sex differences in prevalence or clinical presentation have been observed in many diseases including autoimmune disorders, cardiovascular diseases, cancer, and psychiatric disorders (Appelman et al., 2015; Dong et al., 2020; Erol et al., 2015; Riecher‐Rössler, 2017; Voskuhl, 2011), leading to hypotheses that X chromosome genetic variation may contribute to some of these differences. Therefore, interest in analyzing X chromosome variants is growing and researchers are beginning to incorporate X chromosome variants into GWAS (Chang et al., 2014; Khramtsova et al., 2019; MacArthur et al., 2017; Stahl et al., 2019). However, often, little attention is paid to XCI biology when analyzing X chromosome genotype data (Chen et al., 2020; Wang et al., 2017). A number of approaches have been proposed to analyze single nucleotide polymorphisms (SNPs) on the X chromosome, and several studies have compared different approaches (Clayton, 2008; Gao et al., 2015; König et al., 2014; Özbek et al., 2018; Wang et al., 2014; Xu & Hao, 2018). Most studies have focused on power when presenting results and comparing approaches, whereas biases and the interpretability of coefficients have not been well investigated and discussed. As risk prediction methods such as polygenic risk scores (PRS) increase in popularity (Lambert et al., 2019; Lloyd‐Jones et al., 2019), a focus on the properties of SNP effect estimates, including coefficient biases and concerns regarding interpretability, will become more important to integrate X chromosome variants into these predictive models.
We previously proposed using an XCI‐robust approach for X chromosome genetic variant analysis, by including a sex–SNP interaction term, which allows for different effects of the genetic variants between males and females, and thus, increases the flexibility of the model. We used this approach in a study of bipolar disorder (Jons et al., 2019); but as with other methodological approaches, discussion of the utility of the model primarily focused on power to detect effects. In this study, we performed simulations to examine the impact of model assumptions and SNP coding scheme on biases of model coefficients, in scenarios with and without sex differences in SNP effect, and using models with and without SNP × Sex interaction terms in the analysis. We also illustrate our key findings through an example of an X chromosome SNP previously shown to be associated with body mass index.
2. METHODS
2.1. Common SNP coding schemes
Because of the underlying biological process of XCI, two genotype coding schemes are commonly used in the analysis of X chromosome SNP data; one corresponds to an assumption of “XCI” (formerly referred to as “Clayton”) (Clayton, 2008) while the other is consistent with escape from XCI (“eXCI,” formerly referred to as “PLINK”) (Purcell et al., 2007). Denoting the two alleles at a SNP as “a” and “A,” assuming additive allele effects, both XCI and eXCI coding schemes code “aa”, “aA” and “AA” female genotypes as 0, 1, 2. For males, XCI coding assigns genotype “a” a value of 0 and “A” a value of 2, while eXCI assigns “a” and “A” genotypes values of 0 and 1, respectively. It should be noted that the choice of coding “a” or “A” as the effect allele may impact the coefficient estimates beyond just a change in sign, particularly for eXCI coding which codes the male genotypes on a smaller scale relative to females; therefore, it is important to include sex as a covariate (Chen et al., 2019).
2.2. Simulation: Data generation
Data were simulated under a variety of scenarios including assuming a locus undergoing XCI or escaping from XCI, as well as with and without SNP × Sex interactions. The simulated variables were sex (female and male), SNP genotype (aa, Aa, or AA for females; a or A for males) and outcomes (0,1). Each simulated data set consisted of roughly 500 females and 500 males, with female taken as the reference level (sex = 0) and male sex coded as 1. The frequencies of the minor allele was set at 0.3 and 0.5, and random XCI was assumed.
After simulating the sex and genotype data, binary outcomes were randomly generated using a logistic model conditional on sex and genotypes; specifically, two sets of outcomes were generated corresponding to the assumptions of a locus undergoing or escaping from XCI (referred to as “XCI” and “eXCI”) based on XCI (Clayton) and eXCI (PLINK) coded genotypes, respectively. For data generated under both the XCI and eXCI assumptions, outcomes were generated in two ways, using models with and without SNP × Sex interaction terms (i.e., in the absence and presence of sex differences in SNP effect).
Table 1a,b shows the data‐generating models considered in the absence of sex differences in SNP effects. Specifically, a binary outcome Y was generated from a model with only main effects of sex and SNP, using the equation:
where SNP was coded assuming XCI or eXCI. The intercept was fixed at 0, and five combinations of β sex and β SNP coefficients were used (Table 1a,b). We generated 100 data sets under each parameter combination.
Table 1.
Data‐generating models in the absence of SNP × Sex interaction effects using (a) XCI (Clayton) coding and (b) eXCI (PLINK) coding
| Coding | Model coefficients | OR for effect of sex | ORs for effect of SNP, given sex | Prevalence | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | # Copies of effect allele | βsex | βSNP | ORsex (eβ sex) | ORSNP|M (e2βSNP) | ORSNP|W1 (eβSNP) | ORSNP|W2 (e2βSNP) | Overall | Female | Male | ||
| (a) XCI (Clayton) coding | ||||||||||||
| 0 | 1 | 2 | 0 | 0.75 | e0 | e1.5 | e0.75 | e1.5 | 0.664 | 0.668 | 0.660 | |
| M | 0 | 2 | NA | 0.1 | 0.5 | e0.1 | e1 | e0.5 | e1 | 0.628 | 0.618 | 0.638 |
| F | 0 | 1 | 2 | 0.2 | 0.2 | e0.2 | e0.4 | e0.2 | e0.4 | 0.574 | 0.550 | 0.598 |
| 0.5 | 0.1 | e0.5 | e0.2 | e0.1 | e0.2 | 0.585 | 0.514 | 0.646 | ||||
| 0.75 | 0 | e0.75 | e0 | e0 | e0 | 0.589 | 0.500 | 0.678 | ||||
| (b) eXCI (PLINK) coding | ||||||||||||
| 0 | 1 | 2 | 0 | 0.75 | e0 | e0.75 | e0.75 | e1.5 | 0.629 | 0.668 | 0.590 | |
| M | 0 | 1 | NA | 0.1 | 0.5 | e0.1 | e0.5 | e0.5 | e1 | 0.602 | 0.618 | 0.586 |
| F | 0 | 1 | 2 | 0.2 | 0.2 | e0.2 | e0.2 | e0.2 | e0.4 | 0.562 | 0.550 | 0.574 |
| 0.5 | 0.1 | e0.5 | e0.1 | e0.1 | e0.2 | 0.579 | 0.524 | 0.634 | ||||
| 0.75 | 0 | e0.75 | e0 | e0 | e0 | 0.589 | 0.500 | 0.678 | ||||
Note: With the coding scheme used when generating the data specified on the left, we give how SNPs are coded within sex under each coding scheme. The “Model” column provides the five coefficient combinations we used to generate the data in this simulation study. We then calculated the odds ratio for the effect of sex and for the effect of SNP given sex. ORsex refers to the odds ratio for the effect of sex with female as the reference level and male equal to 1. ORSNP|M refers to the odds ratio for the effect of SNP, either comparing SNP = 0 with SNP = 2 in XCI (Clayton) or with SNP = 1 in eXCI (PLINK) coding, given sex = male. ORSNP|W1 refers to the odds ratio for the effect of SNP comparing SNP = 0 with SNP = 1 and ORSNP|W2 refers to the odds ratio for the effect of SNP comparing SNP = 0 with SNP = 2, given sex = female. In the “Prevalence” column, we calculated the proportion of cases in the overall population (1000 cases), in females (500 cases), and in males (500 cases).
Table 2a,b shows the data‐generating models considered in the presence of sex differences in SNP effects, introduced by including a Sex × SNP interaction term when we generated the data. The general form of the equation is:
Table 2.
Data‐generating models in the presence of SNP × Sex interaction effects using (a) XCI (Clayton) coding and (b) eXCI (PLINK) coding
| Model | ORs for effect of sex, given SNP | ORs for effect of SNP, given Sex | Prevalence | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | # Copies of effect allele | βsex | βSNP | βint | ORsex|SNP0 (eβsex) | ORsex|SNP2 (eβsex+2βint) | ORSNP|M (e2βSNP+2βint) | ORSNP|W1 (eβSNP) | ORSNP|W2 (e2βSNP) | Overall | Female | Male | ||
| (a) XCI (Clayton) coding | ||||||||||||||
| 0 | 1 | 2 | 0.2 | 0.2 | 0.1 | e0.2 | e0.4 | e0.6 | e0.2 | e0.4 | 0.585 | 0.550 | 0.620 | |
| M | 0 | 2 | NA | 0.2 | 0.2 | 0.2 | e0.2 | e0.6 | e0.8 | e0.2 | e0.4 | 0.595 | 0.550 | 0.640 |
| F | 0 | 1 | 2 | 0.2 | 0.2 | 0.3 | e0.2 | e0.8 | e1 | e0.2 | e0.4 | 0.604 | 0.550 | 0.658 |
| (b) eXCI (PLINK) coding | ||||||||||||||
| 0 | 1 | 2 | 0.2 | 0.2 | 0.1 | e0.2 | e0.3 | e0.3 | e0.2 | e0.4 | 0.568 | 0.550 | 0.586 | |
| M | 0 | 1 | NA | 0.2 | 0.2 | 0.2 | e0.2 | e0.4 | e0.4 | e0.2 | e0.4 | 0.574 | 0.550 | 0.598 |
| F | 0 | 1 | 2 | 0.2 | 0.2 | 0.3 | e0.2 | e0.5 | e0.5 | e0.2 | e0.4 | 0.579 | 0.550 | 0.608 |
Note: with the coding scheme used when generating the data specified on the left, we give how SNPs are coded within sex under each coding scheme. The “Model” column provides the three coefficient combinations we used to generate the data in this simulation study. We then calculated the odds ratio for the effect of sex given SNP and for the effect of SNP given sex. ORsex|SNP0 refers to the odds ratio for the effect of sex (with female as the reference level and male equals to 1) given SNP = 0 for both coding schemes. For XCI (Clayton), ORsex|SNP2 refers to the odds ratio for the effect of sex given SNP = 2 (with female as the reference level); for eXCI (PLINK) coding, ORsex|SNP1 refers to the odds ratio for the effect of sex given SNP = 1 (with female as the reference level). ORSNP|M refers to the odds ratio for the effect of SNP, either comparing SNP = 0 with SNP = 2 in XCI or with SNP = 1 in eXCI coding, given sex = male. ORSNP|W1 refers to the odds ratio for the effect of SNP comparing SNP = 0 with SNP = 1 and ORSNP|W2 refers to the odds ratio for the effect of SNP comparing SNP = 0 with SNP = 2, given sex = female. In the “Prevalence” column, we calculated the proportion of cases in the overall population (1000 cases), in females (500 cases), and in male (500 cases).
Again, the intercept was fixed at 0, and either XCI or eXCI coding was used for the SNP variable. Three combinations of β sex, β SNP, and β int were chosen (Table 2a,b), and 100 data sets were generated under each combination.
2.3. Simulation: Data analysis
The simulated data were analyzed in multiple ways using XCI (Clayton) or eXCI (PLINK) coding and with and without SNP × Sex interaction terms. For each generated data set, regardless of whether the outcome was generated assuming XCI or eXCI, we fit four different models (Table 3).
Table 3.
Logistic regression models fit to each of the simulated data sets, using either XCI (Clayton) or eXCI (PLINK) coding for the SNP effects, and with and without SNP × Sex interaction terms
| 1 | Logit (Y) = intercept + β sex × Sex + β SNP × SNPXCI |
| 2 | Logit (Y) = intercept + β sex × Sex + β SNP × SNPeXCI |
| 3 | Logit (Y) = intercept + β sex × Sex + β SNP × SNPXCI + βint × Sex × SNPXCI |
| 4 | Logit (Y) = intercept + β sex × Sex + β SNP × SNPeXCI + βint × Sex × SNPeXCI |
We first fit models including only main effects for sex and SNP. Among them, the first model used the XCI coding for the SNP variable (Model 1), while the second model used the eXCI coding for the SNP variable (Model 2). These models allowed us to study the coefficient estimates and p‐values when the coding scheme used to generate data (reflecting assumptions about XCI) is inconsistent with the coding scheme used to fit data (i.e., the genotype‐phenotype model), as well as when they are consistent. We coded sex = 0 for females and sex = 1 for males, and coded the SNP genotypes in terms of the same allele as in the data generation. We stored the coefficients and p‐values for each model, and then calculated the bias of the coefficients (fitted value minus true value).
We also fit additional models that included interaction terms between sex and SNP (Models 3 and 4 in Table 3). Both the main effect SNP term and the interaction term used the same SNP coding within a model. In addition to assessing bias and p‐values of the individual model terms, we conducted likelihood ratio χ 2‐tests (LRT). First, we compared all models with the model “logit (Y) = intercept + β sex × Sex” to test the overall effect of the SNP coefficients; this would be either a one or 2‐df likelihood ratio χ 2‐test depending on which model we are testing (e.g., df = 1 for testing SNP effects in Model 1, but df = 2 for jointly testing SNP and SNP × Sex interaction effects in Model 3). Second, for the models with interaction terms we performed a 1‐df likelihood ratio χ 2‐test comparing to a model “logit (Y) = intercept + β sex × Sex + βSNP × SNP” (comparing Model 3 with Model 1 and comparing Model 4 with Model 2), to test for sex differences in SNP effect.
For all combinations of data generation scenarios and analysis methods, we plotted the estimated coefficients/bias and p‐values using boxplots, and plotted the proportions of p‐values from likelihood ratio χ 2 tests below a prespecified significance threshold to display power using bar‐plots.
In addition to the coefficient combinations shown in Tables 1a,b and 2a,b, we also assessed additional scenarios with lower prevalence or a negative interaction term (Supporting Information Material). In the following sections, we will focus on results with MAF = 0.5 and with coefficient combinations and prevalence shown in Tables 1a,b and 2a,b. Key findings from additional scenarios will be discussed, without showing detailed results.
2.4. Simulation: Nonrandom XCI
We also considered how the presence of XCI skewness or, in other words, nonrandom XCI, impacts coefficient biases when the genetic model is misspecified because it does not account for skewness. As shown previously, nonrandom/XCI skewness is equivalent to a genetic model that includes a dominance deviation (Chen et al., 2019). Therefore to generate data consistent with XCI skewness, we added a dominance variable (D) coded as (0, 1, 0) for female genotypes (aa, Aa, AA) and (0, 0) for male genotypes (a, A). The coefficient for this non‐additive effect term D was set to be less than the additive effect (SNP term coefficient) to mimic the situation of skewness. The general form of the equation is:
The coefficient combinations of sex and SNP terms were the same as above (Tables 1a,b and 2a,b) and the coefficient of the dominance effect term was set at 0.1 for all scenarios. As above, we fit Models 1–4 (Table 3) without adding a nonadditive effect term and performed likelihood ratio χ 2 tests. Results were summarized similar to the scenarios without dominance effects.
2.5. Application to genetic associations with obesity
We sought to examine the observed changes in coefficient estimates from the four genetic models that were fit in simulations in the context of an applied example. Previously, the minor T allele of rs1316982, an X chromosome SNP in an intron of the gene IL13RA1, was identified as significantly associated with body mass index (BMI) in a GWAS (Hoffmann et al., 2018). Using data from the UK Biobank, we re‐analyzed the relationship between this SNP and obesity (defined as BMI > 30) in a sample of N = 173,557 males and N = 201,630 females of European ancestry. Genotyping, imputation, and quality control procedures have been previously described (Hoffmann et al., 2018). We fit the four logistic regression models described in Table 3. For each model, we also included additional covariates for age, assessment center, genotyping batch, and the first 20 principal components to capture population stratification. We also fit a model with sex and the additional covariates, but without a SNP or SNP × Sex interaction term.
3. RESULTS
3.1. Part 1: Data generated in the absence of sex differences in SNP effect
3.1.1. Fitting models without SNP × Sex interaction
Figure 1 displays results for data generated in the absence of sex differences in SNP effect (Table 1a,b) and analyzed using either XCI (Clayton) (Model 1) or eXCI (PLINK) coding (Model 2) with no SNP × Sex interaction term (Figure 1 and Table S1) for situations with MAF = 0.5; results for MAF = 0.3 were similar (Figures S1.1–S1.6). As expected, we observed biases in the SNP and sex coefficients when there was model misspecification (i.e., inconsistency in the coding schemes used to generate and fit the data, e.g., generate data under XCI coding, but use eXCI coding to fit, or vice versa). The biases were greatest when the true effect of SNP (i.e., the magnitude of true SNP coefficient) was greatest. The direction of the bias (positive or negative) depends on how the variables are coded, in particular the chosen reference levels. As we stated previously, we fixed allele frequencies at 0.5 and coded female as 0 and male as 1. Under such circumstances, for data sets generated using eXCI coding, we observed negative biases (fitted < true) in both SNP and sex coefficients when analyzed using XCI coding. For data sets generated using XCI coding, we observed positive biases (fitted > true) in both sex and SNP coefficients when analyzed with eXCI coding. Notably, we also observed false‐positive tests of the sex effects along with the coefficient biases, while the tests for the SNP effect had no type 1 error inflation.
Figure 1.
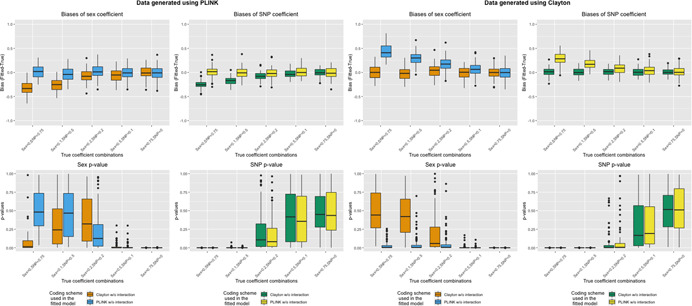
Bias and p‐values of sex and SNP coefficients when generating data in the absence of sex differences in SNP effect and fitting models without SNP–sex interaction terms. Top row: Boxplots of bias (Y‐axis; estimate minus true coefficient) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). Bottom row: Boxplots of p‐values (Y‐axis) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI coding (left) or XCI coding (right). Color indicates the model that was fit (Model 1 or Model 2, XCI or eXCI coding without a SNP–sex interaction term)
When we changed the prevalence to be below 50%, as opposed to above 50% shown in Tables 1a,b and 2a,b, we observed the same patterns but with a change in the direction of the biases (Figures S2.1–S2.6).
3.1.2. Fitting models with SNP × Sex interaction terms
Figure 2 displays results for data generated in the absence of sex differences in SNP effect (Table 1a,b) and analyzed using either XCI (Clayton) coding (Model 3) or eXCI (PLINK) coding (Model 4) with a SNP × Sex interaction term. When an interaction term was included in the model to fit the data, the coefficients (and corresponding p‐values) for sex and SNP were unbiased regardless of whether the SNP coding was correctly specified in the model (Figure 2 and Table S2). However, we observed biases in the interaction terms if there was an inconsistency between the coding schemes used to generate the data and to fit the data, especially in the scenarios with a stronger SNP effect. The p‐values for interaction terms in those models were also significantly lower than expected under the null hypothesis of no interaction, leading to false‐positive interaction signals under misspecification of the SNP coding.
Figure 2.
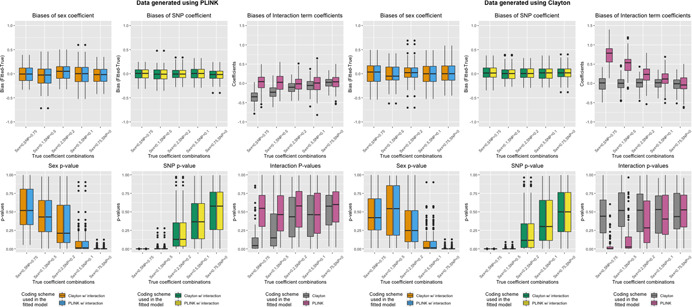
Bias and p‐values of sex and SNP coefficients when generating data in the absence of sex differences in SNP effect and fitting models with SNP–sex interaction terms. Top row: Boxplots of bias (Y‐axis; estimate minus true coefficient) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). Bottom row: Boxplots of p‐values (Y‐axis) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI coding (left) or XCI coding (right). Color indicates the model that was fit (Model 3 or Model 4, XCI or eXCI coding with a SNP–sex interaction term)
Although false‐positive evidence for interaction terms from the 1‐df test was observed when the SNP coding was misspecified, the p‐values from the 2‐df test (joint test of SNP and SNP–sex interaction) were the same for both coding schemes (Figure 3a), even under misspecification, and the power estimates based on a p‐value threshold of 0.01 (Figure 3b) were similar as well, as expected.
Figure 3.
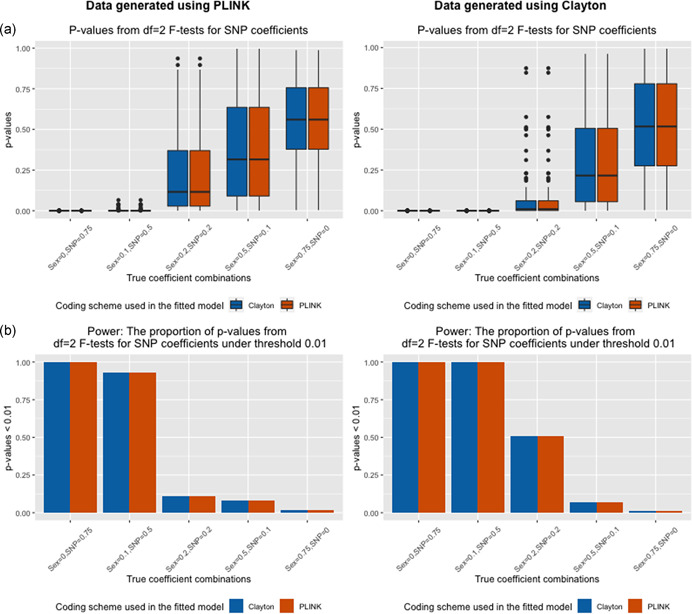
Two degree‐of‐freedom F tests for SNP coefficients for data generated in the absence of sex differences and fitting models with SNP‐sex interaction terms. (a) Boxplots of p‐values (Y‐axis) of df = 2F tests across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). (b) Power defined as the proportion of p < 0.01 (Y‐axis) across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI coding (left) or XCI coding (right). Color indicates the model that was fit (Model 3 or Model 4, XCI or eXCI coding with a SNP–sex interaction term)
Again, when we changed the prevalence to be below 50%, the biases in the coefficient for interaction term has the opposite direction from what we show below (Figures S2.1–S2.6). We also had more significant p‐values and higher powers due to the coefficient combinations we selected in the simulations with lower prevalence (i.e., further from 0).
3.2. Part 2: Data generated in the presence of sex differences in SNP effects
3.2.1. Fitting models without SNP × Sex interaction terms
When we generated data under the assumption of sex differences in SNP effects (Table 2a,b), both SNP and sex coefficients were biased in all models without interaction terms (Figure 4 and Table S3). When the data was generated assuming XCI (Table 2a), biases were greater among models with SNP coding misspecification (Model 2, analyzed using eXCI (PLINK) coding). Interestingly, in our scenarios with data generated using eXCI coding (Table 2b), the biases of the SNP and sex coefficients when analyzed using XCI coding (Model 1, misspecified SNP coding) were smaller than the biases observed when analyzed using eXCI coding (Model 2, consistent SNP coding). Additionally, we observed false‐positive sex and SNP effects in all models without interaction terms, except for the sex coefficient when data was generated with eXCI coding, but analyzed using XCI coding. The p‐values also were smaller (i.e., false‐positive rates were larger) when the true interaction term coefficients were bigger.
Figure 4.
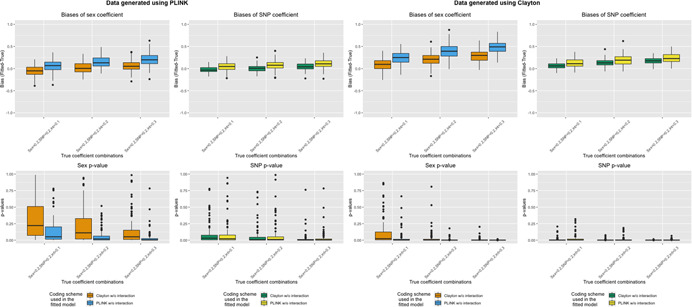
Bias and p‐values of sex and SNP coefficients when generating data in the presence of sex differences in SNP effect and fitting models without SNP‐sex interaction terms. Top row: Boxplots of bias (Y‐axis; estimate minus true coefficient) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). Bottom row: Boxplots of p‐values (Y‐axis) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI coding (left) or XCI coding (right). Color indicates the model that was fit (Model 1 or Model 2, XCI or eXCI coding without a SNP–sex interaction term)
Biases with opposite directions were observed when data was generated with prevalence less than 50% (Figures S2.1–S2.6), but the patterns are preserved. When the interaction term coefficients were changed from positive to negative (Figures S3.1–S3.3), we observed that analyzing using eXCI coding had lower biases in both sex and SNP coefficients regardless of data generation assumption (XCI or eXCI, misspecified or consistent) compared to lower biases using XCI coding when we had positive interaction terms as shown in Figure 4. We also had larger p‐values due to smaller effect sizes arising from the negative interaction terms.
3.2.2. Fitting models with SNP × Sex interaction terms
When the data was generated under SNP × Sex interactions (Table 2a,b) and the model was fit with an interaction term (Models 3 and 4), there were no biases in the sex coefficient regardless of whether the SNP coding was misspecified (Figure 5 and Table S4). The SNP coefficients were also unbiased given that female was coded as the sex reference level (sex = 0). However, there were biases in the interaction terms when the SNP coding was misspecified, with coefficients biased in the same way as Part 1.b. In general, the amount of bias in interaction term coefficients increases as the true value of interaction term coefficients increases.
Figure 5.
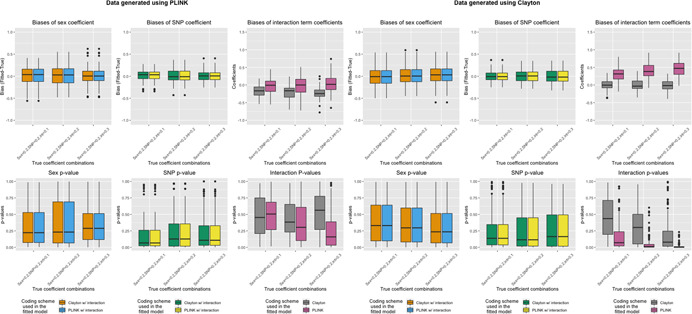
Bias and p‐values of sex and SNP coefficients when generating data in the presence of sex differences in SNP effect and fitting models with SNP–sex interaction terms. Top row: Boxplots of bias (Y‐axis; estimate minus true coefficient) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). Bottom row: Boxplots of p‐values (Y‐axis) of sex and SNP coefficients across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI coding (left) or XCI coding (right). Color indicates the model that was fit (Model 3 or Model 4, XCI or eXCI coding with a SNP‐sex interaction term)
The findings (Figure 6) from the 2‐df likelihood ratio χ 2 test for the SNP effect were similar to those observed in Part 1.b. The power, or proportion of p‐values less than 0.01, for models with inconsistency in coding schemes was the same as those without inconsistency.
Figure 6.
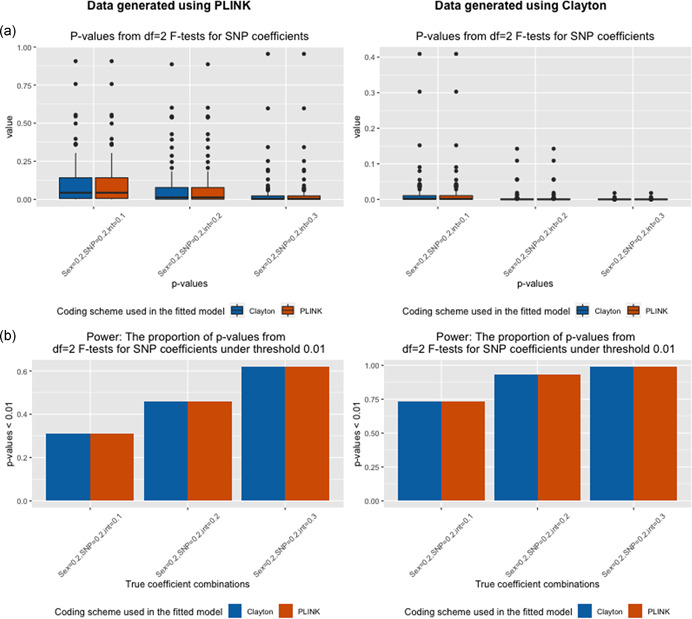
Two degree‐of‐freedom F tests for SNP coefficients for data generated in the presence of sex differences and fitting models with SNP–sex interaction terms. (a) Boxplots of p‐values (Y‐axis) of df = 2 F tests across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). (b) Power defined as the proportion of p < 0.01 (Y‐axis) across 1000 simulation runs for various simulation settings (X‐axis) when data is generated using eXCI (PLINK) coding (left) or XCI (Clayton) coding (right). Color indicates the model that was fit (Model 3 or Model 4, XCI (Clayton) or eXCI (PLINK) coding with a SNP–sex interaction term)
When we lowered the prevalence to below 50%, the direction of biases of the interaction term coefficients changed, as expected (Figures S2.1–S2.6). When we changed the interaction term coefficients to negative (Figures S3.1–S3.3), biases for the interaction term were minimal even when the SNP coding is miss‐specified. Generally, p‐values were also higher than for the positive interactions, and there are less “false positives”; but also the power for the 2‐df likelihood ratio tests were lower.
3.3. Part 3: Exploration of dominance deviations from an additive genetic model
When we considered skewness in our data generation, we observed similar results as when data were generated under random XCI (Figures S4.1–S4.6), although the biases observed in the sex coefficient were greater. The inclusion of the interaction term in our model reduced the biases in both sex and SNP terms when there is coding scheme misspecification. The p‐values from the 2 df likelihood ratio χ 2 test were also the same regardless of coding scheme consistency or misspecification, and the power estimates based on a p‐value threshold of 0.01 were similar as well.
3.4. Part 4: Real data application to obesity
Results of the four models evaluating the association of obesity with the X chromosome SNP rs1316982 are shown in Table 4. In the UK Biobank data, males have a higher rate of obesity (defined as BMI > 30) compared to females (odds ratio [OR] = 1.118; 95% confidence interval [CI] = 1.101–1.135; p < 2E−16). In all four SNP models, the association between sex and obesity is evident for participants homozygous for the major allele (SNP = 0), where OR's for the sex effect range from 1.116 to 1.129, with the model using eXCI coding without SNP × Sex interaction having the highest OR. As expected, OR for the sex effect given SNP = 0, as well as the OR for the SNP effect given sex are equivalent in the two models with SNP × Sex interactions regardless of the coding scheme. In both of these models, the OR for the SNP effect is closer to the model with XCI coding and no SNP × Sex interaction, where the OR in males (1.099) is more similar to the OR for the female rare homozygotes (OR = 1.082) than the OR for the female heterozygotes (OR = 1.040), consistent with XCI. Note that the SNP effect estimate for the model using XCI coding without SNP × Sex interaction is similar to both models including SNP × Sex interaction. This is consistent with prior studies showing that the gene IL13RA1 (where rs1316982 resides) undergoes XCI across most tissues (Balaton et al., 2015) (Tukiainen et al., 2017). Taken together, these results support that the coding assuming XCI is most appropriate. Under this coding, the SNP × Sex interaction term is not statistically significant, indicating no evidence of sex differences in SNP effect on obesity assuming XCI. When assuming XCI and no SNP × Sex interaction, the minor T allele of rs1316982 is significantly associated with increased rate of obesity at the genome‐wide level (p = 1.15E−13).
Table 4.
Results of Table 3 logistic regression models on obesity (defined as BMI > 30) in UK Biobank sample
| SNP coding | Interaction | Effect | Beta | SE | P | exp(beta) | ORsex|0 | ORsex|1 | ORsex|2 | ORSNP|M | ORSNP|W1 | ORSNP|W2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| XCI/Clayton | No | Sex | 0.111 | 0.008 | 5.77E−48 | 1.118 | 1.118 | 1.118 | 1.091 | 1.044 | 1.091 | |
| SNP | 0.044 | 0.006 | 1.15E−13 | 1.044 | ||||||||
| eXCI/PLINK | No | Sex | 0.121 | 0.008 | 1.55E−54 | 1.129 | 1.129 | 1.129 | 1.057 | 1.057 | 1.118 | |
| SNP | 0.056 | 0.008 | 9.11E−12 | 1.057 | ||||||||
| XCI/Clayton | Yes | Sex | 0.109 | 0.009 | 1.26E−35 | 1.116 | 1.116 | 1.123 | 1.096 | 1.040 | 1.082 | |
| SNP | 0.039 | 0.010 | 6.79E−05 | 1.040 | ||||||||
| Sex × SNP | 0.006 | 0.012 | 6.10E−01 | 1.006 | ||||||||
| eXCI/PLINK | Yes | Sex | 0.109 | 0.009 | 1.26E−35 | 1.116 | 1.116 | 1.175 | 1.096 | 1.040 | 1.082 | |
| SNP | 0.039 | 0.010 | 6.79E−05 | 1.040 | ||||||||
| Sex × SNP | 0.052 | 0.018 | 3.12E−03 | 1.053 |
Note: Female is coded as the reference level, and logistic regression models are adjusted for age, assessment center, genotyping batch, and PC's.
Abbreviations: ORsex|SNP0, odds ratio for the effect of sex, given SNP = 0; ORsex|SNP2, odds ratio for the effect of sex, given SNP = 2; ORsex|SNP1 = odds ratio for the effect of sex, given SNP = 1; ORSNP|M, odds ratio for the effect of SNP, either comparing SNP = 0 with SNP = 2 in XCI or with SNP = 1 in eXCI coding, given sex = male; ORSNP|W1 = odds ratio for the effect of SNP comparing SNP = 0 with SNP = 1, given sex = female; ORSNP|W2, odds ratio for the effect of SNP comparing SNP = 0 with SNP = 2, given sex = female.
4. DISCUSSION
In this simulation study, we investigated the coefficient biases of the SNP and sex effects under commonly used models and coding schemes for X chromosome SNPs, including the previously introduced “XCI‐Robust Approach” that includes a SNP–sex interaction term (Jons et al., 2019). By including a SNP–sex interaction term in the model, it becomes more flexible, requiring no prior knowledge about whether the SNPs are in a region of inactivation or escape from XCI. We focused on the interpretation of the results and explored how we can overcome issues including biases in coefficients and false‐positive tests of SNP and sex effects.
We demonstrated sex and SNP coefficient biases in several situations, particularly if the assumptions about XCI made by the coding scheme used and the assumptions made about sex differences in SNP effect of the fitted model were incorrect. When data were generated assuming no sex differences (i.e., no interaction), biases arose when the fitted models did not include interaction terms and used a different coding scheme from the XCI assumptions of the true model; if the coding scheme in the fitted models was correctly specified regarding assumptions about XCI, no biases were observed (as expected). However, if the fitted model included an interaction term, all biases in the sex and SNP coefficients were eliminated regardless of the misspecification of coding schemes. This is because we coded female sex = 0; thus under an interaction model, the SNP coefficient represents the SNP effect in females, which is not dependent on XCI (Clayton) versus eXCI (PLINK) coding. Of note, if we reverse how sex is coded and use males as the reference, biases in the SNP coefficients with misspecification are observed as expected. For analysis of X chromosome SNPs, coding females as the reference is a strategic choice because the SNP coding for females is the same regardless of whether we assume XCI or eXCI, and the SNP coefficient can be interpreted as the effect of one allele in females regardless of potential XCI model misspecification.
If the data‐generating model assumed sex differences in SNP effect, then there were biases in all models without interaction terms. Interestingly, we also observed smaller biases when we generated data assuming eXCI, but analyzed assuming XCI (Model 1, coding misspecification), than when we analyzed assuming eXCI (Model 2, coding consistency). Upon examining the data‐generating model from Table 2b, this is not surprising. The particular interactions that we generated under eXCI coding had the property that ORSNP|M was close to ORSNP|W2, which is the assumption of the XCI model without interaction (Model 1); and therefore, Model 1 fit the generated sex differences in SNP effect in a similar way as the true Model 4. We could also interpret this observation as the cancellation of biases caused by SNP coding misspecification and misspecification of interaction, conditional on how sex is coded. Here the biases due to the effect of misspecification (SNP coding or interaction) may be offset by how we coded sex in the fitted model (i.e., female sex = 0); of note, if we reverse how sex is coded and use males as the reference, biases with misspecification are observed as expected. Similarly, this would also explain the smaller biases we get when analyzing using eXCI coding compared to using XCI coding regardless of the XCI/eXCI assumption we made when generating the data when we lowered the prevalence to below 50% or when we changed the interaction term coefficients to negative.
We also observed large interaction term coefficient biases and related false‐positive tests of sex–SNP interaction effects. Two degree‐of‐freedom tests for SNP and interaction terms overcome this issue. Therefore, interaction terms are important to include to avoid biased coefficients in sex and SNP variables. However, the sex and SNP coefficients themselves are not interpretable from these models, and it is necessary to report sex‐specific odds ratios/estimates and the results for the 2 df tests. Furthermore, multiple statistical models (e.g., with and without SNP–sex interaction) and SNP coding schemes (e.g., assuming XCI or eXCI) can capture the same odds ratios across male and female genotypes, as was observed above for the models we simulated under eXCI with SNP × Sex interaction that were similar to a model under XCI with no SNP × Sex interaction. Therefore in addition to reporting the sex‐specific genotype ORs, it is important to report assumptions that were made by the model and coding.
As with any statistical analysis, it is critical to interpret results of SNP analyses (autosomal and X chromosome) in the context of the model that was used to analyze the data. This is especially critical for X chromosome analyses, particularly regarding the XCI assumptions underlying the chosen SNP coding and presence of a SNP–sex interaction effect on the phenotype. The biases and type 1 error inflations that we observed may not be errors or biases when considered in the context of the model assumptions. For instance, if SNP coding assumes that the phenotypic difference between “A” and “a” males is the same as the phenotypic difference between “AA” and “aa” females (i.e., XCI Clayton coding) and this coding scheme yields a significant SNP–sex interaction term, this indicates that there is a departure from the assumption that the phenotypic difference between “A” and “a” males is the same as the phenotypic difference between “AA” women and “aa” females. This could suggest that (1) there is a sex‐difference in SNP effect for a SNP in a region of XCI (i.e., XCI coding and the SNP–sex interaction are correct), or (2) the SNP is in a region not undergoing XCI, leading to the departure from the expected phenotypic effects under XCI (i.e., XCI coding is not correct). This suggests that multiple models with differing assumptions may need to be considered to gain insight into the findings. A comparison of effect estimates under the different models may be informative about XCI status. Potentially this observation could be used to develop a formal test of XCI assumptions, although this needs to be investigated further.
These observations are further supported by our real data example, where exploration of different models gave us additional insight into the genetic association between rs1316982 and BMI/obesity beyond what was previously reported, where effect size estimates were reported without context to the analyzed genetic model (Hoffmann et al., 2018). Comparison of ORsex and ORSNP across the models combined with the SNP residing within a gene thought to undergo inactivation suggest that the assumption of XCI is most appropriate. Unlike the model under XCI coding, the SNP × Sex interaction term is statistically significant under the model with eXCI coding, which may falsely lead to a conclusion of the presence of sex differences in SNP effect that may better reflect a deviation from the eXCI model.
This study underscores that the coding scheme selected when modeling the SNP effect, whether XCI or eXCI coding, should be carefully chosen since they represent different underlying XCI assumptions. Often in published analyses of X chromosome SNPs, these choices are not explicitly stated or are given without explanation of the underlying assumptions. It is important that the SNP coding scheme, details of the fitted model, and assumptions being made about the process of XCI are reported, as these are critical when interpreting SNP effects as well as for reproducibility or validation of findings.
Many of the observations we described are supported by recent work from Chen et al (Chen et al., 2019), which also noted the importance of carefully specifying the model and coding schemes when X‐chromosome is included in the GWAS. Theoretical justifications and insights are provided for several points we highlight, such as that sex should always be included as a covariate since it is an confounder for analysis involving X‐chromosome SNPs with traits that have sexual differences. They also highlighted the value of the inclusion of gene–sex interaction terms which statistically eliminates the differences resulting from the choices of baseline allele and XCI assumption when a 2‐df LRT is performed, while it also has advantages in terms of power (Chen et al., 2019).
We also considered the impact of nonrandom XCI or XCI skewness in our simulations. XCI skewness towards one parental allele is a property of the individual female (i.e., some females have higher degrees of skewness than others), and can even vary across the cells and tissues within a female (e.g., some cells/tissues may be skewed towards the paternal allele whereas others towards the maternal allele). XCI skewness in some females and in some cells and tissues adds additional variability that cannot be properly assessed with GWAS genotype data alone, and requires additional information regarding either DNA methylation or gene expression to determine the particular degree of skewness within an individual. However, if the XCI skewness has an impact on the phenotype at the population level, this is equivalent to a nonadditive or dominance genetic model, as noted in Chen et al (2019). It should be noted that in our study we only considered a single scenario when the nonadditive effect is smaller than the additive effect, but more scenarios should be considered in future research. In our analysis, the biases for the SNP term were quite small and the sex term captured most of the additional biases from not including a nonadditive/dominance term in our fitted model. If we increase the nonadditive effect, we expect to see higher biases in all sex, SNP, and interaction terms. However, the inclusion of the interaction term should reduce the magnitude of biases when there is a coding scheme misspecification in the model. Further data simulated under a dominant genetic model would likely lead to additional situations of biases similar to those observed with autosomal SNPs. To overcome these issues, Chen et al suggests modeling a dominance deviation parameter in addition to the SNP × Sex interaction term that we suggested here. Consideration of these issues are an important point for future research.
In some GWAS that include X chromosome SNPs, sex‐stratified analyses are conducted, followed by meta‐analysis of the results (Magi et al., 2010). Investigation of this approach was beyond the scope of this study, and we have not directly compared this approach to fitting the models we describe here, although previous studies have shown that analyzing males and females separately may result in a loss in power (Loley et al., 2011). Importantly, the meta‐analysis approach still depends on the choice of SNP coding in males and females, and makes the critical assumption that the estimated SNP effect is the same in males and females, so the potential biases and challenges with interpretation that we have identified here will likely still apply. This approach also does not allow for estimating the sex effect. We also acknowledge that the number of scenarios we considered was limited. Results from additional scenarios with a change of MAF, prevalence, or direction in interaction term when generating the data were shown in Supporting Information Material. Of those, we observed similar results and our main conclusions remained the same as discussed earlier in the paper.
Unlike most prior literature on analysis of X chromosome SNP data, which focused on the power to detect X chromosome SNP effects (König et al., 2014; Özbek et al., 2018; Wang et al., 2014; Xu & Hao, 2018), this study focused on interpretation of X chromosome SNP effects. As polygenic methods, and in particular, PRS approaches, become more commonplace, it becomes increasingly important to consider the properties of the coefficient estimates themselves. Currently, PRS methods exclude SNPs from the X chromosome due to the complexity in modeling these effects. To be able to incorporate X chromosome SNPs into PRS models, we need to understand potential biases in SNP effect estimates and modeling strategies that can overcome these biases. The work here is a first step in this direction. Standard PRS approaches (Choi & O'Reilly, 2019; Lloyd‐Jones et al., 2019; Vilhjálmsson et al., 2015) do not include interaction terms. Because our work suggests that models including SNP–sex interaction terms may be most appropriate for modeling X chromosome SNPs, these standard PRS approaches would need to be adapted to accommodate estimates from models with SNP × Sex interaction terms.
In summary, this is the first study to examine the coefficient biases that may result from model misspecification of X chromosome SNP effects. Assumptions made about the X chromosome SNP effects should be made clear when reporting and interpreting X chromosome associations. Fitting SNP × Sex interaction terms can avoid coefficient bias regardless of whether or not there are true sex differences in SNP effect, which should be incorporated into future models of polygenic risk prediction including X chromosome SNPs.
Supporting information
Supporting information.
ACKNOWLEDGEMENTS
We thank Ann Westphal and Debbi Strain for assistance with manuscript preparation.
CONFLICT OF INTERESTS
The authors declare that there are no conflict of interests.
Song, Y., Biernacka, J. M., & Winham, S. J. (2021). Testing and estimation of X‐chromosome SNP effects: Impact of model assumptions. Genetic Epidemiology, 45, 577–592. 10.1002/gepi.22393
DATA AVAILABILITY STATEMENT
The data described in the manuscript are simulated data. Code to generate and analyze the data is available from the authors upon request. This study has been conducted using the UK Biobank Resource under Application Number 55108.
REFERENCES
- Appelman, Y., van Rijn, B. B., Ten Haaf, M. E., Boersma, E., & Peters, S. A. (2015). Sex differences in cardiovascular risk factors and disease prevention. Atherosclerosis, 241(1), 211–218. 10.1016/j.atherosclerosis.2015.01.027 [DOI] [PubMed] [Google Scholar]
- Balaton, B. P., Cotton, A. M., & Brown, C. J. (2015). Derivation of consensus inactivation status for X‐linked genes from genome‐wide studies. Biology of Sex Differences, 6, 35. 10.1186/s13293-015-0053-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrel, L., & Willard, H. F. (1999). Heterogeneous gene expression from the inactive X chromosome: An X‐linked gene that escapes X inactivation in some human cell lines but is inactivated in others. Proceedings of the National Academy of Sciences of the United States of America, 96(13), 7364–7369. 10.1073/pnas.96.13.7364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, D., Gao, F., Slavney, A., Ma, L., Waldman, Y. Y., Sams, A. J., Billing‐Ross, P., Madar, A., Spritz, R., & Keinan, A. (2014). Accounting for eXentricities: Analysis of the X chromosome in GWAS reveals X‐linked genes implicated in autoimmune diseases. PLOS One, 9(12), e113684. 10.1371/journal.pone.0113684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, B., Craiu, R. V., Strug, L. J., & Sun, L. (2019). The X factor: A robust and powerful approach to x‐chromosome‐inclusive whole‐genome association studies. https://arxiv.org/abs/1811.00964 [DOI] [PMC free article] [PubMed]
- Chen, B., Craiu, R. V., & Sun, L. (2020). Bayesian model averaging for the X‐chromosome inactivation dilemma in genetic association study. Biostatistics, 21(2), 319–335. 10.1093/biostatistics/kxy049 [DOI] [PubMed] [Google Scholar]
- Choi, S. W., & O'Reilly, P. F. (2019). PRSice‐2: Polygenic Risk Score software for biobank‐scale data. GigaScience, 8(7). 10.1093/gigascience/giz082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton, D. (2008). Testing for association on the X chromosome. Biostatistics, 9(4), 593–600. 10.1093/biostatistics/kxn007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, M., Cioffi, G., Wang, J., Waite, K. A., Ostrom, Q. T., Kruchko, C., Lathia, J. D., Rubin, J. B., Berens, M. E., Connor, J., & Barnholtz‐Sloan, J. S. (2020). Sex differences in cancer incidence and survival: A pan‐cancer analysis. Cancer Epidemiology, Biomarkers and Prevention, 29(7), 1389–1397. 10.1158/1055-9965.Epi-20-0036 [DOI] [PubMed] [Google Scholar]
- Erol, A., Winham, S. J., McElroy, S. L., Frye, M. A., Prieto, M. L., Cuellar‐Barboza, A. B., Fuentes, M., Geske, J., Mori, N., Biernacka, J. M., & Bobo, W. V. (2015). Sex differences in the risk of rapid cycling and other indicators of adverse illness course in patients with bipolar I and II disorder. Bipolar Disorders, 17(6), 670–676. 10.1111/bdi.12329 [DOI] [PubMed] [Google Scholar]
- Gao, F., Chang, D., Biddanda, A., Ma, L., Guo, Y., Zhou, Z., & Keinan, A. (2015). XWAS: A software toolset for genetic data analysis and association studies of the X chromosome. Journal of Heredity, 106(5), 666–671. 10.1093/jhered/esv059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heard, E., & Disteche, C. M. (2006). Dosage compensation in mammals: Fine‐tuning the expression of the X chromosome. Genes and Development, 20(14), 1848–1867. 10.1101/gad.1422906 [DOI] [PubMed] [Google Scholar]
- Hoffmann, T. J., Choquet, H., Yin, J., Banda, Y., Kvale, M. N., Glymour, M., Schaefer, C., Risch, N., & Jorgenson, E. (2018). A large multiethnic genome‐wide association study of adult body mass index identifies novel loci. Genetics, 210(2), 499–515. 10.1534/genetics.118.301479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jons, W. A., Colby, C. L., McElroy, S. L., Frye, M. A., Biernacka, J. M., & Winham, S. J. (2019). Statistical methods for testing X chromosome variant associations: application to sex‐specific characteristics of bipolar disorder. Biology of Sex Differences, 10(1), 57. 10.1186/s13293-019-0272-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khramtsova, E. A., Davis, L. K., & Stranger, B. E. (2019). The role of sex in the genomics of human complex traits. Nature Reviews Genetics, 20(3), 173–190. 10.1038/s41576-018-0083-1 [DOI] [PubMed] [Google Scholar]
- König, I. R., Loley, C., Erdmann, J., & Ziegler, A. (2014). How to include chromosome X in your genome‐wide association study. Genetic Epidemiology, 38(2), 97–103. 10.1002/gepi.21782 [DOI] [PubMed] [Google Scholar]
- Lambert, S. A., Abraham, G., & Inouye, M. (2019). Towards clinical utility of polygenic risk scores. Human Molecular Genetics, 28(R2), R133–r142. 10.1093/hmg/ddz187 [DOI] [PubMed] [Google Scholar]
- Lloyd‐Jones, L. R., Zeng, J., Sidorenko, J., Yengo, L., Moser, G., Kemper, K. E., Wang, H., Zheng, Z., Magi, R., Esko, T., Metspalu, A., Wray, N. R., Goddard, M. E., Yang, J., & Visscher, P. M. (2019). Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nature Communications, 10(1), 5086. 10.1038/s41467-019-12653-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loley, C., Ziegler, A., & König, I. R. (2011). Association tests for X‐chromosomal markers—A comparison of different test statistics. Human Heredity, 71(1), 23–36. 10.1159/000323768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacArthur, J., Bowler, E., Cerezo, M., Gil, L., Hall, P., Hastings, E., Junkins, H., McMahon, A., Milano, A., Morales, J., Pendlington, Z. M., Welter, D., Burdett, T., Hindorff, L., Flicek, P., Cunningham, F., & Parkinson, H. (2017). The new NHGRI‐EBI Catalog of published genome‐wide association studies (GWAS Catalog). Nucleic Acids Research, 45(D1), D896–d901. 10.1093/nar/gkw1133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magi, R., Lindgren, C. M., & Morris, A. P. (2010). Meta‐analysis of sex‐specific genome‐wide association studies. Genetic Epidemiology, 34(8), 846–853. 10.1002/gepi.20540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özbek, U., Lin, H. M., Lin, Y., Weeks, D. E., Chen, W., Shaffer, J. R., Purcell, S. M., & Feingold, E. (2018). Statistics for X‐chromosome associations. Genetic Epidemiology, 42(6), 539–550. 10.1002/gepi.22132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell, S., Neale, B., Todd‐Brown, K., Thomas, L., Ferreira, M. A., Bender, D., Maller, J., Sklar, P., de Bakker, P. I., Daly, M. J., & Sham, P. C. (2007). PLINK: A tool set for whole‐genome association and population‐based linkage analyses. American Journal of Human Genetics, 81(3), 559–575. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riecher‐Rössler, A. (2017). Sex and gender differences in mental disorders. Lancet Psychiatry, 4(1), 8–9. 10.1016/s2215-0366(16)30348-0 [DOI] [PubMed] [Google Scholar]
- Ross, M. T., Grafham, D. V., Coffey, A. J., Scherer, S., McLay, K., Muzny, D., Platzer, M., Howell, G. R., Burrows, C., Bird, C. P., Frankish, A., Lovell, F. L., Howe, K. L., Ashurst, J. L., Fulton, R. S., Sudbrak, R., Wen, G., Jones, M. C., Hurles, M. E., … Joseph, S. S. (2005). The DNA sequence of the human X chromosome. Nature, 434(7031), 325–337. 10.1038/nature03440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahl, E. A., Breen, G., Forstner, A. J., McQuillin, A., Ripke, S., Trubetskoy, V., Mattheisen, M., Wang, Y., Coleman, J., Gaspar, H. A., de Leeuw, C. A., Steinberg, S., Pavlides, J., Trzaskowski, M., Byrne, E. M., Pers, T. H., Holmans, P. A., Richards, A. L., Abbott, L., … Reif, A. (2019). Genome‐wide association study identifies 30 loci associated with bipolar disorder. Nature Genetics, 51(5), 793–803. 10.1038/s41588-019-0397-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tukiainen, T., Villani, A. C., Yen, A., Rivas, M. A., Marshall, J. L., Satija, R., Aguirre, M., Gauthier, L., Fleharty, M., Kirby, A., Cummings, B. B., Castel, S. E., Karczewski, K. J., Aguet, F., Byrnes, A., GTEx, C., Laboratory, Data Analysis & Coordinating Center (LDACC)—Analysis Working, G., Statistical Methods Groups—Analysis Working Group, Enhancing GTEx (eGTEx) Group , … MacArthur, D. G. (2017). Landscape of X chromosome inactivation across human tissues. Nature, 550(7675), 244–248. 10.1038/nature24265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilhjálmsson, B. J., Yang, J., Finucane, H. K., Gusev, A., Lindström, S., Ripke, S., Genovese, G., Loh, P. R., Bhatia, G., Do, R., Hayeck, T., Won, H. H., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Discovery, Biology, and Risk of Inherited Variants in Breast Cancer (DRIVE), s, Kathiresan, S., Pato, M., Pato, C., Tamimi, R., Stahl, E., Zaitlen, N., … Price, A. L. (2015). Modeling linkage disequilibrium increases accuracy of polygenic risk scores. American Journal of Human Genetics, 97(4), 576–592. 10.1016/j.ajhg.2015.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voskuhl, R. (2011). Sex differences in autoimmune diseases. Biology of Sex Differences, 2(1), 1. 10.1186/2042-6410-2-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., Talluri, R., & Shete, S. (2017). Selection of X‐chromosome Inactivation model. Cancer Informatics, 16, 1176935117747272. 10.1177/1176935117747272 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., Yu, R., & Shete, S. (2014). X‐chromosome genetic association test accounting for X‐inactivation, skewed X‐inactivation, and escape from X‐inactivation. Genetic Epidemiology, 38(6), 483–493. 10.1002/gepi.21814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise, A. L., Gyi, L., & Manolio, T. A. (2013). eXclusion: Toward integrating the X chromosome in genome‐wide association analyses. American Journal of Human Genetics, 92(5), 643–647. 10.1016/j.ajhg.2013.03.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, W., & Hao, M. (2018). A unified partial likelihood approach for X‐chromosome association on time‐to‐event outcomes. Genetic Epidemiology, 42(1), 80–94. 10.1002/gepi.22097 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting information.
Data Availability Statement
The data described in the manuscript are simulated data. Code to generate and analyze the data is available from the authors upon request. This study has been conducted using the UK Biobank Resource under Application Number 55108.


