Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Sep 9;60(18):13950–13954. doi: 10.1021/acs.inorgchem.1c01838

Photoinduced Low-Spin → High-Spin Mechanism of an Octahedral Fe(II) Complex Revealed by Synergistic Spin-Vibronic Dynamics

Mátyás Pápai 1,*
PMCID: PMC8456406  PMID: 34498843

Abstract

graphic file with name ic1c01838_0007.jpg

The Fe(II) low-spin (LS; 1A1g, t2g6eg) → high-spin (HS; 5T2g, t2g4eg) light-induced excited spin state trapping (LIESST) mechanism solely involving metal-centered states is revealed by synergistic spin-vibronic dynamics simulations. For the octahedral [Fe(NCH)6]2+ complex, we identify an initial ∼100 fs 1T1g → 3T2g intersystem crossing, controlled by vibronic coupling to antisymmetric Fe–N stretching motion. Subsequently, population branching into 3T1g, 5T2g (HS), and 1A1g (LS) is observed on a subpicosecond time scale, with the dynamics dominated by coherent Fe–N breathing wavepackets. These findings are consistent with ultrafast experiments, methodologically establish a new state of the art, and will give a strong impetus for further intriguing dynamical studies on LS → HS photoswitching.

Short abstract

The low-spin (LS) → high-spin (HS) light-induced excited spin-state trapping (LIESST) mechanism solely involving metal-centered states is revealed by synergestic spin-vibronic dynamics simulations. For the [Fe(NCH)6]2+ complex, we observe <100 fs 1T1g → 3T2g intersystem crossing and subsequent population branching into the 3T1g, 5T2g (HS), and 1A1g (LS) states. The intersystem crossing dynamics is found to be controlled by vibronic coupling to antisymmetric Fe−N stretching modes and coherent breathing wavepackets.

Photoinduced low-spin (LS) → high-spin (HS) transition in transition-metal complexes, known as light-induced excited spin state trapping (LIESST), has attracted great interest since its discovery in 1984.1 LIESST is an intriguing phenomenon both from the point of view of the fundamentals of excited-state processes and revolutionary applicational areas, such as molecular data storage.2 It is known that the LS-to-HS transition can also be triggered by varying the temperature, pressure, and magnetic field;3 in fact, the first discovery of these so-called spin-crossover (SCO) complexes is dated way back to 1931.4

In the past two decades, the LIESST mechanism has been a very “hot” research topic; this is motivated by the fact that the gained knowledge may allow control of excited-state pathways and thus can lead to the design of improved functional molecules and technologies. In the case of switchable hexacoordinated complexes with a FeIIN6 core, which by far dominate the known LIESST-exhibiting systems, irradiation of light converts the singlet ground state [1A1g(LS), t2g6eg] into a quintet metastable state [5T2g(HS), t2g4eg]; thus, a ΔS = 2 net change of the spin momentum occurs. The LIESST mechanism was first investigated in 1991 by Hauser5 for the 1-propyltetrazole [Fe(ptz)6](BF4)2 pseudooctahedral SCO Fe(II) complex, promoted to the lowest singlet metal-centered (MC) state. Utilizing UV/vis/near-IR absorption spectroscopy, he identified a triplet intermediate state, which at 10 K decays via branching into a quintet metastable state [5T2g(HS), 75%] and the ground state [1A1g(LS), 25%], occurring via intersystem crossing (ISC), as illustrated in Figure 1. More recently, for the Zn-doped crystal [Zn0.9Fe0.1(ptz)6](BF4)2, probed at 125 K by time-resolved absorption spectroscopy, Hauser and co-workers identified the upper triplet 3T2g as the intermediate state, which is formed from 1T1g in <150 fs and decays into the 5T2g HS state in 1.2 ps.6 The HS state is metastable at low temperatures (T < 50 K), and its lifetime is determined by quantum-mechanical tunneling.

Figure 1.

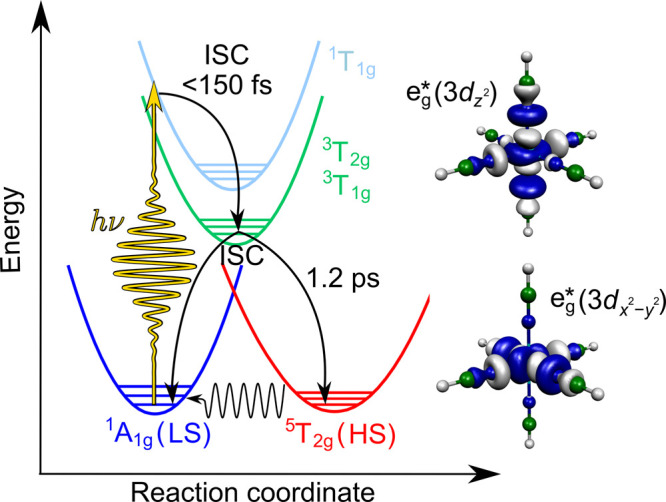
Figure 1

Open in a new tab

Schematic mechanistic picture of the LIESST effect in the case of excitation into the lowest 1MC (1T1g) state by 530 nm light. The wavy arrow illustrates the low-temperature HS → LS relaxation by tunneling. The excited-state lifetimes are taken for [Zn0.9Fe0.1(ptz)6](BF4)2 from ref (6). The electronic state labels are consistent with Oh point group symmetry. Also shown are the eg* antibonding orbitals of the complex investigated in the present work, [Fe(NCH)6]2+, which are populated in the excited states.

Despite these valuable mechanistic insights, several unknowns remain, in most cases, because of the ambiguities in the interpretation of the experimental data. An excellent example is the more complicated case of [Fe(bipy)3]2+ (bipy = 2,2′-bipyridine), a LS Fe(II) complex, which became the LS ↔ HS photoswitching prototype for time-resolved investigations. [Fe(bipy)3]2+ is converted to the HS state in <100 fs, initiated by irradiation into the optically active singlet metal-to-ligand charge-transfer (MLCT) band. This <100 fs time scale and the HS lifetime (ca. 650 ps in aqueous solution) are consistent for various experimental studies, but it is strongly debated how the HS state is populated.7−9 A final consensus is yet to be established; in order to achieve this goal, theory, which has the potential to complement and support time-resolved experiments, has a crucial role. However, the computational state of the art for light-induced singlet-to-quintet transitions has so far been limited to analysis of the static potential energy surfaces (PESs)10/couplings11 and estimation of the excited-state lifetimes by Fermi’s golden rule.12,13 Albeit often useful, these approaches face severe shortcomings when it comes to fast electronic relaxation such as LIESST, with a time scale comparable to that of nuclear motion. In fact, this nuclear–electronic coupling, leading to a dynamic mixing of the electronic states, is among the main sources for the complexity of the obtained time-resolved experimental data, which theory is intended to alleviate.

In this Communication, we present the first theoretical dynamics study on LS → HS photoswitching with excitation into 1MC states (1T1g, [Fe(ptz)6]2+ prototype; Figure 1). In order to achieve feasibility at a high computational level, we investigate the excited-state dynamics of [Fe(NCH)6]2+, a well-established model14−17 for metastable Fe(II)-based SCO systems. Its validity, with a special emphasis on LIESST, is discussed in the Supporting Information (SI). Employing a synergistic spin-vibronic approach,18,19 we achieve an invaluable mechanistic understanding, whose adequacy is assessed and confirmed by its consistency with the above-discussed experiments.

Herein, we employ a synergistic approach, which exploits the complementary character of trajectory surface hopping (TSH; full dimensionality) and quantum dynamics (QD; fully quantum description). We utilize full-dimensional TSH on potentials computed on-the-fly to select the dominant nuclear degrees of freedom and QD on high-level ab initio (CASPT2) precomputed surfaces along the selected modes for the accurate simulation of LIESST excited-state dynamics. A brief methodological description is provided in the Computational Methods section, with details given in the SI.

Figure 2 presents the normal-mode activity of the vibrational motion, obtained from the excited-state TSH trajectories. As is clear from the figure, three modes, ν13, ν14, and ν15, dominate the excited-state nuclear motion. As shown in Figure 3, all three modes have Fe–N stretching character, but while the 2-fold-degenerate ν13 and ν14 modes are antisymmetric, ν15 is a totally symmetric (breathing) mode. These three Fe–N stretching modes are in excellent agreement with the natural choice of coordinates upon the occupation of eg* antibonding orbitals, shown in Figure 1, in MC excited states.

Figure 2.

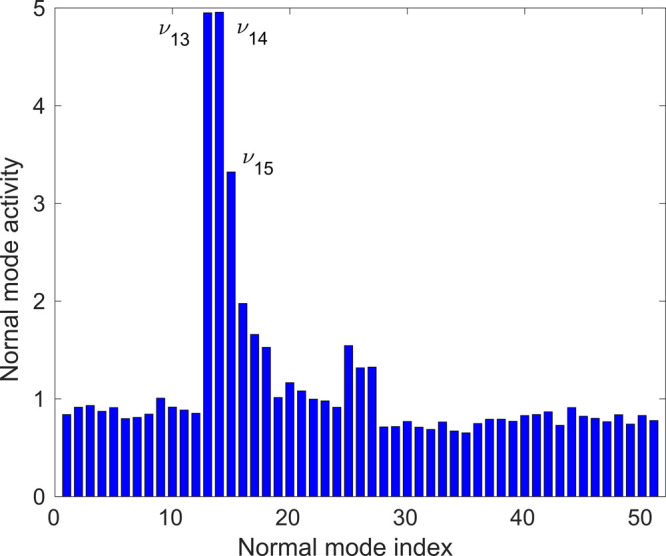
Figure 2

Open in a new tab

Dynamic normal-mode activity, as determined from the standard deviation of nuclear displacements, projected onto the ground-state normal modes. This was obtained from the singlet–triplet TSH simulations. The labels of the three dominant normal modes, ν13, ν14, and ν15, are depicted. As illustrated in Figure 3, the character of these three modes is Fe–N stretching.

Figure 3.

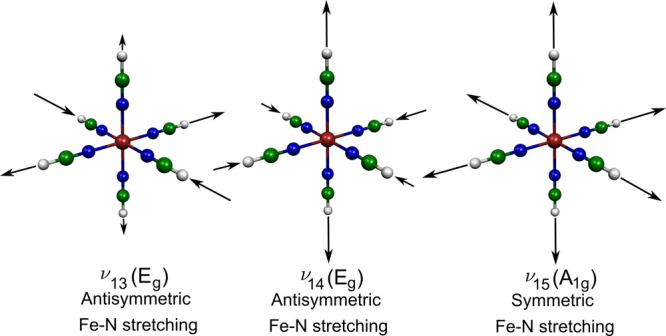
Figure 3

Open in a new tab

Illustration of the three dominant modes of [Fe(NCH)6]2+, ν13 (antisymmetric Fe–N stretching), ν14 (antisymmetric Fe–N stretching), and ν15 (symmetric Fe–N stretching), identified by the TSH simulations. Also shown are the Oh symmetry labels of the modes.

Figure 4 shows the PESs along modes ν15 and ν14; the PESs along ν13 are shown in Figure S7. While the ν15 breathing mode is crucial to connect the LS (1A1g) and HS (5T2g) states (Figure 4a), it maintains the octahedral symmetry and does not allow the different singlet and triplet MC components to cross. The reason for this is that, in the singlet and triplet excited states, a single eg* orbital is populated, which activates antisymmetric Fe–N stretching modes, while the ν15 breathing mode is totally symmetric. Indeed, as seen in Figure 4b, the excited-state potentials split along ν14, allowing the possibility of singlet–triplet ISC and triplet internal conversion (IC) via the intersection of the corresponding MC PESs.

Figure 4.

Figure 4

Open in a new tab

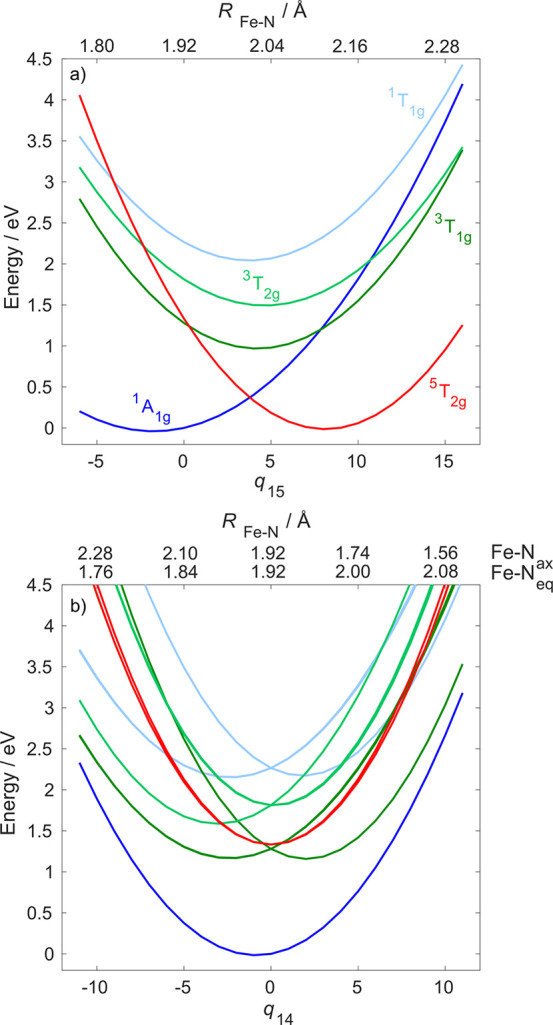
One-dimensional cuts of the diabatic CASPT2 PESs along (a) ν15 and (b) ν14. Nuclear displacements are given in dimensionless mass-frequency-scaled normal coordinates and Fe–N distances (Å).

In Figure 5, we present the electronic population dynamics, as obtained from the three-dimensional QD simulation utilizing the selected modes and all relevant singlet–triplet–quintet states. As shown in the figure, the 1T1g population decay has two components, characterized by the 39 and 168 fs exponential time constants. These time scales are in excellent agreement with the experimentally observed <150 fs ISC.6 As proposed by Marino et al.,6 the 1T1g states indeed deactivate via the 3T2g states. Subsequently, the excited-state population flows on a subpicosecond time scale to 3T1g by triplet IC and to the 5T2g manifold via triplet–quintet ISC; as a minor component, the ground state 1A1g is recovered. The 3T1g population is stable on the 1 ps time duration of the simulation, which is consistent with its 39 ps6 lifetime detected experimentally.20 Crucially, the simulated dynamics captures all important aspects of the LIESST mechanism revealed by experiments: very fast singlet–triplet ISC, the role of 3T2g states as intermediates, and branching into the HS/LS states. This consistency supports the presented results, which for certain aspects, such as the singlet–triplet ISC, reach even a quantitative agreement with experiment.6

Figure 5.

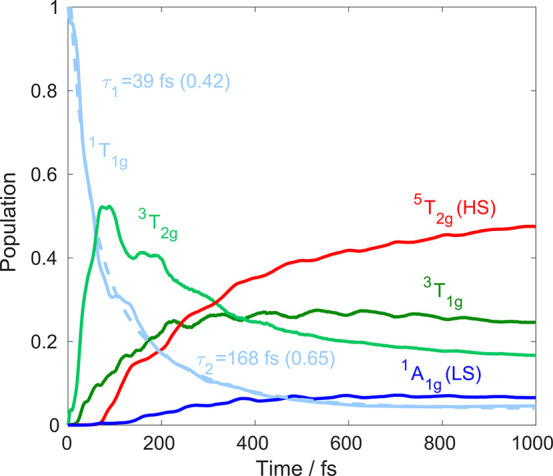
Figure 5

Open in a new tab

Simulated population dynamics upon excitation into the 1T1g manifold. The 1T1g population curve (light blue) is fitted with a biexponential functional (dashed line); the numbers in parentheses denote the coefficients of the two exponential components.

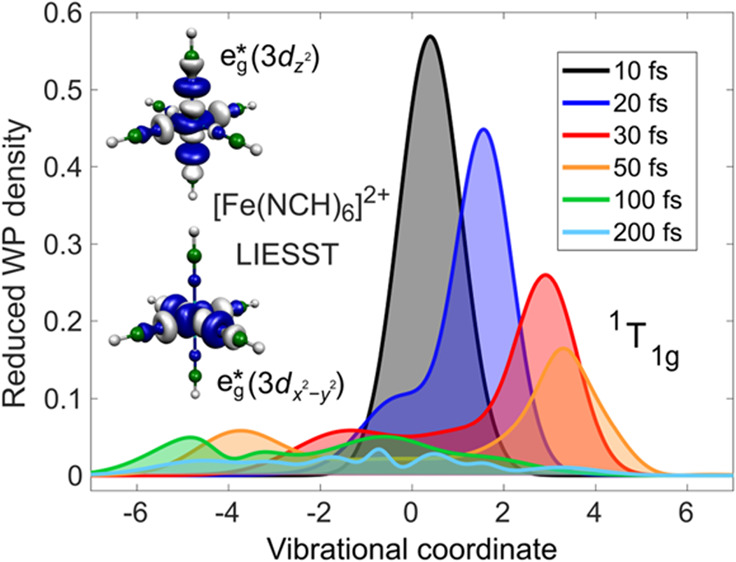
Finally, we reveal fine details of the LIESST mechanism based on the time evolution of excited-state nuclear wavepackets. We now analyze the singlet–triplet ISC along ν14, which is the natural choice for the involved 1T1g/3T2g states (occupation of a single eg* orbital). Figure 6a shows snapshots of the excited-state singlet wavepacket along ν14 for the initial 200 fs. The 1T1g wavepacket immediately starts to propagate away from q14 = 0, entering the 1T1g/3T2g crossing region. This, combined with a sizable spin–orbit coupling (∼175 and 250 cm–1), allows efficient ISC to the 3T2g manifold, which is indeed what is observed in Figure 5. On the 100–200 fs time scale, the wavepacket becomes more diffuse, which is the reason why the ISC is slower for >100 fs. These results highlight the importance of vibronic motion, as confirmed by the discrepancy between the 36 ps 1T1g → 3T2g ISC time constant of ref (13) for [Fe(mtz)6]2+, based on Fermi’s golden rule, and the <150 fs experimental6 and simulated 39/168 fs values obtained in this work.

Figure 6.

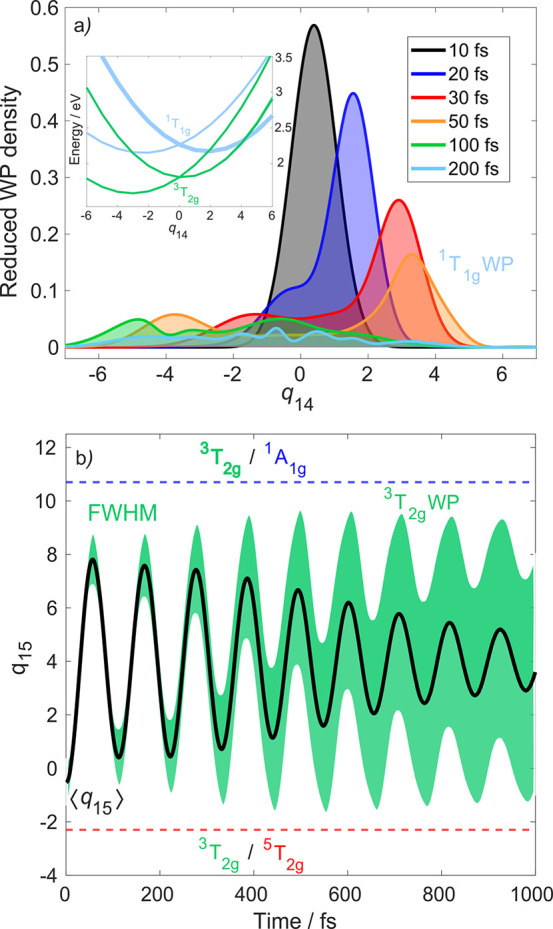
Figure 6

Open in a new tab

(a) Wavepacket (WP) dynamics along ν14 (1T1g WP). The inset shows the relevant excited-state potentials (the 1T1g component, from which the dynamics is initiated, is displayed using a thick light-blue line). (b) WP dynamics along ν15 (3T2g WP), illustrated by the wavepacket centroid (black) and Gaussian width (green; fwhm). Also shown are the positions of the relevant intersections (3T2g/5T2g and 3T2g/1A1g) along ν15 (dashed lines).

In Figure 6b, we analyze the wavepacket motion in the intermediate 3T2g state along ν15. Clearly, a coherent wavepacket oscillation is induced, with a period of ∼110 fs. The wavepacket dephases and spreads, and, importantly, the Gaussian full width at half-maximum (fwhm, green) does not reach the crossings with the 5T2g and 1A1g states (dashed lines in Figure 6b). This is to say that the 3T2g wavepacket only slightly leaks into the crossing region, which is the reason why the quintet population rises relatively slowly (in [Fe(bipy)3]2+, the HS state is populated in <100 fs7,8). Although the wavepacket gains more access to the 3T2g/5T2g intersection along ν14, this channel does not allow significant net population flow to the 5T2g states. This is due to very efficient 5T2g → 3T1g deactivation, favored by the energetics and easy access to the crossing region (located just at the 5T2g minimum) along ν14, as is clear from Figure 4b.

In this Communication, we revealed the Fe(II) LIESST mechanism of Fe[(NCH)6]2+ using synergistic spin-vibronic dynamics simulations. The obtained mechanistic picture is consistent with the experimental findings and includes assignment of the principal intermediate 3T2g, whose dynamics are controlled by the key antisymmetric (ν14) and symmetric (ν15) Fe–N stretching vibrations. Importantly, the present work establishes a new theoretical state of the art for LS → HS photoswitching and will certainly motivate intriguing dynamical studies, both experimental and theoretical ones.

Computational Methods. The TSH simulations are based on Tully’s fewest switches,21 a three-step propagator technique22 (with transformations between the adiabatic–spin diabatic and diagonal representations), and local diabatization.23 The QD simulations are based on a diabatic vibronic-coupling24,25/spin-vibronic26−29 Hamiltonian and the multiconfigurational time-dependent Hartree (MCTDH) method.30 Our methodology uses the following implementations: TSH, SHARC2.1(31) interfaced to ORCA4.2(32,33) utilizing time-dependent density functional theory (TD-DFT; B3LYP*,34,35 singlet–triplet states including spin–orbit coupling); QD, Heidelberg MCTDH8.4;30 CASPT2 (12 electrons/14 orbitals: five–five Fe 3d/4d-based, two-σFe–N bonding and a pair of Fe 3s/4s correlating active orbitals), OpenMolcas20.10.36 Further details of the utilized methodology are described in the SI.

Acknowledgments

The research leading to the presented results has received funding from the Hungarian National Research, Development and Innovation Fund (Grant NKFIH PD 134976). The author acknowledges support from the János Bolyai Scholarship of the Hungarian Academy of Sciences. The author is grateful to Tamás Rozgonyi for fruitful discussions. Guest access to the central HPC cluster of the Technical University of Denmark is acknowledged.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.1c01838.

  • Validity of the [Fe(NCH)6]2+ model, normal-mode frequencies and characters, methodological and computational details of the TSH and QD simulations, and optimized ground-state geometries (PDF)

The author declares no competing financial interest.

Supplementary Material

ic1c01838_si_001.pdf (4.2MB, pdf)

References

  1. Decurtins S.; Gütlich P.; Köhler C.; Spiering H.; Hauser A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron (II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. 10.1016/0009-2614(84)80403-0. [DOI] [Google Scholar]
  2. Létard J.-F.; Guionneau P.; Goux-Capes L.. Spin Crossover in Transition Metal Compounds III; Springer: Berlin, 2004; pp 221–249. [Google Scholar]
  3. Bousseksou A.; Molnár G.; Matouzenko G. Switching of Molecular Spin States in Inorganic Complexes by Temperature, Pressure, Magnetic Field and Light: Towards Molecular Devices. Eur. J. Inorg. Chem. 2004, 2004, 4353–4369. 10.1002/ejic.200400571. [DOI] [Google Scholar]
  4. Cambi L.; Szegö L. Über die magnetische Susceptibilität der komplexen Verbindungen. Ber. Dtsch. Chem. Ges. B 1931, 64, 2591–2598. 10.1002/cber.19310641002. [DOI] [Google Scholar]
  5. Hauser A. Intersystem crossing in the [Fe(ptz)6](BF4)2 spin crossover system (ptz = 1-propyltetrazole). J. Chem. Phys. 1991, 94, 2741–2748. 10.1063/1.459851. [DOI] [Google Scholar]
  6. Marino A.; Chakraborty P.; Servol M.; Lorenc M.; Collet E.; Hauser A. The Role of Ligand-Field States in the Ultrafast Photophysical Cycle of the Prototypical Iron(II) Spin-Crossover Compound [Fe(ptz)6](BF4)2. Angew. Chem., Int. Ed. 2014, 53, 3863–3867. 10.1002/anie.201310884. [DOI] [PubMed] [Google Scholar]
  7. Zhang W.; Alonso-Mori R.; Bergmann U.; Bressler C.; Chollet M.; Galler A.; Gawelda W.; Hadt R.; Hartsock R.; Kroll T.; et al. Tracking excited-state charge and spin dynamics in iron coordination complexes. Nature 2014, 509, 345–348. 10.1038/nature13252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Auböck G.; Chergui M. Sub-50-fs photoinduced spin crossover in [Fe(bpy)3]2+. Nat. Chem. 2015, 7, 629–633. 10.1038/nchem.2305. [DOI] [PubMed] [Google Scholar]
  9. Moguilevski A.; Wilke M.; Grell G.; Bokarev S. I.; Aziz S. G.; Engel N.; Raheem A. A.; Kühn O.; Kiyan I. Y.; Aziz E. F. Ultrafast Spin Crossover in [FeII(bpy)3]2+: Revealing Two Competing Mechanisms by Extreme Ultraviolet Photoemission Spectroscopy. ChemPhysChem 2017, 18, 465–469. 10.1002/cphc.201601396. [DOI] [PubMed] [Google Scholar]
  10. Vankó G.; Bordage A.; Pápai M.; Haldrup K.; Glatzel P.; March A. M.; Doumy G.; Britz A.; Galler A.; Assefa T.; et al. Detailed Characterization of a Nanosecond-Lived Excited State: X-ray and Theoretical Investigation of the Quintet State in Photoexcited [Fe(terpy)2]2+. J. Phys. Chem. C 2015, 119, 5888–5902. 10.1021/acs.jpcc.5b00557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sousa C.; Llunell M.; Domingo A.; de Graaf C. Theoretical evidence for the direct 3MLCT-HS deactivation in the light-induced spin crossover of Fe(II)–polypyridyl complexes. Phys. Chem. Chem. Phys. 2018, 20, 2351–2355. 10.1039/C7CP08098K. [DOI] [PubMed] [Google Scholar]
  12. Sousa C.; de Graaf C.; Rudavskyi A.; Broer R.; Tatchen J.; Etinski M.; Marian C. M. Ultrafast Deactivation Mechanism of the Excited Singlet in the Light-Induced Spin Crossover of [Fe(2,2’-bipyridine)3]2+. Chem. - Eur. J. 2013, 19, 17541–17551. 10.1002/chem.201302992. [DOI] [PubMed] [Google Scholar]
  13. Sousa C.; de Graaf C.; Rudavskyi A.; Broer R. Theoretical Study of the Light-Induced Spin Crossover Mechanism in [Fe(mtz)6]2+ and [Fe(phen)3]2+. J. Phys. Chem. A 2017, 121, 9720–9727. 10.1021/acs.jpca.7b10687. [DOI] [PubMed] [Google Scholar]
  14. Kepenekian M.; Robert V.; Le Guennic B.; De Graaf C. Energetics of [Fe(NCH)6]2+ via CASPT2 calculations: A spin-crossover perspective. J. Comput. Chem. 2009, 30, 2327–2333. 10.1002/jcc.21236. [DOI] [PubMed] [Google Scholar]
  15. Droghetti A.; Alfè D.; Sanvito S. Assessment of density functional theory for iron(II) molecules across the spin-crossover transition. J. Chem. Phys. 2012, 137, 124303. 10.1063/1.4752411. [DOI] [PubMed] [Google Scholar]
  16. Lawson Daku L. M.; Aquilante F.; Robinson T. W.; Hauser A. Accurate Spin-State Energetics of Transition Metal Complexes. 1. CCSD(T), CASPT2, and DFT Study of [M(NCH)6]2+ (M = Fe, Co). J. Chem. Theory Comput. 2012, 8, 4216–4231. 10.1021/ct300592w. [DOI] [PubMed] [Google Scholar]
  17. Fumanal M.; Wagner L. K.; Sanvito S.; Droghetti A. Diffusion Monte Carlo Perspective on the Spin-State Energetics of [Fe(NCH)6]2+. J. Chem. Theory Comput. 2016, 12, 4233–4241. 10.1021/acs.jctc.6b00332. [DOI] [PubMed] [Google Scholar]
  18. Capano G.; Penfold T. J.; Chergui M.; Tavernelli I. Photophysics of a copper phenanthroline elucidated by trajectory and wavepacket-based quantum dynamics: a synergetic approach. Phys. Chem. Chem. Phys. 2017, 19, 19590–19600. 10.1039/C7CP00436B. [DOI] [PubMed] [Google Scholar]
  19. Gómez S.; Heindl M.; Szabadi A.; González L. From Surface Hopping to Quantum Dynamics and Back. Finding Essential Electronic and Nuclear Degrees of Freedom and Optimal Surface Hopping Parameters. J. Phys. Chem. A 2019, 123, 8321–8332. 10.1021/acs.jpca.9b06103. [DOI] [PubMed] [Google Scholar]
  20. The 3T1g lifetime was measured through the reverse LIESST process, in which the HS state is converted to the LS state by irradiation with 830 nm light.
  21. Tully J. C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
  22. Mai S.; Marquetand P.; González L. A general method to describe intersystem crossing dynamics in trajectory surface hopping. Int. J. Quantum Chem. 2015, 115, 1215–1231. 10.1002/qua.24891. [DOI] [Google Scholar]
  23. Granucci G.; Persico M.; Zoccante A. Including quantum decoherence in surface hopping. J. Chem. Phys. 2010, 133, 134111. 10.1063/1.3489004. [DOI] [PubMed] [Google Scholar]
  24. Cederbaum L. S.; Köppel H.; Domcke W. Multimode vibronic coupling effects in molecules. Int. J. Quantum Chem. 1981, 20, 251–267. 10.1002/qua.560200828. [DOI] [Google Scholar]
  25. Köppel H.; Domcke W.; Cederbaum L. S.. Advances in Chemical Physics; John Wiley & Sons, Ltd., 1984; pp 59–246. [Google Scholar]
  26. Capano G.; Chergui M.; Rothlisberger U.; Tavernelli I.; Penfold T. J. A Quantum Dynamics Study of the Ultrafast Relaxation in a Prototypical Cu(I)–Phenanthroline. J. Phys. Chem. A 2014, 118, 9861–9869. 10.1021/jp509728m. [DOI] [PubMed] [Google Scholar]
  27. Eng J.; Gourlaouen C.; Gindensperger E.; Daniel C. Spin-Vibronic Quantum Dynamics for Ultrafast Excited-State Processes. Acc. Chem. Res. 2015, 48, 809–817. 10.1021/ar500369r. [DOI] [PubMed] [Google Scholar]
  28. Pápai M.; Vankó G.; Rozgonyi T.; Penfold T. J. High Efficiency Iron Photosensitiser Explained with Quantum Wavepacket Dynamics. J. Phys. Chem. Lett. 2016, 7, 2009–2014. 10.1021/acs.jpclett.6b00711. [DOI] [PubMed] [Google Scholar]
  29. Penfold T. J.; Gindensperger E.; Daniel C.; Marian C. M. Spin-Vibronic Mechanism for Intersystem Crossing. Chem. Rev. 2018, 118, 6975–7025. 10.1021/acs.chemrev.7b00617. [DOI] [PubMed] [Google Scholar]
  30. Beck M.; Jäckle A.; Worth G.; Meyer H.-D. The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. 10.1016/S0370-1573(99)00047-2. [DOI] [Google Scholar]
  31. Mai S.; Marquetand P.; González L. Nonadiabatic Dynamics: The SHARC Approach. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1370 10.1002/wcms.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
  33. Neese F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1327 10.1002/wcms.1327. [DOI] [Google Scholar]
  34. Reiher M.; Salomon O.; Artur Hess B. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. 10.1007/s00214-001-0300-3. [DOI] [Google Scholar]
  35. Reiher M. Theoretical Study of the Fe(phen)2(NCS)2 Spin-Crossover Complex with Reparametrized Density Functionals. Inorg. Chem. 2002, 41, 6928–6935. 10.1021/ic025891l. [DOI] [PubMed] [Google Scholar]
  36. Fdez Galván I.; Vacher M.; Alavi A.; Angeli C.; Aquilante F.; Autschbach J.; Bao J. J.; Bokarev S. I.; Bogdanov N. A.; Carlson R. K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. 10.1021/acs.jctc.9b00532. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic1c01838_si_001.pdf (4.2MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES