Inverse Probability Weighted Estimators of Vaccine Effects Accommodating Partial Interference and Censoring

Summary:

Estimating population-level effects of a vaccine is challenging because there may be interference, i.e., the outcome of one individual may depend on the vaccination status of another individual. Partial interference occurs when individuals can be partitioned into groups such that interference occurs only within groups. In the absence of interference, inverse probability weighted (IPW) estimators are commonly used to draw inference about causal effects of an exposure or treatment. Tchetgen Tchetgen and VanderWeele (2012) proposed a modified IPW estimator for causal effects in the presence of partial interference. Motivated by a cholera vaccine study in Bangladesh, this paper considers an extension of the Tchetgen Tchetgen and VanderWeele IPW estimator to the setting where the outcome is subject to right censoring using inverse probability of censoring weights (IPCW). Censoring weights are estimated using proportional hazards frailty models. The large sample properties of the IPCW estimators are derived, and simulation studies are presented demonstrating the estimators’ performance in finite samples. The methods are then used to analyze data from the cholera vaccine study.

1. Introduction

Estimating population-level effects of a vaccine is challenging because there may be interference, i.e., the outcome of one individual may depend on the vaccination status of another individual. Partial interference is a special case of interference where individuals can be partitioned into groups such that interference does not occur between individuals in different groups but may occur between individuals in the same group (Sobel 2006). Partial interference might be a reasonable assumption if groups of individuals are sufficiently separated geographically, socially, and/or temporally. In this paper we consider assessing the effects of cholera vaccination based on a study in Matlab, Bangladesh (Ali et al. 2005), assuming partial interference based on the spatial location of residences of study participants (Perez-Heydrich et al. 2014). Effects due to interference, also known as spillover effects or peer effects, are of interest in many areas, including criminology, developmental psychology, econometrics, education, political science, social media and network analysis.

Inferential methods about spillover effects have been developed for randomized experiments (Rosenbaum, 2007; Hudgens and Halloran, 2008; Baird et al., 2018). However, in some settings it may not be feasible or ethical to randomize groups or individuals to different treatment or exposure conditions. In the observational setting, Tchetgen Tchetgen and VanderWeele (henceforth TV) (2012) proposed inverse probability weighted (IPW) estimators for different causal effects when there may be partial interference. Large sample properties of these IPW estimators were considered by Perez-Heydrich et al. (2014) and Liu et al. (2016). While motivated by observational studies, these estimators may also be applied in cluster randomized trials where partial interference is assumed and there is non-compliance, i.e., not all individuals receive the treatment assigned to their cluster. These estimators are also applicable to settings such as the cholera vaccine study where all individuals in the study were randomized but only a subset chose to participate in the trial.

In settings where the outcome of interest is a time to event, the outcome may be subject to right censoring due to study completion or participant drop-out. For example, in the Bangladesh cholera vaccine trial, some study participants emigrated out of the field trial area and hence were lost to follow-up. To date most methods that permit interference do not allow for right censored outcomes. One exception is Loh et al. (2020), who allow for right censored outcomes and interference, but require treatment to be randomized. In the absence of interference, censoring is often accommodated via inverse probability of censoring weights along with inverse probability treatment weights (e.g., Robins and Finkelstein (2000)).

In this paper, an extension of the TV IPW estimator is considered for observational studies where there may be partial interference and the outcome is subject to right censoring using inverse probability of censoring weights (IPCW). The proposed methods are developed in Section 2. In Section 3 simulation results are presented demonstrating the empirical performance of the proposed methods in finite sample settings. In Section 4 the methods are used to analyze the Bangladesh cholera vaccine study. Section 5 concludes with a discussion.

2. Methods

2.1. Estimands

Suppose data are observed from m groups of individuals, with n_i individuals per group for i = 1, … , m. In the cholera vaccine study analysis presented below, participants are partitioned into m = 700 groups (neighborhoods) according to the geographical location of their household of residence. Let A_ij = 1 if individual j in group i receives treatment (e.g., vaccine) and A_ij = 0 otherwise. Let A_i = (A_i1, A_i2, …, A_ini) and A_i,−j (A_i1, A_i2, …, A_ij−1, A_ij+1 …, A_ini). Let a_i and a_i,−j denote possible realizations of A_i and A_i,−j, and let $\mathcal{A}(n)$ denote the set of all possible 2ⁿ treatments for a group size of n = 1, 2, …. Assume partial interference and denote the potential time to event for individual j in group i if, possibly counter to fact, group i receives treatment a_i by T_ij(a_i). In the motivating vaccine study, we are interested in time until incident cholera. The notation T_ij(a_i) reflects the partial interference assumption, i.e., the potential outcome of individual j in group i does not depend on the treatment of individuals outside group i. Below the notation T_ij(a, a_i,−j) is sometimes used to make explicit the treatment for individual j and the treatment for all other individuals in group i. Let ${\mathbf{T}}_i(.)=\{T_{ij}({\mathbf{a}}_i):{\mathbf{a}}_i\in \mathcal{A}(n_i),j=1,2,\dots ,n_i\}$ denote the set of all potential event times for individuals in group i.

Suppose the event times are subject to right censoring, e.g., due to loss to follow-up or study completion. Let C_ij denote the potential censoring times for individual j in group i. Let Δ_ij = 1 if T_ij(A_i) ⩽ C_ij and Δ_ij = 0 otherwise, and let X_ij = min(T_ij(A_i), C_ij). Define X_i = (X_i1, X_i2, … , X_ini) and Δ_i = (Δ_i1, Δ_i2, … , Δ_ini). Denote by L_ij the vector of baseline covariates for subject j in group i and by L_i baseline covariates for all subjects in group i, i.e., L_i = (L_i1, L_i2, … , L_ini). Assume that the m groups are randomly sampled from an infinite superpopulation of groups such that the observed data are m i.i.d. copies of O_i = (L_i, A_i, X_i, Δ_i).

In the absence of interference, treatment effects are typically defined as contrasts in mean potential outcomes for different counterfactual scenarios, e.g., the average treatment effect is usually defined as the difference in the mean potential outcome had all individuals received treatment versus had no individuals received treatment. Similarly, in the setting where there is partial interference, causal effects may be defined as contrasts in mean potential outcomes for different counterfactual scenarios. Here we consider counterfactual scenarios where the marginal probability that an individual receives treatment, Pr_α(A_ij = 1), equals α for different values of α ∈ (0, 1). The notation Pr_α(·) indicates that the probability corresponds to the distribution under the counterfactual scenario. Specifically, the Bernoulli treatment allocation strategy (or policy) described in TV is considered wherein individuals independently select treatment with probability α. Let π(a_i, α) denote the probability that group i receives treatment a_i under Bernoulli allocation strategy α. That is, $\pi ({\mathbf{a}}_i,\alpha )={\text{Pr}}_{\alpha }({\mathbf{A}}_i={\mathbf{a}}_i)={\prod }_{k=1}^{n_i}{\alpha }^{a_{ik}}(1-\alpha {)}^{1-a_{ik}}$. Similarly let $\pi ({\mathbf{a}}_{i,-j},\alpha )={\text{Pr}}_{\alpha }({\mathbf{A}}_{i,-j}={\mathbf{a}}_{i,-j}\mid A_{ij}=a)={\prod }_{k=1,k\ne j}^{n_i}{\alpha }^{a_{ik}}(1-\alpha {)}^{1-a_{ik}}$.

The causal estimands of interest defined below are contrasts in the risk of having an event by time t for different combinations of treatment a and allocation strategies α. To define these estimands, let

$${\overline{F}}_{ij}(t,a,\alpha )=\sum _{{\mathbf{a}}_{i,-j}\in \mathcal{A}(n_i-1)}I\{T_{ij}(a,{\mathbf{a}}_{i,-j})⩽t\}\pi ({\mathbf{a}}_{i,-j},\alpha ),$$

and

$${\overline{F}}_{ij}(t,\alpha )=\sum _{{\mathbf{a}}_i\in \mathcal{A}(n_i)}I\{T_{ij}({\mathbf{a}}_i)⩽t\}\pi ({\mathbf{a}}_i,\alpha ).$$

In words, ${\overline{F}}_{ij}(t,a,\alpha )$ is the probability that individual j in group i will have an event by time t when receiving treatment a and the group adopts policy α. Likewise, ${\overline{F}}_{ij}(t,\alpha )$ is the probability that individual j in group i will have an event by time t when the group adopts allocation strategy α. Denote the group average risks by ${\overline{F}}_i(t,a,\alpha )=n_i^{-1}{\sum }_{j=1}^{n_i}{\overline{F}}_{ij}(t,a,\alpha )$ and ${\overline{F}}_i(t,\alpha )=n_i^{-1}{\sum }_{j=1}^{n_i}{\overline{F}}_{ij}(t,\alpha )$. Let $\mu (t,a,\alpha )=E_{\alpha }\{{\overline{F}}_i(t,a,\alpha )\}$ and $\mu (t,\alpha )=E_{\alpha }\{{\overline{F}}_i(t,\alpha )\}$ where E_α{.} denotes the expected value under the counterfactual setting when policy α is adopted in the superpopulation of groups. In the cholera vaccine study described in Section 4, μ(t, a, α) denotes the average risk of acquiring cholera by time t when an individual receives treatment a and other individuals receive vaccine with probability α.

Various effects of treatment can be defined by contrasts in μ(t, a, α) and μ(t, α). The direct effect is obtained by comparing the probability of an event when an individual receives treatment versus when not receiving treatment for a fixed allocation strategy. In particular, the direct effect at time t corresponding to policy α is defined to be DE(t, α) = μ(t, 0, α) – μ(t, 1, α). The indirect (or spillover) effect is the difference in the probability of an event by time t for two different policies when the individual does not receive treatment. Specifically, the indirect effect is given by IE(t, α₁, α₂) = μ(t, 0, α₁) – μ(t, 0, α₂) for allocation strategies α₁ and α₂. An indirect effect can analogously be defined when an individual is vaccinated. The total effect is the difference between the probability of an event by time t when an individual does not receive treatment under policy α₁ and when an individual receives treatment under policy α₂, i.e., TE(t, α₁, α₂) = μ(t, 0, α₁) – μ(t, 1, α₂). Finally, the overall effect is the difference between the probability of an event by time t for policy α₁ versus α₂, i.e., OE(t, α₁, α₂) = μ(t, α₁) – μ(t, α₂).

2.2. Assumptions

Assume the following:

1. Conditional independent treatment: A_i ⫫ T_i(.) ∣ L_i

2. Treatment positivity: Pr(A_i = a_i ∣ L_i) > 0 for all ${\mathbf{a}}_i\in \mathcal{A}(n_i)$

3. Conditional independent censoring: C_ij ⫫ T_ij(A_i) ∣ {L_i, A_i}

4. Non-censoring positivity: Pr(Δ_ij = 1 ∣ L_i, A_i) > 0

Assumption I states that the potential event times for individuals within the same group are conditionally independent of the treatment received by the group given covariates; this is a group-level generalization of the usual individual-level no unmeasured confounders assumption often made in the absence of interference. In the cholera vaccine study, Assumption I would be violated if there was an unobserved common cause of one or more components of vaccination status and time to cholera. For instance, individuals who were more concerned about cholera may have been more likely to participate in the trial and also more likely to practice other measures (e.g., hand washing) to prevent cholera. Treatment positivity assumes that each group has a non-zero probability of being assigned every possible treatment combination given covariates for the group (Perez-Heydrich et al., 2014). Assumption II is reasonable in the cholera study because all women and children in Matlab were invited to participate in the vaccine trial. Assumption III supposes that conditional on baseline group covariates and group treatment, an individual’s failure time is independent of their censoring time. Assumption III would be violated in the cholera study if there was some variable other than L_i and A_i which were prognostic of both the censoring and time to cholera. For example, this assumption might not hold if individuals living in areas of Matlab with a high burden of cholera were more likely to emigrate outside of the study area. Note censoring times between individuals within the same cluster need not be independent; indeed, the frailty model introduced below allows for such dependency via a cluster random effect. Finally Assumption IV indicates that each individual has a non-zero probability of not being censored at each observation time (Rotnitzky et al., 2007). In the next section IPW estimators are proposed and shown to be consistent (and asymptotically normal) for the direct, indirect, total, and overall effects under Assumptions I-IV.

2.3. Proposed Estimator

In the absence of censoring, the IPW estimator proposed by TV can be used to draw inference about μ(t, a, α) and μ(t, α), i.e., the mean potential outcomes under the counterfactual setting where policy α is adopted. In particular, letting Y_ij = I(X_ij ⩽ t) be the indicator variable that the observation time for individual j in group i is less than or equal to t, the TV IPW estimators are ${\widehat{\mu }}^{TV}(t,a,\alpha )=m^{-1}{\sum }_{i=1}^m{\widehat{F}}_i^{TV}(t,a,\alpha )$ and ${\widehat{\mu }}^{TV}(t,\alpha )=m^{-1}{\sum }_{i=1}^m{\widehat{F}}_i^{TV}(t,\alpha )$ where

$${\widehat{F}}_i^{TV}(t,a,\alpha )=n_i^{-1}\sum _{j=1}^{n_i}\frac{\pi ({\mathbf{A}}_{i,-j};\alpha )I(A_{ij}=a)Y_{ij}}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })},{\widehat{F}}_i^{TV}(t,\alpha )=n_i^{-1}\sum _{j=1}^{n_i}\frac{\pi ({\mathbf{A}}_i;\alpha )Y_{ij}}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })},$$

and $\widehat{\beta }$ is an estimator of the vector of parameters for the propensity model Pr(A_i∣L_i, β). Details of the propensity model are discussed in the next sections.

In the presence of censoring, the following extension of the TV IPW estimators is proposed: $\widehat{\mu }(t,a,\alpha )=m^{-1}{\sum }_{i=1}^m{\widehat{F}}_i(t,a,\alpha )$ and $\widehat{\mu }(t,\alpha )=m^{-1}{\sum }_{i=1}^m{\widehat{F}}_i(t,\alpha )$ where

$${\widehat{F}}_i(t,a,\alpha )=n_i^{-1}\sum _{j=1}^{n_i}\frac{\pi ({\mathbf{A}}_{i,-j};\alpha )I(A_{ij}=a)I({\Delta }_{ij}=1)I(X_{ij}⩽t)}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })S_C(X_{ij}\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\widehat{\gamma })},$$

$${\widehat{F}}_i(t,\alpha )=n_i^{-1}\sum _{j=1}^{n_i}\frac{\pi ({\mathbf{A}}_i;\alpha )I({\Delta }_{ij}=1)I(X_{ij}⩽t)}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })S_C(X_{ij}\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\widehat{\gamma })},$$

$S_C(t\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\widehat{\gamma })=\text{Pr}(C_{ij}>t\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\widehat{\gamma })$ and $\widehat{\gamma }$ is an estimator of the vector of the parameters for the censoring model. Details of the censoring model are discussed in the next sections. Estimates of the direct, indirect, total, and overall effects are given by $\widehat{DE}(t,\alpha )=\widehat{\mu }(t,0,\alpha )-\widehat{\mu }(t,1,\alpha )$, $\widehat{IE}(t,{\alpha }_1,{\alpha }_2)=\widehat{\mu }(t,0,{\alpha }_1)-\widehat{\mu }(t,0,{\alpha }_2)$, $\widehat{TE}(t,{\alpha }_1,{\alpha }_2)=\widehat{\mu }(t,0,{\alpha }_1)-\widehat{\mu }(t,1,{\alpha }_2)$ and $\widehat{OE}(t,{\alpha }_1,{\alpha }_2)=\widehat{\mu }(t,{\alpha }_1)-\widehat{\mu }(t,{\alpha }_2)$.

The proposition below shows that if the group level propensity scores and the individual censoring probabilities are known, then the proposed IPCW estimators are unbiased. A proof of the proposition is given in Web Appendix A.

Proposition. If Pr(A_i∣L_i) and S_C(X_ij∣L_i, A_i) are known for j = 1, 2, … , n_i and i = 1, … , m, then $E\{\widehat{\mu }(t,a,\alpha )\}=\mu (t,a,\alpha )$ and $E\{\widehat{\mu }(t,\alpha )\}=\mu (t,\alpha )$.

In observational studies, the conditional distribution of treatment given covariates is un-known. Likewise, in both observational studies as well as randomized trials, the conditional distribution of censoring given covariates is typically not known (one exception being studies or trials without drop-out such that the only cause of censoring is the end of administrative follow-up at some fixed time point). Therefore, we consider finite dimensional parametric models to estimate the group propensity scores and conditional probability of censoring; these estimates are then plugged into the IPCW estimators defined above.

The conditional probability of censoring is estimated using a shared frailty model (Munda et al., 2012) where the conditional hazard for C_ij is assumed to have the proportional hazards form g_ij(c∣L_i, A_i, e_i) = g₀(c; θ_h)e_i exp (${\tilde{\mathbf{L}}}_{ij}{\theta }_c$) where g₀ is the baseline hazard function, θ_h is the q′-dimensional parameter vector of the baseline hazard function, e_i is a random effect with density f_e(e_i; θ_r), ${\tilde{\mathbf{L}}}_{ij}$ is some user specified function of {L_i, A_i}, and θ_c is the q-dimensional column vector of coefficients. The row vector ${\tilde{\mathbf{L}}}_{ij}$ could include, for example, covariates and treatment for individual j (i.e., L_ij and A_ij) as well as the proportion of others in the group who receive treatment (i.e., ${\sum }_{k\ne j}{A}_{ik}∕(n_i-1)$). Below the dependence of g₀ on θ_h is suppressed for notational convenience. Let $\gamma =({\theta }_c^{\mathsf{T}},{\theta }_h^{\mathsf{T}},{\theta }_r)$ be the vector of parameters for the frailty model. Maximum likelihood theory can be used to draw inference about γ. Under assumption III, the contribution of group i to the log-likelihood corresponding to the frailty censoring model, denoted by l(X_i, Δ_i, L_i, A_i, γ), equals

$$\sum _{j=1}^{n_i}(1-{\Delta }_{ij})[\log \{g_0(X_{ij})\}+{\tilde{\mathbf{L}}}_{ij}{\theta }_c]+\log \{(-1{)}^{d_i}{\mathcal{L}}^{(d_i)}(\sum _{j=1}^{n_i}{G}_0(X_{ij})\text{exp}({\tilde{\mathbf{L}}}_{ij}{\theta }_c))\},$$

where $d_i={\sum }_{j=1}^{n_i}(1-{\Delta }_{ij})$ is the number of censored observations in group i, $G_0(\omega )={\int }_0^{\omega }{g}_0(\kappa )d\kappa$, $\mathcal{L}(s)={\int }_0^{\infty }\text{exp}(-e_{i}s)f_e(e_i;{\theta }_r)d{e}_i$ and ${\mathcal{L}}^{(k)}$ is the k^th-derivative of $\mathcal{L}$ (Munda et al., 2012). Therefore, the maximum likelihood estimator of γ solves the following estimating equations

$$\sum _i{\psi }_{ck}({\mathbf{X}}_i,{\Delta }_i,{\mathbf{L}}_i,{\mathbf{A}}_i,\gamma )=0\text{for}k=1,\dots ,q+q^{\prime }+1,$$

where ψ_ck = ψ_ck(X_i, Δ_i, L_i, A_i, γ) = ∂l(X_i, Δ_i, L_i, A_i, γ)/∂γ_k and γ_k is the k-th element of γ. Below, the baseline hazard for the censoring model is assumed to be constant and equal to θ_h, and the frailty term e_i is assumed to follow a Gamma distribution with mean 1 and variance θ_r, such that censoring weights for an uncensored individual can be computed via

$$\begin{gathered} S_C(t,\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\gamma )=\int \text{Pr}(C_{ij}>t\mid {\tilde{\mathbf{L}}}_{ij},\gamma ,e_i)f_e(e_i;{\theta }_r)d{e}_i \\ =\int \text{exp}\{-{\theta }_{h}t\text{exp}({\tilde{\mathbf{L}}}_{ij}{\theta }_c)e_i\}\frac{e_i^{1∕{\theta }_r-1}\text{exp}(-e_i∕{\theta }_r)}{{\theta }_r^{1∕{\theta }_r}\Gamma (1∕{\theta }_r)}d{e}_i \\ ={\left\{{\theta }_r{\theta }_{h}t\text{exp}({\tilde{\mathbf{L}}}_{ij}{\theta }_c)+1\right\}}^{-1∕{\theta }_r} \end{gathered}$$

Following TV (2012), a mixed effects model may be assumed for the treatment allocation, i.e., Pr(A_ij = 1∣L_ij, b_i) = logit⁻¹(L_ijθ_x + b_i) where b_i is a random effect following density f_b(b_i; θ_s). (In the application below the mixed effects model has a slightly more complicated form owing to the study design.) Let $\beta =({\theta }_x^{\mathsf{T}},{\theta }_s)$ denote the (p + 1) dimensional vector of parameters for the mixed effects model. Again, maximum likelihood theory can be used to draw inference about β. The contribution of group i to the log-likelihood for the mixed effects model is given by l(A_i, L_i, β) = log Pr(A_i∣L_i, β) where

$$\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\beta )=\int \prod _{j=1}^{n_i}{h}_{ij}(b_i,{\mathbf{L}}_i,{\theta }_x{)}^{A_{ij}}\{1-h_{ij}(b_i,{\mathbf{L}}_i,{\theta }_x){\}}^{(1-A_{ij})}{f}_b(b_i;{\theta }_s),$$

and h_ij (b_i, L_i, β) = Pr(A_ij = 1∣L_ij, b_i). The maximum likelihood estimator of β is the solution to the score equations

$$\sum _i{\psi }_{xk}({\mathbf{A}}_i,{\mathbf{L}}_i,\beta )=0\text{for}k=1,\dots ,p+1,$$

where ψ_xk = ψ_xk(A_i, L_i, β) = ∂l(A_i, L_i, β)/∂β_k and β_k is the k-th element of β.

Inference about the causal effects of interest is then based on solving the vector of estimating equations

$$\sum _i\psi ({\mathbf{O}}_i,\theta )=0,$$ (1)

where θ = (γ, β, θ), ψ(O_i, θ) = (ψ_c, ψ_x, ψ_aα)⊺, ψ_c = (ψ_c1, ψ_c2, …, ψ_cq+q′+1), ψ_x = (ψ_x1, ψ_x2, …, ψ_xp+1),

$${\psi }_{a\alpha }={\psi }_{a\alpha }({\mathbf{O}}_i,\theta )=\frac{g^{\ast }({\mathbf{O}}_i,a,\alpha ,\gamma )}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\beta )}-\theta ,$$

and

$$g^{\ast }({\mathbf{O}}_i,a,\alpha ,\gamma )=n_i^{-1}\sum _{j=1}^n\frac{\pi ({\mathbf{A}}_{i,-j};\alpha )I(A_{ij}=a)I({\Delta }_{ij}=1)I(X_{ij}⩽t)}{S_C(X_{ij}\mid {\mathbf{L}}_i,{\mathbf{A}}_i,\gamma )}.$$

Let $\widehat{\theta }=(\widehat{\gamma },\widehat{\beta },\widehat{\mu }(t,a,\alpha ))$ denote the solution to (1). Denote the true value of θ by θ₀ = (γ₀, β₀, μ(t, a, α)) and note that

$$\int {\psi }_{a\alpha }(\mathbf{o},{\gamma }_0,{\beta }_0,\mu (t,a,\alpha ))d{F}_{\mathbf{O}}(\mathbf{o})=E\left\{\frac{g^{\ast }({\mathbf{O}}_i,a,\alpha ,{\gamma }_0)}{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,{\beta }_0)}-\mu (t,a,\alpha )\right\}=0,$$

where F_O denotes the joint distribution of the complete observed random variable O and the last equality follows from the Proposition above. Therefore, assuming the parametric models above are correctly specified, it follows that $\int \psi (\mathbf{o},{\theta }_0)d{F}_O(\mathbf{o})=0$. By M-estimation theory (Stefanski and Boos, 2002), $\widehat{\theta }\stackrel{p}{\to }{\theta }_0$ and $\sqrt{m}(\widehat{\theta }-{\theta }_0)$ converges in distribution to a Normal distribution with mean 0 and covariance matrix £ equal to U(θ₀)⁻¹V(θ₀){U(θ₀)⁻¹}^T where $U({\theta }_0)=E\{-\stackrel{.}{\psi }({\mathbf{O}}_i,{\theta }_0)\}$, V(θ₀) = E{ψ(O_i, θ₀)ψ(O_i, θ₀)^T}, and $\stackrel{.}{\psi }({\mathbf{O}}_i,\theta )=\partial \psi ({\mathbf{O}}_i,\theta )∕\partial {\theta }^T$. Consistency and asymptotic normality of the direct, indirect and total effect estimators follows from the delta method. Similar techniques can be used to show that $\widehat{\mu }(t,\alpha )$ and the overall effect estimator are also consistent and asymptotically Normal. The asymptotic variance Σ can be consistently estimated by $\widehat{\Sigma }=\widehat{U}(\widehat{\theta }{)}^{-1}\widehat{V}(\widehat{\theta })\{\widehat{U}(\widehat{\theta }{)}^{-1}{\}}^T$ where $\widehat{U}(\widehat{\theta })=m^{-1}{\sum }_{i=1}^m\{-\stackrel{.}{\psi }({\mathbf{O}}_i,\widehat{\theta })\}$ and $\widehat{V}(\widehat{\theta })=m^{-1}{\sum }_{i=1}^m\{\psi ({\mathbf{O}}_i,\widehat{\theta })\psi ({\mathbf{O}}_i,\widehat{\theta }{)}^T\}$. The empirical sandwich variance estimator $\widehat{\Sigma }$ can be computed using the R package geex (Saul and Hudgens, 2020) and can be used to construct Wald confidence intervals (CIs).

3. Simulation Study

A simulation study was conducted to assess the finite sample bias of the IPCW estimator and coverage of the corresponding Wald confidence intervals. The data generating model used in the simulation study was motivated by aspects of the cholera vaccine study analysis presented in the next section. Following Perez-Heydrich et al. (2014), data were simulated according to the following steps.

1. First, two baseline covariates L_1ij and L_2ij were randomly generated. In the application presented in Section 4, conditional independence (assumption I) is assumed given an individual’s age (in decades) and the distance of their residence to the nearest river. Motivated by this example, L_1ij (age) and L_2ij (distance to river) were randomly generated as follows. First, V_ij was randomly generated from an Exponential distribution with mean 20, and r_1i and r_2ij were independently sampled from Normal(0, 0.1), i.e., a mean-zero Gaussian distribution with standard deviation 0.1. Then L_1ij was set to min(V_ij + r_1i + r_2ij, 100)/10 and L_2ij randomly generated such that log L_2ij ~ Normal(r_1i + r_2ij, 0.75).

2. The random effects for the treatment model b_i were randomly sampled from a Normal distribution with mean 0 and variance 1.0859.

3. The treatment indicators A_ij were randomly sampled from a Bernoulli distribution with mean p_ij = expit(0.2727 – 0.0387L_1ij + 0.2179L_2ij + b_i).

4. The potential times to event T_ij(a_i) were randomly sampled from an Exponential distribution with mean μ_ij = 200 + 100a_ij – 0.98L_1ij – 0.145L_2ij + 50 ${\sum }_{k\ne j}{a}_{ik}∕n_i$.

5. The random effects for the censoring model e_i were randomly generated from a Gamma distribution with mean 1 and variance θ_r = 1.25.

6. Censoring times C_ij were randomly sampled from an Exponential distribution with mean 1/λ₀ where λ₀ = 0.015 exp (0.002L_1ij + 0.015L_2ij)e_i.

7. Individual censoring indicators were determined, i.e., Δ_ij = 0 if C_ij T_ij(A_i).

Steps i through vii were used to stochastically generate 1000 data sets, with each data set containing 500 groups with 10 individuals per group. For each simulated data set, the IPCW estimator of μ(100, a, α) was evaluated for a = 0, 1 and α = 0.1, 0.2, … , 0.9. Estimated standard errors based on the empirical sandwich variance estimator and Wald 95% confidence intervals were also calculated for each simulated data set. Empirical standard errors were calculated by taking the standard deviation of the point estimates from all simulations.

The true value of the estimand was obtained by simulating counterfactual outcomes for m = 10⁶ groups of individuals. Note that, according to the model used to generate the data, potential survival times depend only on ${\sum }_{k\ne j}{a}_{ik}$ SO, μ(t, a, α) was approximated by (Perez-Heydrich et al., 2014)

$$m^{-1}\sum _{i=1}^m{n}_i^{-1}\sum _{j=1}^{n_i}\sum _{k=0}^{n_i-1}\left(\begin{array}{c}\hfill n_i-1\hfill \\ \hfill k\hfill \end{array}\right)I\{T_{ij}(a,k)⩽t\}{\alpha }^k(1-\alpha {)}^{n_i-k-1}.$$

The true value of μ(t, α) was determined in a similar fashion.

Results from the simulation study are presented in Table 1. Bias of the IPCW estimator was negligible for all values of a and α. Likewise, the median estimated standard error was close to the empirical standard error. Coverage of the 95% Wald CIs generally approximated the nominal level. However, the results in Table 1 and from other simulations described below indicate coverage may differ from the nominal level when α is close to 0 or 1. For the observed data generating distribution in the simulations, the probability an individual received treatment was approximately 0.6. This suggests caution should be used when drawing inferences for values of α far from the observed proportion of individuals treated.

Table 1.

Results from simulation study described in Section 3, where: α denotes the allocation probability; μ_a denotes the value of the target parameters μ(100, a, α) for a = 0, 1; Bias is the average of $\mu (100,a,\alpha )-\widehat{\mu }(100,a,\alpha )$ for a = 0, 1; ESE is the empirical standard error; MSE is the median of the sandwich variance-based standard error estimates; EC denotes the empirical coverage of the 95% Wald confidence intervals based on the Normal distribution; and EC_t denotes empirical coverage of t-distribution-based Wald confidence intervals.

α	μ 0	Bias	ESE	MSE	EC	ECt		α	μ 1	Bias	ESE	MSE	EC	ECt
0.1	0.39	−0.02	0.07	0.07	95%	95%		0.1	0.28	−0.01	0.08	0.08	92%	92%
0.2	0.38	−0.01	0.04	0.04	95%	95%		0.2	0.28	0.00	0.04	0.04	95%	95%
0.3	0.38	−0.01	0.03	0.03	95%	95%		0.3	0.27	0.00	0.03	0.03	94%	94%
0.4	0.37	0.00	0.03	0.02	95%	95%		0.4	0.27	0.00	0.02	0.02	94%	94%
0.5	0.37	0.00	0.03	0.02	96%	96%		0.5	0.27	0.00	0.02	0.02	94%	94%
0.6	0.36	0.00	0.02	0.02	94%	95%		0.6	0.27	0.00	0.02	0.02	94%	94%
0.7	0.35	0.01	0.02	0.02	95%	95%		0.7	0.26	0.00	0.01	0.01	96%	96%
0.8	0.35	0.00	0.03	0.03	96%	96%		0.8	0.26	0.00	0.02	0.02	96%	96%
0.9	0.34	0.00	0.05	0.05	95%	95%		0.9	0.26	0.00	0.02	0.02	96%	96%

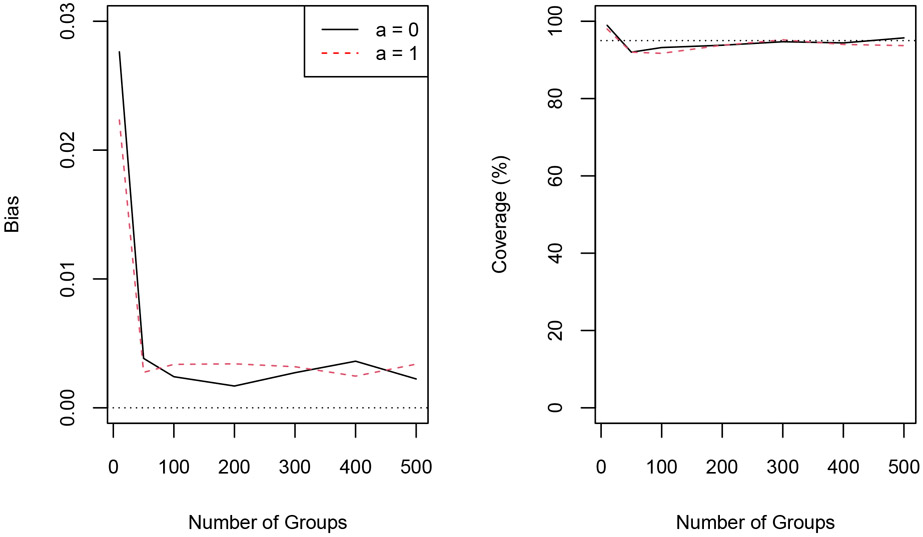
Additional simulation studies were conducted to assess the performance of the proposed methods for different values of m, the total number of groups, ranging from 10 to 500. The number of individuals per group was 10, as in the previous simulations. For each m ∈ {10, 50, 100, 200, 300, 400, 500}, 1000 data sets were simulated according to steps i through vii above. Results are depicted in Figure 1. Bias of the IPCW estimator was small and coverage of the Wald CIs was close to the nominal level, especially as the number of groups increased. Details regarding these simulation results are provided in Web Tables 1-6.

Figure 1.

Absolute bias of the IPCW estimator (left) and corresponding Wald 95% confidence interval coverage (right) for different numbers of groups for α = 0.5. The dotted line in the right plot corresponds to 95% coverage. This figure appears in color in the electronic version of this article.

In cluster randomized trials with small numbers of clusters, Wald CIs are often constructed using a t distribution with m – r degrees of freedom, where r is the number of parameters being estimated, rather than a Normal distribution; empirical coverage of Wald CIs using the t distribution is also shown in Table 1 and Web Tables 1-6, and was similar to coverage based on the Normal distribution, except when m = 10 in which case the t-based CI has coverage closer to the nominal level.

Additional simulations for m = 500 and n_i ∈ {30, 50, 75, 100, 200} are provided in Web Tables 7-11. Bias of the IPCW estimator remained negligible in these scenarios, however Wald CIs tended to undercover as the size of the groups increased. Simulations were also conducted for a range of censoring rates; see Web Tables 12-14. These tables also include performance of the TV IPW estimator, which does not account for censoring; as expected the estimator is biased and the corresponding CIs fail to cover at the nominal level, with performance worsening as censoring increases.

Validity of the IPCW estimator relies on correct specification of the treatment allocation and censoring models. Therefore additional simulations were conducted to assess robustness to mis-specification of these models. Web Tables 15-22 summarize performance of the IPCW estimator to incorrect specification of the random effect distribution in the treatment model. For these simulations, the random effect b_i was generated from the distributions in Web Figure 1 but assumed to be Gaussian when calculating the IPCW estimator. These results demonstrate robustness to mild departures from the assumed random effect distribution, whereas more severe mis-specification (e.g., for skewed or bimodal distributions) may result in bias and CI undercoverage. Web Table 23 demonstrates robustness of the method when the censoring model is mis-specified due to covariate omission. Finally Web Table 24 summarizes performance of the IPCW estimator when censoring depends on treatment; as expected, the results are similar to Table 1, demonstrating the estimator performs well in this scenario.

In summary, these empirical results suggest the proposed methods: (i) appropriately account for right censoring, unlike the TV estimator; (ii) are best suited for applications where there are many groups and the number of individuals per group is not large; and (iii) tend to be robust to mild mis-specification of the treatment allocation and censoring models.

4. Application

4.1. Cholera Vaccine Study and Analysis

In this section, the methods described in Section 2 are used to analyze a cholera vaccine study in Matlab, Bangladesh (Ali et al., 2005). Eligible study participants were children 2–15 years of age and women greater than 15 years old. All 121, 975 eligible individuals in the population were randomized to one of three vaccination groups: B subunit-killed whole cell oral cholera vaccine, killed whole-cell-only cholera vaccine, and E. coli K12 placebo. As in Perez-Heydrich et al. (2014), no distinction is made between the two vaccines in the analysis presented here. Individuals were considered to have participated in the randomized trial component of the study if they received two or more doses of vaccine or placebo. The primary endpoint of the trial was incident cholera. Three health centers in the Matlab area served as surveillance centers and collected endpoint data on all individuals, regardless of whether they participated in the randomized trial. The analysis presented here includes data from all individuals, i.e., trial participants as well as those who chose not to participate. Thus an approach which accounts for possible confounding, such as the IPW method described in Section 2, should be utilized to assess the effects of vaccination.

Previous analyses of this study suggest the presence of interference (Ali et al., 2005; Perez-Heydrich et al., 2014). Interference is plausible in this setting because the vaccine may (i) prevent an individual from contracting cholera or (ii) decrease the infectiousness or contagiousness of an individual who does contract cholera; for either (i) or (ii), the vaccine would make it less likely that such an individual would subsequently infect other individuals. However, these previous analyses did not formally account for censoring. Here individuals are considered right censored if they were not diagnosed with cholera during the study. Individuals who emigrated from the study location or died during the follow-up period prior to cholera infection were right censored at the time of emigration or death. Individuals who did not emigrate or die and who did not develop cholera during the study were right censored at the end of the study period.

Related individuals in Matlab live in collections of houses called baris. There were a total of 6,415 baris at the time of the vaccine trial. Perez-Heydrich et al. (2014) used a clustering algorithm to form groups (neighborhoods) based on the spatial location of the baris, with the number of groups pre-specified to be 700. The analysis here is based on the same groups as in Perez-Heydrich et al. and assumes that there is no interference between individuals in different groups, i.e, vaccination of an individual in one group has no effect on whether an individual in another group contracts cholera. When fitting the propensity model Pr(A_i∣L_i, β) described below, the largest 15 groups had estimated group propensity scores that were effectively equal to zero, and therefore these groups were omitted.

Individuals participating in the vaccine trial were not all vaccinated on the same calendar day, such that the level of vaccine coverage within a group varied over a relatively brief period of calendar time at the study onset. For simplicity and because the methods developed above do not accommodate time varying treatment, the start of follow-up for all individuals in a particular group was set to the latest date of second vaccination among all individuals in that group. Observations were excluded if individuals contracted cholera (60), died (346), or emigrated (3671) prior to the start of follow-up for their group. In total, 94,234 individuals were included in the analysis. Among these individuals, 55,413 were unvaccinated, either because they received placebo or they did not participate, and 38,821 were vaccinated with one of the two vaccines. During follow-up, there were 280 incident cases of cholera among the unvaccinated individuals and 74 cholera cases among the vaccinated individuals. Most (96%) of censoring was due to end of study follow-up (n = 89, 956), 3.5% of censoring was due to emigration (n = 3, 340), and < 1% due to death (n = 584).

As in Perez-Heydrich et al., the group propensity score was modeled using a mixed effects model. The particular form of the model derives from the fact that for an individual to have received a vaccine, they must have (i) chosen to participate in the trial, and (ii) been randomized to receive one of the two vaccines. To account for (i), a logistic regression model for participation was assumed. Covariates in the participation component of the model were age, squared age, distance to nearest river, and squared distance to nearest river. Accommodating (ii) in the propensity model is straightforward because, due to randomization, individuals who elected to participate in the trial were known to receive one of the two vaccines with probability 2/3. Combining these two aspects of the model, the propensity score for group i was estimated by

$$\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })=\int \prod _{j=1}^{n_i}\{(2∕3)h_{ij}(b_i,{\mathbf{L}}_{ij},{\widehat{\theta }}_x){\}}^{A_{ij}}\{1-(2∕3)h_{ij}(b_i,{\mathbf{L}}_{ij},{\widehat{\theta }}_x){\}}^{(1-A_{ij})}{f}_b(b_i;{\widehat{\theta }}_s),$$

where h_ij(b_i, L_i, θ_x) = Pr(B_ij = 1∣b_i, L_ij, θ_x) = expit(L_ijθ_x + b_i), B_ij is the indicator of participation, i.e., B_ij = 1 if individual j in group i participated in the randomized trial and B_ij = 0 otherwise, and (${\widehat{\theta }}_x$, ${\widehat{\theta }}_s$) is the maximum likelihood estimate of (θ_x, θ_s). Censoring was modeled using the Gamma frailty model described above, and included only age as a covariate as no other variables were associated with censoring. Estimated parameters and standard errors for the treatment and censoring models are given in Web Table 25. Over 70% of individuals belonged to groups where the vaccine coverage was between 0.3 and 0.6. Therefore, the analysis was conducted for allocation strategies ranging from 0.3 to 0.6.

4.2. Results

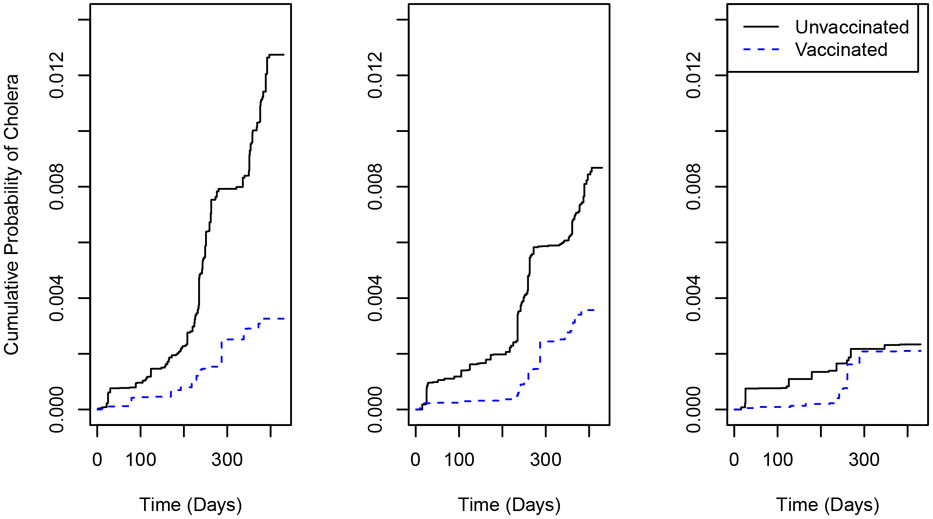
Figure 2 shows the IPCW estimates of the cumulative probability of cholera over time for allocation strategies 0.3, 0.45, and 0.6, both when an individual receives a vaccine and when an individual is unvaccinated. The IPCW estimates can be viewed as weighted averages, with uncensored individuals weighted by $w_{ij}=\pi ({\mathbf{A}}_{i,-j};\alpha )∕\{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })S_C(X_{ij}\mid {\mathbf{L}}_i,\widehat{\gamma })\}$ and ${\tilde{w}}_{ij}=\pi ({\mathbf{A}}_i;\alpha )∕\{\text{Pr}({\mathbf{A}}_i\mid {\mathbf{L}}_i,\widehat{\beta })S_C(X_{ij}\mid {\mathbf{L}}_i,\widehat{\gamma })\}$; histograms of w_ij and ${\tilde{w}}_{ij}$ for α = 0.30, 0.45, 0.60 are presented in Web Figures 2-3. Figure 2 shows that the estimated risk of cholera when an individual is unvaccinated decreases dramatically as α increases, suggesting the presence of interference. This decrease is more modest when an individual is vaccinated, indicating a stronger indirect effect when unvaccinated. At all time points the estimated risk of cholera is higher when an individual is unvaccinated, suggesting a beneficial, direct effect of vaccination, especially at lower coverage levels. For α = 0.3 and α = 0.45, the estimated risk when unvaccinated increases suddenly between 200 and 300 days, and then again between 300 and 400 days. These results might be attributable to the known bimodal seasonality of cholera in Bangladesh (Longini et al., 2002). Note that, because the study start date varied across groups, the time scale in this analysis does not exactly coincide with calendar time. Nonetheless, 95% of individuals had a start date within a two calendar month range, such that there is a strong correlation between the analysis time scale and calendar time, and thus cholera seasonality may explain these periods of marked increase in risk.

Figure 2.

Estimated cumulative probability of cholera over time when vaccinated or unvaccinated for α = 0.3 (left), α = 0.45 (center) and α = 0.6 (right). This figure appears in color in the electronic version of this article.

Direct, indirect, total and overall effect estimates and 95% CIs (×1000) for different allocation strategies at time t = 1 year are shown in Figure 3. The direct effect estimates generally decrease as α increases. For example, the direct effect estimate for α = 0.35 is 3.6 (95% CI 1.1, 6.2) whereas for α = 0.5 the direct effect estimate is 1.5 (95% CI −0.5, 3.5). The indirect, total, and overall effect estimates in Figure 3 compare the risk of cholera over a range of allocation probabilities α₁ ∈ [0.3, 0.6] versus α₂ = 0.4. Here the indirect effect contrasts risk of cholera infection when individuals are unvaccinated. For larger values of α₁ the 95% CIs for these effects exclude the null value of zero. For example, for α₁ = 0.6 the indirect effect estimate is 2.8 (95% CI 1.1, 4.5), providing statistical evidence of the presence of interference. These results indicate that when individuals are unvaccinated, the risk of cholera infection is significantly reduced by increasing the level of vaccine coverage in their neighborhood. The total effect estimates quantify the combined direct and indirect effects of the vaccine. The overall effect estimates may be of greatest interest from a public health or policy perspective. For α₁ = 0.6, the overall effect estimate is 2.2 (95% CI 0.9, 3.4); in words, fewer cases of cholera per 1000 individuals per year are expected if 60% of individuals are vaccinated compared to if only 40% of individuals receive vaccine.

Figure 3.

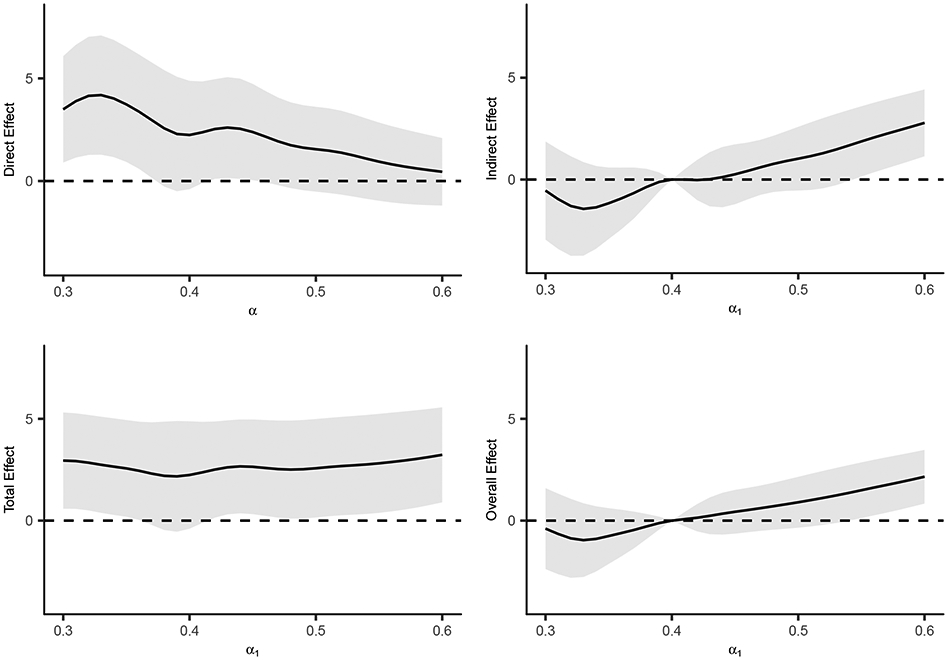
Direct, indirect, total and overall effect estimates (×1000) for different allocation strategies at time t = 1 year. Indirect, total, and overall effects are with respect to α₂ = 0.4. The shaded regions denote pointwise 95% confidence intervals of the estimates.

In previous analyses of these data, Perez-Heydrich et al. also estimated the direct, indirect, total and overall effects using a binary outcome indicating whether an individual was infected with cholera during the first year of follow-up. The IPCW estimates for t = 1 are similar to these previous results, e.g., Perez-Heydrich et al. estimated the direct effect for α = 0.32 to be 5.3 (95% CI 2.5, 8.1) whereas the IPCW estimate of this effect at t = 1 is 4.0 (95% CI 1.6, 6.5). However, the Perez-Heydrich et al. estimates may be biased because they did not account for right censoring. That said, the IPCW results should still be viewed cautiously and only have valid causal interpretation if Assumptions I - IV hold and the treatment and censoring models are correctly specified.

5. Discussion

In this paper, the TV IPW estimator for partial interference was extended to allow for right censored outcomes. The proposed estimator was obtained by weighting the original TV estimator by censoring weights calculated from a parametric frailty model of the censoring times. The estimator was shown to be consistent and asymptotically Normal (under identifiability Assumptions I - IV), and a consistent estimator of the asymptotic variance was proposed. A simulation study demonstrated that the proposed methods performed well in finite samples provided the number of groups is sufficiently large. Analysis of a cholera vaccine study using the proposed methods suggests vaccination had both a direct and indirect effect against cholera infection. These results are in accordance with findings by Ali et al. (2005) and Perez-Heydrich et al. (2014), but are likely more accurate since these previous analyses did not formally account for right censoring.

There are several areas of possible future research related to the methods developed here. For example, further research could entail developing estimators which perform well in settings where the number of groups (m) is small. The IPCW estimator considered here also presents computational challenges when group sizes (n_i’s) are large because the corresponding estimated group propensity scores can be approximately zero. As a result, in the cholera vaccine analysis in Section 4 the largest 15 groups were excluded, inefficiently discarding data and limiting the generalizability of the results. Other approaches are needed to better accommodate larger groups. Extensions of the IPCW estimator which allow for competing risks could also be considered. In the cholera example, such extensions would permit death to be considered a competing risk rather than treating such observations as censored. Validity of the IPCW estimator requires correct specification of parametric models, such that it is important to assess model fit in application of this method. Further research could entail developing estimators which are robust to model mis-specification; e.g., in the absence of censoring, doubly robust estimators have been developed which allow for partial interference and are consistent even if the treatment model is mis-specified (Liu et al., 2019).

Extensions of the IPCW estimator could also be considered for the setting where there is general interference, i.e., where interference is not restricted to individuals within the same group. One such approach might entail extending existing methods for observational studies with arbitrary interference (e.g., Sofrygin and van der Laan (2016); Tchetgen Tchetgen et al. (2020)) to allow for right censored outcomes, perhaps by incorporating inverse probability of censoring weights. In the cholera study, interference may have been present between individuals in different groups; for instance, Root et al. (2011) found that the risk of cholera among placebo recipients was inversely associated with level of vaccine coverage in their social networks, suggesting possible interference between socially connected individuals from different groups. Methods for observational studies with general interference and right censored outcomes could also be helpful when there is partial interference but the number of groups is small.

Methods could also be developed which allow the assumed interference structure to change over time. For example, when individuals in the cholera study were censored due to emigration out of the study area, it may be considered unlikely that those individuals would continue to interfere with others in the study; in which case, the assumed interference structure could be updated at the time when the individuals were censored.

Finally, following Tchetgen Tchetgen and VanderWeele (2012) and Perez-Heydrich et al. (2014), here we consider causal estimands corresponding to counterfactual scenarios where individuals independently select treatment with probability α. In future research alternative estimands, as in Papadogeorgou et al. (2019) and Barkley et al. (2020), could be considered which target counterfactual estimands that allow for within group treatment selection dependence. For example, if a particular vaccine is made widely available in Matlab, we might expect vaccine uptake to be positively correlated between individuals in the same bari. Thus such estimands may be more relevant to public health officials determining vaccine policy.

Data Availability Statement

The data that support the findings in this paper are available on request from the International Centre for Diarrhoeal Disease Research, Bangladesh. The data are not publicly available due to privacy or ethical restrictions.