Abstract
The effect of a mutation on fitness may differ between populations depending on environmental and genetic context, but little is known about the factors that underlie such differences. To quantify genome-wide correlations in mutation fitness effects, we developed a novel concept called a joint distribution of fitness effects (DFE) between populations. We then proposed a new statistic w to measure the DFE correlation between populations. Using simulation, we showed that inferring the DFE correlation from the joint allele frequency spectrum is statistically precise and robust. Using population genomic data, we inferred DFE correlations of populations in humans, Drosophila melanogaster, and wild tomatoes. In these species, we found that the overall correlation of the joint DFE was inversely related to genetic differentiation. In humans and D. melanogaster, deleterious mutations had a lower DFE correlation than tolerated mutations, indicating a complex joint DFE. Altogether, the DFE correlation can be reliably inferred, and it offers extensive insight into the genetics of population divergence.
Keywords: population genetics, distribution of fitness effects, population divergence
Introduction
New mutations that alter fitness are the key input into the evolutionary process. Typically, the majority of new mutations are deleterious or nearly neutral, and only a small minority are adaptive. These three categories constitute a continuum of fitness effects—the distribution of fitness effects (DFE) of new mutations (Eyre-Walker and Keightley 2007). The DFE is central to many theoretical evolutionary topics, such as the maintenance of genetic variation (Charlesworth 1994) and the evolution of recombination (Barton 1995), in addition to being key to applied evolutionary topics, such as the emergence of pathogens (Gandon et al. 2013) and the genetic architecture of complex disease (Durvasula and Lohmueller 2021).
The DFE can be quantified by either experimental approaches or statistical inference. Experimental approaches measure the DFE using random mutagenesis (Elena et al. 1998) or mutation accumulation (Fry et al. 1999); however, these approaches are limited to studying a small number of mutations. Most of our knowledge regarding the DFE has come from statistical inferences based on contemporary patterns of natural genetic variation. In these inferences, genetic data are typically summarized by the allele frequency spectrum (AFS; also known as the site frequency spectrum, SFS). In some methods, a demographic model is inferred from the AFS of putatively neutral variants, and the DFE is estimated from the AFS of variants under selection, conditional on the best fit demographic model (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008; Kim et al. 2017). In other methods, the background pattern of variation is accounted for by the inclusion of nuisance parameters when fitting a DFE model to the AFS of variants under selection (Eyre-Walker et al. 2006; Tataru et al. 2017; Barton and Zeng 2018). In an alternative approach, a recent study applied approximate Bayesian computation to simultaneously infer the DFE and a demographic model (Johri et al. 2020). Moreover, a linear regression method can be used to infer the DFE from nucleotide diversity (James et al. 2017). These approaches has been applied to numerous organisms, including plants (Chen et al. 2017; Huber et al. 2018; Chen et al. 2020), Drosophila melanogaster (Keightley and Eyre-Walker 2007; Castellano et al. 2017; Huber et al. 2017; Barton and Zeng 2018; Johri et al. 2020), and primates (Boyko et al. 2008; Huber et al. 2017; Kim et al. 2017; Ma et al. 2013; Castellano et al. 2019).
Using these inference methods, several studies have found evidence for differences in DFEs among different populations (Boyko et al. 2008; Ma et al. 2013; Kim et al. 2017; Castellano et al. 2019; Tataru and Bataillon 2019). These studies, however, have been limited by the implicit assumption that the fitness effects of a given mutation in different populations are independent draws from distinct DFEs. Moreover, these studies only compared DFEs from the AFS of single populations and therefore cannot investigate differences in fitness effects in new environments after population divergence. Intuitively, we expect the fitness effects of a given mutation in different contexts to be correlated. Wang et al. (2009) experimentally measured the fitness effects of twenty dominant mutations in two environments in D. melanogaster and found a strong positive correlation. But the generality of their results is unclear, and it is not known what factors affect the strength of the correlation.
Considering deleterious mutations, here we developed a novel concept called the joint DFE of new mutations, which can be inferred from the joint AFS of pairs of populations. We then defined the correlation of mutation fitness effects between populations using the joint DFE. With simulation, we showed that inferring the joint DFE and correlation requires only modest sample sizes and is robust to many forms of model misspecification. We then applied our approach to data from humans, D. melanogaster, and wild tomatoes. We found that the correlation of mutation fitness effects between populations is lowest in wild tomatoes and highest in humans. In D. melanogaster and wild tomatoes, we found differences in the correlation among genes with different functions. We also found that mutations with more deleterious effects exhibit lower correlations. Together, our results show that the joint DFE and correlation of mutation fitness effects offer new insight into the population genetics of these species.
Results
Definition
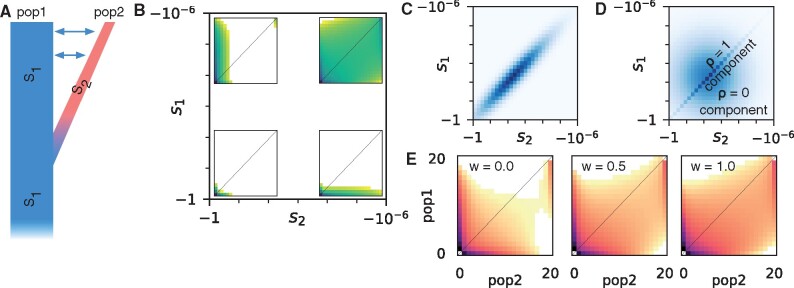
To define the joint DFE, we considered two populations that have recently diverged, one of which may have entered a new environment (fig. 1A). We also considered that a mutation has selection coefficient s1 in the ancestral population and s2 in the recently diverged population. For two populations, the joint AFS is a matrix in which each entry i, j corresponds to the number of variants observed at frequency i in population 1 and j in population 2 in a sequenced sample of individuals from the two populations. Different combinations of s1 and s2 lead to distinct patterns in the joint AFS (fig. 1B). We refer to the joint probability distribution for (s1, s2) as the joint DFE (fig. 1C), and we refer to the marginal probability distributions for s1 or s2 as the marginal DFEs for population 1 or population 2, respectively. The observed AFS from a pair of populations results from integrating spectra for different values of s1 and s2 over the joint DFE.
Fig. 1.
The joint allele frequency spectrum (AFS) and joint distribution of fitness effects (DFE). (A) We considered populations that have recently diverged with gene flow between them. Some genetic variants will have a different effect on fitness in the diverged population (s2) than in the ancestral population (s1). (B) The joint DFE is defined over pairs of selection coefficients (s1, s2). Insets show the joint AFS for pairs of variants that are strongly or weakly deleterious in each population. In each spectrum, the number of segregating variants at a given pair of allele frequencies is exponential with the color depth. (C) One potential model for the joint DFE is a bivariate lognormal distribution, illustrated here for strong correlation. (D) We focus on a model in which the joint DFE is a mixture of components corresponding to equality (ρ = 1) and independence (ρ = 0) of fitness effects. (E) As illustrated by these simulated allele frequency spectra, stronger correlations of mutation fitness effects lead to more shared polymorphism. Here, w is the weight of the ρ = 1 component in the mixture model.
Little is known about the shape of the joint DFE, so we considered multiple parametric models. The best fit DFEs for single populations tend to be lognormal or gamma distributions (Boyko et al. 2008), although discrete distributions may sometimes fit better (Kousathanas and Keightley 2013; Johri et al. 2020). We first considered a bivariate lognormal distribution (fig. 1C), because it has an easily interpretable correlation coefficient. However, accurate numerical integration over the bivariate lognormal distribution becomes challenging when the correlation coefficient approaches one, because probability density becomes concentrated in a small number of sampled grid points (supplementary fig. S1, Supplementary Material online). We also considered another popular probability distribution for modeling DFEs, the gamma distribution, but there are multiple ways of defining a bivariate gamma distribution (Nadarajah and Gupta 2006). We thus focused on a mixture model that consisted of a component corresponding to perfect correlation with weight w, and a component corresponding to zero correlation with weight (fig. 1D). To limit the complexity of the model, we assumed that the marginal DFEs were identical for both populations. In this case, the correlation of the overall distribution is equal to the mixture proportion w. We thus interpret and discuss w as a DFE correlation coefficient.
The DFE correlation profoundly affects the expected AFS (fig. 1E). Qualitatively, if the correlation is low, there is little shared high-frequency polymorphism. In this case, alleles that are nearly neutral in one population are often deleterious in the other, driving their frequencies lower in that population. If the correlation of the joint DFE is larger, more shared polymorphism is preserved. To calculate the expected AFS for a given demographic model and DFE, we first cached calculations of the expected AFS for a grid of selection coefficient pairs. Assuming independence among sites, the expectation for the full DFE is then an integration over values of s1, s2, weighted by the DFE (supplementary fig. S1, Supplementary Material online) (Ragsdale et al. 2016; Kim et al. 2017). We based our approach on the fitdadi framework developed by Kim et al. (2017), and our approach is integrated into our dadi software (Gutenkunst et al. 2009). More detail can be found in the Materials and Methods section.
Simulation
We focused our simulation studies on cases in which the correlation of the DFE was high, because those cases turned out to be most relevant to our empirical analyses.
To evaluate the precision of our approach, we first stochastically simulated unlinked single nucleotide polymorphisms (SNPs) under a known demographic model (supplementary table S1 and fig. S2, Supplementary Material online) and a symmetric lognormal mixture model for the joint DFE (fig. 1; eqs. 4 and 6). We then inferred the three joint DFE parameters: the mean μ and standard deviation σ of the marginal lognormal distributions and the DFE correlation w. The demographic and joint DFE parameters for these simulations were similar to those we later inferred for human populations under a demographic model of divergence, growth, and migration. When we fit the joint DFE to these simulated data, we found that the variance of the inferred parameters grew only slowly as the sample size decreased (supplementary fig. S3A, Supplementary Material online). This suggests that only modest sample sizes are necessary to confidently infer the joint DFE, similar to how only modest sample sizes are necessary to infer the mean and variance of the univariate DFE (Keightley and Eyre-Walker 2010).
Because our inference approach focuses on shared variation, we expected precision to depend on the divergence time between the populations. To test this, we simulated data sets with sample size similar to our real Drosophila data and varied the divergence time in the demographic model. We found that the variance of the inferred μ and σ parameters was always small (supplementary fig. S3B and C, Supplementary Material online), but the variance of the inferred DFE correlation w depended on the divergence time (supplementary fig. S3B and C, Supplementary Material online). That variance in w was large for small divergence times (). This is expected, because in this case selection has had little time act differently in the two populations. That variance in w was also large if the divergence time was large and there was no migration between the populations (supplementary fig. S3C, Supplementary Material online). This is also expected, because in this scenario there is little shared variation between populations. However, the variance of the inferred DFE correlation w was small when the divergence time was between and 10° (supplementary fig. S3B and C, Supplementary Material online). Moreover, the variance of w was not large unless FST in the simulated data was substantially larger than found in the empirical data we analyzed. Ancestral state misidentification could bias our inference (Baudry and Depaulis 2003). To account for this, in our empirical analyses we included a model parameter for such misidentification. Tests with simulated data showed that the degree of misidentification could be precisely inferred (supplementary fig. S4, Supplementary Material online), and including this parameter in our model does not strongly affect other inferences (supplementary table S14, Supplementary Material online).
Having found good precision for our inference, we then turned to testing the robustness of our inference to model misspecification. Since these tests focused on biases in the average inference, we did not stochastically sample data for these analyses, but rather used the expected AFS under each scenario as the data.
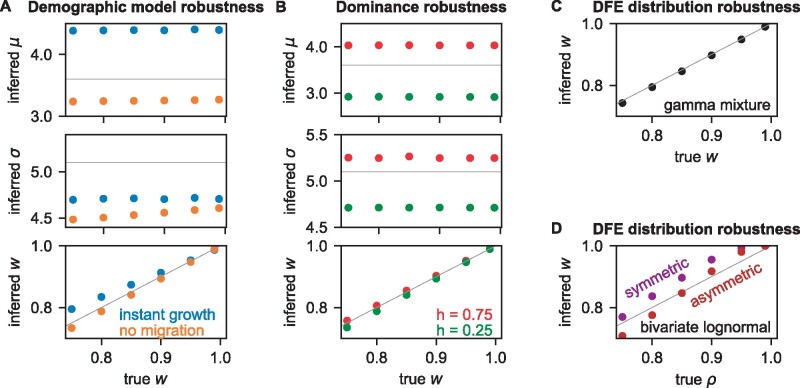
The demographic model is a key assumption of our joint DFE inference procedure. To test how imperfect modeling of demographic history would bias our inference, we simulated both neutral and selected data under a demographic model that included divergence, exponential growth in both populations, and asymmetric migration between populations (supplementary fig. S2B, Supplementary Material online). We then fit models that either lacked migration or that modeled instantaneous growth and symmetric migration to the neutral data (supplementary fig. S2C, Supplementary Material online). We then used these misspecified models to infer the DFE correlation w from the selected data. For both misspecified demographic models, although the inferred μ and σ were biased, we found that the inferred w was not strongly biased, particularly for large correlations (fig. 2A).
Fig. 2.
Robustness of joint DFE inference to model misspecification. Simulated neutral and selected data were generated under a demographic model with exponential growth and migration (supplementary table S1, Supplementary Material online), and lognormal mixture DFE models were fit to the data. The DFE parameters are: μ, the mean log population-scaled selection coefficient; σ, the standard deviation of those log coefficients; and w, the correlation of the DFE. The gray lines indicate true values, and the data plotted in these figures can be found in supplementary tables S4–S6, Supplementary Material online. (A) In this case, simpler demographic models with instantaneous growth or symmetric migration were fit to the neutral data. The resulting misspecified model was then used when inferring the DFE. This misspecification biased μ and σ, but not w. (B) In this case, selected data were simulated assuming dominant or recessive mutations, but the DFE was inferred assuming no dominance (h = 0.5). Again, μ and σ are biased, but w is not. (C) In this case, selected data were simulated using a mixture of gamma distributions. When these data were fit using our mixture of lognormal distributions, w was not biased. (D) In this case, selected data were simulated using bivariate lognormal models, with either symmetric or asymmetric marginal distributions. When these data were fit using our symmetric mixture of lognormal distributions, w was only slightly biased.
Dominance is a potential confounding factor when inferring the joint DFE, since dominance influences allele frequencies differently in populations that have and have not undergone a bottleneck (Balick et al. 2015). Typically, mutation fitness effects in diploids are assumed to be additive, corresponding to a dominance coefficient of h = 0.5. To test the effects of dominance on our inference, we simulated nonsynonymous frequency spectra with dominance coefficients of h = 0.25 and h = 0.75 and then optimized joint DFE parameters under the assumption that h = 0.5. We found that an incorrect assumption about dominance did not substantially bias the inferred w, although it did bias the inferred μ and σ (fig. 2B).
The probability distribution assumed for the joint DFE is another potential confounding factor. To test how this might bias inference, we first simulated a true mixture model in which the marginal distributions were gamma (eq. 7), rather than lognormal (eq. 6). In this case, we found that inferred w was not substantially biased (fig. 2C). We also considered fitting the lognormal mixture model (fig. 1D) to data simulated under a bivariate lognormal model (fig. 1C and eq. 8). In this case, we found that the inferred mixture component w was larger than the simulated bivariate lognormal correlation coefficient ρ, although they were similar (fig. 2D). The mixture model assumes symmetric marginal distributions between the two populations, but the bivariate lognormal model is more general and permits asymmetric marginal distributions. When we simulated data under a bivariate model with asymmetric means and variances of the marginal distributions, but fit with a symmetric mixture model, we found only slight bias, similar to the symmetric bivariate case (fig. 2D).
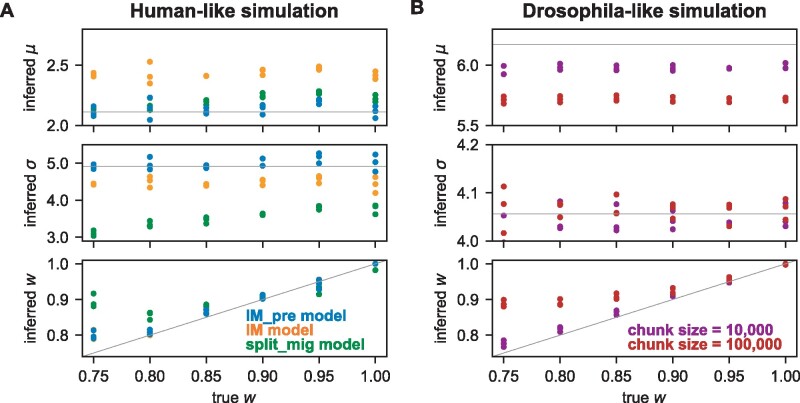
Finally, background selection (BGS) may also bias our joint DFE inference. To examine the effects of BGS on our inference, we simulated data with linkage using SLiM 3 (Haller and Messer 2019). We simulated genome-scale data for both human- and Drosophila-like scenarios using the best fit demographic models we inferred for our real data (supplementary fig. S6A and B, Supplementary Material online). For each data set, we fit a demographic model to the simulated synonymous mutations then used that demographic model to infer the joint DFE from the simulated nonsynonyous mutations. For human-like simulations, we also carried out the analysis using simpler demographic models in the inference. As expected, we found that BGS biased our demographic model inferences. For example, if we used the same human demographic model in the inference and simulation, the inferred divergence time increased as the DFE correlation w decreased (supplementary table S7, Supplementary Material online). As w decreased, the strength of BGS increased (supplementary fig. S5 and table S8, Supplementary Material online). However, we found that the joint DFE correlation w could be robustly inferred in the presence of BGS (fig. 3). The inferred μ and σ were biased if the demographic model was misspecified (fig. 3A). But the inferred w was overestimated only if w was <0.8 with misspecified demographic models (fig. 3A). In our Drosophila-like simulations, we simulated under two different regimes to modulate the strength of BGS (supplementary fig. S5, Supplementary Material online). To make those simulations tractable, we scaled D. melanogaster population sizes down by a factor of 1,000 and scaled other parameters to attempt to compensate (see Materials and Methods), but rescaling may distort various genetic statistics (Uricchio and Hernandez 2014). Nevertheless, similar to the human simulations, we found bias in the inference of μ, but inference of w was biased only if the simulated w was <0.9. Because we observed larger values of w in our real data analyses, these simulations suggest that those analyses are robust to BGS.
Fig. 3.
Robustness of joint DFE inference to background selection. Simulated genome-scale data were generated with background selection and different DFE correlations. (A) Data were simulated using the best fit demographic model for humans in supplementary figure S6A, Supplementary Material online with and . Beside fitting the true model, simpler demographic models (supplementary fig. S2, Supplementary Material online) were also fit to test robustness to model misspecification in the presence of background selection. (B) Data were simulated using the best fit demographic model for Drosophila melanogaster in supplementary figure S6B, Supplementary Material online with and . To modulate the strength of background selection, data were simulated with different genomic chunk sizes. The larger chunk size yields stronger background selection. Points indicate inferences from distinct data sets and colors indicate different simulation scenarios. Gray lines indicate true values. The data plotted in these figures can be found in supplementary table S7, Supplementary Material online.
Together, our tests on simulated data suggest that inferring the DFE correlation w from the joint AFS can be done with high precision and is robust to multiple confounding factors, including misspecification of the demographic model and DFE distribution as well as the presence of BGS.
Application
We applied our joint DFE inference approach to humans, D. melanogaster, and wild tomatoes. For humans, we considered the joint DFE between Yoruba in Ibadan (YRI) and Utah residents (CEPH) with Northern and Western European ancestry (CEU) populations, because the Yoruba are a well-studied proxy for the ancestral human population and European populations parallel the history of French D. melanogaster. For D. melanogaster, we considered the joint DFE between Zambian and French populations, because the Zambian population is representative of the ancestral population (Lack et al. 2015) and France is a distinct environment. For wild tomatoes, we considered the joint DFE between two closely related species, Solanum chilense and Solanum peruvianum, because they still share substantial polymorphism and have overlapping ranges.
We first fit demographic models to synonymous variants in each population pair. For all the three species, we fit relatively simple models of divergence with gene flow, although for humans we also found it necessary to include predivergence population growth. Broadly, these models fit the data well (supplementary figs. S6 and S7, Supplementary Material online).
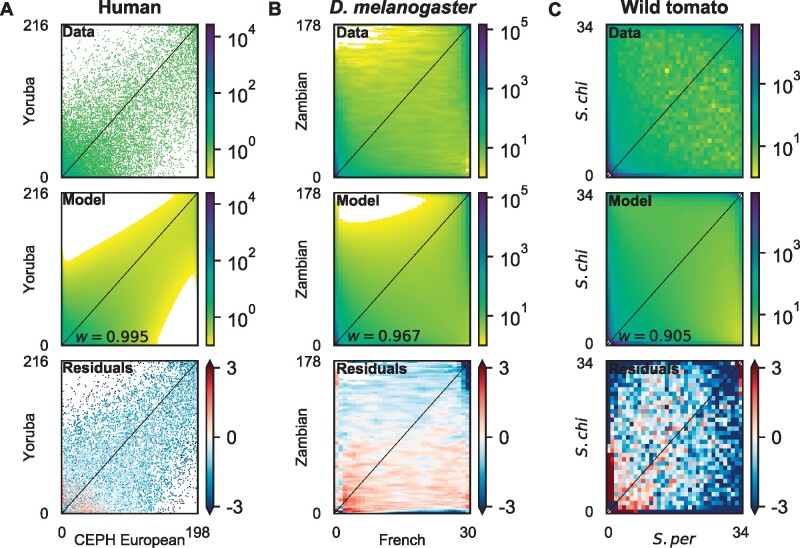
We next estimated the joint DFE using all nonsynonymous variants in the whole exome data from each species with our lognormal mixture model (fig. 1D). In all the cases, the resulting models fit the nonsynonymous joint frequency spectrum well, with similar patterns of residuals to the demographic models fit to synonymous data (fig. 4 and supplementary fig. S7, Supplementary Material online). For humans, we found the highest DFE correlation in our study (fig. 5 and supplementary table S9, Supplementary Material online), which was statistically indistinguishable from perfect correlation w = 1. For D. melanogaster, we found that mutation fitness effects between Zambian and French populations were highly correlated, with (fig. 5 and supplementary table S10, Supplementary Material online). For wild tomatoes, we found the lowest DFE correlation, (fig. 5 and supplementary table S11, Supplementary Material online). In humans, CpG dinucleotides have elevated mutation rates, which might affect DFE inference. To control for this effect, we repeated our exome analysis in humans using only regions outside annotated CpG islands. We also did a similar analysis in D. melanogaster, although their CpG dinucleotides do not have elevated mutation rates. The resulting estimates of w (supplementary fig. S12 and supplementary tables S9, S10, Supplementary Material online) were statistically indistinguishable from those using the whole exome data. We further inferred DFE correlation using only GC-conservative mutations (A ↔ T and C ↔ G) in humans, because GC-biased gene conversion (gBGC), which is common in mammals but not in D. melanogaster (Zhen et al. 2021), may bias DFE inference (Castellano et al. 2019). These GC-conservative mutations are not affected by gBGC. Similar to the whole exome data, the resulting w was statistically indistinguishable from 1 (supplementary fig. S12 and table S9, Supplementary Material online). Among these three population pairs, the inferred DFE correlation was negatively related to genetic divergence, as measured by FST (fig. 5A).
Fig. 4.
Model fits to joint allele frequency spectra (AFS) using nonsynonymous data. (A) Joint AFS for the human nonsynonymous data, the best fit model with DFE correlation w = 0.995, and the residuals between model and data. (B) Joint AFS for the Drosophila melanogaster nonsynonymous data and the best fit model with DFE correlation w = 0.967. (C) Joint AFS for the wild tomato nonsynonymous data and the best fit model with DFE correlation w = 0.905. In all three cases, residuals are small for almost all entries in the AFS, so to increase contrast the color range has been restricted to ±3. See supplementary figure S8, Supplementary Material online for plots showing the full residual range.
Fig. 5.
Exome-wide DFE correlations. (A) Plotted are maximum likelihood inferences of the DFE correlation w with 95% confidence intervals versus genetic divergence FST of the considered population pair. (B) Plotted are maximum likelihood inferences of the DFE correlation w with 95% confidence intervals for nonsynonymous SNPS with different predicted effects from SIFT. Colors indicate FDR adjusted P-values from two-tailed z-tests as to whether the confidence interval overlaps w = 1. FST was estimated using whole-exome synonymous mutations.
For simplicity, we assumed that the DFE correlation w is constant throughout the distribution, but the correlation may depend on how deleterious the mutation is. To test this assumption, rather than adding complexity to the DFE model, we instead segregated our data by applying SIFT scores to predict whether a nonsynonymous mutation is likely to be tolerated or deleterious based on evolutionary conservation (Vaser et al. 2016). We then fit DFE models to the SNPs in each class. As expected, we inferred a more negative mean fitness effect for the deleterious class than the tolerated class (supplementary fig. S12 and tables S9–S11, Supplementary Material online). Moreover, we found that the DFE correlation w was dramatically smaller for the deleterious class than the value from the tolerated class in humans and D. melanogaster, but not in wild tomatoes (fig. 5B). To test whether this effect extended beyond individual mutations to whole genes, we also separated our data by the dN/dS ratio in humans and D. melanogaster. We found no significant difference in DFE correlations among genes with different dN/dS ratios (supplementary fig. S12, Supplementary Material online). However, we did observe that the average strength of purifying selection increases as the dN/dS ratio decreases (supplementary fig. S12, Supplementary Material online).
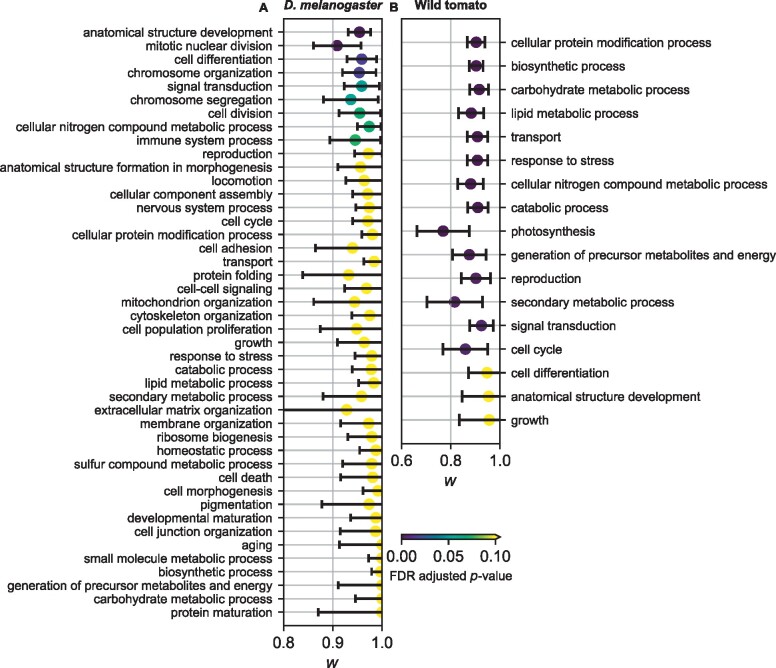
To investigate the biological basis of the joint DFE, we considered genes of different function based on Gene Ontology (GO) terms (Gene Ontology Consortium 2000). For D. melanogaster, we found a wide range of inferred DFE correlations, with the lowest maximum likelihood estimate corresponding to mutations in genes involved in the mitotic nuclear division at (fig. 6 and supplementary table S10, Supplementary Material online). For wild tomatoes, we found an even wider range of inferred DFE correlations, with the lowest maximum likelihood estimate being genes involved in photosynthesis at (fig. 6 and supplementary table S11, Supplementary Material online). For humans, we found that all GO terms yielded values of w that were statistically indistinguishable from one (supplementary table S9 and fig. S9, Supplementary Material online). Among the D. melanogaster GO terms, we found no correlation between the inferred w and the mean and standard deviation of the marginal DFEs (supplementary fig. S13, Supplementary Material online), suggesting that the variation we see in w is not driven simply by variation in overall constraint. In humans, we further explored the biological context of the joint DFE by considering genes that are involved in disease and that interact with viral pathogens. We found no statistically significant differences in DFE correlations among these gene groups, although we did find that the DFE for genes involved in disease or that interact with viruses was shifted toward more negative selection (supplementary table S9 and fig. S12, Supplementary Material online).
Fig. 6.
DFE correlation for different GO terms in Drosophila melanogaster and wild tomatoes. Plotted are maximum likelihood inferences with 95% confidence intervals. Colors indicate FDR-adjusted P-values from two-tailed z-tests as to whether the confidence interval overlaps w = 1. The data plotted in these figures can be found in supplementary tables S10 and S11, Supplementary Material online. (A) Inferred DFE correlation in D. melanogaster. (B) Inferred DFE correlation in wild tomatoes.
To test the robustness of our analyses in the real data to various modeling choices, we used the variation among our inferences among D. melanogaster GO terms. We fit simpler models of demographic history with instantaneous growth in the two diverged populations with and without symmetric migration to the synonymous data and used those models as the basis of joint DFE analysis. Although these demographic models fit the data much less well than our main model (supplementary figs. S7 and S14, Supplementary Material online), the inferred values of w for the GO terms were highly correlated with those from our main model (supplementary fig. S15A and B, Supplementary Material online). We also tested our approach using a DFE model with a bivariate lognormal model instead of a lognormal mixture model. The inferred values for ρ in the bivariate model were highly correlated with the values for the inferred w (supplementary fig. S15C, Supplementary Material online). Together, these results suggest that the robustness we observed in simulated data (fig. 2) holds true for real data.
Discussion
In this study, we introduced the concept of a joint DFE between pairs of populations, and we developed and applied an approach for inferring it. We tested our approach with simulation studies and found that inferring the DFE correlation between populations does not require excessive data and is robust to many forms of model misspecification (supplementary fig. S3, Supplementary Material online and figs. 2 and 3). We then applied our approach to humans, D. melanogaster, and wild tomatoes. Among these species, we found the lowest exome-wide DFE correlation in wild tomatoes and the highest in humans (fig. 5A). In humans and D. melanogaster, we found that the DFE correlation is lower for deleterious mutations than tolerated mutations (fig. 5B). And in D. melanogaster and tomatoes, we found that the DFE correlation varied with gene function (fig. 6). These results illustrate the biological insights that can be gained by considering the joint DFE between populations.
The first step of our analyses is fitting a demographic model, although our DFE correlation inferences are robust to details of that model (fig. 2A and supplementary fig. S14, Supplementary Material online). Nevertheless, our inferred demographic models (supplementary fig. S6, Supplementary Material online) are comparable to other inferences. For D. melanogaster, our inferred relative population sizes and divergence time for African and European populations are similar to those of Arguello et al. (2019) (supplementary table S16, Supplementary Material online), although we used different populations and different models. For humans, our demographic parameters were similar to those of Gravel et al. (2011) (supplementary table S17, Supplementary Material online), although their model also included an East Asian population. For wild tomatoes, we obtained a demographic model close to the result of Beddows et al. (2017) (supplementary table S18, Supplementary Material online).
The fitness effect of a mutation may differ between populations due to differences in both environmental and genetic context. The wild tomato species we analyzed overlap in range and are more genetically differentiated than the D. melanogaster or human populations we studied. In this case, we speculate that differences in fitness effects are primarily driven by differences in genetic background, although S. chilense does exhibit adaptations for more arid habitats (Moyle 2008). Among the species we studied, humans exhibited the highest correlation of mutation fitness effects, which was statistically indistinguishable from perfect correlation w = 1, suggesting little difference in mutation fitness effects between YRI and CEU populations. Huang et al. (2021) also estimated the genome-wide differences of selection coefficients between Africans and Europeans were almost 0 with a different approach (He et al. 2015). It is unclear whether this is caused by our relatively low genetic differentiation or our ability to control our local environment. Experiments suggest that stressful environments can alter DFEs between populations (Wang et al. 2014). Previous population genetic studies also have found evidence for differences in marginal DFEs between populations of humans (Boyko et al. 2008; Lopez et al. 2018) and also between populations of other primates (Ma et al. 2013; Castellano et al. 2019; Tataru and Bataillon 2019). Although we assumed that the mean and the variance of mutation fitness effects did not differ between the two populations in our models for the joint DFE, those previous studies found only slight differences and our simulation study suggests that inferences of the DFE correlation are robust to relatively large differences in marginal DFEs (fig. 2D). Recently, Martin and Lenormand (2015) extended Fisher’s Geometrical Model to consider the relationship between mutation fitness effects in two different environments, represented by two optima in trait space. Unfortunately, they could not derive an analytic joint DFE for their model, so we could not apply it here. In related work, Keightley et al. (2000) used Caenorhabditis elegans mutation accumulation data to infer bivariate gamma distributions of mutation effects on pairs of life history traits, although with low precision. Overall, our simple models of the joint DFE fit the data well, but more complex models may be more informative. Over the long term, assessing the joint DFE between multiple populations of multiple species may reveal the relative importance of environmental and genetic context in determining the mutation fitness effects.
We focused on the deleterious component of the DFE in this study, and positive selection or local adaptation may affect joint DFE inference. However, Castellano et al. (2019) found that including beneficial mutations or not did not affect the DFE model for the deleterious components in humans. Moreover, Zhen et al. (2021) estimated the proportion of new beneficial mutations to be ∼1.5% in humans and close to 0 in D. melanogaster. Therefore, we do not expect beneficial mutations to significantly affect our inference in humans and D. melanogaster. Further studies that include local adaptation when inferring the joint DFE may improve our analysis of populations with low DFE correlations, such as wild tomatoes.
Finally, the concept of a joint DFE could be widely applicable. For example, we recently inferred a joint DFE between mutations at the same protein site, using triallelic variants (Ragsdale et al. 2016). Remarkably, we found that biochemical experiments in a variety of organisms yielded a similar correlation of pairwise fitness effects to the value we inferred from D. melanogaster population genetic data. Other potential applications of a joint DFE include modeling ancient DNA data to infer DFE correlations across time and modeling linkage to infer DFE correlations across genomic positions. We thus anticipate that extending the concept of the DFE from one population to two or more will significantly advance our understanding of population evolution and have broad impact in population genetics.
Materials and Methods
Inferring the Joint DFE from the Joint AFS
If we sample n1 chromosomes from population 1 and n2 chromosomes from population 2, then the joint AFS for these two populations can be written as
| (1) |
Here, denotes the number of mutations in the sample that have i copies of derived alleles among the n1 chromosomes from population 1 and j copies of derived alleles among the n2 chromosomes from population 2. We denote the joint spectra for neutral and selected mutations as and , respectively.
Let be the expected joint AFS for demographic parameters , population-scaled selection coefficients γ1 in the ancestral and first contemporary population and γ2 in the second contemporary population, and population-scaled mutation rate θ= 1. The population-scaled selection coefficient γ is , where Na is the ancestral population size. For a mutation with selection coefficient s, a diploid individual has its fitness multiplied by if homozygous and by if heterozygous, where h is the dominance coefficient. The population-scaled mutation rate θ is , where μ is the mutation rate. The vector of demographic parameters depends on the demographic model assumed, but it typically contains parameters for relative population sizes, divergence times, and rates of gene flow. Then the expected neutral joint AFS is
| (2) |
where is the population-scaled neutral mutation rate (Gutenkunst et al. 2009). The expected selected joint AFS is
| (3) |
Here is the population-scaled mutation rate for selected mutations, and is the joint DFE.
In most of our analyses, we modeled the joint DFE as a mixture of two components, and , where is a DFE with equal selection coefficients in the two populations, and is a DFE with statistically independent selection coefficients and marginal distributions . Letting w be the mixture proportion of , we have
| (4) |
And considering only deleterious mutations we have
| (5) |
We typically worked with lognormal distributions, so
| (6) |
Here, μ and σ are the mean and standard deviation of the logs of the population-scaled selection coefficients, respectively.
To test the robustness of our approach, we also considered other models for the joint DFE. When using a mixture of gamma distributions,
| (7) |
Here, α is the shape parameter and β is the scale parameter. When using a bivariate lognormal distribution, which is potentially asymmetric,
| (8) |
Here, ρ is the correlation coefficient.
Calculating the expected selected joint AFS (eqs. 3 and 5) is computationally expensive, because spectra must be calculated for many pairs of selection coefficients. Simultaneously inferring the demographic parameters and the DFE parameters is thus infeasible. We thus first inferred the demographic parameters using the putative neutral data and then held those parameters constant while inferring the DFE parameters.
Ancestral state misidentification creates an excess of high-frequency derived alleles (Baudry and Depaulis 2003), which may bias demographic history and DFE inference. To account for this effect, when fitting demographic history and DFE models we included separate parameters for ancestral state misidentification (Ragsdale et al. 2016). Then, for example,
| (9) |
when ancestral state misidentification is applied to the neutral demographic history model.
We inferred the demographic parameters by maximizing the composite likelihood of the neutral joint AFS, including as a free parameter (Gutenkunst et al. 2009). To then infer the DFE parameters , we modeled the selected joint AFS as a Poisson Random Field (Sawyer and Hartl 1992) and maximized the composite likelihood
| (10) |
Here, represents the demographic parameters inferred from the neutral data. And in this step we fixed to a multiple of determined by the expected ratio of new selected to new neutral mutations, based on base-specific mutation rates and genome composition.
Numerically, to calculate the expected selected joint AFS, we first cached expected spectra for a range of selection coefficient pairs. The cached values of γ1, γ2 were from 50 points logarithmically spaced within , for a total of 2,500 cached spectra (supplementary fig. S1, Supplementary Material online). We then evaluated equation (3) using the trapezoid rule over these cached points. To test whether the accuracy of this integration affected our results, we repeated our exome-wide analyses for humans and D. melanogaster using 100 cache points, for a total of 10,000 cached spectra. The results of these analyses were statistically indistinguishable from those using 50 cache points (supplementary table S13, Supplementary Material online). For the mixture model (eq. 5), the component was calculated as a one-dimensional integral over a cache of spectra. Probability density for the joint DFE may extend outside the range of cached spectra. To account for this density, we integrated outward from the sampled domain to γ= 0 or to estimate the excluded weight of the joint DFE. We then weighted the closest cached joint AFS F by the result and added it to the expected joint AFS. For the edges of the domain, this was done using the SciPy method quad, and for the corners it was done using dblquad (Virtanen et al. 2020).
Simulated Data
For our precision tests (supplementary fig. S3, Supplementary Material online), we used dadi to simulate data sets without linkage. Unless otherwise specified, for supplementary figure S3, Supplementary Material online and figure 2, the “truth” simulations were performed with an isolation-with-migration (IM) demographic model (supplementary fig. S2B, Supplementary Material online) with parameters as in supplementary table S1, Supplementary Material online, a joint lognormal mixture DFE model with marginal mean and standard deviation , and with sample sizes of 216 for population 1 and 198 for population 2. For supplementary figure S3, Supplementary Material online, data were simulated with w = 0.9 and the nonsynonymous population-scaled mutation rate by Poisson sampling from the expected joint AFS. For supplementary figure S3A, Supplementary Material online, the resulting average number of segregating polymorphisms varied with sample size, ranging from 6,953 for sampling two chromosomes to 45,691 for sampling 100 chromosomes. For supplementary figure S3B and C, Supplementary Material online, the sample size was fixed at 20 chromosomes per population.
For our robustness tests (fig. 2), we were interested in bias rather than variance, so misspecified models were fit directly to the expected frequency spectrum under the true model without Poisson sampling noise. For figure 2A, the best fit model with no migration had s = 0.937, , T = 0.0639, m = 0, and the best fit model with instantaneous growth and symmetric migration had , T = 0.23, m = 0.42. For figure 2C, the true joint DFE was a mixture model with marginal gamma distributions with , β = 1400. For figure 2D, the true joint DFE was a symmetric bivariate lognormal distribution with and , and for the asymmetric case in figure 2D, . We then simulated data with different correlation coefficients ρ to examine the relationship between ρ and the DFE correlation w.
To examine the effects of BGS, we used SLiM 3 (Haller and Messer 2019) to simulate data with linkage. We replicated our simulation and inference three times for each w with different demographic models in the human simulations and an IM model in the D. melanogaster simulations (supplementary fig. S2, Supplementary Material online). For humans, we simulated the exome in chromosome 21 using the demographic parameters in supplementary figure S6A, Supplementary Material online, the joint DFE parameters μ and σ from the whole human exome in supplementary table S9, Supplementary Material online with , and sample sizes of 216 for population 1 and 198 for population 2. We assumed the mutation rate was per nucleotide per generation ( Ségurel et al. 2014) and an ancestral population size of 8,000. We further assumed the ratio of the nonsynonymous to synonymous mutations in humans was 2.31 (Huber et al. 2017). In our simulation, we used the human exome based on the reference genome hg19 from UCSC Genome Browser and the deCODE human genetic map (Kong et al. 2010). For each w, we first simulated human chromosome 21 twenty times, then obtained 20 synonymous frequency spectra and 20 nonsynonymous frequency spectra from these sequences. We combined these 20 synonymous frequency spectra into a single one and inferred the demographic models. We then combined the 20 nonsynoymous frequency spectra into one spectrum and inferred the joint DFEs. We inferred the joint DFEs using both the true (IM_pre model) and wrong (IM model with asymmetric migration & split_mig model without migration) demographic models (supplementary fig. S2, Supplementary Material online). For D. melanogaster, we simulated small sequences instead of a whole chromosome, because the large population size of D. melanogaster made our simulation extremely slow. We used the demographic parameters for the IM model in supplementary figure S6B, Supplementary Material online, the joint DFE parameters μ and σ from the whole D. melanogaster exome in supplementary table S10, Supplementary Material online with , and sample sizes of 178 for population 1 and 30 for population 2. For each w, we simulated 2000 small sequences with a length of 10,000 bp, then obtained 2,000 synonymous frequency spectra and 2,000 nonsynonymous frequency spectra. We combined these 2,000 synonymous frequency spectra into a single one and inferred the demographic models. We then combined the 2,000 nonsynonymous frequency spectra into one spectrum and inferred the joint DFEs. This was equivalent to a total sequence size of 20 Mb. We also replicated the above simulation with 200 small sequences with a length of 100,000 bp. We inferred the demographic and DFE parameters from the combined synonymous frequency spectrum and nonsynonymous frequency spectrum of these 200 small sequences. We assumed that the mutation rate was per nucleotide per generation, that the recombination rate was per nucleotide per generation (Keightley et al. 2014), and that the ancestral population size was 1.38 million. We also assumed the ratio of the nonsynonymous to synonymous mutations in D. melanogaster was 2.85 (Huber et al. 2017). For D. melanogaster, to accelerate our simulation, we used a factor of 1,000 to rescale the population size, mutation rate, and recombination rate (Hoggart et al. 2007). To quantify the strength of BGS in our simulations, we simulated data under neutral models and compared the expected number of pairwise differences between two chromosomes in the nonneutral scenarios with the neutral ones (Hudson and Kaplan 1995). The strength of BGS (supplementary fig. S5, Supplementary Material online) in the simulated data for both humans and D. melanogaster was comparable to or stronger than the estimated strength from the empirical studies (Charlesworth 2013).
Genomic Data
In all analyses, we only considered biallelic SNPs from automosomes. For humans, we obtained 108 and 99 unrelated individuals (216 and 198 haplotypes) from YRI and CEU populations in the 1000 Genomes Project Phase 3 genotype data (1000 Genomes Project Consortium 2015). We removed those regions that were not in the 1000 Genomes Project phase 3 strict mask file. We only considered biallelic exonic SNPs that were annotated as synonymous_variant or missense_variant by the 1000 Genomes Project. We further excluded SNPs without reported ancestral alleles. We also used the CpG table from the UCSC Genome Browser to distinguish SNPs in CpG regions. We further used mutations unaffected by gBGC (only A ↔ T and C ↔ G mutations) to repeat our analysis.
For D. melanogaster, we obtained Zambian and French D. melanogaster genomic data from the Drosophila Genome Nexus (Lack et al. 2016). The Zambian sequences were 197 haploids from the DPGP3 and the French were 87 inbred individuals. We removed those SNPs in the IBD and/or admixture masks. In these data, many SNPs were not called in all individuals. We thus projected downward to obtain a consensus AFS with maximal genome coverage. For these data, that was to a sample size of 178 Zambian and 30 French haplotypes (supplementary fig. S16, Supplementary Material online). We used Drosophila simulans as the outgroup and downloaded the alignment between the reference genome for D. simulans (drosim1) and the reference genome for D. melanogaster (dm3) from UCSC Genome Browser to determine the ancestral allele of each SNP. We then used GATK (version: 4.1.4.1) (McKenna et al. 2010) to liftover the genomic coordinates from dm3 to dm6 with the liftover chain file from the UCSC Genome Browser. To annotate SNPs to their corresponding genes and as synonymous or nonsynonymous mutations, we used ANNOVAR (version: 20191024) (Wang et al. 2010) with default settings and the dm6 genome build. We downloaded the CpG table from the UCSC Genome Browser to distinguish SNPs in CpG regions.
For wild tomatoes, we obtained S. chilense and S. peruvianum DNA sequencing data from Beddows et al. (2017) and followed their scheme for assigning individuals to species. We only analyzed 17 S. chilense and 17 S. peruvianum individuals sequenced by Beddows et al. (2017) because of their high quality. We used an Solanum lycopersicoides individual sequenced by Beddows et al. (2017) to determine the ancestral allele of each SNP. We further removed variants with heterozygous genotype in this S. lycopersicoides individual. To more easily apply SIFT, we used the NCBI genome remapping service to convert the data from SL2.50 coordinates to SL2.40.
Fitting Demographic Models to Genomic Data
We used dadi to fit models for demography to spectra for synonymous mutations (Gutenkunst et al. 2009), including a parameter for ancestral state misidentification (Ragsdale et al. 2016). For the human analysis, we used dadi with grid points of [226,236,246], and we found that an IM model with an instantaneous growth in the ancestral population (IM_pre) fit the data well (supplementary fig. S6A, Supplementary Material online). For the D. melanogaster analysis, we used dadi with grid points of [188,198,208], and we found that an IM model fit the data well (supplementary fig. S6B, Supplementary Material online). For the wild tomato analysis, we used dadi with grid points of [44,54,64] and fit a split-migration model with asymmetric migration (supplementary fig. S6C, Supplementary Material online), as Beddows et al. (2017) did.
Fitting Joint DFEs to Genomic Data
Cached allele frequency spectra were created for the corresponding demographic models. For humans and D. melanogaster, we used the same grid points settings as the grid points used when inferring demographic models. For wild tomatoes, we used dadi with grid points of to generate caches with selection. Models of the joint DFE were then fit to nonsynonymous data by maximizing the likelihood of the data, assuming a Poisson Random Field (Sawyer and Hartl 1992). In these fits, the population-scaled mutation rate for nonsynonymous mutations θNS was held fixed at a given ratio to the rate for synonymous mutations θS in the same subset of genes, as inferred from our demographic history model. For D. melanogaster this ratio was 2.85 and for humans it was 2.31 (Huber et al. 2017). This ratio was 5.21 for the gBGC unaffected mutations in humans (Zhen et al. 2021). For wild tomatoes, this ratio was assumed to be 2.5, which was between the ratios in humans and D. melanogaster. For the lognormal mixture model, the three parameters of interest are the DFE correlation w as well as the mean μ and standard deviation σ of the marginal distributions. In addition, we included a separate parameter for ancestral state misidentification for each subset of the data tested, because the rate of misidentification depends on the strength of selection acting on the sites of interest. To mitigate the effect of BGS, we separately inferred demographic parameters for each subset of the data (supplementary tables S9–S11, Supplementary Material online) with the best fit demographic model inferred from the whole exome data (supplementary fig. S6, Supplementary Material online).
We separately analyzed SNPs from genes associated with different GO terms. We downloaded the Generic GO subset from http://geneontology.org/docs/download-ontology/ on August 12, 2020. This is a set of curated terms that are applicable to a range of species (Gene Ontology Consortium 2000). We considered the direct children of GO: 0008510 “Biological Process,” and any gene annotated with a child of a given term was assumed to also be annotated by the parent term. Thus, a given gene may be present in multiple GO terms in our analysis. We used Ensembl Biomart (Cunningham et al. 2019) to retrieve the annotated GO terms for each gene. For humans, we downloaded the GO annotation from https://grch37.ensembl.org/biomart/martview/ with Ensembl Genes 101 database and Human genes (GRCh37.p13) on August 19, 2020. For D. melanogaster, we downloaded the GO annotation from https://www.ensembl.org/biomart/martview/ with Ensembl Genes 101 database and D. melanogaster genes (BDGP6.28) on September 10, 2020. For tomatoes, we downloaded the GO annotation from https://jul2018-plants.ensembl.org/biomart/martview/ with Ensembl Plants Genes 40 database and Solanum lycopersicum genes (SL2.50) on September 26, 2020. To ensure convergence in our inference, we removed those GO terms with <2,000 either synonymous or nonsynonymous mutations (supplementary tables S9–S11, Supplementary Material online).
We also separately analyzed SNPs classified by SIFT as deleterious (SIFT score 0.05) or tolerated (SIFT score > 0.05) (Vaser et al. 2016). We downloaded SIFT predictions from https://sift.bii.a-star.edu.sg/sift4g/ on October 2, 2020. We used the SIFT prediction data with GRCH37.74 for humans, with BDGP6.83 for D. melanogaster, and with SL2.40.26 for tomatoes. To carry out our DFE analysis, we needed to estimate an appropriate population-scaled nonsynonymous mutation rate θNS for deleterious and tolerated mutations. To do so, we estimated the proportions of deleterious and tolerated mutations in the downloaded SIFT prediction data sets. This is because all the possible mutations and their SIFT scores were predicted in the downloaded data sets. We then obtained the population-scaled mutation rates for deleterious and tolerated mutations by multiplying θNS from the whole exome data with the proportions of deleterious and tolerated mutations, respectively. More specifically, if we assumed the mutation rate for the ith type nucleotide mutation to be ui, the count for deleterious mutations from the ith type nucleotide mutation to be di in the SIFT data sets, and the count for tolerated mutations from the ith type nucleotide mutation to be ti in the SIFT data sets, then the proportions for deleterious and tolerated mutations were and , respectively. In total, we have 12 different types of nucleotide mutations: A → T, T → A, C → G, G → C, A → C, C → A, C → T, T → C, A → G, G → A, G → T, and T → G. We obtained the mutation rates for different types of mutations from Jónsson et al. (2017) for humans and Singh et al. (2007) for drosophila. For wild tomatoes, we used the Arabidopsis thaliana nucleotide mutation rates from Ossowski et al. (2010), because these mutation rates have not been directly measured in wild tomatoes.
We further considered differences between regions of the genome that experience different levels of evolutionary conservation, as estimated from the ratio of nonsynonymous to synonymous divergence dN/dS. For humans, we separated SNPs into categories based on the estimated dN/dS values of the gene in which they are found from a previous study (Gayà-Vidal and Albà 2014). For D. melanogaster, we separated SNPs based on the dN/dS estimate of the surrounding 10 kb genomic region from PopFly (Hervas et al. 2017).
For humans, we also divided genes into classes based on their role in disease and interactions with viruses. Following Struck et al. (2018), we classified genes as associated with Mendelian disease, complex disease, or no disease using Online Mendelian Inheritance in Man (OMIM, Amberger et al. 2015) and the European Bioinformatics Institute’s genome-wide association studies (GWAS) catalog (MacArthur et al. 2017). We used the data of Enard and Petrov (2018) to annotate 4,534 genes as encoding virus-interacting proteins (VIPs). We defined the set of non-VIP genes as the 17,603 Ensembl genes that were not annotated as encoding VIPs. We identified 1,728 genes as known to interact with 2 or more viruses, leaving 2,806 genes known to interact with only a single virus.
To estimate the uncertainty of our inferences, we used an approach based on the Godambe Information Matrix (Coffman et al. 2016), which is computationally more efficient than conventional bootstrap parameter optimization. To generate the requisite bootstrap data sets, we divided the reference genomes into 1 Mb chunks. Because gene content varied among bootstraps, θNS also needed to vary. To estimate the appropriate θNS for each bootstrap, we scaled corresponding θNS from the real data by the ratio of the number of segregating sites in the AFS of the bootstrap versus real data. We found good agreement between the uncertainties estimated by the Godambe approach and those from directly fitting the bootstrap data sets (supplementary fig. S17, Supplementary Material online). Note that this process does not propagate uncertainty in the demographic parameter inference, so our uncertainties are somewhat underestimated.
To estimate P-values for inferred DFE correlation w, we used the two-tailed z-test by assuming w = 1 under the null hypothesis and using the standard deviation estimated from the Godambe approach. To compare inferred DFE correlations between tolerated and deleterious mutations, we used two-tailed z-tests to calculate P-values by assuming no difference under the null hypothesis and using the standard deviations estimated from the Godambe approach. For multiple testing correction, we estimated false discovery rate (FDR) adjusted P-values by the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995). These multiple hypothesis tests are from different types of data, including whole-exome data, whole-exome data without CpG regions, different GO terms, genes with different dN/dS values, genes with different SIFT scores, genes associated with no/simple/complex diseases, and genes associated with no/single/multiple VIPs (supplementary tables S9–S11, Supplementary Material online).
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
We thank Laura Rose and Thorsten Kloesges for sharing their tomato data and assistance with the analysis. We also thank David Enard for sharing his virus-interacting-proteins data. We also thank Christian Huber and Kirk Lohmuller for discussing SLiM simulation with background selection. Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM127348.
Author Contributions
R.N.G. designed the study. X.H., A.L.F., A.J.C., T.J.S., M.N.I., J.E.J., J.E.L., A.P.R., and R.N.G. designed the analysis method and simulated and analyzed the data. X.H., A.L.F., T.J.S., J.E.J., and R.N.G. wrote the manuscript.
Data Availability
The software tools used in this study are dadi (https://bitbucket.org/gutenkunstlab/dadi) and SLiM 3 (https://github.com/MesserLab/SLiM/).
References
- 1000 Genomes Project Consortium 2015. A global reference for human genetic variation. Nature 526(7571):68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amberger JS, Bocchini CA, Schiettecatte F, Scott AF, Hamosh A.. 2015. OMIM.org: Online Mendelian Inheritance in Man (OMIM[textregistered]), an Online catalog of human genes and genetic disorders. Nucleic Acids Res. 43(Database issue):D789–D798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arguello JR, Laurent S, Clark AG.. 2019. Demographic history of the human commensal Drosophila melanogaster. Genome Biol Evol. 11(3):844–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balick DJ, Do R, Cassa CA, Reich D, Sunyaev SR.. 2015. Dominance of deleterious alleles controls the response to a population bottleneck. PLoS Genet. 11(8):e1005436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton HJ, Zeng K.. 2018. New methods for inferring the distribution of fitness effects for INDELs and SNPs. Mol Biol Evol. 35(6):1536–1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton NH.1995. A general model for the evolution of recombination. Genet Res. 65(2):123–144. [DOI] [PubMed] [Google Scholar]
- Baudry E, Depaulis F.. 2003. Effect of misoriented sites on neutrality tests with outgroup. Genetics 165(3):1619–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beddows I, Reddy A, Kloesges T, Rose LE.. 2017. Population genomics in wild tomatoes-the interplay of divergence and admixture. Genome Biol Evol. 9(11):3023–3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y.. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B. 57(1):289–300. [Google Scholar]
- Boyko AR, Williamson SH, Indap AR, Degenhardt JD, Hernandez RD, Lohmueller KE, Adams MD, Schmidt S, Sninsky JJ, Sunyaev SR, et al. 2008. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 4(5):e1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellano D, James J, Eyre-Walker A.. 2017. Nearly neutral evolution across the Drosophila melanogaster genome. Mol Biol Evol. 35(11):2685–2694. [DOI] [PubMed] [Google Scholar]
- Castellano D, MacIà MC, Tataru P, Bataillon T, Munch K.. 2019. Comparison of the full distribution of fitness effects of new amino acid mutations across great apes. Genetics 213(3):953–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B.1994. The effect of background selection against deleterious mutations on weakly selected, linked variants. Genet Res. 63(3):213–227. [DOI] [PubMed] [Google Scholar]
- Charlesworth B.2013. Background selection 20 years on. J Heredity. 104(2):161–171. [DOI] [PubMed] [Google Scholar]
- Chen J, Glémin S, Lascoux M.. 2017. Genetic diversity and the efficacy of purifying selection across plant and animal species. Mol Biol Evol. 34(6):1417–1428. [DOI] [PubMed] [Google Scholar]
- Chen J, Glémin S, Lascoux M.. 2020. From drift to draft: how much do beneficial mutations actually contribute to predictions of Ohta’s slightly deleterious model of molecular evolution? Genetics 214(4):1005–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman AJ, Hsieh P, Gravel S, Gutenkunst RN.. 2016. Computationally efficient composite likelihood statistics for demographic inference. Mol Biol Evol. 33(2):591–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham F, Achuthan P, Akanni W, Allen J, Amode MR, Armean IM, Bennett R, Bhai J, Billis K, Boddu S, et al. 2019. Ensembl 2019. Nucleic Acids Res. 47(D1):D745–D751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durvasula A, Lohmueller KE.. 2021. Negative selection on complex traits limits phenotype prediction accuracy between populations. 10.1101/721936. [DOI] [PMC free article] [PubMed]
- Elena SF, Ekunwe L, Hajela N, Oden SA, Lenski RE.. 1998. Distribution of fitness effects caused by random insertion mutations in Escherichia coli. Genetica 102–103(1–6):349–358. [PubMed] [Google Scholar]
- Enard D, Petrov DA.. 2018. Evidence that RNA viruses drove adaptive introgression between Neanderthals and modern humans. Cell 175(2):360–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD.. 2007. The distribution of fitness effects of new mutations. Nat Rev Genet. 8(8):610–618. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Woolfit M, Phelps T.. 2006. The distribution of fitness effects of new deleterious amino acid mutations in humans. Genetics 173(2):891–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry JD, Keightley PD, Heinsohn SL, Nuzhdin SV.. 1999. New estimates of the rates and effects of mildly deleterious mutation in Drosophila melanogaster. Proc Natl Acad Sci USA. 96(2):574–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandon S, Hochberg M, Holt RD, Martin G, Day T.. 2013. What limits the evolutionary emergence of pathogens? Philos Trans R Soc B. 368(1610):20120086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gayà-Vidal M, Albà M.. 2014. Uncovering adaptive evolution in the human lineage. BMC Genomics 15:599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gene Ontology Consortium 2000. Gene Ontology: tool for the unification of biology. Nat Genet. 25(1):25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravel S, Henn BM, Gutenkunst RN, Indap AR, Marth GT, Clark AG, Yu F, Gibbs RA, Bustamante CD, Altshuler DL, et al. ; The 1000 Genomes Project. 2011. Demographic history and rare allele sharing among human populations. Proc Natl Acad Sci USA. 108(29):11983–11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD.. 2009. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5(10):e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, Messer PW.. 2019. SLiM 3: forward genetic simulations beyond the Wright–Fisher model. Mol Biol Evol. 36(3):632–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Wang M, Huang X, Li R, Xu H, Xu S, Jin L.. 2015. A probabilistic method for testing and estimating selection differences between populations. Genome Res. 25(12):1903–1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hervas S, Sanz E, Casillas S, Pool JE, Barbadilla A.. 2017. PopFly: the Drosophila population genomics browser. Bioinformatics 33(17):2779–2780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoggart CJ, Chadeau-Hyam M, Clark TG, Lampariello R, Whittaker JC, De Iorio M, Balding DJ.. 2007. Sequence-level population simulations over large genomic regions. Genetics 177(3):1725–1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, Wang S, Jin L, He Y.. 2021. Dissecting dynamics and differences of selective pressures in the evolution of human pigmentation. Biol Open. 10(2):bio.056523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber CD, Durvasula A, Hancock AM, Lohmueller KE.. 2018. Gene expression drives the evolution of dominance. Nat Commun. 9(1):2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber CD, Kim BY, Marsden CD, Lohmueller KE.. 2017. Determining the factors driving selective effects of new nonsynonymous mutations. Proc Natl Acad Sci USA. 114(17):4465–4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL.. 1995. Deleterious background selection with recombination. Genetics 141(4):1605–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James J, Castellano D, Eyre-Walker A.. 2017. DNA sequence diversity and the efficiency of natural selection in animal mitochondrial DNA. Heredity 118(1):88–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johri P, Charlesworth B, Jensen JD.. 2020. Toward an evolutionarily appropriate null model: jointly inferring demography and purifying selection. Genetics 215(1):173–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jónsson H, Sulem P, Kehr B, Kristmundsdottir S, Zink F, Hjartarson E, Hardarson MT, Hjorleifsson KE, Eggertsson HP, Gudjonsson SA, et al. 2017. Parental influence on human germline de novo mutations in 1,548 trios from Iceland. Nature 549(7673):519–522. [DOI] [PubMed] [Google Scholar]
- Keightley PD, Davies EK, Peters AD, Shaw RG.. 2000. Properties of ethylmethane sulfonate-induced mutations affecting life-history traits in Caenorhabditis elegans and inferences about bivariate distributions of mutation effects. Genetics 156(1):143–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A.. 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics 177(4):2251–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A.. 2010. What can we learn about the distribution of fitness effects of new mutations from DNA sequence data? Philos Trans R Soc B. 365(1544):1187–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Ness RW, Halligan DL, Haddrill PR.. 2014. Estimation of the spontaneous mutation rate per nucleotide site in a Drosophila melanogaster full-sib family. Genetics 196(1):313–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim BY, Huber CD, Lohmueller KE.. 2017. Inference of the distribution of selection coefficients for new nonsynonymous mutations using large samples. Genetics 206(1):345–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong A, Thorleifsson G, Gudbjartsson DF, Masson G, Sigurdsson A, Jonasdottir A, Walters GB, Jonasdottir A, Gylfason A, Kristinsson KT, et al. 2010. Fine-scale recombination rate differences between sexes, populations and individuals. Nature 467(7319):1099–1103. [DOI] [PubMed] [Google Scholar]
- Kousathanas A, Keightley PD.. 2013. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics 193(4):1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lack JB, Cardeno CM, Crepeau MW, Taylor W, Corbett-Detig RB, Stevens KA, Langley CH, Pool JE.. 2015. The Drosophila Genome Nexus: a population genomic resource of 623 Drosophila melanogaster genomes, including 197 from a single ancestral range population. Genetics 199(4):1229–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lack JB, Lange JD, Tang AB, Corbett-Detig RB, Pool JE.. 2016. A thousand fly genomes: an expanded drosophila genome nexus. Mol Biol Evol. 33(12):3308–3313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez M, Kousathanas A, Quach H, Harmant C, Mouguiama-Daouda P, Hombert JM, Froment A, Perry GH, Barreiro LB, Verdu P, et al. 2018. The demographic history and mutational load of African hunter-gatherers and farmers. Nat Ecol Evol. 2(4):721–730. [DOI] [PubMed] [Google Scholar]
- Ma X, Kelley JL, Eilertson K, Musharoff S, Degenhardt JD, Martins AL, Vinar T, Kosiol C, Siepel A, Gutenkunst RN, et al. 2013. Population genomic analysis reveals a rich speciation and demographic history of orang-utans (Pongo pygmaeus and Pongo abelii). PLoS One 8(10):e77175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacArthur J, Bowler E, Cerezo M, Gil L, Hall P, Hastings E, Junkins H, McMahon A, Milano A, Morales J, et al. 2017. The new NHGRI-EBI Catalog of published genome-wide association studies (GWAS Catalog). Nucleic Acids Res. 45(D1):D896–D901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G, Lenormand T.. 2015. The fitness effect of mutations across environments: fisher’s geometrical model with multiple optima. Evolution 69(6):1433–1447. [DOI] [PubMed] [Google Scholar]
- McKenna A, Hanna M, Banks E, Sivachenko A, Cibulskis K, Kernytsky A, Garimella K, Altshuler D, Gabriel S, Daly M, et al. 2010. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 20(9):1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moyle LC.2008. Ecological and evolutionary genomics in the wild tomatoes (Solanum Sect. Lycopersicon). Evolution 62(12):2995–3013. [DOI] [PubMed] [Google Scholar]
- Nadarajah S, Gupta AK.. 2006. Some bivariate gamma distributions. Appl Math Lett. 19(8):767–774. [Google Scholar]
- Ossowski S, Schneeberger K, Lucas-Lledo JI, Warthmann N, Clark RM, Shaw RG, Weigel D, Lynch M.. 2010. The rate and molecular spectrum of spontaneous mutations in Arabidopsis thaliana. Science 327(5961):92–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale AP, Coffman AJ, Hsieh P, Struck TJ, Gutenkunst RN.. 2016. Triallelic population genomics for inferring correlated fitness effects of same site nonsynonymous mutations. Genetics 203(1):513–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer SA, Hartl DL.. 1992. Population genetics of polymorphism and divergence. Genetics 132(4):1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ségurel L, Wyman MJ, Przeworski M.. 2014. Determinants of mutation rate variation in the human germline. Annu Rev Genomics Hum Genet. 15(1):47–70. [DOI] [PubMed] [Google Scholar]
- Singh ND, Bauer DuMont VL, Hubisz MJ, Nielsen R, Aquadro CF.. 2007. Patterns of mutation and selection at synonymous sites in Drosophila. Mol Biol Evol. 24(12):2687–2697. [DOI] [PubMed] [Google Scholar]
- Struck TJ, Mannakee BK, Gutenkunst RN.. 2018. The impact of genome-wide association studies on biomedical research publications. Hum Genomics. 12(1):38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tataru P, Bataillon T.. 2019. polyDFEv2.0: testing for invariance of the distribution of fitness effects within and across species. Bioinformatics 35(16):2868–2869. [DOI] [PubMed] [Google Scholar]
- Tataru P, Mollion M, Glémin S, Bataillon T.. 2017. Inference of distribution of fitness effects and proportion of adaptive substitutions from polymorphism data. Genetics 207(3):1103–1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uricchio LH, Hernandez RD.. 2014. Robust forward simulations of recurrent hitchhiking. Genetics 197(1):221–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaser R, Adusumalli S, Leng SN, Sikic M, Ng PC.. 2016. SIFT missense predictions for genomes. Nat Protoc. 11(1):1–9. [DOI] [PubMed] [Google Scholar]
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. ; SciPy 1.0 Contributors. 2020. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 17(3):261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang A, Sharp N, Spencer C, Tedman-Aucoin K, Agrawal A.. 2009. Selection, epistasis, and parent-of-origin effects on deleterious mutations across environments in Drosophila melanogaster. Am Nat. 174(6):863–874. [DOI] [PubMed] [Google Scholar]
- Wang AD, Sharp NP, Agrawal AF.. 2014. Sensitivity of the distribution of mutational fitness effects to environment, genetic background, and adaptedness: a case study with Drosophila. Evolution 68(3):840–853. [DOI] [PubMed] [Google Scholar]
- Wang K, Li M, Hakonarson H.. 2010. ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data. Nucleic Acids Res. 38(16):e164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhen Y, Huber CD, Davies RW, Lohmueller KE.. 2021. Greater strength of selection and higher proportion of beneficial amino acid changing mutations in humans compared with mice and Drosophila melanogaster. Genome Res. 31(1):110–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The software tools used in this study are dadi (https://bitbucket.org/gutenkunstlab/dadi) and SLiM 3 (https://github.com/MesserLab/SLiM/).