Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2021 Sep 1;1(9):1389–1398. doi: 10.1021/jacsau.1c00184

Structural and Spectroscopic Evidence for a Side-on Fe(III)–Superoxo Complex Featuring Discrete O–O Bond Distances

Hung-Ruei Pan †, Hsin-Jou Chen †, Zong-Han Wu †, Pu Ge ‡, Shengfa Ye §,⊥,*, Gene-Hsiang Lee ∥, Hua-Fen Hsu †,*
PMCID: PMC8479760  PMID: 34604849

Abstract

graphic file with name au1c00184_0007.jpg

The O–O bond length is often used as a structural indicator to determine the valence states of bound O2 ligands in biological metal–dioxygen intermediates and related biomimetic complexes. Here, we report very distinct O–O bond lengths found for three crystallographic forms (1.229(4), 1.330(4), 1.387(2) Å at 100 K) of a side-on iron–dioxygen species. Despite their different O–O bond distances, all forms possess the same electronic structure of Fe(III)–O2•–, as evidenced by their indistinguishable spectroscopic features. Density functional theory and ab initio calculations, which successfully reproduce spectroscopic parameters, predict a flat potential energy surface of an η2-O2 motif binding to the iron center regarding the O–O distance. Therefore, the discrete O–O bond lengths observed likely arise from differential intermolecular interactions in the second coordination sphere. The work suggests that the O–O distance is not a reliable benchmark to unequivocally identify the valence state of O2 ligands for metal–dioxygen species in O2-utilizing metalloproteins and synthetic complexes.

Keywords: iron−superoxo complex, superoxo, O2 ligand, non-heme iron, intermediate

Introduction

Reactive metal–dioxygen species, including metal–superoxide and −(hydro)peroxide, play important roles in various biological processes performed by O2-utilizing metalloproteins.1−4 The O–O bond length typically serves as an important indicator to identify the electronic state of these O2-bound intermediates. For instance, free O2, O2•–, and O22– have distinct O–O distances of 1.21, 1.33, and 1.49 Å, respectively.5,6 Thus, based on the short O–O bond length of 1.23 Å, CuI–O2 or CuII–O2•– were both considered in peptidylglycine-α-hydroxylating monooxygenase.7 The structures of several iron-containing oxygenases featuring O–O bond lengths of 1.3–1.4 Å have been proposed as representatives of iron–superoxide complexes;8−11 an O–O distance of 1.45 Å suggests an iron–peroxide species.12 For nickel-containing quercetinase, the O–O bond length only can be refined to a range of 1.20–1.35 Å; therefore, the valency of the O2 ligand cannot be unequivocally assigned.13 Due to the low-resolution of X-ray structures of enzymes, geometric parameters obtained from well-defined synthetic analogues usually serve as references for comparison. Unfortunately, careful examination of individual categories of structurally characterized metal–superoxo or −peroxo complexes reveals that each has a wide range of O–O distances. Furthermore, abnormally short O–O distances have been attributed to librational motions of the diatomic O2 ligand as signified by large thermal displacement parameters,14,15 which can be mitigated by collecting the crystallographic data at low temperatures. Notably, even for X-ray crystallographic data of acceptable quality, the O–O bond length still varies over a wide range (Tables S114−21 and S2(16,22−51)). In particular, for metal–superoxo examples, an O–O bond distance of 1.231(6) Å was found for a Cr(III)–-η1-O2•– complex, but that of 1.383(2) Å was resolved for a Cu(II)−η2-O2•– species.15,17 Similarly, for metal–peroxo compounds, an O–O bond length of 1.361(5) Å was observed for a Co(III)–-η2-O22– complex,32 and that of 1.463(6) Å was obtained for [FeIII(14-TMC)(O2)]+ (TMC = tetramethyl cyclam).25 A copper–dioxygen complex supported by a β-diketiminate ligand featuring an O–O bond length of 1.392(12) Å was initially proposed to be a Cu(III)−η2-O22– species,22 but this formulation was later revised to Cu(II)−η2-O2•– after re-evaluation using Cu K pre-edge X-ray absorption spectroscopy.52 The correlation of O–O bond length and the valence state of bound O2 ligands in metal–dioxygen complexes seems specious if not unclear. The discrepancy in O–O bond lengths for O2 ligands with the same valence state can be ascribed, at least in part, to dissimilarity in the geometry or coordination environment among complexes; therefore, solid evidence remains lacking.

In this work, we report a side-on iron–dioxygen complex, [Fe(PS3″)(O2)]− (1) (PS3″ = [P(C6H3-3-SiMe3-2-S)3]3–), showing various O–O bond lengths in different crystallographic forms where iron centers all possess similar geometry. However, the spectroscopic features of all forms are indistinguishable and conclude an electronic formulation of Fe(III)–O2•– species. All of our structural data are of excellent quality, and thermal displacement parameters of O atoms in the bound O2 units are in an acceptable range, thus librational motion of the O2 ligand is not a factor for their O–O distances. Instead, we propose that the subtle difference in crystal packing is likely responsible for the phenomena. This proposition is supported by the wave-function-based multireference calculations that predict a rather flat potential energy surface of side-on O2 bonding to the Fe center with respect to the O–O distance.

Results and Discussion

Synthesis, Characterization, and Reactivity of Complex 1

Reactions of trigonal-bipyramidal Fe(II) precursors, [X][Fe(PS3″)(CH3CN)] (PS3″ = [P(C6H3-3-SiMe3-2-S)3]3–, X = PPh4+,53 and AsPh4+; Figure S1 and Tables S3 and S4) with O2 in CH3CN at −20 °C or below generate a deep-blue solution with three intense bands at 504, 557, and 655 nm (Scheme 1 and Figure 1A). As monitored by UV–vis–NIR spectroscopy, this is a clean conversion with three isosbestic points at 400, 471, and 893 nm. The crystalline solids of the resulting species, complex 1, were isolated by removing CH3CN from the solution, followed by dissolving the residue in THF and hexane. The single crystals of [X][1]·2THF suitable for X-ray diffraction analyses were obtained by slow precipitation at −40 °C within several days. Complex 1 represents a rare example of structurally characterized non-heme Fe(III)-O2•– biomimetic complex, and the only other case is [FeIII(TAML)(O2)]2– (TAML is a tetraamido macrocyclic ligand), which is, however, generated by treating an Fe(III) precursor with KO2.16 Other synthetic Fe(III)–O2•– species have been only spectroscopically detected.18,54−60

Scheme 1. Formation of [Fe(PS3″)(O2)]− (1) from the reaction of [Fe(PS3″)(CH3CN)]− with O2.

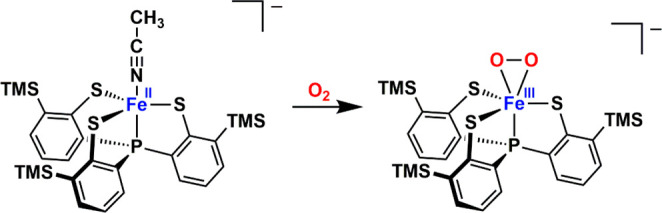
Scheme 1

Open in a new tab

Figure 1.

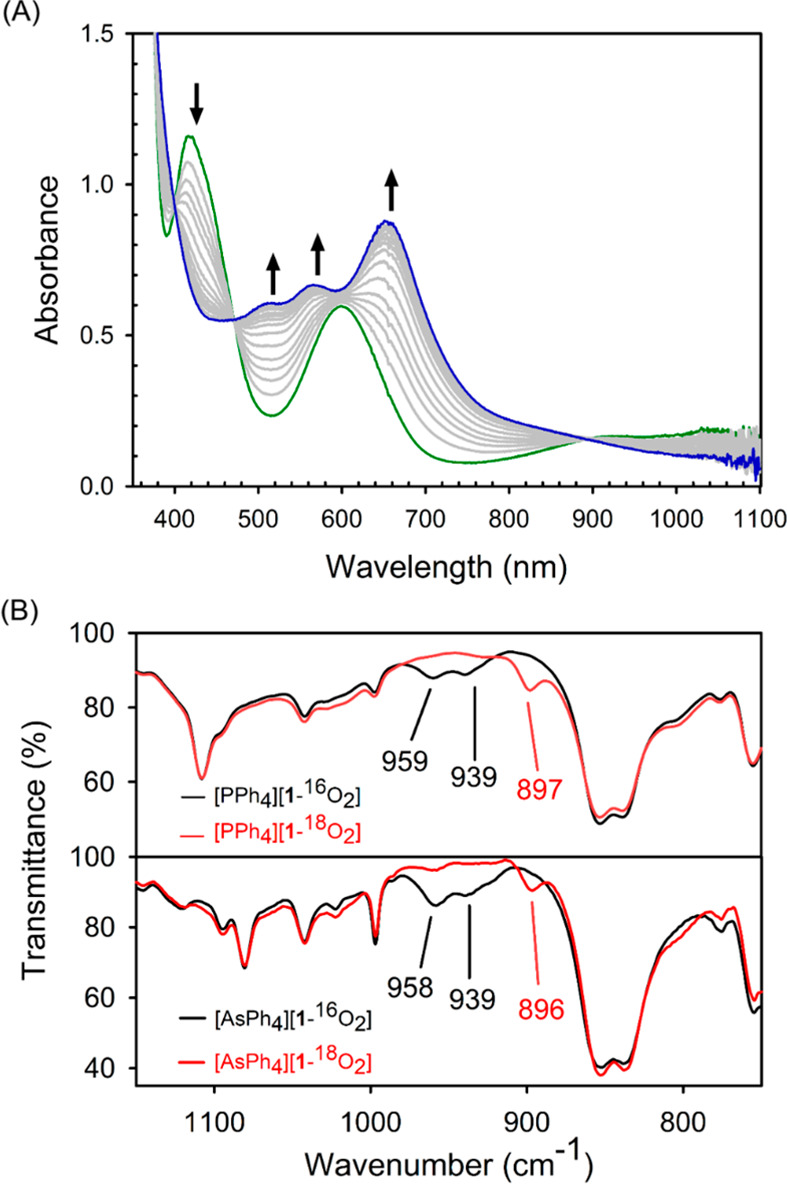
Figure 1

Open in a new tab

(A) Variation of the UV–vis–NIR spectrum of [Fe(PS3″)(CH3CN)]– (green) reacting with O2 to form 1 (blue) at −20 °C. (B) Infrared spectra of [PPh4][1] and [AsPh4][1] in KBr; 16O2 sample (black) and 18O2 sample (red).

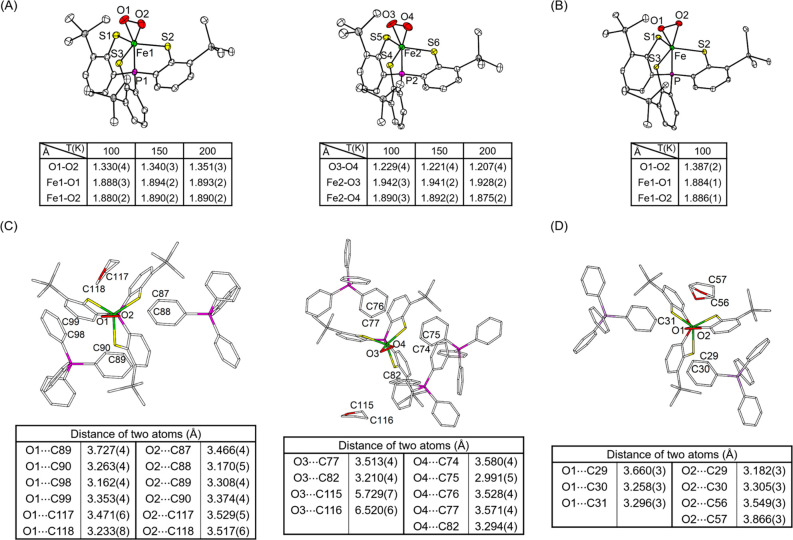
The molecular structures of [PPh4][1]·2THF were determined by X-ray crystallography at 100, 150, and 200 K and that of [AsPh4][1]·2THF at 100 K. Four sets of data are all of high quality without any detectable crystallographic disorder (Tables S5–S8). The geometry of all iron centers can be viewed as a pseudotrigonal-bipyramid formed by a PS3″ ligand and an η2-O2 moiety (Figure 2A,B and Figure S2). The average Fe–S distances (2.31–2.32 Å) in all structures are similar and are close to those reported for related trigonal-bipyramidal complexes, [FeIII(PS3″)L]− (L = Cl– and OCH3–), containing intermediate-spin Fe(III) centers.61 However, the two independent molecules in a crystallographic asymmetric unit of the PPh4+ salt exhibit two distinguishable O–O distances irrespective of the temperature (tables in Figure 2A). Specifically, one with nearly identical Fe–O1 and Fe–O2 bond lengths displays an O1–O2 distance of 1.33–1.35 Å, and the other featuring a slightly asymmetrically coordinated O2 motif possesses an O3–O4 length of 1.21–1.23 Å. In the structure of [AsPh4][1], the η2-O2 ligand binds to the iron center symmetrically and has an O1–O2 distance of 1.387(2) Å (table in Figure 2B). The O–O bond distances observed for the symmetric Fe–O2 unit in [PPh4][1] and [AsPh4][1] are in the longer end of the range (1.23–1.38 Å) found for all structurally characterized metal–superoxo complexes reported thus far (Table S1),14−21 including [FeIII(TAML)(O2)]2– (1.323(3) and 1.306(7) Å).16 It should be noted that [Mn(PS3″)(O2)]−, the Mn derivative of 1, possesses an O–O distance of 1.379(3) Å but is formulated as a Mn(IV)–peroxo species.40 In contrast, the O–O bond lengths determined for the asymmetric Fe–O2 unit in [PPh4][1] are in the shortest end of the range and are even close to that of free O2 (1.21 Å). More importantly, the Ueq values for the two O atoms of the O2 ligand fall into the reasonable range and only marginally increase with the temperature (Table S9). Thus, in the present case, such a large variation in the O–O distances cannot be simply rooted back to the librational motion of the O2 ligand.

Figure 2.

Figure 2

Open in a new tab

ORTEP diagrams (35% probability) of (A) two independent molecules of [PPh4][1]·2THF and (B) the molecule of [AsPh4][1]·2THF. The cations, solvated THF, and H atoms are omitted for clarity. The selected bond distances (Å) obtained at 100, 150, and 200 K for PPh4+ and 100 K for AsPh4+ salts are listed in the tables. (C) Two independent molecules of [PPh4][1]·2THF and (D) the molecule of [AsPh4][1]·2THF showing the neighboring groups of bound O2 moieties. The selected distances between bound O2 and neighboring C atoms of PPh4+ (or AsPh4+) and solvated THF are listed in the tables.

After scrutinizing all of the crystallographic data of [PPh4][1] and [AsPh4][1], we found subtle differences in the second coordination sphere among three sets of the Fe–O2 units (Figure 2C,D). The symmetrically bound O1–O2 moieties of [PPh4][1] and [AsPh4][1] are well surrounded by two phenyl rings of the countercation and a solvated THF molecule. Notably, the distances between both O atoms and a plethora of neighboring C atoms in these groups are 3.2–3.7 Å, implying the presence of a weak hydrogen bonding C–H···O network.62 In contrast, the solvated THF molecule is further away from the bound O3–O4 ligand of [PPh4][1] (O3···C115 = 5.729(7) Å and O3···C116 = 6.520(6) Å). In addition, only one side of the O3–O4 unit (nearby O4) is more tightly encircled with three phenyl rings of PPh4+ compared to the other side (nearby O3).

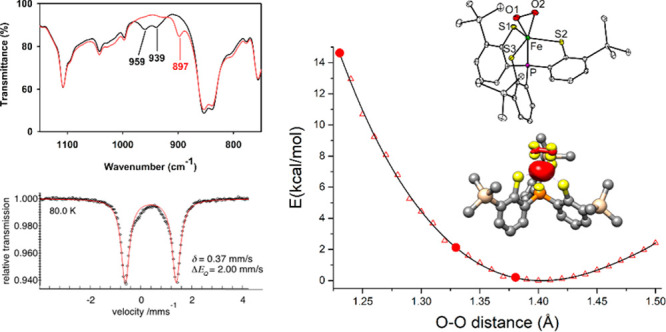
To elucidate the electronic structure origin for the distinct geometries of 1, we carried out detailed spectroscopic characterizations. The KBr infrared (IR) spectrum of [AsPh4][1] revealed a Fermi doublet at 958 and 939 cm–1, which is shifted to 896 cm–1 upon 18O substitution (Figure 1B). Therefore, this doublet should be attributed to the O–O stretch (νO–O) because the observed isotopic shift of 53 cm–1 is in excellent agreement with that (54 cm–1) calculated for a diatomic O–O harmonic oscillator. Remarkably, although two different forms of 1 were found in the crystal structure of [PPh4][1], its solid IR spectrum showed the same features as those for [AsPh4][1] (Figure 1B). More importantly, a broad νO–O band at 958 cm–1, which is shifted to 896 cm–1 for the 18O-isotope-substituted sample, was identified in the IR spectrum of a THF solution of [PPh4][1] (Figure S3). Compared to those reported for metal–superoxo complexes (1260–961 cm–1) (Table S10), the νO–O frequencies measured for 1 are in the lower end. In line with this notion, a Badger’s rule analysis of the O–O stretch at 950 cm–1 predicts a long O–O bond distance of 1.40 Å.63 This value is substantially greater than that determined for the asymmetrically bound O2 ligand of [PPh4][1], although it is close to those for the symmetrically coordinated O2 moiety of [PPh4][1] and [AsPh4][1]. As elaborated elsewhere,64 the bond-length/bond-strength correlations are just empirical relationships rather than physical laws, and due to various reasons, numerous exceptions have been reported already. Therefore, although the bound O2 ligands in three crystallographic forms featured distinct O–O distances, they would have similar O–O force constants and stretching frequencies such that the low resolution of the measured IR spectra especially on solid samples failed to distinguish their differences.

Furthermore, both complexes possess well-isolated S = 1 ground states, as established by the temperature-dependent magnetic susceptibility measurements (Figures S4 and S5). The 1H NMR spectra of both cation salts recorded at 223 K in THF-d8 consistently displayed three peaks at the paramagnetic region, 14.56, −2.54, and −46.03 ppm, associated with the protons in the phenyl rings of the PS3″ ligand (Figure S6). These spectroscopic findings evidence that, despite having distinct O–O bond distances, all forms of 1 feature nearly identical electronic structure irrespective whether in a solid state or in solution.

The zero-field Mössbauer spectra of [PPh4][1] and related PS3″ complex with varying Fe oxidation states are depicted in Figure 3. The isomer shift (δ) determined for 1 is comparable to those found for intermediate-spin ferric species [FeIII(PS3″)Cl]− and [FeIII(PS3″)(OCH3)]− but deviates by more than 0.1 mm/s from those for Fe(II) complex [FeII(PS3″)(CH3CN)]− and Fe(IV) complex [FeIV(PS3″)Cl]. Therefore, Mössbauer data clearly indicate that 1 likely contains an intermediate-spin ferric center, as found for [FeIII(PS3″)Cl]− and [FeIII(PS3″)(OCH3)]−.61 The different quadrupole splitting (ΔEQ) measured for them can be attributed to their distinct coordination geometries.

Figure 3.

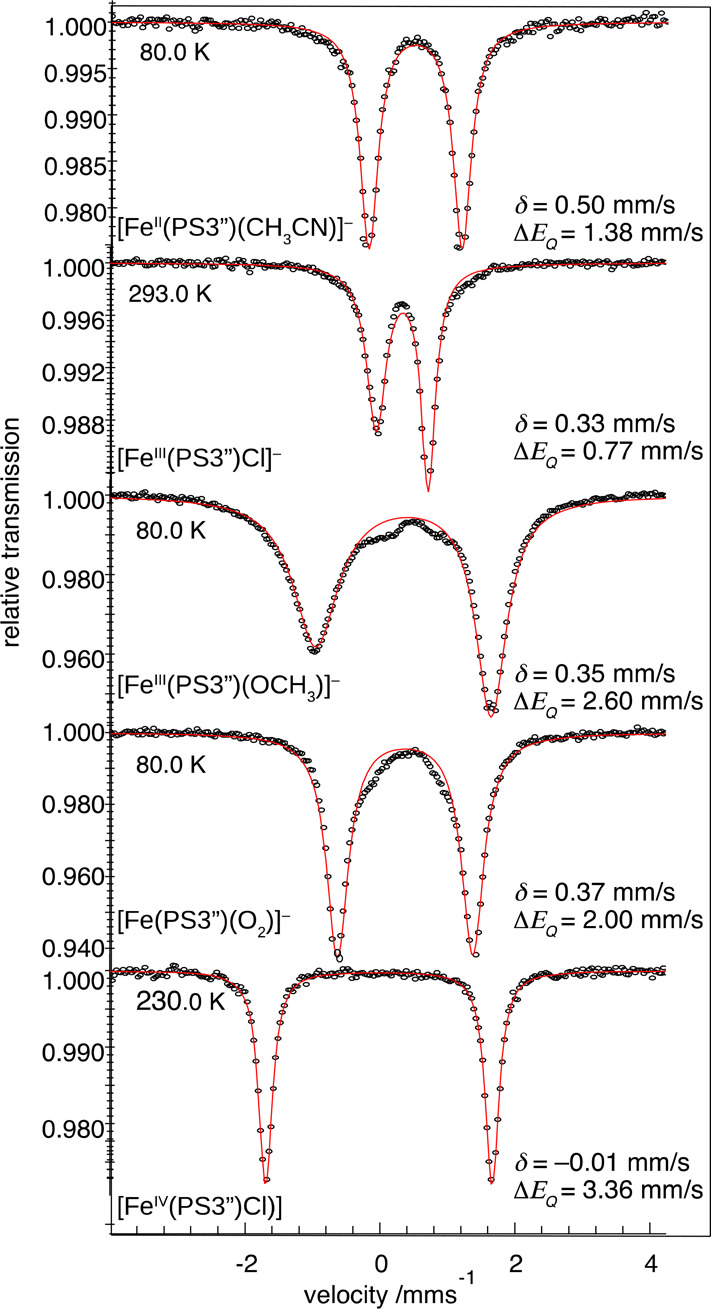
Figure 3

Open in a new tab

Zero-field Mössbauer spectra of 1 and related complexes measured at indicated temperatures. The asymmetric line shape found for [FeIII(PS3″)Cl]− and [FeIII(PS3″)(OCH3)]− originates from not perfectly fast spin relaxation for half-integer spin systems. For details, see the Supporting Information, Figure S7).

Computational Studies on the Electronic Structure and the Potential Energy Surface of Complex 1

To gain in-depth insight into the electronic structure of 1, density functional theory (DFT) calculations were undertaken. The quintet and septet states of 1 were estimated to lie 13.4 and 22.0 kcal/mol, respectively, above the triplet ground state. Furthermore, the B3LYP computed key metrics (Table S11) and spectroscopic parameters (νO–O = 1049 cm–1, δ = 0.35 mm/s, and |ΔEQ| = 2.26 mm/s) all match the experimental values within the uncertainty range of the calculations. In particular, considering that DFT computations often slightly overestimate O–O stretching frequencies, as exemplified by related Mn–superoxo and hydroperoxo complexes.65,66 All findings thus lend credence to the computed electronic structure of 1 (Figure S8).

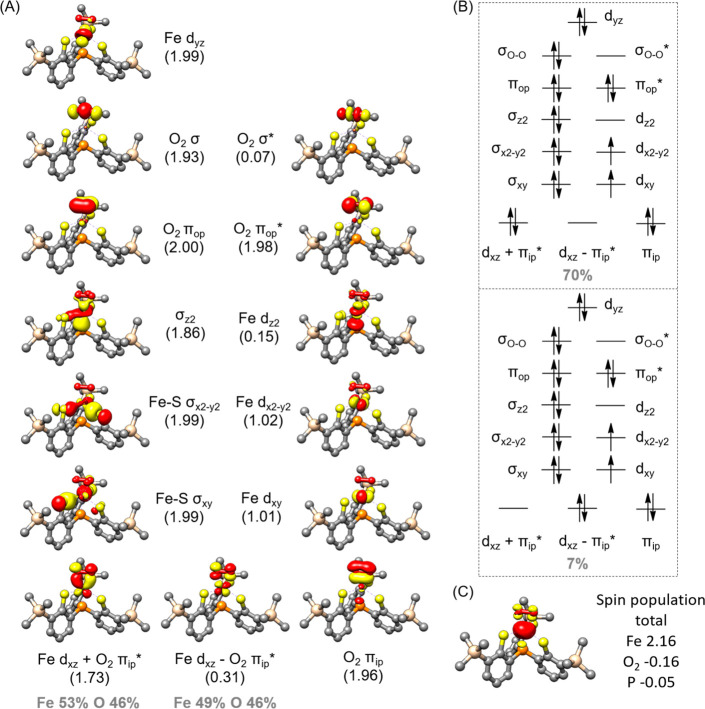
To further elucidate the bonding of complex 1, we carried out wave-function-based multireference CASSCF(20,14) calculations on its S = 1 ground state. The active space comprises five Fe 3d based orbitals, O–O σ, σ*, πip, πip*, πop, and πop* orbitals (ip = in the Fe–O–O plane, op = out of the Fe–O–O plane), the two Fe–S σ bonding orbitals (σxy,x2–y2) with respect to the interactions between Fe dxy,x2–y2 and the three equatorial S donors, and the P 3p centered bonding counterpart of the Fe dz2 orbital (σz2) (Figure 4A). As depicted in Figure 4B, the ground state wave function of 1 consists of two dominant electron configurations, viz., (σz2)2(σxy)2(σx2–y2)2(πop)2(πop*)2(πip)2(dyz)2(dxz + πip*)2(dxy)1(dx2–y2)1(dxz – πip*)0(σz2*)0(σO–O*)0 (70%) and (σz2)2(σxy)2(σx2–y2)2(πop)2(πop*)2(πip)2(dyz)2(dxz + πip*)0(dxy)1(dx2–y2)1(dxz – πip*)2(σz2*)0(σO–O*)0 (7%), where dxz + πip* and dxz – πip* denote the bonding and antibonding combinations derived from the interaction between Fe dxz and O2 πip*. The latter configuration, in fact, corresponds to a double excitation from the bonding dxz + πip* orbital to its antibonding dxz – πip* one. Consequently, the occupation numbers of these two orbitals differ substantially from 2 and 0, respectively, as expected for a doubly occupied and a vacant orbital, but their sum (2.04) is very close to 2. As elaborated elsewhere, such an orbital occupation pattern signifies that 1 possesses considerable diradical character, which can be quantified by diradical index (d).67,68 A value of d = 0% means that the two unpaired electrons interact so strongly that a covalent bond is formed, whereas the vanishing interaction between them is distinguished by d = 100%; consequently, 0% < d < 100% implies antiferromagnetic coupling between them with a hindered overlap. For complex 1, d was computed to be 57%. This d value suggests that it contains an S = 3/2 ferric center that is strongly antiferromagnetically coupled to a superoxo radical, thereby yielding an overall triplet state. This electronic structure description is consistent with the sizeable negative spin population observed for the O2 ligand (Figure 4C). By contrast, the negative spin population found for the anchor P atom stems from spin polarization of the fully occupied σz2 orbital induced by the unpaired electrons residing in the Fe dxy,x2–y2 orbitals.

Figure 4.

Figure 4

Open in a new tab

(A) Electronic structure of complex 1 with the O–O distance of 1.40 Å (the local minimum shown in Figure 5D) derived from CASSCF(20,14) calculations. Natural orbitals with occupation number in parentheses and contribution from atomic orbitals. (B) Two dominant electron configurations. (C) Spin density plot and important atomic spin population.

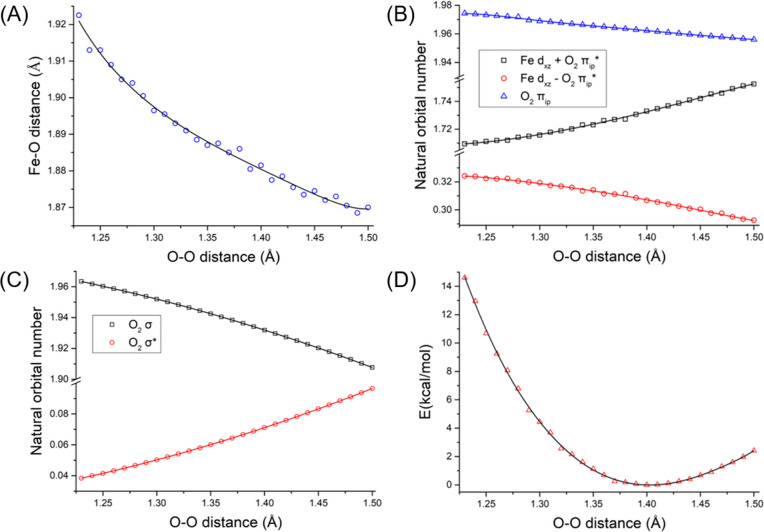
To shed light on how the distinct O–O distance impacts the electronic structure of 1, we performed a series of relaxed surface scans with the Perdew–Burke–Ernzerhof (PBE) density functional in which the O–O bond distance was systematically varied (Figures 5 and S9). On top of that, the electronic energy of each structure was further evaluated using the ab initio CASSCF(20,14)/NEVPT2 methods with the same active space discussed above. Theoretical results revealed that lengthening the O–O bond from 1.23 to 1.50 Å only causes a slight contraction of 0.07 Å for the average Fe–O2 bond lengths (Figure 5A). More importantly, during this process, the bonding situation of 1 is nearly identical, as evidenced by the minute changes of the occupation numbers of the orbitals describing the dominant Fe–O2 interaction, viz. dxz + πip* and dxz – πip* as well as O2 σ and σ* (Figure 5B,C and Figures S10 and S11). In support, the computed Mössbauer parameters based on the crystal structures are also in reasonable agreement with the experiment (Table S11). Consistent with such minimal electronic structure adjustments is that the energy variation is less than 6 kcal/mol for the O–O bond distance in the range of 1.29–1.50 Å (Figure 5D). However, upon shortening the O–O bond length from 1.28 to 1.23 Å, the energy difference increases from 6.8 to 14.6 kcal/mol. As shown in Figure S12, the CASSCF(20,14) computations without NEVPT2 corrections predict an even greater energy gap of 15.6 kcal/mol for the complex with an O–O bond distance of 1.23 Å relative to the minimum. These theoretical findings thus indicated that, due to lack of proper treatment of dynamic electron correlations, the present CASSCF(20,14)/NEVPT2 calculations still overestimate the energy separation of complex 1 with the slightly different O–O bond distance, especially for that less than 1.28 Å. To verify this notion, we also computed the energies of the three different forms found in the crystals (not shown in Figure 5). To do so, prior to ab initio calculations, only the positions of H atoms in the crystal structures were optimized while keeping those of the remaining atoms unchanged. The CASSCF(20,14)/NEVPT2 computations delivered an energy gap as large as 22.7 kcal/mol for the form having a short O–O distance of 1.229 Å, although the other two with the O–O distances of 1.330 and 1.387 Å were found to lie 5.2 and 2.1 kcal/mol, respectively, above the minimum shown in Figure 5D. These results hence suggest that, to compute a more accurate potential energy surface (PES), a formidable active space consisting of more than 14 active orbitals has to be employed, which will be perused in our further study. Nevertheless, our theoretical findings unambiguously revealed that the side-on O2 addition to the Fe center with respect to the varying O–O distance induces negligible electronic structure changes and hence likely has a rather flat PES. As a consequence, a subtle difference in weak interactions arising from the slightly different second coordination sphere likely affects their O–O distances considerably. This notion rationalizes why 1 exhibits three distinct O–O bond lengths in the crystals, but spectroscopic measurements cannot distinguish them. PBE calculations demonstrated that the end-on O2 congener of 1 is destabilized by 4.8 kcal/mol relative the side-on one and features a considerably higher νO–O value (1151 cm–1), which can be attributed to σ-type donation from the doubly occupied O2 πip * to the empty Fe dz2 orbital (Figure S13).

Figure 5.

Figure 5

Open in a new tab

Average Fe–O2 bond length (A), CASSCF(20,14)/NEVPT2 computed occupation–number variations of the dxz + πip* and dxz – πip* orbitals (B), those of O2 σ and σ* orbitals (C), and computed energy change of 1 (D) as a function of the O–O bond distance.

The reactivity of 1 exhibits an amphoteric nature, acting either as an electrophile or as a nucleophile. On one hand, its electrophilicity is demonstrated by its moderate capability of abstracting hydrogen atoms. Treatment of complex 1 with 2,6-di-tert-butylphenol (BDEO–H = 82.8 kcal/mol) yields, primarily, 4,4′-dihydroxy-3,3′,5,5′-tetra-tert-butyldiphenyl as identified by electrospray ionization mass spectrometry (ESI-MS) measurements (Figure S14). The quantitative product analyses were performed by liquid chromatography (LC) and gave a yield of 88% (Figure S15). However, complex 1 fails to activate C–H bonds such as those in xanthene, 9,10-dihydroanthrene, and fluorene. On the other hand, complex 1 can perform a nucleophilic oxidative reaction with benzaldehyde to furnish a dominant product of benzoate (detected by ESI-MS and quantified by LC, 95% yield, Figures S16 and S17). Kinetic measurements of complex 1 reacting with both substrates were taken by monitoring the disappearance of the characteristic band at 655 nm in UV–vis–NIR spectra (Figures S18 and S19). The obtained second-order rate constants (k2) at 253 K were 1.61 × 10–4 and 3.86 × 10–4 M–1 s–1, respectively (Figure S20).69 Although the majority of reported Fe(III)–superoxo complexes were found to only exhibit electrophilic reactivity,18,57,59,60 such an amphoteric behavior is also found for [Fe(TAML)(O2)]2–,16 which further affirmed the notion that both complexes feature a similar electronic structure.

Conclusion

In summary, we have obtained a ferric–superoxo complex by addition of O2 to an Fe(II) precursor bearing a tris(benzenethiolato)phosphine derivative. The X-ray structures revealed distinct O–O bond lengths in three different crystallographic forms, but they all shared the same spectroscopic features in the solid state and in solution. Consequently, their electronic structure is best described as an intermediate-spin ferric center antiferromagnetically coupled to a superoxo radical, giving an overall triplet state. The variation in O–O bond lengths across different crystallographic forms likely results from the subtle difference in the second coordination sphere environment of the side-on bound O2 moiety because the computed PES of side-on O2 bonding with respect to the O–O bond distance is rather flat. Thus, one should keep in mind that the assignment of valence states of O2 moieties in metal−η2-O2 complexes simply using the O–O bond length alone is unsatisfactory. The overall implication provides a basis to question the electronic structure of metal–dioxygen intermediates when solely judged by the structural parameter of the O–O bond length.

Experimental Section

Materials and Methods

All experiments were carried out under dinitrogen with standard Schlenk techniques or N2-filled glovebox. H3[PS3″] (H3[P(C6H3-3-Me3Si-2-S)3]) was synthesized according to the literature procedures.70 [PPh4][Fe(PS3″)Cl], [PPh4][Fe(PS3″)(OCH3)], and [Fe(PS3″)Cl] were prepared for Mössbauer measurements using synthetic protocols reported in the literature.61,71 Solvents were dried and distilled by standard procedures. Otherwise, all starting materials were obtained commercially and used without further purification. The crystals were mounted on a glass fiber and quickly coated in epoxy resin. Diffraction measurements were performed with a Bruker SMART CCD diffractometer. The experimental temperature was controlled using an Oxford Cryosystems cooler. Least-squares refinement of the positional and anisotropic thermal parameters for the contribution of all non-hydrogen atoms and fixed hydrogen atoms was based on F2. A SADABS absorption correction was made.72 The SHELXTL structural refinement program was employed.73 All non-hydrogen atoms were refined with anisotropic displacement factors. All hydrogen atoms were calculated using the riding model. UV–vis–NIR spectra were measured with a Hewlett-Packard 8453 spectrophotometer. 1H NMR samples were characterized by a Bruker AMX500 spectrometer. A PerkinElmer Spectrum RX I spectrophotometer was used as the tool to record Fourier transform infrared spectroscopy. Elemental analysis data were measured with Elemetar vario EL III. ESI-MS spectra was performed by Q-Orbitrap MS. Product analysis for the reactivity was quantified by high-performance liquid chromatography (Agilent 1260 Infinity). Magnetic susceptibility data were measured from powder samples of solid material in the temperature range of 2–300 K using a SQUID susceptometer with a field of 0.1 T (MPMS-7, Quantum Design, calibrated with standard palladium reference sample, error <2%). Mössbauer spectra were recorded on conventional spectrometers with alternating constant acceleration of the γ source. The minimum experimental line width was 0.24 mm/s (full width at half-height). The sample temperature was maintained constant in an Oxford Instruments Variox cryostat. Isomer shifts are quoted relative to iron metal at 300 K. The zero-field spectra were simulated with Lorentzian doublets with the program mf.SL developed by Dr. Eckhard Bill at the Max-Planck Institute for Chemical Energy Conversion. Kinetic studies of complex 1 reacting with 2,6-DTBP and benzaldehyde were performed. Different equivalents of substrates were reacted with complex 1 (0.2 mM) in THF at −20 °C. The reactions were monitored by UV–vis–NIR spectroscopy with the disappearance of the characteristic band at 655 nm. The pseudo-first-order rate constants (kobs) increase linearly as a function of the substrate concentration, giving second-order rate constants. The product analyses were quantified by LC. The product yield was compared against the standard curves with authentic samples.74 Benzil and phenol were used as internal standards for the reactions with 2,6-di-tert-butylphenol and benzaldehyde, respectively.

Synthesis of [AsPh4][Fe(PS3″)(CH3CN)]·5CH3CN

H3PS3″ (0.1000 g, 0.174 mmol) and Li (0.0037 g, 0.522 mmol) were dissolved in CH3OH to generate a pale yellow solution. After FeCl2 (0.0221g, 0.174 mmol) was added to the reaction mixture, the solution color changed to emerald immediately. The solvent was removed, and the residue was dissolved in CH3CN. After AsPh4Cl·H2O was added, the solution was stored at −40 °C. The dark green crystals of [AsPh4][Fe(PS3″)(CH3CN)]·5CH3CN were produced after 1–2 days. Yield: 63.1%. Electronic absorption in CH3CN (λ, nm; ε, M–1 cm–1): 417 (4.48 × 103); 601, (2.33 × 103). Anal. Calcd for C53H59AsFeNPS3Si3 ([AsPh4][Fe(PS3″)(CH3CN)]): C, 60.50; H, 5.65; N, 1.33; S, 9.14. Found: C, 60.37; H, 5.82; N, 1.37; S, 9.07.

Synthesis of [PPh4][Fe(PS3″)(16/18O2)]·2THF ([PPh4][1]·2THF)

Adding O2 into [PPh4][Fe(PS3″)(CH3CN)] (0.005 g, 5 × 10–3 mmol) in CH3CN at −40 °C generated a blue solution. The solvent was removed, and the residue was recrystallized from THF/hexane at −40 °C to give a dark blue crystalline solid of [PPh4][1]·2THF in a quantitative yield. Electronic absorption in THF (λ, nm; ε, M–1 cm–1): 504 (1.88 × 103); 557 (1.99 × 103); 655 (2.59 × 103). Anal. Calcd for C51H56FeO2P2S3Si3 ([PPh4][1]): C, 61.30; H, 5.65; S, 9.63. Found: C, 60.51; H, 5.98; S, 9.28. IR (KBr, ν, cm–1): 959, 939 (16O–16O); 897 (18O–18O).

Synthesis of [AsPh4][Fe(PS3″)(16/18O2)]·2THF ([AsPh4][1]·2THF)

Adding O2 into [AsPh4][Fe(PS3″)(CH3CN)] (0.005 g, 4.7 × 10–3 mmol) in CH3CN at −40 °C generated a blue solution. The solvent was removed, and the residue was recrystallized from THF/hexane at −40 °C to give a dark blue crystalline solid of [AsPh4][1]·2THF in a quantitative yield. Electronic absorption in THF (λ, nm; ε, M–1 cm–1): 504 (2.634 × 103); 557 (2.701 × 103); 655 (3.407 × 103). Anal. Calcd for C55H64AsFeO3PS3Si3 ([AsPh4][1]·THF): C, 59.23; H, 5.78; S, 8.63. Found: C, 58.19; H, 5.706; S, 8.805. IR (KBr, ν, cm–1): 958, 939 (16O–16O); 896 (18O–18O).

Computational Setup

Geometry optimizations were performed with the PBE75 and B3LYP76,77 density functionals, and the RI78 and RIJCOSX79 approximations were used to accelerate the calculations, respectively. The def2-TZVP for the first coordination sphere and def2-SVP basis sets80 for the remaining atoms were applied in combination with the auxiliary basis sets def2/J.81 As shown in Table S11, the estimated geometric metrics using both density functionals are in reasonable agreement with experiment (for details, see the Supporting Information). In line with this finding, the computed electronic structures are nearly identical. However, the B3LYP calculations predicted that 1 with a side-on O2 moiety lies above its corresponding isomer with an end-on O2 motif by 9.5 kcal/mol, whereas the PBE calculations suggested that the latter is destabilized by 4.8 kcal/mol. Therefore, relaxed scans of the O–O bond distance were carried out using the PBE density functional only. The Mössbauer spectroscopic parameters were computed using the B3LYP density functional. The CP(PPP)82 basis set for Fe was employed, and the def2-TZVP83 basis set for O, P, and S and the def2-SV(P) basis set84 for remaining atoms were used.

Isomer shifts δ were calculated from the electron densities r0 at the Fe nuclei by employing the linear regression:

graphic file with name au1c00184_m001.jpg

Here, C is a prefixed value, and α and β are the fit parameters. Their values for different combinations of the density functionals and basis sets can be found in our earlier work (α = −0.366, β = 2.852, C = 111810).85,86

Quadrupole splittings, ΔEQ, were obtained from electric field gradients Vij (i = x, y, z; Vii are the eigenvalues of the electric field gradient tensor) using a nuclear quadrupole moment Q(57Fe) = 0.16 barn:87

graphic file with name au1c00184_m002.jpg

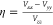Here, Inline graphic is the asymmetry parameter.

All calculations were performed by using the ORCA quantum chemical program package.88

Acknowledgments

We thank Ms. Shu-Yi Sun, Mr. Tsung-Lun Kan, and Mr. Bo-Rong Su at Instrument Center of National Cheng Kung University for assisting the measurements of elemental analysis, NMR, and ESI-MS, respectively. We thank the Ministry of Science and Technology in Taiwan for financial support (MOST 109-2113-M-006-007). H.-R.P. gratefully acknowledges the Ph.D. fellowship from Science College of National Cheng Kung University and Ministry of Science and Technology in Taiwan. S.Y. gratefully acknowledges the financial support from the Max-Planck Society, in particular, the joint work space of MPI-CEC and MPI-KOFO. G.P. gratefully acknowledges the financial support from the National Natural Science Foundation of China (No. 22006008).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00184.

  • Crystallographic data for [AsPh4][1] (CIF)

  • Crystallographic data for [PPh4][1] at 100 K (CIF)

  • Crystallographic data for [PPh4][1] at 150 K (CIF)

  • Crystallographic data for [PPh4][1] at 200 K (CIF)

  • Crystallographic data for [AsPh4][Fe(PS3″)(CH3CN)] (CIF)

  • ORTEP diagrams, NMR spectra, data tables (PDF)

The authors declare no competing financial interest.

Supplementary Material

au1c00184_si_001.cif (740KB, cif)
au1c00184_si_002.cif (1.4MB, cif)
au1c00184_si_003.cif (1.4MB, cif)
au1c00184_si_004.cif (2.1MB, cif)
au1c00184_si_005.cif (750.9KB, cif)
au1c00184_si_006.pdf (2MB, pdf)

References

  1. Huang X.; Groves J. T. Oxygen Activation and Radical Transformations in Heme Proteins and Metalloporphyrins. Chem. Rev. 2018, 118 (5), 2491–2553. 10.1021/acs.chemrev.7b00373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Elwell C. E.; Gagnon N. L.; Neisen B. D.; Dhar D.; Spaeth A. D.; Yee G. M.; Tolman W. B. Copper–Oxygen Complexes Revisited: Structures, Spectroscopy, and Reactivity. Chem. Rev. 2017, 117 (3), 2059–2107. 10.1021/acs.chemrev.6b00636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Nam W. Dioxygen Activation by Metalloenzymes and Models. Acc. Chem. Res. 2007, 40 (7), 465–465. 10.1021/ar700131d. [DOI] [Google Scholar]
  4. Jasniewski A. J.; Que L. Dioxygen Activation by Nonheme Diiron Enzymes: Diverse Dioxygen Adducts, High-Valent Intermediates, and Related Model Complexes. Chem. Rev. 2018, 118 (5), 2554–2592. 10.1021/acs.chemrev.7b00457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Valentine J. S. The Dioxygen Ligand in Mononuclear Group VIII Transition Metal Complexes. Chem. Rev. 1973, 73 (3), 235–245. 10.1021/cr60283a002. [DOI] [Google Scholar]
  6. Vaska L. Dioxygen-Metal Complexes: Toward a Unified View. Acc. Chem. Res. 1976, 9 (5), 175–183. 10.1021/ar50101a002. [DOI] [Google Scholar]
  7. Prigge S. T.; Eipper B. A.; Mains R. E.; Amzel L. M. Dioxygen Binds End-On to Mononuclear Copper in a Precatalytic Enzyme Complex. Science 2004, 304 (5672), 864. 10.1126/science.1094583. [DOI] [PubMed] [Google Scholar]
  8. Kovaleva E. G.; Lipscomb J. D. Crystal Structures of Fe2+ Dioxygenase Superoxo, Alkylperoxo, and Bound Product Intermediates. Science 2007, 316 (5823), 453. 10.1126/science.1134697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jeoung J.-H.; Bommer M.; Lin T.-Y.; Dobbek H. Visualizing the substrate-, superoxo-, alkylperoxo-, and product-bound states at the nonheme Fe(II) site of homogentisate dioxygenase. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (31), 12625. 10.1073/pnas.1302144110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Wang Y.; Liu K. F.; Yang Y.; Davis I.; Liu A. Observing 3-hydroxyanthranilate-3,4-dioxygenase in action through a crystalline lens. Proc. Natl. Acad. Sci. U. S. A. 2020, 117 (33), 19720. 10.1073/pnas.2005327117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Schlichting I.; Berendzen J.; Chu K.; Stock A. M.; Maves S. A.; Benson D. E.; Sweet R. M.; Ringe D.; Petsko G. A.; Sligar S. G. The Catalytic Pathway of Cytochrome P450cam at Atomic Resolution. Science 2000, 287 (5458), 1615. 10.1126/science.287.5458.1615. [DOI] [PubMed] [Google Scholar]
  12. Karlsson A.; Parales J. V.; Parales R. E.; Gibson D. T.; Eklund H.; Ramaswamy S. Crystal Structure of Naphthalene Dioxygenase: Side-on Binding of Dioxygen to Iron. Science 2003, 299 (5609), 1039. 10.1126/science.1078020. [DOI] [PubMed] [Google Scholar]
  13. Jeoung J.-H.; Nianios D.; Fetzner S.; Dobbek H. Quercetin 2,4-Dioxygenase Activates Dioxygen in a Side-On O2–Ni Complex. Angew. Chem., Int. Ed. 2016, 55 (10), 3281–3284. 10.1002/anie.201510741. [DOI] [PubMed] [Google Scholar]
  14. Cramer C. J.; Tolman W. B.; Theopold K. H.; Rheingold A. L. Variable character of O-O and M-O bonding in side-on (η2) 1:1 metal complexes of O2. Proc. Natl. Acad. Sci. U. S. A. 2003, 100 (7), 3635–3640. 10.1073/pnas.0535926100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cho J.; Woo J.; Nam W. An “End-On” Chromium(III)-Superoxo Complex: Crystallographic and Spectroscopic Characterization and Reactivity in C-H Bond Activation of Hydrocarbons. J. Am. Chem. Soc. 2010, 132 (17), 5958–5959. 10.1021/ja1015926. [DOI] [PubMed] [Google Scholar]
  16. Hong S.; Sutherlin K. D.; Park J.; Kwon E.; Siegler M. A.; Solomon E. I.; Nam W. Crystallographic and spectroscopic characterization and reactivities of a mononuclear non-haem iron(III)-superoxo complex. Nat. Commun. 2014, 5, 5440. 10.1038/ncomms6440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Iovan D. A.; Wrobel A. T.; McClelland A. A.; Scharf A. B.; Edouard G. A.; Betley T. A. Reactivity of a stable copper–dioxygen complex. Chem. Commun. 2017, 53 (74), 10306–10309. 10.1039/C7CC05014C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Oddon F.; Chiba Y.; Nakazawa J.; Ohta T.; Ogura T.; Hikichi S. Characterization of Mononuclear Non-heme Iron (III)-Superoxo Complex with a Five-Azole Ligand Set. Angew. Chem., Int. Ed. 2015, 54 (25), 7336–7339. 10.1002/anie.201502367. [DOI] [PubMed] [Google Scholar]
  19. Qin K.; Incarvito C. D.; Rheingold A. L.; Theopold K. H. A Structurally Characterized Chromium(III) Superoxide Complex Features “Side-on” Bonding. Angew. Chem., Int. Ed. 2002, 41 (13), 2333–2335. . [DOI] [PubMed] [Google Scholar]
  20. Würtele C.; Gaoutchenova E.; Harms K.; Holthausen M. C.; Sundermeyer J.; Schindler S. Crystallographic Characterization of a Synthetic 1:1 End-On Copper Dioxygen Adduct Complex. Angew. Chem., Int. Ed. 2006, 45 (23), 3867–3869. 10.1002/anie.200600351. [DOI] [PubMed] [Google Scholar]
  21. Yao S.; Bill E.; Milsmann C.; Wieghardt K.; Driess M. A “Side-on” Superoxonickel Complex [LNi(O2)] with a Square-Planar Tetracoordinate Nickel(II) Center and Its Conversion into [LNi(μ-OH)2NiL]. Angew. Chem., Int. Ed. 2008, 47 (37), 7110–7113. 10.1002/anie.200802234. [DOI] [PubMed] [Google Scholar]
  22. Aboelella N. W.; Kryatov S. V.; Gherman B. F.; Brennessel W. W.; Young V. G.; Sarangi R.; Rybak-Akimova E. V.; Hodgson K. O.; Hedman B.; Solomon E. I.; Cramer C. J.; Tolman W. B. Dioxygen Activation at a Single Copper Site: Structure, Bonding, and Mechanism of Formation of 1:1 Cu-O2 Adducts. J. Am. Chem. Soc. 2004, 126 (51), 16896–16911. 10.1021/ja045678j. [DOI] [PubMed] [Google Scholar]
  23. Aboelella N. W.; Lewis E. A.; Reynolds A. M.; Brennessel W. W.; Cramer C. J.; Tolman W. B. Snapshots of Dioxygen Activation by Copper: The Structure of a 1:1 Cu/O2 Adduct and Its Use in Syntheses of Asymmetric Bis(μ-oxo) Complexes. J. Am. Chem. Soc. 2002, 124 (36), 10660–10661. 10.1021/ja027164v. [DOI] [PubMed] [Google Scholar]
  24. Annaraj J.; Cho J.; Lee Y.-M.; Kim S. Y.; Latifi R.; de Visser S. P.; Nam W. Structural Characterization and Remarkable Axial Ligand Effect on the Nucleophilic Reactivity of a Nonheme Manganese(III)–Peroxo Complex. Angew. Chem., Int. Ed. 2009, 48 (23), 4150–4153. 10.1002/anie.200900118. [DOI] [PubMed] [Google Scholar]
  25. Cho J.; Jeon S.; Wilson S. A.; Liu L. V.; Kang E. A.; Braymer J. J.; Lim M. H.; Hedman B.; Hodgson K. O.; Valentine J. S.; Solomon E. I.; Nam W. Structure and reactivity of a mononuclear non-haem iron(III)–peroxo complex. Nature 2011, 478 (7370), 502–505. 10.1038/nature10535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Cho J.; Kang H. Y.; Liu L. V.; Sarangi R.; Solomon E. I.; Nam W. Mononuclear nickel(ii)-superoxo and nickel(iii)-peroxo complexes bearing a common macrocyclic TMC ligand. Chem. Sci. 2013, 4 (4), 1502–1508. 10.1039/c3sc22173c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Cho J.; Sarangi R.; Annaraj J.; Kim S. Y.; Kubo M.; Ogura T.; Solomon E. I.; Nam W. Geometric and electronic structure and reactivity of a mononuclear ’side-on’ nickel(iii)–peroxo complex. Nat. Chem. 2009, 1 (7), 568–572. 10.1038/nchem.366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Cho J.; Sarangi R.; Kang H. Y.; Lee J. Y.; Kubo M.; Ogura T.; Solomon E. I.; Nam W. Synthesis, Structural, and Spectroscopic Characterization and Reactivities of Mononuclear Cobalt(III)-Peroxo Complexes. J. Am. Chem. Soc. 2010, 132 (47), 16977–16986. 10.1021/ja107177m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Colmer H. E.; Geiger R. A.; Leto D. F.; Wijeratne G. B.; Day V. W.; Jackson T. A. Geometric and electronic structure of a peroxomanganese(iii) complex supported by a scorpionate ligand. Dalton Trans. 2014, 43 (48), 17949–17963. 10.1039/C4DT02483D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Crump D. B.; Stepaniak R. F.; Payne N. C. Charge distribution in dioxygen complexes of cobalt(III). The crystal structure and absolute configuration of (+)546-Δ-cis-β-[{2,13-dimethyl-6,9-diphenyl-2,6,9,13-tetraarsatetradecane}(dioxygen)cobalt(III)] perchlorate. Can. J. Chem. 1977, 55 (3), 438–446. 10.1139/v77-065. [DOI] [Google Scholar]
  31. de Sousa D. P.; Bigelow J. O.; Sundberg J.; Que L.; McKenzie C. J. Caught! Crystal trapping of a side-on peroxo bound to Cr(iv). Chem. Commun. 2015, 51 (14), 2802–2805. 10.1039/C4CC08785B. [DOI] [PubMed] [Google Scholar]
  32. DeRosha D. E.; Mercado B. Q.; Lukat-Rodgers G.; Rodgers K. R.; Holland P. L. Enhancement of C-H Oxidizing Ability in Co–O2 Complexes through an Isolated Heterobimetallic Oxo Intermediate. Angew. Chem., Int. Ed. 2017, 56 (12), 3211–3215. 10.1002/anie.201612010. [DOI] [PubMed] [Google Scholar]
  33. Halpern J.; Goodall B. L.; Khare G. P.; Lim H. S.; Pluth J. J. Reaction of oxygen with dicyanotris(dimethylphenylphosphine)cobalt(II). Synthesis, structure, and reactivity of a novel cobalt-dioxygen adduct. J. Am. Chem. Soc. 1975, 97 (8), 2301–2303. 10.1021/ja00841a068. [DOI] [Google Scholar]
  34. House D. A.; Garner C. S. Diperoxodiethylenetriamminechromium(IV) 1-hydrate: a New Chromium(IV) Peroxo Compound. Nature 1965, 208 (5012), 776–777. 10.1038/208776b0. [DOI] [Google Scholar]
  35. Hu X.; Castro-Rodriguez I.; Meyer K. Dioxygen Activation by a Low-Valent Cobalt Complex Employing a Flexible Tripodal N-Heterocyclic Carbene Ligand. J. Am. Chem. Soc. 2004, 126 (41), 13464–13473. 10.1021/ja046048k. [DOI] [PubMed] [Google Scholar]
  36. Kang H.; Cho J.; Cho K.-B.; Nomura T.; Ogura T.; Nam W. Mononuclear Manganese–Peroxo and Bis(μ-oxo)dimanganese Complexes Bearing a Common N-Methylated Macrocyclic Ligand. Chem. - Eur. J. 2013, 19 (42), 14119–14125. 10.1002/chem.201301641. [DOI] [PubMed] [Google Scholar]
  37. Kim J.; Shin B.; Kim H.; Lee J.; Kang J.; Yanagisawa S.; Ogura T.; Masuda H.; Ozawa T.; Cho J. Steric Effect on the Nucleophilic Reactivity of Nickel(III) Peroxo Complexes. Inorg. Chem. 2015, 54 (13), 6176–6183. 10.1021/acs.inorgchem.5b00294. [DOI] [PubMed] [Google Scholar]
  38. Kishima T.; Matsumoto T.; Nakai H.; Hayami S.; Ohta T.; Ogo S. A High-Valent Iron(IV) Peroxo Core Derived from O2. Angew. Chem., Int. Ed. 2016, 55 (2), 724–727. 10.1002/anie.201507022. [DOI] [PubMed] [Google Scholar]
  39. Kitajima N.; Komatsuzaki H.; Hikichi S.; Osawa M.; Moro-Oka Y. A Monomeric Side-On Peroxo Manganese(III) Complex: Mn(O2)(3,5-iPr2pzH)(HB(3,5-iPr2pz)3). J. Am. Chem. Soc. 1994, 116 (25), 11596–11597. 10.1021/ja00104a061. [DOI] [Google Scholar]
  40. Lee C.-M.; Chuo C.-H.; Chen C.-H.; Hu C.-C.; Chiang M.-H.; Tseng Y.-J.; Hu C.-H.; Lee G.-H. Structural and Spectroscopic Characterization of a Monomeric Side-On Manganese(IV) Peroxo Complex. Angew. Chem., Int. Ed. 2012, 51 (22), 5427–5430. 10.1002/anie.201201735. [DOI] [PubMed] [Google Scholar]
  41. Noh H.; Jeong D.; Ohta T.; Ogura T.; Valentine J. S.; Cho J. Distinct Reactivity of a Mononuclear Peroxocobalt(III) Species toward Activation of Nitriles. J. Am. Chem. Soc. 2017, 139 (32), 10960–10963. 10.1021/jacs.7b04479. [DOI] [PubMed] [Google Scholar]
  42. Rahman A. F. M. M.; Jackson W. G.; Willis A. C. The First Sideways-Bonded Peroxo Complex for a Tetraaminecobalt(III) Species. Inorg. Chem. 2004, 43 (24), 7558–7560. 10.1021/ic040044z. [DOI] [PubMed] [Google Scholar]
  43. Ramsey C. M.; Cage B.; Nguyen P.; Abboud K. A.; Dalal N. S. Ligand Dependence of Magnetic Dimensionality in Chromium(IV) Complexes: Layered vs Three-Dimensional Antiferromagnets. Chem. Mater. 2003, 15 (1), 92–99. 10.1021/cm020721s. [DOI] [Google Scholar]
  44. Reynolds A. M.; Gherman B. F.; Cramer C. J.; Tolman W. B. Characterization of a 1:1 Cu-O2 Adduct Supported by an Anilido Imine Ligand. Inorg. Chem. 2005, 44 (20), 6989–6997. 10.1021/ic050280p. [DOI] [PubMed] [Google Scholar]
  45. Schaefer W. P.; Huie B. T.; Kurilla M. G.; Ealick S. E. Oxygen-carrying cobalt complexes. 10. Structures of N, N’-ethylenebis(3-tert-butylsalicylideniminato)cobalt (II) and its monomeric dioxygen adduct. Inorg. Chem. 1980, 19 (2), 340–344. 10.1021/ic50204a013. [DOI] [Google Scholar]
  46. Seo M. S.; Kim J. Y.; Annaraj J.; Kim Y.; Lee Y.-M.; Kim S.-J.; Kim J.; Nam W. [Mn(tmc)(O2)]+: A Side-On Peroxido Manganese(III) Complex Bearing a Non-Heme Ligand. Angew. Chem., Int. Ed. 2007, 46 (3), 377–380. 10.1002/anie.200603414. [DOI] [PubMed] [Google Scholar]
  47. Singh U. P.; Sharma A. K.; Hikichi S.; Komatsuzaki H.; Moro-Oka Y.; Akita M. Hydrogen bonding interaction between imidazolyl N–H group and peroxide: Stabilization of Mn(III)-peroxo complex TpiPr2Mn(η2-O2)(imMeH) (imMeH = 2-methylimidazole). Inorg. Chim. Acta 2006, 359 (13), 4407–4411. 10.1016/j.ica.2006.06.033. [DOI] [Google Scholar]
  48. Terry N. W.; Amma E. L.; Vaska L. Molecular oxygen binding in a monomeric cobalt complex. Crystal and molecular structure of dioxygen-bis[cis-1,2-bis(diphenylphosphino)ethylene]cobalt tetrafluoroborate. J. Am. Chem. Soc. 1972, 94 (2), 653–655. 10.1021/ja00757a066. [DOI] [Google Scholar]
  49. VanAtta R. B.; Strouse C. E.; Hanson L. K.; Valentine J. S. Peroxo(tetraphenylporphinato)manganese(III) and chloro(tetraphenylporphinato)manganese(II) anions. Synthesis, crystal structures, and electronic structures. J. Am. Chem. Soc. 1987, 109 (5), 1425–1434. 10.1021/ja00239a024. [DOI] [Google Scholar]
  50. Yokoyama A.; Han J. E.; Cho J.; Kubo M.; Ogura T.; Siegler M. A.; Karlin K. D.; Nam W. Chromium(IV)–Peroxo Complex Formation and Its Nitric Oxide Dioxygenase Reactivity. J. Am. Chem. Soc. 2012, 134 (37), 15269–15272. 10.1021/ja307384e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zhang Q.; Bell-Taylor A.; Bronston F. M.; Gorden J. D.; Goldsmith C. R. Aldehyde Deformylation and Catalytic C–H Activation Resulting from a Shared Cobalt(II) Precursor. Inorg. Chem. 2017, 56 (2), 773–782. 10.1021/acs.inorgchem.6b02127. [DOI] [PubMed] [Google Scholar]
  52. Tomson N. C.; Williams K. D.; Dai X.; Sproules S.; DeBeer S.; Warren T. H.; Wieghardt K. Re-evaluating the Cu K pre-edge XAS transition in complexes with covalent metal–ligand interactions. Chem. Sci. 2015, 6 (4), 2474–2487. 10.1039/C4SC03294B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Chang Y.-H.; Chan P.-M.; Tsai Y.-F.; Lee G.-H.; Hsu H.-F. Catalytic Reduction of Hydrazine to Ammonia by a Mononuclear Iron(II) Complex on a Tris(thiolato)phosphine Platform. Inorg. Chem. 2014, 53 (2), 664–666. 10.1021/ic402108w. [DOI] [PubMed] [Google Scholar]
  54. Momenteau M.; Reed C. A. Synthetic Heme-Dioxygen Complexes. Chem. Rev. 1994, 94 (3), 659–698. 10.1021/cr00027a006. [DOI] [Google Scholar]
  55. Shan X.; Que L. Intermediates in the oxygenation of a nonheme diiron(II) complex, including the first evidence for a bound superoxo species. Proc. Natl. Acad. Sci. U. S. A. 2005, 102 (15), 5340. 10.1073/pnas.0409640102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Zhao M.; Helms B.; Slonkina E.; Friedle S.; Lee D.; DuBois J.; Hedman B.; Hodgson K. O.; Fréchet J. M. J.; Lippard S. J. Iron Complexes of Dendrimer-Appended Carboxylates for Activating Dioxygen and Oxidizing Hydrocarbons. J. Am. Chem. Soc. 2008, 130 (13), 4352–4363. 10.1021/ja076817a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Chiang C.-W.; Kleespies S. T.; Stout H. D.; Meier K. K.; Li P.-Y.; Bominaar E. L.; Que Jr L.; Münck E.; Lee W.-Z. Characterization of a Paramagnetic Mononuclear Nonheme Iron-Superoxo Complex. J. Am. Chem. Soc. 2014, 136 (31), 10846–10849. 10.1021/ja504410s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Fischer A. A.; Lindeman S. V.; Fiedler A. T. A synthetic model of the nonheme iron–superoxo intermediate of cysteine dioxygenase. Chem. Commun. 2018, 54 (80), 11344–11347. 10.1039/C8CC06247A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Blakely M. N.; Dedushko M. A.; Yan Poon P. C.; Villar-Acevedo G.; Kovacs J. A. Formation of a Reactive, Alkyl Thiolate-Ligated FeIII-Superoxo Intermediate Derived from Dioxygen. J. Am. Chem. Soc. 2019, 141 (5), 1867–1870. 10.1021/jacs.8b12670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Kim H.; Rogler P. J.; Sharma S. K.; Schaefer A. W.; Solomon E. I.; Karlin K. D. Heme-FeIII Superoxide, Peroxide and Hydroperoxide Thermodynamic Relationships: FeIII-O2•– Complex H-Atom Abstraction Reactivity. J. Am. Chem. Soc. 2020, 142 (6), 3104–3116. 10.1021/jacs.9b12571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Chang K.-C.; Huang C.-J.; Chang Y.-H.; Wu Z.-H.; Kuo T.-S.; Hsu H.-F. Reactivity of a Fe(III)-Bound Methoxide Supported with a Tris(thiolato)phosphine Ligand: Activation of C-Cl Bond in CH2Cl2 by Nucleophilic Attack of a Fe(III)-OCH3 Moiety. Inorg. Chem. 2016, 55 (2), 566–572. 10.1021/acs.inorgchem.5b02135. [DOI] [PubMed] [Google Scholar]
  62. Desiraju G. R. The C-H O Hydrogen Bond in Crystals: What Is It?. Acc. Chem. Res. 1991, 24 (10), 290–296. 10.1021/ar00010a002. [DOI] [Google Scholar]
  63. Holland P. L. Metal–dioxygen and metal–dinitrogen complexes: where are the electrons?. Dalton Trans. 2010, 39 (23), 5415–5425. 10.1039/c001397h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Kaupp M.; Danovich D.; Shaik S. Chemistry is about energy and its changes: A critique of bond-length/bond-strength correlations. Coord. Chem. Rev. 2017, 344, 355–362. 10.1016/j.ccr.2017.03.002. [DOI] [Google Scholar]
  65. Lin Y.-H.; Kutin Y.; van Gastel M.; Bill E.; Schnegg A.; Ye S.; Lee W.-Z. A Manganese(IV)-Hydroperoxo Intermediate Generated by Protonation of the Corresponding Manganese(III)-Superoxo Complex. J. Am. Chem. Soc. 2020, 142 (23), 10255–10260. 10.1021/jacs.0c02756. [DOI] [PubMed] [Google Scholar]
  66. Lin Y.-H.; Cramer H. H.; van Gastel M.; Tsai Y.-H.; Chu C.-Y.; Kuo T.-S.; Lee I. R.; Ye S.; Bill E.; Lee W.-Z. Mononuclear Manganese(III) Superoxo Complexes: Synthesis, Characterization, and Reactivity. Inorg. Chem. 2019, 58 (15), 9756–9765. 10.1021/acs.inorgchem.9b00767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Mondal B.; Neese F.; Bill E.; Ye S. Electronic Structure Contributions of Non-Heme Oxo-Iron(V) Complexes to the Reactivity. J. Am. Chem. Soc. 2018, 140 (30), 9531–9544. 10.1021/jacs.8b04275. [DOI] [PubMed] [Google Scholar]
  68. Herebian D.; Wieghardt K. E.; Neese F. Analysis and Interpretation of Metal-Radical Coupling in a Series of Square Planar Nickel Complexes: Correlated Ab Initio and Density Functional Investigation of [Ni(LISQ)2] (LISQ = 3,5-di-tert-butyl-o-diiminobenzosemiquinonate(1-)). J. Am. Chem. Soc. 2003, 125 (36), 10997–11005. 10.1021/ja030124m. [DOI] [PubMed] [Google Scholar]
  69. Jo Y.; Annaraj J.; Seo M. S.; Lee Y.-M.; Kim S. Y.; Cho J.; Nam W. Reactivity of a cobalt(III)-peroxo complex in oxidative nucleophilic reactions. J. Inorg. Biochem. 2008, 102 (12), 2155–2159. 10.1016/j.jinorgbio.2008.08.008. [DOI] [PubMed] [Google Scholar]
  70. Block E.; Ofori-Okai G.; Zubieta J. 2-Phosphino- and 2-Phosphinylbenzenethiols: New Ligand Types. J. Am. Chem. Soc. 1989, 111 (6), 2327–2329. 10.1021/ja00188a071. [DOI] [Google Scholar]
  71. Niemoth-Anderson J. D.; Clark K. A.; George T. A.; Ross C. R. Five-Coordinate Diamagnetic Iron(IV) Complexes With A Trigonal Planar Arrangement of Thiolate Ligand Atoms: Synthesis and Crystal Structure of [FeX(PS3)] (X = Cl, Br or I; PS3H3 = [P(C‘‘‘6H3-3-Me3Si-2-SH)3]). J. Am. Chem. Soc. 2000, 122 (16), 3977–3978. 10.1021/ja993988+. [DOI] [Google Scholar]
  72. Sheldrick G. M.SADABS; University of Göttingen: Germany, 1996.
  73. Sheldrick G.SHELXTL, version 5; Siemens Analytical Xray Systems. Inc.: Madison, WI, 1994.
  74. van der Vlugt J. I.; Hewat A. C.; Neto S.; Sablong R.; Mills A. M.; Lutz M.; Spek A. L.; Müller C.; Vogt D. Sterically Demanding Diphosphonite Ligands – Synthesis and Application in Nickel-Catalyzed Isomerization of 2-Methyl-3-Butenenitrile. Adv. Synth. Catal. 2004, 346 (8), 993–1003. 10.1002/adsc.200303240. [DOI] [Google Scholar]
  75. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  76. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37 (2), 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  77. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98 (7), 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  78. Eichkorn K.; Treutler O.; Öhm H.; Häser M.; Ahlrichs R. Auxiliary basis sets to approximate Coulomb potentials (Chem. Phys. Letters 240 (1995) 283–290). Chem. Phys. Lett. 1995, 242 (6), 652–660. 10.1016/0009-2614(95)00838-U. [DOI] [Google Scholar]
  79. Neese F.; Wennmohs F.; Hansen A.; Becker U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356 (1), 98–109. 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
  80. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7 (18), 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  81. Weigend F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8 (9), 1057–1065. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
  82. Neese F. Prediction and interpretation of the 57Fe isomer shift in Mössbauer spectra by density functional theory. Inorg. Chim. Acta 2002, 337, 181–192. 10.1016/S0020-1693(02)01031-9. [DOI] [Google Scholar]
  83. Schäfer A.; Huber C.; Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100 (8), 5829–5835. 10.1063/1.467146. [DOI] [Google Scholar]
  84. Schäfer A.; Horn H.; Ahlrichs R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97 (4), 2571–2577. 10.1063/1.463096. [DOI] [Google Scholar]
  85. Römelt M.; Ye S.; Neese F. Calibration of Modern Density Functional Theory Methods for the Prediction of 57Fe Mössbauer Isomer Shifts: Meta-GGA and Double-Hybrid Functionals. Inorg. Chem. 2009, 48 (3), 784–785. 10.1021/ic801535v. [DOI] [PubMed] [Google Scholar]
  86. Ye S.; Bill E.; Neese F. Electronic Structures of the [Fe(N2)(SiPiPr3)]+1/0/–1 Electron Transfer Series: A Counterintuitive Correlation between Isomer Shifts and Oxidation States. Inorg. Chem. 2016, 55 (7), 3468–3474. 10.1021/acs.inorgchem.5b02908. [DOI] [PubMed] [Google Scholar]
  87. Sinnecker S.; Slep L. D.; Bill E.; Neese F. Performance of Nonrelativistic and Quasi-Relativistic Hybrid DFT for the Prediction of Electric and Magnetic Hyperfine Parameters in 57Fe Mössbauer Spectra. Inorg. Chem. 2005, 44 (7), 2245–2254. 10.1021/ic048609e. [DOI] [PubMed] [Google Scholar]
  88. Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2 (1), 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au1c00184_si_001.cif (740KB, cif)
au1c00184_si_002.cif (1.4MB, cif)
au1c00184_si_003.cif (1.4MB, cif)
au1c00184_si_004.cif (2.1MB, cif)
au1c00184_si_005.cif (750.9KB, cif)
au1c00184_si_006.pdf (2MB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES