Abstract
The discovery of conductive and magnetic two-dimensional (2D) materials is critical for the development of next generation spintronics devices. Coordination chemistry in particular represents a highly versatile, though underutilized, route toward the synthesis of such materials with designer lattices. Here, we report the synthesis of a conductive, layered 2D metal–organic kagome lattice, Mn3(C6S6), using mild solution-phase chemistry. Strong geometric spin frustration in this system mediates spin freezing at low temperatures, which results in glassy magnetic dynamics consistent with a rare geometrically frustrated (topological) spin glass. Notably, we show that this geometric frustration engenders a large, tunable exchange bias of 1625 Oe in Mn3(C6S6), providing the first example of exchange bias in a coordination solid or a topological spin glass. Exchange bias is a critical component in a number of spintronics applications, but it is difficult to rationally tune, as it typically arises due to structural disorder. This work outlines a new strategy for engineering exchange bias systems using single-phase, crystalline lattices. More generally, these results demonstrate the potential utility of geometric frustration in the design of new nanoscale spintronic materials.
Short abstract
Classic exchange bias relies on a disordered interface between a ferromagnet and antiferromagnet, impeding the design of next generation systems. We show that magnetic disorder due to geometric frustration engenders a large, tunable exchange bias in the metal−organic kagome lattice, Mn3(C6S6). As Mn3(C6S6) is a topological spin glass, the exchange bias may be a tuning handle for exotic nonequilibrium states. This work designates designer metal−organic lattices as a platform for novel emergent physical phenomena.
Introduction
The nascent field of two-dimensional (2D) magnetism has outlined a path toward nanoscale spintronics devices that leverage magnetic degrees of freedom.1 Along these lines, materials that exhibit exchange bias, characterized by a horizontal shift in the origin of the magnetic hysteresis loop, are of particular interest. Exchange bias is widely employed in spin valves used in hard disk read heads,2 is used to stabilize magnetic storage media,3 and shows promise for more exotic spintronics applications, such as electrical switching of magnetic logic devices.4 While exchange bias has been extensively demonstrated in antiferromagnetic/ferromagnetic thin film interfaces5 and nanoparticle systems,6 this property has yet to be demonstrated in 2D materials suitable for the development of nanoscale spintronics devices. Although the microscopic origin of exchange bias is yet unresolved,6 recent studies underscore the critical role that spin frustration may play—most explicitly demonstrated by the observation of exchange bias not only at ferromagnetic/spin glass interfaces,7 but also in single phase, amorphous spin glasses.8 In such systems, disorder-induced spin frustration engenders glassy behavior, which has been linked to the observation of exchange bias. Indeed, recent work by some of us has outlined qualitative relationships between glassy dynamics and the magnitude of the exchange bias in disordered systems.9 Despite this, structural disorder, whether it occurs at interfaces or in single phase glasses, hinders efforts toward rationally tuning exchange bias.
We hypothesized that spin frustration arising not from structural disorder but from geometrically frustrated lattices may also result in exchange bias, providing a crystallographically precise platform for the design of novel exchange bias systems. Such lattices, comprising spins arranged in a triangular pattern, engender frustration when antiferromagnetic coupling is dominant, since three spins at the corners of a triangle cannot all align in an antiparallel fashion, resulting in a number of energetically degenerate magnetic configurations. The kagome lattice, composed of magnetic ions arranged in a trihexagonal tiling, is a paradigmatic example, where the ground state degeneracy scales macroscopically with the number of spins. As the temperature is lowered, fluctuating correlated spins in such lattices may dynamically slow down in certain circumstances, forming a disordered magnetic phase termed a topological spin glass or spin jam.10−13 The magnetic transition from a correlated spin liquid state to the glass state in geometrically frustrated lattices is unconventional. The current consensus suggests an interplay of quantum fluctuations10−13 and crystal anisotropy underpins the glass transition,10,11 drawing parallels to spin liquid physics.14,15 This scenario is quite distinct from that of structurally disordered glasses, resulting in a uniquely nonhierarchical energy landscape of nearly degenerate magnetic configurations, and thus distinctive magnetic dynamics, which have been considered evidence of nonequilibrium topological glassy states.12
More generally, the design of 2D frustrated magnetic lattices is of inherent interest for studies at the nanoscale, as these lattices are implicated in a variety of exotic correlated phenomena, such as quantum spin liquid behavior,16 superconductivity,17 and spin neumaticity.18 Saliently, a number of layered metal–organic coordination solids with kagome-like frustrated 2D lattices have recently been reported,19 wherein π–d conjugation gives rise to materials exhibiting varied charge transport behavior, ranging from semiconductors to strongly correlated superconductors.19,20 However, experimental realization of the diverse magnetic behavior predicted in these materials remains limited,19,21,22 likely due to the synthetic difficulty of achieving the requisite square planar coordination geometry with transition metals of interest.
Here, we report the layered 2D coordination solid Mn3(C6S6), which consists of high-spin Mn2+ ions templated into a kagome lattice by benzenehexathiol. This material displays conductivity values reaching ∼1.50 S/cm at room temperature, while magnetic characterization reveals a high degree of spin frustration, with antiferromagnetic coupling at room temperature and a spin canted antiferromagnetic glassy state at low temperatures. Remarkably, Mn3(C6S6) also displays a large exchange bias upon magnetic field annealing. The dynamic magnetic properties of this solid are consistent with geometric, rather than disorder-induced, spin frustration, indicating that Mn3(C6S6) is a topological spin glass. These results highlight a potentially powerful strategy for the design of novel exchange bias systems that relies on crystalline frustrated lattices rather than serendipitously disordered interfaces. Beyond potential applications in biased spintronics devices, Mn3(C6S6) stands as a tunable platform for the fundamental study of frustrated and topological magnetism at the nanoscale.
Results
Synthesis and Structure of Mn3(C6S6)
The material Mn3(C6S6) was synthesized at the liquid–liquid interface of an aqueous solution of Mn(CH3CO2)2·4H2O and a dichloromethane solution of benzenehexathiol under an atmosphere of 95% N2 and 5% H2. Slow addition of these solutions to pure layers of their respective solvents produced a yellow-gold film with an iridescent sheen (SI Figure 1). Scanning electron microscopy characterization of this film revealed a morphology similar to the previously reported Cu3(C6S6) phase, wherein the side of the film facing the organic phase is smooth and the opposite side is composed of smaller crystallites (SI Figure 2).23
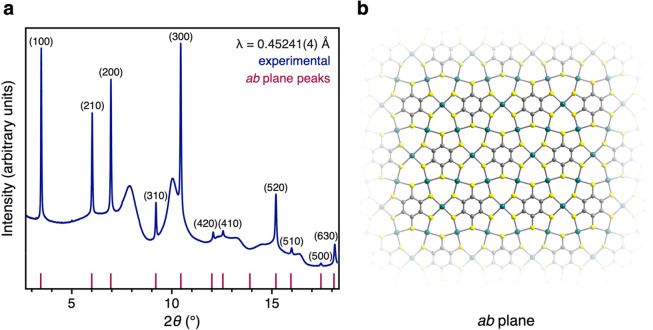
Synchrotron powder X-ray diffraction data for Mn3(C6S6) revealed a crystalline material with a structure similar to that of Cu3(C6S6) (Figure 1), where the sharp peaks correspond to the ab plane, and broad peaks are reflections associated with the c axis.23 Simulated powder X-ray diffraction patterns for eclipsed and staggered stacking models of Mn3(C6S6) (SI Figure 3) suggest that the structure is closer to one with an eclipsed conformation. Broadening in the peaks corresponding to c-axis reflections is attributed to the inherent anisotropy of the flake-like crystals, with a Scherrer analysis suggesting a c-axis particle size of ∼25 nm, consistent with the SEM (SI Figures 2b and 3), although minor stacking disorder may contribute as well. Peak indexing revealed a hexagonal lattice with an in-plane lattice parameter of 8.62 Å and an estimated interlayer distance of 3.77 Å, where the interlayer distance is estimated by taking the center of the primary broad peaks at 2θ = 8.90° and 10.05°, with Miller indices (101) and (201) (further discussion in Supporting Information). Inductively coupled plasma–mass spectrometry analysis of the crystalline solid afforded an empirical formula of Mn0.49:S1, consistent with the expected formula of Mn0.5:S1. The infrared spectrum of Mn3(C6S6) (SI Figure 4) features C–S stretches consistent with those reported in Cu3(C6S6),20 establishing the ligand as C6S66–, while the absence of C–H and O–H stretching frequencies from 2800 to 3500 cm–1 indicated the absence of coordinated solvent, as expected given the calculated interlayer distance. The X-ray photoelectron spectrum of Mn3(C6S6) could be fit assuming the presence of only one Mn, S, and C species (SI Figure 5), further supporting the conclusion that the manganese and ligand are valence pure.24 In the Mn K-edge X-ray absorption near edge structure (XANES) spectrum of Mn3(C6S6), the rising edge energy of ∼6548 eV coincides with that of a MnS standard, while a small pre-edge feature is consistent with local inversion symmetry, as would be expected for the proposed square planar geometry (SI Figure 6). Together, the diffraction and spectroscopic data are consistent with an assignment of Mn2+3(C6S6)6–, in which divalent manganese ions are trihexagonally tiled by diamagnetic benzenehexathiolate to form a 2D kagome lattice.
Figure 1.
Structural characterization of Mn3(C6S6). (a) Synchotron powder X-ray diffractogram of Mn3(C6S6), with simulated peaks from the ab plane as reference. (b) Structure of the ab plane of Mn3(C6S6). Teal, yellow, and gray spheres represent Mn, S, and C atoms, respectively.
Conductivity and Electronic Structure
An average room temperature conductivity value of σ = 0.39 S/cm was determined from van der Pauw conductivity measurements on thin film (100–200 nm thick) samples of Mn3(C6S6), with a champion device exhibiting a value of 1.48 S/cm. The variance in conductivity values (SI Table 1) is similar to that characterized in other metal–organic materials25 and likely stems from differences in interparticle contacts and film continuity across devices. Variable-temperature conductivity measurements were performed on a pressed pellet of Mn3(C6S6) using a 2-point screw cell with copper contacts. The data were adequately fit using an Efros–Shklovskii variable-range hopping model (SI Figures 7 and 8), as is typical for charge transport in low-dimensional and polycrystalline materials limited by interparticle contacts.26,27 Thermopower measurements on the thin film samples afforded Seebeck coefficients as high as 169 μV K–1 (SI Table 1), suggesting that Mn3(C6S6) is a p-type semiconductor. Indeed, the UV–vis–NIR spectrum of Mn3(C6S6) displays a monotonic increase in absorption in the near-IR region that is indicative of thermally activated charge carriers (SI Figure 9).27−30 Notably, the corresponding power factor of 4.08 μW/mK2 surpasses values obtained for structurally similar metal–organic materials.23,31 Density functional theory calculations on bulk crystals with spin canted configurations, including spin–orbit coupling and van der Waals corrections, are consistent with semiconducting behavior, yielding calculated direct gaps on the order of ∼1 eV (Figure 2, left). Notably, the valence band contains significant Mn, S, and C orbital character, highlighting the importance of covalency in enabling electronic coupling within the material (Figure 2, right).
Figure 2.
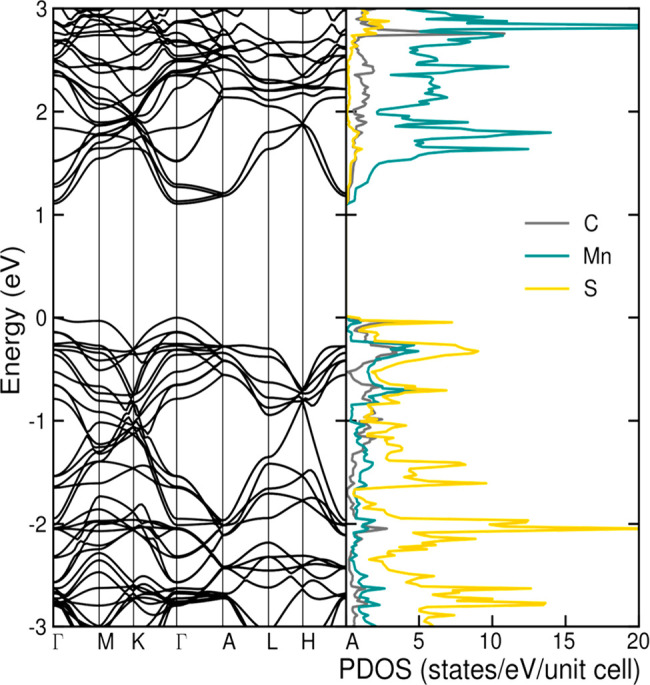
Calculated band structure and density of states of Mn3(C6S6). Representative band structure of bulk Mn3(C6S6) with a canted antiferromagnetic spin configuration (left) and corresponding density of states (right). Various canted antiferromagnetic spin configurations give nearly identical band structures (see SI Figure 11). The plots are results from density functional theory calculations, using an optimized structure (see Computational Methods and SI Figure 10).
Magnetic Properties
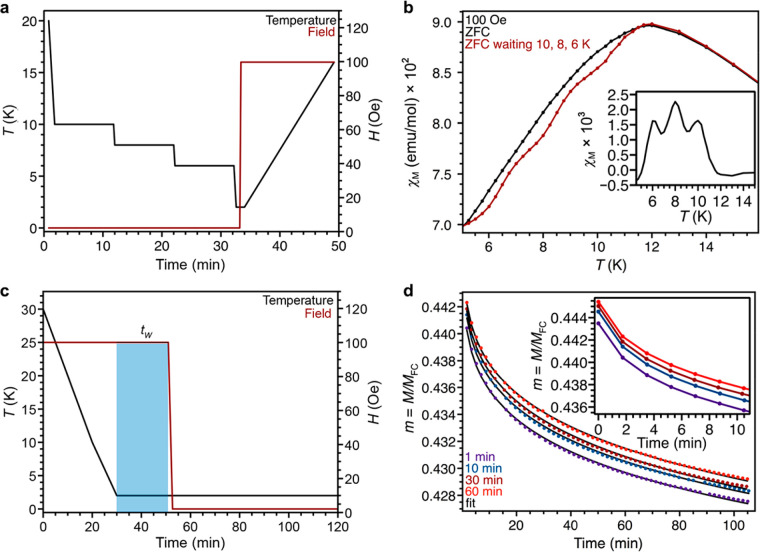
Strong antiferromagnetic interactions in Mn3(C6S6) at room temperature are evidenced by a magnetic susceptibility-temperature product of χMT = 6.94 emu·K/mol, far below the 13.13 emu·K/mol expected for three isolated high-spin MnII centers (SI Figure 11). This is corroborated by a Curie–Weiss analysis, which gives Θ = −253 K, while the calculated Curie constant of 13.03 emu K/mol is consistent with three S = 5/2 MnII ions per formula unit (SI Figure 12). In the χM versus T data, a peak at ∼12 K and the divergence between field-cooled (FC) and zero field-cooled (ZFC) traces (Figure 3a) are indicative of the onset of a spin freezing transition, TF. The disparity between |Θ| and this transition temperature is attributed to geometric frustration induced by the kagome lattice, which is well-known to give lower ordering temperatures than those expected from the strength of magnetic interactions. The Ramirez ratio, f = |Θ|/TF, is commonly used to quantify spin frustration, and the value of f ≈ 20 obtained for Mn3(C6S6) is indicative of a high degree of frustration.16 Moreover, ac magnetic susceptibility data reveal a frequency dependence of TF, with a Mydosh parameter of ∼0.015 (Figure 3b–c), consistent with spin glass behavior associated with frustrated magnets.32
Figure 3.
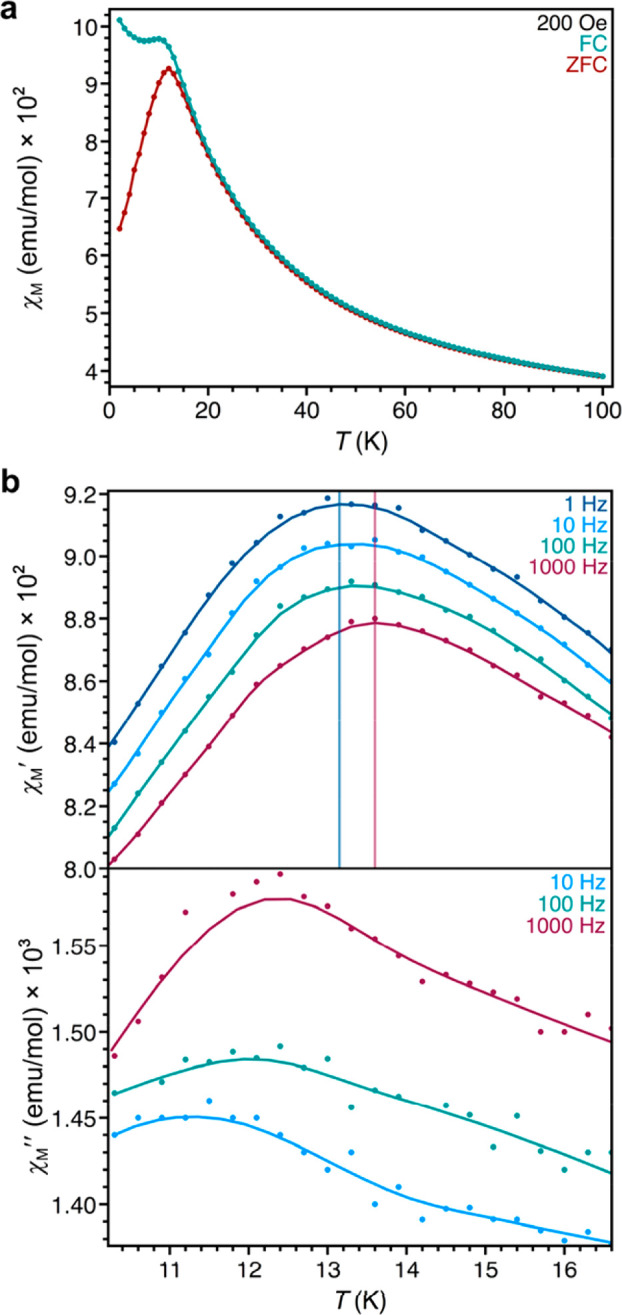
Magnetic susceptibility data for Mn3(C6S6). (a) Field-cooled (under 200 Oe, teal) and zero field-cooled (red) molar magnetic susceptibility data for Mn3(C6S6) collected between 2 and 300 K under an applied field of 200 Oe. (b) Variable temperature molar in-phase (χM′) and out-of-phase (χM″) ac susceptibility data for Mn3(C6S6) collected at the indicated frequencies under a dc field of 25 Oe to reduce noise. Smoothed lines are guides for the eyes, while the vertical lines for 1 and 1000 Hz highlight the frequency dependence.
Spin glasses are characterized by an energy landscape featuring numerous, nearly degenerate states that arise from spin frustration. This landscape can be probed by monitoring changes in magnetization with changing temperature, applied magnetic field, and time, perhaps most uniquely through the demonstration of a thermal memory.32,33 To examine this memory effect, a sample of Mn3(C6S6) was cooled under zero field from 30 K and held for 10 min at 10, 8, and 6 K temperature points (Figure 4a). At each temperature pause, the material will traverse the available energy landscape to reach an associated metastable state. After these temperature pauses, ZFC magnetic susceptibility data were collected under 100 Oe, revealing thermal memory at the set wait points, as evidenced by “memory dips” in the measured susceptibility (Figure 4b, red trace). A partial rejuvenation of the susceptibility (an increase after a dip) is observed upon warming as the system gains the requisite thermal energy to re-equilibrate within the energy landscape. In this context, bifurcation of the FC and ZFC dc susceptibility data (Figure 3a) is consistent with a spin glass state, for which application of a magnetic field enables access to higher moment, metastable states.
Figure 4.
Spin glass behavior of Mn3(C6S6). (a) Illustration of a memory dip experiment protocol. The material was first cooled from 30 to 10 K under zero field and held for 10 min; cooled to 8 K and held for 10 min; cooled to 6 K and held for 10 min; and finally cooled to 2 K. A 100 Oe field was then applied, and the susceptibility trace was collected upon warming. (b) Data from thermal memory effect experiments. The red trace displays the ZFC curve after following the protocol illustrated in (a). Memory dips at 10, 8, and 6 K are consistent with the thermal annealing protocol. The black trace displays standard ZFC data collected under 100 Oe in the absence of the memory dip protocol. Lines are guides for the eye. (Inset) Difference plot between red and black curves. (c) Illustration of thermoremanent relaxation experiment. The material was first cooled under a 100 Oe applied field and held for a designated wait time, tw, at 2 K; the field was then removed and the thermoremnant magnetization data were collected. (d) Thermoremnant magnetization data collected from the protocol in (c) with different colors indicating designated wait times. The magnetization clearly increases with longer wait times. Solid lines are fits to the curves as described in the Supporting Information. (Inset) Expanded view between 0 and 10 min highlighting the magnetic aging characteristic of spin glasses.
The complex energy landscape of a spin glass engenders nontrivial magnetic relaxation processes. To investigate the glassy relaxation dynamics of Mn3(C6S6), thermoremanent magnetization experiments were performed following the protocol outlined in Figure 4c. The material was first cooled from 30 to 2 K under a 100 Oe field and held for a given waiting time (tw); the field was then zeroed and the change in magnetization was monitored. As seen in the decay curves in Figure 4d, longer tw values are associated with higher magnetization values, characteristic of a glassy magnetic system.32,33 Fits of the magnetization decay curves using a stretched exponential function yielded τ values on the order of 102 years (SI Table 2). Electronic structure calculations performed on five possible spin conformations in Mn3(C6S6) (SI Table 3) indicate that coplanar antiferromagnetic spin arrangements are lowest in energy. The resulting small energy differences between the various antiferromagnetic configurations are likely critical to the observation of glassy behavior. Variable-field magnetization data collected at 2 K after cooling under zero field revealed an open hysteresis loop with a coercive field, Hc, of 2000 Oe that does not saturate as high as 7 T, which could indicate spin canting similar to that observed in S = 5/2 Heisenberg kagome lattices (SI Figure 13).34
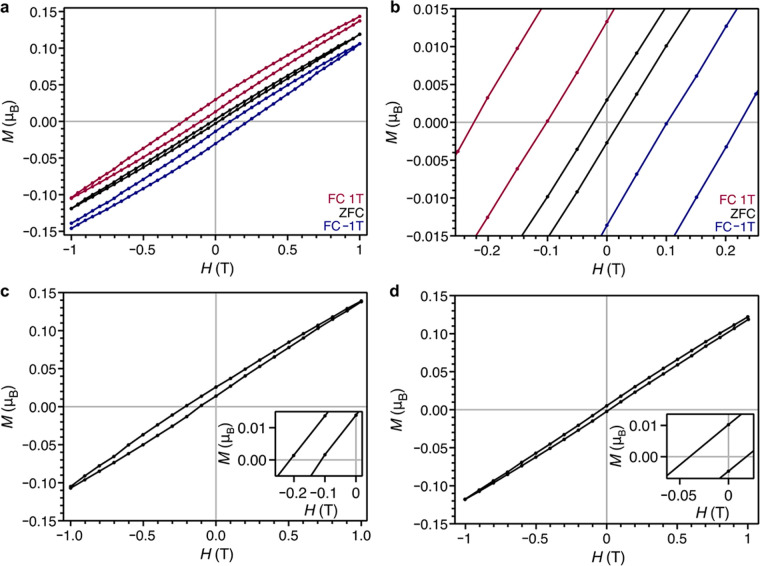
Variable-field magnetization data collected upon cooling under ±1 T revealed hysteresis with a pronounced lateral origin shift from zero to ∓1625 Oe, accompanied by an increase in Hc by 395 Oe (Figure 5a–b), consistent with the exchange bias effect.5,6,32 The stability of the exchange bias was examined by cooling Mn3(C6S6) under 1 T, ramping the field to 0 T, and then collecting hysteresis data after a 60 min waiting period (Figure 5c). The corresponding loop is essentially unchanged from that characterized immediately after cooling under 1 T, indicating that the exchange bias is nonvolatile. Several successive hysteresis loops were also collected after cooling the sample under 1 T. Both Hc and the exchange bias field, He, trend toward a constant value with increasing cycle number (SI Figure 14), consistent with the magnetic training effect in exchange biased systems. Hysteresis data collected after cooling Mn3(C6S6) under different fields revealed that He achieves a maximum at fields of approximately 1 T (SI Figure 15). As such, the exchange bias likely cannot be attributed to the small crystallite morphology of Mn3(C6S6), given that single-phase, superparamagnetic particles displaying exchange bias do so even under large applied fields, owing to the presence of a well-behaved magnetic core coupled with surface states exhibiting glassy dynamics.5,6,35 An exchange bias is also observed following application of a 1 T field for a 1 h induction period after zero field cooling, indicating that isothermal magnetic switching is possible in this system (Figure 5d). Importantly, this observation is entirely at odds with the existence of a minor loop phenomenon (see discussion in Supporting Information). Further, this isothermal switching is not observed in heterostructured antiferromagnetic/ferromagnetic exchange bias systems, suggesting a unique glassy mechanism is responsible for the behavior observed here.
Figure 5.
Variable field magnetization data for Mn3(C6S6). (a) Data collected after cooling under 1 T (red curve), −1 T (blue curve), and zero field (black curve). The hysteresis loops collected under applied fields exhibit symmetric shifts relative to the zero-field loop. (b) Expanded view of the region between −0.25 and 0.25 T in Figure 4a. (c) Hysteresis data obtained after cooling under 1 T and a 1 h waiting period at zero field. The observed exchange bias is similar to that in (a) (red curve). (Inset) Expanded view of the exchange bias intercepts. (d) Isothermal exchange bias. The sample was cooled under zero field, and a field of 1T was then applied for 1 h. (Inset) Expanded view of the exchange bias intercepts. All data was collected at 2 K.
Glassy magnetic behavior typically originates from significant structural disorder; however, the myriad structural data for Mn3(C6S6) establish the homogeneous, crystalline nature of the 2D plane. To elucidate whether the spin glass state mediating exchange bias originates from small amounts of local/stacking disorder or is a consequence of system geometric frustration, we employed a suite of magnetic characterization methods capable of probing the unique history-dependent dynamics inherent to the energy landscape of a geometrically frustrated glass.12,13 The conventional, structurally disordered spin glass has a rugged, funnel-like energy landscape with a hierarchical magnetic configuration space.13 In contrast, geometrically frustrated glasses have a nonhierarchical configuration space, where the macroscopic degeneracy of the kagome lattice ground states is lifted by quantum and classical spin fluctuations, resulting in a flattened, corrugated energy landscape with numerous nearly degenerate states.13 Consequently, these dissimilar landscapes have distinctive responses to temperature, time, and field perturbations. Specifically, the susceptibility of the geometrically frustrated glass is significantly less sensitive to such perturbations.13,36 This is attributed to the plethora of essentially degenerate minima in the energy landscape, as well as the relative insensitivity of the potential energy barriers between these configurational states to such environmental disturbances. In essence, because the energy landscape is significantly more homogeneous (and thus less energetically distinct), the geometric glass is less able to adapt to environmental perturbations, resulting in nonequilibrium glassy dynamics: the state evolution of a geometrically frustrated glass is akin to a random walk.
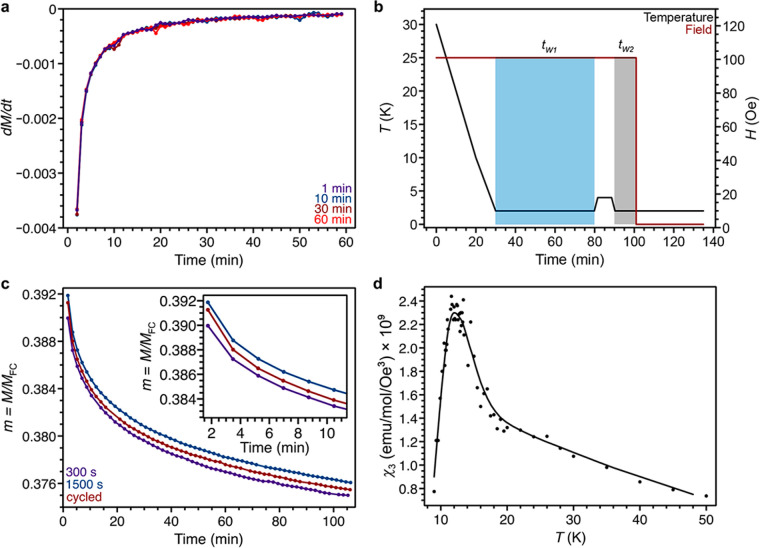
We probe these unique dynamics using established dc magnetic relaxation analyses. First, in disordered spin glasses, a distinct peak associated with tw is typically observed in the time-dependent derivative of the thermoremanent magnetization, which is caused by a distribution of superparamagnetic clusters with individual relaxation times; those with relaxation times on the order of tw magnetize during aging and subsequently relax on that same time scale.32,33 In contrast, dM/dt versus t curves derived from the data in Figure 4d overlay, suggesting that the characteristic relaxation time of the glass is essentially unaffected by the aging history of the material (Figure 6a and SI Table 2). In other words, the spin-reversal barriers within the energy landscape of Mn3(C6S6) are significantly less dynamic in response to the time-dependent history of the material compared to structurally disordered glasses. Magnetization relaxation in Mn3(C6S6) was also examined following the temperature perturbation protocol illustrated in Figure 6b, wherein after cooling from 30 to 2 K under 100 Oe, separate waiting periods of 1500 and 300 s are punctuated by a 60 s period at 4 K. The thermoremanent magnetization curve collected after this temperature cycling sequence (Figure 6c, red trace) exhibits a larger frozen moment than that for a magnetization decay curve collected after a tw of 300 s without a temperature perturbation (Figure 6c, purple trace). A similar phenomenon has been observed for the topological spin glass (H3O)Fe3(SO4)2(OH)6 and is distinct from the behavior of disordered glasses, where temperature cycling resets aging.36 This result for Mn3(C6S6) is further corroborated by the incomplete rejuvenation of the memory dip curve to the baseline curve, as well as the shallow profile of the dips: the energy landscape of a geometrically frustrated glass is less sensitive to temperature and time perturbation (Figure 4b).12,13 Together, these findings suggest that the energy landscape of Mn3(C6S6) is significantly less dynamic than that of a disordered spin glass, but rather is consistent with a topological spin glass.
Figure 6.
Glassy topological dynamics of Mn3(C6S6). (a) Derivatives of 2 K thermoremanent magnetization decay curves collected at the indicated waiting times. Curves overlay. (b) Illustration of a temperature cycling experiment. The sample was cooled from 30 to 2 K under an applied field, held for tw1 = 1500 s, heated to 4 K and held for 60 s, and then cooled to 2 K and held for tw2 = 300 s. The field is then set to zero, and the thermoremanent magnetization decay curve is collected. (c) Data resulting from the temperature cycled aging experiment illustrated in (b) (red curve). Data collected after 300 and 1500 s wait times (absent cycling) are shown for comparison in purple and blue, respectively. Temperature cycling does not reset the initial state of the glass, as the red curve lies above the purple curve. (Inset) Expanded view of the magnetization decay curves between 2 and 10 min. (d) χ3 versus T data. The peak at ∼12 K is consistent with the freezing temperature observed in the ac and dc magnetic susceptibility data. The data indicate significant spin correlations far above the freezing temperature. Smoothed lines are guides for the eyes.
The canonical magnetic glass transition is a second-order phenomenon, and therefore a higher-order magnetic susceptibility term is needed to interrogate the phase transition.32 The nonlinear susceptibility, χ3, of Mn3(C6S6) was extracted from a series of magnetization isotherms around TF. In disordered spin glasses, χ3(T) ∝ (T–Tg)−γ (2 < γ < 3) for temperatures approaching TF.32,37 In the case of Mn3(C6S6), χ3 versus T is both nonzero as high as 50 K and diverges to a far lesser degree than is observed in canonical spin glasses, such that the data could not be fit to the aforementioned power law (Figure 6d). This behavior indicates a buildup of correlated spin dynamics well above the glass transition, as predicted by topological spin glass theory10,11 and previously observed in the topological spin glass candidate hydronium iron jarosite.37,38 The divergence of the FC and ZFC traces (Figure 3a) far above the glass transition temperature corroborates this observation, as it suggests that temperature and field are dynamically modifying correlated, unfrozen spins. These data are unsurprisingly consistent with the large frustration parameter of Mn3(C6S6), as disordered glasses typically have TF ≈ Θ, resulting in a Ramirez ratio near unity.12 We further note that, in the magnetically relevant temperature regimes, Mn3(C6S6) is functionally insulating, and the MnII ion lacks first-order orbital degrees of freedom, which summarily indicate that our interpretations are not predicated on an inappropriate topological spin glass model.12 Together, these experiments demonstrate that the glassy dynamics of Mn3(C6S6) likely originate from geometric frustration, rather than from structural disorder, doping effects, or long-range magnetic interactions. This finding is consistent with previous theoretical and experimental studies, which show that significant disorder (on the order of 20% substitutional disorder) is necessary to shift the glassy dynamical behavior of a frustrated lattice into the disordered regime.37,39−41
Discussion
Classical exchange bias is driven by a structurally disordered interface between antiferromagnetic and ferromagnetic thin films.5−7 Numerous studies have shown that this disordered interface is itself primarily responsible for the exchange bias phenomenon and is intimately related to spin glass physics. In this study, we omit the bilayer, and instead focus in on a crystallographically precise, single phase spin glass, toward inferring a more general understanding of the exchange bias phenomenon.
Given that structural and magnetic data do not support disorder in Mn3(C6S6), we propose an alternative explanation for the exchange bias that invokes an interplay of antisymmetric exchange and magnetic field-mediated chiral induction of the spin texture.42,43 Field-dependent chiral magnetic order has been theoretically proposed43 and experimentally verified34 in Heisenberg kagome antiferromagnets, in particular, in potassium iron jarosite, a spin congener of Mn3(C6S6). Importantly, theoretical studies suggest that the chiral order observed in these magnetically ordered systems is retained locally in topological spin glasses.10,11 These local, correlated spin objects, termed topological domain wall defects, “spin folds”, or weathervane modes, have likewise been predicted to select specific chirality based on field-dependent anisotropic exchange interactions.10,11 We posit that that the application of a magnetic field polarizes and selects the chirality of these weathervane modes, while the strength of the field determines the number of correlated spins within each mode, as well as its anisotropy field. Only a fraction of the spin folds is repolarized upon a reverse field sweep, resulting in the shifted hysteresis loop. This explanation has similarities to what has been proposed in canonical spin glasses,42,44 but with a key distinction. In the case of canonical spin glasses, the first field-intercept of the hysteresis loop is independent of the annealing field, which has been interpreted as arising from the introduction of a rigid chiral spin texture in the material, even in the presence of a small magnetic field. In Mn3(C6S6), this first intercept gradually grows until it reaches a set value, instead suggesting that chiral induction is dependent on external variables until a critical field is applied (SI Figure 17). A complex chiral equilibrium such as this has been previously invoked to explain the unusual relaxation behavior in topological spin glasses.36 A comparison of hysteresis loops collected after zero field cooling and field annealing for two different wait times (30 and 300 s) highlights this point further (SI Figure 18). While the initial magnetization of the hysteresis loop is unaffected, suggesting the absence of aging and domain growth, the exchange bias increases by 14% with the longer induction period. In this context, the bias field may be seen as a probe of the net chirality of the system.
Outlook
The foregoing results demonstrate that bulk topological spin glasses alone can engender exchange bias. Initial investigations of several other site-ordered, geometrically frustrated spin glasses suggest that this design principle holds generally (SI Figure 19 details an exchange bias experiment on the aforementioned (H3O)Fe3(SO4)2(OH)6).45 Modification of the magnetic and electronic properties of Mn3(C6S6) through isoreticular chemistry and/or doping stands as a promising avenue toward accessing materials exhibiting a large exchange bias at even higher temperature.19,22,24 Moving forward, engineering more strongly anisotropic topological spin glasses, in both organometallic and solid state materials, will likely result in weaker frustration, technologically relevant glass transition temperatures, and larger exchange bias.10,11
These results reveal a new direction in the study of frustrated magnetism, where correlated spins in topologically frustrated glasses may be modulated and observed through exchange bias experiments. Specifically, in the context of field-dependent chiral weathervane modes, the observed isothermal exchange bias in these systems may ultimately provide a field-tunable handle toward controlling nonequilibrium topologically glassy states. Finally, spin glass theory underpins a range of technologically important fields, from neural networks to quantum annealing,32,33 highlighting the importance of further study of the predicted non-Abelian dynamics11 in low-dimensional topological spin glasses, such as Mn3(C6S6), at the nanoscale.
Acknowledgments
The synthesis and magnetic characterization of this material were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0019356. Powder X-ray diffraction data were collected at beamline 17-BM-B at the Advanced Photon Source, a US Department of Energy, Office of Science User Facility operated by the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02- 06CH11357. Thin film conductivity and thermopower measurements were performed at the Molecular Foundry, Lawrence Berkeley National Laboratory, and were supported by the Department of Energy, Office of Science, Office of Basic Energy Sciences, Scientific User Facilities Division of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. Computational resources were provided by the National Energy Research Scientific Computing Center (NERSC). X-ray absorption spectroscopy experiments were supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences Heavy Elements Chemistry program of the US DoE under contract number DE-AC02-05CH11231 (D.J.L. and D.K.S.), as well as the US DoE, Office of Science, Office of Basic Energy Sciences under award number DE-SC0016961 (M.W.M.), and data were collected with the X-ray absorption spectroscopy user resources of beamline 10.3.2 at the Advanced Light Source, which is a DoE Office of Science User Facility under contract number DE-AC02-05CH11231. We thank the Quantum Information Science and Engineering Network for support for R.A.M. through NSF award DMR-1747426, and the US National Science Foundation for providing graduate fellowship support to L.E.D. and E.O.V. We further thank the staff at the Biomolecular Technology Center of the California Institute for Quantitative Biosciences (QB3) at Berkeley for assistance with XPS measurements, D. Jorgens at the University of California Berkeley Electron Microscope Laboratory for advice and assistance in electron microscopy sample preparation and data collection, J. Oktawiec for collecting synchrotron powder diffraction data, J. G. Analytis, E. Maniv, and E. Lachman for helpful discussions, and K. R. Meihaus and T. D. Harris for editorial assistance.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.1c00568.
Materials and Methods with tables and figures (PDF)
Author Contributions
R.A.M. and J.R.L. designed this project with assistance from L.E.D. E.A.P and J.B.N. performed band structure and magnetic structure density functional theory calculations and analyses. E.W.Z. and J.J.U. collected and analyzed thin film conductivity and thermopower measurements. M.W.M., D.J.L., and D.K.S. collected and analyzed X-ray absorption spectra. E.O.V. and R.A.M. performed scanning electron microscopy. R.A.M. synthesized the materials, and collected and analyzed all data unless otherwise noted, with initial guidance from L.E.D. and M.E.Z. R.A.M and J.R.L. wrote the manuscript, and all authors contributed to manuscript revision.
The authors declare no competing financial interest.
Safety Statement
The synthesis of the ligand benzenehexathiol involves condensed ammonia, which is poisonous and presents an inhalation hazard, and also involves elemental sodium, which is pyrophoric.
Supplementary Material
References
- Gong C.; Zhang X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science 2019, 363, 4450. 10.1126/science.aav4450. [DOI] [PubMed] [Google Scholar]
- Gider S.; Runge B.-U.; Marley A. C.; Parkin S. S. P. The Magnetic Stability of Spin-Dependent Tunneling Devices. Science 1998, 281, 797–799. 10.1126/science.281.5378.797. [DOI] [PubMed] [Google Scholar]
- Skumryev V.; Stoyanov S.; Zhang Y.; Hadjipanayis G.; Givord D.; Nogués J. Beating the superparamagnetic limit with exchange bias. Nature 2003, 423, 850–853. 10.1038/nature01687. [DOI] [PubMed] [Google Scholar]
- He X.; Wang Y.; Wu N.; Caruso A. N.; Vescovo E.; Belashchenko K. D.; Dowben P. A.; Binek C. Robust isothermal electric control of exchange bias at room temperature. Nat. Mater. 2010, 9, 579–585. 10.1038/nmat2785. [DOI] [PubMed] [Google Scholar]
- O’Grady K.; Fernandez-Outon L. E.; Vallejo-Fernandez G. A new paradigm for exchange bias in polycrystalline thin films. J. Magn. Magn. Mater. 2010, 322, 883–899. 10.1016/j.jmmm.2009.12.011. [DOI] [Google Scholar]
- Kiwi M. Exchange bias theory. J. Magn. Magn. Mater. 2001, 234, 584–595. 10.1016/S0304-8853(01)00421-8. [DOI] [Google Scholar]
- Ali M.; Adie P.; Marrows C. H.; Grieg D.; Hickey B. J.; Stamps R. L. Exchange bias using a spin glass. Nat. Mater. 2007, 6, 70–75. 10.1038/nmat1809. [DOI] [PubMed] [Google Scholar]
- Monod P.; Préjean J. J.; Tissier B. Magnetic hysteresis of CuMn in the spin glass state. J. Appl. Phys. 1979, 50, 7324–7. 10.1063/1.326943. [DOI] [Google Scholar]
- Maniv E.; Murphy R. A.; Haley S.; Doyle S.; John C.; Maniv A.; Ramakrishna S. K.; Tang Y.-L.; Ercius P.; Ramesh R.; et al. Exchange bias due to coupling between coexisting antiferromagnetic and spin-glass orders. Nat. Phys. 2021, 17, 525–530. 10.1038/s41567-020-01123-w. [DOI] [Google Scholar]
- Chandra P.; Coleman P.; Ritchey I. The anisotropic kagomé antiferromagnet: a topological spin glass?. J. Phys. I 1993, 3, 591–610. 10.1051/jp1:1993104. [DOI] [Google Scholar]
- Ritchey P.; Chandra P. Coleman, Spin folding in the two-dimensional Heisenberg kagomé antiferromagnet. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 15342. 10.1103/PhysRevB.47.15342. [DOI] [PubMed] [Google Scholar]
- Yang J.; Samarakoon A.; Dissanayake S.; Ueda H.; Klich I.; Iida K.; Pajerowski D.; Butch N. P.; Huang Q.; Copley J. R. D.; et al. Spin jam induced by quantum fluctuations in a frustrated magnet. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 11519–11523. 10.1073/pnas.1503126112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samarakoon A.; Sato T. J.; Chen T.; Chern G.-W.; Yang J.; Klich I.; Sinclair R.; Zhou H.; Lee S.-H. Aging, memory, and nonhierarchical energy landscape of spin jam. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 11806–11810. 10.1073/pnas.1608057113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keren A.; Uemura Y. J.; Luke G.; Mendels P.; Mekata M.; Asano T. Magnetic dilution in the geometrically frustrated SrCr9pGa12–9pO19 and the role of local dynamics: A muon spin relaxation study. Phys. Rev. Lett. 2000, 84, 3450–3453. 10.1103/PhysRevLett.84.3450. [DOI] [PubMed] [Google Scholar]
- Bono D.; Limot L.; Mendels P.; Collin G.; Blanchard N. Correlations, spin dynamics, defects: The highly frustrated kagome bilayer. Low Temp. Phys. 2005, 31, 704–721. 10.1063/1.2008131. [DOI] [Google Scholar]
- Balents L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. 10.1038/nature08917. [DOI] [PubMed] [Google Scholar]
- Anderson P. W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. 10.1126/science.235.4793.1196. [DOI] [PubMed] [Google Scholar]
- Damle K.; Senthil T. Spin Nematics and Magnetization Plateau Transition in Anisotropic Kagome Magnets. Phys. Rev. Lett. 2006, 97, 453–4. 10.1103/PhysRevLett.97.067202. [DOI] [PubMed] [Google Scholar]
- Maeda H.; Sakamoto R.; Nishihara H. Coordination Programming of Two-Dimensional Metal Complex Frameworks. Langmuir 2016, 32, 2527–2538. 10.1021/acs.langmuir.6b00156. [DOI] [PubMed] [Google Scholar]
- Takenaka T.; Ishihara K.; Roppongi M.; Miao Y.; Mizukami Y.; Makita T.; Tsurumi J.; Watamabe S.; Takeya J.; Yamashita M.; et al. Strongly correlated superconductivity in a copper-based metal-organic framework with a perfect kagome lattice. Sci. Adv. 2021, 7, eebf3996. 10.1126/sciadv.abf3996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao M.; Wang A.; Zhang X. Half-metallicity of a kagome spin lattice: the case of a manganese bis-dithiolene monolayer. Nanoscale 2013, 5, 10404–10405. 10.1039/c3nr03323f. [DOI] [PubMed] [Google Scholar]
- Chakravarty B.; Mandal S. Sarkar, Bis(dithioline)-Based Metal–Organic Frameworks with Superior Electronic and Magnetic Properties: Spin Frustration to Spintronics and Gas Sensing. J. Phys. Chem. C 2016, 120, 28307–28319. 10.1021/acs.jpcc.6b09416. [DOI] [Google Scholar]
- Huang X.; Sheng P.; Tu Z.; Zhang F.; Wang J.; Geng H.; Zou Y.; Di C-a; Yi Y.; Sun Y.; et al. A two-dimensional π–d conjugated coordination polymer with extremely high electrical conductivity and ambipolar transport behaviour. Nat. Commun. 2015, 6, 666–668. 10.1038/ncomms8408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kambe T.; Sakamoto R.; Kusamoto T.; Pal T.; Fukui N.; Hoshiko K.; Shimojima K.; Wang Z.; Hirahara T.; Ishizaka K.; et al. Redox Control and High Conductivity of Nickel Bis(dithiolene) Complex π-Nanosheet: A Potential Organic Two-Dimensional Topological Insulator. J. Am. Chem. Soc. 2014, 136, 14357–14360. 10.1021/ja507619d. [DOI] [PubMed] [Google Scholar]
- Sun L.; Park S. S.; Sheberla D.; Dinca M. Measuring and Reporting Electrical Conductivity in Metal–Organic Frameworks: Cd2(TTFTB) as a Case Study. J. Am. Chem. Soc. 2016, 138, 14772–14782. 10.1021/jacs.6b09345. [DOI] [PubMed] [Google Scholar]
- Mott N. F. Conduction in non-crystalline materials. Philos. Mag. 1969, 19, 835–852. 10.1080/14786436908216338. [DOI] [Google Scholar]
- Ziebel M. E.; Darago L. E.; Long J. R. Control of Electronic Structure and Conductivity in Two-Dimensional Metal–Semiquinoid Frameworks of Titanium, Vanadium, and Chromium. J. Am. Chem. Soc. 2018, 140, 3040–3051. 10.1021/jacs.7b13510. [DOI] [PubMed] [Google Scholar]
- Chung T.-C.; Kaufman J. H.; Heeger A. J.; Wudl F. Charge storage in doped poly(thiophene): Optical and electrochemical studies. Phys. Rev. B: Condens. Matter Mater. Phys. 1984, 30, 702–710. 10.1103/PhysRevB.30.702. [DOI] [Google Scholar]
- Dickens P. G.; Neild D. J. Some Electronic Properties of the Molybdenum Bronzes. Trans. Faraday Soc. 1968, 64, 13–18. 10.1039/tf9686400013. [DOI] [Google Scholar]
- Aubrey M. L.; Wiers B. M.; Andrews S. C.; Sakurai T.; Reyes-Lillo S. E.; Hamed S. M.; Yu C.-J.; Darago L. E.; Mason J. A.; Baeg J.-O.; et al. Electron delocalization and charge mobility as a function of reduction in a metal–organic framework. Nat. Mater. 2018, 17, 625–632. 10.1038/s41563-018-0098-1. [DOI] [PubMed] [Google Scholar]
- Sun L.; Liao B.; Sheberla D.; Kraemer D.; Zhou J.; Stach E. A.; Zakharov D.; Stavila V.; Talin A. A.; Ge Y.; et al. A Microporous and Naturally Nanostructured Thermoelectric Metal-Organic Framework with Ultralow Thermal Conductivity. Joule 2017, 1, 168–177. 10.1016/j.joule.2017.07.018. [DOI] [Google Scholar]
- Mydosh J. A.Spin Glasses: An Experimental Introduction; Taylor and Francis: London, 1993. [Google Scholar]
- Mydosh J. A. Spin glasses: redux: an updated experimental/materials survey. Rep. Prog. Phys. 2015, 78, 052501. 10.1088/0034-4885/78/5/052501. [DOI] [PubMed] [Google Scholar]
- Grohol D.; Matan K.; Cho J.-H.; Lee S.-H.; Lynn J. W.; Nocera D. G.; Lee Y. S. Spin chirality on a two-dimensional frustrated lattice. Nat. Mater. 2005, 4, 323–328. 10.1038/nmat1353. [DOI] [PubMed] [Google Scholar]
- Martinez B.; Obradors X.; Balcells L.; Rouanet A.; Monty C. Low Temperature Surface Spin-Glass Transition in γ-Fe2O3 Nanoparticles. Phys. Rev. Lett. 1998, 80, 181–184. 10.1103/PhysRevLett.80.181. [DOI] [Google Scholar]
- Wills S.; Dupuis V.; Vincent E.; Hammann J.; Calemczuk R. Aging in a topological spin glass. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, R9264–R9267. 10.1103/PhysRevB.62.R9264. [DOI] [Google Scholar]
- Earle S. A.; Ramirez A. P.; Cava R. J. The Effect of Gallium Substitution for Iron on the Magnetic Properties of Hydronium Iron Jarosite. Phys. B 1999, 262, 199–204. 10.1016/S0921-4526(98)00165-3. [DOI] [Google Scholar]
- Wills S.; Oakley G. S.; Visser D.; Frunzke J.; Harrison A.; Andersen K. H. Short-range order in the topological spin glass (D3O)Fe3(SO4)2(OD)6 using xyz polarized neutron diffraction. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 64, 094436. 10.1103/PhysRevB.64.094436. [DOI] [Google Scholar]
- Walton A.; McCleary C. V.; Stager N. P. Raju, Effect of disorder on the magnetization of a spin glass. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 135–137. 10.1103/PhysRevB.59.135. [DOI] [Google Scholar]
- Bisson W. G.; Wills A. S. Anisotropy-driven spin glass transition in the kagome antiferromagnet hydronium jarosite, (H3O)Fe3(SO4)2(OH)6. J. Phys.: Condens. Matter 2008, 20, 452204. [Google Scholar]
- Shender F.; Cherepanov V. B.; Holdsworth P. C. W.; Berlinsky A. J. Kagomé Antiferromagnet with Defects: Satisfaction, Frustration, and Spin Folding in a Random Spin System. Phys. Rev. Lett. 1993, 70, 3812. 10.1103/PhysRevLett.70.3812. [DOI] [PubMed] [Google Scholar]
- Kawamura H. Chiral ordering in Heisenberg spin glasses in two and three dimensions. Phys. Rev. Lett. 1992, 68, 3785–3788. 10.1103/PhysRevLett.68.3785. [DOI] [PubMed] [Google Scholar]
- Elhajal M.; Canals B.; Lacroix C. Symmetry breaking due to Dzyaloshinsky-Moriya interactions in the kagomé lattice. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 66, 014422. 10.1103/PhysRevB.66.014422. [DOI] [Google Scholar]
- Hudl M.; Mathieu R.; Nordblad P. Tunable exchange bias in dilute magnetic alloys – chiral spin glasses. Sci. Rep. 2016, 6, 19964. 10.1038/srep19964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachman E.; Murphy R. A.; Maksimovic N.; Kealhofer R.; Haley S.; McDonald R. D.; Long J. R.; Analytis J. G. Exchange biased anomalous Hall effect driven by frustration in a magnetic kagome lattice. Nat. Commun. 2020, 11, 560. 10.1038/s41467-020-14326-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.