Effectiveness of face masks in reducing the spread of COVID-19: A model-based analysis

Abstract

Background

The World Health Organization and US Centers for Disease Control and Prevention recommend that both infected and susceptible people wear face masks to protect against COVID-19.

Methods

We develop a dynamic disease model to assess the effectiveness of face masks in reducing the spread of COVID-19, during an initial outbreak and a later resurgence, as a function of mask effectiveness, coverage, intervention timing, and time horizon. We instantiate the model for the COVID-19 outbreak in New York, with sensitivity analyses on key natural history parameters.

Results

During the initial epidemic outbreak, with no social distancing, only 100% coverage of masks with high effectiveness can reduce the effective reproductive number R_e below 1. During a resurgence, with lowered transmission rates due to social distancing measures, masks with medium effectiveness at 80% coverage can reduce R_e below 1, but cannot do so if individuals relax social distancing efforts. Full mask coverage could significantly improve outcomes during a resurgence: with social distancing, masks with at least medium effectiveness could reduce R_e below 1 and avert almost all infections, even with intervention fatigue. For coverage levels below 100%, prioritizing masks that reduce the risk of an infected individual from spreading the infection rather than the risk of a susceptible individual from getting infected yields the greatest benefit.

Limitations

Data regarding COVID-19 transmission are uncertain, and empirical evidence on mask effectiveness is limited. Our analyses assume homogeneous mixing, providing an upper bound on mask effectiveness.

Conclusions

Even moderately effective face masks can play a role in reducing the spread of COVID-19, particularly with full coverage, but should be combined with social distancing measures to reduce R_e below 1.

1. Introduction

Since its recognized emergence in early 2020 in Wuhan, China, COVID-19 has spread rapidly around the globe with more than 135 million confirmed infections and more than 3 million deaths as of April 2021.¹ In the US alone, more than 30 million cases have been confirmed and more than 550,000 deaths have occurred.²

Until widespread vaccination of the public occurs, prevention remains the only way to reduce the spread of the infection. SARS-CoV-2, the virus that causes COVID-19, is believed to spread from person to person primarily through respiratory droplets from coughing or sneezing when individuals are in close contact (within 6 feet of each other).³ Prevention measures include quarantine and self-isolation for individuals with confirmed or possible infection, shelter-in-place restrictions, hygiene measures such as frequent hand washing and cleaning of potentially contaminated surfaces, social distancing, and the wearing of face masks. The US Centers for Disease Control and Prevention (CDC) recommends “wear[ing] cloth face coverings in public settings when around people outside of their household, especially when other social distancing measures are difficult to maintain.”⁴ The World Health Organization similarly recommends the wearing of face masks.⁵

Face masks have been recommended for previous outbreaks of respiratory disease such as the 2003 SARS outbreak and the 2009 H1N1 epidemic.^6,7 Previous modeling studies (e.g.,^8–10) showed that face masks could help reduce the spread of H1N1. Similarly, empirical studies comparing SARS-CoV-2 transmission between populations with and without mandatory mask wearing have concluded that requiring face masks could help mitigate the spread of the virus.^11,12

A number of empirical studies have evaluated the effectiveness of face masks in preventing the transmission of SARS-CoV-2 and influenza-like illnesses. Ranges for mask effectiveness vary widely, even across studies that analyze the same type of mask. A meta-analysis of 39 observational and comparative studies of SARS-CoV-2 estimated that face mask use by susceptible individuals in non-healthcare settings led to a relative infection risk of .56 (95% CI [.40, .79]).¹³ The meta-analysis estimated that N95 masks were more effective than surgical masks, which in turn were more effective than single-layer cloth masks. Data from a cohort study in Beijing, China indicates that face mask use by asymptomatic infected individuals and family member contacts led to a relative SARS-CoV-2 infection risk of .32.¹⁴ A recent randomized controlled trial in Denmark estimated that surgical face mask use led to a relative SARS-CoV-2 infection risk of 0.82 in a setting where other social distancing measures were in effect.¹⁵ A cluster randomized controlled trial found that medical mask use by individuals infected with influenza-like illnesses led to a relative transmission risk of .32 (95% CI [.03, 3.13]).¹⁶ Two other randomized controlled trials investigating the transmission of influenza-like illnesses found that wearing a surgical face mask led to a relative infection risk of .85 and .51.^17,18

Several empirical studies have shown that mask effectiveness is affected by traits such as mask fit, material, and number of layers.^19–21 For example, a study that considered five medical procedure mask modifications including changing the positioning of ear loops and enhancing the mask/face seal found that these procedures increased the fitted filtration efficiency of masks by 60.3%-80.3%.¹⁹

Several studies have used compartmental models to evaluate the impact of masks on SARS-CoV-2 spread. Eikenberry et al.²² developed an SEIR model which they calibrated to New York state and Washington state to assess the impact of masks worn by the general population, considering different mask effectiveness and coverage levels. They estimated that moderately effective masks with 80% coverage could avert up to 45% of deaths over two months. Li et al.²³ analyzed the impact of mask coverage, availability, and aerosol reduction during an initial outbreak and in combination with social distancing, and concluded that mask wearing can potentially decrease the basic reproductive number (R₀) of the epidemic. Ngonghala et al.²⁴ considered combinations of interventions, including the use of face masks in public, social distancing, contact tracing, quarantine, and isolation. Ngonghala et al.²⁵ extended this work to incorporate lockdown measures and found that consistent use of face masks could prevent post-lockdown resurgence of COVID-19. Stutt et al.²⁶ used an epidemic model to show that face masks combined with lockdown periods can significantly decrease the spread of the disease and flatten secondary and tertiary waves of infection.

However, it remains unclear whether the timing of intervention, coverage level, or effectiveness of the mask is most important in slowing the spread of the epidemic, nor how these traits combine with social distancing measures to impact the epidemic’s trajectory. Further, it remains to be explored how short-term effects differ from long-term effects. In this paper, we aim to understand how face masks alone (i.e., without consideration of other interventions such as shelter-in-place) can reduce the spread of the epidemic during an initial outbreak, and then how masks and social distancing measures can synergize to slow the spread of the epidemic during a later resurgence.

To answer these questions, we develop a model to assess the potential effectiveness of face masks in reducing the spread of COVID-19. Since empirical evidence of the effectiveness of masks is highly variable, we assess the impact of masks as a function of how effective they are. Unlike other studies, we distinguish between the effectiveness of masks worn by confirmed and unconfirmed infected individuals. Because the supply of masks with high effectiveness is limited, confirmed infected individuals are assumed to wear the most effective masks, while we vary the effectiveness of masks worn by the remaining population. We instantiate the model for the COVID-19 outbreak in New York state. We show how the impact of masks on infection spread varies as a function of mask effectiveness (reduction in infectivity and susceptibility), coverage (percentage of people wearing masks), timing (when people begin wearing masks), and time horizon (period over which the epidemic is simulated) both during an initial outbreak when no interventions are in place and during a resurgence when social distancing measures are in place. We also perform sensitivity analyses to explore how the findings might change with different values of the disease natural history parameters.

2. Methods

2.1. Epidemic Model

We develop a dynamic compartmental model of SARS-CoV-2 transmission and progression (Figure 1) based on a modified SEIR model.²⁷ Dynamic compartmental models are based on a system of ordinary differential equations that separate the population into compartments based on an individual’s state of infection. Such models are widely used to study the dynamics of infectious diseases and assess the impact of interventions on their trajectory.

Figure 1:

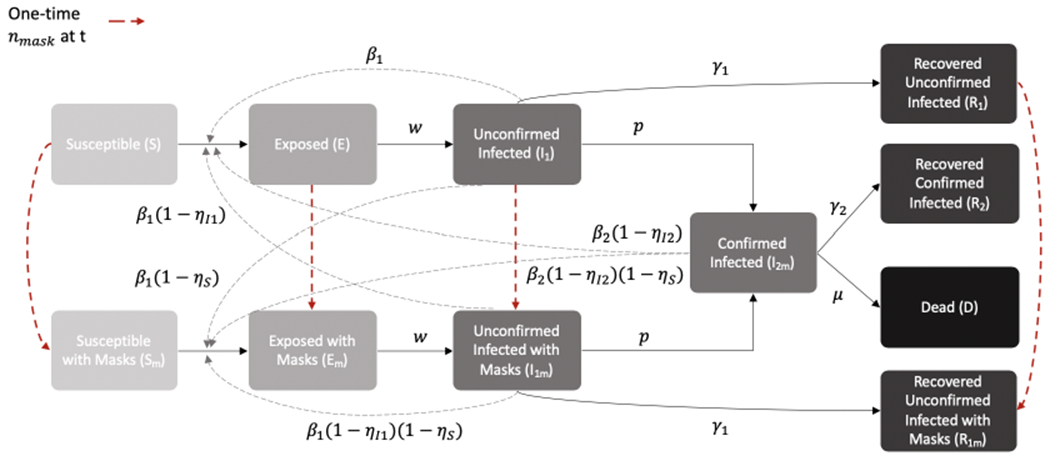
Dynamic compartmental model of the spread of SARS-CoV-2

In our model, the compartments include individuals who are susceptible (S), exposed (E), unconfirmed infected (I₁), recovered from unconfirmed infected (R₁), confirmed infected (I_2m), recovered from confirmed infected (R₂), and dead (D). We assume that exposed individuals are infected but not infectious; unconfirmed infected individuals are infectious but not confirmed to be infected; and confirmed infected individuals are those who have been identified by testing. We assume that some individuals in the unconfirmed infected state do not have enough symptoms to warrant testing, and that individuals with enough symptoms to warrant testing will be identified at rate p. We separate the confirmed and unconfirmed cases because a large proportion of COVID-19 cases are undetected and play a significant part in transmission.^28–30 We assume that all people identified as infected wear masks with high effectiveness. Additional states reflect individuals who are wearing cloth face masks: susceptible with mask (S_m), exposed with mask (E_m), unconfirmed infected with mask (I_1m), and recovered unconfirmed infected with mask (R_1m).

In the model, a susceptible person who becomes infected moves to an exposed compartment. Infection progresses to unconfirmed infection (at rate w), and in some cases to confirmed infection (at rate p). Individuals can recover from any of the infected states (at rates γ₁ or γ₂), and can die only from the confirmed infected state (at rate μ). Because we consider a relatively limited period of time in our analyses, we do not model births into the population nor deaths from non-COVID-related causes.

The compartmental model is governed by the following differential equations:

$$\begin{gathered} \frac{\mathrm{d}S}{\mathrm{d}t}=-S\left[{\beta }_1(I_1+(1-{\eta }_{I1})I_{1m})+{\beta }_2(1-{\eta }_{I2})I_{2m}\right] \\ \frac{\mathrm{d}{S}_m}{\mathrm{d}t}=-S_m(1-{\eta }_S)\left[{\beta }_1(I_1+(1-{\eta }_{I1})I_{1m})+{\beta }_2(1-{\eta }_{I2})I_{2m}\right] \\ \frac{\mathrm{d}E}{\mathrm{d}t}=S\left[{\beta }_1(I_1+(1-{\eta }_{I1})I_{1m})+{\beta }_2(1-{\eta }_{I2})I_{2m}\right]-wE \\ \frac{\mathrm{d}{E}_m}{\mathrm{d}t}=S_m(1-{\eta }_S)\left[{\beta }_1(I_1+(1-{\eta }_{I1})I_{1m})+{\beta }_2(1-{\eta }_{I2})I_{2m}\right]-w{E}_m \\ \frac{\mathrm{d}{I}_1}{\mathrm{d}t}=wE-I_1({\gamma }_1+p) \\ \frac{\mathrm{d}{I}_{1m}}{\mathrm{d}t}=w{E}_m-I_{1m}({\gamma }_1+p) \\ \frac{\mathrm{d}{I}_{2m}}{\mathrm{d}t}=p(I_1+I_{1m})-I_{2m}({\gamma }_2+\mu ) \\ \frac{\mathrm{d}{R}_1}{\mathrm{d}t}={\gamma }_1{I}_1 \\ \frac{\mathrm{d}{R}_{1m}}{\mathrm{d}t}={\gamma }_1{I}_{1m} \\ \frac{\mathrm{d}{R}_2}{\mathrm{d}t}={\gamma }_2{I}_{2m} \\ \frac{\mathrm{d}D}{\mathrm{d}t}=\mu I_{2m} \end{gathered}$$

In the above equations, β₁ is the transmission rate for unconfirmed infected individuals and β₂ is the transmission rate for confirmed infected individuals. Masks decrease the risk of a susceptible individual from getting infected by η_S (which we refer to as the decrease in susceptibility) and decrease the risk of an infected individual from spreading the infection by η_I1 and η_I2 for unconfirmed and confirmed cases, respectively (which we refer to as the decrease in infectivity).

We assume that at time t, a fixed percentage n_mask of susceptible (S), exposed (E), unconfirmed infected (I₁), and recovered unconfirmed infected individuals (R₁) begin to wear masks. This fixed percentage is applied to all four groups because it is impossible to distinguish between these cohorts without widespread testing. Once an individual begins wearing a mask, we assume the person wears a mask until they recover (if identified as infected) or die.

2.2. Reproductive Numbers

The effective reproductive number R_e for an epidemic model (sometimes referred to as the controlled reproduction number³¹) is the average number of secondary infections per infected individual in a population that includes both susceptible and non-susceptible individuals. When R_e is above 1, an epidemic will spread exponentially; when R_e is below 1, the number of new cases will decline and the epidemic will die out. The basic reproductive number, R₀, is the average number of secondary infections per infected individual in a fully susceptible population.

We derive R_e for our model using the next-generation method^32,33 (details in Supplement A). We obtain

$$R_e=\frac{S\left({\beta }_1({\gamma }_2+\mu )+{\beta }_2(1-{\eta }_{I2})p\right)+S_m(1-{\eta }_S)\left({\beta }_1(1-{\eta }_{I1})({\gamma }_2+\mu )+{\beta }_2(1-{\eta }_{I2})p\right)}{({\gamma }_1+p)({\gamma }_2+\mu )}$$

At the onset of the epidemic, S = 1 and, assuming no individuals wear masks, we have S_m = 0 and η_I2 = η_I1 = η_S = 0. Substituting these values into the expression for R_e we obtain

$$\begin{gathered} R_0=\frac{1}{{\gamma }_1+p}({\beta }_1+p\frac{{\beta }_2}{{\gamma }_2+\mu }) \\ =\frac{{\beta }_1}{{\gamma }_1+p}+\frac{p}{{\gamma }_1+p}(\frac{{\beta }_2}{{\gamma }_2+\mu }). \end{gathered}$$

The above expression is very interpretable. The average unconfirmed infectious period is $\frac{1}{{\gamma }_1+p}$ , and the average confirmed infectious period is $\frac{1}{{\gamma }_2+\mu }$. Therefore, the number of secondary infections from an unconfirmed infected individual is $\frac{{\beta }_1}{{\gamma }_1+p}$, and the number of secondary infections from a confirmed infected individual is $\frac{{\beta }_2}{{\gamma }_2+\mu }$. Finally, noticing that the proportion of unconfirmed infected individuals who become confirmed infected is $\frac{p}{{\gamma }_1+p}$ yields the basic reproductive number R₀.

2.3. Model Instantiation and Calibration

We instantiate the model using data for New York state before shelter in place. Although the situation in New York state has greatly improved, New York state before shelter in place provides a good example of how COVID-19 can spread without widespread non-pharmaceutical interventions. Using the estimates based on New York state, we assess the impact of masks during an initial outbreak without other interventions. We obtain values for model parameters from the literature and public sources (Table 1). Details of parameter value derivations from the cited sources are contained in Supplement B. We use data that includes confirmed cases and deaths by day for New York state, which are released daily by the New York Times and accumulated on a Github account.³⁴

Table 1:

Values and sources for model parameters

Parameter	Description	Value	Source
w	Daily rate of progression from exposed to infected	0.20	35–37
d 1	Average duration of unconfirmed infection (days)	6	35,38
d 2	Average duration of confirmed infection (days)	8	39,40
f 1	Fraction of infections that remain unconfirmed	0.8	35,40
f 2	Fraction of infections that are confirmed	0.2	35, 40
ξ	Infected fatality ratio	0.014	41
γ 1	Daily rate at which individuals with unconfirmed infection recover and become immune	0.133	Calculated
γ 2	Daily rate at which individuals with confirmed infection recover and become immune	0.116	Calculated
p	Daily rate at which unconfirmed cases progress to confirmed	0.033	Calculated
μ	Daily death rate for individuals with confirmed infection	0.0090	Calculated
ηS	Decrease in susceptibility due to masks	0.2 - 0.6	13, 15
η I1	Decrease in infectivity due to masks for unconfirmed infected individuals	0.3 - 0.7	14, 16–18
η I2	Decrease in infectivity due to masks for confirmed infected individuals	0.70	14, 16

We compute the transition rates as follows (details in Supplement C):

$$\begin{gathered} {\gamma }_1=\frac{f_1}{d_1} \\ p=\frac{1-f_1}{d_1} \\ \mu =\frac{1}{d_2}\times \frac{\xi }{f_2} \\ {\gamma }_2=\frac{1}{d_2}-\mu \end{gathered}$$

We determine values for the transmission rate parameters β₁ and β₂ and the initial number of infected confirmed individuals, I_2m(0), via model calibration assuming no individuals wear masks and keeping all other parameter values as shown in Table 1. We assume that asymptomatic individuals are less infectious than symptomatic individuals, and thus assume that β₁ < β₂ because confirmed infected individuals are more likely to have symptoms and be tested. As there is evidence that the total number of cases could be many times higher than the number of confirmed cases,^28,42 we do not directly calibrate to the number of confirmed cases but instead calibrate to reported deaths. Specifically, we calibrate to the number of new daily deaths in New York state over the period March 1 - April 4, 2020. We calibrate to daily deaths only up until April 4th, since the New York state Pause Program began and all non-essential statewide businesses closed on March 22nd,⁴³ and we want to capture the trend of the epidemic before any other interventions took place. We calibrate to a 7-day rolling average of reported deaths (Supplemental Figure E.1a) and compare our model projections to multiples of the 7-day rolling average of new confirmed cases (Supplemental Figure E.1b).

We use Latin Hypercube Sampling for calibration, uniformly sampling 50,000 times from a range of values for each parameter. ⁴⁴ We measure goodness of fit using the sum of squared errors. The calibrated parameter values are:

$$\begin{gathered} {\beta }_1=0.60 \\ {\beta }_2=0.67 \\ {I}_{2m}(0)=1.81\times {10}^{-5} \end{gathered}$$

The resulting R₀ value is 4.67, which is consistent with other sources (e.g.,^45–47) that aim to estimate R₀ for the initial outbreak taking into account not only confirmed cases but also extrapolating to unconfirmed cases given various assumptions.

Figure 2 compares the calibrated model’s output to the New York state data on deaths and multiples of confirmed cases. The model output closely matches the calibration target of reported deaths (Figure 2a). Figure 2b shows the model’s projected total number of infected individuals compared to 5 times, 10 times, and 20 times that of the daily confirmed cases in New York state. We initiated the model with 5 times more total cases than confirmed cases. Because there is a lag in the number of confirmed cases, the ratio between the total number of cases and the number of confirmed cases changes over time, which is why we initially observe a higher ratio for the first few weeks of the epidemic, before the ratio decreases to 5.

Figure 2:

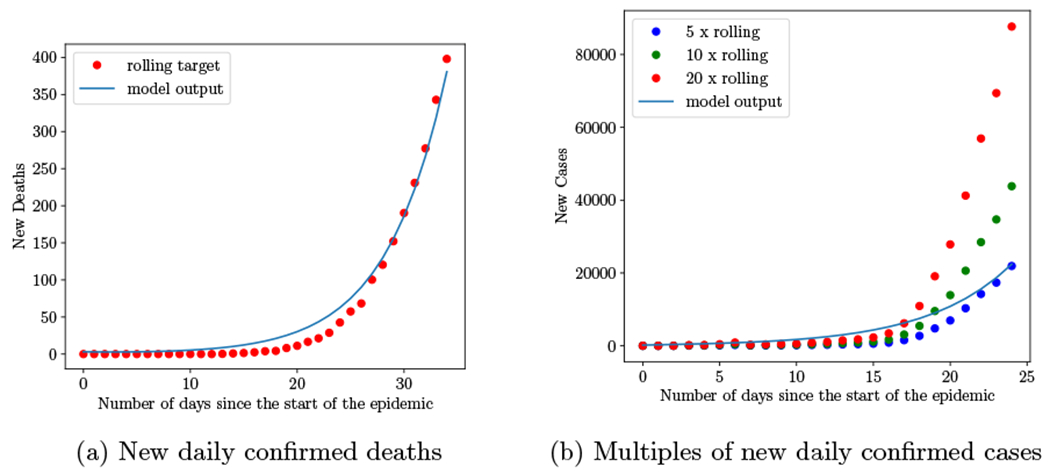
Calibrated model’s daily number of deaths and total cases (confirmed and unconfirmed) compared to reported values (7-day rolling averages) for New York state.

Because there is uncertainty regarding COVID-19 natural history, we vary the parameters with the greatest uncertainty reported in the literature and consider their lower and upper bounds (Supplemental Table D.1), creating six one-way sensitivity analyses. For each case, we recalibrate the model to New York state, as done for our base case.

Ranges cited in literature for the effectiveness of masks vary greatly and there have been few randomized controlled trials evaluating the effectiveness of masks in preventing SARS-CoV-2 transmission. Therefore, we consider three levels of mask effectiveness, reflecting a low, medium and high range of mask effectiveness found in the empirical studies. We derive the range of reduction in susceptibility η_Sto be 0.2 – 0.6 from a meta-analysis and a randomized controlled trial which found, respectively, that face mask use by susceptible individuals led to a relative infection risk of of 0.56 (95% CI [0.40, 0.79]) and 0.82.^13,15 From randomized controlled trials and cohort studies,^14,16–18 we estimate the range of reduction in infectivity for unconfirmed infected individuals η_I1 to be 0.15 – 0.68. Since the reduction in infectivity is greater than the reduction in susceptibility,^{8, 48} we estimate the range of η_I1 to be 0.3 – 0.7. Lastly, we take the upper bound of this range for the reduction in infectivity for confirmed infected individuals η_I2. Combining these estimates, we assume η_S = 0.6, η_I1 = 0.7 for masks with high effectiveness; η_S = 0.4, η_I1 = 0.5 for masks with intermediate effectiveness; and η_S = 0.2., η_I1 = 0.3, for masks with low effectiveness.

3. Results

We consider the effect of masks during the initial epidemic outbreak when no interventions are in place (Section 3.1) and then during a resurgence when social distancing measures are in place (Section 3.2). We assess the fraction of infections averted and the impact on the effective reproductive number, R_e.

3.1. Analyses: Initial Outbreak

If masks are only worn by confirmed infected individuals and no other interventions are introduced during the initial outbreak, the model projects that 97.7% of the population will become infected within 100 days (Figure 3). These results are similar to those of Stutt et al.²⁶ who estimated that nearly the entire population would become infected by day 100 without any interventions.

Figure 3:

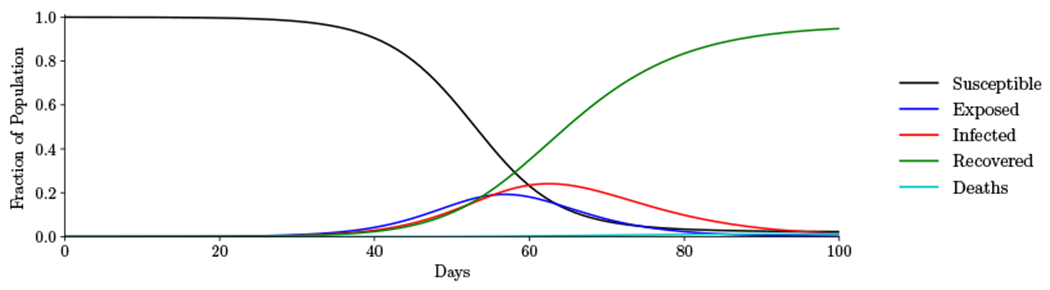
Initial outbreak. Trajectory of the epidemic assuming only confirmed infected individuals wear masks.

As Figure 3 shows, mask wearing by only confirmed infected individuals is insufficient to stop the initial outbreak. This is due to the spread of the infection by individuals with unconfirmed infection. We now consider the impact of masks worn by susceptible and unconfirmed infected individuals.

3.1.1. Infections Averted

Figure 4 shows the fraction of infections averted as a function of mask effectiveness in reducing infectivity and susceptibility, coverage level (n_mask, 0% to 100% in increments of 10%), and number of days until people begin wearing masks (0, 10, 20, …, 50 days after (1.81 × 10⁻³)% of the population is confirmed infected), over different time horizons (T = 100, 365 days). Below we describe key results as they relate to the characteristics we varied.

Figure 4:

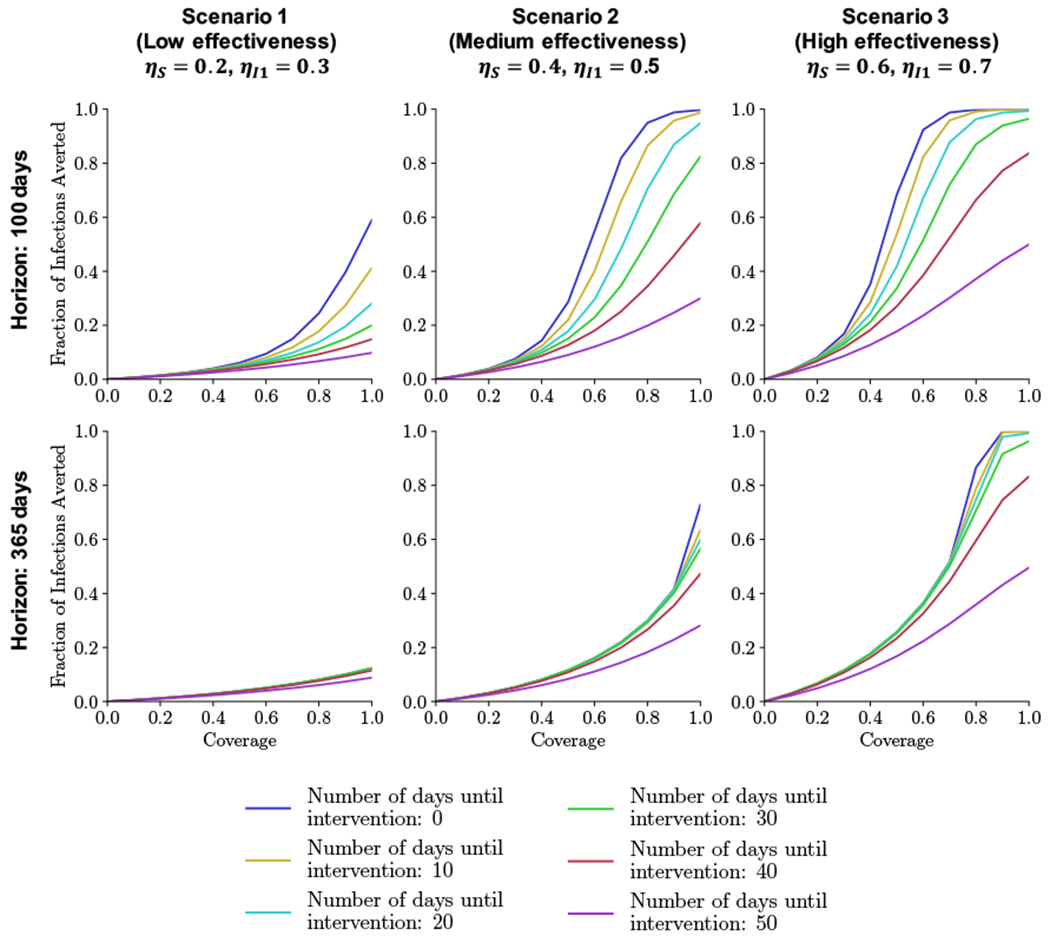
Initial outbreak. Fraction of infections averted over two time horizons (100 and 365 days) as a function of coverage (n_mask = 0% to 100%) and number of days until susceptible and unconfirmed people begin wearing masks (0, 10, …, 50 days) for different levels of mask effectiveness (Scenarios 1-3).

Mask Effectiveness

Comparing across scenarios in Figure 4, it is evident that mask effectiveness significantly affects transmission. For example, if masks are worn beginning at the onset of the epidemic with 100% coverage, then 12.4% of infections are averted over one year if the masks have low effectiveness (Scenario 1 in Figure 4), increasing to 72.8% if the masks have medium effectiveness (Scenario 2) and to 100% if the masks have high effectiveness (Scenario 3). With 50% coverage, these fractions are 3.9%, 11.6%, and 25.7%, respectively. Similar trends hold for a 100-day time horizon.

The difference in the fraction of infections averted is smaller across mask effectiveness levels as the time of intervention is delayed. For example, if masks are worn beginning on day 50 after the start of the epidemic with 100% coverage, then 8.8% of infections are averted over one year if the masks have low effectiveness, increasing to 28.1% if the masks have medium effectiveness and to 49.5% if the masks have high effectiveness. The difference in the fraction of infections averted is smaller when there is only 50% coverage; then the fractions are 3.1%, 8.3%, and 16.7%, respectively.

Coverage Level

Increasing returns generally occur in the fraction of infections averted as the coverage level increases. For example, for masks with high effectiveness and immediate intervention, increasing coverage from 60% to 70% and then from 70% to 80% increases the fraction of infections averted by 42% and 68%, respectively, over one year. One exception is for a short time horizon (100 days) and masks with higher effectiveness (Scenarios 2 and 3) introduced early: in this case, decreasing returns in averted infections occur for high coverage levels. This happens because the early interventions occur when the number of infections is still very low. If the intervention is later, the epidemic is already near its peak at the time of intervention and masks are not sufficient to flatten the infection curve.

Intervention Timing

As one would expect, the potential to reduce infections decreases the later masks are introduced. For example, for masks with high effectiveness and 100% coverage, 100% of infections are averted over one year with masks beginning on day 0, decreasing to 96.3% if masks begin on day 30, and decreasing to 49.5% if masks begin on day 50. Similarly, for masks with low effectiveness, these percentages measured over a 100-day time horizon are 59.0%, 20.0%, and 9.8%, respectively.

Time Horizon

Figure 4 shows that when effects are measured over shorter time horizons, masks beginning on day 0 are best, whereas for longer time horizons, effects are similar for masks beginning on any day up to day 30.

Supplemental Figure E.2 shows infections averted for each scenario for different time horizons. The pattern in the beginning of the epidemic is similar for all three levels of mask effectiveness: an initial peak in infections averted occurs between days 55 and 65, when the incidence of cases without any interventions reaches its peak; with intervention, the peak is delayed. With full coverage and immediate intervention, masks with high and medium effectiveness can both initially avert up to 99% of infections; however, this value drops after 150 days for masks with medium effectiveness, while masks with high effectiveness can continue to avert nearly all infections thereafter because R_e is below 1. This finding demonstrates the need to consider both the time horizon and level of mask effectiveness when assessing interventions.

Combined Findings

Figure 5 shows the proportion of the population that has been infected as a function of the time horizon for different coverage levels and mask effectiveness. As can be seen in the figure, higher coverage levels and mask effectiveness delay and reduce the infection peak.

Figure 5:

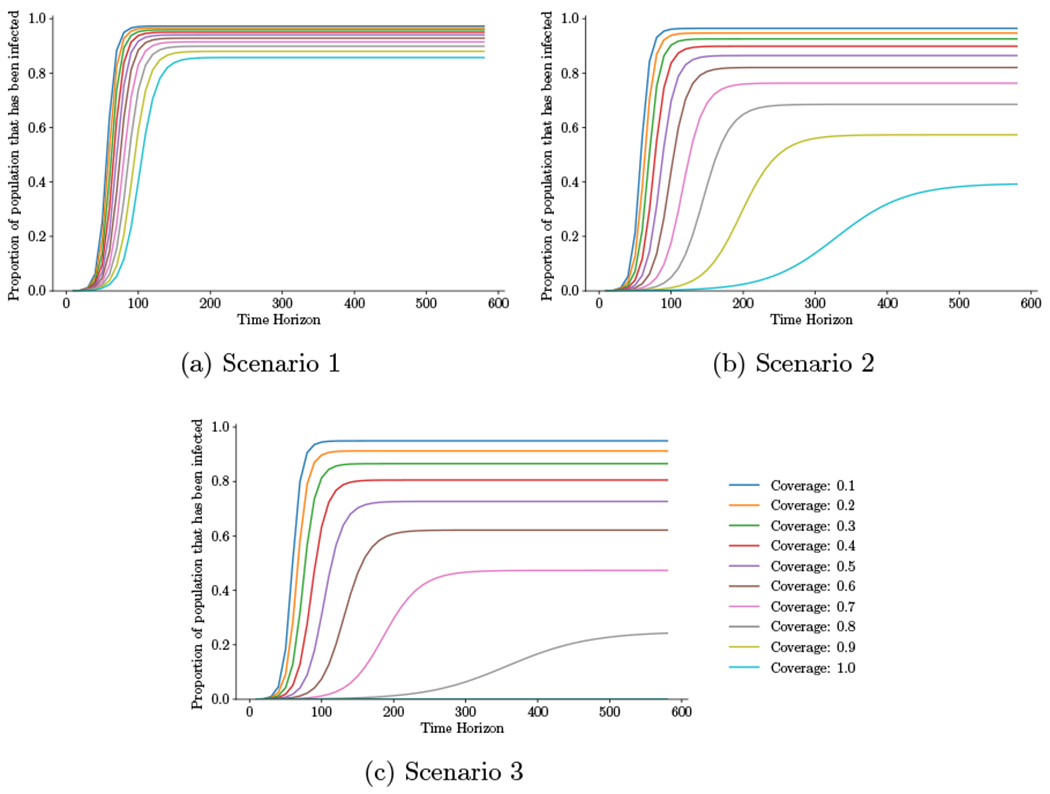
Initial outbreak. Proportion of the population that has been infected for different time horizons (ranging from 10 to 600 days in 10 day increments) as a function of coverage level, assuming immediate intervention. Scenario 1: η_S = 0.2, η_I1 = 0.3; Scenario 2: η_S = 0.4, η_I1 = 0.5; Scenario 3: η_S = 0.6, η_I1=0.7, where η_S = reduction in susceptibility for an uninfected person wearing a mask, η_I1 = reduction in infectivity for an unconfirmed infected person wearing a mask.

Combining the findings from the four characteristics of the mask interventions, with the exception of the most extreme interventions (masks with high effectiveness with at least 90% coverage and intervention within 10 days of the outbreak), we find that masks alone are insufficient to end the spread of the epidemic, and further interventions (such as social distancing, isolation, and quarantine) should be implemented quickly during the initial outbreak. However, if mask interventions are implemented early with high coverage and at least medium effectiveness, they can avert significant numbers of infections and flatten the infection curve, reducing the burden on healthcare systems⁴⁹ and giving valuable time for policymakers to implement future interventions.

When we compare the fraction of infections averted across the six cases with different natural history parameters, varying mask effectiveness, coverage level and intervention timing, results are qualitatively unchanged from the base case (Supplemental Table D.3). As in the base case, mask effectiveness greatly influences the fraction of infections averted, with the difference in infections averted across mask effectiveness levels decreasing as coverage decreases or as intervention start is delayed; increasing returns occur in infections averted as the coverage level increases; and fewer infections can be averted across all levels of mask effectiveness as intervention timing is delayed.

3.1.2. Threshold Analysis of R_e

We perform a threshold analysis of the effective reproductive number R_e (details in Supplement D.1.1). We find that only 100% coverage of masks with high effectiveness can reduce R_e below 1. This trend holds across the natural history sensitivity analyses (Supplemental Table D.2). If mask coverage is only 80%, then masks with higher effectiveness are necessary to decrease R_e below 1 compared to 100% coverage. Additionally, we find that prioritizing masks that reduce the risk of an infected individual from spreading the infection rather than the risk of a susceptible individual from getting infected yields the greatest benefit.

3.2. Analyses: Resurgence

During the first months of the COVID-19 outbreak in the US, interventions such as shelter-in-place orders were imposed to curb the epidemic. These measures prevented most of the population from becoming infected in the first 60 days (Figure 3). However, many of these orders have been lifted across the US as states loosen restrictions and allow some businesses to reopen.^50,51 With restrictions lifted, a resurgence of COVID-19 has occurred in many states.^52,53

Using our model, we estimate the effectiveness of masks during a resurgence. To model other measures that remain in place to prevent the spread of the epidemic (e.g., frequent hand washing, social distancing), we assume the transmission rates are halved compared to the initial outbreak: β₁ = 0.30, β₂ = 0.34.^54–56 We initialize the model with an estimate of the proportion of individuals in each compartment on June 15 in New York state, the date on which the first region moved to Phase 3.⁵⁷ Since the transmission rates are halved and the starting susceptible population is lower (S(0) + S_m(0) = 0.90 compared to 1 in the initial outbreak), we also have a lower reproductive number: R_e = 2.10 compared to R₀ = 4.67 in the initial outbreak.

Since the effective reproductive number R_e is halved, we consider two longer time horizons, 150 and 500 days. Less than 2% of the population will be newly infected after 150 days when only confirmed infected individuals wear masks because the initial number of infected individuals is higher, and only 65% of the population becomes infected during the resurgence. After 500 days, the percentage of the population that will be newly infected is at most 0.7% across all mask intervention strategies.

3.2.1. Infections Averted

Figure 6 shows the fraction of infections averted for varying coverage levels and timing over the two time horizons (T = 150, 500 days). We find that masks are generally much more effective in slowing the spread of the epidemic during resurgence because the R_e at the time of resurgence is much lower, as noted above. Moreover, the fraction of infections averted is close to 1 for more intervention strategies.

Figure 6:

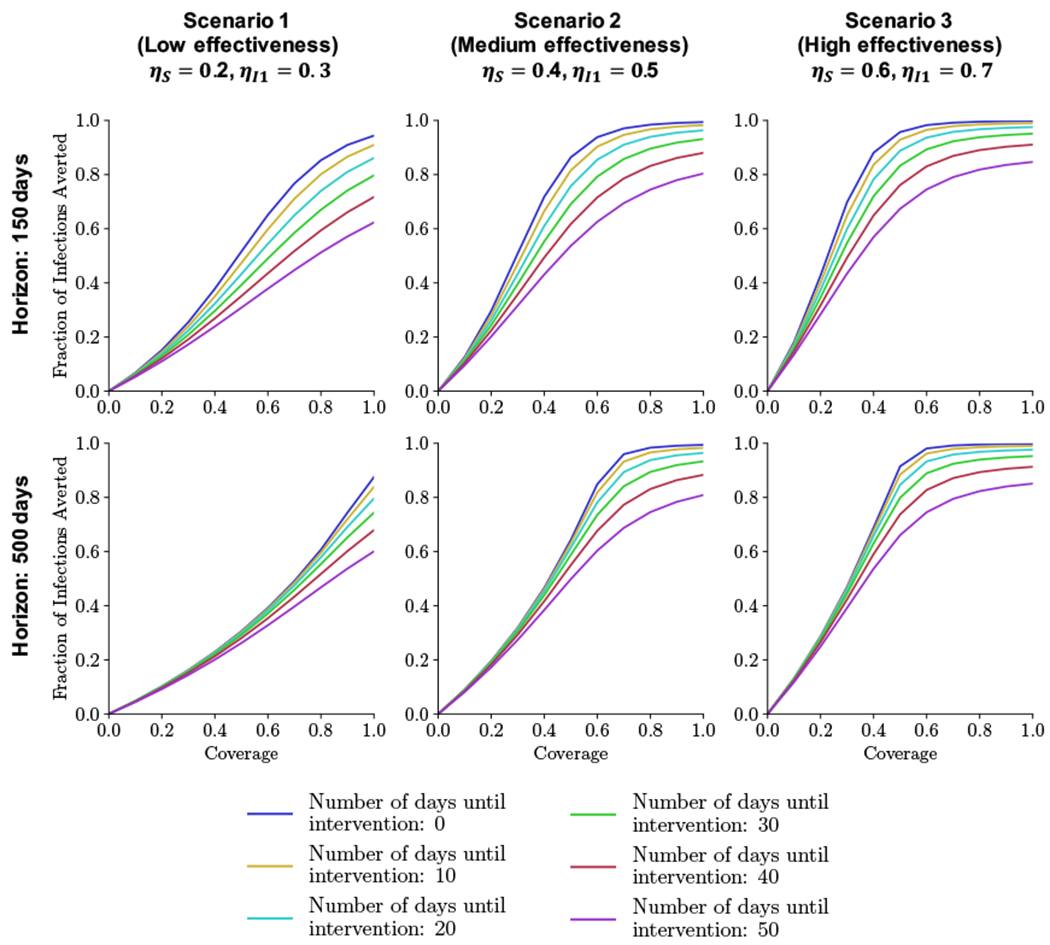
Resurgence. Fraction of infections averted across two time horizons (150, 500 days) and for three mask effectiveness scenarios as a function of coverage and number of days until people begin wearing masks.

The fraction of infections averted is less sensitive to coverage, timing, mask effectiveness, and time horizon than during the initial outbreak. For example, for masks with high effectiveness and intervention within 10 days, coverage levels between 60% and 100% result in similar fractions of infections averted (above 95%) over 500 days; during the initial outbreak, 60% coverage can only avert 36% of infections compared to 99.9% for 100% coverage over 365 days. Similarly, later interventions can avert a larger fraction of infections compared to the initial outbreak. For instance, an intervention 50 days after the start of the resurgence using masks with medium effectiveness at 100% coverage averts 81% of infections over 500 days (compared to only 28% during the initial outbreak over 365 days). Even masks with low effectiveness if implemented early can avert 80% of infections over 500 days, compared to only 12% of infections during the initial outbreak over 365 days. Finally, regardless of time horizon, masks with medium effectiveness, early intervention (within 30 days), and high coverage (above 70%) can avert more than 80% of infections.

3.2.2. Threshold Analysis on R_e

We perform a threshold analysis on R_e during resurgence (details in Supplement D.1.2). We find that, unlike in the initial outbreak, masks with high and medium effectiveness at 80% coverage can decrease R_e below 1. We further find synergies between social distancing and masks by comparing the trajectory of the epidemic under three scenarios (Supplemental Figure D.3): only social distancing; only masks with low effectiveness, immediate intervention, and 100% coverage; both intervention strategies combined.

3.2.3. Effects of Intervention Fatigue

With long-term social distancing measures in place, individuals may begin to develop so-called “intervention fatigue” and follow safety guidelines less stringently.^58–60 For example, suppose that individuals relax social distancing efforts such that the transmission rate is reduced by only 25% compared to the initial outbreak.⁵⁶ Assuming immediate intervention, introduction of masks with medium effectiveness at 80% or 100% coverage leads to an R_e of 1.22 and 0.86, respectively (Figure 7). In this case, masks with medium effectiveness at 80% coverage are no longer sufficient to reduce R_e below 1. These trends generally hold across the natural history sensitivity analyses as well (Supplemental Table D.2).

Figure 7:

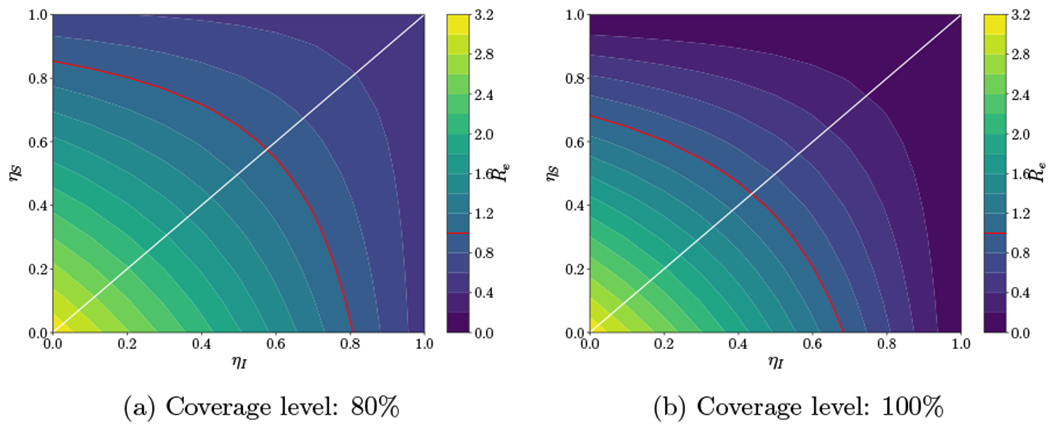
Resurgence. Sensitivity analysis for R_e varying η_S and η_I with a red contour line at R_e = 1 and a white line at which η_S = η_I assuming two coverage levels (80% and 100%) and a 25% reduction in the transmission rates (β₁, β₂) due to social distancing.

Suppose that in addition individuals do not wear masks properly (e.g., only covering their mouth with the mask). If the effectiveness of masks decreases by 25% compared to masks with medium effectiveness (η_S = 0.3, η_I = 0.375), then even immediate intervention with full coverage cannot reduce R_e below 1 when social distancing measures are relaxed. Therefore, if masks are to be effective in reducing the spread of the epidemic, it is important that individuals wear properly and adhere to social distancing measures.

3.2.4. Mandatory Masks

A number of countries around the world have mandated masks for all individuals in public enclosed spaces.⁶¹ In the US, approximately two-thirds of states have issued mask requirements, and there have been increasing calls for a federal mask mandate covering all states (e.g.,⁶²). Recent studies have shown that mandatory mask laws increase mask compliance.^63,64 For example, a study in Wisconsin found that 96% of the population wore a mask once a state mandate was put in place.⁶⁴

To estimate the full potential of masks in curbing the epidemic, we model mandatory masks as full coverage with immediate intervention, assuming that confirmed infected individuals wear masks with high effectiveness and that social distancing reduces the transmission rate during a resurgence by 50% compared to the initial outbreak. Full coverage of masks with low, medium, and high effectiveness would avert 87.5%, 99.4%, and 99.8% of infections, respectively, over 500 days (Figure 6) and would decrease R_e to 1.02, 0.57, and 0.25, respectively. In this case, masks with full coverage with at least medium effectiveness can decrease R_e below 1 and avert almost all infections.

If individuals relax social distancing efforts such that the transmission rate during a resurgence is only 25% lower than in the initial outbreak, then the fraction of infections averted with medium effectiveness masks over 500 days is 98.1% and 66.0% and R_e is 0.86 and 1.22, respectively, for masks with 100% and 80% coverage. Therefore, even with relaxed social distancing measures during a resurgence, full coverage of masks with medium effectiveness can decrease R_e below 1 and avert almost all infections.

3.2.5. More Effective Social Distancing Measures

There is limited available data on the effectiveness of social distancing measures, and existing data shows a wide range of observed behavior over the course of the epidemic.⁵⁴ Therefore, it is possible that more effective social distancing measures could be put in place in response to a resurgence. We consider the case of such measures leading to a 75% or 90% reduction in transmission.⁵⁶ We find that with a reduction in transmission of 75% or higher, all masks with at least 80% coverage can reduce R_e below 1 (Supplemental Table D.4).

4. Discussion

Our analyses highlight the role that masks can play in reducing the spread of COVID-19 and reveal synergies between social distancing measures and masks. We find that without social distancing measures, masks are able to avert infections and flatten the infection curve, but only masks with high effectiveness and full coverage can reduce R_e below 1. We also evaluate the impact of masks during a resurgence, assuming the combined effect of all social distancing interventions at that time could range from 25% to 90%, reflecting the wide range of behavior that has been observed over the course of the epidemic. Social distancing behaviors have fluctuated widely with, for example, significant spikes in new cases after the holidays and significant spikes in new cases emerging in different regions at different times. We find that during a resurgence, when there is a lowered transmission rate due to existing social distancing measures, masks with at least medium effectiveness at 80% coverage can reduce R_e below 1, whereas masks with low effectiveness cannot do so. However, if individuals relax social distancing efforts during a resurgence, masks with medium effectiveness at 80% coverage cannot reduce R_e below 1. Masks with full coverage could significantly improve outcomes during a resurgence: with social distancing, masks with at least medium effectiveness could reduce R_e below 1, even with intervention fatigue. We also find that prioritizing masks with higher reduced infectivity rather than masks that provide greater reductions in susceptibility yields the greatest benefits.

Our compartmental model provides a general theoretical framework for understanding how key characteristics of masks influence their effectiveness in mitigating the spread of COVID-19. We assume low, medium, and high values for mask effectiveness based on ranges reported in the literature. A recent Danish randomized controlled trial estimated that surgical face mask use led to a relative risk of 0.82.¹⁵ This estimated effectiveness aligns closest with our parameters for masks with low effectiveness, in which case our results emphasize the importance of sustained social distancing. However, randomized controlled trials evaluating the effectiveness of various masks in reducing the transmission of SARS-CoV-2 in the general community are lacking. Furthermore, empirical evidence on the effectiveness of different types of face masks to prevent SARS-CoV-2 spread (e.g., N95, KN95, surgical, and various types of cloth masks) is still emerging, and estimates of mask effectiveness in preventing transmission vary widely, even for the same type of mask. Many observational studies focus on mask use in Asia, which may not be relevant for Western societies, and only evaluate mask use in controlled environments. Moreover, the majority of empirical studies evaluate mask use only over a short period of time; however, prolonged mask use could lead to lower compliance by the general population and lead to lower mask effectiveness. We explore such a scenario in our intervention fatigue analysis. Further knowledge of the effectiveness of different types of masks can be used to refine policy recommendations.

While we model mandatory masks as full coverage, compliance might be lower in practice and specific coverage levels may be difficult to achieve. In many states in the US, masks have been met with resistance. For example in Florida, masks are recommended but not required in all counties, and even in counties where there are mask requirements, the local authorities may not assess fines in cases of noncompliance.⁶⁵ Policymakers will need to consider compliance levels that can be achieved in practice when considering the potential impact of mask policies.

Our analysis has several additional limitations. Data on COVID-19 is uncertain and evolving. For example, deaths in the beginning of the epidemic may have been underreported.⁶⁶ In that case, our analysis would underestimate the transmission rates, and therefore overestimate the impact of masks. However, in our sensitivity analyses the trends we see when varying effectiveness, coverage, timing of intervention and time horizon are robust to changes in parameter values. We assume that individuals have no natural immunity to COVID-19, and that individuals who recover after being infected become immune. Uncertainty remains about the extent to which an individual is immune to COVID-19 after contracting it;⁶⁷ a study of SARS found only temporary immunity lasting three years.⁶⁸ All time horizons considered in this paper are less than three years, so if immunity for COVID-19 is similar to that for SARS, our results still hold. Our model assumes homogeneous mixing, and thus our results provide an upper bound on the effectiveness of masks.

Compartmental models of the type we have used implicitly assume exponentially distributed time spent in disease stages.²⁷ This assumption may not be completely realistic as it implies that a patient is more likely to die from COVID-19 on the first day after being confirmed infected than on any subsequent day. However, use of such models is standard practice in modeling epidemics at the population level and provides an accessible framework with a minimal number of parameters for generating insights into the course of an epidemic.^{22,24–27,69–71} A more sophisticated agent-based microsimulation model could capture different distributions for the time spent in disease states and illuminate the effects of these simplifying assumptions in compartmental models, assuming sufficient data are available. However, use of such a model would be unlikely to change our basic conclusions regarding mask effectiveness and social distancing. Our model also does not incorporate age stratification. This would be valuable future work given the changing distribution of new COVID-19 cases across age groups.

Our analysis assumes a constant rate of testing, p. In many US states, testing of the population has increased (e.g.,^72,73). Therefore, the proportion of the infected population that is confirmed is likely larger than in the earlier stages of the epidemic, although it is likely that a large part of the infected population has not been identified.^53,74 In one-way sensitivity analysis we considered a lower value for f₁, the fraction of infections that are unconfirmed, and thus a higher value for p, and found that results were qualitatively unchanged. An area for future work would be to model a resurgence with a higher rate of testing than in the initial outbreak. With a higher testing rate, more individuals will move into the confirmed infected state and more individuals will thus potentially wear masks with the highest effectiveness, leading to lower transmission. In this case, a lower level of mask coverage than we estimated could reduce R_e below 1. Modeling increased testing would require data on the distribution of asymptomatic, mild, and severe cases among tested individuals (in order to calculate the duration of the confirmed infected state and recovery and death rates), as well as an estimate of the fraction of cases that are still unconfirmed.

As of April 2021, more than 60,000 new COVID-19 cases occur in the US each day, and it is becoming clear that slowing the spread of the disease will require significant time and effort. Our analysis suggests that, until widespread vaccination of the public occurs, even moderately effective face masks can play a role in reducing the spread of COVID-19, particularly with full coverage, but should be combined with social distancing measures to reduce the effective reproductive number R_e below 1.

Highlights.

• We develop a model to assess the effectiveness of face masks in reducing the spread of COVID-19.

• For coverage levels below 100%, prioritizing masks that reduce the risk of an infected individual from spreading the infection rather than the risk of a susceptible individual from getting infected yields the greatest benefit.

• Even moderately effective face masks can play a role in reducing the spread of COVID-19, particularly with full coverage, but should be combined with social distancing measures to reduce the effective reproductive number below 1.