Abstract
Mortality inequalities remain substantial in many countries, and large shocks such as pandemics could amplify them further. The unequal distribution of COVID-19 confirmed cases suggests that this is the case. Yet, evidence on the causal effect of the epidemic on mortality inequalities remains scarce. In this paper, we exploit exhaustive municipality-level data in France, one of the most severely hit country in the world, to identify a negative relationship between income and excess mortality within urban areas, that persists over COVID-19 waves. Over the year 2020, the poorest municipalities experienced a 30% higher increase in excess mortality. Our analyses can rule out an independent contribution of lockdown policies to this heterogeneous impact. Finally, we find evidence that both labor-market exposure and housing conditions are major determinants of the epidemic-induced effects of COVID-19 on mortality inequalities, but that their respective role depends on the state of the epidemic.
Keywords: COVID-19, Poverty, Mortality inequality, Labor market, Housing conditions
1. Introduction
Despite an unprecedented worldwide decline in mortality over the last century, a substantial income gradient still persists within most countries (Case et al., 2002, Cutler et al., 2006, Chetty et al., 2016, Currie et al., 2020). These structural inequalities result primarily from individual differences between the rich and the poor in health behaviors, information, economic or social stress (Butikofer et al., 2021) and from ecological factors, like the living environment or public health institutions (Chetty et al., 2016, LeClere et al., 1997, Robert, 1999, Pickett and Pearl, 2001). However, sudden exogenous events like pandemics can also significantly affect these inequalities. Historical studies have shown that past epidemics had unequal effects on the mortality of different socio-economic groups, either because they revealed latent inequalities in individual health capital or because they spread differently across living environments (Snowden, 2019, Alfani, 2021, Beach et al., 2021).
The COVID-19 crisis epitomizes such massive mortality shock, on a worldwide scale. In 2020, about 100 million people have tested positive for COVID-19 – among which 2.2% died – with a large number of infections and deaths also remaining undetected.1 Assessing the causal impact of this pandemic on mortality inequalities is therefore key, not only to inform public policy in the context of the crisis, but also to study the role of pandemics in shaping mortality inequalities from a historical perspective. However, while a growing literature has pointed out that most vulnerable socioeconomic groups were more often affected in the early months of the pandemic, most of the existing evidence remains essentially correlational.
A first challenge in measuring the causal impact of the epidemic on mortality inequality consists in isolating the specific contribution of COVID-19. Even in the absence of a pandemic, structural socioeconomic inequalities in health would have likely resulted in an income gradient in 2020 mortality. A second challenge mostly ignored by the literature is to disentangle the respective effects of the pandemic on the one hand and of the policy responses such as lockdown on the other hand. Finally, a third challenge relates to the dynamics of the pandemic: many studies are based on early and short-term measures. It is unclear whether these results only reflect harvesting effects due to a temporary mortality shock on individuals particularly at risk. In particular, one cannot exclude that the income gradient gradually disappears, or is even reversed, as time goes by and the disease spreads.
In this paper, we address these challenges in the context of France, one of the most severely hit country in the world. Using exhaustive administrative data sets, we are able to study the links between income and the 2020-specific excess mortality at a very local level, for the entire country and over a long time period. We combine daily death records of all-cause mortality provided by the French National Statistical Institute (INSEE) for the three entire years 2018–2020 with information on the municipality of residency, a very detailed geographic scale (1,600 inhabitants and 15 sq.km per municipality, on average). Leveraging the precision of our data, we study what happens, on average, between municipalities within urban areas exposed to COVID-19. While working at the municipality level does not allow us to adequately capture the individual income-related factors driving differential COVID-19 lethality, it does allow us to better capture the ecological factors related to poor environments that promote the spread of the virus. In particular, working at such a fine geographic scale means that we can account for local interactions between individuals that are central to the development of health inequalities (LeClere et al., 1997, Robert, 1999, Pickett and Pearl, 2001), and all the more so in the case of an epidemic.2
There are three main results in this paper. First, we confirm the existence and persistence of an income gradient in the 49,495 excess deaths that occurred in French urban areas over the two distinct waves of the epidemic (in Spring and late Fall 2020). Within a given urban area, and once population size and age are controlled for, the difference in excess mortality rates between the poorest municipalities (bottom quartile of the income distribution) and the richer ones equals 2.6 deaths per 10k. inhabitants, i.e. 30% of the excess mortality in the non-poor municipalities in 2020. Given the respective average median income in poor (17,108 euros) and non-poor municipalities (22,204 euros), this result implies an elasticity of excess mortality with respect to income of 1.32 at the municipality level.3 We show that the gradient uncovered during the first wave is not compensated during the second wave, but rather reappears with regularity every time the epidemic returns, so that it is the strongest in areas that got most affected by COVID-19 in 2020. Second, we propose a decomposition of the total impact of COVID-19 on mortality that contrasts the effects arising from the lockdown policy with those more directly related to the epidemic (such as deaths attributed to COVID-19, hospital congestion, etc.). While lockdown policies could theoretically have an independent impact on the mortality gradient even in the absence of COVID-19, we find no empirical support for such an effect in our setting. Third, examining potential mechanisms, we find suggestive evidence that labor-market exposure and housing conditions are important determinants of the variation in COVID-19 mortality and largely capture the income gradient. This last result suggests that COVID-19 had a greater impact on poor municipalities because of a higher virus transmission among individuals living in these municipalities.
This article makes several contributions to the literature on the income gradient in the specific case of COVID-19. Many papers have shown that the first wave affected more strongly deprived neighborhoods and individuals based on confirmed cases (Chen and Krieger, 2021, Abedi et al., 2020, Ashraf, 2020, Kim and Bostwick, 2020, Williamson et al., 2020, Drefahl et al., 2020, Jung et al., 2020, Caul, 2020).4 Our data improve the measurement of the specific contribution of COVID-19 to health inequalities in two ways. First, confirmed cases underestimate the number of deaths attributable to the pandemic. In particular, they do not account for false negatives or deaths on which no test has been carried out, either because testing material was lacking in hospital or simply because they occurred at home. Unreported cases are highly unlikely to be independent of income and may therefore bias the results of the literature based on confirmed cases. To avoid such bias, we favor all-cause mortality to confirmed cases in our estimations. Second, our approach allows to better account for the structural income heterogeneity in mortality that is found absent COVID-19. A large literature documents mortality inequalities between socio-economic groups and it could then be the case that the income heterogeneity in COVID-19 confirmed deaths reflect only these. In particular, structural health inequalities may be especially strong in the US (where most of the evidence on the income gradient comes from), a country where access to health care is very unevenly distributed among the population.5 We therefore use all-cause excess mortality as our main dependent variable, defined as the deviation in 2020 all-cause mortality with respect to a counterfactual (pre-COVID) period — namely the average of all-cause mortality in 2019 and 2018.6
To our knowledge, very few articles have worked on all-cause excess mortality, and all of them focused on the first wave (Calderón-Larrañaga et al., 2020, Krieger et al., 2020, Decoster et al., 2021). By using two successive waves in France, our paper adds to this literature by evaluating the evolution of the income gradient over time. Our analysis reveals that the relationship between income and COVID-19 mortality applies with regularity to each wave of the epidemic and that the mortality differential created does not disappear over time.7 The epidemic caused an increase in differential mortality between rich and poor municipalities that is not a simple one-time shock or anticipation effect but is rather deepening after each wave.
This article is also the first to distinguish between epidemic-induced and lockdown-induced effects on mortality. The COVID-19 epidemic had many effects on mortality: directly on infected individuals but also more indirectly by increasing the pressure on health infrastructures (thereby delaying other types of treatment) and by modifying individuals’ behavior. Likewise, lockdown policies may impact mortality in a way that is non-orthogonal to income (e.g. through mental-health consequences, increased domestic violence, reduced road accidents, etc.; cf. Banerjee et al., 2020, Belot et al., 2020, Caul, 2020, Mulligan, 2021, McIntyre and Lee, 2020, Bullinger et al., 2020, Calderon-Anyosa and Kaufman, 2021), reinforcing or, on the contrary, mitigating the effects of the epidemic on mortality inequalities. We exploit the quasi-natural experiment provided by the first lockdown in France to disentangle between the epidemic- and the lockdown-induced mortality dimensions. The uniform implementation of a lockdown over the territory froze the epidemic at very different stages of development. In zones with a low level of infection at the start of the lockdown, the propagation of the virus was stopped before it could have a significant impact on mortality. By contrast, in the high-infection zone, the virus had already circulated enough to have a large impact on mortality, despite the lockdown. We find no income gradient in the within-urban-area mortality in the low-infection zone, suggesting that lockdown policies alone do not play a major role. Instead, the overall income gradient seems to be driven by the effect of COVID-19 infections and related health issues. Among these effects, we further argue that COVID-19 (immediate) mortality represents the main driver of excess mortality in 2020.
Finally, our paper speaks to the literature on the mechanisms underlying the relationship between income and COVID-19 mortality. Other papers have highlighted the importance of labor-market exposure or housing conditions (including the first version of this paper, as of July 2020, as well as Almagro and Orane-Hutchinson, 2020, Almagro et al., 2020, Glaeser et al., 2020, Naticchioni et al., 2020). Building on exhaustive administrative data, we confirm the role of increased exposure inside and outside the house.8 We complement the literature by examining the dynamics of the mechanism effect over both waves and by trying to quantify the respective contribution of each mechanism in explaining the income gradient in excess mortality.9 The contribution of the share of essential workers remains high in both waves, while the effect of the share of workers with frequent social contact at work decreases in magnitude during the second wave. It suggests that employers have partly adjusted the management of the occupational risk over time. Housing conditions also matter less during the second wave, as the lockdown was less stringent. While we acknowledge that other mechanisms could be at play, a horse race performed between variables related to occupational exposure and housing conditions indicates that our variables – and especially the share of essential workers and of overcrowding housing – capture a substantial share of the income gradient in COVID-19 related mortality.
The remainder of the paper is organized as follows: Section 2 describes the data and the construction of our outcome variable, while Section 3 explains the context. In Section 4, we present the first evidence of an income gradient in COVID-19 mortality in France that persists across waves. In Section 5, we disentangle between the epidemic-induced and the lockdown-induced effects of COVID-19 on excess mortality. Given these results, Section 6 explores potential mechanisms and Section 7 concludes.
2. Data and measurement
Data sources
In this paper, we gather various individual-level data sets that we match using municipality-level identifiers. In France, municipalities are very small administrative units of 1,600 inhabitants and 15.3 sq.km on average; there are about 35,000 of them in 2020. Our analysis compares municipalities within urban areas. Urban areas are groups of neighboring municipalities, defined by the French National Statistical Institute (INSEE) on the basis of commuting patterns. We consider 16,640 municipalities distributed across 621 urban areas, each being made of 27 municipalities and hosting 85,000 inhabitants on average.10 The majority of our sources are exhaustive administrative data sets made available by INSEE. We provide more details on all data in Appendix A.1.
Measuring the impact of the epidemic on mortality
Most other works studying the unequal impact of the pandemic are based on COVID-19 confirmed cases (infection or death). These measures suffer from several conceptual limitations.11 First, the total impact of an epidemic on mortality is a function of both the direct effects of infections (), and the indirect effects of infections, including the effect of public policies taken as a response to infections, (). Indirect effects include, among others, (i) physical, psychological, and social effects of distancing;12 (ii) economic changes (Banerjee et al., 2020); (iii) deaths due to altered access to health services. Furthermore, can be broken down into reported infection-caused deaths () and unreported infection-caused deaths (). Studies based on confirmed cases not only ignore the indirect effects of the epidemic but can also suffer from severe biases arising from the salience of unreported cases and the saturation of health services.
A growing literature confirms that measures based on COVID-19 reported cases actually include significant biases. First, testing capacities and strategies have proven to vary substantially over space and time, not only across countries but even across regions or neighborhoods (Kung et al., 2020, Rivera et al., 2020, Borjas, 2020, Balmford et al., 2020, Silverman et al., 2020, Yorifuji et al., 2021, Wu et al., 2021). France is no exception to this rule: it ranked among the worst OECD countries in number of tests per inhabitant by the end of the first wave, in May 2020 (Scarpetta et al., 2020, Foucart and Horel, 2020). Another source of bias comes from the non-random testing of the population in a context of a shortage in testing resources. Typically, tests are more often conducted on symptomatic persons, the elderly or socio-economic vulnerable people, leading to overestimation of infection rates (Beaney et al., 2020, Böttcher et al., 2021). Finally, some individuals who die from COVID-19 are not accurately identified, due to difficulties in attributing the cause of death. This may particularly bias the number of reported cases in France, where no system existed to report the COVID-19 mortality at home (Fouillet et al., 2020).
A second limitation of analyses using only measures based on COVID-19 confirmed cases is that they ignore counterfactual mortality. To conclude about an income gradient from COVID-19 observed death actually presumes that such gradient would not exist absent the epidemic. In other words, it fails to take into account structural health inequalities between socio-economic groups. Such inequalities have been consistently documented in a wide range of countries (Case et al., 2002, Cutler et al., 2006, Adler and Rehkopf, 2008, Cutler et al., 2012, Currie and Schwandt, 2016, Mackenbach et al., 2019) and have been recently highlighted in the case of France, where the richest 5% men (resp. women) have a life expectancy of 13 (resp. 8) years longer than the poorest 5% on average over the 2012–2016 period (Blanpain, 2018).13 As a consequence, accounting for the baseline inequality in mortality between rich and poor (in the absence of COVID-19) is key to accurately identify the specific contribution of the epidemic on inequality in mortality.
To address these issues, we build measures of all-cause excess mortality at the municipality level based on daily counts of deaths from INSEE. For every single individual who died in France in 2018, 2019 or 2020, this data set provides the municipality and place of death (hospital or clinic, home, care home, etc.) as well as a set of individual-level characteristics such as sex, date of birth and municipality of residency.14 Such data makes it possible to compare the mortality for the residents of a given municipality, during a given period in 2020, to the mortality in the same municipality during the same period in the two previous years,15 before the COVID-19 outbreak. For each municipality , we therefore define excess mortality during period as follows:
| (1) |
where is the number of deaths among residents of municipality during period of year and is the total number of inhabitants (/10,000) of municipality , as recorded in 2014. The superscript only indicates that excess mortality is computed using similar calendar periods across different years (e.g. the excess mortality for March 2020 is computed based on mortality in March 2020, March 2019 and March 2018, where ); to simplify the notation, we do not include it in following equations.
Using all-cause excess mortality allows us to study the impact of the COVID-19 epidemic on mortality based on a measure that is of constant quality over space and time and that is available at a fine level for a very large territory. We are therefore able to avoid the usual biases found in the literature that are due to testing or death reporting issues. Furthermore, our counterfactual analysis also allows us to take into account the structural inequalities between rich and poor municipalities in terms of mortality in order to accurately identify the impact of the epidemic on these inequalities. Finally, our measure allows us to account for both the effects induced by the epidemic itself and those induced by the policy response, the latter being generally ignored in the literature. In Section 5, we develop a triple-difference strategy based on a quasi-experimental setting, which exploits natural variations in infection rates over the French territory at a very early stage of the epidemic to net out the potential effects induced by the lockdown policy. This strategy allows us to isolate the overall effect of COVID-19 infections and to study how it is distributed based on a reliable and unbiased measure of mortality.
A municipality-level analysis
The main goal of this paper is to estimate the impact of the COVID-19 epidemic on inequalities in mortality. Our approach at the municipal level allows us to study this issue from a geographical point of view, at a fine local level, and to estimate the average effect of COVID-19 on the mortality of individuals living in a poor area.16 This approach captures mortality inequalities that primarily relate to ecological (or local) factors. Such factors are known to influence the income gradient in life expectancy in normal times (Chetty et al., 2016). And given the nature of an epidemic, they are likely to be central to the spread of the virus. In other words, we think that location is an important source of heterogeneity in the impact of COVID-19 on mortality and we thus conduct our analysis at a fine geographic scale.
Because poorer individuals tend to both locate in poorer municipalities (by construction) and suffer from poorer health status, mortality spatial inequalities may also come from individual factors, that would be better captured using individual-level data. Local and individual aspects are equally important but relate to somewhat different and complementary questions. In particular, we think that only a local approach is able to take into account the interactions between individuals living or working in the same area. It is therefore especially suited for the analysis of an epidemic where one’s risk spills over to his neighbors. To the best of our knowledge, the only study able to look at both individual and local levels is the one by Decoster et al. (2021), who exploit mortality data from the first wave of the epidemic (March–May) in Belgium. Their results indicate that individual income has only a small insignificant effect once one controls for local income. That is, during the epidemic, people died more like their neighbors than like their own income’s category.
Municipalities are very small geographic units and a good approximation of individuals’ living environments. This precision allows us to ask how mortality differs across different municipalities (neighborhoods) of a same urban area (agglomeration). It also drives our focus on ecological aspects in Section 6.
3. COVID-19 in France: context and background
3.1. The temporal dynamics of the epidemic in 2020
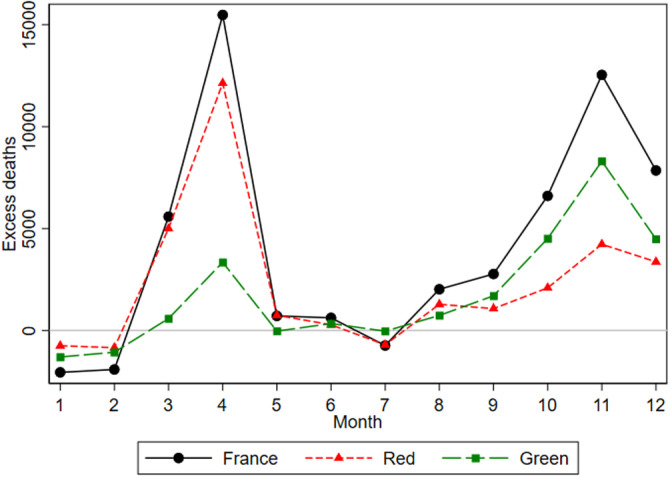
Overall in 2020, there was 49,495 deaths in excess in French urban areas in comparison with the average of 2018 and 2019. Fig. 1 represents the distribution across months of these extra deaths in France in 2020 (black line). It clearly appears that, as in many European countries, excess deaths in 2020 essentially occurred over two distinct waves that peaked in April (15,479 deaths) and November (12,537 deaths), respectively. In the remainder of this paper, we will refer to the period covering March and April 2020 as the “first wave”; and the period October to December 2020 as the “second wave”.
Fig. 1.
Monthly counts of excess deaths in French urban areas.
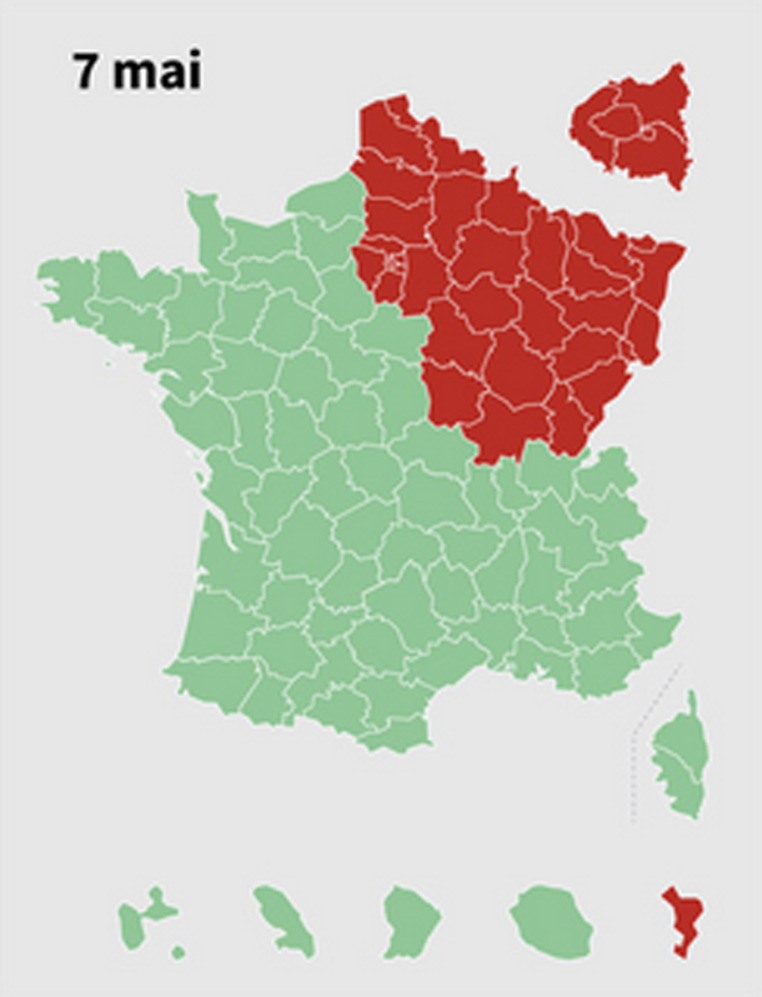
NOTE: The figure represents the difference between the monthly number of deaths in 2020 and its average over 2019 and 2018 in the relevant zone. The “red” zone corresponds to the areas that were the most severely hit by the first wave, and that are located in the North-Eastern quarter of the country. This zone covers about 44% of the urban population of (mainland) France. The “green” zone encompasses the rest of the French territory.
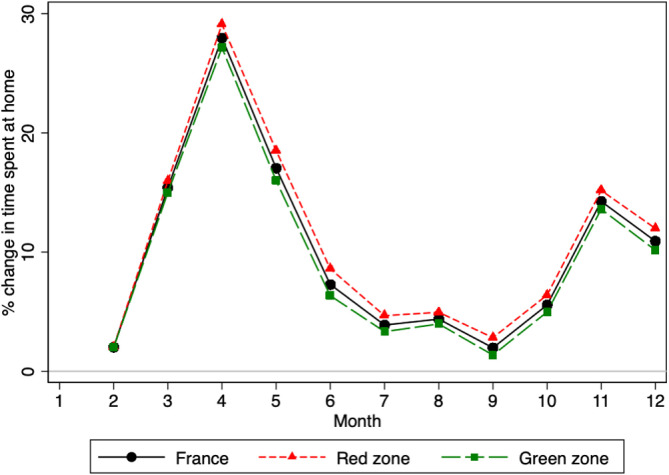
In both cases, the French government reacted by taking extraordinary containment measures. As COVID-19 first spread in the country in early 2020, the government decided of a national lockdown on March 17 and that eventually lasted until May 11. This first lockdown was the most stringent and seems to have reduced the spread of COVID-19 drastically. All workers stayed home except if their activity was deemed essential for the country and visits to elderly care homes (hereafter EHPADs) were forbidden. After a lull in the summer, the epidemic developed again until a second lockdown was decided on October 30 and continued until December 15. This second lockdown was less stringent however: (i) on top of essential private industries, factories, firms from the construction sector as well as most public services remained open; (ii) to the exception of universities most schools kept on receiving students; (iii) visits to EHPADs were allowed; (iv) parks and gardens remained open. The second lockdown got also repealed quicker, with the end of a first phase after a month when all shops opened again. We provide anecdotal evidence on that aspect in Fig. B.1 (black line) using Google mobility data (Google LLC, 2021). The increase in time spent at home appears much higher when a lockdown policy is in place, and more so during the first lockdown than the second.
Fig. B.1.
Percentage change in time spent at the place of residence in 2020.
NOTE: Based on Google mobility data (Google LLC, 2021), the graph plots the percentage change in the time spent at the place of residence relative to a baseline measured between January 3, 2020 and February 6, 2020. For more information on the methodology, please refer to this Google webpage. The “red” zone corresponds to the areas that were the most severely hit by the first wave, and that are located in the North-Eastern quarter of the country. This zone covers about 44% of the urban population of (mainland) France. The “green” zone encompasses the rest of the French territory.
3.2. Spatial heterogeneity in excess deaths
An important feature of the French case is that the spread of the epidemic was still very uneven across the country when the first lockdown was implemented (March 17, 2020). While the North-East was severely hit, the West and the South were then almost spared by the epidemic. In the remainder of this paper we call the former region the “red zone” and the latter the “green zone”. Fig. 1 exhibits this spatial heterogeneity in excess deaths during the first wave. We reproduce the death toll separately for the North-East (red line) and the rest of the country (green line), the former indicating regions where COVID-19 was highly active when the first lockdown started. As is clear in the Figure, the first wave mostly hit the red zone, which accounts for 80% of French excess deaths in April 2020 — while it only represents 44% of the total urban population. By contrast, the green zone suffered a much smaller increase in mortality over the same period.17
Fig. 1 thus summarizes the spatio-temporal dynamics of the COVID-19 epidemic in France in 2020. We distinguish four phases, 1: January and February are marked by a relatively low mortality in all regions of France.18 2: March and April represent the “first wave” that mostly hit the North-Eastern quarter (red zone) of the country. 3: May to September, mortality is close to normal. 4: October to December, a second wave hit the country, this time more homogeneously across the territory.
As shown in appendix (Table B.3, Table B.4), the red zone contains less urban areas than the green zone (191 vs. 430) but these are bigger on average (39 municipalities and 12,000 inhabitants vs 22 municipalities and 6,800 inhabitants) and have more deprived municipalities (25% vs. 20%). Breaking down these statistics at the municipality level reveals however that municipalities in both zone are not so dissimilar. The median mortality rates in 2018 and 2019 (72 vs. 75 deaths per 10k inhabitants) are very similar, and so are the share of elderly (16% vs. 17%) and median income (22,000 vs. 21,000 euros).
4. The impact of COVID-19 on the income gradient in mortality
This section highlights a key heterogeneity in all-cause excess mortality in France that appears consistently over the two waves: an income gradient in the total impact of the COVID-19 epidemic on mortality.
4.1. A first stylized fact
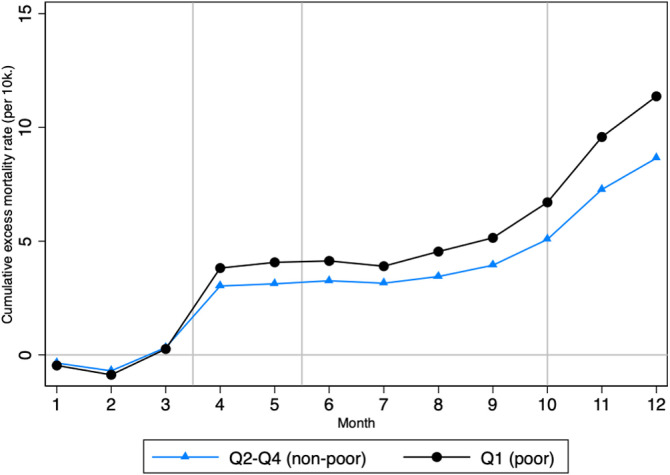
In 2020, poorest municipalities in France suffered from a greater increase in mortality, as compared to other municipalities. This stylized fact appears very clearly in Fig. 2, which displays the (non-parametric) monthly cumulative number of excess deaths (per 10k inhabitants) in 2020, separately for the poorest municipalities and other municipalities.19
Fig. 2.
Cumulative excess mortality rate per 10,000 inh. by poverty status.
NOTE: The graph plots the cumulative sum of all excess deaths per 10,000 inhabitants from January 2020 for poor and non-poor municipalities. Poor is defined as belonging to the bottom quartile of the national distribution of municipal median income weighted by the municipality size.
To categorize a municipality as poor, we first rank all municipalities according to the median income of their inhabitants and we define as “poor” all the municipalities that fall into the first quartile () of this distribution (cf. A.1, A.2 for details and data). We weight each municipality by its total population in order to give an equal weight to each individual. The municipalities included in therefore represent the 25% of the French urban population living in the municipalities with the lowest median income.
Fig. 2 shows no specific pattern in the cumulative excess mortality rate in the first three months of 2020 (phase 1, in Section 3.1), followed by a marked increase from April (phase 2), that further grows as the second wave takes place (phase 4). By the end of 2020, there was, on average, 11.4 more deaths per 10k inhabitants than usual in the poorest municipalities in France, against 8.7 in richer municipalities. In the following paragraphs, we employ an econometric approach to check whether this stylized fact holds after accounting for the influence of age and local factors.
4.2. Empirical approach
We check that the descriptive evidence displayed in Fig. 2 holds parametrically and test its robustness. We contrast the evolution of excess mortality in poor municipalities with that of richer municipalities over the whole French territory, taking a synthetic year (the average of 2018 and 2019) as the baseline. Our main model writes:
| (2) |
where indicates the municipality, an urban area. represents municipalities’ excess mortality rate as defined in Section 2 (i.e. as the deviation to the average 2018 and 2019 mortality rate of the same municipality over the same calendar period). In our analysis, every municipality belongs to one single urban area , and we therefore drop this redundant subscript in subsequent models. is a vector of controls including the total population size and the share of the population above 65 years old. Importantly, we introduce , an urban-area fixed effect so that we only exploit differences between municipalities located within a contiguous urban environment. This is an important aspect of our model since it absorbs specific local factors that may foster or hinder the spread of the epidemic and are unlikely to be independent from municipalities’ income. Our results are thus based on comparisons at a very fine spatial level. Municipalities are weighted by their total population. Standard errors are clustered at the urban-area level.
Our model can be viewed as a difference-in-differences design where the coefficient of interest is . It estimates the difference in excess mortality rate (time dimension) between municipalities from the poorest () and the other quartiles (comparison group). This model identifies the heterogeneity in the causal (total) effect of the pandemic on excess mortality under the sole hypothesis that, absent COVID-19 and the associated public policies, the average difference in the evolution of mortality over a given calendar period (in 2020 vs. before) between rich and poor municipalities of the same urban area would have remained stable. Below, we use falsification tests to provide evidence that this assumption is sensible.
4.3. Results
Table 1 reports the estimates associated with Eq. (2). Column 1 is estimated on all urban areas from mainland France and using the cumulative excess mortality rate over 2020 as a dependent variable. On average, within a given urban area, and once population size and age are controlled for, municipalities of the poorest quartile had an excess mortality rate of 2.627 (deaths per 10k inhabitants) higher than other municipalities. This has to be compared with the baseline average of 8.668 (deaths per 10k inhabitants) across municipalities of the other quartiles. Given the respective average median income in poor (17,108 euros) and non-poor municipalities (22,204 euros), this result implies an elasticity of excess mortality with respect to income of 1.32 at the municipality level.
Table 1.
Excess mortality rate by municipality income .
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| 2020 | Wave 1 | Wave 2 | No wave | |
| Q1 (poor) | 2.627*** | 1.178* | 1.083*** | 0.366 |
| (0.996) | (0.672) | (0.359) | (0.297) | |
| Controls | ✓ | ✓ | ✓ | ✓ |
| Urban area FE. | ✓ | ✓ | ✓ | ✓ |
| Non poor average | 8.668 | 3.661 | 4.825 | 0.182 |
| Observations | 16640 | 16640 | 16640 | 16640 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table reports the coefficients associated with Eq. (2). The independent variable, excess mortality rate, is computed considering four different time periods: the whole year (column 1), wave 1 (March to April, column 2), wave 2 (October to December, column 3) and other months in 2020 outside the two waves (January, February and from May to September, column 4). By construction, column 1 is the sum of columns 2 to 4. The non-poor average line reports the average of the predicted value of the dependent variable in non-poor municipalities. Controls include total population size and the share of the population over 65 years old.
We next consider three sub-periods for 2020 that correspond to the dynamics of the epidemic described in Section 3.1. In column (2) we report the coefficients associated with Eq. (2) when considering only the first wave, that is for March and April, while in column (3) we consider the second wave, from October to December. The income gradient is significant in both waves and slightly higher than 1 extra dead per 10,000 inhabitants. By contrast, we observe no gradient when we focus on excess mortality outside of the two waves. In column (4), we consider a synthetic period made of all the months in 2020 that we did not classify in either wave. In these months, mortality was really close to baseline (i.e. 0 excess death).
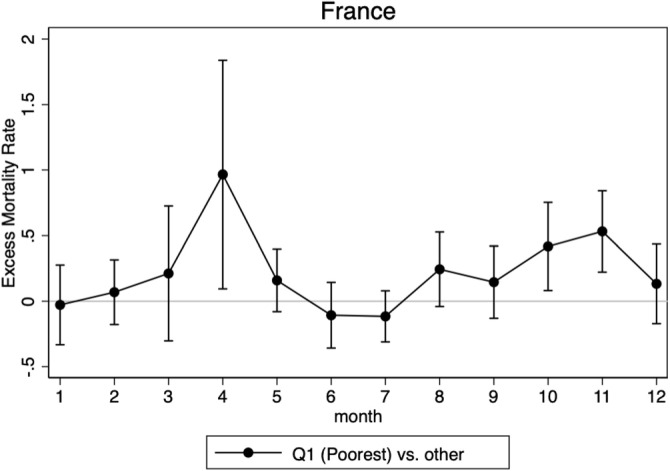
We then further decompose the effect and estimate the model for each of the 12 months separately. Fig. 3 plots the estimated coefficients. The difference in monthly all-cause excess mortality between municipalities of the poorest quartile and richer municipalities closely follows the dynamics of the epidemic depicted in Fig. 1 and the only differs from 0 at the peak of the first and second waves. In other words, in each epidemic wave, mortality increases on average (Fig. 1) but even more so in the poorest municipalities (Fig. 3).20
Fig. 3.
Monthly difference in all-cause excess mortality rate by income.
NOTE: The graph plots the point estimate and the 95% confidence intervals of the estimation of from Eq. (2) evaluated each month. It accounts for the monthly difference in all-cause excess mortality between the poor municipalities and the rest, where poor is defined as belonging to the bottom quartile of the national distribution of municipal median income weighted by the municipality size.
Taken together, these results support the idea that the income gradient we estimate for the whole 2020 year actually reflects the causal (total) effect of COVID-19 on mortality inequalities. They also provide evidence that this causal effect appears with regularity in each wave of the epidemic. We provide clearer and more detailed evidence on this last finding in Section 4.4.
About the definition of poverty
Our main model compares municipalities from the poorest quartile () to the others. This approach has the advantage of simplicity: by discretizing income into a simple “poor” vs. “non-poor” comparison, it greatly reduces the dimension of the problem and allows the exploration of heterogeneity and mechanisms in the following sections. In Appendix C.1 we explain this definition carefully. In particular, we show that contrasting the evolution of mortality in each of the four quartiles leads to a clear monotonic pattern. That is, within an urban area, the increase in excess mortality (during COVID-19 waves) decreases in municipalities’ income. This monotonicity is robust to a number of alternative partitioning of the distribution. Given this monotonic income gradient, pooling non-poor municipalities together to form a comparison group actually attenuates the differences in mortality rates that we estimate (as is closer to the - average).
Robustness
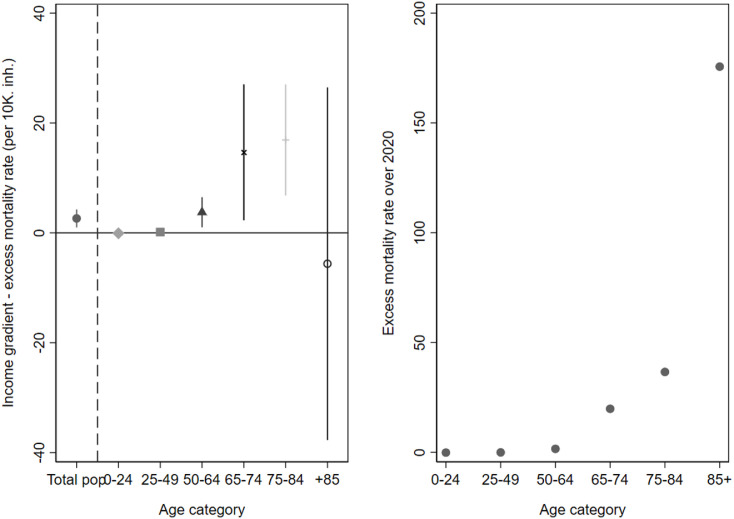
The presence of a stronger increase in mortality of the poorest municipalities is robust to a number of alternative specifications. We only summarize these results here; comprehensive analysis can be found in Appendix C. As already mentioned, we test alternative grouping of municipalities into distinct quartiles (Table C.1) or deciles (Table C.2) of the income distribution. We further implement a log-linear model which relates excess mortality per 10k inhabitants to the log of municipalities’ median income (Table C.2). The table shows that comparing a municipality to another with a 10% higher median income is associated with a reduction of observed excess mortality by almost 1 death per 10k inhabitants over the 2020 year. Our main result also holds when excluding elderly care homes. These were severely hit during the epidemic and one may worry that their location could drive a spurious correlation between municipality-level income and mortality. Removing all death records in such institutions does not alter our conclusion (Table C.3). Next, we compute the income gradient separately for different age categories (Fig. C.2): death toll and the income gradient increase with age, except for the category of people over 85 years old, who may represent a particularly vulnerable population irrespective of the level of income. In other words, except for the very old, the size of the gradient increases with the size of the death toll.
Fig. C.2.
Income gradient (LHS) and Excess mortality rate (RHS) over 2020 by age category.
NOTE: This Figure plots on the left-hand side the coefficient as estimated from Eq. (2) run separately on excess mortality over 2020 for different age categories. The first point reports the coefficient estimated on the whole population. 95% confidence intervals are reported. On the right-hand side, we show the magnitude of excess mortality defined as the number of excess deaths per 10,000 inhabitants over 2020, for the same age categories.
Finally, we run an additional falsification test which compares mortality in 2019 and 2020 to the same baseline of 2018. Reassuringly, we find a gradient in 2020 excess mortality but none in 2019 excess mortality (see Appendix C.2.2).
4.4. Urban area analysis
Fig. 3 suggests that there is a proportional link between the income gradient and excess mortality at the country level. Our data allows us to test this relation at a much finer scale, namely the urban area level. To do so we proceed in three steps. First we estimate the gradient (for each month of 2020) separately for each of the 421 urban areas that include both poor and non-poor municipalities. This new urban-area specific gradient measures how unequal the increase in mortality has been within each urban areas. Second, we measure mortality shocks faced by each urban area. For this, we simply compute urban-area specific (monthly) excess mortality. Finally, we study the link between the measured (urban area specific) gradient and contemporary (urban area specific) mortality shocks. (See Appendix D for more details.)
This exercise yields a clear message: when a given urban area faces an increase in excess mortality rate by one (death per 10k inhabitant) in a given month, we also observe an increase of that urban area’s gradient that same month by a bit more than 0.3 (more death per 10k inhabitant) on average (cf. Table D.1). This means that an increase in the intensity of an epidemic wave in given urban area will disproportionately affect poorer municipalities of this urban area.
Fig. 3 also shows that the gradient exists in both waves. Two different hypotheses could explain such finding. In a “structural” hypothesis, there could be specific features of poorer municipalities that strengthen the mortality response to COVID-19. In a “circumstancial” hypothesis, poorer municipalities may have simply been hit first; and one could expect mortality in non-poor areas to subsequently catch up. The “circumstancial” hypothesis is potentially compatible with the reappearance of the gradient because our result could be driven by different urban areas in each wave. For instance, it could be that Paris was hit in both waves but displayed a gradient only in the first; while Marseille was unaffected in the first wave but displayed an important gradient in the second wave. To the best of our knowledge, there are no papers disentangling between these two hypotheses. Our data allows to test these two scenarii over a one-year and two-waves span.
To discriminate between both hypotheses, we simply consider the 243 (among 421) urban areas that suffered positive excess mortality in each of the two waves.21 We find that, for these hit-twice urban areas, the average income gradient in both wave is positive (cf. Table D.2). We interpret this result as an evidence that, in these urban areas, although residents of poorer municipalities suffered more in the first wave, they also did so in the second wave. In other words, over a one year period, we find no evidence of catch-up of the richer municipalities.
This longer-term perspective provides new evidence on the impact of COVID-19 on mortality inequalities: it shows that the income gradient identified in the first wave is a regular feature of the pandemic that is not compensated later in 2020. It also indicates that there may be structural features of poorest municipalities that drive the heterogeneous impact of COVID-19 on mortality.
5. The role of lockdown: evidence from a quasi-natural experiment
The previous section has established evidence of an income-related heterogeneity in the total impact of the pandemic on mortality in France. This income gradient can result directly from COVID-19 infections, from the related effect on health system and individual behaviors, or because of important economic and social changes. In particular, it may be that lockdown policies have an independent impact on mortality that is heterogeneous between poor and non-poor municipalities, thereby playing a role in the observed mortality gradient. We call “epidemic channels” the COVID-19 impact on the health situation (broadly understood as infection and any indirect effect that increases with the level of infection, such as hospital congestion, increased anxiety, etc.) and “policy channel” the mortality changes caused by lockdown policies alone.22 In this section, we take advantage of the quasi-natural experiment induced by the first lockdown to isolate the independent impact of lockdown policies on mortality inequalities and to estimate the impact of the epidemic net of this effect.
5.1. Identification strategy
At the core of our strategy is the fact that the first lockdown was implemented uniformly over the country while the epidemic was at very heterogeneous stages of development across regions. In particular, based on an external classification provided by the government on May 7, we can distinguish regions strongly hit by the epidemic as early as mid-March (the red zone), from regions where the epidemic was at a much earlier stage of development when the first lockdown was decided (the green zone). Although this classification was only provided toward the end of the first lockdown, it strongly correlates with indicators of the spread of COVID-19 before the lockdown (in mid-March): (i) the average occupancy rate of intensive care beds was 26.5% in red départements, against 7.0% on average in the green départements 23 ; (ii) the likelihood to visit an emergency unit for suspicion of COVID-19 was twice as large in red départements (12.0% on average in the red départements vs 6.3% in the low-infection ones).24 Importantly for what follows, we also show that there is no differential pre-trend in mortality between both zones in the years, months, and weeks preceding the epidemic (Table 2). The table also confirms that COVID-19 infection rates were already quite high in the red zone in early March 2020, while the virus was almost absent from the green zone where excess mortality was still very close to 0 during the last two weeks of March. Finally, we show in Section 5.2 that trends in differential mortality between rich and poor municipalities are very similar across zones during pre-COVID periods, in line with Le Bras, 2020, Fouillet et al., 2020 who provide evidence on the absence of a relationship between the location of the first epicenters and socio-demographic characteristics at the département level.
Table 2.
Mortality trends in the red and green zones .
| (1) | (2) | (3) | |
|---|---|---|---|
| Red zone | Green zone | Difference | |
| 2019 excess mortality rates (2019 vs 2018) | |||
| Annual excess mortality rate | 0.239 | 1.473 | −1.234 |
| March–April | −1.357 | −0.685 | −0.672 |
| 2020 excess mortality rates (2020 vs 2018–2019) | |||
| January (pre-COVID) | −0.225 | −0.457 | 0.232 |
| February (pre-COVID) | −0.355 | −0.434 | 0.080 |
| March | 0.816 | −0.087 | 0.904*** |
| - first 2 weeks | −0.252 | −0.165 | −0.088 |
| - last 2 weeks | 1.139 | 0.216 | 0.923*** |
| April | 2.696 | 0.333 | 2.364*** |
| May | 0.341 | 0.359 | −0.018 |
| Nb municipalities | 7,358 | 9,947 | 1,7305 |
| Total population | 23,457,888 | 30,460,492 | 53,918,380 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table shows excess mortality rates separately computed in the red and the green zones over different time windows. Figures are expressed as number of deaths per 10,000 inhabitants. The first two rows exhibit measures comparing mortality between 2019 and 2018; the other rows compare mortality in 2020 to the average mortality over 2018 and 2019 (as in Eq. (1)). One can see no statistical difference between the two zones before the last two weeks of March 2020 (v.s. 2018–2019). Excess mortality rates then increase significantly more in the red zone than in the green zone and this pattern remains during the first wave. In May 2020 (v.s. 2018–2019) the two zones do not differ anymore in terms of excess mortality rates.
This quasi-experimental setting provides a unique opportunity to compare the evolution of excess mortality in two zones equally affected by lockdown restrictions25 and sharing similar characteristics (health care system, other institutions, etc.) but unequally exposed to COVID-19. As before, we analyze within-urban areas gradient. Our claim is that the evolution of the within-urban-area gradient would have been comparable (on average between green and red zones) absent COVID-19 and the associated public policies. In other words, we assume that the probability for an urban area to be exposed to COVID-19 is independent of the evolution of its poor vs. non-poor mortality differential that would have occurred absent COVID-19.
To disentangle the epidemic effects of COVID-19 on excess mortality from lockdown effects, we treat the green zone as a control group: we consider the income gradient in excess mortality found in this zone during wave 1 as a measure of the differentiated impact (between poor and non-poor municipalities) of the lockdown. By contrast, the income gradient found in the red zone captures both the effects of the epidemic and those of the lockdown. The difference between the two estimated gradients can thus be attributed to the aforementioned “epidemic channels”. These channels are diverse: from direct death caused by infection to any indirect effect that increases with the level of infection (e.g. due to hospital congestion or any behavioral response such as increased anxiety or greater fear of commuting caused by the important circulation of the virus in the area). We argue, however, that direct death from COVID-19 infection remains the main driver of the 2020 excess mortality. First because aggregate numbers suggest so: confirmed COVID-19 fatalities amount to 118% of 2020 excess mortality in France (Le Minez and Roux, 2021). Second, the heterogeneity across age bins shows no excess mortality or income gradient among the youngest. Such pattern restricts the set of possible confounding factors to those only affecting mortality of older people. Although we do not exclude other contributions, these are likely to be secondary at most.
5.2. Income gradient and the direct impact of COVID-19
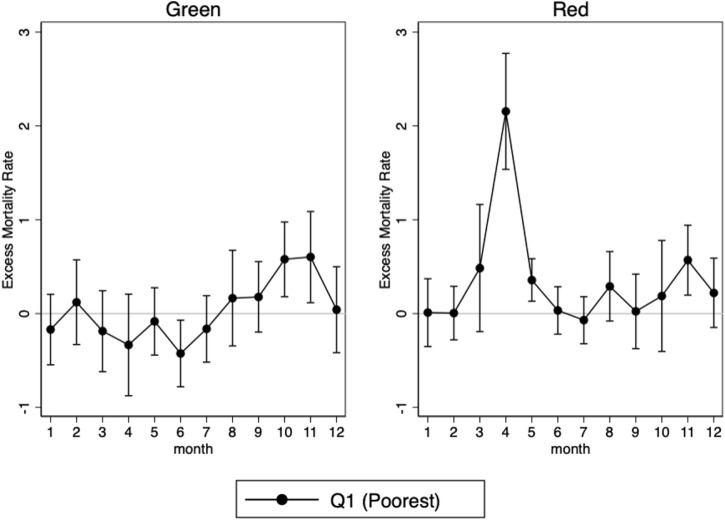
Double-differences by zone
We first re-estimate Eq. (2) for each zone in each month and we plot the coefficients of interest on Fig. 4 (the zone-specific equivalent of Fig. 3). It clearly appears that no gradient is found in the green zone during the first wave, unlike in the red zone and despite common lockdown restrictions. This leads us to conclude that lockdown policies did not have a significant independent contribution to the excess mortality income gradient. By contrast, the Figure shows a marked income gradient in excess mortality whenever the level of infection is high (i.e. wave 1 in the red zone; wave 2 in both zones). This suggests that the income gradient is only to be found in the epidemic effect of COVID-19.
Fig. 4.
Gradient in excess mortality by zone.
NOTE: The graph plots the point estimate and the 95% confidence intervals of the estimation of from Eq. (2) evaluated each month on each zone separately. It accounts for the monthly difference in all-cause excess mortality between the poor municipalities and the rest in each zone, where poor is defined as belonging to the bottom quartile of the national distribution of municipal median income weighted by the municipality size. The red zone corresponds to the areas that were the most severely hit by the first wave, and that are located in the North-Eastern quarter of the country. This zone covers about 44% of the urban population of (mainland) France. The green zone encompasses the rest of the French territory.
A triple-difference strategy
To test more formally the existence of an income gradient in the effect of the epidemic, we exploit the lockdown natural experiment by employing a triple-difference strategy. That is, we add the red vs. green dimension (defined at the département level) to the difference-in-differences setting used in Section 4. Formally, we estimate the following model:
| (3) |
The main coefficient of interest estimates the difference between red and green zones in the within urban-area difference between rich and poor municipalities’ excess mortality. represents a vector of controls and the full set of urban-area fixed effects,26 both defined as in Eq. (2). measures the causal impact of the pandemic cleared of the lockdown-induced effect on excess mortality under the sole hypothesis that, absent COVID-19 infections, the average difference in the evolution of excess mortality in a given month between rich and poor municipalities of the same urban area would have been the same in red and green zones.27 Standard errors are clustered at the département level, the most aggregated level of treatment status in this setting.28
In this setting the period of interest is that of March and April (first wave), and estimating Eq. (3) both before the pandemic broke (January and February) and between waves (May–September) provides several tests of our identification assumption. Furthermore, evaluating the equation during the second wave (October–December), when no clear difference in mortality between the two zones stood out, ensures that both zones are comparable.
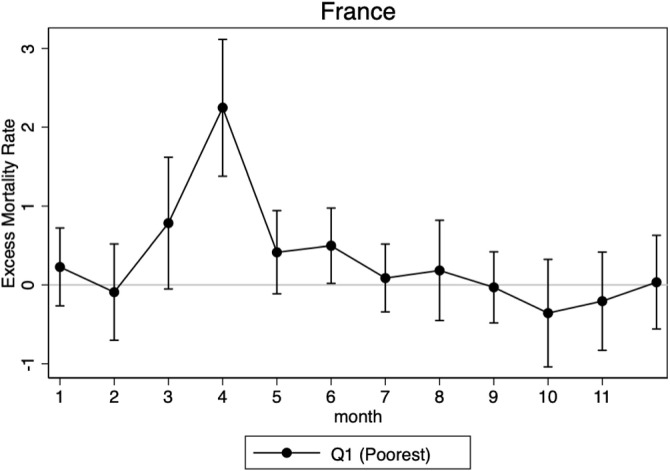
All monthly coefficients are reported in Fig. 5. Consistent with our hypothesis, the figure shows no significant difference in excess mortality between zones outside of the first wave. This difference first increases in March, due to the early direct effects of the epidemic, but remains insignificant at a 5% level. Conversely, in April, at the peak of wave 1, the main coefficient is strongly significant and is even stronger than in the difference-in-differences setting.
Fig. 5.
Income gradient in the direct effect of COVID-19 on mortality.
NOTE: The graph plots the point estimate and the 95% confidence intervals of the estimation of from Eq. (3) evaluated each month. It accounts for the monthly difference in all-cause excess mortality between the poor municipalities and the rest in the red and in green zones, where poor is defined as belonging to the bottom quartile of the national distribution of municipal median income weighted by the municipality size.
Robustness
To check the robustness of our results, we take advantage of the panel nature of our data to estimate an explicit triple-difference model, which includes municipality fixed effects and uses death toll as the main dependent variable. Formally, we estimate the following model:
| (4) |
where is the number of deaths in year , municipality in urban area and département . This alternative specification allows us to control for municipality fixed effects , which capture all time-invariant factors influencing municipality-level mortality between 2018 and 2020.29 This implies that urban-area fixed effects cannot be estimated (each municipality belongs to a single urban area). It follows that in this model, we do not restrict ourselves to comparing adjacent municipalities within the same urban area.
We estimate this model on the first wave of the epidemic (March–April), when the situation was suited for the use of a triple difference. As shown in Table E.1, the nature of the result remains: over March–April, mortality increased in 2020, more so in red than in green areas, and more so in poor than non-poor municipalities. This result holds true regardless of whether we include municipalities located in rural areas (column 1) or not (column 2) in the estimation sample.30 Finally, this result is also robust to the exclusion of elderly care homes.31 In total, this set of results confirms that the most severely hit municipalities are those belonging to the poorest quartile and to the red zone.
6. Potential mechanisms
6.1. Identifying relevant mechanisms
The heterogeneous impact of COVID-19 on excess mortality between rich and poor municipalities can cover many mechanisms. While we acknowledge that we cannot examine all the potential underlying channels, we choose to study closely the occupational and housing exposure mechanisms, based on three reasons: (i) these mechanisms have been mentioned as potential powerful channels of transmission very early on, both by economists and public health experts; (ii) they relate to ecological infection factors; (iii) the availability of high-quality data. We provide more explanations on the two first rationales in the following paragraphs.
Both the scientific literature and newspapers have extensively covered the key role of housing conditions and occupational exposure from the beginning of the epidemic (Almagro and Orane-Hutchinson, 2020, Almagro et al., 2020, Glaeser et al., 2020, Naticchioni et al., 2020, Angelucci et al., 2020).32 Informed by the state of the scientific knowledge at that time and given the likely positive association of housing and occupational exposure with poverty, we focus on these mechanisms.
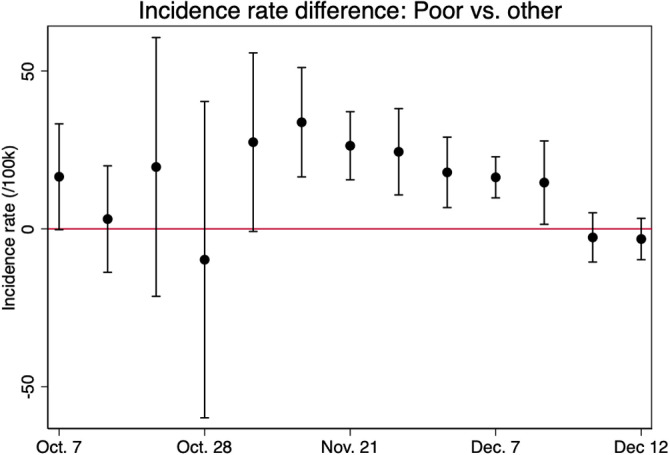
The second reason that leads us to focus on these mechanisms relates to the ecological approach that we follow throughout the paper. The probability of dying from COVID-19 can be decomposed as follows: , where the first component is the probability of being infected (the transmission component) and the second component is the probability of dying, conditional on being infected (the lethality component). Given our use of municipality-level data, we are primarily interested in mechanisms affecting the probability of getting infected, rather than the probability of dying conditional on being infected. While we cannot directly distinguish between both components due to the lack of individual data, we can argue, however, that the transmission component matters and is correlated with income.33 To rule out the hypothesis that the entire gradient comes from a difference in lethality (because, for instance, all individuals with a comorbidity may also locate in poor municipalities) and make sure that there exists a difference in transmission, we use data on tests. Finding a gradient in incidence rate would suggest that the mortality gradient comes at least in part from differential transmission. We use administrative testing data at the municipality level from the French public health agency (SI-DEP), which we describe in Appendix A.1. The weekly incidence rate is computed as the number of positive tests per 100,000 inhabitants over the period October 6th–December 28th 2020 covered by the data. Test data suffers from caveats that we already mentioned in Section 2 and that make us favor all-cause excess mortality in our main analysis. We describe these caveats in Appendix A.2. With these limitations in mind,34 we regress the incidence rate on our variable along with our standard controls, urban-area fixed effects and we cluster standard errors at the urban-area level (as in Eq. (2)). Fig. 6 exhibits a pronounced gradient in infection at the peak of the second wave, in November and beginning of December.35
Fig. 6.
Weekly difference in infection rate by income.
NOTE: The graph plots the point estimate and the 95% confidence intervals of the estimation of from Eq. (2) evaluated each week with the incidence rate as the dependent variable. It accounts for the weekly difference in incidence rate between the poor municipalities and the rest, where poor is defined as belonging to the bottom quartile of the national distribution of municipal median income weighted by the municipality size.
From this exercise we conclude that the entire gradient in mortality cannot be explained by a (simple) difference in underlying health conditions, but that ecological dimensions matter to a great extent. In the following subsections, we first describe how we measure such potential mechanisms and confirm that each of our measures is positively correlated with poverty (Section 6.2). We then try to quantify the extent to which these mechanisms explain the income gradient in COVID-19 related mortality and to understand which of them prevails (Section 6.3).
6.2. Housing and labor-market conditions: measurement and relation with poverty
Highly-exposed occupations are successively defined as occupations with frequent direct contact with the public in usual (pre-COVID-19) business conditions, and as occupations in sectors which kept operating during lockdown periods (the so-called essential workers). Informed by administrative data on the occupational distribution in each municipality, we compute (i) the worker-weighted average frequency of contact (hereafter “index of frequent contact”) and (ii) the share of essential workers, in every municipalities. Regarding housing conditions, we use census data at the household level to measure the share of overcrowded housing units in the municipality. This variable improves on some other measures of household size used in the literature (Almagro and Orane-Hutchinson, 2020) since it is a function of household size, dwelling size and number of rooms. At the interaction between labor-market and housing dimensions, we finally compute the share of municipalities’ households that gather at least one member aged 65 or more and one member from a younger generation who is currently employed. This measure requires occupation information from the Census, which is only available for municipalities with at least 2000 inhabitants. With respect to other papers establishing a link between physical contact (at home or at work) or maintained activity in the workplace during lockdown and COVID-19 exposure, we are able to provide evidence at a fine level both geographically — since we have administrative data at the municipal level while covering the whole national territory – and sector-wise – as the definition of essential workers is at the 3-digit occupation level.36 We are also able to uncover the role of the interaction of labor-market and housing channels: workers increase their risk of catching the disease in their workplace, and transmit it to vulnerable persons when living in multigenerational households. We provide more details on the construction of these measures in Appendix A.2 and reference the sources in Appendix A.1. Table F.1 shows descriptive statistics on the different mechanism variables.
Table F.2 shows the strength of the link between poverty and our (normalized) labor-market and housing measures, once included our baseline controls and urban-area fixed effects. Municipalities of the poorest quartile have more occupations in contact with the public (column 1) and more essential workers (column 2). A one standard-deviation increase in the share of essential workers (respectively in the index of frequent contact) makes the probability to fall in the bottom quartile of the national weighted income distribution increase by 16pp (respectively 14pp). The association is even stronger with the housing-crowding variable (column 3): a one standard-deviation increase in the share of over-crowded housing amounts to a 29pp rise in the probability to be living in a poor municipality. Poorest municipalities are also more likely to have multigenerational households (column 4), although the reduced sample size of municipalities with more than 2,000 inhabitants decreases the precision.37
6.3. Disentangling the role of each mechanism
In order to understand which mechanism prevails and to better inform public policy, we perform a horse race between our mechanism variables. Table 3 reports the results on excess mortality for the first wave (top panel) and the second wave (bottom panel) in all urban areas. The last column is a multivariate regression where all mechanism variables are added on top of the poverty indicator.38
Table 3.
Horse-race between mechanism variables .
| (1) | (2) | (3) | (4) | (5) | |
| Excess mortality rate, wave 1 | |||||
| Poor | 0.51309* | 0.40407* | 0.33580 | 0.01338 | −0.09418 |
| (0.29809) | (0.22907) | (0.27580) | (0.13489) | (0.14011) | |
| Index of frequent contact | 0.54991** | −0.11774 | |||
| (0.26948) | (0.16746) | ||||
| Share of essential workers | 0.51327*** | 0.42277*** | |||
| (0.10279) | (0.12855) | ||||
| Share of over-crowded housing | 1.50339*** | 1.45786*** | |||
| (0.28401) | (0.30927) | ||||
| Urban areas FE | ✓ | ✓ | ✓ | ✓ | ✓ |
| Controls | ✓ | ✓ | ✓ | ✓ | ✓ |
| Control outcome mean | 3.689 | 3.709 | 3.687 | 3.795 | 3.786 |
| Adjusted R2 | 0.1710 | 0.1720 | 0.1722 | 0.1762 | 0.1768 |
| Observations | 16267 | 16267 | 16267 | 16267 | 16267 |
| Excess mortality rate, wave 2 | |||||
| Poor | 0.45548*** | 0.39177*** | 0.17436 | 0.41355** | 0.16927 |
| (0.15906) | (0.14304) | (0.13468) | (0.20919) | (0.17754) | |
| Index of frequent contact | 0.32137* | −0.36327* | |||
| (0.16477) | (0.21621) | ||||
| Share of essential workers | 0.81386*** | 0.98330*** | |||
| (0.12239) | (0.14665) | ||||
| Share of over-crowded housing | 0.12615 | 0.05592 | |||
| (0.24226) | (0.22109) | ||||
| Urban areas FE | ✓ | ✓ | ✓ | ✓ | ✓ |
| Controls | ✓ | ✓ | ✓ | ✓ | ✓ |
| Control outcome mean | 4.870 | 4.882 | 4.868 | 4.879 | 4.858 |
| Adjusted R2 | 0.1274 | 0.1276 | 0.1298 | 0.1274 | 0.1299 |
| Observations | 16267 | 16267 | 16267 | 16267 | 16267 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
This table shows the result of regressing municipalities’ excess mortality on a variable measuring either poverty, housing conditions or occupational exposure. The upper part of the table shows results for the first wave (March–April) while the bottom part of the table shows results for the second wave (October–December) on municipalities in all urban areas. The first column only examines the poverty channel. Columns (2) to (4) respectively include one additional variable capturing either the occupation or housing mechanism. Column (5) includes both the poverty dummy and all the mechanism variables. The last column for wave 2 includes the same variables but uses the incidence rate as the dependent variable instead. All regressions include urban-area fixed-effects and control for total population and for the share of inhabitants over 65 y.o. in the municipality. The mechanism variables have been normalized such that coefficients can be interpreted in terms of the effect of a one standard-deviation change, and can be compared with each other. The control outcome mean line reports the average excess mortality rate per 10k inhabitants or incidence rate per 100K inhabitants in each wave in non-poor municipalities (conditional on controls and urban-area fixed effects).
Column (1) of Table 3 reports the difference in excess mortality between poor and non-poor municipalities. In the first wave, each of the mechanism variables is positively related to excess mortality, when included along with the poverty indicator.39 Including the frequent contact variable, however, has only a minor effect on the poverty coefficient (column (2)) whereas the inclusion of the share of essential workers (column (3)) and overcrowded housing (column (4)) makes the coefficient of poverty shrink. In the first wave, the initial coefficient of poverty diminishes by 35% when the share of essential worker is included, and by 97% when the share of over-crowded housing is included. The last column shows that the covariates altogether absorb all of the poverty coefficient, which is not significant anymore, while housing conditions and the share of essential workers are still significantly related to excess mortality.
Similarly, in wave 2, a high share of the poverty coefficient is absorbed by the mechanism variables (63%), but here the share of essential workers appears as the main channel of the income gradient. It alone absorbs 62% of the poverty coefficient, whereas the relationship between housing conditions and excess mortality decreases in magnitude, consistent with the less strict implementation of the lockdown policy (see Section 3 for more details). It is reasonable to think that there is an overlap between the group of workers with frequent contacts in their job and essential workers (e.g. cashiers, bus drivers, etc.).40 The coefficient of the frequent contact variable drops when the share of essential worker is included during the first wave. It suggests that non-essential workers with frequent contacts in normal business conditions do not suffer more from the pandemic during the first wave, since the lockdown probably prevents them from having such contacts. Conversely, being an essential worker alone is associated with a higher risk of COVID-19 related mortality. During the second wave, the inclusion of both occupational exposure variables even yields a negative coefficient on the contact variable. If we do not want to put too much emphasis on this result, one explanation could be that more protective measures have been taken for these over-exposed workers, maybe to the extent that they become more protected than the average worker.41 Essential workers, however, continue to be hit more severely by COVID-19 despite these protective measures because they are going to the workplace more frequently.
Examining the dynamics of the effect, Almagro and Orane-Hutchinson, 2020, Almagro et al., 2020 highlight a growing importance of housing crowding over time compared with commuting in explaining COVID-19 infection, that they justify by the fact that essential workers were gradually laid off over time. The different policies implemented and the lower incidence of layoffs in France compared with the US during the pandemic may explain why we do not find a similar pattern.
In Appendix F, we reproduce the horse race on the incidence rate to check that our mechanism variables affect mortality through the transmission channel. Table F.3 indicates that both horse races on excess mortality and incidence rate give very similar results: all mechanisms are positively associated with the incidence rate when sequentially added with the poverty variable. The last column of Table F.3 that includes the mechanism variables altogether with the poverty measure reports a poverty coefficient close to zero and non-significant. The table also suggests that housing conditions are more crucial in explaining differences in infection than in the probability of dying conditional on being infected, as compared to labor market measures.
All in all, Table 3 suggests that both housing conditions and the share of essential workers are important determinants of the relatively higher excess mortality due to COVID-19 in poor municipalities. The relative importance of housing conditions diminishes over time, potentially due to a less strict lockdown during the second wave, whereas remote work was prevalent throughout the period. The whole set of covariates explain about 13% to 18% of the overall variation in excess mortality according to the adjusted . Additional evidence that our mechanism variables channel a significant share of the income gradient by affecting transmission is that the of columns 2 to 5 of Table F.3 is much higher, at about 70%.
7. Conclusion
In this paper, we provide clear evidence that COVID-19 contributes to increasing inequalities in mortality through an unequal impact across municipalities. We find that the epidemic caused 2.6 more deaths per 10k inhabitants on average in the poorest municipalities in 2020, relative to a baseline of 8.7 in non-poor municipalities (i.e. a 30% higher effect in the poorest municipalities). Importantly, the income gradient measured in the first wave (March–April) persists in the second wave (October–December), even within cities strongly affected during the first wave. We further show that lockdown policies do not appear to have a significant independent contribution to this gradient. Finally, our analysis suggests a key mediating role of labor market and housing conditions, in line with the idea that ecological factors are important determinants of the spread of epidemics. More specifically, we find that labor-market exposure remains an important determinant of COVID-19 mortality across both waves, while the role of housing conditions decreases over time.
Our results show that the correlation between income and COVID-19 mortality highlighted in the recent literature does not only mirror existing health inequalities but that the baseline income gradient in mortality is rather amplified during each epidemic wave. Observing such an effect in both waves in a country with relatively egalitarian access to health care also reinforces the idea that the income gradient in mortality is a very robust feature of the epidemic. Potential future epidemic waves of COVID-19 or similar infectious diseases are likely to follow the same pattern and further amplify existing health inequalities.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We would like to thank Philippe Askenazy, Luc Behaghel, Simone Bertoli, Aline Bütikofer, Paul Dutronc-Postel, Gabrielle Fack, François Fontaine, Laurent Gobillon, Camille Hémet, Miren Lafourcade, Clément Malgouyres, Eric Maurin, Dominique Meurs, Alexandra Roulet, Mariona Segu, Marianne Tenand as well as participants of the following seminars and conferences for their valuable comments: Labor Chair seminar at PSE, Economic Policy seminar at the Univ. of Lausanne, BM at NHH, Health and Inequality seminar at CBS, European Meeting of the UEA 2021, ADRES 2020, AFSE 2021, JMA 2021, LAGV 2021, SEW 2021 and ESPE 2021 annual conferences. We thank the CASD (10.34724/CASD) for providing us access to some of the confidential data used in this work. We also thank the support of the EUR (Ecoles Universitaires de Recherche, Paris Graduate School of Economics) grant ANR-17-EURE-0001. We benefited from the Labor Chair at PSE, the LABEX OSE - ouvrir la Science Économique and Cepremap funding for data access.
Footnotes
Individual characteristics affecting one’s likelihood of infection also affect infection risks of others living or working nearby. Note that we introduce in our models urban-area fixed effects, so that we absorb specific local factors that may foster or hinder the spread of the epidemic and are unlikely to be independent from municipalities’ income.
Decoster et al. (2021) find that a 10% increase in the average municipality income is roughly associated with 2 fewer excess deaths per 10k. inhabitants in Belgium. Our estimate is a bit lower (1.1), potentially because France was less severely hit than Belgium during the first wave of the epidemic. However, the orders of magnitude are fairly close.
A few exceptions should be mentioned. Comparing US counties, Brown and Ravallion, 2020, Desmet and Wacziarg, 2020, Knittel and Ozaltun, 2020 find no association between median income or poverty rates and COVID-confirmed deaths. Jung et al. (2020) finds a positive relation between poverty rates and confirmed deaths in counties with a low density but rather a U-shaped relation in dense areas. According to Sa (2020), the positive association between socioeconomic deprivation and confirmed COVID-19 deaths in the UK turns negative once self-declared health quality is taken into account.
By contrast, measuring the income gradient in a country like France is informative on the unequal impact of COVID-19 despite a rather equal access to health care. Comparing the income gradients found in both countries is interesting to the extent that France and the US systematically rank at both ends of the distribution of OECD countries in terms of equality of access to health care ( source, see also Currie et al. (2020) for a comparison of mortality trends in the US and in France).
Two exceptions to the literature using confirmed cases should be mentioned: Caul (2020) describes both confirmed cases and all-cause mortality — but with no counterfactual; Chen and Krieger (2021) use a counterfactual but do not consider all-cause mortality.
More specifically, a surplus of 1.18 (resp. 1.08) excess deaths per 10k. inhabitants is found in the bottom income quartile in the first wave (resp. second wave), as compared to richer municipalities.
Although we argue that occupational and housing conditions capture a substantial share of this inside and outside the house exposure, we acknowledge the potential role of other mechanisms, such as: greater levels of air pollution in poorer areas (Cole et al., 2020, Persico and Johnson, 2020), lower levels of compliance to lockdown and to self-protection measures among low-income individuals (Papageorge et al., 2020), more comorbidities among individuals living in poor areas (Wiemers et al., 2020, Raifman and Raifman, 2020) among others. While population density is also an often debated mechanism, we do not treat it as a potential mechanism given its non-significant correlation with poverty in our data.
Almagro et al. (2020) also examine the dynamics of the effect of labor-market exposure and housing conditions in New York City but over a shorter time period and under a different institutional context.
Due to our within urban area approach, we exclude smallest urban areas made of only one municipality from the analysis. Table B.1, Table B.2 provide more descriptive statistics on our sample at the urban area and the municipality level, respectively.
See Böttcher et al. (2021) for a detailed discussion on this topic.
For instance, evidence suggests that the lockdown have reduced the transmission of the seasonal flu and of norovirus (Kraay et al., 2020).
We also find such inequalities in our data in 2018 and 2019 (see Section 5.1).
In the emergency of the COVID-crisis, INSEE made the data set available at a high frequency rate: this has induced potential measurement errors although INSEE applies corrections at each iteration. However municipalities have about one week to inform INSEE about new death. As the version of the data that we are currently using got updated on February 5, 2021, our measures should be accurate. For a discussion on the quality of the data, see the information provided by INSEE.
We use the average of years 2018 and 2019 because taking several years makes our measure less sensitive to random events occurring in a given year. For data availability reasons, we cannot go further back in time, since death data before 2018 do not include, at the moment, information on the municipality of residency.
Currie and Schwandt (2016) take a similar approach to study the link between poverty and mortality from a historical perspective.
The classification between green and red zones follows a map (see Fig. A.1) issued by the Government at the end of the first lockdown (on May 7) that we detail in Appendix A.2. The map is defined at the département level. A département is an administrative unit in France that encompasses on average 363 municipalities and 645,000 inhabitants. There is a total of 101 départements in France. Table B.3, Table B.4 detail the total number of urban areas, municipalities, and inhabitants in each zone.
The seasonal flu was particularly strong in 2018.
The cumulative number of excess deaths in month corresponds to our excess mortality variable computed over the period from January to the month .
It is also important to note that the standard errors are much greater in the first wave than in any other month. This is because the excess mortality only occurred in some part of the country, as explained in Section 3.2, an heterogeneity we discuss at length in Section 5.
These represent 72% (96%) of urban areas (population) in the red zone and 43% (69%) in the green zone.
According to McIntyre and Lee (2020), unemployment in time of lockdown is expected to have a strong impact on suicide rates — and we know that poor individuals are more likely to have jobs that cannot be done remotely and were therefore more often laid off during the lockdown (Gottlieb et al., 2021, Palomino et al., 2020). Bullinger et al. (2020) have shown that stay-at-home orders increase domestic violence in poor households but not in households with above-median income. The strong variation in car crashes and in pollution levels due to the lockdown could also differently affect municipalities depending on their income (Brodeur et al., 2021).
Note that red départements have more intensive care beds per inhabitant (7.58 vs 5.86 per 100K. inhabitants on December 31, 2018) so that the high occupancy rate of intensive care beds in the North-East of France is very unlikely to be driven by worse preliminary health care infrastructures.
An alternative possibility could have been to group départements based on these figures form mid-March. While the nature of our results is similar with this alternative classification, we preferred to rely on an external classification provided by the government, which cuts France in half and minimizes the share of areas classified as highly infected that are contiguous with areas classified as low-infected.
Fig. B.1 (Appendix B) supports the idea of a very uniform enforcement of the lockdown policy, since the increase in time spent at home compared to normal conditions is very similar across zones.
Note that these urban-area fixed effects account for the risk that: (i) coincidentally, the differences in COVID-19 infection intensity across urban areas at a given point in time could be non-orthogonal to their income level; (ii) people may adapt their behavior to the local level of infection which would bias our results (Almagro et al., 2020).
Note that this assumption is much less demanding than (for instance) assuming that the impact of the lockdown alone is the same in both zones.
Note that clustering at the level of urban areas does not change the nature of our results.
We, therefore, do not need to divide the number of deaths by the population in the dependent variable, because we measure the population only once in 2014.
Because we do not need to include urban-area fixed effects anymore, we can estimate this model on the whole sample of French municipalities, including those in rural areas.
Results available upon request.
We regret the absence of individual data on health and cause of death or high-quality measures of health in municipalities at the municipality level that could directly control for lethality. We therefore notably ignore the role of comorbidities known to be related with poverty and that most likely played a role in the observed mortality gradient (Wiemers et al., 2020, Raifman and Raifman, 2020). Controlling for age, proven to be one of the main individual determinants of COVID-19 mortality (Zhou et al., 2020), presumably mitigates this concern. Furthermore, using Belgian individual-level data, Decoster et al. (2021) find that the effect of individual income is not significant once one controls for place of residency.
One of the main limitations of the testing data – the fact that testing is limited and not random – is presumably less of a concern during the second wave where testing was more generalized.
We confirm this result by further decomposing the gradient into four quartiles (as in Eq. (5)). Here again, we observe a monotonous gradient in infection from early November to mid-December. Results available upon request.
Almagro et al. (2020) exploit both occupation data from the American Community Survey and ZIP-code level and individual geolocation data to track time spent outside of home, but they focus on New York City only. Angelucci et al. (2020) use individual survey data in the US but they define essential workers based on the ability to work remotely before COVID-19.
The coefficient indicates that a one standard-deviation increase in the share of multigenerational households increases the probability to be in the poorest quartile by 7pp, but the -value is only equal to 0.177.
Although these mechanisms are likely to be correlated with each other, we also looked at their independent association with excess mortality and its dynamic. We checked, in particular, that this association is insignificant outside of the two epidemic waves. Results are available upon request.
A one standard-deviation increase in the mechanism variables is associated with an increase from around 0.5 death per 10k inhabitants for the occupational variables to around 1.5 deaths per 10k inhabitants for the housing variable.
The correlation between both variables is 0.4. Out of the ten occupation codes with the highest index of frequent contact, six include essential workers.
Think for example of a shop assistant, who must constantly wear a face mask and use hydro-alcoholic gel, compared to a clerical worker sharing his office and not constantly wearing a face mask.
Workers are localized according to their municipality of residency and regardless of their municipality of work.
Essential workers include: health workers, auxiliary nurses, pharmacists, ambulance drivers, post office clerks, the police, public transport and funeral services, firefighters, persons working in the sale of food products, delivery workers, tobacconists and cleaning staff. On average, they include about 19.5% of workers in each municipality. The French National Statistical Institute also used this list in one of their paper (Papon and Robert-Bobée, 2020).
We tried an alternative approach based on sectors that remained active during the lockdown. Our results got very noisy as we could not systematically identify firms that remained open and workers that kept on going to their workplace at a disaggregated level.
One could also have used 2019 as baseline, but all three measures are very close (with correlations between 0.5 and 0.9).
To insist on the difference between the coefficients of interest in (2), (6), we indicate both and with a .
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.euroecorev.2021.103923.
Appendix A. Data sources and measurement
A.1. Data sources
by alphabetical order
DADS.
(for “Déclarations Annuelles des Données Sociales”) is a matched employer–employee exhaustive dataset that covers all employees in private and public sectors (outside of agriculture) in the year 2016. The DADS is an administrative data set that all employers must report yearly to social security authorities and tax administration. The version available to researchers is provided by the INSEE. In particular, the DADS contain information about all positions occupied by any worker in a specific year, with start and end date at the daily level. For each position held by one individual we observe: the occupation, the firm and sector, both locations of work and residency and the number of hours spent. When using DADS to build municipality-level indicators we rely on the municipality of residency. DOI: 10.34724/CASD.21.3038.V2.
Daily deaths files.
(“Fichier des Décès Quotidiens”) from INSEE record each death that occurred between January 1, 2018 and December 31, 2020. For each death, we observe information relative to the event (the date and municipality of death as well as a category about the place of death — hospital or clinic, home, care home, etc.) and the individual (municipality of residency, sex, date of birth). INSEE made these files available at a higher frequency during the Covid-19 crisis, but this comes at the expense of some quality checks. The files are originally recorded by municipalities and then gradually added to the INSEE data sets. In theory, municipalities have about one week to inform INSEE about new deaths. In practice, one cannot fully exclude that the files were incomplete by the time of our analysis (especially for the most recent months) although we updated them frequently (last update: February 5th, 2021). URL: https://www.insee.fr/fr/statistiques/4487988
DEFIS .
(“Dispositif d’Enquêtes sur les Formations et Itinéraires des Salariés”) is a database produced by the Céreq. It comes from a survey led on 4,500 firms and 16,000 of their workers as of 2013. Firms with more than 10 workers are representative of the whole private sector, but smaller ones are only representative for some sub-sectors. In this paper, we use the survey led on workers in 2015. The question of interest relates to the frequency of on-the-job contacts with the public. It refers to the current job of workers who have not changed firm since 2013, and to the one of 2013 for workers who changed firm since then. URL: https://www.cereq.fr/en/data-access-lifelong-learning-and-vocational-training-surveys-defis-cvts-base-reflet/defis-employee
Filosofi database.
(a French acronym for “Localised Disposable Income System”), 2014 version, contains a series of local measures on income and poverty. INSEE uses fiscal and social benefits data to compute these indicators at the municipality level. In particular, we are interested in the median standard of living of each municipality’s inhabitants. The concept of standard of living corresponds to the household disposable income divided by consumption units (using the OECD scale), to account for the size of the household. DOI: 10.34724/CASD.179.2668.V1. URL: https://www.insee.fr/fr/metadonnees/source/operation/s1451/presentation
Population censuses.
are used to compute a series of measures at the municipality level. Each year: (i) a fifth of municipalities with less than 10,000 inhabitants are covered by an exhaustive census and (ii) a sample of 8% of the population of municipalities with 10,000 or more inhabitants are surveyed. In-depth questions relative to economic activity and family structure of households are only available for about 20% of the households of municipalities under 10,000 inhabitants and about 40% of the households in the other municipalities (10,000 inhabitants or more). Analyses of in-depth questions cannot be done for municipalities with less than 2,000 inhabitants as samples get too small. We use INSEE annual population counts and both exhaustive and partial census data files. DOI: 10.34724/CASD.10.3255.V1 and 10.34724/CASD.10.3254.V1. URL: https://www.insee.fr/fr/information/2383265
SI-DEP data.
is provided by Santé Publique France. These testing data cover the period from October 6th, 2020 to December 28th 2020. On that period and for (almost) every day, we obtain the weekly incidence rate at the municipality level. The incidence rate is computed as the number of positive tests per 100,000 inhabitants. Open-access data deviates from the actual measure of the daily incidence rate in two dimensions. First, the reported incidence rate is computed over a rolling window of 7 days from d-9 to d-3. This methodology aims at reducing measurement error. Second, for privacy reason, the open-data file transforms the continuous variable into a right-censored discrete variable taking 8 values.
Urban areas.
are defined by the INSEE as a group of neighboring municipalities encompassing an urban center and its periphery made of municipalities where at least 40% of employed inhabitants works in the urban center, as of 2010. Big urban areas represent 85% of the French mainland population in 2014.
A.2. Measurement
A.2.1. Poor municipalities
We assign each municipality its median income as computed by INSEE from fiscal and social benefits data. We next order each municipality from the poorest to the richest.
Next, we classify municipalities into bins of equal population-weighted size. Put differently, we divide the French urban population into equal groups based on their municipality of residency. In our favorite specification we consider four quartiles, from the poorest to the richest. Because municipalities have different sizes, each group is made of a different number of municipalities. This weighting follows our empirical specifications.
A.2.2. Red and green zones
When deciding the gradual lifting of the lockdown, the Ministry of Public Health provided a map differentiating red (high-infection) and green (low-infection) départements on May 7. A département is an administrative unit in France that encompasses on average 645,000 inhabitants. There is a total of 101 départements in France, 94 of which are on continental Europe (we call “mainland”). This map distinguishes high- and low-infection areas on the basis of: (i) the share of ER visits for a COVID-19 suspicion; (ii) the occupancy rate of intensive care beds relative to the initial one; (iii) the testing rate relative to the needs. High-infection départements correspond to 44% of the urban population and to roughly 30% of mainland France départements, all in the North-Eastern quarter of the country (see Fig. A.1).
Fig. A.1.
High- (red) and low-infection (green) Départements as of May 7, 2020.
Note: Map of Départements issued by the Government on May 7, 2020. See source.
Although published in May, we use this distinction as a proximate measure of COVID-19 spread intensity before and during lockdown. We discuss this aspect in Section 5.1.
A.2.3. Incidence rate
We exploit incidence data provided by the French Public Health Institute on a weekly basis (see Appendix A.1 for more details). For each day , the incidence rate is given as a moving average from to . The graphical evidence (Fig. 6) therefore reports the coefficients on 12 key dates, corresponding to each day numbered 1, 7, 14, 21 or 28 of each of the 3 months of the observed period. We call this measure a weekly incidence rate for simplification in the core of the paper. The regression reported in Table 3 averages over dates every 7-day after the first one observed (October 6th, 2020), which corresponds to the average of the daily incidence rate over the observed period. We note the following important caveats about the data:
-
•
Unfortunately, it does not allow us to consider the first wave;
-
•
The data is categorized and right-censored, creating measurement error;
-
•
The data suffers the limitations we describe in Section 2 which is that people do not get tested systematically and that individuals’ propensity to get tested often reacts to local intensity of the infection;
In our analyses, we treat the incidence rate as a continuous variable and ignore right-censoring, that is: we transform each bin-indicator into the value of the center of the bin. For the last right-censored bin, there is no mid-point. We extrapolate the increasing trend of mid-points of the lower bins to get the 8th bin mid-point.
A.2.4. Labor market conditions
One novelty of this paper is to use administrative data to test whether labor market conditions explain the differential in excess mortality between poor and rich municipalities. We focus on two main characteristics of jobs that we expect to be key vectors for spreading the disease: (i) whether the worker kept on going to her workplace during the lockdown; (ii) whether the job involves frequent contacts with the public in usual business conditions (i.e. as measured before the lockdown).
As for the first dimension, for each municipality, we compute the share of essential workers42 based on individual employment data from the DADS and on a list of essential occupations built by the Paris Region Health Observatory (Mangeney et al., 2020).43 Note that, although this list was built by an administrative organization, it remains arbitrary by nature. However, to our knowledge, there is no better way at the moment to characterize workers that kept on going to their workplace during the lockdown.44
As for the second dimension, our proxy is based on the question “In your job, are you in direct contact with the public” that is available in a survey called DEFIS (see Appendix A.1). For each occupation code (at the 3-digit level), we compute the share of workers answering “Often” (v.s. “Sometimes” or “Never”). Using the DADS, we then compute the average of this index at the municipality level based on the occupation distribution of workers living in each municipality.
A.2.5. Housing conditions
Our last dimension of interest is the relation between housing conditions and excess mortality due to COVID-19. We use the average share of housing units that are overcrowded provided by INSEE at the municipality level. Overcrowded accommodations are those that have less than “one living room, one room for each couple, one room for each other adult aged 19 or older, one room for two children if they are of the same sex or are under 7 years of age, and one room per child otherwise”.
A.2.6. Interaction between labor market and housing conditions
To investigate the interactions between both mechanisms, we finally build an index at the municipality level, based on the partial census data files available for municipalities with more than 2,000 inhabitants. We compute the share of households with both an elderly person (over 65 y.o.) and a worker that is younger by at least 18 years (“multi-generational households” hereafter). This variable is meant to capture the fact that having different generations living in the same apartment increases the likelihood to get infected, and to potentially die for the elderly. This likelihood increases further if at least one of the younger members of the household works, as it potentially multiplies her social interactions.
Appendix B. Descriptive statistics
B.1. Sample
See Tables B.1 to B.4
Table B.1.
Descriptive statistics: Urban areas .
| Urban Areas |
|||||
|---|---|---|---|---|---|
| mean | sd | min | p50 | max | |
| Nb. Municipalities | 27 | 83 | 2 | 7 | 1738 |
| Population (10k) | 8.5 | 53 | .25 | 1.4 | 1247 |
| Poor (%) | 21 | 25 | 0 | 13 | 100 |
| Observations | 621 | ||||
Descriptive statistics across the 621 urban areas (UA). On average there are 27 municipalities in an UA, with an average total population of 85,000 inhabitants. On average, within an UA, 21% of municipalities are classified as poor.
Table B.2.
Descriptive statistics: Municipalities .
| Municipalities |
|||||
|---|---|---|---|---|---|
| mean | sd | min | p50 | max | |
| Mort. rate 2018 (10k) | 84 | 62 | 0 | 74 | 1545 |
| Mort. rate 2019 (10k) | 84 | 63 | 0 | 74 | 1254 |
| Mort. rate 2020 (10k) | 90 | 67 | 0 | 79 | 1691 |
| Population | 3188 | 11881 | 65 | 784 | 466351 |
| Share 65y.o. (%) | 17 | 6.6 | 0 | 17 | 63 |
| Median Income (1k) | 22 | 3 | 12 | 21 | 46 |
| Observations | 16640 | ||||
Descriptive statistics across the 16,640 municipalities. The average mortality rate (per 10,000 inhabitants) was 84 in 2018 and 2019 and rose to 90 in 2020. The average population of municipalities is 3,188, of which 17% are aged 65 or older. Municipalities’ median income is, on average, 22,000 euro.
Table B.3.
Descriptive statistics: Urban areas, by zone .
| mean | sd | min | p50 | max | count | |
|---|---|---|---|---|---|---|
| Red zone | ||||||
| Nb. Municipalities | 39 | 133 | 2 | 8 | 1738 | 191 |
| Population (10k) | 12 | 91 | .25 | 1.4 | 1247 | 191 |
| Poor (%) | 25 | 26 | 0 | 18 | 100 | 191 |
| Green zone | ||||||
| Nb. Municipalities | 22 | 46 | 2 | 6 | 505 | 430 |
| Population (10k) | 6.8 | 20 | .25 | 1.3 | 225 | 430 |
| Poor (%) | 20 | 24 | 0 | 10 | 100 | 430 |
Descriptive statistics across the urban areas (UA) of red (191 UA) and green (430 UA) zones.
Table B.4.
Descriptive statistics: Municipalities, by zone .
| mean | sd | min | p50 | max | count | |
|---|---|---|---|---|---|---|
| Red zone | ||||||
| Mort. rate 2018 (10k) | 81 | 65 | 0 | 72 | 1545 | 7000 |
| Mort. rate 2019 (10k) | 81 | 65 | 0 | 72 | 1254 | 7000 |
| Mort. rate 2020 (10k) | 89 | 73 | 0 | 79 | 1691 | 7000 |
| Population | 3330 | 12154 | 65 | 606 | 276219 | 7000 |
| Share 65y.o. (%) | 16 | 6.2 | 0 | 16 | 51 | 7000 |
| Median Income (1k) | 22 | 3.4 | 13 | 22 | 43 | 7000 |
| Green zone | ||||||
| Mort. rate 2018 (10k) | 85 | 59 | 0 | 75 | 915 | 9640 |
| Mort. rate 2019 (10k) | 86 | 61 | 0 | 76 | 1085 | 9640 |
| Mort. rate 2020 (10k) | 90 | 63 | 0 | 79 | 949 | 9640 |
| Population | 3085 | 11678 | 80 | 931 | 466351 | 9640 |
| Share 65y.o. (%) | 18 | 6.7 | 0 | 17 | 63 | 9640 |
| Median Income (1k) | 21 | 2.7 | 12 | 21 | 46 | 9640 |
Descriptive statistics across the 16,640 municipalities divided into red (7,000 municipalities) and green (9,640 municipalities) zones.
B.2. Lockdown
Appendix C. Income gradient: robustness and falsification
C.1. Income gradient: alternative definitions and robustness
C.1.1. Empirical approach
In this appendix we take a more comprehensive approach and contrast the evolution of excess mortality rate in all four quartiles of municipalities’ median income, taking the richest () as the reference. To do so, we estimate the following model:
| (5) |
Where all definitions (concept, subscripts, controls and standard errors) are the same as in Eq. (2). The coefficients of interest are , and . They estimate the difference in excess mortality rate between richest municipalities () and each of the three other quartiles (, and ), respectively.
The identification assumption remains: the three coefficients identify the heterogeneity in the causal (total) effect of the pandemic on excess mortality under the hypothesis that, absent COVID-19 and the associated public policies, the average difference in the evolution of mortality in a given calendar period (in 2020 vs. before) between rich and poor municipalities of the same urban area would have remained stable.
C.1.2. Main results
Table C.1 reports the estimates of coefficients , and from Eq. (5). It is the equivalent of Table 1. On average, within a given urban area, and once population size and age are controlled for, municipalities of the poorest quartile had an excess mortality rate of 4.216 (deaths per 10k inhabitants) higher than the richest municipalities. This has to be compared with the baseline average of 6.584 (deaths per 10k inhabitants) across municipalities of the richest quartile. Excess mortality is also significantly higher in municipalities of the two other quartiles than in municipalities of the richest quartile, but for both and the difference with is half smaller than the one observed between and .
Columns (2) and (3) consider the first (i.e. March–April) and second (i.e. October–December) waves, respectively. The income gradient is striking in both waves and of very similar size. We observe no gradient when we focus on excess mortality outside of these two waves (column (4)).
Table C.1.
Excess mortality rate by municipality income .
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| 2020 | Wave 1 | Wave 2 | No wave | |
| Q1 (poor) | 4.216*** | 1.986** | 1.975*** | 0.255 |
| (1.157) | (0.796) | (0.416) | (0.347) | |
| Q2 | 2.280** | 1.170** | 1.476*** | −0.365 |
| (0.926) | (0.484) | (0.406) | (0.380) | |
| Q3 | 2.229*** | 1.122*** | 1.041** | 0.0661 |
| (0.585) | (0.339) | (0.440) | (0.328) | |
| Controls | ✓ | ✓ | ✓ | ✓ |
| Urban area FE. | ✓ | ✓ | ✓ | ✓ |
| Q4 average | 6.584 | 2.674 | 3.682 | 0.228 |
| Observations | 16640 | 16640 | 16640 | 16640 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table reports the coefficients associated with Eq. (5). The independent variable, excess mortality rate, is computed considering four different time periods: the whole year (column 1), wave 1 (March to April, column 2), wave 2 (October to December, column 3) and other months in 2020 outside the two waves (January, February and from May to September, column 4). By construction, column 1 is the sum of column 2 to 4. The average line reports the average of the predicted value of the dependent variable in municipalities. Controls include total population size and the share of the population over 65 years old.
C.1.3. Alternative grouping
The monotonic gradient can also be seen when using alternative grouping in municipalities instead of quartiles. In Table C.2 below we estimate two alternative specifications of Eq. (5). Columns (1) to (4) reproduce Table C.1 using 10 deciles of income (instead of four quartiles) to group municipalities. Similarly, columns (5) to (8) repeat the exercise using directly the continuous (log of) municipalities’ median income.
Table C.2.
Excess mortality rate by municipality income .
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| 2020 | Wave 1 | Wave 2 | No wave | 2020 | Wave 1 | Wave 2 | No wave | |
| Q1 (poor) | 6.822*** | 3.235** | 3.109*** | 0.478 | ||||
| (1.402) | (1.283) | (0.557) | (0.444) | |||||
| Q2 | 5.543*** | 2.589*** | 2.030*** | 0.924 | ||||
| (1.036) | (0.444) | (0.520) | (0.587) | |||||
| Q3 | 3.629*** | 1.960*** | 1.932*** | −0.263 | ||||
| (0.913) | (0.397) | (0.499) | (0.551) | |||||
| Q4 | 4.343*** | 2.080*** | 2.155*** | 0.108 | ||||
| (1.096) | (0.550) | (0.516) | (0.491) | |||||
| Q5 | 3.439*** | 1.964*** | 1.354** | 0.121 | ||||
| (1.119) | (0.412) | (0.552) | (0.603) | |||||
| Q6 | 4.052*** | 1.994*** | 1.714*** | 0.344 | ||||
| (0.647) | (0.272) | (0.497) | (0.428) | |||||
| Q7 | 3.647*** | 1.865*** | 1.500** | 0.281 | ||||
| (1.010) | (0.361) | (0.676) | (0.565) | |||||
| Q8 | 3.277*** | 1.795*** | 0.677* | 0.805 | ||||
| (0.760) | (0.350) | (0.377) | (0.510) | |||||
| Q9 | 1.818*** | 0.970*** | 0.553* | 0.294 | ||||
| (0.450) | (0.314) | (0.331) | (0.323) | |||||
| log Median Income | −10.07*** | −4.311*** | −4.820*** | −0.934 | ||||
| (1.993) | (1.479) | (0.751) | (0.766) | |||||
| Controls | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Urban area FE. | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Richest average | 5.079 | 1.945 | 3.232 | −0.0984 | ||||
| Observations | 16640 | 16640 | 16640 | 16640 | 16640 | 16640 | 16640 | 16640 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table reports the coefficients associated to Eq. (5). The independent variable, excess mortality rate, is computed considering four different time periods: the whole year (column 1), wave 1 (Mars to April, column 2), wave 2 (October to December, column 3) and other months in 2020 outside the two waves (January, February and from May to September, column 4). By construction, column 1 (5) is the sum of columns 2 to 4 (6 to 8). The average line reports the average of the predicted value of the dependent variable in municipalities.
C.2. Robustness checks
C.2.1. Excluding elderly care homes
Elderly care homes (EHPADs in the French acronym) were strongly hit by the COVID-19 epidemics. If EHPADs are not distributed homogeneously across municipalities, they could drive the difference between income groups (in one way or another). To exclude the threat of this confounding factor, we exclude deaths recorded from such institutions from our sample and re-estimate our model of Eq. (2). Table C.3 displays the results in the same format as Table 1. Although lower in numbers, the main conclusion remains: an income gradient appears during epidemic waves.
The gradient in wave 1 is both large (+1.021 per 10k inhabitants) and insignificant. As explained in the core of the paper, this is largely due to the unequal spread of COVID-19 when the first lockdown started. If one considers only the red zone, the estimated coefficient is 1.945 (***). We therefore conclude from this exercise that EHPADs do not explain the entire increase in the gradient.
Table C.3.
No elderly care homes .
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| 2020 | Wave 1 | Wave 2 | No wave | |
| Q1 (poor) | 2.524** | 1.021 | 1.139*** | 0.363 |
| (1.004) | (0.648) | (0.310) | (0.327) | |
| Controls | ✓ | ✓ | ✓ | ✓ |
| Urban area FE. | ✓ | ✓ | ✓ | ✓ |
| Non poor average | 6.486 | 2.784 | 3.831 | −0.129 |
| Observations | 16640 | 16640 | 16640 | 16640 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table reports the coefficients associated to Eq. (2). The independent variable, excess mortality rate, is computed considering four different time periods: the whole year (column 1), wave 1 (Mars to April, column 2), wave 2 (October to December, column 3) and other months in 2020 outside the two waves (January, February and from May to September, column 4). By construction, column 1 is the sum of column 2 to 4. The non-poor average line reports the average of the predicted value of the dependent variable in non-poor municipalities.
C.2.2. Falsification test
Fig. C.1 shows the results from the estimation of Eq. (5) using excess mortality rate based on 2018 as the sole baseline. This implies that the mortality rate of 2020 is now compared to 2018 instead of the average mortality of 2018 and 2019.45 We also run a falsification test comparing mortality in 2019 to 2018.
Fig. C.1.
Falsification test.
Note: This Figure plots the coefficient as estimated from Eq. (2) using two alternative dependent variables. The black solid line shows the relative evolution of excess mortality in 2019 for poorest municipalities () as compared to others. For the sake of comparison, we also display the excess mortality of 2020 as compared to the same, 2018 baseline.
The gray dotted line shows that using 2018 as the only reference point does not alter our main results too much, although having only one year of reference makes our measure more sensitive to year-specific shocks. Nevertheless, two take away points emerge from the black line. Overall, comparing 2019 to 2018 yields no significant difference in yearly excess mortality between poor and non-poor municipalities. Excess mortality is smaller for richer municipalities over some short periods (in August and September) but the estimated effects always remain smaller than 1 death per 10,000 inhabitants (i.e. about 0.3 death in the average municipality of our sample).
C.3. Income gradient by age
See Fig. C.2.
Appendix D. Urban-area level analysis
To explore the validity of our results at the urban-area level, we first measure urban-area specific gradients by estimating the following model:
| (6) |
We include our baseline controls: population and share of residents older than 65 years old. The main difference from the model of Eq. (2) lies in the which is urban area-specific (while in (2) is not). Put differently, this model adds an interaction between the urban area indicators () and the indicator.46 That is to say, this model estimates one gradient per urban area. It follows that (6) can only be estimated on the 421 urban areas that host both poor and non-poor municipalities.
Next, we measure the intensity of the mortality shocks at the urban-area level. To do this, we simply compute each urban-area specific excess mortality in 2020. This is Eq. (1) at the urban-area level (instead of municipality level). When measuring the urban-area excess mortality, we sum all excess deaths from every municipality, irrespective of their income level.
In Table D.1 below we regress urban-area month-specific gradient as measured in Eq. (6) on urban-area month-specific excess mortality. This is to understand how the local gradients evolve with the magnitude of the mortality shock. The coefficient in column (1) corresponds to a pooled regression where each of the 421 urban areas is present 12 times (one per month; and we cluster standard errors by urban area). The coefficient indicates that increasing urban-area level excess mortality rate by one death (per 10k inhabitants) also increases the income gradient in mortality by 0.373 death (per 10k inhabitants). Column (2) next introduces an urban-area fixed effect and therefore only considers the changes across months to identify the effect. Columns (3) and (4) reproduce columns (1) and (2), respectively, weighting observations by urban-area population. They mostly ensure that the correlation between excess mortality and gradient is not driven by small urban areas only. Columns (2) to (4) report results that are qualitatively similar to column (1). That is to say: on average, when an urban area faces a greater mortality, a within urban area gradient appears (the share of all death coming from the poorest municipalities of the urban area increases).
We next investigate whether the 234 urban areas that suffered increased mortality in both waves also display an income gradient in the second wave. This amounts to testing the hypothesis that the positive relationship between the income gradient and excess mortality is a “structural” feature of the epidemics. The alternative would be that the income gradient only captures a difference in the timing of deaths between inhabitants of poor and non-poor municipalities. Table D.2 shows that, in both waves, the average (and median) gradient of these 234 urban areas was greater than 0. That indicates that residents of poorer municipalities within an urban area were more likely to die (more) in 2020 (than before) than residents of non-poor municipalities. Importantly, the positive gradient is also found in the second wave indicating that there has been no convergence in mortality rates between poorer and richer municipalities of these urban areas over the two waves.
Table D.1.
Gradient and excess mortality .
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Gradient | Gradient | Gradient | Gradient | |
| UA excess m.r. | 0.373*** | 0.356*** | 0.319*** | 0.319*** |
| (0.0767) | (0.0833) | (0.0369) | (0.0358) | |
| Constant | −0.126 | −0.111 | −0.0418 | −0.0425 |
| (0.149) | (0.0754) | (0.115) | (0.0276) | |
| UA FE | ✓ | ✓ | ||
| Weights | ✓ | ✓ | ||
| Observations | 5052 | 5052 | 5052 | 5052 |
| UA | 421 | 421 | 421 | 421 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
NOTE: This table reports the coefficients associated with a regression of urban areas’ month-specific gradient and excess mortality. 421 urban areas have an estimated income gradient and they are observed in the 12 months (5,052 observations). Column (1) is a pooled regression while column (2) introduces an urban area fixed effect. Column (3) and (4) repeat (1) and (2), respectively, weighting by urban areas population.
We remain cautious in interpreting the relative size of these gradients. The reduction of the average gradient (between wave 1 and 2) indicates a slower divergence between poorer and richer municipalities in the second wave. But such effect could be the product of many factors: a) we document in the paper that wave 2 is more diffuse over France than wave 1 (an aspect that is mirrored in the higher dispersion of gradients in wave 2 shown in Table D.2), b) first- and second-wave policy response differed, c) there is potential learning from municipalities (i.e. residents, governing bodies, etc.).
Table D.2.
Persistence of a gradient .
| mean | sd | p50 | min | max | count | weights | |
|---|---|---|---|---|---|---|---|
| Gradient, Wave 1 | 2.84 | 15.91 | 1.05 | −67.27 | 72.55 | 234 | 234.00 |
| Gradient, Wave 2 | 1.37 | 19.60 | 0.28 | −103.15 | 76.70 | 234 | 234.00 |
| Gradient, Wave 1 | 1.49 | 5.67 | 1.62 | −67.27 | 72.55 | 234 | 4053.86 |
| Gradient, Wave 2 | 1.02 | 5.82 | 1.72 | −103.15 | 76.70 | 234 | 4053.86 |
NOTE: This table describes the income gradient in both waves across the 234 urban areas that suffered excess mortality in both waves. The last two row are weighted by urban-area population (their total weights are expressed in 10k inhabitants).
Appendix E. Red and green zones
See Table E.1.
Table E.1.
Triple-difference regression on the number of deaths, wave 1 .
| Number of deaths, wave 1 | ||
|---|---|---|
| 2020 1 | 0.12952*** | 0.18605*** |
| (0.03773) | (0.05675) | |
| 2020 1 ×Red area 1 | 0.51121*** | 0.75283*** |
| (0.17458) | (0.26704) | |
| 2020 1 ×Poor 1 | −0.05089 | 0.19666* |
| (0.03267) | (0.11114) | |
| 2020 1 ×Red area 1 ×Poor 1 | 0.81664* | 2.41010** |
| (0.41663) | (1.08131) | |
| Municipality FE | ✓ | ✓ |
| Sample | All | Major urban centers |
| municipalities | and their outskirts | |
| Control outcome mean | 1.736 | 2.290 |
| Observations | 188688 | 100686 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the département level.
NOTE: This table reports coefficients from a triple-difference regression on the number of deaths in wave 1 (March–April) over the years 2018–2020. The three dimensions are (i) time, with 2020 being the post period; (ii) the level of infection in the département before the first wave; (iii) the poverty status of the municipality, defined as the bottom quartile of the national distribution of municipal income weighted by the municipal population size. We include municipality fixed-effects to account for time-invariant factors at the municipal level, such as the population measured in 2014. The control outcome mean is the mean number of deaths in March–April in the years 2018–2019 in non-poor municipalities in green zones.
Appendix F. Mechanisms
See Table F.1, Table F.2, Table F.3
Table F.1.
Summary statistics of mechanism variables .
| France |
Poor |
Non-Poor |
||||
|---|---|---|---|---|---|---|
| mean | sd | mean | sd | mean | sd | |
| Share of over-crowded housing | 0.0554 | 0.0559 | 0.0778 | 0.0716 | 0.0479 | 0.0472 |
| Index of frequent contact | 0.5999 | 0.0294 | 0.6077 | 0.0285 | 0.5972 | 0.0293 |
| Share of essential workers | 0.2063 | 0.0522 | 0.2375 | 0.0392 | 0.1959 | 0.0519 |
| Share of multi-generational households | 0.0225 | 0.0104 | 0.0240 | 0.0116 | 0.0218 | 0.0097 |
| Observations | 16640 | 1851 | 14789 | |||
This table describes the different mechanism variables for the whole country and by poverty status. Being poor means living in a municipality belonging to the bottom 25% of the national income distribution weighted by population size.
Table F.2.
Relationship between poverty status and mechanism variables .
| Index of frequent contact | Share of essential workers | Share of over-crowded housing | Multigenerational hh | |
|---|---|---|---|---|
| Main coefficient | 0.13598*** | 0.15640*** | 0.28968*** | 0.06955 |
| (0.04143) | (0.01664) | (0.04138) | (0.05136) | |
| Urban areas FE | ✓ | ✓ | ✓ | ✓ |
| Controls | ✓ | ✓ | ✓ | ✓ |
| Control outcome mean | 0.251 | 0.251 | 0.251 | 0.272 |
| Observations | 16267 | 16267 | 16267 | 3971 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses are clustered at the département level. This table shows the result of regressing the poverty dummy on mechanism variables measuring either housing conditions or occupational exposure and the interaction of these variables via the variable multigenerational household. The poverty dummy is equal to one for the bottom 25% of the national distribution of municipal median income weighted by population size. Each column reports the result of a separate regression examining one mechanism. The main coefficient corresponds to the correlation between each of the mechanism variable and poverty. The mechanism variables have been standardized such that coefficients can be interpreted in terms of the effect of a one standard-deviation change, and can be compared with each other. All regressions include urban areas fixed-effects and control for total population and for the share of inhabitants over 65 y.o. in the municipality.
Table F.3.
Horse-race between mechanism variables .
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Incidence rate (per 100k. inh.), wave 2 | |||||
| Poor (Q1) | 5.92693*** | 5.02211** | 4.18254* | 0.04053 | −1.06828 |
| (2.11590) | (2.36330) | (2.15177) | (2.56955) | (2.17981) | |
| Index of frequent contact | 4.55486* | −3.46067 | |||
| (2.45458) | (3.40661) | ||||
| Share of essential workers | 5.04624* | 4.89758 | |||
| (2.98801) | (4.02379) | ||||
| Share of over-crowded housing | 17.69906*** | 18.00957*** | |||
| (1.73201) | (2.18879) | ||||
| Urban areas FE | ✓ | ✓ | ✓ | ✓ | ✓ |
| Controls | ✓ | ✓ | ✓ | ✓ | ✓ |
| Control outcome mean | 236.111 | 236.277 | 236.096 | 237.359 | 237.241 |
| Adjusted R2 | 0.6922 | 0.6928 | 0.6934 | 0.6990 | 0.6997 |
| Observations | 16267 | 16267 | 16267 | 16267 | 16267 |
* 0.1, ** 0.05, *** 0.01. Standard errors in parentheses clustered at the urban-area level.
This table shows the result of regressing municipalities’ incidence rate on a variable measuring either poverty, housing conditions or occupational exposure. The table only shows results for the second wave (October–December) – that is when test data are available – on municipalities in all urban areas. The first column only examines the poverty channel. Columns (2) to (4) respectively include one additional variable capturing either the occupation or housing mechanism. The last column includes both the poverty dummy and all the mechanism variables. All regressions include urban-area fixed-effects and control for total population and for the share of inhabitants over 65 y.o. in the municipality. The mechanism variables have been normalized such that coefficients can be interpreted in terms of the effect of a one standard-deviation change, and can be compared with each other. The outcome-mean line reports the mean of the incidence rate per 100K inhabitants (conditional on controls and fixed effects) in each wave.
Appendix G. Supplementary data
The following is the Supplementary material related to this article.
The supplementary material contains the code and data necessary to reproduce the paper’s results.
References
- Abedi V., Olulana O., Avula V., Chaudhary D., Khan A., Shahjouei S., Li J., Zand R. Racial, economic, and health inequality and COVID-19 infection in the United States. J. Racial Ethn. Health Dispar. 2020 doi: 10.1007/s40615-020-00833-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adler N.E., Rehkopf D.H. US disparities in health: descriptions, causes, and mechanisms. Annu. Rev. Publ. Health. 2008;29:235–252. doi: 10.1146/annurev.publhealth.29.020907.090852. [DOI] [PubMed] [Google Scholar]
- Alfani G. Epidemics, inequality, and poverty in preindustrial and early industrial time. J. Econ. Lit. 2021 [Google Scholar]
- Almagro M., Coven J., Gupta A., Orane-Hutchinson A. 2020. Racial disparities in frontline workers and housing crowding during COVID-19: Evidence from geolocation data. Available At SSRN 3695249. [Google Scholar]
- Almagro M., Orane-Hutchinson A. Covid Economics: Vetted and Real-Time Papers, vol. 13. 2020. The determinants of the differential exposure to COVID-19 in new york city and their evolution over time. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelucci M., Angrisani M., Bennett D., Kapteyn A., Schaner S.G. Institute of Labor Economics (IZA); 2020. Remote Work and the Heterogeneous Impact of COVID-19 on Employment and Health: Technical Report 13620 13620. Publication Title: IZA Discussion Papers. URL https://ideas.repec.org/p/iza/izadps/dp13620.html. [Google Scholar]
- Ashraf B.N. Socioeconomic conditions, government interventions and health outcomes during COVID-19. Covid Econ. 2020;37:141–162. [Google Scholar]
- Balmford B., Annan J.D., Hargreaves J.C., Altoè M., Bateman I.J. Cross-country comparisons of COVID-19: Policy, politics and the price of life. Environ. Resour. Econ. 2020;76(4):525–551. doi: 10.1007/s10640-020-00466-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee A., Pasea L., Harris S., Gonzalez-Izquierdo A., Torralbo A., Shallcross L., Noursadeghi M., Pillay D., Sebire N., Holmes C., et al. Estimating excess 1-year mortality associated with the COVID-19 pandemic according to underlying conditions and age: a population-based cohort study. Lancet. 2020 doi: 10.1016/S0140-6736(20)30854-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beach B., Clay K., Saavedra M.H. The 1918 influenza pandemic and its lessons for COVID-19. J. Econ. Lit. 2021 [Google Scholar]
- Beaney T., Clarke J.M., Jain V., Golestaneh A.K., Lyons G., Salman D., Majeed A. Excess mortality: the gold standard in measuring the impact of COVID-19 worldwide? J. R. Soc. Med. 2020;113(9):329–334. doi: 10.1177/0141076820956802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belot M., Choi S., Jamison J.C., Papageorge N.W., Tripodi E., Van den Broek-Altenburg E. 2020. Unequal Consequences of Covid 19 Across Age and Income: Representative Evidence from Six Countries: CEPR Discussion Paper No. DP14908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanpain N. L’espérance de vie par niveau de vie: chez les hommes, 13 ans d’écart entre les plus aisés et les plus modestes. INSEE Première. 2018;(1687) [Google Scholar]
- Borjas G.J. Social Science Research Network; Rochester, NY: 2020. Demographic Determinants of Testing Incidence and COVID-19 Infections in New York City Neighborhoods: SSRN Scholarly Paper ID 3572329. URL https://papers.ssrn.com/abstract=3572329. [DOI] [Google Scholar]
- Böttcher L., D’Orsogna M., Chou T. 2021. Using excess deaths and testing statistics to improve estimates of COVID-19 mortalities. arXiv preprint arXiv:2101.03467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodeur A., Cook N., Wright T. On the effects of COVID-19 safer-at-home policies on social distancing, car crashes and pollution. J. Environ. Econ. Manag. 2021;106 doi: 10.1016/j.jeem.2021.102427. URL https://www.sciencedirect.com/science/article/pii/S0095069621000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown C.S., Ravallion M. National Bureau of Economic Research; 2020. Inequality and the Coronavirus: Socioeconomic Covariates of Behavioral Responses and Viral Outcomes Across US Counties: Technical Report w27549. URL https://www.nber.org/papers/w27549. [DOI] [Google Scholar]
- Bullinger L.R., Carr J.B., Packham A. National Bureau of Economic Research; 2020. COVID-19 and Crime: Effects of Stay-at-Home Orders on Domestic Violence: Technical Report w27667. URL https://www.nber.org/papers/w27667. [DOI] [Google Scholar]
- Butikofer A., Karadakic R., Salvanes K.G. 2021. Income Inequality and Mortality: A Norwegian Perspective: NHH Dept. of Economics Discussion Paper, No. 04. [Google Scholar]
- Calderon-Anyosa R.J., Kaufman J.S. Impact of COVID-19 lockdown policy on homicide, suicide, and motor vehicle deaths in Peru. Prevent. Med. 2021;143 doi: 10.1016/j.ypmed.2020.106331. URL https://www.sciencedirect.com/science/article/pii/S0091743520303625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calderón-Larrañaga A., Vetrano D.L., Rizzuto D., Bellander T., Fratiglioni L., Dekhtyar S. High excess mortality in areas with young and socially vulnerable populations during the COVID-19 outbreak in Stockholm Region, Sweden. BMJ Glob. Health. 2020;5(10) doi: 10.1136/bmjgh-2020-003595. URL https://gh.bmj.com/content/5/10/e003595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case A., Lubotsky D., Paxson C. Economic status and health in childhood: The origins of the gradient. Amer. Econ. Rev. 2002;92(5):1308–1334. doi: 10.1257/000282802762024520. [DOI] [PubMed] [Google Scholar]
- Caul S. Deaths involving Covid-19 by local area and socioeconomic deprivation: Deaths occurring between 1 March and 31 July 2020. Stat. Bull. 2020 [Google Scholar]
- Chen J.T., Krieger N. Revealing the unequal burden of COVID-19 by income, race/Ethnicity, and household crowding: US county versus zip code analyses. J. Publ. Health Manag. Pract. 2021;27(1):S43–S56. doi: 10.1097/PHH.0000000000001263. [DOI] [PubMed] [Google Scholar]
- Chetty R., Stepner M., Abraham S., Lin S., Scuderi B., Turner N., Bergeron A., Cutler D. The association between income and life expectancy in the United States, 2001–2014. JAMA. 2016;315(16):1750–1766. doi: 10.1001/jama.2016.4226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole M., Ozgen C., Strobl E. Institute of Labor Economics (IZA); 2020. Air Pollution Exposure and COVID-19: Technical Report. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie J., Schwandt H. Mortality inequality: the good news from a county-level approach. J. Econ. Perspect. 2016;30(2):29–52. doi: 10.1257/jep.30.2.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie J., Schwandt H., Thuilliez J. Pauvreté, Egalité, Mortalité: mortality (in) equality in France and the United States. J. Popul. Econ. 2020;33(1):197–231. [Google Scholar]
- Cutler D., Deaton A., Lleras-Muney A. The determinants of mortality. J. Econ. Perspect. 2006;20(3):97–120. [Google Scholar]
- Cutler D.M., Lleras-Muney A., Vogl T. The Oxford Handbook of Health Economics. 2012. Socioeconomic status and health: Dimensions and mechanisms. [Google Scholar]
- Decoster A., Minten T., Spinnewijn J. The income gradient in mortality during the covid-19 crisis: evidence from belgium. The Journal of Economic Inequality. 2021:1–20. doi: 10.1007/s10888-021-09505-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmet K., Wacziarg R. National Bureau of Economic Research; 2020. Understanding Spatial Variation in COVID-19 across the United States: Technical Report w27329. URL https://www.nber.org/papers/w27329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drefahl S., Wallace M., Mussino E., Aradhya S., Kolk M., Brandén M., Malmberg B., Andersson G. A population-based cohort study of socio-demographic risk factors for COVID-19 deaths in Sweden. Nature Commun. 2020;11(1):5097. doi: 10.1038/s41467-020-18926-3. URL https://www.nature.com/articles/s41467-020-18926-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foucart S., Horel S. Dépistage du coronavirus : les raisons du fiasco français sur les tests. Le Monde.Fr. 2020 URL https://www.lemonde.fr/planete/article/2020/04/24/nous-attendons-d-etre-contactes-par-l-ars-mais-il-ne-se-passe-rien-le-fiasco-des-tests-en-france_6037647_3244.html. [Google Scholar]
- Fouillet A., Pontais I., Caserio-Schönemann C. Excess all-cause mortality during the first wave of the COVID-19 epidemic in France, March to May 2020. Eurosurveillance. 2020;25(34) doi: 10.2807/1560-7917.ES.2020.25.34.2001485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaeser E.L., Gorback C.S., Redding S.J. National Bureau of Economic Research; 2020. How much does COVID-19 Increase with Mobility? Evidence from New York and Four other US Cities: Technical Report. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Google LLC E.L. 2021. Google COVID-19 community mobility reports. Accessed 02/15/2021, https://www.google.com/covid19/mobility/ [Google Scholar]
- Gottlieb C., Grobovšek J., Poschke M., Saltiel F. Working from home in developing countries. Eur. Econ. Rev. 2021;133 doi: 10.1016/j.euroecorev.2021.103679. URL https://www.sciencedirect.com/science/article/pii/S0014292121000325. [DOI] [Google Scholar]
- Jung J., Manley J., Shrestha V. Social Science Research Network; Rochester, NY: 2020. Coronavirus Infections and Deaths by Poverty Status: The Effects of Social Distancing: SSRN Scholarly Paper ID 3623430. URL https://papers.ssrn.com/abstract=3623430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.J., Bostwick W. Social vulnerability and racial inequality in COVID-19 deaths in chicago. Health Educ. Behav. 2020;47(4):509–513. doi: 10.1177/1090198120929677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knittel C.R., Ozaltun B. National Bureau of Economic Research; 2020. What Does and Does Not Correlate with COVID-19 Death Rates: Technical Report w27391. URL https://www.nber.org/papers/w27391. [DOI] [Google Scholar]
- Kraay A.N., Han P., Kambhampati A.K., Wikswo M.E., Mirza S.A., Lopman B.A. Impact of non-pharmaceutical interventions for SARS-CoV-2 on norovirus outbreaks: an analysis of outbreaks reported by 9 US states. MedRxiv. 2020 doi: 10.1101/2020.11.25.20237115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krieger N., Waterman P.D., Chen J.T. COVID-19 and overall mortality inequities in the surge in death rates by zip code characteristics: Massachusetts, January 1 to May 19, 2020. Am J Public Health. 2020;110(12):1850–1852. doi: 10.2105/AJPH.2020.305913. URL https://ajph.aphapublications.org/doi/full/10.2105/AJPH.2020.305913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kung S., Doppen M., Black M., Braithwaite I., Kearns C., Weatherall M., Beasley R., Kearns N. Underestimation of COVID-19 mortality during the pandemic. ERJ Open Res. 2020 doi: 10.1183/23120541.00766-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bras H. L’épidémie et son terrain social. Fondation Jean-Jaurès. 2020 Library Catalog: jean-jaures.org. URL https://jean-jaures.org/nos-productions/l-epidemie-et-son-terrain-social. [Google Scholar]
- Le Minez S., Roux V. 2021. 2020 : une hausse des décès inédite depuis 70 ans. INSEE Première, no. 1847. [Google Scholar]
- LeClere F.B., Rogers R.G., Peters K.D. Ethnicity and mortality in the United States: individual and community correlates. Soc. Forces. 1997;76(1):169–198. [Google Scholar]
- Mackenbach J.P., Valverde J.R., Bopp M., Brø nnum Hansen H., Costa G., Deboosere P., Kalediene R., Kovács K., Leinsalu M., Martikainen P., et al. Progress against inequalities in mortality: register-based study of 15 European countries between 1990 and 2015. Eur. J. Epidemiol. 2019;34(12):1131–1142. doi: 10.1007/s10654-019-00580-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangeney C., Bouscaren N., Telle-Lamberton M., Saunal A., Féron V. Paris Region Health Observatory; 2020. La Surmortalité Durant l’Epidémie de Covid-19 dans les Départements Franciliens: Technical report. URL https://www.ors-idf.org/nos-travaux/publications/la-surmortalite-durant-lepidemie-de-covid-19-dans-les-departements-franciliens.html. [Google Scholar]
- McIntyre R.S., Lee Y. Projected increases in suicide in Canada as a consequence of COVID-19. Psychiatry Res. 2020;290 doi: 10.1016/j.psychres.2020.113104. URL https://www.sciencedirect.com/science/article/pii/S0165178120310386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulligan C.B. National Bureau of Economic Research; 2021. Deaths of Despair and the Incidence of Excess Mortality in 2020: Technical Report. [Google Scholar]
- Naticchioni P., Scrutinio V., di Porto E., et al. Centre for Economic Performance, LSE; 2020. Partial Lockdown and the Spread of Covid-19: Lessons from the Italian Case: Technical Report. [Google Scholar]
- Palomino J.C., Rodríguez J.G., Sebastian R. Wage inequality and poverty effects of lockdown and social distancing in Europe. Eur. Econ. Rev. 2020;129 doi: 10.1016/j.euroecorev.2020.103564. URL https://www.sciencedirect.com/science/article/pii/S001429212030194X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papageorge N.W., Zahn M.V., Belot M., van den Broek-Altenburg E., Choi S., Jamison J.C., Tripodi E., et al. Institute of Labor Economics (IZA); 2020. Socio-Demographic Factors Associated with Self-Protecting Behavior during the COVID-19 Pandemic: Technical Report. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papon S., Robert-Bobée I. French National Statistical Institute (INSEE); 2020. Une hausse des décès deux fois plus forte pour les personnes nées à l’étranger que pour celles nées en France en mars-avril 2020: Technical Report. URL https://www.insee.fr/fr/statistiques/4627049. [Google Scholar]
- Persico C., Johnson K.R. 2020. The effects of increased pollution on COVID-19 cases and deaths. Available At SSRN 3633446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickett K.E., Pearl M. Multilevel analyses of neighbourhood socioeconomic context and health outcomes: a critical review. J. Epidemiol. Commun. Health. 2001;55(2):111–122. doi: 10.1136/jech.55.2.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raifman M.A., Raifman J.R. Disparities in the population at risk of severe illness from COVID-19 by race/Ethnicity and income. Am. J. Prev. Med. 2020;59(1):137–139. doi: 10.1016/j.amepre.2020.04.003. URL https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7183932/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera R., Rosenbaum J.E., Quispe W. Excess mortality in the United States during the first three months of the COVID-19 pandemic. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268820002617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert S.A. Socioeconomic position and health: the independent contribution of community socioeconomic context. Annu. Rev. Sociol. 1999;25(1):489–516. [Google Scholar]
- Sa F. Institute of Labor Economics (IZA); 2020. Socioeconomic Determinants of COVID-19 Infections and Mortality: Evidence from England and Wales: Technical Report. [Google Scholar]
- Scarpetta S., Pearson M., Colombo F., Guanais F. 2020. Testing for COVID-19: A way to lift confinement restrictions. OECD Policy Responses To Coronavirus (COVID-19). URL https://www.oecd.org/coronavirus/policy-responses/testing-for-covid-19-a-way-to-lift-confinement-restrictions-89756248/#boxsection-d1e31. [Google Scholar]
- Silverman J.D., Hupert N., Washburne A.D. Using influenza surveillance networks to estimate state-specific prevalence of SARS-CoV-2 in the United States. Sci. Transl. Med. 2020 doi: 10.1126/scitranslmed.abc1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snowden F.M. Yale University Press; 2019. Epidemics and Society: From the Black Death to the Present. [Google Scholar]
- Wiemers E.E., Abrahams S., AlFakhri M., Hotz V.J., Schoeni R.F., Seltzer J.A. Disparities in vulnerability to severe complications from COVID-19 in the United States. MedRxiv. 2020 doi: 10.1101/2020.05.28.20115899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson E.J., Walker A.J., Bhaskaran K., Bacon S., Bates C., Morton C.E., Curtis H.J., Mehrkar A., Evans D., Inglesby P., Cockburn J., McDonald H.I., MacKenna B., Tomlinson L., Douglas I.J., Rentsch C.T., Mathur R., Wong A.Y., Grieve R., Harrison D., Forbes H., Schultze A., Croker R., Parry J., Hester F., Harper S., Perera R., Evans S.J., Smeeth L., Goldacre B. Factors associated with COVID-19-related death using OpenSAFELY. Nature. 2020;584(7821):430–436. doi: 10.1038/s41586-020-2521-4. URL https://www.nature.com/articles/s41586-020-2521-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J., McCann A., Katz J., Peltier E., Deep Singh K. The Pandemic’s hidden toll: Half a million deaths. New York Times. 2021 URL https://www.nytimes.com/interactive/2020/04/21/world/coronavirus-missing-deaths.html. [Google Scholar]
- Yorifuji T., Matsumoto N., Takao S. Excess all-cause mortality during the COVID-19 outbreak in Japan. J. Epidemiol. 2021;31(1):90–92. doi: 10.2188/jea.JE20200492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X., et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet. 2020;395(10229):1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The supplementary material contains the code and data necessary to reproduce the paper’s results.