A joint deep learning model enables simultaneous batch effect correction, denoising, and clustering in single-cell transcriptomics

Abstract

Recent developments of single-cell RNA-seq (scRNA-seq) technologies have led to enormous biological discoveries. As the scale of scRNA-seq studies increases, a major challenge in analysis is batch effects, which are inevitable in studies involving human tissues. Most existing methods remove batch effects in a low-dimensional embedding space. Although useful for clustering, batch effects are still present in the gene expression space, leaving downstream gene-level analysis susceptible to batch effects. Recent studies have shown that batch effect correction in the gene expression space is much harder than in the embedding space. Methods such as Seurat 3.0 rely on the mutual nearest neighbor (MNN) approach to remove batch effects in gene expression, but MNN can only analyze two batches at a time, and it becomes computationally infeasible when the number of batches is large. Here, we present CarDEC, a joint deep learning model that simultaneously clusters and denoises scRNA-seq data while correcting batch effects both in the embedding and the gene expression space. Comprehensive evaluations spanning different species and tissues showed that CarDEC outperforms Scanorama, DCA + Combat, scVI, and MNN. With CarDEC denoising, non-highly variable genes offer as much signal for clustering as the highly variable genes (HVGs), suggesting that CarDEC substantially boosted information content in scRNA-seq. We also showed that trajectory analysis using CarDEC's denoised and batch-corrected expression as input revealed marker genes and transcription factors that are otherwise obscured in the presence of batch effects. CarDEC is computationally fast, making it a desirable tool for large-scale scRNA-seq studies.

Single-cell RNA sequencing (scRNA-seq) analysis has substantially advanced our understanding of cellular heterogeneity and transformed biomedical research. However, the analysis of scRNA-seq data remains confounded by batch effects, which are inevitable in analyses of human tissue and are prevalent in many scRNA-seq studies in general (Hicks et al. 2018; Lähnemann et al. 2020). Several methods have been developed to remove batch effects in scRNA-seq data analysis (Haghverdi et al. 2018; Lopez et al. 2018; Barkas et al. 2019; Korsunsky et al. 2019; Stuart et al. 2019; Welch et al. 2019; Li et al. 2020; Polanski et al. 2020). These methods can be divided into two categories: (1) batch correction in the low-dimensional embedding space, and (2) batch correction in the original gene expression space. Most published papers belong to the first category (Barkas et al. 2019; Korsunsky et al. 2019; Welch et al. 2019; Li et al. 2020; Polanski et al. 2020). Although useful for profiling the overall characteristics of cells such as clustering and trajectory reconstruction, these methods cannot be used for downstream gene-level analysis like differential expression and coexpression analysis.

A recent benchmarking study has shown that correcting batch effects in the gene expression space is much more challenging than in the embedding space (Luecken et al. 2020). Popular methods such as Seurat 3.0 (Stuart et al. 2019) rely on the mutual nearest neighbor (MNN) approach (Haghverdi et al. 2018) to remove batch effects in the gene expression space, but MNN can only analyze two batches at a time. Its performance is affected by the order in which batches are corrected and it quickly becomes computationally infeasible when the number of batches gets large. Moreover, our evaluations indicate that MNN performs poorly for removing batch effects for genes that are not highly variable. Non-highly variable genes represent the majority of genes in the genome, in which batch effects constitute a larger fraction of variance in the transcriptome and are much harder to correct.

To address this gap in the literature, we present count-adapted regularized deep embedded clustering (CarDEC), a joint deep learning framework for simultaneous batch effect correction, denoising, and clustering of scRNA-seq data. Rather than explicitly modeling batch effect, CarDEC jointly optimizes its reconstruction loss with a self-supervised clustering loss. By minimizing a clustering loss iteratively, the batch effects in the embedding are reduced and cell type signal is improved (Li et al. 2020). The denoised gene expression values, computed from this embedding using a decoder, are then corrected for batch effects as well. To address the difficulty of batch correcting genes that are not highly variable, which suffer from a lower cell type signal-to-noise ratio, we designed CarDEC using a branching architecture that treats highly variable genes (HVGs) and the remaining genes, which we designate as lowly variable genes (LVGs), as distinct feature blocks.

CarDEC is unique among batch effect correction methods in that it implicitly corrects for batch effects through joint optimization of its dual objective function rather than explicitly modeling batch effects using batch indicators as in methods such as MNN (Haghverdi et al. 2018) and scVI (Lopez et al. 2018). Moreover, it corrects batch effects both in the low-dimensional embedding space and the original gene expression space. CarDEC's architecture is founded on the idea of treating HVGs and LVGs as different “feature blocks,” which enables CarDEC to use the HVGs to drive the clustering loss, while still allowing the LVG reconstructions to depend on the rich, batch-corrected embedding learned from the HVGs, to help remove batch effects in the LVGs.

Results

Overview of CarDEC and evaluation

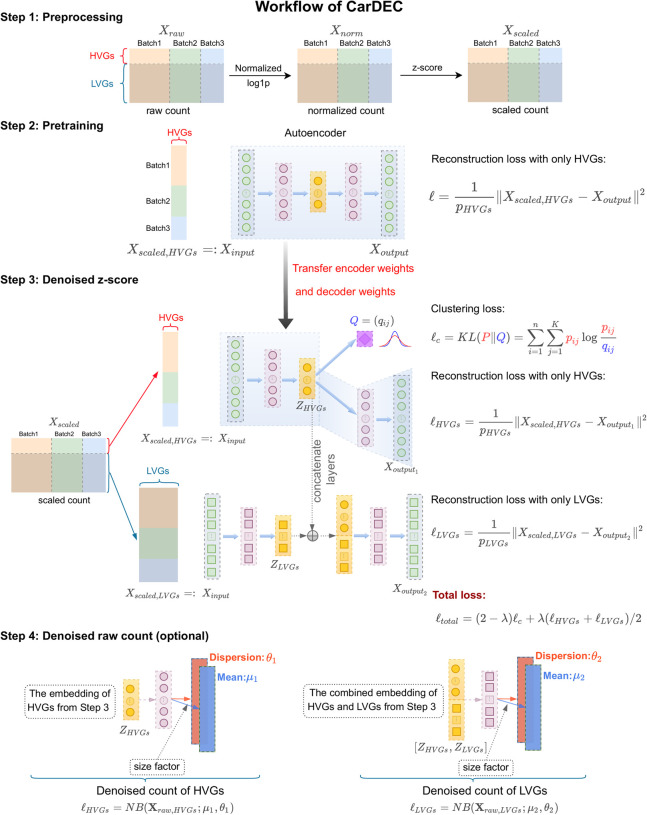
An outline of the CarDEC workflow is shown in Figure 1. CarDEC starts with data preprocessing and pretraining of an autoencoder using HVGs with a mean squared error reconstruction loss function. After pretraining, the weights learned from the pretrained autoencoder are transferred over to the main CarDEC model, which treats HVGs and LVGs as different feature blocks. The main CarDEC loss function is a weighted combination of the reconstruction losses for the HVGs and the LVGs, and a self-supervised clustering loss function driven by the HVGs. This combined loss function allows CarDEC to preserve local structure of the data during clustering (Guo et al. 2017). By minimizing this self-supervised combined loss function, CarDEC not only improves the low-dimensional embedding for clustering but the reconstructed genewise features, which are computed as a function of the low-dimensional embedding, are also denoised and batch effect–corrected, leading to improved gene expression quality.

Figure 1.

The workflow of CarDEC. The CarDEC workflow can be summarized in four steps that are depicted here: preprocessing, pretraining, denoising, and optionally, denoising on the count scale.

We evaluated CarDEC on a diverse set of challenging real data sets that range from human to mouse and have different flavors of batch effects. In our evaluations, we wished to assess two properties of CarDEC: (1) its ability to recover biological signals in the data, and (2) its ability to remove spurious technical signals driven by batch effects. An ideal method should strive to remove batch effects while maintaining true biological variations. We compared CarDEC with several state-of-the-art scRNA-seq methods for denoising, batch effect correction, and clustering. scVI (Lopez et al. 2018) and DCA (Eraslan et al. 2019) are multiuse methods that provide denoised counts in the gene expression feature space and also a low-dimensional embedding that can be used for tasks like clustering and visualization. scVI also attempts to correct for batch effects by conditioning on batch annotation when modeling the denoised counts with a zero-inflated negative binomial distribution. Because DCA is not designed for batch effect correction, to make a fair comparison, we applied Combat (Johnson et al. 2007) to DCA denoised gene expression. MNN (Haghverdi et al. 2018) is a batch correction method that merges batches in a pairwise manner and generates batch-corrected gene expression on a cosine scale. We used the implementation of the MNN method provided in the R programming language (R Core Team 2020). Scanorama (Hie et al. 2019) is also based on the mutual nearest neighbor idea, but it finds matching elements among all batches at once, thus speeding it up computationally and making the method invariant to batch order. scDeepCluster (Tian et al. 2019) is a clustering method that also draws inspiration from the self-supervised clustering loss (Guo et al. 2017). We provide the exact software implementations of these packages that we used in Supplemental Table S3.

To measure the degree of batch mixing, we examined the batchwise centroids after denoising and/or batch correction with each method by calculating a coefficient of variation (CV) metric. For each gene, a CV is calculated for a given cell type using the centroid of each batch in that cell type. Then, to obtain a single CV score, we take the weighted average of the cell type–specific CVs, in which the weight of a cell type is the fraction of the data set's cells that belong to that cell type. The reason for computing CV scores within cell types is that we expect minimal biological heterogeneity within cell types, so in the absence of batch effects we expect batch centroids to be similar to one another within, but not between, cell types. A higher value of CV corresponds to greater variation of gene expression among batches and less batch mixing, whereas a good batch effect removal method should drive the CV value close to zero.

Application to human pancreatic islet data from four protocols

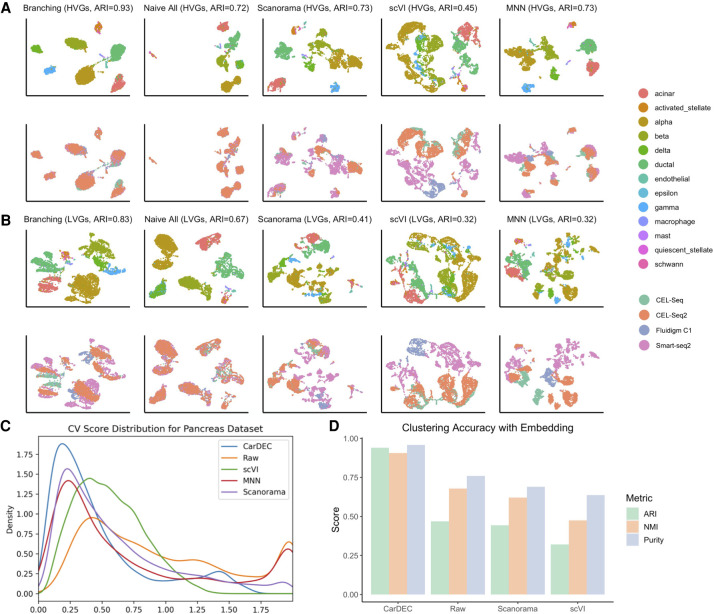
A unique feature of CarDEC is the branching architecture for both the HVGs and the LVGs. To show that this architecture is key in removing batch effects, we combined four data sets consisting of scRNA-seq expression data in human pancreas generated using Fluidigm C1 (Lawlor et al. 2017), Smart-seq2 (Segerstolpe et al. 2016), CEL-Seq (Grün et al. 2016), and CEL-Seq2 (Muraro et al. 2016). This is a challenging task because there are strong batch differences among these different scRNA-seq protocols, and analysis using the raw data as input yielded low adjusted Rand indexes (ARIs) (Supplemental Fig. S1). The branching architecture was designed with two objectives in mind. First, we wish to show that when correcting batch effects and denoising both the HVGs and the LVGs, using a branching model that treats these feature blocks differently improves the quality of denoised expression values relative to a naive architecture that treats these feature blocks the same. Second, we hope to design a model architecture such that including the LVGs in the model does not worsen denoising and batch effect correction quality of the HVGs, relative to a naive model that only denoises the HVGs and does not attempt to denoise LVGs.

As shown in Figure 2, the branching architecture posts significant performance boosts over the naive architecture that treated all genes as the same feature block in the input. The branching architecture performed better for denoising both the HVGs (ARI of 0.93 over 0.72) and the LVGs (ARI of 0.83 over 0.67) relative to the naive architecture (Fig. 2A,B), underscoring the necessity of using the branching architecture to denoise all genes as efficiently as possible. We also observed that for the purpose of denoising and batch correcting only the HVGs, the branching architecture performed just as well as a naive model that only included the HVGs and completely discarded the LVGs (ARI of 0.93 vs. 0.95) (Supplemental Fig. S2). This verifies that the branching architecture does not trade off denoising and batch correction effectiveness on the HVGs at all to denoise the LVGs. Additionally, the denoised counts from CarDEC showed less batch effects compared to denoised expression from Scanorama, scVI, and batch-corrected expression from MNN (Fig. 2A,B). Figure 2C shows that genewise CV scores obtained from CarDEC are the closest to zero among all compared methods. We also noticed that the clustering accuracy obtained when clustering is performed using denoised values in the gene expression space is similar to the clustering accuracy obtained when using the embedding of CarDEC to do clustering (Fig. 2D).

Figure 2.

Justification for the branching architecture in CarDEC. The CarDEC API splits the input matrix into HVGs and LVGs and treats them separately with a “Branching” architecture as in Figure 1. Alternatively, we can use a “Naive” model that treats all features the same regardless of gene expression variance. The naive model consists of an autoencoder with a clustering loss in addition to the reconstruction loss. Here, we show the utility of the branching architecture. The HVGs and LVGs were clustered separately, and the ARI of assignments is provided along with a UMAP plot. The top row was colored by cell type, the bottom row by scRNA-seq protocol. (A) UMAP embedding computed from the denoised HVG counts for each method: CarDEC with Branching architecture, CarDEC with Naive Architecture, Scanorama, scVI, and MNN. (B) UMAP embedding computed from the denoised LVG counts for each method. Figure legends are the same as those in A. (C) Density plot of genewise coefficient of variation (CV) among batch centroids. Density plots are provided for HVGs and LVGs separately. (D) Clustering accuracy metrics were obtained using the embedding-based methods to cluster the data, rather than running Louvain on the full gene expression space. Results for “Raw” were obtained by using Louvain's algorithm on the original HVG counts and are provided as a baseline to which embedding-based clustering results may be compared.

Application to macaque retina data with multilevel batch effect

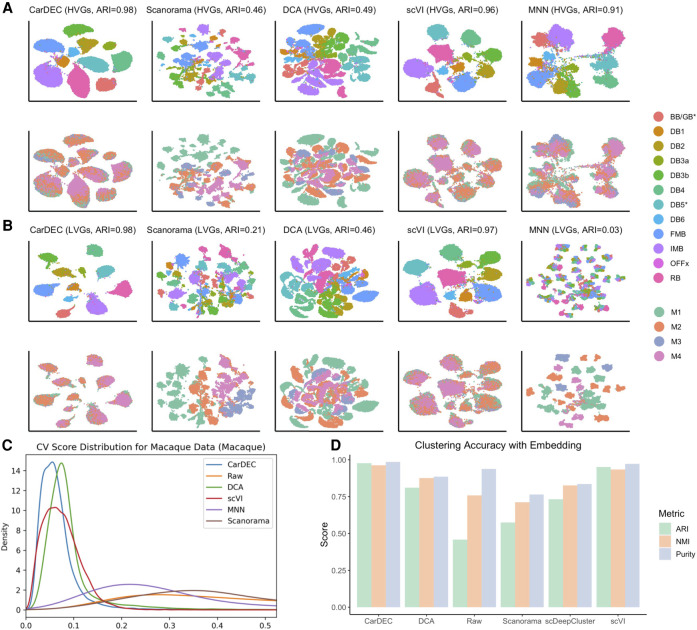
After finalizing the CarDEC architecture, we next evaluated the performance of CarDEC on a macaque retina data set (Peng et al. 2019). This data set poses a great challenge for batch effect correction and denoising because it features strong, multilevel batch effects, with cells sequenced from two different regions, four different macaques, and 30 different samples (Supplemental Fig. S3).

For the task of denoising and batch effect correction in the gene expression space, CarDEC was again the best performing method (Fig. 3; Supplemental Figs. S4, S5), followed by scVI whose ARIs are close to CarDEC. CarDEC and scVI not only removed the multilevel batch effects but also preserved inter–cell type variation. The ARI for clustering using the LVG denoised and batch effect–corrected counts from CarDEC is 0.98 and is 0.97 for scVI (Fig. 3B), which is as high as that when using the HVGs to do clustering (Fig. 3A). As a comparison, the ARI is only 0.15 using the LVG raw counts as input for clustering (Supplemental Fig. S3). This suggests that the denoising and batch correction in CarDEC and scVI substantially boosted the signal-to-noise ratio in the LVGs. Moreover, CarDEC's and scVI's genewise CVs are the closest to zero, providing evidence that cells were mixed well by batch by these two methods (Fig. 3C; Supplemental Fig. S6).

Figure 3.

Comparison of different methods on the macaque retina data set. (A) UMAP embedding computed from the denoised HVG counts for each method. The top row was colored by cell type; the bottom row was colored by Macaque ID. Cells were also clustered with Louvain's algorithm. (B) UMAP embedding computed from the denoised LVG counts for each method. Figure legends are the same as those in A. (C) Density plot of genewise CV among batch centroids. Density plots are provided for HVGs and LVGs separately. Centroids computed with sample ID as batch definition. (D) Clustering accuracy metrics were obtained using the embedding-based methods to cluster the data, rather than running Louvain on the full gene expression space. Results for “Raw” were obtained by using Louvain's algorithm on the original HVG counts and are provided as a baseline to which embedding-based clustering results may be compared.

The other methods all struggled with batch effects in the denoised counts. Scanorama largely failed to correct batch effects: when using Scanorama batch-corrected gene expression as input, the cells were separated primarily by batch rather than by cell type. For the LVGs, its ARI is as low as that when using the LVG raw counts as input for clustering (Scanorama 0.21 vs. raw 0.15) (Fig. 3B; Supplemental Fig. S3). DCA had slightly higher ARIs than Scanorama for both the HVGs and the LVGs, although both are significantly lower than CarDEC and scVI (Fig. 3A,B). MNN performed much better than Scanorama and DCA for batch correcting the HVG counts, achieving an ARI of 0.91 (Fig. 3A). However, it still fell short of CarDEC and scVI for this evaluation (CarDEC ARI 0.98 and scVI ARI 0.96). Looking more closely at the HVG UMAP plots, the batches were mixed less thoroughly with MNN than they were for CarDEC and scVI, and the cells were separated less by cell type, indicating that MNN failed to completely recover cell type variation. This is further confirmed by the genewise CV density plot in which the MNN density curve is further away from zero than CarDEC and scVI (Fig. 3C). For removing batch effects in the LVG counts, MNN was the worst performing method because it removed nearly all biological variations, leaving only batch effects.

For the simpler task of clustering using the low-dimensional embedding representation, existing methods did considerably better than they did at batch effect correction in the gene expression space, but still fell short of CarDEC and scVI (Fig. 3D; Supplemental Fig. S7). CarDEC and scVI achieved ARIs of nearly 1 for clustering using the embedding. DCA and scDeepCluster performed better than Louvain's algorithm using raw HVGs, but still fell short of achieving as high an ARI as CarDEC and scVI. Scanorama struggled on this data set with an ARI of only 0.57.

Application to mouse cortex and PBMC data from four protocols

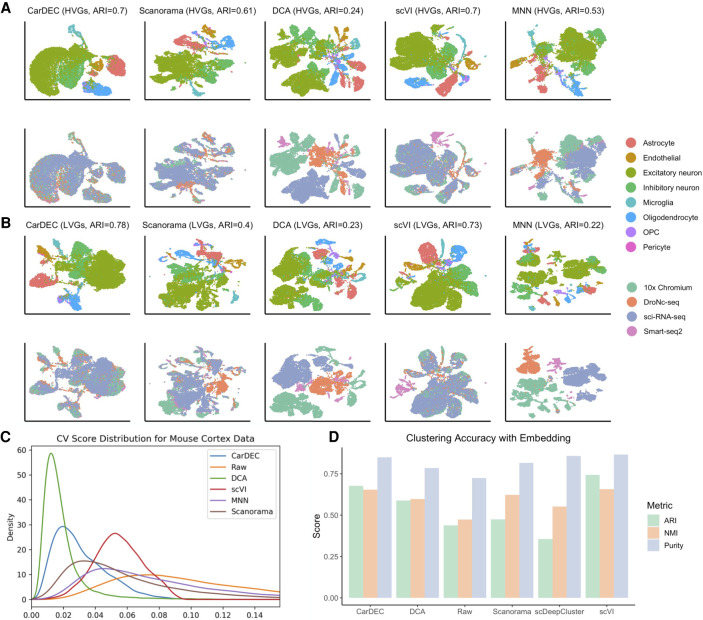
We next compared different methods using a mouse cortex data set (Ding et al. 2020). This data set poses a great challenge for batch correction and denoising on two fronts (Supplemental Fig. S9). First, it shows very serious batch effects because cells were generated using four different scRNA-seq protocols. Furthermore, this data set is heavily dominated by excitatory and inhibitory neurons, and the other cell types are rare, so preserving biological variation is especially imperative for detecting and analyzing these rarer subpopulations.

For the task of denoising and batch correcting the gene expression space, CarDEC and scVI performed considerably better than the other methods (Fig. 4). CarDEC performed the best, followed closely by scVI, at balancing between removing batch effects while preserving as much cell type variability as possible. For both CarDEC and scVI, the ARIs are similar when using the HVG denoised counts and the LVG denoised counts as input for clustering (Fig. 4A,B). As a comparison, the ARIs are only 0.28 and 0.26 when using the HVG and the LVG raw counts as input for clustering, respectively (Supplemental Fig. S9). The relatively low ARI when using the HVG raw counts as input for clustering shows the strong batch effects in this data set. However, for this challenging data set, using CarDEC denoised and batch-corrected LVG counts, the ARI increased to 0.78, suggesting that CarDEC substantially boosted the signal-to-noise ratio in the LVGs by simultaneous denoising and batch effect removal. We observed a similar signal boost by scVI in which the ARI for the LVGs is 0.73. The genewise CVs for CarDEC are also the closest to zero among all methods (Fig. 4C). Although scVI achieved high ARIs for both the HVG and LVG denoised gene expression, the cells appeared to be less well mixed than CarDEC (Fig. 4A,B), which is in agreement with its larger CVs than CarDEC.

Figure 4.

Comparison of different methods on the mouse cortex data set. (A) UMAP embedding computed from the denoised HVG counts for each method. The top row was colored by cell type; the bottom row was colored by batch. Cells were also clustered with Louvain's algorithm, and the resultant ARI is provided. (B) UMAP embedding computed from the denoised LVG counts for each method. Figure legends are the same as those in A. (C) Density plot of genewise CV among batch centroids. Density plots are provided for HVGs and LVGs separately. (D) Clustering accuracy metrics obtained using the embedding-based methods to cluster the data, rather than running Louvain on the full gene expression space. Results for “Raw” were obtained by using Louvain's algorithm on the original HVG counts and are provided as a baseline against which embedding-based clustering results may be compared.

DCA largely failed for this data set (Fig. 4A,B), although its denoised gene expression was also batch corrected by Combat. For both the HVGs and the LVGs, DCA separated the cells purely by scRNA-seq protocol with no mixing of cells from different batches. After denoising using DCA and batch correction with Combat, cell variation was driven entirely by batch, rendering the denoised counts ineffective for downstream analyses. For batch correcting the HVGs, Scanorama was the third-best performer (Fig. 4A), followed by MNN. MNN did not merge batches to the extent that CarDEC did and failed to preserve as much cell type variability, causing cell types to mix more. For removing batch effects in the LVGs, MNN did considerably worse than CarDEC and scVI (Fig. 4B). It suffered from the same problems as DCA for the LVGs in that cell type variation was lost and all variability was driven by batch. We also noticed that the CVs for DCA are the closest to zero; however, the small CVs are mainly a result of the overcorrection of Combat as the ARIs are low for both the HVGs and the LVGs.

Owing to the strong batch effects in this data set, even the simpler task of clustering using embedding was very difficult (Fig. 4D; Supplemental Fig. S10). In particular, scDeepCluster performed poorly at this task, scoring a lower ARI than a straightforward application of Louvain's algorithm to the raw data. The ARI for Scanorama is only slightly better than that obtained from the raw data. For this task, scVI was the leader, achieving an ARI of 0.74, followed closely by CarDEC with an ARI of 0.73.

We also analyzed a data set of human PBMCs from the same study (Ding et al. 2020) as the mouse cortex data. This data set was similar to the cortex data set, featuring eight batches spanning five scRNA-seq protocols and the results were largely the same: CarDEC and scVI were the best performers for denoising/batch correcting the HVGs and also the best for denoising/batch correcting the LVGs (Supplemental Figs. S12–S14).

Application to human monocyte data with pseudotemporal structure

We next show the utility of CarDEC for improving trajectory analysis for cells with pseudotemporal structure. We analyzed an scRNA-seq data set generated from monocytes derived from human peripheral blood mononuclear cells by Ficoll separation followed by CD14- and CD16-positive cell selection (Li et al. 2020). This data set includes 10,878 monocytes from one healthy subject. The cells were processed in three batches from blood drawn on three different days. Although monocytes can be classified as classical (CD14⁺⁺/CD16⁻), intermediate (CD14⁺⁺/CD16⁺), and nonclassical patrolling (CD14⁻/CD16⁺⁺) subpopulations based on surface markers, our previous analysis based on scRNA-seq data indicates that these cells show continuous transcriptional characteristics and trajectory analysis is an appropriate approach to characterize them (Li et al. 2020). This data set has strong batch effects (Supplemental Fig. S16). To reconstruct the trajectories of these cells, for each method, we first denoised and/or batch corrected the gene expression matrix, which was then fed into Monocle 3 (Cao et al. 2019) to estimate the pseudotime of each cell.

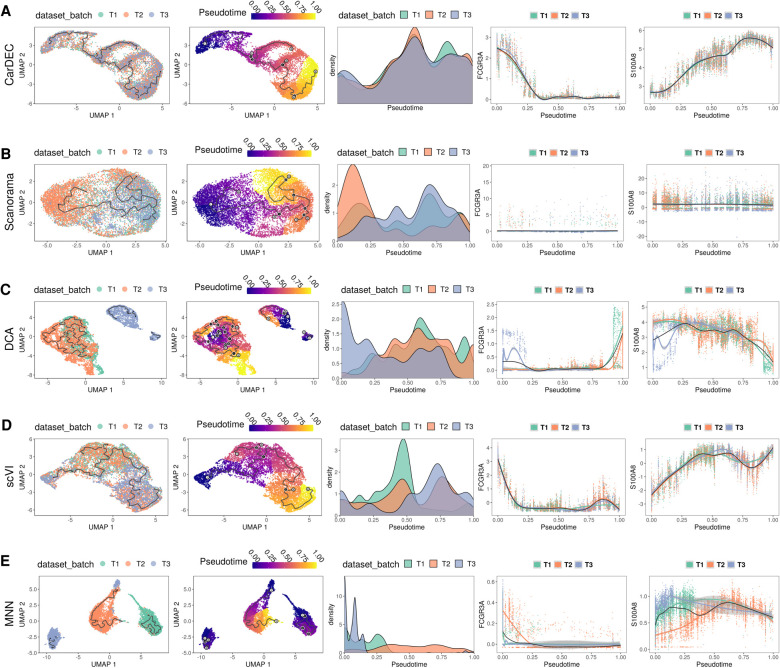
Figure 5A shows that CarDEC yields the best pseudotime analysis results with cells from the three batches well mixed, and a clear pseudotemporal path emerged. The batchwise density plots show that the three batches have similar pseudotime distributions, suggesting that CarDEC successfully removed batch effects. The plots of FCGR3A (known marker gene for nonclassical monocytes) and S100A8 (known marker gene for classical monocytes) gene expression also showed expected patterns (Supplemental Fig. S17). There are two key points of evidence from these marker gene plots suggesting that CarDEC recovered biological signal. First, for each marker gene, the expression levels are virtually identical across batches for all pseudotime points, which indicates that batch effects were removed for each gene expression and pseudotime relationship. Also, FCGR3A gene expression decreases monotonically with pseudotime, whereas S100A8 expression increases monotonically with pseudotime. This is exactly the kind of behavior we expect from these marker genes. Because FCGR3A and S100A8 are markers for the nonclassical and classical monocytes, respectively, we expect a good pseudotime analysis to segment the monocytes from nonclassical to classical (or vice versa) and for FCGR3A and S100A8 expressions to be monotonic functions of pseudotime with opposite trends. By denoising and batch correcting gene counts, CarDEC successfully mixed batches and recovered biological signal down to the individual marker gene level.

Figure 5.

Comparison of different methods for pseudotime analysis in the human monocyte data. The analysis is performed on monocytes derived from three technical replicates from the same subject. For each method, the full data set was denoised/batch corrected and then fed to Monocle 3 for pseudotime analysis. We show the UMAP embedding colored by batch (column 1) and estimated pseudotime (column 2). We also visualize the kernel density distribution of pseudotime by batch (column 3) and plot the distributions of marker genes FCGR3A and S100A8 against pseudotime (columns 4 and 5, respectively). (A) Pseudotime analysis when using denoised/batch-corrected gene expression matrix from CarDEC as input. (B) Pseudotime analysis when using batch-corrected gene expression matrix from Scanorama as input. (C) Pseudotime analysis when using denoised gene expression matrix from DCA but with Combat post hoc batch correction as input. (D) Pseudotime analysis when using denoised/batch-corrected gene expression matrix from scVI as input. (E) Pseudotime analysis when using batch-corrected gene expression matrix from MNN as input.

In contrast, no other methods were able to achieve CarDEC's success in improving pseudotime analysis. Scanorama (Fig. 5B), DCA (Fig. 5C), and MNN (Fig. 5E) all failed to mix batches in the UMAP embedding from Monocle 3. Although scVI (Fig. 5D) mixed batches well in the UMAP embedding, the pseudotime distributions showed substantial variation across batches. For Scanorama, DCA, and MNN, neither of the marker genes show strong monotonic trends as a function of the pseudotime, and for each marker gene, the relationship between expression and pseudotime varied by batch. These issues suggest that Scanorama, DCA, and MNN confounded biological signal and obscured signals from canonical markers of established subpopulations, FCGR3A and S100A8, as marker genes.

There are other approaches to using these denoising and batch correction methods for pseudotime analysis. For example, one can subset the denoised and batch-corrected matrix to include only the HVGs and then feed this into Monocle 3 (Supplemental Figs. S18, S20). Alternatively, one can use the embedding from CarDEC, Scanorama, DCA, or scVI as the reduced dimension space to build the Monocle 3 pseudotime graph (Supplemental Figs. S19, S21). In both these other cases, the conclusions are largely the same: CarDEC is the best method for improving pseudotime analysis.

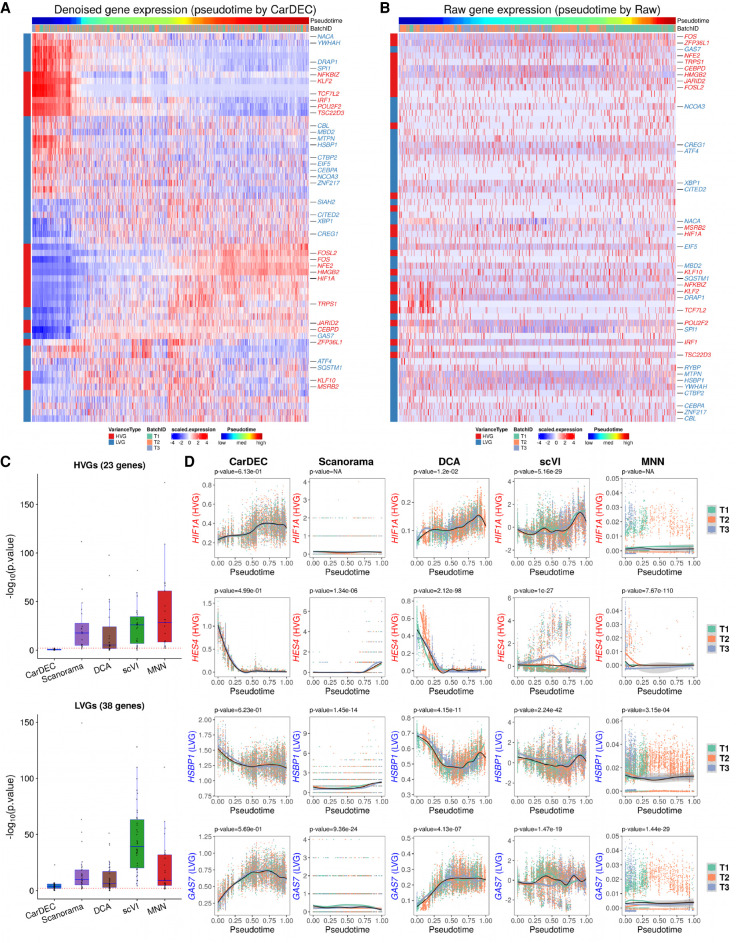
Next, we examined whether the denoised and batch-corrected gene expression values can help improve gene expression quality for biological discovery. We focused our analyses on 61 transcription factors (TFs) that were expressed in the monocyte data and also found to be differentially expressed among classical, intermediate, and nonclassifcal monocytes by Wong et al. (2011). Among these 61 TFs, 23 were selected as HVGs and the remaining 38 were designated LVGs. Figure 6A shows that the CarDEC denoised gene expression revealed a gradually decreasing trend from nonclassical to classical for TFs that are known to be highly expressed in nonclassical monocytes, for example, TCF7L2, POU2F2, CEBPA, and HSBP1. We also observed expected gene expression increase from nonclassical to classical for TFs that are known to be highly expressed in classical monocytes, for example, NFE2, CEBPD, GAS7, and MBD2. Notably, some of the TFs with these expected expression patterns were not selected as HVGs, suggesting that denoising and batch correction in CarDEC helped recover the true biological variations in both HVGs and LVGs. In contrast, when using raw UMI counts as input, the heat map did not reveal any meaningful biological patterns even for those TFs that were selected as HVGs (Fig. 6B).

Figure 6.

Comparison of different methods for differential expression analysis of transcription factors in the human monocyte data. (A) Heat map of scaled gene expression for CarDEC. Pseudotime was inferred based on embedding obtained from CarDEC using Monocle 3. (B) Heat map of scaled raw UMI counts. Pseudotime was inferred based on embedding obtained from the scaled raw UMI counts using Monocle 3. (C) P-values obtained from differential expression analysis among the three batches over pseudotime. For each method, the pseudotime was inferred based on embedding obtained from the corresponding method. The red dotted line corresponds to P-value = 0.01. The top panel is for the 23 HVG TFs, and the bottom panel is for the 38 LVG TFs. (D) Denoised and batch-corrected gene expression for CarDEC, batch-corrected gene expression for Scanorama, denoised gene expression for DCA with Combat post hoc batch correction, denoised and batch-corrected gene expression for scVI, and batch-corrected gene expression for MNN over pseudotime for four selected TFs: HIF1A, HES4, HSBP1, and GAS7. For each method, the pseudotime was inferred based on embedding from the corresponding method.

An important task in trajectory analysis is to identify genes whose expression values change over pseudotime and whether the expression patterns are different between conditions (e.g., healthy vs. diseased) over pseudotime. Avoiding false positive results is critical because failure of doing so may lead to follow-up of a wrong signal. Because the three batches were obtained from the same subject, we do not expect to detect significant gene expression differences over pseudotime among them. To this end, we performed differential expression analysis and compared the distributions of gene expression changes over pseudotime across the three batches. We performed hypothesis tests using the “gam” function in R package mgcv and tested whether gene expression patterns for the three batches are significantly different over pseudotime. Figure 6C shows the P-values from this differential expression analysis for each method. CarDEC is much more effective in removing batch effects than Scanorama, DCA, scVI, and MNN. For the 23 HVG TFs, the median −log₁₀ P-value for CarDEC is 0.30, whereas the median −log₁₀ P-values for Scanorama, DCA, scVI, and MNN are 18.37, 5.29, 25.90, and 28.52, respectively. For the 38 LVG TFs, the median −log₁₀ P-value for CarDEC is increased to 3.70, but still much lower than the other methods (9.81 for Scanorama, 6.36 for DCA, 39.19 for scVI, and 9.07 for MNN). These results indicate that failure to correct for batch effects could lead to a severe inflation of false positive results. Figure 6D shows four selected TFs, for which the denoised and batch-corrected gene expression for CarDEC agreed well among the three batches, further confirming the effectiveness of CarDEC in removing batch effects in the gene expression space.

CarDEC is scalable to large data sets

As the scale of scRNA-seq continues to grow, it becomes increasingly important for a method to be scalable to large data sets. To evaluate the scalability of CarDEC, we leveraged a data set of 104,694 human fetal liver cells (Popescu et al. 2019). Because we are principally interested in the problem of denoising and batch correcting in the full gene expression space, we retained all 21,521 genes after initial filtering for this analysis. For CarDEC we benchmarked two variations: a version that provides only denoised/batch-corrected expression in the Z-score space (CarDEC Z-score) and a version that provides denoised/batch-corrected expression in the count space (CarDEC Count).

We evaluated the run time needed to process 10%, 20%, 40%, 60%, 80%, and 100% of cells in the human fetal liver data set for CarDEC, Scanorama, DCA, scVI, and MNN. All evaluations were performed on a 2019 edition MacBook Pro with 2.4 GHz 8-Core Intel Core i9 CPU and 32 GB of memory. CarDEC, DCA, and scVI were all trained with early stopping to halt training upon convergence. The results are shown in Supplemental Figure S22. Both versions of CarDEC as well as DCA scaled approximately linearly with the number of cells and all three of these methods finished the analysis in <3.5 h. We were unable to train scVI on >60% of the cells, because the jupyter kernel crashed midtraining for 80% of the cells. scVI also took considerably longer to run. At 60% of the data, CarDEC Z-score, DCA, and CarDEC Count took ∼40 min, 1 h, and 1.5 h, respectively. In contrast, scVI took ∼3 h and 45 min to analyze this data. Scanorama had serious scalability issues. Like scVI, we could not run Scanorama for >60% of the data. Among the data points that we do have, Scanorama's run time is clearly not O(n_cells), whereas CarDEC, DCA, and scVI scale roughly linearly owing to the minibatch gradient descent algorithm that trains all of them (any non-monotonicity is a result of early stopping variation). Scanorama's run time appears to be parabolic as a function of sample size. MNN also has serious scalability issues, which is consistent with a recent benchmarking study (Haghverdi et al. 2018). It took >12 h to analyze 20% of the data and >47 h to analyze 40% of the data. We could not run MNN in <48 h using >40% of the data.

CarDEC is robust to hyperparameters

CarDEC involves several parameters that need to be tuned. To evaluate if CarDEC is robust to different choices of these parameters, we conducted additional analyses. First, we evaluated the performance of CarDEC for the α weight parameter, which is used when combining the self-supervised clustering loss and the reconstruction losses. The α parameter can be set to any value in the range of [0, 2]. Because a weight of 1 is the midpoint of this range, we chose it as a natural default. To evaluate the robustness of CarDEC to the choice of α, we varied its value across the set [0.1, 0.55, 1.0, 1.45, 1.9] and measured how the ARI changes for both the HVGs and the LVGs for each chosen value of α with all other parameters held equal. As shown in Supplemental Figure S23, CarDEC is robust to this choice of parameter.

Next, we evaluated the performance of CarDEC when varying the number of clusters for clustering. To show that CarDEC is robust to this parameter, we cannot rely on ARI, because the maximum achievable ARI for any clustering method decreases the more the number of clusters is misspecified relative to the number of labels/cell types in the set of gold standard labels. Instead, we chose to show that increasing the number of clusters specified for CarDEC just splits existing clusters, without substantially changing cell type signals/separation. To do this, we fit CarDEC on the pancreas data set repeatedly, varying the number of clusters with each fit. The numbers of clusters selected were 5, 9, 11, 14, and 18, respectively. As shown in Supplemental Figure S24A, even when the number of clusters is increased from 5 to 18, the cells were still separated mainly by their gold standard cell type labels. Closer examination of the UMAPs revealed that increasing the number of clusters usually just split cell types into two or more cluster label bins to accommodate surplus cluster labels, without changing the underlying structure of the UMAP plot. The CV score distributions shown in Supplemental Figure S24B further supports that CarDEC is robust to the choice of the number of clusters because the CV score distributions were largely unchanged when the number of clusters varied. We also visualized how cells in a cluster were split when CarDEC was refit with an increasing number of clusters using a Sankey Plot. As shown in Supplemental Figure S24C, in nearly all cases, increasing the number of clusters just split existing clusters.

Discussion

We developed CarDEC, a joint deep learning model, that removes batch effects not only in the low-dimensional embedding space but also across the entire gene expression space. As shown in our evaluations and a recent benchmarking study (Luecken et al. 2020), it is considerably harder to correct for batch effects in the gene expression space than in the embedding space, and especially hard to correct for batch effects in LVGs, which constitute the majority of the transcriptome. CarDEC was built to tackle these challenges. To remove batch effects in the gene expression space, we minimize a loss function that combines clustering and reconstruction losses. The self-supervised clustering loss, driven by HVGs, regularizes the embedding and removes batch effects in the embedding. The rich, batch-corrected embedding is then used to compute an effectively batch-corrected representation in the original gene expression space. To address the difficulty associated with batch correcting LVGs, we implemented a branching architecture, for which embeddings are computed separately for HVGs and LVGs and in which only the HVG embedding is used to compute the clustering loss. Using the pancreatic islet data sets generated from four scRNA-seq protocols, we showed that this branching architecture substantially improved batch effect removal on both the HVG and LVG gene expression spaces, as compared to the naive architecture.

Across a variety of data sets, with batch effects spanning multiple complexities in level and strength, we showed that CarDEC consistently led in its ability to remove batch effects. CarDEC was consistently the best for removing batch effects in all capacities: in the embedding space, the HVG expression space, and the LVG expression space. We showed that with appropriate denoising and batch correction, the LVGs offer as much signal for clustering as the HVGs, suggesting that CarDEC has substantially boosted the amount of information content in scRNA-seq. We also showed that by batch correcting gene expression counts, CarDEC improved pseudotemporal analysis of human monocytes, an example of how batch correction can be used to improve downstream analyses.

CarDEC removes batch effects in the LVG denoised gene expression based on the embedding layer that concatenates the HVG embedding. A potential concern of this concatenation is that the denoised LVG expression values might contain artificially introduced signals from the HVGs. To examine this, we focused on the bottom 16,215 genes in the pancreas data set by variance and evaluated the performance of CarDEC when varying the number of HVGs. Then, we fit CarDEC for various numbers of HVGs and evaluated the ARI obtained from clustering the denoised expression for these 16,215 genes. If the LVGs contain artificial signals from the HVGs, then we would expect the ARI computed from the bottom 16,125 genes to vary by how many HVGs were used to train CarDEC. As shown in Supplemental Figure S25, this is not the case. We observed that ARI on the LVG set increased modestly when the number of HVGs was increased from 500 to 1000, likely because 500 HVGs were too few highly variable features. From 1000 up to 3000 inclusive, the ARI on the LVG set was very stable. After 3000 HVGs, there was a modest drop in the LVG set's ARI, but this is likely because too many noisy features were introduced into the HVG set, which hurt the quality of the KL divergence gradients. Because the 16,125 LVG set's ARI is fairly invariant to the number of HVGs used, especially in the range of 1000 to 3000 HVGs, we can infer that the model architecture is not adding significant artificial signals from the HVGs to the LVGs.

In this article, we focused on the analyses when using all genes as input. Because Scanorama, DCA, scVI, and MNN are intended to be used with HVGs only, we reanalyzed every data set with only HVGs selected as the input using every method. As expected, many methods performed better when only HVGs were modeled (Supplemental Figs. S2, S8, S11, S15). However, for the macaque retina data, Scanorama still struggled to remove its batch effects even when only HVGs were considered. For this challenging data set, the ARI from Scanorama is only 0.18, which is much lower than all the other methods (Supplemental Fig. S8).

Current scRNA-seq studies often include a large number of cells generated from many samples, across multiple conditions, and possibly using different protocols. Removing batch effects is critical for data integration. Because CarDEC provides efficient batch correction in the full gene expression space, it can be used for a wide array of analyses to facilitate biological discovery. Harmonized counts in the gene expression space can be used to estimate unbiased, batch-corrected log fold changes, which can be used to identify marker genes for different cell types. These counts can also be used to reconstruct trajectories and identify genes showing pseudotemporal patterns. Last, CarDEC is computationally fast and memory efficient, making it a desirable tool for analyses of complex data in large-scale single-cell transcriptomics studies.

Methods

The CarDEC workflow (Fig. 1) involves four steps: preprocessing, pretraining, gene expression denoising in Z-score space, and (optionally) denoising in count space. Below we briefly describe each of these steps. Details of the implementation is described in Supplemental Note 1, and the hyperparameters of CarDEC are shown in Supplemental Table S1.

Step 1: preprocessing

We first remove any cells expressing less than 200 genes and then remove any genes expressed in less than 30 of the remaining cells. Let X be an n × p gene count matrix with n cells and p genes after filtering. The gene expression values are normalized. In the first step, cell-level normalization is performed, in which gene expression for a given gene in each cell is divided by the total gene expression across all genes in the cell, multiplied by the median total expression across all cells, and then transformed to a natural log scale. In the second step, gene-level normalization is performed, in which the cell-level normalized values for each gene are standardized by subtracting the mean and dividing by the standard deviation across all cells within the same batch for the given gene. Highly variable genes (HVGs) are selected based on the log-normalized counts using the approach introduced by Stuart et al. (2019) and implemented in the “pp.highly_variable_genes” function with “batch_key” parameter in the SCANPY package (version ≥1.4) (Wolf et al. 2018). The remaining genes that are not selected as HVGs are considered lowly variable genes (LVGs). We note that many of the LVGs still show cell-to-cell variability and are useful for clustering analysis after appropriate denoising and batch effect correction. We select 2000 HVGs for all analyses in this article.

Step 2: pretraining using the HVGs

The pretraining step is a straightforward implementation of an autoencoder. Let p_HVG be the number of HVGs selected in Step 1, and Y_HVG be the corresponding n × p_HVG matrix of normalized expression, subsetted to include only the HVGs. Define a standard autoencoder for Y_HVG with encoder and decoder represented by f_E,HVG (·; W_E,HVG) and f_D,HVG (·; W_D,HVG), respectively. The weights W_E,HVG and W_D,HVG are randomly initialized using the glorot uniform approach and are tuned during pretraining. We use the tanh activation for the output of the encoder, and the linear activation function for the output of the decoder. For all intermediate hidden layers in the encoder and decoder, we use the ReLu activation function. The autoencoder is pretrained with mean squared error loss using minibatch gradient descent with the Adam optimizer (Kingma and Ba 2015).

Step 3: denoising Z-scores

In this step, we use an expanded, branching architecture to accommodate LVGs and introduce a clustering loss that regularizes the embedding and improves batch mixing and denoising especially in the gene space. Let p_LVG be the number of LVGs selected in Step 1, and Y_LVG be the corresponding n × p_LVG matrix of normalized expression, subsetted to include only the LVGs, and y_{i, HVG} and y_{i, LVG} be the vectors of HVGs and LVGs, respectively in cell i. We retain the encoder and decoder mappings for HVGs, f_E,HVG (·; W_E,HVG) and f_D,HVG (·; W_D,HVG) from Step 2, including the learned weights W_E,HVG and W_D,HVG. We introduce a clustering layer that takes the HVG embedding z_i,HVG = f_E,HVG ( y_{i, HVG} ; W_E,HVG) as input and returns for each cell a vector of cluster membership probabilities for h clusters, where h is a user-specified number. For this clustering layer, we introduce an h × d matrix of trainable weights/cluster centroids M, where the jth row of M is a cluster centroid μ_j, and d is dimension of the embedding.

To initialize M, we run Louvain's algorithm on the embeddings {z_i,HVG :i ∈ {1, 2, …, n}} learned from the pretrained autoencoder and find the cluster centroid for each cluster. The clustering layer computes a vector of cluster membership probabilities for cell i, denoted by q_i. Let q_ij, the jth element of q_i, denote the probability that cell i belongs to cluster j. Then the membership probabilities are computed using a t-distribution kernel as follows:

$$q_{ij}=\frac{{\left(1+{\parallel {\mathit{z}}_{i,\mathrm{HVG}}-{\mu }_j\parallel }^2\right)}^{-1}}{\sum j^{\mathrm{\prime }}{\left(1+{\parallel {\mathit{z}}_{i,\mathrm{HVG}}-{\mu }_{j^{\mathrm{\prime }}}\parallel }^2\right)}^{-1}}.$$

Because we do not have cell type labels in an unsupervised analysis, we create “pseudolabels” that can be used in place of real labels for optimizing clustering weights. Inspired by Xie et al. (2016), these pseudolabels are computed from the membership probabilities q_ij as follows:

$$p_{ij}=\frac{q_{ij}^2/{\sum }_i{q}_{ij}}{{\sum }_{j^{\mathrm{\prime }}}{q}_{i{j}^{\mathrm{\prime }}}^2/{\sum }_i{q}_{i{j}^{\mathrm{\prime }}}}.$$

Let p_i be an h-dimensional vector whose jth element is p_ij. Then the clustering loss for cell i is defined as the following Kullback–Leibler divergence (KLD):

$$l_{i,c}=\mathrm{KLD}\left({\mathit{p}}_i\right||{\mathit{q}}_i)=\sum _j{p}_{ij}\log \left(\frac{p_{ij}}{q_{ij}}\right).$$

This loss is a component of the total loss defined later. Because it takes the embedding vectors z_i,HVG as input, minimizing this objective function can refine the embedding and help to remove batch effects from denoised counts computed using this embedding as input. The use of this KLD loss function was inspired by DESC (Li et al. 2020), which has shown that batch effects can be gradually removed over iterations. The intuition is to use “easy-to-cluster” cells, that is, cells with “pseudolabels,” to guide the neural network to learn cluster-specific gene expression features while ignoring other unwanted noises such as batch effects. Over iterations, the algorithm ignores information unrelated to cell clustering by adjusting the network weights using the gradient descent algorithm and learns cluster-specific information. During the iterative update procedure, cells that are initially assigned to the same cluster are moved closer and closer to the cluster centroid, hence removing batch effects in the embedding space. Because the algorithm learns information on cell clusters from those “easy-to-cluster cells” while ignoring other irrelevant information by constructing the auxiliary distribution P and optimizing the KL divergence between P and Q, then as long as technical differences (e.g., between batches) are smaller than biological differences (e.g., between cell types), it can remove batch effect successfully.

We also introduce encoder and decoder mappings f_E,LVG (·; W_E,LVG) and f_D,LVG (·; W_D,LVG) to address the problem of denoising and batch correction for the LVGs. Unlike the HVG decoder f_D,HVG, the LVG decoder f_D,LVG (·; W_{D, LVG}) does not map the low-dimension embedding z_i,LVG alone to reconstruct ${\hat{\mathit{y}}}_{i,\mathrm{LVG}}$ in the original p_LVG-dimension space. Rather, we concatenate the HVG and LVG embeddings together, and feed the combined vector [z_i,HVG z_i,LVG] into the decoder to denoise and batch correct LVG expression in the original p_LVG-dimension space. That is,

$${\hat{\mathit{y}}}_{i,\mathrm{LVG}}=f_{D,\mathrm{LVG}}\left(\left[{\mathit{z}}_{i,\mathrm{HVG}}{\mathit{z}}_{i,\mathrm{LVG}}\right];W_{D,\mathrm{LVG}}\right).$$

This concatenated embedding is critical because it allows CarDEC to only use the high signal-to-noise ratio HVGs to drive the clustering loss, while still using the rich, batch-corrected embedding that is refined using this clustering loss to denoise and batch correct LVGs. The activation functions for the encoder and decoder of the LVGs are similarly defined as the autoencoder in Step 2.

To train this branching model, we first introduce two reconstruction losses, one for the HVGs and one for the LVGs computed as follows for cell i:

$$l_{i,\mathrm{HVG}}=\frac{1}{p_{\mathrm{HVG}}}{\parallel {\hat{\mathit{y}}}_{i,\mathrm{HVG}}-{\mathit{y}}_{i,\mathrm{HVG}}\parallel }^2$$

$$l_{i,\mathrm{LVG}}=\frac{1}{p_{\mathrm{LVG}}}{\parallel {\hat{\mathit{y}}}_{i,\mathrm{LVG}}-{\mathit{y}}_{i,\mathrm{LVG}}\parallel }^2.$$

Then the total loss is calculated as a multicomponent loss function as follows:

$$l_i=\alpha l_{i,c}+\left(2-\alpha \right)\frac{l_{i,\mathrm{HVG}}+l_{i,\mathrm{LVG}}}{2},$$

where α is a hyperparameter ranging from 0 to 2 that balances reconstruction loss with clustering loss. We set α at 1 as default value. The total loss is minimized in an iterative fashion until certain convergence criteria are satisfied.

Step 4: denoising gene expression counts

In Step 3, the denoised expression values obtained from the decoder are on a Z-score scale and are not naturally comparable to raw UMI counts. To remedy this, we offer an optional downstream modeling step that provides denoised expression values on the original count scale. This strategy involves finding mean and dispersion parameters that maximize a negative binomial likelihood. We choose the negative binomial distribution because previous studies have shown that UMI counts are not zero-inflated, and the negative binomial distribution fits the data well (Chen et al. 2018; Wang et al. 2018; Svensson 2020).

After the training in Step 3, we have obtained batch-corrected low-dimension embeddings, z_i,HVG and z_i,LVG for each cell i from the fine-tuned HVG and LVG encoders. We will use two separate neural networks to maximize the negative binomial losses: one for the HVGs and one for the LVGs. These models are completely separate from one another but are trained almost identically with only minor differences. The goal is to map the embeddings into the full gene space to obtain mean and dispersion parameters for each gene. Without loss of generality, we use the HVGs as an example to illustrate how the neural network is built.

The vector of genewise means μ_i,HVG and vector genewise dispersions θ_i,HVG are given below:

$${\mathit{\mu }}_{i,\mathrm{HVG}}=s_i\times \exp \left({\mathbf{W}}_{\mu ,\mathrm{HVG}}\times {\tilde{\mathit{z}}}_{i,\mathrm{HVG}}\right),$$

$${\mathit{\theta }}_{i,\mathrm{HVG}}=\mathrm{softplus}\left({\mathbf{W}}_{\theta ,\mathrm{HVG}}\times {\tilde{\mathit{z}}}_{i,\mathrm{HVG}}\right),$$

where s_i is the size factor for cell i, W_μ,HVG and W_θ,HVG are trainable weight matrices, and exp and softplus are activation functions that are applied elementwise. For each gene j in cell i, we compute the negative log likelihood of the negative binomial distribution as

$$l_{ij}=-\log \left(\frac{\mathrm{\Gamma }\left(x_{ij}+{\theta }_{ij}\right)}{\mathrm{\Gamma }\left({\theta }_{ij}\right)}{\left(\frac{{\theta }_{ij}}{{\theta }_{ij}+{\mu }_{ij}}\right)}^{{\theta }_{ij}}{\left(\frac{{\mu }_{ij}}{{\theta }_{ij}+x_{ij}}\right)}^{x_{ij}}\right),$$

where x_ij is the original count in HVG gene j for cell i, and where μ_ij and θ_ij are the jth elements of μ_i,HVG and θ_i,HVG, respectively. For the HVG count model, the full loss for cell i is then $l_i=\left(1/p_{\mathrm{HVG}}\right){\sum }_{j=1}^{p_{\mathrm{HVG}}}{l}_{ij}$. The loss for the LVG count model can be similarly defined. Both the HVG and LVG count models are trained using their own early stopping and learning rate decay convergence monitoring.

Evaluation of batch effect removal in the gene expression space and the embedding space

Here, we briefly describe the workflow to evaluate batch effect removal and comparison between different methods (for details, see Supplemental Note 2). First, we evaluated the performance of different methods in removing batch effect in the gene expression space. For this evaluation, we considered CarDEC, Scanorama, DCA with post hoc batch effect correction by Combat, scVI, and MNN. We ran all denoising/batch correction methods on the full data matrix and then presented clustering results for denoised HVGs and denoised LVGs separately by subsetting the HVGs and LVGs from the full denoised/batch-corrected expression matrix. The subsetted matrix that includes only the HVGs (or LVGs) is then passed down to the Louvain's clustering algorithm. All steps in this workflow are identical for both the HVGs and the LVGs, and all methods used the same HVGs and LVGs as input for clustering. Furthermore, on a given data set, we benchmarked all methods with the same number of clusters. Second, we evaluated batch effect removal for the embedded representations of scRNA-seq. For this evaluation we considered CarDEC, Scanorama, DCA with post hoc batch effect correction by Combat, scVI, and scDeepCluster. We excluded MNN because it has no embedding functionality. We included “raw” as a control method for comparison, which is just subsetting the raw data to include only the HVGs, and then running the clustering workflow.

Coefficient of variation (CV) analysis

To measure batch mixing, we examined the batchwise centroids before and after denoising. Let X^′ be a matrix of gene expression counts (including both HVGs and LVGs). X^′ can be the matrix of raw counts or the denoised/batch-corrected counts from any of CarDEC, Scanorama, DCA with post hoc batch effect correction by Combat, scVI, or MNN. For CarDEC, we only considered denoised counts, not denoised expression in the Z-score space. If X^′ consists of MNN-corrected expression, then we did not preprocess the data because MNN denoised expression is on a cosine scale. In the case of MNN, Scanorama, and DCA after Combat correction, a fraction of expression counts can be negative, which poses difficulties when computing coefficients of variation. To circumvent this issue, any expression values after correction by these methods that are negative were truncated to zero for the CV analysis. For all other methods we have denoised expression in the non-negative count space, so we performed cell normalization and log normalization on X^′, exactly in the same way described in the Step 1 (preprocessing) of CarDEC.

Next, we describe how the CV scores are calculated. Let $x_{ij}^{\mathrm{\prime }}$ be the expression value in gene j of cell i in X^′. Let S_ab be a set of integers defined such that i ∈ S_ab if and only if cell i belongs to cell type a and is sequenced from batch b. Furthermore, let $c_{ajb}={\sum }_{i\in S_{ab}}{x}_{ij}/{\sum }_{i\in S_{ab}}1$ be the centroid (mean expression) of batch b for gene j of cell type a. Let C_aj = {c_ajb} be the collection of batch centroids for gene j in cell type a. We can now define a cell type–specific CV as follows:

$${\mathrm{CV}}_{aj}=\frac{\sqrt{\mathrm{Var}\left(C_{aj}\right)}}{\mathrm{Mean}\left(C_{aj}\right)+\gamma },$$

where γ = 10⁻¹² is a small constant to mitigate computational instability. A higher value of CV_aj corresponds to greater variation among batches and less batch mixing for cell type a, so a good batch effect removal method should drive CV_aj closer to zero. Normalizing by mean expression adjusts the metric for how highly expressed the gene is, so that CVs from more highly expressed genes are comparable to CVs from less highly expressed genes.

To consolidate our results across cell types, so that we can present a single distribution of CV scores across all cell types, we combine the cell type–specific CV score s. Then we summarize the cell type–specific CV scores by taking a weighted average of these scores across cell types, in which the weight of a cell type is proportional to that cell type's frequency in the data set. Specifically, the weight for cell type a is computed as $c\left(a\right)={\sum }_{i}I\left(a_i=a\right)/{\sum }_{i}1$, where a_i is the cell type of cell i. The combined CV score is calculated as follows:

$${\mathrm{CV}}_j=\sum _{a}c\left(a\right){\mathrm{CV}}_{aj}.$$

Evaluation metrics for clustering

For all our benchmark data sets, we used the cell type labels reported in the original papers as the gold standard. The clustering performance of each method was mainly evaluated using the adjusted Rand index (ARI), calculated as follows:

$$\mathrm{ARI}=\frac{{\sum }_{ij}\left(\begin{array}{c}{n}_{ij}\\ 2\end{array}\right)-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{c}n\\ 2\end{array}\right)}{{\displaystyle \frac{1}{2}\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right)+{\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{c}n\\ 2\end{array}\right)}},$$

where n_ij is the number of cells in both cluster i from the cluster assignments obtained when benchmarking and in cell type j according to the gold standard cell type labels. a_i is the total number of cells in cluster i from the cluster assignments obtained when benchmarking, b_j is the total number of cells in cell type j according to the gold standard cell type labels from the original study, and n is the total number of cells. Additionally, we also computed normalized mutual information (NMI) and purity, calculated as follows:

$$\mathrm{NMI}=2\times \frac{{\sum }_{ij}{\displaystyle \frac{n_{ij}}{n}\log \left(\frac{n\times n_{ij}}{a_i\times b_j}\right)}}{{\sum }_i{\displaystyle \frac{a_i}{n}\log \left(\frac{n}{a_i}\right)}+{\sum }_j{\displaystyle \frac{b_j}{n}\log \left(\frac{n}{b_j}\right)}},$$

$$\mathrm{Purity}=\frac{1}{n}\sum _i\underset{j}{max}{n}_{ij}.$$

Data sets

We analyzed multiple published scRNA-seq data sets, which are available through the accession numbers reported in the original articles: (1) human pancreatic islet data: CEL-Seq (NCBI Gene Expression Omnibus [GEO; https://www.ncbi.nlm.nih.gov/geo/] GSE81076), CEL-Seq2 (GEO GSE85241), Fluidigm C1 (GEO GSE86469), and Smart-seq2 (ArrayExpress [https://www.ebi.ac.uk/arrayexpress/] E-MTAB-5061); (2) bipolar cells from mouse retina (GEO GSE81904); (3) bipolar cells from macaque retina (GEO GSE118480); (4) mouse cortex data (Single Cell Portal [https://singlecell.broadinstitute.org/single_cell] SCP425); (5) human PBMC data (Single Cell Portal SCP424); (6) human monocyte data (GEO GSE146974); and (7) human fetal liver data (Array Express E-MTAB-7407). Details of these data sets are described in Supplemental Table S2.

Software availability

An open-source implementation of the CarDEC algorithm can be downloaded from GitHub (https://github.com/jlakkis/CarDEC) and is available as Supplemental Code. Code to reproduce all our analyses can be found on GitHub (https://github.com/jlakkis/CarDEC_Codes) and is also available as Supplemental Code.

Competing interest statement

The authors declare no competing interests.