The use of differential privacy for census data and its impact on redistricting: The case of the 2020 U.S. Census

New Census privacy protections may introduce both bias and noise into redistricting and voting rights analysis.

Abstract

Census statistics play a key role in public policy decisions and social science research. However, given the risk of revealing individual information, many statistical agencies are considering disclosure control methods based on differential privacy, which add noise to tabulated data. Unlike other applications of differential privacy, however, census statistics must be postprocessed after noise injection to be usable. We study the impact of the U.S. Census Bureau’s latest disclosure avoidance system (DAS) on a major application of census statistics, the redrawing of electoral districts. We find that the DAS systematically undercounts the population in mixed-race and mixed-partisan precincts, yielding unpredictable racial and partisan biases. While the DAS leads to a likely violation of the “One Person, One Vote” standard as currently interpreted, it does not prevent accurate predictions of an individual’s race and ethnicity. Our findings underscore the difficulty of balancing accuracy and respondent privacy in the Census.

INTRODUCTION

In preparation for the official release of the 2020 Census data, the U.S. Census Bureau has developed a disclosure avoidance system (DAS) to prevent Census responses from being linked to specific individuals (1). The DAS is based on differential privacy technology, which adds a certain amount of random noise to Census tabulations. The Bureau has been required by law to prevent the disclosure of information about Census participants (13 U.S. Code § 9) and has implemented disclosure avoidance methods since 1960. However, their decision to incorporate differential privacy and the necessary subsequent postprocessing steps in the 2020 Census, as implemented in the DAS, has been controversial. Some scholars have voiced concerns about the potential negative impacts of noisy data on public policy and social science research, which critically rely upon Census data (2–6).

The U.S. decennial census serves as an important and unique case study on the impact of differential privacy. Its statistics define the drawing of legislative districts, determine the distribution of federal funds for more than a hundred government programs, and are extensively analyzed by social scientists (7, 8). Other countries and international organizations, including the European Union, United Kingdom, and Australia, have adopted or are considering the adoption of differential privacy technology (9–11). In addition to its decennial census, the U.S. Census Bureau has recently used differential privacy as their “privacy definition” in a national block-level data release on commuting patterns (12). The Bureau is now considering adopting a similar approach for other data products, such as the American Community Survey (13).

It is a common misconception that a differentially private census only involves injecting random noise (14, 15). Simple noise injection may lead to geographies with negative population values, create small discrepancies in population counts even at high levels of aggregation like states, and create inconsistencies across millions of tabulations that the Census must publish. Therefore, the U.S. Census Bureau has adjusted its differentially private counts with various postprocessing steps to prevent these negative counts and ensure that population counts at several geographies are exact and tables are consistent. Although this postprocessing is not formally part of differential privacy, the two are inseparable because national statistical agencies must ensure the facial validity of census products while simultaneously protecting respondents’ privacy. The question is whether these sensible adjustments unintentionally induce systematic (instead of random) discrepancies in reported Census statistics (16).

Here, we empirically evaluate the impact of the DAS, both the noise injection and postprocessing, on redistricting and voting rights analysis across local, state, and federal contexts. These districts vary greatly in their size and underlying geographies. This heterogeneity makes redistricting an interesting case for assessing the impact of differential privacy in national statistical products. Although the Census Bureau plans to only release the DAS-protected 2020 Census tabulations, in April 2021, they published a DAS version of the 2010 tabulations to collect public comment. Using these demonstration data, we conduct our empirical evaluation under a likely scenario, in which practitioners, map drawers and analysts alike, treat these DAS-protected data “as is” as they have done in the past, without accounting for the DAS noise generation mechanism.

First, we find systematic biases in the DAS-protected data along racial and partisan lines. The DAS has a tendency to transfer population across geographies in ways that artificially reduce racial and partisan heterogeneity. This is, in part, due to the postprocessing procedure, which gives a priority to the accuracy of population counts for the largest racial group in a given area.

Second, we use a set of recently developed simulation methods that can generate large numbers of realistic redistricting maps under a set of legal and other relevant constraints, including contiguity, compactness, population parity, and preservation of communities of interest and counties (17–24). These simulation methods are useful because they allow us to understand the systematic impacts of DAS on the redistricting process and evaluation by generating a large number of realistic redistricting plans under various conditions. They also have been extensively used by expert witnesses in recent court cases on redistricting, including Common Cause v. Lewis (2020), Rucho v. Common Cause (2019), Ohio A. Philip Randolph Institute v. Householder (2020), and League of Women Voters of Michigan v. Benson (2019).

We find that the noise introduced by the DAS can prevent map drawers from creating districts of equal population according to current statutory and judicial standards. For example, over the past half century, the Supreme Court has firmly established the principle of “One Person, One Vote”, requiring states to minimize the population difference across districts based on the Census data. This applies even if differences are theoretically smaller than known enumeration error (Karcher v. Daggett 1983). In many cases, actual deviations from equal population, as measured using the original Census data, will be several times larger than as reported under the DAS-protected data. The magnitude of this problem is especially acute for smaller districts, such as state legislative districts and school boards.

The noise introduced by the DAS also has partisan and racial implications. We find that DAS yields unpredictable changes to district-level partisan outcomes and may change the conclusions of redistricting analyses used to identify partisan gerrymandering. Our analyses demonstrate that precincts that are heterogeneous along racial and partisan lines are systematically undercounted by the DAS. In some cases, these perturbations can lead to a change in the number of majority-minority districts (MMDs) if one follows the current standard set by courts (e.g., Thornburg v. Gingles 1986, Shaw v. Reno 1993, Bartlett v. Strickland 2009, and Shelby County v. Holder 2013).

Last, we find that the noise-induced DAS data do not degrade the overall prediction accuracy of individuals’ race based on the Bayesian Improved Surname Geocoding (BISG) methodology, which combines the Census block-level proportion of each race with a voter’s name and address (25–27). Redistricting analysis for voting rights cases often necessitates this individual-level prediction because most states’ voter lists do not include individual race. We also show that the DAS-protected data can still alter individual-level race predictions constructed from voter names and addresses. These changes can have a large impact on the analysis of local redistricting cases. In a reanalysis of a recent Voting Rights Act case, we find that predictions generated using DAS-protected data underpredict minority voters and result in fewer MMDs.

We conclude by discussing the implications of our findings for future redistricting and voting rights analysis under the privacy-protected Census data. Our article represents the broadest look at the impact of the new DAS methodologies on redistricting use to date. Prior research applied related redistricting simulation methodologies to simulated DAS data, as we do, but used an old version of the DAS algorithm rather than the latest demonstration data release (28). These authors make a valuable contribution by demonstrating the continued usability of weighted regressions for voting rights analysis. While their primary focus is on the analysis of one county in one state, we cover several levels of redistricting across many states. We can thus examine the consequences of DAS-induced error across a variety of contexts and use cases.

RESULTS

Differential privacy and postprocessing

The Census Bureau has developed the TopDown algorithm as the DAS of the 2020 Census (1). The algorithm adds statistical noise to implement differential privacy and then makes postprocessing adjustments. Differentially private systems such as the Census DAS provide some protection against the risk of “reconstruction attacks,” which attempt to identify a specific individual in the dataset using external information. We examine the April 2021 demonstration data before the Census release of 2020 P.L. 94-171 data, which many states use for redistricting. The demonstration data are a reprocessed release of the decennial census data from 2010 for the purpose of analyzing the suitability of data processed through the DAS.

The DAS is a new approach to privacy in decennial data releases. Releases from 1990 to 2010 relied on “swapping” for disclosure limitation (29). Swapping is the process of switching data entries in a controlled way to provide some protection to those with “rare and unique responses” (30).

Below, we briefly summarize the most recently released version of the DAS algorithm, which combines differentially private noise injection with postprocessing. We then document the nature of the discrepancies induced by these demonstration data when compared to the original release of 2010 Census data. In particular, we find that the DAS artificially shifts populations from racially mixed areas to homogeneous areas. In the subsequent section, we use redistricting simulation analysis to show how these population discrepancies are likely to affect redistricting plans.

The U.S. Census DAS

The first step of the DAS pipeline is to add independent, symmetric Laplace or geometric noise to counts in each of numerous published Census tables. The differential privacy provides a specific definition of privacy: a probabilistic guarantee that empirical conclusions are relatively unaffected by the inclusion or exclusion of a particular individual from the dataset (31). In the case of noise injection as in the DAS, the amount of noise in each file is controlled by the privacy loss budget, denoted by ϵ. Higher values of ϵ exponentially increase the tolerance of what is an acceptable degree of disclosure probability. Formally, differential privacy caps at exp(ϵ) the ratio between the likelihoods of a certain output in a pair of datasets that only vary in the inclusion of a single individual. Thus, the additional certainty (in terms of odds) that someone can gain about a particular conclusion will change by at most a factor of exp(ϵ) if an individual is included in the dataset. We note that, because census takers will attempt to enumerate every individual in the country regardless of voluntary participation, it is debatable whether differential privacy is a suitable definition of privacy for census data.

In April 2021, the Bureau implemented DAS-12.2 on the 2010 Census and released it as a demonstration of the version of the DAS that they plan to use in the release of the 2020 decennial census statistical tables. The numbers in the version name represent the privacy loss budget. DAS-12.2 represents a relatively high privacy loss budget [ϵ = 12.2, with exp(12.2) ≈ 2.0 × 10⁵] to achieve the accuracy targets at the expense of greater privacy loss, whereas an earlier version, DAS-4.5, used a lower privacy loss budget at the expense of worse accuracy [ϵ = 4.5, with exp(4.5) ≈ 9.0 × 10¹]. Both of these privacy loss budgets are high (that is, enforce less stringent privacy guarantees and retain higher accuracy) relative to standard reference points (32). There may not be an overlap between the values of ϵ that are considered stringent enough for privacy purposes and high enough for redistricting purposes.

In addition, the Census Bureau postprocesses the noisy tabulation data to ensure that the resulting public release data meet a handful of criteria. First, they must be self-consistent such that, for example, the total population for each block nested within a tract adds up to the tract population. In addition, they must abide by several common sense constraints, including the avoidance of negative counts. Last, certain aggregate statistics such as state-level total population counts must exactly equal the Census Bureau’s best estimate. Counts that remain fixed are considered invariant counts in the Census Bureau’s terms. This postprocessing works by using an optimizing routine to find a set of integer counts that meet all the constraints and are as close as possible to the noise-infused data. However, the exact specifics of this optimizing routine are not currently public.

The aggregate geographic levels for which the Census officially accounts, such as states, counties, and tracts, are called on-spine geographies, while off-spine geographies include precincts and voting districts (VTDs). The DAS postprocessing is targeted for accuracy and consistency of on-spine geographies. Notably, to increase accuracy on off-spine units, the Census Bureau has defined special block groups that do not directly correspond to the block groups in the final data release.

The Census Bureau has not released demonstration data that only contain added noise (the first step) before postprocessing (the second step). Without these noisy tabulation data, it is impossible to cleanly separate the effects of postprocessing from those of noise injection. Nonetheless, the existence of the 2010 demonstration data alongside the released 2010 Census allows us to analyze the suitability of the totality of the demonstration data for redistricting purposes.

Last, a complete theoretical investigation of the DAS remains difficult partly because of its complex postprocessing procedure and is beyond the scope of this article. Cohen et al. (28) examine a previous version of the TopDown algorithm and present some theoretical analysis of its simplified version, which they call “ToyDown.” Our empirical investigation complements their theoretical study and shows how the most up-to-date DAS affects redistricting in practice.

Racial and partisan undercounting biases

To evaluate the impact of the new DAS on redistricting plan drawing and analysis, we generated 10 sets of redistricting datasets, described in Table 1. These cases cover federal, state, and local offices across a diverse set of states. Using R packages “geomander” and “ppmf” (33, 34), we create precinct-level datasets that have three versions of total population counts: the original 2010 Census, the DAS-12.2 data, and the DAS-4.5 data.

Table 1. States and districts studied.

We compared the Census 2010, DAS-12.2, and DAS-4.5 datasets in seven states and three levels of elections. Simulations indicate the number of simulations for each of those three different comparison datasets. States that we only use for precinct-level modeling and not for redistricting simulations are denoted by a dashed entry.

State	Office	Districts	Precincts	Simulations
Alabama	–	–	1992	–
Delaware	State Senate	21	434	10,000
Louisiana	State Senate	39	3668	35,000
Louisiana*	State House	15	361	90,000
Mississippi	State Senate	52	1969	50,000
New York†	School Board	9	1207	10,000
North Carolina	U.S. House	13	2692	200,000
Pennsylvania	U.S. House	18	9256	10,000
South Carolina	U.S. House	7	2122	200,000
South Carolina	State House	124	2122	100,000
Utah	–	–	2337	–
Washington	–	–	7312	–

*Examines the Baton Rouge area.

†Examines the East Ramapo school district, using Census blocks instead of voting precincts.

We first examine the nature of the population variation induced by differential privacy and postprocessing at the level of VTDs. Almost by definition of differential privacy, there is meaningful variation in how VTDs’ populations change as a result of the DAS, even among those with similar racial and partisan characteristics. As a result, it is difficult to discern systematic patterns by observation alone. We therefore fit a generalized additive model (GAM) to the precinct-level population errors using various characteristics of the precinct. This model decomposes the overall changes into a systematic component, which varies according to the racial and partisan composition of a precinct, and a residual noise component, which has a mean of zero conditional on the local demographic composition. While the residual noise may lead to concentrated harms in certain small geographic communities, once aggregated to larger geographic areas, it will tend to cancel out. The systematic component, however, will not necessarily cancel, and hence, it is of particular interest to identify and quantify any such systematic error.

Our predictors for the GAM include the two-party Democratic vote share of elections in the precinct, turnout as a fraction of the voting age population, log population density, the fraction of the population that is White, and the Herfindahl-Hirschman index of race as a measure of racial heterogeneity (35). The GAM regresses the difference in precinct population between the DAS-12.2 and the Census data on the following function of these predictors

$$P_{\text{DAS},i}-P_{\text{Census},i}=t(\text{Democrati}{\mathrm{c}}_i,\text{Turnou}{\mathrm{t}}_i,\text{log}(\text{Densit}{\mathrm{y}}_i))+\mathrm{}s(\text{Whit}{\mathrm{e}}_i)+s(\text{HH}{\mathrm{I}}_i)+{\mathrm{\epsilon }}_i$$

where i indexes precincts or VTDs, P_D,i denotes i’s population as reported by data source D, and HHI denotes the Herfindahl-Hirschman index, which is a measure of diversity ranging from 0 (most diverse) to 1 (least diverse). The function t indicates the smoothed tensor product cubic regression, while the function s denotes thin-plate regression splines. Last, ε_i represents the error term. The model explains about 9 to 12% of the overall variance in population change.

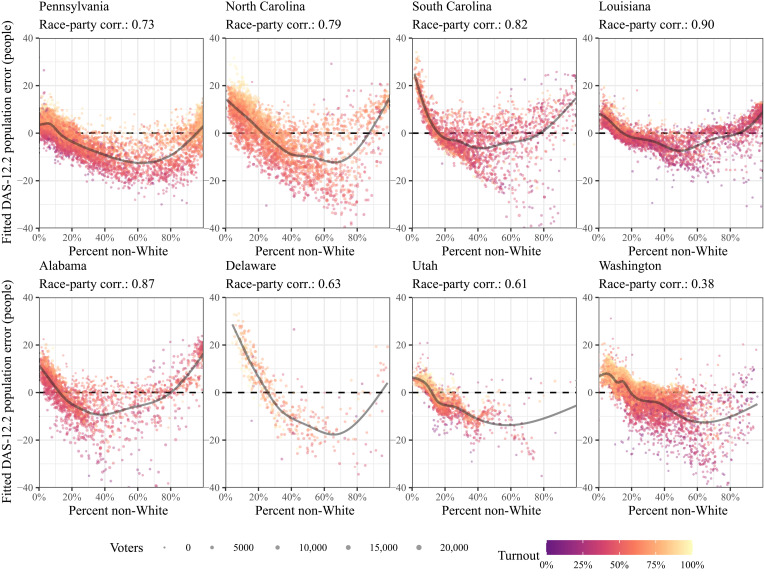
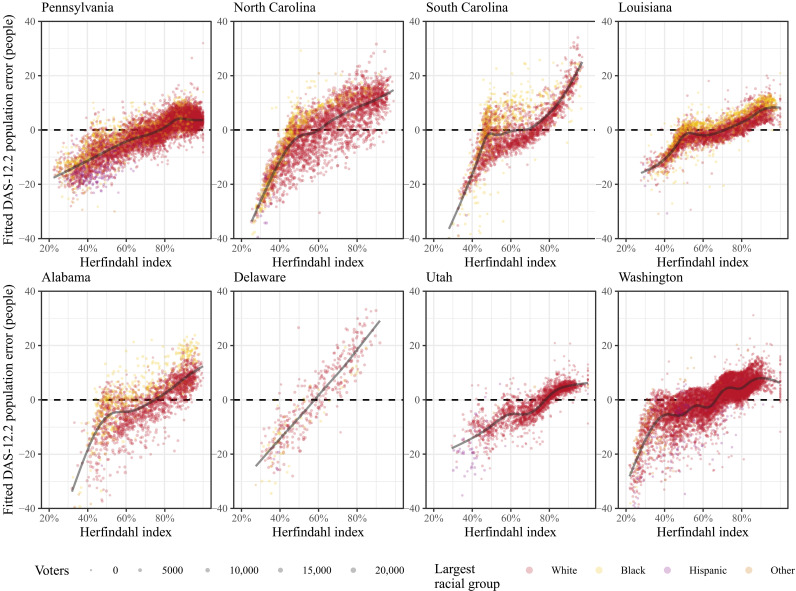
Figure 1 plots the fitted values from this model using deviations of the DAS-12.2 data against the minority fraction of the population in each precinct for eight states. We chose to study a variety of states including those frequently studied in redistricting (Pennsylvania and North Carolina), the Deep South (South Carolina, Louisiana, and Alabama), small states (Delaware), and heavily Republican (Utah) or Democratic (Washington) western states. Consistent patterns emerge across these diverse states. As indicated by U-shaped patterns, mixed White/non-White precincts lose the most population relative to more homogeneous precincts. Figure 2 more clearly shows this pattern with racially homogeneous precincts (see fig. S3.3 for the results based on DAS-4.5). We plot the error against the Herfindahl-Hirschman index and find that the fitted error in estimated population steeply declines as the precinct becomes more racially diverse.

Fig. 1. Model-smoothed error in precinct populations by the minority fraction of voters, with color indicating turnout.

A GAM-smoothed curve is overlaid to show the mean error by minority share.

Fig. 2. Model-smoothed error in precinct populations by the Herfindahl-Hirschman index.

A Herfindahl-Hirschman index of 100% indicates that the precinct is composed of only one racial group.

These patterns can be partially explained by the adopted DAS targets, which prioritize accuracy for the largest racial group in a given area (36). By doing so, the DAS procedure appears to undercount heterogeneous areas where the population is most racially diverse. In highly heterogeneous precincts, the largest racial group is smaller, so the magnitude of the accuracy guarantees is much smaller. As precincts are the building blocks of political districts, our results demonstrate that precincts that are heterogeneous along racial and partisan lines would see their electoral power diluted under the DAS. In aggregate, the reallocation of population from heterogeneous to homogeneous precincts would tend to increase the apparent spatial segregation by race.

We find a similar pattern of undercounting bias along a partisan dimension, which is detailed in section S3. The Census Bureau does not tabulate partisan data, so this must be a result of the relationship between party and race. To compute election results, we use precinct-level data from statewide elections (to avoid uncontested races and differences idiosyncratic to candidates) sourced from the Voting and Election Science Team (37). In Pennsylvania, we use the two-party vote share averaged across all statewide and presidential races, 2004–2008, and adjust to match 2008 turnout levels. In North Carolina, we use the 2012 gubernatorial election at the precinct level. In South Carolina, we use the 2018 gubernatorial election, while in Louisiana, we use the 2019 Secretary of State election, each estimated at the voting tabulation district level, allocated on the basis of the 2010 Census block voting age population. Last, in Delaware, we use the precinct-level returns from the 2020 presidential election.

Moderately Democratic precincts are, on average, assigned less population under the DAS than the actual 2010 Census. Furthermore, higher-turnout precincts are, on average, assigned more population under the DAS than they should otherwise have. These effects are on the order of 5 to 15 voters per precinct, on average, although some are larger. The corresponding effects for the DAS-4.5 data display an identical pattern but with roughly double the magnitude of fitted error (fig. S3.4).

Aggregated across the hundreds of precincts that comprise the average district, the DAS-12.2 errors may become substantial, as we discuss in more detail in the sections below. In the 70 congressional districts in the states that we examine statewide, the average district’s population changes by 308 people when measured with DAS-12.2 counts. However, in two Pennsylvania congressional districts in the Philadelphia area, the population changes by 2151 people on average. This measured difference under the DAS is orders of magnitude larger than the difference under block population numbers released in 2010.

It is difficult to know exactly how these partisan and racial biases arise without knowing more detail about the DAS postprocessing system and parameters. Regardless, the presence of differential bias in the precinct populations according to partisanship, turnout, and racial diversity can have important implications.

Simulation analysis

Simulating realistic districts allows us to understand how the DAS would affect a variety of potential redistricting plans beyond the enacted 2010 districts. These analyses are particularly relevant because map drawers will soon be using DAS-processed data to create new districts for the 2020 cycle. The DAS-12.2 data yield precinct population counts that are roughly 1.0% different from the original Census, and the DAS-4.5 data are about 1.9% different. For the average precinct, this amounts to a discrepancy of 18 people (for DAS-12.2) or 33 people (for DAS-4.5) moving across precinct boundaries. Therefore, our main simulation results should be considered as a study of how such precinct-level differences propagate at the district level by exploring many realistic redistricting plans.

Of the 10 states in Table 1, we further analyze 7 for simulation. In our modal analysis, we simulate district plans under the scenario that map drawers only have access to one of the three versions of population counts (the original 2010 Census, the DAS-12.2, or the DAS-4.5). Congressional district simulations were conducted with the sequential Monte Carlo (SMC) redistricting sampler of (23), while most of the state legislative district simulations use a merge-split Markov chain Monte Carlo (MCMC) sampler building from (19, 20). Both of these sampling algorithms are implemented in the open-source software package “redist” (24). The package allows simulating districts while imposing a population parity constraint so that all simulated maps are realistic (for more detail, see Materials and Methods).

Mirroring enacted maps, congressional district maps were sampled so that population deviations were at most 0.1 to 1%, and state legislative district population deviations were at most 5 to 10%, depending on the state. We generated Monte Carlo samples until the standard diagnostics including the number of effective samples indicated accurate sampling and adequate sample diversity. In the state legislative district simulations in South Carolina with more than 100 districts and Mississippi with 52 districts, ensuring sampling diversity required running several chains of the merge-split algorithm in parallel, initiated from a sample generated from (23).

Impacts on population parity

Perhaps the strongest constraint on modern redistricting is the requirement that districts be nearly equal in population. Deviations in population between districts have the effect of diluting the power of voters in larger-population districts. The importance of this principle stems from a series of Supreme Court cases in the 1960s, beginning with Gray v. Sanders (1963), in which the court held that political equality comes via a standard known as One Person, One Vote. As for acceptable deviations from population equality, Wesberry v. Sanders (1964) set the basic terms by holding that the Constitution requires that “as nearly as is practicable one [person’s] vote in a congressional election is to be worth as much as another’s.” Even minute differences in population parity across congressional districts must be justified, including those smaller than the expected error in decennial census figures (Karcher v. Daggett 1983).

For congressional districts, the majority of states thus balance population to within one person of perfect population parity (38). For state legislative districts, Reynolds v. Sims (1964) held that they must be drawn to near population equality. However, subsequent rulings stated that states may allow for small population deviations when seeking other legitimate interests (Mahan v. Howell 1972; Gaffney v. Cummings 1973). It remains to be seen whether the Supreme Court will see deviations due to Census privacy protection as legitimate.

When measuring population equality, states must rely on Census data, which was viewed as the most reliable source of population figures (Kirkpatrick v. Preisler 1969). We therefore empirically examine how the DAS affects the ability to draw redistricting maps that adhere to this equal population principle. We simulate maps for Pennsylvania congressional districts and Louisiana State Senate districts constrained at various levels of population parity, where populations are defined by one of the three data sources. We then examine the degree to which the resulting maps satisfy the same population parity criteria using another data source.

Deviation from population parity across n_d districts is generally defined as

$$\text{Deviation from parity}=\underset{1\le k\le n_d}{\text{max}}\frac{\mid P_k-\overline{P}\mid }{\overline{P}}$$

where P_k denotes the population of district k and $\overline{P}$ denotes the target district population. In other words, we track the percent difference in the district population P_k from the average district size $\overline{P}$ and report the maximum deviation. Our redistricting simulations generate plans that do not exceed a user-specified deviation. After generating these plans, we then reevaluate the deviation from parity using the precinct populations from the three data sources.

We find that the noise introduced by the DAS prevents the drawing of equal-population maps with commonly used population deviation thresholds. Because only one dataset will be available in practice, redistricting practitioners who attempt to create equal-population districts with DAS data should expect the actual deviation from parity to be orders of magnitude larger than what they can observe in the data. Because of the asymmetric postprocessing within the DAS algorithm, there is no clear way to improve estimates or to be confident in the magnitude of the error for any particular case. Below, we conduct simulations on congressional and state legislative districts. We find that this problem is more acute in state legislative districts, where there are more districts and each district is composed of fewer precincts. This is likely a consequence of the DAS procedure, for which noise is relatively larger at smaller scales.

Congressional districts in Pennsylvania

First, we analyze how the parity of the 2010 enacted Pennsylvania congressional districts varies when measured with each dataset. Congressional districts are generally drawn as to be nearly equal as possible. The enacted Pennsylvania congressional map has a maximum population difference between districts of 283 people (or 0.04%). When measured under the DAS, however, these differences are considerably larger, at 3893 people for DAS-4.5 (0.57%) and 2287 for DAS-12.2 (0.32%).

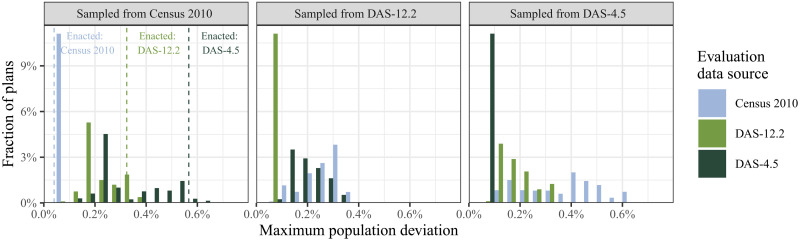
Investigating a singular enacted plan only allows us to measure how DAS influences parity in one particular instance. However, simulations allow us to generate many potential maps and investigate how likely parity errors would be under various intended tolerances. Figure 3 shows the maximum deviation from population parity for the 30,000 simulated redistricting plans in Pennsylvania, when evaluated according to the three different data sources. We simulated 10,000 plans from each data source, with every plan satisfying a 0.1% population parity constraint. The simulation algorithm also ensured that no more than 17 counties were split across the entire state, reflecting the requirement in Pennsylvania that district boundaries align with the boundaries of political subdivisions to the greatest extent possible.

Fig. 3. Maximum deviation from population parity among Pennsylvania redistricting plans simulated from the three data sources.

All plans were sampled with a population constraint of 0.1%, corresponding to the deviation measured from the Census 2010 precinct data and marked with the dashed line. Deviation from parity was then evaluated using the three versions of population data.

Consistently, plans that were generated under one set of population data and drawn to have a maximum deviation of no more than 0.1% had much larger deviations when measured under a different set of population data. For example, of the 10,000 maps simulated using the DAS-12.2 data (the middle panel of the figure), 9915 exceeded the maximum population deviation threshold, according to the 2010 Census data. While nearly every plan failed to meet the population deviation threshold, the exact amount of error varied greatly across the simulation set. As a result, redistricting practitioners who attempt to create equal-population districts according to similar thresholds can expect the actual deviation from parity to be larger than reported but of unknown magnitude.

State legislative districts in Louisiana

We expect smaller districts such as state legislative districts to be more prone to discrepancies in population parity. For example, the average Louisiana congressional district comprises about 600 precincts, but a State Senate district comprises about 90 and a State House district comprises only 35. Therefore, deviations due to DAS are more likely to result in larger percent deviations from the average.

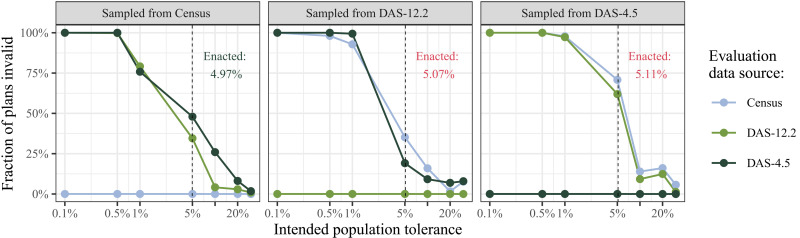
First, we calculate how the DAS influences the parity of the enacted map. Louisiana’s state constitution places no legal parity requirements beyond that districts be created “as equally as practicable on the basis of population shown by the census.” However, their adopted guidelines for the 2010 redistricting cycle set 5% as a target for all maps drawn for the State House (39). The State Senate map, with a parity of 4.97%, appears to have been drawn to target this goal as well. However, we find that both enacted plans under the DAS have population parities of above 5%, rendering the enacted plan invalid under the state’s own guidelines.

Second, we use simulations to examine whether this pattern is also found in other realistic maps. We compare 30,000 Louisiana State Senate plans generated from each of the three data sources (90,000 in total) and population parity constraints ranging from 0.1 to 30%, measuring the plans’ population deviation against the three different data sources. We simulated 5000 plans for each data source/population parity pair. Figure 4 plots the results of this comparison.

Fig. 4. Fraction of Louisiana State Senate plans simulated under one data source with a population parity constraint that is invalid when measured under another.

The horizontal axis shows the tolerance constraint for the original simulation on the log₁₀ scale. The vertical axis shows the percent of plans that exceed the intended tolerance according to the evaluation data. The dashed lines show the maximum deviation from parity of the enacted 2010 State Senate map as measured under each dataset. The enacted plan meets the 5% target when measured with the Census, but parity exceeds 5% in both DAS datasets.

As expected, we see complete acceptance for plans measured with the dataset from which they were generated. However, plans generated under one dataset can exceed the population threshold under another. Specifically, plans generated under DAS data can be highly likely to be invalid when evaluated using the true Census data. The rate of invalid plans grows as the tolerance becomes more precise.

Also note that even at tolerances as generous as 1 or 5%, plans generated from both versions of DAS data can regularly be invalid. Compared to Pennsylvania congressional districts, with a parity tolerance of 0.1%, simulated districts for the Louisiana State Senate fail to meet the cutoffs much more often, as the DAS-added noise is relatively larger at smaller scales. This suggests that map drawers using the DAS-adjusted demonstration data should anticipate actual population differences between districts to be larger than reported, although they will not be able to know the true magnitude of the errors.

Impacts on partisan composition

If changes in reported population in precincts affect the districts in which they are assigned to, then this has implications for which parties win those districts. While a change in population counts of about 1% may seem small, differences in vote counts of that magnitude can reverse some election outcomes. Across the five U.S. House election cycles between 2012 and 2020, 25 races were decided by a margin of less than a percentage point between the Republican and Democratic party’s vote shares, and 228 state legislative races were decided by less than a percentage point between 2012 and 2016.

Partisan implications also raise the concern of gerrymandering, where political parties draw district boundaries to systematically favor their own voters. Simulation methods have been regularly used in redistricting litigation over partisan gerrymanders, including Common Cause v. Lewis, Rucho v. Common Cause, Ohio A. Philip Randolph Institute v. Householder, League of Women Voters of Michigan v. Benson, and League of Women Voters v. Pennsylvania. To evaluate the impact of the DAS on the analysis of potential partisan gerrymanders, we used the simulations from four states (Table 1) and compared the partisan attributes of the simulated plans from the three data sources.

How does the systematic undercounting and overcounting of precinct-level populations in the DAS data affect the conclusions that we draw about the partisan and racial biases of legislative redistricting plans? We first assess the impact of DAS data in identifying partisan packing and cracking, following a common approach in redistricting analysis. Practitioners and researchers compare enacted plans against a distribution of election results from each simulated plan, for example, adding up each precinct-level vote tabulation to each simulated district. Plans that are partisan gerrymanders stand out from the simulated ensemble as yielding more seats for one party over the other. The argument that ensemble analysis is sufficient for this purpose has been made in various academic contexts, including (40, 41), and litigation contexts, most recently (42, 43).

The results from nonsimulation analysis (figs. S1 and S2) suggest that the DAS-induced noise may not cancel out if diverse areas are spatially clustered. The systematic patterns at the district level clearly depend on the spatial adjacency of diverse and homogeneous precincts. Simulations can evaluate these implications beyond particular enacted plans.

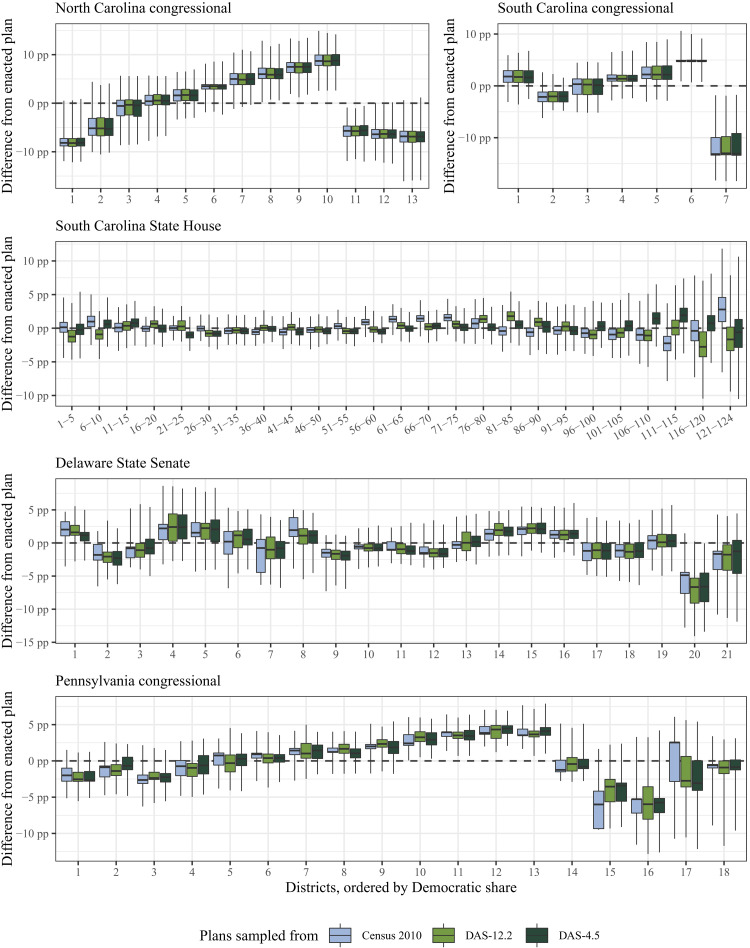
We find that across tens of thousands of simulated plans, the DAS leads to unpredictable differences in the distribution state-level party outcomes under the three data sources. Figure 5 summarizes the differences in simulations with the aforementioned ensemble approach. To compare district-level partisan outcomes across simulations, we sort districts in ascending order of the Democratic candidate’s vote share in each simulation so that district number 1 in North Carolina is always the most Republican district in each simulated plan and district number 13 is the most Democratic district in the same plan. For each ordered district in each simulation, we subtract off the enacted plan’s Democratic vote share and plot the differences in a box plot (whiskers extend the entire range of simulated data). A box plot completely above zero indicates that the enacted plan had fewer Democratic voters in that district than would be expected under a partisan-neutral baseline, in other words, that the district cracked Democratic voters.

Fig. 5. The distribution of the simulated Democratic vote share relative to the enacted redistricting plan in percentage points, comparing the original Census with DAS versions.

Districts are ordered by the level of the Democratic vote in each simulation. Districts are grouped for the South Carolina State House because of the large number of districts. Whiskers extend to cover the full range of the simulated data. pp, percentage points.

Figure 5 shows that while in some cases, such as the congressional districts in North and South Carolina, there are no discernible differences across the three data sources, for others, the differences can be substantial. For the South Carolina State House, a pattern of cracking in the 61st to 75th most Democratic districts under the Census 2010 data disappears under the DAS-protected data. Moreover, evidence of packing in the 111th to 115th most Democratic state legislative districts under the Census 2010 data is reversed under the DAS-4.5 data. In Pennsylvania, results are relatively stable across data sources for the relatively Republican districts 1 to 14 but display considerable differences for the most Democratic districts (15 and 17), with median discrepancies moving as much as five percentage points.

Given that redistricting litigation often must focus on a single district or set of districts (44), discrepancies of this magnitude at the district level could change the conclusions regarding the presence or absence of a partisan gerrymander. The fact that the presence and magnitude of the discrepancies are not consistent even within the same state can complicate efforts to take into account these potential biases in research and decision-making.

Impacts on racial composition

The Voting Rights Act of 1965, its subsequent amendments, and a series of Supreme Court cases all center race as an important feature of redistricting. A large number of these cases focus on the creation of MMDs (e.g., Thornburg v. Gingles 1986, Shaw v. Reno 1993, Miller v. Johnson 1995, and Shelby County v. Holder 2013). First, we analyze whether the DAS data systematically undercount or overcount certain areas across racial lines. In doing so, we focus on the consequences of the Bureau’s decision to target accuracy to the majority racial group in a given area in their postprocessing procedure (36).

We also explore how DAS data can influence the creation of MMDs. To do so, we empirically examine how using the DAS data to create MMDs differs from the same process undertaken using the 2010 Census data. We simulate maps in the Louisiana State House using various levels of a constraint targeted to create MMDs and examine the degree to which maps generated using the Census and DAS data lead to different results at the precinct level.

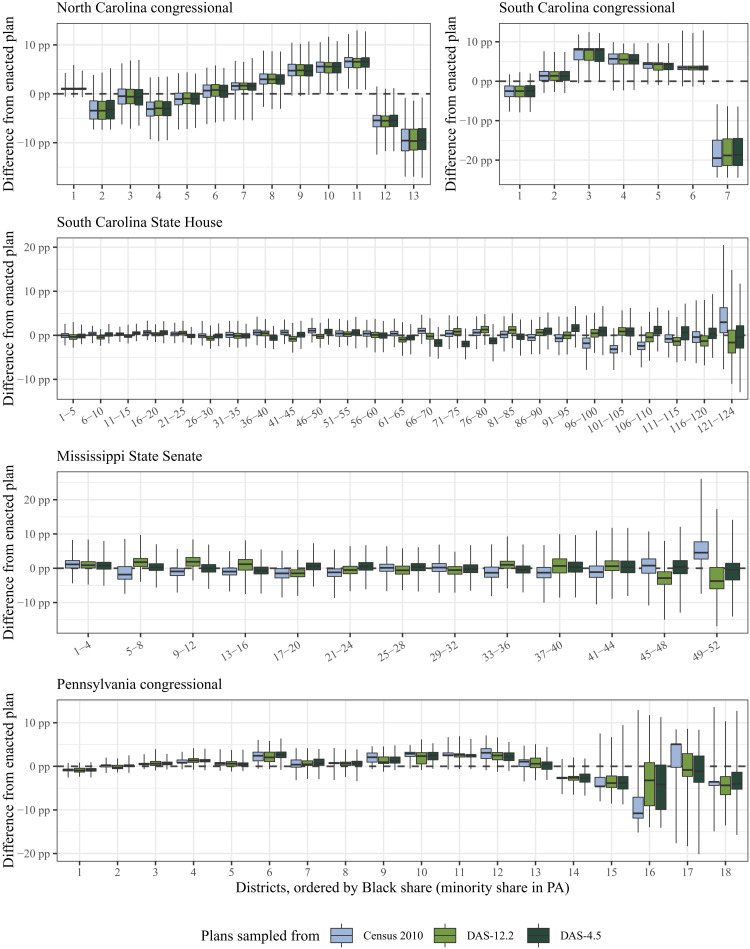
Figure 6 compares the simulations drawn from the three data sources in a way similar to Fig. 5 but by ordering the districts by their Black population share instead of Democratic vote share. As in Fig. 5, there are inconsistent patterns across states and district sizes. The racial makeup of congressional districts in North and South Carolina does not appear to be affected. For the South Carolina State House, patterns of cracking in the districts with the largest racial minorities (districts ordered 121 to 124) under the Census 2010 data disappear or are even reversed under the DAS-12.2 and DAS-4.5 data. In districts ranked to be the 96th to 110th most Black, patterns of packing are reversed in the DAS data. Similarly, in the Mississippi State Senate, evidence of cracking in the most Black districts (ordered 49 to 52) becomes evidence of packing under the DAS-12.2 data. In Pennsylvania’s 18 congressional districts, patterns are generally stable across the data sources for the 14 most White congressional districts but display considerable differences for the heavily non-White districts ordered 16 and 17, with median discrepancies moving as much as seven percentage points.

Fig. 6. The distribution of the simulated Black population share relative to the enacted redistricting plan in percentage points, comparing the original Census with DAS versions.

Districts are numbered in ascending order of the Black or minority population share in each simulation. Districts are grouped for the South Carolina State House and Mississippi State Senate because of the large number of districts. Whiskers extend to cover the full range of the data.

These district-level findings may still mask the variability around which individual precincts are included in MMDs. To explore this, we run simulations using several levels of a Voting Rights Act constraint, which we did not apply in previous sections, to encourage the formation of MMDs at various strengths. We focus on Louisiana State House districts in the Baton Rouge area and run 10,000 simulations of the merge-split MCMC sampler for each dataset-constraint pair. We then calculate the probability that each precinct is assigned to an MMD (as defined by Black population) by the proportion of Monte Carlo samples in which the precinct is assigned to an MMD.

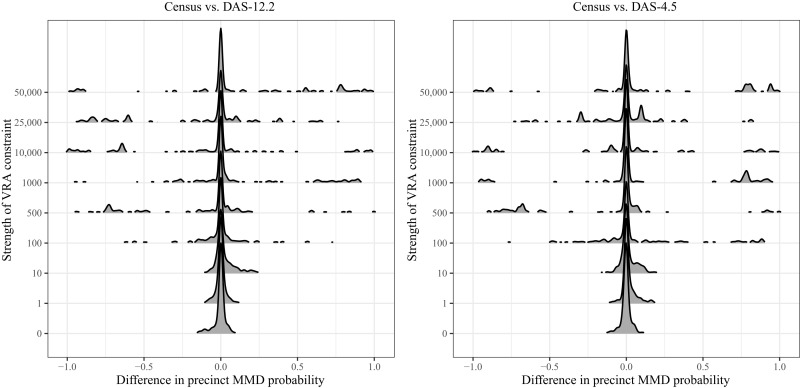
The left and right columns of Fig. 7 show the difference between these probabilities for the Census versus DAS-12.2 and Census versus DAS-4.5. With no Voting Rights Act constraint (corresponding to the Voting Rights Act strength of zero on the y axis), each precinct has similar probabilities of being in an MMD, regardless of the dataset used. However, as the strength of this constraint increases (making the algorithm search for MMDs more aggressively), we see that the noise introduced to the DAS data systematically alters the district membership of individual precincts. Precincts with a value of 1 or −1 in Fig. 7 are never in an MMD under one data source but are always in an MMD when the same mapmaking process is undertaken with a different data source.

Fig. 7. The difference in calculated probabilities of being assigned to an MMD under the DAS compared to the original Census.

VRA, Voting Rights Act. Strength of VRA constraint is a weight that controls the preference for MMDs in the simulation’s target distribution (see Materials and Methods, Eq. 1).

This means that how the Census implements the DAS could influence the political representation of voters in particular precincts. The simulation methods used are probabilistic, and assignment differences are expected and even desired between many created districts. However, these results illustrate a potential scenario in which real map drawers decide to add or remove precincts from a particular district to keep minority groups together because of population deviation introduced by DAS.

Impacts on ecological inference and voting rights analysis

Researchers have developed methods to predict the race and ethnicity of individual voters using Census data. Since Gingles, voting rights cases have required evidence that an individual’s race is highly correlated with candidate choice. Statistical methods must therefore estimate this individual quantity from aggregate election results and aggregate demographic statistics (45–47). A key input to these methods is accurate racial information on voters. To produce these data, recent litigation has used BISG to impute race and ethnicity into a voter file (25–27). This methodology provides improved classification of the degree of racially polarized voting and racial segregation.

We first examine how the accuracy of prediction changes between the DAS and original Census data. While differential privacy should not prevent statistical prediction, race is the most sensitive information included in the P.L. 94-171 data release. Hence, it is of interest to examine whether the DAS will degrade the prediction accuracy of individual race and ethnicity. We follow up on this analysis by revisiting a recent Voting Rights Act Section 2 court case about the East Ramapo school board election and investigate whether this change in racial prediction alters the conclusions of the racial redistricting analysis.

Prediction of individual voters’ race and ethnicity

We first compare the accuracy of predicting individual voters’ race and ethnicity using the original 2010 Census data, the DAS-12.2 data, and the DAS-4.5 data. To obtain the benchmark, we use the North Carolina voter file acquired in February 2021. All voter files used here were obtained through L2 Inc., a leading national nonpartisan firm that supplies voter data and related technology. In the United States, voter files are particularly widespread because of the Help America Vote Act of 2002. In several southern states—Alabama, Florida, Georgia, Louisiana, North Carolina, and South Carolina—the voter files contain the self-reported race of each registered voter. This information can then be used to assess the accuracy of the BISG prediction methodology (see Materials and Methods).

We compare estimates by changing the data source from which the geographic prior is estimated, from the 2010 Census to each of the two DAS datasets. Estimates of the other race prediction probabilities are obtained by merging three sources: the 2010 Census surname list (48), the Spanish surname list from the Census, and the voter files from six states in the U.S. South, where state governments collect racial and ethnic data about registered voters for Voting Rights Act compliance. The middle and first name probabilities are derived exclusively from the voter files.

We evaluate the accuracy of the BISG methodology on approximately 5.8 million registered voters included in the North Carolina February 2021 voter file. Among them, approximately 70% are White and 22.5% are Black, with smaller contingents of Hispanic (3.4%), Asian (1.5%), and other (2.4%) voters.

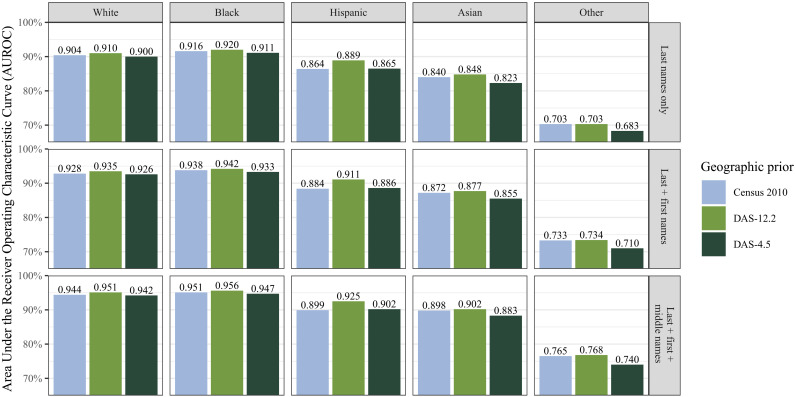
Figure 8 summarizes the accuracy of the race prediction with the area under the receiver operating characteristic curve (AUROC), which ranges from 0 (perfect misclassification) to 1 (perfect classification). Across all racial and ethnic groups except Hispanics, we find the same unexpected pattern. Relative to the 2010 Census data, the DAS-12.2 data yield a small improvement in prediction performance, while the DAS-4.5 data give a slight degradation. Among Hispanics, both forms of DAS-protected data result in slightly improved predictions over the original Census data.

Fig. 8. AUROC percentage values for the prediction of individual voter’s race and ethnicity using North Carolina voter file.

Bars represent AUROC with geographic priors given by each of three datasets: 2010 Census, DAS-12.2, and DAS-4.5.

The strong performance of the DAS data in this setting is counterintuitive. It is possible that the noise added to the underlying data has somehow mirrored the true patterns of population shift from 2010 to 2021 or that this noise makes the DAS-12.2 data more reflective of the registered voter population relative to the total population. In addition, the DAS may degrade or attenuate individual probabilities without having a meaningful impact on the overall ability to classify, something that AUROC is not designed to measure (49). Despite this, AUROC has been used to measure the disclosure risk from differentially private data in pharmacogenomic research (50).

Results are substantively similar if we consider the classification error, under the heuristic that we assign each individual to the racial and ethnic group with the highest posterior probability. Using the true Census data to establish geographic priors, we achieve posterior misclassification rates of 15.1, 12.1, and 10.0% when using the last name; last name and first name; and last, first, and middle names for prediction, respectively. The analogous misclassification rates are slightly higher for the DAS-4.5 priors—15.6, 12.5, and 10.3%—but the same or slightly lower for the DAS-12.2 priors: 15.1, 12.0, and 9.9%.

Our analysis shows that across three main racial and ethnic groups, the predictions based on the DAS data appear to be as accurate as those based on the 2010 Census data. The finding suggests that, although the new DAS methodology may protect differential privacy, it may not prevent accurate prediction of sensitive attributes any more than the swapping methodology used in the 2010 Census.

Implications for evidence in voting rights cases

How might these differences in BISG result affect findings in voting rights cases? We reexamine the remedy in NAACP of Spring Valley v. East Ramapo Central School District (2020) as a case study. The BISG methodology played a central role in this recent case regarding Section 2 of the Voting Rights Act. The East Ramapo Central School District (ERCSD) nine-member school board was elected using at-large elections. This often led to an all-White school board, despite 35% of the voter-eligible population being Black or Hispanic. However, within the district, nearly all White school children attend private yeshivas, whereas nearly all Black and Hispanic children attend the ERCSD public schools. As a result of the court ruling for the plaintiffs, the district moved to a ward system. That is, the school district adopted a system with seven geography-based election districts.

We reexamine the remedy of this case by focusing on plans with MMDs. We estimate how many MMDs the move to a district system would create in this case, based on imputations of individual race and ethnicity using either the DAS-12.2 or the Census 2010 data. The move from at-large elections to district systems has been shown to improve representation for minority candidates in local elections with high residential segregation, like the ERCSD (51).

To approximate the data used by an expert witness who testified in the court case, we obtain the New York voter file (as of 16 November 2020) from the state Board of Elections. We subset the voters to active voters with addresses in Rockland County where the ERCSD is located. Using the R package “censusxy,” which interfaces with the Census Bureau’s batch geocoder, we match each voter to a block and subset the voters to those who live within the geographic bounds of the ERCSD (52). This leaves 58,253 voters, for whom we impute races using the same machinery behind the R package “wru” (53), as described in (27). This process closely mimics the one used in the original case.

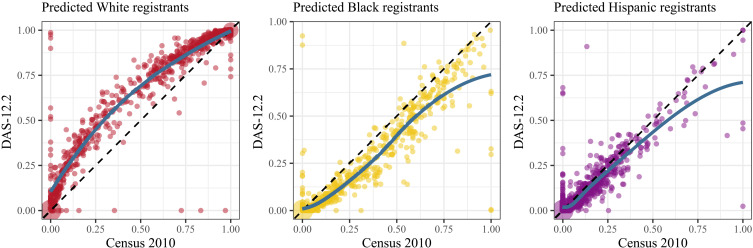
We first examine how BISG results differ at smaller levels, before simulating how these differences manifest in the number of MMDs that can be drawn. Figure 9 compares these two predictions using the proportions of (predicted) White, Black, and Hispanic registered voters for each Census block. As in the case, we aggregate predicted probabilities for each individual’s race to the block level rather than classifying each individual by their most likely predicted race. We find that the predictions based on the DAS-12.2 tend to produce blocks with more White registered voters than those based on the original Census data. As a consequence, the predicted proportions of Black and Hispanic registrants are much smaller, especially in the blocks where they form a majority group.

Fig. 9. Differences in imputed racial registrants by census blocks.

The x axis represents the percent of a group, as measured by aggregating predicted probabilities for race from racial imputation using the Census 2010 data. The y axis represents the corresponding imputation using the DAS-12.2 data.

The precise reason for these biases is unclear. The DAS tends to introduce more error for minority groups than for White voters and even more error for a racial group that is a minority in its Census block. This additional noise, when carried through a nonlinear transformation such as the Bayes’ rule calculation for racial imputation, may introduce some bias. In addition, the large bias for White and Black voters relative to Hispanic voters suggests that the similarity of surnames between the White and Black populations, compared to the Hispanic population, may also be a factor. Regardless, it is clear that the DAS-injected noise differentially biases voter race imputations at the block level. This pattern may not always yield greater inaccuracies when aggregated to the statewide level, as seen in the prior section, but it is especially prevalent within the ERCSD.

We further find that the systematic differences in racial prediction at the block level result in the underestimation of the number of MMDs that can be drawn from the data. We simulate 10,000 redistricting plans using DAS-12.2 population and a 5% population parity tolerance. As in the original court case, an MMD is defined as a district in which more than 50% of its registered voters are either Black or Hispanic. We find that the number of MMDs based on the DAS-12.2 data never exceeds that based on the 2010 Census for all simulated plans. Notably, among 6774 plans that are estimated to yield two MMDs according to the Census data, 56% of them are predicted to have only one MMD. For a complete accounting of simulation evidence in this local case, see table S4.2.

While this single case of local redistricting does not represent the entire universe of local redistricting, our analysis suggests that in small electoral districts, such as those of school board elections, the DAS can generate bias that may favor one racial group over another. Local governments generally do not lie on-spine so they may be especially victim to the random seed used in privatizing the data. Although the number of MMDs is underestimated under the DAS data in this case, the direction and magnitude of racial effects are difficult to predict, as they depend on how the choice of tuning parameters in the DAS algorithm interact with a number of geographical and other factors.

DISCUSSION

Significance

Here, we study how the DAS and subsequent postprocessing steps could affect the process of redistricting. Our analysis shows that the added noise makes it impossible to follow the principle of One Person, One Vote, as it is currently interpreted by courts and policy-makers. The principle requires states to minimize population differences between districts as much as possible. Given the magnitude of population errors introduced by the DAS, our analysis shows that current practices of redistricting will make it difficult and, in some cases, effectively impossible to meet these existing standards relative to the Census’ best estimates of total population. In the near future, courts may decide to treat this new type of error as is or loosen the bounds on these standards. Such a move will change the precedents and alter our understanding of redistricting in the United States. It may also affect the partisan balance of power.

The complex nature of the DAS postprocessing procedure masks the original source of these biases. Our findings suggest that they are likely a combination of several factors. First, the bias against heterogeneous areas could be driven by the Bureau’s decision to target accuracy to the population count of the majority racial group in a given area (36). Second, the choice to not prioritize accuracy at the block level leads to an additive effect in many cases. Our precinct-level population tabulations reveal around a 1% average deviation in the DAS-12.2 data compared to the 2010 Census data, and these errors do not always cancel out. Ensuring that population is accurate at this off-spine geography would help minimize population deviations among the majority of states that rely on these geographies to draw and evaluate their districts.

One general strength of the differential privacy framework is that the noise generation mechanism is known. However, the asymmetric and deterministic nature of the postprocessing procedure of the DAS makes a proper statistical adjustment difficult for many commonly used models and nearly impossible for others. For this reason, many analysts are likely to treat the DAS-protected data as the basis for evaluating districts, as they have done with the past versions of the Bureau’s disclosure avoidance methods.

One possible approach is for the Bureau to additionally release the noisy DAS data without postprocessing so that analysts can use it for their statistical analysis. This will not solve the problems in map drawing but would allow researchers to properly calibrate uncertainty for at least some analyses when evaluating redistricting maps. However, new methodological developments are needed to properly incorporate the DAS noise generation mechanism into redistricting simulation analyses. In addition, it remains to be seen whether the addition of noise significantly reduces the statistical power to detect racial and partisan gerrymandering in litigation.

Implications

When considering the fundamental trade-off between privacy protection and data accuracy, it is critical to understand what individual data are at risk. The decennial census collects information on individual age, sex, race, relationship to the head of household, and basic housing information but not other, more sensitive information, such as citizenship, income, and disability status. The basic demographic variables in the decennial census play an essential role in public policy, including redistricting, the subject of this article, and the disbursement of federal and state funds. Individuals’ race and ethnicity are perhaps the most sensitive variable to be protected in the decennial census microdata.

The ability to reveal the race of 17% of respondents through a microdata reconstruction experiment (using a compendium of five commercial databases) provided key motivation for the Bureau’s decision to adopt differential privacy (54). Combining the Census data with a publicly available voter file, we find that the prediction of individual race is as accurate with the DAS data as with the original Census data. We expect these findings to be relevant even where public voter files are not available but where the commercial databases as used in (54) still are.

Although accurate individual-level prediction does not necessarily constitute a violation of differential privacy, we believe that this finding needs to be considered when weighing the benefits and costs of privacy protection in the decennial census. Our empirical findings on racial imputation accuracy point to the fact that differential privacy does not necessarily prevent accurate prediction of individuals’ sensitive information better than the prior privacy protection method.

Based in part on an earlier version of this article, along with input from other researchers and practitioners, the Census Bureau has altered the DAS algorithm to address some of the aforementioned problems. According to the Census Bureau’s 9 June 2021 press release, the Bureau now plans to further increase the privacy loss budget and modify the postprocessing algorithm. In addition, its 1 July 2021 newsletter states that this latest change has lowered the total error at areas above the optimized block group but has increased the amount of error introduced by the DAS at the block level. We plan to analyze new demonstration data based on this updated DAS algorithm once released.

It is important to point out that the Census Bureau claimed that the DAS-12.2 analyzed here met all internal accuracy targets “established for redistricting, Voting Rights Act enforcement, and other priority uses of the redistricting data” (55). Nonetheless, we are still able to identify systematic biases across several states in that data on precisely the topic for which these accuracy guarantees were designed. If the same flaws are not resolved in the 2020 Census data, then they may have important ramifications for the upcoming redistricting cycle and for years to come.

Many national statistics agencies around the world face the difficult task of balancing the statutory requirements to protect respondent privacy with the accuracy of their reported count. Full enumeration censuses must pay special attention to disclosure risks due to the inclusion of data from every person that can be counted. At the same time, since censuses are used to allocate political power between geographic areas, it is equally important to ensure the accuracy and usability of the reported counts.

The U.S. Census Bureau’s DAS clearly reflects this critical trade-off. The DAS relies on differential privacy, adding random noise to the raw Census counts, while it also uses a complex postprocessing procedure to avoid negative counts and maintain consistency of published population counts across several levels of geographical units. This two-step algorithm creates counts that appear to be usable and are consistent within and across tables. This feature makes it likely that a similar algorithm will be used in other contexts. Our findings suggest, however, that the complex and nonlinear nature of the DAS can increase the chances of systematic errors and biases.

This article focused on the impacts of the DAS on redistricting analyses using the latest versions of the demonstration data released before the 2020 Census data are delivered. This offered a framework for evaluation that was completely within the stated use for the data. We considered a likely scenario, in which map drawers and analysts treat the noise-injected DAS data as is, without performing any additional accounting for the DAS noise. We find that the DAS has profound effects on standard redistricting analyses and procedures. Despite the efforts of the Bureau to minimize error, we find that the added noise artificially shifts population counts from racially heterogeneous and mixed-partisanship areas to more homogeneous areas. These nonrandom local errors can aggregate into substantively large and unpredictable biases at district levels, especially for small districts. Fixing these systematic biases is of fundamental importance, as they will have partisan and racial impacts on the upcoming redistricting.

Privacy protection in the decennial census is not free; it comes with the societal cost of decreasing accuracy, which has ripple effects in making and evaluating public policy. Therefore, we must ask what private information we wish to protect and what cost we are willing to pay for it. The burden of privacy should not be borne disproportionately by people of certain races or political preferences.

POSTSCRIPT

On 12 August 2021, about 6 weeks before the planned release, the Census Bureau released the finalized demonstration data for the 2020 Census. The Bureau announced several important changes to the DAS. These changes were based on the comments and feedback submitted during a public comment period in May 2021, where the initial version of this article was also submitted. First, the Bureau announced a greater privacy loss budget (ϵ = 19.61) than for either of the previous releases (ϵ = 12.2 and 4.5). According to the Bureau’s presentation on 1 July 2021, they have resolved the problems due to “geographic bias” (“the accuracy of population counts being different at larger and smaller geographies”) and “characteristic bias” (“counts of racially or ethnically diverse geographies being different than more racially or ethnically homogeneous areas”). This constitutes a 1000-fold increase (on the probability ratio scale) in the leniency of the privacy guarantee since exp(19.61)/ exp(12.2) ≈ 1.6 × 10³. Second, the Bureau announced several changes to the postprocessing algorithm with the goal of reducing biases of the type that we demonstrated in our article. Third, according to the Bureau, they modified the postprocessing algorithm to reduce the total error at high levels of geography above the block group. As a side effect, this will likely increase total error at the block level.

In this section, we repeat our analyses above using the DAS-19.61 data. The Census Bureau reports that the DAS-19.61 corrects for racial and partisan biases at on-spine geographical units higher than the block group. Unfortunately, we still observe these biases at the VTD level because the Bureau did not attempt to minimize VTD-level errors as part of their postprocessing. This fact has important implications for redistricting simulation analyses, which are typically based on VTDs. We find that, although the differences in population counts between the DAS-19.61 and 2010 census data are an order of magnitude smaller than before at the congressional district level, strict population parities may still not be attainable in some cases. In addition, racial and partisan effects of the DAS-19.61 data on simulation analyses remain qualitatively similar to those of the prior DAS releases. It appears that the evaluation of redistricting maps based on the DAS-19.61 can sometimes yield conclusions different from that based on the census data. Last, like before, the latest DAS does not degrade the overall prediction accuracy of individual voters’ race and ethnicity. However, these predictions are sufficiently different to possibly affect the conclusions of simulation analysis for the voting rights of minority groups.

In summary, the latest release of DAS-protected data improves over previous releases in many ways but fails to address all of the problems identified here, particularly those affecting the drawing and simulation of districting plans. Biases remain at the VTD level even after increasing the total privacy loss budget. These biases would likely not be resolved by any increase in the privacy loss budget. Instead, these biases likely come from the decision to maintain accuracy at geographies other than VTDs and voting precincts, such as census tracts. The imperfect overlap between these boundaries, combined with the increase in errors at small geographic levels such as census blocks, could still affect redistricting analyses. At the same time, using the latest DAS-protected data, we are still able to accurately predict individual’s race, which is the most sensitive information of the decennial census.

Racial and partisan biases

Figures S4.1, S4.2, and S4.3 replicate Figs. 1 and 2 and fig. S3.1 on the DAS-19.61 data. For VTDs, we observe the same pattern of bias as before, albeit around half the magnitude, and despite the Bureau’s assurances that racial biases had been corrected by changes to the postprocessing system.

However, it does appear to be the case that the Bureau has largely eliminated these errors for on-spine geographies. Consequently, for larger geographical areas such as congressional districts, which can be decomposed as a large number of tracts plus several additional block groups or blocks, the racial biases only manifest in the latter additions and are relatively small in magnitude. In contrast, the previous DAS-12.2 contained racial biases for on-spine geographies as well, which were magnified by aggregation and did not disappear, leading to large population shifts in current congressional districts. Table S4.3 shows that deviations from 2010 Census totals among all the enacted congressional districts in the states that we studied ranged from −2153 to 2164 under the DAS-12.2 data, but under the DAS-19.61 data, the range of deviations is only −216 to 319. This constitutes a nearly 10-fold improvement.

Simulation analysis

Population parity in redistricting

By increasing the privacy loss budget to 19.61, we expect total population errors at large geographic levels such as complete districts to be smaller than in previous releases. The population of congressional districts (as of 2019) according to the DAS-19.61 differs from the actual Census counts by an order of magnitude smaller than that according to the DAS-12.2 (table S4.3). However, leaving VTDs “off-spine” means that discrepancies could still be present.

We repeat the parity analysis with the new DAS-19.61 data. As before, we generated 35,000 Louisiana State Senate maps (5000 for each of seven tolerances) under each dataset (for 70,000 total) and measured the fraction of plans that would be rendered invalid. Figure S4.4 shows the results from this analysis. Unlike the previous releases of DAS-4.5 and DAS-12.2, the enacted map would still be valid at an intended population tolerance of 5% under DAS-19.61. These errors are lower than those found in Fig. 4 for DAS-12.2 and DAS-4.5, rendering the majority of plans at generous tolerances such as 5% valid in both cases.

However, plans generated with strict parity goals can still be found invalid at high rates. This means that plans created with a particular parity goal in mind may, in reality, exceed that goal in some cases, with the likelihood of such a mistake happening increasing as the parity tolerance is lowered.

Partisan effects on redistricting

Our reanalysis of racial and partisan biases found that biases persist at the VTD level but generally disappear when VTDs are aggregated to larger, fixed, geographic areas. Here, we reanalyze the effect of these smaller-scale VTD biases on simulation analyses of partisan and racial gerrymandering. Do the small-scale errors continue to cause spurious shifts and incorrect conclusions from redistricting simulations, as in Fig. 5? Or does the large size of the simulated legislative districts compared to individual VTDs protect against bias?

Unfortunately, as fig. S4.5 shows, DAS-19.61 data display qualitatively similar patterns to the DAS-12.2 and DAS-4.5 data. While, for many simulated districts, there is close agreement between the results for Census 2010 and DAS-protected data, for some districts (see Pennsylvania, ordered district 15, and South Carolina State House, ordered districts 111 to 115 and 121 to 124), the DAS-based simulations differ by several percentage points, which can shift the direction of a plan’s measured partisan bias.

Racial effects on redistricting

The results for racial gerrymandering are similarly troubling. Figure S4.6 shows DAS-19.61 results following the layout of its counterpart in Fig. 6. The same areas for which the DAS-12.2 and DAS-4.5 simulations diverged from the 2010 Census ground truth prove problematic for the DAS-19.61 as well (South Carolina State House, ordered districts 96 to 110 and 121 to 124; Mississippi State Senate, ordered districts 49 to 52; and Pennsylvania, ordered district 16).

How should we reconcile these findings with the fact that biases in the overall population totals at the legislative district level appear to have been rectified by DAS-19.61? We suspect that the simulation process, which constantly makes calculations from and reassigns districts for individual VTDs, is driven more by local considerations than fixed tabulations are. Analogous to population parity simulations, the aggregated calculations performed by the simulation algorithms and resulting analyses depend on the noisy data themselves; this is crucially different from tabulations of existing geographic areas that have been defined without reference to it.

We next examine how the DAS-19.61 affects which VTDs belong to an MMD. We again simulate 50,000 maps using each dataset at a wide variety of constraint strengths that target the creation of MMDs. The results are shown in fig. S4.7, and they are substantively similar to the results based on the prior demonstration data presented in Fig. 7. Specifically, we find that some precincts are always contained in an MMD when maps are drawn using the original Census but never under DAS (or vice versa). As before, the magnitude of these differences is generally larger for higher values of the constraint than for lower values.

Ecological inference and voting rights analysis

Prediction of individual voters’ race and ethnicit

We examine whether the DAS-19.61 affects the prediction of individual voters’ race and ethnicity. Figure S4.8 presents the AUROC results for different racial groups using this final demonstration dataset. We compare the results against those in Fig. 8. We find that, by and large, our conclusions are unchanged. The DAS-19.61 data allow for the prediction of individual voters’ race and ethnicity with almost identical levels of accuracy to the 2010 Census data. The empirical performance of the BISG methodology based on the DAS-19.61 has a similar pattern: It typically performs about the same for White and Black voters, slightly better for Hispanic voters, and slightly worse for Asian and other voters. Although the unexpected finding of the DAS-12.2 analysis, superior predictive performance using the privacy-protected data, is no longer present here, there is also no significant degradation in prediction quality relative to the 2010 Census data.

Table S4.1 reports misclassification rates of the BISG methodology based on the DAS-19.61 data where we assign each individual to the single ethnic group with the highest posterior probability. We can compare these against the analogous results for the 2010 census, DAS-12.2, and DAS-4.5 data given in tables S1.1, S1.2, and S1.3. The conclusions are largely similar using these metrics too: Classification error for individual voters’ race and ethnicity is at the same level using the DAS-19.61 data, as it is using the 2010 Census data.

Ecological inference in the voting rights analysis

We repeat our analysis of the ERCSD to examine the effect of the final DAS-19.61 on local redistricting. Using the same geocoded voter file, we impute race onto the voter file using the BISG with the geographic priors from the DAS-19.61 data. Figure S4.9 displays the imputed races, aggregated to the block level, which is the basic geographic unit for building districts in this case. Consistent with the DAS-12.2 data, the DAS-19.61 data tend to result in overestimates of White voters and thus underestimates of Black and Hispanic voters.

We find that similar to the previous demonstration data, the block-level undercounts of minority voters do not disappear at the school board ward level in this case. Under DAS-19.61, we find underestimation of majority-minority wards in line with findings under DAS-12.2. As shown in table S4.2, among sampled districts, MMDs are always underestimated in this local case.

MATERIALS AND METHODS

Redistricting simulation methodology

The goal of redistricting simulation methods is to generate a collection of redistricting plans that are representative of the set of all plans that satisfy applicable redistricting criteria. These criteria may be set out explicitly in state law or may be derived from traditional principles or court cases. The simulation methods applied here were designed to sample plans from a specific probability distribution that reflects the most common redistricting requirements: that each district (i) be geographically contiguous, (ii) have a population that deviates by no more than a specified amount from a target population that corresponds to population equality across districts, (iii) be compact (we use a graph-theoretic measure of compactness that counts how many internal edges must be removed to form the districts), and (iv) avoid splitting counties so as to follow political subdivision boundaries where possible.

Some simulations here also reflect a fifth constraint, which is that the districts satisfy the requirements of the federal Voting Rights Act. This is accomplished by changing the sampling distribution to put more probability mass on plans that have a certain fraction of minority voters in a district. Formally, the target probability distribution can be written as

$$\mathrm{\pi }(\mathrm{\xi })\propto \text{exp} \{-J(\mathrm{\xi })\}\mathrm{\tau }{(\mathrm{\xi })}^{\mathrm{\rho }}{1}_{\{\mathrm{\xi } \text{connected}\}}{1}_{\{\text{dev}(\mathrm{\xi })\le D\}}$$ (1)

where ξ is a redistricting map, τ(ξ) measures the degree of compactness (operationalized as the number of spanning forests on a partitioned graph), ρ is a parameter chosen to control the level of compactness, dev(ξ) measures the percent deviation from population parity as defined in the article, and J(ξ) is an additional constraint such as those related to the Voting Rights Act. This probability distribution is desirable because it represents the unique maximum entropy distribution on the set of redistricting maps that satisfy contiguity and population party requirements as well as moment conditions implied by compactness and additional constraints. The distribution is also able to accommodate a variety of constraints that are used in real-world redistricting processes.

We use two algorithms to sample from this target distribution: an SMC algorithm (23) and a merge-split–type MCMC algorithm that uses the same transition kernel (19, 20). Both of these sampling algorithms are implemented in the open-source software package “redist” (24). The SMC algorithm operates by drawing districts one at a time on a blank map. Each district is formed by drawing a random spanning tree and removing a certain edge from it, creating a “split” in the map that forms a new district. As redistricting plans are formed from these districts, they are periodically weighted and reshuffled so that the sampled plans approximate the target distribution. The MCMC algorithm also forms districts by drawing a random spanning tree and splitting it, but rather than drawing redistricting plans from scratch, it starts with an existing plan and modifies it, merging a random pair of districts and then splitting them a new way. Diagnostic measures exist for both these algorithms that allow users to identify issues in accurate sampling from the target probability distribution. The original papers for these algorithms provide more detail on the algorithm specifics, empirical validation of their performance, and the appropriateness of the chosen target distribution.

Prediction of individual race and ethnicity using names and residence location

Our approach follows that of (27). We denote by E_i the race and ethnicity of voter i, N_i as the name of voter i, and G_i as the geography in which voter i resides. For each choice of race and ethnicity e ∈ ℰ = {White, Black, Hispanic, Asian, Other}, Bayes’ rule implies

$$\text{Pr} (E_i=e\mid N_i=n,G_i=g)=\frac{\mathit{\text{Pr}} (N_i=n\mid E_i=e)\mathit{\text{Pr}} (E_i=e\mid G_i=g)}{{\sum }_{e\prime \in ℰ}\mathit{\text{Pr}} (N_i=n\mid E_i=e\prime )\mathit{\text{Pr}} (E_i=e\prime \mid G_i=g)}$$

where we have assumed conditional independence between the surname of a voter and their geolocation within each racial category, i.e., N_i ⫫ G_i∣E_i.

In the presence of multiple names, e.g., first name f, middle name m, and surname s, we make the further conditional independence assumption (56)

$$\begin{array}{c}\text{Pr} (N_i=\{f,m,s\}\mid E_i=e)\\ =\text{Pr} (F_i=f\mid E_i=e)\text{Pr} (M_i=m\mid E_i=e)\text{Pr} (S_i=s\mid E_i=e)\end{array}$$

where F_i, M_i, and S_i represent individual i’s first, middle, and surnames, respectively.

Supplementary Materials

This PDF file includes:

Correspondence Table

Sections S1 to S4

Figs. S3.1 to S3.4 and S4.1 to S4.9

Tables S1.1 to S1.3, S2.1, and S4.1 to S4.3

View/request a protocol for this paper from Bio-protocol.