Abstract
Purpose:
To introduce, develop, and evaluate a novel denoising technique for diffusion MRI that leverages nonlinear redundancy in the data to boost the SNR while preserving signal information.
Methods:
We exploit nonlinear redundancy of the dMRI data by means of kernel principal component analysis (KPCA), a nonlinear generalization of PCA to reproducing kernel Hilbert spaces. By mapping the signal to a high-dimensional space, a higher level of redundant information is exploited, thereby enabling better denoising than linear PCA. We implement KPCA with a Gaussian kernel, with parameters automatically selected from knowledge of the noise statistics, and validate it on realistic Monte Carlo simulations as well as with in vivo human brain submillimeter and low-resolution dMRI data. We also demonstrate KPCA denoising on multi-coil dMRI data.
Results:
SNR improvements up to 2.7× were obtained in real in vivo datasets denoised with KPCA, in comparison to SNR gains of up to 1.8× using a linear PCA denoising technique called Marchenko-Pastur PCA (MPPCA). Compared to gold-standard dataset references created from averaged data, we showed that lower normalized root mean squared error was achieved with KPCA compared to MPPCA. Statistical analysis of residuals shows that anatomical information is preserved and only noise is removed. Improvements in the estimation of diffusion model parameters such as fractional anisotropy, mean diffusivity, and fiber orientation distribution functions were also demonstrated.
Conclusion:
Nonlinear redundancy of the dMRI signal can be exploited with KPCA, which allows superior noise reduction/SNR improvements than the MPPCA method, without loss of signal information.
Keywords: denoising, diffusion MRI, kernel, low-rank, noise, PCA, SNR
1 ∣. INTRODUCTION
Diffusion MRI (dMRI) is a noninvasive imaging modality that allows the characterization of tissue microstructure of biological tissues with an unrivaled level of quality and detail. When diffusion-encoding gradients are played out, the MR signal becomes sensitive to the diffusion of water molecules and their interaction with the surrounding microstructure.1 Hence, the dMR signal, carrying unique information, can be used to probe the microstructural environment of tissues. The characteristic attenuation of the dMRI signal during the diffusion probing time, however, makes the signal-to-noise ratio (SNR) of the diffusion-weighted (DW) MR images inherently low.2 This is of particular concern for high-resolution dMRI, as the SNR decreases even further due to a decrease in the voxel size. Low SNR not only complicates visual inspection but hampers quantitative analysis of informative tissue parameters, for example, by reducing the accuracy and precision of the parameter estimates.3
Increasing the SNR in dMRI is a major goal for the MRI community. Ultrahigh field dMRI,4-6 advanced dMRI acquisition protocols,7-14 or noise reduction techniques,3,15-17 to name a few, are complementary approaches that have been shown to enhance the SNR. In this work, we focus on noise removal techniques, in particular, the thermal noise at the reception of the radiofrequency signal,15 which further propagates to the dMRI signal domain during image reconstruction.18
Noise reduction or denoising can be done by averaging16: the subject is imaged several times with identical image parameters, and the resulting images averaged. Under some statistical assumptions, this simple technique can increase the SNR by a factor of with Nscans the number of repetitions. Evidently, this approach requires additional scan time and, as the acquisition time of a conventional dMRI protocol is already relatively long, averaging becomes impractical for routine use.
From a signal processing perspective, denoising can be seen as a post-processing approach, where an algorithm attempts to remove the noise, that is, reduce the noise standard deviation, while maintaining the noise-tree signal undistorted. Trivially formulated, denoising has been a longstanding problem in image processing, where many challenges need to be confronted, which are further aggravated in quantitative image modalities such as diffusion MRI. Indeed, early computer vision-based denoising algorithms applied to dMRI have shown to be detrimental to parameter estimation quality.3 Some exemplar cases are the popular total variation–based noise removal techniques19,20 or more recently, nonlocal means algorithms.21,22 Other shortcomings are the loss of spatial resolution due to blurring in the presence of partial volume effects.
On the other hand, denoising algorithms that depart from exploiting spatial similarity but leverage “redundancy” of the dMRI signal along diffusion direction have been shown to suppress noise significantly while preserving the dMRI signal, with no apparent blurring or biases. Principal component analysis (PCA)–based methods belong to this category of methods. PCA-based methods were first used in,23 and ever since, have been thoroughly validated for diffusion MRI parameter quantification and substantially refined and improved. Most of the improvements that PCA algorithms have witnessed are based on the estimation of the number of signal-only principal components. By removing the rest of the components, attributed to noise, denoising is performed. While this threshold was heuristically set in,23 the criterion was formalized in,3 where an elegant approach was proposed relying on the theory of random covariance matrix theory, in particular, exploiting the universal Marchenko-Pastur law for eigenvalues. The MPPCA method of3 has also been extended to general noise models other than the additive white Gaussian noise case.24
All dMRI PCA denoising methods are limited by the degree of redundancy in the signal with respect to the dimensionality of the data, that is, the number of gradient directions. Several factors, including spatial resolution, number of b-values, number of gradient directions, determine the amount of redundancy in the data. The capability for noise reduction is hampered if the SNR is very low as in high-resolution diffusion MRI. We would like to emphasize here that this limitation is not attributable to the PCA method at hand but in the assumption that the covariance matrix of the signal is of sufficiently low rank.
Fortunately, there exist nonlinear redundancies which are not captured by the linearity assumption implicitly adopted in PCA, but that can be exploited to enhance the SNR of dMRI substantially more than possible with current state-of-the-art approaches. The fundamental idea is to look for high-dimensional nonlinear spaces where the covariance matrix of the transformed dMRI signal turns out to be of low rank. Enforcing this prior knowledge, that is, applying PCA in the transformed domain, we can denoise the signal in the high-dimensional space and map it back to the original space. As a unified approach, this operation exploits the nonlinear relationships within the data, and is referred to as a nonlinear generalization of PCA. The whole process can be carried out by a technique called kernel principal component analysis (KPCA),25 where a kernel function implicitly determines the mapping of the dMRI signal to a high-dimensional Hilbert space.26
In this work, we introduce KPCA denoising to the dMRI community and showcase it with a Gaussian kernel that maps the dMRI signal to an infinite dimensional space where redundancy is exploited. The parameters of the kernel as well as the rank of the covariance matrix are chosen in a data-driven manner, as those that provide the best signal representation according to the mean square error (MSE) between the denoised and the underlying noise-free signal. The Stein unbiased risk estimate (SURE) is used as a proxy of the MSE,27-29 circumventing the need for the unobservable noise-free signal. Only knowledge of the noise statistics is required, which we input to the algorithm with state-of-the-art noise mapping techniques.
We thoroughly validate KPCA with realistic Monte Carlo simulations as well as with several in vivo human brain datasets acquired with submillimeter spatial resolution. In addition, KPCA was validated on a conventional (low-resolution) multi-shell dMRI dataset. Finally, KPCA denoising was demonstrated in an in vivo human brain multi-coil dMRI dataset, capturing nonlinear redundancies in the coil and gradient directional domains simultaneously. In all cases, we confirmed superior noise reduction compared to the linear MPPCA method, which immediately translates to higher SNR enhancement, while preserving signal reliably, as confirmed by residual analysis. Finally, improved diffusion parameter estimation was invariably found when dMRI datasets were denoised with KPCA. A preliminary version of this work has been presented as an abstract at the ISMRM 2020.30
2 ∣. THEORY
2.1 ∣. Redundancy of dMRI signals in canonical spaces: PCA denoising
In dMRI, it is often assumed that the diffusion signal carries redundant information between the gradient directions (also referred to as q-space). Redundancy can be elegantly captured by covariance matrix analysis. Let be the diffusion MR signal with M the number of gradient diffusion directions. Its second-order statistical characterization is given by its mean and covariance matrix . The diffusion signal x is said to be “redundant” if Cx is rank-deficient, with rank K substantially smaller than the dimensionality M. In that case, Cx, a low-rank matrix, can be written with eigenvalue decomposition . The low-rank diffusion signal x with these statistical properties is given by the so-called “spike” model31:
| (1) |
where vk are independent and identically distributed (IID) random variables with zero mean and unit variance. The diffusion signal is always corrupted by noise, , which is typically modeled as additive and with zero mean, that is, y = x + w. Denoising the signal y can be formulated as an estimation problem, where the goal is to estimate the noise-free signal x from the observed data y. As Cw is a full-rank matrix (noise is not redundant), it is precisely the low-rank nature of Cx in comparison to Cw (K < < M) that allows to “separate” signal from noise, that is, estimating x reliably. Low-rank denoising is usually performed in image patches, each one containing N diffusion signals xn, n = 1, …, N, with mean μ and covariance matrix Cx. For the noisy spike model,
| (2) |
the optimal estimate of xn in terms of the norm (assuming rank K known) is given by32
| (3) |
where , and are obtained from the singular value decomposition (SVD) of the noisy data matrix , that is,
| (4) |
by nullifying components with index k > K, and being the sample mean of yn. This denoising framework is also called PCA denoising, with as the principal components. As already mentioned in the introduction, all of the PCA-based dMRI denoising methods3,22,24,33 fundamentally differs in the the way K is estimated. No improvements are made in the intrinsic data model. In this work, we instead reconsider the low-rank model of Equation (3). In particular, we are interested in the intrinsic redundancy in the noise-free image x. If K is comparable to M, the optimal solution of Equation (3) can hardly denoise, no matter which PCA algorithm we employ. MRI artifacts, partial volume effects, higher spatial resolution, nonconventional dMRI sequences, to name a few, all of these factors may increase the original rank K of the signal. A possible way to increase the redundancy is to focus on M, rather than K, and increase the dimensionality of the signal by adding more gradient directions. Theoretically appealing, this modus operandi will necessarily necessitate additional scan time, which is often of concern in clinical settings.
In the quest for data redundancy, we look for information redundancy in data domains which are not necessarily the canonical space where conventional PCA is applied. The next section is devoted to motivate and formalize our approach, after which we present the novel denoising method in Section 3.1.1.
2.2 ∣. Redundancy of dMRI signals in high-dimensional Hilbert spaces
Our starting point is a function ϕ( · ) that maps the diffusion signal x from the native space to a “feature” space , often high-dimensional, P > > M, with . We will deal with the definition of ϕ( · ) later, but for now let us assume that the transformed data ϕ(x) is redundant, that is, the covariance matrix of ϕ(x) is of rank , even if native rank K is high. For example, any mapping which makes data “sparser” in the feature domain will “compress” the information more than in the native space. This redundancy translates into a low-rank covariance matrix Cϕ(x). We can exploit this redundancy to denoise data in the feature space and eventually return to the native space to get the denoised signals . Note that the entire process can be seen as a way to exploit nonlinear redundancy that the dMRI signal can carry, and that could be otherwise difficult to capture with conventional PCA.
In , similar to PCA, the optimal estimates of ϕ(xn) of rank are those minimizing the error . They can be shown to be the projection of the mapped noisy signals ϕ(yn), n = 1, …, N, onto the feature space, Pϕ(yn),
| (5) |
In Equation 5, is the mean of ϕ(yn), n = 1, …, N, are the nonlinear principal component directions, and the rest of parameters are obtained (we maintain the notation of Equation 3) from the SVD of centered noisy projected data matrix
| (6) |
While the low-rank denoising is performed in , we would like to come back to the native space. If we want to denoise the signal y* at the center of the patch, we then look for that x which, after being mapped to the feature space, ϕ(x), turns out to be the closest to the projection Pϕ(y*) (Equation 5), that is,
| (7) |
A fundamental result that is of high relevance for this work is the following. To apply PCA in the feature space defined by the mapping ϕ( · ), and to solve Equation 7 in order to return to the native space, we do not need to know ϕ( · ) explicitly, but just the inner product of the form ⟨ϕ(x), ϕ(y)⟩ for x and y in . Since ⟨ϕ( · ), ϕ( · )⟩ is a symmetric, positive definite function, it automatically defines a kernel function in as k(x, y) = ⟨ϕ(x), ϕ(y)⟩. Conversely, choosing a kernel function k( ·, · ) implicitly defines a mapping ϕ( · ).26 Therefore, it is the kernel function that implicitly defines the feature space. Features spaces with this property are called reproducing kernel Hilbert spaces, and applying PCA in the feature space is termed KPCA.26 In the next section, we present our Kernel PCA denoising method in detail, elaborating on the selection of the kernel as well as the rank .
3 ∣. METHODS
3.1 ∣. KPCA denoising
3.1.1 ∣. KPCA algorithm
Given a kernel k( ·, · ), the denoised signal in the feature space defined by k( ·, · ) can be written as34
| (8) |
with , 1 an N-dimensional column vector with all entries equal to one, and αk, the first eigenvectors that solve the following eigenvalue problem:
| (9) |
where is a “center” matrix and K, the so-called kernel matrix (N × N), Kmn = k(yn, ym). Finally, the coefficients βk, the components of projection of ϕ(y*) onto the k-th nonlinear principal component , can be computed as
| (10) |
with αkn the nth coefficient of αk, and equal to35
| (11) |
The interested reader can find the mathematical proof of the derivation of KPCA in34 and in Section 1.1 of the Supporting Information of this submission.
3.1.2 ∣. The choice of the kernel function
We showcase KPCA denoising for dMRI with a Gaussian kernel function,
| (12) |
with h the scale parameter. Gaussian kernels have shown excellent performance in machine learning tasks and are particularly interesting for dMRI denoising for the following reasons. The implicit feature space that the Gaussian kernel function generates can be shown to be infinite-dimensional.26 As data tend to be sparser in high-dimensional spaces, higher redundancy is achieved by mapping the data with ϕh( · ). As implied by the notation, we can control the shape of the mapping with the scale parameter h, and, in fact, the components of ϕh(yn) decay with increasing h. In that sense, by varying h, we can adapt the level of redundancy of the dMRI signal in the feature space. This aspect will be of high interest for the automatic selection of parameters. Finally, it is possible to demonstrate that, when h → ∞, KPCA with a Gaussian kernel behaves as linear PCA in the canonical space.36 Hence, linear PCA is a particular case of KPCA with Gaussian kernel functions. It is therefore expected that our KPCA denoising will perform typically better, as we confirm in this paper. More details about the implicit mapping related to the Gaussian kernel and the demonstration of the asymptotic equivalence of KPCA and PCA are given in the Supporting Information, (Section 1.2 and 1.3, respectively).
In addition, there are computational advantages in choosing the Gaussian kernel. The solution of Equation 8 can be obtained in very short computational time with the approximation given in37
| (13) |
being calculated analytically. Details are given in Section 1.4 of Supporting Information. Finally, in the discussion session, we elaborate on possible improvements of KPCA denoising by selecting more complex kernels.
3.1.3 ∣. Automatic parameter selection driven by noise statistics
Two parameters need to be selected for our KPCA method: the scale parameter h and the rank . Ideally, we would like to select those that best represent the noise-free signal x*, for example, by quantifying the mean squared error, (risk) for different choices of h and . Obviously, the ground-fruth signal x* is unobservable, and hence the MSE is not computable. Instead, we use the SURE.27 Minimizing SURE can act as a surrogate for minimizing the MSE, with the critical difference that it does not require knowledge of x*.28 For an AWGN model like that of Equation 2, SURE can be computed from the noisy signals yn, the denoised signal , and the standard deviation of the noise, σ. We estimate the noise maps of the DWI images using the method presented in,38 with the assumption of Gaussian distributed data, which holds in our experiments as we show in the subsequent section. Then, for every voxel in the image patches, we fix σ and applied grid search minimization to get the optimal h and with respect to the SURE cost-function. We used the efficient implementation of the SURE method based on Monte Carlo sampling.29 We refer the reader to Section 1.5 of the Supporting Information for more details about the SURE method for optimal parameter selection. In addition, a discussion is provided at the end of the paper about the extension of SURE to other noise models as well as different techniques to estimate h and that may be of interest.
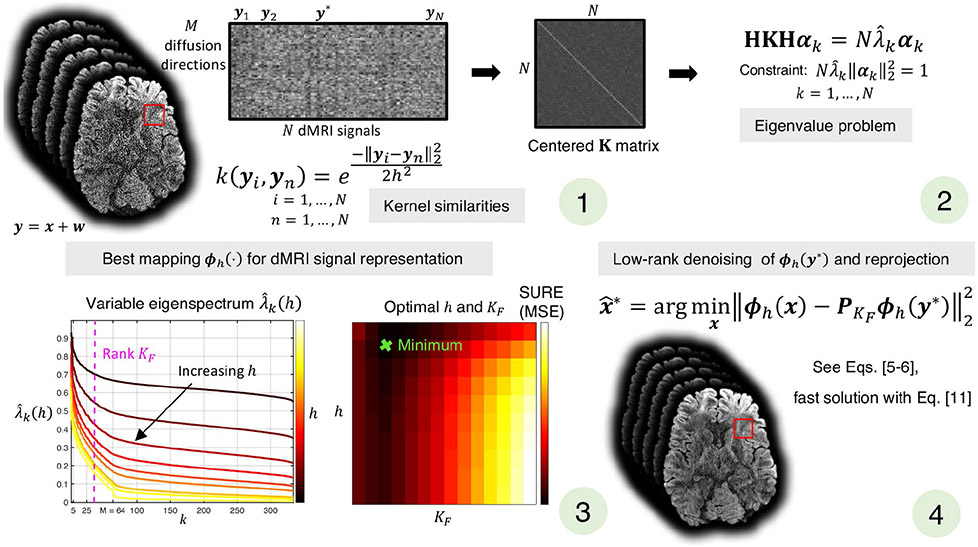
An illustrative scheme of the KPCA denoising method used in this work is presented in Figure 1. Code will be publicly available at https://github.com/gabrll and https://github.com/pnlbwh.
FIGURE 1.
Sliding-window version of KPCA denoising. For a given patch of N dMRI noisy signals, (1) the similarity between each pair, yi, yn, are calculated as k(yi, yn), and represented by the centered K matrix, HKH. Solving the eigenvalue problem (2), we obtain the eigenvectors αk and eigenvalues associated to the mapping ϕh( · ), which defines the feature space where linear PCA is performed. The best feature space, that is, optimal h, and optimal rank are selected as those that, after reprojection of the low-rank denoised signal to the native space, give the best signal representation in terms of the Stein Unbiased Risk Estimate (SURE) (3). Finally, the denoising signal at the center of the patch (4) is obtained by applying low-rank denoising (with optimal ) in the optimal feature space and reprojecting
3.2 ∣. Experimental validation
We validated KPCA denoising using simulated and in vivo human brain dMRI data, both quantitatively and qualitatively, and compared our results with MPPCA denoising.3 Both algorithms were implemented in a sliding-window fashion, where for each patch, only the signal at the center was denoised. The selection of the parameters for KPCA was done as follows. The standard deviation of the noise was estimated with the method of.38 The set of possible values of to minimize the SURE was chosen to be in the range [1, 30], and the scale parameter of the Gaussian kernel h, was parameterized by h = c σmin-class where σmin-class is the average minimum distance between all pairs of signals in the patch,37 and the values for c was chosen from ten equidistant points in the interval [0.6, 6] (see Section 1.4 of the Supporting Information).
3.2.1 ∣. Simulations
A Monte Carlo–based experiment was conducted to assess the benefits of KPCA denoising in subsequent diffusion parameter estimation. Similar to the patch-based simulation experiment in,3 we generated 5 × 5 × 5 signals based on a diffusion tensor (axially symmetric) model and a total of M gradient directions uniformly spread on the sphere with a given b-value, b. The underlying fractional anisotropy (FA) and mean diffusivity (MD) for each tensor in the pach was sampled from a distribution with fixed mean FAGT and MDGT, and a standard deviation of 10% with respect to the mean. MC = 5000 zero-mean uncorrelated Gaussian noise realizations were added to each of the noise-free N = 125 signals. The standard deviation of the noise was parameterized by a nominal SNR value, that is, σ = 1/SNR.
The MC = 5000 noisy patches were then denoised with MPPCA and KPCA, and the denoised signals were compared to the ground-truth signal. Experiments were conduced for different (a) number of diffusion directions, M ∈ [32, 64, 128], (b) b-values, b ∈ [1200, 1500, 2500]s/mm2, (c) SNR values, SNR ∈ [5, 8, 15], and (d) representative FA in both gray and white matter, FAGT ∈ [0.2, 0.6]. MDGT = 8 · 10−4 mm2/s was considered in both cases.
The normalized root mean square error (NRMSE) was used to compare the denoised signals with respect to the ground-truth signal. Diffusion tensor parameters were estimated from the log-linearized signals with a Linear Least Squares (LLS) estimator. Next, the FA and MD were estimated and compared to the ground-truth FA and MD, FAGT and MDGT. To assess how denoising affects accuracy and precision, the bias and standard deviation of the estimates of the dMRI signals, FA and MD were calculated.
3.2.2 ∣. In vivo human brain submillimeter resolution dMRI data
Whole human brain in vivo submillimeter dMRI data were acquired and reconstructed with the generalized slice dithered enhanced resolution (gSlider) technique,8 and denoised with KPCA and MPPCA. Two datasets with different spatial resolutions were considered. Both datasets were acquired in accordance with the IRB approval from Massachusetts General Hospital for obtaining in vivo human MRI scans.
660 μm isotropic gSlider data
A total of 46 thick sagittal slices were acquired (Siemens 3T Connectom scanner) with in-plane resolution 660 μm and matrix size 332 × 180, covering the full brain (FOV = 220 × 118 × 151.8 mm3). The diffusion protocol consisted of M = 64 DW images (diffusion directions uniformly distributed along sphere) with b = 1500 s/mm2 and 7 b0-images. Data was acquired10 with a single-shot EPI sequence: 32 coil channels, Muti-Band = 2, partial Fourier = 6/8, phase-encoding (superior-inferior axis) under-sampling factor Rin-plane = 2, TR/TE = 4400/80 ms, 5 radiofrequency encoding pulses. The total acquisition time was about 25 minutes. Three repetitions were acquired to construct a gold-standard reference. Conventional gSlider8 was used to reconstruct the data and obtain whole brain isotropic 660 μm resolution. Prior to gSlider reconstruction, slice and in-plane GRAPPA was used for k-space and SMS reconstruction, and real-valued data was obtained with background phase correction.16 Eddy-current and motion were corrected between all acquisitions using the FSL technique FLIRT. The 3 datasets were then denoised with KPCA and MPPCA, and compared to the averaged dataset, which is considered here as the gold-standard reference. Both algorithms were implemented in a voxel-wise fashion, with a sliding window of [5 × 5 × 5] voxels.
860 μm isotropic gSlider data
Whole human brain gSlider-SMS data were collected from a healthy male volunteer on a Siemens 3T Prisma scanner. Four scans of the full brain (FOV = 220 × 220 × 163 mm3) were obtained. A total of 38 thick axial slices were acquired with in-plane resolution of 860 μm and matrix size 256 × 256. The diffusion protocol consisted of 64 DW images (diffusion directions uniformly distributed along sphere) at b = 2000 s/mm2 and 8 b0-images. Data were acquired11 with a single-shot EPI sequence: 32 coil channels, Muti-Band = 2, partial Fourier = 6/8, phase-encoding (posterior-anterior axis) under-sampling factor Rin-plane = 3, TR/TE = 3500/81 ms, 5 radiofrequency encoding pulses. The total acquisition time was about 20 min. Four repetitions were acquired to construct a gold-standard reference. Data was preprocessed and reconstructed as described for the 660 μm case. After affine registration, one of the datasets was denoised with KPCA and MPPCA (identical window size as before), and compared to the averaged dataset, the gold-standard reference.
2.2.1 ∣. Quantitative validation
We assessed the performance of KPCA denoising in signal preservation and parameter estimation, quantitatively. The NRMSE was used to compare the signal of the denoised DW images with the signal of the averaged dataset. As in the simulation experiment, accuracy and precision results were reported. To assess the ability of KPCA denoising for SNR enhancement, we estimated the noise maps (noise standard deviation) of the denoised datasets with the homomorphic approach.38 The SNR gain was defined as the ratio between the standard deviation of the noise in the original dataset and that of the denoised datasets. To demonstrate that KPCA preserves the underlying diffusion signal reliably, we calculated the normalized residuals between the noisy datasets and the denoised versions, and checked if any anatomical structure was present.3
We conducted DTI analysis and high angular resolution diffusion imaging (HARDI) validation. FA and MD maps were estimated with dtifit from FSL, and compared to the maps from the reference set. The NRMSE, bias, and standard deviation were used to assess the improved quality in parameter estimation. HARDI analysis was carried out with MRtrix3.39 Fiber orientation distribution functions (fODFs) were calculated in white matter area only, with the single-shell single-tissue constrained spherical deconvolution (CSD) technique.40 For each voxel, main fiber peaks were extracted, and the angular error compared to those from the reference set were calculated. The variability in the estimation of the ODF peaks was probed with the coherence metric, κ, (κ ∈ [0, 1]), which was originally proposed in41 and used in.3 A high value of κ indicates low angular variability, that is, high angular precision.
3.2.3 ∣. In vivo human brain low-resolution dMRI multi-shell data
KPCA denoising was validated on a more conventional multi-shell dMRI dataset, with an isotropic spatial resolution of 1.5 mm. From a healthy male volunteer, whole brain data was acquired on a SIEMENS 3T Prisma scanner with a 2D single-shot EPI sequence and the following acquisitions parameters: 32 coil channels, Multi-band = 2, matrix size = 160 × 160 × 93, partial Fourier = 6/8, phase-encoding (posterior-anterior axis) under-sampling factor Rin-plane = 2, and TR/TE = 2515/96 ms. K-space data were reconstructed with GRAPPA and coil-combined with the adaptive combine algorithm. The diffusion protocol consisted of 30 diffusion directions (equally spread along the sphere) for b-values of 1500 and 3000 s/mm2, and 7 b0-images. Magnitude data was corrected for EPI distortions with FSL’s tool eddy.42 Five repetitions were acquired. The average of the acquired 5 scans was considered as the ground-truth dataset. KPCA and MPPCA denoising use information for the 2 shells simultaneously (eg, M = 30 × 2 = 60), with a window size of [5 × 5 × 5]. All data were acquired in accordance with the IRB approval from Brigham and Women’s Hospital for obtaining in vivo human MRI scans. Accuracy, precision, and NRMSE were reported for denoised dMRI signal, FA and MD results, as well as mean kurtosis (MK). Residual analysis was also carried out, and result for SNR-enhancement were also given.
3.2.4 ∣. Capturing nonlinear coil and diffusion redundancy simultaneously
We investigated whether KPCA denoising can work at the reconstruction level, for example, by denoising multi-coil and diffusion data simultaneously. To that end, we used an in vivo human brain DW image dataset comprising of 1 b0-image and 15 diffusion gradient directions that were uniformly spread over the sphere (b = 1200 s/mm2). The acquisition protocol was as follows: With a 3T Philips scanner, an axial slice was acquired with a single-shot EPI sequence, matrix size = 70 × 91, in-plane resolution of 2 mm, multi-coil system with eight channels and no undersampling factor. All data were acquired in accordance with the IRB approval from the University of Valladolid, Spain, for obtaining in vivo human MRI scans. To create a gold-standard reference, 20 repetitions of the same axial slice were obtained. Prior to denoising, k-space data were transformed into image space with an inverse Fourier transform. Similar to approaches in,24,33 complex-valued images were transformed into real-valued images with the background phase estimation technique.16 Phase estimation was obtained by taking the complex argument of the image resulting from the inverse Fourier transform of low-pass filtered k-space data (center of the k-space with Hamming window). Complex conjugate phase correction was applied, and the real part was retained. Note that this technique preserves Gaussian statistics if the background phase is accurately estimated.5 No statistical correlation was assumed between the noise properties of the different coils. To apply denoising, the coil and the diffusion dimension were merged into a single dimension, M = 8 channels × 15 diffusion directions = 120. The size of the patch was [7 × 7]. As in the previous experiment, the NRMSE, the noise maps, and the normalized residuals were calculated both from the denoised dataset with MPPCA and KPCA. NRMSE maps for diffusion derived metrics, FA and MD were also computed.
4 ∣. RESULTS
4.1 ∣. Simulations
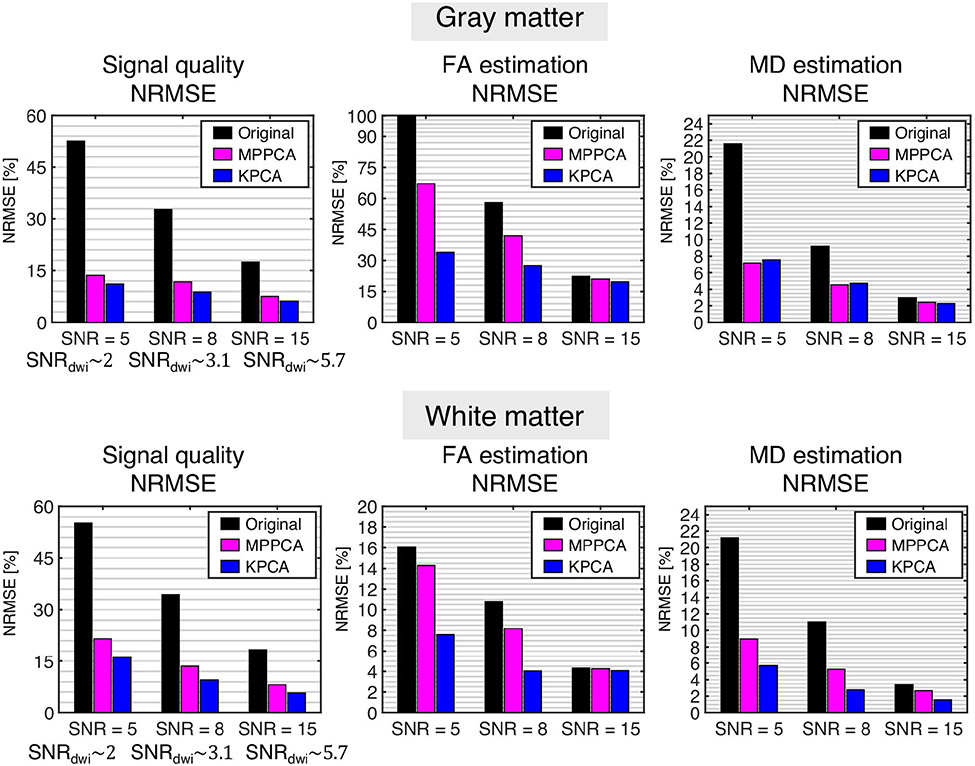
NMRSE results for the case b = 1200 s/mm2 and M = 64 directions are shown as bar plots in Figure 2, whereas the rest of results, including bias and standard deviation of the estimates, are shown in Table format in the Supporting Information (Tables S1-S9). In general, KPCA achieves the lowest NRMSE results in signal quality, FA and MD, and shows a significant improvement in estimation of FA for low SNR values, for example, SNR = 5 and SNR = 8, which correspond to real SNR values (defined as the the noise-free dMRI signal divided by sigma) of 2 and 3, typically encountered in real data noisy scenarios as those like submillimeter resolution data shown in this paper. The lower NRMSE of KPCA in comparison to MPPCA comes from a simultaneous reduction of bias and precision. In practically all cases, results are statistically significant as confirmed with a Welch’s t-test (see caption on Tables S1-S9).
FIGURE 2.
Quantitative results from the MC-based simulation experiment. For representative cases of both white and gray matter, b = 1200 s/mm2 and M = 64, the NRMSE (%) of the dMRI signal, FA and MD estimates are shown for different SNR values (the corresponding mean SNR over all diffusion directions, SNRdwi, is given as a reference). Differences are statistically significant as confirmed by a Welch’s t-test (P < .01)60
Interestingly, the improved performance of KPCA over MPPCA denoising is quite evident for reduced number of diffusion directions M = 32 or M = 64. This is attributed to the lack of enough “linear” redundancy of the dMRI signal K compared to low values of dimensionality M. KPCA, however, as it performs low-rank denoising in a high-dimensional space (P > > M), can achieve superior noise reduction, and hence, improved parameter estimation.
4.2 ∣. In vivo human brain submillimeter resolution dMRI data
Denoised images with MPPCA and KPCA from the 660 and 860 μm resolution datasets are shown in Figures 3 and 4, respectively. The original dataset (no denoising) as well as the gold-standard reference, 3 averages for the 660 μm case and 4 averages for 860 μm case, are also shown.
FIGURE 3.
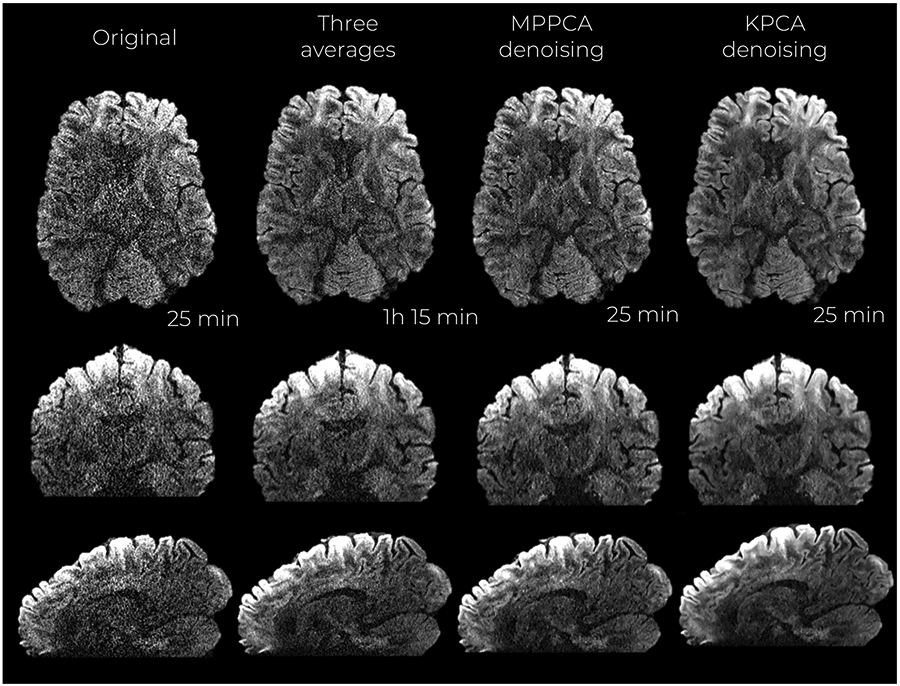
Mid-axial, coronal and sagittal slices of denoised DW images at 660 μm isotropic resolution and b-value of b = 1500 s/mm2. Acquisition times are reported as well
FIGURE 4.
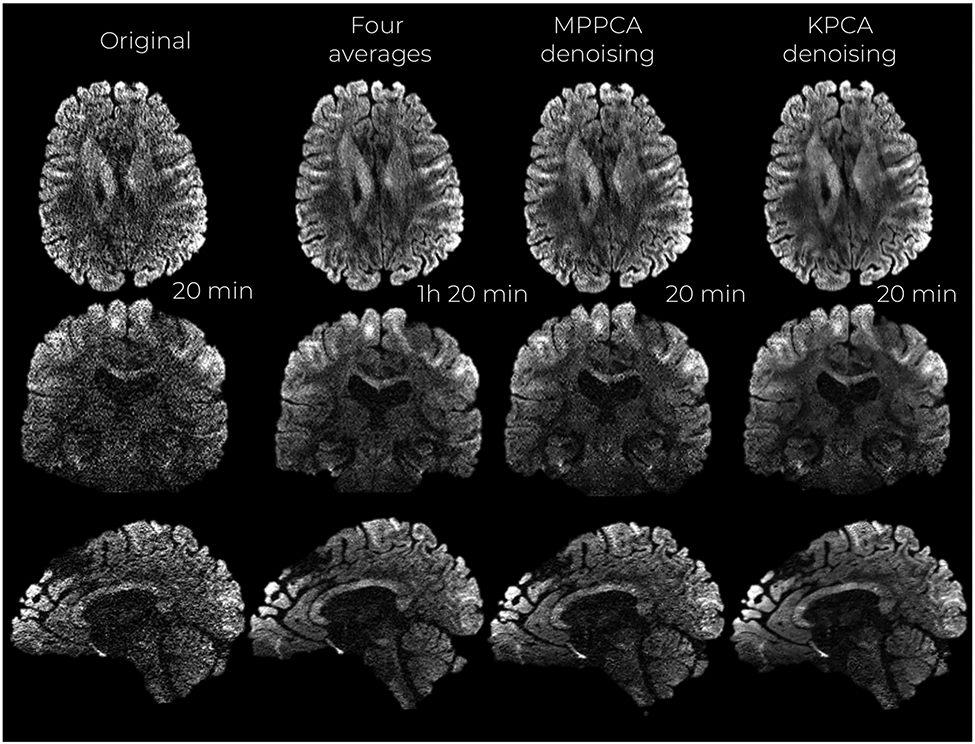
Mid-axial, coronal and sagittal slices of denoised DW images at 860 μm isotropic resolution and b-value of b = 2000 s/mm2. Acquisition times are reported as well
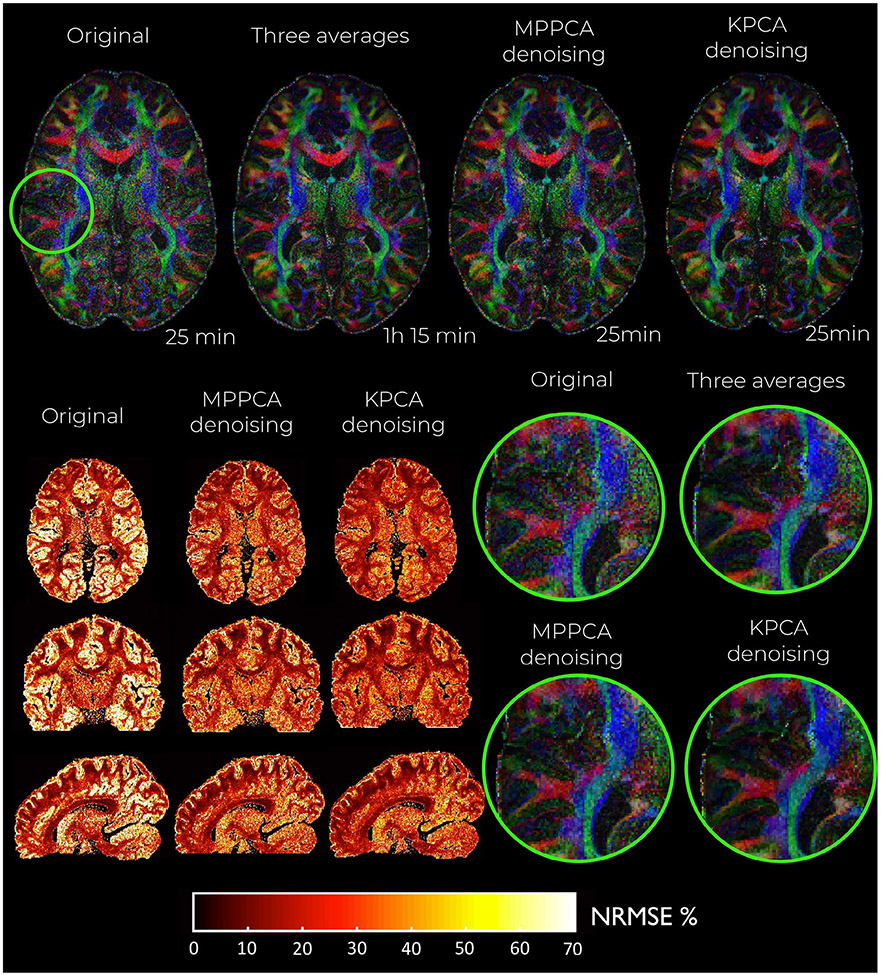
Visually, KPCA denoising achieves a higher noise suppression than MPPCA without signal loss. No anatomical structure can be seen in the ‘residual’ images (original—denoised DW image) shown in Figure 5 and Figure S2 of the Supporting Information (860 μm dataset).
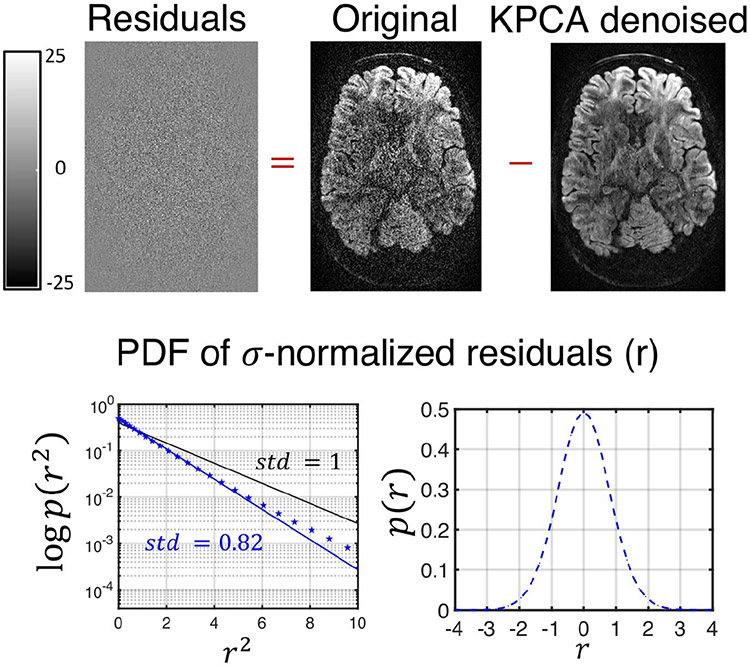
FIGURE 5.
Residual maps from the 660 μm resolution datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Note that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid-line the optimal analytical zero-mean Gaussian distribution that best fits the data (maximum likelihood sense). Note that the standard deviation of the normalized residual, 0.82, is lower than 1 (black-line represents a zero-mean standard Gaussian distribution)
Statistical analysis of residuals confirms signal preservation in KPCA denoising. Any anatomical structure in the residual dataset will make the standard deviation higher than the noise standard deviation σ.3 By analyzing the σ-normalized residuals r,3 we found that in both cases, 660 and 860 μm resolution data, r approximately follows a zero-mean Gaussian distribution with standard deviation 0.82 and 0.79, respectively, see blue dotted-blue line graphs representing the estimated pdf, p(r), of normalized residuals (logarithmic plot on the left, linear plot on the right). As the standard deviation is lower than the unit (see solid black-line representing zero-mean standard Gaussian distribution), we then can conclude that no anatomical structure is lost in KPCA denoising. The pdf p(r) was estimated with a kernel density estimator. The solid blue-line represents the analytical Gaussian pdf that best fits the data in a Maximum Likelihood sense.
The estimated noise maps after denoising are presented in Figure 6 and Figure S3 of the Supporting Information. Note that the noise mapping method38 we use to estimate σ assumes either a Gaussian or Rician distribution. Since, by assumption, the original data is Gaussian distributed (real-value phase corrected images16) and the residuals are shown to be Gaussian, our assumptions are well founded.
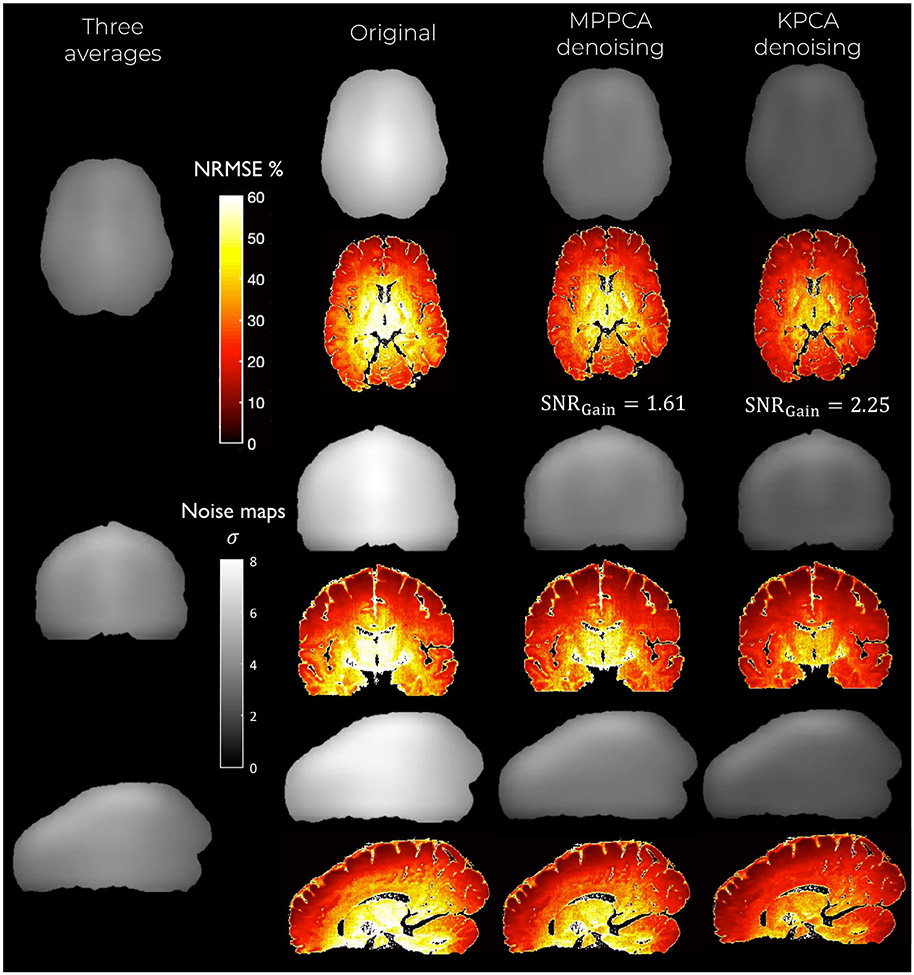
FIGURE 6.
Maps of the NRMSE (hot colormap) and noise level (gray colormap) for the denoised DW images at 660 μm isotropic resolution and b-value of b = 1500 s/mm2. Observe that KPCA denoising obtains the lowest level of noise (highest SNR gains) and lowest NRMSE
KPCA achieves higher noise suppression while still reliably preserving signal, supported by the previous experiment with residuals. The lowest levels of noise are found when the original data is denoised with KPCA, indicating that KPCA enhances the SNR to a greater extent than what is achievable with MPPCA denoising. The SNR gain is more than 60% higher compared to MPPCA, see Table 1. Superior noise removal performance as well as reliable signal preservation make the NMRSE (compared to the averaged data case) substantially lower than MPPCA, both in white and gray matter (Table 1).
TABLE 1.
Quantitative results from experiment with in vivo human brain submillimeter resolution dMRI data. Note that in all cases, that is, brain, white matter (WM), and gray matter (GM), KPCA denoising achieves better results than MPPCA
| Signal (NRMSE (%)) | SNR gain (X) | FA (NRMSE (%)) | MD (NRMSE (%)) | Angular error (°) | Angular precision | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Brain | WM | GM | Brain | Brain | WM | GM | Brain | WM | GM | WM | WM | |
| Original-660μm | 32 | 34 | 29 | 1 | 43 | 29 | 61 | 14 | 8 | 16 | 15.7 | 0.709 |
| MPPCA-660μm | 28 | 29 | 25 | 1.63 | 32 | 23 | 40 | 9 | 6 | 10 | 14.3 | 0.757 |
| KPCA-660μm | 22 | 23 | 20 | 2.25 | 27 | 21 | 30 | 8 | 5 | 9 | 13.1 | 0.787 |
| Original-860μm | 52 | 57 | 48 | 1 | 51 | 39 | 65 | 21 | 26 | 14 | 15.8 | 0.705 |
| MPPCA-860μm | 40 | 42 | 36 | 1.81 | 38 | 32 | 44 | 15 | 20 | 9 | 13.7 | 0.705 |
| KPCA-860μm | 32 | 34 | 33 | 2.71 | 32 | 29 | 35 | 14 | 19 | 8 | 12.6 | 0.731 |
In good agreement with the findings from the simulation experiment, denoising improves diffusion parameter estimation, and in particular, KPCA denoising helps estimate quantitative parameters with lower statistical error. NRMSE of both estimated FA and MD are considerably lower (Table 1) when DTI is applied after KPCA denoising compared to MPPCA. The improvement is significantly noticeable in gray matter. Cortical gray matter seems better delineated in the FA maps that are obtained after denoising data with KPCA (see color-encoded FA maps in Figure 7). This is highly relevant since mapping cortical gray matter is one of the main motivations of ultra-high resolution dMRI protocols.43. In fact, error maps also suggest that the estimation of FA is improved to a greater extent in cortical areas. Color-encoded FA maps as well as errors map for the 860 μm case are shown in Figure S4 of the Supporting Information. The improvement in NRMSE comes from a marked reduction in both accuracy and precision, see Table S10 and S11, respectively. For comparison, NRMSE values in FA, MD, and signal are similar to those reported in the reconstruction method presented in,10 where the same 660 μm gSlider dataset was used. It should be noted though that establishing a rigorous comparison is complicated since, in the work of,10 NRMSE results were given over the whole brain and not classified into different brain tissues (eg, WM and GM), as we do here. Furthermore, no metrics related with accuracy and precision were provided.
FIGURE 7.
Color-encoded FA maps of the denoised DW images at 660 μm isotropic resolution and b-value of b = 1500 s/mm2 as well as corresponding NRMSE maps. Note the better delineation of cortical gray matter in KPCA denoising
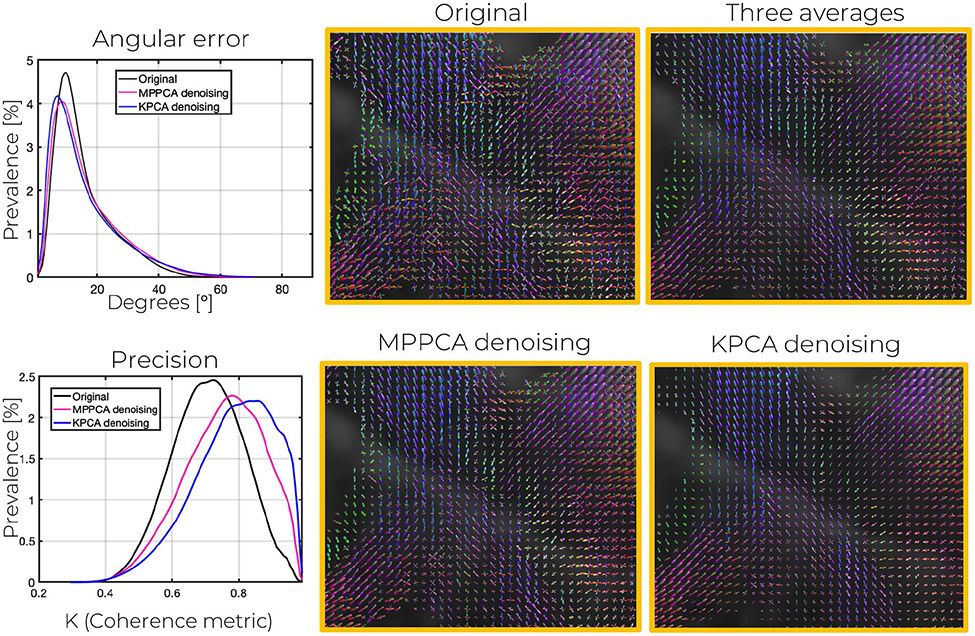
fODF estimation becomes more robust after denoising, and more accurate and precise angular directions can be achieved if data is first denoised with KPCA. As shown in Table 1, lower angular errors (mean of the errors for the first, second, and third peak) are achieved with KPCA. Graphs of the prevalence/probability of angular errors in the 660 μm data are shown in Figure 8 and Figure S5 (860 μm). Results are statistically significant as confirmed by a Wilconson signed-rank test.44,45 In particular, the null hypothesis of the median of the angular errors of MPPCA and KPCA being equal was rejected with P < .01. Similar conclusions can be reached when comparing the angular errors of the noisy data to those of KPCA.
FIGURE 8.
Angular error as well as angular precision, probed by coherence metric κ, for the peaks of the fODFS estimated with CSD after denoising the 660 μm isotropic resolution DW images (b = 1500 s/mm2). Further, corresponding fODFs maps in a representative crossing-fibers area are displayed. Observe the lower variability in the fODFs of KPCA denoising compared to MPPCA
Clearly, the distribution of the KPCA angular errors is shifted to the left more than that of MPPCA and the original data, demonstrating lower angular errors in the white matter map obtained from the dataset denoised with KPCA rather than that obtained from the MPPCA denoised or original data. Graphs of the fODFs plotted in the 3-fiber crossing area of Figure 8 shows lower peak variability with KPCA denoising, a direct consequence of higher noise suppression. The coherence metric, κ, proposed in41 is in agreement with this observation. As shown in the plot, both in Figure 8 and Figure S5, the prevalence graphs of κ for the KPCA are shifted to the right more than that of MPPCA or the original data. As a result, overall coherence metric values are higher for KPCA (Table 1), indicating higher angular precision could be achieved if data is denoised first with KPCA.
4.3 ∣. In vivo human brain low-resolution dMRI multi-shell data
KPCA denoising achieves superior noise removal performance than MPPCA in the conventional low-resolution dMRI multi-shell dataset, see Figure S6. Denoised DWI images are comparable to the 5-average scan, which serves as ground-truth. SNR enhancement was 2 times bigger than that obtained of MPPCA (Figure S7), and NMRSE maps contain substantially lower NMRSE values in the case of KPCA compared to the MPPCA and noisy map. As in the previous experiment, no anatomical structure can be seen in the residual maps (Figure S8), suggesting good signal preservation. Improved accuracy, precision, and lower NRMSE were found when estimating FA, MD, and MK from data that were denoised with KPCA compared to MPPCA. All of these results can be found in Tables S12-S14 of the Supporting Information.
4.4 ∣. Capturing nonlinear coil and diffusion redundancy simultaneously
Coil DWI images as well as coil-combined DW images are presented in Figure 9. The sum of squares (SoS) method was employed for coil combination.
FIGURE 9.
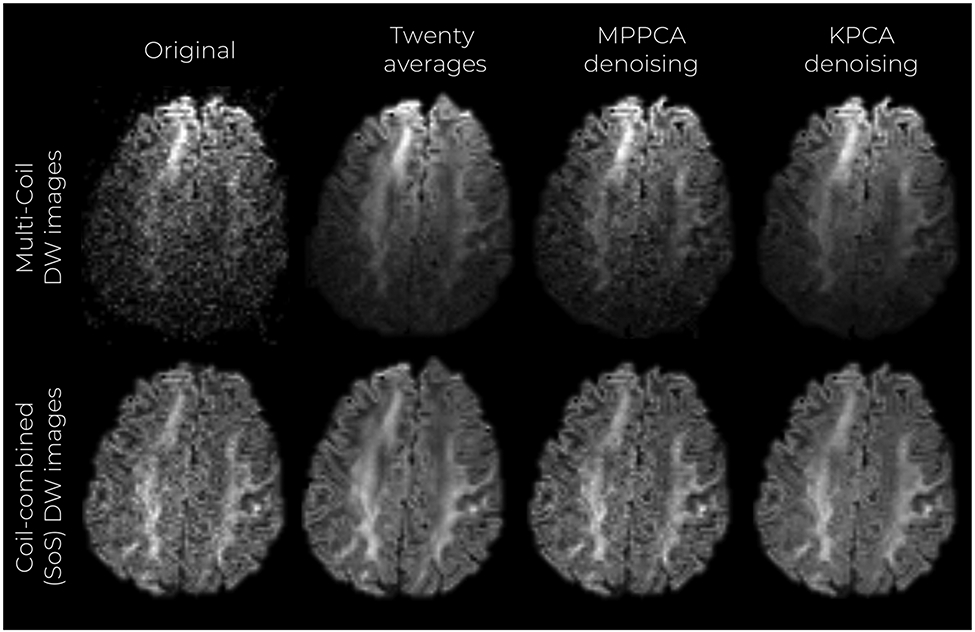
Mid-axial, coronal, and sagittal slices of multi-coil denoised DW images. DW images coil-combined with the SoS method are also shown
As in the previous experiments, KPCA achieves higher noise suppression than MPPCA, and the result is comparable to the twenty average case. As expected, differences in noise reduction are less notorious in the SoS images, as this technique already denoises the data due to averaging. However, higher noise reduction and good structure preservation is still observed by inspecting the DW images that are denoised with KPCA. Similar to the experiment with high-resolution dMRI data, σ-normalized residual maps of the multi-coil data show no anatomical features, and signal preservation is confirmed by statistical residual analysis (Figure S12 of the Supporting Information). Furthermore, normalized residuals follow a Gaussian distribution with standard deviation less than one. Noise maps presented in Figure S13 show higher SNR enhancement when KPCA denoising is applied, compared to MPPCA, ie, 2.48× and 1.73×, respectively. NRMSE values (maps in Figure S14) in the whole brain were also lower for KPCA than MPPCA. Improved estimation of FA and MD compared to MPPCA is achieved as well, please see Table S15-S17 in the Supporting Information.
5 ∣. DISCUSSION
We have shown using realistic simulations and in vivo dMRI experiments that it is possible to achieve superior noise suppression than state-of-the-art linear PCA denoising (MPPCA) while preserving the dMRI image structure, if nonlinear redundancies in the data are exploited. No signal structure is removed, as confirmed by the residual analysis. The KPCA denoising methodology can be used to enhance the typically low SNR of dMRI protocols, without compromising signal integrity.
To exploit nonlinear redundancy of the dMRI signal the key point is to apply PCA in a reproducing kernel Hilbert space where the low-rank assumption of the covariance matrix holds to a greater extent than in the canonical linear PCA space. It is precisely at very low SNR and reduced number of diffusion directions where the benefits of KPCA denoising over linear PCA are highly evident. If the rank K is not much lower than M, the portion of the eigenspectrum that is suppressed with linear PCA-based methods may not be large. Therefore, the percentage of accumulated noise in the preserved principal components will be substantial. With KPCA, this problem is bypassed, as the eigenspectrum is “augmented’ in the high-dimensional feature space , where thresholding is applied. Thereby, a large amount of the spectrum is suppressed, that is, more level of noise is reduced.
As the kernel determines the feature space, the choice of the kernel is an interesting problem that deserves to be discussed. We motivated the selection of the Gaussian kernel in Section 3.1.2. Though it provided excellent results, other kernels that are specifically tailored to certain features of the dMRI signal, for example the angular information, can be used. This could be accomplished by defining a corresponding spherical covariance function for the diffusion directions, as done in,46,47 and incorporating this covariance matrix into the conventional Gaussian kernel.
The selection of the rank and the kernel parameters clearly affects the performance. The SURE method allows us to rely on the statistical distribution model of the data, providing the optimal representation in the MSE sense. Originally, the SURE approach was conceived for additive noise models where the covariance of the noise is diagonal and parameterized by a single noise level σ. This case gives excellent results in all of our experiments. However, it can be extended to other statistical distributions,48 including Gaussian noise models with arbitrarily complex covariance matrices. This could be of interest in scenarios where noise correlation does exist. That could be the case of the multi-coil data experiment of this paper, where correlation between channels may exist and different noise levels can be measured. It could be of help too in cases where there exist noise correlation between different images, which could happen if they are preprocessed in a joint fashion.
We have demonstrated that KPCA can work at the reconstruction level, for example, denoising data with joint information from coil channels and diffusion directions, with accurate signal preservation and substantial noise reduction. Denoising at this early stage in the processing pipeline has some advantages. The most obvious is the possibility of modeling noise distribution accurately,24 which permits an optimal selection of rank and kernel parameters with the SURE method. As mentioned in the previous paragraph, we have assumed an uncorrelated Gaussian distribution for all of our experiments with excellent results. While this assumption is reasonable in most of the cases considered in his paper, the actual distribution may deviate from the Gaussian distribution, due to data processing algorithms (eg, motion correction). Therefore, the performance of denoising could be suboptimal. However, noise distributions in the reconstruction step, (after GRAPPA or SENSE reconstruction) have been studied/modeled extensively,18 and Gaussian distributions have shown to be a very accurate model for real-valued images obtained with GRAPPA/SENSE plus background phase correction. Superior denoising capabilities of KPCA are expected if denoising is done at this stage. It is important to recognize possible risks of denoising at the reconstruction level. The phase correction technique considerably influences the denoising step (see [24] for a more comprehensive analysis). Phase estimation should be accurately estimated to remove random phase variations between directions and channels. Otherwise, remaining artifacts/variations can reduce the signal redundancy and hence undermine the benefits of KPCA denoising at this early stage.
It is worth noting that random matrix theory in kernel matrices has received less interest for optimal rank selection than in the conventional PCA case. The difficulty of tracking noise statistics over the kernel transformation, and the asymptotic approximations necessary to obtain meaningful theoretical results49 makes this line of action impractical. This is one of the main benefits of the SURE method. Indeed, though KPCA denoising performs the low-rank decomposition in the feature transformed space, where noise statistics are difficult to model, the optimal selection of the rank and the scale parameter is done in the native space after reconstruction, where the assumed noise distribution model is well defined.
We would like to emphasize the broad applicability of KPCA denoising beyond conventional dMRI pulse sequences. We envisage even further benefits of using KPCA denoising compared to conventional PCA in situations where the complexity of the dMRI signal increases. New developments in diffusion sequences such as multidimensional dMRI50-53 are highly attractive applications for KPCA denoising. It is part of our future work to extensively evaluate KPCA denoising in tensor-encoding dMRI data54 and extend our preliminary experiments on this kind of data. Combination of relaxometry and diffusion MRI data may be another application where the nontrivial redundancy between different modalities could be better exploited with KPCA.55-58
It is very common to incorporate denoising mechanisms into reconstruction problems as regularization terms.10,11,59 In this regard, we believe KPCA denoising could be easily accommodated into this framework, and superior results cold be obtained than those algorithms that employ linear PCA-based regularization terms. We are currently exploring this line in our future work.
Finally, we would like to discuss some limitations of the current implementation of KPCA, for example, computation time. In general, computation time of KPCA is higher than that of MPPCA. This is due to the calculation of kernel distance as well as the SURE-method to select rank and optimal kernel parameters. Nevertheless, we foresee a considerable reduction in time with improvement in code-programming as well as with numerical approximations for nonlinear distances involved in the kernel (eg, Gaussian functions).
6 ∣. CONCLUSION
We introduce to the dMRI community a novel denoising technique, Kernel PCA, which goes beyond the linear compressibility assumption of PCA-based methods and exploits the nonlinear redundancies that is intrinsic to dMRI data. Substantially superior SNR-enhanced dMRI data can be obtained compared to PCA, without compromising signal integrity, in a short-computation time, and with no manual parameter tunning. We showcase the power of KPCA denoising with several in vivo whole human brain submillimeter resolution datasets as well as conventional spatial resolution multi-coil dMRI data. Improved diffusion parameter estimation was observed in all cases compared to state-of-the-art PCA denoising, for example, MPPCA. We believe KPCA denoising could be beneficial in any diffusion MRI processing pipeline and particularly critical when processing very low SNR data, as in high-resolution dMRI.
Supplementary Material
FIGURE S1 MSE and SURE as 2-dimensional functions of rank and mapping parameter h (parameterized by c and σmin–class. SURE can act as as surrogate for the unobservable MSE in optimal parameter design tasks
FIGURE S2 Residual maps from the 860 μm resolution datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid-line the optimal analytical zero-mean Gaussian distribution that best fits the data (Maximum Likelihood sense). Note that the standard deviation of the normalized residual, 0.79, is lower than 1 (black-line represents a zero-mean standard Gaussian distribution)
FIGURE S3 Maps of the NRMSE (hot colormap) and noise level (gray colormap) for the denoised DW images at 860 μm isotropic resolution and b-value of b = 2000 s/mm2. Observe that KPCA denoising obtains lowest level of noise (highest SNR gains) and NRMSE
FIGURE S4 Color-encoded FA maps of the denoised DW images at 860 μm isotropic resolution and b-value of b = 2000 s/mm2 as well as corresponding NRMSE maps
FIGURE S5 Angular error as well as angular precision, probed by coherence metric κ, for the peaks of the fODFS estimated with CSD after denoising the 860 μm isotropic resolution DW images (b = 2000 s/mm2). Further, corresponding fODFs maps in a representative crossing-fibers area are displayed. Observe the lower variability in the fODFs of KPCA denoising compared to MPPCA
FIGURE S6 Absolute error maps of FA and MD for the 660 μm gSlider dataset
FIGURE S7 Absolute error maps of FA and MD for the 860 μm gSlider dataset
FIGURE S8 Mid-axial, coronal, and sagittal slices of denoised multi-shell conventional DWI images
FIGURE S9 Maps of the NRMSE (hot colormap) and noise level (gray colormap) for the denoised multi-shell conventional DW images. Observe that KPCA denoising obtains the lowest level of noise (highest SNR gains) and NRMSE
FIGURE S10 Residual maps from the conventional mutilshell dMRI datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid line the optimal analytical zero-mean Gaussian distribution that best fits the data (maximum likelihood sense). Note that the standard deviation of the normalized residual, 0.98, is lower than 1 (black line represents a zero-mean standard Gaussian distribution)
FIGURE S11 Absolute error maps of FA, MD, and MK for the conventional low-resolution dMRI dataset
FIGURE S12 Residual maps from the multi-coil dMRI datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid line the optimal analytical zero-mean Gaussian distribution that best fits the data (maximum likelihood sense). Note that the standard deviation of the normalized residual, 0.79, is lower than 1 (black line represents a zero-mean standard Gaussian distribution)
FIGURE S13 Estimated noise maps for the denoised multi-coil DW images. Observe that KPCA denoising obtains the lowest level of noise (highest SNR gains)
FIGURE S14 NRMSE maps for the denoised multi-coil DW images. Maps of errors for the signal and the fractional anisotropy are shown Observe that KPCA denoising obtains the lowest NRMSE in both type of maps
FIGURE S15 Absolute error maps of FA and MD for the multi-coil dMRI dataset
TABLE S1 Absolute bias (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S2 Standard deviation (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S3 NRMSE (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test P < .01)60
TABLE S4 Absolute bias (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S5 Standard deviation (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S6 NRMSE (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S7 Absolute bias (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S8 Standard deviation (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S9 NRMSE (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S10 Accuracy results for the experiment with in vivo human brain submillimeter resolution dMRI data
TABLE S11 Precision results for the experiment with in vivo human brain submillimeter resolution dMRI data
TABLE S12 NRMSE and SNR-based results from the experiment with conventional multi-shell dMRI data. Note that in all cases KPCA denoising achieves better results than MPPCA
TABLE S13 Accuracy results for the experiment with conventional multi-shell dMRI data
TABLE S14 Precision results for the experiment with conventional multi-shell dMRI data
TABLE S15 NRMSE and SNR-based results from the experiment with multi-coil dMRI data. Note that in all cases KPCA denoising achieves better results than MPPCA
TABLE S16 Accuracy results for the experiment with multi-coil dMRI data
TABLE S17 Precision results for the experiment with multi-coil dMRI data
ACKNOWLEDGEMENTS
We acknowledge funding support from the following National Institute of Health (NIH) grants: R01MH116173 (PIs: Setsompop, Rathi), K25HL143278 (PI: Vegas Sanchez-Ferrero, Gonzalo), P41EB015902 (PI: Westin, Carl-Fredrik)
Footnotes
SUPPORTING INFORMATION
Additional Supporting Information may be found online in the Supporting Information section.
REFERENCES
- 1.Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42:288–292. [Google Scholar]
- 2.Jones DK. Diffusion MRI. Oxford University Press; 2010. [Google Scholar]
- 3.Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage. 2016;142:394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gallichan D. Diffusion MRI of the human brain at ultra-high field (UHF): a review. NeuroImage. 2018;168:172–180.Neuroimaging with Ultra-high Field MRI Present and Future. [DOI] [PubMed] [Google Scholar]
- 5.Eichner C, Setsompop K, Koopmans PJ, et al. Slice accelerated diffusion-weighted imaging at ultra-high field strength. Magn Reson Med. 2014;71:1518–1525. [DOI] [PubMed] [Google Scholar]
- 6.Kleinnijenhuis M, van Mourik T, Norris DG, Ruiter DJ, van Walsum AMvC, Barth M. Diffusion tensor characteristics of gyrencephaly using high resolution diffusion MRI in vivo at 7T. Neuroimage. 2015;109:378–387. [DOI] [PubMed] [Google Scholar]
- 7.Setsompop K, Cohen-Adad J, Gagoski B, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. NeuroImage. 2012;63:569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Setsompop K, Fan Q, Stockmann J, et al. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gslider-SMS). Magn Reson Med. 2018;79:141–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liao C, Stockmann J, Tian Q, et al. High-fidelity, high-isotropic-resolution diffusion imaging through gSlider acquisition with and T1 corrections and integrated b0/rx shim array. Magn Reson Med. 2020;83:56–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Haldar JP, Liu Y, Liao C, Fan Q, Setsompop K. Fast submillimeter diffusion MRI using gslider-SMS and SNR-enhancing joint reconstruction. Magn Reson Med. 2020;84:762–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ramos-Llordén G, Ning L, Liao C, et al. High-fidelity, accelerated whole-brain submillimeter in vivo diffusion MRI using gSlider-spherical ridgelets (gslider-SR). Magn Reson Med. 2020;84:1781–1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu W, Poser BA, Douaud G, et al. High-resolution diffusion MRI at 7t using a three-dimensional multi-slab acquisition. NeuroImage. 2016;143:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wu W, Koopmans PJ, Frost R, Miller KL. Reducing slab boundary artifacts in three-dimensional multislab diffusion MRI using nonlinear inversion for slab profile encoding (NPEN). Magn Reson Med. 2016;76:1183–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Eichner C, Paquette M, Mildner T, et al. Increased sensitivity and signal-to-noise ratio in diffusion-weighted MRI using multi-echo acquisitions. NeuroImage. 2020;221:117–172. [DOI] [PubMed] [Google Scholar]
- 15.Macovski A. Noise in MRI. Magn Reson Med. 1996;36:494–497. [DOI] [PubMed] [Google Scholar]
- 16.Eichner C, Cauley SF, Cohen-Adad J, et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage. 2015;122:373–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aja-Fernández S, Niethammer M, Kubicki M, Shenton ME, Westin CF. Restoration of DWI data using a rician LMMSE estimator. IEEE Trans Med Imag. 2008;27:1389–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aja-Fernández S, Vegas-Sánchez-Ferrero G. Statistical analysis of noise in MRI. Springer; 2016. [Google Scholar]
- 19.Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60:259–268. [Google Scholar]
- 20.Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med. 2011;65:480–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Descoteaux M, Wiest-Daesslé N, Prima S, Barillot C, Deriche R. Impact of rician adapted non-local means filtering on HARDI. Med Image Comput Comput Assist Interv. Springer; 2008:122–130. [DOI] [PubMed] [Google Scholar]
- 22.Manjón JV, Coupé P, Martí-Bonmatí L, Collins DL, Robles M. Adaptive non-local means denoising of MR images with spatially varying noise levels. J Magn Reson Imaging. 2010;31:192–203. [DOI] [PubMed] [Google Scholar]
- 23.Manjón JV, Coupé P, Concha L, Buades A, Collins DL, Robles M. Diffusion weighted image denoising using overcomplete local PCA. PLOS ONE. 2013;8:021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage. 2019;200:391–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schölkopf B, Smola A, Müller KR. Kernel principal component analysis. International conference on artificial neural networks: Springer; 1997:583–588. [Google Scholar]
- 26.Scholkopf B, Mika S, Burges CJ, et al. Input space versus feature space in kernel-based methods. IEEE Trans Neural Netw Learn Syst. 1999;10:1000–1017. [DOI] [PubMed] [Google Scholar]
- 27.Stein CM. Estimation of the mean of a multivariate normal distribution. Ann Stat. 1981;1135–1151. [Google Scholar]
- 28.Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. J Am Stat Assoc. 1995;90:1200–1224. [Google Scholar]
- 29.Ramani S, Blu T, Unser M. Monte-carlo SURE: a black-box optimization of regularization parameters for general denoising algorithms. IEEE Trans Image Process. 2008;17:1540–1554. [DOI] [PubMed] [Google Scholar]
- 30.Ramos-Llordén G, Vegas-Sánchez-Ferrero G, Liao C, et al. Structure preserving noise removal in hilbert space from ultra-high resolution diffusion MRI data. In Proceedings of the ISMRM & SMRT Virtual Conference & Exhibition. 2020;28. [Google Scholar]
- 31.Johnstone IM, Paul D. PCA in high dimensions: an orientation. Proc IEEE. 2018;106:1277–1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nadakuditi RR. Optshrink: an algorithm for improved low-rank signal matrix denoising by optimal, data-driven singular value shrinkage. IEEE Trans Inf Theory. 2014;60:3002–3018. [Google Scholar]
- 33.Lemberskiy G, Baete S, Veraart J, Shepherd TM, Fieremans E, Novikov DS. Achieving sub-mm clinical diffusion mri resolution by removing noise during reconstruction using random matrix theory. Proc Int Soc Mag Reson Med. 2019;27. [Google Scholar]
- 34.Mika S, Schölkopf B, Smola AJ, Müller KR, Scholz M, Rätsch G. Kernel PCA and de-noising in feature spaces. Adv Neural Inf Process Syst. 1999;536–542. [Google Scholar]
- 35.Kwok JY, Tsang IH. The pre-image problem in kernel methods. IEEE Trans Neural Netw Learn Syst. 2004;15:1517–1525. [DOI] [PubMed] [Google Scholar]
- 36.Jorgensen KW, Hansen LK. Model selection for gaussian kernel PCA denoising. IEEE Trans Neural Netw Learn Syst. 2011;23:163–168. [DOI] [PubMed] [Google Scholar]
- 37.Rathi Y, Dambreville S, Tannenbaum A. Statistical shape analysis using kernel PCA. Image processing: algorithms and systems, neural networks, and machine learning. Int Soc Optics Photonics; 2006:60–641B. [Google Scholar]
- 38.Aja-Fernández S, Pie T, Vegas-Sánchez-Ferrero G, et al. Spatially variant noise estimation in MRI: a homomorphic approach. Med Image Anal. 2015;20:184–197. [DOI] [PubMed] [Google Scholar]
- 39.Tournier JD, Smith R, Raffelt D, et al. MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation. NeuroImage. 2019;202:137. [DOI] [PubMed] [Google Scholar]
- 40.Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007;35:1459–1472. [DOI] [PubMed] [Google Scholar]
- 41.Jones DK. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn Reson Med. 2003;49:7–12. [DOI] [PubMed] [Google Scholar]
- 42.Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion mr imaging. Neuroimage. 2016;125:1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.McNab JA, Jbabdi S, Deoni SC, Douaud G, Behrens TE, Miller KL. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage. 2009;46:775–785. [DOI] [PubMed] [Google Scholar]
- 44.Wilcoxon F Individual comparisons by ranking methods. Breakthroughs in Statistics. Springer; 1992:196–202. [Google Scholar]
- 45.Hollander M, Wolfe DA, Chicken E. Nonparametric Statistical Methods, Vol. 751, John Wiley & Sons; 2013. [Google Scholar]
- 46.Andersson JL, Sotiropoulos SN. Non-parametric representation and prediction of single-and multi-shell diffusion-weighted MRI data using gaussian processes. Neuroimage. 2015;122:166–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wu W, Koopmans PJ, Andersson JL, Miller KL. Diffusion acceleration with gaussian process estimated reconstruction (DAGER). Magn Reson Med. 2019;82:107–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Eldar YC. Generalized SURE for exponential families: Applications to regularization. IEEE Trans Signal Process. 2008;57:471–481. [Google Scholar]
- 49.elKaroui N, et al. The spectrum of kernel random matrices. Ann Stat. 2010;38:1–50. [Google Scholar]
- 50.Westin CF, Szczepankiewicz F, Pasternak O, et al. Measurement tensors in diffusion MRI: generalizing the concept of diffusion encoding. Med Image Comput Comput Assist Interv. Springer; 2014:209–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Westin CF, Knutsson H, Pasternak O, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage. 2016;135:345–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Topgaard D Multidimensional diffusion MRI. J Magn Reson. 2017;275:98–113. [DOI] [PubMed] [Google Scholar]
- 53.Topgaard D, ed. Advanced Diffusion Encoding Methods in MRI. New Developments in NMR. The Royal Society of Chemistry; 2020. [Google Scholar]
- 54.Szczepankiewicz F, Hoge S, Westin CF. Linear, planar and spherical tensor-valued diffusion MRI data by free waveform encoding in healthy brain, water, oil and liquid crystals. Data Brief. 2019;25:208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion-relaxation correlation spectroscopic imaging: a multidimensional approach for probing microstructure. Magn Reson Med. 2017;78:2236–2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ning L, Gagoski B, Szczepankiewicz F, Westin CF, Rathi Y. Joint relaxation-diffusion imaging moments to probe neurite microstructure. IEEE Trans Med Imag. 2019;39:668–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lampinen B, Szczepankiewicz F, Mårtensson J, et al. Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding. Magn Reson Med. 2020;84:1605–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Grussu F, Battiston M, Veraart J, et al. Multi-parametric quantitative in vivo spinal cord MRI with unified signal readout and image denoising. Neuroimage. 2020;116–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hu Y, Wang X, Tian Q, et al. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magn Reson Med. 2020;83:1596–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Welch BL. The generalization of Student’s’ problem when several different population variances are involved. Biometrika. 1947;34:28–35. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 MSE and SURE as 2-dimensional functions of rank and mapping parameter h (parameterized by c and σmin–class. SURE can act as as surrogate for the unobservable MSE in optimal parameter design tasks
FIGURE S2 Residual maps from the 860 μm resolution datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid-line the optimal analytical zero-mean Gaussian distribution that best fits the data (Maximum Likelihood sense). Note that the standard deviation of the normalized residual, 0.79, is lower than 1 (black-line represents a zero-mean standard Gaussian distribution)
FIGURE S3 Maps of the NRMSE (hot colormap) and noise level (gray colormap) for the denoised DW images at 860 μm isotropic resolution and b-value of b = 2000 s/mm2. Observe that KPCA denoising obtains lowest level of noise (highest SNR gains) and NRMSE
FIGURE S4 Color-encoded FA maps of the denoised DW images at 860 μm isotropic resolution and b-value of b = 2000 s/mm2 as well as corresponding NRMSE maps
FIGURE S5 Angular error as well as angular precision, probed by coherence metric κ, for the peaks of the fODFS estimated with CSD after denoising the 860 μm isotropic resolution DW images (b = 2000 s/mm2). Further, corresponding fODFs maps in a representative crossing-fibers area are displayed. Observe the lower variability in the fODFs of KPCA denoising compared to MPPCA
FIGURE S6 Absolute error maps of FA and MD for the 660 μm gSlider dataset
FIGURE S7 Absolute error maps of FA and MD for the 860 μm gSlider dataset
FIGURE S8 Mid-axial, coronal, and sagittal slices of denoised multi-shell conventional DWI images
FIGURE S9 Maps of the NRMSE (hot colormap) and noise level (gray colormap) for the denoised multi-shell conventional DW images. Observe that KPCA denoising obtains the lowest level of noise (highest SNR gains) and NRMSE
FIGURE S10 Residual maps from the conventional mutilshell dMRI datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid line the optimal analytical zero-mean Gaussian distribution that best fits the data (maximum likelihood sense). Note that the standard deviation of the normalized residual, 0.98, is lower than 1 (black line represents a zero-mean standard Gaussian distribution)
FIGURE S11 Absolute error maps of FA, MD, and MK for the conventional low-resolution dMRI dataset
FIGURE S12 Residual maps from the multi-coil dMRI datasets after being denoised with KPCA. On top of the figure, the residual map from a given DW image, which shows no anatomical information. On the bottom, the probability density function of the residuals (r) normalized by the level of noise, σ. For the statistics, the normalized residuals are taken for all diffusion directions and number of repetitions. Observe that the residuals for KPCA approximately follows a Gaussian distribution (blue dotted line on both plots representing the estimated pdf). On blue solid line the optimal analytical zero-mean Gaussian distribution that best fits the data (maximum likelihood sense). Note that the standard deviation of the normalized residual, 0.79, is lower than 1 (black line represents a zero-mean standard Gaussian distribution)
FIGURE S13 Estimated noise maps for the denoised multi-coil DW images. Observe that KPCA denoising obtains the lowest level of noise (highest SNR gains)
FIGURE S14 NRMSE maps for the denoised multi-coil DW images. Maps of errors for the signal and the fractional anisotropy are shown Observe that KPCA denoising obtains the lowest NRMSE in both type of maps
FIGURE S15 Absolute error maps of FA and MD for the multi-coil dMRI dataset
TABLE S1 Absolute bias (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S2 Standard deviation (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S3 NRMSE (%) of the original, MPCA-denoised, and KPCA- denoised dMRI signals, compared to the ground truth dMRI signal. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test P < .01)60
TABLE S4 Absolute bias (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S5 Standard deviation (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S6 NRMSE (%) of the FA estimates (compared to ground-truth FA) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S7 Absolute bias (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S8 Standard deviation (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S9 NRMSE (%) of the MD estimates (compared to ground-truth MD) obtained after LLS estimation of the diffusion tensor from the original dMRI signal and denoised signals with MPPCA and KPCA. MC-based simulation experiment. Differences in cases marked with * are not statistically significant as confirmed with a Welch’s t-test (P < .01)60
TABLE S10 Accuracy results for the experiment with in vivo human brain submillimeter resolution dMRI data
TABLE S11 Precision results for the experiment with in vivo human brain submillimeter resolution dMRI data
TABLE S12 NRMSE and SNR-based results from the experiment with conventional multi-shell dMRI data. Note that in all cases KPCA denoising achieves better results than MPPCA
TABLE S13 Accuracy results for the experiment with conventional multi-shell dMRI data
TABLE S14 Precision results for the experiment with conventional multi-shell dMRI data
TABLE S15 NRMSE and SNR-based results from the experiment with multi-coil dMRI data. Note that in all cases KPCA denoising achieves better results than MPPCA
TABLE S16 Accuracy results for the experiment with multi-coil dMRI data
TABLE S17 Precision results for the experiment with multi-coil dMRI data