A matter of time: Using dynamics and theory to uncover mechanisms of transcriptional bursting

Abstract

Eukaryotic transcription generally occurs in bursts of activity lasting minutes to hours; however, state-of-the-art measurements have revealed that many of the molecular processes that underlie bursting, such as transcription factor binding to DNA, unfold on timescales of seconds. This temporal disconnect lies at the heart of a broader challenge in physical biology of predicting transcriptional outcomes and cellular decision-making from the dynamics of underlying molecular processes. Here, we review how new dynamical information about the processes underlying transcriptional control can be combined with theoretical models that predict not only averaged transcriptional dynamics, but also their variability, to formulate testable hypotheses about the molecular mechanisms underlying transcriptional bursting and control.

A disconnect between transcriptional bursting and its underlying molecular processes

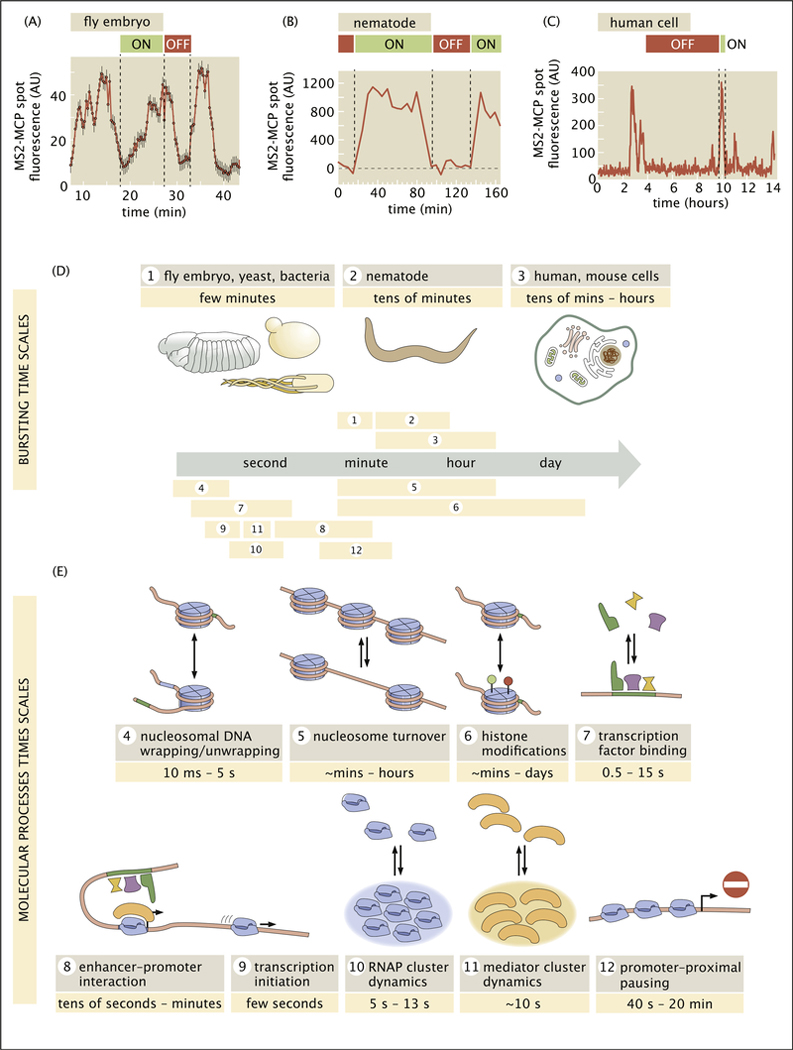
Over the past two decades, new technologies have revealed that transcription is a fundamentally discontinuous process characterized by transient bursts of transcriptional activity interspersed with periods of quiescence. Although electron microscopy provided early hints of bursty transcription [1], the advent of single-molecule fluorescence in situ hybridization (smFISH) [2,3], was key to establishing its central role in transcription. The single-cell distributions of nascent RNA and cytoplasmic mRNA molecules obtained using this technology provided compelling, if indirect, evidence for the existence and ubiquity of gene expression bursts, and indicated that their dynamics were subject to regulation by transcription factors [4,5]. These fixed-tissue inferences have been confirmed with new in vivo RNA fluorescence labeling technologies such as the MS2/MCP [6] and PP7/PCP systems [7], which directly reveal stochastic bursts of transcriptional activity in living cells in culture and within animals (Figure 1A–C) [8–11].

Figure 1. Separation of timescales between transcriptional bursting and its underlying molecular processes.

(a,b,c) Transcriptional bursting in (a) an embryo of the fruit fly Drosophila melanogaster, (b) the nematode Caenorhabditis elegans, and (c) human cells. (d) In these and other organisms, bursting dynamics (average period of ON and OFF) span a wide range of timescales from a few minutes to tens of hours. (e) Timescales of the molecular processes behind transcription range from fast seconds-long transcription factor binding to slower histone modifications, which may unfold across multiple hours or days. A detailed summary of measurements leading to these numbers, including references, is provided in Appendix A. (a, adapted from Ref. [16]; b, adapted from Ref. [17]; c, adapted from Ref. [18]).

What is the role of transcriptional bursting in cellular decision-making? One possibility is that bursty gene expression is intrinsically beneficial, helping (for instance) to coordinate gene expression or to facilitate cell-fate decision-making [12]. Alternatively, bursting may not itself be functional but might instead be a consequence of key underlying transcriptional processes, such as proofreading transcription factor identity [13,14].

Bursting and its regulation are intimately tied to the molecular mechanisms that underlie transcriptional regulation as a whole. In this article, we argue that, to make progress toward predicting transcriptional outcomes from underlying molecular processes, we can start with the narrower question of how the burst dynamics emerge from the kinetics of molecular transactions at the gene locus. To illustrate the importance and challenge of taking kinetics into account, we highlight two interrelated molecular puzzles that arise from new measurements of the dynamics of key transcriptional processes in vivo.

First, as illustrated in Figure 1D and reviewed in detail in Appendix Table A.1, despite qualitatively similar bursty traces from different organisms, bursts unfold across markedly distinct timescales ranging from several minutes [15,16], to tens of minutes [17,18], all the way to multiple hours [19]. Is this wide range of bursting timescales across organisms reflective of distinct molecular mechanisms or is it the result of a common set of highly malleable molecular processes?

Second, recent live imaging experiments have revealed a significant temporal disconnect between transcription factor binding events, which generally last for seconds, and the transcriptional bursts that these events control, which may last from a few minutes to multiple hours.

The majority of the molecular processes underlying transcriptional control are highly transient (Figure 1E), with timescales ranging from milliseconds to seconds (see Appendix Table A.2 and accompanying text for a detailed tabulation and discussion of these findings).

In this article, we seek to address this second puzzle by surveying key theoretical and experimental advances that, together, should shed light on the molecular origins of transcriptional bursting and transcriptional regulation. We leverage this framework to examine two kinds of molecular-level models that explain how slow burst dynamics could arise from fast molecular processes. Finally, we present concrete experimental strategies based on measuring variability in the timing of bursts that can be used to discern between molecular models of transcriptional bursting.

Overall, we seek to illustrate how iterative discourse between theory and experiment sharpens our molecular understanding of transcriptional bursting by reformulating cartoon models as concrete mathematical statements. Throughout this article, we focus on illustrative recent experimental and theoretical efforts; we therefore do not attempt to provide a comprehensive review of the current literature (see Ref. [20–25] for excellent reviews).

The two-state model: a simple quantitative framework for bursting dynamics

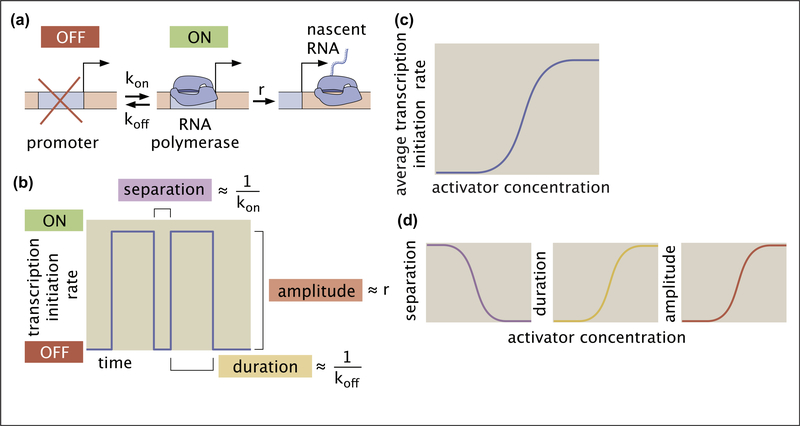
To elucidate the disconnect between molecular timescales and transcriptional bursting, we invoke a simple and widely used model of bursting dynamics: the two-state model of promoter switching. While the molecular reality of bursting is likely more complex than the two-state model suggests [26–28], there is value in examining where this simple model breaks down. This model posits that the promoter can exist in two states: a transcriptionally active ON state and a quiescent OFF state (Figure 2A). The promoter stochastically switches between these states with rates k_on and k_off and loads new RNA polymerase II (RNAP) molecules at a rate r when in the ON state [22,29–31]. Figure 2B shows a hypothetical activity trace for a gene undergoing bursty expression, where a burst corresponds to a period of time during which the promoter is in the ON state. The average burst duration, amplitude, and separation are given by 1/k_off, r, and 1/k_on, respectively.

Figure 2. The two-state model of transcriptional bursting.

(a) A two-state model of transcriptional bursting by a promoter switching between ON and OFF states. (b) Mapping the bursting parameters k_on, k_off, and r to burst duration, separation, and amplitude, respectively. (c) The action of an activator results in an increase in the average rate of transcription initiation. (d) In the two-state model, this upregulation can be realized by decreasing burst separation, increasing burst duration, increasing burst amplitude, or any combination thereof.

Because the instantaneous transcription initiation rate during a burst is r and zero otherwise, the average initiation rate is equal to r times the fraction of time the promoter spends in this ON state p_on,

$$\langle \text{initiation}\text{rate}\rangle =r{p}_{on},$$ (1)

where brackets indicate time-averaging. As shown in Appendix B, in steady state, p_on can be expressed as a function of the transition rates k_on and k_off:

$$p_{on}=\frac{k_{on}}{k_{on}+k_{off}}.$$ (2)

Plugging this solution into Equation (1) results in the average rate of mRNA production as a function of the bursting parameters given by.

$$\langle \text{initiation}\text{rate}\rangle =\underset{\text{in}\text{ON}\text{state}}{\underset{\text{transcription}\text{rate}}{\underbrace{r}}}\underset{\text{ON}\text{state}}{\underset{\text{probability}\text{of}}{\underbrace{\frac{k_{\text{on}}}{k_{\text{on}}+k_{\text{off}}}}}}.$$ (3)

Equation (3) shows that, within the two-state model, transcription factors can influence the mean transcription rate by modulating any one of the three burst parameters (or a combination thereof). For example, consider an activator that can increase the mean transcription rate (Figure 2C) by decreasing k_off, increasing k_on or r, or any combination thereof (Figure 2D). Both live-imaging measurements and smFISH have revealed that the vast majority of transcription factors predominantly modulate burst separation by tuning k_on [5,11,15,16,32–35]. There are also examples of the control of burst amplitude and duration, however [17,33,36].

Although experiments have identified which bursting parameters are under regulatory control, the question of how this regulation is realized at the molecular level remains largely open (with a handful of notable exceptions in bacteria [37], yeast [65], and mammalian cell culture [66]). This is because the two-state model is a phenomenological model: we can use it to quantify burst dynamics without making any statements about the molecular identity of the burst parameters. Nonetheless, by putting hard numbers to bursting and identifying which parameter(s) are subject to regulation, this framework constitutes a useful quantitative tool to formulate and test hypotheses about the molecular mechanisms underlying transcriptional control.

For instance, consider the observation that many activators modulate burst separation. A simple way to explain this fact is to posit that transitions between the ON and OFF states reflect the binding and unbinding of individual factors to regulatory DNA. Here, k_off would be the activator DNA-unbinding rate and k_on would be a function of activator concentration [A],

$$k_{on}([A])=[A]k_0^b,$$ (4)

where $k_0^b$ is the rate constant for activator binding.

A recent study in yeast lent credence to this picture, finding that activator affinity (k^u) might indeed play a role in dictating burst duration [65]. However, for most genes and organisms surveyed so far, the two-state model indicates that transcription factor unbinding alone cannot set the timescale for bursting: if k_off were an activator unbinding rate, then it would be on the order of 1 s⁻¹ (Figure 1D and E, box 7). However, measurements of burst duration reveal that k_off must be orders of magnitude smaller (≲ 0.01s⁻¹, Figure 1D). Thus, the two-state model lends a quantitative edge to the disconnect in Figure 1, reaffirming that transcriptional bursting is unlikely to be solely determined by the binding kinetics of the transcription factors that regulate it. We must therefore extend our simple two-state framework to incorporate molecular mechanisms that allow rapid transcription factor binding and transcriptional bursts that are orders of magnitude slower.

Bridging the timescale gap: kinetic traps and rate-limiting steps

Recent works have considered kinetic models of transcription that describe transition dynamics between distinct microscopic transcription factor binding configurations. These models make it possible to investigate how molecular interactions facilitate important behaviors such as combinatorial regulatory logic, sensitivity to changes in transcription factor concentrations, the specificity of interactions between transcription factors and their targets, and transcriptional noise reduction [13,14,38–41,67].

We illustrate how these kinetic models can shed light on the disconnect between the timescales of transcription factor binding and bursting using the activation of the hunchback minimal enhancer by Bicoid in the early fruit fly embryo as a case study [34,38,41–44]. Recent in vivo single-molecule studies have revealed that Bicoid specifically binds DNA in a highly transient fashion (~ 1 – 2 s) [45,46], suggesting that Bicoid binding cannot dictate the initiation and termination of hunchback transcriptional bursts, which happen over minutes [34]. We seek molecular models that recapitulate two key aspects of bursting: (1) the emergence of effective ON and OFF transcriptional states and (2) “slow” (>1 min) fluctuations between these states. We sketch out the mathematical basis of these efforts and review key results below; more detailed calculations can be found in Appendix C.

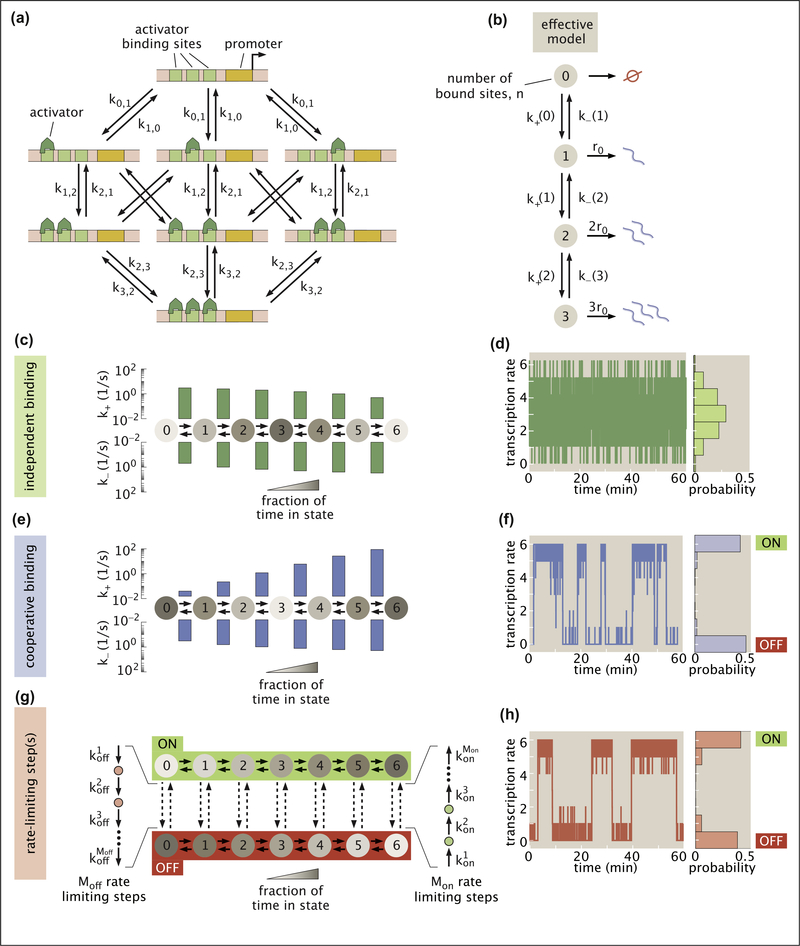
Following [38], we consider a simple activation model featuring an enhancer with identical activator binding sites. While the full model for the hunchback minimal enhancer consists of six binding sites, we first use a simpler version with three binding sites to introduce key features of our binding model before transitioning to the more realistic six binding sites version when discussing our results. We capture the dynamics of activator binding and unbinding at the enhancer by accounting for the transitions between all possible binding configurations (Figure 3A). Our assumption of identical activator binding sites leads to two simplifications: (1) the same rate, k_i,j governs the switching from any configuration with i activators bound to any configuration with j bound and (2) all binding configurations with the same number n of activators bound have the same rate of transcription, r_n = r₀ n, which we posit to be proportional to the number of bound activators. As a result we need not track specific binding configurations and may condense the full molecular representation in Figure 3A into a simpler four-state chain-like model with one state for each possible value of n (Figure 3B).

Figure 3. Using theoretical models to understand the origin of ON/OFF bursting dynamic.

(a) Model with three activator binding sites. The transition rates between states with i and j activators are given by k_i,j. (b) The model in (a) can be simplified to an effective four-state chain model in which each state corresponds to a certain number of bound molecules and the transcription rate is proportional to the number of bound activators. (c) Independent activator binding model with effective binding and unbinding rates plotted above and below, respectively. Shading indicates the fraction of time that the system spends in each state. (d) Stochastic simulations indicate that rapid activator binding alone drives fast fluctuations about a single transcription rate. (e) Cooperative binding model in which already-bound activators enhance the binding rate of further molecules. (f) Simulation reveals that cooperativity can cause the system to exhibit bimodal rates of transcription and slow fluctuations between effective ON and OFF states. (g) Rate-limiting step model in which several molecular steps can connect a regime where binding is favored (ON) and a realization where binding is disfavored (OFF). (h) Simulations demonstrate that rate-limiting steps can lead to bimodal transcriptional activity reminiscent of transcriptional bursting. Simulation results were down-sampled to a resolution of 0.5 s to ensure plot clarity in d, f, and h. Scripts used to generate plots in d, f, and h are available on Github [68]. (Parameters: c, d, k^b = k^u = 0.5s⁻¹; e, f, k^b = 0.004s⁻¹, k^u = 0.5s⁻¹; and ω = 6.7; G,H, $k_{on}^u=k_{\mathit{off}}^u=0.5{\text{s}}^{-1}$, $k_{\mathit{off}}^b=0.01{\text{s}}^{-1}$, $k_{on}^b=21{\text{s}}^{-1}$, M_off = 1, M_on = 2, $k_{off}^1=0.0023$, $k_{on}^1=k_{on}^2=0.0046{\text{s}}^{-1}$.)

Transitions up and down the chain in Figure 3B are governed by the effective binding and unbinding rates k₊(n) and k₋(n). To calculate these rates from the microscopic transition rates k_i,j, consider, for example, that there are three possible ways of transitioning from the 0 state to the 1 state, each with rate k_0,1. Thus, the effective transition rate between states 0 and 1 is given by 3k_0,1. More generally, in the effective model, activator binding rates are

$$k_{+}\left(n\right)=(N-n)k_{n,n+1},$$ (5)

where n indicates the current number of bound activators and N is the total number of binding sites. Similarly, activator unbinding rates are given by

$$k\_\left(n\right)=n{k}_{n,n-1}.$$ (6)

These transition rates allow us to generalize to the more realistic enhancer with six binding sites.

We first examine a system in which activator molecules bind and unbind independently from each other (Figure 3C). There are only two unique microscopic rates in this system: activator molecules bind at a rate $k_{i,i+1}=k^b=k_0^b[A]$, with [A] being the activator concentration and $k_0^b$ the binding rate constant, and unbind at a rate k_i,i−1 = k^u. We fix the unbinding rate k^u = 0.5 s⁻¹ to ensure consistency with recent experimental measurements of Bicoid in Ref. [45,46]. For simplicity, we also set k^b = 0.5 s⁻¹ (see Appendix C.2.3 for details).

To gain insight into the model’s transcriptional dynamics, we use stochastic simulations based on the Gillespie Algorithm [47]; however a variety of alternative analytic and numerical approaches exist [40,41,44]. Our simulations reveal that independent binding leads to a unimodal output behavior in which the transcription rate fluctuates rapidly about a single average (Figure 3D). This result is robust to our choices of k^b or k^u, as well as the number of binding sites in the enhancer (Appendix C.2.2). The observed lack of slow, bimodal fluctuations leads us to conclude that the independent binding model fails to recapitulate transcriptional bursting.

One way to extend the independent binding model is to allow for cooperative protein-protein interactions between activator molecules. Specifically, we consider a model where bound activator molecules [69] act to catalyze the binding of additional activators. Here, the activator binding rate is increased by a factor ω for every activator already bound, leading to

$$k_{i,i+1}=k^b{\omega }^i.$$ (7)

Because we assume that activator unbinding still occurs independently, the effective unbinding rates remain unchanged (Equation (6)).

Stochastic simulations of the cooperative binding model in Figure 3F reveal that the output transcription rate now takes on an all-or-nothing character, fluctuating between high and low values that act as effective ON and OFF states. Further, our simulation indicates that these emergent fluctuations are quite slow (0.13 transitions/min for the system shown), despite fast activator binding kinetics. Both of these phenomena result from large imbalances between k₊(n) and k₋(n) that act as “kinetic traps.”

Consider the case with five bound activators. If k₊(5) ≫ k₋(5), then the enhancer is much more likely to bind one more activator molecule and move to state six than to lose an activator and drop to state four. For instance, if k₊(5)/k₋(5) = 23 (Figure 3F), then the system will on average oscillate back and forth between states five and six 23 times before it finally passes to state four. While it is possible to generate this kind of trap without cooperativity at one end of the chain or the other by tuning k^b, cooperative interactions are needed to simultaneously achieve traps at both ends.

While we focused on binding-mediated cooperativity here, we note that all results presented above hold equally well for the unbinding-mediated case where cooperative interactions between bound molecules stabilize binding by reducing k_i,i−1 while maintaining k_i,i+1 unchanged. As discussed in Appendix C.3.4, our analysis of this unbinding-mediated cooperativity scenario makes the intriguing additional prediction that rapid (~1 s) activator dwell times inferred from in vivo experiments could mask the existence of rare long-lived (≥10 s) binding events that, despite their infrequency, play a key role in driving slow transcriptional burst dynamics. Finally, it is important to note that the phenomenon of emergent slow fluctuations is not limited to activator binding: cooperative interactions in fast molecular reactions elsewhere in the transcriptional cycle, such as in the dynamics of pre-initiation complex assembly, could, in principle, also induce slow fluctuations.

Inspired by the MWC model of protein allostery [44,50], a second way to bridge the timescale gap between activator binding and transcriptional bursting is to posit two distinct system configurations: an ON configuration where binding is favored (k^b ≫ k^u) and an OFF configuration that is less conducive to binding (k^b ≪ k^u). From any of the seven binding states, this system can transition from OFF to ON by traversing M_on slow steps, each with rate $k_{on}^i\ll {\mathrm{k}}^{\text{u}}$, where i is the step number (Figure 3G). Similarly, transitions from ON to OFF are mediated by M_off steps with rates given by $k_{off}^i$. Stochastic simulations indicate that this system yields bimodal transcription that fluctuates between high and low activity regimes on timescales set by the rate-limiting molecular steps (Figure 3H). Thus, as long as these steps induce a sufficiently large shift in activator binding (k^b), the rate-limiting step model reconciles rapid activator binding with transcriptional bursting.

Figure 1B suggests candidates for these slow molecular steps. For example, the ON state in Figure 3G could correspond to an open chromatin state that favors binding while the OFF state could indicate that a nucleosome attenuates binding such that M_on = M_off = 1. Our model also allows multiple distinct rate-limiting steps. For instance, chromatin opening could require multiple histone modifications (M_on ≥ 2, M_off = 1), or chromatin opening may need to be followed by enhancer-promoter co-localization to achieve a high rate of transcription (M_on = 2, M_off = 1).

Although they are not the only possible models, the cooperativity and rate-limiting step scenarios discussed above represent two distinct frameworks for thinking about how slow processes like bursting can coincide with, and even arise from, rapid processes like activator binding. The next challenge in identifying the molecular processes that drive transcriptional bursting is to establish whether these models make experimentally distinguishable predictions.

Using bursting dynamics to probe different models of transcription

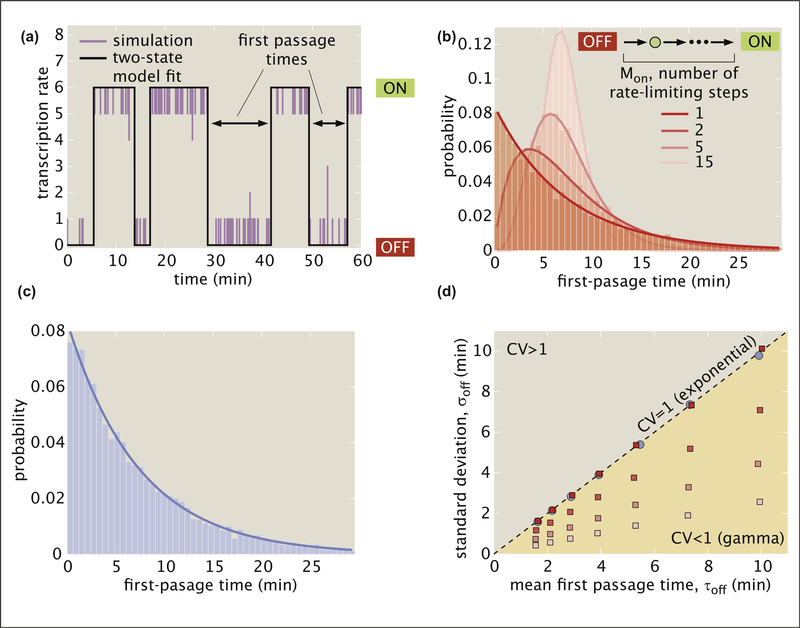
While we cannot yet directly observe the microscopic reactions responsible for bursting in real time, these processes leave signatures in transcriptional dynamics that may distinguish molecular realizations of bursting such as those of our cooperative binding (Figure 3E) and rate-limiting step (Figure 3G) models. Inspired by Ref. [27,51–53], we examine whether the distribution of observed burst separation times (Figure 4A) distinguishes between these two models. In keeping with literature convention, we refer to these separation times as first-passage times from OFF to ON.

Figure 4. Using first-passage time distributions to discriminate between models of transcriptional bursting.

(a) The outcome of stochastic simulations like those in Figure 3d, f, and g (purple) is fit to a two-state model (black) and the first-passage times out of the OFF state are measured. (b) First-passage times for the rate-limiting step model as a function of the number of rate-limiting steps M_on calculated using stochastic simulations. A single step results in an exponential distribution, but distributions break from this behavior when more steps are added, yielding increasingly peaked gamma distributions. (c) In contrast, first-passage times for the cooperative binding model follow an exponential distribution. (d) Standard deviation as a function of mean first-passage time for various parameters choices of the cooperative binding (blue) and the rate-limiting step models (red, with color shading indicating the M_on values considered in (b)). Distributions with CV = 1, such as the exponential distribution, fall on the line of slope one while gamma distributions, with CV < 1, fall in the region below this line. Scripts use to generate plots in a, b, c, and d are available on GitHub [68]. (Parameters: B, $k_{on}^u=k_{off}^u=0.5{\text{s}}^{-1}$, $k_{off}^b=0.01{\text{s}}^{-1}$, $k_{on}^u=21{\text{s}}^{-1}$, M_off = 1, $k_{off}^1=0.0023{\text{s}}^{-1}$, $k_{on}^i=M_{on}0.0023{\text{s}}^{-1}$; C, k^b = 0.004 s⁻¹. k^u = 0.5 s⁻¹, and ω = 6.7; D (rate-limiting-step model), $k_{on}^u=k_{off}^u=0.5{\text{s}}^{-1}$, $k_{off}^b=0.01{\text{s}}^{-1}$, $k_{on}^b=21{\text{s}}^{-1}$, M_off = 1, τ_off ∈ [1.6, 10.9] min, $k_{off}^1=1/{\tau }_{off}{\text{s}}^{-1}$, $k_{on}^i=M_{on}/{\tau }_{off}{\text{s}}^{-1}$; D (cooperativity model), k^b ∈ [0.01, 0.003] s⁻¹, k^u = 0.5 s⁻¹; and ω ∈ [4.5, 7.4]).

The variability in reactivation times provides clues into the number of hidden steps in a molecular pathway. For instance, suppose that bursts are separated by an average time τ_off = 1/k_on, as defined in the two-state model in Figure 2A and B. If there is only a single rate-limiting molecular step in the reactivation pathway (M_on = 1 in Figure 3G), then the first-passage times will follow an exponential distribution (Figure 4B) such that the variability, defined as the standard deviation (σ_off), will simply be equal to the mean (τ_off). Now, consider the case where two distinct molecular steps, each taking an average τ_off/2, connect the OFF and ON states (M_on = 2). To calculate the variability in the time to complete both steps and reactivate, we need to add the variability of each step in quadrature:

$${\sigma }_{off}=\sqrt{\frac{{{\tau }_{off}}^2}{2}+\frac{{{\tau }_{off}}^2}{2}}=\frac{{\tau }_{off}}{\sqrt{2}}.$$ (8)

More generally, in the simple case in which each step has the same rate, given an average first-passage time of τ_off, the variability in the distribution of measured first-passage times will decrease as the number of rate-limiting steps, M_on, increases following

$${\sigma }_{off}\left(M_{on}\right)=\frac{{\tau }_{off}}{\sqrt{M_{on}}}.$$ (9)

As predicted by Equation (9), increasing the rate-limiting step number reduces the width of the distribution for the rate-limiting step model obtained from stochastic simulations, shifting passage times from an exponential distribution when M_on = 1 to increasingly peaked gamma distributions when M_on > 1 (Figure 4B).

On the basis of these results, since the fluctuations between high- and low-activity regimes reflect transitions through many individual binding states in the cooperative binding model (Figure 3E), we might also expect this model to exhibit nonexponential first passage times. Instead, the first-passage times are exponentially distributed (Figure 4C). This result is consistent with earlier theoretical work that examined a chain model similar to ours and found that sufficiently large reverse rates (k^u in our case) cause first-passage time distributions to exhibit approximately exponential behavior [54].

The coefficient of variation (CV = σ_off/τ_off) provides a succinct way to summarize the shape of passage time distributions for a wide range of model realizations. Figure 4D plots σ_off against τ_off for each of the model architectures considered in Figure 4B and C for a range of different τ_off values. Points representing distributions with CV = 1 will fall on the line with slope one and points for distributions with CV < 1 will fall below it. We see that both the cooperative binding model and the single rate-limiting step model have CV values of approximately one for a wide range of τ_off values, consistent with exponential behavior. Conversely, all models with multiple rate-limiting steps have slopes that are significantly less than one.

Thus, by moving beyond experimentally measuring average first-passage time for a given gene and examining its distribution, it is possible to rule out certain molecular mechanisms. For example, a nonexponential distribution would be evidence against the cooperative binding and single rate-limiting step models (see Appendix C.1 and Appendix C.4 for details about stochastic simulations and first-passage time calculations). While these conclusions are specific to the models considered here, the general approach of invoking the distributions rather than means and using stochastic simulations to derive expectations for different models can be employed to discriminate between molecular hypotheses in a wide variety of contexts. Indeed, the examination of distributions has been revolutionary throughout biology by making it possible to, for example, reveal the nature of mutations [55], uncover mechanisms of control of transcriptional initiation [56] and elongation [57,58], measure translational dynamics [59], and even count molecules [60].

Note that, while appropriate for qualitatively estimating the order of magnitude of bursting timescales, raw fluorescence measurements from MS2 and PP7 experiments such as those in Figure 1A–C do not directly report on the promoter state. Rather, the signal from these experiments is a convolution of the promoter state and the dwell time of each nascent RNA molecule on the gene body [16]. As a result, inference techniques like those developed in Refs. [16,26] are often required to infer underlying burst parameters and promoter states that can be used to estimate first-passage time distributions. Other techniques, such as measuring the short-lived luminescent signal from reporters [27], have also successfully estimated first-passage times.

The first-passage time analyses discussed here are just one of an expansive set of approaches to determining the best model to describe experimental data. For instance, direct fits of models to experimental time traces could be used to identify the most appropriate model (see, e.g. Refs. [26,61]). A discussion of this and other approaches falls beyond the scope of this work, but we direct the reader to several excellent introductions to elements of this field [61–64].

Conclusions

The rapid development of live-imaging technologies has opened unprecedented windows into in vivo transcriptional dynamics and the kinetics of the underlying molecular processes. We increasingly see that transcription is complex, emergent, and—above all—highly dynamic, but experiments alone still fail to reveal how individual molecular players come together to realize processes that span a wide range of temporal scales, such as transcriptional bursting.

Here we have argued that theoretical models can help bridge this crucial disconnect between single-molecule dynamics and emergent transcriptional dynamics. By committing to mathematical formulations rather than qualitative cartoon models, theoretical models make concrete quantitative predictions that can be used to generate and test hypotheses about the molecular underpinnings of transcriptional control. We have also shown how, although different models of biological phenomena might be indistinguishable in their averaged behavior, these same models often make discernible predictions at the level of the distribution of such behaviors.

Moving forward, it will be critical to continue developing models that are explicit about the kinetics of their constituent molecular pieces, as well as statistical methods for connecting these models to in vivo measurements in an iterative dialogue between theory and experiment. In particular, robust model selection frameworks are needed to navigate the enormous space of possible molecular models for transcriptional control. Such theoretical advancements will be key if we are to synthesize the remarkable experimental findings from recent years into a truly mechanistic understanding of how transcriptional control emerges from the joint action of its molecular components.