Abstract
We analyse officially procured data detailing the COVID-19 transmission in Romania’s capital Bucharest between 1st August and 31st October 2020. We apply relational hyperevent models on 19,713 individuals with 13,377 infection ties to determine to what degree the disease spread is affected by age whilst controlling for other covariate and human-to-human transmission network effects. We find that positive cases are more likely to nominate alters of similar age as their sources of infection, thus providing evidence for age homophily. We also show that the relative infection risk is negatively associated with the age of peers, such that the risk of infection increases as the average age of contacts decreases. Additionally, we find that adults between the ages 35 and 44 are pivotal in the transmission of the disease to other age groups. Our results may contribute to better controlling future COVID-19 waves, and they also point to the key age groups which may be essential for vaccination given their prominent role in the transmission of the virus.
Keywords: Covid-19, age-group transmission, network analysis, relational hyperevent models, Romania
1. Introduction
The ongoing pandemic of coronavirus disease (COVID-19) unfolded, at the end of December 2019, in Wuhan, China, and, in only 3 months (as of March 2020), swiftly spread worldwide to 208 countries and territories [1]. Large-scale non-pharmaceutical interventions (NPIs) have been implemented ever since, with tremendous social, health and economic costs [2]. Many of the NPIs (closing schools and workplaces, cancelling public events, restricting private gatherings, limiting internal movement, public transport and travel, etc.) have aimed to supervise and control people’s locations. Nevertheless, further research is still needed to inform about the relationship between how people interact and infections [3, 4].
The Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-COV-2) spreads through direct (inter-personal) contact (through aerosols or droplets containing the virus) [5, 6]. Inherently, person-to-person virus transmission is shaped or decisively influenced by human behaviour. Markedly, the spread of close-contact viruses has been shown to be largely related to how people interact [7, 8] and to how individuals are embedded in social networks [9–11]. Or, briefly, to how social relationships are organized within society [12, 13]. In effect, ideas and statistical models from the network science [14] have already been applied to various topics related to the COVID-19 pandemic, such as the global and local spread of the virus [1, 15, 16], the exploration of SARS-COV-2 contact tracing data [6, 17, 18], the assessment of vaccination strategies [19, 20], the analysis of vaccine patents [21], the evaluation of distancing strategies [22], etc.
As hitherto documented [23–26], human interactions may prove determinant in understanding the transmission of respiratory close-contact infectious diseases. Thus, our paper addresses the relationship between contact patterns and the spread of COVID-19 infections, by employing a network science approach. We rely our investigation on two theoretical perspectives [8]. The first is the assortative perspective which argues that social relationships are given rise by the compatibility and complementarity of actors’ attributes [8]. Mixing patterns, either assortative (homophily) [27, 28] or disassortative (heterophily) [29], have been deemed salient drivers in the formation of human connections. The second is the relational perspective which suggests that the disease spread (diffusion) is affected by the structural features of the social networks (the configurations of the positions occupied by the individuals) [30]. Building on these two perspectives, we look at how the infection spreads throughout networks and assess the positive role of age in patterning COVID-19 contact transmission. Additionally, we control for network effects as well as for the sex of the embedded actors (both positive cases and their potential sources of infection). To this aim, we apply a recently proposed family of statistical models—relational hyperevent models (RHEM) [31–34]—to the real-world data describing the spread of COVID-19 in Bucharest (Romania), between 1 August and 31 October 2020. RHEM can specify and estimate the relative risk that a confirmed positive case nominates a set of actors as her/his close contacts (and therefore, possible origins of infection), as a function of given covariates and of the actors’ embedding into the network of previous case-contact ties.
Understanding how contact patterns affect the circulation of SARS-COV-2 is critical for devising sustainable control programs to shield health-care country-level infrastructures. The examination of transmissibility by accounting for socio-demographic covariates and network factors (configurations of the transmission networks) avail of comprehending the inner mechanisms of the disease spread. Currently, the role of human covariates and tie patterns in the SARS-COV-2 circulation [35] remains unclear, due to the precarity of corresponding real-world data. Evidence on how COVID-19 infections are transmitted between and within age-groups may inform vaccination strategies: either to prioritize specific age-groups (for countries with a poor supply of vaccines), or to appraise the aftermath of unsuccessful vaccination campaigns (when the vaccination goals are not reached).
1.1 Background
The available evidence about the role of age in the SARS-COV-2 transmission is limited, heterogeneous and inconclusive. For instance, a large-quantitative pre-pandemic study showed that children and adolescents tend to have in their personal networks larger numbers of alters similar in age, that is, 5 to 19-year olds are more assortative mixing in their contacts [36]. Given this age-homophily effect, children and adolescents were predicted to have the highest incidence, at least during the initial phase of an epidemic. A contact tracing study [37] implemented in South Korea during the COVID-19 outbreak showed that the contacts of symptomatic young people (aged 10–19) contracted the disease, in households, in 18.6% of cases (a percent larger than any other age group). Moreover, people aged 70 and 79 were the most likely to spread SARS-COV-2 outside the households (4.8% of their non-household contacts became infected). Conversely, it has been argued [38] that, in the USA, as of October 2020, at least 65 of 100 COVID-19 infections originated from individuals aged 20 to 49. Also, this particular age group was deemed to be the only one to sustain resurgent SARS-COV-2 transmission with reproduction numbers higher than one. Further, a study on the COVID-19 outbreak in Wuhan, China, claimed that people of 23–44 years had played a key role in spreading the infection within households and among friends [39].
Regarding the disease spread within the same age-group, available research shows that mitigation of community spread may be achieved by diminishing mixing in younger adults (individuals aged 18–35) [35]. Concurrently, evidence available for India [40] marks that enhanced transmission risk in similar-age pairs is strongest for children 0–14 years and among adults aged 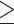 65 years. On top of that, infections in most age groups originated in individuals aged 20–44. Contact survey data [4] collected during the early stage of the COVID-19 pandemic, in Wuhan, China, revealed that the 0–14 years were less susceptible to SARS-COV-2 than adults (15–64 years old) while, in contrast, individuals over 65 years were more susceptible. Comparable results were reported by fitting age-structured mathematical models to data collected from China, Italy, Japan, Singapore, Canada and South Korea. These models marked that susceptibility to infection among people under 20 years was approximately half that of adults aged 20 years, whereas clinical symptoms were manifesting in 69% of infected people aged over 70 years [41]. Instead, a retrospective cohort study, conducted in Shenzhen, China, showed that children (<10 years) were at a similar risk of infection to the general population even if less likely to develop severe symptoms [42].
65 years. On top of that, infections in most age groups originated in individuals aged 20–44. Contact survey data [4] collected during the early stage of the COVID-19 pandemic, in Wuhan, China, revealed that the 0–14 years were less susceptible to SARS-COV-2 than adults (15–64 years old) while, in contrast, individuals over 65 years were more susceptible. Comparable results were reported by fitting age-structured mathematical models to data collected from China, Italy, Japan, Singapore, Canada and South Korea. These models marked that susceptibility to infection among people under 20 years was approximately half that of adults aged 20 years, whereas clinical symptoms were manifesting in 69% of infected people aged over 70 years [41]. Instead, a retrospective cohort study, conducted in Shenzhen, China, showed that children (<10 years) were at a similar risk of infection to the general population even if less likely to develop severe symptoms [42].
These findings should be context-wise interpreted and carefully addressed as changes in the contact patterns explain changes in disease incidence [43], while some age groups could experience, on average, milder symptoms if any. We may infer that individuals of different age have a different impact on the SARS-COV-2 transmission [44]. For example, young people tend to have larger networks (more contacts) than adults and the elderly. At the same time, the seemingly reduced susceptibility of children as well as their propensity to show milder symptoms may decrease the probability of them being detected [40].
2. Methods
On 7 March 2020, Romanian authorities were officially confirming the first COVID-19 case in Bucharest city (the capital of Romania—a European Union member state), that is, a return traveller from Italy who entered Bucharest on 27 February 2020 [45]. As of 6 July 2021, the number of people tested positive for COVID-19 in Bucharest was 183,739 (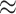 17% of all 1,081,090 cases reported in Romania) [46]. Bucharest, located in southern Romania is the largest city (area: 228 km
17% of all 1,081,090 cases reported in Romania) [46]. Bucharest, located in southern Romania is the largest city (area: 228 km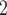 , a population of 1.83 million, and a density of 8.026 people/km
, a population of 1.83 million, and a density of 8.026 people/km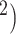 and the most important commercial centre [Gross Domestic Product (GDP) —per capita in 2019: EUR 20.573, and a total nominal GDP of EUR 52.2 billion—23.9% of Romania]. In this observational study, we analyse anonymized real world COVID-19 human to human transmission data procured from the Department of Public Health Bucharest (Ministry of Health, Romania). These data describe all the infections officially recorded between 1 August and 31 October 2020, in Bucharest. Put it differently, we analyse the complete set of confirmed cases in Bucharest in that period. The observations are available for replication [47].
and the most important commercial centre [Gross Domestic Product (GDP) —per capita in 2019: EUR 20.573, and a total nominal GDP of EUR 52.2 billion—23.9% of Romania]. In this observational study, we analyse anonymized real world COVID-19 human to human transmission data procured from the Department of Public Health Bucharest (Ministry of Health, Romania). These data describe all the infections officially recorded between 1 August and 31 October 2020, in Bucharest. Put it differently, we analyse the complete set of confirmed cases in Bucharest in that period. The observations are available for replication [47].
Backward contact tracing is employed by the public health authorities to monitor human-to-human disease spread, even if the actual directionality of infection, in COVID-19 epidemiological studies, is difficult to ascertain [18]. Particularly, individuals, officially confirmed as COVID-19 positive cases (the red circles in Fig. 1), are required to nominate the people they considered potential origin of their infection (the grey nodes in Fig. 1).
Fig. 1.
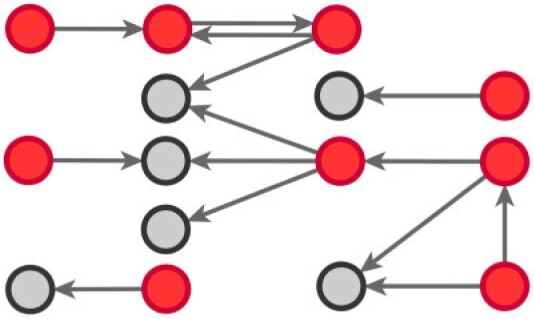
Human-to-human COVID-19 spread by backward contact tracing. Arrows stem from COVID-19 officially confirmed cases (red circles) to their potential origin of infection (grey circles).
We make use of the data provided by the public health authorities to create infection chains (real-world infection networks)—similar to the ones exhibited in Fig. 1. In these chains, we may notice various scenarios. First, COVID-19 confirmed cases nominate as a potential origin of infection other COVID-19 confirmed cases (pairs of red circles, in the form positive (referee)  positive (referral) arcs). Second, COVID-19 confirmed cases nominate each other as infection sources (pairs of red circles and reciprocated arrows, in the form of positive
positive (referral) arcs). Second, COVID-19 confirmed cases nominate each other as infection sources (pairs of red circles and reciprocated arrows, in the form of positive  positive arcs). Third, COVID-19 confirmed cases nominate potential infection origins (pairs wherein an arrow stems from a red circle and targets a grey circle, in the form of positive (referee)
positive arcs). Third, COVID-19 confirmed cases nominate potential infection origins (pairs wherein an arrow stems from a red circle and targets a grey circle, in the form of positive (referee)  contact (referral) arcs). Unlike the red circles (COVID-19 positive cases), the people designated by grey circles are not tested by the medical authorities, but directly placed in quarantine. In effect, we do not know whether the grey circles are also infected individuals.
contact (referral) arcs). Unlike the red circles (COVID-19 positive cases), the people designated by grey circles are not tested by the medical authorities, but directly placed in quarantine. In effect, we do not know whether the grey circles are also infected individuals.
Age and sex information are available for the nodes embedded in the transmission chains, irrespective of their status (either referees or referrals). In our research design, we use the label referee to indicate the individuals who provided information about their possible sources of infection (the number of nominations made by the referees is unbounded). Also, we use the term referral to designate the people nominated as potential origin of infection.
We employ relational hyperevent modelling (RHEM) [31, 32, 34] to estimate the probability of a source (referee) nominating a set of targets (referrals). Our core objective is to assess age-homophily in contact-elicitation (by confirmed positive cases) in a statistically valid way. Statistically, this amounts to specify and estimate the hazard that a possible contact C, taken from a population of actors, is nominated by a confirmed positive case P (referee) as a function of the age-difference of P and C—along with other control variables. However, valid statistical analysis has to deal with two types of dependencies in the given referee-referral data. First, a single positive case P does not only mention one single contact but possibly a set of contacts 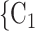 , C
, C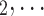 , C
, C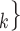 of any size. This property of the data naturally invalidates any assumption of independence of the referee-referral dyads originating from the same positive case. Second, the actors involved (referees and referrals) are embedded into a—largely unobserved—social space [48, 49], which shapes the baseline probability that P ‘knows’ or ‘is close to’ a possible contact C and, also, the baseline probability that two possible contacts C and C’ are close to each other—which can all have an influence on the hazard that P nominates C and C’.
of any size. This property of the data naturally invalidates any assumption of independence of the referee-referral dyads originating from the same positive case. Second, the actors involved (referees and referrals) are embedded into a—largely unobserved—social space [48, 49], which shapes the baseline probability that P ‘knows’ or ‘is close to’ a possible contact C and, also, the baseline probability that two possible contacts C and C’ are close to each other—which can all have an influence on the hazard that P nominates C and C’.
RHEM can deal with these two types of dependencies in a principled way. First, a single observation modelled by RHEM is not given by a positive case P and a single nominated contact C, but by the entire set of contacts 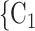 , C
, C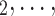 C
C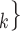 nominated by P. RHEM is a variant of Cox proportional hazard models (CoxPH) that specifies and estimates the hazard of observing a ‘relational hyperevent’, that is, an event on a hyperedge (P,
nominated by P. RHEM is a variant of Cox proportional hazard models (CoxPH) that specifies and estimates the hazard of observing a ‘relational hyperevent’, that is, an event on a hyperedge (P,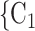 , C
, C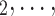 C
C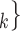 ), estimating the conditional distribution that
), estimating the conditional distribution that 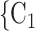 , C
, C C
C is the entire set of contacts, nominated by a given positive case P. This conditional distribution can be a parametric function of covariates of interest—such as the average age-difference between P and the various contacts C
is the entire set of contacts, nominated by a given positive case P. This conditional distribution can be a parametric function of covariates of interest—such as the average age-difference between P and the various contacts C C
C —as well as of other covariates included to control for alternative explanations of co-reference probabilities. By design, RHEM treats a given hyperedge (P,
—as well as of other covariates included to control for alternative explanations of co-reference probabilities. By design, RHEM treats a given hyperedge (P, 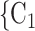 , C
, C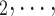 C
C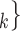 ) as a single observation—avoiding to assume independence of the implied referee-referral dyads (P,C
) as a single observation—avoiding to assume independence of the implied referee-referral dyads (P,C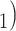 , (P,C
, (P,C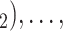 (P,C
(P,C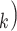 . Secondly, RHEM allows to add further covariates (‘network effects’) that allow to control for further dependencies in contact-elicitation data. For instance, if some of the C
. Secondly, RHEM allows to add further covariates (‘network effects’) that allow to control for further dependencies in contact-elicitation data. For instance, if some of the C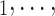 C
C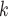 have previously been tested positive and have nominated P, then this implies that those C
have previously been tested positive and have nominated P, then this implies that those C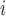 are ‘close to’ P, so that in turn P is more likely to reciprocate this nomination, when being interviewed as a positive case. As another example of a network effect that can be controlled for with RHEM is that if, say, C
are ‘close to’ P, so that in turn P is more likely to reciprocate this nomination, when being interviewed as a positive case. As another example of a network effect that can be controlled for with RHEM is that if, say, C and C
and C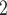 are among the list of contacts of a previously interviewed positive case P’, then the probability that another positive case P also co-nominates C
are among the list of contacts of a previously interviewed positive case P’, then the probability that another positive case P also co-nominates C and C
and C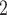 is likely to be higher than the product of their marginal probabilities. This would amount to an effect predicting partial repetition of contact lists. Below, we define and discuss these and other effects in more detail.
is likely to be higher than the product of their marginal probabilities. This would amount to an effect predicting partial repetition of contact lists. Below, we define and discuss these and other effects in more detail.
To estimate RHEM, we compare the observed nomination events (P, 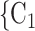 , C
, C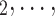 C
C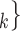 ) with possible alternative hyperedges (P,
) with possible alternative hyperedges (P, 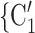 , C’
, C’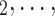 C’
C’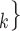 ), where
), where 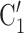 , C’
, C’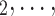 C’
C’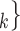 is a set of actors that the positive case P could have nominated as contact set, but did not. Since the number of possible contact sets scales exponentially with the number of actors, we estimate RHEM via ‘case-control sampling’ [31, 32, 34]. For each observed nomination event (P,
is a set of actors that the positive case P could have nominated as contact set, but did not. Since the number of possible contact sets scales exponentially with the number of actors, we estimate RHEM via ‘case-control sampling’ [31, 32, 34]. For each observed nomination event (P, 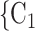 , C
, C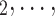 C
C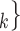 ), we draw one thousand alternative possible contact sets
), we draw one thousand alternative possible contact sets 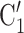 , C’
, C’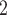 ,
,  , C’
, C’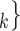 (‘non-events’ or ‘controls’) uniformly at random from all set of actors of size k. Case-control sampling has been shown to yield reliable estimates for large REM [33] and for RHEM [31, 32, 34].
(‘non-events’ or ‘controls’) uniformly at random from all set of actors of size k. Case-control sampling has been shown to yield reliable estimates for large REM [33] and for RHEM [31, 32, 34].
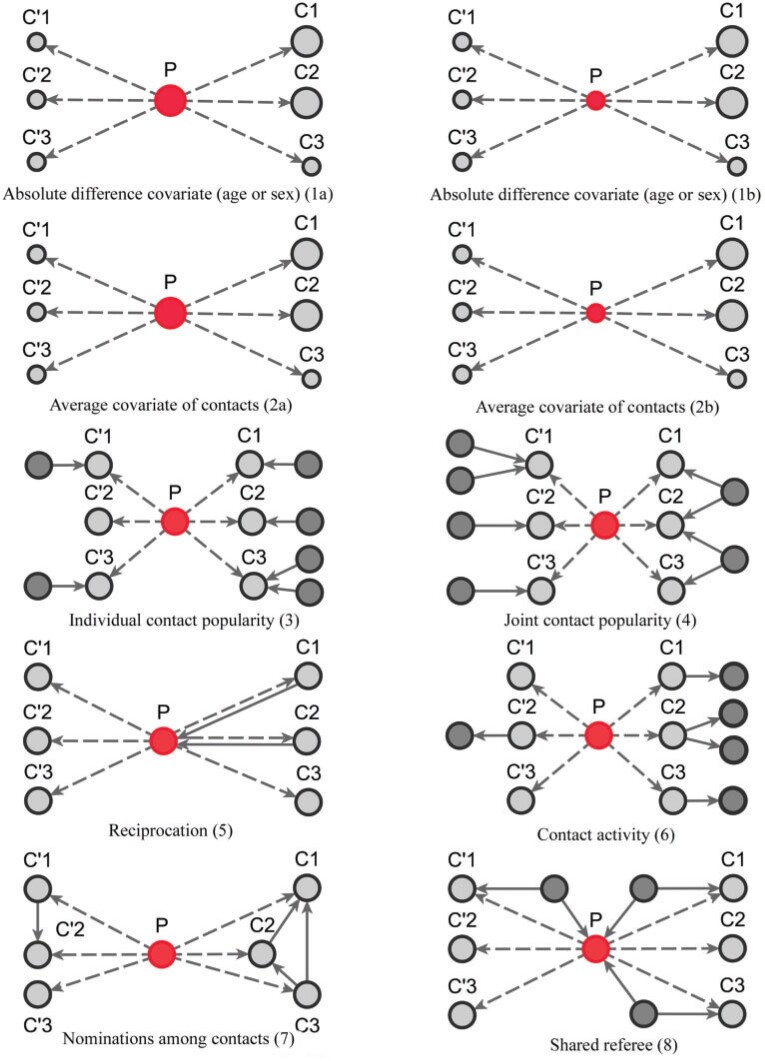
We include, in the RHEM models, several covariate and network effects which are visually described in Fig. 2. All images contain the following elements. A central actor P, displayed in red, is a confirmed positive case (source, referee). When interviewed for contacts, P can theoretically elicit any set of contacts 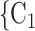 , C
, C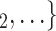 (targets, referrals) of any size taken from a population of actors. Also, the images display two alternative possible sets of contacts,
(targets, referrals) of any size taken from a population of actors. Also, the images display two alternative possible sets of contacts, 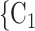 , C
, C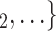 and
and 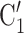 , C’
, C’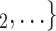 , as light-grey nodes with given labels. The positive case P is connected to the set of contacts
, as light-grey nodes with given labels. The positive case P is connected to the set of contacts 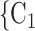 , C
, C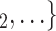 via dashed edges pointing to the right, and P is connected to the set of contacts
via dashed edges pointing to the right, and P is connected to the set of contacts 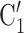 , C’
, C’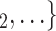 via dashed edges pointing to the left. All other nodes (unlabelled and displayed as dark-grey nodes), as well as all the edges that are displayed as solid lines represent previous referees, referrals, or the respective referee-referral edges. These previous referrals are assumed to shape the probability that P elicits the set
via dashed edges pointing to the left. All other nodes (unlabelled and displayed as dark-grey nodes), as well as all the edges that are displayed as solid lines represent previous referees, referrals, or the respective referee-referral edges. These previous referrals are assumed to shape the probability that P elicits the set 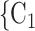 , C
, C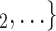 rather than the set
rather than the set 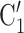 , C’
, C’ . Furthermore, the images for each effect (Fig. 2) are always constructed in a way that if the associated parameter is positive, then P has a preference for eliciting the set of contacts
. Furthermore, the images for each effect (Fig. 2) are always constructed in a way that if the associated parameter is positive, then P has a preference for eliciting the set of contacts  , C
, C on the right, and if the associated parameter is negative, then P has a preference for eliciting the set of contacts
on the right, and if the associated parameter is negative, then P has a preference for eliciting the set of contacts  , C’
, C’ on the left.
on the left.
Fig. 2.
Network effects included in the Relational hyperevent models. The images describe contact-elicitation data wherein the red P nodes are positive (referees) cases, the grey C nodes designate contacts (referrals), while the dark grey unlabelled nodes represent previous referees or referrals.
In terms of covariates effects, for each (possible or observed) contact nomination hyperedge (P, 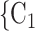 , C
, C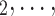 C
C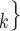 ), we computed assortativity mixing (homophily) scores on both age and sex. Namely, the average absolute difference (abs_diff_age) between the age of a hyperevent source P (positive case or referee) and the age of the hyperevent targets C
), we computed assortativity mixing (homophily) scores on both age and sex. Namely, the average absolute difference (abs_diff_age) between the age of a hyperevent source P (positive case or referee) and the age of the hyperevent targets C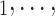 C
C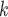 (contacts or referrals). A positive (negative) parameter associated with abs_diff_age would indicate that positive cases P have a tendency to nominate contacts C
(contacts or referrals). A positive (negative) parameter associated with abs_diff_age would indicate that positive cases P have a tendency to nominate contacts C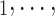 C
C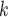 of different (similar) age. Thus, a positive parameter associated with abs_diff_age would point to age-heterophily, or dis-assortative mixing, and a negative parameter to age-homophily, or assortative mixing. A similar covariate (abs_diff_sex) was taken for the average absolute difference in sex between the positive case P and her/his nominated contacts C
of different (similar) age. Thus, a positive parameter associated with abs_diff_age would point to age-heterophily, or dis-assortative mixing, and a negative parameter to age-homophily, or assortative mixing. A similar covariate (abs_diff_sex) was taken for the average absolute difference in sex between the positive case P and her/his nominated contacts C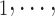 C
C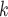 . Males were coded by 1 and females by 2, so that abs_diff_sex is the ratio of contacts that have a different sex than P. Additionally, we also accounted for the average age (avg_age) in the set of contacts as well as for the average sex (avg_sex) in the contact set of each hyperevent. A positive (negative) parameter associated with avg_age would point to a tendency to nominate old (young) contacts and a positive (negative) parameter associated with avg_sex would point to a tendency to nominate females (males).
. Males were coded by 1 and females by 2, so that abs_diff_sex is the ratio of contacts that have a different sex than P. Additionally, we also accounted for the average age (avg_age) in the set of contacts as well as for the average sex (avg_sex) in the contact set of each hyperevent. A positive (negative) parameter associated with avg_age would point to a tendency to nominate old (young) contacts and a positive (negative) parameter associated with avg_sex would point to a tendency to nominate females (males).
In Fig. 2.1 and 2.2, for the covariate effects, we display actors as large nodes if they assume a high value in a given covariate (either high age or sex  female
female 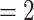 ), and we display them as small nodes if they assume low values in a given covariate (either low age or sex
), and we display them as small nodes if they assume low values in a given covariate (either low age or sex  male
male 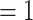 ). Notably, for the case of the absolute difference covariate effects (age and sex), we display two variants of graphics that differ only in the covariate value of the positive case P (Fig. 2.1a,b). Namely, in Fig. 2.1a, P assumes a high covariate value, and, in Fig. 2.1b, P assumes a low covariate value. For both images, the set of contacts
). Notably, for the case of the absolute difference covariate effects (age and sex), we display two variants of graphics that differ only in the covariate value of the positive case P (Fig. 2.1a,b). Namely, in Fig. 2.1a, P assumes a high covariate value, and, in Fig. 2.1b, P assumes a low covariate value. For both images, the set of contacts 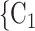 , C
, C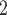 , C
, C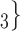 takes higher values in the given covariate than the set of contacts
takes higher values in the given covariate than the set of contacts 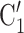 , C’
, C’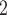 , C’
, C’ . In the network exhibited as Fig. 2.1a, the positive case P is, on average, closer (with respect to covariate values) to the set of contacts
. In the network exhibited as Fig. 2.1a, the positive case P is, on average, closer (with respect to covariate values) to the set of contacts  , C
, C , C
, C than to the set of contacts
than to the set of contacts 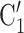 , C’
, C’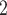 , C’
, C’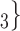 . That is, the absolute difference of the covariate between P and the set of contacts
. That is, the absolute difference of the covariate between P and the set of contacts 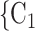 , C
, C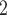 , C
, C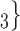 is smaller than the absolute difference of the covariate between P and the set of contacts
is smaller than the absolute difference of the covariate between P and the set of contacts 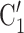 , C’
, C’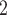 , C’
, C’ . If the absolute difference of covariate (abs_diff_age or abs_diff_sex) is associated with a positive parameter, then—in the network displayed as Fig. 2.1a—the set of contacts
. If the absolute difference of covariate (abs_diff_age or abs_diff_sex) is associated with a positive parameter, then—in the network displayed as Fig. 2.1a—the set of contacts  , C
, C , C
, C would be less likely to be nominated as the set of contacts of the positive case P. (A positive parameter associated with abs_diff_covar would imply that difference leads to nominations). In the network presented in Fig. 2.1b, everything is reversed: since P has a low value in the covariate, P is more different to the set of contacts
would be less likely to be nominated as the set of contacts of the positive case P. (A positive parameter associated with abs_diff_covar would imply that difference leads to nominations). In the network presented in Fig. 2.1b, everything is reversed: since P has a low value in the covariate, P is more different to the set of contacts 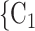 , C
, C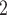 , C
, C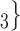 than to the set of contacts
than to the set of contacts 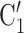 , C’
, C’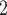 , C’
, C’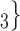 .
.
In Fig. 2.2(a,b), for the average covariate of contacts effects, it does not matter which value the positive case P assumes in the given covariate (age or sex). It only matters which values the contacts take. We nevertheless illustrate this effect with the same images. Specifically, for both Fig. 2.2(a,b) images, the set of contacts 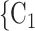 , C
, C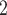 , C
, C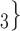 takes higher values in the given covariate than the set of contacts
takes higher values in the given covariate than the set of contacts 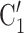 , C’
, C’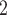 , C’
, C’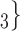 . Thus, in both images, the value of avg_covariate (avg_age or avg_sex) is higher for the set of contacts
. Thus, in both images, the value of avg_covariate (avg_age or avg_sex) is higher for the set of contacts 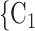 , C
, C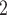 , C
, C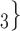 than for the set of contacts
than for the set of contacts 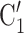 , C’
, C’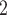 , C’
, C’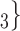 . Thus, if avg_covariate is associated with a positive parameter then—for both networks, Fig. 2.2(a,b)—the set of contacts
. Thus, if avg_covariate is associated with a positive parameter then—for both networks, Fig. 2.2(a,b)—the set of contacts 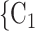 , C
, C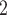 , C
, C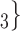 is more likely to be nominated by P than the set of contacts
is more likely to be nominated by P than the set of contacts 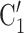 , C’
, C’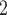 , C’
, C’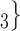 . The covariate value of P does not have any impact for this effect.
. The covariate value of P does not have any impact for this effect.
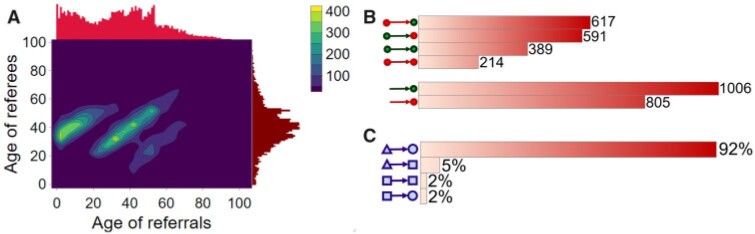
Figure 2.3–2.8 illustrated various networks effects. The individual contact popularity effect refers to how does the risk increase if the contacts 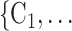 C
C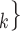 individually have been more often mentioned as contacts before. In Fig. 2.3, the set of possible contacts
individually have been more often mentioned as contacts before. In Fig. 2.3, the set of possible contacts  , C
, C , C
, C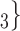 on the right received in total four past nominations, leading to an individual contact popularity
on the right received in total four past nominations, leading to an individual contact popularity  4/3 (the average number of nominations per actor). The set of possible contacts
4/3 (the average number of nominations per actor). The set of possible contacts 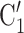 , C’
, C’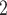 , C’
, C’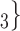 on the left received in total two past nominations, leading to an individual contact popularity
on the left received in total two past nominations, leading to an individual contact popularity 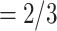 . If individual contact popularity is associated with a positive parameter, then the set of contacts
. If individual contact popularity is associated with a positive parameter, then the set of contacts 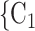 , C
, C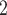 , C
, C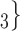 on the right would be more likely to be nominated as the set of contacts of the positive case P. This effect is very important to account for a specific property of our data: the set of actors included in our analysis contains only persons that are ‘active’ as a referee or as a referral at least once. Therefore, all actors in our sample are guaranteed to appear at least once either as a positive case or as a nominated contact and, once they have experienced this first appearance, their probability to participate in another event decreases sharply. Thus, we actually expect a negative parameter associated with individual contact popularity for the way the data has been constructed. Negative estimates mean a decrease in the relative risk. A negative effect is due to the sample selection: each actor is guaranteed to appear in at least one event; once they had this event, their probability to appear in another one decreases.
on the right would be more likely to be nominated as the set of contacts of the positive case P. This effect is very important to account for a specific property of our data: the set of actors included in our analysis contains only persons that are ‘active’ as a referee or as a referral at least once. Therefore, all actors in our sample are guaranteed to appear at least once either as a positive case or as a nominated contact and, once they have experienced this first appearance, their probability to participate in another event decreases sharply. Thus, we actually expect a negative parameter associated with individual contact popularity for the way the data has been constructed. Negative estimates mean a decrease in the relative risk. A negative effect is due to the sample selection: each actor is guaranteed to appear in at least one event; once they had this event, their probability to appear in another one decreases.
The joint contact popularity effect refers to how does the risk increase if the contacts 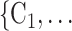 C
C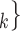 pairwise have been more often co-mentioned as contacts before. In Fig. 2.4, among the three unordered pairs in the set of possible contacts
pairwise have been more often co-mentioned as contacts before. In Fig. 2.4, among the three unordered pairs in the set of possible contacts 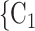 , C
, C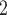 , C
, C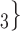 on the right, two, namely
on the right, two, namely 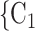 , C
, C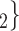 and
and 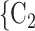 , C
, C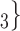 , have been co-nominated before, leading to joint contact popularity
, have been co-nominated before, leading to joint contact popularity  2/3 (the average number of co-nominations per pair of actors). Among the three unordered pairs in the set of possible contacts
2/3 (the average number of co-nominations per pair of actors). Among the three unordered pairs in the set of possible contacts 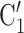 , C’
, C’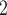 , C’
, C’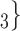 on the left, none has been co-nominated before, leading to joint contact popularity
on the left, none has been co-nominated before, leading to joint contact popularity  0. If joint contact popularity is associated with a positive parameter, then the set of contacts
0. If joint contact popularity is associated with a positive parameter, then the set of contacts 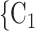 , C
, C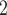 , C
, C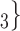 on the right would be more likely to be nominated as the set of contacts of the positive case P. Note that both sets received the same number of previous individual nominations (four each), so that individual contact popularity is equal to 4/3 for both sets.
on the right would be more likely to be nominated as the set of contacts of the positive case P. Note that both sets received the same number of previous individual nominations (four each), so that individual contact popularity is equal to 4/3 for both sets.
The reciprocation effect describes, briefly, the following scenario: if A mention B as a contact then B is more likely to mention A as a contact—if B is interviewed as a confirmed positive case. In Fig. 2.5, among the three ties (P, C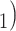 , (P, C
, (P, C and (P, C
and (P, C , in the hyperedge (P,
, in the hyperedge (P, 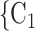 , C
, C , C
, C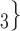 ), on the right, two are characterized by a past nomination in the reverse direction. (Note that both C
), on the right, two are characterized by a past nomination in the reverse direction. (Note that both C and C
and C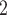 have elicited P as a contact in previous interviews.) Thus, the reciprocation is 2/3. Among the three ties (P, C’
have elicited P as a contact in previous interviews.) Thus, the reciprocation is 2/3. Among the three ties (P, C’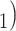 , (P, C’
, (P, C’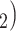 , and (P, C’
, and (P, C’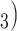 in the hyperedge (P,
in the hyperedge (P, 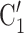 , C’
, C’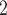 , C’
, C’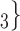 ), on the left, none characterized by a past nomination in the reverse direction. Thus, the reciprocation is 0. If reciprocation is associated with a positive parameter, then the set of contacts
), on the left, none characterized by a past nomination in the reverse direction. Thus, the reciprocation is 0. If reciprocation is associated with a positive parameter, then the set of contacts 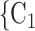 , C
, C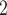 , C
, C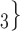 , on the right, would be more likely to be nominated as the set of contacts of the positive case P.
, on the right, would be more likely to be nominated as the set of contacts of the positive case P.
The contact activity effect exhibits the following scenario: if an actor A has already appeared as a positive case (sending out ties) then is there an increase in the likelihood of A appearing in a contact list of another interviewed confirmed positive case? In Fig. 2.6, the three contacts of the hyperedge 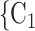 , C
, C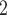 , C
, C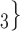 , on the right, have nominated in total four contacts in the past. Thus, the contact activity equals 4/3, which is also the average out-degree of these contacts. The three contacts of the hyperedge
, on the right, have nominated in total four contacts in the past. Thus, the contact activity equals 4/3, which is also the average out-degree of these contacts. The three contacts of the hyperedge 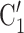 , C’
, C’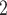 , C’
, C’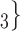 , on the left, have nominated in total one contact in the past. Thus, the contact activity is 1/3, which is also their average out-degree. If contact activity is associated with a positive parameter, then the set of contacts
, on the left, have nominated in total one contact in the past. Thus, the contact activity is 1/3, which is also their average out-degree. If contact activity is associated with a positive parameter, then the set of contacts 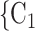 , C
, C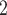 , C
, C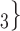 , on the right, would be more likely to be nominated than the set of contacts on the left. Note that, in contrast to reciprocation, for contact activity it does not matter whether the past nominations from the contacts targeted the source of the focal hyperedge or not.
, on the right, would be more likely to be nominated than the set of contacts on the left. Note that, in contrast to reciprocation, for contact activity it does not matter whether the past nominations from the contacts targeted the source of the focal hyperedge or not.
The nominations among contacts effect measures the ratio of previous referee-referral ties in the set of contacts 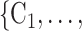 C
C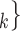 . In Fig. 2.7, all three of the three unordered pairs of contacts
. In Fig. 2.7, all three of the three unordered pairs of contacts 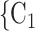 , C
, C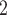 , C
, C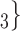 , on the right, have a past nomination tie. Thus, the nominations among contacts is 3/3
, on the right, have a past nomination tie. Thus, the nominations among contacts is 3/3 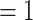 . Among the three unordered pairs of contacts
. Among the three unordered pairs of contacts 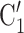 , C’
, C’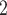 , C’
, C’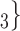 , on the left, only one, namely
, on the left, only one, namely 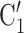 , C’
, C’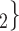 , has a past nomination tie. Thus, in this case the nominations among contacts effect is 1/3. If the effect is associated with a positive parameter, then the set of contacts on the right would be more likely to be nominated by P than the set of contacts on the left. The nominations among contacts effect tests whether an interviewed person is likely to nominate a previous positive case and some of her/his contacts.
, has a past nomination tie. Thus, in this case the nominations among contacts effect is 1/3. If the effect is associated with a positive parameter, then the set of contacts on the right would be more likely to be nominated by P than the set of contacts on the left. The nominations among contacts effect tests whether an interviewed person is likely to nominate a previous positive case and some of her/his contacts.
The shared referee effect measures previous co-nominations of the positive case P and some of her/his contacts C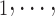 C
C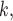 in the contact list of another interviewed positive case P’. In Fig. 2.8, among the three ties (P, C
in the contact list of another interviewed positive case P’. In Fig. 2.8, among the three ties (P, C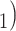 , (P, C
, (P, C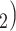 and (P, C
and (P, C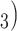 in the hyperedge (P,
in the hyperedge (P, 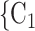 , C
, C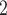 , C
, C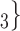 ) on the right, two are characterized by a past joint nomination from a third actor. (Note that both P and C
) on the right, two are characterized by a past joint nomination from a third actor. (Note that both P and C have been co-nominated by a common previous referee, and both P and C
have been co-nominated by a common previous referee, and both P and C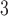 have been co-nominated by a common previous referee.) Thus, the shared referee effect equals
have been co-nominated by a common previous referee.) Thus, the shared referee effect equals 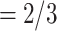 . Among the three ties (P, C’
. Among the three ties (P, C’ , (P, C’
, (P, C’ and (P, C’
and (P, C’ in the hyperedge (P,
in the hyperedge (P, 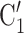 , C’
, C’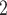 , C’
, C’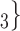 ) on the left, only one is characterized by a past co-nomination from a common referee. Thus, the shared referee effect is 1/3. If shared referee is associated with a positive parameter, then the set of contacts
) on the left, only one is characterized by a past co-nomination from a common referee. Thus, the shared referee effect is 1/3. If shared referee is associated with a positive parameter, then the set of contacts 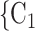 , C
, C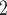 , C
, C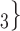 on the right would be more likely to be nominated as the set of contacts of the positive case P.
on the right would be more likely to be nominated as the set of contacts of the positive case P.
In general, RHEM explain the ‘relative risk’ of an event on a hyperedge h (P,
(P, 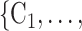 C
C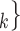 ), where P is a person that tested positive and C
), where P is a person that tested positive and C through C
through C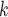 are
are 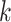 contacts mentioned by P. Relative risk (also relative hazard, relative intensity or relative event rate) refers to the factor by which an event on a hyperedge with the given specific explanatory variables is more likely than an event on a ‘average hyperedge’ (meaning a hyperedge hypothetically taking average values in all explanatory variables). In this article, we give standardized scores (estimates) for the explanatory variables, leading to the following exemplary interpretation. For instance, according to the most complex model reported below (‘combined’ model) a hyperedge that takes a value in abs_diff_age (absolute difference in age between the positive case and her/his contacts) which is by one standard deviation above average has a relative risk that is multiplied with exp(-0.36)
contacts mentioned by P. Relative risk (also relative hazard, relative intensity or relative event rate) refers to the factor by which an event on a hyperedge with the given specific explanatory variables is more likely than an event on a ‘average hyperedge’ (meaning a hyperedge hypothetically taking average values in all explanatory variables). In this article, we give standardized scores (estimates) for the explanatory variables, leading to the following exemplary interpretation. For instance, according to the most complex model reported below (‘combined’ model) a hyperedge that takes a value in abs_diff_age (absolute difference in age between the positive case and her/his contacts) which is by one standard deviation above average has a relative risk that is multiplied with exp(-0.36) 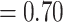 , which implies a decrease by 30%. A hyperedge that takes a value in abs_diff_sex which is by one standard deviation above average, has a relative risk that is multiplied with exp(0.13)
, which implies a decrease by 30%. A hyperedge that takes a value in abs_diff_sex which is by one standard deviation above average, has a relative risk that is multiplied with exp(0.13)  1.14, that is, an increase of 14%. In this article, we build three RHEM models: a RHEM purely with covariate effects (The ‘covariate model’ or Model 1), a RHEM purely based on network effects (the ‘network model’ or Model 2), and a RHEM with both types of effects combined (the ‘combined model’ or Model 3).
1.14, that is, an increase of 14%. In this article, we build three RHEM models: a RHEM purely with covariate effects (The ‘covariate model’ or Model 1), a RHEM purely based on network effects (the ‘network model’ or Model 2), and a RHEM with both types of effects combined (the ‘combined model’ or Model 3).
3. Results
In this study, we examine the spread of COVID-19 infections in Bucharest (Romania), from 1 August to 31 October 2020. We analyse real-world human-to-human transmission data. Particularly, we address contact-elicitation data wherein an infected patient (alternatively, a positive case, a referee) nominates her/his potential source(s) of infection (contacts, targets and referrals). We officially procured the information from local public health authorities. Our data consist of 19,713 unique nodes (individuals) embedded in 13,377 observed referee—referral (transmission) pairs. In our dataset, some people are only referees or referrals whereas others may be both positive cases as well as contacts. Namely, a person may have multiple statuses across different pairs: an individual may be a positive COVID-19 case (a referee) in some dyad(s), whilst, in other dyad(s) she may be a nominee (a contact or referral). We underscore that Romanian authorities collected the data in a backward contact tracing fashion: each patient was requested to nominate the potential source(s) for her/his infection (see Methods section for details).
Figure 3 provides an overall representation of the patterns detected in the disease transmission chains. These chains were reconstructed through inter-connecting the 13,377 pairs through common nodes (people). Figure 3(a) illustrates a referee-referral matrix, with the information arranged by age in the form of a contour plot. We kept in the visualization only those pairs with complete information on the age variable (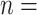 13,298, that is
13,298, that is 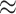 99% of the total number of 13,377 observed pairs). For 79 referee–referral pairs, age data were missing, either for the referee or for the referral. The contour plot marks particular patterns of transmission (the discoloured diagonals): the main diagonal of the matrix indicates homophily (the age of the referee and of the referral are very closed if not identical). Deviations above and below the main diagonal are indicative of heterophily (the age of the referee is higher (lower) than the age of the referral). The age distributions for the referees and referrals are also available as marginal histograms (dark red and dark, respectively). The age distributions have the following characteristics. For the referees: the mean age is 39.97 with S.E.
99% of the total number of 13,377 observed pairs). For 79 referee–referral pairs, age data were missing, either for the referee or for the referral. The contour plot marks particular patterns of transmission (the discoloured diagonals): the main diagonal of the matrix indicates homophily (the age of the referee and of the referral are very closed if not identical). Deviations above and below the main diagonal are indicative of heterophily (the age of the referee is higher (lower) than the age of the referral). The age distributions for the referees and referrals are also available as marginal histograms (dark red and dark, respectively). The age distributions have the following characteristics. For the referees: the mean age is 39.97 with S.E. 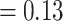 (
(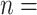 13,374, SD
13,374, SD 14.82, Med
14.82, Med 40, Min
40, Min 0, Max
0, Max  97, IQR
97, IQR  18, MAD
18, MAD  13.34, skewness
13.34, skewness  0.12, kurtosis
0.12, kurtosis  0.61, missing data
0.61, missing data  3). For the referrals: the mean age is 33.66 with S.E.
3). For the referrals: the mean age is 33.66 with S.E.  0.18 (
0.18 (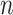
 13,301, SD
13,301, SD 21.02, Med
21.02, Med 34, Min
34, Min 0, Max
0, Max 95, IQR
95, IQR  34, MAD
34, MAD 25.20, skewness
25.20, skewness  0.22, kurtosis
0.22, kurtosis 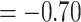 , missing data
, missing data 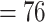 ).
).
Fig. 3.
Visualizations for the overall COVID-19 transmission patterns detected in the empirical data. (a) The contour plot is based on a referee-referral matrix. Individuals (referees and referrals) are arranged by their age. Colours in the plot illustrate the frequency of referee–referral nominations by age. Marginal histograms display age distributions for both referees and referrals (dark-red and red, respectively). (b) The bar plots show the frequency of referee-referral nominations by sex categories (females are indicated by green while males are indicated by red). Arrows designate who nominates whom as a disease origin. Moreover, it is illustrated the frequency of cases wherein the referral is female (male), irrespective of the referee’s sex (male, female or unknown). (c) The bar plots indicate the distribution of various types of pairs in the dataset. We also use three shapes to designate individuals embedded in the transmission dyads: triangles (referees), circles (referrals), and squares (brokers).
Figure 3(b) shows a bias in favour of sex related dis-assortative mixing (heterophily) in the contact-elicitation data. Out of 1,811 pairs, wherein covariate information for each node in a pair is available, 1,208 are mixed dyads (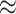 67%): female
67%): female  male (591 nominations) or male
male (591 nominations) or male  female (617). Pairs with full information on sex represent 13.5% of the total 13,377 pairs in the dataset. Overall, females are referrals in 1,006 cases and referees in 7,045. Further, males are referrals in 805 instances and referees in 6,332. Additionally, looking only at the dyads for which the sex of the referrals is missing, we unveil that females were the referees in 6,065 cases, while males in 5,501 situations.
female (617). Pairs with full information on sex represent 13.5% of the total 13,377 pairs in the dataset. Overall, females are referrals in 1,006 cases and referees in 7,045. Further, males are referrals in 805 instances and referees in 6,332. Additionally, looking only at the dyads for which the sex of the referrals is missing, we unveil that females were the referees in 6,065 cases, while males in 5,501 situations.
In Fig. 3(c), we report the distribution of various types of pairs in the dataset, given three categories vertices: referrals (people nominated as origin the infection), referees (COVID-19 confirmed positives), and brokers (people who appear in more than one pair, and who entail two statuses: both referrals and referees). There total number of 19,713 unique nodes are distributed across the three vertex categories in the following way: 13,818 referrals (node-level in-degree centrality spanning from one to four), 6,441 referees (node-level out-degree centrality spanning from 1 to 19), and 454 brokers (node-level degree centrality spanning from two to eight). We record four types of pairs: referee  referral (12,270 arcs, which corresponds to 91.7% of all observed ties), broker
referral (12,270 arcs, which corresponds to 91.7% of all observed ties), broker  referral (611 arcs i.e. 4.8%), referee
referral (611 arcs i.e. 4.8%), referee  broker (250 arcs i.e. 1.9%), and broker
broker (250 arcs i.e. 1.9%), and broker 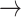 broker (246 arcs i.e. 1.8%). Joining the 13,377 pairs into transmission chains gives rise to a highly fragmented network (the connectedness degree is 0.00013; which is consonant with other similar network studies [50]). This sheer fragmentation is also visually illustrated in Fig. 3(c). The referee
broker (246 arcs i.e. 1.8%). Joining the 13,377 pairs into transmission chains gives rise to a highly fragmented network (the connectedness degree is 0.00013; which is consonant with other similar network studies [50]). This sheer fragmentation is also visually illustrated in Fig. 3(c). The referee 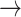 referral pairs account for 92% of all observed dyads. These specific pairs may reflect: isolated dyads (
referral pairs account for 92% of all observed dyads. These specific pairs may reflect: isolated dyads (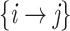 arcs that appear only once in the dataset), or dyads embedded in various larger polyadic structures (e.g. star networks in the form
arcs that appear only once in the dataset), or dyads embedded in various larger polyadic structures (e.g. star networks in the form 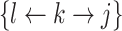 ).
).
Table 1 illustrates a contact–elicitation matrix that points to the nomination intensity across and within age groups. The most origins of infections are reported for the 35–44-year-old group (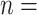 2,312; 17.3% of all nominations). Nearly half of the total contacts (referrals) include people aged 25 and 54 (
2,312; 17.3% of all nominations). Nearly half of the total contacts (referrals) include people aged 25 and 54 (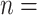 6,477; 48.5%). Conversely, with respect to the positive confirmed patients, we note: the largest category is aged 35–44 (
6,477; 48.5%). Conversely, with respect to the positive confirmed patients, we note: the largest category is aged 35–44 (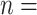 4,125; 30.8% of all referees), while people between 25 and 54 years amass 9,837 cases (73.5%). These results may suggest that adults were pivotal in the disease circulation within the investigated time window.
4,125; 30.8% of all referees), while people between 25 and 54 years amass 9,837 cases (73.5%). These results may suggest that adults were pivotal in the disease circulation within the investigated time window.
Table 1.
Infection spread between and within age-groups
| Age groups of referrals | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–6 | 7–13 | 14–18 | 19–24 | 25–34 | 35–44 | 45–54 | 55–64 | 65–74 | 75–84 | 85
|
NA | Row total | ||
| A. Absolute frequencies by referee count | ||||||||||||||
| Age | 0–6 | 30 | 20 | 2 | 4 | 56 | 84 | 12 | 18 | 12 | 1 | 1 | 2 | 242 |
| groups | 7–13 | 41 | 39 | 18 | 6 | 24 | 146 | 62 | 7 | 12 | 8 | 4 | 3 | 370 |
| of | 14–18 | 13 | 30 | 41 | 17 | 7 | 85 | 121 | 9 | 6 | 6 | 3 | 4 | 342 |
| referees | 19–24 | 25 | 10 | 36 | 177 | 127 | 61 | 254 | 44 | 19 | 12 | 2 | 1 | 768 |
| 25–34 | 564 | 100 | 29 | 138 | 1,042 | 328 | 287 | 268 | 63 | 15 | 4 | 19 | 2,857 | |
| 35–44 | 767 | 837 | 276 | 96 | 321 | 1,066 | 301 | 186 | 202 | 40 | 10 | 23 | 4,125 | |
| 45–54 | 116 | 313 | 340 | 312 | 230 | 273 | 844 | 185 | 96 | 97 | 34 | 15 | 2,855 | |
| 55–64 | 45 | 55 | 38 | 59 | 140 | 135 | 143 | 295 | 66 | 39 | 30 | 5 | 1,050 | |
| 65–74 | 28 | 35 | 21 | 12 | 38 | 110 | 80 | 51 | 123 | 19 | 13 | 3 | 533 | |
| 75–84 | 3 | 8 | 6 | 7 | 7 | 20 | 49 | 13 | 23 | 27 | 8 | 0 | 171 | |
85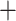
|
0 | 3 | 1 | 2 | 6 | 4 | 12 | 11 | 9 | 8 | 4 | 1 | 61 | |
| NA | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Column total | 1,632 | 1,450 | 809 | 830 | 1,998 | 2,312 | 2,167 | 1,087 | 631 | 272 | 113 | 76 | 13,377 | |
| B. Absolute frequencies by referee count | ||||||||||||||
| Age | 0–6 | 12.4% | 8.3% | 0.8% | 1.7% | 23.1% | 34.7% | 5.0% | 7.4% | 5.0% | 0.4% | 0.4% | 0.8% | 100.0% |
| groups | 7–13 | 11.1% | 10.5% | 4.9% | 1.6% | 6.5% | 39.5% | 16.8% | 1.9% | 3.2% | 2.2% | 1.1% | 0.8% | 100.0% |
| of | 14–18 | 3.8% | 8.8% | 12.0% | 5.0% | 2.0% | 24.9% | 35.4% | 2.6% | 1.8% | 1.8% | 0.9% | 1.2% | 100.0% |
| referees | 19–24 | 3.3% | 1.3% | 4.7% | 23.0% | 16.5% | 7.9% | 33.1% | 5.7% | 2.5% | 1.6% | 0.3% | 0.1% | 100.0% |
| 25–34 | 19.7% | 3.5% | 1.0% | 4.8% | 36.5% | 11.5% | 10.0% | 9.4% | 2.2% | 0.5% | 0.1% | 0.7% | 100.0% | |
| 35–44 | 18.6% | 20.3% | 6.7% | 2.3% | 7.8% | 25.8% | 7.3% | 4.5% | 4.9% | 1.0% | 0.2% | 0.6% | 100.0% | |
| 45–54 | 4.1% | 11.0% | 11.9% | 10.9% | 8.1% | 9.6% | 29.6% | 6.5% | 3.4% | 3.4% | 1.2% | 0.5% | 100.0% | |
| 55–64 | 4.3% | 5.2% | 3.6% | 5.6% | 13.3% | 12.9% | 13.6% | 28.1% | 6.3% | 3.7% | 2.9% | 0.5% | 100.0% | |
| 65–74 | 5.3% | 6.6% | 3.9% | 2.3% | 7.1% | 20.6% | 15.0% | 9.6% | 23.1% | 3.6% | 2.4% | 0.6% | 100.0% | |
| 75–84 | 1.8% | 4.7% | 3.5% | 4.1% | 4.1% | 11.7% | 28.7% | 7.6% | 13.5% | 15.8% | 4.7% | 0.0% | 100.0% | |
85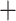
|
0.0% | 4.9% | 1.6% | 3.3% | 9.8% | 6.6% | 19.7% | 18.0% | 14.8% | 13.1% | 6.6% | 1.6% | 100.0% | |
| NA | 0.0% | 0.0% | 33.3% | 0.0% | 0.0% | 0.0% | 66.7% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | |
| Column total | 12.2% | 10.8% | 6.0% | 6.2% | 14.9% | 17.3% | 16.2% | 8.1% | 4.7% | 2.0% | 0.8% | 0.6% | 100.0% | |
Table 2 reports correlation, covariance and standard deviations. We note that correlation among explanatory variables is generally small (between 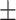 0.2). Table 3 presents parameter estimates of relational hyperevent models explaining the relative risk that a confirmed positive case nominates a set of actors as her/his close contacts. Comparing the model fit (AIC; smaller AIC points to better model fit), we find that the ‘network effects’ (Model 2) improve model fit much more than the ‘covariate effects’ of age and sex (Model 1). The best-fitting model is the joint model including covariate and network effects (Model 3). However, the difference in model fit between the covariate-only model (Model 1) and the joint model (Model 3) is huge while the difference in model fit between the network only model (Model 2) and the joint model is much smaller. Note however that the differences in parameters (values, signs, and significance levels) between the joint model and the two sub-models are rather small. Thus, the covariates and network statistics seem to model orthogonal effects that are hardly influencing each other. Below we provide a quantitative discussion of all findings.
0.2). Table 3 presents parameter estimates of relational hyperevent models explaining the relative risk that a confirmed positive case nominates a set of actors as her/his close contacts. Comparing the model fit (AIC; smaller AIC points to better model fit), we find that the ‘network effects’ (Model 2) improve model fit much more than the ‘covariate effects’ of age and sex (Model 1). The best-fitting model is the joint model including covariate and network effects (Model 3). However, the difference in model fit between the covariate-only model (Model 1) and the joint model (Model 3) is huge while the difference in model fit between the network only model (Model 2) and the joint model is much smaller. Note however that the differences in parameters (values, signs, and significance levels) between the joint model and the two sub-models are rather small. Thus, the covariates and network statistics seem to model orthogonal effects that are hardly influencing each other. Below we provide a quantitative discussion of all findings.
Table 2.
Correlation (above the diagonal), standard deviation (on the diagonal; in bold font), and covariance (below the diagonal) of all explanatory variables used in our models. Note: all variables are standardized (divided by their standard deviation) before estimating the models to yield standardized parameters. The table below reports the standard deviation and covariance of the unstandardized variables. Labels refer to: age homophily (diff.age), average age of contacts (avg.age), sex homophily (diff.sex), average sex of contacts (avg.sex), individual contact popularity (ind.cont.pop), joint contact popularity (joint.cont.pop), reciprocity (recip), contact activity (cont.act), nominations among contacts (nominate.cont), and shared referee (shared.ref)
| ind.cont | joint.cont | nominate | shared | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| diff.age | avg.age | diff.sex | avg.sex | pop | pop | recip | cont.act | cont | ref | |
| diff.age |
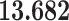
|
 0.139
0.139 |
0.000 | 0.000 | 0.072 | 0.001 | 0.000 |
 0.085
0.085 |
0.000 | 0.001 |
| avg.age |
 32.421
32.421 |
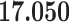
|
0.000 | 0.007 |
 0.051
0.051 |
 0.001
0.001 |
0.001 | 0.074 | 0.000 | 0.000 |
| diff.sex | 0.001 | 0.000 |
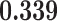
|
 0.055
0.055 |
0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.001 |
| avg.sex | 0.001 | 0.041 |
 0.006
0.006 |
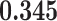
|
0.007 | 0.000 |
 0.001
0.001 |
 0.004
0.004 |
 0.001
0.001 |
 0.001
0.001 |
| ind.cont.pop | 0.416 |
 0.37
0.37 |
0.000 | 0.001 |
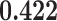
|
0.006 |
 0.002
0.002 |
 0.193
0.193 |
0.004 | 0.003 |
| joint.cont.pop | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
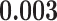
|
0.009 |
 0.001
0.001 |
0.074 | 0.031 |
| recip | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
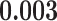
|
0.006 | 0.104 | 0.154 |
| cont.act |
 0.447
0.447 |
0.487 | 0.000 |
 0.001
0.001 |
 0.031
0.031 |
0.000 | 0.000 |
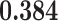
|
0.005 | 0.000 |
| nominate.cont | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
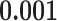
|
0.143 |
| shared.ref | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
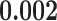
|
Table 3.
Relational hyperevents model estimates
| Covariate model (Model 1) | |||||
|---|---|---|---|---|---|
| coef | exp(coef) | S.E.(coef) | z | Pr(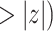
|
|
| Age difference | –0.34639 | 0.70724 | 0.01528 | –22.672 |
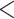 2e
2e 16 16
|
| Average age of contacts | –0.13134 | 0.87692 | 0.0139 | –9.448 |
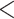 2e
2e 16 16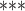
|
| Sex difference | 0.12819 | 1.13677 | 0.0139 | 9.221 |
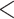 2e
2e 16 16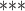
|
| Average sex of contacts | 0.06132 | 1.06324 | 0.02775 | 2.210 | 0.0271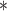
|
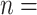 7,547,892; number of events
7,547,892; number of events  7,587. 7,587. | |||||
AIC  104,026.86 104,026.86 | |||||
Concordance  0.58 (S.E. 0.58 (S.E.  0.003); Likelihood ratio test 0.003); Likelihood ratio test  660.8 (df 660.8 (df  4) 4) 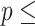 2e-16; Wald test 2e-16; Wald test  608.5 608.5 | |||||
(df  4) 4) 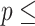 2e-16; Score (logrank) test 2e-16; Score (logrank) test  614.7 (df 614.7 (df  4) 4) 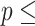 2e-16. 2e-16. | |||||
| Network model (Model 2) | |||||
| coef | exp(coef) | S.E.(coef) | z | Pr(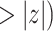
|
|
| Individual contact popularity | –5.291756 | 0.005033 | 0.117836 | –44.91 |
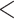 2e
2e 16 16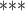
|
| Joint contact popularity | 0.040595 | 1.04143 | 0.002078 | 19.54 |
 2e
2e 16 16
|
| Reciprocation | 0.058597 | 1.060347 | 0.002201 | 26.62 |
 2e
2e 16 16
|
| Contact activity | –3.387140 | 0.033805 | 0.079126 | –42.81 |
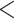 2e
2e 16 16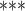
|
| Nominations among contacts | 0.051087 | 1.052415 | 0.00188 | 27.18 |
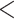 2e
2e 16 16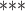
|
| Shared referee | 0.044245 | 1.045238 | 0.001319 | 33.53 |
 2e
2e 16 16
|
 7,547,892; number of events
7,547,892; number of events  7,587. 7,587. | |||||
AIC  854.239. 854.239. | |||||
Concordance  0.797 (S.E. 0.797 (S.E.  0.002); Likelihood ratio test 0.002); Likelihood ratio test  22,837 (df 22,837 (df  6) 6)  2e-16; Wald test 2e-16; Wald test  4,342 (df 4,342 (df  6) 6) 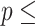 2e-16; Score (logrank) test 2e-16; Score (logrank) test  89,419 (df 89,419 (df  6) 6) 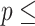 2e-16. 2e-16. | |||||
| Combined model (Model 3) | |||||
| coef | exp(coef) | S.E.(coef) | z | Pr(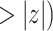
|
|
| Age difference | –0.360909 | 0.697043 | 0.015515 | –23.263 |
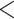 2e
2e 16 16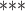
|
| Average age of contacts | –0.114654 | 0.891675 | 0.014062 | –8.153 | 3.54E 16 16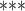
|
| Sex difference | 0.126829 | 1.135223 | 0.014319 | 8.857 |
 2e
2e 16 16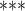
|
| Average sex of contacts | 0.079576 | 1.082828 | 0.028581 | 2.784 | 0.00537
|
| Individual contact popularity | –5.299928 | 0.004992 | 0.118003 | –44.914 |
 2e
2e 16 16
|
| Joint contact popularity | 0.041241 | 1.042103 | 0.00207 | 19.927 |
 2e
2e 16 16
|
| Reciprocation | 0.058644 | 1.060398 | 0.002219 | 26.434 |
 2e
2e 16 16
|
| Contact activity | –3.422744 | 0.032623 | 0.079374 | –43.122 |
 2e
2e 16 16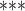
|
| Nominations among contacts | 0.050917 | 1.052235 | 0.001932 | 26.354 |
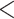 2e
2e 16 16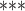
|
| Shared referee | 0.044550 | 1.045557 | 0.001334 | 33.398 |
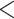 2e
2e 16 16
|
 7,547,892; number of events
7,547,892; number of events  7,587. 7,587. | |||||
AIC  81,181.108. 81,181.108. | |||||
Concordance  0.837 (S.E. 0.837 (S.E.  0.002); Likelihood ratio test 0.002); Likelihood ratio test  23,519 (df 23,519 (df  10) 10)  2e-16; Wald test 2e-16; Wald test  4,913 4,913 | |||||
(df  10) 10)  2e-16; Score (logrank) test 2e-16; Score (logrank) test  90023 (df 90023 (df  10) 10) 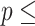 2e-16. 2e-16. | |||||
Signif. codes: *** 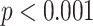 , **
, ** 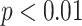 , *
, * 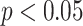 .
.
Age homophily. We find that age difference effect is associated with a significantly negative parameter ( 0.346, in Model 1, and
0.346, in Model 1, and  0.361, in Model 3). Thus, the larger the average difference in age between the confirmed positive case P and a possible set of contacts
0.361, in Model 3). Thus, the larger the average difference in age between the confirmed positive case P and a possible set of contacts 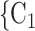 , C
, C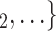 , the less likely P nominates
, the less likely P nominates 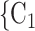 , C
, C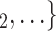 as her/his set of contacts. This points to an age-homophily effect: positive cases are more likely to nominate contacts of similar age. Regarding effect size, we find that if the average age difference between P and
as her/his set of contacts. This points to an age-homophily effect: positive cases are more likely to nominate contacts of similar age. Regarding effect size, we find that if the average age difference between P and 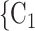 , C
, C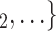 increases by one standard deviation (
increases by one standard deviation ( 13.7 years), then the relative risk that P nominates
13.7 years), then the relative risk that P nominates 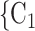 , C
, C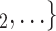 as her/his set of contacts gets multiplied by the factor exp(
as her/his set of contacts gets multiplied by the factor exp( 0.346)
0.346) 0.708, that is, the relative risk decreases by more than 29%.
0.708, that is, the relative risk decreases by more than 29%.
Average age of contacts. We find that the average age of contacts is associated with a significantly negative parameter ( 0.131, in Model 1, and
0.131, in Model 1, and  0.115, in Model 3). Thus, the older the average age of the possible contacts
0.115, in Model 3). Thus, the older the average age of the possible contacts 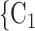 , C
, C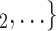 , the less likely a positive case P nominates
, the less likely a positive case P nominates 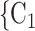 , C
, C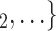 as her/his set of contacts. From the other point of view, positive cases have a tendency to nominate younger contacts. If the average age of
as her/his set of contacts. From the other point of view, positive cases have a tendency to nominate younger contacts. If the average age of 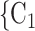 , C
, C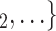 decreases by one standard deviation (
decreases by one standard deviation ( 17.1 years), then the relative risk that
17.1 years), then the relative risk that 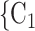 , C
, C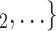 is nominated as a set of contacts gets multiplied by exp(0.131)
is nominated as a set of contacts gets multiplied by exp(0.131)  1.14, that is it increases by 14%.
1.14, that is it increases by 14%.
Sex homophily. We find that the sex difference effect is associated with a significantly positive parameter (0.128, in Model 1, and 0.127, in Model 3). Thus, the larger the average difference in sex between the confirmed positive case P and a possible set of contacts 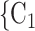 , C
, C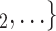 , the more likely P nominates
, the more likely P nominates 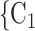 , C
, C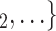 as her/his set of contacts. This points to a sex-heterophily effect: positive cases are more likely to nominate contacts of the opposite sex. Regarding effect size we find that if the average sex difference between P and
as her/his set of contacts. This points to a sex-heterophily effect: positive cases are more likely to nominate contacts of the opposite sex. Regarding effect size we find that if the average sex difference between P and 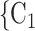 , C
, C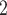 ,
, 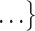 increases by one standard deviation (
increases by one standard deviation ( 0.34; note that this corresponds to a swap of sex of 34% of the contacts towards the sex opposite to P; for instance, if P is female and one third of the contacts
0.34; note that this corresponds to a swap of sex of 34% of the contacts towards the sex opposite to P; for instance, if P is female and one third of the contacts 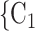 , C
, C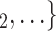 swap their sex from female to male, then the average sex difference increases by 0.33, about one standard deviation), then the relative risk that P nominates
swap their sex from female to male, then the average sex difference increases by 0.33, about one standard deviation), then the relative risk that P nominates 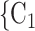 , C
, C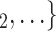 as her/his set of contacts gets multiplied by the factor exp(0.128)
as her/his set of contacts gets multiplied by the factor exp(0.128) 1.14, that is, the relative risk increases by 14%.
1.14, that is, the relative risk increases by 14%.
Average sex of contacts. We find that the average sex of contacts effect is associated with a significantly positive parameter (0.061, in Model 1, and 0.080, in Model 3). Thus, the higher the ratio of females (recall: male  1 and female
1 and female  2) in the set of possible contacts
2) in the set of possible contacts 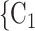 , C
, C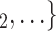 , the more likely a positive case P nominates
, the more likely a positive case P nominates 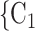 , C
, C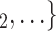 as her/his set of contacts. If the ratio of females in
as her/his set of contacts. If the ratio of females in 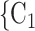 , C
, C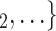 increases by one standard deviation (
increases by one standard deviation ( 0.35, that is, by 35%), then the relative risk that
0.35, that is, by 35%), then the relative risk that 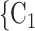 , C
, C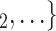 is nominated as a set of contacts gets multiplied by exp(0.061)
is nominated as a set of contacts gets multiplied by exp(0.061)  1.06, that is, it increases by 6%.
1.06, that is, it increases by 6%.
Next, we will discuss the ‘network effects’, in a more concise manner. The general way to compute hazard ratios applies to all effects: if variable 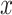 is associated with a parameter equal to beta, then an instance (set of contacts) with
is associated with a parameter equal to beta, then an instance (set of contacts) with 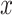 one standard deviation above average has the relative hazard to be nominated as a set of contacts multiplied by exp(beta). If beta is positive, then exp(beta) is larger than one, implying an increased hazard; if beta is negative, then exp(beta) is smaller than one, implying a decreased hazard.
one standard deviation above average has the relative hazard to be nominated as a set of contacts multiplied by exp(beta). If beta is positive, then exp(beta) is larger than one, implying an increased hazard; if beta is negative, then exp(beta) is smaller than one, implying a decreased hazard.
Individual contact popularity. We find that the parameter associated with the individual contact popularity is significantly (and strongly) negative ( 5.29, in Model 2, and
5.29, in Model 2, and  5.30, in Model 3). This implies that the more often the possible contacts
5.30, in Model 3). This implies that the more often the possible contacts 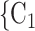 , C
, C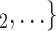 have previously been nominated individually by previous positive cases, the lower the probability that
have previously been nominated individually by previous positive cases, the lower the probability that 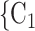 , C
, C is nominated as the set of contacts of the current positive case. We discussed in the Methods section that this finding is due to an aspect in the definition of our data: each actor is guaranteed to appear at least once either as a referee or as a referral. Once an actor has participated in one event (for instance, if the actor has been nominated as a contact), the probability that the same actor participates in another event decreases sharply. Indeed, only a small ratio of all actors have degree larger than one.
is nominated as the set of contacts of the current positive case. We discussed in the Methods section that this finding is due to an aspect in the definition of our data: each actor is guaranteed to appear at least once either as a referee or as a referral. Once an actor has participated in one event (for instance, if the actor has been nominated as a contact), the probability that the same actor participates in another event decreases sharply. Indeed, only a small ratio of all actors have degree larger than one.
Joint contact popularity. We find that the parameter associated with joint contact popularity is significantly positive (0.04, in Models 2 and 3). This means that the more pairs of actors in a given set of possible contacts  , C
, C have previously been co-nominated by a previous positive case, the larger the probability that the current positive case nominates
have previously been co-nominated by a previous positive case, the larger the probability that the current positive case nominates  , C
, C as her/his set of contacts. This effect is a typical network effect, revealing unobserved ‘closeness’ of actors: if, say, C
as her/his set of contacts. This effect is a typical network effect, revealing unobserved ‘closeness’ of actors: if, say, C and C
and C have been co-nominated by some positive case, it is likely that C
have been co-nominated by some positive case, it is likely that C and C
and C are ‘socially close’ in some way which, in turn, increases the probability that C
are ‘socially close’ in some way which, in turn, increases the probability that C and C
and C are co-nominated again.
are co-nominated again.
Reciprocation. We find that the parameter associated with reciprocation is significantly positive (0.06, in Models 2 and 3). This means, the more actors from a possible set of contacts 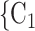 , C
, C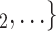 have nominated the current positive case P in a previous interview by health authorities, the larger the probability that P nominates
have nominated the current positive case P in a previous interview by health authorities, the larger the probability that P nominates 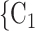 , C
, C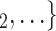 as her/his set of contacts. In the same way as joint contact popularity, reciprocation reveals an effect that social closeness correlates with contact-elicitation probabilities.
as her/his set of contacts. In the same way as joint contact popularity, reciprocation reveals an effect that social closeness correlates with contact-elicitation probabilities.
Contact activity. We find that the parameter associated with the contact activity is significantly (and strongly) negative (-3.39, in Model 2, and -3.42, in Model 3). This implies that the more contacts have been nominated by the actors from a possible set of contacts 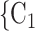 , C
, C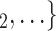 in previous interviews, the lower the probability that
in previous interviews, the lower the probability that 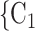 , C
, C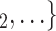 is nominated as the set of contacts of the current positive case. The interpretation of this finding is similar to individual contact popularity: each actor is guaranteed to appear at least once either as a referee or as a referral. Once an actor has participated in one event (for instance, if the actor has been interviewed as a positive case), the probability that the same actor participates in another event decreases sharply. Indeed, only a small ratio of all actors have degree larger than one.
is nominated as the set of contacts of the current positive case. The interpretation of this finding is similar to individual contact popularity: each actor is guaranteed to appear at least once either as a referee or as a referral. Once an actor has participated in one event (for instance, if the actor has been interviewed as a positive case), the probability that the same actor participates in another event decreases sharply. Indeed, only a small ratio of all actors have degree larger than one.
Nominations among contacts. We find that the parameter associated with ‘nominations among contacts’ is significantly positive (0.05, in Models 2 and 3). This means that the more pairs of actors in a given set of possible contacts 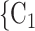 , C
, C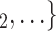 are linked by previous contact nominations, in the sense that one of the actors has nominated the other in a previous interview, the larger the probability that the current positive case nominates
are linked by previous contact nominations, in the sense that one of the actors has nominated the other in a previous interview, the larger the probability that the current positive case nominates 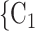 , C
, C as her/his set of contacts. In the same way as joint contact popularity and reciprocation, ‘nominations among contacts’ reveals an effect that social closeness correlates with contact-elicitation probabilities.
as her/his set of contacts. In the same way as joint contact popularity and reciprocation, ‘nominations among contacts’ reveals an effect that social closeness correlates with contact-elicitation probabilities.
Shared referee. We find that the parameter associated with ‘shared referee’ is significantly positive (0.04, in Model 2, and 0.05, in Model 3). This means that the more actors in a given set of possible contacts 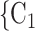 , C
, C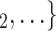 have been co-nominated with the current positive case P by some previously interviewed positive case, the larger the probability that P nominates
have been co-nominated with the current positive case P by some previously interviewed positive case, the larger the probability that P nominates 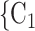 , C
, C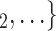 as her/his set of contacts. In the same way as joint contact popularity, reciprocation and nominations among contacts, shared referee reveals an effect that social closeness correlates with contact-elicitation probabilities.
as her/his set of contacts. In the same way as joint contact popularity, reciprocation and nominations among contacts, shared referee reveals an effect that social closeness correlates with contact-elicitation probabilities.
4. Discussion
We provide evidence that age is an important variable for predicting and understanding the spread of the COVID-19 disease. Our results suggest that virus transmission is patterned by age. The relative risk of infection decreases (by 29%, 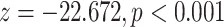 ) as the average difference between a positive case and her/his set of contacts increases (age-homophily). Concomitantly, it is noteworthy that the risk of infection increases (by 14%,
) as the average difference between a positive case and her/his set of contacts increases (age-homophily). Concomitantly, it is noteworthy that the risk of infection increases (by 14%, 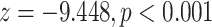 ) as the average age of a patient’s contacts decreases. In other words, infected people have the tendency to nominate younger contacts. These findings emphasize that peer groups of similar age as well as younger people have a sheer importance in the COVID-19 spreading. Similar results are also reported for transmission network data collected during the early outbreak in Japan [50]. We control the age covariate for sex and network effects. We find that the infected people are more likely to nominate contacts of the opposite sex (sex heterophily) and that the relative risk of infection increases (by 6%,
) as the average age of a patient’s contacts decreases. In other words, infected people have the tendency to nominate younger contacts. These findings emphasize that peer groups of similar age as well as younger people have a sheer importance in the COVID-19 spreading. Similar results are also reported for transmission network data collected during the early outbreak in Japan [50]. We control the age covariate for sex and network effects. We find that the infected people are more likely to nominate contacts of the opposite sex (sex heterophily) and that the relative risk of infection increases (by 6%, 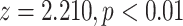 ) as the ratio of female contacts increases.
) as the ratio of female contacts increases.
We also observe that network effects are strong and allow for understanding the role of structure in the dynamics of virus transmission. Notably, we get two different kinds of network effects. First, the two degree statistics (individual contact popularity and contact activity) are found negative due to the property of the data construction (rather than the underlying virus transmission networks). That is actors are only included in the network if they participate in at least one event either as a referee or as a referral. Second, all other network effects are positive and reveal that pairs of actors that are linked by previous contact-elicitation events in any way or direction are likely to be ‘socially close’ which, in turn, increases their probability to be linked again in a future contact-elicitation event.
Descriptive statistics on the spread of the virus indicate that people aged 35 – 44 are the most important group in the diffusion of the disease. Additionally, young and middle-aged people (25–34, 35–44 and 45–54 year-old) account for nearly three quarters of the nominated contacts. Similar work shows, as of October 2020, in the USA, that adults aged 20–34 and 35–49 were the age groups with sustained SARS-COV-2 transmission (the majority of infections were reported to originate from these categories) [38]. Also, young adults (20 – 29 year-old) were shown to have contributed most to the community spread in southern United States, during June- August 2020 (this group accounted for more than 20% of all cases) [51].
The patterns we observe in the disease transmission may have been sustained by a mixture of local context related factors: NPIs relaxation (e.g. opening of public spaces such as restaurants, bars, cinema, gardens and parks etc.), increased domestic mobility and international travelling due to vacations (e.g. August and September are vacation months in Romania). Available evidence in the literature [39] indicates households, workplaces and public spaces to facilitate peer infections for people aged 23–44, and 45–64 year-old. We should also retain households as important conduits for conveying intra-family infections [50]—presumably, in our case, from spouse to spouse (sex heterophily), and from siblings to parents.
Our results should be regarded in the context of some limitations. Firstly, we build our analysis on official information collected by public health authorities in a backward contact tracing data fashion. Notably, this method possesses inherent caveats as it heavily relies on the respondents’ ability to accurately recollect past information. It has already been illustrated that network cognitions are affected by situation and circumstance [52, 53]. Additionally, social contact elicitation has been shown to held various reporting biases, such as masking, the tendency to nominate similar alters, or variation in the volume of the referrals due to respondents’ the cooperativeness [54]. Secondly, our findings provide only part evidence on the viral transmission, as we focused on people’s social interactions at a limited time window (three months). However, our results bring forth the heterogeneity in the circulation of the disease. Moreover, our study findings generalize to populations with similar age distribution and similar cohabitation behaviour: similar household size, age distribution in households etc.
COVID-19 pandemic is currently ongoing. Since its onset, valuable knowledge on the disease spread has cumulated at a rapid pace [6]. Still, many aspects with regard to SARS-COV-2 transmission remain to be unveiled. In this guise, future work is needed to fully comprehend the way in which the network structure of real-world contact patterns, the socio-demographic identifiers (e.g. occupation, economic activity, education, mobility profile, etc.), and the physical contexts (households, schools, universities, workplaces, etc.) interplay. In Bucharest, young and middle-age adults may be at risk for exposure to the disease, given their presence in large shares in frontline occupations and exposed economic activities (retail stores, entertainment, restaurants, bars etc.). Analysing the mixture of interaction patterns and economic activities may prove useful to understand the virus circulation as well as the efficiency of virus local campaign. Also, ascertaining the role that different age groups have in the diffusion of the disease may come as an essential input into assessing the impact of mass vaccination. The scarce current evidence is geographically limited, heterogeneous in terms of the employed research designs, and rather reflective of the early stage of the pandemic. Our results may inform epidemic spreading and vaccination models on social networks, in particular towards a better customization to real-world individual behaviour [55]. Additionally, much work remains to be done in assessing the validity and accuracy of the COVID-19 real world data available for analysis. For instance, the factors determining the efficacy of contact tracing (either backward or forward) has not been fully understood [18].
In sum, our article contributes to the coalescing literature on the role that age plays in patterning the circulation of the COVID-19 disease. We also point out to the age groups which may be essential for vaccination given their role in the transmission. Additionally, our findings may be informative for authorities in their efforts to better control the current epidemiological context as well as future COVID-19 waves [56, 57].
Acknowledgements
We are grateful to the Romanian Ministry of Health, the Department of Public Health Bucharest, and the Rector of the University of Bucharest (Prof. Marian Preda) for the support provided for this study.
Contributor Information
Marian-Gabriel Hâncean, Department of Sociology, University of Bucharest, Bucharest, Panduri 90-92, 050663, Romania.
Jürgen Lerner, Department of Computer and Information Science, University of Konstanz, 78457, Konstanz, Germany.
Matjaž Perc, Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška cesta 160, 2000 Maribor, Slovenia, Department of Medical Research, China Medical University Hospital, China Medical University, Taichung 404332, Taiwan, Alma Mater Europaea, Slovenska ulica 17, 2000 Maribor, Slovenia and Complexity Science Hub Vienna, Josefstädterstraße 39, 1080 Vienna, Austria.
Maria Cristina Ghiţă, Department of Sociology, University of Bucharest, Bucharest, Panduri 90-92, 050663, Romania.
David-Andrei Bunaciu, Department of Sociology, University of Bucharest, Bucharest, Panduri 90-92, 050663, Romania.
Adelina Alexandra Stoica, Department of Sociology, University of Bucharest, Bucharest, Panduri 90-92, 050663, Romania.
Bianca-Elena Mihăilă, Department of Sociology, University of Bucharest, Bucharest, Panduri 90-92, 050663, Romania.
Funding
Executive Unit for Financing Higher Education, Research, Development and Innovation (UEFISCDI) (PN-III-P4-ID-PCE-2020-2828 to M.-G.H.); Deutsche Forschungsgemeinschaft (DFG) (321869138 to J.L.); and Slovenian Research Agency (P1-0403 and J1-2457 to M.P.).
References
- 1. Hâncean, M.-G., Slavinec, M. & Perc, M. (2021) The impact of human mobility networks on the global spread of COVID-19. J. Complex Netw., 8, cnaa041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Dignum, F. et al. (2020) Analysing the combined health, social and economic impacts of the coronanvirus pandemic using agent-based social simulation. Minds Mach., 30, 177–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Askitas, N., Tatsiramos, K. & Verheyden, B. (2021) Estimating worldwide effects of non-pharmaceutical interventions on COVID-19 incidence and population mobility patterns using a multiple-event study. Sci. Rep., 11, 1972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Zhang, J. et al. (2020) Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science, 368, 1481–1486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.WORLD HEALTH ORGANIZATION (2020) Coronavirus disease (COVID-19): how is it transmitted? https://www.who.int/news-room/q-a-detail/coronavirus-disease-covid-19-how-is-it-transmitted (last accessed 14July2021). [Google Scholar]
- 6. Estrada, E. (2020) COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep., 869, 1–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Colizza, V., Barrat, A., Barthelemy, M., Valleron, A.-J. & Vespignani, A. (2007) Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Med., 4, e13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Rivera, M. T., Soderstrom, S. B. & Uzzi, B. (2010) Dynamics of dyads in social networks: assortative, relational, and proximity mechanisms. Annu. Rev. Sociol., 36, 91–115. [Google Scholar]
- 9. Feld, S. L. (1981) The focused organization of social ties. Am. J. Sociol., 86, 1015–1035. [Google Scholar]
- 10. Newman, M. E. J. (2002) Spread of epidemic disease on networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys., 66, 16128. [DOI] [PubMed] [Google Scholar]
- 11. Ventresca, M. & Aleman, D. (2013) Evaluation of strategies to mitigate contagion spread using social network characteristics. Soc. Netw., 35, 75–88. [Google Scholar]
- 12. Watts, D. J. (1999) Networks, dynamics, and the small-world phenomenon. Am. J. Sociol., 105, 493–527. [Google Scholar]
- 13. Barabási, A.-L. & Albert, R. (1999) Emergence of scaling in random networks. Science, 286, 509 – 512. [DOI] [PubMed] [Google Scholar]
- 14. Wasserman, S. & Faust, K. (1994) Social Network Analysis: Methods and Applications. Structural Analysis in the Social Sciences. Cambridge: Cambridge University Press, pp. 3 - 27. [Google Scholar]
- 15. Jo, W., Chang, D., You, M. & Ghim, G.-H. (2021) A social network analysis of the spread of COVID-19 in South Korea and policy implications. Sci. Rep., 11, 8581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Saraswathi, S., Mukhopadhyay, A., Shah, H. & Ranganath, T. S. (2020) Social network analysis of COVID-19 transmission in Karnataka, India. Epidemiol. Infect., 148, e230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Nagarajan, K., Muniyandi, M., Palani, B. & Sellappan, S. (2020) Social network analysis methods for exploring SARS-CoV-2 contact tracing data. BMC Med. Res. Methodol., 20, 233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kojaku, S., Hébert-Dufresne, L., Mones, E., Lehmann, S. & Ahn, Y. Y. (2021) The effectiveness of backward contact tracing in networks. Nat. Phys., 17, 652–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Cheng, S., Arcucci, R., Pain, C. C. & Guo, Y.-K. (2021) Optimal vaccination strategies for COVID-19 based on dynamical social networks with real-time updating. medRxiv, Available at: https://www.medrxiv.org/content/10.1101/2021.03.11.21253356v1 (Accessed: 14July2021). Doi: 10.1101/2021.03.11.21253356. pp. 1–24. [DOI] [Google Scholar]
- 20. Markoviè, R., Šterk, M., Marhl, M., Perc, M. & Gosak, M. (2021) Socio-demographic and health factors drive the epidemic progression and should guide vaccination strategies for best COVID-19 containment. Results Phys., 26, 104433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gaviria, M. & Kilic, B. (2021) A network analysis of COVID-19 mRNA vaccine patents. Nat. Biotechnol., 39, 546–548. [DOI] [PubMed] [Google Scholar]
- 22. Block, P. et al. (2020) Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav., 4, 588–596. [DOI] [PubMed] [Google Scholar]
- 23. Mossong, J. et al. (2008) Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med., 5, e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Li, K., Wei, Z. & Cong, R. (2019) Sentiment contagion dilutes prisoner’s dilemmas on social networks. EPL, 128, 38002. [Google Scholar]
- 25. Liu, L., Chen, X & Szolnoki, A. (2019) Evolutionary dynamics of cooperation in a population with probabilistic corrupt enforcers and violators. Math. Models Methods Appl. Sci, 29, 2127 – 2149. [Google Scholar]
- 26. Li, K., Mao, Y., Wei, Z. & Cong, R. (2021) Pool-rewarding in N-person snowdrift game. Chaos Soliton Fract., 143, 110591. [Google Scholar]
- 27. McPherson, M., Smith-Lovin, L. & Cook, J. M. (2001) Birds of a feather: homophily in social networks. Annu. Rev. Sociol., 27, 415–444. [Google Scholar]
- 28. Duh, M., Gosak, M., Slavinec, M. & Perc, M. (2019) Assortativity provides a narrow margin for enhanced cooperation on multilayer networks. New J. Phys., 21, 123016. [Google Scholar]
- 29. Barranco, O., Lozares, C. & Muntanyola-Saura, D. (2019) Heterophily in social groups formation: a social network analysis. Qual. Quant., 53, 599–619. [Google Scholar]
- 30. Valente, T. W. & Vega Yon, G. G. (2020) Diffusion/contagion processes on social networks. Heal. Educ. Behav., 47, 235–248. [DOI] [PubMed] [Google Scholar]
- 31. Lerner, J. & Hâncean, M.-G. (2021) Micro-level network dynamics of scientific collaboration and impact: relational hyperevent models for the analysis of coauthor networks. Available at: https://arxiv.org/abs/2105.01562 (Accessed: 14July2021). Doi: arXiv:2105.01562. pp. 1–31. [Google Scholar]
- 32. Lerner, J., Lomi, A., Mowbray, J., Rollings, N. & Tranmer, M. (2021) Dynamic network analysis of contact diaries. Soc. Netw., 66, 224–236. [Google Scholar]
- 33. Lerner, J. & Lomi, A. (2020) Reliability of relational event model estimates under sampling: How to fit a relational event model to 360 million dyadic events. Netw. Sci., 8, 97–135. [Google Scholar]
- 34. Lerner, J., Mowbray, J., Tranmer, M. & Hancean, M.-G. (2019) REM beyond dyads: relational hyperevent models for multi-actor interaction networks. Available at: https://arxiv.org/abs/1912.07403 (Accessed: 14July2021). Doi: arXiv:1912.07403. pp. 1–26. [Google Scholar]
- 35. Goldstein, E., Lipsitch, M. & Cevik, M. (2021) On the effect of age on the transmission of SARS-CoV-2 in households, schools, and the community. J. Infect. Dis., 223, 362–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Mossong, J. et al. (2008) social contacts and mixing patterns relevant to the spread of infectious diseases. PLOS Med., 5, e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Park, Y. J. et al. (2020) Contact tracing during coronavirus disease outbreak, South Korea, 2020. Emerg. Infect. Dis., 26, 2465–2468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Monod, M. et al. (2021) Age groups that sustain resurging COVID-19 epidemics in the United States. Science, 371, eabe8372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Liu, Y. et al. (2020) What are the underlying transmission patterns of COVID-19 outbreak? An age-specific social contact characterization. EClinicalMedicine, 22, 100354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Laxminarayan, R. et al. (2020) Epidemiology and transmission dynamics of COVID-19 in two Indian states. Science, 370, 691 – 697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Davies, N. G. et al. (2020) Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med., 26, 1205–1211. [DOI] [PubMed] [Google Scholar]
- 42. Bi, Q. et al. (2020) Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect. Dis., 20, 911–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Eames, K. T. D. & Keeling, M. J. (2003) Contact tracing and disease control. Proc. R. Soc. B Biol. Sci., 270, 2565–2571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Moreno López, J. A. et al. (2021) Anatomy of digital contact tracing: Role of age, transmission setting, adoption, and case detection. Sci. Adv., 7, eabd8750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Hâncean, M.-G., Perc, M. & Lerner, J. (2020) Early spread of COVID-19 in Romania: imported cases from Italy and human-to-human transmission networks. R. Soc. Open Sci., 7, 200780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Sava, J. A. (2021) statista. Number of people infected with COVID-19 in Romania 2021, by region. https://www.statista.com/statistics/1104730/covid-19-infections-by-region-romania/ (last accessed 14July2021). [Google Scholar]
- 47. Hâncean, M.-G. et al. (2021) Replication data for: the role of age in the spreading of COVID-19 across a social network in Bucharest. The dataset is available on Harvard Dataverse Repository at 10.7910/DVN/CSNRR5 (Accessed: 16July2021). Doi: 10.7910/DVN/CSNRR5. [DOI] [Google Scholar]
- 48. McPherson, J. M. & Ranger-Moore, J. R. (1991) Evolution on a dancing landscape: organizations and networks in dynamic Blau space*. Soc. Forces, 70, 19–42. [Google Scholar]
- 49. McPherson, J. M. & Smith, J. A. (2019) Network effects in Blau space: imputing social context from survey data. Socius, 5, 1 - 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Andalibi, A., Koizumi, N., Li, M.-H. & Siddique, A. B. (2021) Symptom and age homophilies in SARS-CoV-2 transmission networks during the early phase of the pandemic in Japan. Biology, 10, 499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Boehmer, T. K. et al. (2020) Changing age distribution of the COVID-19 pandemic - United States, May-August 2020. MMWR. Morb. Mortal. Wkly. Rep., 69, 1404–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Pilny, A. & Huber, C. J. (2021) An egocentric network contact tracing experiment: testing different procedures to elicit contacts and places. Int. J. Environ. Res. Public Health, 18, 1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Smith, E., Brands, R., Brashears, M. & Kleinbaum, A. (2020) Social networks and cognition. Annu. Rev. Sociol., 46, 159 - 174. [Google Scholar]
- 54. Heckathorn, D. D. (1997) Respondent-driven sampling: a new approach to the study of hidden populations*. Soc. Probl., 44, 174–199. [Google Scholar]
- 55. Wang, Z. et al. (2016) Statistical physics of vaccination. Phys. Rep., 664,1 – 113. [Google Scholar]
- 56. Priesemann, V. et al. (2021) Calling for pan-European commitment for rapid and sustained reduction in SARS-CoV-2 infections. Lancet, 397, 92 – 93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Priesemann, V. et al. (2021) An action plan for pan-European defence against new SARS-CoV-2 variants. Lancet, 397, 469 – 470. [DOI] [PMC free article] [PubMed] [Google Scholar]