Focusing of in-plane hyperbolic polaritons in van der Waals crystals with tailored infrared nanoantennas

Focusing of in-plane hyperbolic PhPs into deep subwavelength focal spots provides enhanced field confinement and absorption.

Abstract

Phonon polaritons (PhPs)—light coupled to lattice vibrations—with in-plane hyperbolic dispersion exhibit ray-like propagation with large wave vectors and enhanced density of optical states along certain directions on a surface. As such, they have raised a surge of interest, promising unprecedented manipulation of infrared light at the nanoscale in a planar circuitry. Here, we demonstrate focusing of in-plane hyperbolic PhPs propagating along thin slabs of α-MoO₃. To that end, we developed metallic nanoantennas of convex geometries for both efficient launching and focusing of the polaritons. The foci obtained exhibit enhanced near-field confinement and absorption compared to foci produced by in-plane isotropic PhPs. Foci sizes as small as λ_p/4.5 = λ₀/50 were achieved (λ_p is the polariton wavelength and λ₀ is the photon wavelength). Focusing of in-plane hyperbolic polaritons introduces a first and most basic building block developing planar polariton optics using in-plane anisotropic van der Waals materials.

INTRODUCTION

Focusing of electromagnetic waves to deeply subdiffractional volumes allows for enhancing light-matter interactions, which is the key for a broad range of applications at the nanoscale such as light manipulation (1–3), nanolithography (4, 5), photocatalysis (6, 7), and biosensing (8–10). Recently, hyperbolic phonon polaritons (PhPs) (11) in thin slabs of the van der Waals (vdW) crystal hexagonal Boron Nitride (h-BN) have been intensively investigated as they exhibit extreme field confinement (12, 13) and exotic ray-like propagation (14, 15), with potential for hyperlensing (16) and focusing (15, 17) of mid-infrared light at the nanoscale. However, hyperbolic PhPs in h-BN exhibit out-of-plane hyperbolic propagation, challenging the development of hyperbolic nano-optics compatible with on-chip optical devices (18). In this regard, hyperbolic PhPs with in-plane propagation have recently been demonstrated in artificial h-BN metasurfaces (19) and in the natural vdW crystals α-V₂O₅ (20) and α-MoO₃ (21, 22), which allows fundamental and applied studies of hyperbolic focusing phenomena in a planar configuration (18).

The in-plane hyperbolic propagation of PhPs arises from a different sign of the permittivity of the host material along the two in-plane crystalline directions (Fig. 1A). It can be described by a hyperbolic isofrequency curve (IFC), a slice of the polariton dispersion in the momentum-frequency space defined by a plane of constant frequency (ω), as shown in Fig. 1B for PhPs in an α-MoO₃ slab at infrared frequencies (illuminating wavelength λ₀ = 11.05 μm). According to this IFC, the propagation of PhPs in α-MoO₃ is only allowed along specific directions laying within the sectors $\mid \text{tan}(k_x/k_y)\mid <\sqrt{-{\mathrm{\epsilon }}_y/{\mathrm{\epsilon }}_x}$ between the asymptotes of the hyperbola in the (k_x, k_y) space (x and y corresponding to the α-MoO₃ [001] and [100] crystalline directions, respectively). Another peculiar characteristic is that the Poynting vector $\overrightarrow{S}$, which determines the propagation direction of PhPs in real space (perpendicular to the IFC), is generally noncollinear with the wave vector $\overrightarrow{k}$. This is in stark contrast to the propagation of waves in in-plane isotropic media where $\overrightarrow{S}$ and $\overrightarrow{k}$ are collinear and, thus, leads to exotic and nonintuitive optical phenomena (21–24). When approaching the two asymptotes of the IFC, the number of available wave vectors of PhPs largely increases (high-|$\overrightarrow{k}$| wave vectors, denoted by ${\overrightarrow{k}}_{\mathrm{H}}$), which yields a highly directional ray-like propagation (15, 16).

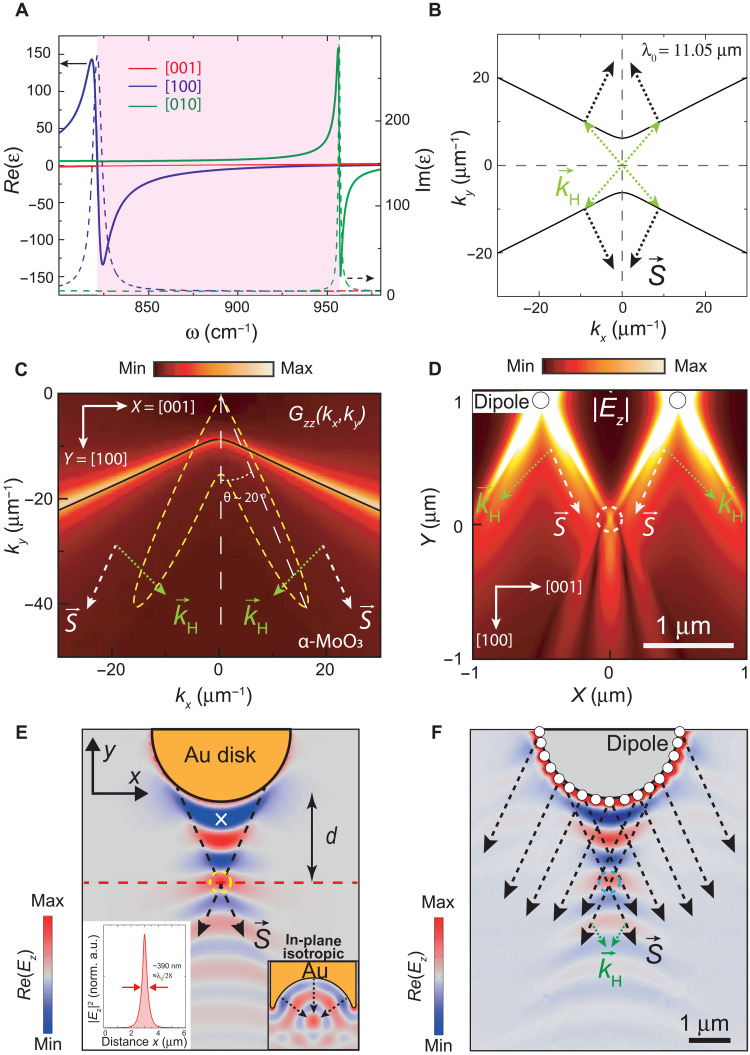
Fig. 1. Focusing of in-plane hyperbolic PhPs.

(A) IR dielectric function of α-MoO₃ for the hyperbolic reststrahlen band studied in this work (shaded region). (B) IFC of in-plane hyperbolic PhPs in a 165-nm-thick α-MoO₃ slab at an illuminating wavelength λ₀ = 11.05 μm. PhPs with high-|$\overrightarrow{k}$| wave vectors are indicated by ${\overrightarrow{k}}_{\mathrm{H}}$, together with their Poynting vector $\overrightarrow{S}$. (C) Color plot (z component of the Dyadic Green’s function) for the density of electromagnetic modes in k-momentum space (k_x, k_y) generated by a point dipole on α-MoO₃ (λ₀ = 11.05 μm). The dashed yellow line represents the pattern of the field emitted by the dipole as a function of the polar angle. (D) Near field, |E_z|, calculated analytically for two vertical point dipoles on α-MoO₃. A focal spot is obtained upon interference of ray-like PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors (dashed circle). (E) Simulated near field, Re(E_z), produced by a metal Au disk nanoantenna: The excitation and interference of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors lead to a focal spot (yellow dashed circle). The right inset shows the analogous case for an in-plane isotropic medium using a rod-like metal nanoantenna with a concave extremity. The left inset shows the electric field amplitude, |E_z|², along the dashed red line (normalized to the intensity at the white cross). (F) Simulated near field, Re(E_z), for a discrete distribution of point electric dipoles localized along the periphery of a virtual disk: A convex interference pattern and focal spot (cyan dashed circle) are revealed, resembling the results obtained in (E).

Here, we develop metallic Au nanoantennas with tailored geometries to excite and focus in-plane hyperbolic PhPs along the surface of an α-MoO₃ slab. Our theoretical and experimental findings show the possibility of obtaining extraordinarily small foci with enhanced near-field confinement and absorption in in-plane hyperbolic media with respect to in-plane isotropic media. This result can be explained by the interference of highly directional hyperbolic polaritons featuring large wave vectors and enhanced density of electromagnetic modes.

RESULTS AND DISCUSSION

To understand the ray-like character of in-plane hyperbolic propagation of PhPs in α-MoO₃, we analyze the near field created by a point source placed above a slab of α-MoO₃. Namely, we use the Dyadic Green’s function (DGF), $\widehat{D}$, which connects the electric vectorial fields created by this point source, $\overrightarrow{E}$, with its dipole moment, $\overrightarrow{p}$, so that $\overrightarrow{E}=\widehat{D}\overrightarrow{p}$. The Fourier transform of the DGF contains the dispersion relation of the modes of our system (given by the poles of DGF) as well as their density, thus being an extremely useful tool for the analytical visualization of the PhPs. Since PhPs in α-MoO₃ have a strong vertical component of the electric field, we consider the vertically polarized dipole source (i.e., polarized along the z axis). The color plot in Fig. 1C renders the zz component of the DGF in momentum space, D_zz(k_x, k_y) (see details in section S1). It can be observed that the maxima are obtained for directions closely aligned with the asymptotes of the IFC (solid black line), i.e., for PhPs with wave vectors ${\overrightarrow{k}}_{\mathrm{H}}$ and Poynting vector $\overrightarrow{S}$: The pattern of the field emitted by the vertical point source exhibits very narrow lobes, indicating the directions along which the density of propagating polaritonic modes is maximum, which form an angle θ ~ 20° with respect to the y axis for an incident wavelength λ₀ = 11.05 μm (dashed yellow lines in Fig. 1C). Our analytical results prove, therefore, that the ray-like propagation of PhPs along slabs of α-MoO₃ is consistent with the high density of electromagnetic modes associated with the asymptotes of the IFCs. To visualize the propagation of these PhPs in real space, we perform calculations of the near-field distribution, ∣E_z(x, y)∣, originated by two distant point sources placed above the surface of an α-MoO₃ slab (Fig. 1D). We observe that the propagation of directional and intense polaritonic rays (dashed white arrows) yields upon constructive interference the formation of a focal spot (dashed white circle).

On the basis of these analytical calculations, in the following, we study the focusing of in-plane hyperbolic PhPs in α-MoO₃. To this aim, we propose the use of optical nanoantennas, which would allow for both effective launching and focusing of the PhPs. We note that the focusing of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors is obtained upon their constructive interference, leading to a focal spot with enhanced field confinement in line with previous works (15, 16). Figure 1E shows the near field, Re(E_z(x, y)), obtained by full-wave numerical simulations for a metal nanoantenna with in-plane circular geometry (disk) located on top of an α-MoO₃ slab for an illuminating wavelength λ₀ = 11.05 μm. We observe PhPs launched by the nanoantenna that exhibit large near-field amplitude and convex wavefronts within a triangular region, in which a focusing spot is formed at its apex (marked with a yellow dashed circle). By plotting a profile of the electric field intensity, ∣E_z(x, y)∣², along the x axis in Fig. 1E (red dashed line), we obtain a full width at half maximum (FWHM) of the spot of ~390 nm (left inset in Fig. 1E), revealing a deep subwavelength size of ~λ₀/28.

The numerical study performed above indicates that focusing of in-plane hyperbolic PhPs can be obtained by using extended optical nanoantennas such as metal disks, i.e., optical elements with convex geometry. Note that this is in stark contrast to the typical concave nanoantennas used to focus polaritons in in-plane isotropic media (see right inset in Fig. 1E). Such anomalous behavior can be understood by considering the Huygens’ principle in hyperbolic media where a circular metal nanoantenna can be seen as an extended source composed of an infinite number of point-like dipoles situated along its edge that launch PhPs whose wavefronts interfere. Figure 1F shows the calculated near field for a discrete number of point electric dipoles placed on an α-MoO₃ slab along a semicircle that mimics the nanoantenna’s periphery. Contrary to in-plane isotropic media where circular fringes parallel to the nanoantenna’s periphery are obtained (see fig. S8) and, thus, the energy flows equally in all the directions, the interference of highly directional PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors launched by point dipoles leads to focusing into a spot of nanometer dimensions (blue dashed circle in Fig. 1F). This result closely reproduces the near-field distribution obtained for a disk nanoantenna in Fig. 1E, thus confirming that the ray-like polaritons with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors along directions closely aligned with the asymptotes of the IFCs are responsible for the foci formation.

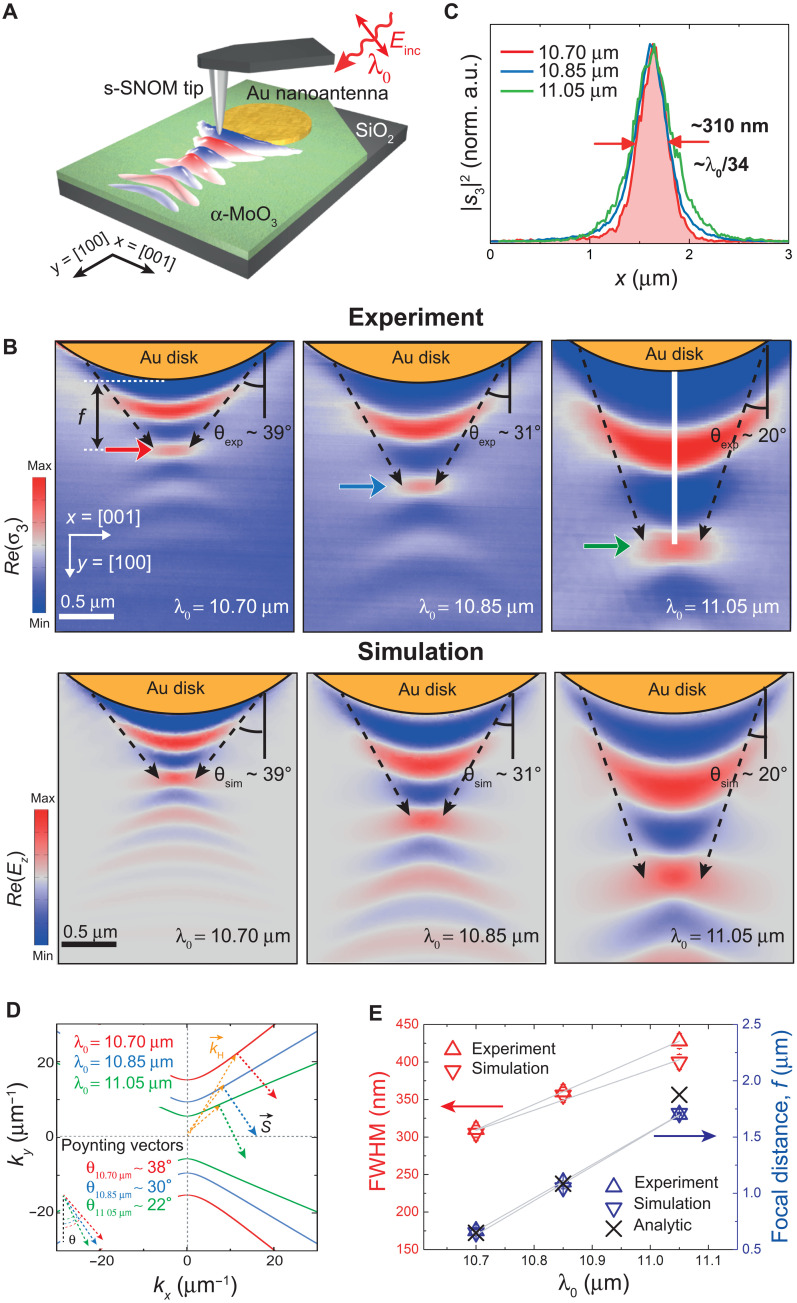
To experimentally demonstrate focusing of in-plane hyperbolic PhPs, we fabricate a Au disk nanoantenna on top of an α-MoO₃ slab and perform near-field nanoimaging using scattering-type scanning near-field optical microscopy (s-SNOM) (see Materials and Methods), as sketched in Fig. 2A (25, 26). The images obtained for three different incident wavelengths λ₀ = 10.70, 10.85, and 11.05 μm are shown in Fig. 2B (top panels). All of them reveal a series of convex fringes that emerge from the disk nanoantennas and narrow with the distance with respect to the disk edge, eventually leading to the formation of a focal spot, in excellent agreement with full-wave numerical simulations (bottom panels). We observe that both the width of the focal spot and its focal distance f (defined as the distance measured from the focal spot to the nanoantenna’s edge along a perpendicular line to the edge) vary as a function of the incident wavelength λ₀. By taking profiles along the [001] α-MoO₃ direction passing through the focal spots (indicated by arrows in the top panels), we extract spot sizes (corresponding to the FWHM) that vary from ~310 nm at λ₀ = 10.70 μm to ~430 nm at λ₀ = 11.05 μm, which reveal a deep subwavelength character, reaching values as small as λ₀/34 (Fig. 2C). On the other hand, f varies strongly from ~0.6 μm at λ₀ = 10.70 μm up to ~1.7 μm at λ₀ = 11.05 μm. This wavelength dependence can be qualitatively understood by the analytically calculated in-plane hyperbolic IFCs (Fig. 2D), which dictates the direction of propagation of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors that yield the formation of the foci [the Poynting vector $\overrightarrow{S}$ denoting the propagation of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors forms an angle θ with respect to the y axis in Fig. 2 (B and D)]. Hence, the particular curvature of the IFC for each of the incident wavelengths λ₀ dictates both the angle θ and the PhP wavelengths λ_H, being $\mid {\overrightarrow{k}}_{\mathrm{H}}\mid =2\mathrm{\pi }/{\mathrm{\lambda }}_{\mathrm{H}}$. Whereas the former leads to a wavelength-dependent focal distance f, which might find interesting applications in frequency-selective waveguiding, the latter determines the size of the focal spot.

Fig. 2. Planar focusing of in-plane hyperbolic PhPs with Au disk nanoantennas.

(A) Schematics of the s-SNOM experiment to image the propagation and focusing of in-plane hyperbolic PhPs excited by a Au disk nanoantenna on an α-MoO₃ slab. The sample is illuminated with p-polarized IR light of wavelength λ₀. (B) Experimental [Re(σ₃); top row] and simulated [Re(E_z); bottom row] near-field images of PhPs launched by a Au disk nanoantenna fabricated on top of a 165-nm-thick α-MoO₃ crystal at λ₀ = 10.70 μm (left), λ₀ = 10.85 μm (middle), and λ₀ = 11.05 μm (right). The interference of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors launched from the edges of the antenna yields a focal spot with varying size and f as a function of λ₀. The dashed arrows mark the angle θ. (C) Experimental near-field amplitude |s₃|² profiles along the x axis at positions marked with an arrow in (B) for λ₀ = 10.70 μm (red), λ₀ = 10.85 μm (blue), and λ₀ = 11.05 μm (green). A deep subwavelength spot size of λ₀/34 (~310 nm) is measured for λ₀ = 10.70 μm. (D) Analytical IFCs for a 165-nm-thick α-MoO₃ crystal at λ₀ = 10.70 μm (red), λ₀ = 10.85 μm (blue), and λ₀ = 11.05 μm (green). The Poynting vector $\overrightarrow{S}$ of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors forms wavelength-dependent angles θ with respect to the y axis. (E) Dependence of the experimental, simulated, and analytically calculated values of the spot size (FWHM) and f with λ₀ (gray lines serve as a guide for the eye).

We note that the focal distance f can be analytically calculated using a simple Eq. 1 derived from the DGF, where the α-MoO₃ crystal is formally treated as a two-dimensional (2D) conductive layer with the thickness-dependent effective 2D conductivity (see the Supplementary Materials)

$$f=R\sqrt{1-\frac{{\mathrm{\epsilon }}_{\mathit{xx}}^{\prime }}{{\mathrm{\epsilon }}_{\mathit{yy}}^{\prime }}}$$ (1)

where ${\mathrm{\epsilon }}_{\mathit{xx}}^{\prime }$ and ${\mathrm{\epsilon }}_{\mathit{yy}}^{\prime }$ are the real part of the α-MoO₃ dielectric function for components “x” and “y”, and R is the radius of the disk nanoantenna. By comparing the experimental values of f with those obtained by numerical simulations and analytical calculations, we obtain an excellent agreement (Fig. 2, D and E). As such, despite its simplicity, Eq. 1 provides a precise mean for the design of disk nanoantennas capable of focusing in-plane hyperbolic PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors at predefined distances.

At this point, we demonstrated that metal disk nanoantennas allow for planar focusing of in-plane hyperbolic PhPs into deep subwavelength spot sizes. However, considering that this focusing phenomenon stems from the interference of PhPs with large wave vectors ${\overrightarrow{k}}_{\mathrm{H}}$, which potentially can take infinitely large values, we assume that the size of the foci can be further reduced upon improvement of the nanoantennas’ design. It should be noted, however, that the minimum achievable size is ultimately conditioned by the extremely short propagation length of PhPs with arbitrarily large wave vectors, thus introducing a trade-off between PhPs’ wave vector and propagation length. In addition, the spot size is also affected by the contribution of PhPs with low-|$\overrightarrow{k}$| (${\overrightarrow{k}}_{\mathrm{L}}$) wave vectors, with relatively larger wavelengths with respect to ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors.

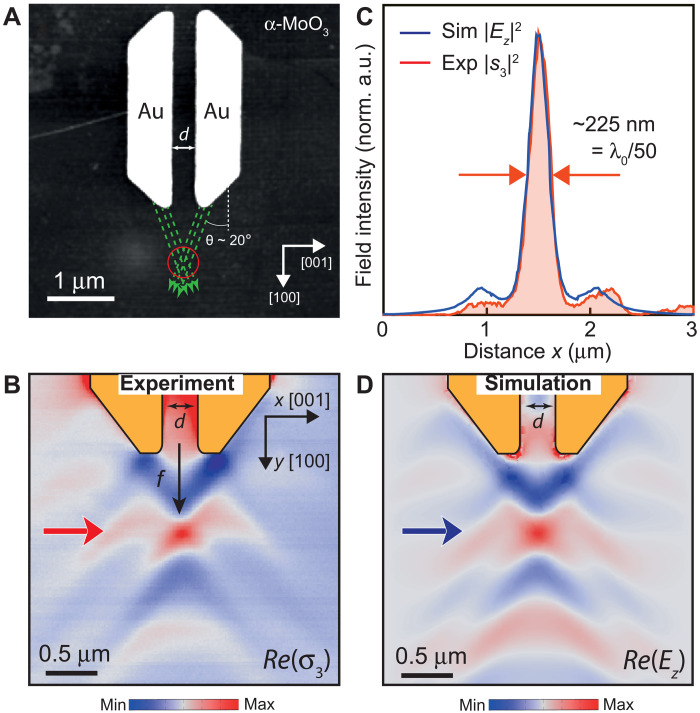
Bearing this in mind, to further reduce the size of the foci, we consider rod-like trapezoidal nanoantennas in which the extremities are tilted at an angle that depends on λ₀, taking a value of ~44° for λ₀ = 11.05 μm (Fig. 3A). Note that the nanoantenna’s geometry needs to be improved to enhance the near-field intensity and absorption at the focus (see the Supplementary Materials). In comparison with the disk nanoantennas shown in Fig. 2, this improved design allows for (i) launching PhPs with${\overrightarrow{k}}_{\mathrm{H}}$ along a unique and well-defined direction (dashed green lines) and (ii) inhibiting the contribution of PhPs with ${\overrightarrow{k}}_{\mathrm{L}}$ wave vectors to the spot size since the central part of the primitive disk-like nanoantenna is absent, i.e., only ray-like PhPs with${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors are contributing to the focal spot. Figure 3B shows the experimental near-field image, Re(σ₃), for a rod-like trapezoidal nanoantenna fabricated on an α-MoO₃ slab. We observe PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors being excited at the edges of the nanoantennas that, upon propagation, interfere, giving rise to the formation of a focal spot at a distance f ~ 790 nm. By taking a profile along the x axis ([001] α-MoO₃ direction) passing through the focus (red curve in Fig. 3C), we extract a spot size (FWHM) as small as ~225 nm, i.e., a deep subwavelength size of ~λ₀/50, or ~λ_p/4.5, with λ_p ~ 1 μm being the polaritonic wavelength along the y axis ([100] α-MoO₃ direction). This result is in excellent agreement with the value obtained from numerical simulations (blue curve in Fig. 3C corresponding to a profile taken through the focal spot in the simulated near-field image of Fig. 3D). We note that such as in the case of the disk-like nanoantenna, the focal distance f for rod-like trapezoidal nanoantennas can also be analytically derived using a simple equation (eq. S28), which gives a value f ~ 760 nm, in excellent agreement with the experiment and numerical simulation (f ~ 790 nm). An in-depth discussion on the theoretical limits of λ₀ to produce a focal spot, as well as achievable focal distances, is shown in section S12.

Fig. 3. Optical nanoantennas for an improved planar nanofocusing of in-plane hyperbolic PhPs.

(A) Topographic image of rod-like trapezoidal Au nanoantennas separated by a distance d = 320 nm on an α-MoO₃ crystal. The slope of the antennas’ edges at both extremities present an angle of ~44° with respect to the [100] direction. The green dashed arrows illustrate the propagation of PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$wave vectors excited from the edges of the antennas (λ₀ = 11.05 μm) that interfere at the focal spot marked with a red circle. (B) Experimental near-field image, Re(σ₃), of rod-like trapezoidal nanoantennas on an α-MoO₃ slab. (C) Comparison between experimental/simulated near-field amplitude |s₃|²/|E_z|² profiles taken along the x axis ([001] direction) at positions marked by a red/blue arrow in (B) and (D), respectively. A deep subwavelength focusing of λ₀/50 (λ_p/4.5) is obtained. (D) Simulated near-field images, Re(E_z), of rod-like trapezoidal nanoantennas on an α-MoO₃ slab.

The above results demonstrate that, by simply tailoring the geometry of Au nanoantennas with a trapezoidal shape, allowing only the interference of polaritons with enhanced density of electromagnetic modes, the near-field confinement at the focus position can be enhanced. Furthermore, the focal distance f of these nanoantennas can be easily tuned by simply varying the separation distance “d” between the trapezoidal rods, thus providing an additional tuning knob for a fixed illuminating wavelength (see the Supplementary Materials).

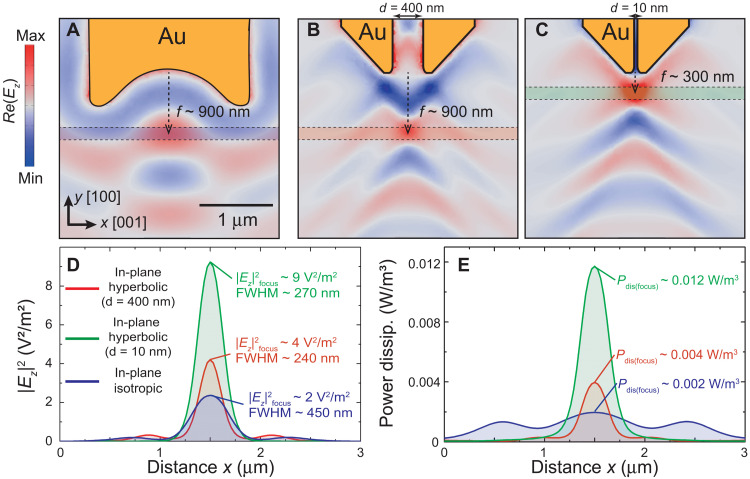
Focusing of light into deep subwavelength regions at the nanoscale has profound implications for fundamental studies on near-field light-matter interactions, energy harvesting, or heat management (27–30). To assess the potential of hyperbolic foci for these applications, we calculate both the averaged power dissipation (P_dis) inside an α-MoO₃ slab and the averaged electric field intensity (|E_z|²) above the slab at the focus spot position (Materials and Methods) and compare them to the case of a focus in in-plane isotropic media (Materials and Methods). Note that, for a fair comparison, the geometry of the nanoantenna in the in-plane isotropic medium was optimized by calculating either its resonant length or the optimal radius of its concave circular extremity that maximizes both the field intensity and FWHM at the focus (see section S8). Specifically, we perform full-wave numerical simulations and plot P_dis and |E_z|² along a horizontal line at the focal spot position produced by a rod-like nanoantenna with a concave circular extremity in an in-plane isotropic medium (shadowed region in Fig. 4A) and a rod-like trapezoidal nanoantenna in the hyperbolic medium (shadowed region in Fig. 4B). The distance between the trapezoidal rods is adjusted to d = 400 nm to guarantee the same focal distance f ~ 900 nm obtained in the in-plane isotropic case. Note that, whereas in the in-plane isotropic medium, it is impossible to obtain a focus for focal distances f < 900 nm owing to the inherent diffraction limit (for a comprehensive comparison, we consider the PhP wavelength along the y axis to be the same in both media, λ_p ~ 1 μm), in the in-plane hyperbolic medium, focal distances f ~ 300 nm are easily obtained by simply setting the distance between the rod-like trapezoidal antennas to a small value d = 10 nm (Fig. 4C).

Fig. 4. In-plane hyperbolic foci in in-plane hyperbolic and isotropic media.

Simulated near-field maps, Re(E_z), showing the propagation and focusing of PhPs on the surface of a 165-nm-thick crystal for an illuminating wavelength λ₀ = 11.05 μm using (A) a rod-like Au nanoantenna with concave extremities in an in-plane isotropic medium and (B and C) rod-like trapezoidal nanoantennas in the in-plane hyperbolic α-MoO₃ with a separation between rods d = 400 nm and d = 10 nm, respectively. (D) Averaged near-field intensity, |E_z|², above the surface of the slab along the blue/red/green shadowed region in (A), (B), and (C), respectively. (E) Averaged power dissipation density P_dis within the slab along the blue/red/green shadowed region in (A), (B), and (C), respectively. The data are normalized to the averaged |E_z|² value on top of the nanoantennas (see Materials and Methods).

We find that the focusing of PhPs in in-plane hyperbolic media leads to a markedly enhanced near-field intensity (|E_z|²), near-field confinement (FWHM), and power dissipation (P_dis) at the focal spot, as depicted in Fig. 4 (D and E, respectively). In particular, in the case of the in-plane hyperbolic medium, the near-field intensity |E_z|² and P_dis can be enhanced with respect to the isotropic case up to a factor of ×4.5 and ×6, respectively. Note that, for a reasonable comparison between the performance of the nanoantennas in in-plane hyperbolic and in-plane isotropic media, the power dissipation and near-field intensity magnitudes are normalized to the field on top of the nanoantennas, respectively (see Materials and Methods). Besides, the focus FWHM is markedly decreased from ~450 nm, i.e., ~λ_p/2 (in-plane isotropic case using rod-like nanoantennas with concave extremities), down to ~225 nm, i.e., ~λ_p/4.5 (in-plane hyperbolic case using rod-like trapezoidal nanoantennas for d = 320 nm in Fig. 3). Together, these results reveal that rod-like trapezoidal nanoantennas give rise to foci in in-plane hyperbolic media with ~2 times larger near-field confinement than that obtained in in-plane isotropic media with conventional concave antennas. These results suggest directional in-plane propagation of in-plane hyperbolic PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors as a key characteristic that offers unprecedented possibilities in nanophotonics. For example, focusing of such PhPs to deep subwavelength volumes would represent an extraordinary resource for harvesting of infrared light and enhancing light-matter interactions (18, 31).

The possibility of exciting and focusing highly directional PhPs with ${\overrightarrow{k}}_{\mathrm{H}}$ wave vectors along the surface of a hyperbolic medium (α-MoO₃) by using optical metal nanoantennas with tailored geometries as first nano-optical elements marks a fundamental step toward the development of a planar nano-optics in hyperbolic media. The enhanced near-field intensity, field confinement, and power density dissipation provided by focusing in-plane hyperbolic PhPs might offer exciting possibilities for applications in nanophotonics such as infrared frequency-selective waveguiding for nanoscale spectrometry, light routing, light-matter interaction experiments, and heat management. On the basis of these findings, we envision a planar nanophotonics field where the joint advantages of enhanced near-field confinement and energy management at the nanoscale in strongly anisotropic media, together with tunability by strain fields, electric gating, or near-field hybridization in vdW heterostructures, might open the door for more efficient applications in biochemical sensing or near-field thermal harvesting.

MATERIALS AND METHODS

Mechanical exfoliation of α-MoO₃ crystals

The α-MoO₃ crystals on SiO₂/Si substrates were obtained by mechanical exfoliation from commercial α-MoO₃ bulk material (Alfa Aesar). The bulk crystals were first thinned down on a Nitto tape (Nitto Denko Co., SPV 224P) and transferred on a transparent polydimethylsiloxane stamp. Afterward, we selected the crystals with proper sizes and thickness by optical microscopy (transmission mode) and finally transferred them on the SiO₂/Si substrate by using the dry transfer technique.

Fabrication of gold nanoantennas

Metal nanoantennas have been demonstrated as an efficient approach for launching PhPs in polar vdW materials due to their strong plasmonic response and large extinction cross section (32). In this work, we fabricated Au nanoantennas with different geometries by electron beam lithography (100 kV) on α-MoO₃ crystals transferred on a substrate where submicrometer gold markers were previously fabricated for localization. Poly(methyl methacrylate) was used as an electron-sensitive resist. A conventional high-resolution developer [1:3 MIBK (methyl isobutyl ketone): IPA (isopropanol)] was used. The metal antennas were obtained upon thermal evaporation of a Cr (5 nm)/Au (30 nm) bilayer. To do the lift-off and remove any organic residues, a hot acetone bath at 60°C was performed for 10 min, followed by a gentle rinse in IPA for 1 min. The samples were dried with dry nitrogen. Note that any ultrasonic treatment was avoided to prevent any degradation of the α-MoO₃ crystals. The rod-like trapezoidal nanoantennas are designed for an illuminating wavelength λ₀ = 11.05 μm at which the polaritons propagate along a direction, forming an angle θ ~ 20° with respect to the [100] crystal direction. To avoid optical losses by scattering and/or reabsorption of the polaritons as they propagate in close proximity to the edge of the antenna, the flat extremities of the antennas were fabricated, forming an angle θ ~ 44° (see the Supplementary Materials for more details).

Near-field nanoimaging

The near-field measurements were performed by using the commercial Neaspec GmbH s-SNOM setup. The setup consists of a modified atomic force microscopy (AFM) setup that is operated in tapping mode at a resonance frequency of ~280 kHz and an oscillation amplitude of ~100 nm. The commercial AFM tips are metal-coated (Pt/Ir) (Arrow NCPt-50, NanoWorld). A CO₂ laser spanning the 10- to 11-μm-wavelength regime was used as excitation source. A set of mirrors allows for varying the incident polarization on the antennas (p-type polarization is used in all the experiments). In particular, the nanoantenna is illuminated by p-polarized infrared light of wavelength λ₀ (incident field E_inc), yielding strongly confined fields with large momenta at the edges of the metal antenna for the excitation of PhPs (32). The near-field signal on the α-MoO₃ crystal is scattered by a metallized AFM tip at every position of its surface and collected on a detector resulting in a 2D near-field map (21, 33, 34). The near-field signal scattered by the tip is collected using a parabolic mirror and focused on an IR detector (Kolmar Technologies). The near-field amplitude and phase signals are obtained upon a pseudo-heterodyne signal processing by interferometry. The contribution due to far-field background scattering is removed by demodulating the detected signal at the third harmonic. We note that, due to the much larger cross section of the nanoantenna in comparison with the AFM tip apex radius and the small reflection coefficient of the PhPs from the nanoantennas, the contribution of tip-launched polaritons to the s-SNOM maps is negligible, and, therefore, only PhPs launched by the antenna are eventually visualized (32).

Full-wave numerical simulations

The numerical simulations were performed by finite element method calculations using the commercial software COMSOL Multiphysics. The dielectric permittivities at each of the illuminating wavelengths used in this work can be found elsewhere (35). The total power dissipation inside the 165-nm-thick α-MoO₃ slab and the vertical component of the electric field intensity above the slab surface in the near-field regime in Fig. 4 are calculated by taking a profile along the [001] direction at the focal spot position. Specifically, we plot the averaged power dissipation (P_dis) and averaged field intensity (|E_z|²) over a cylindrical volume with a radius of ~112 nm (equal to the FWHM value of the focal spot obtained for the modified rod-like trapezoidal antennas with d = 320 nm in the in-plane hyperbolic medium in Fig. 3) and a height of ~165 nm. The integrated averaged field intensity and power-dissipated values are normalized to the averaged value |E_z| on top of the nanoantennas. The case of the in-plane isotropic medium is simulated by considering ε_xx = ε_yy (ε_xx = ε_yy = −4.1323 + 0.3456i and ε_zz = 9.045 + 0.0644i). The height of the Au nanoantennas is set to 40 nm. The lateral dimensions of the nanoantennas are chosen to be at resonance for an illuminating wavelength λ₀ = 11.05 μm on the respective in-plane isotropic and in-plane hyperbolic media (see section S11): diameter of 3 μm (disk in in-plane hyperbolic medium) and length of ~3 μm (trapezoidal rods in in-plane hyperbolic medium and rods with concave extremities in in-plane isotropic medium). The dielectric permittivity used in the simulations for α-MoO₃ is shown in Table 1. The analytical calculation of the IFCs in Fig. 1 (B and C) and fig. S6 is calculated following (36, 37). The dielectric function for SiO₂ is obtained as shown in (38).

Table 1. Infrared dielectric permittivity of α-MoO₃.

The components of the permittivity tensor are given for the crystallographic axes [001] (ε_xx), [100] (ε_yy), and [010] (ε_zz).

	Illuminating wavelength λ0
	10.70 μm	10.85 μm	11.05 μm
εxx	1.5876 + 0.0689i	1.3932 + 0.0741i	1.1205 + 0.0814i
εyy	−1.5029 + 0.1937i	−2.4623 + 0.2435i	−4.1323 + 0.3456i
εzz	14.99 + 0.3525i	11.161 + 0.1405i	9.045 + 0.0644i

Supplementary Materials

This PDF file includes:

Sections S1 to S13

Figs. S1 to S16