Significance
Proteins capable of separating into three-dimensional liquid droplets in the cytoplasm and nuclei of cells sometimes assemble in a two-dimensional form at membranes. These surface densities, enriched in specific proteins and lipids, often play decisive roles in cell signaling and membrane organization. Here a theoretical approach suggests that surface densities resemble prewet surface phases held together through a combination of two-dimensional membrane-mediated forces and three-dimensional protein interactions. The emergent physics of these liquid surface phases enable their roles both as dynamic scaffolds and as cooperative switches that propagate signals between the membrane and bulk.
Keywords: phase separation, membranes, signaling
Abstract
Recent work has highlighted roles for thermodynamic phase behavior in diverse cellular processes. Proteins and nucleic acids can phase separate into three-dimensional liquid droplets in the cytoplasm and nucleus and the plasma membrane of animal cells appears tuned close to a two-dimensional liquid–liquid critical point. In some examples, cytoplasmic proteins aggregate at plasma membrane domains, forming structures such as the postsynaptic density and diverse signaling clusters. Here we examine the physics of these surface densities, employing minimal simulations of polymers prone to phase separation coupled to an Ising membrane surface in conjunction with a complementary Landau theory. We argue that these surface densities are a phase reminiscent of prewetting, in which a molecularly thin three-dimensional liquid forms on a usually solid surface. However, in surface densities the solid surface is replaced by a membrane with an independent propensity to phase separate. We show that proximity to criticality in the membrane dramatically increases the parameter regime in which a prewetting-like transition occurs, leading to a broad region where coexisting surface phases can form even when a bulk phase is unstable. Our simulations naturally exhibit three-surface phase coexistence even though both the membrane and the polymer bulk only display two-phase coexistence on their own. We argue that the physics of these surface densities may be shared with diverse functional structures seen in eukaryotic cells.
Eukaryotic cells are heterogeneous at scales far larger than individual macromolecules, yet smaller than classically defined organelles. Proteins, RNA, and DNA can self-organize into three-dimensional, liquid-like droplets in the cytoplasm and nucleus (1) and lipids and proteins in the plasma membrane similarly organize into two-dimensional domains, often termed “rafts” (2). These domains and droplets are thought to form in part due to a thermodynamic tendency of their components to phase separate into coexisting liquids. Proteins and other molecules within three-dimensional droplets are held together through weak but specific multivalent interactions (3–5). Lipids and other membrane components interact through less specific effective forces that arise from hydrophobic mismatch, from the interaction of lipid headgroups, and from steric interactions between lipid tails (6). Cell-derived vesicles separate into coexisting phases termed liquid ordered () and liquid disordered () when cooled somewhat below growth temperature (7). This transition occurs close to a critical point (8, 9), a region of thermodynamic space where membrane-mediated forces become long range and where local composition fluctuations are large. At growth temperatures, domains arising from proximity to this critical point are expected to resemble corresponding low-temperature phases at small scales but with finite size and lifetime. Some surface densities appear to form due to a combination of these forces. In these systems proteins aggregate in a thin film at a membrane surface with some components strongly attached to membrane lipids (10–14) while others are free to exchange with the bulk. The protein components of these films can phase separate in the bulk, but only at substantially higher concentrations than are seen in vivo (10, 13, 15). Examples of these surface densities include the Nephrin/Nck/NWasp system that plays a role in cell adhesion (10, 16), T cell signaling clusters (11), and the postsynaptic density (12, 15).
Systems that phase separate in three dimensions can undergo wetting transitions (17, 18), where there is a change in the bulk phase that adheres to a surface. In addition to wetting transitions that take place inside of coexistence on the bulk phase diagram, surfaces of bulk fluids can undergo prewetting transitions (19, 20) that occur near to bulk coexistence. In prewetting transitions, a normally unstable bulk phase is stabilized through favorable interactions with a surface, leading to a surface film that resembles the bulk phase, but is molecularly thin.
The behaviors of membrane domains and protein droplets have both been successfully described using theories of phase transitions in fluid systems (6, 21), but there has been less work interpreting these surface aggregates. We use lattice Monte Carlo simulations in conjunction with a minimal Landau theory to explore the physical principles governing these droplets. We argue that surface densities are similar to prewet phases, but with subtlety arising from their adhesion to a two-dimensional liquid embedded with mobile components that interact favorably with bulk components, enlarging the prewetting regime. We show that the prewetting region is further enhanced when the membrane is independently prone to phase separating, leading to surface phases enriched in both membrane and bulk components. We thus predict surface phases sensitive to both membrane and bulk parameters, which we argue describe a wide variety of structures that are already biochemically characterized.
Simulation Results
Model Overview.
In our simulations we describe the membrane using a conserved order parameter two-dimensional (2D) square-lattice Ising model (22, 23). In this model spins roughly represent membrane components—proteins or lipids—which prefer the liquid-ordered (spin up, light color in figures) or liquid-disordered (spin down, dark color in figures) membrane phases. The Ising model introduces two parameters, the coupling between neighboring spins , and , the difference in the number of up and down spins. Experiments suggest that plasma membrane composition is tuned close to the critical composition ( in the Ising model) and that cells reside slightly above the demixing critical point, occurring at (8, 9, 24, 25).
We model phase-separating cytoplasmic proteins as a lattice polymer mixture prone to phase separation. In most of our simulations two types of polymers, each 20 monomers in length, live on a three-dimensional (3D) cubic lattice at equal concentrations or chemical potentials. Red and blue polymers interact attractively with coupling (in the range of ; see Table 1 for exact values of all parameters) when occupying the same lattice position and like polymers cannot occupy the same position. We also include weak () nearest-neighbor interactions between both like and unlike polymers, which drive phases to localize in space (26, 27). The two polymer types roughly represent interacting components of phase-separated droplets in the cytoplasm or oppositely charged, synthetic polymers such as polylysine and polyglutamine (28, 29). In synthetic systems, the coupling between polymers can be modulated by salt and polymer length. Cellular proteins alter their coupling through posttranslational modifications, changes in salt, pH, and changes in valency (30, 31).
Table 1.
Simulation parameters used in figures
| Figure | Tether density | Membrane order | / | |||
| Fig. 1D, dry | 0.0 | 0.5 | 1.0 | 1.0 | 0.0 | 0.06 |
| Fig. 1D, wet | 0.03125 | 0.5 | 0.9 | 1.1 | 0.5 | 0.10 |
| Fig. 1D, surface coexistence | 0.0468 | 0.5 | 0.75 | 1.0 | 1.0 | −5.9 |
| Fig. 1D, single phase | 0.0468 | 0.5 | 0.675 | 1.0 | 1.0 | −5.9 |
| Fig. 2A | 0.0468 | 0.5 | 0.85 | 1.05 | 1.0 | −5.9 |
| Fig. 2 C, Center | 0.0468 | 0.5 | 0.775 | 2.0 | 1.0 | −5.9 |
| Fig. 2 C, Left | 0.0468 | 0.5 | 0.825 | 2.0 | 1.0 | −5.9 |
| Fig. 2 C, Right | 0.046 8 | 0.5 | 0.775 | 1.0 | 1.0 | −5.9 |
| Fig. 3A | 0.062 5 | 0.6 | 0.5 | 0.9 | 1.0 | −4.5 |
| Fig. 4A | 0.094 | 0.5 | 0.55 | 0.9 | 1.0 | −4.5 |
| Fig. 4B | 0.062 5 | 0.5 | 3.31 | 0.9 | 1.0 | −3.5 |
| Fig. 4C | 0.062 5 | 0.5 | 1.64 | 0.0 | 1.0 | −3.0 |
To couple our membrane and bulk models we introduce tethers that may be thought of as membrane-localized proteins. Tethers connect to up spins on the membrane and extend several (five) lattice spacings into the third dimension where they interact with bulk polymers through an attractive interaction . Tethers translate in just two dimensions across the membrane surface. In cells tethers correspond to lipidated or transmembrane proteins that interact with proteins in the cytoplasm (32). In synthetic systems tethers have been engineered through strong noncovalent binding attachment of peptides or proteins to lipid headgroups (10, 11, 15).
All of our simulations are held at a fixed membrane order parameter (fraction of up vs. down spins, corresponding to a membrane of fixed composition) and at a fixed number of tethers. To understand the bulk phase diagram, we conduct some simulations (shown in SI Appendix, Fig. S2) at fixed bulk polymer concentrations. However, for most of our results we hold the bulk polymer mixture at fixed chemical potential, implemented by allowing polymers to exchange with a separate reservoir held at fixed polymer density. This stands in for exchange of polymers with a large bulk, like the cellular interior, important since the third dimension in our simulation is necessarily limited.
Bulk Phase Behavior Is Independent of Surface Properties.
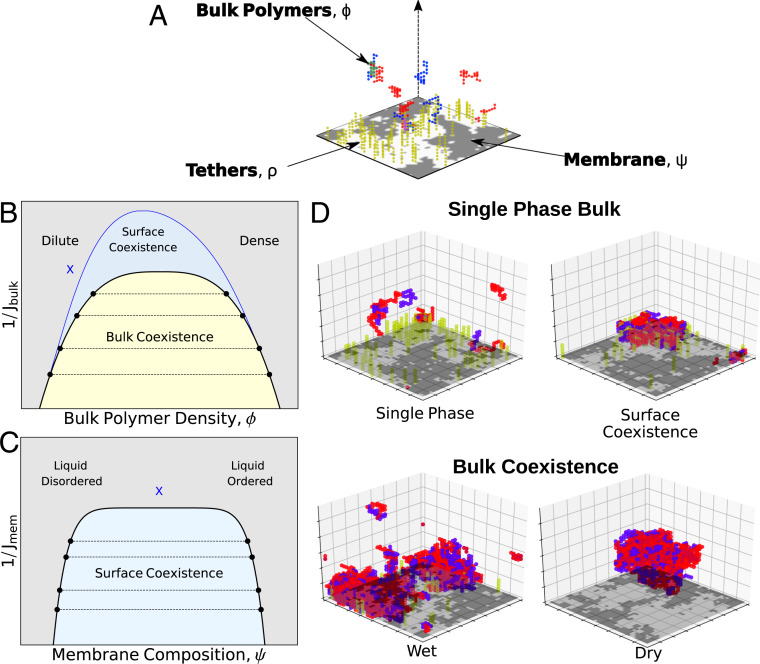
We expect the 3D bulk polymers to have a phase diagram that, in the thermodynamic limit, does not depend on properties of the Ising surface. In the absence of a membrane, at fixed polymer number, the bulk can either be in a uniform state or display coexistence between a polymer dense state enriched in both polymer types and a polymer dilute state. A phase diagram for this is sketched in Fig. 1B in black; at low coupling, , or high temperature, the state is uniform for any bulk concentration. At higher coupling there is a coexistence region where tie-line endpoints, the black circles in Fig. 1B, represent physically accessible polymer densities and where both endpoints have the same chemical potentials and Gibbs free energies. To observe coexistence we perform simulations at fixed polymer number with equal numbers of red and blue polymers. While the coexistence region of the composition-coupling plane does not depend on the properties of the membrane surface, its appearance in simulation does; in a “dry” regime, the polymer dense droplet avoids the surface, while in a “wet” regime it adheres to at least a portion of the surface. Wetting transitions occur when the bulk phase that adheres to the surface changes—here this can be achieved by altering either the bulk properties or the membrane properties and in particular by changing the concentration of tethers. Our focus, however, is on the surface phases that can coexist even in a single-phase region of the bulk.
Fig. 1.
Bulk and surface phases: (A) Cartoon of the minimal model used to describe surface densities. In our simulations red and blue lattice polymers have an attractive interaction in the three-dimensional bulk. An Ising model on the bulk’s boundary contains bright/dark pixels representing liquid ordered/disordered preferring components of a membrane. Tethers (yellow polymers) are connected to up spins and have an attractive interaction with components of the bulk. (B) Schematic bulk phase diagram. On a plot of inverse interaction strength (like temperature) vs. polymer density, the bulk phase diagram contains a single bulk phase region (blue and gray) and a region where a dense phase and a dilute phase coexist (yellow). The shape of the bulk coexistence curve does not depend on location within the surface phase diagram. (C) The region of surface coexistence depends on both bulk and surface parameters. In B and C, we show two two-dimensional slices where surface coexistence occurs in the blue region. The blue X in B corresponds to the location in the bulk phase diagram for which the surface phase diagram is plotted in C; moving this location would change the shape of the blue coexistence curve in C. The blue X in C is the location in the surface parameters for which the surface phase diagram is plotted in B. (D) Example phases observed in Monte Carlo simulations. (Top) Two examples without bulk coexistence, one with surface coexistence and one without. (Bottom) Two examples of coexisting bulk phases. A wet phase adheres to the membrane and a dry phase avoids the membrane.
Multiple Surface Phases Can Coexist on the Boundary of a Single Bulk Phase.
In the absence of tethers, the membrane can phase separate if the interaction strength is lower than a critical value. In this sense, it is possible for the system to display surface phase coexistence even when the bulk is uniform. In the absence of tethers our membrane’s phase diagram is well characterized, with a large coexistence region. When tethers are added that prefer one of these two phases, we qualitatively see that the bulk polymer distribution is different near these two phases (Fig. 1D). This implies that bulk properties should be able to qualitatively change the surface phase diagram even in the absence of bulk phase separation. In particular, increasing bulk coupling should be able to induce phase separation at the surface even when membrane interactions are too weak to induce phase separation on their own (, equivalent to ). We thus expect the surface phase diagram to depend on parameters of the bulk polymer solution and on the membrane and tethers that make up the surface. We sketch two two-dimensional slices through this five-dimensional phase diagram in Fig. 1 B and C. At a given point in the bulk phase diagram (blue x in Fig. 1B) we see a surface coexistence region resembling that for a two-dimensional coexisting liquid prone to phase separating via an Ising transition (blue shaded region in Fig. 1C). Alternatively, by fixing the surface parameters at the blue x in Fig. 1C, the surface coexistence region is plotted in Fig. 1B.
These surface coexistence regions are analogous to prewetting where, for example, a liquid film adheres to a solid surface of a gas phase bulk. In these classical examples there can be either an abrupt or a continuous transition to a prewet state triggered either by increasing bulk density or by lowering temperature. In the limit where where an isolated membrane is ideally mixed our system is analogous to this, albeit with the additional complexity of a mobile surface component in membrane tethers that already widens the prewetting regime. More substantially different, effective interactions between tethers arising from the membrane’s independent phase transition propensity also participate in the prewetting transition by further enhancing the interactions that drive surface aggregation.
Surface and Bulk Properties Together Determine the Surface Phase Diagram.
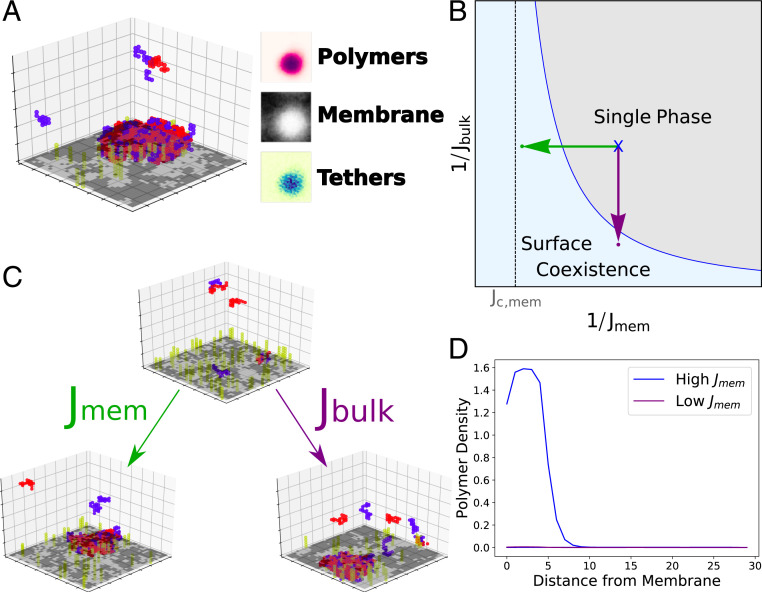
To more quantitatively explore the surface phase diagram in simulation we found a region of parameter space that displays two coexisting phases far from their critical point so that phases could be easily identified in small simulations (Fig. 2A). These two phases differ from each other in their membrane order, their density of tethers, and the density of polymers near them. We expect to be able to move from a single phase to two-phase coexistence by increasing either membrane interactions or bulk interactions (schematically shown in Fig. 2B). This is demonstrated in Fig. 2C; a single-phase surface is brought into the surface coexistence region by increasing the coupling between bulk polymers (Fig. 2 C, Right) or by increasing the interactions between membrane components (Fig. 2 C, Left). Each of these coexisting surface phases has a characteristic polymer density profile with distance from the surface (Fig. 2D). Although we primarily focus on membrane and bulk couplings, we confirmed that prewetting can additionally be triggered by increasing the number of tethers on the membrane.
Fig. 2.
Prewetting of surface densities. (A) (Left) Snapshot of a simulation where a polymer-dense droplet prewets the membrane surface even though droplets are unstable in the bulk. (Right) Time-averaged membrane, tether, and polymer compositions. (B) Schematic phase diagram in terms of membrane and bulk couplings. A single-phase system (black dot) can move into the surface coexistence region by increasing (purple arrow) or increasing (green arrow). The surface coexistence regime expands significantly near critical coupling, , and at larger . (C) Simulations at weak bulk and membrane coupling are brought into the coexistence region through increasing (purple) or (green). (D) Density of polymers as a function of distance from the membrane. A system at weak bulk and membrane couplings sees a single phase (purple; simulation in C, Lower Left) while systems at stronger membrane couplings see two coexisting polymer density profiles (blue; simulation in C, Lower Right).
Our simulation results suggest that the range of in which we see prewetting expands significantly as the membrane critical point is approached (Fig. 2B) or as we bring the membrane toward its critical composition () at fixed coupling strength (SI Appendix). These results imply that the membrane critical point expands the surface coexistence region, which we explore more quantitatively using a Landau theory below.
Simulations Demonstrate Three-Phase Surface Coexistence.
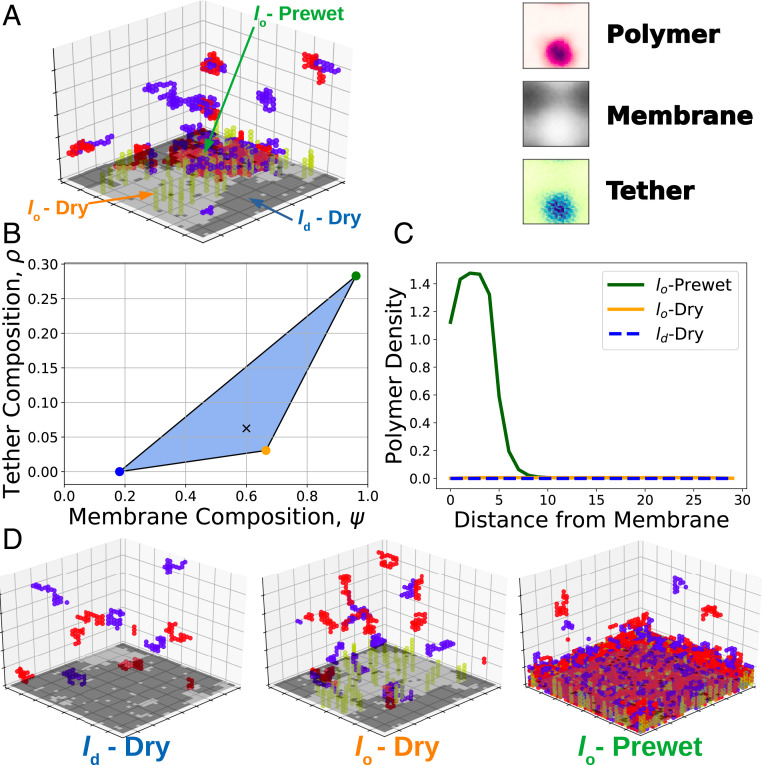
Our model allows for three-phase coexistence by Gibbs phase rule; two conserved quantities on the surface—tether and membrane composition—allow for up to phase coexistence without fine-tuning composition. Simulations can display three-phase coexistence (Fig. 3A), with distinct membrane compositions as well as tether and polymer density profiles. We describe each surface phase by its membrane and polymer compositions. What we denote the -prewet phase is composed of a -like membrane rich in tethers, with an adhered polymer droplet. The -dry phase is an membrane devoid of tethers and depleted of polymers compared to the bulk. The -dry phase consists of an -like membrane somewhat sparse in tethers. This phase may be slightly depleted or enriched in bulk components. Here we assume tethers prefer lipids; -preferring tethers would instead form an analogous -prewet phase.
Fig. 3.
Three-phase coexistence. (A) Simulations display three-phase coexistence where a polymer-dense droplet prewets a phase-separated membrane. Views of time-averaged tether density, membrane composition, and polymer density show a tether and polymer-dense phase rich in ordered components, an ordered membrane phase with a small amount of tethers, and a disordered membrane phase devoid of tethers. (B) Phase diagram over membrane and tether composition extracted from the simulation in A. Membrane and tether compositions falling inside the blue triangle split into three phases, each with a composition given by the vertices of the triangle. Black X corresponds to the surface composition of the simulation in A. (C) Polymer density profiles, as a function of distance from the membrane in each of the three phases. (D) Snapshots of simulations run at compositions corresponding to the endpoints of three-phase coexistence.
Three-phase coexistence generally occurs at polymer couplings that would prewet a single-phase membrane and at membrane couplings that would phase separate even in the absence of any bulk coupling. We extracted the tether and membrane composition of each phase, plotted in Fig. 3B. When tether and membrane composition lie inside the shaded triangle, the system phase separates into phases with tether and membrane compositions given as the vertices of the triangle, each with an accompanying density profile shown in Fig. 3C. We ran simulations at each of these surface compositions to observe individual phases, shown in Fig. 3D.
Alternate Bulk Mixtures Display Surface Phases.
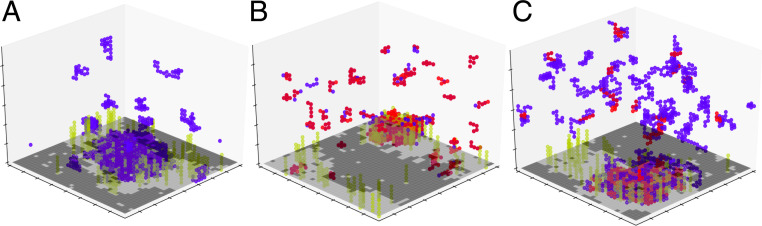
We choose to model cytoplasmic polymers as a lattice coacervate with two polymer types with an attraction between unlike polymers. However, other phase-separating polymer mixtures produce similar results as shown in Fig. 4. A unary, self-avoiding polymer mixture with strong nearest-neighbor interactions (similar to model-protein FUS) (33) gives similar phases and transitions as described below. Similarly, our findings are robust to the underlying details of the coacervate mixture: Polymer mixtures of unequal length (20 and 5 monomers, respectively) and of much shorter length (5 monomers for both types) similarly exhibit behavior qualitatively similar to that detailed for our main polymer simulations.
Fig. 4.
Alternative bulk polymer mixtures display three-phase coexistence. Coexistence of multiple surface phases requires phase separation in the bulk and is robust to the underlying details of the polymer mixture. We observe three-phase surface coexistence in all cases. (A) A unary polymer mixture with strong nearest-neighbor interactions. (B) A mixture of two short (n = 5) polymers. (C) An asymmetric polymer mixture with n = 5 (red) and n = 20 (blue). While we show three-phase coexistence for these systems, we expect all of our results would hold for these and other polymer systems prone to phase separation in the bulk.
Landau Analysis of Surface Phase Behavior
Our lattice simulations serve to give a primarily qualitative and intuitive picture for the phases we see. To more quantitatively understand these surface phases we introduce a Landau free-energy functional, modifying the analysis commonly used to theoretically describe prewetting transitions to incorporate membrane and tethers. As in standard analysis we introduce order parameter fields, and a Landau functional of their configuration, and consider the order parameter of the system to take the configuration that globally minimizes the Landau functional (34). Phase coexistence occurs when two configurations of fields both have the same minimum value of the free energy.
Our Landau functional, , describes a bulk system () with a surface at , with parameterizing the plane parallel to the surface. A single bulk order parameter describes the local density of polymers while two surface order parameters, and , describe the density of tethers and the membrane composition along an - tie line. We define and, suppressing coordinates, we write a Landau free energy for this system as with
| [1] |
where and describe the energy of the surface and bulk systems:
| [2] |
where is the distance from the bulk critical point, the chemical potential of the bulk system, and the distance from the membrane critical point. and are higher-order membrane and bulk couplings. Lagrange multipliers and enforce membrane and tether composition, respectively. The terms in come from an approximation of the Landau free energy of a dilute gas, with coefficients set by mapping the terms onto a Taylor series expansion of tether entropy at (SI Appendix). Membrane–tether and tether–bulk interactions are set by and . We take and , corresponding to a dilute-phase polymer mixture whose components interact favorably with tethers. See Table 2 for values of all Landau theory parameters. Minimizing this Landau functional determines the value of two derivatives and a functional derivative, and .
Table 2.
Landau theory parameters used in figures
| Figure | |||||||||
| Fig. 5 | 0.9 | −0.3 | −2.0 | −0.792 | 2.0 | N/A | N/A | 1 | 1 |
| Fig. 6A | N/A | N/A | −2.0 | N/A | N/A | −0.27 | 0 | 1 | 1 |
| Fig. 6B | 1, 0.75, 0.45, 0.25, 0.1 | 2 | −2.0 | 0.85 | −0.05 | N/A | N/A | 1 | 1 |
| Fig. 6C | 0.45 | 8, 5, 2, 1, 0.5 | −2.0 | 0.85 | 0.05 | N/A | N/A | 1 | 1 |
| Fig. 7 A and B | −0.05 | −0.1 | −2.0 | N/A | N/A | N/A | N/A | 1 | 1 |
| Fig. 7C | −0.05 | −0.1 | −2.0 | −0.56 | 0.52 | N/A | N/A | 1 | 1 |
The 2D Ising model and tethers act as a boundary condition for the bulk and thus cannot influence which bulk phases are stable in the thermodynamic limit. The bulk phase is the value of that globally minimizes , defining . The resulting bulk phase diagram recapitulates Fig. 1A, but with mean-field exponents. The bulk phase diagram describes a demixing transition where at high temperatures or low concentration of polymers there is a single gas-like phase dilute in polymers. At lower temperature or higher concentration of polymers this coexists with a polymer dense phase. Here we use a single order parameter to capture the density of both polymer types.
Analysis of Surface Behavior.
Outside of bulk coexistence, is globally minimized by a unique , where , with the system volume and where is its area. The free energy of the surface, , contains membrane contributions and contributions from surface-induced distortions of the bulk field :
| [3] |
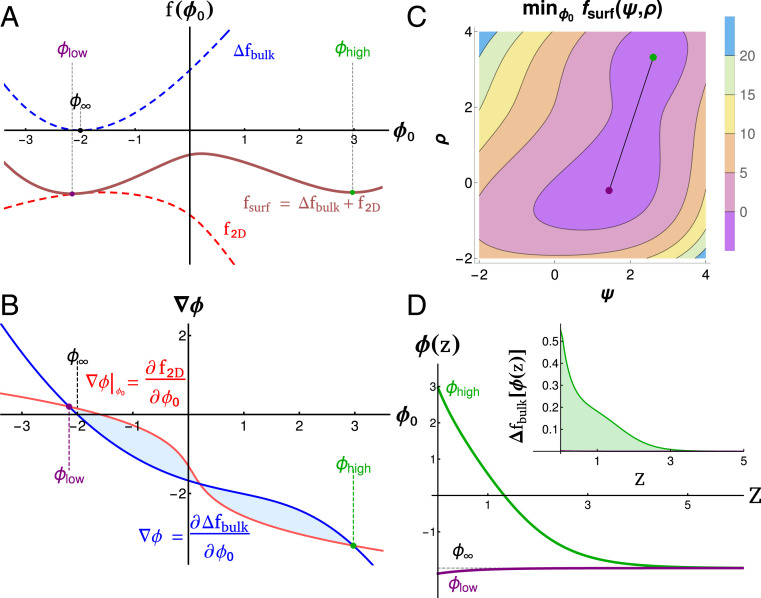
For a given location in the bulk phase diagram the surface can exhibit its own set of phases and transitions that are local minima of . While and cannot be independently minimized, they can be independently minimized for a given value of . Local minima of satisfy the conditions that . Minima of satisfy the differential equation with boundary conditions and . The values of and are plotted in Fig. 5A, along with their sum, . The values of and that minimize are visualized simultaneously in Fig. 5C, each corresponding to the local minima in Fig. 5A.
Fig. 5.
Landau theory of surface phases. (A) Bulk (blue), membrane (red, already minimized over ), and surface (brown) free energies as a function of surface polymer density . There are two energy minima, and in the combined even in the absence of multiple minima in or . (B) Gradient construction used to visualize solutions. Intersections of derivatives of (red) and (blue) give possible surface solutions and . The free energy difference between these solutions is given by the area between these curves, visualized as the shaded regions. Changing the position or slope of surface or bulk lines changes the surface solutions. (C) Surface free energy calculated over values of and , minimized first over . Two minima (purple and green) correspond to surface compositions that minimize the free energy of the membrane and tethers along with their resulting contributions to bulk energy. (D) Density profiles and energy density (Inset) as a function of distance from the membrane for the two physical phases. Both and decay to the bulk density . This adds unfavorable contributions to the free energy that are balanced by contributions from .
Minima can be identified more systematically using the graphical construction in Fig. 5B, plotting and , derivatives of the curves in Fig. 5A. Local minima of the surface free energy occur when these curves cross. In general, two local minima are separated by a local maximum. For two minima to have the same free energy, the areas between the two curves (blue shaded regions in Fig. 5B) must be equal.
Surface Enhancement of Bulk Interactions Diverges near the Membrane Critical Point.
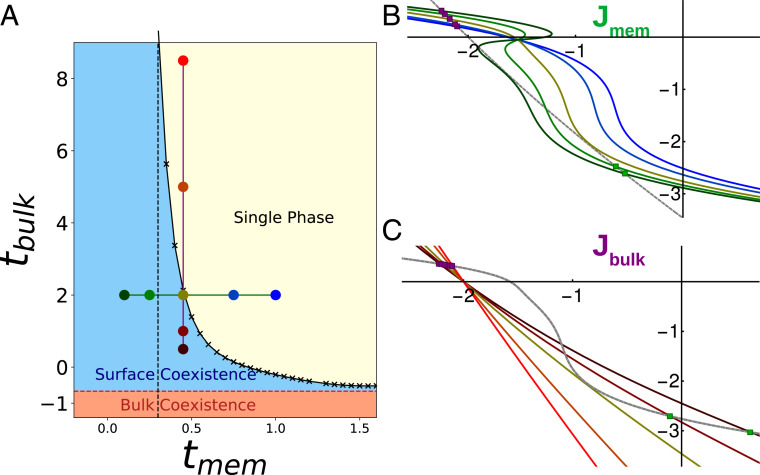
We plotted the regions of surface phase coexistence as a function of bulk and membrane coupling for fixed values of , , and in Fig. 6A. As with simulations we note that the two-phase region expands significantly as . In the absence of interactions with tethers () the membrane of our model () has a line of abrupt phase transitions when , , terminating in a critical phase transition at , . For weak interactions, the location of this first-order line and critical point can shift, but its topology is unchanged—in particular, the location of the critical point shifts toward higher (positive) values of , signifying that the critical point in our simulations should occur at weaker membrane coupling. Thus the surface coexistence line should meet the membrane-only transition line where as in Figs. 2 and 6A, with bulk interactions supplementing membrane ones away from it.
Fig. 6.
Critical point enhancement. (A) Phase diagram over and near the membrane critical point. The surface coexistence region (blue) extends to very weak near , marked by the dashed line. Outside of the coexistence region the surface is single phase (yellow). The bulk coexistence region (red) lies below the surface region. Here the surface would be presented as wet. (B) Gradient construction showing how the 2D curve changes on varying membrane coupling along the green line in A (colors from points in A). The slope of the surface curve increases as , diverging like the susceptibility near the membrane critical point. Polymer density profiles are plotted for each line. (C) Gradient construction varying along the purple line in A. Increasing decreases the slope of the bulk curve, promoting surface phase coexistence.
We can also understand the enlargement of the prewetting regime using the language of classical prewetting theories. In prewetting to a solid surface, is typically assumed to take the simple form . Here is the surface chemical potential and is the surface enhancement (17) quantifying increased attractive interactions between bulk components in proximity to the surface. In most examples the surface enhancement is negative due to loss of effective interactions mediated through negative values of z. However, small positive surface enhancements are possible, for example when magnetic spins interact through contact with a surface with a larger magnetic susceptibility (35, 36).
While our theory explicitly includes only first-order terms in , higher-order terms are generated by minimizing over and contributions, generating an effective surface enhancement. In the graphical construction in Fig. 5B, we can interpret the surface enhancement as the slope of the red line. Near the critical point, components embedded in the membrane feel long-range effective forces mediated by the membrane, sometimes called critical Casimir forces (37, 38). In surface densities these long-range critical Casimir forces provide an effective surface enhancement, mediating an increased interaction between bulk components. The magnitude of this membrane-mediated effective surface enhancement can be understood quantitatively as arising from the integral of the pairwise potential between tethers on the surface. This yields a quantity proportional to the susceptibility (34), which diverges near the critical point. This manifests as a steepening of the surface line as the membrane critical point is approached along increasing (blue to green curves in Fig. 6B). Below the membrane critical point we see the surface line fold back on itself, with two local minima and a local maxima at some values of , implying the membrane can phase separate without bulk interactions.
This analysis show that surface densities form at arbitrarily high near . However, the surface densities in these regimes have only marginal enrichment of polymers at the surface relative to the bulk—far less than would be found in the dense bulk phase—reflecting that they are primarily held together by membrane forces.
While we have focused on membrane-mediated interactions, other surface properties can also impact the formation of surface densities. The tether–bulk interaction strength and the density of tethers both impact the prewetting phase diagram. In particular, polymers can prewet a surface without membrane interactions () but only with higher tether–density and/or strong bulk–tether interactions. With no membrane contributions, the surface phases appear closer to those of classical prewetting, with a polymer density near the surface similar to that in the dense bulk phase. However, because this system is held at fixed tether density rather than fixed surface chemical potential, there is naturally a wider regime of prewetting than is seen with solid surfaces, as the tethers will always be at higher density in the prewet phase than in the membrane as a whole (see SI Appendix for more discussion).
While we expect our phase diagram to be topologically correct, our Landau theory fails to accurately predict the form of these phase boundaries. Mean-field theories like ours generally underestimate fluctuation effects, especially close to the critical point (34). We expect that a more sophisticated renormalization group treatment would predict a larger criticality-mediated enhancement and resulting surface coexistence region as well as a surface coexistence curve with Ising exponents rather than mean-field ones.
Landau Theory Predicts Coexistence of Three Surface Phases.
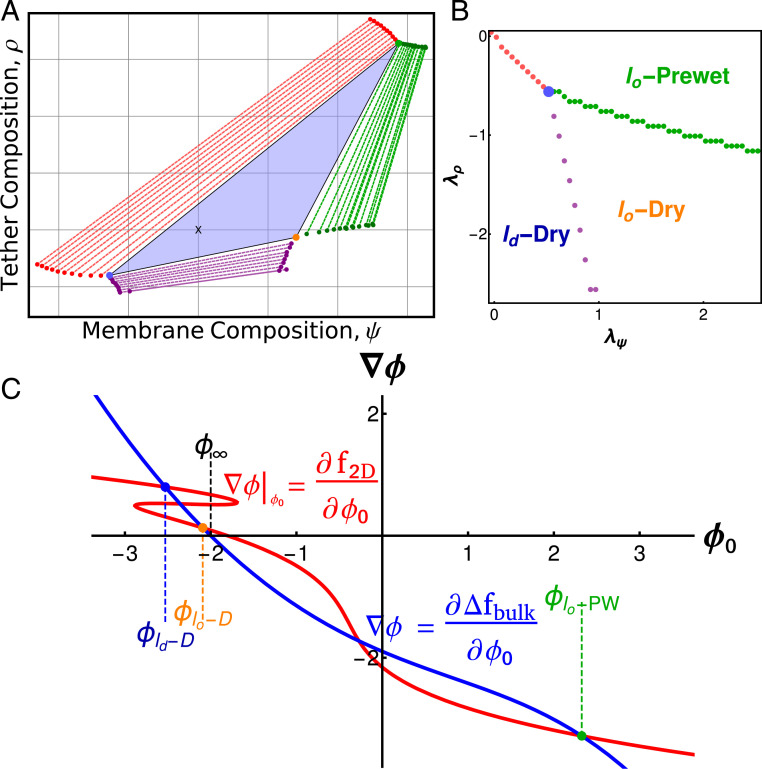
In general, each local minimum has a different value of and . We expect to have two-phase coexistence when the chemical potentials and are such that the global minimum is doubly degenerate and three-phase coexistence when the global minimum is triply degenerate. Coexistence additionally implies that the chemical potentials of each phase are identical. We minimized over a range of chemical potentials searching for regions of two- and three-phase coexistence, shown in Fig. 7B. When surface chemical potentials are tuned instead of composition, we find a single point in the plane of chemical potentials where three phases coexist and there are three lines of two-phase coexistence. This is expected—at fixed chemical potential two-phase coexistence is expected in codimension 1 regions of thermodynamic parameter space (regions of dimension 1 smaller than the total dimension of parameter space), while three-phase coexistence occurs in codimension 2 regions. However, synthetic and biological membrane–tether systems are typically held at fixed composition. In these systems, points of three-phase coexistence in chemical potential become triangles in the space of conserved quantities, with vertices at the physical phases (Fig. 7A). This recapitulates the qualitative findings of our simulations.
Fig. 7.
Three-phase coexistence in Landau theory. (A) Phase diagram over membrane compositions () and tether compositions () calculated from Landau theory. Three phases coexist in the blue triangle, with the surface composition of each phase given by the vertices of the triangle. The positions within the triangle (black x) set the area fraction of phases. Three two-phase coexistence regions (red, purple, green) border the three-phase region and are plotted as tie lines. Surfaces constructed on a tie line split into two phases with compositions given by the ends of the tie line. Single-phase regions border each two-phase region. (B) Phase diagram over the surface chemical potentials for the same system shown in A. The three-phase triangle is represented as the blue point, and each colored line corresponds to the two-phase regions in A. Outside of these lines and the point of three-phase coexistence the system is single phase. (C) Gradient construction within the three-phase region of A. The surface line is phase separated, folding in on itself and intersecting at the blue and yellow points. It additionally intersects with the bulk curve at high densities, green point.
Discussion
We have presented a model for surface densities in which bulk components, a membrane order parameter, and membrane-bound tethers phase separate together in a manner reminiscent of prewetting. In our simulations the membrane is composed of a lattice Ising model, while the bulk is composed of lattice polymers prone to phase separation. The stability of these surface densities can be modulated by membrane interaction strength, by the density and interactions between bulk components, and through the density of tethers that couple membrane and bulk. The fluid nature of the membrane and in particular the mobility of tethers already widen the regime where phase coexistence occurs, as surface domains become enriched in tethers over their average density. Moreover, when the membrane is held close to its critical point, the regime where we see surface phase coexistence widens dramatically, which we trace to membrane-mediated enhancement of bulk polymer interactions. These surface densities are stable thermodynamic phases and their putative roles should be distinguished from roles the membrane may play in nucleating droplets that are already stable in the bulk but face substantial nucleation barriers to their assembly. While our model is not microscopically detailed, we anticipate it captures the coarse-grained behavior of a wide range of surface densities seen in cells.
Stable Surface Densities Can Organize Cellular Processes.
Prewet phases likely facilitate organization of proteins and lipids into stable, long-lived complexes that perform specific functions at distinct sites. Several promising candidate structures are involved in localizing machinery to neuronal synapses. The postsynaptic density of excitatory synapses is composed of phase-separating bulk proteins (12) adhered to a membrane domain enriched in particular ion channels, receptors, and other components. Some of these proteins, like PSD-95 are heavily palmitoylated, a modification that is dynamically regulated and confers a preference for ordered membrane lipids (39). Palmitoylated PSD-95 likely plays a role analogous to the tethers in our model, connecting membrane components to cytoplasmic components of the postsynaptic density. The inhibitory postsynaptic density displays broadly similar organization to its excitatory counterpart, but with different protein–protein interactions that instead localize inhibitory ion channels and the overlapping machinery required there (40). On the presynaptic side, RIM/RIM-BP condensates cluster calcium channels and machinery mediating synaptic vesicle release (14). Common across these examples are liquid structures at the membrane whose components undergo constant turnover yet whose organization and function persist over longer time scales. As in our model, the combination of membrane-mediated forces and bulk interactions allows for a stable domain highly enriched in particular components even while individual components remain mobile.
Formation of Surface Densities Can Transduce Signals.
Prewet surface phases can play a role in signal integration by coupling receptor activation to the creation of an environment that promotes signaling outcomes. While numerous candidate signaling systems exist, the one with the most experimental support is T cell receptor (TCR) signaling, in which ligand binding leads to TCR phosphorylations, the recruitment of scaffolds and signaling mediators that couple to downstream cellular responses. Measurements in reconstituted systems support the idea that these scaffolds are surface densities whose formation is triggered by the phosphorylation of membrane-bound LAT, enhancing interactions with soluble binding partners (11). In the context of our model, LAT phosphorylation is equivalent to strengthening interactions between tethers and bulk polymers, which could nucleate a prewet phase. Moreover, LAT is itself palmitoylated (41), likely conferring a character to LAT tethered surface densities in T cell membranes (42), analogous to the preference for tethers in our model. This may contribute to why the membrane at the TCR and other immune receptor clusters have characteristics associated with domains (43–45). Another possible candidate is the activation of the unfolded protein response in the endoplasmic reticulum (ER), which requires clustering of the integral membrane protein IRE1 (46). IRE1 is thought to form phase-separated clusters both in response to unfolded protein stress (46, 47) and when lipid metabolism is disrupted through sensing membrane disorder (48).
In general, we propose that prewet phases serve natural roles in signaling networks owing to their unique physics. While the specific proteins involved in these signaling networks are diverse, their commonality may be activated receptors seeding domains that bring downstream components into close proximity. In each case a signal leads to increased interactions, between membrane-bound components (like increasing in our model), between membrane and bulk components (like increasing or ), or between particular bulk components (like changing ). Surface transitions depend on bulk, membrane, and tether properties allowing the cell several mechanisms to regulate a single response. Moreover, prewetting is typically a first-order (abrupt) transition, providing a means to transduce a continuous signal into a discrete, switch-like cellular response.
Surface Densities Can Be Driven by Membrane or Bulk Interactions Alone or through a Combination.
The lipid composition of plasma membranes appears to be tuned close to a thermodynamic critical point (8, 24, 25), which we have argued has important consequences for surface phases. Near the membrane critical point, the bulk coupling needed to see surface coexistence rapidly decreases (Fig. 6). We expect that surface densities could be stabilized entirely through membrane criticality-mediated interactions, solely through prewetting interactions between bulk components, or through a mixture of these two forces. We expect the nature of the resulting phases to depend on the relative contributions of membrane- and polymer-mediated interactions. Primarily membrane-dominated surface phases could have only a slight enrichment of bulk polymers over them, while bulk-dominated phases are expected to look more classically prewet, with a molecularly thin layer resembling the bulk phase. Within the membrane, when surface phases are dominated by membrane-mediated interactions, we expect the membrane’s character to resemble that of an independently phase-separated membrane. Alternatively, when polymer forces dominate, the membrane could be just slightly heterogeneous, with enrichment quantitatively predicted by its susceptibility, which is large in the critical region (49).
In cells, proximity of the membrane to its critical point likely allows for weak and diverse interactions between sparse proteins leading to surface phases far outside of their coexistence regime and even far outside of the regime in which they would prewet a single component membrane. While our model assumes that the interaction between tethers is mediated by the membrane’s propensity to phase separate, other attractive interactions between membrane components would likely lead to similar results.
Experimental Signatures of Surface Densities.
Protein-dominated and membrane-only transitions have been well documented in synthetic systems. Synthetic membranes with multiple components can phase separate into coexisting two-dimensional liquid phases in the absence of any proteins (50). Two-dimensional coexisting phases are also observed on single-component membranes, driven by interactions between bulk proteins, some of which adhere (51, 52). Because these interactions are stable outside of the regime of bulk coexistence, they are most likely prewet. Similar experiments coupling multicomponent membranes to proteins highlight the bulk’s ability to mediate interactions between membrane lipids (53, 54).
Two key predictions of our model have not yet been confirmed. First, we predict that three-phase surface coexistence should be possible even in systems where both the surface and the bulk can only independently phase separate into two phases each. We also predict that surface densities can form in regimes where the membrane cannot phase separate on its own and where the bulk cannot phase separate either in three dimensions or onto a uniform membrane. Demonstrating these novel regimes requires mapping the bulk and membrane-only phase diagrams as well as the surface phase diagram for the combined system. We predict that the prewetting regime will expand when membranes have nearly critical compositions, compared to that of single-component membranes. Far from the membrane’s critical point we expect surface densities will molecularly resemble that of the nearby three-dimensional liquid. Conversely, close to the membrane’s transition we expect domains relatively sparse in bulk polymers to be stable far outside of the dome of bulk coexistence.
Many examples in biology display some of the phenomena we investigate here but with additional complications. We do not account for effective forces that may arise from membrane deformation (55–57), the putative prewetting of other biological surfaces such as DNA (58), or the adhesion of multiple membranes (13, 59, 60) so we cannot explore their consequences here.
Prewetting Appears to Be More Common Than Wetting in Cellular Phase Separation.
Nearly all recently described cytoplasmic condensates are observed away from membranes (1, 31), even though our model suggests that only weak, tether-driven interactions are required for membrane wetting. By contrast, a large number of cellular structures appear to be prewet—forming thin films on specific membrane domains outside of bulk coexistence. This may suggest that attractive interactions between droplets and cytoskeletal elements outcompete interactions with membrane components or that these interactions are limited by material properties of the cortex (61, 62). The prediction of prewetting (19) significantly preceded its first experimental realizations (63, 64). Prewet phases outside of biology typically require fine-tuning and subtle experimental considerations to observe. By contrast, in biological contexts, surface densities appear to be common, owing to the presence of a complex membrane with a propensity to phase separate interacting with a dense polymer solution. Our conception of surface densities includes membrane-dominated phases, close to the usual concept of a lipid raft, and bulk-driven phases that closely match the classical concept of prewetting, as well as phases that make use of a combination of these interactions. We hope that future work will clarify the roles these surface densities play in diverse cellular functions.
Materials and Methods
Monte Carlo Simulations.
Monte Carlo simulations were implemented on a three-dimensional lattice () populated with polymers, tethers, and a membrane simulated by an Ising model. The lattice is periodic in the two dimensions and has free boundary conditions at , with the Ising model located at the boundary. Our model is described by a simple Hamiltonian:
| [4] |
where is the interaction strength between polymers of different types (“red” and “blue”), is a nearest-neighbor energy, and is the chemical potential of the 3D system. The spins within the Ising model interact with coupling and components of the bulk interact with tethers through .
Bulk Polymers.
Cytoplasmic proteins are simulated as a mixture of lattice polymers. Bulk polymers occupy the vertices of a 3D cubic lattice. Snake-like moves where the tail of the polymer is moved to a free space adjacent to the head (and vice versa) allow polymers to explore the lattice. Here we simulate just two bulk polymer species and a single tether species. Polymers of the same type cannot inhabit the same lattice position while polymers of opposite type interact through when occupying the same lattice site. All bulk polymers interact equally with tethers. Additionally, all polymers and tethers have small, favorable nearest-neighbor interactions . This nearest-neighbor energy is required to give the droplets tension, without which they do not condense (26, 27).
Tethers.
Tethers move in two dimensions across the surface of the Ising model. Proposed moves translate a tether one lattice space in a random direction. Proposals that move the tether off of an up spin or result in two tethers occupying the same lattice site are immediately rejected.
Membrane.
The membrane is simulated as a conserved order parameter Ising model, implemented on a 2D cubic lattice with periodic boundary conditions. To conserve the total magnetization, or lipid composition, we use a nonlocal Kawasaki move where Ising spins are exchanged rather than flipped. We fix up spins at every tether-occupied site during each sweep.
Simulation Scheme.
Each simulation consists of sweeps through polymers, tethers, and membrane spins. We proposed moves through a randomized sequence of polymers and tethers in the system, followed by a sweep through all Ising spins and proposal of particle exchanges. We equilibrate simulations by raising bulk coupling and tether coupling in increments of 0.05 to with to Monte Carlo sweeps per temperature step. Simulations were sometimes extended from the previous endpoints, for up to Monte Carlo sweeps at a single set of parameters, to ensure equilibration. Single-polymer, tether, and Ising moves are accepted with the Metropolis probability where are the energies of the final and initial system configurations. To accelerate equilibration we propose cluster moves where a connected set of polymers translates one lattice spacing. Cluster moves are proposed with probability and are accepted only if the move does not form or break any bonds, satisfying detailed balance. In simulations at fixed , polymers are exchanged between the system and a noninteracting reservoir. The amount of polymers exchanged per Monte Carlo step is sampled from a Poisson distribution where , ensuring that chemical potential remains constant as particles are added to the system. Exchanges are accepted with probability , where is the change in nearest-neighbor energy. Exchanges that remove or add bonds to the system are immediately rejected. Swapping a particle from the reservoir to the system simply copies the reservoir particle into the system while moving a particle from the system to the reservoir removes the particle from the system but does not place an additional particle in the reservoir. This scheme of “virtual” exchanges is done so the reservoir is effectively infinite while we simulate only a finite amount of particles.
Extracting Surface Composition from Simulations.
To obtain the membrane and tether compositions of simulations that appeared to have three coexisting phases, we analyzed histograms of membrane and tether composition. First, we averaged the membrane spins and tether positions over 50,000 Monte Carlo steps (MCS). From this time-average, we scanned the surface with a 5 × 5 grid, computing the average membrane and tether compositions within. These values are collected over the last half of the simulation run, 2,500,000 MCS, and used to construct a two-dimensional histogram of tether and membrane compositions. We defined the surface composition of coexisting phases as the peaks of this histogram. Because there were multiple peaks likely corresponding to a single phase, we required that the difference in tether density between peaks was greater than 0.05.
Mean-Field Theory.
To minimize the free energy of our system we sought to express the contributions from bulk terms in terms of surface and bulk densities and , as these alone determine the density profile. Following previous work (17, 19), we identify spatial gradients with distance from
where this follows from the functional derivative . We use this identity to express the contributions from spatial variations of in terms of and :
| [5] |
The total free energy of the bulk and surface terms, , can now be written as
| [6] |
which we minimize numerically over values of , , and to obtain results throughout the text. can be minimized independently over , or values to obtain the surface free energy as a function of the remaining terms, as plotted in Fig. 5 A and C.
Numerical Phase Diagrams.
We minimized numerically with Mathematica. We calculated solutions at over a range of values to find coexistence regions. When there were multiple solutions with near-identical energies, within , we declared them coexisting phases. Values of that minimize the free energy at these points terminate tie lines in a fixed composition system. This procedure is visualized in Fig. 7 A and B, where the , values in Fig. 7A correspond to values in Fig. 7B. Multiple phase diagrams in the space of were constructed through combining the tie lines and three-phase regions of phase diagrams calculated at values of and . At specific , values we then determined whether one, two, or three phases were stable.
Supplementary Material
Acknowledgments
We thank Isabella Graf and Jon Machta for helpful comments on a draft and Ilya Levental and Hong-Yin Wang for useful discussions. This work was supported by NSF Grants 1808551 (to S.L.V. and B.B.M.) and 1522467 (to M.R.) and NIH Grants R35GM138341 (to B.B.M.) and R01GM129347 (to S.L.V. and B.B.M.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. K.S. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2103401118/-/DCSupplemental.
Data Availability
All study data are included in this article and/or SI Appendix. Code used in Monte Carlo simulations, Landau theory calculations, example simulation videos, and the SI Appendix can be found on GitHub (https://github.com/SimludDalhec/critical-membrane-prewetting).
References
- 1.Alberti S., Phase separation in biology. Curr. Biol. 27, R1097–R1102 (2017). [DOI] [PubMed] [Google Scholar]
- 2.Sengupta P., Baird B., Holowka D., Lipid rafts, fluid/fluid phase separation, and their relevance to plasma membrane structure and function. Semin. Cell Dev. Biol. 18, 583–590 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brangwynne C. P., et al., Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 324, 1729–1732 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Li P., et al., Phase transitions in the assembly of multivalent signalling proteins. Nature 483, 336–340 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Priftis D., Tirrell M., Phase behaviour and complex coacervation of aqueous polypeptide solutions. Soft Matter 8, 9396–9405 (2012). [Google Scholar]
- 6.Honerkamp-Smith A. R., Veatch S. L., Keller S. L., An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochim. Biophys. Acta – Biomembranes. 1788, 53–63 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baumgart T., et al., Large-scale fluid/fluid phase separation of proteins and lipids in giant plasma membrane vesicles. Proc. Natl. Acad. Sci. U.S.A. 104, 3165–3170 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Veatch S. L., et al., Critical fluctuations in plasma membrane vesicles. ACS Chem. Bio. 3, 287–293, 929 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Burns M., Wisser K., Wu J., Levental I., Veatch S. L., Miscibility transition temperature scales with growth temperature in a zebrafish cell line. Biophys. J. 113, 1212–1222 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Banjade S., Rosen M. K., Phase transitions of multivalent proteins can promote clustering of membrane receptors. eLife 3, e04123 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Su X., et al., Phase separation of signaling molecules promotes T cell receptor signal transduction. Science 352, 595–599 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zeng M., et al., Phase transition in postsynaptic densities underlies formation of synaptic complexes and synaptic plasticity. Cell 166, 1163–1175.e12 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Beutel O., Maraspini R., Pombo-García K., Martin-Lemaitre C., Honigmann A., Phase separation of zonula occludens proteins drives formation of tight junctions. Cell 179, 923–936.e11 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Wu X., et al., RIM and RIM-BP form presynaptic active-zone-like condensates via phase separation. Mol. Cell 73, 971–984.e5 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Zeng M., et al., Reconstituted postsynaptic density as a molecular platform for understanding synapse formation and plasticity. Cell 174, 1172–1187.e16 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Case L. B., Zhang X., Ditlev J. A., Rosen M. K., Stoichiometry controls activity of phase-separated clusters of actin signaling proteins. Science 363, 1093–1097 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.de Gennes P. G., Wetting: Statics and dynamics. Rev. Mod. Phys. 57, 827–863 (1985). [Google Scholar]
- 18.Bonn D., Eggers J., Indekeu J., Meunier J., Rolley E., Wetting and spreading. Rev. Mod. Phys. 81, 739–805 (2009). [Google Scholar]
- 19.Cahn J. W., Critical point wetting. J. Chem. Phys. 66, 3667–3672 (1977). [Google Scholar]
- 20.Nakanishi H., Fisher M. E., Multicriticality of wetting, prewetting, and surface transitions. Phys. Rev. Lett. 49, 1565–1568 (1982). [Google Scholar]
- 21.Brangwynne C. P., Tompa P., Pappu R. V., Polymer physics of intracellular phase transitions. Nat. Phys. 11, 899–904 (2015). [Google Scholar]
- 22.Honerkamp-Smith A. R., et al., Line tensions, correlation lengths, and critical exponents in lipid membranes near critical points. Biophys. J. 95, 236–246 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Machta B. B., Papanikolaou S., Sethna J. P., Veatch S. L., Minimal model of plasma membrane heterogeneity requires coupling cortical actin to criticality. Biophys. J. 100, 1668–1677 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gray E., Karslake J., Machta B. B., Veatch S. L., Liquid general anesthetics lower critical temperatures in plasma membrane vesicles. Biophys. J. 105, 2751–2759 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gray E. M., Díaz-Vázquez G., Veatch S. L., Growth conditions and cell cycle phase modulate phase transition temperatures in RBL-2H3 derived plasma membrane vesicles. PLoS One 10, e0137741 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Freeman Rosenzweig E. S., et al., The eukaryotic CO2-concentrating organelle is liquid-like and exhibits dynamic reorganization. Cell 171, 148–162.e19 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Xu B., et al., Rigidity enhances a magic-number effect in polymer phase separation. Nat. Commun. 11, 1561 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Priftis D., Tirrell M., Phase behaviour and complex coacervation of aqueous polypeptide solutions. Soft Matter 8, 9396–9405 (2012). [Google Scholar]
- 29.Priftis D., Laugel N., Tirrell M., Thermodynamic characterization of polypeptide complex coacervation. Langmuir 28, 15947–15957 (2012). [DOI] [PubMed] [Google Scholar]
- 30.Snead W. T., Gladfelter A. S., The control centers of biomolecular phase separation: How membrane surfaces, PTMs, and active processes regulate condensation. Mol. Cell 76, 295–305 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shin Y., Brangwynne C. P., Liquid phase condensation in cell physiology and disease. Science 357, eaaf4382 (2017). [DOI] [PubMed] [Google Scholar]
- 32.Jiang H., et al., Protein lipidation: Occurrence, mechanisms, biological functions, and enabling technologies. Chem. Rev. 118, 919–988 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qamar S., et al., FUS phase separation is modulated by a molecular chaperone and methylation of arginine cation-π interactions. Cell 173, 720–734.e15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goldenfeld N., Lectures on Phase Transitions and the Renormalization Group (Frontiers in Physics, Addison-Wesley, Advanced Book Program, Reading, MA, 1992), vol. 85. [Google Scholar]
- 35.Binder K., Landau D. P., Wetting and layering in the nearest-neighbor simple-cubic Ising lattice: A Monte Carlo investigation. Phys. Rev. B Condens. Matter 37, 1745–1765 (1988). [DOI] [PubMed] [Google Scholar]
- 36.Binder K., Landau D. P., Wansleben S., Wetting transitions near the bulk critical point: Monte Carlo simulations for the Ising model. Phys. Rev. B Condens. Matter 40, 6971–6979 (1989). [DOI] [PubMed] [Google Scholar]
- 37.Reynwar B. J., Deserno M., Membrane composition-mediated protein-protein interactions. Biointerphases 3, FA117–FA124 (2008). [DOI] [PubMed] [Google Scholar]
- 38.Machta B. B., Veatch S. L., Sethna J. P., Critical Casimir forces in cellular membranes. Phys. Rev. Lett. 109, 138101 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tulodziecka K., et al., Remodeling of the postsynaptic plasma membrane during neural development. Mol. Biol. Cell 27, 3480–3489 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bai G., Wang Y., Zhang M., Gephyrin-mediated formation of inhibitory postsynaptic density sheet via phase separation. Cell Res. 31, 312–325 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhang W., Trible R. P., Samelson L. E., LAT palmitoylation: Its essential role in membrane microdomain targeting and tyrosine phosphorylation during T cell activation. Immunity 9, 239–246 (1998). [DOI] [PubMed] [Google Scholar]
- 42.Levental I., Lingwood D., Grzybek M., Coskun U., Simons K., Palmitoylation regulates raft affinity for the majority of integral raft proteins. Proc. Natl. Acad. Sci. U.S.A. 107, 22050–22054 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Harder T., Rentero C., Zech T., Gaus K., Plasma membrane segregation during T cell activation: Probing the order of domains. Curr. Opin. Immunol. 19, 470–475 (2007). [DOI] [PubMed] [Google Scholar]
- 44.Stone M. B., Shelby S. A., Núñez M. F., Wisser K., Veatch S. L., Protein sorting by lipid phase-like domains supports emergent signaling function in B lymphocyte plasma membranes. eLife 6, e19891 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Holowka D., Baird B., Roles for lipid heterogeneity in immunoreceptor signaling. Biochim. Biophys. Acta Mol. Cell Biol. Lipids 1861, 830–836 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Aragón T., et al., Messenger RNA targeting to endoplasmic reticulum stress signalling sites. Nature 457, 736–740 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Belyy V., Tran N.-H., Walter P., Quantitative microscopy reveals dynamics and fate of clustered IRE1α. Proc. Natl. Acad. Sci. U.S.A. 117, 1533–1542 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Halbleib K., et al., Activation of the unfolded protein response by lipid bilayer stress. Mol. Cell 67, 673–684.e8 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Zhao J., Wu J., Veatch S. L., Adhesion stabilizes robust lipid heterogeneity in supercritical membranes at physiological temperature. Biophys. J. 104, 825–834 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Veatch S. L., Keller S. L., Seeing spots: Complex phase behavior in simple membranes. Biochim. Biophys. Acta Mol. Cell Res. 1746, 172–185 (2005). [DOI] [PubMed] [Google Scholar]
- 51.Last M. G. F., Deshpande S., Dekker C., pH-controlled coacervate-membrane interactions within liposomes. ACS Nano 14, 4487–4498 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Love C., et al., Reversible pH-responsive coacervate formation in lipid vesicles activates dormant enzymatic reactions. Angew. Chem. Int. Ed. Engl. 59, 5950–5957 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lee I.-H., Imanaka M. Y., Modahl E. H., Torres-Ocampo A. P., Lipid raft phase modulation by membrane-anchored proteins with inherent phase separation properties. ACS Omega 4, 6551–6559 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chung J. K., et al., Coupled membrane lipid miscibility and phosphotyrosine-driven protein condensation phase transitions. Biophys. J. 119, S0006349520307281 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yuan F., et al., Membrane bending by protein phase separation. Proc. Natl. Acad. Sci. U.S.A. 118, e2017435118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bergeron-Sandoval L.-P., et al., Endocytosis caused by liquid-liquid phase separation of proteins. bioRxiv [Preprint] (2017). 10.1101/145664 (Accessed 27 January 2021). [DOI]
- 57.Day K. J., et al., Liquid-like protein interactions catalyse assembly of endocytic vesicles. Nat. Cell Biol. 23, 366–376 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Morin J. A., et al., Surface condensation of a pioneer transcription factor on DNA. BioRxiv [Preprint] (2020). 10.1101/2020.09.24.311712 (Accessed 23 January 2021). [DOI]
- 59.Rothman J. E., Jim’s View: Is the Golgi stack a phase-separated liquid crystal? FEBS Lett. 593, 2701–2705 (2019). [DOI] [PubMed] [Google Scholar]
- 60.Rebane A. A., et al., Liquid-liquid phase separation of the Golgi matrix protein GM130. FEBS Lett. 594, 1132–1144 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rosowski K. A., et al., Elastic ripening and inhibition of liquid-liquid phase separation. Nat. Phys. 16, 422–425 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ronceray P., Mao S., Košmrlj A., Haataja M. P., Liquid demixing in elastic networks: Cavitation, permeation, or size selection? arXiv [Preprint] (2021). https://arxiv.org/abs/2102.02787 (Accessed 17 February 2021).
- 63.Rutledge J. E., Taborek P., Prewetting phase diagram of 4He on cesium. Phys. Rev. Lett. 69, 937–940 (1992). [DOI] [PubMed] [Google Scholar]
- 64.Kellay H., Bonn D., Meunier J., Prewetting in a binary liquid mixture. Phys. Rev. Lett. 71, 2607–2610 (1993). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in this article and/or SI Appendix. Code used in Monte Carlo simulations, Landau theory calculations, example simulation videos, and the SI Appendix can be found on GitHub (https://github.com/SimludDalhec/critical-membrane-prewetting).