Significance
How do brains adapt to changing resource constraints? This is particularly relevant in the aging brain, for which the ability of neurons to utilize their primary energy source, glucose, is diminished. Through experiments and modeling, we find that changes to brain activity patterns with age can be understood in terms of decreasing metabolic activity. Specifically, we find that older brains approach a critical point in our model, enabling small changes in metabolic activity to give rise to an abrupt reconfiguration of functional brain networks.
Keywords: fMRI, aging, neurometabolism, synchrony, criticality
Abstract
Brain aging is associated with hypometabolism and global changes in functional connectivity. Using functional MRI (fMRI), we show that network synchrony, a collective property of brain activity, decreases with age. Applying quantitative methods from statistical physics, we provide a generative (Ising) model for these changes as a function of the average communication strength between brain regions. We find that older brains are closer to a critical point of this communication strength, in which even small changes in metabolism lead to abrupt changes in network synchrony. Finally, by experimentally modulating metabolic activity in younger adults, we show how metabolism alone—independent of other changes associated with aging—can provide a plausible candidate mechanism for marked reorganization of brain network topology.
One of the most fundamental questions in neuroscience is how the familiar patterns of collective, brain-wide activity arise from the properties of the constituent neurons and their networks. Here, we study how the brain’s global activity patterns change with age and how those changes might arise from the reduced metabolic activity of constituent regions.
We draw on two types of experimental evidence. First, as established using positron emission tomography, older brains show reduced glucose metabolism (1–3). Second, as established by functional MRI (fMRI), aging is associated with weakened functional connectivity (FC; i.e., reduced communication [on average] between brain regions) (4–6). Combining both observations suggests that impaired glucose metabolism may underlie changes in FC (1, 7). Supporting this link are studies showing disruptions similar to those seen with aging in type 2 diabetic subjects (8, 9).
In healthy brains, resting-state brain activity (states during which subjects are not engaged in any explicit task) alternates between segregating computations within localized functional domains and integrating this information across these domains (7, 10–13). The metabolic cost of these activities increases in proportion to the number and length of functional connections between pairs of brain regions (14), making highly connected (integrated) networks more energetically costly (10). Moreover, connections with the highest cost are the first to weaken with age (6, 7, 15, 16). Thus, it has been hypothesized that declining glucose metabolism in older brains drives the loss of high-cost (integrated) functional activities (14, 16). Yet, the relationship between energetic constraints at the level of individual regions and the apparent reorganization of the functional connectome is still not well understood.
Statistical physics, which interprets the collective properties of complex systems in terms of individual interactions between the underlying parts, provides powerful tools for understanding how brain networks reorganize under constraints (17, 18). In particular, we employ an Ising model (19–21) to describe how pairwise interactions between brain regions give rise to specific profiles of network synchrony, a time-dependent average of the activity over the brain (22–24). The Ising model is a simple yet powerful tool to capture ordered and disordered phases and the transitions between them. It assumes that two things matter in understanding the collective behaviors of a system of agents (brain regions in this case): the topological relationships among the agents and their strength of interaction. This perspective can provide insight into global changes in FC observed in the data by assuming that brain regions are fully connected with a single average interaction strength.
While the Ising model provides a general tool for describing the collective properties of complex systems, we adapt it to examine the specific relationship between brain aging and metabolic activity. To achieve this, we analyzed four resting-state fMRI datasets. We utilized two large-scale resting-state 3T (Tesla) fMRI datasets to identify aging related effects: the Cambridge Centre for Aging and Neuroscience Stage II Study (Cam-CAN; ages 18 to 88, ) (25) and the Human Connectome Project Aging fMRI dataset (HCP-A; ages 36 to 100, ) (26). To assess metabolic effects, we used two 7T fMRI datasets from the Protecting the Aging Brain fMRI data repository: a Bolus dataset (PAgB Bolus; ages 21 to 48, ) consisting of a within-subject experiment in which individuals were scanned following separate administration of calorie-matched glucose and ketones (d--hydroxybutyrate ketone ester [D-Hb]) and a Diet dataset (PAgB Diet; ages 21 to 43, ) consisting of an independent within-subject experiment of healthy, young adults scanned at resting state while on glycolytic and ketogenic diets (27). Ketone bodies decrease the relative free energy of adenosine triphosphate (ATP) production by approximately as compared with glucose (28). The additional efficiency of ketone bodies as a cellular fuel source, observed even in healthy subjects, has been shown to increase both cardiac efficiency (28) as well as brain activity (27).
The significance of this work is threefold. First, we demonstrate that the Ising model, with a fully connected topology, provides a mechanism for how FC patterns change in qualitatively abrupt ways as a function of the average interaction between brain regions (18). Second, we establish a direct link between network synchrony and the relative frequencies of integrated (high-cost) and segregated (low-cost) brain activities (10, 14). Finally, we suggest a precise relationship between differences in FC over the life span as well as in response to changes in the brain’s access to energy.
Methods
Life Span and Metabolic Neuroimaging Datasets.
The Cam-CAN life span study was designed to identify neurobiological correlates of normal aging and provides a roughly uniform coverage of age groups, allowing comparison between groups as well as a wide array of behavioral measures. We excluded 10 subjects from analysis due to severe structural atrophy that precluded coregistration to a standard brain template (, 321 female).
The HCP-A study of healthy adults was comparable with the Cam-CAN dataset in terms of both its goals and design but differed in acquisition parameters and preprocessing methods. Given these differences, we used the HCP-A dataset to test the generalizability of our results with respect to aging.
The PAgB Bolus study consisted of two within-subject conditions time locked on separate days: 1) D-Hb ketone ester bolus following a 12-h overnight fast (deltaG, TdeltaS Ltd, Thame, UK) and 2) glucose bolus following a 12-h overnight fast, breaking an overnight fast with a glucose drink (Glucose Tolerance Test Beverages; Fisher Scientific, Inc.). The D-Hb ketone ester was weight dosed for each participant at 395 mg/kg and calorie matched between D-Hb ketone ester and glucose (detailed documentation of the dataset may be found in ref. 27).
The PAgB Diet study scanned participants under three conditions: 1) standard diet: following their standard diet without fasting; 2) fasting: following their standard diet with an overnight (12-h) fast; and 3) ketogenic diet: following a ketogenic (high-fat, moderate-protein, low-carbohydrate [50-g/d]) diet for 1 wk, by which point all participants were in ketosis (0.6 mmol/L ketone blood concentration). Of these, we examined the standard (glycolytic) and ketogenic conditions to test the generalizability of our results in the context of metabolism. All conditions were conducted at resting state. Detailed documentation of the two PAgB metabolic datasets may be found in ref. 27.
MRI Acquisition.
The Cam-CAN life span dataset contains multiple imaging modalities, including blood oxygen level–dependent (BOLD) MRI and magnetoencephalography (MEG). The neuroimaging experiments of the Cam-CAN study were conducted in Cambridge, United Kingdom at the Medical Research Council Cognition and Brain Sciences Unit. We focused on the resting-state BOLD echo-planar imaging (EPI) scans collected at 3T field strength over 8 min and 40 s. The BOLD EPI imaging protocol consisted of repetition time (TR) = 1,970 ms, echo time (TE) = 30 ms, flip angle = , voxel size = mm, slices = 32, and number of measurements = 261. Further acquisition details can be found in ref. 25.
The HCP-A dataset was collected at four different sites while using identical equipment and parameters. Images were acquired at 3T field strength through two separate sessions for each subject. We concatenated the time series from the two sessions within each subject, resulting in a total of 26 min of resting-state fMRI data. The BOLD EPI imaging protocol consisted of TR = 800 ms, TE = 37 ms, flip angle = , voxel size = mm, slices = 72, number of measurements = 2 × 488 per session, and 1,952 volumes in total. Further acquisition details can be found in ref. 29.
The two PAgB metabolic datasets (PAgB Bolus and PAgB Diet) were acquired at the Athinoula A. Martinos Center for Biomedical Imaging. Images were collected at 7T field strength with identical parameters for the two datasets. Resting-state BOLD images were 10 min long each and involved a protocol quantitatively optimized, using a dynamic phantom, for detection sensitivity to resting-state networks (30, 31). The BOLD EPI imaging protocol consisted of TR = 802 ms, TE = 20 ms, flip angle = , voxel size = mm, slices = 85, and number of measurements = 740 in each resting-state session. Further acquisition details can be found in ref. 27.
MRI Preprocessing.
Aside from the HCP-A data, which were provided in an already preprocessed form, we preprocessed all fMRI data using fMRIPrep (20.0.6), which is based on Nipype 1.4.2 (32, 33). First, the T1-weighted (T1w) structural images were corrected for intensity nonuniformity and skull stripped. Brain tissue segmentation of cerebrospinal fluid (CSF), white matter, and gray matter was then performed on the brain-extracted T1w images. Subsequently, volume-based spatial normalization to one standard space (ICBM 2009c Nonlinear Asymmetric template) was carried out through nonlinear registration.
For each of the BOLD runs found per subject, images were skull stripped and motion and slice-time corrected. A deformation field to correct for susceptibility distortions was then estimated based on fMRIPrep’s field mapless approach. The BOLD images were then coregistered to the T1w structural images using a boundary-based registration with nine degrees of freedom and resampled into standard space. To control for nonneuronal systemic effects associated with aging and ketosis, white matter and CSF, but not global, signals along with six motion regressors were regressed out using the nilearn package (https://nilearn.github.io).
Preprocessing of the fMRI images from the HCP-A dataset up to this point involved a different procedure. We accessed these images in an already preprocessed state, as per the steps described in refs. 34 and 35.
Finally, for all four datasets, the cleaned voxel space time series were band-pass filtered to include the neuronal frequencies (0.01 to 0.1 Hz) and were parceled into the Willard 498 functional regions of interest.
fMRI Binarization.
In order to access the time-dependent network properties of our data, we first binarize the fMRI time series. This method simplifies the time series while preserving their FC patterns. In particular, the Pearson correlation is widely used to estimate FC between arbitrary pairs of variables ():
| [1] |
Here, variables ( and for example) are the nodes of a graph, and is the weight of the edge between them. However, these connection strengths often change over time (36). To capture these changes, is calculated over each pair of successive time points (i.e., a window length of one), reducing Eq. 1 to
| [2] |
where and are the signs of the time derivatives of and , respectively, and the time-dependent correlation, , is their product. Thus, the binarized derivative method (BDM) takes a raw signal and binarizes it .
While the binarization provides a simplified representation of the raw time series , it still preserves FC (SI Appendix, Fig. S1). For each subject in the life span dataset, we selected a random interval of fixed length (the window size), computed the region–region correlation matrix for both raw and binarized time series (Eq. 1), and then, computed the correlation between both FC estimates. These estimates were highly correlated, regardless of the number of time points (the averaging window) used (SI Appendix, Fig. S1A) and the age of the subject (SI Appendix, Fig. S1B) (window size TR), suggesting that BDM can be used to simplify functional signals while preserving their connectivity patterns. More broadly, the BDM approach has two key advantages over previous methods (36, 37). First, it simplifies complex, many-variable interactions in terms of dynamical patterns of binary ( and ) variables. Second, it is naturally compatible with Ising models, which have been shown to be powerful tools in isolating latent relationships within networks of neurons (21, 24).
Motivation for the Ising Model.
Here, we provide the Ising model of the network synchrony and demonstrate it on a simple system of three interacting regions. Although first developed to describe ferromagnetism, the Ising model can be more generally derived using maximum entropy (19, 21, 24). For a set of binary nodes, such as what is provided by BDM, synchrony is defined mathematically as
| [3] |
where is the value of the th binarized signal at time (24). The Ising model of the distribution of synchronies P(s) (as derived in SI Appendix, Derivation of the Ising Model of fMRI Network Synchrony) is given by
| [4] |
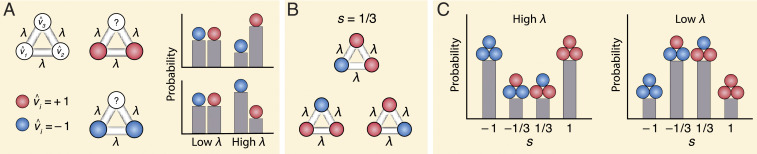
Here, the normalizing constant is called the partition function, a familiar quantity in statistical physics (20). To account for the multiple ways a particular value of synchrony can occur, also contains the binomial prefactor, (Fig. 1). In statistical physics, is equivalent to a well-known model of ferromagnets called the Curie–Weiss (or fully connected) Ising model (38). Conceptually, expresses the average correlation across our N nodes. As a result, represents the average node-to-node interaction strength (over pairs) and is the basic mechanistic quantity of our model (Fig. 1 A, Left). Small values of describe correlational networks in which interactions between nodes are weak and in which the node weights are independent of each other. In contrast, large values of describe networks in which interactions between nodes are strong and node activities are highly correlated (Fig. 1 A, Right). As described earlier, however, a given value of synchrony may be obtained in many different ways (i.e., it is degenerate) (Fig. 1B). Therefore, when is small, is determined by the degeneracy, and low synchronies are most likely. Conversely, when is large, is determined by the interactions between nodes, and higher synchronies are more likely. In particular, as is varied, the relative importance of each of these terms changes. As can be seen in Fig. 1C, this causes to change from a bimodal (Fig. 1 C, Left) to a unimodal (Fig. 1 C, Right) distribution. For the Ising model, this shift occurs at the critical point (38). To simplify our future analysis, we will now refer only to the rescaled interaction : .
Fig. 1.
The Ising model predicts network probabilities from interactions between its nodes. (A) The Ising model maps binary variables onto a fully connected network (Left). Each variable (1, 2, N) is a node with binary weight (represented by the colors red and blue), and each pair of nodes is connected by an edge with weight . Here, we show the example of . The value of () describes the average interaction strength between nodes; the larger is, the more likely the unknown value of is to be similar to its neighbors (Right). (B and C) The probability of each network is determined by its synchrony (s). (B) Multiple graphs give the same value of synchrony. Since there are three ways to have one blue node and two red nodes, there are three different graphs that give (red minus blue divided by ). This degeneracy effectively triples the probability of . (C) The probability distribution of given by the Ising model is a function of and degeneracy. When (interaction) is large, the probability that is large (Left). However, when is small, degeneracy wins out, and the probability that is large (Right).
Model Fitting.
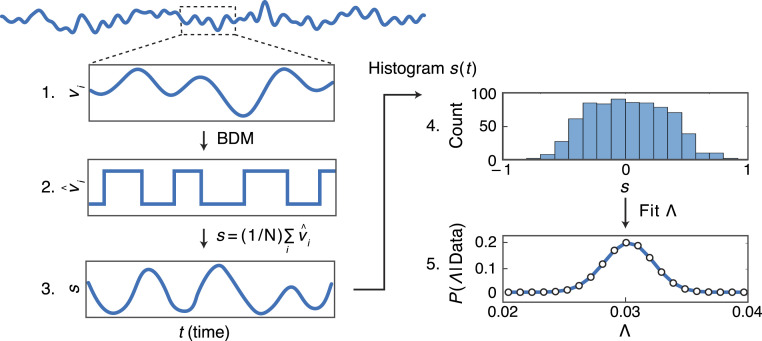
We next fit the Ising model to our data (Fig. 2). First, we took the fMRI signal for each region and time and binarized it using BDM. The model assumes that all regions have, on average, similar FC strengths. We tested this assumption by computing the total (over all pairs) FC for each region, and we used the subject-averaged (over Cam-CAN and PAgB Bolus) FC matrix as our reference (SI Appendix, Fig. S2). From these signals, we selected a subset of 100 positively correlated brain regions with greatly elevated FC in younger (age ) compared with older (age ) subjects. As validation, we find that our theory is robust to this choice (SI Appendix, Fig. S3). For each subject, we then computed the time-dependent synchrony using the binarized fMRI signals from the 100 selected regions of the brain. We then took the histogram of for each subject to get a distribution , giving the variation in synchrony per individual. This was then used to obtain by fitting to the Ising model. Here, the precision of the fit is a function of the Bayesian posterior distribution . We use a uniform (unbiased) prior distribution of ; thus, the posterior is computed directly from the likelihood function , with given by Eq. 4. In practice, we will summarize this posterior by its peak (the maximum likelihood estimate) and its width (error bars). Small relative error bars indicate high confidence in the fitted values of . For the Ising model, the maximum likelihood estimator for satisfies
| [5] |
where is the number of time points used. To account for autocorrelation within the fMRI time series (which effectively reduces the number of independent samples available for each subject), we consider 0.01 likelihood ratio error bars for . This approximately corresponds to one SE with a maximum synchrony autocorrelation time of 10 TR (i.e., at minimum, of the samples are uncorrelated) or three SEs if all points are independent.
Fig. 2.
How we obtain the Ising model parameter from fMRI data. 1) The fMRI signal from the th brain region (of 100) as a function of time . 2) We binarize it to give . 3) The binarized signals are then averaged over all brain regions, giving that individual’s time-dependent synchrony . 4) We then histogram into the different values over time to express the variations in an individual’s synchrony levels. 5) We find the value of that best fits for each individual. expresses the Bayesian posterior probability (with a uniform prior distribution over ) that our data were generated from an Ising model (Eq. 4) with relative interaction strength .
Network Identification and Analysis.
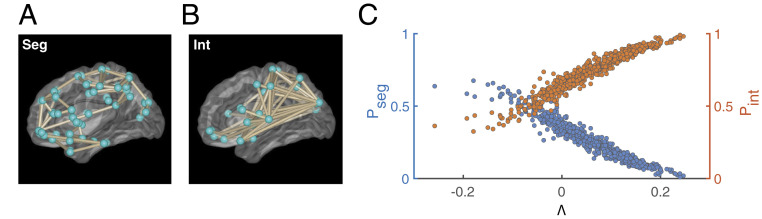
To establish the relationship between and brain network reorganization, we isolated specific functional patterns associated with different values of synchrony. The binarized data were combined across all Cam-CAN subjects () and classified into two categories of synchrony: low () and high (). Time points corresponding to intermediate values of synchrony were excluded (at this stage only) in order to obtain a clear separation between groups. Network connectivity was computed (separately for each group) as the Pearson correlation between each pair of brain regions. During periods of low synchrony, functional connections were found to be sparse, favoring connections between local (segregated) networks of regions. In contrast, periods of high synchrony were characterized by dense connections (integrated) between multiple functional domains across the brain (10). Reflecting these differences, we further refer to these networks as Seg and Int, respectively.
To relate the occupation probabilities of these different networks to , we decomposed the FC matrix (, computed over all synchronies) of each subject into a weighted contribution of Seg and Int:
The weights associated to each subject ( and ) were then computed using a least-squares fit. As a preprocessing step, we zeroed the artificial, diagonal elements and then normalized both networks (by dividing by the total correlation across all elements) to account for differences in scale. To compare these weights across subjects and different values of , we only consider the ratio of these weights:
For each subject, represents the relative proportion of FC explained by the Seg network. In other words, represents the fraction of time spent in segregated networks as compared with integrated networks ().
Results
Here, we analyze the collective properties of fMRI signals and how they change with age and metabolic activity. The collective property of our interest is the observed network synchrony , a measure of the average coordination between the 100 Willard Atlas brain regions selected for our analysis (Model Fitting) (24, 39). In general, collective properties can often be described using mean-field models, where every component of interest is approximated as being connected to every other component with the same strength (24, 40). In addition, the Ising model is known to describe how pairwise interactions among microscopic, binary () elements give rise to macroscopic behaviors (20, 21). Thus, to model how the observed frequencies of different synchronies vary across experimental conditions, we utilize a mean-field Ising model, with a single average interactions strength (assumed positive) between all pairs of brain regions (Fig. 1; SI Appendix, Fig. S2 has further justification).
We find the value of the interaction strength, , that best fits the experimentally observed synchrony values for each subject (Fig. 2). This is equivalent to choosing such that the average value of predicted by the Ising model matches precisely with the empirical estimate for each subject and condition (Eq. 5 and Methods). In addition, we find that this model reasonably captures the full distribution of synchrony observed in the data (SI Appendix, Fig. S4). Most importantly, the Ising model predicts the two qualitatively distinct regimes present in the data: one characterized by a unimodal distribution of synchrony and the other by a broad or bimodal distribution of synchrony.
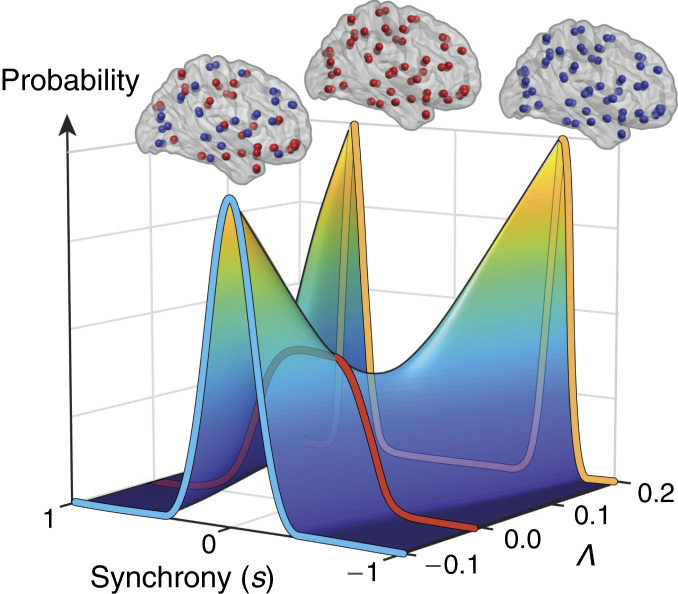
Ising models are useful in understanding how changes in smaller-scale properties (such as the interactions between brain regions) can give rise to abrupt and qualitatively distinct collective phenomena at larger scales. Much like water at its boiling point, which discontinuously changes from liquid to vapor, these changes occur at an intermediate value of the interaction strength, called the critical point. Here, we use to denote the deviation from the critical interaction strength () of the Ising model. Fig. 3 illustrates how the distribution of synchronies (with example brain networks shown for comparison) changes as a function of , from unimodal (low synchrony, ; blue) when to bimodal (high synchrony, ; orange) when . Here, the distributions (which are discrete by nature) are smoothed to simplify the visualization. While both low- and high-synchrony networks are equally likely at the critical point (Fig. 3, red) (), small changes in lead to large, abrupt changes in this balance.
Fig. 3.
The Ising model applied to brain synchrony. Shown is the probability distribution of synchrony (s) for different values of the dimensionless quantity , reflecting the distance of the actual interaction strength, from the critical point : . For (weak interactions), there is a single unimodal population having a peak at (blue line). For (strong interactions), the population is bimodal, with peaks at and (orange line). Above each peak is an example network; nodes are brain regions, and colors are states (red , blue ). defines the critical point, where changes from a minimum to a maximum and P(s) rapidly changes (red line). At the critical point, low- and high-synchrony networks are equally probable.
Different values of synchrony also correspond to different functional network patterns (Fig. 4 and Network Identification and Analysis). In particular, low-synchrony patterns (near ) reflect short-range, domain-specific (segregated) activities (Fig. 4A). In contrast, high-synchrony patterns () capture integration, or long-range communication between distant regions (Fig. 4B). Consequently, just as with synchrony (Fig. 3), different values of change the relative time spent in segregated () and integrated () networks (in Fig. 4C, each colored marker is a subject). When , low synchronies (i.e., segregated networks) occur more frequently, while the opposite holds when . In both cases, this balance rapidly shifts at the critical point, .
Fig. 4.
controls the balance between segregated (low s) and integrated (high s) networks. (A and B) FC (averaged over all Cam-CAN subjects) during low (A) and high (B) synchrony, visualized using the BrainNet Viewer showing the top five percentages of connections (41). (A) Low synchrony () reflects segregation (Seg). (B) High synchrony () reflects integration (Int). (C) The fraction of time each subject (each data point and the specific value of ) spends in integrated (; orange) and segregated (; blue) networks. corresponds to large and small , while corresponds to the opposite. The cross-over in C occurs at the critical point, .
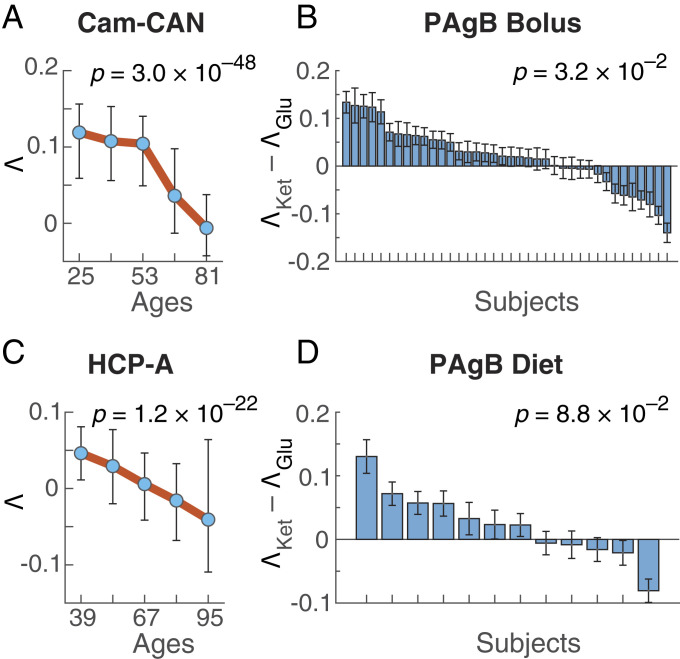
Both age and metabolism-related changes in FC can be described by changes in the region-to-region interaction strength . In particular, we find that significantly decreases with age (Cam-CAN, Spearman rank permutation test, , ) (Fig. 5A), suggesting that aging is associated with a marked shift from integrated toward more segregated network activities. In contrast, upon administration of a more metabolically efficient (higher-energy) ketone bolus compared with a less metabolically efficient (lower-energy) glucose bolus, increases (PAgB Bolus, Wilcoxon one-sided signed rank test, , ) (Fig. 5B) on average by about ( to ) of the decrease seen over the entire life span (28). Thus, by toggling the relative frequencies of segregated and integrated networks, reflects an average cost of functional activity and as suggested by our metabolic manipulation, the energy available to the brain. As aging brains gradually become less efficient in metabolizing glucose, one way that they may conserve energy is by decreasing .
Fig. 5.
significantly decreases with age and increases with a ketogenic metabolism compared with a glycolytic metabolism. (A) Each point (as well as the orange curve connecting them) reflects the median best-fit values for each (of five) equal width (14-y) age groups across Cam-CAN subjects. Error bars represent the upper and lower quartiles. We used a Spearman rank permutation test [, , ] to test significance of the nonlinear relationship between and age. (B) Change in for each PAgB Bolus subject after a higher-energy ketone bolus (Ket) compared with a lower-energy glucose (Glu) bolus. Error bars reflect a 0.01 likelihood ratio CI. A Wilcoxon one-sided signed rank test was used to test if ketones significantly increased (, , ). (C and D) Independent replicates of our findings for both age and metabolism using HCP-A (C) and PAgB Diet (D), respectively.
The application of the Ising model to fMRI is dependent on the magnitude, rather than differences, in the functional connections measured from the data. Consequently, such an analysis could be sensitive to differences in data acquisition, preprocessing, and head motion. To assess reproducibility, we thus replicated our life span and metabolic analyses on two independent resting-state datasets: HCP-A (Spearman rank permutation test, , ) (Fig. 5C) and PAgB Diet (Wilcoxon one-sided signed rank test, , ) (Fig. 5D), respectively. Both sets of analyses qualitatively replicated our original findings, suggesting that our original results were robust to differences in processing pipelines and experimental design. Furthermore, we tested and found no relationship between our results and head motion (SI Appendix, Fig. S6).
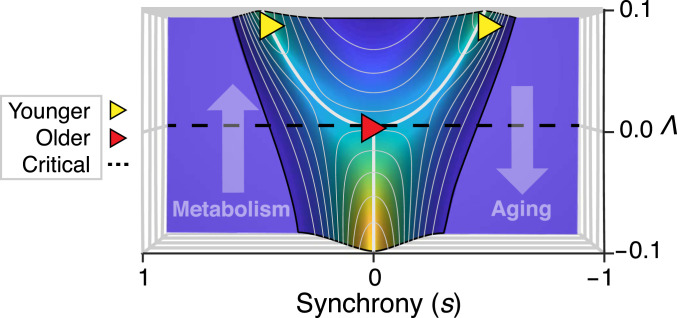
Precisely because aging brains approach the critical point (), however, very small changes in the interaction strength between regions () lead to a sharp transition in the ratio of integrated to segregated networks (20, 21). Fig. 6 expresses this in terms of the probability distribution of , now viewed from the top down. Here, we observe that as brains age, from younger (yellow; age , ) to older (red; age , ), [a proxy for metabolism (14)] decreases toward the critical point (black). Consequently, aging induces a sharp reconfiguration of the distribution of synchrony.
Fig. 6.
Older brains approach a critical point, a behavior we have shown to be consistent with decreased metabolism. Shown is the probability distribution of synchrony () vs. , viewed from the top down. At the critical point (; black line), peak synchrony (indicated by a white line) changes from low () toward high () values. Decreased metabolic activity causes [through associated decreases in FC (14)] to decrease toward a critical point. Thus, aging from younger (yellow) to older (red) induces a sharp reconfiguration in the distribution of synchrony. Here, the plotted triangles correspond to the values (from Cam-CAN) centered at ages 25 (younger) and 81 (older) (Fig. 5).
Discussion
Our results suggest that disrupted transitioning between integrated vs. segregated networks, as seen with aging, can be quantitatively modeled by an Ising model, in which the range of synchronies observed for each individual is controlled by an average interaction strength () between pairs of brain regions. We find that governs a trade-off between lower–metabolic cost, segregated and higher–metabolic cost, integrated neural activity patterns (16). Specifically, the observed link between global resting-state FC patterns and synaptic activity, as measured through the local field potential (22), suggests that reflects the average synaptic connectivity across the brain. Indeed, synaptic connections weaken with age (42, 43) and are particularly vulnerable to metabolic disruptions (44–47). Utilizing subject-matched fMRI and MEG data provided by Cam-CAN, we also find to be significantly correlated with alpha-band MEG coherence, thus providing a potential, more direct link between our findings and disrupted neural dynamics in the aging brain (SI Appendix, Fig. S5) (25, 48). Consistent with our findings, we hypothesize that is decreased in older brains to compensate for encroaching glucose hypometabolism. However, because older brains approach a critical point, even very small metabolic changes will result in large reconfigurations of FC.
Both aging and ketosis exert independent systemic effects that we considered in interpreting our results. For example, older subjects often have cardiovascular changes that affect neurovascular coupling (49) and thus, by extension, the BOLD response measured by fMRI. Likewise, ketosis has systemic effects, such as diuresis and thus, lowered blood pressure, as well as reduced cellular need for oxygen, all of which also could affect BOLD (50). In addition, FC is known to be affected by changes in cerebrovascular reactivity (CVR), which in turn, decreases with age (51). However, there are several reasons to suspect that these alternative mechanisms are not the sole causal influence of shifts in . First, we used a hybrid global signal regression on white matter and CSF voxels, but not gray matter, to minimize the influence of nonneuronal confounds (52, 53). Second, while systemic effects might introduce spurious global correlations across the brain (54–56), they would not be expected to differentiate between integrated and segregated networks. Third, both CVR and MEG alpha-power are modulated by systemic (a by-product of cellular metabolism), suggesting a common metabolic mechanism for these age-associated changes (51, 57). Nevertheless, experimentally dissociating metabolic from more systemic influences of aging and ketosis (e.g., by replicating our results using M/EEG or arterial spin labeling in a large-scale life span dataset that also experimentally modulates metabolism) is one important direction for future research.
In conclusion, the Ising model provides a mechanism for how the brain adapts to resource constraints, such as age-related glucose hypometabolism. By shifting the balance between integration and segregation toward the critical point, the brain may be able to modulate its fuel efficiency without the need to invest in new synaptic connections (7, 14, 16). Thus, toggling may reflect an optimal strategy for the brain, enabling the greatest adaptation for the smallest energetic cost. At the same time, the brain’s protective strategy in conserving energy may produce discontinuous trajectories for cognitive changes associated with aging.
Supplementary Material
Acknowledgments
The research was funded by the W. M. Keck Foundation (K.A.D. and L.R.M.-P.), NSF Brain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiative Grants ECCS1533257 (to K.A.D. and L.R.M.-P.) and NCS-FR 1926 781 (to K.A.D. and L.R.M.-P.), and the Stony Brook University Laufer Center for Physical and Quantitative Biology (K.A.D.).
Footnotes
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2025727118/-/DCSupplemental.
Data Availability
Lifespan fMRI and MEG data are publicly available from Cam-CAN (25). Metabolic fMRI data are located on OpenNeuro (https://openneuro.org/datasets/ds003453 and https://openneuro.org/datasets/ds003437). fMRI data from the HCP-A dataset are publicly available from ref. 26 and were accessed in an already preprocessed state as described in refs. 34 and 35. Additional details, including links to custom MATLAB used in the analyses of data, can be found at GitHub (https://github.com/lcneuro/synch).
References
- 1.Mosconi L., Glucose metabolism in normal aging and Alzheimer’s disease: Methodological and physiological considerations for PET studies. Clin. Transl. Imaging 1, 217–233 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Goyal M. S., et al., Loss of brain aerobic glycolysis in normal human aging. Cell Metab. 26, 353–360.e3 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Castellano C.-A., et al., Lower brain 18F-fluorodeoxyglucose uptake but normal 11C-acetoacetate metabolism in mild Alzheimer’s disease dementia. J. Alzheimers Dis. 43, 1343–1353 (2015). [DOI] [PubMed] [Google Scholar]
- 4.Andrews-Hanna J. R., et al., Disruption of large-scale brain systems in advanced aging. Neuron 56, 924–935 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Geerligs L., Renken R. J., Saliasi E., Maurits N. M., Lorist M. M., A brain-wide study of age-related changes in functional connectivity. Cereb. Cortex 25, 1987–1999 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Achard S., Bullmore E., Efficiency and cost of economical brain functional networks. PLOS Comput. Biol. 3, e17 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bullmore E., Sporns O., The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349 (2012). [DOI] [PubMed] [Google Scholar]
- 8.Profenno L. A., Porsteinsson A. P., Faraone S. V., Meta-analysis of Alzheimer’s disease risk with obesity, diabetes, and related disorders. Biol. Psychiatry 67, 505–512 (2010). [DOI] [PubMed] [Google Scholar]
- 9.Liu D., et al., Disrupted balance of long-and short-range functional connectivity density in type 2 diabetes mellitus: A resting-state fMRI study. Front. Neurosci. 12, 875 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zalesky A., Fornito A., Cocchi L., Gollo L. L., Breakspear M., Time-resolved resting-state brain networks. Proc. Natl. Acad. Sci. U.S.A. 111, 10341–10346 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Friston K. J., Modalities, modes, and models in functional neuroimaging. Science 326, 399–403 (2009). [DOI] [PubMed] [Google Scholar]
- 12.Sporns O., Network attributes for segregation and integration in the human brain. Curr. Opin. Neurobiol. 23, 162–171 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Bassett D. S., Bullmore E., Small-world brain networks. Neuroscientist 12, 512–523 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Tomasi D., Wang G.-J., Volkow N. D., Energetic cost of brain functional connectivity. Proc. Natl. Acad. Sci. U.S.A. 110, 13642–13647 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tomasi D., Volkow N. D., Aging and functional brain networks. Mol. Psychiatry 17, 549–558 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Manza P., et al., Brain network segregation and glucose energy utilization: Relevance for age-related differences in cognitive function. Cereb. Cortex 30, 5930–5942 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Albert R., Barabási A.-L., Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47 (2002). [Google Scholar]
- 18.Betzel R. F., Bassett D. S., Generative models for network neuroscience: Prospects and promise. J. R. Soc. Interface 14, 20170623 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tkacik G., Schneidman E., Berry M. J. II, Bialek W., Spin glass models for a network of real neurons. arXiv [Preprint] (2009). https://arxiv.org/abs/0912.5409 (Accessed 1 September 2021).
- 20.Mora T., Bialek W., Are biological systems poised at criticality? J. Stat. Phys. 144, 268–302 (2011). [Google Scholar]
- 21.Schneidman E., Berry M. J. II, Segev R., Bialek W., Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schölvinck M. L., Maier A., Ye F. Q., Duyn J. H., Leopold D. A., Neural basis of global resting-state fMRI activity. Proc. Natl. Acad. Sci. U.S.A. 107, 10238–10243 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhao L., Alsop D. C., Detre J. A., Dai W., Global fluctuations of cerebral blood flow indicate a global brain network independent of systemic factors. J. Cereb. Blood Flow Metab. 39, 302–312 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tkačik G., et al., Searching for collective behavior in a large network of sensory neurons. PLOS Comput. Biol. 10, e1003408 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Taylor J. R., et al., The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. Neuroimage 144 (Pt B), 262–269 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bookheimer S. Y., et al., The lifespan Human Connectome Project in aging: An overview. Neuroimage 185, 335–348 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mujica-Parodi L. R., et al., Diet modulates brain network stability, a biomarker for brain aging, in young adults. Proc. Natl. Acad. Sci. U.S.A. 117, 6170–6177 (2020)). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sato K., et al., Insulin, ketone bodies, and mitochondrial energy transduction. FASEB J. 9, 651–658 (1995). [DOI] [PubMed] [Google Scholar]
- 29.Harms M. P., et al., Extending the Human Connectome Project across ages: Imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.DeDora D. J., et al., Signal fluctuation sensitivity: An improved metric for optimizing detection of resting-state fMRI networks. Front. Neurosci. 10, 180 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kumar R., et al., Ground-truth “resting-state” signal provides data-driven estimation and correction for scanner distortion of fMRI time-series dynamics. Neuroimage 227, 117584 (2021). [DOI] [PubMed] [Google Scholar]
- 32.Esteban O., et al., fMRIPrep: A robust preprocessing pipeline for functional MRI. Nat. Methods 16, 111–116 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gorgolewski K., et al., Nipype: A flexible, lightweight and extensible neuroimaging data processing framework in python. Front. Neuroinform. 5, 13 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Glasser M. F., et al., The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Glasser M. F., et al., Using temporal ICA to selectively remove global noise while preserving global signal in functional MRI data. Neuroimage 181, 692–717 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hutchison R. M., et al., Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage 80, 360–378 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shine J. M., et al., Estimation of dynamic functional connectivity using multiplication of temporal derivatives. Neuroimage 122, 399–407 (2015). [DOI] [PubMed] [Google Scholar]
- 38.Friedli S., Velenik Y., Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction (Cambridge University Press, 2017). [Google Scholar]
- 39.Altmann A., Ng B., Landau S. M., Jagust W. J., Greicius M. D.; Alzheimer’s Disease Neuroimaging Initiative, Regional brain hypometabolism is unrelated to regional amyloid plaque burden. Brain 138, 3734–3746 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Landau L. D., Lifshitz E. M., Reichl L. E., Statistical physics, part 1. Phys. Today 34, 74 (1981). [Google Scholar]
- 41.Xia M., Wang J., He Y., BrainNet Viewer: A network visualization tool for human brain connectomics. PLoS One 8, e68910 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Geinisman Y., deToledo-Morrell L., Morrell F., Persina I. S., Rossi M., Age-related loss of axospinous synapses formed by two afferent systems in the rat dentate gyrus as revealed by the unbiased stereological dissector technique. Hippocampus 2, 437–444 (1992). [DOI] [PubMed] [Google Scholar]
- 43.Foster T. C., Norris C. M., Age-associated changes in Ca(2+)-dependent processes: Relation to hippocampal synaptic plasticity. Hippocampus 7, 602–612 (1997). [DOI] [PubMed] [Google Scholar]
- 44.Harris J. J., Jolivet R., Attwell D., Synaptic energy use and supply. Neuron 75, 762–777 (2012). [DOI] [PubMed] [Google Scholar]
- 45.Camandola S., Mattson M. P., Brain metabolism in health, aging, and neurodegeneration. EMBO J. 36, 1474–1492 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yin F., Boveris A., Cadenas E., Mitochondrial energy metabolism and redox signaling in brain aging and neurodegeneration. Antioxid. Redox Signal. 20, 353–371 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kapogiannis D., Mattson M. P., Disrupted energy metabolism and neuronal circuit dysfunction in cognitive impairment and Alzheimer’s disease. Lancet Neurol. 10, 187–198 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sahoo B., Pathak A., Deco G., Banerjee A., Roy D., Lifespan associated global patterns of coherent neural communication. Neuroimage 216, 116824 (2020). [DOI] [PubMed] [Google Scholar]
- 49.D’Esposito M., Deouell L. Y., Gazzaley A., Alterations in the bold fMRI signal with ageing and disease: A challenge for neuroimaging. Nat. Rev. Neurosci. 4, 863–872 (2003). [DOI] [PubMed] [Google Scholar]
- 50.Cox P. J., et al., Nutritional ketosis alters fuel preference and thereby endurance performance in athletes. Cell Metab. 24, 256–268 (2016). [DOI] [PubMed] [Google Scholar]
- 51.Chen J. J., Gauthier C. J., The role of cerebrovascular-reactivity mapping in functional MRI: Calibrated fMRI and resting-state fMRI. Front. Physiol. 12, 657362 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Windischberger C., et al., On the origin of respiratory artifacts in BOLD-EPI of the human brain. Magn. Reson. Imaging 20, 575–582 (2002). [DOI] [PubMed] [Google Scholar]
- 53.Murphy K., Birn R. M., Bandettini P. A., Resting-state fMRI confounds and cleanup. Neuroimage 80, 349–359 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen J., Herman P., Keilholz S., Thompson G. J., Origins of the resting-state fMRI signal. Front. Neurosci. 14, 594990 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Billings J., Keilholz S., The not-so-global blood oxygen level-dependent signal. Brain Connect. 8, 121–128 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Liu T. T., Nalci A., Falahpour M., The global signal in fMRI: Nuisance or information? Neuroimage 150, 213–229 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Xu F., et al., The influence of carbon dioxide on brain activity and metabolism in conscious humans. J. Cereb. Blood Flow Metab. 31, 58–67 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Lifespan fMRI and MEG data are publicly available from Cam-CAN (25). Metabolic fMRI data are located on OpenNeuro (https://openneuro.org/datasets/ds003453 and https://openneuro.org/datasets/ds003437). fMRI data from the HCP-A dataset are publicly available from ref. 26 and were accessed in an already preprocessed state as described in refs. 34 and 35. Additional details, including links to custom MATLAB used in the analyses of data, can be found at GitHub (https://github.com/lcneuro/synch).