Study of real-valued distance prediction for protein structure prediction with deep learning

Abstract

Motivation

Inter-residue distance prediction by convolutional residual neural network (deep ResNet) has greatly advanced protein structure prediction. Currently, the most successful structure prediction methods predict distance by discretizing it into dozens of bins. Here, we study how well real-valued distance can be predicted and how useful it is for 3D structure modeling by comparing it with discrete-valued prediction based upon the same deep ResNet.

Results

Different from the recent methods that predict only a single real value for the distance of an atom pair, we predict both the mean and standard deviation of a distance and then fold a protein by the predicted mean and deviation. Our findings include: (i) tested on the CASP13 FM (free-modeling) targets, our real-valued distance prediction obtains 81% precision on top L/5 long-range contact prediction, much better than the best CASP13 results (70%); (ii) our real-valued prediction can predict correct folds for the same number of CASP13 FM targets as the best CASP13 group, despite generating only 20 decoys for each target; (iii) our method greatly outperforms a very new real-valued prediction method DeepDist in both contact prediction and 3D structure modeling and (iv) when the same deep ResNet is used, our real-valued distance prediction has 1–6% higher contact and distance accuracy than our own discrete-valued prediction, but less accurate 3D structure models.

Availability and implementation

https://github.com/j3xugit/RaptorX-3DModeling.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Immense progress has been made on protein structure prediction due to the application of convolutional residual neural network (deep ResNet) that can accurately predict inter-residue (atom) relationships (Abriata et al., 2019; Senior et al., 2020; Shrestha et al., 2019; Wang et al., 2017; Xu, 2019; Yang et al., 2020) and recently Transformer-like network implemented in AlphaFold2. The predicted inter-residue contact or distance is a key to currently many successful structure prediction methods (Xu and Wang, 2019). Early contact predictors such as SVMcon and MetaPSICOV use machine learning methods like support vector machines or neural networks to predict contacts individually (Jianlin Cheng, 2007; Jones et al., 2015). However, this is suboptimal because they predict contacts between two atoms regardless of the other atoms. To address this, RaptorX predicts all contacts of a protein (or a big chunk) simultaneously by ResNet (Wang et al., 2017), which may learn complex sequence-structure relationships and make use of high-order contact correlation to achieve much better accuracy. Right after its success on contact prediction, RaptorX moved to distance prediction by ResNet because distance conveys more information for structure modeling (Xiu, 2019; Zhu et al., 2018). Distance prediction is also adopted by AlphaFold1 (Senior et al., 2020), a leading method in CASP13. However, both RaptorX and AlphaFold1 formulate distance prediction as a multi-class classification problem.

Alternatively, as suggested by RaptorX (Xu et al., 2020), it is also possible to predict real-valued distance. A natural question to ask is how well real-valued distance can be predicted and how useful it is for 3D structure modeling. DeepDist (Wu et al., 2020) is one of the very few methods that predict real-valued distance by ResNet. For 3D structure modeling, DeepDist converts real-valued prediction to distance bounds and then feeds them into CNS (Brunger, 2007), a software designed for experimental structure determination. However, DeepDist did not report how well real-valued distance prediction alone can fold a protein, but only showed that protein folding may be improved by adding real-valued and discrete-valued predictions. Ding et al. developed another real-valued prediction method by adding generative adversarial networks (GANs) on top of ResNet to enforce global distance consistency (Ding and Gong, 2020). Similar to DeepDist, Ding et al. also derived distance bounds from real-valued prediction, which are then fed into CNS for 3D structure modeling. However, it is challenging to train and scale GANs (Salimans et al., 2016). Neither DeepDist nor Ding et al. have compared their real-valued prediction to discrete-valued prediction by the same deep network and thus, cannot accurately evaluate the strength and weakness of real-valued and discrete-valued predictions.

Here, we present a new method for real-valued prediction of distance and inter-residue orientation. Our method differs from DeepDist and Ding et al.’s method in that we predict both mean and standard deviation (i.e. a normal distribution) of distance and orientation while they predict only a single value (which can be interpreted as mean). Our prediction pipeline is much simpler than DeepDist and easier to train than GANs. We also introduce a novel way of using the predicted mean and deviation to build 3D models that is distinct from how discrete distance is used. Our experimental results show that our real-valued prediction exceeds the best in CASP13 in terms of both contact accuracy and 3D structure modeling and that our method greatly outperforms DeepDist and compares favorably to Ding et al.’s method. Finally, we rigorously compare real-valued and discrete-valued predictions based upon the same deep network, which is missing in both DeepDist and Ding et al.’s work. We find that with the same ResNet, real-valued prediction has slightly higher contact and distance accuracy, but less accurate 3D models than discrete-valued prediction.

2 Materials and method

Method overview. Our real-valued prediction method consists of two steps (i) predicting the mean and standard deviation of backbone conformation attributes by deep ResNet. We simultaneously predict the distance of backbone atom pairs (Cb–Cb, Ca–Ca and N–O) and inter-residue orientation angles defined in trRosetta (Yang et al., 2020); (ii) fitting the harmonic function $(\frac{x-u}{\sigma }{)}^{2\mathrm{ }}$ with the predicted mean and deviation as constraints to build 3D structure models by gradient descent where u is the mean and $\sigma$ the standard deviation. We use PyRosetta to build 3D models by performing gradient-based minimization and then the fast relaxation protocol to pack side chains and reduce steric clashes (Chaudhury et al., 2010). In contrast, our discrete-valued prediction uses a spline function to construct distance and orientation potential (Zhao and Xu, 2012).

For both real-valued and discrete-valued predictions, we train six ResNet models of the same architecture on different subsets of data and ensemble them to make predictions. Please see (Xiu, 2019) for a detailed description of our ResNet. Here our ResNet has ∼60 ResNet blocks, each consisting of two 2D convolution layers and 2 batch normalization layers. On average, each convolutional layer has ∼170 filters and in total a ResNet model has ∼50 million parameters. More ResNet blocks tend to produce more accurate predictions, so we use as many blocks as we can fit into the GPU. We use mixed-precision training to reduce the training time and GPU memory usage without losing accuracy (Micikevicius et al., 2017). The ResNets for our real-valued and discrete-valued predictions are the same except the output layer. For real-valued prediction, the output layer generates two values for an atom (or residue) pair, representing predicted mean and standard deviation. For discrete-valued prediction, the output layer yields one value for each discrete bin, representing its predicted probability.

We use the following input features for ResNet: (i) primary sequence represented by one-hot encoding; (ii) sequence profile derived from multiple sequence alignments (MSA) that encode evolutionary information at individual residues. We also use secondary structure and solvent accessibility predicted from sequence profile; (iii) co-evolution information including mutual information and the CCMpred output matrices (Seemayer et al., 2014).

Training and validation data. We train and validate our models on the Cath S35 protein dataset downloaded in December 2019, which has 32511 CATH domains (https://www.cathdb.info/), any two domains sharing at most 35% sequence identity. We remove short domains (<25 residues) and those containing too many Ca and Cb atoms without valid 3D coordinates in their structure files. For each protein domain, we generate its multiple sequence alignment (MSA) by running HHblits with E-value = 0.001 on uniclust30 dated in October 2017 and then derive its input features (Mirdita et al., 2017; Remmert et al., 2012). We randomly split the dataset into a train and validation set (1800 domains). We generate six splits and train ResNets on each split. As shown in Xu et al. (2020), there is very little difference between this Cath S35 and the version dated in March 2018. The ResNet models trained on them have almost the same (contact prediction and 3D modeling) performance on the CASP13 FM and FM/TBM targets.

Independent test data. We use the 45 CASP13 hard targets (32 FM targets and 13 FM/TBM targets) to evaluate all methods. Since T0953s1 and T0955 have very few long-range contacts, they are not used to evaluate contact or distance accuracy. We use HHblits (with E-value = 0.01) and TMalign to check sequence profile and structural similarity between the CASP13 FM targets and our training set. HHblits returns a large E-value (>10) for all 32 FM targets but T0975 and T1015s1. T0975 is related to 4ic1D (HHblits E-value = 4.2E-12) and T1015s1 is related to 4iloA (HHblits E-value = 0.024). However, both 4ic1D and 4iloA were deposited to PDB well before 2018 and structurally they are not similar to T0975 and T1015s1 (TMscore < 0.5), it is fair to include them into our training set.

MSA generation and input features. To generate MSAs for the test targets, we run HHblits (Remmert et al., 2012) with E-value = 1E-3 and 1E-5 on uniclust30 dated in October 2017 and jackhammer (Johnson et al., 2010) with E-value = 1E-3 and 1E-5 on uniref90 dated in March 2018. If any target has a shallow MSA depth (ln(Meff)<6), we search metaclust dated in June 2018 to see if more sequence homologs can be found. All these databases were created before the start of CASP13, so they ensured fairness for comparisons. The input features include both sequential and pairwise features. For sequential features, we use (i) primary sequence represented as a one-hot encoding; (ii) sequence profiles derived from MSAs encoding evolutionary information at each residue; (iii) secondary structure and solvent accessibility predicted from sequence profile by RaptorX-Property (Wang et al., 2016). Our pairwise features include both mutual information and CCMpred (Seemayer et al., 2014) output. The CCMpred output includes one L × L co-evolution matrix and one full precision matrix of dimension L × L × 21 × 21 where L is the protein sequence length.

Protein structure representation. We represent protein backbone conformation using inter-atom distance matrices (C_a–C_a, C_b–C_b and N–O) and inter-residue orientation matrices as employed by trRosetta (Yang et al., 2020). When training the real-valued ResNet models, all distances greater than 20 Å are set to 20 Å so that our ResNet focuses on learning small distances but not large distances. We tried setting the distance limit to 16 Å, but did not obtain better performance. We normalize distances and angles to be bounded by 0 and 1 and the dihedral angles to be bounded by -1 and 1. This normalization not only allows the gradients to flow more easily in the deep ResNet, but it also equally weights the loss function across the inter-atom predictions. For discrete-valued prediction, we discretize distance into 47 bins: 0–2 Å, 2–2.4 Å, 2.4–2.8 Å,…,19.6–20 Å and >20 Å.

Deep model training. In training we randomly sample 40–60% of the sequence homologs from an MSA (with at least 2 sequences) and then derive input features from the sampled MSA. To save training time, we generated 10 different samples on disk for each MSA so that our training program just needs to load one sample from the disk. Our ResNet learns to predict the mean and standard deviation of a normal distribution for real-valued distances and orientations by minimizing the negative log-likelihood. Because it is challenging to learn the mean and standard deviation simultaneously, we train our ResNet in two steps: (i) the first step fixes the standard deviation to be 1 and trains the model to predict the mean distance; (ii) the second step trains the parameters specific to standard deviation by freezing all the other parameters. The actual loss function of the first step is $(p-g{)}^2$where p and g are predicted distance and ground truth, respectively, and p can be interpreted as the mean of the normal distribution. The loss function of the second step is $(p-g{)}^2/{{\sigma }^2+\frac{1}{2}\mathrm{ }\mathit{log}(\sigma )}^{}$ where $\sigma$ is the standard deviation to be predicted and p is mean distance calculated from the trained parameters. We use the AdamW (Loshchilov and Hutter, 2017) optimizer with β₁ set to 0.1, β₂ set to 0.001 and L₂ regularization factor of 0.35. We train our ResNet to predict the mean for 20 epochs with a learning rate of 0.0002, 1 more epoch with a learning rate of 0.00004, and the last epoch with a learning rate of 0.000008. We train the parameters specific to standard deviation similarly, but for only 10 epochs because it converges much more quickly. We train six ResNet models of the same hyperparameters and architecture on different subsets of our data and ensemble them to predict the mean and standard deviation. Instead of predicting a normal distribution for the dihedral angles, we tried to predict the von Mises distribution (Gao et al., 2018) along with the normal distributions for atom pairs. However, it is very hard for ResNet to learn two very different loss functions (for distance and orientation) simultaneously. The validation loss of those models plateaued early and underperformed the deep models that predict the normal distribution of both distance and orientation. We also tried to train our models to predict discrete-valued and real-valued distance simultaneously but failed for similar reasons. Even if only the von Mises function is trained, the Adam optimizer does not always converge possibly because the function is periodic. We did not use SGD since it is much slower than Adam.

Building protein 3D models and model clustering. We build our 3D models from distance and orientation prediction with PyRosetta as follows: (i) convert the predicted distance mean $\mu$ and deviation $\sigma$ to energy potential by fitting them to the harmonic function. That is, the potential of an orientation angle $x$ is $\frac{(x\mathrm{ }-\mathrm{ }\mu {)}^2}{{\sigma }^2}$ and the potential of a distance d function is $\frac{(d\mathrm{ }-\mathrm{ }\mu {)}^2}{{\sigma }^2}$ if d is <19, otherwise $\frac{(19.0\mathrm{ }-\mathrm{ }\mu {)}^2}{{\sigma }^2}$; (ii) we use harmonic function for angles and circular harmonic function for dihedral; (iii) minimize the energy potential by gradient-based algorithm LBFGS. To get out of a local minimum, we perturb all phi/psi angles by a small deviation and then apply LBFGS again to see if a lower energy may be reached. We apply PyRosetta fast relaxation to add side-chain atoms and reduce steric clashes. We generate 20 decoys for each test target and select 5 lowest-energy decoys as predictions. We have also tried the Gaussian function for energy potential, but it is slower in folding than the harmonic function since the latter has a simpler derivative to compute. The harmonic function also improves the average TMscore by about 0.01. For discrete-valued prediction, we convert predicted distance probability distribution into potential using the spline function and then build 3D models by the same protocol. DeepDist selects predicted distances <15Å and adds ±0.1 Å as upper and lower distance bounds to form distance constraints which are then used by CNS to build 3D models. Ding et al. selected predicted distances between 4 and 16 Å and used 0.4 Å around the predicted values as their bounds for CNS. We predict both distance and orientations of atom pairs while DeepDist and Ding et al. only predicts distances.

Performance metrics. We use precision and F1 to evaluate contact prediction. The top L/k (k = 1, 2, 5) precision is the percentage of correct among the L/k contacts with the highest predicted probabilities. The top L/k (k = 1, 2, 5) recall is the number of correctly predicted contacts among the top L/k predictions divided by the number of true contacts. To convert discrete probability distributions over the bins to real-valued distance, we compute a weighted average of the distance bins, which is detailed in Xiu (2019). To evaluate distance accuracy, we use absolute error, relative error, precision, recall, F1, pairwise distance test (PDT) and high-accuracy pairwise distance test (PHA). For all these metrics, we only consider distance <15Å. Absolute error is the absolute difference between predicted and native distance while the relative error is the absolute error normalized by the average of predicted and native distance. We measure the recall by the ratio of atom pairs with native distance <15Å that are predicted to have distance <15Å and precision by the ratio of atom pairs with predicted distance <15Å that have native distance <15Å. To calculate PDT and PHA, we calculate the fraction (R(i)) of predicted distance with an absolute error less than i (i = 0.5, 1, 2, 4 and 8 Å). PDT as the average of R(1), R(2), R(4) and R(8) and PHA is the average of R(0.5), R(1), R(2) and R(4). We use TMscore (Xu and Zhang, 2010) to evaluate quality of a 3D model, which measures its structure similarity with its experimental structure. TMscore ranges from 0 to 1 and a 3D model with TMscore ≥ 0.5 is assumed to have a correct fold.

3 Results

3.1 Accuracy of predicted contacts on CASP13 FM and FM/TBM targets

Using the predicted mean and deviation, we may estimate the probability of two residues forming a contact (i.e. having distance < 8Å). As shown in Table 1, our real-valued contact prediction has slightly better accuracy than our discrete-valued prediction, both outperforming the best methods in CASP13 by a good margin. Our real-valued method greatly outperforms DeepDist, a very new method for real-valued distance prediction. While our top L/5, L/2 and L contact precisions (L is sequence length) for the 43 FM and FM/TBM targets are 84.6%, 72.6% and 61.8%, DeepDist’s contact precisions are 78.6%, 64.5% and 49.6% (Wu et al., 2020). Our methods also have better contact precision than trRosetta (Yang et al., 2020), a method developed after CASP13 that employs discrete-valued prediction, although trRosetta used a newer sequence database uniclust30 (dated in August 2018) and larger metagenome databases to generate MSAs.

Table 1.

Precision and F1 (%) of long-range contact prediction of FM and FM/TBM CASP13 targets by several competing methods

	31 CASP13 FM targets			12 CASP13 FM/TBM targets
	Top L/5	Top L/2	Top L	Top L/5	Top L/2	Top L
	F1 of long-range contact prediction
AlphaFold in CASP13	22.7	36.9	41.9	31.4	48.7	55.1
RaptorX in CASP13	23.3	36.2	41.1	28.8	43.2	51.8
Zhang in CASP13	21.2	34.1	39.2	28.4	43.3	49.5
Discrete (our work)	27.5	44.1	51.1	31.9	52.9	62.0
Real-Valued (our work)	27.9	44.6	51.8	31.8	52.4	62.4
	Precision of long-range contact prediction
RaptorX in CASP13	70.0	58.0	45.0	85.8	70.1	56.9
Zhang in CASP13	65.7	54.8	39.1	82.3	70.0	54.8
trRosetta	78.5	66.9	51.9	NA	NA	NA
Discrete (our work)	80.2	67.6	57.6	93.9	83.5	70.7
Real-Valued (our work)	81.2	68.7	58.1	93.6	82.8	71.3

Note: The F1 of AlphaFold is taken from Xu (2019). The trRosetta result is taken from Yang et al. (2020).

Real-valued versus discrete-valued prediction. We use the same hyperparameters that are optimized on the discrete-valued ResNet for our real-valued ResNet. Our real-valued prediction has marginally better (0.5–1.0%) top L long-range contact accuracy than our discrete-valued prediction. When the extra long-range contact prediction is evaluated, our real-valued method achieves a top L/5, L/2 and L precision of 65.5%, 55.4% and 49.2%, respectively, whereas our discrete-valued prediction has precision 63.1%, 53.6% and 47.8%, respectively. We say one contact is extra long-range if its two involving residues are separated by at least 48 residues along the primary sequence. There is a high correlation (CC = 0.98) between our discrete-valued and real-valued L/5 contact precision on the 43 hard targets, but there are still 9 test proteins with precision difference greater than 5%, indicating that there are situations where real-valued prediction may be more useful (Fig. 1).

Fig. 1.

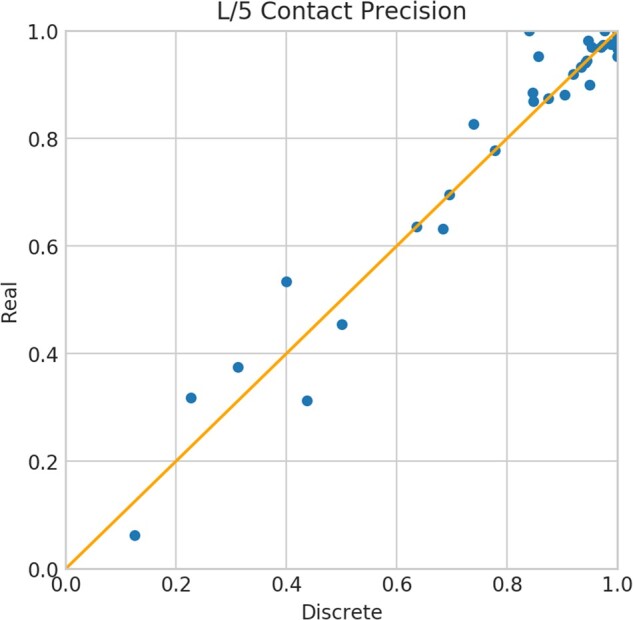
Top L/5 contact precision of our discrete-valued and real-valued methods on the 43 FM and FM/TBM CASP13 targets. A dot above the diagonal line indicates that real-valued prediction is better than its corresponding discrete-valued prediction

3.2 Distance prediction accuracy on CASP13 FM and FM/TBM targets

We use a few metrics to evaluate distance accuracy of our real-valued and discrete-valued predictions, including absolute error, relative error, precision, recall, F1, pairwise distance test (PDT) and high-accuracy pairwise distance test (PHA), which are explained in section Methods. While evaluating distance prediction, we consider only those long-range atom pairs with predicted distance <15Å and native distances <15Å. To evaluate our discrete-valued prediction, we convert discrete probability distributions to real-valued distance by computing the expected value of a discrete distribution, which is detailed in Xiu (2019). As shown in Table 2 and Supplementary Figure S1, our real-valued distance prediction is better than our own discrete-valued prediction by 1–6% in terms of all the metrics except recall. We do not compare our distance accuracy with Ding et al.’s method because they only reported distance accuracy on their validation set but not on the CASP13 targets. In addition, because it is not clear how DeepDist precisely defines their distance measures, it is challenging for us to compare our distance accuracy with DeepDist, but we have much better contact accuracy than DeepDist.

Table 2.

Average distance accuracy of our real-valued and discrete-valued prediction methods compared across CbCb, CaCa or NO atom distances

	CbCb		CaCa		NO
	Real	Discrete	Real	Discrete	Real	Discrete
Abs. error	4.069335	4.232118	3.759566	3.974853	3.643687	3.872508
Rel. error	0.241389	0.251571	0.220723	0.232381	0.215353	0.227033
Precision	0.682059	0.650375	0.691564	0.670452	0.692480	0.676140
Recall	0.712129	0.736852	0.728711	0.745034	0.748851	0.759924
F1	0.686266	0.679169	0.698683	0.694299	0.710045	0.705230
PHA	0.431603	0.412376	0.462826	0.444350	0.481869	0.464568
PDT	0.610425	0.589494	0.637133	0.617010	0.650349	0.630967

Note: The accuracy is measured by absolute error, relative error, precision, recall, F1, PHA and PDT.

3.3 Accuracy of predicted 3D models on CASP13 FM and FM/TBM targets

We use the predicted real-value attributes to generate only 20 decoys for each target and then select 5 decoys with the lowest energy as predicted 3D models. On the 32 CASP13 FM targets, the average quality [measured by TMscore (Xu and Zhang, 2010)] of the first and best (of 5) models is 0.582 and 0.599, respectively. On the 13 FM/TBM targets, the average TMscore of the first and best models is 0.641 and 0.651, respectively. When the best models are considered and TMscore > 0.5 is used to judge if a predicted 3D model has a correct fold or not, our real-valued method predicts correct folds for 23 of the 32 FM targets and 11 of the 13 FM/TBM targets. Despite generating only 20 decoys per target, our real-valued method performs as well as AlphaFold in CASP13, which has an average TMscore 0.583 for the first models of the 32 FM targets and correctly folds 23 of the 32 targets (Senior et al., 2020). Note that AlphaFold generated thousands of decoys per target (Senior et al., 2020).

DeepDist reported an average TMscore 0.487 and 0.522 for the first and best models of the 43 CASP13 FM and FM/TBM targets, respectively. In total DeepDist predicted correct folds for 23 of the 43 targets (Table 3). In contrast, our real-valued prediction method obtains an average TMscore of 0.604 and 0.619 for the first and best models, respectively, and predicts correct folds for 33 of the 43 targets. Our method also vastly outperforms another distance-based folding method DMPfold (Greener et al., 2019), which has average TMscore 0.438 for the first models. Ding et al. evaluated their real-valued prediction on only 20 FM and FM/TBM targets and reported an average TMscore of 0.620, whereas we can achieve a similar TMscore of 0.612 with real-valued prediction (Ding and Gong, 2020; Greener et al., 2019). However, the comparison with Ding et al.’s result is not rigorous, as they used the official domain sequences as inputs while we do not. To simulate the real-world prediction scenarios, we predicted 3D models on the domains determined by our server during the CASP13 season in the absence of the native structures. When evaluating the quality of our predicted 3D models, we only count the segments that overlap with the official domains. As such, when our own domain definition deviates significantly from the official one, our predicted 3D models have low quality score.

Table 3.

Average TMscore obtained by 3 competing methods on the 43 CASP13 FM and FM/TBM targets

Method	Top 1	Top 5	No. of correct folds
Ours	0.604	0.619	33
DeepDist	0.487	0.522	23
DMPfold	0.438	0.449	16

Note: The DeepDist and DMPfold results are taken from the DeepDist paper (Wu et al., 2020).

Real-valued versus discrete-valued prediction. Similarly, we also generate 20 decoys for each target using our discrete-valued prediction and select the 5 lowest-energy decoys as predicted 3D models. On the 32 CASP13 FM targets, the average TMscore of the first and best models generated by our discrete-valued prediction is 0.646 and 0.672, respectively. On the 13 FM/TBM targets, the average TMscore of the first and best 3D models is 0.671 and 0.683, respectively. Our discrete-valued method can predict correct folds for 26 of the 32 FM targets and 11 of the FM/TBM targets. That is, although our real-valued prediction generates better contact accuracy, its 3D modeling accuracy is worse than our discrete-valued prediction. The correlation between our real-valued 3D model quality (measured by TMscore) and discrete-valued model quality is 0.95, but our discrete-valued method predicts better 3D models for nearly all targets (Fig. 2). The correlation between the top L/2 contact precision of the 31 FM targets with their first model TMscore is 0.626 for discrete-valued prediction and 0.543 for real-valued prediction. That is, there is still room for improvement in real-value-based 3D structure modeling. This also implies that contact precision is a better indicator for 3D model quality of discrete-valued prediction than real-valued prediction. The correlation between the logarithm of MSA depth [i.e. ln(Meff)] and model quality for real-valued and discrete-valued predictions is 0.572 and 0.557, respectively. When ln(Meff)>4.0, our discrete-valued method can predict the correct folds for all targets while our real-valued method fails on one target (Supplementary Fig. S2).

Fig. 2.

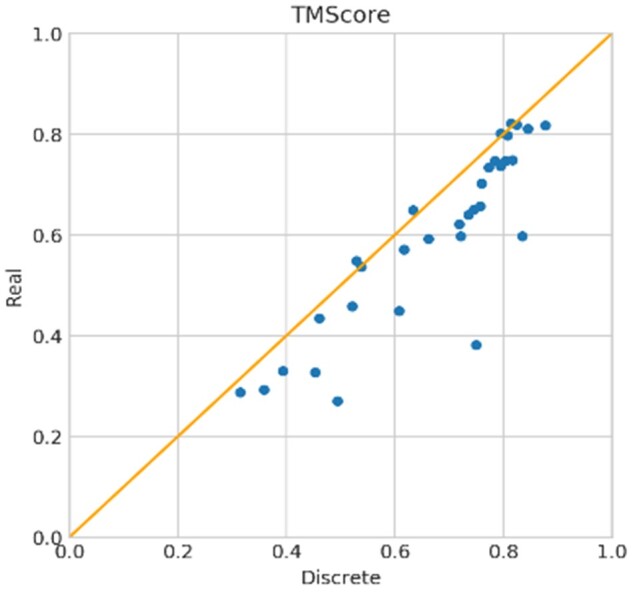
TMscore of the first models of our discrete-valued versus real-valued predictions for the 32 CASP13 FM targets

3.4 Strength and weakness of real-valued prediction

Real-valued prediction has both advantages and down-sides. First, only two parameters (mean and standard deviation) are used for real-valued prediction while dozens of parameters are used for a discrete distance distribution. Second, discretizing distance possibly reduces the amount of information that can be learned by a machine learning method. Indeed, our experiments showed that real-valued prediction has slightly better contact and distance accuracy. Since we use the harmonic function of only two parameters to represent our real-valued energy function, it is symmetric across the mean and much smoother than our discrete-valued potential. As shown in Supplementary Figure S3, discrete distance potentials have troughs followed by peaks followed by another through, which is an undesirable characteristic for energy minimization. The smoothness of real-valued energy function makes gradient-based minimization easier. However, discrete-valued prediction uses dozens of parameters to define a probability distribution and thus, result in a higher resolution energy function than real-valued prediction. With only two parameters, our real-valued energy function may not be very accurate at a distance far away from the predicted mean distance. Contact prediction depends on only the predicted probability of distance falling in the interval [0, 8Å] while 3D modeling depends on the predicted potential of all the distance up to 15 or 20Å, so it is not unexpected that real-valued prediction may lead to better contact precision but worse 3D modeling.

3.5 Case study

Our real-valued and discrete-valued methods perform differently on two CASP13 hard targets T0990-D1 and T1008-D1. For T0990-D1, our discrete-valued prediction works better, while for T1008-D1 our real-valued prediction works better. T0990-D1 has 76 residues and the logarithm of its MSA depth is 3.308. Our real-valued and discrete-valued predictions have similar contact precision. The top L/5, L/2 and L long-range contact precision of both methods are 0.933, 0.605 and 0.6. The top L/5 short-range contact precision is 0.733. But our real-valued prediction has better top L/5 medium-range contact precision (0.8) than discrete-valued prediction (0.667). Both methods have slightly different distance accuracy. Our discrete-valued prediction has a smaller relative and absolute distance prediction error (0.124, 1.424) than our real-valued prediction (0.145, 1.624). Our discrete-valued prediction also has slightly better PDT and PHA (0.794, 0.619) than our real-valued prediction (0.764, 0.580). However, our discrete-valued prediction produces much better 3D models than real-valued prediction in terms of TMscore (0.75 versus 0.382), RSMD (2.512 versus 9.819), GHA (0.536 versus 0.276) and GDT (0.75 versus 0.418). This suggests that contact accuracy may not necessarily be a good predictor of 3D model quality as it does not capture the overall information of the predicted distance map. In addition, the real-valued prediction may not necessarily predict better distance than the discrete-valued method.

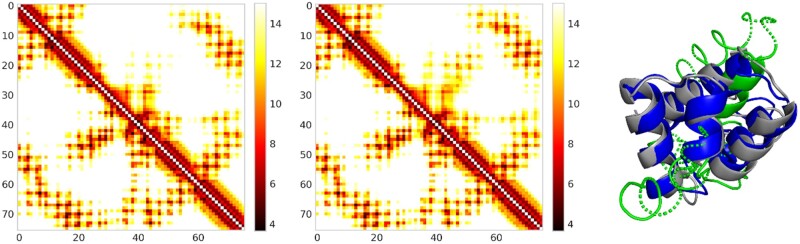
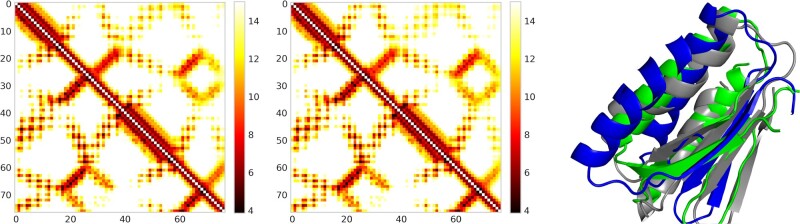
For T1008-D1, our discrete-valued prediction has top L/5, L/2 and L long-range contact precision 0.933, 0.684 and 0.508, respectively, better than our real-valued prediction (0.933, 0.631 and 0.492). Our real-valued prediction has better predicted distance accuracy in terms of relative error (2.633 versus 3.014), absolute error (0.213 versus 0.231), PDT (0.608 versus 0.574) and PHA (0.385 versus 0.352). The 3D model built from our real-valued prediction is better across all metrics, including TMscore (0.587 versus 0.433), GDT (0.444 versus 0.416), RMSD (3.671 versus 7.923) and GHA (0.393 versus 0.312). This suggests that an improved distance prediction can help improve 3D structure modeling (Figs 3 and 4).

Fig. 3.

Distance map for T0990-D1 predicted by real-valued ResNet (Left) and discrete-valued ResNet (Middle). Only distances less than 15 Å are displayed in colors. In each picture, native and predicted distance is shown below and above the diagonal line, respectively. The right picture shows the superimposition of T990-D1 native structure (gray), real-valued model (green) and discrete-valued model (blue)

Fig. 4.

Distance map for T1008-D1 predicted by real-valued ResNet (Left) and discrete-valued ResNet (Middle). Only distances less than 15 Å are displayed in colors. In each picture, native and predicted distance is shown below and above the diagonal line, respectively. The right picture shows the superimposition of T1008-D1 native structure (gray), real-valued model (green) and discrete-valued model (blue)

4 Conclusion and discussions

We have presented a new method for real-valued distance prediction by ResNet. This method can achieve a top L/5 contact precision of 81.2%, more than 10% greater than the best methods in CASP13. Even generating only 20 decoys per target, our method can correctly fold the same number of CASP13 FM targets as the best human group in CASP13. Our method outperforms existing real-valued prediction methods such as DeepDist in terms of both contact accuracy and 3D modeling. With the same ResNet our real-valued prediction can achieve a 1–6% improvement over its discrete version in terms of contact and distance accuracy, but it falls short in 3D structure modeling. Even though the energy function predicted by our real-valued method is smoother and more symmetric, its resolution is not as high as our discrete-valued prediction.

There is still much room to improve real-valued prediction. For example, DeepDist trains both real and discrete predictions at the same time to improve contact accuracy and 3D modeling. Ding et al. show that using the GAN on top of ResNet can further improve the global consistency of distance prediction, which is something worth trying. It is also possible that we can employ better loss functions to deal with the class imbalances in distance prediction (Cao et al., 2019). Recently, there has been much progress in making convolution layers more efficient and powerful, and it would be interesting to see how this can improve (Bello et al., 2019; Chen et al., 2018; Tan and Le, 2019a,b; Wang et al., 2020). There has also been interest in end-to-end training for protein structure prediction, which can improve the learned relationship between structure and output while speeding up prediction (AlQuraishi, 2018; Ingraham et al., 2019; Li, 2019). And lastly, we would continue to investigate ways in which we can reduce the gap between real-valued and discrete-valued prediction in 3D modeling. For example, we may develop a custom real-valued constraint function that can better take advantage of real-valued predictions as opposed to using the out-of-the-box harmonic function.

Funding

This work was supported by National Institutes of Health [R01GM089753 to J.X.].

Conflict of Interest: none declared.