A General Model of the Relationship between the Apportionment of Human Genetic Diversity and the Apportionment of Human Phenotypic Diversity

Abstract

Models that examine genetic differences between populations alongside a genotype–phenotype map can provide insight about phenotypic variation among groups. We generalize a simple model of a completely heritable, additive, selectively neutral quantitative trait to examine the relationship between single-locus genetic differentiation and phenotypic differentiation on quantitative traits. In agreement with similar efforts using different models, we show that the expected degree to which two groups differ on a neutral quantitative trait is not strongly affected by the number of genetic loci that influence the trait: neutral trait differences are expected to have a magnitude comparable to the genetic differences at a single neutral locus. We discuss this result with respect to population differences in disease phenotypes, arguing that although neutral genetic differences between populations can contribute to specific differences between populations in health outcomes, systematic patterns of difference that run in the same direction for many genetically independent health conditions are unlikely to be explained by neutral genetic differentiation.

1. Introduction

Since Lewontin’s (1972) landmark partitioning of human genetic diversity, many studies have supported his claim that allele-frequency differences between geographically defined groups of people are relatively modest (Barbujani et al. 1997; Brown and Armelagos 2001; Rosenberg et al. 2002; Li et al. 2008). The findings of these previous studies have often been reported as estimates of F_ST, which can be interpreted as the proportion of variance in an allelic indicator variable attributable to allele-frequency differences between populations (Holsinger and Weir 2009). Estimates of worldwide human F_ST and F_ST-like quantities have ranged from ~0.05 (e.g., Rosenberg et al. 2002) to ~0.15 (e.g., Barbujani et al. 1997).

Human F_ST estimates suggest that for phenotypes governed by a single typical genetic locus, population membership is likely to account for a relatively small proportion of the total variance of the trait. However, phenotypes are generally influenced by many loci, not just one. Large sets of loci can contain a great deal of information about population membership and can permit highly accurate ancestry inference, even if each locus has a small F_ST (Smouse et al. 1982; Bowcock et al. 1994; Mountain and Cavalli-Sforza 1997; Rosenberg et al. 2002; Bamshad et al. 2003; Edwards 2003; Li et al. 2008). Should we expect traits that are influenced by many loci to aggregate information about population membership across loci, leading to differences between populations that are more pronounced than those observed for traits influenced by fewer loci?

This question has been examined in many population-genetic and quantitative-genetic studies, both in theoretical models (Felsenstein 1973, 1986; Chakraborty and Nei 1982; Rogers and Harpending 1983; Lande 1992; Spitze 1993; Lynch and Spitze 1994; Whitlock 1999; Berg and Coop 2014; Edge and Rosenberg 2015) and in empirical applications in humans (Roseman 2004; Roseman and Weaver 2004; Weaver et al. 2007; Relethford 2010) and other organisms (for reviews, see Whitlock 2008; Leinonen et al. 2013), finding that, in the absence of selection, the expected degree to which groups differ on an additive, genetically determined trait does not depend on the number of loci that influence the trait. Put differently, a typical neutral trait conveys roughly the same degree of information about population membership as a single neutral locus, even if the trait is influenced by a large set of loci that would, if considered directly, permit accurate classification by population of origin.

Recently, to facilitate direct comparisons of multilocus genetic classification, single-locus genetic differentiation, and phenotypic differentiation, we developed a model that combines a simple model of multilocus genetic classification with a simple genotype–phenotype map. Our model enables genotype–phenotype comparisons to be performed in a statistical framework that permits exact computation and does not require detailed evolutionary assumptions (Edge and Rosenberg 2015). Our results agreed with those found with other models, highlighting the differences between polygenic phenotypic differentiation and information about population membership at multiple genetic loci.

In our past work (Edge and Rosenberg 2015), we applied strong assumptions about the allele-frequency distribution, and we examined only haploids. Here, we extend our earlier model to allow arbitrary allele-frequency distributions and arbitrary ploidy. Our results provide another way of establishing the result that between-group differentiation on a neutral trait mirrors between-group genetic differentiation at a neutral locus, one that makes minimal evolutionary assumptions. In Section 2, we describe our extended model. In Section 3, we define several measurements of between-group genetic differentiation. In Sections 4 and 5, we describe properties of two statistics that summarize the degree of difference between two populations on a quantitative trait. In Section 6, we introduce two simplifying assumptions that allow us to analyze the problem of inferring an individual’s population of origin using either genetic or phenotypic information. Finally, we discuss the results with respect to the interpretation of population differences in disease phenotypes. Figure 1 provides a conceptual map of the structure of the article.

FIGURE 1.

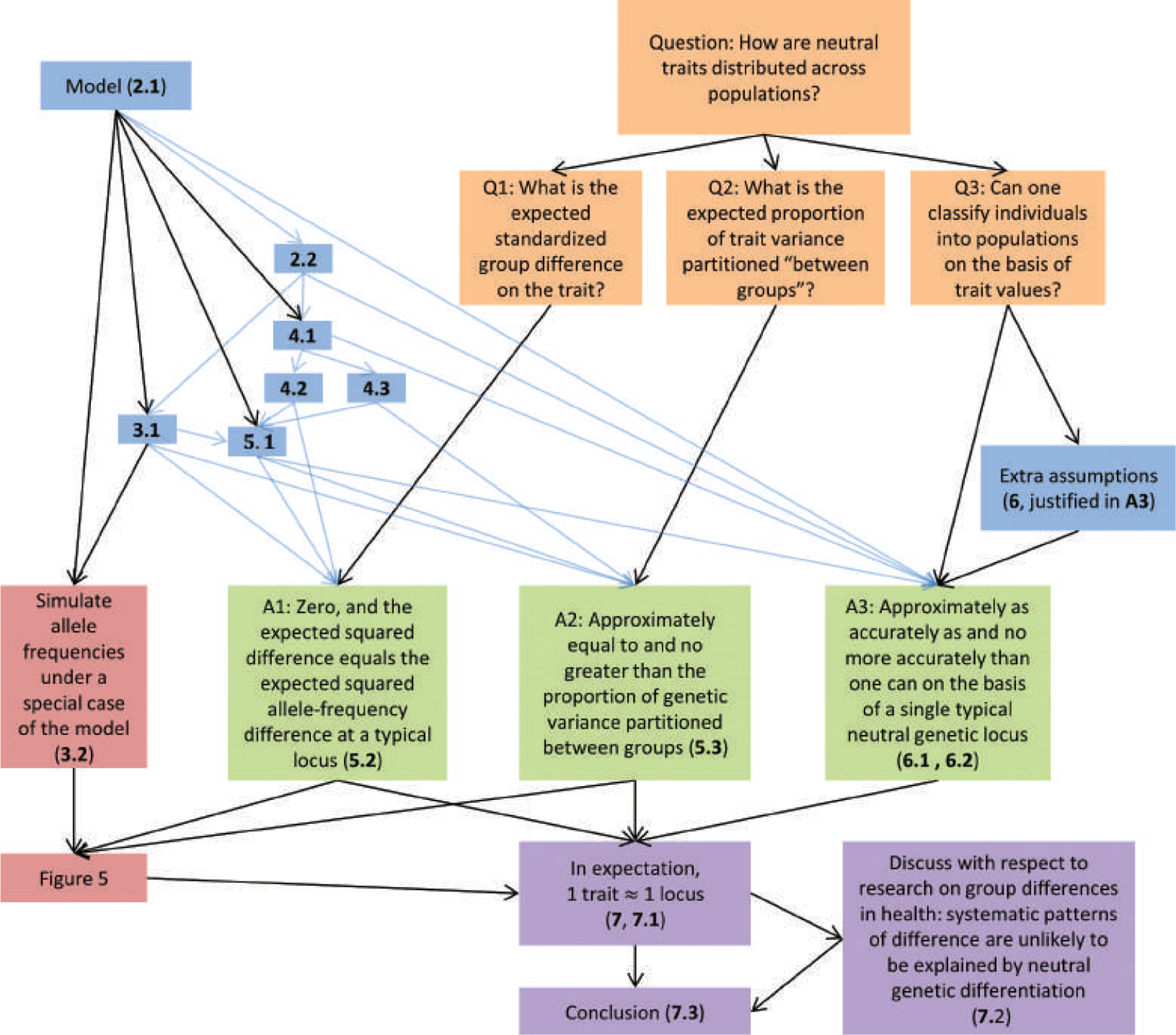
A conceptual map of this article. For boxes that correspond to specific subsections of the article, the subsection number is displayed in bold. Arrows indicate conceptual dependence, with blue arrows indicating that a subsection cites mathematical results obtained in another subsection. Motivating questions are in orange, mathematical machinery is in blue, simulations are in red, mathematical answers are in green, and interpretation of results is in purple.

2. Preliminaries

2.1. Model

Our extended model is parallel to our previously reported model (Edge and Rosenberg 2015) and is similar to models used by Risch et al. (2002), Edwards (2003), and especially Tal (2012) to investigate the problem of classifying individuals into populations using multilocus genetic data. For a summary of our notation, see Table 1.

Table 1.

Summary of Notation

Symbol	Meaning
k	The number of loci that influence a quantitative trait
ℓ	The ploidy of the individuals being considered
M	An individual’s population membership; takes values A and B
L ij	An individual’s allelic type at the jth allele at the ith locus; takes values 0 and 1
p i	The frequency of the 1 allele at locus i in population A (Eq. 1)
q i	The frequency of the 1 allele at locus i in population B (Eq. 1)
$\overline{p}$	The mean frequency of the 1 allele across loci in population A (Eq. 2)
$\overline{q}$	The mean frequency of the 1 allele across loci in population B (Eq. 2)
$s_p^2$	The variance across loci in the frequency of the 1 allele in population A (Eq. 3)
$s_q^2$	The variance across loci in the frequency of the 1 allele in population B (Eq. 3)
V ij	An indicator for whether an individual’s jth allele at the ith locus is a + allele (Eq. 4)
T	An individual’s value for a quantitative trait (Eq. 4)
X i	An indicator for whether the 0 or the 1 allele is also the + allele at locus i (Eq. 5)
S	The number of 1 alleles an individual carries (Eq. 6)
δ i	The difference between populations in the frequency of the 1 allele at locus i (Eq. 8)
$\overline{\delta }$	The mean allele-frequency difference between populations, or $\overline{q}-\overline{p}$ (Eq. 9)
$\overline{{\delta }^2}$	The mean squared difference between populations in the frequency of the 1 allele (Eq. 10)
$F_{ST}^k$	The ratio of the mean (across k loci) within-population variance in an allelic indicator variable to the mean (across k loci) total variance in an allelic indicator variable (Eq. 14)
$D_L^2$	A function of $F_{ST}^k$ that bears the same relationship to $F_{ST}^k$ as the square of Cohen’s d does to r2 (Eq. 15)
$F_{ST(\ell )}^k$	A generalization of $F_{ST}^k$ for the sum of ℓ independent allelic indicator variables (Eq. 16)
$D_{L(\ell )}^2$	A function of $F_{ST(\ell )}^k$ that bears the same relationship to $F_{ST(\ell )}^k$ as the square of Cohen’s d does to r2 (Eq. 17)
U i	A transformation of the Xi: if Xi = 1, then Ui = 1; if Xi = 0, then Ui = −1 (Eq. 18)
D T	The standardized difference between populations A and B on the trait (Eqs. 25, 34)
${\rho }_T^2$	The proportion of the total variance in the trait attributable to between-population difference on the trait (Eqs. 26, 27, 41)
Q ST	A quantitative-trait analogue of FST: if ℓ = 1(haploid organisms), then $Q_{ST}={\rho }_T^2$ (Eq. 28)
W S	A quantity that equals 1 if an individual is classified into the wrong population on the basis of its value of S, and that equals 0 otherwise (Eq. 55)
W T	A quantity that equals 1 if an individual is classified into the wrong population on the basis of its value of T, and that equals 0 otherwise (Eq. 56)

We consider two populations of equal size, labeled A and B. In each individual, we consider k biallelic genetic loci. Each individual is ℓ-ploid (ℓ ≥ 1), carrying ℓ copies of each locus. At each locus, the allelic type more common in population B than in population A is labeled “1,” and the other allelic type is labeled “0.” Conditional on population membership, all of an individual’s alleles are independent—both alleles at the same locus, as under Hardy-Weinberg equilibrium, and alleles at distinct loci, as under linkage equilibrium.

Let L_ij be an indicator random variable denoting whether the jth allele (1 ≤ j ≤ ℓ) at locus i is the “1” allele, and let M be a random variable that represents an individual’s population membership and that takes values A and B. The conditional probabilities that L_ij = 1 are

$$\begin{gathered} P\left(L_{ij}=1\mid M=A\right)=p_i, \\ P\left(L_{ij}=1\mid M=B\right)=q_i. \end{gathered}$$ (1)

The p_i and q_i obey 0 ≤ p_i ≤ q_i ≤ 1. The constraint q_i ≥ p_i holds because, by definition, the 1 allele is more common in population B than in population A. We also assume that, for at least one value of i, p_i or q_i does not equal 0 or 1; and for the limiting results in Section 6, we assume that, as the number of loci k approaches infinity, the number of loci at which p_i ∈ (0, 1) and the number of loci at which q_i ∈ (0, 1) both approach infinity.

Define $\overline{p}$ and $\overline{q}$ as the means across loci of the allele frequencies p_i and q_i:

$$\begin{gathered} \overline{p}=\frac{1}{k}\sum _{i=1}^k{p}_i, \\ \overline{q}=\frac{1}{k}\sum _{i=1}^k{q}_i. \end{gathered}$$ (2)

Define $s_p^2$ and $s_q^2$ as the variances across loci of the p_i and q_i, though they are not probabilistic variances because the p_i and q_i are nonrandom:

$$\begin{gathered} s_p^2=\frac{1}{k}\sum _{i=1}^k{\left(p_i-\overline{p}\right)}^2, \\ {s}_q^2=\frac{1}{k}\sum _{i=1}^k{\left(q_i-\overline{q}\right)}^2. \end{gathered}$$ (3)

We model a completely heritable, selectively neutral, additively determined trait as a function of the k loci described above. Specifically, an individual’s value on the trait—represented by a random variable T—is a weighted sum of the individual’s L_ij values. As in our previous work (Edge and Rosenberg 2015, Eq. 9), the weights are determined by labels at each locus, where for each trait we label one allele at each locus—either the 0 allele or the 1 allele—as the “+” allele and the other allele as the “−” allele. T is then equal to the number of + alleles carried by the individual. That is,

$$T=\sum _{i=1}^k\sum _{j=1}^{\ell }{V}_{ij},$$ (4)

where V_ij = 1 if the jth allele at the ith locus is a + allele and V_ij = 0 otherwise.

Again following our previous work (Edge and Rosenberg 2015, Eq. 7), we assume that whether an allele is more common in population B than in population A (i.e., labeled “1”) is independent of whether it is associated with larger trait values than the other allele (i.e., labeled “+”). This claim amounts to assuming that the alleles at k loci have not been under selection and have reached their current frequencies independently of their effect on the trait. We express this assumption with the random variable X_i, with X_i = 0 if the 0 allele and the + allele are identical at the ith locus and X_i = 1 if the 1 allele and the + allele are identical at the ith locus. Each trait is associated with a set of k values for the X_i, and for each of the k loci,

$$P\left(X_i=0\right)=P\left(X_i=1\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$ (5)

independently of the X_i for the other loci.

We introduce a statistic for comparison with the trait value T. We summarize the information about population membership available at an individual’s k loci with the genotypic statistic S, the total number of 1 alleles—that is, alleles that are more common in population B than in population A—at k loci:

$$S=\sum _{i=1}^k\sum _{j=1}^{\ell }{L}_{ij}.$$ (6)

S is not generally an optimal basis for distinguishing members of population A and B (e.g., Tal 2012)—in principle, we could improve classification by more heavily weighting loci that have a greater allele frequency difference between populations—but we will show that classifications based on S approach perfect accuracy as k increases, as long as $\overline{p}\ne \overline{q}$.

Figure 2 shows a schematic of our model. The model reduces to the one described in Edge and Rosenberg (2015) if one assumes (a) that p_i = p and q_i = q for all i, (b) that q = 1 − p, and (c) that the organisms being examined are haploid (ℓ = 1).

FIGURE 2.

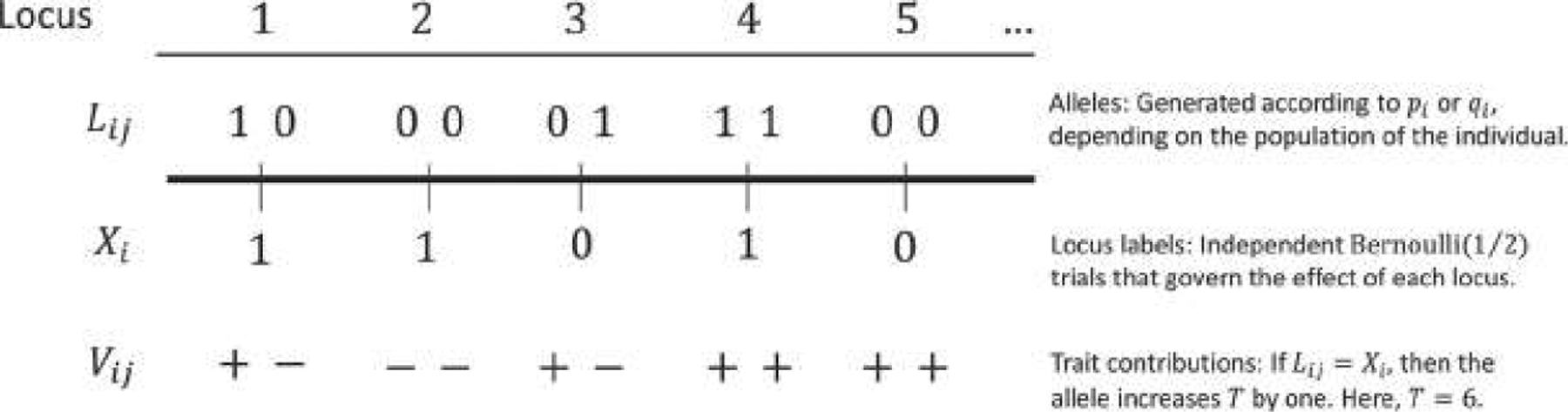
A schematic of our model for generating a quantitative trait. Five loci are shown for a diploid individual. The L_ij are the individual’s alleles, which, conditional on population membership, are independent Bernoulli trials with probability at locus i equal either to p_i (if the individual is drawn from population A) or to q_i (if the individual is drawn from population B). At each locus, the frequency of the 1 allele is at least as large in population B as it is in population A. The X_i are labels indicating which allele at locus i leads to larger values of T; they are independent Bernoulli trials, each with probability ½. If an individual’s jth allele at locus i (L_ij) matches the allele that leads to larger values of the trait for that locus (X_i), then V_ij takes the value “+”; otherwise, V_ij takes the value “−”. T is equal to the sum of + alleles carried by the individual. In the case pictured, T = 6.

2.2. The Poisson Binomial Distribution

Under our model, many relevant quantities have a Poisson binomial distribution, which arises when independent Bernoulli trials with possibly varying success probabilities are summed. By the central limit theorem, the Poisson binomial distribution converges to a normal distribution as the number of terms summed increases without bound, provided that the sum of the variances of the Bernoulli random variables approaches infinity (Deheuvels et al. 1989, Theorem 1.1). If Z is a Poisson binomial random variable with probabilities p₁, …, p_k, then

$$\begin{gathered} E(Z)=\sum _{i=1}^k{p}_i=k\overline{p}, \\ \text{Var}(Z)=\sum _{i=1}^k{p}_i\left(1-p_i\right)=k\overline{p}(1-\overline{p})-k{s}_p^2, \end{gathered}$$ (7)

where $\overline{p}$ is as in Eq. 2 and $s_p^2$ is as in Eq. 3 (e.g., Edwards 1960).

3. Genetic Differentiation between Populations at a Single Locus

On the basis of our model, we define several statistics measuring the degree of genetic differentiation between populations at a single typical locus. In Section 5, we use these statistics to compare the degree of genetic differentiation at a typical locus to the expected degree of difference between populations in a neutral trait.

3.1. Single-Locus Differentiation Measures

One summary of the degree of single-locus genetic differentiation between populations is the difference between populations in the frequency of the 1 allele at the locus:

$${\delta }_i=q_i-p_i.$$ (8)

We also define

$$\overline{\delta }=\frac{1}{k}\sum _{i=1}^k{\delta }_i=\overline{q}-\overline{p},$$ (9)

$$\overline{{\delta }^2}=\frac{1}{k}\sum _{i=1}^k{\delta }_i^2={\overline{\delta }}^2+s_{\delta }^2,$$ (10)

where $s_{\delta }^2={\sum }_{i=1}^k{\left({\delta }_i-\overline{\delta }\right)}^2/k$, and

$$\overline{{\delta }^4}=\frac{1}{k}\sum _{i=1}^k{\delta }_i^4={\overline{{\delta }^2}}^2+s_{{\delta }^2}^2,$$ (11)

where $s_{{\delta }^2}^2={\sum }_{i=1}^k{\left({\delta }_i^2-\overline{{\delta }^2}\right)}^2/k$.

The quantity δ (Eq. 8), the difference in population frequencies of one specific allele at a biallelic locus, is closely related to F_ST for a single locus. Specifically, with two populations and dropping the subscript i, single-locus F_ST, which we write as $F_{ST}^1$, is

$$\begin{gathered} F_{ST}^1=\frac{{\delta }^2}{4\left(\frac{p+q}{2}\right)\left(1-\frac{p+q}{2}\right)} \\ =\frac{{\delta }^2}{2[p(1-p)+q(1-q)]+{\delta }^2} \end{gathered}$$ (12)

(e.g., Weir 1996; Rosenberg et al. 2003, Eq. 8; Holsinger and Weir 2009, Eq. 4). $F_{ST}^1\in \left[{\delta }^2,\delta /(2-\delta )\right]$, and δ² never deviates from $F_{ST}^1$ by more than (5√5 − 11)/2 ≈ 0.0902 (Rosenberg et al. 2003). $F_{ST}^1$ can be interpreted in terms of a ratio involving heterozygosity in the subpopulations and in the total population (Nei 1973), or as a ratio of variance components (Holsinger and Weir 2009); we emphasize the latter interpretation. Specifically, if L is an allelic indicator variable representing a single copy of a locus and M denotes population membership, then for a single locus,

$$F_{ST}^1=\frac{{\text{Var}}_M[E(L\mid M)]}{\text{Var}(L)}.$$ (13)

The subscript M indicates that the variance in the numerator is taken with respect to group membership. Equation 13 can be verified using the law of total variance, noting that Var_M[E(L|M)] = δ²/4 and that E_M[Var(L|M)] = [p(1 − p) + q(1 − q)]/2, and comparing with Eq. 12.

To summarize the overall degree of genetic differentiation at a group of k loci, we define an F_ST measure that summarizes the typical degree of differentiation at a locus chosen from a set of k loci, which we write as $F_{ST}^k$. For locus i, L_i1 is an allelic indicator variable representing one copy of the locus. To compute $F_{ST}^k$, we sum the variance components that appear in Eq. 13 across all k loci and take their ratio:

$$\begin{gathered} F_{ST}^k=\frac{\sum _{i=1}^k{\text{Var}}_M\left[E\left(L_{i1}\mid M\right)\right]}{\sum _{i=1}^k\text{Var}\left(L_{i1}\right)} \\ =\frac{\overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\overline{{\delta }^2}}. \end{gathered}$$ (14)

This ratio is analogous to estimators of F_ST that involve a ratio of two variance estimates (e.g., Weir and Cockerham 1984, Eq. 10). In our model, however, $F_{ST}^k$ is known and not estimated because the allele frequencies are known. Though $F_{ST}^k$ is intended as an index of the degree of genetic differentiation at a single typical locus, $F_{ST}^k$ is not equal to the mean of the $F_{ST}^1$ values computed for each locus separately. Rather, it is the ratio of the mean across loci of the between-group variance in allelic type to the mean across loci of the total variance in allelic type.

One interpretation of F_ST is as the proportion of the variance removed from an indicator variable for one copy of an allele by conditioning on population membership. F_ST is thus analogous to r², a measurement of effect size commonly used in meta-analysis, which can be interpreted as the proportion of variance in a dependent variable that is removed by conditioning on an independent variable (Fox 1997: 94). Another commonly used effect-size measurement applicable to differences between two groups is Cohen’s d (Cohen 1988), the difference in group means on a dependent variable divided by the square root of the mean across groups of within-group variances of the independent variable. For equally sized groups, Cohen’s d is related to r² by d² = 4r²/(1 − r²) (by inverting Rosenthal 1994, Eqs. 16–24). By analogy, we define another measurement of between-group genetic differentiation across a set of loci:

$$\begin{gathered} D_L^2=\frac{4F_{ST}^k}{1-F_{ST}^k} \\ =\frac{\overline{{\delta }^2}}{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}. \end{gathered}$$ (15)

$D_L^2$ for a set of loci is not generally equal to the mean across loci of the value that would result by applying Eq. 15 to each locus separately. Rather, like $F_{ST}^k$, $D_L^2$ is a ratio of two means across loci—the mean of the ${\delta }_i^2$ and the mean within-group variance in allelic type.

$F_{ST}^k$ is a variance partition for allelic indicator variables representing one copy of a locus. At a diploid or polyploid biallelic locus, each copy of the locus provides information about population membership, so more information is available at the locus than is reflected in one copy. We thus define an analogue of $F_{ST}^k$ for a set of ℓ-ploid loci by partitioning the variance of the sum of the number of 1 alleles at each locus into between-group and within-group components. For a single locus, the between-group variance of the sum is

$$\begin{gathered} {\text{Var}}_M\left[E\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M\right)\right] \\ =\sum _{m\in \{A,B\}}P(M=m){\left[E\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M=m\right)-E\left(\sum _{j=1}^{\ell }{L}_{ij}\right)\right]}^2 \\ =\frac{1}{4}{\left[E\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M=A\right)-E\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M=B\right)\right]}^2 \\ =\frac{{\ell }^2}{4}{\delta }_i^2, \end{gathered}$$

and by the independence of the allelic copies at a single locus, the within-group variance is

$$\begin{gathered} E_M\left[\text{Var}\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M\right)\right] \\ =\sum _{m\in \{A,B\}}P(M=m). \\ \sum _{j=1}^{\ell }P\left(L_{ij}=1\mid M=m\right)\left[1-P\left(L_{ij}=1\mid M=m\right)\right] \\ =\frac{\ell }{2}\left[p_i\left(1-p_i\right)+q_i\left(1-q_i\right)\right]. \end{gathered}$$

To define $F_{ST(\ell )}^k$, we sum these terms across loci to construct a ratio of the between-group variance to the total variance:

$$\begin{gathered} F_{ST(\ell )}^k=\frac{\sum _{i=1}^k{\text{Var}}_M\left[E\left(\sum _{j=1}^{\ell }{L}_{ij}\mid M\right)\right]}{\sum _{i=1}^k\text{Var}\left(\sum _{j=1}^{\ell }{L}_{ij}\right)} \\ =\frac{\ell \overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\ell \overline{{\delta }^2}}. \end{gathered}$$ (16)

We show in Appendix 1 that $F_{ST(\ell )}^k\in \left[F_{ST}^k,\ell F_{ST}^k\right)$ with $F_{ST(\ell )}^k=F_{ST}^k$ if and only if $F_{ST}^k=0$ or $F_{ST}^k=1$. Figure 3 shows the relationship between $F_{ST}^k$ and $F_{ST(\ell )}^k$ for several values of ℓ, illustrating the relative increase in $F_{ST(\ell )}^k$ compared with $F_{ST}^k$ as ℓ increases. Figure 3 also illustrates, as shown in Appendix 1, that $F_{ST(\ell )}^k$ is comparable to $\ell F_{ST}^k$ for $F_{ST}^k$ close to 0 and comparable to $F_{ST}^k$ for $F_{ST}^k$ close to 1.

FIGURE 3.

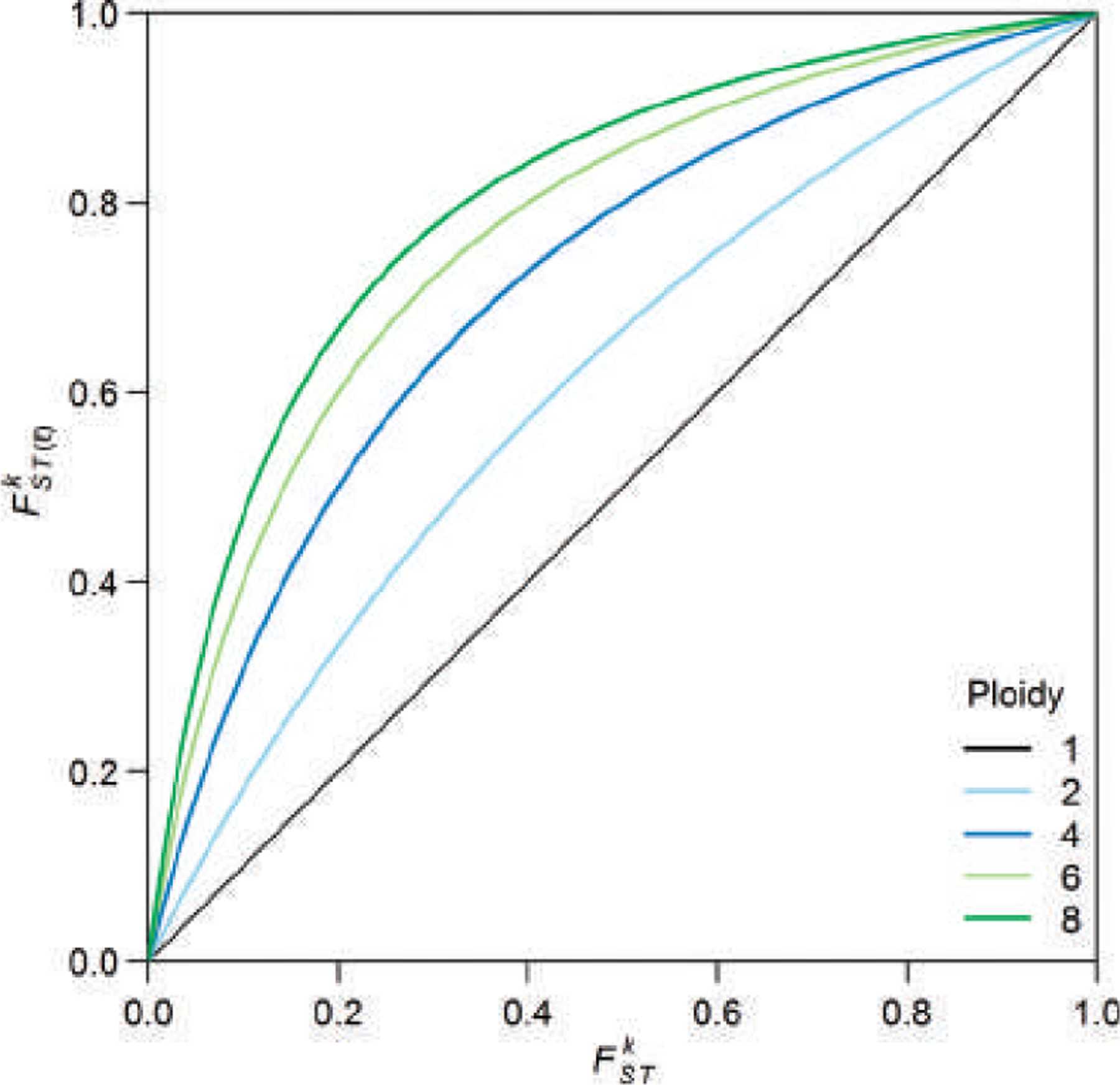
The relationship between $F_{ST}^k$ (Eq. 14), which partitions the variance of allelic indicator variables representing a single copy of each locus, and $F_{ST(\ell )}^k$ (Eq. 16), which partitions the variance of sums of ℓ allelic indicator variables at each locus. Thus, for haploids (ℓ = 1), $F_{ST(\ell )}^k=F_{ST}^k$. For higher ploidy, $F_{ST(\ell )}^k\in \left[F_{ST}^k,\ell F_{ST}^k\right)$, with $F_{ST(\ell )}^k=F_{ST}^k$ if and only if $F_{ST}^k=0$ or $F_{ST}^k=1$ (see Appendix 1). The plot is obtained from Eq. A1.4.

Similarly, we can define an analogue of $D_L^2$ for an ℓ-ploid locus:

$$\begin{gathered} D_{L(\ell )}^2=\frac{4F_{ST(\ell )}^k}{1-F_{ST(\ell )}^k} \\ =\frac{\ell \overline{{\delta }^2}}{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2} \\ =\ell D_L^2. \end{gathered}$$ (17)

Whereas $F_{ST}^k$ and $D_L^2$ can be viewed as indices of the amount of information about population membership available in a single copy of a typical locus, $F_{ST(\ell )}^k$ and $D_{L(\ell )}^2$ assess the total amount of population membership information at a typical locus, considering all ℓ copies.

3.2. Simulation-Based Allele Frequency Differences

Because some of our results depend on specific characteristics of the p_i and q_i, we simulated allele frequencies under a model similar to that of Nicholson et al. (2002) to obtain suitable example distributions for the p_i and q_i (see Figure 4 for a schematic). Specifically, we generated allele frequencies for derived alleles in an ancestral population according to the neutral site frequency spectrum with 2N = 20,000, choosing each allele frequency π_i according to P(π_i = j/(2N)) ∝ 1/j (Charlesworth and Charlesworth 2010, Eq. B6.6.1). To simulate drift after divergence, we produced postdivergence allele frequencies by adding to each “ancestral” allele frequency π_i an independently drawn Normal(0, 0.3π_i(1 − π_i)) random number, where 0.3 is chosen so that $F_{ST}^k$ approximates worldwide human F_ST estimates. Any postdivergence allele frequencies less than 0 or greater than 1 were set to 0 or 1, respectively. After simulating postdivergence frequencies of the derived allele independently in two populations, we assigned the frequencies of either the ancestral or the derived allele in each population to be p_i and q_i, requiring q_i ≥ p_i. We generated 10⁶ pairs of allele frequencies (p_i, q_i) after removing loci at which the same allele fixed in both populations. (Such loci do not contribute to $F_{ST}^k$ or $D_L^2$.) For our simulated allele frequencies, $\overline{p}\approx 0.457$, $\overline{q}\approx 0.542$, $s_p^2\approx s_q^2\approx 0.191$, $\overline{\delta }\approx 0.086$, $\overline{{\delta }^2}\approx 0.025$, $\overline{{\delta }^4}\approx 0.006$, $F_{ST}^k\approx 0.099$, and $D_L^2\approx 0.440$.The $F_{ST}^k$ value of 0.099 is similar to estimates of F_ST for human populations.

FIGURE 4.

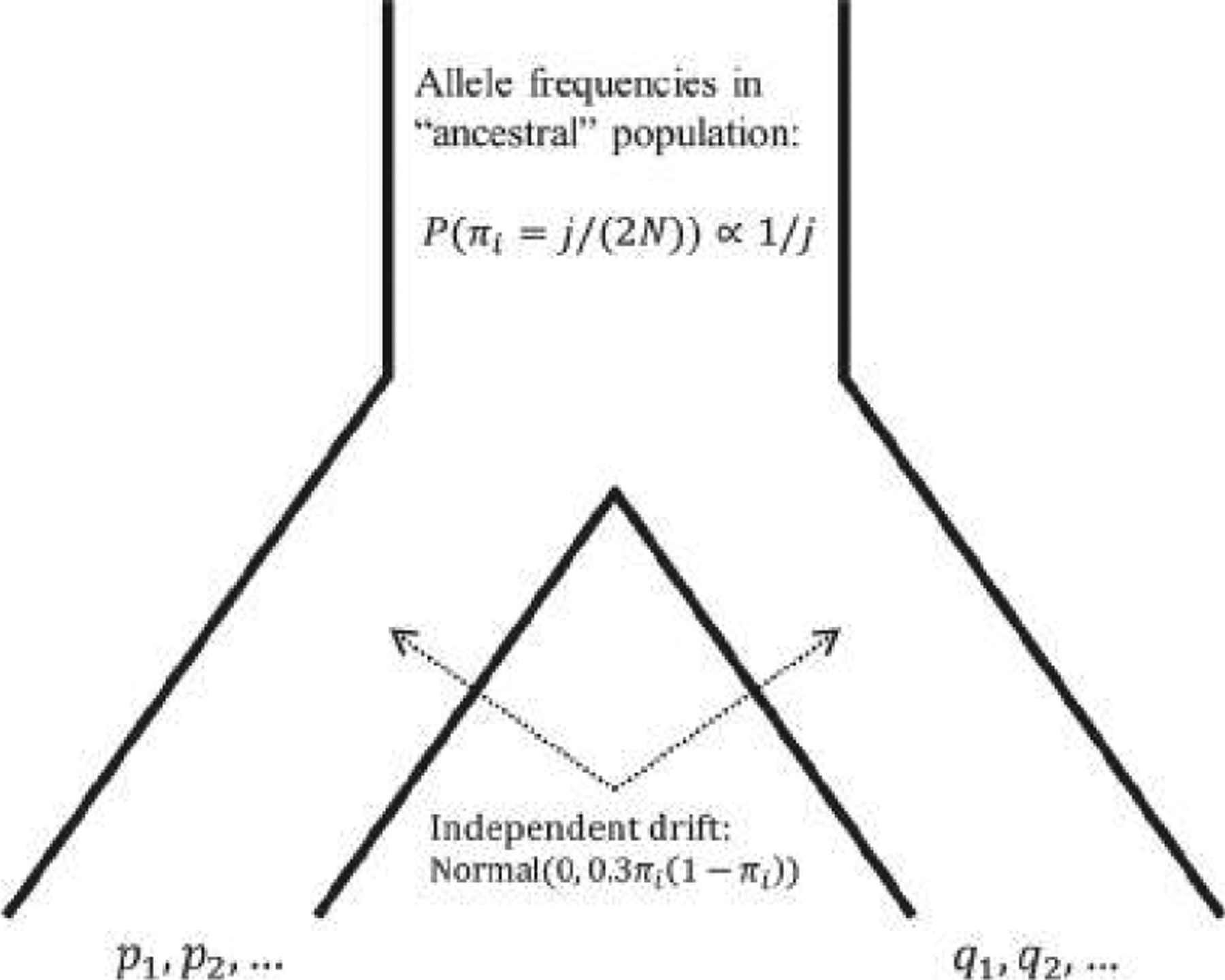
A schematic of the drift model used to simulate allele frequencies (see Section 3.2). Derived allele frequencies in an “ancestral” population are drawn according to the neutral site frequency spectrum. Following a split, the two subpopulations drift independently, with the drift represented by a truncated normal variate with expectation 0. After drift, for each locus i, the allele with greater frequency in population B than in population A is identified, its frequency in population A is labeled p_i, and its frequency in population B is labeled q_i.

4. Properties of the Trait Value T Conditional on the Labeling X_i

We next consider the distribution and properties of the trait value T in each population. In this section, we condition on the labeling of the alleles at each locus X₁, X₂, …, X_k. These labels determine, for each locus, whether the 1 or the 0 allele increases an individual’s trait value. In Section 5, we remove this condition and consider the expected behavior of the trait value under random assignment of the labels.

It is convenient to define a transformation of the labels:

$$U_i=2X_i-1.$$ (18)

If X_i = 1 and the 1 allele is the + allele, then U_i = 1, and if X_i = 0 and the 1 allele is the − allele, then U_i = −1.

4.1. Distribution of T within Each Population Given the Labeling of the Alleles

In either population, conditional on the labeling of the alleles,

$$\begin{gathered} \left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ =\sum _{i:x_i=1}\sum _{j=1}^{\ell }{L}_{ij}+\sum _{i:x_i=0}\sum _{j=1}^{\ell }\left(1-L_{ij}\right). \end{gathered}$$

Because the L_ij are independent Bernoulli random variables with different success probabilities, T has a Poisson binomial distribution in each population. Specifically, within population A, each of the ℓ allelic copies at each locus at which x_i = 1 increases T by 1 with probability p_i, and each of the ℓ allelic copies at each locus at which x_i = 0 increases T by 1 with probability 1 − p_i. Within population B, the same statement holds if p_i is replaced by q_i.

By the properties of the Poisson binomial distribution (Eq. 7), the expectations of T in populations A and B conditional on the labeling are then

$$\begin{gathered} E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right) \\ =\ell \left[\sum _{i:x_i=1}{p}_i+\sum _{i:x_i=0}\left(1-p_i\right)\right], \\ E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=B\right) \\ =\ell \left[\sum _{i:x_i=1}{q}_i+\sum _{i:x_t=0}\left(1-q_i\right)\right]. \end{gathered}$$ (19)

The difference in the conditional expectations is then

$$\begin{gathered} E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=B\right) \\ -E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right) \\ =\ell \left[\sum _{i:x_i=1}{q}_i+\sum _{i:x_i=0}\left(1-q_i\right)\right]-\ell \left[\sum _{i:x_i=1}{p}_i+\sum _{i:x_i=0}\left(1-p_i\right)\right] \\ =\ell \left[\sum _{i:x_i=1}\left(q_i-p_i\right)-\sum _{i:x_i=0}\left(p_i-q_i\right)\right]=\ell \sum _{i=1}^k{\delta }_i{u}_i, \end{gathered}$$ (20)

where, analogously to Eq. 18, u_i = 2x_i − 1.

By Eq. 20 and the fact that the populations have equal size so that P(M = A) = P(M = B) = ½, the variance across populations of the conditional expectation of T is

$$\begin{gathered} {\text{Var}}_M[E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M\right] \\ =\frac{{\ell }^2}{4}{\left(\sum _{i=1}^k{\delta }_i{u}_i\right)}^2. \end{gathered}$$ (21)

By the properties of the Poisson binomial distribution (Eq. 7), the conditional variance of the trait in population A is

$$\begin{gathered} \text{Var}\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right) \\ =\sum _{i:x_i=1}\sum _{j=1}^{\ell }{p}_i\left(1-p_i\right)+\sum _{i:x_i=0}\sum _{j=1}^{\ell }{p}_i\left(1-p_i\right) \\ =\ell \sum _{i-1}^k{p}_i\left(1-p_i\right)=\ell k\left[\overline{p}(1-\overline{p})-s_p^2\right]; \end{gathered}$$

the last step follows from the simplification of the variance in Eq. 7. Because this quantity does not depend on {X₁, …, X_k}, we can remove the condition on {x₁, …, x_k}, giving

$$\text{Var}(T\mid M=A)=\ell k\left[\overline{p}(1-\overline{p})-s_p^2\right].$$ (22)

Similarly, the variance of T in population B is

$$\text{Var}(T\mid M=B)=\ell k\left[\overline{q}(1-\overline{q})-s_q^2\right].$$ (23)

We use the conditional expectations and variances of T in the two populations to define several measurements of the degree of difference between populations on the trait.

4.2. The Standardized Difference in Trait Means, D_T, Given the Labeling of the Alleles

We consider three indices of the degree of difference between populations on the trait—two here, and a third we defer to Section 6. The first is the standardized difference in population means for the trait, D_T, which is the difference between population trait means divided by the square root of the mean across populations of within-population trait variances. D_T is an instance of the Cohen’s d measure of effect size (Cohen 1988). In this case, conditional on the labeling, D_T is

$$\begin{gathered} \left(D_T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ =[E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=B\right) \\ -E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right)]/ \\ \sqrt{\frac{\text{Var}(T\mid M=A)+\text{Var}(T\mid M=B)}{2}}. \end{gathered}$$

The numerator is given in Eq. 20. By Eqs. 22 and 23 and the fact that the two populations are assumed to be the same size, the square of the denominator is

$$\begin{gathered} E_M[\text{Var}(T\mid M)] \\ =\frac{\text{Var}(T\mid M=A)+\text{Var}(T\mid M=B)}{2} \\ =\frac{\ell k}{2}\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]. \end{gathered}$$ (24)

Therefore, combining Eqs. 20 and 24,

$$\begin{gathered} \left(D_T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ =\frac{\sqrt{\ell }\sum _{i=1}^k{\delta }_i{u}_i}{\sqrt{k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}}, \end{gathered}$$ (25)

where again, as in Eq. 18, u_i = 2x_i − 1. In Section 5, we study the distribution of D_T across different labelings of the alleles.

4.3. Partitioning the Variance of the Trait Given the Labeling of the Alleles: ${\rho }_T^2$ and Q_ST

A second measure of between-population difference on the trait is the proportion of the trait’s variance attributable to difference between populations. We label this proportion ${\rho }_T^2$, with

$$\begin{gathered} {\rho }_T^2=\frac{{\text{Var}}_M[E(T\mid M)]}{\text{Var}(T)} \\ =\frac{{\text{Var}}_M[E(T\mid M)]}{E_M[\text{Var}(T\mid M)]+{\text{Var}}_M[E(T\mid M)]}. \end{gathered}$$ (26)

The last step follows from the law of total variance. Conditional on the labeling {X₁, …, X_k}, the numerator appears in Eq. 21, and the denominator is the sum of the expressions in Eqs. 21 and 24. Thus, by Eq. 26, conditional on the labeling of the alleles for a given trait,

$$\begin{gathered} \left({\rho }_T^2\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ =\frac{\ell {\left(\sum _{i=1}^k{\delta }_i{u}_i\right)}^2}{2k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\ell {\left(\sum _{i=1}^k{\delta }_i{u}_i\right)}^2}. \end{gathered}$$ (27)

The proportion ${\rho }_T^2$ is related to Q_ST, which is an analogue of F_ST developed for quantitative traits. For haploids, Q_ST is the proportion of the heritable variance in a quantitative trait attributable to genetic differences between populations (Whitlock 2008). Because we have assumed that the trait we examine is completely heritable, ${\rho }_T^2=Q_{ST}$ for haploids. Q_ST is defined so that, like F_ST, it does not depend on ploidy, which means that ${\rho }_T^2\ne Q_{ST}$ for ploidy ℓ > 1 (unless ${\rho }_T^2=0$ or ${\rho }_T^2=1$). For diploids, again invoking the assumption of perfect heritability of the trait, Q_ST is

$$Q_{ST}=\frac{{\text{Var}}_M[E(T\mid M)]}{2E_M[\text{Var}(T\mid M)]+{\text{Var}}_M[E(T\mid M)]}$$

(Whitlock 2008), and by analogy, for ℓ-ploid organisms,

$$\begin{gathered} Q_{ST}=\frac{{\text{Var}}_M[E(T\mid M)]}{\ell E_M[\text{Var}(T\mid M)]+{\text{Var}}_M[E(T\mid M)]} \\ =\frac{{\left(\sum _{i=1}^k{\delta }_i{u}_i\right)}^2}{2k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+{\left(\sum _{i=1}^k{\delta }_i{u}_i\right)}^2}. \end{gathered}$$ (28)

Thus, regardless of ploidy ℓ, Q_ST is obtained from the expression in Eq. 27 by setting ℓ to 1. The relationship between Q_ST and ${\rho }_T^2$ is exactly the same as the relationship between $F_{ST}^k$ and $F_{ST(\ell )}^k$ (Figure 3 and Appendix 1); that is, if $Q_{ST}=F_{ST}^k$, then ${\rho }_T^2=F_{ST(\ell )}^k$.

5. Properties of D_T and ${\rho }_T^2$ across Different Labelings of the Alleles

In this section, we consider properties of the trait value T across different traits, which may have different allelic labels (X_i), so that each trait has its own locus-specific effects for the alleles. Specifically, we consider two indices of the degree of difference between populations on the trait defined in Section 4, the standardized group difference, D_T (Section 4.2), and the proportion of trait variance that is attributable to between-group differences, ${\rho }_T^2$ (Section 4.3).

5.1. Properties of ${\sum }_{i=1}^k{\delta }_i{U}_i$

One random variable that appears in expressions for both D_T (Eq. 25) and ${\rho }_T^2$ (Eq. 27) is ${\sum }_{i=1}^k{\delta }_i{U}_i$, where U_i is a function of the labels X_i that determine which allele at locus i is the + allele (Eq. 18), taking a value of either −1 or 1 with probability ½ each, and δ_i is the difference between populations in the frequency of the 1 allele (Eq. 8). We give the relevant moments of ${\sum }_{i=1}^k{\delta }_i{U}_i$ here for later reference.

We note first that, for all i and for integers n ≥ 0, the odd and even moments of the U_i obey

$$E\left(U_i^{2n+1}\right)=0,$$ (29)

$$E\left(U_i^{2n}\right)=1.$$ (30)

Thus, by Eq. 29, for n ∈ {0, 1, 2, …},

$$E\left[{\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^{2n+1}\right]=0.$$ (31)

The second moment is

$$\begin{gathered} E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^2\right] \\ =\sum _{i=1}^k{\delta }_i^{2}E\left(U_i^2\right)+\sum _{i=1}^k\sum _{j\ne i}{\delta }_i{\delta }_{j}E\left(U_i{U}_j\right) \\ =\sum _{i=1}^k{\delta }_i^2=k\overline{{\delta }^2}, \end{gathered}$$ (32)

by Eq. 30 and because, by the independence of the U_i, E(U_iU_j) = E(U_i)E(U_j) = 0 for all i ≠ j.

We show in Appendix 2 that the fourth moment is

$$E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^4\right]=3k^2{\overline{{\delta }^2}}^2-2k\left({\overline{{\delta }^2}}^2+s_{{\delta }^2}^2\right).$$ (33)

5.2. The Standardized Group Difference in Trait Means, D_T

Removing the condition on the labels in Eq. 25, u_i becomes the random variable U_i (Eq. 18), and D_T becomes the random variable

$$D_T=\frac{\sqrt{\ell }\sum _{i=1}^k{\delta }_i{U}_i}{\sqrt{k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}}.$$ (34)

By Eq. 29,

$$E\left(D_T\right)=\frac{\sqrt{\ell }\sum _{i=1}^k{\delta }_{i}E\left(U_i\right)}{\sqrt{k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}}=0.$$ (35)

Equation 35 reflects the symmetry of the distribution of D_T around 0. By Eqs. 32, 34, and 35,

$$\begin{gathered} \text{Var}\left(D_T\right)=E\left(D_T^2\right)-E{\left(D_T\right)}^2=E\left(D_T^2\right) \\ =E\left[{\left(\frac{\sqrt{\ell }{\sum }_{i=1}^k{\delta }_i{U}_i}{\sqrt{k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}}\right)}^2\right] \\ =\frac{\ell \overline{{\delta }^2}}{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]/2}, \end{gathered}$$ (36)

where $\overline{{\delta }^2}$ is as defined in Eq. 10.

$E\left(D_T^2\right)$ (Eq. 36) is one measurement of the typical size of the between-group difference in trait means, irrespective of its direction. For fixed $\overline{p}$ and $\overline{q}$, $E\left(D_T^2\right)$ is usually larger if k > 1 than if k = 1 because of variation in the allele frequencies: $s_p^2=s_q^2=s_{\delta }^2=0$ if k = 1, but each may be positive if k > 1, and positive values of each of these terms increase $E\left(D_T^2\right)$. Nonetheless, $E\left(D_T^2\right)$ does not grow without bound as k increases, and it is equal to one of our indices of between-group genetic differentiation at a single locus, $D_{L(\ell )}^2$ (Eq. 17),

$$E\left(D_T^2\right)=D_{L(\ell )}^2=\ell D_L^2.$$ (37)

Thus, though $E\left(D_T^2\right)$ increases with higher ploidy, it does not necessarily increase as the number of loci k influencing the trait increases (Figure 5A). Equation 36 reduces to the results we showed for $D_T^2$ in our previous work (Edge and Rosenberg 2015, Eqs. 37, 38) under the more restrictive assumptions we used there. The correspondences between the main results in this article and the main results in Edge and Rosenberg (2015) are summarized in Table 2.

FIGURE 5.

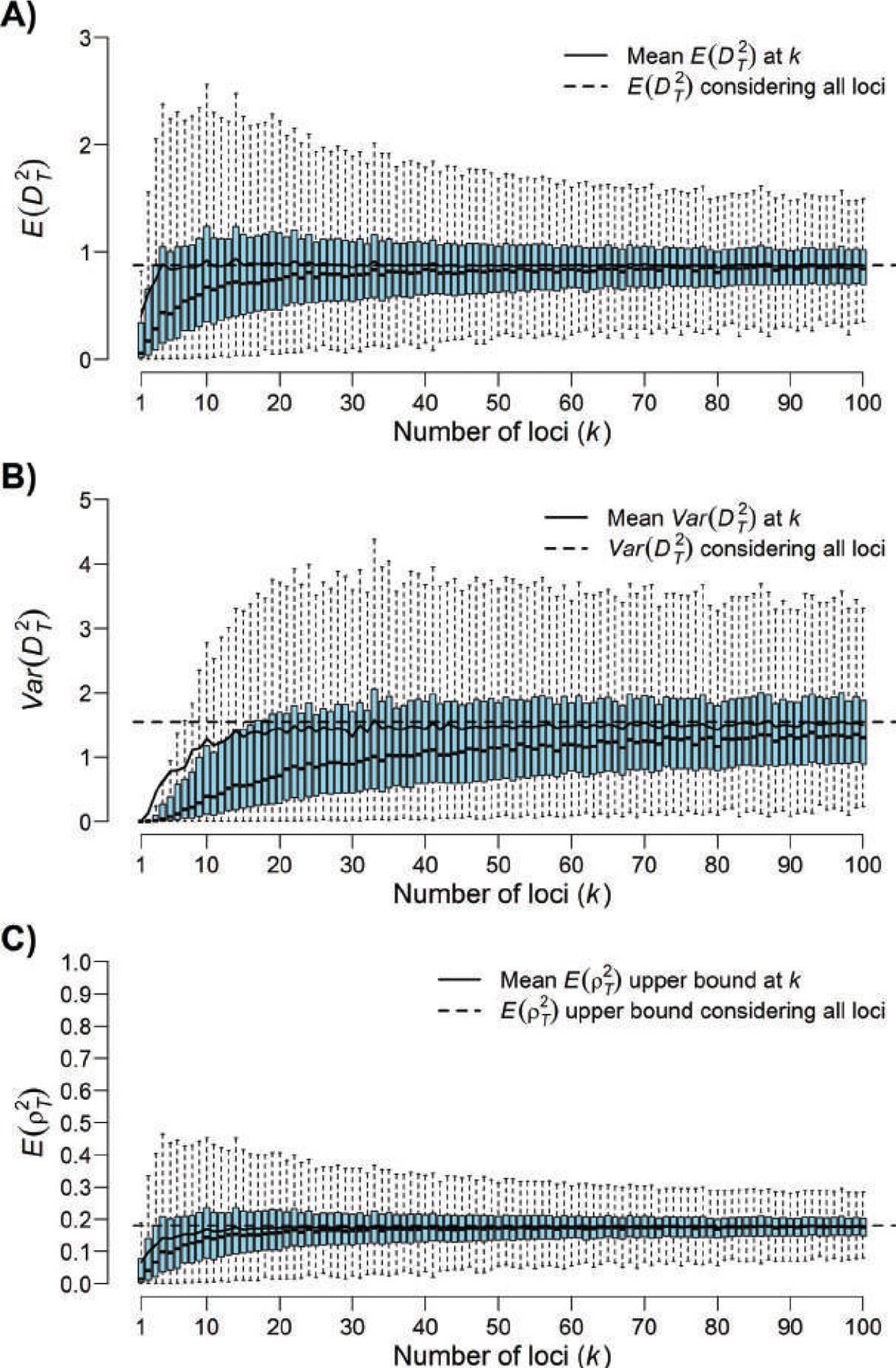
The behavior of expected measures of trait differentiation as the number of randomly selected loci influencing the trait increases. We simulated allele frequencies at 10⁶ neutral loci for a pair of populations that have undergone independent drift since divergence from an ancestral population, with F_ST ≈ 0.1 (see Section 3.2). For each k ∈ {1, …, 100}, we selected 1,000 size-k random subsets of the 10⁶ pairs of simulated allele frequencies and computed three quantities for each subset, assuming diploidy (ℓ = 2). (A) The expected squared standardized trait difference between groups, $E\left(D_T^2\right)$ (Eq. 36). (B) The variance of the squared standardized trait difference between groups, $\text{Var}\left(D_T^2\right)$ (Eq. 39). (C) The upper bound on (and approximate value of) the expected proportion of variance in a neutral trait attributable to allele-frequency differences between groups, $E\left({\rho }_T^2\right)$ (Eqs. 43, 44). For each quantity, box plots of the 1,000 values for each k are shown. Boxes represent the middle 50% of data at each k, and whiskers extend 1.5 times the interquartile range beyond the edge of the box or to the most extreme observation, whichever is shorter. Outliers beyond 1.5 times the interquartile range from the edge of the box are not shown. For all three quantities, as k increases, the mean value at k loci (solid line) converges to the value obtained using all loci (dashed line) because larger random sets of loci more precisely reflect the overall degree of between-group differentiation than do smaller sets of loci.

Table 2.

Correspondence between the Main Results in This Article and in Edge and Rosenberg (2015)

Result	Equation Number
	This Article	Edge and Rosenberg (2015)
E(DT) = 0 due to symmetry around 0 of the distribution of DT.	35	36
$\text{Var}\left(D_T\right)=E\left(D_T^2\right)$ does not increase without bound with the number of loci and is equal to $D_L^2$, where DL is an analogue of DT for the allelic count at a single locus.	36, 37	37, 38
FST ≈ QST.	45, 47, 48	42, 43
As the number of loci k increases without bound, the genetic misclassification rate approaches 0.	55	5
The expectation of the approximate trait-based misclassification rate is closely related to the genetic misclassification rate obtained using one locus.	57	47

The main results in this article reduce to the main results in Edge and Rosenberg (2015) under the following assumptions: (a) The allele frequencies are the same at each locus, meaning that $p_i=\overline{p}=p$ for all i, $q_i=\overline{q}=q$ for all i, ${\delta }_i=\overline{\delta }=q-p$ for all i, and $s_p^2=s_q^2=s_{\delta }^2=0$. (b) The allele frequencies are symmetric, meaning that $\overline{q}=1-\overline{p}$. In conjunction with assumption (a), (b) implies that $F_{ST}={\overline{\delta }}^2=1-4pq$. (c) The organisms are haploid, or in the present article’s notation, ℓ = 1. Assumption (c) implies that $Q_{ST}={\rho }_T^2$ (Eqs. 26–28).

In addition to the expectation of $D_T^2$, we may wish to know its variance—do traits influenced by many loci vary widely in their level of between-population difference? By Eq. 33,

$$\begin{gathered} E\left(D_T^4\right)=\frac{{\ell }^2\left[3k^2{\overline{{\delta }^2}}^2-2k\left({\overline{{\delta }^2}}^2+s_{{\delta }^2}^2\right)\right]}{k^2{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]}^2/4} \\ =\frac{{\ell }^2}{{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]}^2/4}\times \left(3{\overline{{\delta }^2}}^2-2\left({\overline{{\delta }^2}}^2+s_{{\delta }^2}^2\right)/k\right). \end{gathered}$$ (38)

The required variance, calculated as $E\left(D_T^4\right)-E{\left(D_T^2\right)}^2$, is, by Eqs. 36 and 38,

$$\text{Var}\left(D_T^2\right)=\frac{2{\ell }^2}{{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]}^2/4}\times \left({\overline{{\delta }^2}}^2-\left({\overline{{\delta }^2}}^2+s_{{\delta }^2}^2\right)/k\right).$$ (39)

If k = 1, then $s_{{\delta }^2}^2=0$, and $\text{Var}\left(D_T^2\right)=0$. As k increases, $\text{Var}\left(D_T^2\right)$ approaches

$$\begin{gathered} \underset{k\to \infty }{\text{lim}}\text{Var}\left(D_T^2\right)= \\ =\frac{2{\ell }^2{\overline{{\delta }^2}}^2}{{\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]}^2/4} \\ =2\text{Var}{\left(D_T\right)}^2. \end{gathered}$$ (40)

Equations 39 and 40 indicate that as the number of loci k increases, the variance of $D_T^2$ does increase, but it asymptotes to a limit that does not depend on k (Figure 5B).

5.3. Properties of ${\rho }_T^2$ and Q_ST

Removing the condition on the labels in Eq. 27, u_i becomes the random variable U_i (Eq. 18), and ${\rho }_T^2$ becomes a random variable

$$\begin{gathered} {\rho }_T^2=\ell {\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2/ \\ \{2k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right] \\ +\ell {\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2\}. \end{gathered}$$ (41)

To describe the behavior of ${\rho }_T^2$ across different traits, we approximate $E\left({\rho }_T^2\right)$ by replacing ${\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2$ in Eq. 41 with its expectation, motivated by a Taylor approximation argument. Making the substitution $Y=(\ell /2){\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2$, we have

$$\begin{gathered} {\rho }_T^2=\frac{Y}{k\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+Y} \\ =g(Y). \end{gathered}$$ (42)

Defining μ_Y = E(Y), a first-order Taylor series expansion for g(Y) around Y = μ_Y gives

$${\rho }_T^2=g(Y)\approx g\left({\mu }_Y\right)+g^{\prime }\left({\mu }_Y\right)\left(Y-{\mu }_Y\right),$$

and taking the expectation gives

$$E\left({\rho }_T^2\right)=E[g(Y)]\approx g\left({\mu }_Y\right)+g^{\prime }\left({\mu }_Y\right)E\left(Y-{\mu }_Y\right)=g\left({\mu }_Y\right).$$

By Eq. 32, $E\left[{\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2\right]=k\overline{{\delta }^2}$. Substituting $E(Y)=(\ell /2)k\overline{{\delta }^2}$ for Y in Eq. 42 gives

$$E\left({\rho }_T^2\right)\approx \frac{\ell \overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\ell \overline{{\delta }^2}}.$$ (43)

The expression on the right side of Eq. 43 is an approximation of $E\left({\rho }_T^2\right)$, but it is also a strict upper bound on $E\left({\rho }_T^2\right)$. To see that it is an upper bound, note that ${\rho }_T^2$ is concave in $Y=(\ell /2){\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2$ (Eq. 42). Thus, by Jensen’s inequality, which states that if g is a concave function of a random variable X, then E[g(X)] ≤ g[E(X)], we have

$$E\left({\rho }_T^2\right)\le \frac{\ell \overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\ell \overline{{\delta }^2}}.$$ (44)

As we observed for $E\left(D_T^2\right)$, if $\overline{p}$ and $\overline{q}$ are fixed, then $E\left({\rho }_T^2\right)$ can take larger values if k > 1 than if k = 1 because increasing $s_p^2$ or $s_q^2$ increases the upper bound on $E\left({\rho }_T^2\right)$. Nonetheless, $E\left({\rho }_T^2\right)$ does not grow without bound as k increases (Figure 5C). Comparing Eqs. 43 and 44 with Eq. 16,

$$\begin{gathered} E\left({\rho }_T^2\right)\approx F_{ST(\ell )}^k, \\ E\left({\rho }_T^2\right)\le F_{ST(\ell )}^k. \end{gathered}$$ (45)

The expected value of ${\rho }_T^2$ is thus approximately equal to, and no greater than, the ratio of the mean across loci of the between-group variance of ${\sum }_{j=1}^{\ell }{L}_{ij}$ to the mean across loci of the total variance of ${\sum }_{j=1}^{\ell }{L}_{ij}$ , where ${\sum }_{j=1}^{\ell }{L}_{ij}$ is a random variable representing the number of 1 alleles carried by an ℓ-ploid individual at locus i.

Because Q_ST is equal to the expression for ${\rho }_T^2$ in Eq. 41 with ℓ set to 1 (Eq. 28), Eqs. 43 and 44 imply that

$$\begin{gathered} Q_{ST}\approx \frac{\overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\overline{{\delta }^2}}, \\ {Q}_{ST}\le \frac{\overline{{\delta }^2}}{2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right]+\overline{{\delta }^2}}. \end{gathered}$$ (46)

By Eq. 14, the expression on the right side of Eq. 46 is equal to $F_{ST}^k$, so

$$Q_{ST}\approx F_{ST}^k,$$ (47)

$$Q_{ST}\le F_{ST}^k.$$ (48)

Equation 47 is consistent with previous work on the relationship between $F_{ST}^k$ and Q_ST under different models (e.g., Lande 1992; Whitlock 1999), and it provides one justification for the claim that the degree of between-group difference on a neutral trait is approximately equal to the degree of between-group genetic differentiation at a typical locus.

6. Adding Assumptions Inspired by Equal Drift since a Recent Divergence

Having addressed the relationship between neutral genetic and neutral phenotypic differentiation between populations in the context of standardized differences and variance partitioning (Sections 4 and 5), we now consider the accuracy with which individuals can be classified into populations using neutral genetic and phenotypic information. We require two assumptions that will allow us to consider approximate misclassification rates that would arise if we attempted to identify an individual’s population of origin by examining k loci directly or by examining a trait determined additively by those k loci. The case in which these assumptions are met is a restriction of the general case we have been examining. The special case in this section can be viewed as the expectation under a model in which the allele frequencies in populations A and B have experienced equal amounts of drift since a recent divergence (see Appendix 3).

The first assumption is symmetry of average frequency of the 1 allele across loci in populations A and B,

$$\overline{q}=1-\overline{p},$$ (49)

where both $\overline{p}$ and $\overline{q}$ are assumed to be nonzero. By Eq. 9, Eq. 49 implies that

$${\overline{\delta }}^2=1-4\overline{p}\overline{q}.$$ (50)

The quantity in Eq. 50 is the $F_{ST}^1$ value of a locus that has the average frequency of the 1 allele in each population, lending ${\overline{\delta }}^2$ a new interpretation (Eq. 12). The second assumption is that the variance of the allele frequencies has the same value in each population:

$$s_p^2=s_q^2.$$ (51)

6.1. Multilocus Classification

We now consider the problem of identifying the population of an individual of unknown origin. In this subsection, we examine the misclassification rates that arise from an examination of the number of 1 alleles carried by an individual across k loci, S.

Recall that the genotypic statistic S (Eq. 6) is the number of alleles carried by an individual that are more common in population B than in population A. If X_i = 1 for all i, then T = S. Within each population, the Ls are independent Bernoulli random variables with possibly different probabilities. Thus, within each population, S has a Poisson binomial distribution. By the properties of the Poisson binomial distribution (Eq. 7),

$$\begin{gathered} E(S\mid M=A)=\sum _{i=1}^k\sum _{j=1}^{\ell }{p}_i=\ell k\overline{p}, \\ \text{Var}(S\mid M=A)=\sum _{i=1}^k\sum _{j=1}^{\ell }{p}_i\left(1-p_i\right) \\ =\ell k\left[\overline{p}(1-\overline{p})-s_p^2\right]; \\ E(S\mid M=B)=\sum _{i=1}^k\sum _{j=1}^{\ell }{q}_i=\ell k\overline{q}, \\ \text{Var}(S\mid M=B)=\sum _{i=1}^k\sum _{j=1}^{\ell }{q}_i\left(1-q_i\right) \\ =\ell k\left[\overline{q}(1-\overline{q})-s_q^2\right], \end{gathered}$$ (52)

where $\overline{p}$, $\overline{q}$, $s_p^2$, and $s_q^2$ are as defined in Eqs. 2 and 3. The variances of S within each population are the same as the variances of T within each population (Eqs. 22, 23).

We consider the normal approximation of the misclassification rate obtained if the genotypic statistic S is used for classification. If the assumptions in Eqs. 49 and 51 hold, then the within-population variances of S in the two populations are equal:

$$\begin{gathered} \ell k\left[\overline{p}(1-\overline{p})-s_p^2\right]=\ell k\left[\overline{q}(1-\overline{q})-s_q^2\right] \\ =\ell k\left[\overline{p}\overline{q}-s_p^2\right]. \end{gathered}$$ (53)

Further, when k is large, as a sum of independent Bernoulli variables the sum of whose variances increases without bound, the distribution of S is approximately normal:

$$\begin{gathered} (S\mid M=A)~\text{Normal}\left(\ell k\overline{p},\ell k\left[\overline{p}\overline{q}-s_p^2\right]\right), \\ (S\mid M=B)~\text{Normal}\left(\ell k\overline{q},\ell k\left[\overline{p}\overline{q}-s_p^2\right]\right). \end{gathered}$$ (54)

(Deheuvels et al. 1989, Theorem 1.1).

Denoting the normal density that approximates the distribution of S in population A by f_A(s) and the corresponding normal density for population B by f_B(s), then when we observe that S = s, we classify the individual into population A if f_A(s) > f_B(s) and into population B if f_A(s) < f_B(s). In this case, f_A(s) > f_B(s) if $s<\ell k(\overline{p}+\overline{q})/2$ and f_A(s) < f_B(s) if $s>\ell k(\overline{p}+\overline{q})/2$. We ignore the case of $s=\ell k(\overline{p}+\overline{q})/2$, which is negligible for large k. By the assumption in Eq. 49, $\overline{p}+\overline{q}=1$, and we therefore classify an individual into population A if S < ℓk/2 and into population B if S > ℓk/2.

We represent the event that an individual is misclassified on the basis of S with the random indicator variable W_S, which equals 1 if and only if an individual is misclassified on the basis of S and equals 0 otherwise. In population A, the approximate probability of misclassification is

$$\begin{gathered} P\left(W_s=1\mid M=A\right)\approx P(S>\ell k/2\mid M=A) \\ \approx 1-\Phi \left(\sqrt{\ell k}\frac{\overline{\delta }}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\right), \end{gathered}$$

where Φ is the cumulative distribution function of the standard normal distribution. A similar calculation for population B gives the same misclassification rate. Thus, in both populations, the approximate misclassification probability obtained using S is

$$\begin{gathered} P\left(W_s=1\right)\approx 1-\Phi \left(\sqrt{\ell k}\frac{\overline{\delta }}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\right) \\ =1-\Phi \left(\sqrt{\ell k}\frac{\overline{q}-\overline{p}}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\right). \end{gathered}$$ (55)

As k increases, with $\overline{p}$, $\overline{q}$, and $s_p^2$ held constant, the argument to the cumulative distribution function in Eq. 55 approaches infinity, and the value of the cumulative distribution function approaches 1. Thus, as the number of loci increases, the misclassification probability obtained when using the genotypic statistic S, P(W_S = 1), approaches 0.

6.2. Trait-Based Classification

Next we consider the approximate misclassification rate obtained on the basis of an individual’s trait value. We represent the event that an individual is misclassified on the basis of T with the random indicator variable W_T, which equals 1 if an individual is misclassified on the basis of its trait value and equals 0 otherwise. Using an argument similar to the one used to justify Eq. 55 (detailed in Appendix 4), the approximate trait-based misclassification rate, conditional on X₁, …, X_k, is

$$\begin{gathered} P\left(W_T=1\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ \approx 1-\Phi \left[\frac{\sqrt{\ell }\left|{\sum }_{i=1}^k{\delta }_i{u}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right], \end{gathered}$$ (56)

where Φ is the cumulative distribution function of the standard normal distribution.

To understand how the misclassification rate is expected to behave across different labelings of the loci, we consider the expectation of the normal approximation of the misclassification rate obtained using the trait value T, P(W_T = 1). Removing the condition on the allelic labeling in Eq. 56 and rearranging gives

$$1-P\left(W_T=1\right)\approx \Phi \left[\frac{\sqrt{\ell }\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right],$$

where U_i is as defined in Eq. 18. Taking the expectation of both sides gives

$$1-E\left[P\left(W_T=1\right)\right]\approx E\left(\Phi \left[\frac{\sqrt{\ell }\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right]\right).$$

Noticing that Φ is concave for positive values of its argument gives, by Jensen’s inequality,

$$E\left(\Phi \left[\frac{\sqrt{\ell }\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right]\right)\le \Phi \left[\frac{\sqrt{\ell }E\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right].$$

Because $\left|\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)\right|={\left[{\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, and because the square root is a concave function, Jensen’s inequality gives

$$E\left(\left|\sum _{i=1}^k{\delta }_i{U}_i\right|\right)=E\left(\sqrt{{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^2}\right)\le \sqrt{E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^2\right]}.$$

Then

$$\Phi \left[\frac{\sqrt{\ell }E\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right]\le \Phi \left[\frac{\sqrt{\ell E[{\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2}]}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right].$$

Because $E\left[{\left({\sum }_{i=1}^k{\delta }_i{U}_i\right)}^2\right]=k\overline{{\delta }^2}$ (Eq. 32),

$$\Phi \left[\frac{\sqrt{\ell E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^2\right]}}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right]=\Phi \lceil \frac{\sqrt{\ell \overline{{\delta }^2}}}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\rceil =\Phi \lceil \frac{\sqrt{\ell \left({\overline{\delta }}^2+s_{\delta }^2\right)}}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\rceil .$$

We then have an approximate lower bound on the expected probability of misclassification on the basis of T:

$$E\left[P\left(W_T=1\right)\right]\approx 1-E\left(\Phi \left[\frac{\sqrt{\ell }\left|{\sum }_{i=1}^k{\delta }_i{U}_i\right|}{2\sqrt{k\left(\overline{p}\overline{q}-s_p^2\right)}}\right]\right)\ge 1-\Phi \left[\frac{\sqrt{\ell \left({\overline{\delta }}^2+s_{\delta }^2\right)}}{2\sqrt{\overline{p}\overline{q}-s_p^2}}\right].$$ (57)

If ${\text{s}}_{\delta }^2=0$, then Eq. 57 produces the same result as Eq. 55 with k = 1. The expectation of the approximate misclassification probability on the basis of the trait is therefore, if ${\text{s}}_{\delta }^2=0$, greater than or equal to the approximate misclassification probability obtained using a single locus.

For fixed $\overline{p}$, $\overline{q}$, and $s_p^2$, as k increases, the argument to the cumulative distribution function in Eq. 57 does not approach infinity. The value of the cumulative distribution function approaches an asymptotic value obtained as the increasingly many loci converge on large-k values of ${\text{s}}_{\delta }^2$ and $s_p^2$. Thus, as the number of loci considered increases, the misclassification probability obtained when using the trait value T, P(W_T = 1) does not approach 0.

7. Discussion

We have extended a model of multilocus allele frequency differences and polygenic trait differences between groups to accommodate more general allele-frequency distributions and arbitrary ploidy. Our results recapitulate our original conclusion (Edge and Rosenberg 2015): a single neutral trait provides approximately the same amount of information about population membership as does a single neutral genetic locus. This general claim is reflected in three specific ways of asking about the relative magnitude of population-membership information in genotypes and in phenotypes: using the standardized trait difference between groups (D_T, Eq. 37), using the between-group variance in the trait (${\rho }_T^2$ and D_ST, Eqs. 45, 47), and using the misclassification rate obtained when attempting to classify individuals into groups by their trait values (P(W_T = 1), Eq. 57). We also provide two main updates to our previous work. First, under our model, within-population variation in allele frequency across loci tends to increase the degree of expected difference between groups on a polygenic trait (Eq. 36). Second, the degree of information about population membership is greater for a diploid (or polyploid) than for a haploid locus (Figure 3), and it is also correspondingly greater for a trait in a diploid (or polyploid) organism than in a haploid (Eq. 37).

What accounts for the difference between the ancestry information of multiple genetic loci and that of a trait governed by those same loci? When examining multiple genetic loci, information about population membership can be cumulated from multiple sites—for example, by counting in an individual the alleles that are more common in population A than in population B. In contrast, although an individual’s trait value implicitly encodes information about its genotype at many loci, random genetic drift prevents the trait from accumulating information about population membership. In our model, for every locus at which the allele at higher frequency in population A is associated with larger trait values, there is likely to be another locus at which the “A-like” allele is associated with smaller trait values. The cumulative effect of this locus-by-locus shuffling of the choice of population associated with the higher trait value is that a single neutral trait is, in expectation, approximately as informative about population membership as a single neutral locus.

7.1. Models of Genotypic and Phenotypic Differentiation

Our results accord with those of previous efforts to address similar questions with different models (Felsenstein 1973, 1986; Rogers and Harpending 1983; Lande 1992; Spitze 1993; Lynch and Spitze 1994; Whitlock 1999; Berg and Coop 2014), which have repeatedly found that group or population differences in neutral, completely heritable traits mirror neutral genetic differentiation. Previous examinations of trait differentiation have often proceeded by relating assumptions about quantitative traits to models of evolutionary change in allele frequencies, such as a Wright–Fisher model (Felsenstein 1973), an island migration model (Lande 1992), or a coalescent framework (Whitlock 1999). The use of such evolutionary models can suggest connections with other areas of evolutionary genetics and can also provide insights with considerable generality; for example, Whitlock’s (1999) results hold for coalescent models with arbitrary population structure.

In contrast with some previous models of phenotypic diversity, our models here and in our previous work (Edge and Rosenberg 2015) are more similar to the genetic classification models of Risch et al. (2002), Edwards (2003), and Tal (2012) in that we directly consider allele frequencies, using simple probabilistic arguments and minimal evolutionary assumptions. This approach complements earlier evolutionary work on the relationship of genetic and phenotypic differentiation in at least two ways. First, our model allows for computations with quantities that are of interest in epidemiological and biomedical studies but that do not necessarily arise naturally under evolutionary models, such as Cohen’s d (equal to our D_T for a completely heritable trait) and the effect size r² (equal to our ${\rho }_T^2$ for a completely heritable trait). Second, the fact that our model makes only minimal evolutionary assumptions shows that similar results obtained under evolutionary models are robust in that they are also produced via a substantially different modeling approach.

7.2. Interpreting Group Differences in Phenotype

How can this work aid in the interpretation of phenotypic differences between human groups? Consider health outcomes, an important set of phenotypes for which genetic and phenotypic differentiation across populations have been of interest.

Among people in the United States, for example, well-established differences exist between socially defined racial groups in the incidence of many health conditions, including heart disease (e.g., Lloyd-Jones et al. 2010), various cancers (e.g., Ward et al. 2004; Siegel et al. 2013), and diabetes (e.g., LaVeist et al. 2009), with African Americans having worse health outcomes than European Americans across many domains (reviewed in Dressler et al. 2005; Adler and Rehkopf 2008). Such phenotypic differences between pairs of groups arise from a combination of interacting factors, which can be viewed as modifications of a baseline prediction made on the basis of neutral genetic differences. Evolutionary genetics can then contribute to understanding group differences in health outcomes by providing models that predict the degree to which phenotypic differences between human groups are likely to be based in neutral genetic differences. Such models do not necessarily explain the source of any particular phenotypic difference, but they do provide an idea of what patterns of difference are expected.

Using population-genetic models to build intuition about phenotypic differences between human groups does not require that group classifications are reducible to, caused by, or primarily based in genetic differences between populations. Rather, population-genetic models of neutral genetic variation are applicable to sets of groups that are correlated with some degree of genetic population structure and that thus distinguish groups that differ in allele frequency at sites across the genome. Although the relationship between population-genetic groupings and socially defined groupings is complex (e.g., Kittles and Weiss 2003; Bamshad et al. 2004; Kitcher 2007; Hunley et al. 2016), we can gain some intuition about the possible sources of a group difference in phenotype for socially defined groups by comparing its size to the associated degree of between-group differentiation at a typical genetic locus.

Two possible causes of group phenotypic differences that are larger or smaller than the degree of between-group differentiation at a typical selectively neutral locus are natural selection and environmental difference. If a trait has been under selection in two populations in a manner that leads to divergence—for example, if the trait is advantageous in one population and disadvantageous or neutral in the other—then the between-group difference on the trait will typically exceed the average between-group genetic difference. An example relevant to health differences between socially defined racial groups is skin pigmentation: lighter skin has been positively selected among populations at higher latitudes (Jablonski and Chaplin 2000; Relethford 2002; Berg and Coop 2014), but it is also a risk factor for skin cancer (Lin and Fisher 2007). In turn, European Americans, most of whose recent ancestors generally lived at high latitude, have substantially higher rates of skin cancer than do African Americans (Halder and Bridgeman-Shah 1995), a larger fraction of whose recent ancestors generally lived at lower latitudes. In contrast, many other health-related traits are likely associated with similar reproductive fitness wherever they occur. Such conditions would be expected to experience convergent selection, which would lead to smaller between-group trait differences than might be predicted from neutral genetic diversity. Thus, one explanation for larger-than-expected phenotypic differences among groups is divergent selection, and one explanation for smaller-than-expected phenotypic differences among groups is convergent selection. This reasoning is the basis for the use of comparisons between Q_ST and F_ST to test hypotheses about phenotypic evolution, a productive approach for model organisms that can be raised in a “common garden” situation (Whitlock 2008; Leinonen et al. 2013).

In humans, assessing whether selection has magnified health differences beyond the neutral prediction is difficult. In some specific cases, divergent selection is regarded as an important driver of group difference in disease burden—including, for example, sickle-cell disease, which occurs at higher rates in malarial regions of Africa and the Mediterranean (e.g., Piel et al. 2010). In many other cases of phenotypic difference, hypotheses of divergent selection—sometimes paired with gene–environment interaction—have also been proposed (Knowler et al. 1983; Meindl 1987; Zlotogora et al. 1988; Wilson and Grim 1991; Bindon and Baker 1997). Many such hypotheses have been criticized individually (Curtin 1992; Risch et al. 2003), and concern has been raised that selective explanations for differences in health outcomes often assume a degree of endurance and importance unwarranted by the evidence (Kaufman and Hall 2003). As new cases connecting selection pressures to molecular evidence of adaptation emerge (e.g., Fumagalli et al. 2015), the empirical basis for assessing the role of divergent selection in explaining differences in health outcomes will expand.

Much recent discussion has focused on an alternative approach to examining worldwide consequences of selection, considering demographic factors that influence the strength of selection against deleterious mutations in different populations (Lohmueller 2014; Henn et al. 2015). Recent studies have not found pronounced difference between groups of primarily European and African descent in the overall frequency of putatively deleterious alleles (Fu et al. 2014; Simons et al. 2014; Do et al. 2015), but populations differ in how these alleles are distributed among individuals, with Europeans carrying more genotypes homozygous for putatively deleterious alleles compared with Africans (Lohmueller et al. 2008; Fu et al. 2014; Do et al. 2015). Though these studies do not identify differences between populations in the influence of experienced selective pressures, their results suggest that a systematic difference across populations in the outcomes of selection on disease phenotypes, if it exists at all, would likely tilt toward a greater disease burden in non-Africans.

Finally, environmental differences between groups are important sources of between-group trait differences. Environmental differences and associated differences in the effect of gene–environment interactions can act in concert with or in opposition to any genetic differences that influence a trait, leading to between-group trait differences that are larger or smaller than would be expected on the basis of neutral genetic differences alone (Pujol et al. 2008). In the United States, the environments of people of different socially defined races differ in myriad factors that could contribute to differences in health outcomes (Williams and Jackson 2005), including socioeconomic status (Adler and Newman 2002), education (Non et al. 2012), residential segregation (Williams and Collins 2001), discrimination (Williams and Mohammed 2009), targeting by the criminal justice system (Iguchi et al. 2005), access to medical care (Mayberry et al. 2000), and doctor–patient communication (Ashton et al. 2003).

We can examine an environmental hypothesis about group differences in health outcomes in relation to the predicted pattern of differences across outcomes for our neutral model of two groups. Under the neutral model, each group has an equal chance of having a larger trait value for each trait. Thus, each population would have a larger mean value for roughly half the traits on which the groups differed, with each trait independent if there are no genetic correlations. An environmental explanation of differences in health outcomes might hold that social differences, such as differences in access to health care, are likely to cause a pattern in which differences between groups run in the same direction across many diseases and causes of mortality. Under this reasoning, the fact that African Americans suffer more than do European Americans from a wide variety of diseases is more consistent with environmental sources of phenotypic difference than with a neutral-genetic explanation. As an example, Wong et al. (2002) tabulated racial differences in causes of death in 36 categories over a 9-year period. After adjusting for age, sex, and years of education, they estimated that black Americans lost more life years than white Americans on average in 28 of those categories. Informally, assuming under our neutral model that no genetic correlation exists between phenotypic outcomes and that for each outcome the larger value has equal probability of occurring in either group, the binomial probability that one population would have a larger trait value than the other on at least 28 of 36 independent phenotypes is only 0.001. A single systematic environmental effect that simultaneously inflates many nongenetic risk factors in African Americans, on the other hand, can provide a simple explanation for such skewed outcomes.

7.3. Conclusions

Our model provides a general framework for describing the relevance of single-locus genetic diversity partitioning for predictions about the sources of phenotypic differences between groups. For neutral, heritable traits, group differences in phenotype will be random in direction and will reflect the degree of genetic difference at a single locus—modest in size for humans, but likely not zero—regardless of how many loci influence the trait. Such neutral differences are a baseline on top of which selection and environmental influences act (Figure 6). In the case of health-related differences between socially defined races in the United States, the occurrence of genetic differentiation as measured by F_ST suggests that neutral genetic differences are likely to exist for many heritable health outcomes that are not under selection. Such genetically based differences may run in the opposite direction of the apparent phenotypic difference between groups, and typical values of human F_ST suggest that they will likely be modest in size on average. Nonetheless, their existence supports the view that genetic research designs that capitalize on group differences (e.g., Winkler et al. 2010; Zaitlen et al. 2014) can be informative about genetic architecture or the genetic variants that influence phenotypes (Rosenberg et al. 2010; Teo et al. 2010). At the same time, any patterns of difference in which one group suffers more than others from the majority of many genetically independent diseases are unlikely to be explained by neutral genetic variation. For humans, our model supports the view that coordinated group differences across a preponderance of independent health-related traits suggest an important role for systematic differences in environmental risk factors.

FIGURE 6.

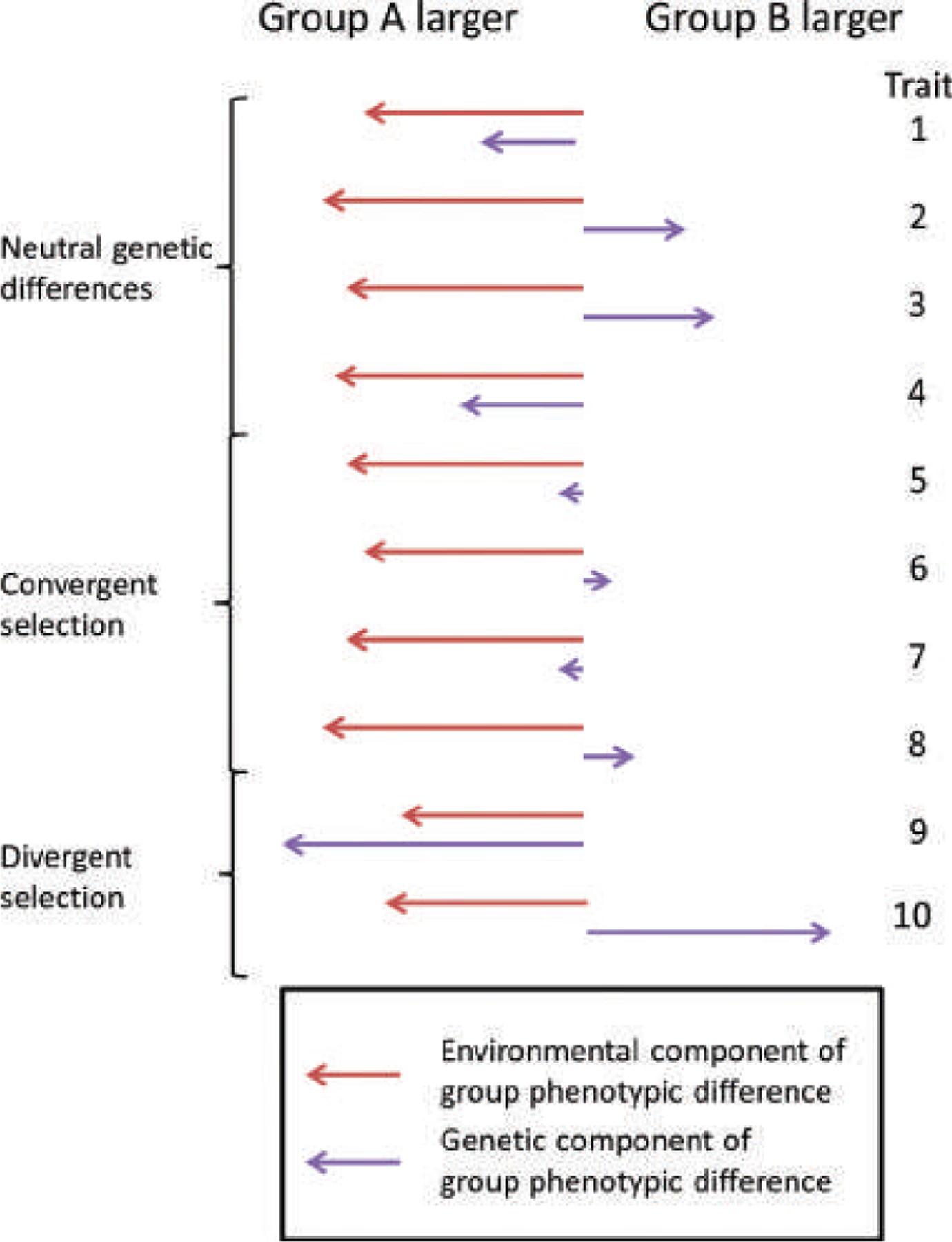
A schematic for thinking about health differences between socially defined racial groups in the United States. Groups such as African Americans face environmental differences likely to lead to worse health outcomes across a range of different diseases (red arrows). For health phenotypes that have been selectively neutral, genetic differences between groups will be random in direction and comparable in size to genetic differences at a single locus—modest for humans, but usually not zero, depending on the groups being considered (purple arrows in traits 1–4). For health phenotypes under convergent selection, such as those that lead to reduced reproductive success in most or all human environments, genetic differences will be random in direction and smaller than for neutral phenotypes (purple arrows in traits 5–8). Some health outcomes, such as skin cancer and sickle-cell disease, differ between groups in part because of divergent selection. (These differences do not necessarily coincide neatly with socially relevant racial divisions.) For such phenotypes, the genetic component of a group difference in phenotype can be large (purple arrows in traits 9 and 10). Not considered in this simple diagram are gene–environment interactions, which often are especially important in cases of divergent selection. For example, in the case of skin cancer, the degree to which genetic variants that lead to darker skin are protective depends on sun exposure.

Appendix 1: $F_{ST}^k$ and $F_{ST(\ell )}^k$

In this appendix, we derive some results about the relationship between $F_{ST}^k$ (Eq. 14), which summarizes the information about population membership available in one copy of a typical locus chosen from within a set of k loci, and $F_{ST(\ell )}^k$ (Eq. 16), which summarizes the corresponding population membership information available in ℓ independent copies of a typical locus chosen from within the set of k loci.

For convenience, define v as

$$v=2\left[\overline{p}(1-\overline{p})-s_p^2+\overline{q}(1-\overline{q})-s_q^2\right],$$ (A1.1)

where $\overline{p}$, $\overline{q}$, $s_p^2$, and $s_q^2$ are as defined in Eqs. 2 and 3. Then by Eq. 14,

$$F_{ST}^k=\frac{\overline{{\delta }^2}}{v+\overline{{\delta }^2}},$$ (A1.2)

and by Eq. 16,

$$F_{ST(\ell )}^k=\frac{\ell \overline{{\delta }^2}}{v+\ell \overline{{\delta }^2}},$$ (A1.3)

where ℓ is the number of copies of the locus being considered and $\overline{{\delta }^2}$ is defined in Eq. 10. Because v, $\overline{{\delta }^2}$, and ℓ are all nonnegative, $F_{ST}^k\in [0,1]$ and $F_{ST(\ell )}^k\in [0,1]$. Equations A1.2 and A1.3 also imply that $F_{ST}^k=0$ if and only if $F_{ST(\ell )}^k=0$.

By Eqs. 14 and 16, for $F_{ST(\ell )}^k>0$,

$$\frac{F_{sT}^k}{F_{ST(\ell )}^k}=\frac{\frac{\overline{{\delta }^2}}{v+\overline{{\delta }^2}}}{\frac{\ell \overline{{\delta }^2}}{v+\ell \overline{{\delta }^2}}}=\frac{\ell \overline{{\delta }^2}+v}{\ell \left(v+\overline{{\delta }^2}\right)}.$$

Noting that

$$1-F_{ST}^k=\frac{v}{v+\overline{{\delta }^2}},$$

we then have, for $F_{ST(\ell )}^k>0$,

$$\begin{gathered} \frac{F_{ST}^k}{F_{ST(\ell )}^k}=\frac{\overline{{\delta }^2}}{\nu +\overline{{\delta }^2}}+\frac{v}{\ell \left(v+\overline{{\delta }^2}\right)} \\ =F_{ST}^k+\frac{1-F_{ST}^k}{\ell }=\frac{1+(\ell -1)F_{ST}^k}{\ell }. \end{gathered}$$

Consequently, for $F_{ST(\ell )}^k>0$,

$$\frac{F_{sT(\ell )}^k}{F_{ST}^k}=\frac{\ell }{1+(\ell -1)F_{ST}^k}.$$ (A1.4)

Because $F_{ST}^k\in [0,1]$ and $F_{ST}^k=0$ if $F_{ST(\ell )}^k=0$, Eq. A1.4 implies that

$$F_{ST(\ell )}^k\in \left[F_{ST}^k,\ell F_{ST}^k\right),$$

with $F_{ST}^k=F_{ST(\ell )}^k$ if ℓ =1 or if either $F_{ST}^k=1$ or $F_{ST}^k=0$, but with ${\text{lim}}_{F_{ST}^k\to 0}{F}_{ST(\ell )}^k=\ell F_{ST}^k$. In other words, if ℓ > 1, for very small but nonzero $F_{ST}^k,F_{ST(\ell )}^k\approx \ell F_{ST}^k$, but for $F_{ST}^k$ near 1, $F_{ST(\ell )}^k\approx F_{ST·}^k$ The relationship between $F_{ST}^k$ and $F_{ST(\ell )}^k$ is plotted in Figure 3.

Appendix 2: The Fourth Moment of ${\sum }_{i=1}^k{\delta }_i{U}_i$

In this appendix, we show that the fourth moment of ${\sum }_{i=1}^k{\delta }_i{U}_i$ is equal to the expression in Eq. 33.

By the independence of the U_i and Eqs. 29 and 30,

$$\begin{gathered} E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^4\right] \\ =E\left(\sum _{i=1}^k{\delta }_i^4{U}_i^4+3\sum _{i=1}^k\sum _{j\ne i}{\delta }_i^2{\delta }_j^2{U}_i^2{U}_j^2\right) \\ =\sum _{i=1}^k{\delta }_i^4+3\sum _{i=1}^k\sum _{j\ne i}{\delta }_i^2{\delta }_j^2. \end{gathered}$$ (A2.1)

To simplify the sum in Eq. A2.1, notice that ${\sum }_{j\ne i}{\delta }_j^2=k\overline{{\delta }^2}-{\delta }_i^2$, so

$$\begin{gathered} \sum _{i=1}^k\sum _{j\ne i}{\delta }_i^2{\delta }_j^2 \\ ={\delta }_1^2\left(k\overline{{\delta }^2}-{\delta }_1^2\right)+{\delta }_2^2\left(k\overline{{\delta }^2}-{\delta }_2^2\right)+\dots +{\delta }_k^2\left(k\overline{{\delta }^2}-{\delta }_k^2\right) \\ =k\overline{{\delta }^2}\sum _{i=1}^k{\delta }_i^2-\sum _{i=1}^k{\delta }_i^4=k^2{\overline{{\delta }^2}}^2-k\overline{{\delta }^4}, \end{gathered}$$ (A2.2)

where $\overline{{\delta }^4}$ is as defined in Eq. 11. Plugging the expression for ${\sum }_{i=1}^k{\Sigma }_{j\ne i}{\delta }_i^2{\delta }_j^2$ from Eq. A2.2 into Eq. A2.1 gives

$$\begin{gathered} E\left[{\left(\sum _{i=1}^k{\delta }_i{U}_i\right)}^4\right]=3k^2{\overline{{\delta }^2}}^2-2k\overline{{\delta }^4} \\ =3k^2{\overline{{\delta }^2}}^2-2k\left({\overline{{\delta }^2}}^2+s_{{\delta }^2}^2\right), \end{gathered}$$ (A2.3)

which proves the statement in Eq. 33.

Appendix 3: Allele Frequencies in a Drift Model

In this appendix, we show that the assumptions in Eqs. 49 and 51 are the expectations of allele frequencies under a population-genetic model in which the two populations experience equal degrees of drift since a recent divergence. The model we use for drift is similar to some models used in previous work (Nicholson et al. 2002; Falush et al. 2003). Note that, although the allele frequencies and p_i and q_i are treated as fixed quantities in the main text, they are treated as random variables in this appendix.

A.3.1. Drift Model

Let π₁, π₂, …, π_k, represent the frequencies of one of two alleles at each of k loci in a predivergence population. The π_i may be outcomes of a random process with arbitrary distribution. After a divergence event, the predivergence population splits into two populations—populations A and B—that undergo drift. The amount of drift at each locus is represented by a set of continuous random variables, α_A1, α_A2, …, α_Ak for population A and α_B1, α_B2, …, α_Bk for population B. For all i, conditional on π_i, the α_Ai and α_Bi are independent, and E(α_Ai) = E(α_Bi) = 0. Further, if the two subpopulations have experienced equal amounts of drift, then conditional on π_i, the α_Ai and α_Bi are identically distributed. The postdrift allele frequencies in population A are π₁ + α_A1, π₂ + α_A2, …, π_k + α_Ak, and in population B they are π₁ + α_B1, π₂ + α_B2, …, π_k + α_Bk.

At each locus, define the 1 allele as the allele that is more frequent in population B than in population A. If the allele frequencies are the same in both populations at a locus, then the 1 allele at that locus is chosen randomly, with probability ½ for each allele. The frequency of the 1 allele at locus i is p_i in population A and q_i in population B.

A.3.2. Proposition 1

Proposition 1:

If populations A and B have experienced equal amounts of drift since divergence, then E(p_i) + E(q_i) = 1.

Proof:

Under the drift model outlined above,

1. if α_Ai < α_Bi, then p_i = π_i + α_Ai and q_i = π_i + α_Bi;

2. if α_Ai = α_Bi, then p_i = q_i = τ_i, where τ_i is either π_i + α_Ai or 1 − π_i − α_Ai with probability ½ of each possibility; and

3. if α_Ai > α_Bi, then p_i = 1 − π_i − α_Ai and q_i = 1 − π_i − α_Bi.

If the two subpopulations have experienced equal amounts of drift since divergence, then conditional on π_i, the drift variables α_Ai and α_Bi are independent and identically distributed. Thus, P(α_Ai < α_Bi) = P(α_Ai > α_Bi), and therefore

$$P\left(p_i={\pi }_i+{\alpha }_{Ai}\right)=P\left(p_i=1-{\pi }_i-{\alpha }_{Ai}\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right..$$

Conditional on π_i = w, we have

$$E\left(p_i\mid {\pi }_i=w\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(w+E\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(1-w-E\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right).$$

Similarly,

$$E\left(q_i\mid {\pi }_i=w\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(w+E\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(1-w-E\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right).$$

And so, conditional on π_i = w,

$$\begin{gathered} E\left(p_i+q_i\mid {\pi }_i=w\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(w+E\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right) \\ +\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(1-w-E\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right) \\ +\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(w+E\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right) \\ +\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(1-w-E\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]\right) \\ =1. \end{gathered}$$

Because E(p_i + q_i|π_i = w) = 1 for all w, the unconditional expectation is

$$E\left(p_i+q_i\right)=E_{{\pi }_i}\left[E\left(p_i+q_i\mid {\pi }_i=w\right)\right]=1.$$

This completes the proof of Proposition 1.

Thus, taking the mean across loci, $\text{E}(\overline{q})=1-\text{E}(\overline{p})$, and the assumption in Eq. 49 characterizes the expectations of allele frequencies under the model of equal drift since a recent divergence.

A.3.3. Proposition 2

Proposition 2:

If populations A and B have experienced equal amounts of drift since divergence, then $E\left(s_p^2\right)=E\left(s_q^2\right)$.

Proof:

Define a random indicator variable G_i with the property

$$\begin{gathered} G_i=0\iff p_i={\pi }_i+{\alpha }_{Ai}, \\ {G}_i=1\iff p_i=1-{\pi }_i-{\alpha }_{Ai}. \end{gathered}$$

This property implies that

$$\begin{gathered} G_i=0\Rightarrow p_i={\pi }_i+\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right), \\ {G}_i=1\Rightarrow p_i=1-{\pi }_i-\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right), \end{gathered}$$

because p_i ≤ q_i. By the law of total variance,

$$\text{Var}\left(p_i\mid {\pi }_i=w\right)={\text{Var}}_{G_i}\left[E\left(p_i\mid {\pi }_i=w,G_i=g\right)\right]+E_{G_i}\left[\text{Var}\left(p_i\mid {\pi }_i=w,G_i=g\right)\right].$$

Under the assumption of equal drift since divergence, P(G_i = 0) = P(G_i = 1) = ½. Thus, Var(p_i|π_i = w) is equal to the sum of

$$\begin{gathered} {\text{Var}}_{G_i}\left[E\left(p_i\mid {\pi }_i=w,G_i=g\right)\right] \\ =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[E\left(p_i\mid {\pi }_i=w,G_i=0\right)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[E\left(p_i\mid {\pi }_i=w,G_i=0\right){+E\left(p_i\mid {\pi }_i=w,G_i=1\right)]]}^2 \\ +\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[E\left(p_i\mid {\pi }_i=w,G_i=1\right)-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[E\left(p_i\mid {\pi }_i=w,G_i=0\right){+E\left(p_i\mid {\pi }_i=w,G_i=1\right)]]}^2 \\ =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.{\left[E\left(p_i\mid {\pi }_i=w,G_i=0\right)-E\left(p_i\mid {\pi }_i=w,G_i=1\right)\right]}^2 \\ =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.[2w-1+E\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]{+E\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]]}^2 \end{gathered}$$

and

$$\begin{gathered} E_{G_i}\left[\text{Var}\left(p_i\mid {\pi }_i=w,G_i=g\right)\right] \\ =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[\text{Var}\left(p_i\mid {\pi }_i=w,G_i=0\right)+\text{Var}\left(p_i\mid {\pi }_i=w,G_i=1\right)\right] \\ =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.[\text{Var}\left[\text{min}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right] \\ +\text{Var}\left[\text{max}\left({\alpha }_{Ai},{\alpha }_{Bi}\right)\mid {\pi }_i=w\right]]. \end{gathered}$$

A parallel calculation for q_i reveals that Var(q_i| π_i = w) is equal to the sum of two equivalent terms, meaning that for all i, Var(p_i| π_i = w) = Var(q_i| π_i = w). Because this claim holds for all i and because π_i is by definition the same for populations A and B,

$$\text{Var}\left(p_i\right)=\text{Var}\left(q_i\right).$$

Finally, by Eq. 3, $s_p^2$ is the biased sample variance of the p_i and $s_p^2$ is the biased sample variance of the q_i. Applying Bessel’s correction to the biased sample variance, the expectations of $s_p^2$ and $s_q^2$ under the drift model are, for k loci,

$$E\left(s_p^2\right)=\frac{k-1}{k}\text{Var}\left(p_i\right),$$

$$E\left(s_q^2\right)=\frac{k-1}{k}Var\left(q_i\right),$$

and because Var(p_i) = Var(q_i),

$$E\left(s_p^2\right)=E\left(s_q^2\right).$$

Thus, the assumption in Eq. 51 represents the expectation for properties of the variance of allele frequencies across loci under a model of equal drift since a recent divergence. This completes the proof of Proposition 2.

Appendix 4: The Approximate Trait-Based Misclassification Rate, Conditional on the Labeling of the Alleles

In this appendix, we justify Eq. 56 using an argument similar to the one used to justify Eq. 55. We assume the conditions that apply in Section 6, stated in Eqs. 49 and 51.

W_T is an indicator variable that equals 1 if an individual is misclassified on the basis of its value for T. Conditional on the allelic labels X₁, …, X_k, T has a Poisson binomial distribution (see Section 4.1), which, for large k, is well approximated by a normal distribution (Deheuvels et al. 1989, Theorem 1.1). By the conditional expectations and variances in Eqs. 19, 22, and 23 and the assumptions in Eqs. 49 and 51, the large-k distributions of T in the two populations are approximately

$$\begin{gathered} \left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right) \\ ~\text{Normal}\left(\ell \left[\sum _{i:x_i=1}{p}_i+\sum _{i:x_i=0}\left(1-p_{i)}\right)\right],\ell k\left[\overline{p}\overline{q}-s_p^2\right]\right), \\ \left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=B\right) \\ ~\text{Normal}\left(\ell \left[\sum _{i:x_i=1}{q}_i+\sum _{i:x_i=0}\left(1-q_i\right)\right],\ell k\left[\overline{p}\overline{q}-s_p^2\right]\right)\text{, } \end{gathered}$$

conditional on the labeling of the alleles, X₁, …, X_k.

Denoting the normal density that approximates the distribution of T in population A by f_A.T(t) and the corresponding normal density for population B by f_B.T(t), then after observing that T = t, we classify the individual into population A if f_A.T(t) > f_B.T(t) and into population B if f_A.T(t) < f_B.T(t). Because the variances of the two limiting normal distributions are equal, the relationship of the densities depends only on whether the observed trait value t is closer to its expectation in population A or population B. That is, defining

$$\begin{gathered} {\mu }_{A.T}=E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=A\right), \\ {\mu }_{B.T}=E\left(T\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},M=B\right), \end{gathered}$$

we have

$$\begin{gathered} f_{A.T}(t)>f_{B.T}(t)\iff \left|t-{\mu }_{A.T}\right|<\left|t-{\mu }_{B.T}\right|, \\ {f}_{A.T}(t)<f_{B.T}(t)\iff \left|t-{\mu }_{A.T}\right|>\left|t-{\mu }_{B.T}\right|. \end{gathered}$$

Consider an individual drawn from population A, who will be misclassified if f_A.T(t) < f_B.T(t). If μ_A.T < μ_B.T, then

$$f_{A.T}(t)<f_{B.T}(t)\iff t>\left({\mu }_{A.T}+{\mu }_{B.T}\right)/2,$$

whereas if μ_A.T > μ_B.T, then

$$f_{A.T}(t)<f_{B.T}(t)\iff t<\left({\mu }_{A.T}+{\mu }_{B.T}\right)/2.$$

(We defer for a moment the case μ_A.T = μ_B.T.) Thus, the approximate probability of misclassifying an individual from population A on the basis of its trait value is, if μ_A.T < μ_B.T,

$$\begin{gathered} P\left(W_T=1\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},{\mu }_{A.T}<{\mu }_{B.T},M=A\right) \\ \approx P\left(T>\frac{{\mu }_{A.T}+{\mu }_{B.T}}{2}\right) \\ \approx 1-\Phi \left(\frac{\frac{{\mu }_{A.T}+{\mu }_{B.T}}{2}-{\mu }_{A.T}}{\sqrt{\ell k\left[\overline{p}\overline{q}-s_p^2\right]}}\right) \\ =1-\Phi \left(\frac{\left|{\mu }_{B.T}-{\mu }_{A.T}\right|}{2\sqrt{\ell k\left[\overline{p}\overline{q}-s_p^2\right]}}\right) \\ =1-\Phi \left(\frac{\sqrt{\ell }\left|\sum _{i=1}^k{\delta }_i{u}_i\right|}{2\sqrt{k\left[\overline{p}\overline{q}-s_p^2\right]}}\right), \end{gathered}$$ (A4.1)

where the last step follows from Eq. 20. Similarly, if μ_A.T > μ_B.T, then

$$\begin{gathered} P\left(W_T=1\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\},{\mu }_{A.T}>{\mu }_{B.T},M=A\right) \\ \approx P\left(T<\frac{{\mu }_{A.T}+{\mu }_{B.T}}{2}\right) \\ \approx \Phi \left(\frac{{\mu }_{A.T}-\frac{{\mu }_{A.T}+{\mu }_{B.T}}{2}}{\sqrt{\ell k\left[\overline{p}\overline{q}-s_p^2\right]}}\right) \\ =1-\Phi \left(\frac{\left|{\mu }_{B.T}-{\mu }_{A.T}\right|}{2\sqrt{\ell k\left[\overline{p}\overline{q}-s_p^2\right]}}\right) \\ =1-\Phi \left(\frac{\sqrt{\ell }\left|\sum _{i=1}^k{\delta }_i{u}_i\right|}{2\sqrt{k\left[\overline{p}\overline{q}-s_p^2\right]}}\right). \end{gathered}$$ (A4.2)

The expressions in Eqs. A4.1 and A4.2 are equal. Further, the expression they provide also applies to the case of μ_A.T = μ_B.T. If μ_A.T = μ_B.T, then P(W_T = 1) = ½ because the trait has the same distribution in each population. The expression in Eqs. A4.1 and A4.2 applies because if μ_A.T = μ_B.T, then by Eq. 20, ${\sum }_{i=1}^k{\delta }_i{u}_i=0$, and Φ(0) = ½ as required. A similar set of calculations for population B gives the same expression, so we remove the condition on population membership, arriving at the statement in Eq. 56:

$$\begin{gathered} P\left(W_T=1\mid \left\{X_1,\dots ,X_k\right\}=\left\{x_1,\dots ,x_k\right\}\right) \\ \approx 1-\Phi \left(\frac{\sqrt{\ell }\left|\sum _{i=1}^k{\delta }_i{u}_i\right|}{2\sqrt{k\left[\overline{p}\overline{q}-s_p^2\right]}}\right). \end{gathered}$$