SUMMARY
Two commonly used approaches to study interactions among neurons are spike count correlation, which describes pairs of neurons, and dimensionality reduction, applied to a population of neurons. Although both approaches have been used to study trial-to-trial neuronal variability correlated among neurons, they are often used in isolation and have not been directly related. We first established concrete mathematical and empirical relationships between pairwise correlation and metrics of population-wide covariability based on dimensionality reduction. Applying these insights to macaque V4 population recordings, we found that the previously reported decrease in mean pairwise correlation associated with attention stemmed from three distinct changes in population-wide covariability. Overall, our work builds the intuition and formalism to bridge between pairwise correlation and population-wide covariability and presents a cautionary tale about the inferences one can make about population activity by using a single statistic, whether it be mean pairwise correlation or dimensionality.
In brief
Pairwise correlations and dimensionality reduction are widely used approaches for measuring how neurons covary. Umakantha, Morina, Cowley, et al. establish concrete mathematical relationships between the two approaches and empirically investigate these relationships for visual cortical neurons. The findings provide a cautionary tale for summarizing population-wide covariability using any single activity statistic.
Graphical Abstract
INTRODUCTION
A neuron can respond differently to repeated presentations of the same stimulus. These variable responses are often correlated across pairs of neurons from trial to trial, measured using spike count correlations (rsc, also referred to as noise correlation; Cohen and Kohn, 2011). Studies have reported changes in spike count correlation across various experimental manipulations and cognitive phenomena, including attention (Cohen and Maunsell, 2009; Mitchell et al., 2009; Herrero et al., 2013; Gregoriou et al., 2014; Ruff and Cohen, 2014a; Snyder et al., 2018), learning (Gu et al., 2011; Jeanne et al., 2013; Ni et al., 2018), task difficulty (Ruff and Cohen, 2014b), locomotion (Erisken et al., 2014), stimulus drive (Maynard et al., 1999; Kohn and Smith, 2005; Smith and Kohn, 2008; Miura et al., 2012; Ponce-Alvarez et al., 2013; Ruff and Cohen, 2016b), decision making (Nienborg et al., 2012), task context (Bondy et al., 2018), anesthesia (Ecker et al., 2010), adaptation (Adibi et al., 2013), and more (Figure 1A). Spike count correlation also depends on timescales of activity (Bair et al., 2001; Kohn and Smith, 2005; Smith and Kohn, 2008; Mitchell et al., 2009; Runyan et al., 2017), neuromodulation (Herrero et al., 2013; Minces et al., 2017), and properties of the neurons themselves, including their physical distance from one another (Lee et al., 1998; Smith and Kohn, 2008; Smith and Sommer, 2013; Ecker et al., 2014; Solomon et al., 2015; Rosenbaum et al., 2017), tuning preferences (Lee et al., 1998; Romo et al., 2003; Kohn and Smith, 2005; Huang and Lisberger, 2009), and neuron type (Qi and Constantinidis, 2012; Snyder et al., 2016). Theoretical work has posited that changes in correlations affect neuronal computations and sensory information coding (Zohary et al., 1994; Shadlen and Newsome, 1998; Abbott and Dayan, 1999; Averbeck et al., 2006; Moreno-Bote et al., 2014; Sharpee and Berkowitz, 2019; Rumyantsev et al., 2020; Bartolo et al., 2020). Given such widespread empirical observations and theoretical insight, spike count correlation has been and remains instrumental in our current understanding of how neurons interact.
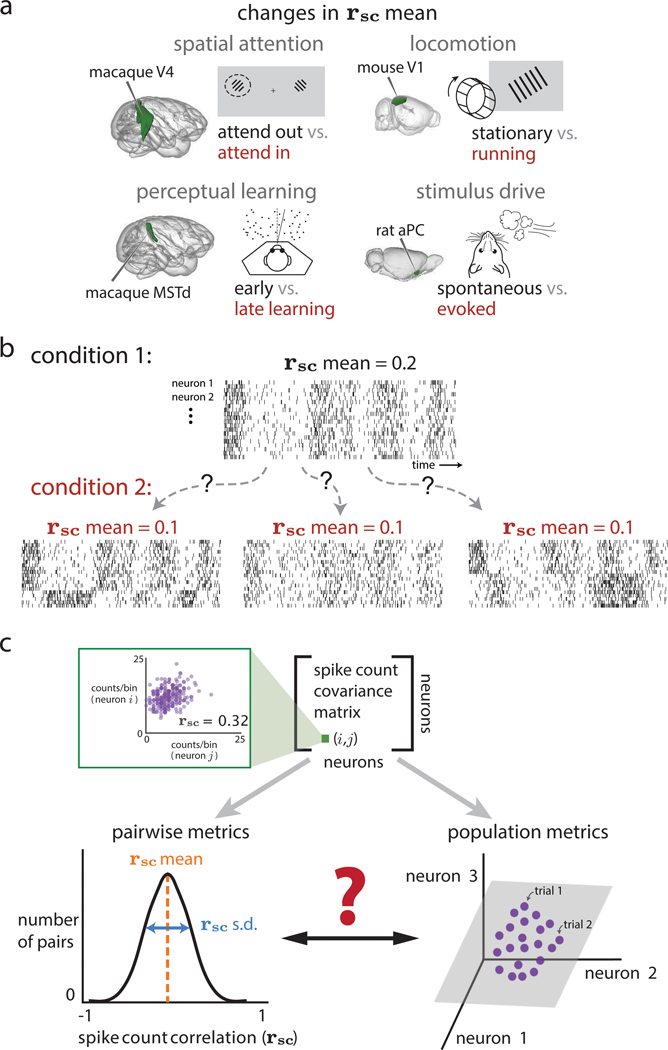
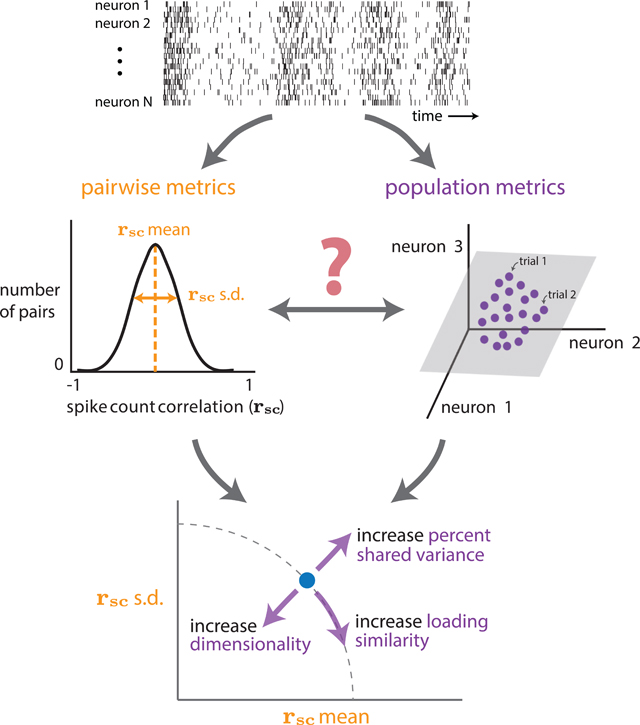
Figure 1. How do spike count correlations between pairs of neurons (i.e., pairwise metrics) relate to how the entire population co-fluctuates (i.e., population metrics)?
(A) Four example experiments in which mean spike-count correlation (rsc mean) has been observed to change between experimental conditions. These include spatial attention (macaque visual area V4; Cohen and Maunsell, 2009; Mitchell et al., 2009; Gregoriou et al., 2014; Luo and Maunsell, 2015; Snyder et al., 2018), perceptual learning (macaque dorsal medial superior temporal area; Gu et al., 2011), locomotion (mouse visual area V1; Erisken et al., 2014), and stimulus drive (rat anterior piriform cortex; Miura et al., 2012).
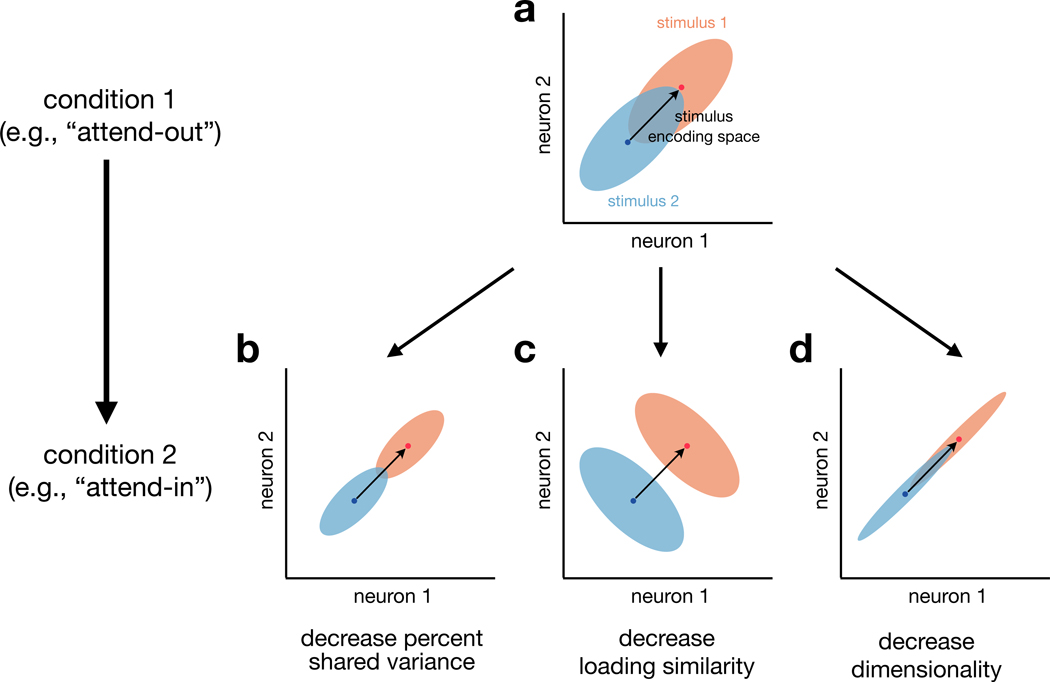
(B) The same change in rsc mean (from 0.2 to 0.1 between conditions 1 and 2) could correspond to multiple distinct changes in the activity of the population of neurons. Condition 2, left: a decrease in rsc mean could correspond to some neurons becoming anti-correlated with others in the population; in this case, some neurons that were previously positively correlated are now anti-correlated with the rest of the population (bottom rows of raster plot). Condition 2, middle: a decrease in rsc mean could correspond to a decrease in how strongly neurons co-fluctuate together; in this case, neurons covary as in condition 1, but each neuron does not co-fluctuate with other neurons as strongly. Condition 2, right: a decrease in rsc mean could correspond to the introduction of another “mode” of covariation (i.e., an increase in the dimensionality of population activity); in this case, neurons in the top half of the raster covary as in condition 1, but neurons in the bottom half of the raster covary in a manner independent from those in the top half.
(C) Pairwise (rsc) and population (dimensionality reduction) metrics both arise from the same spike count covariance matrix, but the precise relationship between these two sets of metrics remains unknown. Top row: each element of the spike count covariance matrix corresponds to the covariance across responses to repeated presentations of the same stimulus for two simultaneously recorded neurons (e.g., neurons i and j, left inset). Bottom row: pairwise metrics (left) typically summarize the distribution of spike count correlation with the mean (rsc mean); in this work, we propose additionally reporting the standard deviation (rsc SD). Population metrics (right) of the spike count covariance matrix are identified by applying dimensionality reduction to the population activity (e.g., gray plane depicts a low-dimensional space describing how neurons covary; see also Figure S5). By understanding the relationship between pairwise and population metrics, we can better interpret how changes in pairwise statistics (e.g., experiments in A) correspond to changes in population metrics and vice versa.
Most studies compute the average spike count correlation over pairs of recorded neurons for different experimental conditions, periods of time, neuron types, etc. A decrease in this mean correlation is commonly attributed to a reduction in the size (or gain) of shared co-fluctuations (Shadlen and Newsome, 1998; Rabinowitz et al., 2015; Lin et al., 2015; Ecker et al., 2016; Huang et al., 2019; Ruff et al., 2020), e.g., a decrease in the strength of “common shared input” that drives each neuron in the population. However, other distinct changes at the level of the entire neuronal population can manifest as the same decrease in mean pairwise correlation (Figure 1B). For example, a common input that drives the activity of all neurons up and down together could be altered to drive some neurons up and other neurons down. Alternatively, that first common input signal might remain the same, but a second input signal could be introduced that drives some neurons up and others down. It is difficult to differentiate these distinct possibilities using a single summary statistic, such as mean spike count correlation.
Distinguishing among these changes to the population-wide covariability might be possible by considering additional statistics that measure how the entire population of neurons co-fluctuates together. In particular, one may use dimensionality reduction to compute statistics that characterize multiple distinct features of population-wide covariability (Cunningham and Yu, 2014). Dimensionality reduction has been used to investigate decision making (Harvey et al., 2012; Mante et al., 2013; Kiani et al., 2014; Kaufman et al., 2015), motor control (Churchland et al., 2012; Gallego et al., 2017), learning (Sadtler et al., 2014; Ni et al., 2018; Vyas et al., 2018), sensory coding (Mazor and Laurent, 2005; Pang et al., 2016), spatial attention (Cohen and Maunsell, 2010; Rabinowitz et al., 2015; Snyder et al., 2018; Huang et al., 2019), interactions between brain areas (Perich et al., 2018; Ruff and Cohen, 2019a; Ames and Churchland, 2019; Semedo et al., 2019; Veuthey et al., 2020), and network models (Williamson et al., 2016; Mazzucato et al., 2016; Recanatesi et al., 2019), among others. As with mean spike count correlation, the statistics computed from dimensionality reduction can also change with attention (Rabinowitz et al., 2015; Huang et al., 2019), stimulus drive (Churchland et al., 2010; Cowley et al., 2016; Snyder et al., 2018), motor output (Gallego et al., 2018), learning (Athalye et al., 2017), and anesthesia (Ecker et al., 2014). However, unlike mean spike count correlation (henceforth referred to as a “pairwise metric”), which averages across pairs of neurons, the statistics computed from dimensionality reduction (henceforth referred to as “population metrics”) consider the structure of population-wide covariability (Figure 1C). Although dimensionality reduction is often applied to trial-averaged activity (removing trial-to-trial variability), here, we focus on using dimensionality reduction to study trial-to-trial variability (around the trial-averaged mean). An example of a commonly reported population metric is dimensionality (Yu et al., 2009; Rabinowitz et al., 2015; Cowley et al., 2016; Williamson et al., 2016; Mazzucato et al., 2016; Gao and Ganguli, 2015; Gallego et al., 2017; Stringer et al., 2019a; Recanatesi et al., 2019). Dimensionality is used to assess whether the number of population co-fluctuation patterns (possibly reflecting the number of common inputs) changes across experimental conditions (Figure 1B, condition 1 versus condition 2, right panel). Thus, population metrics could help to distinguish among the distinct ways in which population-wide covariability can change, especially those that lead to the same change in mean spike count correlation (Figure 1B).
Both pairwise and population metrics aim to characterize how neurons covary, and both can be computed from the same spike count covariance matrix (Figure 1C). Still, studies rarely report both, and the relationship between the two is not known. In this study, we establish the relationship between pairwise metrics and population metrics both analytically and empirically using simulations. We find that changes in mean spike count correlation could correspond to several distinct changes in population metrics, including (1) the strength of shared variability (e.g., the strength of a common input), (2) whether neurons co-fluctuate together or in opposition (e.g., how similarly a common input drives each neuron in the population), or (3) the dimensionality (e.g., the number of common inputs). Furthermore, we show that a rarely reported statistic—the standard deviation of spike count correlation—provides complementary information to the mean spike count correlation about how a population of neurons co-fluctuates. Applying this understanding to recordings in area V4 of macaque visual cortex, we found that the previously reported decrease in mean spike count correlation with attention stems from multiple distinct changes in population-wide covariability. Overall, our results demonstrate that common ground exists between the literatures of spike count correlation and dimensionality reduction and provides a cautionary tale for attempting to draw conclusions about how a population of neurons covaries using one, or a small number of, statistics. Our framework builds the intuition and formalism to navigate between the two approaches, allowing for a more interpretable and richer description of the interactions among neurons.
RESULTS
Defining pairwise and population metrics
We first define the metrics that we will use to summarize (1) the distribution of spike count correlations (i.e., pairwise metrics) and (2) dimensionality reduction of a population covariance matrix (i.e., population metrics). For pairwise metrics, we consider the mean and standard deviation (SD) of rsc across all pairs of neurons, which summarize the rsc distribution (Figure 1C, bottom left panel). For population metrics, which are derived from factor analysis (FA), we consider loading similarity, percent shared variance (abbreviated to %sv), and dimensionality (described below and in more detail in STAR Methods). These metrics each describe some aspect of population-wide covariability and thus represent natural, multivariate extensions of rsc.
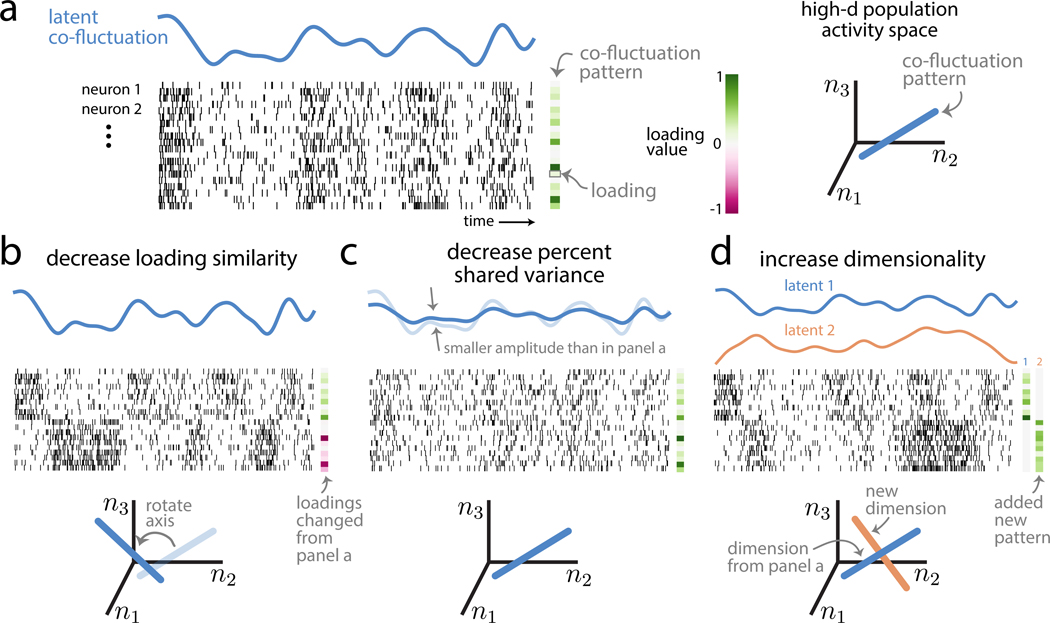
To illustrate these three population metrics, consider the activity of a population of neurons over time (Figure 2A, spike rasters). If the activity of all neurons goes up and down together, we would find the pairwise spike count correlations between all pairs of neurons to be positive. A more succinct way to characterize this population activity is to identify a single time-varying latent co-fluctuation that is shared by all neurons (Figure 2A, blue line). The way in which neurons are coupled to this latent co-fluctuation is indicated by a loading for each neuron. In this example, because the latent co-fluctuation describes each neuron’s activity going up and down together, the loadings have the same sign (Figure 2A, green rectangles). We refer to the latent co-fluctuation’s corresponding set of loadings as a co-fluctuation pattern. A co-fluctuation pattern can be represented as a direction in the population activity space, where each coordinate axis corresponds to the activity of one neuron (Figure 2A, right panel). The first population metric is loading similarity, a value between 0 and 1 that describes to what extent the loadings differ across neurons within a co-fluctuation pattern. A loading similarity close to 1 indicates that the loadings have the same sign and are of similar magnitude (Figure 2A, green rectangles). A loading similarity close to 0 indicates that many of the loadings differ, either in magnitude, sign, or both (Figure 2B, green and pink squares). In this case, some neurons may have positive loadings and co-fluctuate in the same direction as the latent co-fluctuation (Figure 2B, top rows of neurons show high firing rates when blue line is high and low firing rates when blue line is low), whereas other neurons may have negative loadings and co-fluctuate in the opposite direction as the latent co-fluctuation (Figure 2B, bottom rows of neurons show low firing rates when blue line is high and high firing rates when blue line is low). One can view changing the loading similarity as rotating the direction of a co-fluctuation pattern in population activity space (Figure 2B, bottom plot).
Figure 2. Intuition about population metrics: loading similarity, percent shared variance (%sv), and dimensionality.
(A) Population activity (where each row is the spike train for one neuron over time; simulated data) is characterized by a latent co-fluctuation (blue) and a co-fluctuation pattern made up of loadings (green rectangles). Each neuron’s time-varying firing rate is a product of the latent co-fluctuation and that neuron’s loading (which may either be positive or negative). One may also view population activity through the lens of the population activity space (right plot), where each axis represents the activity of one neuron (n1; n2; n3 represent neuron 1, neuron 2, and neuron 3). In this space, a co-fluctuation pattern corresponds to an axis whose orientation depends on the pattern’s loadings (right plot, blue line).
(B) Population activity with a lower loading similarity than in (A). The loadings have both positive and negative values (i.e., dissimilar loadings), leading to neurons that are anti-correlated (compare top rows with bottom rows of population activity). Changing the loading similarity will rotate a pattern’s axis in the population activity space (bottom plot, “rotate axis”).
(C) Population activity with a lower %sv than in (A). The latent co-fluctuation shows smaller amplitude changes over time than in (A), which leads to a lower %sv. Changing %sv leads to no changes of the co-fluctuation pattern (bottom plot, axis is same as that in A).
(D) Population activity with a dimensionality of 2, compared to a dimensionality of 1 in (A). Adding a new dimension leads to a new latent co-fluctuation (orange line) and a new co-fluctuation pattern (“added new pattern”). Each neuron’s time-varying firing rate is expressed as a weighted combination of the latent co-fluctuations, where the weights correspond to the neuron’s loadings in each co-fluctuation pattern. Here, each dimension corresponds to a distinct subset of neurons (top rows versus bottom rows); in general, this need not be the case, as each neuron typically has non-zero weights for both dimensions. In the population activity space (bottom plot), the activity varies along the two axes (i.e., a 2D plane) defined by the two co-fluctuation patterns. See also Figure S5. The spike trains shown in this figure were created for the sole purpose of illustrating the population metrics in this figure and were not used in subsequent analyses. The spike trains were generated by first creating latent co-fluctuations using Gaussian processes. These latent co-fluctuations were then linearly combined using loading weights (drawn from a standard normal distribution), yielding a time-varying firing rate for each neuron. Spike trains were generated according to an inhomogeneous Bernoulli process based on the time-varying firing rates. The intended duration of each spike train plotted is around 10 s.
The second population metric is percent shared variance or %sv, which measures the percentage of spike count variance explained by the latent co-fluctuation. This percentage is computed per neuron and then averaged across all neurons in the population (Williamson et al., 2016). A %sv close to 100% indicates that the activity of each neuron is tightly coupled to the latent co-fluctuation, with a small portion of variance that is independent to each neuron (Figure 2A). A %sv close to 0% indicates that neurons fluctuate almost independently of each other and their activity weakly adheres to the time course of the latent co-fluctuation (Figure 2C). By changing %sv, one does not change the co-fluctuation pattern in population activity space (Figure 2, blue lines are the same in panels A and C) but rather the strength of the latent co-fluctuation (Figure 2C, blue line has smaller amplitude than in panel A).
The third population metric is dimensionality. We define dimensionality as the number of co-fluctuation patterns (or dimensions) needed to explain the shared variability among neurons (see STAR Methods). The variable activity of neurons may depend on multiple common inputs, e.g., top-down signals like attention and arousal (Rabinowitz et al., 2015; Cowley et al., 2020) or spontaneous and uninstructed behaviors (Stringer et al., 2019b; Musall et al., 2019). Furthermore, these common inputs may differ in how they modulate neurons. This may result in two or more dimensions of the population activity (Figure 2D, blue and orange latent co-fluctuations). For illustrative purposes, each dimension might correspond to a single group of tightly coupled neurons (Figure 2D, neurons in top rows have non-zero loadings for pattern 1, whereas neurons in bottom rows have non-zero loadings for pattern 2). However, in general, each neuron can have non-zero loadings for multiple patterns. In population activity space, adding a new dimension adds a new axis along which neurons covary (Figure 2D, orange line). We use the term “dimension” to refer either to a latent co-fluctuation or its corresponding co-fluctuation pattern, depending on context.
Varying population metrics to assess changes in pairwise metrics
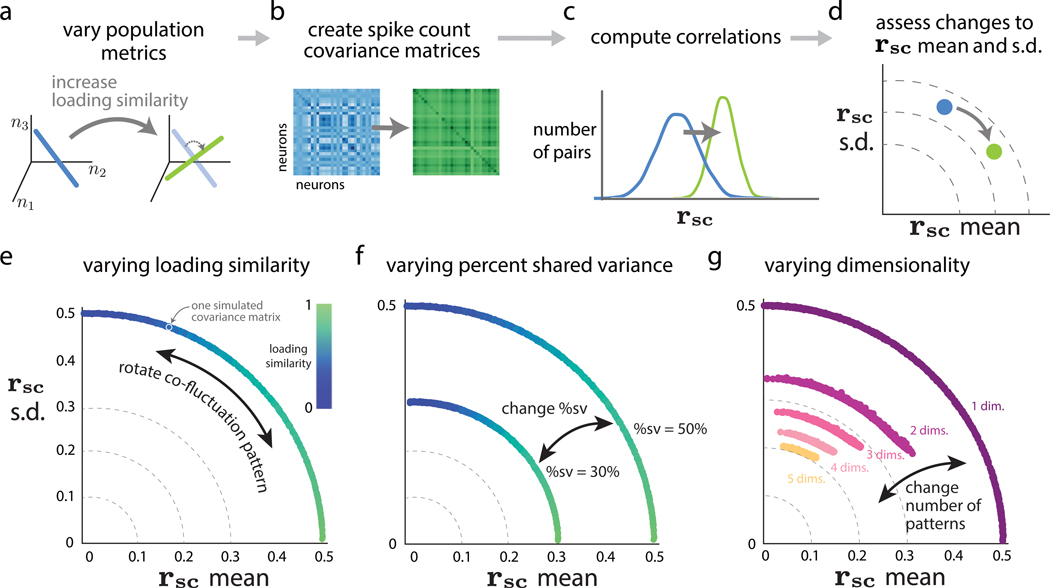
Given that both pairwise and population metrics are computed from the same spike count covariance matrix (Figure 1C), a connection should exist between the two. We establish this connection by deriving mathematical relationships and carrying out simulations. In simulations, we assessed how systematically changing one of the population metrics (e.g., increasing loading similarity; Figure 3A) changes the spike count covariance matrix (Figure 3B) and the corresponding rsc distribution (Figure 3C), which we summarized using its mean and standard deviation (Figure 3D). The covariance matrix was parameterized in a way that allowed us to create covariance matrices with specified population metrics (see STAR Methods). Thus, our simulation procedure does not simulate neuronal activity but rather creates covariance matrices that are consistent with the specified population metrics.
Figure 3. Relationship between population metrics and pairwise metrics.
(A–D) The simulation procedure to assess how systematic changes in population metrics lead to changes in pairwise metrics.
(A) We first systematically varied one of the population metrics while keeping the others fixed. For example, we can increase the loading similarity from a low value (left, blue) to a high value (right, green), while keeping %sv and dimensionality fixed.
(B) Then, we constructed covariance matrices corresponding to each value of the population metric in (A) (see STAR Methods), without generating synthetic data.
(C) For each covariance matrix from (B), we directly computed the correlations (i.e., the rsc distributions).
(D) We computed rsc mean and rsc SD from the rsc distributions in (C) and then assessed how the change in a given population metric from (A) changed pairwise metrics. In this case, the increase in loading similarity increased rsc mean and decreased rsc SD (blue dot to green dot).
(E) Varying loading similarity with a fixed %sv of 50% and dimensionality of 1. Each dot corresponds to the rsc mean and rsc SD of one simulated covariance matrix with specified population metrics (dots are close together and appear to form a continuum). The color of each dot corresponds to the loading similarity (see STAR Methods), where a value of 1 indicates that all loading weights have the same value.
(F) Varying %sv. The same setting as in (E), except we consider two different values of percent shared variance (50% and 30%).
(G) Varying dimensionality (i.e., number of co-fluctuation patterns) while sweeping loading similarity between 0 and 1 and keeping %sv fixed at 50%. In this simulation, the relative strengths of each dimension uniform across dimensions (i.e., flat eigenspectra; see STAR Methods).
See also Figure S7.
Loading similarity has opposing effects on rsc mean and SD
We first asked how the loading similarity of a single co-fluctuation pattern (i.e., one dimension) affected rsc mean and SD. Intuitively, a high loading similarity indicates that the activity of all neurons increases and decreases together (Figure 2A), resulting in values of rsc that are all positive and similar in value. Indeed, in simulations, we found that high loading similarity corresponded to large rsc mean and rsc SD close to 0 (Figure 3E, green dots near horizontal axis). On the other hand, a low loading similarity indicates that, when some neurons increase their activity, others decrease their activity (Figure 2B), resulting in some positive rsc values (for pairs that change their activity in the same direction) and some negative rsc values (for pairs that change their activity in opposition). In simulations, a low loading similarity indeed corresponded to an rsc mean close to 0 and a large rsc SD (Figure 3E, blue dots near vertical axis). By varying the loading similarity, we surprisingly observed an arc-like trend in the rsc mean versus rsc SD plot (Figure 3E). In Math Note A, we derive the analytical relationship between loading similarity and rsc. In Math Note B, we show mathematically why the rsc mean versus rsc SD relationship follows a circular arc.
Decreasing %sv reduces rsc mean and SD
We next asked how %sv, which measures the percentage of each neuron’s variance that is shared with other neurons in the population, is related to rsc mean and SD. Intuitively, one might expect % sv and rsc mean to be closely related because rsc measures the degree to which the activity of two neurons is shared (Cohen and Kohn, 2011). We investigated this in simulations and found that how closely %sv and rsc mean were related depended on the loading similarity. When loading similarity was high (Figure 3F, green dots), there was a direct relationship between %sv and rsc mean (specifically, %sv equals rsc mean). However, when loading similarity was low (Figure 3F, blue dots), the relationship between %sv and rsc mean was less direct. Namely, rsc mean remained close to zero, regardless of %sv. This illustrates that rsc mean and %sv are not the same. It is possible for a population of neurons with high %sv (e.g., Figure 3F, blue dots in outer arc) to have smaller rsc mean than a population with lower %sv (e.g., Figure 3F, green dots in inner arc).
These relationships that we have shown through simulation can be captured mathematically. First, if we have knowledge of the loading weights in the co-fluctuation pattern, the rsc between a pair of neurons can be expressed in terms of the %sv and loading values of the two neurons (Math Note A),
| (Equation 1) |
where is the rsc between neurons i and j, and are the %sv of each neuron (expressed as a proportion per neuron, in contrast to %sv in Figure 3F, which shows the average %sv across all neurons), and wi and wj are the loadings of the neurons in the co-fluctuation pattern. The rsc mean is the average of values across all neuron pairs. From Equation 1, we observe that, when loading similarity is high (i.e., most loading weights have the same sign), %sv and rsc mean are directly related (i.e., ). However, when loading similarity is low (i.e.,some loading weights are positive and others are negative), mean is small, regardless of %sv, because some pairs have and others have .
Second, if we have information about the rsc SD (instead of loading weights), we can establish the following relationship between %sv, rsc mean, and rsc SD (Math Note B):
In other words, in the rsc mean versus rsc SD plot, %sv is reflected in the distance of a point from the origin (Figure 3F). This relationship holds, regardless of the loading similarity. The intuition is that the %sv corresponds to the magnitude of rsc values (i.e., the from Equation 1).
These findings highlight the pitfalls of considering a single statistic (e.g., rsc mean) on its own and the benefits of considering multiple statistics (e.g., both rsc mean and SD) when trying to draw conclusions about how neurons covary. By considering rsc mean and SD together, one can gain insight into the loading similarity (Figure 3E) and the %sv (Figure 3F) of a neuronal population. Thus far, we have only considered the specific case where activity co-fluctuates along a single dimension in the firing rate space. We next considered how pairwise metrics change in the more general case where neuronal activity co-fluctuates along multiple dimensions.
Adding more dimensions tends to reduce rsc mean and SD
We sought to assess how dimensionality (i.e., the number of co-fluctuation patterns) is related to pairwise metrics. In simulations, we increased the number of co-fluctuation patterns (compare Figure 2A to 2D; see STAR Methods), while sweeping loading similarity and fixing the total %sv. We found that increasing dimensionality tended to reduce rsc mean and SD (Figure 3G, dots for larger dimensionalities lay closer to the origin than dots for smaller dimensionalities).
It seems counterintuitive that adding a new way in which neurons covary reduces the magnitude of rsc. The intuition is that, if multiple distinct (i.e., orthogonal) dimensions exist, then a neuron pair interacts in opposing ways along different dimensions. For example, consider two neurons with loadings of the same sign in one co-fluctuation pattern and opposite sign in the second pattern. If only the first dimension exists, the two neurons would go up and down together and be positively correlated. If only the second dimension exists, the two neurons would co-fluctuate in opposition and be negatively correlated. When both dimensions exist, the positive correlation from the first dimension and the negative correlation from the second dimension offset, and the resulting correlation between the neurons would be smaller than if only the first dimension were present. We formalize the above intuition in Math Note C. We also show analytically that increasing dimensionality tends to move points closer to the origin in the rsc mean versus rsc SD plot (i.e., decrease rsc mean and SD; Math Note D).
An increase in dimensionality does not imply that both rsc mean and rsc SD necessarily decrease. For example, in the case where the first dimension has high loading similarity, adding more dimensions means it is less likely for rsc SD to be 0 (Figure 3G, compare dot closest to horizontal axis for “1 dim.” to that for “2 dims.”). The intuition is that, if the first dimension has a loading similarity of 1, the loading weights for all neurons are the same and thus rsc values between all pairs are the same, resulting in rsc SD of 0. Adding an orthogonal dimension to this pattern necessarily means adding a pattern with low loading similarity (Math Note E), making it less likely for rsc across all pairs to be the same. Therefore, rsc SD is unlikely to be 0 for two dimensions (Figure 3G; the smallest rsc SD for 2 dims. is around 0.2). Still, in Figure 3G, the dots for 2 dims. are closer to the origin than the dots for 1 dim., implying that, even if rsc SD increases with an increase in dimensionality, the rsc mean must decrease to a larger extent (Math Note D). As another example, in the case where the first dimension has low loading similarity, adding a second dimension with high loading similarity would increase rsc mean. The rsc SD would decrease to a larger extent than the increase in rsc mean such that the dot for two dimensions is closer to the origin than that for one dimension (Math Note D).
The relative strength of each dimension impacts pairwise metrics
In the previous simulation (Figure 3G), we assumed that each dimension explained an equal proportion of the overall shared variance (e.g., for two dimensions, each dimension explained half of the shared variance; see STAR Methods). However, it is typically the case for recorded neuronal activity that some dimensions explain more shared variance than others; in other words, neuronal activity co-fluctuates more strongly along some patterns than others (Sadtler et al., 2014; Williamson et al., 2016; Mazzucato et al., 2016; Gallego et al., 2018; Huang et al., 2019; Stringer et al., 2019a; Ruff et al., 2020). We sought to assess the influence of the relative strength of each dimension on pairwise metrics.
We reasoned that stronger dimensions would play a larger role than weaker dimensions in determining the rsc distribution and pairwise metrics. Extending Equation 1 to multiple dimensions, we show that the rsc between a pair of neurons can be expressed as the sum of a contribution from each constituent dimension (Math Note C). The stronger a dimension, the larger the magnitude of its contribution to rsc and thus the larger its impact on rsc mean and SD.
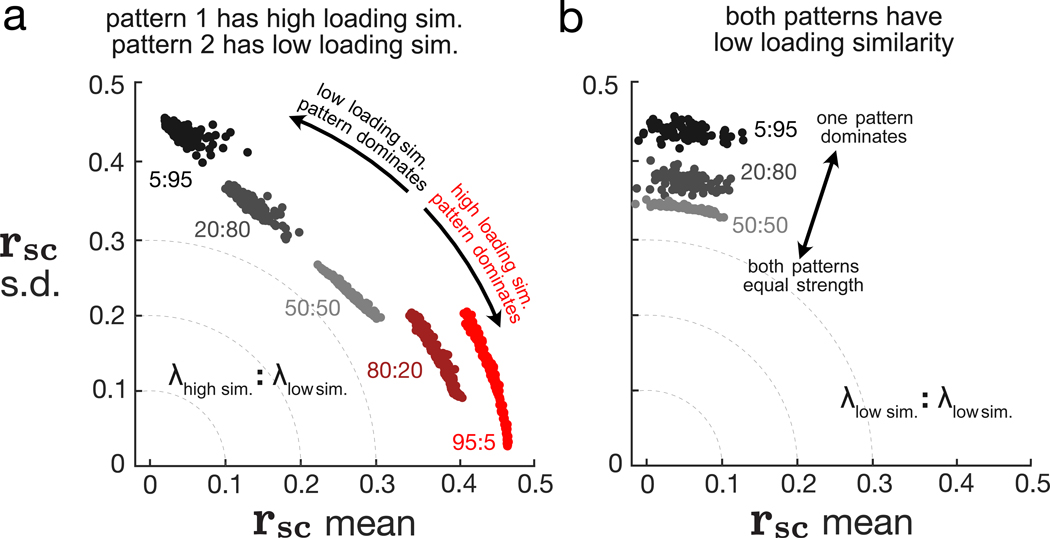
To test this empirically, we performed a simulation with two dimensions while systematically varying the relative strength of each dimension. We considered two scenarios: (1) one dimension has a pattern with high loading similarity and one dimension has a pattern with low loading similarity (Figure 4A) and (2) both dimensions have patterns with low loading similarity (Figure 4B). Note that both dimensions cannot have patterns with high loading similarity because they would not be orthogonal (Math Note E).
Figure 4. Relative strengths of dimensions affect rsc distributions.
With dimensionality of 2, we systematically varied the relative strengths of the two dimensions with a fixed total %sv of 50%. We considered two scenarios: (1) one dimension has high loading similarity and the other dimension has low loading similarity (A) and (2) both dimensions have low loading similarity (B). Each dot represents one simulated covariance matrix and rsc distribution. The colors of the dots indicate different relative strengths between the two dimensions, and numbers next to each cloud of dots indicate the ratio between the relative strength associated with each dimension. For example, in (A), red dots correspond to the high loading similarity dimension being 19 times stronger (95:5) than the low loading similarity dimension. Black dots correspond to the low loading similarity dimension being 19 times stronger (5:95) than the high loading similarity dimension. In (B), because both patterns have low loading similarity, clouds for 80:20 and 95:5 are very similar to clouds for 20:80 and 5:95, respectively, and are thus omitted for clarity. See also Figure S1.
In scenario (1), where one dimension’s pattern has high loading similarity and the other has low loading similarity, rsc mean and rsc SD reflect the loading similarity of the dominant dimension (Figure 4A). When the dimension with a high loading similarity pattern dominated, rsc mean was large and rsc SD was small (Figure 4A, red dots are close to horizontal axis). When the dimension with a low loading similarity pattern dominated, rsc mean was small and rsc SD was large (Figure 4A, black dots are close to vertical axis). When the two dimensions were of equal strength (i.e., neither dimension dominated), rsc mean and rsc SD were both intermediate values (Figure 4A, light gray dots are between red and black dots). Thus, the dimensions along which neuronal activity co-fluctuates more strongly have a greater influence on pairwise metrics (Figure S1).
In scenario (2), where both dimensions have patterns of low loading similarity, rsc mean was low and rsc SD was high (Figure 4B), similar to when there is one dimension with low loading similarity (Figure 3E, blue dots). When we made one dimension stronger than the other, rsc mean remained low and rsc SD remained high (Figure 4B, light gray dots and black dots are both close to vertical axis) because both patterns had low loading similarity. However, the radius of the arc increased (Figure 4B, black dots farther from the origin than light gray dots) and was close to the arc that would have been produced with a single dimension (Figure 3G, 1 dim.). Thus, whereas changing the number of dimensions causes discrete jumps in the arc radius (Figure 3G), changing the relative strength of each dimension allows for rsc mean and rsc SD to vary continuously between the arcs for different dimensionalities. Put another way, changing the relative strength of each dimension varies the “effective dimensionality” of population activity in a continuous manner. Neuronal activity for which one dimension dominates another (Figure 4B, black dots) has a lower effective dimensionality than when both dimensions have equal strength (Figure 4B, light gray dots).
Reporting only a single statistic provides an incomplete description of population covariability
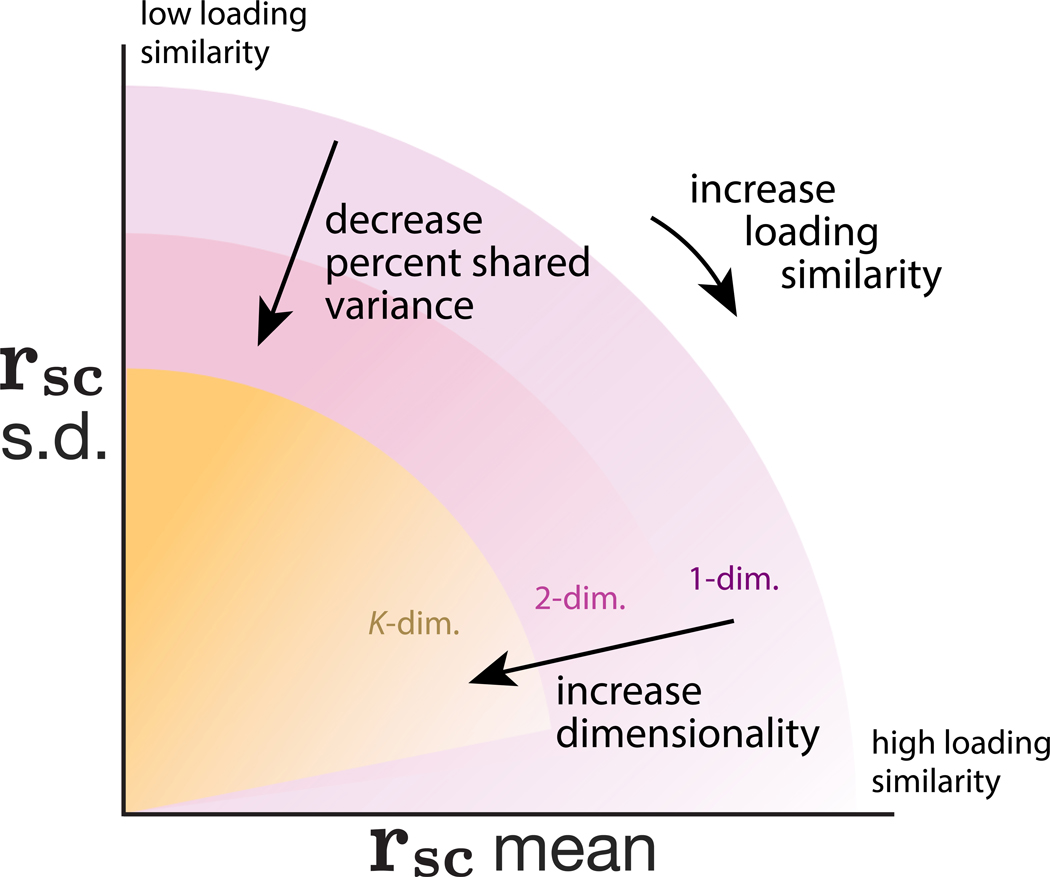
Figure 5 summarizes the relationships that we have established between pairwise metrics and population metrics. Rotating a co-fluctuation pattern from a low loading similarity to a high loading similarity increases rsc mean and decreases rsc SD along an arc (Figure 5, arrow outside pink arc). Decreasing %sv decreases both rsc mean and SD (Figure 5, arrow pointing toward origin), and increasing dimensionality also tends to decrease rsc mean and SD (Figure 5, pink to yellow shaded regions).
Figure 5. Summary of relationship between pairwise and population metrics.
A change in rsc mean and rsc SD may correspond to changes in loading similarity, %sv, dimensionality, or a combination of the three. Shaded regions indicate the possible rsc mean and rsc SD values for different dimensionalities; increasing dimensionality tends to decrease rsc mean and rsc SD (shaded regions for larger dimensionalities become smaller). Within each shaded region, decreasing %sv decreases both rsc mean and SD radially toward the origin. Finally, rotating co-fluctuation patterns such that the loadings are more similar (going from low to high loading similarity) results in moving clockwise along an arc such that rsc mean increases and rsc SD decreases. We also note two subtle trends. First, there are more possibilities for loading similarity to be low than high (Math Note E), suggesting that rsc SD will generally tend to be larger than rsc mean if neuronal activity varied along a randomly chosen co-fluctuation pattern (shading within each region is darker near the vertical axis than the horizontal axis). Second, this effect becomes exaggerated for higher dimensional neuronal activity, as many dimensions can have low loading similarity but only one dimension can have high loading similarity (Math Note E). Thus, it becomes progressively unlikely for rsc SD to be 0 as dimensionality increases (shaded regions for larger dimensionalities lifted off the horizontal axis).
These results provide a cautionary tale that using a single statistic on its own provides an opaque description of population wide covariability. For example, a change in rsc mean could correspond to changes in loading similarity, %sv, dimensionality, or a combination of the three. Likewise, reporting dimensionality on its own would be incomplete because the role of a dimension in explaining population-wide covariability depends how much shared variance it explains and the loading similarity of its co-fluctuation pattern. For example, consider a decrease in dimensionality by 1. This would have little impact on population-wide covariability if the removed dimension explains only a small amount of shared variance, whereas it could have a large impact if the removed dimension explains a large amount of shared variance.
Considering multiple statistics together provides a richer description of population-wide covariability. For example, in the case where population activity co-fluctuates along a single dimension, rsc mean and rsc SD can be used together to approximate %sv (using distance from the origin) and deduce whether loading similarity is low (rsc SD > rsc mean) or high (rsc mean > rsc SD), whereas rsc mean alone would not provide much information about %sv or loading similarity (cf. Figure 5). In the next section, we further demonstrate using neuronal recordings how relating pairwise and population metrics using the framework we have developed (Figure 5) provides a richer description of how neurons covary than using a single statistic (e.g., rsc mean) alone.
Case study: V4 neuronal recordings during spatial attention
When spatial attention is directed to the receptive fields of neurons in area V4 of macaque visual cortex, rsc mean among those neurons decreases (Cohen and Maunsell, 2009; Mitchell et al., 2009; Gregoriou et al., 2014; Snyder et al., 2016, 2018). This decrease has often been attributed to a reduction in shared modulations among the neurons. However, we have shown both mathematically and in simulations that several distinct changes in population metrics (e.g., decrease in loading similarity, decrease in %sv, or an increase in dimensionality) could underlie this decrease in rsc mean (Figure 5). Here, we sought to assess which aspects of population-wide covariability underlie, and how each of them contribute to, the overall decrease in rsc mean.
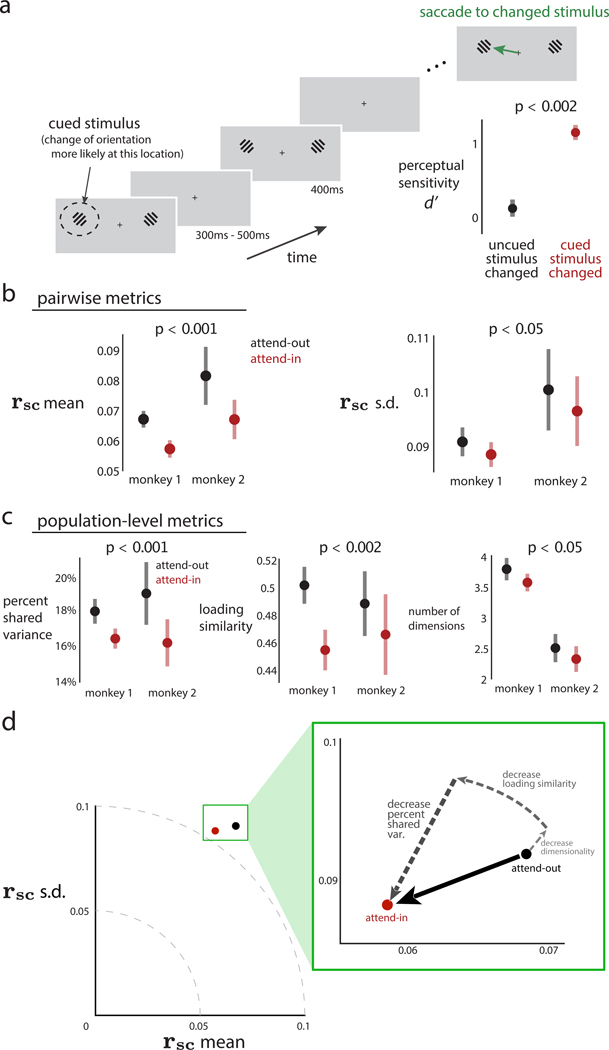
We analyzed activity recorded simultaneously from tens of neurons in macaque V4 while the animal performed an orientation-change detection task (Figure 6A; previously reported in Snyder et al., 2018). To probe spatial attention, we cued the animal to the location of the stimulus that was more likely to change in orientation. As expected, perceptual sensitivity increased for orientation changes in the cued stimulus location (Figure 6A, inset, red dot above black dot). “Attend-in” trials were those in which the cued stimulus location was inside the aggregate receptive fields (RFs) of the recorded V4 neurons, whereas “attend-out” trials were those in which the cued stimulus location was in the opposite visual hemifield.
Figure 6. An observed decrease in rsc mean of macaque V4 neurons during a spatial attention task corresponds to changes in multiple population metrics.
(A) Experimental task design. On each trial, monkeys maintained fixation while Gabor stimuli were presented for 400 ms (with 300–500 ms in between presentations). When one of the stimuli changed orientation, animals were required to saccade to the changed stimulus to obtain a reward. At the beginning of a block of trials, we performed an attentional manipulation by cuing animals to the location of the stimulus that was more likely to change for that block (dashed circle denotes the cued stimulus and was not presented on the screen). The cued location alternated between blocks. Animals were more likely to detect a change in stimulus at cued rather than uncued locations (inset in bottom right, p < 0.002 for both animals; data for monkey 1 are shown). During this task, we recorded activity from V4 neurons whose receptive fields (RFs) overlapped with one of the stimulus locations.
(B) rsc mean (left panel) and rsc SD (right panel) across recording sessions for two animals. Black denotes “attend-out” trials (i.e., the cued location was outside the recorded V4 neurons’ RFs), and red denotes “attend-in” trials (i.e., the cued location was inside the RFs). Data were pooled across both animals to compute p values reported in titles for comparison of attend-out (black) and attend-in (red). For individual animals, rsc mean was lower for attend-in than attend-out (p < 0.001 for each animal). rsc SD was also lower for attend-in than attend-out (p < 0.05 for monkey 1 and p = 0.148 for monkey 2).
(C) Population metrics identified across recording sessions for two animals (same data as in B). Black denotes attend-in trials; red denotes attend-out trials. Data were again pooled across animals to compute p values reported in titles for comparing attend-out and attend-in. %sv was lower for attend-in than attend-out (p < 0.001 for monkey 1 and p < 0.02 for monkey 2). Loading similarity was lower for attend-in than attend-out (p < 0.001 for monkey 1 and p = 0.162 for monkey 2). Dimensionality was lower for attend-in than attend-out (p = 0.113 for monkey 1 and p = 0.174 for monkey 2). In (A)–(C), dots indicate means and error bars indicate 1 SEM, both computed across recording sessions. See also Figure S2.
(D) Summary of the real data results. Attention decreases both rsc mean and rsc SD (black dot to red dot). These decreases in pairwise metrics correspond to a combination of decreases in %sv, loading similarity, and dimensionality (dashed arrows).
See also Figures S3, S4, and S6.
For pairwise metrics, rsc mean decreased when attention was directed into the RFs of the V4 neurons (Figure 6B, left panel), consistent with previous studies (Cohen and Maunsell, 2009; Mitchell et al., 2009; Gregoriou et al., 2014; Snyder et al., 2016, 2018). We further found that rsc SD was lower for attend-in trials than for attend-out trials, an effect not reported previously (Figure 6B, right panel).
The decrease in both rsc mean and rsc SD could arise from several different types of distinct changes in population-wide covariability (Figure 5). To compute the population metrics, we applied FA separately to attend-out and attend-in trials (see STAR Methods). FA is the most basic dimensionality reduction method that characterizes shared variance among neurons (Cunningham and Yu, 2014) and is consistent with how we created covariance matrices in Figures 3 and 4. We found three distinct changes in population metrics. First, neuronal activity during attend-in trials had lower %sv than during attend-out trials (Figure 6C, left), consistent with previous interpretations that attention reduces the strength of shared modulations (Rabinowitz et al., 2015; Ecker et al., 2016; Huang et al., 2019; Ruff et al., 2020). Second, we also found lower loading similarity for attend-in trials than attend-out trials for the dominant dimension (i.e., the dimension that explains the largest proportion of the shared variance; Figure 6C, middle; see also Figure S2B). This implies that, with attention, neurons in the population co-fluctuate in a more heterogeneous manner (i.e., more pairs of neurons co-fluctuate in opposition and fewer pairs co-fluctuate together). Third, we found that dimensionality was slightly lower for attend-in than attend-out trials (Figure 6C, right). Thus, on average, a smaller number of distinct shared signals were present when attention was directed into the neurons’ RFs. The small change in dimensionality is consistent with the relative strength of each dimension (i.e., eigenspectrum shape) being similar for attend-in and attend-out (Figure S2A). Taken together, this collection of observations of both pairwise and population metrics leads to a more refined view of how attention affects population-wide covariability.
The pairwise (Figure 6B) and population (Figure 6C) metrics are computed based on the same recorded activity, and each represents a different view of population activity. The central contribution of our work is to provide a framework by which to understand these two perspectives and five different metrics in a coherent manner. Using the relationships between pairwise and population metrics we have established in the rsc mean versus rsc SD space (Figure 5), we can decompose the decrease in rsc mean and SD into (1) a small decrease in dimensionality (Figure 6D, small dashed arrow), (2) a decrease in loading similarity (Figure 6D, medium dashed arrow), and (3) a substantial decrease in %sv (Figure 6D, large dashed arrow). We quantify these contributions in Figure S3. The rsc mean and SD decreased despite the decrease in dimensionality (which alone would have tended to increase rsc mean and SD) because of the larger contributions of loading similarity and %sv to pairwise metrics in these V4 recordings. We have also applied the same analysis to population recordings in visual area V1 (Zandvakili and Kohn, 2015; available on http://crcns.org) and found that, although rsc mean and SD both decreased (like in the V4 recordings), the population metrics changed in a different way compared to the V4 recordings (Figure S4). Together, these analyses demonstrate the need for considering both pairwise and population metrics together when studying correlated variability, with a bridge that allows one to navigate between the two.
DISCUSSION
Coordinated variability in the brain has long been linked to the neural computations underlying a diverse range of functions, including sensory encoding, decision making, attention, learning, and more. In this study, we sought to relate two major bodies of work investigating the coordinated activity among neurons: studies that measure spike count correlation between pairs of neurons and studies that use dimensionality reduction to measure population-wide covariability. We considered three population metrics and established analytically and empirically that (1) increasing loading similarity corresponds to increasing rsc mean and decreasing rsc SD, (2) decreasing %sv corresponds to decreasing both rsc mean and SD, and (3) increasing dimensionality tends to decrease rsc mean and SD. Applying this understanding to recordings in macaque V4, we found that the previously reported decrease in mean spike count correlation associated with attention stemmed from a decrease in %sv, a decrease in loading similarity, and decrease in dimensionality. This analysis revealed that attention involves multiple changes in how neurons interact that are not well captured by a single statistic alone. Overall, our work demonstrates that common ground exists between the literatures of spike count correlation and dimensionality reduction approaches and builds the intuition and formalism to navigate between them.
Our work also provides a cautionary tale for attempting to summarize population-wide covariability using one, or a small number of, statistics. For example, reporting only rsc mean is incomplete because several distinct changes in population-wide covariability can correspond to the same change in rsc mean. In a similar vein, reporting only dimensionality is incomplete because it does not indicate how strongly the neurons covary or their co-fluctuation patterns. For this reason, we recommend reporting several different pairwise and population metrics (e.g., the five used in this study along with the eigenspectrum of the shared covariance matrix), as long as they can be reliably measured from the data available. This not only allows for a deeper and more complete understanding of how neurons covary, but also it allows one to make tighter connections to previous literature that uses the same metrics. Future work may seek to revisit previous results of correlated neuronal variability that are based on a single statistic (e.g., rsc mean) and reinterpret them within a framework that considers multiple perspectives and statistics of population-wide covariability, such as that presented here.
There are some situations where it is not feasible to reliably measure population statistics, such as recording from a small number of neurons in deep brain structures (Nevet et al., 2007; Liu et al., 2013) or when the number of trials is small relative to the number of neurons recorded (Wainwright, 2019). In such situations, the rsc can be measured between pairs of neurons recorded in each session and then averaged across sessions to obtain the rsc mean. Based on our findings, we recommend that studies that report rsc mean also report rsc SD because the latter provides additional information about population-wide covariability. For example, in the special case of one latent dimension (typically not known in advance for real data), measuring rsc mean and rsc SD allows one to estimate the loading similarity and %sv (cf. Figures 3E and 3F). In general, even when there is more than one latent dimension in the population, rsc SD provides value in situating the data in the rsc mean versus rsc SD plot (Figure 5). Changes in rsc mean and SD can then inform changes in population metrics based on the relationships established in this work (cf. Figure 6D).
The reason that our work, and many previous studies, have focused on trial-to-trial variability is that it has important implications for information coding. Early work on information-limiting correlations typically focused on rsc mean (e.g., Zohary et al., 1994; Shadlen and Newsome, 1998; Cohen and Maunsell, 2009; Cohen and Kohn, 2011), which reflects the strength of shared variability among neurons. Recent theoretical work (Averbeck et al., 2006; Moreno-Bote et al., 2014; Kohn et al., 2016) and experimental evidence (Ni et al., 2018; Ruff and Cohen, 2019a; Cowley et al., 2020; Rumyantsev et al., 2020; Bartolo et al., 2020) have shown that it is not only the strength of shared trial-to-trial variability but also the directions of shared variability relative to stimulus tuning (Figure 7A) that need to be considered for information coding. These properties of shared trial-to-trial variability are precisely what are measured by the population metrics used here. In particular, the %sv measures how strongly trial-to-trial variability is shared among neurons (Figure 7B), loading similarity measures the direction(s) of variability (Figure 7C), and dimensionality measures how many different directions of variability exist in the data (Figure 7D). By considering these three population metrics together, along with the way in which mean population responses vary across conditions (i.e., the stimulus-encoding directions), we can more incisively characterize how trial-to-trial variability impacts information coding than by using rsc mean alone. Understanding how patterns of shared variability are related to (e.g., align with or are orthogonal to) patterns of stimulus encoding and downstream readouts will be likely critical for understanding information coding in the brain.
Figure 7. Population metrics and information coding.
For illustrative purposes, we consider the responses of two neurons to two different stimuli. (A) In “condition 1” (e.g., attend-out in our V4 analyses), the two neurons have positively correlated trial-to-trial variability (blue and orange clouds each have positive correlation) and a stimulus encoding space (black arrow) defined by the span of the trial-averaged responses (blue and orange dots). Then, we consider how changes in trial-to-trial neuronal variability (i.e., shapes of the clouds) from one experimental condition to another (e.g., spatial attention) can influence decoding of the two stimuli. For simplicity, we construct examples in which the stimulus encoding space remains constant between the two conditions. We illustrate here the changes in population metrics that we observed in our V4 data (Figure 6D).
(B) First, a decrease in percent shared variance (both clouds are smaller in size) results in more accurate decoding of the population responses to the two stimuli (the blue and orange ellipses are less overlapping here than in A).
(C) Second, a decrease in the loading similarity of the strongest dimension (both clouds have been rotated to have negative correlation) also leads to an improvement in decoding performance. In this case, the improvement stems from the fact the stimulus encoding space (black arrow) and the strongest dimension of trial-to-trial variability (negative correlation) are misaligned (Averbeck et al., 2006; Moreno-Bote et al., 2014; Ruff and Cohen, 2019a).
(D) Third, a decrease in dimensionality (the less dominant dimension has been squashed for both clouds) could either improve or have no impact on decoding performance. Here, the dimension that was squashed (negative correlation direction) was orthogonal to the stimulus encoding dimension (black arrow), leading to no impact on decoding performance. In general, all else being equal, higher dimensional trial-to-trial variability (distinct from high-d signal; Rigotti et al., 2013) is more likely to overlap with stimulus encoding dimensions and thus limit the amount of information encoded.
We considered three population metrics—dimensionality, % sv, and loading similarity—that summarize the structure of population-wide covariability and are rooted in well-established concepts in existing literature. First, dimensionality has been used to describe how neurons covary across conditions (i.e., an analysis of trial-averaged firing rates; Churchland et al., 2012; Rigotti et al., 2013; Mante et al., 2013; Cowley et al., 2016; Kobak et al., 2016; Sohn et al., 2019), as well as how neurons covary from trial to trial (Yu et al., 2009; Santhanam et al., 2009; Sadtler et al., 2014; Rabinowitz et al., 2015; Mazzucato et al., 2016; Williamson et al., 2016; Bittner et al., 2017; Athalye et al., 2017; Williams et al., 2018; Stringer et al., 2019a; Recanatesi et al., 2019). We focused on the latter in our study to connect with the rsc literature, which also seeks to understand the shared trial-to-trial variability between neurons. To focus on the shared variability among neurons, we used FA to measure dimensionality. Another commonly used dimensionality reduction method, principal-component analysis (PCA), although appropriate for studying trial-averaged activity, does not distinguish between variability that is shared among neurons and variability that is independent to each neuron. Second, investigating the loading similarity has provided insight about whether shared variability among neurons arises from a shared global factor that drives neurons to increase and decrease their activity together (Ecker et al., 2014; Okun et al., 2015; Lin et al., 2015; Rabinowitz et al., 2015; Williamson et al., 2016; Huang et al., 2019) or whether the co-fluctuations involve a more intricate pattern across the neuronal population (Snyder et al., 2018; Insanally et al., 2019; Cowley et al., 2020). Third, we have previously reported %sv for area V1 (Williamson et al., 2016), area M1 (Hennig et al., 2018), and network models (Williamson et al., 2016; Bittner et al., 2017). Conceptually, %sv and rsc mean are both designed to capture the strength of shared variability in a population of neurons. Thus, we might initially think that there should be a one-to-one correspondence between the two quantities. Indeed, if the population activity is described by one co-fluctuation pattern with a high loading similarity, there is a direct relationship between %sv and rsc mean (Figure 3F). However, in general, %sv and rsc mean do not have a one-to-one correspondence between them (Figure 3F, moderate or low loading similarity).
We focus here on studying trial-to-trial activity fluctuations that are shared between neurons. Many studies have considered the source of these shared fluctuations in the context of pairwise correlations (Cohen and Kohn, 2011). Most commonly, pairwise correlations have been suggested to originate through common input (Zohary et al., 1994; Shadlen and Newsome, 1998). However, there are, in fact, numerous mechanisms that can shape the trial-by-trial shared variability of neuronal populations, including neuromodulation (Harris and Thiele, 2011; Herrero et al., 2013; Minces et al., 2017), coupled inhibition (Haider et al., 2006), or distinct patterns of neuronal connectivity (Mazzucato et al., 2016; Williamson et al., 2016; Huang et al., 2019; Recanatesi et al., 2019). These mechanisms likely produce distinct signatures in population metrics, such as %sv, loading similarity, and dimensionality. The framework that we have developed here can be applied to spiking network models with different underlying mechanisms of shared cortical variability to identify signatures in population metrics (Mazzucato et al., 2016; Williamson et al., 2016; Huang et al., 2019; Recanatesi et al., 2019). We can then assess whether any of those signatures are present in neuronal recordings to gain insight into the underlying mechanisms of shared variability in the brain.
Although pairwise correlation and dimensionality reduction have most commonly been computed based on spike counts, several studies have also computed these metrics on neuronal activity recorded using other modalities, such as calcium imaging (Harvey et al., 2012; Ahrens et al., 2012; Dechery and MacLean, 2018; Stringer et al., 2019a; Rumyantsev et al., 2020). The relationships that we established here between pairwise and population metrics are properties of covariance matrices in general and do not rely on or assume recordings of neuronal spikes. Thus, the intuition built here can be applied to other recording modalities.
Our work here focused on studying interactions within a single population of neurons. Technological advances are enabling recordings from multiple distinct populations simultaneously, including neurons in different brain areas, neurons in different cortical layers, or different neuron types (e.g., Ahrens et al., 2013; Jiang et al., 2015; Jun et al., 2017). Studies are dissecting the interactions between these distinct populations using pairwise correlation (Smith et al., 2013; Pooresmaeili et al., 2014; Oemisch et al., 2015; Zandvakili and Kohn, 2015; Ruff and Cohen, 2016a; Snyder et al., 2016) and dimensionality reduction (Semedo et al., 2014; Buesing et al., 2014; Bittner et al., 2017; Perich et al., 2018; Semedo et al., 2019; Ames and Churchland, 2019; Ruff and Cohen, 2019a; Veuthey et al., 2020; Cowley et al., 2020). As we have shown here for a single population of neurons, considering a range of metrics from both the pairwise correlation and dimensionality reduction perspectives and understanding how they relate to one another will provide rich descriptions of how different neuronal populations interact.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Byron M. Yu (byronyu@cmu.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
Original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table. Additional information or data are available upon request from the lead contact (byronyu@cmu.edu).
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: organisms/strains | ||
|
| ||
| Rhesus macaque (Macaca mulatta) | 1 animal from Covance, 1 from Tulane National Primate Research Center | N/A |
|
| ||
| Software and algorithms | ||
|
| ||
| MATLAB | MathWorks | RRID: SCR_001622; https://www.mathworks.com/products/matlab.html |
| Custom spike-sorting software | Kelly et al., 2007 | https://github.com/smithlabvision/spikesort |
| Code to reproduce simulations | Original code | https://zenodo.org/record/5028023 |
| Code to compute activity statistics | Original code | https://zenodo.org/record/5028018 |
|
| ||
| Other | ||
|
| ||
| 96-electrode array | Blackrock Microsystems | http://www.blackrockmicro.com/neuroscience-research-products/neural-data-acquisition-systems/ |
| Eyelink 1000 eye tracker | SR research | RRID: SCR_009602; https://www.sr-research.com/ |
METHOD DETAILS
Spike count covariance matrix
Both pairwise metrics and population metrics are computed directly from the spike count covariance matrix of size n × n for a population of n neurons. Each entry in is the covariance between the activity of neuron i and neuron j:
| (Equation 2) |
where xi and xj represent the activity of neurons i and j, respectively, and and represent the mean activity of neurons i and j, respectively. The variance of the ith neuron is equal to .
Pairwise metrics
We computed the spike count correlation between neurons i and j directly from the spike count covariance matrix:
| (Equation 3) |
We then summarized the distribution of rsc values across all pairs of neurons in the population with two pairwise metrics: the rsc mean and rsc standard deviation (SD).
Population metrics
The metrics we use for characterizing population-wide covariability are based on factor analysis (FA; Santhanam et al., 2009; Yu et al., 2009; Churchland et al., 2010; Harvey et al., 2012; Williamson et al., 2016; Bittner et al., 2017; Athalye et al., 2017; Huang et al., 2019), a dimensionality reduction method. We chose FA because it is the most basic dimensionality reduction method that explicitly separates variance that is shared among neurons from variance that is independent to each neuron. This allows us to relate the population metrics provided by FA to spike count correlation, which is designed to measure shared variability between pairs of neurons. One might consider using principal component analysis (PCA), but it does not distinguish shared variance from independent variance. Thus, FA is more appropriate than PCA for studying the shared variability among a population of neurons.
Decomposing the spike count covariance matrix
FA decomposes the spike count covariance matrix into a low-rank shared covariance matrix, which captures the variability shared among neurons in the population, and an independent variance matrix, which captures the portion of variance of each neuron unexplained by the other neurons (Figure S5A):
| (Equation 4) |
where is the shared covariance matrix for n neurons, and is a diagonal matrix containing the independent variance of each neuron. The low-rank shared covariance matrix can be expressed using the eigendecomposition as (Figure S5A):
| (Equation 5) |
where and , with . The rank (i.e., dimensionality) of the shared covariance matrix, d, indicates the number of latent variables. Each column of U is an eigenvector and represents a co-fluctuation pattern containing the loading weights of each neuron (i.e., how much each neuron contributes to that dimension). The matrix is a diagonal matrix where each diagonal element is an eigenvalue and represents the amount of variance along the corresponding co-fluctuation pattern (e.g., in Figure 2A has larger eigenvalue than 2C).
Based on this matrix decomposition, we defined the three metrics that describe the population-wide covariability:
Loading similarity: the similarity of loading weights across neurons for a given co-fluctuation pattern. Scalar value between 0 (the weights are maximally dissimilar, defined precisely below) and 1 (all weights are the same).
Percent shared variance (%sv): the percentage of each neuron’s variance that is explained by other neurons in the population. Percentage between 0% and 100%.
Dimensionality: the number of dimensions (i.e., co-fluctuation patterns). Integer value.
We give the precise definitions of these population metrics below and in Figure S5B.
Loading similarity
We sought to define loading similarity such that, for a given co-fluctuation pattern, if the weights for all neurons are the same, we would measure a loading similarity of 1. When the weights are as different as possible, we would measure a loading similarity of 0. We define the loading similarity based on the variance across the n weights (for n neurons) in a co-fluctuation pattern uk. The smallest possible variance is 0; the largest possible variance, for a unit vector uk, is 1/n (Math Note F). Thus, we define loading similarity for a co-fluctuation pattern as:
| (Equation 6) |
where the loading similarity is computed on unit vectors (i.e., uk has a norm of 1). The notation denotes that the variance is being taken across the n elements of the vector uk. The denominator of Equation 6 acts as a normalizing factor, bounding the loading similarity value between 0 and 1.
The loading similarity distinguishes between a co-fluctuation pattern along which all neurons in the population have the same weight in which case they change their activity up and down together (Figure 2A; loading similarity of 1), from one in which weights are different and some neurons increase their activity when others decrease their activity (Figure 2B; loading similarity of 0). The loading weights we use here are closely related to ‘population coupling’ (Okun et al., 2015) and ‘modulator weights’ (Rabinowitz et al., 2015). For some types of shared fluctuations, these weights are similar across neurons in a population (i.e., high loading similarity; Okun et al., 2015; Rabinowitz et al., 2015; Huang et al., 2019). For other types of shared fluctuations, the weights vary substantially across neurons in the population (i.e., low loading similarity; Snyder et al., 2018; Cowley et al., 2020).
We show in Math Note E why, if one dimension has high loading similarity, the other dimensions must have low loading similarity. The reason is that co-fluctuation patterns are defined to be mutually orthogonal. If one co-fluctuation pattern has all weights close to the same value (i.e., high loading similarity), then all other co-fluctuation patterns must have substantial diversity in their weights (i.e., low loading similarity) to satisfy orthogonality.
Percent shared variance
The percent shared variance (%sv) measures the percentage of each neuron’s spike count variance that is explained by other neurons in the population (Williamson et al., 2016; Bittner et al., 2017; Hennig et al., 2018). Equivalently, we can think of %sv in terms of latent co-fluctuations. Because latent co-fluctuations capture the shared variability among neurons, the %sv measures how much of each neuron’s variance is explained by the latent co-fluctuations. The activity of neurons may be tightly linked to the latent co-fluctuation (e.g., Figure 2A), in which case a large percentage of each neuron’s variance is shared with other neurons, or may only be loosely linked to the latent co-fluctuation (e.g., Figure 2C), in which case a small percentage of each neuron’s variance is shared with other neurons. Mathematically, we define the %sv for a neuron i:
| (Equation 7) |
where si is the ith entry along the diagonal of the shared covariance matrix (Figure S5A, ), and is the ith entry along the diagonal of the independent covariance matrix (Figure S5A, ). A %sv of 0% indicates that the neuron does not covary with (i.e., is independent of) other neurons in the population, whereas a %sv of 100% indicates that the neuron’s activity can be entirely accounted for by the activity of other neurons in the population. To compute %sv for an entire population of neurons, we averaged the %sv of the individual neurons. All %sv values reported in this study are the %sv for the neuronal population.
Dimensionality
Dimensionality refers to the number of latent co-fluctuations needed to describe population-wide covariability. For example, the population-wide covariability can be described by one latent co-fluctuation (Figure 2A) or by several latent co-fluctuations (Figure 2D). In the population activity space, dimensionality corresponds to the number of axes along which the population activity varies (see Figure 2D, bottom inset). Mathematically, the dimensionality is the rank of the shared covariance matrix (i.e., the number of columns in U, Figure S5A).
Creating the spike count covariance matrices with specified population metrics
To relate pairwise and population metrics, we created spike count covariance matrices of the form in Equation 4 with specified population metrics. Importantly, we did not simulate spike counts, nor fit a factor analysis model to simulated data. Rather, we created covariance matrices using (4) and computed pairwise correlations directly from the entries of the covariance matrix, as shown in (3). Across simulations (Figures 3 and 4), we simulated with n = 30 neurons and set independent variances (i.e., diagonal elements of in Equation 4) to 1.
Specifying co-fluctuation patterns to obtain different loading similarities
Each co-fluctuation pattern uk is a vector with n = 30 entries (one entry per neuron). We generated a single co-fluctuation pattern by randomly drawing 30 independent samples from a Gaussian distribution with a mean of 2.5. We choose a nonzero mean so that we could obtain co-fluctuation patterns with loading similarities close to 1 when drawing from the Gaussian distribution (i.e., a mean of 0 would have resulted in almost all co-fluctuation patterns having a loading similarity close to 0). To get a range of loading similarities between 0 and 1, we used different standard deviations for the Gaussian. For a small standard deviation value, all entries in the co-fluctuation pattern are close to 2.5, resulting in a high loading similarity. For larger standard deviations, some loading weights are positive and some negative, with large variability in their values, resulting in co-fluctuation patterns with low loading similarity. We increased the Gaussian standard deviation from 0.1 to 5.5 with increments of size 0.1. For each increment, we generated 50 patterns and normalized them to have unit norm. In total, we created a set of 2,750 random patterns.
The following procedure describes the construction of shared covariance matrices with one co-fluctuation pattern. We chose a single pattern (i.e., U has only 1 column) from the set of 2,750. We constructed the shared covariance matrix by computing , where was chosen to achieve a desired percent shared variance (see below). The covariance matrix was then computed according to Equation 4. We created a covariance matrix, yielding a spread of loading similarities between 0 and 1 (Figures 3E and 3F). In the next section, we describe the procedure for creating a covariance matrix with more dimensions.
Specifying the percent shared variance
To achieve a given %sv, either the independent variance or the amount of shared variability (i.e., the eigenvalues) of each dimension can be adjusted. In the main text, we set the independent variance of each neuron to , and changed the total amount of shared variability by multiplying each eigenvalue (each diagonal element in from Equation 5) by the same constant value, a. To obtain a specified %sv, we identified a by searching through a large set of possible values (from 10−4 to 103 with step size 10−3). We allowed for a tolerance of between the desired %sv and the %sv that was achieved after scaling the eigenvalues by a. In other analyses (not shown), we allowed the independent variances to be different across neurons (e.g., drawn from an exponential distribution), and the relationships between pairwise and population metrics were qualitatively similar to those in the main text.
Increasing dimensionality
To assess how changing dimensionality affects pairwise metrics, we created covariance matrices whose shared covariance matrix comprised more than 1 dimension. To create a shared covariance matrix with d dimensions, we randomly chose d patterns from the set of 2,750 we had generated above (see ‘Specifying co-fluctuation patterns to obtain different loading similarities’). We then orthogonalized the chosen patterns using the Gram-Schmidt process to obtain d orthonormal (i.e., orthogonal and unit length) co-fluctuation patterns . We formed the shared covariance matrix using , where is a diagonal matrix containing the eigenvalues (i.e., the strength of each dimension; see ‘Specifying the relative strengths of each dimension’ below). We repeated this procedure to produce 3,000 sets of d orthonormal patterns (i.e., 3,000 different U matrices), each of which was used to create a shared covariance matrix. The spike count covariance was computed according to Equation 4.
Specifying the relative strengths of each dimension
In simulating shared covariance matrices with more than one dimension, we chose the relative strength of each dimension by specifying the eigenspectrum (diagonal elements of in Equation 5). We worked with three sets of eigenspectra. First, a flat eigenspectrum had eigenvalues that were all equal (Figure 3G). Second, for two dimensions, we varied the ratio of the two eigenvalues between 95:5, 80:20, 50:50, 20:80, and 5:95 (Figure 4). Third, we considered an eigenspectrum in which each subsequent eigenvalue falls off according to an exponential function (Figure S1). Only the relative (and not the absolute) eigenvalues (i.e., the shape of the eigenspectrum) affect the results, because the eigenspectrum was subsequently scaled to achieve a desired %sv (see ‘Specifying the values of percent shared variance’).
Analysis of V4 neuronal recordings from a spatial attention task
Electrophysiological recordings
We analyzed data from a visual spatial attention task reported in a previous study (Snyder et al., 2018). Briefly, we implanted a 96-electrode “Utah” array (Blackrock Microsystems; Salt Lake City, UT) into visual cortical area V4 of an adult male rhesus macaque monkey (data from two monkeys were analyzed; in our study, monkey 1 corresponds to “monkey P” and monkey 2 corresponds to “monkey W” from Snyder et al., 2018). After recording electrode voltages (Ripple Neuro.; Salt Lake City, UT), we used custom software to perform offline spike sorting (Kelly et al., 2007, freely available at https://github.com/smithlabvision/spikesort). This yielded 93.2 ± 8.9 and 61.9 ± 27.4 candidate units per session for monkey 1 and 2, respectively. Experiments were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and were performed in accordance with the United States National Research Council’s Guide for the Care and Use of Laboratory Animals.
To further ensure the isolation quality of recorded units, we removed units from our analyses according to the following criteria. First, we removed units with a signal-to-noise ratio of the spike waveform less than 2.0 (Kelly et al., 2007). Second, we removed units with overall mean firing rates less than 1 Hz, as estimates of rsc for these units tends to be poor (Cohen and Kohn, 2011). Third, we removed units that had large and sudden changes in activity due to unstable recording conditions. For this criterion, we divided the recording session into ten equally-sized blocks and for each unit computed the difference in average firing rate between adjacent blocks. We excluded units with a change in average firing rate greater than 60% of the maximum firing rate (where the maximum is taken across the ten equally-sized blocks). Fourth, we removed an electrode from each pair of electrodes that were likely electrically-coupled. We identified the coupled electrodes by computing the fraction of threshold crossings that occurred within 100 μs of each other for each pair of electrodes. We then removed the fewest number of electrodes to ensure this fraction was less than 0.2 (i.e., pairs with an unusually high number of coincident spikes) for all pairs of electrodes. Fifth, we removed units that did not sufficiently respond to the visual stimuli used in the experiment. Evoked spike counts (i.e., a neuron’s response after stimulus presentation) were taken between 50 ms to 250 ms after stimulus onset, and spontaneous spike counts (i.e., a neuron’s response during a blank screen) were taken in a 200 ms window that ended 50 ms before stimulus onset. For each unit, we computed a sensitivity measure d′ between evoked and spontaneous activity:
for mean spike counts μevoked and μspontaneous and spike count variances and . We removed units with from analyses, as these units had spontaneous and evoked responses that were difficult to distinguish.
After applying these five criteria, 44.5 ± 11.3 and 18.8 ± 6.7 units per session (mean ± s.d. over sessions) remained for monkeys 1 and 2, respectively. Although these remaining units likely contained both single-unit and multi-unit activity, we refer to each unit as a neuron for simplicity. In this study, we restricted analyses to sessions with at least 10 neurons remaining after applying the above criterion (23 sessions for monkey 1, and 14 sessions for monkey 2).
Visual stimulus change-detection task
Animals were trained to perform a change-detection task with a spatial attention cue to the location of the visual stimulus that was more likely to change (Snyder et al., 2018). In the visual change-detection task (Figure 6A), animals fixated a central dot while Gabor stimuli were presented in two locations on a computer screen. One location was chosen to be within the aggregate receptive fields (RFs) of the recorded V4 neurons (mapped prior to running the experiment), and the other location was placed at the mirror symmetric location in the opposite hemifield. Animals maintained fixation while a sequence of Gabor stimuli were presented. Each drifting Gabor stimulus (oriented at either 45° or 135°) was presented for 400 ms, followed by a blank screen presented for a random interval (between 300 and 500 ms). The sequence continued, with a fixed probability for each presentation, until one of the two stimuli changed orientation when presented (i.e., the ‘target’). Upon target presentation, animals were required to make a saccade to the target to earn a juice reward. We manipulated spatial attention in the experiment by cueing the more probable target location in blocks. At the beginning of each block, the cue was denoted by presenting only one Gabor stimulus at the more probable target location (90% likely), and requiring animals to detect orientation changes at this location for 5 trials. Consistent with the results of previous studies, we found that animals had greater perceptual sensitivity for orientation changes at the cued (i.e., attended) location than the uncued location (Figure 6A, inset in the bottom right) and shorter reaction times (Snyder et al., 2018).
Data processing and computing spike counts
We first separated the trials into two groups: (1) “attend in” trials, for which the cued stimulus was inside the recorded neurons’ RFs and (2) “attend out” trials, for which the cued stimulus was outside the RFs. Since the initial orientation of the stimulus at the cued location could be one of two values (i.e., 45° or 135°), we further divided trials, resulting in a total of 4 groups of trials per session (attend in & 45°, attend out & 45°, attend in & 135°, attend out & 135°). Each combination of cued location and stimulus orientation was treated as an independent sample. The same neurons were used for each of the 4 groups within each session, ensuring a fair comparison between the attend-in and attend-out conditions.
We analyzed all stimulus presentations for which the target stimulus did not change. For each stimulus presentation, we took spike counts in a 200 ms window starting 150 ms after stimulus onset. For each of the 4 groups, we formed a spike count matrix , containing the spike counts of the n recorded neurons for the t trials belonging to that group. These spike count matrices were then used to compute both the pairwise and population metrics (described below). For all analyses (Figure 6), we excluded recording sessions with fewer than 10 neurons. Additionally, because population metrics depend on the number of trials (Williamson et al., 2016), for each session we equalized the number of trials across the 4 groups by randomly subsampling from groups with larger numbers of trials.
Computing pairwise metrics for V4 spike counts
We computed pairwise metrics on each combination of attention state (‘attend in’ and ‘attend out’) and stimulus orientation. We computed the correlation as described above in ‘Pairwise metrics’ and then computed rsc mean and rsc SD For each attention state, we averaged the rsc mean and rsc SD over sessions and different stimulus orientations.
Computing population metrics for V4 spike counts
We fit the parameters of a factor analysis model (see Figure S5A) to each spike count matrix X (as described above) using the expectation-maximization (EM) algorithm (Dempster et al., 1977). For each session, this was performed separately for each attention state and stimulus orientation. Using the FA parameters, we then computed the three population metrics (Figure S5B). For dimensionality, we first found the number of dimensions d that maximized the cross-validated data likelihood. We fit an FA model with d dimensions, and then found the number of dimensions required to explain 95% of the shared variance, termed dshared (Williamson et al., 2016). We report dshared because it tends to be a more reliable estimate of dimensionality than the number of dimensions that maximizes the cross-validated data likelihood. We computed %sv as described by Equation 7. We report the loading similarity as defined in Equation 6 for the co-fluctuation pattern that explained the most shared variability (i.e., the eigenvector with the largest eigenvalue; see Figure S1 for why the loading similarity of this dimension is most informative), since it contributes most to describing the population-wide covariability. For ‘attend in’ and ‘attend out’ conditions, we averaged the population metrics across sessions and stimulus orientations.
Much of our work focuses on systematically changing a single population metric and assessing changes in pairwise metrics (Figures 3A–3D). When analyzing neuronal recordings, one needs to fit factor analysis to the recordings in order to estimate the population metrics. When estimating the population metrics together, it could be the case that changes in one population metric impacts or biases the estimation of another population metric. We characterized these estimation errors in Figure S6. Moreover, in Figure S7, we show that our main findings (Figure 5) are the same when estimating population metrics from Poisson simulated data, which resembled realistic neuronal activity.
Statistics
We employed paired permutations tests for all statistical comparisons of pairwise metrics and population metrics between ‘attend-in’ and ‘attend-out’ conditions (Figures 6B and 6C). First, for a given metric, we computed its value separately for each stimulus type (i.e., 45° or 135°), condition (i.e., attend-in or attend-out), and session. We then averaged the difference between attend-in and attend-out across stimulus types and sessions. To compute a null distribution, we randomly permuted the pair of attend-in and attend-out labels for each stimulus type and condition combination and recomputed the average difference. We ran 10, 000 permutations to obtain a null distribution of 10, 000 samples. We computed p-values as the proportion of samples in the null distribution that were more extreme than the average difference in the data, corresponding to p < 0:0001 as the highest attainable level of significance in our statistical analyses.
Math Notes
A). Relationship between correlation, loading similarity, and %sv (one latent dimension)
We establish here the mathematical relationship between rsc, loading similarity, and %sv. This will provide the formalism for understanding why decreasing %sv decreases both rsc mean and SD (Figure 3F), that a high loading similarity corresponds to large rsc mean and low rsc SD (Figure 3E), and that a low loading similarity corresponds to small rsc mean and large rsc SD (Figure 3E).
Let n be the number of neurons, and let w be the co-fluctuation pattern (i.e., loading vector ), be the strength of the co-fluctuation pattern (i.e., eigenvalue of the shared covariance matrix), and be a diagonal matrix specifying the independent variance of each neuron . Then the covariance matrix of the population activity is (see STAR Methods and Figure S5):
From this, we observe that for the off-diagonal entries (i.e., if ). Along the diagonal, and . The correlation (i.e., rsc if is a spike count covariance matrix) between neurons i and j can be written as:
| (Equation 8) |
where and represent the %sv (as proportions) for neurons i and j, respectively, and if or −1 if . The last line follows from the fact that %sv for neuron i is defined in Equation 7 as:
| (Equation 9) |
Equations 8 and 9 provide a basis for understanding the relationships between rsc, %sv, and loading similarity. The rsc mean and SD are computed across all pairs of neurons , for i < j.
For establishing a relationship between pairwise metrics and %sv, consider decreasing the overall %sv of the population while keeping the loadings fixed. This corresponds to decreasing in Equation 9, which implies for each neuron decreases, and thus the product decreases for all pairs. The magnitude of each decreases (i.e., each moves closer to 0). As such, decreasing %sv of the population decreases the distance of a point from the origin in the rsc mean versus rsc SD plot, all else being equal (Figure 3F).
For establishing a relationship between pairwise metrics and loading similarity, consider two extreme cases: 1) when loading similarity is 1 (as high as possible) 2) when it is 0 (as low as possible). We first assume that each neuron has the same independent variance for simplicity, as we did in Figure 3. A loading similarity of 1 corresponds to each or each . In either case, is always + 1. Furthermore, is the same for every neuron and (i.e., the %sv of the population, expressed as a proportion) for every pair of neurons. Thus, all for all pairs of neurons i and j. In this case, rsc mean = %sv and rsc SD = 0. If the independent variances are different across neurons, we can still get each and each to be the same by setting each or each . This would also result in for all pairs of neurons i and j, and thus rsc mean = %sv and rsc SD = 0. In this case, the loading similarity is still high (all wi are the same sign; we can show that load. sim.>0:5), but not equal to 1.
Now, consider a scenario in which half the loadings are and the other half are (and assume again that are the same for every neuron). This is one way to obtain a loading similarity of 0. In this case, are still the same for every neuron, so for all pairs. However, for pairs, and for pairs. We can show that rsc and, by using Equation 10 from Math Note B below, rsc . Thus, for a large number of neurons n, this case (where loading similarity = 0) corresponds to small negative rsc mean (close to 0), and large rsc SD (close to the %sv). As an example, for 30 neurons and %sv = 50%, this corresponds to rsc mean = −0.0172 and rsc SD = 0.4997. With this analysis, we have established that for one latent dimension:
Decreasing %sv decreases the magnitudes of correlations (i.e., each closer to 0). rsc mean and SD both decrease (as seen empirically in Figure 3F).
Starting from a loading similarity near 1, a decrease in loading similarity involves flips in the signs of some correlations (i.e., some become ). rsc mean decreases but rsc SD increases (as seen empirically in Figure 3F).
Both rsc mean and %sv measure shared variance among neurons, but they are not always equal. Equation 8 shows that the two quantities are equal if all are the same (i.e., when loading similarity is high). However, in general rsc mean and shared variance (%sv) are not the same—e.g., when loading similarity is low, or when there are multiple dimensions (Math Note C).
In this section, we consider the extremes of loading similarity. In the next section, we analyze how gradual changes in loading similarity affect rsc mean and SD for a fixed %sv.
B). Circular arc in rsc mean versus rsc SD plot for one latent dimension and fixed %sv
We establish here mathematically that gradually varying the loading similarity for one latent dimension and fixed %sv results in an arc-like relationship between rsc mean and rsc SD, and that the radius of the arc is approximately equal to the %sv (Figures 3E and 3F).
We use the same notation as in Math Note A. Let and denote the mean and variance across all neurons or all pairs of neurons, depending on context. In particular, we are interested in mean, , where the expectation and variance are computed across for all pairs of neurons in a given population (i.e., the upper triangle of the correlation matrix, for i > j).
Let c be the distance of a point (corresponding to one instance of the population activity covariance matrix) from the origin in the rsc mean versus rsc SD plot (i.e., . We want to know whether c is the same for all population activity covariance matrices with one latent dimension and fixed %sv. This would correspond to a point being equidistant from the origin, and thus a circular arc. We can write c as:
Thus, the squared distance (i.e., squared radius) is equal to , the mean of across all pairs in the population. Let m be the number of pairs (i.e., ). Now, using Equations 8 and 9 derived in Math Note A:
where and are the %sv of neurons i and j (expressed as proportions), as defined in Math Note A. We can show that . Intuitively, if we have a symmetric matrix with entries , and we want to find the sum of the off-diagonal elements , then we can take the sum of all elements and subtract the diagonal . Using this equivalence, it follows:
| (Equation 10) |
This provides an equation for the squared radius (i.e., squared distance from the origin) of a point in the rsc mean versus rsc SD plot. In the above derivation, and are taken across the percent shared variance of each neuron in the population . Thus, is equal to our population metric %sv. Now, we will bound , which by definition is greater than or equal to 0. Since , one instance where the maximum variance occurs is when there are an equal number of and (and = 0.5). Then,
So . For a small number of neurons n, the second term in Equation 10 is non-negligible. For example, for a model with 6 neurons and %sv = 50%, the radius of the data points may vary between 0.4472 and 0.5. As the number of neurons increases, the second terms becomes negligible, and data points lie approximately along an arc with radius equal to %sv. For example, for 30 neurons as in our simulations and a %sv of 50%, the radius only varies between 0.4913 and 0.5.
To summarize, Equation 10 computes the distance from the origin of a point for a given population of neurons. For a fixed %sv, can be the same or differ across many simulation runs. If = 0 or is the same across runs, then the points will lie perfectly along an arc, with radius specified by Equation 10. However, if is different across runs, the distances of each point from the origin will differ slightly, so they will lie close to, but not exactly along, an arc.
With this analysis, we have shown that in the case of one latent dimensions:
A point (i.e., corresponding to a given population of neurons, simulated or real) on the rsc mean versus rsc SD plot has distance from the origin (i.e., radius) less than or equal to %sv.
If the %sv for individual neurons are all the same (see Math Note A), then the radius equals %sv.
As the number of neurons increases, the radius becomes asymptotically closer to %sv.
C). Relationship between correlation, loading similarity, and %sv (multiple latent dimensions)
In Math Note A, we established a mathematical relationship between rsc, loading similarity, and %sv in the case of one latent dimension. Here, we generalize Equation 8 to include multiple dimensions in order to better understand the relationship between rsc and dimensionality. We demonstrate here that the general relationships between rsc, %sv, and loading similarity for one latent dimension also hold true for multiple latent dimensions. For multiple latent dimensions, the relative strengths of each dimension is an important consideration—a stronger dimension plays a bigger role in determining the rsc distribution. Finally, we consider the relationship between dimensionality itself and rsc. We will discover below that increasing dimensionality tends to decrease the magnitude of rsc values.
First, consider the case of two latent dimensions. Again, let n be the number of neurons, let w be the co-fluctuation pattern (i.e., loading vector ) with eigenvalue , let v be another pattern orthogonal to w , with eigenvalue , and let be a diagonal matrix specifying the independent variance of each neuron . Then the covariance is . On the off-diagonals entries (i.e., if ), . Along the diagonal, and .
Because the shared covariance matrix can be expressed as a sum of two component matrices , we can express the %sv of neuron as
where is the %sv variance of neuron i explained by dimension w and is the %sv variance of neuron i explained by dimension v.
With this decomposition of , and following similar steps as in Equation 8:
| (Equation 11) |
where %sv values are represented as proportions. Equation 11 relates rsc, %sv, and loading similarity for the case of two latent dimensions. Next, we compare these relationships for one versus two latent dimensions.
We will show that, for two latent dimensions, the relative strength of each dimension (i.e., the ratio : ) is an important consideration. For two latent dimensions, decreasing the overall %sv by decreasing both and equally (e.g., and both decrease equally) pushes each closer to 0; rsc mean and SD will decrease. This is similar to what happens for one latent dimension when %sv is decreased. On the other hand, even if the overall %sv is held constant, but increases relative to (i.e., increase the strength of w relative to v), pairwise correlations could change. Each will largely be determined by and mean and SD will be more similar to what they would be if only w existed (Figure 4A). In other words, each for two latent dimensions is the sum of the that would have been produced by each of the two constituent dimensions on their own. The dimension with larger relative strength will have larger ; the stronger dimension will play a larger role in determining each value of and thus the resulting rsc distribution.
Using this logic, we can deduce that increasing the loading similarity of one of the dimensions would increase rsc mean and decrease rsc SD for the same reasons as for one latent dimension (Math Note A). Doing so for a relatively stronger dimension would result in larger changes in rsc than doing so for a relatively weaker dimension.
We have shown how having multiple latent dimensions can affect the relationship between rsc, %sv, and loading similarity. Now, we show that dimensionality itself and rsc are related—a larger dimensionality tends to decrease rsc mean and SD. To see this, we can generalize Equation 11 for d < n orthogonal latent dimensions .
Considering the sign of one term, could have the same sign for across all dimensions ; in this case, a larger dimensionality acts to increase the correlation between neurons i and j above the level corresponding to a single dimension. However, because the loading vectors are orthogonal, a pair of neurons i and j is likely to have many of opposite sign across dimensions; in this case, a larger dimensionality pushes the correlation between neurons i and j closer to 0. Thus, we would expect the magnitude of correlations to decrease as more dimensions are added (i.e., a tendency for rsc mean and SD to decrease; Figure 3G). In the next section, we show this relationship mathematically.
D). Increasing dimensionality decreases arc radius
We establish here that increasing dimensionality results in a decrease in the radius of the arc in the rsc mean versus rsc SD plot (Figure 3G). We extend the math for an arc for one latent dimension (Math Note B) to multiple latent dimensions. We will refer to the one latent dimension as the ‘1-d case’ and multiple (k) latent dimensions as the ‘k-d case’.
We use the same notation as in Math Note C. Consider the distance c of a point (corresponding to one instance of the population activity covariance matrix) from the origin in the rsc mean versus rsc SD plot. From Math Note B, . For this 2-d case, the correlation between neurons i and j is . Thus we can write as:
where the % shared variance of neuron i in this 2-d case is .
Then letting m be the number of pairs in the population, and following similar steps to Equation 10 in Math Note B, we arrive at:
| (Equation 12) |
Not including the negative sign in front, note that this final term is non-negative (given that and are non-negative, as for any covariance matrix). Thus, comparing the final line in Equation 12 to the final line from Equation 10, we observe that the distance of the point for the 2-d case in the rsc mean versus rsc SD plot is necessarily smaller than or equal to the distance for the corresponding 1-d case.
More generally, for a k-dimensional case we can show that:
| (Equation 13) |
where the sum is taken over all unique pairs of loading vectors . Indeed, as more latent dimensions are subsequently added, the radius of the rsc mean versus rsc SD plot decreases (Figure 3G). Intuitively, this final term accounts for how population activity covaries along many different dimensions in the high-d firing rate space. As more orthogonal dimensions are added, population activity is further pulled in different directions in the high-d space, more interaction terms come into play, and the magnitude of correlations is further decreased. This tends to decrease both rsc mean and rsc SD, explaining why the radius of the arc in the rsc mean versus rsc SD plot tends to decrease as dimensionality increases.
We note that rsc mean and rsc SD do not necessarily both need to decrease. For example, consider a pattern with a loading similarity of 1; loading weights for all neurons would have the same value, rsc across all pairs would be the same value, and thus rsc SD would be 0 (see Math Note A). When a second pattern of necessarily low loading similarity (see Math Note E) is added, rsc values across pairs of neurons would differ, and rsc s.d. would be larger than 0. Therefore, rsc SD can increase when going from the 1-d case to the 2-d case. However, the corresponding decrease in rsc mean would be larger in magnitude than the increase in rsc SD, resulting in an overall decrease in arc radius (Figure 3G, 1 to 2 dimensions, data points closest to the horizontal axis).
The third term in Equation 13 can also help explain variability of the radius across different random instantiations with the same population metrics (Figures 3G and 4). Consider a fixed %sv. For the 1-d case, the radius is determined by the first two terms of the above equation, and any variability in radius will be caused by different values of across different instantiations. For the 2-d case, the third term also plays a factor in determining the radius, and this term varies across different random instantiations, typically to a larger degree than the second term for large numbers of neurons n (see Math Note B). Thus, the 2-d and k-d cases have greater variability in than 1-d cases (Figures 3G and 4). Other subtle factors can affect the variability of . For example, variability in can increase or decrease depending on the relative strengths of each dimension and their corresponding loading similarities (Figures 4 and S1). This can be explained by the third component of Equation 13, in particular by the terms involving and .
E). Properties of loading similarities across different co-fluctuation patterns
We asked whether there was a relationship between the loading similarities of different co-fluctuation patterns in the same model. In our simulations and V4 data analysis, we ensured that we obtain unique co-fluctuation patterns by constraining dimensions to be orthogonal. Thus, we might conjecture that if one pattern has high loading similarity (e.g., ), then another pattern in the same model necessarily has low loading similarity (e.g., ). Indeed, this is true because the sum across the loading similarities of each pattern in a model is at most 1. We show this property of loading similarity here.
Let w and v be vectors representing two co-fluctuation patterns in the same model. We use the notation to refer to the elementwise product between w and v, resulting in a vector that is the same size as w and v. Furthermore, we use , and as shorthand to refer to computations across the elements of a vector (and not as operations on a random variable): e.g , and . Also, in this section we refer to the loading similarity of vector w as for shorthand.
We first show a constraint on loading similarities for a model with two co-fluctuation patterns (i.e., loading vectors for each dimension). Let n be the number of neurons and let be two loading vectors. As in our simulations and data analysis (see Methods), w and v are orthogonal unit vectors: , , and . Then, using these constraints,
| (Equation 14) |
Because correlation is bounded between −1 and 1, we know that . It follows that:
| (Equation 15) |
The last step follows from the definition of loading similarity:
The final inequality in Equation 15 proves the intuition provided at the beginning of this section–if is large, then must be small (at most 1 − ). More strongly, if , then .
Generally, for a model with d dimensions and patterns , we can show that . To see this, we can construct a matrix C with entries for , and (derived from the constraints in Equation 14). Note that , with variances on the diagonal and covariances on off-diagonals, is a covariance matrix, which implies . For a 3-d model,
which implies . In general, for a d-dimensional model (with ):
| (Equation 16) |
Equation 16 has several implications:
If one knows the loading similarities of all dimensions in a model, then the maximum possible loading similarity of any new dimension is . It follows that two dimensions with high loading similarity cannot co-exist in the same model.
If one dimension has ls = 1, then all other dimensions in the model (or that would be added to the model) necessarily have Is = 0. Note that there is only one possibility for a pattern to have Is = 1 (i.e., , such that ). This implies that there are many possibilities for a pattern to have . More loosely, there are relatively few ways for a pattern to have high loading similarity, but many more ways for a pattern to have low loading similarity.
F). Maximum variance of a unit vector
We defined loading similarity for a co-fluctuation pattern u (normalized to have norm 1) of n neurons to be , where the variance is computed along the elements of u. This value lies between 0 and 1 because the maximum variance across the elements of u is . We now show this mathematically.
Let be a unit vector. Because u is a unit vector, . Using these facts
This holds with equality when (i.e., when the mean across the elements in a co-fluctuation pattern is 0). This implies that the smallest loading similarity is 0 (when ), and the largest loading similarity is 1 (when ).
Supplementary Material
Highlights.
Pairwise correlation and dimensionality reduction characterize how neurons covary
Pairwise and population metrics are closely related mathematically and empirically
Decrease in V4 pairwise correlation corresponds to multiple population-level changes
Multiple activity statistics should be used when describing population covariability
ACKNOWLEDGMENTS
The authors would like to thank Samantha Schmitt for help with data collection and Joȧo Semedo for helpful discussions. B.R.C. was supported by CV Starr Foundation Fellowship. A.C.S. was supported by NIH grant K99EY025768. M.A.S. and B.M.Y. were supported by NIH CRCNS R01 MH118929, NIH R01 EB026953, and NSF NCS BCS 1954107/1734916. M.A.S. was supported by NIH R01 EY022928, NIH R01 EY029250, and NIH P30 EY008098. B.M.Y. was supported by Simons Foundation 364994 and 543065, NIH R01 HD071686, NIH CRCNS R01 NS105318, and NSF NCS BCS 1533672.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.neuron.2021.06.028.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Abbott LF, and Dayan P. (1999). The effect of correlated variability on the accuracy of a population code. Neural Comput. 11, 91–101. [DOI] [PubMed] [Google Scholar]
- Adibi M, McDonald JS, Clifford CW, and Arabzadeh E. (2013). Adaptation improves neural coding efficiency despite increasing correlations in variability. J. Neurosci 33, 2108–2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahrens MB, Li JM, Orger MB, Robson DN, Schier AF, Engert F, and Portugues R. (2012). Brain-wide neuronal dynamics during motor adaptation in zebrafish. Nature 485, 471–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahrens MB, Orger MB, Robson DN, Li JM, and Keller PJ (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nat. Methods 10, 413–420. [DOI] [PubMed] [Google Scholar]
- Ames KC, and Churchland MM (2019). Motor cortex signals for each arm are mixed across hemispheres and neurons yet partitioned within the population response. eLife 8, e46159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athalye VR, Ganguly K, Costa RM, and Carmena JM (2017). Emergence of coordinated neural dynamics underlies neuroprosthetic learning and skillful control. Neuron 93, 955–970.e5. [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, and Pouget A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci 7, 358–366. [DOI] [PubMed] [Google Scholar]
- Bair W, Zohary E, and Newsome WT (2001). Correlated firing in macaque visual area MT: time scales and relationship to behavior. J. Neurosci 21, 1676–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolo R, Saunders RC, Mitz AR, and Averbeck BB (2020). Information-limiting correlations in large neural populations. J. Neurosci 40, 1668–1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittner SR, Williamson RC, Snyder AC, Litwin-Kumar A, Doiron B, Chase SM, Smith MA, and Yu BM (2017). Population activity structure of excitatory and inhibitory neurons. PLoS ONE 12, e0181773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bondy AG, Haefner RM, and Cumming BG (2018). Feedback determines the structure of correlated variability in primary visual cortex. Nat. Neurosci 21, 598–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buesing L, Machado TA, Cunningham JP, and Paninski L. (2014). Clustered factor analysis of multineuronal spike data. In NIPS’14: Proceedings of the 27th International Conference on Neural Information Processing Systems (MIT), pp. 3500–3508.
- Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen MR, Corrado GS, Newsome WT, Clark AM, Hosseini P, Scott BB, et al. (2010). Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci 13, 369–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, and Shenoy KV (2012). Neural population dynamics during reaching. Nature 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Kohn A. (2011). Measuring and interpreting neuronal correlations. Nat. Neurosci 14, 811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Maunsell JH (2009). Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci 12, 1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, and Maunsell JH (2010). A neuronal population measure of attention predicts behavioral performance on individual trials. J. Neurosci 30, 15241–15253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley BR, Smith MA, Kohn A, and Yu BM (2016). Stimulus-driven population activity patterns in macaque primary visual cortex. PLoS Comput. Biol 12, e1005185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley BR, Snyder AC, Acar K, Williamson RC, Yu BM, and Smith MA (2020). Slow drift of neural activity as a signature of impulsivity in macaque visual and prefrontal cortex. Neuron 108, 551–567.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham JP, and Yu BM (2014). Dimensionality reduction for large-scale neural recordings. Nat. Neurosci 17, 1500–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dechery JB, and MacLean JN (2018). Functional triplet motifs underlie accurate predictions of single-trial responses in populations of tuned and un-tuned V1 neurons. PLoS Comput. Biol 14, e1006153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, and Rubin DB (1977). Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 39, 1–22. [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, and Tolias AS (2010). Decorrelated neuronal firing in cortical microcircuits. Science 327, 584–587. [DOI] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Cotton RJ, Subramaniyan M, Denfield GH, Cadwell CR, Smirnakis SM, Bethge M, and Tolias AS (2014). State dependence of noise correlations in macaque primary visual cortex. Neuron 82, 235–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Denfield GH, Bethge M, and Tolias AS (2016). On the structure of neuronal population activity under fluctuations in attentional state. J. Neurosci 36, 1775–1789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erisken S, Vaiceliunaite A, Jurjut O, Fiorini M, Katzner S, and Busse L. (2014). Effects of locomotion extend throughout the mouse early visual system. Curr. Biol 24, 2899–2907. [DOI] [PubMed] [Google Scholar]
- Gallego JA, Perich MG, Miller LE, and Solla SA (2017). Neural manifolds for the control of movement. Neuron 94, 978–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallego JA, Perich MG, Naufel SN, Ethier C, Solla SA, and Miller LE (2018). Cortical population activity within a preserved neural manifold underlies multiple motor behaviors. Nat. Commun 9, 4233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao P, and Ganguli S. (2015). On simplicity and complexity in the brave new world of large-scale neuroscience. Curr. Opin. Neurobiol 32, 148–155. [DOI] [PubMed] [Google Scholar]
- Gregoriou GG, Rossi AF, Ungerleider LG, and Desimone R. (2014). Lesions of prefrontal cortex reduce attentional modulation of neuronal responses and synchrony in V4. Nat. Neurosci 17, 1003–1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Liu S, Fetsch CR, Yang Y, Fok S, Sunkara A, DeAngelis GC, and Angelaki DE (2011). Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron 71, 750–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider B, Duque A, Hasenstaub AR, and McCormick DA (2006). Neocortical network activity in vivo is generated through a dynamic balance of excitation and inhibition. J. Neurosci 26, 4535–4545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, and Thiele A. (2011). Cortical state and attention. Nat. Rev. Neurosci 12, 509–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennig JA, Golub MD, Lund PJ, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Yu BM, and Chase SM (2018). Constraints on neural redundancy. eLife 7, e36774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrero JL, Gieselmann MA, Sanayei M, and Thiele A. (2013). Attention-induced variance and noise correlation reduction in macaque V1 is mediated by NMDA receptors. Neuron 78, 729–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, and Lisberger SG (2009). Noise correlations in cortical area MT and their potential impact on trial-by-trial variation in the direction and speed of smooth-pursuit eye movements. J. Neurophysiol 101, 3012–3030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C, Ruff DA, Pyle R, Rosenbaum R, Cohen MR, and Doiron B. (2019). Circuit models of low-dimensional shared variability in cortical networks. Neuron 101, 337–348.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Insanally MN, Carcea I, Field RE, Rodgers CC, DePasquale B, Rajan K, DeWeese MR, Albanna BF, and Froemke RC (2019). Spike-timing-dependent ensemble encoding by non-classically responsive cortical neurons. eLife 8, e42409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeanne JM, Sharpee TO, and Gentner TQ (2013). Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron 78, 352–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X, Shen S, Cadwell CR, Berens P, Sinz F, Ecker AS, Patel S, and Tolias AS (2015). Principles of connectivity among morphologically defined cell types in adult neocortex. Science 350, aac9462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jun JJ, Steinmetz NA, Siegle JH, Denman DJ, Bauza M, Barbarits B, Lee AK, Anastassiou CA, Andrei A, Aydιn Ҫ, et al. (2017). Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2015). Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. eLife 4, e04677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RC, Smith MA, Samonds JM, Kohn A, Bonds AB, Movshon JA, and Lee TS (2007). Comparison of recordings from microelectrode arrays and single electrodes in the visual cortex. J. Neurosci 27, 261–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Cueva CJ, Reppas JB, and Newsome WT (2014). Dynamics of neural population responses in prefrontal cortex indicate changes of mind on single trials. Curr. Biol 24, 1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D, Brendel W, Constantinidis C, Feierstein CE, Kepecs A, Mainen ZF, Qi X-L, Romo R, Uchida N, and Machens CK (2016). Demixed principal component analysis of neural population data. eLife 5, e10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A, and Smith MA (2005). Stimulus dependence of neuronal correlation in primary visual cortex of the macaque. J. Neurosci 25, 3661–3673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn A, Coen-Cagli R, Kanitscheider I, and Pouget A. (2016). Correlations and neuronal population information. Annu. Rev. Neurosci 39, 237–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Port NL, Kruse W, and Georgopoulos AP (1998). Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J. Neurosci 18, 1161–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin I-C, Okun M, Carandini M, and Harris KD (2015). The nature of shared cortical variability. Neuron 87, 644–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S, Gu Y, DeAngelis GC, and Angelaki DE (2013). Choice-related activity and correlated noise in subcortical vestibular neurons. Nat. Neurosci 16, 89–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo TZ, and Maunsell JH (2015). Neuronal modulations in visual cortex are associated with only one of multiple components of attention. Neuron 86, 1182–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard EM, Hatsopoulos NG, Ojakangas CL, Acuna BD, Sanes JN, Normann RA, and Donoghue JP (1999). Neuronal interactions improve cortical population coding of movement direction. J. Neurosci 19, 8083–8093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazor O, and Laurent G. (2005). Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron 48, 661–673. [DOI] [PubMed] [Google Scholar]
- Mazzucato L, Fontanini A, and La Camera G. (2016). Stimuli reduce the dimensionality of cortical activity. Front. Syst. Neurosci 10, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minces V, Pinto L, Dan Y, and Chiba AA (2017). Cholinergic shaping of neural correlations. Proc. Natl. Acad. Sci. USA 114, 5725–5730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, and Reynolds JH (2009). Spatial attention de-correlates intrinsic activity fluctuations in macaque area V4. Neuron 63, 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura K, Mainen ZF, and Uchida N. (2012). Odor representations in olfactory cortex: distributed rate coding and decorrelated population activity. Neuron 74, 1087–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, and Pouget A. (2014). Information-limiting correlations. Nat. Neurosci 17, 1410–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevet A, Morris G, Saban G, Arkadir D, and Bergman H. (2007). Lack of spike-count and spike-time correlations in the substantia nigra reticulata despite overlap of neural responses. J. Neurophysiol 98, 2232–2243. [DOI] [PubMed] [Google Scholar]
- Ni AM, Ruff DA, Alberts JJ, Symmonds J, and Cohen MR (2018). Learning and attention reveal a general relationship between population activity and behavior. Science 359, 463–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nienborg H, Cohen MR, and Cumming BG (2012). Decision-related activity in sensory neurons: correlations among neurons and with behavior. Annu. Rev. Neurosci 35, 463–483. [DOI] [PubMed] [Google Scholar]
- Oemisch M, Westendorff S, Everling S, and Womelsdorf T. (2015). Interareal spike-train correlations of anterior cingulate and dorsal prefrontal cortex during attention shifts. J. Neurosci 35, 13076–13089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M, Steinmetz N, Cossell L, Iacaruso MF, Ko H, Barthó P, Moore T, Hofer SB, Mrsic-Flogel TD, Carandini M, and Harris KD (2015). Diverse coupling of neurons to populations in sensory cortex. Nature 521, 511–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang R, Lansdell BJ, and Fairhall AL (2016). Dimensionality reduction in neuroscience. Curr. Biol 26, R656–R660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perich MG, Gallego JA, and Miller LE (2018). A neural population mechanism for rapid learning. Neuron 100, 964–976.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponce-Alvarez A, Thiele A, Albright TD, Stoner GR, and Deco G. (2013). Stimulus-dependent variability and noise correlations in cortical MT neurons. Proc. Natl. Acad. Sci. USA 110, 13162–13167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pooresmaeili A, Poort J, and Roelfsema PR (2014). Simultaneous selection by object-based attention in visual and frontal cortex. Proc. Natl. Acad. Sci. USA 111, 6467–6472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi X-L, and Constantinidis C. (2012). Correlated discharges in the primate prefrontal cortex before and after working memory training. Eur. J. Neurosci 36, 3538–3548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinowitz NC, Goris RL, Cohen M, and Simoncelli EP (2015). Attention stabilizes the shared gain of V4 populations. eLife 4, e08998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanatesi S, Ocker GK, Buice MA, and Shea-Brown E. (2019). Dimensionality in recurrent spiking networks: global trends in activity and local origins in connectivity. PLoS Comput. Biol 15, e1006446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK, and Fusi S. (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romo R, Hernández A, Zainos A, and Salinas E. (2003). Correlated neuronal discharges that increase coding efficiency during perceptual discrimination. Neuron 38, 649–657. [DOI] [PubMed] [Google Scholar]
- Rosenbaum R, Smith MA, Kohn A, Rubin JE, and Doiron B. (2017). The spatial structure of correlated neuronal variability. Nat. Neurosci 20, 107–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2014a). Attention can either increase or decrease spike count correlations in visual cortex. Nat. Neurosci 17, 1591–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2014b). Global cognitive factors modulate correlated response variability between V4 neurons. J. Neurosci 34, 16408–16416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2016a). Attention increases spike count correlations between visual cortical areas. J. Neurosci 36, 7523–7534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2016b). Stimulus dependence of correlated variability across cortical areas. J. Neurosci 36, 7546–7556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2019a). Simultaneous multi-area recordings suggest that attention improves performance by reshaping stimulus representations. Nat. Neurosci 22, 1669–1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff DA, Xue C, Kramer LE, Baqai F, and Cohen MR (2020). Low rank mechanisms underlying flexible visual representations. Proc. Natl. Acad. Sci. USA 117, 29321–29329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumyantsev OI, Lecoq JA, Hernandez O, Zhang Y, Savall J, Chrapkiewicz R, Li J, Zeng H, Ganguli S, and Schnitzer MJ (2020). Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105. [DOI] [PubMed] [Google Scholar]
- Runyan CA, Piasini E, Panzeri S, and Harvey CD (2017). Distinct timescales of population coding across cortex. Nature 548, 92–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC, Yu BM, and Batista AP (2014). Neural constraints on learning. Nature 512, 423–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santhanam G, Yu BM, Gilja V, Ryu SI, Afshar A, Sahani M, and Shenoy KV (2009). Factor-analysis methods for higher-performance neural prostheses. J. Neurophysiol 102, 1315–1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semedo J, Zandvakili A, Kohn A, Machens CK, and Yu BM (2014). Extracting latent structure from multiple interacting neural populations. In NIPS’14: Proceedings of the 27th International Conference on Neural Information Processing Systems (MIT), pp. 2942–2950.
- Semedo JD, Zandvakili A, Machens CK, Yu BM, and Kohn A. (2019). Cortical areas interact through a communication subspace. Neuron 102, 249–259.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, and Newsome WT (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci 18, 3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpee TO, and Berkowitz JA (2019). Linking neural responses to behavior with information-preserving population vectors. Curr. Opin. Behav. Sci 29, 37–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, and Kohn A. (2008). Spatial and temporal scales of neuronal correlation in primary visual cortex. J. Neurosci 28, 12591–12603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, and Sommer MA (2013). Spatial and temporal scales of neuronal correlation in visual area V4. J. Neurosci 33, 5422–5432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Jia X, Zandvakili A, and Kohn A. (2013). Laminar dependence of neuronal correlations in visual cortex. J. Neurophysiol 109, 940–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Morais MJ, and Smith MA (2016). Dynamics of excitatory and inhibitory networks are differentially altered by selective attention. J. Neurophysiol 116, 1807–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AC, Yu BM, and Smith MA (2018). Distinct population codes for attention in the absence and presence of visual stimulation. Nat. Commun 9, 4382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohn H, Narain D, Meirhaeghe N, and Jazayeri M. (2019). Bayesian computation through cortical latent dynamics. Neuron 103, 934–947.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon SS, Chen SC, Morley JW, and Solomon SG (2015). Local and global correlations between neurons in the middle temporal area of primate visual cortex. Cereb. Cortex 25, 3182–3196. [DOI] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Carandini M, and Harris KD (2019a). High-dimensional geometry of population responses in visual cortex. Nature 571, 361–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019b). Spontaneous behaviors drive multidimensional, brain-wide activity. Science 364, 255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veuthey TL, Derosier K, Kondapavulur S, and Ganguly K. (2020). Single-trial cross-area neural population dynamics during long-term skill learning. Nat. Commun 11, 4057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyas S, Even-Chen N, Stavisky SD, Ryu SI, Nuyujukian P, and Shenoy KV (2018). Neural population dynamics underlying motor learning transfer. Neuron 97, 1177–1186.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wainwright MJ (2019). High-Dimensional Statistics: A Non-Asymptotic Viewpoint (Cambridge University; ). [Google Scholar]
- Williams AH, Kim TH, Wang F, Vyas S, Ryu SI, Shenoy KV, Schnitzer M, Kolda TG, and Ganguli S. (2018). Unsupervised discovery of demixed, low-dimensional neural dynamics across multiple timescales through tensor component analysis. Neuron 98, 1099–1115.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson RC, Cowley BR, Litwin-Kumar A, Doiron B, Kohn A, Smith MA, and Yu BM (2016). Scaling properties of dimensionality reduction for neural populations and network models. PLoS Comput. Biol 12, e1005141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, and Sahani M. (2009). Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol 102, 614–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandvakili A, and Kohn A. (2015). Coordinated neuronal activity enhances corticocortical communication. Neuron 87, 827–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, and Newsome WT (1994). Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370, 140–143. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table. Additional information or data are available upon request from the lead contact (byronyu@cmu.edu).
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental models: organisms/strains | ||
|
| ||
| Rhesus macaque (Macaca mulatta) | 1 animal from Covance, 1 from Tulane National Primate Research Center | N/A |
|
| ||
| Software and algorithms | ||
|
| ||
| MATLAB | MathWorks | RRID: SCR_001622; https://www.mathworks.com/products/matlab.html |
| Custom spike-sorting software | Kelly et al., 2007 | https://github.com/smithlabvision/spikesort |
| Code to reproduce simulations | Original code | https://zenodo.org/record/5028023 |
| Code to compute activity statistics | Original code | https://zenodo.org/record/5028018 |
|
| ||
| Other | ||
|
| ||
| 96-electrode array | Blackrock Microsystems | http://www.blackrockmicro.com/neuroscience-research-products/neural-data-acquisition-systems/ |
| Eyelink 1000 eye tracker | SR research | RRID: SCR_009602; https://www.sr-research.com/ |