Gating current noise produced by Brownian models of a voltage sensor

Abstract

The activation of voltage-dependent ion channels is associated with the movement of gating charges, which give rise to gating currents. Although gating currents from a single channel are too small to be detected, analysis of the fluctuations of macroscopic gating currents from a population of channels allows a good guess of their magnitude. The analysis of experimental gating current fluctuations, when interpreted in terms of a rate model of channel activation and assuming sufficiently high bandwidth, is in accordance with the presence of a main step along the activation pathway carrying a charge of 2.3–2.4 e₀. To give a physical interpretation to these results and to relate them to the known atomic structure of the voltage sensor domain, we used a Brownian model of voltage-dependent gating based on atomic detail structure, that follows the laws of electrodynamics. The model predicts gating currents and gating current fluctuations essentially similar to those experimentally observed. The detailed study of the model output, also performed by making several simplifications aimed at understanding the basic dependencies of the gating current fluctuations, suggests that in real channels the voltage sensor moves along a sequence of intermediate states separated by relatively low (<5 kT) energy barriers. As a consequence, crossings of successive gating charges through the gating pore become very frequent, and the corresponding current shots are often seen to overlap because of the relatively high filtering. Notably, this limited bandwidth effect is at the origin of the relatively high single-step charge experimentally detected.

Significance

In this work, computational models of voltage-dependent gating treating the voltage sensor as a Brownian particle are used to understand the significance of the gating current fluctuations that have been experimentally determined. The study suggests that the relatively high single-step charge experimentally determined from gating current fluctuations is produced by the relatively low energy barriers associated to the limited bandwidth at which recordings have been done. This occurrence is due to low energy barriers separating successive intermediate states of the voltage sensor position.

Introduction

The activation of voltage-dependent Na and K channels in response to a depolarization is a vital step in the action potential, the long-range signal of the nervous system and skeletal and cardiac muscle. This process produces a small but detectable component of current—the gating current—produced by the movement of protein charges, shown to be mostly associated with the voltage sensors for channels gating (1,2). Experimental techniques today amplify the gating current by increasing the cell membrane density of voltage sensors enormously.

Although transitions of individual voltage sensors do not generate experimentally detectable currents, even with the new experimental techniques, they do produce noticeable fluctuations in the macroscopic gating current (3,4). The analysis of the variance of these fluctuations allows estimates of the magnitude and time distribution of the elementary charge movements when reasonable assumptions about the underlying process are made, as done by (4) in Na channels and (3) in Shaker K channels. Both studies found that these fluctuations, assumed to originate from the individual movements of voltage sensors, produce a variance in measured current proportional to the mean current, a typical feature of shot noise (5, 6, 7, 8, 9).

Shot noise is expected from traditional discrete state rate models when the voltage sensor moves instantaneously from one stable position to the next along the activation pathway (5). The interpretation of the experimental data on gating current fluctuation with a sequential step rate model suggests the presence of a main step along the activation pathway carrying a charge of 2.3–2.4 e₀ (3,4). Notably, this conclusion is only valid under the assumption of sufficiently high energy barriers and recording bandwidth.

Later studies performed with a drift-diffusion model of the voltage sensor showed that a charge diffusing along an energy profile produces a shot noise only if the energy profile encountered by the voltage sensor during its activation includes a high energy barrier (6). It has long been known that a high energy barrier converts the drift-diffusion of the particle into a movement that, under some conditions, may be approximated by discrete state rate models, as formulated in the so-called Kramers’ approximation, and studied extensively by physical chemists and applied mathematicians (10, 11, 12). By contrast, the drift-diffusion model predicts a variance independent of the mean current when the energy profile does not include a high barrier (6).

Thus, a simple system of a charge moving along an energy profile (without a significant barrier) does not produce shot noise. But a structurally more complex system that approximates a voltage sensor might have different properties and different shot noise. Much structural and functional data show that during activation, gating charges move across two large vestibules separated by a short and highly hydrophobic gating pore impermeable to ions and water (13,14). Several studies show that the electric field is negligible in the large vestibules because of the high ion mobility there and because a significant voltage drop is only present inside the short hydrophobic gating pore (15, 16, 17). Although the gating charges on the voltage sensor are in the vestibules, their movements hardly produce any gating current. On the other hand, when the gating charge moves out of the vestibules and through the gating pore, gating current noise is produced with particular properties, as we will see in this study.

We recently proposed a computer model of the voltage-dependent gating of Shaker channels in which the voltage sensor is treated as a charged Brownian particle moving within a voltage sensor domain having geometrical and electrostatic properties taken from structural data. Notably, in this model the energy profile experienced by the voltage sensor during its movement is self-consistently evaluated using the laws of electrodynamics (18, 19, 20). The model was shown to produce macroscopic gating currents quite similar to those experimentally observed.

In this work, we investigated in depth the properties of the gating current fluctuations produced by the model, and the main parameters modulating them. To do this, we first constructed a simplified model of the voltage sensor domain that differs from our full model (18) and also from a realistic ion channel because it does not include the permanent charges present near the voltage sensor domain. The simplified model also has a voltage sensor that moves over an energy profile that we choose arbitrarily instead of being assessed self-consistently from all the charges present in the system. Although we are fully aware that this is a heavy simplification of the reality, this model allows us to connect with the existing biophysical literature and to investigate how the gating current fluctuations vary with conditions. With the knowledge acquired with the simplified model, we will then calculate and study the fluctuations of gating current using an unsimplified and self-consistent model of voltage gating.

Materials and methods

In this work, we deal with two different Brownian models of the voltage sensor, referred to as the “simplified” and the “full” model. In the full model, already presented in the original study (18) and slightly improved in (19), the geometry and charge distribution of the voltage sensor domain have been deduced from the structural atomic model of the Shaker K channel (21), and the voltage sensor dynamics are computed from the Langevin equation while self-consistently assessing the electrostatic potential that drives the voltage sensor dynamics. The potential is computed self-consistently from the Poisson equation, considering all the charges present in the model. The self-consistency is an important part of these models, as potentials change when charges move. If models were not self-consistent, the change in potential could not be included. The change in potential can have large effects in circumstances difficult to predict ahead of time. To construct the simplified model, we started from the full model, in which we made several simplifications in the geometry and charge distribution that would allow us to better understand the qualitative properties of the gating current fluctuations and compare them to the existing literature. Most importantly, in this model we were able to arbitrarily choose the energy profile driving the voltage sensor dynamics, a shortcoming that allowed us to simulate it under different energy profiles, essential to understanding several key concepts at the origin of gating current fluctuations. Although the main equations used in the two models are the same and have already been presented in the previous studies (18), we will present them again in the context of the simplified model so that the reader can have a deeper understanding of the simplifications performed, compared to the full model.

Structure of the voltage sensor domain

In our model, the voltage sensor domain (VSD) was approximated by an hourglass-shaped geometrical structure consisting of a water-inaccessible cylindrical gating pore having a length of 0.4 nm and a diameter of 1 nm, flanked by internal and external water-accessible vestibules having a length of 3.1 nm each, and a conical shape opening with a half angle of 15° into two hemispherical subdomains of bath solution, both having radii of 1 μm. Each vestibule had a total volume of 7.9 nm³, thus allowing the simultaneous presence of only few ions at physiological conditions. This geometry allows the formulation of the model in one spatial dimension, consisting of a main axis perpendicular to the membrane and passing through the gating pore. In the numerical simulation, the main axis was divided into subdomains of constant step size within the VSD, and a step size increasing geometrically going outwards in the two bath solutions. Using this subdivision, the surfaces separating adjacent subvolumes (or slabs) were circles inside the gating pore, spherical caps in the vestibules, and hemispheres in the baths, each one perpendicularly contacting the channel wall (Fig. 2 A). The S₄ segment does not occupy space in either vestibule, as it contributes to form the vestibule walls together with the other segments of the VSD (S₁–S₃), as seen in the available crystal structure. The crystal structure shows that the extracellular vestibule is formed by a departure of the S₃–S₄ segments from the S₁–S₂ (14). We included the charges on the S₄ segment as charge density in the volume grids of the model. The S₄ charge profile (Z_S4, expressed in e₀ units) was built by considering either one or four positive charges (depending on the simulation performed), each giving rise to a charge profile normally distributed with a standard deviation (SD) of 0.1 nm (in some cases, we varied the SD of the distribution). In our model, the S₄ segment was assumed to be a rigid body, and its position was represented by the variable x_S4, expressing the distance of its midpoint from the center of the gating pore. During the simulation, the voltage sensor was allowed to move through the gating pore and vestibules up to a maximal displacement x_S4 of ±1.8 nm by imposing fully reflective boundary conditions (i.e., if movement exceeds that displacement, the particle is reflected inside the boundary by an amount equal to the exceeded displacement). Although a traveling distance for the voltage sensor of 36 Å may seem too large, several points need to be considered. First, in our full model, this traveling distance allowed the movement of the voltage sensor by the distance separating R1 from K5 (28 Å), which was assessed by taking the charge-to-charge distance in the 3D structure of the VSD (18). Considering that this distance corresponds to the passage through the pore of the first four gating charges (R1–R4), those relevant to gating, the average distance each of them has to travel along the longitudinal axis to cross the gating pore is ∼7 Å, an amount in accordance with the available literature. Indeed, although the current consensus (22) indicated a maximal vertical motion of 10 Å, the simulations showed that the sensor moved along a path that was about 40° off the membrane normal, thus giving a motion along the main axis of the voltage sensor of 12.5 Å. We also need to consider the position of the voltage sensor at rest. It is now clear that there is more than one “resting” state, whose specific occupancies depend on the level of hyperpolarization, which is different in different studies. In this respect, the model of (22) took as “closed state” the one that is most populated at moderate negative voltage (the “penultimate resting state,” as it was called by (23)), as opposed to the resting state reported, for instance, by (24) and (25), with R1 in the catalytic center (which is reached only at high negative voltages), that we can call the “deep resting state.” This state has been also proposed by (21) for Shaker channels using a combination of modeling and experiment work and named C4, in which R1 lies below F290 and interacts with E293. The model proposed suggests an S₄ movement of at least 12 Å to pass from the active state, O, to the C3 state, whereas the deeper resting state C4 of the VSD could be reached with an S₄ movement of ∼17 Å (21). Now, even taking 17 Å as a reliable guess of the distance traveled by the voltage sensor for full VSD activation, our data are still significantly higher than this. The gap in our view derives in large part from the fact that in our model, the charge is glued on the S₄ segment instead of extending out by 6–7 Å (the arginine length), which decreases by about another 4–5 Å, considering that the first and last gating charges—R1 and R4—are thought to be tilted by 30–45° from S₄ normal and in the opposite way when bound to the catalytic center, containing in this way the voltage sensor movement. All this considered, the difference between our data and literature can be considered minor.

Figure 2.

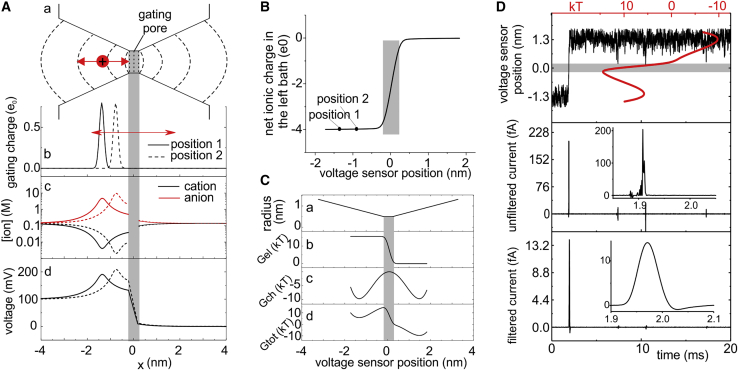
Properties and output of the simplified model. (A) (a) shows a sketch of the voltage sensor domain considered in the simplified model, with the gating pore and two adjacent vestibules. The dashed lines represent surfaces used to divide the space into subvolumes. (b)–(d) are plots of the position-dependent gating charge density, anion and cation concentrations, and electrostatic potential, assessed at 0 mV of applied potential. The concentration and electrostatic potential profiles are shown for two different positions of the voltage sensor (solid and dashed lines, respectively). Notice that at the ion concentrations reached, only a few ions will be present inside the vestibule at each time. (B) Plot of the ionic net charge in the left compartment (bath and vestibule) as a function of the position of the voltage sensor. The two positions labeled “1” and “2” correspond to the two positions of the voltage sensor considered in (A). (C) Electrostatic, chemical, and total (electrostatic + chemical) energy profiles experienced by the voltage sensor during its movement through the gating pore. As stated in the text, in The simplified model, we arbitrarily choose the energy profile experienced by the particle. This profile contains the overall energy charges experienced by the sensor, including the electrostatic voltage profile created by the voltage sensor and ions, and all other kinds of chemical and electrostatic interaction with the voltage sensor domain. (D) Trial simulation performed with our simplified model, using the energy profile shown in (Cd) and a friction coefficient of 2 × 10⁻⁶ kg/s. From top to bottom, the panel shows the position of the voltage sensor (i.e., of the gating charge) from the center of the gating pore, the unfiltered gating current produced by the movement of the voltage sensor, and the same gating current filtered with a digital, eight-pole Bessel filter with a cutoff frequency of 8 kHz. The red line in the top panel represents the energy profile encountered by the voltage sensor. It is superimposed on the time course of the voltage sensor position to show that the voltage sensor spends most of its time in the energy wells present in the two vestibules (we used the same graphic style used by (6) to make comparisons with earlier work easier). To see this figure in color, go online.

Ion electrodiffusion

We assumed that the intracellular and extracellular walls of the VSD are bathed by ionic solutions containing 140 mM of positively and negatively charged monovalent ions that can freely move in the baths and vestibules of the VSD but cannot enter the gating pore because of water and ion inaccessibility. Given the very small volume of the vestibules (∼7.9 nm³), a concentration of 140 mM there would correspond to a mean number of ions present inside close to one. The gating pore was assumed to have a relative dielectric constant (ε = 4) much lower than in the bathing solution (ε = 80); water and ions do not enter the gating pore. Ions were subjected to electrodiffusion governed by the following flux conservative equation:

$$\frac{d{C}_j\left(x,t\right)}{dt}=-\nabla F_j\left(x,t\right),$$ (1)

where C_j(x, t) is the concentration of ion j, t is the time, $\nabla$ is the spatial gradient operator, and F_j(x, t) is the flux (mole per second per unit area) of ion j, given by the Nernst-Planck equation

$$F_j\left(x,t\right)=-D_j\left(x\right)\left[\nabla C_j\left(x,t\right)+\frac{z_{j}F}{RT}\nabla V\left(x,t\right)\right],$$ (2)

where D_j(x) and z_j are the diffusion coefficient profile and the valence of ion j, respectively; F, R, and T have their usual meanings; and V(x, t) is the electrical voltage profile.

As also done in our previous model of voltage gating, we assumed steady state for the dynamics of the electrolyte ions:

$$\frac{d{C}_j}{dt}=0.$$ (3)

The validity of this approximation, which is based on the finding that ions relax on a timescale much faster than the movement of the S₄ segment, has been fully demonstrated in (18) and is a valid and necessary approximation in nearly all Langevin models (11).

The electrical voltage profile V(x) was assessed from the net charge density profile ρ(x), using the Poisson’s equation

$${\epsilon }_0\left[\frac{d}{dx}\left(\epsilon \left(x\right)\frac{dV\left(x\right)}{dx}\right)+\epsilon \left(x\right)\frac{dV\left(x\right)}{dx}\frac{d\mathit{ln}A\left(x\right)}{dx}\right]=-\rho \left(x\right),$$ (4)

where ε₀ = 8.854 × 10⁻¹² F ⋅ m⁻¹ is the vacuum permittivity, ε(x) is the position-dependent dielectric coefficient, V(x) is the electric potential, and A(x) is the position-dependent surface. The charge density profile was generated from the gating charges and the ions in solution:

$$\rho \left(x\right)=\frac{e_0{z}_{s4}\left(x\right)}{A\left(x\right)dx}+F{\sum }_j{z}_j{C}_j\left(x\right).$$ (5)

Equations 1 and 4 were iteratively solved until finding a steady-state solution for each allowed position of the voltage sensor, and the resulting ion concentration profiles were stored for the assessment of the gating currents (see later). The iteration made the treatment self-consistent, and always converged in our experience. In the Supporting materials and methods, we report details of the numerical solution of Eqs. 1 and 4.

Movement of the S₄ segment

In our model, whereas ions were described by their concentration profiles (i.e., their mean number densities) (see above), the voltage sensor was treated explicitly as a moving particle occupying a well-defined position. More specifically, the S₄ segment was assumed to move in one dimension as a charged Brownian particle, with dynamics governed by the following Langevin’s equation:

$$m{x}_{S4}^{··}\left(t\right)=F_{ex}\left(x_{S4},t\right)-\gamma x_{S4}^{·}\left(t\right)+R\left(t\right).$$ (6)

Here, x_S4(t) represents the position of the voltage sensor, m is the mass of the particle, F_ex(x_S4, t) is the external force acting on the particle, and R(t) is a random force due to the collision of the fluid and the rest of the protein on the S₄ segment, which has a probability distribution with zero mean and second moment given by

$$⟨R\left(t\right)R\left(t^{\prime }\right)⟩=2k_{B}T\gamma \delta \left(t-t^{\prime }\right),$$ (7)

where k_B is the Boltzmann constant, T is absolute temperature, and δ is the delta function. γ, the friction coefficient of the S₄ voltage sensor, was chosen to give, under the various conditions tested, gating current kinetics in reasonable agreement with the experimental data. More specifically, the approach we used to set this parameter was to change it until the time course of the output gating currents was similar to that observed experimentally. For instance, when we varied the energy profile experienced by the particle, the time course of the gating currents varied accordingly (it was very sensitive to the height of the barrier). Thus, we had to change γ to obtain gating currents with time courses similar to those observed experimentally.

In our gating model, the friction experienced by the moving voltage sensor, γ, was assumed to be the same everywhere (and at any time, i.e., to be position and time independent). We considered this simplification reasonable even though the friction for the S₄ segment is certainly very different inside the hydrophobic plug as compared to the solution. The reason for this assumption is that a portion of the S₄ segment of essentially constant length is always inside the hydrophobic plug, and this part is arguably the one that mostly contributes to the overall friction of the moving sensor (as compared to the portions moving in the solutions outside the hydrophobic plug). We believe that this is true regardless of the specific residues on the S₄ segment that are in the hydrophobic plug at different times during activation.

In the very high friction limit, the inertial term $m\left({\partial }^2{x}_{S4}/\partial t^2\right)$ in Eq. 7 is much smaller than the friction term $\gamma \stackrel{.}{x_{S4}^{·}\left(t\right)}$, and thus we arrive at the following stochastic differential equation (11,26, 27, 28):

$$x_{S4}^{·}\left(t\right)=F_{ex}\left(x_{S4}\right)/\gamma +r\left(t\right),$$ (8)

where r(t) is a random Gaussian term with zero mean and second moment <R(t)R(t′)> = $2k_{B}T/\gamma$ δ(t − t′). Equation 8 may be written in the form of the following stochastic differential equation, discretized with a Euler scheme (29):

$$\Delta x_{S4}\left(t\right)=\left(\raisebox{1ex}{$F_{ex}\left(x_{S4}\right)$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.\right)\Delta t+\sqrt{\frac{2k_{B}T\Delta t}{\gamma }}\phi \left(t\right),$$ (9)

where φ(t) represents a normally distributed random variable with zero mean and unitary variance. Based on Eq. 9, the position of the particle may be found at each time step Δt as x_S4 = $x_{S4}^{old}$ + Δx_S4, where $x_{S4}^{old}$ represents the initial position of the particle. The particle, as already stated, was allowed to freely move in the range x_S4 = ± 1.8 nm by imposing elastic boundary conditions. More specifically, we applied a totally reflecting boundary condition using the following algorithm: if, at a certain time step, the particle reaches a position x₁ > 1.8 nm, its new position is set to 1.8 − (x₁ − 1.8), that is, the particle is redirected inside the allowed spatial range by an amount exactly equal to the excess displacement. Similarly, if the particle in a certain time step reaches the position x₂ < −1.8 nm, then the new position of the particle will be −1.8 + (−1.8 − x₂).

In our model, the external force acting on the S₄ segment, F_ex(x_S4), is assessed as the negative gradient of the energy profile experienced by the voltage sensor, G_tot(x_S4), which was arbitrarily chosen and varied during the study:

$$F_{ex}\left(x_{S4},t\right)=-\frac{d{G}_{tot}\left(x_{S4}\right)}{d{x}_{S4}}.$$ (10)

In our simulations of a single S₄ segment, Eq. 9 was solved using a Euler scheme, with a time step of 1 μs and using a normally distributed random number generator from (30). We verified that the variance-mean current plot, resulting from thousands of simulations, as well as the properties of the microscopic current, did not vary when further reducing the time step.

Assessment of gating current

As our main goal was to compare the output of the model with the experimental results, we computed the gating current exactly as it is normally done in experiments, that is, by assessing the ionic current measured at the intracellular and extracellular electrodes positioned far from the voltage sensor domain (I_gL and I_gR, respectively). More specifically, the gating current was assessed by analyzing the net charge changes (with time) in the left (or alternatively, in the right) bath, on the assumption that ions cannot pass through the gating pore, and by applying charge conservation equations (31):

$$\begin{array}{l}{I}_{gL}\left(x,t\right)=\frac{d}{dt}{\int }_0^{x_{pl}}A\left(x\right)F\left({\sum }_{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)dx\hfill \\ I_{gR}\left(x,t\right)=\frac{d}{dt}{\int }_{x_{pr}}^{L}A\left(x\right)F\left({\sum }_{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)dx\hfill \end{array},$$ (11)

where x_pl and x_pr are the left and right edges of the gating pore, F is the Faraday constant, and z_j and c_j(x, t) are the valence and the concentration of ion j. We verified in every situation that identical results were obtained for I_gL and I_gR.

Maxwell’s equations guarantee that the total current in a series system is equal everywhere, at any time, no matter what the microphysics of conduction (32, 33, 34). The total current is the [flow of ionic charge] + [the flow of gating charge] + [the displacement current], which is usually over approximated as ε₀ε_r ∂E/∂t. We thus checked our model for the spatial conservation of current in the calculation of the microscopic gating current. As shown in Fig. S1, the model respects the spatial conservation of the total current throughout the entire domain, suggesting that the lack of a self-consistent treatment of the potential barrier is not injecting significant current into the system, as it might.

Filtering of the current

The microscopic gating current is very noisy because of the high-frequency thermal (Brownian) movements of the voltage sensor. The noise obscured individual shot current events and required the application of a digital filter. Because one of our goals was to compare our observation with experimental results, we usually used a digital low-pass filter reproducing the effect of an eight-pole Bessel filter with a cutoff frequency of 8 kHz, which is the same condition used in the experimental determination of the gating current fluctuations from Shaker K channels (3). The C code for this filter was from https://github.com/university-of-york/cs-www-users-fisher. Because our digital filter, like any Bessel filter, produces a characteristic ringing, in the detailed analysis of shot currents (Fig. 5) we used a well-behaved Gaussian digital filter, which in addition allows the use of analytical expressions for its output (35). In the implementation of the Gaussian filter, the output of each data point in the time course was

$$y\left(i\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{\sum }_{j=-n}^n{x}_{i+j}{e}^{-\frac{j^2}{2{\sigma }^2}},$$ (12)

where σ = 0.1325/f_c, f_c is the cutoff frequency expressed in units of the sampling rate x_i+j of the unfiltered point at the (i+j) -th position, and n was set to 70 to cover all the Gaussian coefficients significantly higher than zero.

Figure 5.

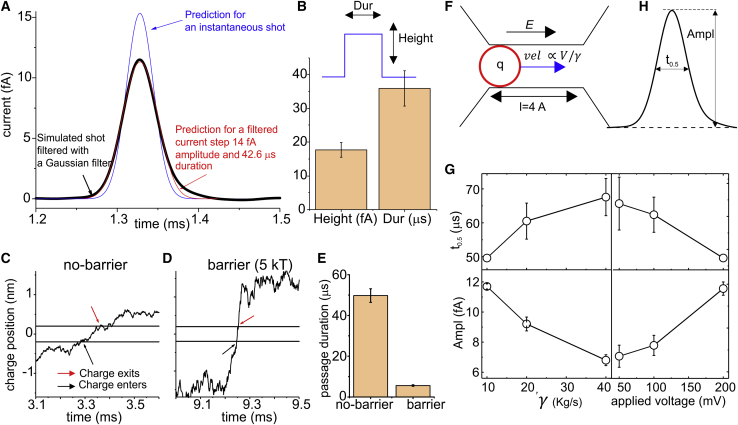
Analysis of the shot current observed in absence of energy barrier. (A) The plot shows a typical shot current observed under no-barrier conditions (black line), filtered with a Gaussian filter with B = 8 kHz. The blue line represents the response predicted for an instantaneous shot of charge filtered by a Gaussian filter, namely i(t) = q h(t), where q is the gating charge and h(t) is the Gaussian response function, reported in the Appendix of the Supporting materials and methods. The red line is a fit of a squared shot current of duration Dur = 42.6 μs and amplitude Height = 14 fA with the following equation for Gaussian filtered current steps from (35): i(t) = $\left(Height/2\right)\left[erf\left(\sqrt{2/ln2}\pi Bt\right)-erf\left(\sqrt{2/ln2}\pi B\left(t-Dur\right)\right)\right]$. (B) Plot of the mean height and Dur parameters obtained by fitting 10 shot currents as shown in (A), with the equation for a filtered current step. (C) Time-dependent position of the voltage sensor obtained from a simulation with the simplified model, with 100 mV of applied potential and no energy barrier. The black and red arrows indicate the time of entrance and exit of the voltage sensor into (from) the gating pore. (D) Same plot as in (C), except for the 5 kT energy barrier (same condition as in Fig. 2A). (E) Plot showing the mean time taken by the voltage sensor to pass across the gating pore in the no-barrier and 5 kT barrier cases. (F) Proposed physical mechanism of the generation of a shot current in our simplified model with an applied voltage and with no energy barrier. Because of the presence of an electric field inside the gating pore, the gating charge is subjected to an electric force, thus generating a current. This current is predicted to be directly proportional to the applied voltage and inversely proportional to the friction coefficient experienced by the voltage sensor during its movement. (H) Illustration of a shot current and the parameters used to quantify it, namely the amplitude (Ampl) and duration at half amplitude (t_0.5). (G) Plot showing the parameters Ampl and t_0.5 of shot currents, defined in (H), as a function of the friction coefficient and of the applied potential. To see this figure in color, go online.

Overall algorithm for the simplified model

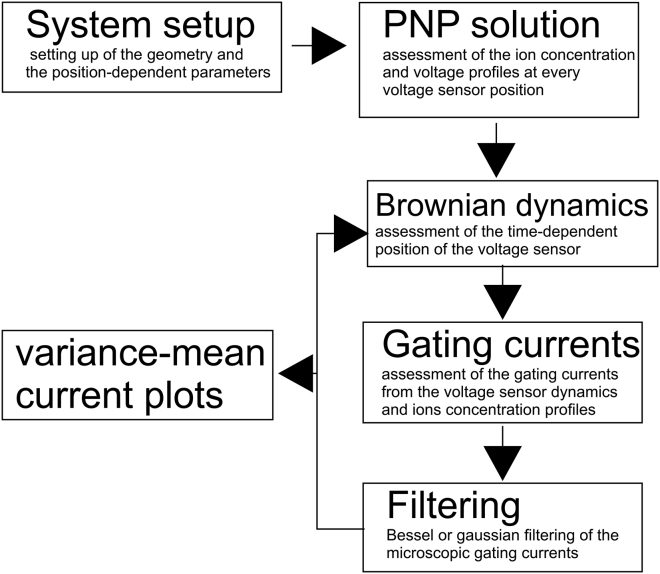
In this section, we report the overall algorithm used for the assessment of the time course of a microscopic gating current and of the variance versus mean current plots (Fig. 1). At the beginning of the computation, the spatial profile of all the geometrical parameters (center position, surface, and volume of the slabs over the whole spatial domain) as well as of the various position-dependent parameters (dielectric constant, diffusion coefficients, charge density carried by the voltage sensor) were set. At this stage, for the simplified model, we also set the energy profile experienced by the voltage sensor instead of being computed later from the solution of the PNP system, as in the case of the full model. We then proceeded with the solution of the PNP system (Eqs. 1, 2, 3, 4, and 5) for each possible position of the voltage sensor, using the numerical algorithm reported in the Supporting materials and methods. Namely, the voltage sensor was positioned within each allowed volume slab (those having a center position in the range of ±1.8 nm), and the ion concentrations and electric potential profiles at equilibrium were assessed and stored for later use. More specifically, the ion concentration profiles will be used for the assessment of the microscopic gating currents, whereas the electric potential profiles will be used in the full model to assess the energy profile experienced by the voltage sensor and driving its movement (18). Once the concentration and electric potential profiles for each possible position of the voltage sensor have been assessed, the time course of the voltage sensor position was assessed from Eqs. 8 and 9. More specifically, starting from an initial position, at each time step Δt the position of the voltage sensor (x_s4) is uploaded by x_s4(new) = x_s4(old) + Δx_s4, where Δx_s4 is assessed by Eq. 9 using a random number generator to obtain φ(t). During the computation of the time course of the voltage sensor position, we also assessed the microscopic gating current using Eq. 11 (to calculate the time derivative present in this equation, we used as information the overall ionic charge in the right (or left) bath at the current and previous time steps). At the end of the simulation, we filtered the gating current using either a Bessel or Gaussian filter as reported in Filtering of the current. The variance versus mean current plot was made by repeating the simulation of the voltage sensor dynamics (Eqs. 8 and 9) tens of thousands of times, and at each time step, we assessed the mean and variance of the signal. In this routine, there was no need to assess at each simulation the geometrical parameters or the voltage and concentration profiles associated to each voltage sensor position, as the conditions of the simulations were maintained constant.

Figure 1.

Scheme showing the various steps performed during the simulation of the microscopic gating currents and of the variance versus mean current plots. See text for details.

Results

The simplified model

The main properties of our simplified model, derived from the full model of Catacuzzeno and Franciolini (18), are shown in Fig. 2 A. The voltage sensor domain consists of a short, cylindrical gating pore with adjacent conical vestibules and bath domains. Ions and water can freely move in the baths and vestibules but cannot access and cross the gating pore. The four gating charges on the voltage sensor were initially concentrated in one single point, with a charge density normally distributed in space. They were allowed to move back and forth across the gating pore and part of the adjacent vestibules (red arrow in Fig. 2 A b), and this movement was modeled as a discretized Brownian stochastic process. Because of the very slow motion of the voltage sensor as compared to the ions in solution, we assumed that at each time step, anions and cations would instantaneously modify their concentration profiles to screen the gating charge (18). More specifically, the gating charge, together with the cations and anions in the baths, creates an electrostatic potential (Fig. 2 A d) that in turn rearranges the ion concentration profiles in the bath (Fig. 2 A c). Anions concentrate close to the gating charge (red lines), and cations deplete at the same location (black lines). When the gating charge moves, the ion concentration and the electric potential profiles will move accordingly, as shown by the two positions represented in Fig. 2, A b–d (continuous and dashed lines, respectively).

In our simplified model, the gating current recorded by the bath electrodes (located far from the gating pore) equals the charge (per unit time) that the electrodes need to put into the baths (for simplicity, from here on baths and vestibules on either side of the gating pore will be considered as a single environment and referred to as “bath”) or absorb from them to maintain electroneutrality. This means that a (gating) current is detected by the electrode only when the movement of the gating charge results in the addition or subtraction of charges into or from the baths. If, during the time step Δt, the net charge in one bath changes by ΔQ, this means that the movement of the gating charge has added to (or subtracted from) the bath and, as a result, to the electrode that same amount of charge, resulting in a recorded gating current of ΔQ/Δt. Fig. 2 B reports the net ion charge contained in the left bath as a function of the position of the voltage sensor. When the voltage sensor is in position 1, i.e., it is well inside the left bath, the net ionic charge there is −4 e₀ (to compensate for the +4 e₀ of the gating charge and keep electroneutrality in the bath). Slightly moving the voltage sensor to the right, for instance, from position 1 to position 2 in Fig. 2 A b, we see that the net ionic charge remains close to −4 e₀, as expected given that the position of the voltage sensor remains well inside the left bath. In other words, this movement does not generate any gating current because the gating charge has not entered the gating pore and thus has not subtracted charges from the left bath. Only when the voltage sensor enters inside the gating pore (gray region) is a sensible change in the net charge of the left bath detected, and this produces a gating current.

Finally, in our simplified models, the voltage sensor moves along an energy profile that we choose arbitrarily. Although we are aware that any physical model of voltage-dependent gating should self-consistently compute the energy profile, as we did in (18), this shortcut turned out to be decisive in helping us understand how the gating current depends on the shape of the energy profile and on many other parameters. Later, we will show results for which this approximation is removed. As shown in Fig. 2 C, the energy profiles experienced by the gating charge can be thought of as the sum of an electric component (G_el), produced by an imposed membrane potential entirely and linearly dropping within the gating pore (Fig. 2 C b), and a “chemical component” (G_ch) shaped as two wells and one barrier, with the energy barrier centered in the middle of the hydrophobic gating pore and the wells located in the baths, where the gating charges are balanced by countercharges (Fig. 2 C c). (Notice that the chemical component of the energy might also include the electrostatic interaction between the gating charges as countercharges present on the vestibules. Fig. 2 C d shows the overall energy profile experienced by the gating charge, resulting from the addition of the electric and chemical components. Given the symmetry of the chemical component in the simplified models and the resulting identical intracellular and extracellular energy minima, at zero applied potential the voltage sensor does not experience a net force in either direction, and thus, it is expected to spend equal time in the left and in the right vestibule.

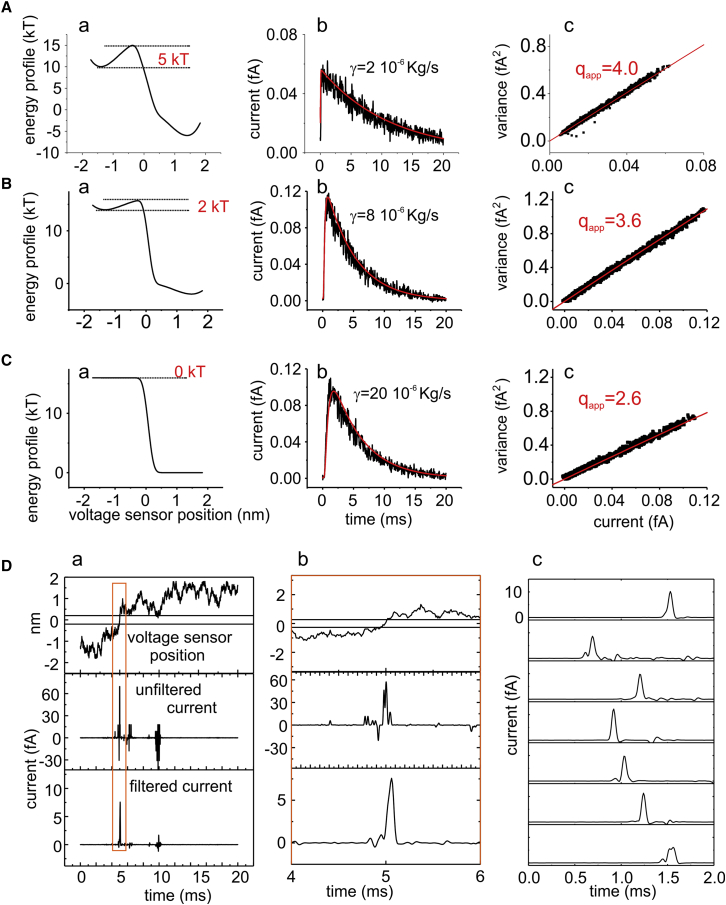
Fig. 2D shows a typical outcome of the simulation of a microscopic gating current, obtained with an energy profile that includes a high barrier (>5 kT) across the gating pore, in addition to a voltage drop of 100 mV (cf. Fig. 2 C). The top panel shows the position of the gating charge with respect to the gating pore as function of time. Superimposed, in red, the same plot also reports the total energy profile encountered by the voltage sensor (the same as in Fig. 2 C d). Because of the presence of a high barrier separating the two wells, the gating charge is virtually always in one well or the other, except for the few tens of microseconds during which the gating charge is crossing the gating pore (or the barrier). The central panel also shows that the fluctuating movement of the charge within the vestibules produces a negligible amount of current. By contrast, the passage of the gating charge across the gating pore causes a needle-like current (expanded on the time domain in the inset). The features of this current spike, which coincides with the gating charge crossing the gating pore, recall the shot current postulated to occur when the voltage sensor crosses the membrane (3,4). The bottom panel displays the same current trace after being filtered at 8 kHz with an eight-pole digital Bessel filter.

Constructing variance-mean current plots and recovering the apparent gating charge

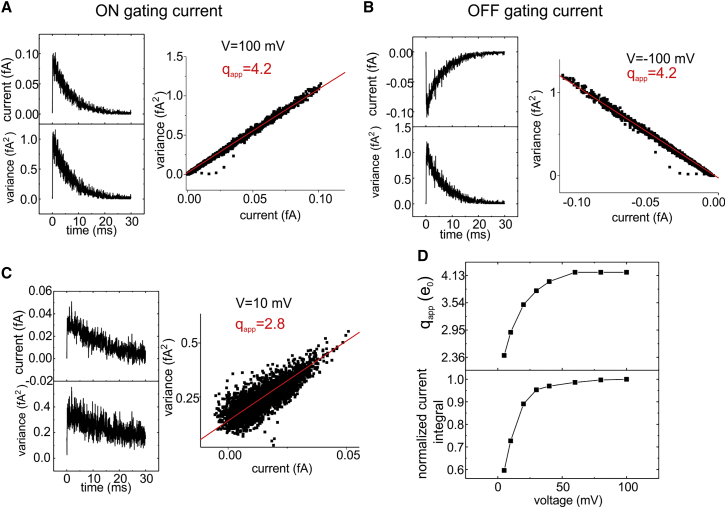
The variance-mean current plots have been classically used to estimate the gating charge that moves across the gating pore during channel activation or deactivation. The mean current and the corresponding variance with our simplified model were obtained from the ensemble of thousands of filtered microscopic gating currents and used to construct the variance-mean current plot (Fig. 3), which shows a clear linear dependence between the two variables. To be connected to the widely used literature, the data were fitted using the following equation, valid for a two-state rate model, at applied potentials at which the activation process becomes essentially irreversible:

$${\sigma }^2\left(t\right)=2B{q}_{app}⟨i\left(t\right)⟩-{⟨i\left(t\right)⟩}^2,$$ (13)

where B is the effective bandwidth of the filter, q_app is the apparent gating charge (we call this charge apparent because, as we will see, it does not always assume the value corresponding to the effective gating charge moving through the gating pore), σ²(t) is the variance, and $⟨i\left(t\right)⟩$ is the mean current. In the case considered in Fig. 3, A and B, i.e., ON or OFF gating currents obtained in the presence of a relatively high energy barrier and at a potential at which the process can be considered essentially irreversible, the fit gave an apparent gating charge q_app for both the ON and the OFF gating currents of 4.2 e₀, a value close to the amount of gating charge considered in the model. We verified that the small overestimate of the gating charge originates from the ringing property of the Bessel filter we used, and could be mostly eliminated using a Gaussian filter. By contrast, at lower voltages that activate the voltage sensor only partially (consider that the activation V_1/2 in the model is 0 mV), the resulting q_app was sensibly lower (Fig. 3 C), in accordance with the limit that Eq. 13 holds only for irreversible processes.

Figure 3.

Simulations of variance versus mean current plots with the simplified model. (A–C) The left panels show the time course of the mean (top) and variance (bottom) assessed from 10,000 simulated microscopic gating currents, and the right panels represent in black symbols the variance versus mean current plot obtained from the same data. The red lines represent the fit of the data with Eq. 13, to which a constant, current-independent variance was added (6), giving the reported q_app. (A) and (C) were obtained with the voltage sensor initially placed at the intracellular well (−1.67 nm), and stepping the applied voltage to either +100 or +10 mV. They thus represent ON gating currents produced by the forward movement of the voltage sensor. By contrast, in (B) the voltage sensor started from the extracellular well (+1.67 nm), and the applied voltage was maintained at −100 mV (OFF gating currents). (D) Plot shows q_app and normalized current integral (that is, a measure of the activation degree) as a function of the applied voltage. Whereas at high voltages that ensure an essentially irreversible activation, q_app results are close to the real charge carried by the voltage sensor, at lower voltages this parameter tends to be sensibly lower. All simulations shown in this figure were obtained with a barrier height of 10 kT (cf. Fig. 2C). To see this figure in color, go online.

Dependence of the fluctuation properties on the voltage sensor energy profile

We then repeated this type of analysis using an energy barrier of lower amplitude to verify whether in our model a q_app close to the actual gating charge is also obtained only in the presence of a high energy barrier. Since varying the barrier height also changes the time course of the gating currents, we changed the friction coefficient γ in the various simulations to keep the time course of gating currents approximately the same. A q_app close to 4 was still obtained upon reducing the barrier height to 5 kT (Fig. 4 A). However, as shown in Fig. 4 B, on further reducing the barrier height while keeping the same voltage drop, the slope of the variance-mean current plot decreased (to give q_app = 3.6 e₀ for a barrier height of 2 kT), as expected for the particle dynamics being not well described by a state rate model. Notably, a significant slope of the variance-mean current plot (with a q_app = 2.6 e₀) remained even after the energy barrier within the gating pore had been set to zero (Fig. 4 C), suggesting that a shot current is present even in the absence of well-defined discrete states for the voltage sensor. This conclusion seems to be supported by the simulations reported in Fig. 4 D, in which the microscopic gating current is shown for a model not including an energy barrier. Fig. 4, D a and b show that although the gating charge roams in the bath where no voltage gradient is present, no gating current is generated (see lower panels). A clear and significant current flickering is instead observed as soon as the gating charge enters and swiftly and unidirectionally traverses the gating pore, under the drive of the voltage gradient present. This rapid crossing of the gating pore produces a current resembling the shot observed in presence of an energy barrier, as clearly shown at the bottom of Fig. 4 D b. Fig. 4 D c reports representative traces showing the microscopic gating currents and shot events generated as the gating charge crosses the gating pore in seven different trials.

Figure 4.

Presence of a shot noise in the absence of an energy barrier. (A–C) Assessment of the variance-mean current plot for models including a double-well energy profile characterized by different barrier heights, with the simplified model. (A) (a), (B) (a), and (C) (a) report the energy profiles encountered by the gating charge during its movement across the gating pore. (A) (b), (B) (b), and (C) (b) report the mean current resulting from 10,000 simulations of the microscopic current. Each simulated current was filtered with an eight-pole Bessel filter with a cutoff frequency of 8 kHz. (A) (c), (B) (c), and (C) (c) show the variance-mean current plots. The red lines are the best fits of the raw data with Eq. 1, resulting from a one-step Markov model. (D) Typical outcome of simulations in the absence of an energy barrier (cf. C a). (a) shows the gating charge position (top), unfiltered current (middle), and filtered microscopic gating current (eight-pole Bessel, f_c = 8 kHz; bottom) for a typical simulation. (b) reports a time expansion of the same simulation shown in (a). (c) reports the filtered microscopic currents obtained in seven different simulations performed under the same conditions as (a) and (b). To see this figure in color, go online.

As a first attempt to analyze in detail the shape of the shot events in the absence of an energy barrier, using the simplified model, we tried to increase the cutoff frequency of the filter. As shown in Fig. S2, both the amplitude and duration of the unitary events (shots) were strongly influenced by the filter cutoff frequency included in our model, suggesting a very fast underlying signal that has been significantly smoothed by our low-pass filter. However, the increase in the filter cutoff frequency also resulted in the appearance of a high-amplitude noise due to the currents generated from the high-frequency Brownian motion of the gating charge, which obscured the shot current. We thus tried to deduce the shape of the signal underlying the filtered shot by taking into account the effect of the filter. For the purpose of this analysis, we filtered the microscopic current with a Gaussian filter (f_c = 8 kHz), as it is better behaved and avoids most of the ringing usually observed with Bessel and other filters available for analog signals. As shown in Fig. 5 A, the filtered signal (black line) deviates significantly from the prediction of an instantaneous shot of charge filtered with a Gaussian filter (blue line), suggesting that the assumption made in rate models of an instantaneous movement of the gating charge across the gating pore is not appropriate, as expected for a model including no barrier in its energy profile. We also found that the shots could be well fit by an equation predicting the observed time course of a filtered current step (Fig. 5 A, red line) (35), resulting in a mean amplitude and duration of the underlying current step of 17.6 ± 2.1 fA and 35.9 ± 5.3 μs, respectively (Fig. 5 B). We also observed that under the no-barrier condition, the voltage sensor required a relatively long time to cross the gating pore, as measured by directly looking at the time course of the position of the voltage sensor (Fig. 5, C and E). This time was, however, much shorter in the model with a high energy barrier (Fig. 5, D and E; same energy profile as Fig. 4 A a). To put it crudely, the voltage sensor took much longer to diffuse across the gating pore than to jump across a barrier.

The drawing in Fig. 5 F sketches a possible physical mechanism for the shots observed in absence of an energy barrier. As shown earlier, the gating charge will generate a current only when it enters and moves inside the gating pore, where it senses the electric field. Here, it will experience an electrical force given by F = qV/l, where q is the gating charge, V the applied voltage, and l the length of the gating pore. This force will remain constant for the entire length of the gating pore, and will drive the particle toward the right vestibule at a constant drift velocity vel = F/γ = qV/(l γ). The mean time taken to cross the gating pore will be given by $\overline{t}$ = (l − a)/vel = l(l − a), where the parameter a takes into account the fact that in our model the charge is not a point charge, thus it needs to be a good way inside the gating pore to experience most of the electric field (similar reasoning holds when the charge exits from the right boundary of the gating pore). Notably, as the charge moves inside the gating pore at a constant drift velocity, for the averaged time $\overline{t}$ it will produce a constant current i = q/$\overline{t}$ = q²V/[l(l − a)γ]. Using parameters V = 100 mV, l = 4 Å, q = 4e₀, γ = 20∗10⁻⁶ kg/s, and a = 0.5 Å, we obtain $\overline{t}$ = 35 μs and i = 18.2 fA, values reasonably in accordance with those obtained from fitting the signal to a filtered current step (Fig. 5 B). This simple treatment shows that duration and amplitude of shot currents observed in absence of an energy barrier should depend on V and γ, as the analysis of the unitary events confirmed (Fig. 5 G).

We also looked for V- and γ-dependent shot noise by performing noise analysis. As shown in the Fig. S3, we did find a marked dependence of noise fluctuations on both parameters (in the absence of energy barriers), as assessed from the slope of the variance-mean current plot. Under these conditions, the slope of the variance-mean current plot displayed a clear dependence on the friction coefficient (with a four-fold change in γ resulting in a two-fold change in the slope) and on voltage (increasing ∼50% on doubling the voltage step). By contrast, no dependence on both parameters was found in presence of a high energy barrier, as expected from Eq. 13.

Analysis of the fluctuation properties with distributed charges on the voltage sensor

It is now well established that the first four arginines, positioned every third residue on the S₄ segment, are the main carriers of the gating charge. These residues are separated by an α-carbon distance of 4.5–6.0 Å, depending on the assumed secondary structure for the S₄ segment (α-helix or 3₁₀ helix). We thus verified the consequences of a more realistic situation, with four unitary gating charges evenly distributed along the voltage sensor, each spread according to a Gaussian distribution with an SD of 1 Å.

Dependence of the fluctuations on the intercharge distance and energy barrier height

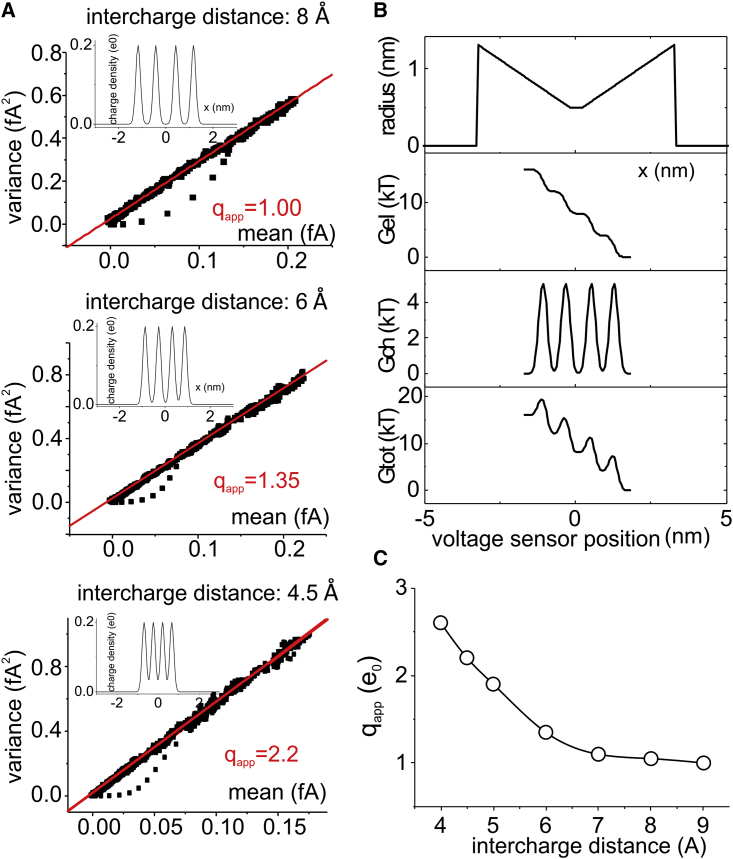
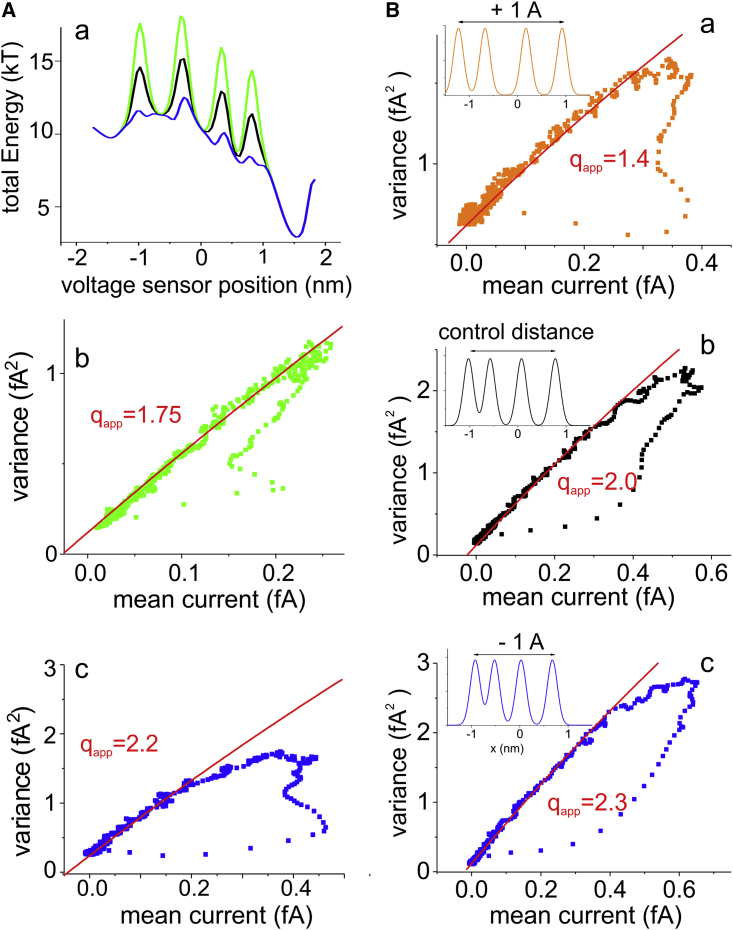
As before, we assumed a linear voltage drop within the gating pore, resulting in an electric component of the energy profile with a staircase shape (Fig. 6 B). Four energy barriers were then added in correspondence of the four electric energy drops and thus associated with the passage of each unitary charge through the gating pore (Fig. 6 B). This was done by making the chemical energy component proportional to the gradient of the electric energy component, thus ensuring that an increase in G_ch was always associated to the entry of charge inside the gating pore. Fig. 6 A shows three different simulations, all performed with the same electric and chemical energy components but using three different intercharge distances, ranging from 4.5 to 8 Å. For a distance of 8 Å, the simulations resulted in a q_app of 1 e₀. This result agrees with a four-step rate model process, with each gating charge going through the gating pore as a separate step. It has indeed been shown that under the assumption of a filter frequency sufficiently high to allow the temporal discrimination of the individual shot currents originating from the four different steps (high bandwidth conditions), Eq. 13 may be applied also to a multistep process, with q_app assuming a value not larger than the largest transition charge, which in the four-step rate model would be equal to 1 e₀ (3).

Figure 6.

Gating current fluctuations with multiple gating charges on the voltage sensor. (A) Variance-mean current plots obtained in simulations performed with the simplified model, with four gating charges on the voltage sensor (charge density was normally distributed with an SD of 1 Å). The three plots correspond to different intercharge distances (indicated). The insets in each plot show the corresponding gating charge distribution. (B) Plots of the radius, electrical, chemical, and total energy profiles for the simulation shown in (A), with an intercharge distance of 8 Å. (C) Plot of the apparent charge estimated from simulations performed at different intercharge distances. To see this figure in color, go online.

However, as the intercharge distance gets smaller and more similar to a realistic distance between charges located on an α-helix, q_app increases, deviating significantly from 1 e₀. In Fig. 6 C, we report the results of simulations performed at various intercharge distances, showing that q_app as high as 2.5 may be reached at intercharge distances not far from those at which gating charges are in an α-helix.

The increase in the apparent charge for low intercharge distances might be caused by the fact that when the charges get closer, the charge density distributions of two consecutive charges may partially be found simultaneously inside the gating pore. As expected on the basis of this interpretation, the q_app was found to be related to the spreading of the gating charge distribution. Increasing σ, the SD of the Gaussian charge distribution, results in an increase in q_app while decreasing σ, and thus, decreasing the charge overlap results in a decrease in q_app (see Fig. S4).

Features of elementary shot events produced by distributed charges

We also studied in detail the shot events produced by models having two different intercharge distances (8 and 4.5 Å) to find a mechanistic interpretation for the increased slope of the variance-mean current plot at shorter intercharge distances. (In this study, we used relatively high energy barriers of ∼4.6 kT; see Fig. 9 C.) Fig. 7, A and E show the chemical energy profiles associated with the passage through the gating pore of the voltage sensor with intercharge distances of 8 and 4.5 Å. In the first case (8 Å), the energy barriers to be crossed are well separated from one another, giving relatively low interbarrier energy minima. On the contrary, for an intercharge distance of 4.5 Å, we observe a marked superimposition of the single energy barriers, with the result of considerably shallower energy minima.

Figure 9.

Gating current fluctuations in the full model. (A) Plots of the mean current and variance assessed from 10,000 simulated microscopic gating currents obtained in response to a depolarizing step to 0 mV (initial position of the voltage sensor −1.67 nm). Each simulated microscopic current was filtered with an eight-pole Bessel filter with a cutoff frequency of 8 kHz. (B) Plot of variance versus mean current made with the data shown in (A). The solid line represents the fit of the data from the decaying part of the gating current with Eq. 13, with qapp = 2.0 e₀. (C) Total energy profile experienced by the voltage sensor during its movement, at an applied potential of 0 mV. Notice that this energy profile, differently from those arbitrarily chosen in the simplified model, is self-consistently assessed with the Poisson equation, considering the effect of all the charges present in the system. (D) Plot of the mean current and variance assessed from 10,000 simulated microscopic gating currents obtained in response to a depolarizing step to −40 mV (initial position of the voltage sensor −1.67 nm). (E) Apparent charge obtained at various applied potentials. (F) Plot of variance versus mean current made from data obtained with a repolarization to −140 mV (from an initial position of the voltage sensor of +1.56 nm). The solid line represents the fit of the data from the decaying part of the gating current with Eq. 13, with qapp = 1.35 e₀. To see this figure in color, go online.

Figure 7.

Evidence for multicharge steps at low intercharge distance. (A and E) Chemical energy profiles for the multicharge models with an intercharge distance of either 8 or 4.5 Å. (B and F) Filtered current responses for the two models, showing that although at a relatively high intercharge distance, multiple peaks are clearly visible in the response, at lower intercharge distance often the passage of the four gating charges occurs in only one step. (C and G) Running integrals for the responses shown in (B) and (F). (D and H) Histograms of the charge carried by the current peaks, accumulated from 20 (D) or 60 (H) responses as those shown in (B) and (F). It is evident that for large intercharge distances, most of the current peaks carry a single gating charge, whereas for lower intercharge distance, peaks carrying multiple gating charges are significantly represented. To see this figure in color, go online.

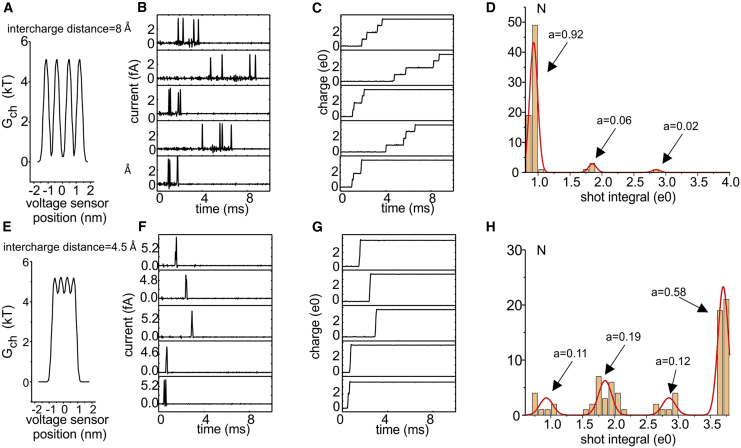
As shown in Fig. 7, A–C, at an intercharge distance of 8 Å, the passage of the voltage sensor through the gating pore most often (15 out of 20 simulations) produced four clearly distinct current peaks (see the four topmost responses in Fig. 7 B). In four simulations we found three peaks (see bottom response in Fig. 7 B) and in one we found only two peaks. As clearly shown in the running integral of the microscopic current (Fig. 7 C), in the four-peak responses each peak corresponds to the passage of about one unitary charge through the gating pore. In contrast, in the four responses with three peaks, we found that one of the peaks carried two unitary charges. In the simulation with two peaks, one peak carried one charge, and the other carried three charges (data not shown). These different responses are also evident in the charge amplitude histogram shown in Fig. 7 D, showing that most of the current peaks we detected under these conditions carry a charge of ∼1 e₀. These results show that with the gating charges positioned quite far from one another, the current shots produced by each charge crossing the gating pore are detected as well separated from each other, even at the moderate filter bandwidth of 8 kHz, presumably because the movement of the voltage sensor among adjacent intermediate states is relatively slow. It is thus not surprising that in this condition, the variance-mean current plot gives a q_app ∼1 e₀ (cf. Fig. 6 A, upper plot), as predicted by a rate model with a four-step sequential activation process that should represent the sequential passage of the four gating charges through the pore.

When the intercharge distance is reduced to 4.5 Å, the scenario emerging from the analysis of the shot events is radically different, with many of them appearing lumped together, giving bigger current shots (Fig. 7, E–H). This could be expected because of the strongly reduced well depth in the energy profile, which will greatly speed up the movement of the voltage sensor between adjacent intermediate states. In most of the simulations (40 out of 60), we see in fact only one current peak, corresponding to the passage of a charge of ∼4 e₀ through the gating pore in only one step. There were, however, several instances (20 out of 60) in which the voltage sensor moved in two steps, each carrying 1, 2, or 3 unitary charges (see one such outcome in the bottom trial in Fig. 7, F and G). This suggests that when the gating charges are relatively close, they can pass through the gating pore at very high rate, and their individual passages will not be resolved at the filter conditions used. In this case, it appears obvious that the variance-mean current plot will have a q_app higher than 1 e₀, as most of the shots (∼90% under these conditions; cf. Fig. 7 H) carry a charge higher than 1 e₀.

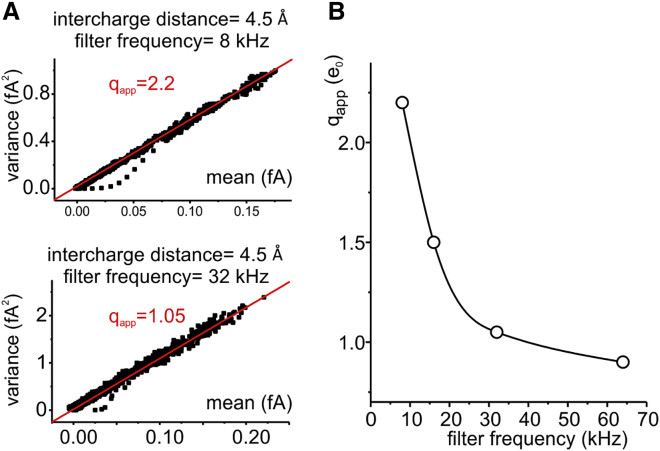
The results presented above suggest that a q_app higher than 1 e₀ reflects gating charges passing so rapidly through the gating pore that at the filter bandwidth used, it is not possible to discriminate all their individual passages. To confirm this view, we performed simulations of gating current fluctuations using an intercharge distance of 4.5 Å and varying filter frequencies, higher than 8 kHz, that would allow a better discrimination of the single-charge passages through the gating pore. As shown in Fig. 8, increasing the filter cutoff frequency results in a decrease of q_app to values more congruent with the theoretical expectations.

Figure 8.

Effect of filtering on the q_app in a multicharge model. (A) Simulated variance versus mean current relationships obtained for a model containing four gating charges at an intercharge distance of 4.5 Å and chemical energy barrier of 5 kT, using a Bessel filter at cutoff frequency of 8 kHz (top) or 32 kHz (bottom). (B) Relationship between q_app and the filter cutoff frequency, showing that higher filter frequency results in a smaller q_app. To see this figure in color, go online.

Conclusions from the simplified model

The results reported above suggest that caution should be used when interpreting the slope of the variance-mean current plot using the classic relationships of state rate models (i.e., slope = 2Bq_app, where q_app is the overall gating charge for a single-step process, or the charge carried by the highest charge-carrying single step for a multistep process). In fact:

• 1)The slope of the variance-mean current curve may be substantially lower than the value of 2Bq_app expected from state rate models because of the presence of not sufficiently high energy barriers (Figs. 4 and 6 C).
• 2)The slope of the variance-mean current curve may be substantially higher than zero even in the complete absence of energy barriers, i.e., when stable states cannot be defined (Figs. 4 and 5).
• 3)In a multistep process, as likely occurs in real channel gating, the slope of the variance-mean current curve may result substantially higher than the maximal charge carried by a single step because of insufficient bandwidth recording (Figs. 6, 7, and 8).

The full model

The results presented so far were obtained with a simplified model of voltage gating, in which no fixed charges on the voltage sensor domain were considered, the gating pore had a uniform dielectric constant, and most notably the energy profile for the voltage sensor movement had an arbitrary shape, not assessed self-consistently. With the knowledge acquired with the simplified model, we are now ready to evaluate the gating current fluctuations produced by our full model of voltage gating (36, 19). This will allow us to verify how well the model predicts the experimentally observed variance-mean current relationship and provide clues to understand its origin.

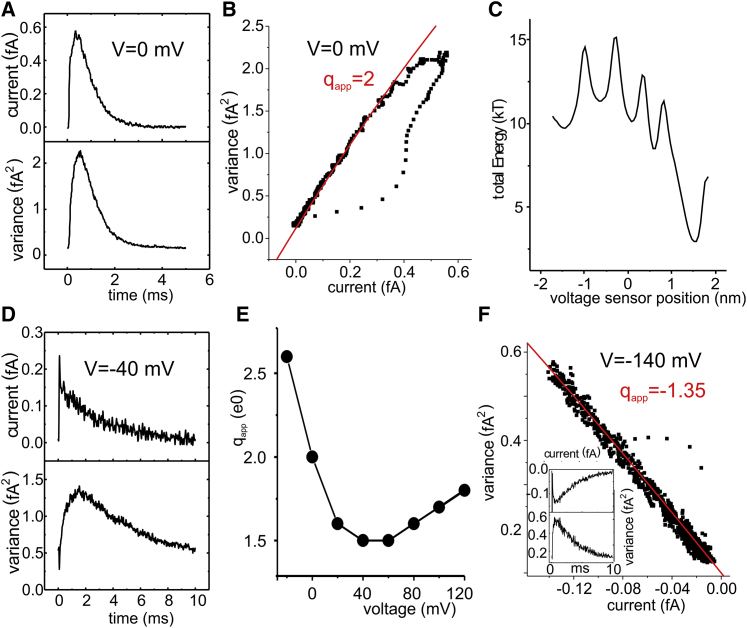
Fig. 9 shows that the full model is consistent with experimental data. Fig. 9, A and B show the variance-mean current plot obtained with the full model by pulsing to 0 mV, assessing the microscopic gating currents resulting from the motion of the voltage sensor, and filtering the response with a four-pole Bessel filter at a cutoff frequency of 8 kHz. When the variance-mean current plot derived from the gating current decay was fitted with the equation resulting from rate model theory (Eq. 13), we obtained a q_app of ∼2.0 e₀. This value was not much different from the 2.4 e₀ obtained experimentally on Shaker channels (3).

Fig. 9D shows the mean current and variance time courses obtained for a depolarizing step to −40 mV. A marked delay in reaching the variance peak, compared to the current peak, is observed under these conditions, a result also obtained in experiments (3). We also assessed the dependence of the q_app on the membrane potential and observed a somewhat complex situation, with a U-shaped q_app-V_m relationship (Fig. 9 E). Notably, a U-shaped dependence of the q_app has also been found experimentally (37).

When the noise analysis was performed on data obtained with a hyperpolarizing step to −140 mV, starting with the voltage sensor in the activated position (at +1.56 nm), we obtained a q_app much lower than that resulting from depolarization to 0 mV (1.35 vs. 2.0, Fig. 9, E and F). This result is not in accordance with experiments, in which a similar value of q_app is obtained from the analysis of the ON and OFF gating current noise. We explain the different q_app for the ON and OFF test as deriving from the asymmetry of the energy profile of our model.

When we saw the energy profile encountered by the voltage sensor during its movement through the gating pore (Fig. 9 C), we were initially rather surprised with the relatively high q_app predicted by the model. As already discussed in (18), the profile displays five energy wells corresponding to the five stable positions of the voltage sensor (S₄) as it moves through the VSD. Without the results obtained from our simplified model, this energy profile could have suggested that a four-step rate model, with each step carrying one charge through the gating pore, might be adequate to describe the activation process.

We imagined that the failure of a four-step rate model to describe the gating process of the Shaker channel (i.e., to output a q_app = 1.0 e₀), as simulated with our full Brownian model, could come from too-low energy barriers existing between the intermediate states. As we have learned, under this condition the current shots resulting from the movement of charges relatively close together tend to be unresolved because of bandwidth limitation, thus enhancing the gating current fluctuations and overestimating q_app. In addition, barriers between energy wells (measured in the forward direction) all lower than 5 kT (cf. Fig. 9 C) and highly asymmetric may prevent the rate model theory from accurately describing the system even in the absence of bandwidth limitations (Fig. 4; see also Barcilon et al., 38).

Dependence of the fluctuations on barrier height and filter frequency

We first changed the height of the four barriers by adding or subtracting Gaussian-shaped energy components to see whether the energy barriers present are not high enough for the full model to be consistent with the rate model predictions (Fig. 10 A a). As shown in Fig. 10 A b, an increase in the energy barrier results in a lower q_app estimated from the variance-mean current plot (from 2.0, as shown in Fig. 9 B, to 1.75). These results tell us that the height of the barriers in the energy profile are not sufficient to allow the use of Eq. 13 coming from the rate models. If the barrier heights are increased, the voltage sensor seems to activate more like a four-step movement, each carrying one charge (i.e., q_app moves toward unity; Fig. 10 A). By contrast, reducing the energy barriers results in an apparent increase in the gating current noise and q_app (Fig. 10 A c). We imagine that lower barriers increase the frequency of the gating charges passing through the gating pore, and this will result in unresolved passages of single charges because of the limited bandwidth conditions. We also verified that the short intercharge distance of our model (as reflection of real channels) is the cause of the partial overlap of energy barriers, leading to increased current fluctuations and q_app. As shown in Fig. 10 B, changes in the fluctuations were found upon changing the intercharge distance of the four gating charges in both directions, with longer intercharge distances giving an apparent charge closer to one.

Figure 10.

Dependence of the gating current fluctuations on the height of the energy barriers, the friction coefficient, and the applied voltage. (A) (b) and (c) show the plots of variance versus mean current produced by altering the total energy profiles as shown in (a) (black line is the original energy profile of the full model, green and blue lines are the altered energy profiles). An increase in the barrier height results in a decrease in the apparent charge. (B) Variance-mean current plots obtained with the full model with the original setting (black data points) and with the intercharge distance increased or decreased by 1 Å (orange and blue, respectively). Insets show the corresponding gating charge distributions. To see this figure in color, go online.

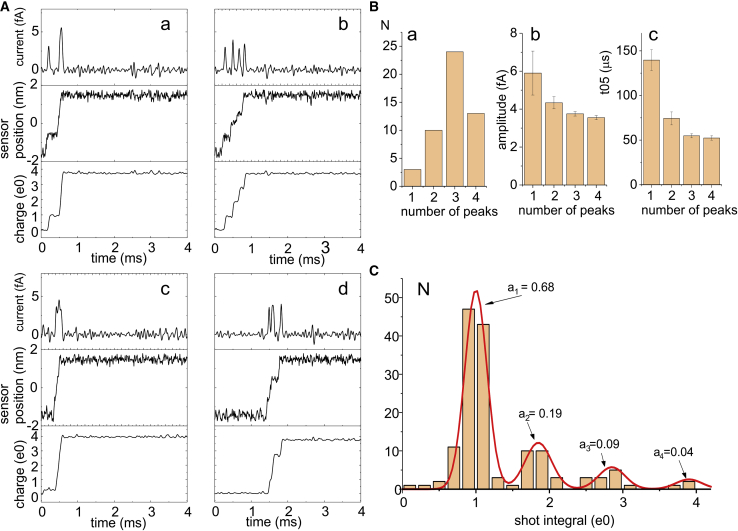
We also studied in detail the unitary events underlying the shot noise in the full model at 8 kHz filter frequency to see whether a significant superimposition of shot current events is present. We found a highly variable shape of the shots evoked by a depolarizing pulse to 0 mV, with the responses consisting of one to four well-defined and distinct peaks, as shown in Fig. 11 B. From the analysis of 49 responses (these were selected from a computation of 60 responses by discarding trials in which the current peaks were not very well defined because of the superimposition of negative peaks coming from short backward movements of the voltage sensor), we found that those with three peaks were the most frequently observed (Fig. 11 A). In addition, we found that the amplitude and duration of the peaks appeared to decrease in the responses with a higher number of peaks (Fig. 11, B b and c). From both the spatial trajectory of the voltage sensor and the time integral of the microscopic current shown in Fig. 11 A (central and bottom plots in each panel, respectively), it is possible to conclude that 1) in the responses with four peaks, each of them corresponds to the passage of one unitary charge through the gating pore (in other words, the passage of each charge is temporally separated from the passage of the other ones)—activation process develops in four distinct steps (Fig. 11 A b); 2) in the responses characterized by only one peak, the whole activation process develops in one single step that moves the four gating charges through the pore simultaneously, without an appreciable time lag between them (Fig. 11 A c); and 3) in the responses with two or three peaks, the integrals of current have values of 1, 2, or 3 e₀, suggesting that two or three gating charges can simultaneously pass through the gating pore. In this case, a single step in the activation process may actually represent the passage of two or three gating charges (Fig. 11, A a and d). Fig. 11 C shows the charge amplitude histogram obtained from the 147 peaks detected in the 49 responses analyzed. The histogram displays four clearly defined peaks, approximately corresponding to 1, 2, 3, and 4 unitary charges, with frequencies of 0.68, 0.19, 0.09, and 0.04, respectively. These data are further evidence that the passage of gating charges through the gating pore in rapid succession can go unresolved, giving rise to shot currents carrying multiple charges. Notably, the single-shot analysis of the OFF gating current at −140 mV shows a lower number of multicharge responses, especially those characterized by 3 and 4 unitary charges (data not shown). This may explain the reduced q_app obtained in these conditions (cf. Fig. 9 F).

Figure 11.

Evidence for multicharge steps in the full model. (A) Four typical microscopic current responses obtained at 0 mV are reported for the full model, showing the presence of single (b) and multicharge steps (a, c, and d). For each simulation, the filtered current, the voltage sensor position, and the charge (time integral of the current) are shown. (B) (a) shows the number of responses with 1–4 peaks. (b) and (c) show the mean amplitude and duration of the current peaks taken from responses with 1–4 peaks. (C) Histogram of the charge carried by the current peaks, accumulated from 40 responses as those shown in (B). To see this figure in color, go online.

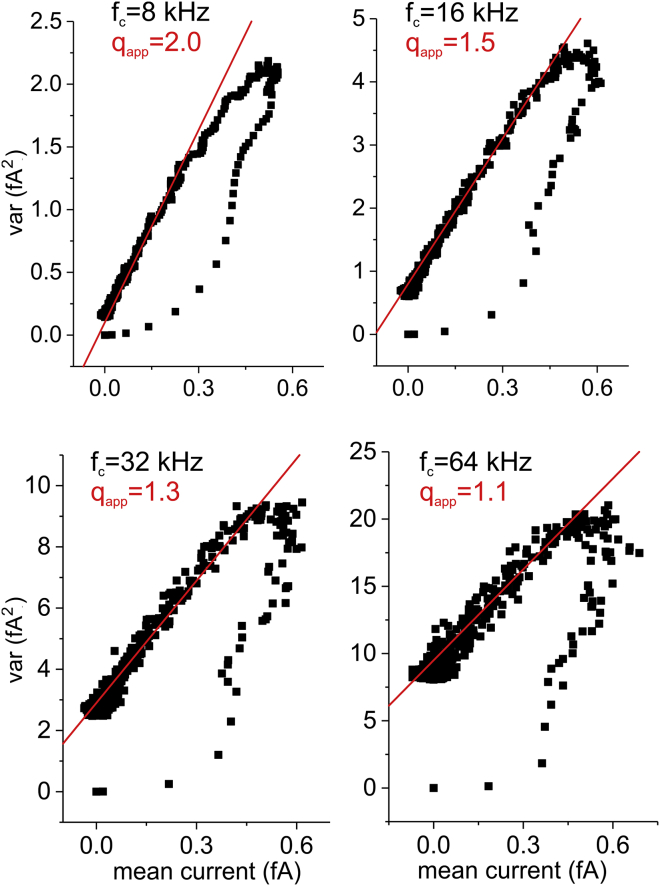
Finally, we performed simulations at increased filter cutoff frequency to further support the notion that the relatively high q_app seen in our full model derives from the low bandwidth condition used. As shown in Fig. 12, an increase in the cutoff frequency resulted in a clear decrease of q_app until obtaining a q_app close to unity for a filter frequency of 64 Hz.

Figure 12.

Effect of filtering on the q_app in our full model of voltage gating. -Simulated variance versus mean current relationships obtained for the full model using a Bessel filter at varying cutoff frequencies (indicated). To see this figure in color, go online.

Test of a four sequential steps rate model

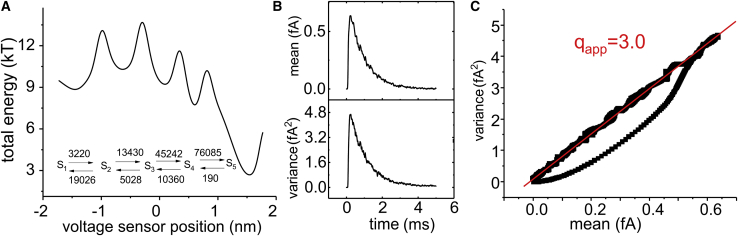
We finally asked whether a four-step rate model mirroring the passage of the four relevant gating charges through the pore, as suggested by the shape of our energy profile, would give gating current fluctuations and q_app similar to our Brownian model of voltage gating. To this end, we performed Monte Carlo simulations using the rate model shown in the inset of Fig. 13 A, with a charge of 1 e₀ associated to each step. The numerical values of the forward and backward rate constants of the model, also shown in the inset of Fig. 13 A, were obtained from the energy profile of our full model, using mean first-passage time theory (39). We performed 10,000 simulations in which we associated to each state transition a single-shot current shaped according to the response predicted by a Gaussian filter set at 8 kHz. Fig. 13 B illustrates the mean current and variance resulting from these simulations. Notably, at this filter cutoff frequency, the variance-mean current relationship gave a q_app of 3.0 e₀ (Fig. 13 C), a value much higher than that obtained with our full model (2.0 e₀). This result possibly indicates that the underlaying process (translocation of the voltage sensor) cannot be well reproduced by a state rate model. In line with this, the rate model was also unable to reproduce the initial rising phase of the gating current (see Fig. 13 B), well visible instead in our Brownian model (Fig. 9 A) and in the experiments.

Figure 13.

Simulations of gating current fluctuations using a four-step sequential rate model. (A) Energy profile from our full model of voltage gating, used for the estimation of the rate constants associated to the rate model (shown in inset), assessed using the mean first-passage time theory (39). (B) Mean current and variance obtained from 10,000 simulations performed at 0 mV of applied potential using rate model theory and the kinetic scheme shown in (A). The Gaussian filter was set at a cutoff frequency of 8 kHz. (C) Variance versus mean current plot obtained for the model shown in (A). To see this figure in color, go online.

Conclusions

In this study, we revisited previous experimental data on gating charge movements by Conti and Stühmer (4) and Sigg et al. (3) in light of current understanding of the voltage sensor architecture. We used computational models of voltage-dependent gating, with the voltage sensor treated as a Brownian particle, to understand the significance of the fluctuations (noise) of the gating current and infer the dynamics of gating charges translocation across the gating pore during VSD activation.

Gating current fluctuations were first studied experimentally by Conti and Stühmer (4) on Nav channels and by Sigg et al. (3) on Kv channels. Applying a classical two-state rate model, both groups found a main charge translocation of 2.3 or 2.4 e₀ during VSD activation and interpreted it as corresponding to a late step in the activation process associated with a bigger translocation of charge than unity.

On reexamining Conti and Stühmer data on Nav in the attempt to generalize their conclusions to other voltage-gated channels, Crouzy and Sigworth (5) postulated that because of the limited filter bandwidth used in their experiments (8 kHz), a rapid passage of consecutive unitary (gating) charges through the pore would not appear as single passages but become indistinguishable from a single large charge movement. As a consequence, the 2.3 e₀ obtained by Conti and Stühmer, and likewise the 2.4 e₀ later obtained by Sigg et al. (3), might not reflect the true size of the actual charge crossing the pore but the sum of charges passing rapidly through the gating pore to not be seen individually. In other words, it would be an experimental artifact due to limited filter bandwidth.

Our study substantiates in large part the predictions of Crouzy and Sigworth (5) by showing that under the experimental conditions of Conti and Stühmer (4) and Sigg et al. (3), i.e., with a filter bandwidth of 8 kHz, the individual current shots resulting from the passage of individual gating charges through the gating pore, which our model was capable of reproducing and identifying individually, could not be seen as such but lumped together to give a higher charge translocation. As for the size of charge translocation upon activation, our model gave a q_app of 2.0 e₀, a value sensibly lower than observed experimentally. To back up this notion that the relatively high q_app seen in our full model derives from the low bandwidth condition used, we tested the q_app output at higher filter bandwidths and found a corresponding decrease in q_app to a value close to unity for a filter frequency of 64 kHz.

One result worth briefly commenting on further is the q_app of 2.0 e₀ generated by our model compared with 2.3/2.4 e₀ found experimentally on real channels. Our model, in its present form, considers the independent movement of the voltage sensors. It is well known, however, that their coupling with the pore introduces some form of cooperativity or concerted movement of the voltage sensors that could possibly affect the dynamics of the gating currents and the underlying fluctuations. In Shaker channels, a final cooperative step leading to the pore opening has been shown to involve the concerted movement of the four S₄ voltage sensors (40, 41, 42). This synchronized movement of the voltage sensors would result in the fourth gating charges of the four sensors crossing (near) simultaneously the gating pore, thus inevitably superimposing the resulting current shots and give a higher q_app than our model that lacks this provision. This might also be the reason of the failure of our model to correctly predict the gating current fluctuation properties on repolarization, as the pore interaction is expected to exert substantial influence on OFF gating in real channels.

We are currently working to enrich our model with explicit models of pore coupling and the final cooperative step to see whether significant improvements in the prediction of gating currents and their fluctuations are brought about; we are aware, however, of the several uncertainties in the structural features and mechanism of this coupling that are still under investigation and debate (43,44).

Author contributions

L.C. performed the computer simulations. L.C. and F.F. discussed model results and wrote an initial version of the manuscript. L.C., F.F., F.B., and R.S.E. discussed the results and wrote the final version of the manuscript.

Editor: Brad Rothberg.