Genetic prediction of complex traits with polygenic scores: A statistical review

Abstract

Accurate genetic prediction of complex traits can facilitate disease screening, improve early intervention, and aid in the development of personalized medicine. Genetic prediction of complex traits requires the development of statistical methods that can properly model polygenic architecture and construct polygenic scores (PGS). Here, we present a comprehensive review on 46 methods for PGS construction. We connect the majority of these methods through a multiple linear regression framework, which can be instrumental for understanding their prediction performance for traits with distinct genetic architectures. We discuss the practical considerations of PGS analysis as well as challenges and future directions of PGS method development. We hope our review serves as a useful reference both for statistical geneticists who develop PGS methods and for data analysts who perform PGS analysis.

Polygenic Scores for Genetic Prediction of Complex Traits

Complex traits are traits that do not perceivably follow simple Mendelian inheritance laws. Example complex traits include binary ones such as type 2 diabetes and hypertension as well as continuous ones such as body mass index and standing height. Complex traits are influenced by multiple genetic factors including genotypes, gene expression, epigenomic modifications, chromatin structure as well as multiple environmental factors including occupational, lifestyle and environmental exposures [1,2]. Among these factors, genotypes, in the form of single nucleotide polymorphisms (SNPs; See Glossary), represent one of the earliest, most stable and accurately measurable factors underlying complex traits [3]. In particular, an individual’s genotypes remain the same across somatic cells and tissues over lifetime, with mutations being extremely rare and often neutral [4]. In addition, an individual’s genotypes can be accurately measured in a cost-effective way through various array-based and sequencing-based technologies and can be further imputed across millions of genomic locations [5–7]. Therefore, genotypes can be used to predict complex traits and reconstruct an individual’s genetic predisposition underlying diseases long before disease onset [8,9]. Such genetic prediction of complex traits can facilitate disease screening and prevention at population scale, improve symptom diagnosis and intervention at an early stage, and aid in the development of precision medicine with individual based treatment choices [10–13].

Genetic prediction of complex traits is often carried out by constructing polygenic scores (PGS). PGS for a trait, in its simplest form, is a weighted summation of genotypes across SNPs with the weights being the estimated genetic effect sizes [10,14–16]. PGS is commonly referred to as the polygenic risk score (PRS) or genetic risk score (GRS) when the trait of interest is a binary trait of disease status [13,16,17]. PGS becomes increasingly popular (Figure 1A) with the abundant availability of genotype and phenotype information collected from various genome-wide association studies (GWASs) [15,18,19]. In the past decade, GWASs have not only successfully identified many SNPs associated with various complex traits [17,20–22], but also demonstrated that most complex traits have a polygenic [23–25] or omnigenic architecture [26] with an appreciable heritable component. Indeed, many complex traits are influenced by thousands of small-effect SNPs [27,28], which together can explain a substantial proportion of phenotypic variance, a quantity known as SNP heritability [29,30]. Consequently, using a handful of SNPs that pass the stringent genome-wide significance level for predicting complex traits is not optimal [20,31]. Instead, genetic prediction of complex traits requires PGS methods that can jointly model genome-wide SNPs.

Figure 1. An overview of PGS methods.

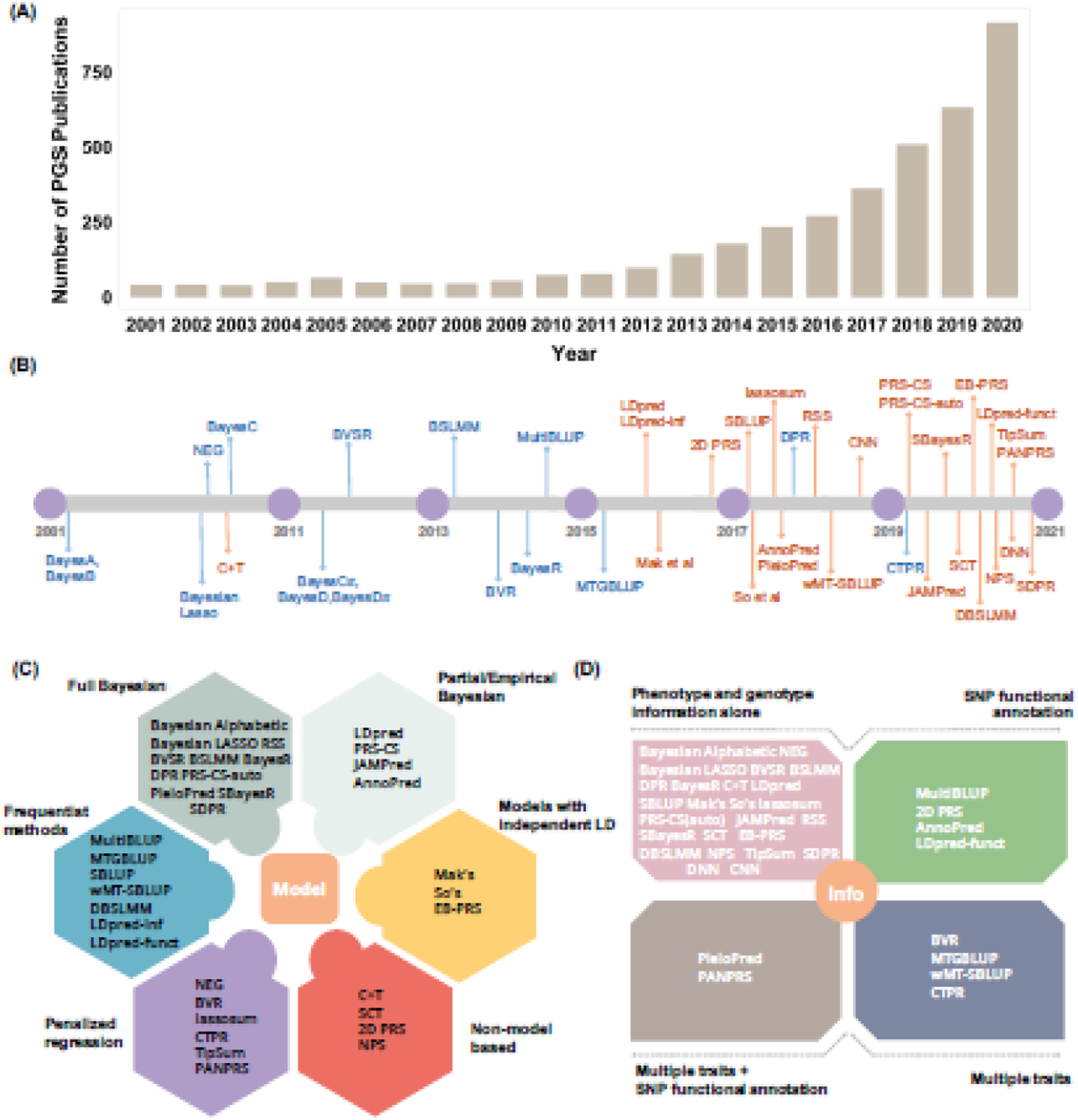
(A) The number of publications on polygenic scores increased substantially from 2001 to 2020, highlighting the popularity of PGS analysis. The number of publications is obtained by searching the key terms of “polygenic + score + or + polygenic + risk + score” on PubMed. (B) Timeline of the commonly used PGS methods that were developed in the past two decades. These PGS methods either use individual-level genotype and phenotype data as input (blue) or use summary statistics as input (orange). (C) PGS methods can be categorized into six categories based on their model and fitting strategy. Specifically, some PGS methods are model based and are described as a formal model with a corresponding fitting algorithm (colors other than red), while others are algorithm-based and are described as an algorithm or a fitting procedure without an explicit model (red). The model-based PGS methods can be further categorized based on the underlying inference algorithm: some are fully Bayesian and use Markov chain Monte Carlo (MCMC) for model fitting (grey); some are partial/empirical Bayesian, optimizing certain hyperparameters through grid search while obtaining other parameter estimates through MCMC (light grey); some are approximate approaches that assume independence across SNPs and use optimization for effect size estimation (yellow); some are frequentist in nature and can obtain an analytic solution without optimization (blue); and some are based on penalized regression and use iterative algorithms for parameter estimation (purple). (D) PGS methods can also be categorized in terms of the information used for PGS construction. Most PGS methods use only genotype and phenotype information from the GWAS on the trait of interest (pink). Some recent PGS methods can use additional SNP annotation information obtained from external data sources (green) and/or other phenotype information in addition to the phenotype of interest (taupe and navy blue).

Development of PGS methods has a long standing history in both animal breeding programs and human genetics [32]. In animal breeding programs, PGS methods are commonly used for predicting animals’ breeding values, which are the expected phenotypic values of an individual’s offspring. There, PGS is referred to as the genomic estimated breeding value (GEBV) and PGS based selective breeding is also referred to as genomic selection. Since the seminal paper of Meuwissen et al [33], genomic selection has achieved remarkable progress in many animal programs and has led to substantial increases in many breeding values such as dairy cattle traits [34]. In human genetics, Wray et al [35] evaluated the feasibility and accuracy of predicting genetic risk to disease using dense genome-wide SNP panels. Later, the predicted genetic risk to disease is coined as PRS [24]. For certain diseases, PGS have established initial clinical success [36,37] and are applied in counselling, prophylactic intervention, and embryonic screening [38–41]. For majority of common diseases and quantitative traits, PGS currently have relatively low overall prediction accuracy across individuals in the general population but can be effective for risk stratification that aims to identify individuals with high disease risks [17,18]. In addition, PGS has many other applications beyond phenotype prediction. For example, PGS for a trait of interest can be treated as a covariate in phenome-wide association study (PheWAS) for identifying clinical phenotypes and risk factors that are associated with the genetic predisposition of the trait [42,43]. PGS can also be viewed as the combined effects of multiple instrumental variables and is applied in Mendelian randomization analysis to study the causal relationship among complex traits [42,44]. Importantly, the accuracy of PGS is expected to improve along with increasing GWAS sample size, availability of new genomic information from omics studies, as well as the development of advanced PGS methods. A plethora of PGS methods have already been developed in recent years (Figures 1B–1D) [45]. These methods take advantage of the polygenic architecture underlying complex traits and model it in different ways. Here, we present a comprehensive review of 46 PGS methods (Supplementary Information Table S1), with a primary focus on methods that make use of summary statistics. For completeness and methodological coherence, we have included early individual-level data based PGS methods and will introduce PGS methods not in a chronological order. Different from the previous PGS reviews that were focused on the practical interpretation and clinical applications of PGS analysis [11,12,16,17,40], we focus on the methodological aspect of PGS methods and review them from a statistical perspective. In particular, we connect the majority of PGS methods through a multiple linear regression modeling framework and show how different PGS methods can be viewed as making distinct modeling assumptions on the distribution of SNP effect sizes across the genome. We show that such modeling framework can be instrumental for understanding the behavior and prediction accuracy of different PGS methods for traits with distinct genetic architectures. Based on the framework, we discuss the practical considerations of PGS analysis as well as current challenges and future directions of PGS method development.

A Multiple Linear Regression Framework

We begin by introducing a simple multiple linear regression model that relates genotypes to the phenotype of interest. To do so, we denote y as a n-vector of phenotypes measured on n individuals in the GWAS. We assume for now that the phenotype of interest is quantitative, but we will discuss the case of binary phenotypes in a later section. We denote X as the n by p matrix of genotypes collected across p SNPs on the same set of individuals. Genotypes are often coded as the number of reference allele for each SNP and can be represented as continuous values between 0 and 2 after imputation. To simplify discussion, we assume that the phenotype vector y and each column of the genotype matrix X have been centered to have a mean of zero. Centering does not influence results and allows us to ignore the intercept in the following equation. We consider the following multiple linear regression model that relates X to y,

$$y=X\beta +\mathit{ϵ},$$ (1)

where β is a p-vector of SNP effect sizes; and ∈ is a n-vector of residual errors, with each element following an independent normal distribution, or ${\mathit{ϵ}}_i~N\left(0,{\sigma }_e^2\right)$.

Despite its simplicity, the above model is instrumental for understanding almost all existing PGS methods. In particular, most PGS methods can be viewed as making distinct modeling assumptions on the SNP effect sizes β in the model and rely on different algorithms to obtain the estimates $\widehat{\beta }$. The SNP effect size estimates $\widehat{\beta }$ subsequently serve as the SNP weights for constructing PGS for newly observed individuals (See Box 1). Because the model includes genome-wide SNPs that are in potential linkage disequilibrium (LD) with each other as covariates, the resulting PGS naturally accounts for SNP LD.

Box 1. Predicting New Observations through PGS Construction.

We can predict phenotypes for newly observed individuals using the estimated SNP effect sizes $\widehat{\beta }$ from the above model. Specifically, once we obtained the p-vector of genotypes, x_l, for a new individual l, we can simply plug in the SNP effect estimates to obtain the predicted phenotype value, i.e., PGS, as ${\widehat{y}}_l=x_l\widehat{\beta }$.

Common Modeling Assumptions on SNP Effect Sizes

Because p >> n, we will need to make additional modeling assumptions on the effect sizes β to make the model in Equation (1) identifiable. Both sparse and polygenic modeling assumptions have been proposed on β. A common sparse modeling assumption on β is the point normal distribution, which assumes that the effect size of j’th SNP comes from a mixture of a normal distribution and a point mass at zero, denoted as

$${\beta }_j~\pi N\left(0,{\sigma }_{\beta }^2\right)+(1-\pi ){\delta }_0,$$ (2)

where, with proportion π, the SNP effect size follows a normal distribution with mean zero and variance ${\sigma }_{\beta }^2$; and with proportion 1-π, the effect size is exactly zero – hence the point mass at zero, δ₀. In the point-normal distribution, π is usually assumed to be small, representing the prior belief that a small proportion of SNPs have non-zero effects.

A common polygenic modeling assumption on β is the normal assumption, which assumes that all SNPs have non-zero effects and that each effect size follows a normal distribution:

$${\beta }_j~N\left(0,{\sigma }_{\beta }^2\right),$$ (3)

with mean zero and variance ${\sigma }_{\beta }^2$. The model in Equation (1), when paired with the normality assumption on β in Equation (3), has a wide variety of applications and has many names. For example, it is referred to as the linear mixed model (LMM) per the resulting random effects term of the combined genetic effects; as the infinitesimal model per its polygenic assumption on the effect sizes Xβ; as the ridge regression in statistics literature; as the L2 regularization when viewed as a penalized regression; as the best linear unbiased prediction (BLUP) when the focus is on the predicted values; or as the restricted maximum likelihood (REML) when the REML algorithm is used for inference. All these names are used interchangeably in the PGS literature and we simply refer to the model as the LMM in the present review.

Sparse Modeling Assumptions on SNP Effect Sizes

One common modeling assumption on the effect sizes β in the multiple linear regression model is sparsity, and one common sparsity assumption is a point-normal distribution (See Box 1). The point-normal distribution assumes that only a small proportion of SNPs have non-zero effects and that their effect sizes follow a normal distribution with mean zero and variance ${\sigma }_{\beta }^2$ PGS methods that use the point-normal distribution include the Bayesian variable selection regression (BVSR) [46,47], the Bayesian alphabetic method BayesCπ [48], LDpred [31] and JAMPred [49]. The first two methods use individual-level data of GWAS while the last two use GWAS summary statistics. These sparse PGS methods also have subtle differences in their assumptions on the hyper-parameters as well as their Markov chain Monte Carlo (MCMC) fitting algorithms.

The point normal distribution assumes that the effect sizes of the non-zero effect SNPs follow a normal distribution. The normality assumption on SNP effect sizes is highly effective in many genetic applications including SNP heritability estimation [20,30] and is commonly referred to as the global shrinkage approach [50]. However, the normality assumption has one potential drawback: the normal distribution has a thin tail, which corresponds to a relatively low prior probability of observing large effect sizes.

Consequently, normality assumption can lead to over-shrinkage of large effect estimates that are crucial for accurate prediction. Because of the drawback in the normality assumption, several PGS methods have been developed to introduce heavy tailed distributions on the non-zero effects to ensure adaptive shrinkage, also known as local shrinkage [50]. These methods often assume a SNP specific non-zero effect size variance ${\sigma }_j^2$ for the j-th SNP and place another prior distribution on ${\sigma }_j^2$ The prior on ${\sigma }_j^2$ can be either continuous or discrete, effectively leading to a scale-mixture of normal distribution on the non-zero effect sizes. For example, BayesB [33,48] places an inverse gamma (IG) distribution on ${\sigma }_j^2$, leading to a point-t distribution on β. BayesD [48] and BayesDπ [48] place a mixture of IG distributions on ${\sigma }_j^2$, leading to a point-t mixture distributions on β. BayesR [51] places a discrete distribution on ${\sigma }_j^2$, leading to a mixture of three normal distributions along with a point mass at zero for β. BayesR is further extended by SBayesR [52] to take summary statistics as input. All these methods rely on MCMC for model inference.

The above PGS methods make explicit sparse modeling assumptions to induce sparsity on effect size estimates. Several PGS methods that were initially described as an algorithm can also be viewed as making implicit sparse modeling assumptions. For example, the most commonly used PGS method, C+T [24,35,53], relies on LD clumping and p-value thresholding to select a subset of approximately independent SNPs with strong association signal for PGS construction. The C+T strategy ensures a sparse set of SNPs to be used for constructing PGS and thus corresponds to making a sparse assumption on SNP effect sizes. Similarly, SCT [54] extends C+T by examining an extended set of hyper-parameters for SNP selection. These hyper-parameters include p-value threshold, LD window size, LD correlation threshold and imputation score. PGS scores in SCT are constructed for different combination of the hyper-parameters and are further selected through a penalized regression in the validation data.

Polygenic Modeling Assumptions on SNP Effect Sizes

An alternative to the sparse modeling assumption on the effect sizes is the polygenic modeling assumption, and the most common polygenic modeling assumption is normality (See Box 1). The model in Equation (1), when paired with the normality assumption β on in Equation (3), has a wide variety of applications and has many names (See Box 1). Here, we simply refer to the model as the LMM, which has been implemented in many software. For example, GEMMA [47] implements LMM for prediction using individual-level data. LDpred-inf [31], SBLUP [55], and DBSLMM [56] all implement the same model using summary statistics as input.

Similar to sparse modeling, multiple PGS methods have been proposed to extend the normality assumption in the polygenic models to enable more accurate prediction. For example, BayesA [25,33,57] places an IG distribution on the SNP specific variance ${\sigma }_j^2$ to induce a t distribution on the effect sizes β. NEG [58] places an exponential-gamma distribution on ${\sigma }_j^2$ to induce a normal-exponential-gamma distribution on β. PRS-CS [59] decomposes ${\sigma }_j^2$ as a product of two parameters: a global shrinkage parameter either placed with a half Cauchy prior or optimized through a grid search, and a local shrinkage parameter with a gamma-gamma prior. Both BayesA and NEG use individual-level data as input while PRS-CS uses summary statistics. As another popular example, the Bayesian version of LASSO [60] effectively places an exponential distribution on ${\sigma }_j^2$ to induce a t distribution on the effect sizes β. NEG [58] places an exponential-gamma distribution on ${\sigma }_j^2$ to induce a Laplacian/double exponential prior on β. The Bayesian LASSO is fitted through either MCMC [61,62] or EM algorithm [63] to obtain the posterior mean of β. In contrast, the frequentist LASSO is expressed in the form of an L1 penalized regression and often fitted through a gradient descent algorithm to effectively obtain the posterior mode of β. While the posterior mean of β is not sparse, the posterior mode is. For PGS construction, the lassosum [64] fits the frequentist LASSO using summary statistics as input. TlpSum [65] extends lassosum by selectively penalizing small effect SNPs via the truncated lasso penalty.

Besides placing a continuous prior on ${\sigma }_j^2$, several PGS methods also place a discrete prior on ${\sigma }_j^2$ to effectively induce a mixture of normal distributions on β. For example, the Bayesian Sparse Linear Mixed Model (BSLMM) [66] assumes that each effect size comes from a mixture of two normal distributions. By segregating SNPs into two categories, BSLMM can place different shrinkages on the SNP effect sizes in the two categories separately, leading to proper shrinkage of small effects without over-shrinkage of large effects. BSLMM is implemented in GEMMA [47], which takes individual level data as input and relies on MCMC for inference. BSLMM is also implemented in DBSLMM [56], which takes summary statistics and relies on an efficient deterministic algorithm for scalable inference. As another example, BayesC [57,67] places a mixture of IG distributions on ${\sigma }_j^2$, thus inducing a mixture of t distributions on β. The two types of polygenic extensions on normality based on continuous and discrete priors on ${\sigma }_j^2$ have different modeling benefits. Specifically, a continuous prior on ${\sigma }_j^2$ often leads to an effect size distribution that is relatively easy to perform inference on, while a discrete distribution on ${\sigma }_j^2$ often allows for more adaptive shrinkage of effect sizes and robust prediction performance across traits. A common feature of both extensions is that they are parametric in nature, relying on using a limited number of parameters to characterize the effect size distribution, which can be restrictive. To enable more flexible effect size modeling, the latent Dirichlet process regression (DPR) [68] uses a Bayesian non-parametric model and places a distribution on ${\sigma }_j^2$, with the distribution to be inferred based on the data at hand. The non-parametric distribution on ${\sigma }_j^2$ in DPR leads to a normal mixture with infinitely many components on the effect sizes, making DPR robust and adaptive to a wide range of phenotypes with different genetic architectures. DPR is implemented in the DPR package that uses individual-level data as input and relies on either MCMC or variational Bayes for inference. DPR is also implemented in SDPR [69], which takes summary statistics as input.

The above PGS methods make explicit polygenic modeling assumptions. A few PGS methods that were originally described as a fitting algorithm can also be viewed as making implicit polygenic modeling assumptions. For example, Mak et al [70] constructs PGS by weighting SNP marginal effect size estimates using local true discovery rates that are estimated through either maximum likelihood or kernel density estimation. Because the local true discovery rate ranges between zero and one, Mak et al method implicitly assumes that all SNPs are included for PGS construction. So et al [71] extends Mak’s approach by applying a Tweedie’s formula [72] to further correct for the SNP effect size estimates before weighting.

Modeling Assumptions and Other Factors that Influence Performance

Given that the majority of PGS methods make distinct modeling assumptions on the effect sizes, one naturally wonders which PGS method to choose for a given trait. Intuitively, if the prior effect size distribution can closely match the true effect size distribution underlying the trait, then the inferred effect size estimates would approximate well the underling polygenic architecture, thus leading to accurate prediction performance. Indeed, it has been shown that polygenic PGS methods often perform well for polygenic traits [24,66,73,74] while sparse PGS methods often perform well for traits in which a small proportion of SNPs have moderate or large effect sizes [26,59,66]. Because the genetic architecture underlying a trait is often unknown and varies across traits [75], it is often beneficial to use a PGS method with a flexible modeling assumption that can adaptively approximate the true effect size distribution across a range of traits. For example, methods that rely on a mixture of normal distributions (e.g., BSLMM, BayesR, DPR) for adaptive modeling of effect sizes often outperforms standard LMM that assumes a single normal distribution.

Certainly, how well the effect size assumption matches the underlying truth is only one modeling factor, albeit a major one, that determines prediction performance. Other modeling factors, such as the choice of inference algorithms and the inference strategies on the hyper-parameters, can also substantially impact prediction performance. Specifically, given the same model and sufficient computational resources, exact inference algorithms often outperform approximate ones. For example, MCMC algorithm for DPR outperforms the variational Bayesian approximation of DPR across traits. However, with limited computational resources, approximate inference algorithm may become the only viable option. For example, DBSLMM relies on an approximate deterministic algorithm to perform inference on BSLMM and is much more scalable than the original MCMC algorithm for fitting BSLMM. In addition, it is generally beneficial to infer various hyper-parameters in the model rather than fixing them to certain pre-assigned values. For example, while both BVSR and BayesCπ fit a similar sparse model, BVSR often outperforms BayesCπ by inferring the hyper-parameters instead of fixing them to a prior set of values. The ability to use a large number of parameters and explore a large parameter space can also help with prediction performance. For example, SCT outperforms C+T by performing SNP selection with additional criteria and exploring a larger hyper-parameter space. Fitting algorithms that use individual-level data as input usually have higher prediction performance than algorithms that take summary statistics, as the later have to approximate the LD matrix (more below). However, due to LD matrix approximation, algorithms using summary statistics are often much more computationally scalable than those using individual-level data. Besides the above modeling factors, PGS performance also depends on the quality of input data [45], GWAS sample size, as well as the trait SNP heritability [76,77], which represents the potential performance upper limit for PGS [78].

Finally, multiple factors also influence the computational cost of different PGS methods. For example, PGS methods based on global shrinkage of LMM are often faster than PGS methods with local shrinkage or sparsity inducing priors, as the former can be fitted based on an analytic solution. For the same model, approximate inference algorithms are computationally faster and use less memory than exact inference algorithms. On the extreme, algorithm-based PGS methods such as CT and SCT are generally more computationally scalable than model-based PGS methods that specify explicit effect size priors and perform formal inference. In addition, PGS methods that rely on summary statistics as input make explicit approximations on the LD matrix, which can alleviate much of the computational burden associated with modeling of SNP correlation. Software implementation, use of multithreading or parallel computing environment, and choice of computational language can also influence the computational cost of PGS methods.

Adaptation of PGS Methods Towards using Summary Statistics

While early PGS methods use individual-level genotype and phenotype as input, a growing number of PGS methods can make use of summary statistics or are specifically designed to do so. Fitting with summary statistics requires LD approximation, which can lead to reduced accuracy as compared to fitting with individual-level data on the same model [79]. However, fitting with summary statistics can take advantage of the easily accessible summary statistics from various GWASs without privacy concerns and logistic hurdles [18,19] and can lead to substantial computational gains through LD approximation. Therefore, summary statistics based PGS methods facilitate PGS applications towards large-scale data, which is a key for ensuring accurate prediction performance.

Two general strategies exist for fitting PGS models using summary statistics, with subtle methodological differences between them. The first strategy is to formulate the model with individual-level data and derive the inference algorithm using summary statistics, while the second strategy is to model summary statistics directly (See Box 2). Both strategies require two forms of summary statistics as input: the p-vector of marginal z-scores z and the p by p SNP correlation matrix D, which is also known as the LD matrix. The input z can be easily obtained through simple linear regression in the original GWAS while the input D is often estimated in a reference panel with individuals of the same ethnicity (e.g., from the 1,000 Genomes project). Because of the relatively small sample size in the reference panel, the estimated D requires further regularization and approximation to ensure numerical stability for PGS inference. Some PGS methods approximate D with a block-diagonal matrix computed either based on LD [31,56,59,64] or through index-sorting [69], sometimes further adjusted for cross-block correlations due to long range LD [49]; some approximate D with a banded matrix based on a sliding window for LD computation [31,55]; some shrink D towards a diagonal matrix with D = ΛD + (1_n×n−Λ)I, where each element λ_ij is a function of recombination rate between SNPs i and j [52,80]; and some approximate D with a sparse matrix by setting small matrix elements to zero [81]. Regardless of the estimation form, a match between the estimated D from the reference panel and the true D in the study sample is critical to ensure accurate prediction performance [56,82,83].

Box 2. Modeling of Summary Statistics.

Two general strategies exist for fitting PGS models using summary statistics. The first strategy is to formulate the model with individual-level data and derive the inference algorithm using summary statistics. Specifically, the likelihood for the model in Equation (1) can be expressed as a function of two terms: X^Ty and X^TX. Subsequently, instead of using individual-level data X and y as input for modeling fitting, one only needs to obtain these two forms of summary statistics. X^Ty can be obtained through the p-vector of marginal z-scores which is equivalently the marginal effect size estimate $\tilde{\beta }$ when both the phenotype and the genotypes for each SNP are standardized to have mean zero and unit standard deviation. In that case, the z-scores are in the form of $z=\frac{X^{T}y}{\sqrt{N}}$ when SNP effect sizes are small, where N is the GWAS sample size. X^TX for the standardized genotype matrix can be obtained through a p by p SNP correlation matrix $D=\frac{X^{T}X}{N}$, which is also referred to as the LD matrix. With z and D as input, likelihood-based inference can be carried out as if individual-level data are available.

The second strategy for fitting PGS models with summary statistics is to model summary statistics directly. For example, the regression with summary statistics (RSS) models the marginal effect size estimates $\tilde{\beta }$ as a function of the underlying effect sizes β in the form of

$$\tilde{\beta }\mid \beta ~N\left(D\beta ,{\sigma }_e^{2}D\right),$$ (4)

where $D=\frac{X^{T}X}{N}$, which is also referred to as the LD matrix; and ${\sigma }_e^2$ is the same error variance as in Equation (1). The conditional likelihood of β given the hyper-parameters (e.g. ${\sigma }_e^2$) based on Equation (4) is the same as the conditional likelihood of β based on Equation (1). Therefore, if the hyper-parameters are known, both strategies for fitting PGS models with summary statistics lead to the same likelihood on β. The likelihood for the hyper-parameters based on Equation (4), however, is different from that based on Equation (1). Note that a more complicated form of RSS is available in [80] when the SNP genotypes are not standardized.

Incorporating Additional Information to Improve Prediction

Several recent PGS methods have been developed to incorporate additional and external information beyond what is available in the GWAS data. Such external information can be either in the form of SNP functional annotations or in the form of other phenotypes in addition to the phenotype of interest. Incorporating external information often improves the accuracy of PGS.

Incorporating SNP functional annotations

SNP functional annotations for a given SNP are continuous or binary annotations that characterize the functional importance of the genetic variant [84–86]. SNP functional annotations are obtained through functional genomic studies [87–91] and can serve as crucial predictors for SNP effects. For example, SNPs with certain functional annotations are more likely to be causal [92], tend to have larger effect sizes, and explain more heritability than SNPs with other annotations [93,94]. Several PGS methods have been developed to incorporate SNP functional annotations to improve prediction. For example, 2D PRS [95] categorizes SNPs into two disjoint sets: one containing high-priori SNPs likely associated with the trait of interest and the other containing low-priori SNPs less likely associated with the trait. The two sets of SNPs are determined based on a separate GWAS and are then subject to the C+T procedure separately with a less stringent p-value threshold for the high-priori SNPs. MultiBLUP [96] divides SNPs into separate groups based on their genomic location and induces different effect size shrinkage in different groups. AnnoPred [97] incorporates SNP functional annotations directly into the prior distribution of effect sizes based on BVSR: it either models the j’th SNP’s probability of having a non-zero effect as a function of its annotations, or models its non-zero effect variance as a function of its annotations. LDpred-funct [98] builds upon LMM and models ${\sigma }_j^2$ as a function of its annotations.

Modeling pleiotropy across multiple traits

Another external information that can facilitate trait prediction is pleiotropic association information. Pleiotropic association characterizes SNP effects similarity across multiple correlated traits and can be used to improve SNP effect size estimation on the trait of interest [99–101]. PGS methods that take advantage of pleiotropy are often based on the multivariate linear mixed model (mvLMM) [102,103], also known as the MT-BLUP in prediction settings. The mvLMM is an extension of LMM and assumes that the effects of j’th SNP across phenotypes follow a multivariate normal distribution, with a covariance matrix capturing the genetic covariance across traits. By jointly modeling SNP effect size similarity across traits, mvLMM can borrow information of effect size estimates from other traits to improve the estimates on the trait of interest. Li et al [104] implements a bivariate version of mvLMM that models two phenotypes jointly. MTGBLUP [100] implemented a general form of mvLMM with individual-level data as input. wMT-SBLUP [99] implements mvLMM with summary statistics as input. Besides mvLMM, CTPR [105] imposes a sparse effect size assumption on each trait and uses an L2 penalty to model effect size similarity across traits. Other methods also incorporate SNP functional annotations into pleiotropic modeling. For example, PleioPred [101] partitions SNPs into multiple annotation categories while jointly modeling two correlated traits together. PANPRS [106] specifies an annotation specific L1 penalty for SNPs in each annotation category to incorporate annotation into prediction and uses a group lasso type penalty to encourage SNP effect size similarity across traits.

Moving Beyond Multiple Linear Regression

While the multiple linear regression framework in Equation (1) includes majority of PGS methods, several notable exceptions exist. For example, the non-parametric shrinkage (NPS) method [81] performs a linear transformation on the SNP genotypes before placing a non-parametric effect size distribution on the transformed genotypes. Subsequently, the resulting prior distribution on the original genotypes from NPS is not straightforward to characterize and does not directly correspond to a known distribution. As another example, deep learning methods [107,108] rely on deep convolutional neural networks connected through the leaky rectified linear unit (ReLU) activation functions for modeling non-linear effects, which can be particularly effective for predicting traits with appreciable genetic heterogeneity [107].However, the performance of deep learning methods is heavily dependent on the availability of large-scale training data, the choice of network architecture, and tuning of hyper-parameters; the latter two require expertise and extensive trial and error due to a lack of standard theory guiding architecture selection and model training. For case-control studies, the binary case-control labels are often treated as continuous traits and directly modeled through the multiple linear regression framework [66,68]. Such modeling could be justified by recognizing the linear model as a first-order Taylor approximation to a generalized linear model [66,68]. However, several recent PGS methods directly use either a logistic regression [106], its approximation [109], or a liability threshold model [66], to directly model ascertainment and the binary nature of case control outcome. Finally, recent studies have started to explore the development of PGS methods to predict a person’s absolute risk of developing a disease over a certain period of time using the Cox proportional hazard model [110]. Validating such absolute risk model in prospective studies will be of particular clinical importance [40].

Evaluating PGS Methods: Cross-validation and Cross-ethnicity Performance

Fitting and evaluating PGS methods rely on a multistage procedure commonly referred to as cross-validation (Figure 2). Cross-validation requires two or three datasets: a training data, an optional validation data, and a test data. PGS methods are fitted in a training data; if needed, have their hyper-parameters determined in a validation data (Supplementary Information Table S1); and eventually have their performance evaluated in a test data. The relative size of the training versus test data represents a bias-variance trade-off in estimating the prediction error. In particular, a small training data and a large test data would likely lead to an over-estimation of the prediction error. A large training data and a small test data, on the other hand, would result in less bias but higher variance in estimating the prediction error. In addition, methods that perform automatic inference on all parameters using the training data alone can potentially combine the validation data into the training data to benefit from the larger sample size. On the other hand, methods that tune hyper-parameters in a separate validation data are often computationally easier to fit, requiring estimating the SNP effect sizes conditional on the hyper-parameters in the training data instead of jointly estimating both, although their performance may also be influenced by the size of the validation data. In the cross-validation, the evaluation metrics in the test data include R² and mean squared error (MSE) for quantitative traits, and area under the curve (AUC) and pseudo-R² for binary traits. Among these metrics, AUC and R² are easier to interpret as both range between zero and one, but neither account for the predicted trait mean like MSE does and thus may not be suited for settings where predicting the absolute trait value is of interest. Importantly, tuning of hyper-parameters in the validation data may only require summary statistics, as is computing R² [56,65,99] or AUC [111] in the test data. Using summary statistics for hyper-parameter tuning and R² computation facilitates the application of PGS methods towards a wide variety of datasets [56]. Finally, we note that an unfortunate mistake practitioners commonly make in the cross-validation procedure is to use the test data instead of a separate validation data to tune the hyper-parameters. Using the same test data to both tune hyper-parameters and evaluate PGS performance would lead to model over-fitting, resulting in underestimation of the prediction error.

Figure 2. A general pipeline for PGS construction and applications.

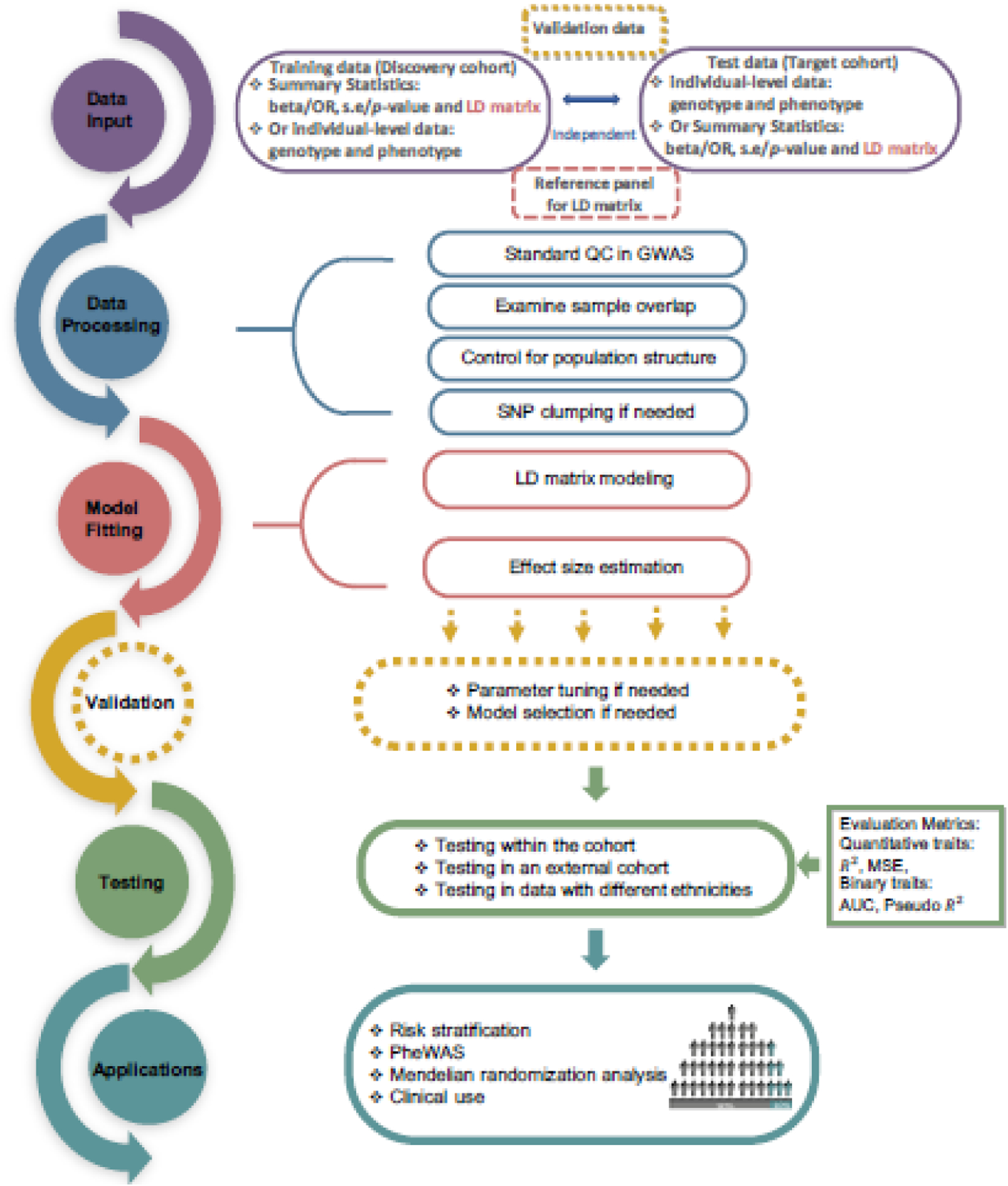
PGS methods require either two or three datasets as input: a training data, a test data, and if necessary, a validation data. These datasets need to undergo multiple steps of stringent quality control that include SNP filtering, overlap sample removal, adjustment of population stratification etc. The training data is then used to fit the desired PGS model for estimating the SNP effect sizes. For certain PGS methods, a validation data is needed to tune parameters in the model or perform model selection. The estimated SNP effect sizes are then used to construct PGS in a test data, where the predictive performance of PGS method is tested based on standard metrics. The constructed PGS are used for different applications, including risk stratification, PheWAS, and Mendelian randomization. Here, a dotted line box represents a step that is not necessary for all PGS methods.

Most cross-validations have thus far been performed on a single GWAS with samples of European ancestry [112]. Several recent studies have explored PGS evaluation either through cross-study validation where the training and test data are from two separate GWASs, or through cross-ethnic group validation where the training and test data are from two GWASs with samples of different ethnicity [56]. Cross-study and cross-ethnicity PGS applications are challenging because of the potential mismatch in allele frequency and LD pattern between the training and test data [81]. Indeed, models trained with European individuals are often 2–3 times less accurate when applied to Asian or African populations as compared to European populations [56,113,114]. Consequently, special PGS methods have been developed to enhance cross-ethnicity prediction. For example, a weighted multi-ethnic PGS is proposed to combine PGS trained in Europeans and non-Europeans to improve prediction in both populations [115]. PolyPred and PolyPred+ [116] rely on functionally informed fine-mapping in different populations to improve causal effect estimation and subsequent cross-ethnicity prediction accuracy. PRS-CSx [117], an extension of PRS-CS, directly assumes shared causal effects and borrows information across populations for accurate effect size estimation. With methodological advances and increased availability of GWASs in under-represented populations [112,114], PGS accuracy in diverse populations will be further improved.

Concluding Remarks

We summarize the discussed PGS methods in a reference guide to facilitate practical applications (Figure 4). The performance of different PGS methods have been evaluated in multiple human traits in both PGS method studies (Figure 3, Figure S1) and method comparison studies [83,118,119]. These studies have shown that C+T is the mostly commonly compared method due to its simplicity and computational efficiency, while PRS-CS and BSLMM tend to have higher performance than the others whenever they are compared, presumably due to their flexible modeling assumptions. However, these studies have also shown that different PGS methods have distinct performance across traits and that the same method may have different performance on the same trait in different studies due to varying cross-validation designs. Therefore, comprehensive comparisons are needed to systematically evaluate the performance of various PGS methods in the future.

Figure 4. A decision tree on which methods to use for PGS analysis.

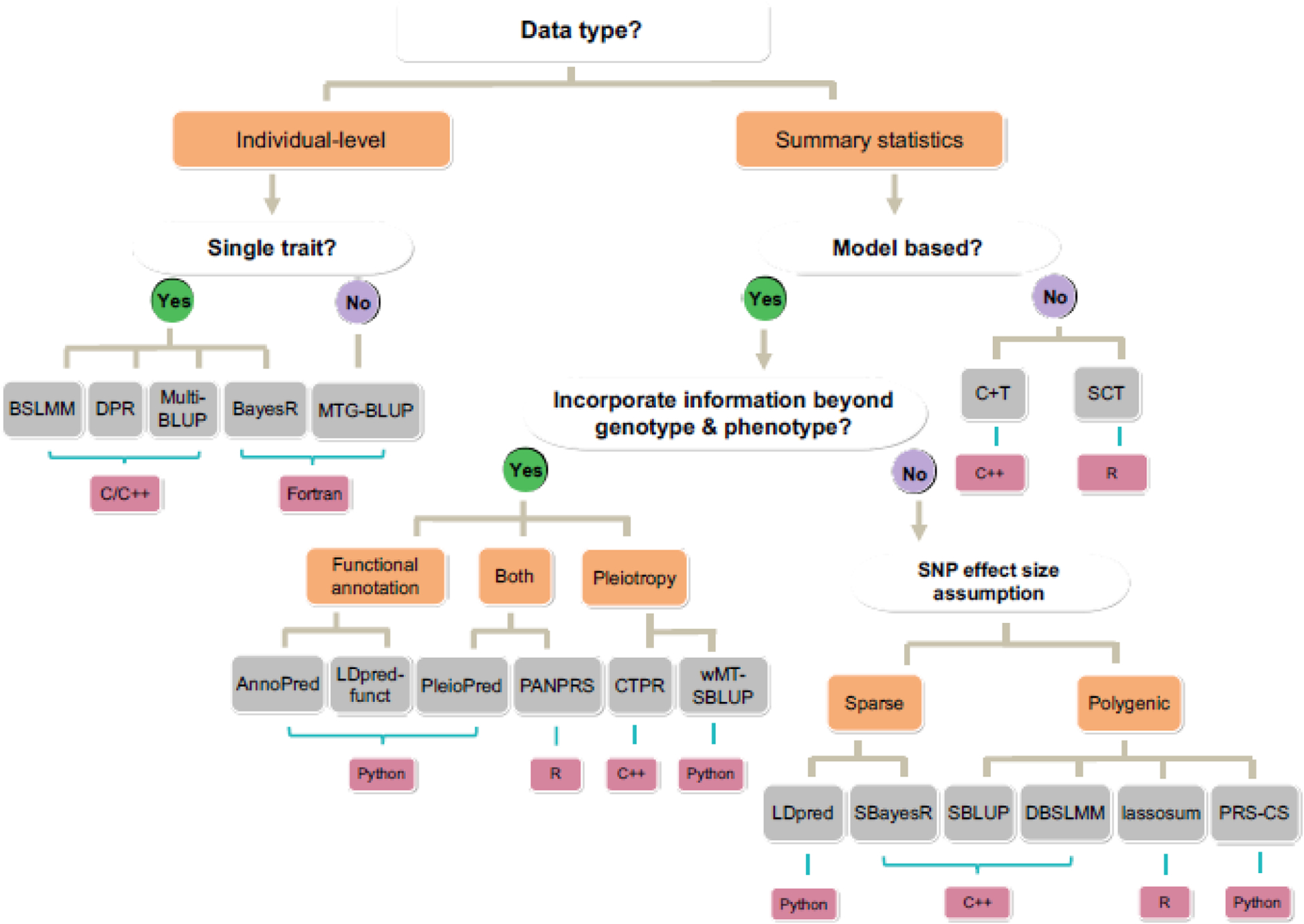
The decision tree begins with input data type, followed by the choices of analyzing single versus multiple traits, using model-based methods versus algorithm-based methods, whether to incorporate information beyond genotype and phenotype, as well as the detailed SNP effect size assumptions (blue brackets). The choices include Yes/No answers (Yes in green circles and No in purple circles) or other qualitative options (orange brackets). Different choices lead to different PGS methods (grey brackets), which are implemented with different computing language (pink brackets).

Figure 3. Predictive performance of common PGS methods as revealed in the PGS methodological publications.

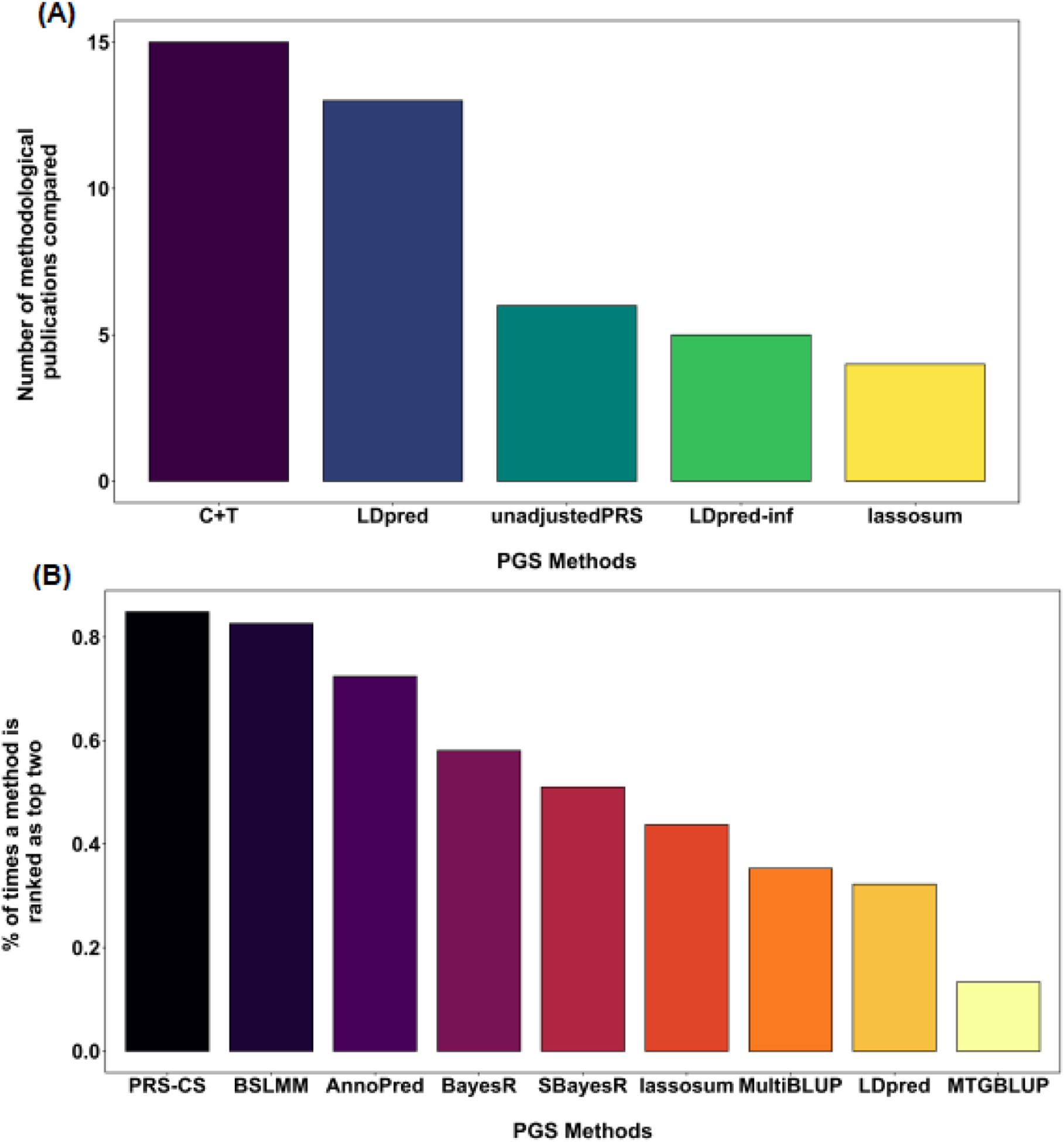
(A) The bar plot shows the top five PGS methods that have been compared the most in the real data applications in the 26 PGS methodological publications listed in Figure S1. y-axis denotes the number of times a specific PGS method is compared in a different PGS methodological publication. Note that PGS methods developed earlier tend to be compared more often than methods developed later. (B) The bar plot shows the percentage of times a PGS method is ranked as the top two methods in terms of prediction performance in human traits in the PGS methodological publications. The percentage is calculated both across publications and across traits examined in all PGS methodological publications listed in Figure S1. In both A and B, we only considered PGS methods that have been compared for at least one time in a PGS methodological publication from a different research group.

We note that the development of PGS methods is in close connection with the development of methods for SNP heritability estimation, with many common methods shared between the two areas [30]. For example, the sparse PGS methods BVSR [46] and BayesR [51] and the polygenic PGS methods LMM [20], BSLMM [66] and DPR [68] are all commonly used for SNP heritability estimation. Among them, LMM is perhaps the most widely applied one [20], with multiple software implementations [47,120] and multiple available fitting algorithms including REML and method of moments for SNP heritability estimation [121]. Besides analyzing a single quantitative trait, LMM has also been extended for SNP heritability estimation for binary [66,122,123] and count [124–126] traits as well as for genetic and environmental covariance estimation across multiple phenotypes [103,127]. With the same model, PGS methods focus on estimating SNP effect sizes while heritability estimation methods focus on estimating a variance component hyper-parameter that represents SNP heritability. The estimated SNP heritability depicts a potential up limit of PGS performance and is served as an initial input for many PGS methods [56]. As with PGS methods, the accuracy of SNP heritability estimation is highly dependent on how well the prior effect size distribution matches the truth [66]. Indeed, a similar trend in SNP heritability estimation is to develop methods with flexible SNP effect size distributional assumptions, often by incorporating SNP annotations or modeling the SNP effect size dependence on the minor allele frequency (MAF) and LD score [121,128]. For example, LDAK assumes that the variance of SNP effect size is a function of MAF and LD, while GREML-MS [129] and stratified LDSC [128] induce such dependence by stratifying SNPs into different MAF and LD bins and assuming different per-SNP heritability values in different strata. Finally, several SNP heritability estimation methods have been developed to take GWAS summary statistics as input. These summary statistics-based methods include LDSC [130] and MQS [121] algorithms for LMM and SumHer algorithm [131] for LDAK, all of which rely on method of moments to achieve scalable computation. A recent review on SNP heritability estimation from a statistical perspective is available in [30]. Taking advantage of the methods developed for SNP heritability estimation and incorporating the lessons and experiences gained in that research area can potentially benefit the development of PGS methods.

While existing PGS methods have shown promising performance across many complex traits, many future improvements are warranted (See Outstanding Questions). For example, annotation facilitated PGS methods have thus far focused on a limited number and types of annotations. Evaluating a large variety of annotations and exploring the benefits of annotation selection [132] may improve prediction further. Incorporating other types of external information such as transcriptomics through other integrative analysis frameworks such as the transcriptome-wide association study may have added benefits. Combining PGS scores from different methods and across multiple GWAS sources and distinct populations, in a principled way, such as through bagging or boosting, may ensure robust prediction performance. Incorporating rare genetic variants especially the ones with high penetrance, modeling allele frequency and LD dependent effect size distribution, accounting for gene-gene interactions and gene-environmental interactions, may all improve prediction. Finally, recent studies have suggested that some fraction of the constructed PGS from certain PGS methods may be correlated with and accounted for by non-genetic risk factors [133]. Thus, investigating the benefits of including the constructed PGS on top of the existing non-genetic risk factors used in the baseline risk model for individual disease or all-cause mortality is especially important for assessing the practical performance of PGS methods and the clinical impact of PGS [133,134].

Outstanding Questions.

• What is the best approach to borrow information across multiple ethnic groups to improve the portability of PGS across ethnicity while maintaining its accuracy in specific ethnic groups?

• What is the best way to approximate the LD matrix, so that we can maintain the accuracy of individual-level based PGS methods while keeping the computation benefits from summary statistics based PGS methods?

• Would modeling the SNP effect size dependence on the minor allele frequency and LD help improve PGS accuracy?

• Can we incorporate other integrative approaches recently developed in various omics studies into PGS modeling to improve prediction performance?

• Would selecting informative functional annotations and/or selecting correlated traits from a large group of candidates help further improve PGS performance on the trait of interest?

• Can we measure prediction uncertainty through the predictive posterior distribution in a computational efficient fashion, and can we quantify the calibration of such prediction uncertainty through posterior predictive checks?

• How do we extend the current PGS methods to predict a person’s absolute risk of developing a disease over a certain period of time?

• How do we appropriately communicate PGS results, especially its relatively low accuracy in the general population, to patients and consumers who obtained their PGS through clinical and lab tests?

Highlights.

• Polygenic scores (PGS) aggregates association information from genome-wide SNPs to enable genetic prediction of complex traits.

• PGS analysis is becoming increasingly popular with the abundant availability of genome-wide association studies and the development of PGS methods.

• Different PGS methods model the polygenic architecture underlying traits in different ways and often make distinct modeling assumptions on the effect size distribution. These modeling assumptions can help understand the performance of PGS methods across traits with distinct genetic architectures.

• Recent PGS methods focus on making use of summary statistics as input, specify flexible effect size assumptions, incorporate additional information including SNP functional annotations and pleiotropy association evidence across multiple traits, perform multi-ethnic prediction, and rely on computationally efficient algorithms for scalable inference.

• The development of PGS methods is in close connection with the development of methods for SNP heritability estimation, with many common methods shared between the two areas. Experience and lessons learned from SNP heritability estimation can potentially benefit the methodological development for PGS construction.

• For certain diseases, PGS have established initial clinical success and can be especially useful for risk stratification. For the majority of complex traits, however, PGS methods have yet to achieve high prediction accuracy in the general population.

Glossary

Best linear unbiased prediction (BLUP)

BLUP is used in linear mixed models for estimating and predicting the random effects. BLUP is a linear function of the outcome, is an unbiased predictor of the random effects, and is best in the sense that the variance of the prediction error, in the form of the mean squared difference between the estimated values and truth, is not greater than that obtained from any other linear unbiased predictors. The BLUPs of random effects are similar to the best linear unbiased estimates (BLUEs) of fixed effects.

Breeding values

The expected phenotypic values of an individual’s offspring.

Clumping

The procedure of selecting a subset of SNPs that are approximately independent of each other.

Effect size

The coefficient of a SNP genotype on an outcome phenotype of interest. It is closely related to the proportion of phenotypic variance explained by the genotype.

Genome-wide association studies (GWASs)

An experimental design that aims to identify SNPs or other genetic variations associated with traits of interest based on samples collected from populations.

Linkage disequilibrium (LD)

LD describes the phenomenon that two alleles at different loci occur together in the same gamete more often than would be expected by chance alone. The coefficient of LD is defined as the difference between the frequency of gametes carrying the pair of two alleles at two loci and the product of the frequencies of those two alleles. For PGS studies, LD is often calculated as the correlation between SNP genotypes using potentially unphased genotype data.

Phenome-wide association study (PheWAS)

A study that focuses on identifying phenotypes associated with a covariate of interest, which is often a genetic variant or the PGS of another phenotype.

Restricted maximum likelihood (REML)

REML is a particular form of maximum likelihood estimation procedure for linear mixed models to produce unbiased estimates for variance and covariance parameters. It is based on a likelihood function defined on a restricted subset of parameters after integrating out the nuisance parameters.

Risk stratification

The procedure of systemically categorizing individuals into subgroups based on their predicted risks, with a special emphasis on identifying individuals with a particularly high disease risk for optimized medical decision making. Risk stratification is conceptually different from risk prediction which aims to predict disease risk well for all individuals in a population.

Single nucleotide polymorphisms (SNPs)

The most common type of genetic variation at a single position in the DNA sequence. A SNP occurs when a single nucleotide in the genome differs between individuals or between paired chromosomes in an individual.

SNP heritability

The proportion of phenotypic variance in the outcome trait explained by measured SNP genotypes in a GWAS. Most often only additive genetic factors are considered.