Summary
Cancers are routinely classified into subtypes according to various features, including histopathological characteristics and molecular markers. Previous genome-wide association studies have reported heterogeneous associations between loci and cancer subtypes. However, it is not evident what is the optimal modeling strategy for handling correlated tumor features, missing data, and increased degrees-of-freedom in the underlying tests of associations. We propose to test for genetic associations using a mixed-effect two-stage polytomous model score test (MTOP). In the first stage, a standard polytomous model is used to specify all possible subtypes defined by the cross-classification of the tumor characteristics. In the second stage, the subtype-specific case–control odds ratios are specified using a more parsimonious model based on the case–control odds ratio for a baseline subtype, and the case–case parameters associated with tumor markers. Further, to reduce the degrees-of-freedom, we specify case–case parameters for additional exploratory markers using a random-effect model. We use the Expectation–Maximization algorithm to account for missing data on tumor markers. Through simulations across a range of realistic scenarios and data from the Polish Breast Cancer Study (PBCS), we show MTOP outperforms alternative methods for identifying heterogeneous associations between risk loci and tumor subtypes. The proposed methods have been implemented in a user-friendly and high-speed R statistical package called TOP (https://github.com/andrewhaoyu/TOP)
Keywords: Cancer subtypes, EM algorithm, Etiologic heterogeneity, Susceptibility variants, Score tests, Two-stage polytomous model
1. Introduction
Genome-wide association studies (GWAS) have identified hundreds of single nucleotide polymorphisms (SNPs) associated with various cancers (MacArthur and others, 2016). However, many cancer GWAS have often defined cancer endpoints according to specific anatomic sites, and not according to subtypes of the disease. Many cancers consist of etiologically and clinically heterogeneous subtypes that are defined by multiple correlated tumor characteristics. For instance, breast cancer is routinely classified into subtypes defined by tumor expression of estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER2) (Perou and others, 2000 ; Prat and others, 2015).
Increasing numbers of epidemiologic studies with tumor specimens are allowing the characterization of cancers at the histological and molecular levels (Cancer Genome Atlas Network, 2012; Cancer Genome Atlas Research Network, 2014), providing tremendous opportunities to investigate for potential distinct etiological pathways between cancer subtypes. For example, a breast cancer ER-negative specific GWAS reported 20 SNPs that were more strongly associated with the risk of developing ER-negative than ER-positive disease (Milne and others, 2017). Previous studies also suggested traditional breast cancer risk factors, such as age, obesity, and hormone therapy use, were heterogeneously associated with the risk of breast cancer subtypes (Barnard and others, 2015).
The most common procedure for testing for associations between risk factors and cancer subtypes is by fitting a standard logistic regression for each subtype versus a control group, then accounting for multiple testing. However, this procedure has several limitations. First, its common for cancer cases to have missing tumor marker data, leading to many cancer cases with no subtype definition, and often these cases are dropped from the model. Second, the tumor markers that defined the subtypes are commonly highly correlated with each other. Testing each subtype separately without modeling the correlation limits the power of the model. Finally, as the number of tumor markers increases, the number of cancer subtypes dramatically increases, thus the increased degrees of freedom penalizes the power of the model.
A two-stage polytomous logistic regression was previously proposed to characterize subtype heterogeneity of a disease according to the underlying disease characteristics (Chatterjee, 2004). The first stage of this method uses a polytomous logistic regression (Dubin and Pasternack, 1986) to model subtype-specific case–control odds ratios. In the second stage, the subtype-specific case–control odds ratios are decomposed into a case–control odds ratio for a reference subtype, a case–case odds ratio for each tumor characteristic, and higher-order interactions between the tumor characteristics. The two-stage model can reduce the degrees of freedom by constraining some or all of the higher-order interactions to be 0. Moreover, the second stage case–case odds ratios can be interpreted as the measures of etiological heterogeneity for tumor characteristics.
Although the two-stage model can improve the power compared to fitting standard logistic regressions for each subtype (Chatterjee, 2004; Zabor and Begg, 2017), the two-stage model does have notable limitations and has not been widely applied to analyze data on multiple tumor characteristics. First, similar to standard logistic regression, the two-stage model cannot handle missing tumor characteristics, which is common in epidemiologic studies. Second, the two-stage model estimation algorithm places high demands on computing power and is therefore not readily applicable to large datasets. Finally, although the two-stage model can reduce the multiple testing burdens compared to traditional methods, as the number of tumor characteristics increases, the two-stage model can still have substantial power loss due to the degrees of freedom penalty.
In this article, we propose a series of computational and statistical innovations to perform computationally scalable and statistically efficient association tests in large cancer GWASs that incorporate tumor characteristic data. Within this two-stage modeling framework, we propose three alternative types of hypotheses for testing genetic associations in the presence of tumor heterogeneity. As the degrees of freedom for the tests can be large in the presence of many tumor characteristics, we propose modeling parameters associated with exploratory tumor characteristics using a random-effect model. We then derive the score tests under the resulting mixed-effect model while taking into account missing data on tumor characteristics using an efficient EM algorithm (Dempster and others, 1977). All combined, our work represents a conceptually distinct and practically important extension of earlier methods based on mixed-/fixed-effect models (Lin, 1997; Zhang and Lin, 2003; Wu and others, 2011; Sun and others, 2013) to the novel setting of modeling genetic associations with multiple tumor characteristics.
The article is organized as follows. In Section 2, we describe the proposed three different hypothesis tests, the missing data algorithm, and the score tests. In Section 3, we present the simulation results for type I error, power, and computation time. In Section 4, the proposed methods are illustrated with applications using data from the Polish Breast Cancer Study (PBCS). In Section 5, we discuss the strengths and limitations of the methods and future research directions.
2. Method
2.1. Two-stage polytomous logistic model
The details of the two-stage polytomous logistic model have been described earlier (Chatterjee, 2004). We briefly summarize them for completeness. Suppose a disease can be classified using  disease characteristics, and each characteristic
disease characteristics, and each characteristic 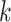 can be classified into
can be classified into 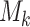 categories; thus, the disease can be classified into
categories; thus, the disease can be classified into 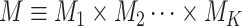 subtypes. For example, breast cancer can be classified into eight subtypes by three tumor characteristics (ER, PR, and HER2), each of which is defined as either positive or negative.
subtypes. For example, breast cancer can be classified into eight subtypes by three tumor characteristics (ER, PR, and HER2), each of which is defined as either positive or negative.
Let 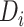 denote the disease status of subject
denote the disease status of subject 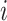 in the study such that
in the study such that 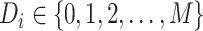 and
and 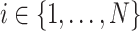 .
. 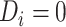 represents a control, and
represents a control, and 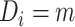 represents a case with disease subtype
represents a case with disease subtype 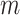 . Let
. Let 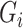 be the genotype for subject
be the genotype for subject 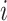 , and
, and 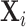 be a
be a 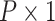 vector of other covariates, where P is the total number of other covariates. In the first stage model, a “saturated” polytomous logistic regression model is constructed as follows:
vector of other covariates, where P is the total number of other covariates. In the first stage model, a “saturated” polytomous logistic regression model is constructed as follows:
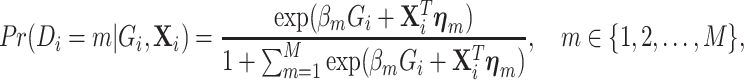 |
(2.1) |
where 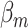 and
and 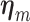 are the regression coefficients for the SNP and other covariates with the
are the regression coefficients for the SNP and other covariates with the 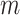 th subtype, respectively.
th subtype, respectively.
Because each cancer subtype is defined through a unique combination of the 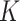 tumor characteristics, we can always alternatively index the parameters
tumor characteristics, we can always alternatively index the parameters 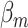 as
as 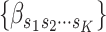 , where
, where 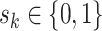 for binary tumor characteristics, and
for binary tumor characteristics, and 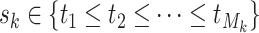 for ordinal tumor characteristics with
for ordinal tumor characteristics with 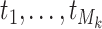 as a set of ordinal scores for
as a set of ordinal scores for 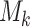 different levels. With this new index, the log odds ratios in the first stage can be represented as follows:
different levels. With this new index, the log odds ratios in the first stage can be represented as follows:
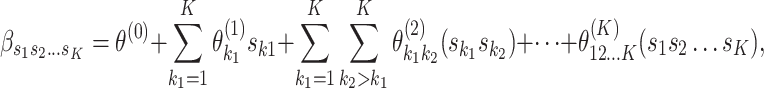 |
(2.2) |
where 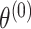 represents the case–control log odds ratio for a reference disease subtype,
represents the case–control log odds ratio for a reference disease subtype, 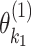 represents the main effect of
represents the main effect of 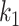 th tumor characteristic,
th tumor characteristic, 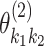 represents the second order interaction between
represents the second order interaction between 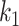 th and
th and 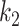 th tumor characteristics , and so on. A reference level can be defined for each tumor characteristic, and the reference disease subtype is jointly defined by the combination of the K tumor characteristics.
th tumor characteristics , and so on. A reference level can be defined for each tumor characteristic, and the reference disease subtype is jointly defined by the combination of the K tumor characteristics.
The reparameterization in (2.2) provides a way to decompose the first stage parameters to a lower dimension. We can constrain different main effects or interaction effects to be 0 to specify different second stage models. The first stage and second stage parameters can be linked with a matrix form, 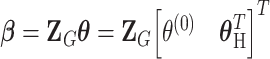 , where
, where 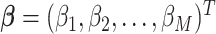 is a vector of first stage case–control log odds ratios for all the M subtypes,
is a vector of first stage case–control log odds ratios for all the M subtypes, 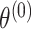 is the case–control log odds ratio for a reference subtype, and
is the case–control log odds ratio for a reference subtype, and 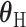 is a vector containing the main effects and interactions effects in the second stage. We will refer to
is a vector containing the main effects and interactions effects in the second stage. We will refer to 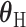 as case–case parameters, and
as case–case parameters, and 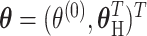 as the vector of second stage parameters.
as the vector of second stage parameters. 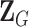 is the second stage design matrix connecting the first stage and second stage parameters. By constraining different second stage main effects or interaction effects to be 0, we can construct different
is the second stage design matrix connecting the first stage and second stage parameters. By constraining different second stage main effects or interaction effects to be 0, we can construct different 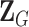 to build different two-stage models.
to build different two-stage models.
Up to now, we have only described second stage decomposition for the regression coefficients of 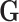 . The second stage decomposition can also be applied to the other covariates, the details of which are in Section 1 of the Supplementary material available at Biostatistics online. We suggest not to perform second stage decomposition on the intercepts parameters of the first stage polytomous model, i.e., the coefficients of intercepts are saturated, because decomposing the intercepts equates to making assumptions on the prevalence of different cancer subtypes, which can potentially lead to bias. Moving forward, we use
. The second stage decomposition can also be applied to the other covariates, the details of which are in Section 1 of the Supplementary material available at Biostatistics online. We suggest not to perform second stage decomposition on the intercepts parameters of the first stage polytomous model, i.e., the coefficients of intercepts are saturated, because decomposing the intercepts equates to making assumptions on the prevalence of different cancer subtypes, which can potentially lead to bias. Moving forward, we use 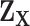 to denote the second stage design matrix for the other covariates
to denote the second stage design matrix for the other covariates 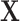 ,
, 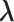 to denote the second stage parameters for
to denote the second stage parameters for 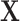 , and
, and 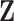 to denote the second stage design matrix for all the covariates.
to denote the second stage design matrix for all the covariates.
2.2. Hypothesis test under two-stage model
The first stage case–control log odds ratios of subtypes can be decomposed into the second stage case–control log odds ratio of the reference subtype, main effects and interaction effects of tumor characteristics. This decomposition presents multiple options for comprehensively testing for the association between a SNP and cancer subtypes. The first hypothesis test is the global association test, 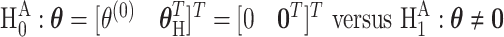 , which tests for an overall association between the SNP and the disease. Because
, which tests for an overall association between the SNP and the disease. Because 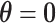 implies
implies  , rejecting this null hypothesis means the SNP is associated with at least one of the subtypes. The null hypothesis can be rejected if the SNP is significantly associated with a similar effect size across all subtypes (i.e.,
, rejecting this null hypothesis means the SNP is associated with at least one of the subtypes. The null hypothesis can be rejected if the SNP is significantly associated with a similar effect size across all subtypes (i.e.,  ,
, 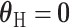 ), or if the SNP has heterogeneous effects on different subtypes (
), or if the SNP has heterogeneous effects on different subtypes (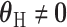 ).
).
The second hypothesis test is the global heterogeneity test, 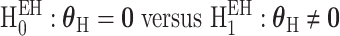 . This test simultaneously evaluates the etiologic heterogeneity with respect to a SNP and all the tumor characteristics. Rejecting this null hypothesis indicates that the first stage case–control log odds ratios are significantly different between at least two different subtypes.
. This test simultaneously evaluates the etiologic heterogeneity with respect to a SNP and all the tumor characteristics. Rejecting this null hypothesis indicates that the first stage case–control log odds ratios are significantly different between at least two different subtypes.
Notably, the global heterogeneity test does not identify which tumor characteristic(s) is/are driving the heterogeneity. To identify the tumor characteristic(s) responsible for observed heterogeneity, we propose the individual tumor marker heterogeneity test, 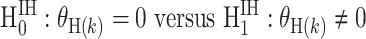 , where
, where 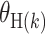 is one of the case–case parameters of
is one of the case–case parameters of 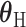 . The case–case parameter (
. The case–case parameter (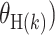 provides a measurement of etiological heterogeneity according to a specific tumor characteristic (Begg and Zhang, 1994). In the breast cancer example, we can directly test
provides a measurement of etiological heterogeneity according to a specific tumor characteristic (Begg and Zhang, 1994). In the breast cancer example, we can directly test 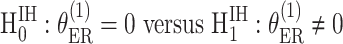 . Rejecting the null hypothesis provides evidence that the case–control log odds ratios of ER+ and ER
. Rejecting the null hypothesis provides evidence that the case–control log odds ratios of ER+ and ER subtypes are significantly different.
subtypes are significantly different.
2.3. EM algorithm accounting for cases with incomplete tumor characteristics
In the previous sections, all the tumor characteristics were assumed to have no missing data. However, in epidemiological research, it is very common to have missing tumor characteristics. This problem becomes exacerbated as the number of tumor characteristics grows. Restricting to cases with complete tumor characteristics can reduce statistical power and potentially introduce selection bias. To solve this problem, we propose to use the EM algorithm (Dempster and others, 1977) to find the maximum likelihood estimate (MLE) of the two-stage model, while incorporating all available information from the study. Let 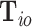 be the observed tumor characteristics of subject
be the observed tumor characteristics of subject 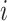 , and
, and 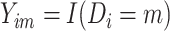 denote whether the
denote whether the 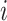 th subject is disease subtype
th subject is disease subtype 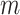 . Given
. Given 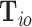 , the possible subtypes for subject
, the possible subtypes for subject 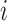 , denoted as
, denoted as 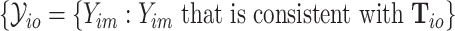 , are within a limited subset of all possible tumor subtypes. We assume that
, are within a limited subset of all possible tumor subtypes. We assume that 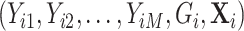 are independently and identically distributed (i.i.d.), and that the tumor characteristics are missing at random (MAR). Let
are independently and identically distributed (i.i.d.), and that the tumor characteristics are missing at random (MAR). Let 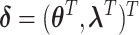 represent the second stage parameters of both
represent the second stage parameters of both 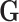 and
and 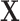 . Given the notation, the E step of them EM algorithm at the
. Given the notation, the E step of them EM algorithm at the 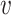 th iteration is
th iteration is
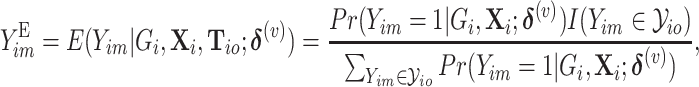 |
(2.3) |
where 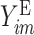 is the probability of the
is the probability of the 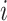 th person to be the
th person to be the 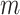 th subtype given his observed tumor characteristics (
th subtype given his observed tumor characteristics (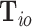 ), genotype (
), genotype (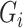 ), and other covariates
), and other covariates 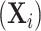 .
. 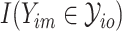 denotes whether the
denotes whether the 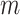 th subtype for the
th subtype for the 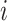 th subject belong to the subsets of possible subtypes given the observed tumor characteristics. The M step at the
th subject belong to the subsets of possible subtypes given the observed tumor characteristics. The M step at the 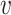 th iteration is
th iteration is
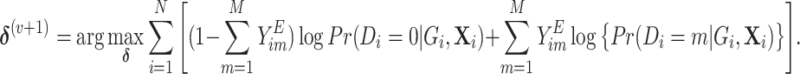 |
(2.4) |
The M step can be solved through a weighted least square iteration. Let 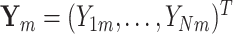 , and
, and 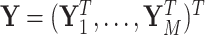 . Let
. Let 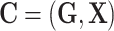 , and
, and 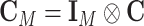 . Let
. Let 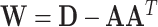 ,
, 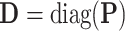 ,
, 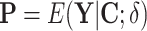 , and
, and 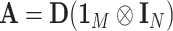 . During the
. During the 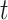 th iteration of the weighted least square,
th iteration of the weighted least square, 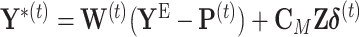 , where
, where 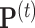 and
and 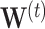 are respectively defined as
are respectively defined as 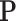 and
and 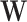 evaluated at the
evaluated at the 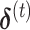 . The weighted least square update is
. The weighted least square update is 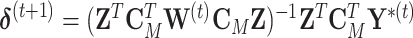 . As
. As 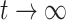 , the weighted least square interaction converges to
, the weighted least square interaction converges to 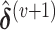 , which will be used in next iteration. The EM algorithm will converge to the MLE of the second stage parameters (denoted as
, which will be used in next iteration. The EM algorithm will converge to the MLE of the second stage parameters (denoted as  ), and the observed information matrix
), and the observed information matrix 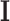 is
is 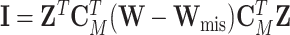 , where
, where 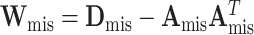 ,
, 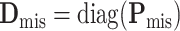 ,
,  , and
, and 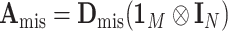 (Louis, 1982). More details of the EM algorithm are in Section 2 of the Supplementary material at Biostatistics online.
(Louis, 1982). More details of the EM algorithm are in Section 2 of the Supplementary material at Biostatistics online.
With the MLE of the second stage parameters of G as 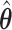 , we can construct the Wald statistics as
, we can construct the Wald statistics as 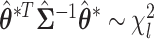 for the global association test, global etiological heterogeneity test, and individual tumor characteristic heterogeneity test using the corresponding second stage parameters and covariance matrix, where the degrees of freedom
for the global association test, global etiological heterogeneity test, and individual tumor characteristic heterogeneity test using the corresponding second stage parameters and covariance matrix, where the degrees of freedom 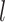 equal the length of
equal the length of 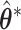 .
.
2.4. Fixed-effect two-stage polytomous model score test
Although the hypothesis tests can be implemented through the Wald test, estimating the model parameters for all SNPs in the genome is time-consuming and computationally intensive. In this section, we develop a score test for the global association test assuming the second stage parameters to be fixed. The score test only needs to estimate the second stage parameters of 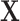 under the null hypothesis once, making it much more computationally efficient than the Wald test. Moreover, the EM algorithm only needs to be implemented once under the null hypothesis. Since we don’t perform any second stage decomposition on the intercept parameters in the first stage polytomous model, the correlations between the tumor characteristics are kept close to the empirical correlations for tumor markers. Most of the imputation power is due to the high correlation between the tumor markers. In the breast cancer example, the correlation between ER and PR is 0.63, between ER and HER2 is
under the null hypothesis once, making it much more computationally efficient than the Wald test. Moreover, the EM algorithm only needs to be implemented once under the null hypothesis. Since we don’t perform any second stage decomposition on the intercept parameters in the first stage polytomous model, the correlations between the tumor characteristics are kept close to the empirical correlations for tumor markers. Most of the imputation power is due to the high correlation between the tumor markers. In the breast cancer example, the correlation between ER and PR is 0.63, between ER and HER2 is  0.16, and between PR and HER2 is
0.16, and between PR and HER2 is  0.17 (Table 1 of the Supplementary material at Biostatistics online). Also, The association of
0.17 (Table 1 of the Supplementary material at Biostatistics online). Also, The association of 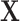 with the tumor markers can improve the power of the EM algorithm. Since a single SNP
with the tumor markers can improve the power of the EM algorithm. Since a single SNP 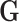 usually has a small effect, the fact that the effect of individual
usually has a small effect, the fact that the effect of individual 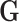 is not incorporated in the EM algorithm itself doesn’t result in much loss of efficiency.
is not incorporated in the EM algorithm itself doesn’t result in much loss of efficiency.
Table 1.
Type I error estimates of MTOP, FTOP with 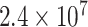 randomly simulated samples. Global association test and global heterogeneity test were applied with FTOP and MTOP. Heterogeneity test for a tumor marker was only applied with FTOP. All of the type error rates are divided by the
randomly simulated samples. Global association test and global heterogeneity test were applied with FTOP and MTOP. Heterogeneity test for a tumor marker was only applied with FTOP. All of the type error rates are divided by the 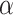 level. If the value is 1, then the type I error is well controlled. If the value is less than 1, then the type I error is conservative.
level. If the value is 1, then the type I error is well controlled. If the value is less than 1, then the type I error is conservative.
| Interested tests | Total sample size |
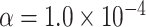
|
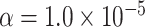
|
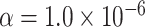
|
|---|---|---|---|---|
| MTOP | ||||
| Global association test | 5000 |
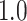
|
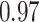
|
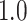
|
| 50 000 |
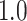
|
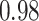
|
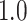
|
|
| 100 000 |
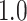
|
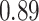
|
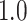
|
|
| Global heterogeneity test | 5000 |
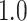
|
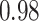
|
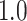
|
| 50 000 |
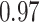
|
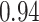
|
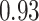
|
|
| 100 000 |
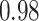
|
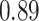
|
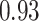
|
|
| FTOP | ||||
| Global association test | 5000 |
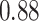
|
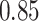
|
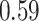
|
| 50 000 |
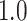
|

|
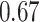
|
|
| 100 000 |
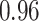
|
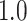
|
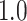
|
|
| Global heterogeneity test | 5000 |
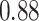
|
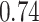
|
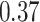
|
| 50 000 |
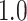
|
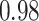
|
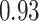
|
|
| 100 000 |
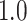
|
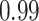
|
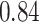
|
|
| Heterogeneity test for | 5000 |
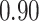
|
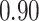
|
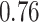
|
| a tumor marker | 50 000 |
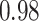
|
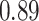
|
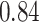
|
| 100 000 |
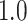
|
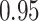
|

|
|
Let 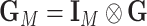 and
and 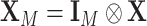 . Under the null hypothesis,
. Under the null hypothesis, 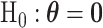 , let
, let 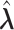 denote the MLE of
denote the MLE of 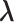 under the null hypothesis. The efficient score of
under the null hypothesis. The efficient score of 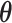 is
is 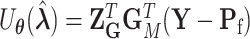 , where
, where 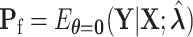 . Let
. Let 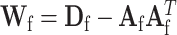 , with
, with 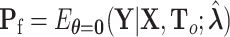 ,
, 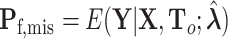 ,
, 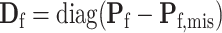 and
and 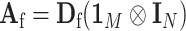 . The corresponding efficient information matrix of
. The corresponding efficient information matrix of 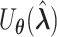 is
is
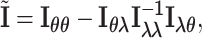 |
(2.5) |
where 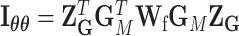 ,
, 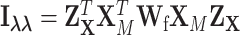 , and
, and 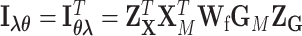 .
.
The score test statistic 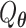 for fixed-effect two-stage model is
for fixed-effect two-stage model is
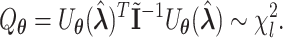 |
(2.6) |
Fixed-effect two-stage polytomous model score test (FTOP) has the same degrees of freedoms and similar asymptotic power (Yi and Wang, 2011) as the Wald test. In GWAS which needs to perform millions of tests, FTOP can be first used to scan the whole genome with global association test, and then select the potential risk regions. In the selected risk regions, each SNP can be tested for global heterogeneity and individual tumor characteristic heterogeneity using Wald test.
2.5. Mixed-effect two-stage polytomous model score test
The two-stage model decreases the degrees of freedom compared to the polytomous logistic regression. However, the power gains in the two-stage model can be reduced as additional tumor characteristics are added into the model. We further propose a mixed-effect two-stage model by modeling some of the second stage case–case parameters as random effects. Let 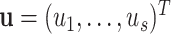 , where each
, where each 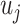 follows an arbitrary distribution
follows an arbitrary distribution 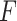 with mean zero and variance
with mean zero and variance 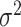 . The mixed-effect second stage model links the first and second stage parameters as follows:
. The mixed-effect second stage model links the first and second stage parameters as follows:
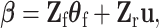 |
(2.7) |
where 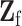 is the second stage design matrix of fixed effect,
is the second stage design matrix of fixed effect, 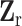 is the second stage design matrix of random effect, and
is the second stage design matrix of random effect, and 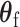 are the fixed-effect second stage parameters. Let
are the fixed-effect second stage parameters. Let 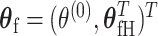 , where
, where 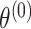 is the case–control log odds ratio of the reference subtype, and
is the case–control log odds ratio of the reference subtype, and 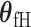 are the fixed case–case parameters. The baseline effect
are the fixed case–case parameters. The baseline effect 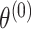 is always kept fixed, since it captures the SNP’s overall effect on all the cancer subtypes.
is always kept fixed, since it captures the SNP’s overall effect on all the cancer subtypes.
The fixed-effect parameters 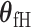 can be used for tumor characters with prior information suggesting that they are a source of heterogeneity, and the random-effect parameters
can be used for tumor characters with prior information suggesting that they are a source of heterogeneity, and the random-effect parameters 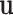 can model tumor characteristics with little or no prior information. In the breast cancer example, the baseline parameter (
can model tumor characteristics with little or no prior information. In the breast cancer example, the baseline parameter (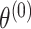 ) and the main effect of ER (
) and the main effect of ER (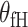 ) can be modeled as fixed effects, since previous evidence indicates ER as a source of breast cancer heterogeneity (García-Closas and others, 2013; Milne and others, 2017). The main effects of PR and HER2 and other potential interactions effects can be modeled as random effects (
) can be modeled as fixed effects, since previous evidence indicates ER as a source of breast cancer heterogeneity (García-Closas and others, 2013; Milne and others, 2017). The main effects of PR and HER2 and other potential interactions effects can be modeled as random effects (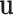 ). In the mixed-effect two-stage model, the global association test is
). In the mixed-effect two-stage model, the global association test is 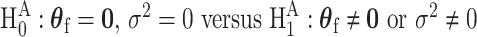 , and the global etiology heterogeneity test is
, and the global etiology heterogeneity test is 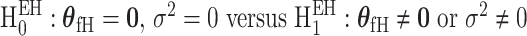 .
.
To derive the score statistic for the global null 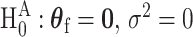 , the common approach is to take the partial derivatives of loglikelihood with respective to
, the common approach is to take the partial derivatives of loglikelihood with respective to 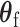 and
and 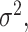 respectively. However, under the null hypothesis, the score for
respectively. However, under the null hypothesis, the score for 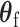 follows a normal distribution, and for
follows a normal distribution, and for  follows a mixture of chi-square distribution (Section 3 of the Supplementary material at Biostatistics online). With the correlation between the two scores, getting the joint distribution between the two becomes very complicated. Inspired by methods for the rare variants testing (Sun and others, 2013), we propose to modify the derivations of score statistic so that two independent scores can be independent. First for
follows a mixture of chi-square distribution (Section 3 of the Supplementary material at Biostatistics online). With the correlation between the two scores, getting the joint distribution between the two becomes very complicated. Inspired by methods for the rare variants testing (Sun and others, 2013), we propose to modify the derivations of score statistic so that two independent scores can be independent. First for 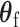 , the score test statistic
, the score test statistic 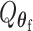 is derived under the global null hypothesis
is derived under the global null hypothesis 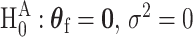 as usual. But for
as usual. But for 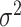 , the score statistic
, the score statistic 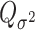 is derived under the null hypothesis
is derived under the null hypothesis 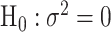 without constraining
without constraining 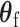 . Through this procedure, the two score test statistics (
. Through this procedure, the two score test statistics (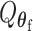 and
and 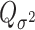 ) can be proved to be independent (Section 4 of the Supplementary material at Biostatistics online), and the Fisher’s procedure (Koziol and Perlman, 1978) can be used to combine the P-value generated from the two independent tests. Similarly to FTOP, the EM algorithm under the null hypothesis of mixed-effect two-stage polytomous model score test (MTOP) can efficiently handle the missing tumor marker problems given the high correlations between the tumor characteristics. However, since MTOP needs to estimate
) can be proved to be independent (Section 4 of the Supplementary material at Biostatistics online), and the Fisher’s procedure (Koziol and Perlman, 1978) can be used to combine the P-value generated from the two independent tests. Similarly to FTOP, the EM algorithm under the null hypothesis of mixed-effect two-stage polytomous model score test (MTOP) can efficiently handle the missing tumor marker problems given the high correlations between the tumor characteristics. However, since MTOP needs to estimate 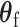 under the null hypothesis
under the null hypothesis 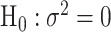 for every single SNP, the computation speed for MTOP is slower than FTOP.
for every single SNP, the computation speed for MTOP is slower than FTOP.
The score statistic of the fixed effect 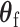 under the global null
under the global null 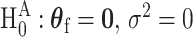 is
is
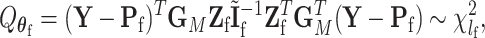 |
(2.8) |
where 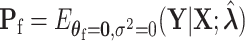 . Here
. Here 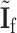 has the same definition as (2.5), but substitute
has the same definition as (2.5), but substitute 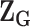 with
with 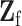 . Under the null hypothesis,
. Under the null hypothesis, 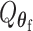 follows a
follows a 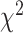 distribution with the degrees of freedom
distribution with the degrees of freedom 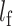 the same as the length of
the same as the length of 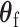 .
.
To explicitly express 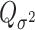 , let
, let 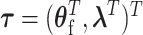 be the second stage fixed effect, and
be the second stage fixed effect, and 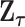 is the corresponding second stage design matrix. The variance component score statistic of
is the corresponding second stage design matrix. The variance component score statistic of 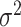 under the null hypothesis
under the null hypothesis 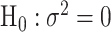 without constraining
without constraining 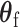 is as follows:
is as follows:
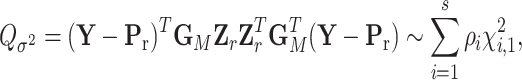 |
(2.9) |
where 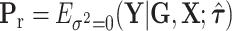 , and
, and 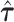 is the MLE under the null hypothesis,
is the MLE under the null hypothesis, 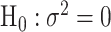 . Under the null hypothesis,
. Under the null hypothesis, 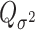 follows a mixture of chi-square distribution (Section 3 of the Supplementary material at Biostatistics online), where
follows a mixture of chi-square distribution (Section 3 of the Supplementary material at Biostatistics online), where 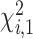 i.i.d. follows
i.i.d. follows 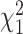 .
. 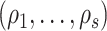 are the eigenvalues of
are the eigenvalues of 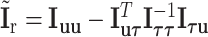 , with
, with 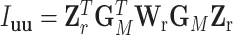 ,
, 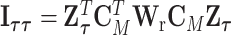 and
and 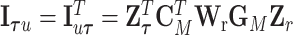 , where
, where 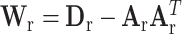 , with
, with 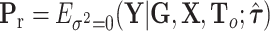 ,
, 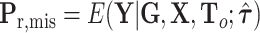 ,
, 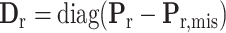 and
and 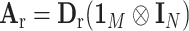 . The Davies exact method (Davies, 1980) is used here to calculate the P-value of the mixture of chi-square distribution.
. The Davies exact method (Davies, 1980) is used here to calculate the P-value of the mixture of chi-square distribution.
Let 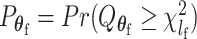 and
and 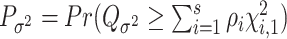 be the P-values of the two independent score statistics. Under the null hypothesis
be the P-values of the two independent score statistics. Under the null hypothesis 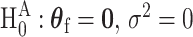 , following the Fisher’s procedure,
, following the Fisher’s procedure, 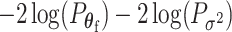 follows
follows 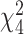 ; thus, the P-value of mixed effect two-stage model under the null hypothesis is
; thus, the P-value of mixed effect two-stage model under the null hypothesis is
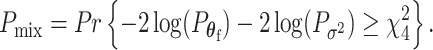 |
(2.10) |
The extension of the score statistics of the global etiology heterogeneity test, 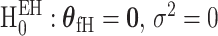 , can be computed following a similar procedure as the global association test.
, can be computed following a similar procedure as the global association test.
3. Simulation experiments
Large scale simulations across a wide range of practical scenarios were conducted to evaluate the type I error (Section 3.1), statistical power (Section 3.2), and computation time (Section 5 of the Supplementary material at Biostatistics online) of the fixed-effect and mixed-effect two-stage models. Data were simulated to mimic the PBCS. We simulated four tumor characteristics: ER (positive vs. negative), PR (positive vs. negative), HER2 (positive vs. negative), and grade (ordinal 1, 2, 3), which collectively defined 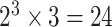 breast cancer subtypes.
breast cancer subtypes.
In each simulation, genotype data 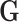 was simulated under the Hardy–Weinberg equilibrium with minor allele frequency (MAF) as 0.25. An additional covariate (
was simulated under the Hardy–Weinberg equilibrium with minor allele frequency (MAF) as 0.25. An additional covariate (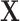 ) was simulated following a standard normal distribution independent of
) was simulated following a standard normal distribution independent of 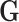 . We simulated a multinomial outcome with 25 groups, one for the control group, and the other 24 for different cancer subtypes, using the polytomous logistic regression model as follows:
. We simulated a multinomial outcome with 25 groups, one for the control group, and the other 24 for different cancer subtypes, using the polytomous logistic regression model as follows:
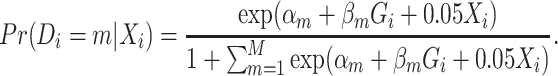 |
(3.1) |
The effect of 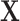 was set as 0.05 for all subtypes. Using the frequency of the breast cancer subtypes from Breast Cancer Association Consortium (Table S2 of the Supplementary material at Biostatistics online) (Michailidou and others, 2017), we computed the corresponding polytomous logistic regression intercept parameters
was set as 0.05 for all subtypes. Using the frequency of the breast cancer subtypes from Breast Cancer Association Consortium (Table S2 of the Supplementary material at Biostatistics online) (Michailidou and others, 2017), we computed the corresponding polytomous logistic regression intercept parameters 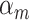 . The case-control ratio was set around 1:1, and the proportions of ER+, PR+, and HER2+ were 0.81, 0.68, and 0.17, respectively. The proportions of grade 1, 2, and 3 were 0.20, 0.48, and 0.32. The missing tumor markers were selected randomly with missing rates of 0.17, 0.25, 0.42, and 0.27 for ER, PR, HER2, and grade, respectively. Under this simulation, approximately
. The case-control ratio was set around 1:1, and the proportions of ER+, PR+, and HER2+ were 0.81, 0.68, and 0.17, respectively. The proportions of grade 1, 2, and 3 were 0.20, 0.48, and 0.32. The missing tumor markers were selected randomly with missing rates of 0.17, 0.25, 0.42, and 0.27 for ER, PR, HER2, and grade, respectively. Under this simulation, approximately 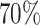 cases had at least one missing tumor characteristic.
cases had at least one missing tumor characteristic.
3.1. Type I error
We evaluated the type I error of the global association test, global heterogeneity test, and individual tumor marker heterogeneity test under the global null hypothesis. The data were generated by setting 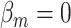 in (3.1), where none of the subtypes was associated with genotypes. The total sample size
in (3.1), where none of the subtypes was associated with genotypes. The total sample size 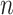 was set to be 5000, 50 000, and 100 000. We conducted
was set to be 5000, 50 000, and 100 000. We conducted 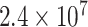 simulations to evaluate the type I error at
simulations to evaluate the type I error at 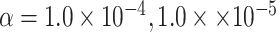 , and
, and 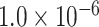 level.
level.
Both MTOP and FTOP were applied with an additive two-stage model by constraining all the interaction terms as 0 in (2.2). The subtype-specific case–control log ORs were specified into the case–control log OR of a baseline disease subtype (ER , PR
, PR , HER2
, HER2 , grade 1) and the main effects associated with the four tumor markers. Furthermore, the MTOP assumed the baseline and ER case–case parameter as fixed effects and the other case–case parameters as random effects. The global association test and global heterogeneity test were implemented using both MTOP and FTOP, but the individual tumor characteristic heterogeneity test could only be implemented with FTOP. For MTOP and FTOP, we removed all the subtypes with fewer than 10 cases to avoid potential nonconvergence of the model.
, grade 1) and the main effects associated with the four tumor markers. Furthermore, the MTOP assumed the baseline and ER case–case parameter as fixed effects and the other case–case parameters as random effects. The global association test and global heterogeneity test were implemented using both MTOP and FTOP, but the individual tumor characteristic heterogeneity test could only be implemented with FTOP. For MTOP and FTOP, we removed all the subtypes with fewer than 10 cases to avoid potential nonconvergence of the model.
Table 1 presents the estimated type I errors under the global null hypothesis. Both MTOP and FTOP correctly control the type I error, especially for the larger sample sizes. FTOP is conservative with 5000 subjects, especially for 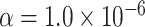 ; however, the method is still valid. The well-controlled type I error also shows that removing rare subtypes doesn’t bias the estimate, as further demonstrated by additional simulations that are presented in Section 6 of the Supplementary material at Biostatistics online. In the later sections, we generally used the additive second stage structure for both MTOP and FTOP unless otherwise specified.
; however, the method is still valid. The well-controlled type I error also shows that removing rare subtypes doesn’t bias the estimate, as further demonstrated by additional simulations that are presented in Section 6 of the Supplementary material at Biostatistics online. In the later sections, we generally used the additive second stage structure for both MTOP and FTOP unless otherwise specified.
3.2. Statistical power
We assessed the statistical power of the proposed methods using various simulation settings with sample sizes as 25 000, 50 000, and 100 000. For each setting, we performed 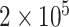 simulations to evaluate the power at
simulations to evaluate the power at 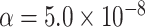 level.
level.
3.2.1. Global association test
The data were simulated with three different scenarios: I. no heterogeneity between tumor markers, II. heterogeneity according to one tumor marker, and III. heterogeneity according to multiple tumor markers. The disease subtypes were generated through (3.1). Under scenario I, we set 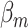 as 0.08 for all the subtypes. For scenarios II and III,
as 0.08 for all the subtypes. For scenarios II and III, 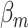 was simulated following the additive two-stage model. Under scenarios II, datasets were simulated with only ER heterogeneity by setting the case–case parameter for ER as 0.08, and all the other as 0. For scenario III, we simulated a scenario with heterogeneity according to all 4 tumor markers by setting the baseline effect to be 0, the ER case–case parameter to be 0.08, and all the other case–case parameters following a normal distribution with mean 0 and variance
was simulated following the additive two-stage model. Under scenarios II, datasets were simulated with only ER heterogeneity by setting the case–case parameter for ER as 0.08, and all the other as 0. For scenario III, we simulated a scenario with heterogeneity according to all 4 tumor markers by setting the baseline effect to be 0, the ER case–case parameter to be 0.08, and all the other case–case parameters following a normal distribution with mean 0 and variance 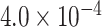 . Under this scenario, all tumor characteristics contributed to the subtype-specific heterogeneity. Moreover, to evaluate different methods under a larger number of tumor characteristics, additional simulations were conducted by adding two additional binary tumor characteristics to the previous four tumor characteristic setting. This defined
. Under this scenario, all tumor characteristics contributed to the subtype-specific heterogeneity. Moreover, to evaluate different methods under a larger number of tumor characteristics, additional simulations were conducted by adding two additional binary tumor characteristics to the previous four tumor characteristic setting. This defined 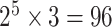 cancer subtypes. The two additional tumor characteristics were randomly selected to be missing with
cancer subtypes. The two additional tumor characteristics were randomly selected to be missing with 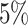 missing rate. Under this setting, around
missing rate. Under this setting, around 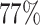 of the cases have at least one tumor characteristic missing. We compared the statistical power to detect the overall association using FTOP, MTOP, standard logistic regression, FTOP with only complete data, and polytomous logistic regression. For MTOP, FTOP, and polytomous model, we removed all the subtypes with fewer than 10 cases to avoid potential nonconvergence of the model.
of the cases have at least one tumor characteristic missing. We compared the statistical power to detect the overall association using FTOP, MTOP, standard logistic regression, FTOP with only complete data, and polytomous logistic regression. For MTOP, FTOP, and polytomous model, we removed all the subtypes with fewer than 10 cases to avoid potential nonconvergence of the model.
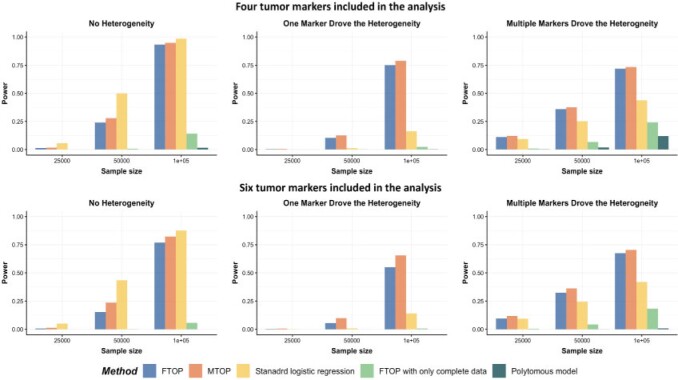
Overall, MTOP had robust power under all scenarios (Figure 1). Standard logistic regression had the highest power when there was no subtype-specific heterogeneity (scenario I), but suffered from substantial power loss when heterogeneity existed between subtypes. MTOP, followed by FTOP, consistently demonstrated the highest power among the five methods when subtype-specific heterogeneity existed (scenarios II and III). The power gain of MTOP over FTOP ranged from 2% to 49%. The power gain was small when there were four tumor characteristics because the difference in the degrees of freedom between MTOP and FTOP was small. However, with six tumor markers, the power gain of MTOP was more apparent owing to the larger difference in the degrees of freedom between the models. FTOP was the least efficient in scenarios with no or little heterogeneity, such as scenarios I and II, but with increasing heterogeneity, such as scenario III, the power of MTOP and FTOP were more similar.
Fig. 1.
Power comparison among MTOP, FTOP, standard logistic regression, two-stage model with only complete data and polytomous model with 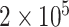 random samples. For the three figures in the first row, four tumor markers were included in the analysis. Three binary tumor marker and one ordinal tumor marker defined 24 cancer subtypes. Around
random samples. For the three figures in the first row, four tumor markers were included in the analysis. Three binary tumor marker and one ordinal tumor marker defined 24 cancer subtypes. Around 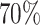 cases would be incomplete. For the three figures in the second row, two extra binary tumor markers were included in the analysis. The six tumor markers defined 96 subtypes. Around
cases would be incomplete. For the three figures in the second row, two extra binary tumor markers were included in the analysis. The six tumor markers defined 96 subtypes. Around 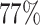 cases would be incomplete. The power was estimated by controlling the type I error
cases would be incomplete. The power was estimated by controlling the type I error 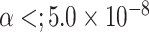 .
.
The simulation study also showed that the incorporation of cases with missing tumor characteristics significantly increased the power of the methods (Figure 1). Under the four tumor markers setting with around 70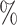 incomplete cases, the power gain of FTOP incorporating the missing data algorithm was at least
incomplete cases, the power gain of FTOP incorporating the missing data algorithm was at least 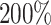 compared to FTOP with only complete data. As expected, under the six tumor markers setting, which resulted in more missing tumor marker data, the power of FTOP with the missing data algorithm was once again significantly higher than FTOP with only complete data. MTOP was the most powerful method when heterogeneity across cancer subtypes was present. Additional power simulations with 5000 subjects are described in Section 7 of the Supplementary material at Biostatistics online.
compared to FTOP with only complete data. As expected, under the six tumor markers setting, which resulted in more missing tumor marker data, the power of FTOP with the missing data algorithm was once again significantly higher than FTOP with only complete data. MTOP was the most powerful method when heterogeneity across cancer subtypes was present. Additional power simulations with 5000 subjects are described in Section 7 of the Supplementary material at Biostatistics online.
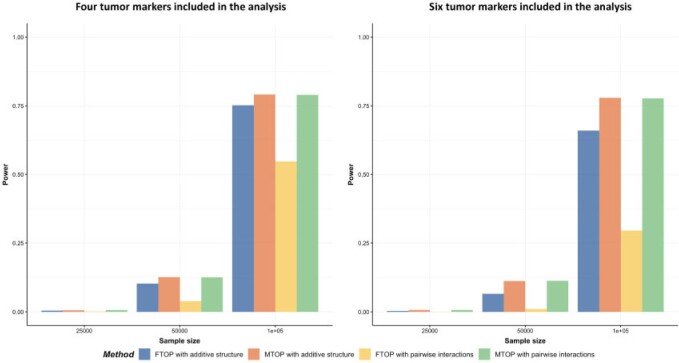
The previous simulations mainly focused on the two-stage model with additive effects. Additional simulations were also implemented with pairwise interactions in the model. We simulated data with 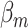 following a second stage model that included main effects and pairwise interactions as shown in (2.2) with the case–case parameter for ER
following a second stage model that included main effects and pairwise interactions as shown in (2.2) with the case–case parameter for ER 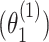 as 0.08, the pairwise interaction effect between ER and HER2
as 0.08, the pairwise interaction effect between ER and HER2  as 0.04, and all the other parameters as 0. Four methods were evaluated including FTOP with/without pairwise interactions and MTOP with/without pairwise interactions (baseline and ER fixed). FTOP without interaction terms still had high power (Figure 2). However, FTOP with pairwise interaction structure had limited power because of the incorporation of the interaction terms as fixed effects. On the other hand, MTOP with/without pairwise interactions maintained a high power even when there were underlying interaction effects.
as 0.04, and all the other parameters as 0. Four methods were evaluated including FTOP with/without pairwise interactions and MTOP with/without pairwise interactions (baseline and ER fixed). FTOP without interaction terms still had high power (Figure 2). However, FTOP with pairwise interaction structure had limited power because of the incorporation of the interaction terms as fixed effects. On the other hand, MTOP with/without pairwise interactions maintained a high power even when there were underlying interaction effects.
Fig. 2.
Power comparison of global association test with pairwise interactions. Four methods were evaluated, including FTOP with additive structure, MTOP with additive structure (ER fixed), FTOP with pairwise interactions and MTOP with pairwise interactions (ER fixed). For the three figures in the first row, four tumor markers were included in the analysis. Three binary tumor marker and one ordinal tumor marker defined 24 cancer subtypes. Around 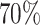 cases were incomplete. For the three figures in the second row, two extra binary tumor markers were included in the analysis. The six tumor markers defined 96 subtypes. Around
cases were incomplete. For the three figures in the second row, two extra binary tumor markers were included in the analysis. The six tumor markers defined 96 subtypes. Around 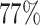 cases were incomplete. The total sample size was 25 000, 50 000, and 100 000. We generated
cases were incomplete. The total sample size was 25 000, 50 000, and 100 000. We generated 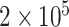 random replicates. The power was estimated by controlling the type I error
random replicates. The power was estimated by controlling the type I error  .
.
3.2.2. Global heterogeneity test
Figure S3 of the Supplementary material at Biostatistics online shows the simulation results for global heterogeneity tests under similar simulation settings as global association tests. MTOP had the highest power when there were heterogeneous associations across the subtypes.
3.2.3. Individual tumor marker heterogeneity test
We further evaluated the power of the individual tumor marker heterogeneity test. The data were generated with four tumor characteristics with the ER case–case parameter (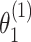 ) as 0.08, and all other parameters as 0. ER was randomly selected to be missing with a rate of 0.17, 0.30, and 0.50. We compared two different methods, FTOP with all four tumor characteristics and the polytomous model. The polytomous model was set up to test each marker at a time. In the polytomous model, we removed cases with missing data only on the relevant tumor marker to avoid penalizing the power of the model by removing cases that were missing tumor marker data on the other tumor markers. FTOP with all four tumor characteristics had smaller power compared to the polytomous model in testing the effect of ER (Figure S4 of the Supplementary material at Biostatistics online). Since FTOP included all four tumor characteristics, and the tumor markers were highly correlated, the variability of underlying parameters was larger. However, the type I errors of the polytomous model in testing PR, HER2 and grade were inflated under this case (Figure S5 of the Supplementary material at Biostatistics online). Under this simulation, these three markers had no effect. On the other hand, FTOP controlled the type I error of all the tests.
) as 0.08, and all other parameters as 0. ER was randomly selected to be missing with a rate of 0.17, 0.30, and 0.50. We compared two different methods, FTOP with all four tumor characteristics and the polytomous model. The polytomous model was set up to test each marker at a time. In the polytomous model, we removed cases with missing data only on the relevant tumor marker to avoid penalizing the power of the model by removing cases that were missing tumor marker data on the other tumor markers. FTOP with all four tumor characteristics had smaller power compared to the polytomous model in testing the effect of ER (Figure S4 of the Supplementary material at Biostatistics online). Since FTOP included all four tumor characteristics, and the tumor markers were highly correlated, the variability of underlying parameters was larger. However, the type I errors of the polytomous model in testing PR, HER2 and grade were inflated under this case (Figure S5 of the Supplementary material at Biostatistics online). Under this simulation, these three markers had no effect. On the other hand, FTOP controlled the type I error of all the tests.
Overall, for the global test for association and the global test for heterogeneity, when there was no heterogeneity, the standard logistic regression was the most powerful method. However, in the presence of subtype heterogeneity, MTOP was the most powerful method, and MTOP had stable power even with a large number of pairwise interactions terms included.
4. Aplication to the PBCS
We applied our proposed methods to the PBCS, a population-based breast cancer case-control study conducted in Poland between 2000 and 2003 (García-Closas and others, 2006). The study consisted of 2078 cases of histologically or cytologically confirmed invasive breast cancer and 2219 women without a history of breast cancer at enrollment. Information on ER, PR, and grade were available from pathology records (García-Closas and others, 2006), and information on HER2 was available from immunohistochemical staining of tissue microarray blocks (Yang and others, 2007). We used genome-wide genotyping data to compare MTOP, FTOP, standard logistic regression, and polytomous logistic regression to detect SNPs associated with breast cancer risk.
Table S4 of the Supplementary material at Biostatistics online presents the sample size of the tumor characteristics. The four tumor characteristics defined 24 mutually exclusive breast cancer subtypes. Subtypes with less than 10 cases were excluded, leaving 17 subtypes in the analysis. Both MTOP and FTOP used the additive second stage design. Besides, we modeled the baseline and ER case–case parameters as fixed effects in MTOP, and all other effects as random effects. We put ER as a fixed effect because of the previously reported heterogeneity in genetic association by ER (García-Closas and others, 2013; Milne and others, 2017). Genotype imputation was done using IMPUTE2 based on 1000 Genomes Project as reference (Michailidou and others, 2017; Milne and others, 2017). In total, 7 017 694 common variants on 22 autochromosomes with MAF 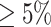 were included in the analysis. In all the models, we adjusted for age and the first four genetic principal components to account for population stratification.
were included in the analysis. In all the models, we adjusted for age and the first four genetic principal components to account for population stratification.
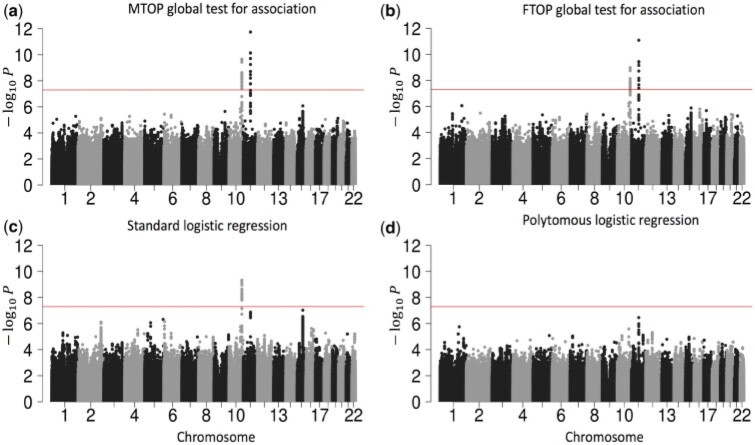
As Figure 3 shows, MTOP, FTOP, and standard logistic regression all identified a known susceptibility variant in the FGFR2 locus on chromosome 10 (Michailidou and others, 2017), with the most significant SNP being rs11200014 (P 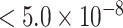 ). Further, both MTOP and FTOP identified a second known susceptibility locus on chromosome 11 (CCND1) (Michailidou and others, 2017), with the most significant SNP in both models being rs78540526 (P
). Further, both MTOP and FTOP identified a second known susceptibility locus on chromosome 11 (CCND1) (Michailidou and others, 2017), with the most significant SNP in both models being rs78540526 (P 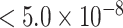 ). The individual heterogeneity test of this SNP showed evidence for heterogeneity by ER (P = 0.011) and grade (P = 0.024). Notably, the CCND1 locus was not genome-wide significant in standard logistic regression or polytomous models. The type I error of the four methods was well controlled (Figure S6 of the Supplementary material at Biostatistics online).
). The individual heterogeneity test of this SNP showed evidence for heterogeneity by ER (P = 0.011) and grade (P = 0.024). Notably, the CCND1 locus was not genome-wide significant in standard logistic regression or polytomous models. The type I error of the four methods was well controlled (Figure S6 of the Supplementary material at Biostatistics online).
Fig. 3.
Manhattan plot of genome-wide association analysis with PBCS using four different methods. PBCS have 2078 invasive breast cancer and 2219 controls. In total, 7 017 694 SNPs on 22 auto chromosomes with MAF more than 5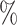 were included in the analysis. ER, PR, HER2, and grade were used to define breast cancer subtypes.
were included in the analysis. ER, PR, HER2, and grade were used to define breast cancer subtypes.
Additional sensitivity analysis of MTOP was implemented by specifying baseline, ER and grade as fixed effects, and PR and HER2 as random effects (Figure S7 of the Supplementary material at Biostatistics online). The results for MTOP with grade as fixed versus random effect were similar. We also implemented MTOP and FTOP incorporating pairwise interactions in the second stage model (Figures S8 and S9 of the Supplementary material at Biostatistics online). With pairwise interactions, both MTOP and FTOP detected FGFR2 and CCND1 with the genome-wide significant threshold. However, the P-value of FTOP with pairwise interactions was less significant compared to FTOP without these interaction terms (for rs11200014, P 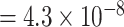 vs. P
vs. P 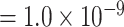 ; for rs78540526, P
; for rs78540526, P 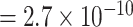 vs. P
vs. P 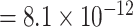 ). The P-value of MTOP with pairwise interactions was also less significant compared to MTOP without interaction terms (for rs11200014, P
). The P-value of MTOP with pairwise interactions was also less significant compared to MTOP without interaction terms (for rs11200014, P 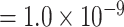 vs. P
vs. P 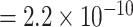 ; for rs78540526, P
; for rs78540526, P 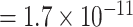 vs. P
vs. P 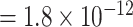 ). In both scenarios with pairwise interactions parameter included, however, the power loss was smaller.
). In both scenarios with pairwise interactions parameter included, however, the power loss was smaller.
Next, we compared the ability of MTOP and standard logistic regressions to detect 178 previously identified breast cancer susceptibility loci (Michailidou and others, 2017). For eight of the 178 loci, the MTOP global association test P-value was more than 10-fold lower compared to the standard logistic regression P-value (Table 2). In the MTOP model, these eight loci all had significant global heterogeneity tests (P 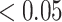 ). Confirming these results, in a previous analysis applying MTOP to 106 571 breast cancer cases and 95 762 controls, these eight loci were reported to have significant global heterogeneity (Ahearn and others, 2019).
). Confirming these results, in a previous analysis applying MTOP to 106 571 breast cancer cases and 95 762 controls, these eight loci were reported to have significant global heterogeneity (Ahearn and others, 2019).
Table 2.
Analysis results of previously identified susceptibility loci. For the listed eight loci, MTOP global association test P-value was more than 10-fold lower compared to the standard logistic regression P-value. All of the loci are significant in global heterogeneity test (P 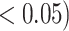 .
.
| SNP |
|
Position |
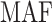
|
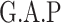
|
Standard analysis P |
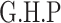
|
|---|---|---|---|---|---|---|
| rs4973768 | 3 | 27 416 013 | 0.47 | 3.1 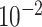
|
9.5 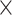 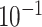
|
9.5 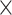 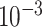
|
| rs10816625 | 9 | 110 837 073 | 0.06 | 5.0 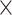 
|
9.8 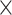 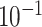
|
2.2 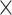 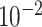
|
| rs7904519 | 10 | 114 773 927 | 0.46 | 6.5 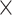 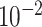
|
8.5 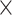 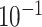
|
3.1 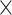 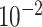
|
| rs554219 | 11 | 69 331 642 | 0.13 | 7.3 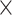 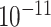
|
1.4 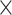 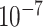
|
5.1 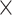 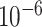
|
| rs11820646 | 11 | 129 461 171 | 0.40 | 1.5 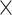 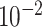
|
8.6 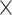 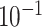
|
4.5 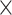 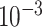
|
| rs2236007 | 14 | 37 132 769 | 0.21 | 2.1 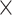 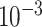
|
1.9 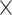 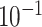
|
3.5 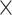 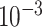
|
| rs1436904 | 18 | 24 570 667 | 0.40 | 7.2 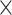 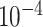
|
6.6 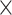 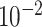
|
9.7 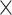 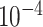
|
| rs1436904 | 22 | 29 121 087 | 0.01 | 9.8 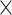 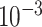
|
1.6 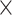 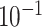
|
2.3 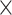 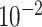
|
Chr. = chromosome; MAF = minor allele frequency; G.A.P = global association test P-value from MTOP; G.H.P = global heterogeneity test P-value from MTOP.
5. Discussion
We present a series of novel methods for performing genetic association testing for cancer outcomes accounting for potential heterogeneity across subtypes. These methods efficiently account for multiple testing, correlations between markers, and missing tumor data. Under the model framework, we develop two computationally efficient score tests, FTOP and MTOP, which model the underlying heterogeneity parameters in terms of fixed effects or mixed effects, respectively. We demonstrate these methods have greater statistical power in the presence of subtype heterogeneity than either standard or polytomous logistic regression analysis.
Several methods have been proposed to study the etiological heterogeneity of cancer subtypes (Chatterjee, 2004; Rosner and others, 2013; Wang and others, 2015). A recent review showed the well-controlled type I error and good statistical power of the two-stage model (Zabor and Begg, 2017). However, previous two-stage models haven’t accounted for missing tumor markers, which is a common problem in epidemiological studies. We show that by incorporating the EM algorithm into the two-stage model we can take advantage of all available information and substantially increase the statistical power (Figure 1). Moreover, the newly proposed mixed effect model can mitigate the degrees of freedom penalty caused by analyzing many tumor characteristics. In a recent large breast cancer GWAS analysis with 106 571 cases and 95 762 controls, the newly developed methods MTOP and FTOP have identified 16 novel loci (Zhang and others, 2019).
Incorporating missing tumor characteristics based on the proposed EM algorithm requires the assumption of MAR, i.e., the mechanism of missing of the individual tumor characteristics can depend only on other observed tumor characteristics and covariates, but not on the unobserved missing value themselves. For the analysis of tumor heterogeneity, information on aggressive types of tumors may be systematically missing. If the missing tumor characteristics are important determinants of aggressiveness, then the underlying assumption is violated. In general, dealing with non-ignorable missing data is a complex problem and certain sensitivity analyses can be performed to explore the degree of bias (Little and Rubin, 2019). In the context of genetic association testing, non-ignorable missingness can lead to inflated type I error only if the missingness mechanism itself is related to the genetic variant. Further research is merited to explore the complex effects of non-ignorable missingness in type I error and power of the proposed tests.
The computation time of MTOP is greater than FTOP (Section 5 of the Supplementary material at Biostatistics online). To construct the score tests in FTOP, the coefficients of covariates need to be estimated once under the null hypothesis, while in MTOP they need to be estimated for every SNP. The computational complexity of FTOP is O(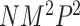 ), with
), with 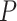 as the number of other covariates
as the number of other covariates 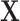 . For MTOP, the computational complexity is O(
. For MTOP, the computational complexity is O(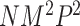 lk), where l and k are respectively the numbers of iteration required for weighted least square and EM algorithm to converge.
lk), where l and k are respectively the numbers of iteration required for weighted least square and EM algorithm to converge.
Currently, we only implement the linear kernel in MTOP, but other common kernels that capture the similarity between tumor characteristics can be used in the future. If there is prior knowledge about the overlapping genetic architecture across different tumor subtypes, this will help to choose the kernel function, and improve the power of the methods.
The proposed methods have been implemented in a user-friendly and high-speed R statistical package called TOP (https://github.com/andrewhaoyu/TOP), which includes all the core functions implemented in C code.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
Funds from the NCI Intramural Research Program, Bloomberg Distinguished Professorship endowment, and NHGRI (1R01 HG010480-01). The simulation experiments and data analysis were implemented using the high performance computation Biowulf cluster at National Institutes of Health, USA.
References
- Ahearn, T. U., Zhang, H., Michailidou, K., Milne, R. L., Bolla, M. K., Dennis, J., Dunning, A. M., Lush, M., Wang, Q., Andrulis, I. L.. and others. (2019). Common breast cancer risk loci predispose to distinct tumor subtypes. bioRxiv, 733402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnard, M. E., Boeke, C. E. and Tamimi, R. M. (2015). Established breast cancer risk factors and risk of intrinsic tumor subtypes. Biochimica et Biophysica Acta (BBA)-Reviews on Cancer 1856, 73–85. [DOI] [PubMed] [Google Scholar]
- Begg, C. B. and Zhang, Z. F. (1994). Statistical analysis of molecular epidemiology studies employing case-series. Cancer Epidemiology and Prevention Biomarkers 3, 173–175. [PubMed] [Google Scholar]
- Cancer Genome Atlas Network. (2012). Comprehensive molecular portraits of human breast tumours. Nature 490, 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cancer Genome Atlas Research Network. (2014). Comprehensive molecular profiling of lung adenocarcinoma. Nature 511, 543–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee, N. (2004). A two-stage regression model for epidemiological studies with multivariate disease classification data. Journal of the American Statistical Association 99, 127–138. [Google Scholar]
-
Davies, R. B. (1980). The distribution of a linear combination of
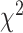 random variables. Journal of the Royal Statistical Society. Series C (Applied Statistics) 29, 323–333. [Google Scholar]
random variables. Journal of the Royal Statistical Society. Series C (Applied Statistics) 29, 323–333. [Google Scholar] - Dempster, A. P., Laird, N. M. and Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39, 1–22. [Google Scholar]
- Dubin, N. and Pasternack, B. S. (1986). Risk assessment for case–control subgroups by polychotomous logistic regression. American Journal of Epidemiology 123, 1101–1117. [DOI] [PubMed] [Google Scholar]
- García-Closas, M. and others. (2006). Established breast cancer risk factors by clinically important tumour characteristics. British Journal of Cancer 95, 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Closas, M. and others. (2013). Genome-wide association studies identify four ER negative-specific breast cancer risk loci. Nature Genetics 45, 392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koziol, J. A. and Perlman, M. D. (1978). Combining independent chi-squared tests. Journal of the American Statistical Association 73, 753–763. [Google Scholar]
- Lin, X. (1997). Variance component testing in generalised linear models with random effects. Biometrika 84, 309–326. [Google Scholar]
- Little, R. J. and Rubin, D. B. (2019). Statistical Analysis with Missing Data, Volume 793. New York, NY: John Wiley & Sons. [Google Scholar]
- Louis, T. A. (1982). Finding the observed information matrix when using the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 44, 226–233. [Google Scholar]
- MacArthur, J., Bowler, E., Cerezo, M., Gil, L., Hall, P., Hastings, E., Junkins, H., McMahon, A., Milano, A., Morales, J.. and others. (2016). The new NHGRI-EBI catalog of published genome-wide association studies (GWAS catalog). Nucleic Acids Research 45, D896–D901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michailidou, K., Lindström, S., Dennis, J., Beesley, J., Hui, S., Kar, S., Lemaçon, A., Soucy, P., Glubb, D., Rostamianfar, A.. and others. (2017). Association analysis identifies 65 new breast cancer risk loci. Nature 551, 92–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milne, R. L. and others. (2017). Identification of ten variants associated with risk of estrogen-receptor-negative breast cancer. Nature Genetics 49, 1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perou, C. M., Sørlie, T., Eisen, M. B., Van De Rijn, M., Jeffrey, S. S., Rees, C. A., Pollack, J. R., Ross, D. T., Johnsen, H., Akslen, L. A.. and others. (2000). Molecular portraits of human breast tumours. Nature 406, 747–52. [DOI] [PubMed] [Google Scholar]
- Prat, A., Pineda, E., Adamo, B., Galván, P., Fernández, A., Gaba, L., Díez, M., Viladot, M., Arance, A. and Muñoz, M. (2015). Clinical implications of the intrinsic molecular subtypes of breast cancer. The Breast 24, S26–S35. [DOI] [PubMed] [Google Scholar]
- Rosner, B., Glynn, R. J., Tamimi, R. M., Chen, W. Y., Colditz, G. A., Willett, W. C., and Hankinson, S. E. (2013). Breast cancer risk prediction with heterogeneous risk profiles according to breast cancer tumor markers. American Journal of Epidemiology 178, 296–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, J., Zheng, Y. and Hsu, L. (2013). A unified mixed-effects model for rare-variant association in sequencing studies. Genetic Epidemiology 37, 334–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, M., Kuchiba, A. and Ogino, S. (2015). A meta-regression method for studying etiological heterogeneity across disease subtypes classified by multiple biomarkers. American Journal of Epidemiology 182, 263–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, M. C., Lee, S., Cai, T., Li, Y., Boehnke, M., and Lin, X. (2011). Rare-variant association testing for sequencing data with the sequence kernel association test. American Journal of Human Genetics 89, 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, X. R., Sherman, M. E., Rimm, D. L., Lissowska, J., Brinton, L. A., Peplonska, B., Hewitt, S. M., Anderson, W. F., Szeszenia-Dąbrowska, N., Bardin-Mikolajczak, A.. and others. (2007). Differences in risk factors for breast cancer molecular subtypes in a population-based study. Cancer Epidemiology and Prevention Biomarkers 16, 439–443. [DOI] [PubMed] [Google Scholar]
- Yi, Y. and Wang, X. (2011). Comparison of Wald, score, and likelihood ratio tests for response adaptive designs. Journal of Statistical Theory and Applications 10, 553–569. [Google Scholar]
- Zabor, E. C. and Begg, C. B. (2017). A comparison of statistical methods for the study of etiologic heterogeneity. Statistics in Medicine 36, 4050–4060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, D. and Lin, X. (2003). Hypothesis testing in semiparametric additive mixed models. Biostatistics 4, 57–74. [DOI] [PubMed] [Google Scholar]
- Zhang, H., Ahearn, T., Lecarpentier, J., Barnes, D., Beesley, J., Qi, G., Jiang, X., O’Mara, T. A., Zhao, N., Bolla, M.K.. and others. (2019). Genome-wide association study identifies 32 novel breast cancer susceptibility loci from overall and subtype-specific analyses. bioRxiv, 778605. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.