The Psychology of Reaching: Action Selection, Movement Implementation, and Sensorimotor Learning

Abstract

The study of motor planning and learning in humans has undergone a dramatic transformation in the 20 years since this journal’s last review of this topic. The behavioral analysis of movement, the foundational approach for psychology, has been complemented by ideas from control theory, computer science, statistics, and, most notably, neuroscience. The result of this interdisciplinary approach has been a focus on the computational level of analysis, leading to the development of mechanistic models at the psychological level to explain how humans plan, execute, and consolidate skilled reaching movements. This review emphasizes new perspectives on action selection and motor planning, research that stands in contrast to the previously dominant representation-based perspective of motor programming, as well as an emerging literature highlighting the convergent operation of multiple processes in sensorimotor learning.

1. INTRODUCTION

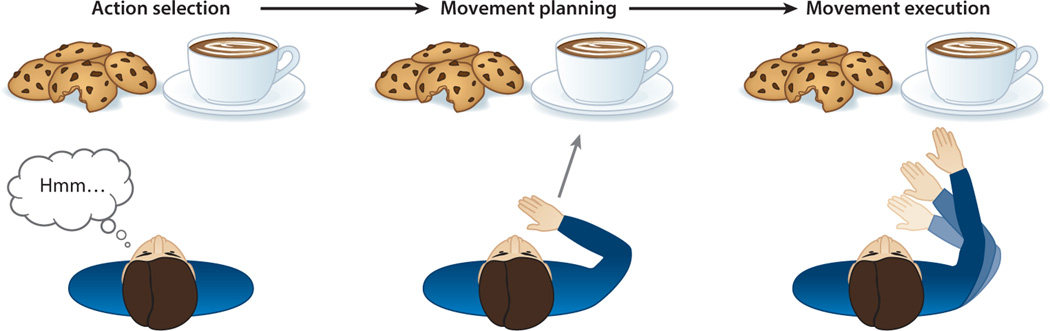
This review focuses on the control of reaching, a fundamental feature of human competence, underlying capacities as diverse as feeding and object manipulation. The organizational structure loosely hews to the temporal structure of a goal-directed reach (Figure 1). Section 2 examines decision-making processes involved in selecting a target, along with the planning processes that specify the motor commands. Section 3 focuses on the execution of a movement, and how the motor system deals with noisy performance through feedback control. In Section 4 we turn to learning, in particular, how error information is used to ensure that the motor system remains both flexible and stable to support reaching in a broad range of contexts.

Figure 1.

Reaching as a multilevel process. Goal-oriented movement begins with the selection of a target from the available options (action selection). Once a choice is defined, the system must specify the appropriate motor commands (movement planning). Forces generated by the muscles change the orientation of the joints such that the hand is brought to the chosen target (movement execution).

2. FROM ACTION SELECTION TO MOVEMENT PLANNING

We live in a world that is rich with appealing stimuli, presenting the sensorimotor system with a plethora of options. How do we decide whether to take a sip of cappuccino or reach for a delicious cookie? And, even after deciding on the goal, there remains the challenge of transforming that decision into an appropriate movement.

2.1. Decision Making in the Motor System

The choice between a cappuccino and a cookie, like all decisions, involves a competitive process. Over the past two decades, an interesting debate has emerged concerning the appropriate way to characterize this competition. One view is that the motor system develops movement plans for all options in parallel, and then executes only one of them. An alternative hypothesis proposes that the system can prepare only a single movement at a time, so that the decision is limited to the action selection stage.

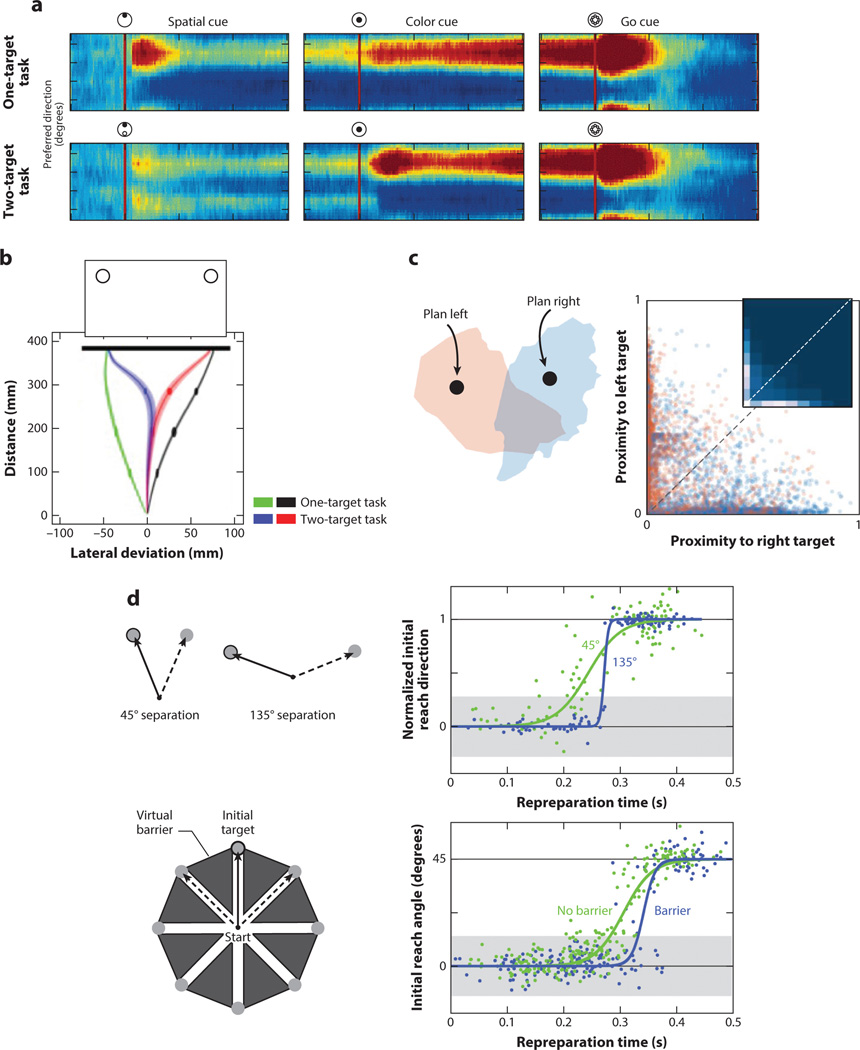
A widely cited neurophysiological study advanced the idea of parallel (and simultaneous) movement plans, at least under conditions of uncertainty about the movement goal (Cisek 2007). When two potential targets were presented to a monkey, activity corresponding to both potential movements was observed in the monkey’s dorsal premotor cortex (PMd). When a subsequent cue indicated the target, the activity became limited to neurons tuned toward that target’s direction (Figure 2a) (Cisek & Kalaska 2005). Importantly, the initial dual representation does not depend on the appearance of multiple targets: It can be observed in response to a single stimulus that is associated with two possible visuomotor transformation rules, for instance, reaching toward or away from the target (Klaes et al. 2011).

Figure 2.

Movement planning amid uncertainty. (a) Population activity in dorsal premotor cortex (PMd) neurons. Preparatory activity is observed in neurons tuned for movement toward the target location following onset of a target (spatial cue in top row). Activity is bimodal when two potential targets are illuminated at the start of the trial (bottom row). This activity coalesces toward a single direction when a secondary preparatory cue specifies the correct target (color cue) (Cisek & Kalaska 2005). (b) Movement averaging. Trajectories follow a relatively straight path to the target when there is a single option (green and black movement paths). However, when presented with two potential targets at movement initiation, the initial trajectory is toward a location between the two targets (blue and red) (Chapman et al. 2010). (c) State-space representation of PMd under uncertainty. Low-dimensional neural states when a single target is presented on either the left (red) or the right (blue). The proximity plot captures the state of the system at a given point in time when two potential targets are present. The distance of the neural state within individual trials is biased toward either the left or right target (along the principal axes), and rarely corresponds to an integrated position (close to the unity line). (Dekleva et al. 2018). (d) Intermediate movements are diminished when decreasing the compatibility between the targets. A larger spatial separation between the potential targets or introduction of virtual barriers reduces the likelihood of intermediate movements (Haith et al. 2015a).

Behavioral studies have provided further support for the parallel planning hypothesis. In these studies, an initial display shows potential targets, and the participant must initiate a movement prior to final target specification. Under such conditions, the initial movement direction corresponds to a weighted average of the potential movements (Figure 2b) (Chapman et al. 2010, Stewart et al. 2013). Consistent with the neural evidence, the behavioral results also indicate that parallel planning is best characterized as arising at the motor rather than the sensory level (Gallivan et al. 2017, Stewart et al. 2014). Moreover, conditions associated with multiple action options influence behavior (e.g., by increasing reaction time and movement variability), not only under uncertainty about the target location but also when there is ambiguity about which hand to use (Oliveira et al. 2010, Oostwoud Wijdenes et al. 2016).

Recent evidence, however, suggests a more constrained organization within the motor system, one in which planning is limited to a single movement. Dekleva et al. (2018) illustrated that the bimodal neurophysiological activity described above may be an artifact of averaging across trials in single-unit recordings. By using simultaneous recordings from multiple neurons, the authors found that PMd activity on any given trial represented only one target (Figure 2c). Behavioral studies have also offered a reconceptualization of the initial trajectories observed in tasks involving goal uncertainty (Wong & Haith 2017). Rather than indicating an averaging process, these trajectories may reflect a deliberate decision regarding how to optimize performance (Hudson et al. 2007). That is, an intermediary trajectory may be optimal to rapidly update a (single) movement plan once the final goal is specified. When this option is no longer optimal—for example, by increasing the distance between candidate targets—the occurrence of intermediate movements is dramatically diminished (Figure 2d) (Haith et al. 2015a).

The influence of abstract properties on behavior provides further evidence that intermediate movements reflect high-level cognitive processes rather than emerging from the blending of motor planning processes (Song & Nakayama 2009). The probability of intermediate movements increases when targets overlap in terms of semantics (Dale et al. 2007), phonology (Spivey et al. 2005), or even truth evaluation (McKinstry et al. 2008). These effects suggest that interference in goal selection may promote an optimal strategy to plan an intermediate movement without committing to the final goal. A similar picture emerges from studies of bimanual coordination. While humans are quite facile in using both hands cooperatively (e.g., in tying shoelaces), we exhibit considerable difficulty when distinct goals require the production of asymmetric movements, such as simultaneously drawing a “C” and a “U” (Ivry et al. 2004). These interference effects are not observed when there is external sensory guidance (Mechsner et al. 2001, Rosenbaum et al. 2006). For example, asymmetric bimanual movements require longer reaction times when cued symbolically, but they exhibit negligible cost when spatial cues indicate the target locations (Diedrichsen et al. 2001). These results suggest that interference originates upstream of motor planning, for instance, when translating the symbolic cues into actions (Derosiere et al. 2018, Klein et al. 2012).

Decision making is a dynamic and multilevel process that encompasses multiple brain networks (Gallivan et al. 2018). It entails the evaluation of the value associated with possible options (Padoa-Schioppa 2011), constrained by the current context. Decision-making processes continue to operate throughout the movement (Wispinski et al. 2018); we can change our minds after movement initiation, replacing one movement with another (van den Berg et al. 2016) or rapidly aborting an initiated movement (Verbruggen et al. 2019). It is reasonable that the optimal decision to make an intermediate movement amid uncertainty takes advantage of our capability to move in a flexible manner, as the ongoing behavior entails the continuous reevaluation of how our actions conform to current goals.

2.2. Transformation of a Target Location to a Motor Plan

Once an action is chosen, a series of complex computations is required to transform that goal into a movement plan. A core problem concerns coordinate transformations, where information extracted from multiple sensory systems is translated into a format appropriate for motor commands (Soechting & Flanders 1989). Visual (and perhaps olfactory) cues that signal the position of the cup of cappuccino have to be reconciled with proprioceptive information about the current position of the arm. The resultant difference vector, the difference between the current position of the limb and the desired position, forms the basis for a movement plan (Shadmehr & Wise 2005). A control theory framework has been adopted to describe this coordinate transformation; this framework builds on the concept of an internal model, a representation of an agent–environment interaction (Jordan & Rumelhart 1992, Shadmehr & Krakauer 2008, Shadmehr & Mussa-Ivaldi 1994, Wolpert et al. 1995). One type of internal model is an inverse model, a controller that specifies the mapping between a kinematic representation, such as a difference vector, and a dynamic representation, namely the motor commands and muscular forces required to produce the desired movement.

These models make a fundamental distinction between feedback and feedforward control. Feedback control refers to the response of the system to the sensory information that arises during the execution of the movement, enabling online corrective changes in the motor commands to improve the performance (Todorov&Jordan2002). However, such control can be unstable, given the delays in transmitting and processing sensory information (Miall et al. 1993, 2007). Feedforward control refers to planning that uses another type of internal model, a forward model, that anticipates the sensory consequences of the motor command. On the face of it, feedforward control seems to demand more complicated computations. A simple feedback controller can keep issuing new commands that follow simple algorithms, such as “get closer to target” (Braitenberg 1986). In contrast, a feedforward controller succeeds only if the initial movement plan and commands are accurate.

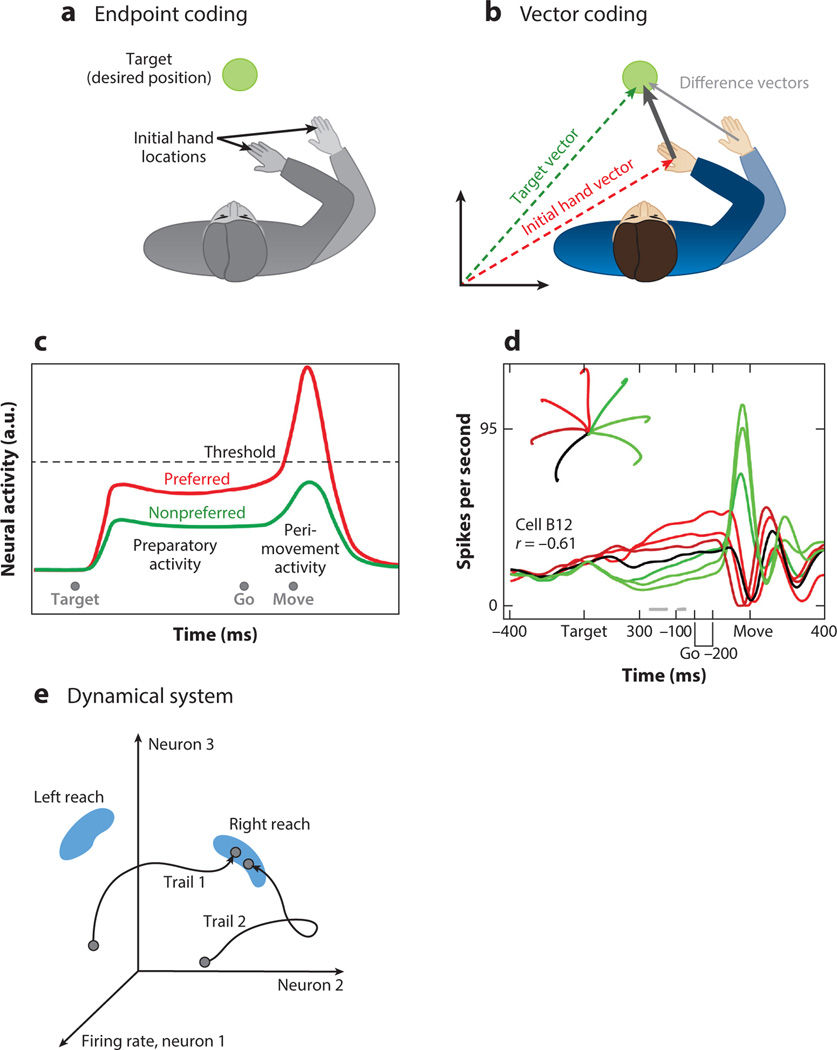
For feedforward systems, it is important to consider how the motor plan is coded. A classic debate centers on whether the movement plan uses endpoint coding, the specification of the desired final location of the limb (Figure 3a) (Feldman 1986, Polit & Bizzi 1979), or vector coding, the specification of the trajectory that would transport the limb from the current position to the desired position (Figure 3b). These two hypotheses generate different predictions in terms of the relevance of the initial arm position for movement accuracy. Surprisingly, endpoint accuracy is maintained when the limb position is perturbed around the time of movement initiation, even when proprioceptive feedback information is absent (Kelso & Holt 1980, Polit & Bizzi 1979). Thus, at some level, the nervous system must specify a desired final position (van den Dobbelsteen et al. 2001) and, by maintaining this representation, be impervious to alterations in limb trajectory. In contrast, vector coding entails a representation of movement direction and extent, specified either in terms of hand path or in terms of muscle activity (Griffin et al. 2015, Kakei et al. 1999), which are features correlated with activity of neurons in many regions of the motor pathway (Fu et al. 1993, Georgopoulos et al. 1982). Behavioral evidence also shows that the initial position impacts planning (Sainburg et al. 2003; Sober & Sabes 2003; Vindras et al. 1998, 2005). When performing center-out reaching movements, the endpoint locations exhibit a variability pattern that is higher in movement extent than in direction (Gordon et al. 1994b). Moreover, errors in extent are more easily corrected compared with errors in direction (Krakauer et al. 2000). These findings support the idea that there are differential constraints on movement features related to direction and extent, features that provide the basis of vectorial planning. It is, of course, possible that movement planning entails both endpoint and vector-based coding, with the former helping to ensure that the movement terminates at the desired position, and the latter providing some degree of flexibility (e.g., movement speed) (Hudson & Landy 2012, Thaler & Todd 2009).

Figure 3.

Representational and dynamical systems perspectives on movement coding. (a) With endpoint coding, planning centers on specifying the desired position, or state, without taking into account the agent’s initial state. (b) With vector coding, planning entails a computation of the difference vector between the target and the initial position of the hand. (c) According to a representational approach, preparatory neural activity should reflect a subthreshold directional preference. During execution, this preference would be maintained, with movement ensuing when the activity level reaches a threshold for initiation. (d) At odds with this hypothesis is the finding that many premotor and primary motor neurons do not exhibit the same pattern of activity during the preparatory and execution phases (Churchland et al. 2010). (e) Schematic illustration of the combined dynamics of neural activity of three neurons, presented in a state space. According to a dynamical system approach, the pattern of neural activity of the neurons over time (black arrows) converges to a state, reflecting the upcoming reach direction. Abbreviation: a.u., arbitrary units.

The above discussion has been from the engineering perspective, which emphasizes the identification of representational features that might be amenable to building controllers for a robot. This approach has also been inspired by the feature-like coding observed in neurons in the motor system, signals that have formed the basis for impressive brain–machine interface systems (Serruya et al. 2002). In this view, one would assume that motor planning is, in one sense, a subthreshold reflection of movement execution itself (Figure 3c) (Bastian et al. 1998, Cisek 2006). However, this hypothesis is not supported empirically: The activity of neurons in premotor and motor cortices can be quite distinct during preparatory and execution phases (Figure 3d), and at the population level, the correlation is modest (Churchland et al. 2010).

These observations have inspired an alternative physiological perspective to capture how the motor system supports movement planning (and execution), one that can be understood only in terms of the pattern of activity of the neural population and how this activity changes over time (Churchland et al. 2010, Shenoy et al. 2013). During preparation, the population activity follows a neural trajectory specific to the forthcoming movement, reaching an optimal preparatory state that is marked by reduced trial-by-trial variability just prior to movement initiation (Figure 3e). The population-level trajectory during the movement period is distinct from that of planning, allowing for the same population to code information for both phases, with the transition between the two trajectory patterns providing the mechanism for movement initiation (Elsayed et al. 2016).

This dynamical system approach does not necessarily contradict the representational approach. The two might describe processes operating at different hierarchal levels (Kakei et al. 1999, 2001; Lara et al. 2018). Thus, it is possible that movement direction and extent are represented upstream, linked to a more cognitive and psychological level of intention about where to move. The dynamical system may be best suited for capturing how the motor system evolves through the planning and execution phases.

3. FROM PLANNING TO EXECUTION

Humans exhibit a rich repertoire of movements that vary in extent, speed, duration, force, and so forth. Despite this flexibility, there are notable features that remain largely invariant. After deciding to eat a cookie, our movement to that goal is not arbitrary: The hand smoothly follows a direct, rather than curved, path to the cookie, even though this may require rather complex, nonlinear changes in joint space (Morasso 1981). Moreover, the velocity profile is bell shaped, reaching a maximum around the middle of the movement. These features have been modeled as an optimization process that minimizes jerk, the third derivative of position with respect to time (Flash & Hogan 1985), thus maximizing movement smoothness. Other minimization criteria have been proposed, such as minimization of lower (Ben-Itzhak & Karniel 2007, Leib & Karniel 2012) or higher (Dingwell et al. 2004) derivatives. These criteria reflect control principles to minimize effort while maintaining performance.

The system must also be flexible, sensitive to the demands of a particular context. Consider the speed of a movement. There is certainly an advantage to moving quickly, either to catch a prey or to avoid a predator. But this comes at a cost. A classic observation in motor control is the speed–accuracy trade-off, a phenomenon formalized as Fitts’s law, relating movement duration (i.e., speed) to target size (Fitts 1954). Importantly, there is also a cost, in terms of metabolic energy consumption, in moving too slowly (Shadmehr et al. 2016).

These principles shed light on the variables the motor system controls during both planning and execution. However, even when attempting to optimize performance, things frequently go wrong, with the actual movement not isomorphic with the intended movement. In this section, we discuss movement variability, considering situations in which variability has a detrimental effect on performance as well as situations in which variability can facilitate motor learning. We also describe how the motor system reoptimizes performance given an unexpected outcome.

3.1. Sources of Motor Variability

A hallmark of skilled behavior is a reduction in variability (Shmuelof et al. 2012b): The novice hopes the dart will land on the board, whereas the expert is only satisfied when the dart lands on the desired number. Influential theories of motor control are premised on the idea that optimal performance comes about by minimizing variability (Harris & Wolpert 1998, Todorov & Jordan 2002). A challenge here is to identify the loci of variability (Dhawale et al. 2017, Faisal et al. 2008), recognizing that this variability will arise at all stages of movement. For example, in a delayed response task, variability in the neural activity in PMd and primary motor cortex (M1) prior to movement onset accounted for more than half of the trial-by-trial variability in movement velocity (Churchland et al. 2006).

In contrast, the fact that movement requires activating an actuator, one subject to biomechanical and physical constraints, will certainly introduce execution-based variability. The variability of an output signal increases with the size of the signal, a phenomenon referred to as signal-dependent noise (Harris & Wolpert 1998). Force variability scales with the magnitude of the produced force (Schmidt et al. 1979), an effect attributed to inherent noise in the neuromuscular junction and muscle activity (Faisal et al. 2008, van Beers et al. 2004) rather than to noise in the motor command (Jones et al. 2002). Increased variability along the axis of movement increases with movement amplitude due to the directional anisotropy of arm inertia (Gordon et al. 1994a, Vindras et al. 2005).

We typically think of variability in a negative light—as something that gets in the way of optimal performance. Moreover, variability may not only influence the accuracy of a specific movement but may also have detrimental effects on learning. For example, there is a negative correlation between reaching variability in an unperturbed environment and the rate at which participants adapt to a perturbed environment (Stark-Inbar et al. 2016). However, in some contexts, elevated variability has been found to be associated with improved learning (Fernandez-Ruiz et al. 2011, Wu et al. 2014). What might be the benefits of a noisy system? One hypothesis is that adding variability promotes flexibility, allowing the system to explore new solutions that might lead to even better performance (Dhawale et al. 2017).

In summary, movement variability can originate at different stages in the cascade of events from planning to execution, and this may be relevant for differentiating between “bad” and “good” variability. Signal-dependent noise arising during movement execution is largely a product of peripheral constraints. Minimizing this noise ensures that the executed movement closely matches the desired movement. In contrast, planning variability may provide a substrate for exploration, helping the system uncover optimal solutions.

3.2. Feedback Control

Regardless of the source of variability, the failure to achieve a desired goal will result in some corrective action. Whether you fail to grasp your coffee because of neural noise or muscular fatigue, or because someone bumped your arm in the crowded café, feedback processes will be engaged to help achieve the goal. As noted above, the inherent delays associated with neural transmission present a challenge for feedback control systems. To overcome delays, evolution has provided us with a multilevel feedback control system, which allows for corrections at different timescales and following different control principles.

Feedback mechanisms are frequently described as reflexive, in the sense that they operate outside awareness or volitional control. These mechanisms are divided into two components. First, there are reflexive responses of spinal origin. With latencies as short as 25 ms, sensory information from the muscles, joints, and skin can modify activity in motor neurons. This sensory information is integrated with descending motor commands by spinal interneurons to assist voluntary drive to the motor neurons to help correct or resist movement errors (Nielsen 2004, Pruszynski et al. 2009). For example, to maintain upright posture, axial and limb muscles must respond automatically to unexpected changes in muscle length caused by perturbations (Marsden et al. 1981).

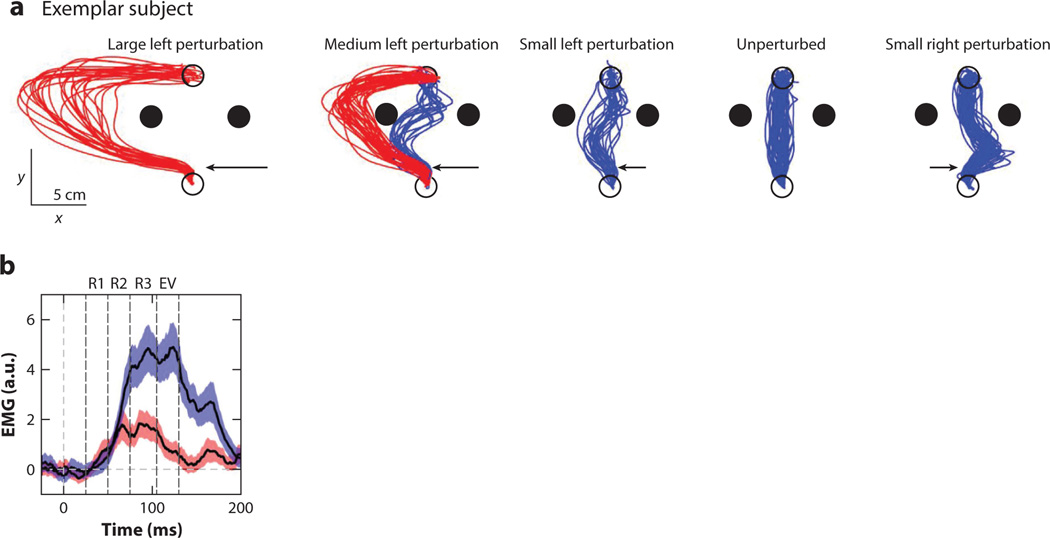
Second, there are more flexible, task-dependent long-latency reflexes, which are under the control of both subcortical and cortical mechanisms (Scott et al. 2015). Long-latency reflexes in response to mechanical perturbations have estimated latencies of 50 to 105 ms (Pruszynski & Scott 2012), whereas the response to visual errors ranges from 150 to 200 ms (Carroll et al. 2019, Day & Lyon 2000, Franklin & Wolpert 2008). In one study, lateral forces were delivered to the arm as the participant attempted to reach a target, necessitating online corrections not only to reach the target but also to avoid contact with virtual obstacles in the workspace (Nashed et al. 2014). While the early spinal reflexes were similar across reaches, adaptive adjustments in muscle activity were observed as early as 45–75 ms following the perturbation, clearly much faster than the latencies associated with voluntary corrections (Gu et al. 2018). Interestingly, the corrective response—whether between or around the obstacles—depended on where in the reach the perturbation was delivered (Figure 4). This flexibility was modeled by assuming that reflex gains were dynamically modified in a task-dependent manner, combining information about the state of the limb (e.g., position, velocity, acceleration) and task-related variables (e.g., target and obstacle position). Thus, long-latency reflex responses are sensitive to task goals and are not simply hardwired.

Figure 4.

Long-latency responses flexibly respond to task demands. (a) Red and blue colors indicate reaches that went around or between the obstacles, respectively. Arrows indicate the position and relative magnitude of the perturbation. The variability in the response is dependent on both the perturbation and state of the limb. (b) Comparison of electromyography (EMG) activity in the posterior deltoid during reaches going between the obstacles (blue) or around them (red). A difference in the reflexive responses to these perturbations is evident as early as 75 ms. R1 represents the short-latency response epoch, R2 and R3 are the long-latency response epochs, and EV indicates the early voluntary response. Abbreviation: a.u., arbitrary units. Figure adapted from Nashed et al. (2014).

Optimal feedback control (OFC) provides a normative framework to help explain the “intelligence” exhibited by fast, automatic responses. A core assumption is that the nervous system prioritizes the minimization of task-relevant variability, using corrective mechanisms to ensure task success while ignoring variability in task-redundant, or task-irrelevant, dimensions (Diedrichsen et al. 2010a, Pruszynski & Scott 2012, Scott 2004, Todorov & Jordan 2002). According to OFC theory, the motor system minimizes a cost function related to the movement goal (e.g., reaching the target) and a regularization term representing the cost to move. Given these constraints, a unique control policy is implemented such that the state estimate (i.e., the internal representation of body and other task-relevant variables) is transformed into a motor command.

OFC theory has proven to be an extremely powerful framework in accounting for feedback-based control across many task contexts (Diedrichsen 2007, Liu & Todorov 2007). The theory provides a unified framework to account for the relationship between planning and control: Control mechanisms enacted during movement are a natural corollary of how reflex gains are set in a task-dependent manner prior to movement initiation. OFC also offers a solution to the degrees-of-freedom problem. Specifically, the brain tends to find a stereotypical manner of producing a movement because reflex gains are set in order to minimize task-relevant variability.

3.3. Fast Online Control and Decision Making

OFC provides an account of how online control mechanisms can be modulated in an efficient way, helping to ensure that a movement is properly executed. More recent extensions of these ideas are inspired by the realization that information that is not directly related to movement execution, such as uncertainty in the choice of target or target-associated value, also alters online feedback control. This research suggests that the normally deliberative, time-consuming decision making processes typically studied with nonmotor tasks can be implemented with striking speed and efficiency by the motor system.

Selen et al. (2012) addressed the question of how uncertainty impacts long-latency reflexes by having participants reach in the direction corresponding to the modal direction of a display of moving dots. The gain on long-latency reflexes (75–105-ms range) scaled with the coherence level of the dot display as well as viewing time, factors that are likely to impact the participants’ confidence in the required reach direction. Thus, long-latency reflexes can also be modulated by subjective evaluations of belief related to decision making.

When a corrective action is required, the challenge is relatively simple when reaching to a static object because the position of the goal is stable. The situation appears to be much more complex when interacting with a dynamic target. Consider a worker on an assembly line, tasked with placing a lid on a container. How does a feedback control system determine its corrective action in response to an error in the estimated future position of the lid versus an error in the initial reach trajectory? This problem has been addressed in studies looking at online corrections in response to displacements of either the target or a cursor representing the hand position (Reichenbach et al. 2014). As might be expected, directing attention to the target improved performance when the target was displaced. Interestingly, directing attention to the cursor had little impact on performance when the cursor was displaced. The authors (Reichenbach et al. 2014) hypothesize that the motor system retains a stable estimate of hand position regardless of attention. In addition, when the display included multiple moving targets and cursors, most of which were task irrelevant, the participants had difficulty identifying task-relevant target displacement amid the visual distractors. However, they were able to ignore these distractors when responding to feedback about hand position. It may be that proprioceptive feedback from the hand is readily combined with visual information to create a stable representation for feedback control. In contrast, vision provides the only source of feedback for responding to errors in the estimate of target position.

In one sense, a feedback control system need not be concerned with determining the source of an error; that is, in terms of the task goal of reaching a moving object, it does not really matter whether a corrective action is required because of an error in estimating the position of the goal or the position of the limb. Indeed, as discussed above, a key computation for goal-oriented reaching is the difference between the location of the target and that of the limb. However, this integrated representation takes time to emerge. If both the target and cursor positions are displaced during a reach, the initial feedback response (∼170 ms) reflects independent, nonlinear responses to both sources of information. Only after 200 ms does the corrective response reflect an integrated representation of the difference vector (Franklin et al. 2016).

Going up another level of abstraction, Carroll et al. (2019) asked how properties of the target itself, specifically reward value, affect online control processes. Participants initially reached toward a center target that was flanked by two outer targets. Immediately following movement initiation, but prior to a cursor jump, a cue was given to indicate which one of the three targets would be rewarded. Feedback responses beginning 170 ms post cursor jump reflected rapid computations normally associated with high-level decision-making processes, as the hand moved toward the rewarding target.

As described in this section, the noisiness of neural signals, muscular responses, and peripheral receptors, as well as the presence of transmission delays, presents major challenges to fast, efficient online control of movement. Despite these challenges, the motor system shows a remarkable ability to make rapid and flexible adjustments in response to feedback information involving contextual variables. OFC has provided an important theory for understanding how these fast, efficient computations are implemented. Together with recent findings highlighting the connections between high-level decision making and rapid online control, the past decade of research has strengthened the argument that reflexes are much “smarter” than previously assumed (Krakauer 2019).

4. LEARNING AFTER MOVEMENT

Motor control is a dynamic process, not only in the act of movement itself but also in how the system requires constant refinement. In picking up a cup of coffee, the speed of the movement and force at the moment of contact will depend on the amount of liquid in the cup. Success also requires taking into account more subtle factors, such as the weight of the actor’s shirt or her current state of fatigue. Errors not only reveal the exquisite ability of the motor system to make online corrections but also show how the system is constantly fine-tuning its input–output properties to compensate for, and thus anticipate, these sources of variation. The latter process, referred to as sensorimotor adaptation, is crucial for optimizing learned movements. Historically, this term was used to refer to an implicit and automatic learning process that keeps the motor system well calibrated. However, recent research has shown that adaptation is not a unitary process. Thus, we use the term in a more general sense, encompassing the many learning processes that allow us to flexibly modify skilled behaviors to be well suited for a range of contexts.

4.1. Error-Based Learning

Investigations of adaptation have a long history, tracing back to some of the earliest laboratories in experimental psychology (Stratton 1896). Hermann von Helmholtz (1867) is credited with being the first to formally study the effect of prism glasses. These lenses distort the visual input in a systematic manner (e.g., impose a lateral shift of 15°), resulting in large reaching errors. However, within several trials, the error is dramatically reduced. The hallmark sign of a sensorimotor remapping, or implicit recalibration, is the presence of an aftereffect, motor errors in the direction opposite the perturbation, immediately following removal of the perturbation.

Prism glasses served as an important tool for researchers studying sensorimotor learning during the cognitive revolution of the 1960s and 1970s (Redding & Wallace 1978, Welch 1974). A second renaissance, beginning in the 1990s, was motivated by methodological advances, specifically, the introduction of devices that could create virtual reality (VR) environments. One such approach is to use computer displays in which vision of the body is occluded but the position of the body or, more commonly, the end effector is indicated by a cursor (Krakauer et al. 1999, 2000). With these displays, the visual feedback can be manipulated, often via rotation in a polar reference frame. Another VR approach is to use robotic devices that allow the experimenter to create an environment with novel force fields. In the most commonly studied version, the participant holds the handle of the device to reach to visual targets, and a velocity-dependent force field is imposed orthogonal to the direction of movement (Shadmehr & Mussa-Ivaldi 1994).

The introduction of a perturbation, whether with prism glasses, force fields, or a visuomotor rotation, elicits a stereotypical learning function that is exponential in shape: The trial-by-trial change in performance is initially large, tapers off over the course of learning, and reaches a final asymptotic level that generally falls just short of nullifying the perturbation. When the perturbation is removed, a prominent aftereffect is observed. This aftereffect has to be unlearned, or “washed out. ” That is, the error-based learning process is now repeated in reverse. The fact that washout must be learned is surprising given that, without the perturbation, the system is simply being asked to return to its natural state. Indeed, there does seem to be some memory of the original state. First, the presence of this attractor can account for the faster learning rate observed during washout compared with the response to the initial perturbation (Huang et al. 2011, Kitago et al. 2013, Taylor et al. 2014). Second, if no feedback is provided during the washout phase, or if the cursor’s movement is clamped such that there is no error (i.e., it moves directly to the target), then there is a slow drift back toward the original state (Brennan & Smith 2015, Kitago et al. 2013, Scheidt et al. 2000, Shmuelof et al. 2012a).

4.2. Internal Models and State-Space Model of Adaptation

An important theoretical construct for understanding sensorimotor adaptation, and motor control in general, is the internal model. As described above, an internal model describes an agent–environment interaction and, as such, affords the possibility to simulate an action by the body within a particular context. In picking up an object, we have an internal model of the inertial forces that must be overcome. And if suddenly placed in an environment with atypical forces—say, one without gravity or one in which movements elicit velocity-dependent force fields—then the motor system has to either modify this internal model or learn a new internal model, one suited for the novel agent–environment context.

In terms of simulation, forward models generate predictions of the sensory consequences of the motor command. This prediction can then be compared with the actual sensory feedback; the difference between the predicted and actual feedback generates a sensory prediction error (SPE). As such, forward models entail the core ingredients for supervised, error-based learning (Jordan & Rumelhart 1992). The forward model can be thought of as the supervisor, providing a prediction of the consequences of an action. The SPE provides the error signal that can be used to update both the inverse and forward models in an iterative manner, striving to keep the output of these models calibrated with one another.

State-space models provide an elegant formalization of this adaptation process, describing how movement errors induce the trial-by-trial changes to maintain calibration of sensorimotor maps (Donchin et al. 2003, Thoroughman & Shadmehr 2000). The simplest form of the state-space model is as follows:

$$e(n)=r(n)-x(n),$$ 1.

$$x(n+1)=Ax(n)+Be(n).$$ 2.

Consider how this set of equations describes learning in a sensorimotor adaptation task in which the visual feedback is rotated by 30°. In this context, x is an internal model representing an estimate of the relationship between the actual position of the hand and the visual feedback indicating the position of the hand, that is, the current estimate of the imposed rotation, r. At the start of the experiment, we initialize the value of x to zero given that, based on experience, we assume the visual feedback of the hand will correspond to the actual position of the hand. But when the perturbation is introduced, the motor system has to modify this internal model by using an error signal derived from the mismatch between the actual rotation and the current estimate of the rotation. The inverse model uses the forward model prediction of the perturbation to generate the opposite signed motor output to counteract the perturbation. (Note that it is assumed, although not typically stated, that the motor output is equal to −x. )

This learning process is dictated by two parameters. The learning rate, B, corresponds to the proportion of the error, e, that the system will correct for from trial to trial. Experiments across a range of adaptation tasks indicate that the value of B typically falls in the range of 0. 1–0. 3, meaning the motor system adjusts for approximately 10–30% of the error on each trial (Gonzalez Castro et al. 2014, Huang et al. 2011, Smith et al. 2006). While higher values would produce faster learning, this comes at a cost of stability, since the system is responding not only to a perturbation but also to random noise. The A term represents the proportion of the current state estimate that is retained from one trial to the next. This value is typically found to be greater than 0. 95. By being less than one, the model accounts for why the system, even if deprived of visual feedback, decays to a baseline state. In its simple form, both learning and forgetting depend on the execution of a response. However, there is also a temporal component to forgetting that is not explicitly captured by the model. The passage of time, even in the absence of movement, leads to a significant decay of adaptation (Criscimagna-Hemminger & Shadmehr 2008, Hadjiosif & Smith 2013, Kitago et al. 2013, Telgen et al. 2014).

The interaction of A and B captures (and predicts) the canonical learning curves observed in studies of sensorimotor adaptation. Because trial-by-trial learning in this model is a constant proportion of the error, the rate of trial-to-trial change decreases over time, which is the signature of an exponential function. The system will reach an asymptote when the effects of B (learning) and A (forgetting) are in equal opposition to one another. Moreover, under the assumption that A is less than one, this asymptote will be less than the actual perturbation (van der Kooij et al. 2015, Vaswani et al. 2015). That is, learning to respond to a perturbation will be less than perfect, assuming there is a baseline attractor state.

One point of contention with the basic state-space model is the assumption that the input for updating the internal model is a fixed proportion of the observed error. While exponential learning functions are consistent with this assumption, they provide a relatively crude way to evaluate a model that predicts trial-to-trial learning. An alternative approach is to use a random perturbation schedule, sampling a range of error sizes and directions. By having a mean error of zero across trials, the retention term is essentially eliminated, allowing the experimenter to directly measure the response to errors of different sizes. The results from this research converge in showing that the proportionality assumption holds only over a small range of errors (Fine & Thoroughman 2007, Hayashi et al. 2019, Marko et al. 2012, Wei & Körding 2009). For larger errors, the response is either attenuated in proportional terms relative to small errors or even invariant (Kim et al. 2018, Morehead et al. 2017).

These results suggest that not all errors are treated equally. The motor system is more responsive, or sensitive, to small errors, and discounts larger errors (Fine & Thoroughman 2006, Marko et al. 2012). One interpretation of this phenomenon draws on the idea of causal inference (Kording 2014, Wei & Körding 2009). Given the assumption that the world is usually stable, small errors are likely to be the result of the agent’s behavior, providing a source of information for refining the calibration of the system. Large errors, in contrast, may be atypical events, or outliers. A strong gust of wind that sends a tennis serve way out of bonds does not require recalibrating the sensorimotor system in the same way as a serve that lands just outside the service box on a calm day.

State-space models have been largely successful in characterizing and predicting behavior in response to a wide array of perturbations (Galea et al. 2015, Roemmich et al. 2016, Smith et al. 2006, Vaswani et al. 2015), as well as in providing a tool to explore the impact of neurologic lesions on adaptation (Charalambous et al. 2018, Smith & Shadmehr 2005, Tseng et al. 2007). In a complementary manner, they have also proven useful in highlighting conditions that produce results at odds with the assumptions of the model, providing insight into how these simple models must be modified to capture the richness of behavior (Donchin et al. 2003, Huang et al. 2011, Kim et al. 2018, Smith et al. 2006, Vaswani et al. 2015).

4.3. Contextual Changes

Generalization, the extent to which the effects of adaptation next ends to contexts beyond that within which learning occurred is relatively limited. Adaptation resulting from a force field applied by a robotic arm is lost when the same movements are made freely (Kluzik et al. 2008), consistent with the general notion that internal models capture specific agent–environment interactions. Similarly, adaptation shows, at best, modest transfer from one arm to the other (Poh et al. 2016, Sainburg & Wang 2002, Taylor et al. 2011, Werner et al. 2019). Even within a consistent experimental context, adaptation is local. If training is limited to one part of the workspace, the generalization function is relatively narrow, showing a Gaussian-like function with a standard deviation of ∼30° (Krakauer et al. 2000, Shadmehr & Moussavi 2000). While this function is often described in terms of extrinsic coordinates, that is, the direction of a movement with respect to the workspace, there is also evidence that some component of the adaptation is based on an intrinsic reference frame such as joint angles (Berniker & Kording 2011, Brayanov et al. 2012, McDougle et al. 2017, Poh & Taylor 2019). One exception to the local generalization constraint is gain adaptation: The modification of a scalar relationship between a movement and its consequences, in terms of movement extent, generalizes across the workspace, at least for movements made with the same limb (Hudson & Landy 2016, Krakauer et al. 2000, Pearson et al. 2010).

Conversely, we can also look at interference effects to understand the constraints on adaptation. Classically, interference has been demonstrated in AB experimental designs in which perturbation A (e.g., clockwise force field) slows learning of perturbation B (e.g., counterclockwise force field) (Brashers-Krug et al. 1996, Miall et al. 2004, Thoroughman & Shadmehr 1999). These findings suggest that training on a task that requires recalibration of one internal model will delay learning when the task changes. Interference effects observed in block designs cannot be captured by a standard state-space model, which would predict similar rates of change from baseline behavior. However, they can be quantitatively characterized by a multirate state-space model that incorporates adaptive processes operating on different timescales (Sing & Smith 2010, Smith et al. 2006).

So, what distinguishes whether learning involves the recalibration of an internal model, or whether it entails the establishment of a separate internal model? Adaptation that occurs when reaching while yoked to a robotic device (i.e., as in force field studies) does not generalize to free reaching. This observation is interpreted as reflecting the engagement of different internal models for these two contexts, a reasonable assumption given their distinct inertial properties. But what about other types of cues? Several studies have shown that salient cues such as color fail to prevent interference. For example, we cannot simultaneously learn to respond to a clockwise rotation in a red environment and to a counterclockwise rotation in a blue environment (Addou et al. 2011, Gandolfo et al. 1996, Gupta & Ashe 2007).

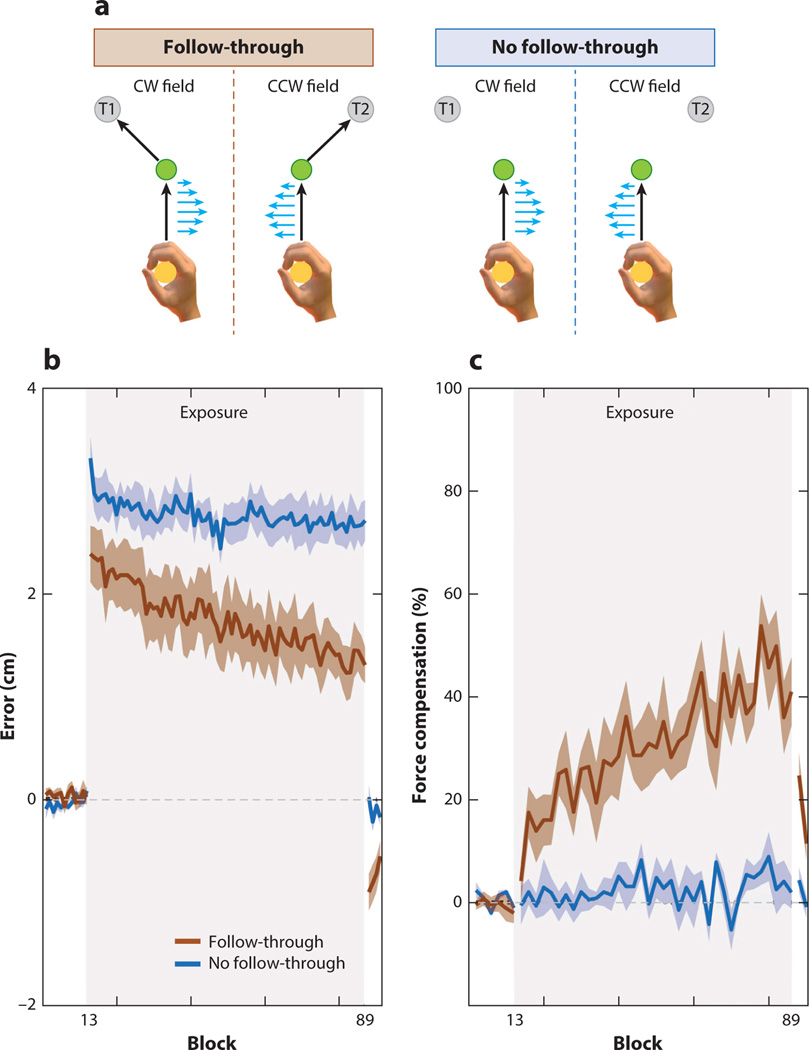
However, as shown in a compelling series of experiments by Wolpert and colleagues (Howard et al. 2012, 2015, 2017; Sheahan et al. 2016), dynamic cues can be sufficient to minimize interference. For example, participants could adapt to both clockwise and counterclockwise force fields applied to the identical segment of a two-segment trajectory, when the second segment required the trajectory to deviate to the left or right (Figure 5). Even though the participant experiences opposing perturbations across trials to a common segment of the overall trajectory, the context defined by the follow-through was sufficient to create distinct internal models.

Figure 5.

Dynamic contextual cues prevent interference. (a) Participants made initial movements to a central target. A velocity-dependent curl field was applied during this segment, with the direction of the field cued by the secondary target location. One group of participants had to immediately follow through to the secondary target after reaching the green target, while the other remained at the green target. (b) Error measured during the initial segment was considerably lower for the follow-through group than the no-follow-through group. (c) The no-follow-through group failed to generate compensatory (opposing) forces in response to the static spatial cues, in contrast to the cue-appropriate forces generated by the follow-through group. Abbreviations: CCW, counterclockwise; CW, clockwise. Figure adapted from Howard et al. (2015).

These results relate to the dynamical systems model discussed in the section on movement planning, which posits that different movement plans create different preparatory states in the motor cortex (Churchland et al. 2006, 2010; Shenoy et al. 2013). With different follow-throughs, or lead-ins (Howard et al. 2012), even movements that share kinematic features (i.e., the initial phase that was near identical in the two contexts) are still associated with different motor plans. In contrast, color cues do not alter the motor plan, as the movement goal remains the same for both colors. Similarly, merely seeing the follow-through target, but never planning, or making, a movement to it, is ineffective in preventing interference; here, the secondary target is a static cue that does not necessitate different motor plans. Interestingly, if participants first learn opposite force fields with different follow-throughs, the reduced interference persists even if the instructions are changed such that they only have to perform the initial segment. As long as different motor plans to the primary target are formed—for instance, by initially showing the secondary target but preventing participants from actually performing the follow-through segment of the movement—participants can adapt to opposite perturbations (Sheahan et al. 2016). From a dynamical systems perspective, separate internal models may be created because the planned follow-throughs to different final target locations necessitate different neural trajectories during motor planning (Churchland et al. 2010).

4.4. Multiple Processes Underlying Adaptation

An appealing feature of the standard state-space model is that learning is attributed to a single process, one that can be characterized by only a few parameters. Moreover, this model fits in nicely with the fact that adaptation, in large part, appears to be an automatic and implicit process. Indeed, the fact that people show pronounced aftereffects after removing prism glasses underscores the automatic nature of adaptation. Even though it is obvious that the perturbing device is no longer present, the participant cannot simply revert to a sensorimotor map that had stood them in good stead for a lifetime. The learning process has to be repeated to reset the system to its default state.

This is not to say that participants are unaware of the perturbations introduced in adaptation studies. It is obvious that the visual world has been translated upon donning a pair of prism glasses, or that a large lateral force is being applied to the arm in a standard force field study. How does this awareness affect learning? One hypothesis is that a second form of learning may be engaged when participants are aware of the perturbation, one that involves the formulation of a strategy to counteract the perturbation. Indeed, while the group average function might suggest a gradual monotonic learning function, individual behavior right after the introduction of a large perturbation (e.g., prism glasses) can be highly variable, one signature of an exploratory process (Harris 1974, Martin et al. 1996).

Additional lines of evidence suggest that a single, implicit learning process might not be sufficient to account for the performance changes observed in many sensorimotor adaptation tasks. Reaction times increase after the introduction of a salient perturbation, and the size of this increase is also predictive of accuracy: Those who show the largest increase tend to learn faster (Fernandez-Ruiz et al. 2011), an observation taken to indicate that extra planning time is required to select an appropriate strategy to counteract the perturbation. Similarly, when participants are required to respond quickly, the behavioral change is more gradual, presumably because this temporal constraint precludes the recall and implementation of a resource-demanding strategy (Haith et al. 2015b).

Even more telling is the aftereffect data in visuomotor adaptation studies. Here, the feedback is eliminated and the instructions emphasize that the participant should reach directly to the target, perhapsevenwiththeadditionaladmonitionto“stopusinganystrategyyoumighthavebeenusing since the perturbation is no longer present. ” Under such conditions, the size of the aftereffect is markedly less than the size of the change in heading angle observed at the end of the perturbation block (Bond & Taylor 2015, Day et al. 2016, Huberdeau et al. 2019, Taylor et al. 2014). While the attenuation may reflect the contextual change of eliminating the feedback, it is also possible that multiple processes were contributing to learning during the perturbation block, with the aftereffect providing a measure of learning limited to implicit adaptation, or recalibration.

4.5. Explicit Contributions to Adaptation

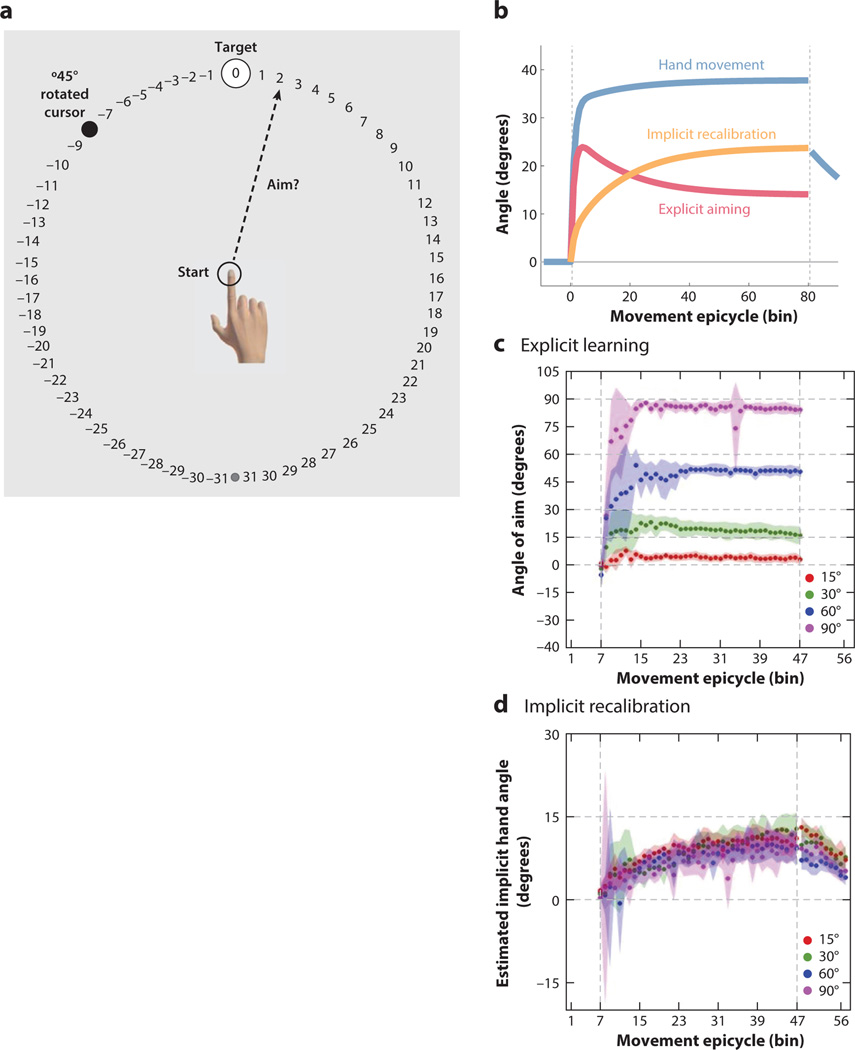
To directly address the question of strategy use, Taylor et al. (2014) modified the standard visuomotor adaptation task, asking participants to report where they planned to reach prior to each movement (Figure 6a). During baseline, the typical participant will report that they are aiming at the target. But with the introduction of the perturbation, the reports reveal that most participants modify their aim, strategically seeking to counteract the perturbation. Interestingly, within a few trials, the actual position of the hand deviates from the reported aim location. This is because, in addition to strategy use, adaptation remains operative, using the observed error to recalibrate an internal model (Figure 6b). As such, one can partition learning into two components, one explicit and one implicit. The aim reports provide a direct measure of explicit strategy use. By subtracting this measure from the actual hand position, one can estimate the magnitude of implicit adaptation.

Figure 6.

Partitioning visuomotor adaptation into explicit and implicit components. (a) In the aim report task, numbered visual landmarks are provided on the display to aid verbal reporting. Aiming strategies are assayed on a trial-by-trial basis, with the participant reporting their aim location prior to reaching. (b) Overall learning decomposed into that associated with explicit aiming and an estimate of implicit recalibration (obtained by subtracting the current aim report from the actual reach direction). (c) Participants modify their explicit aiming strategy in a proportional manner in response to variation of the size of a visuomotor rotation. (d) In contrast, implicit recalibration, either estimated by subtraction or measured in an aftereffect block, is similar across all perturbation sizes. Panel a adapted from Taylor et al. (2014); panels c and d adapted from Bond & Taylor (2015).

As shown by Figure 6b, early learning is dominated by strategy change, leading to a rapid improvement in performance. But over time, the more gradual, cumulative effect of implicit recalibration becomes stronger, necessitating a modification of the aiming strategy to maintain accurate performance. Consistent with the hypothesis that performance is composed of (at least) two processes, the estimated state of recalibration at the end of the perturbation block corresponds nicely to the size of the aftereffect, obtained in a washout block when feedback is eliminated and the participants are instructed to “reach directly to the target” (Figure 6d).

Strategy use is unlikely to be an artifact of the aiming report task. Performance functions and, more importantly, the size of the aftereffects are similar in the aiming report task compared with those observed when participants do not provide reports (Taylor et al. 2014). Subsequent studies have shown that this two-system model is also relevant when considering performance in other adaptation tasks. For example, participants report aiming in the direction opposite to the perturbation imposed by a velocity-dependent force field, and the angle of these reports changes over time (McDougle et al. 2015; see also Schween et al. 2020).

The relative contribution of explicit and implicit learning processes is dependent on the size of the perturbation (Bond & Taylor 2015, Morehead et al. 2015, Werner et al. 2015). Interestingly, most of the variation here is associated with the strategic component. For small rotations (e.g., 15°), strategy use, while evident in the initial perturbation trials, drops to negligible levels by the end of the perturbation block. For large rotations, the magnitude of aiming increases in a near-linear manner with the size of the perturbation (Figure 6c). In contrast, the magnitude of implicit recalibration is relatively invariant, with similar aftereffects observed for rotations ranging from 15° to 90° (Figure 6d) (Bond & Taylor 2015). This finding suggests that the implicit recalibration of a sensorimotor map may be limited in extent; the system is willing to adjust the visuomotor map only to a certain degree. Beyond this, learning requires a process that is more flexible, one that entails a change in action selection (where to reach) rather than action execution (how to reach).

Another point of contrast between explicit and implicit learning can be observed in savings, or faster relearning of a previously experienced perturbation. Several studies have shown that savings is almost entirely due to recall of explicit strategies (Haith et al. 2015b, Huberdeau et al. 2015, Morehead et al. 2015). In contrast, the implicit recalibration component does not increase across repeated exposures to the same perturbation, and even exhibits attenuation (Avraham et al. 2020).

4.6. The Cerebellum: A Critical Subcortical Node in Sensorimotor Learning

An extensive literature involving a range of tasks and species has demonstrated the importance of the cerebellum in sensorimotor recalibration (see reviews in Krakauer et al. 2019, Shadmehr et al. 2010). Damage to the cerebellum results in major impairments in sensorimotor adaptation during reaching (Izawaetal. 2012), walking (Morton & Bastian 2006), and saccadic eye movements (Panouillères et al. 2013), deficits that cannot be accounted for by the increased motor variability associated with ataxia (Martin et al. 1996, Schlerf et al. 2012, Tseng et al. 2007). In terms of a process-based account, the core deficit has been associated with an inability to generate an accurate prediction of the sensory consequences of a movement, an impairment that not only disrupts learning but also underlies the dysmetric movements characteristic of ataxia (Wolpert et al. 1998).

The neuroimaging literature provides a complementary albeit more complex picture. In general, cortical areas including the prefrontal, parietal, and premotor cortices are strongly engaged during the early stages of learning, and exhibit a decrease in activity as performance improves (Bédard & Sanes 2014, Bernardi et al. 2018, Graydon et al. 2005, Krakauer et al. 2004, Shadmehr & Holcomb 1997). Regions within the cerebellum sometimes show a similar pattern (Bernard & Seidler 2013; Imamizu et al. 2000, 2003; Nezafat et al. 2001), consistent with the observation that cerebellar and cortical activity patterns tend to be positively correlated. However, increased activity within subregions of the cerebellum over the course of learning has also been reported (Graydon et al. 2005, Krakauer et al. 2004, Shadmehr & Holcomb 1997). These increases have been interpreted to reflect the establishment of a new internal model or recalibration of an existing internal model (Imamizu et al. 2000).

It is always challenging to relate patterns of hemodynamic activity to function, especially in studies of learning. Increases in activity in response to the introduction of a visual perturbation might reflect surprise at the unexpected feedback, sensitivity to the magnitude of the error, or engagement of motor responses to compensate for the error. Similarly, a decrease in activity as learning proceeds might reflect are duction in error, habituation to the perturbation, or are duction in exploratory behavior. Importantly, the interpretation problem is made even more salient by the fact that most imaging studies of sensorimotor adaptation have used methods that are now known to clearly engage multiple learning processes. For example, learning to compensate for a 45° visuomotor rotation will engage both strategic aiming and implicit recalibration.

With these caveats in mind, several neuroimaging studies have involved methods in which learning is largely implicit, showing evidence for an increase in cerebellar activity over the course of learning. For example, increases localized to the deep cerebellar nuclei were observed when the perturbation of the visual feedback was increased in an incremental manner across trials (Werner etal. 2014), a method designed to minimize awareness of the perturbation. Similarly, random visual perturbations, a method that minimizes strategic changes but engages the adaptation system, is associated with greater activity (relative to nonperturbed movements) in several lobules of the cerebellar cortex (Diedrichsen et al. 2005). Perhaps the strongest support for implicit processing of sensorimotor errors in the cerebellum comes from studies of saccadic adaptation (Desmurget et al. 1998, Liem et al. 2013, van Broekhoven et al. 2009) and eyeblink conditioning (Logan & Grafton 1995), two forms of learning that occur outside awareness.

While the many tools of neuroscience provide compelling evidence that the cerebellum is a key structure for implicit recalibration, an open question concerns the involvement of the cerebellum in other learning processes. Specifically, does the cerebellum also contribute to more cognitive aspects of sensorimotor learning such as strategic aiming? As noted above, activity in certain areas of the cerebellum closely parallels that observed in the prefrontal cortex during studies of visuomotor rotation, with activity decreasing over the course of learning. One interpretation of this pattern is that it reflects the recruitment and implementation of an aiming strategy: Upon introduction of the large perturbation, the participants explore possible ways in which aiming could reduce the large error, with the decrease over time corresponding to the consolidation of a successful strategy (Haith et al. 2015b, McDougle & Taylor 2019). Thus, this neuroimaging research may be taken to indicate multifunctionality within the cerebellum, with certain regions showing a decrease in activation linked to strategy use and other regions showing an increase linked to adaptation.

Indeed, recent neuropsychological studies indicate that the integrity of the cerebellum is required not only for implicit adaptation but also for strategic aiming. In a study involving patients with cerebellar degeneration, Butcher et al. (2017) used the aiming report task to probe strategy use as the participants learned to respond to a 45° rotation (Figure 6a). Consistent with previous reports, the recalibration process was severely compromised, with an aftereffect of only around 3°. Interestingly, the mean aiming angle at the end of the rotation block was only 13°. Thus, the patients failed to increase their aiming direction despite a persistent error of around 30°. Additional research has shown that even when provided with the appropriate aiming strategy in one context, patients fail to generalize to a novel context (Wong et al. 2019). These results demonstrate that the cerebellum is important for implicit recalibration as well as for the generation and implementation of explicit strategies that can facilitate sensorimotor learning. An important question for future research will be to delineate the computational role of the cerebellum in strategy use.

4.7. Interaction Between Implicit and Explicit Learning

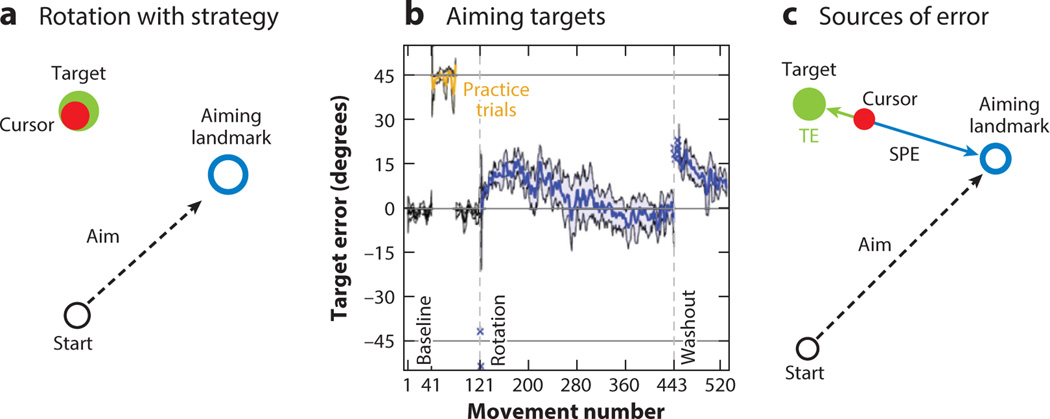
Varying the size of the perturbation provides one way to look at the relative contribution of implicit and explicit processes to adaptation, as well as their interaction. One limitation here, both with the aiming report task and with standard sensorimotor adaptation tasks, is that the error signal results in aligned changes; for example, a counterclockwise rotation leads to changes in aim and adaptation in the clockwise direction. Mazzoni & Krakauer (2006) developed an alternative approach, one in which these two processes work in opposition to one another. In this task, the target was surrounded by a series of circles, or landmarks. After introducing a 45° counterclockwise rotation, the experimenter intervened, explaining the nature of the perturbation and instructing the participant that they could negate this perturbation by aiming to a landmark located 45° in the clockwise direction from the target (Figure 7a). Thus, unlike the aiming report task, designed to probe how participants discover an appropriate strategy, the landmark task provides the participants with an ideal aiming strategy.

Figure 7.

Distinct error signals drive explicit and implicit learning processes. (a) In the aiming landmark task, participants are instructed to aim at a landmark neighboring the target to counteract a 45° rotation. (b) Although the introduction of the strategy results in the cursor landing near the target, the heading error increases over the next 100 trials or so before reversing, with performance eventually being very accurate. A large aftereffect is observed at the beginning of the washout block. (c) Two sources of error drive parallel operation of implicit and explicit learning processes. Sensory prediction error (SPE) is based on the difference between the predicted location of the feedback based on the explicit aim direction (at the aiming landmark) and the cursor. Target error (TE) is based on the difference between the target and cursor. In the aiming landmark task, the directions of these two errors are in opposition to one another, with their relative contributions to learning varying over time due to changes in their respective sizes. Figure adapted from Taylor & Ivry (2011).

As one would expect, after being provided with the strategy, participants were immediately able to achieve accurate performance, with the rotated cursor landing in or close to the target. However, over the course of the next 70 trials, a marked pattern of “drift” was observed. The heading angle deviated further and further from the aiming target, with the cursor eventually missing the target by approximately 20° in the opposite direction of the rotation.

Mazzoni & Krakauer (2006) argued that this paradoxical behavior—where performance becomes worse with practice—reveals how the implicit recalibration process seeks to keep the sensorimotor system well tuned, even at the cost of accurate performance. To appreciate this point, consider the error components when aiming at the landmark. Given the 45° rotation, the cursor lands in the target when reaching to the neighboring landmark. Despite this success, there remains, at least from the perspective of the motor system, a 45° sensory prediction error: The system generates a prediction of the sensory consequences (i.e., feedback at the landmark), but the cursor appears at the target. The recalibration process applies its update rule (see Equation 2), producing the observed drift function. Indeed, the drift would suggest that implicit learning overrides strategy use.

Subsequent research using the landmark task has revealed a more nuanced picture. If the number of trials is increased, the drift function shows a surprising nonmonotonicity, with the mean hand angle eventually returning to 45°, the optimal direction in terms of task success (Figure 7b) (Taylor & Ivry 2011). This finding might suggest that the strategy system eventually overrides the implicit system. However, when the rotation is removed and the participant is instructed to reach directly to the target, a prominent aftereffect is observed. The size of this aftereffect is even larger than the maximum of the drift function. Thus, adaptation appears to have persisted and even continued when the hand direction was going in the opposite direction.

These results, complemented by modeling work, point to the parallel operation of learning processes required for aiming and adaptation. Importantly, these processes are driven by distinct error signals. Whereas adaptation is driven by SPE, the difference between predicted and actual feedback, strategy change is driven by target error (TE), the difference between the actual feedback and the goal (Figure 7c). The nonmonotonicity emerges naturally from the changing magnitude of the two error signals. Early in learning, the SPE signal is large and TE is negligible; over time, TE becomes larger (due to drift) while SPE becomes smaller. The fact that the aftereffect is larger than the peak drift provides further evidence that adaptation continued to operate, even when the effect on behavior was dominated by changes in strategy.

Subsequent research has pointed to weaknesses in the details of the model. In particular, TE-driven changes in strategy use may be better described as an exploratory process rather than error driven gradient descent. But the core idea that adaptation is dependent on SPE and aiming on TE has been confirmed in a range of studies (Brudner et al. 2016, Day et al. 2016, McDougle et al. 2017). These findings make clear not only that multiple processes operate in sensorimotor learning but also that these processes operate at different levels of control. The computational goal of the implicit component of adaptation is to keep the motor system well calibrated, ensuring that motor commands are faithfully implemented (Miyamoto et al. 2020). This system appears impervious to information about task success. In contrast, the computational goal of a strategic process such as aiming is to ensure that the appropriate action is selected to optimize performance. For this to occur, it is essential to monitor how well a selected action achieves its desired goal.

4.8. Characteristics of Implicit and Explicit Adaptation

Recognizing the relevance of multiple learning processes is important for advancing a holistic approach to understanding skill acquisition. Nonetheless, there remains the challenge to specify the constraints associated with each component process. One way to hone in on implicit learning involves creating conditions in which the SPE is fixed (Kim et al. 2018, Morehead et al. 2017, Poh & Taylor 2019, Vandevoorde & Orban de Xivry 2019), exploiting the automatic response of this process to this error signal, even at the expense of task success. In one variant, the timing and radial extent of the feedback cursor are linked to hand motion, but the angular path is invariant, independent of the angular path of the hand. The participant is fully informed of the “clamped” perturbation and is instructed to always aim for the target, ignoring the feedback. Despite these instructions, the behavior shows all of the hallmarks of recalibration (e.g., exponential “learning” function, aftereffects, local generalization) (Morehead et al. 2017, Parvin et al. 2018). Importantly, questionnaire data as well as within-task reports of hand position indicate that participants have no awareness of this change in performance.

Since the size of the error remains invariant (and there is no change in TE), this method provides a new way to examine the sensitivity of the recalibration system to error. In an initial study of this question, both the trial-by-trial rate of change and the asymptotic level of adaptation were found to be largely invariant across errors ranging in size from 7. 5° to 60° (Morehead et al. 2017). Thus, the results from the clamp method converge with earlier findings indicating that the response to large errors is attenuated (Fine & Thoroughman 2006, Marko et al. 2012, Wei & Körding 2009); indeed, these data suggest that the response to errors over this range are saturated. In contrast, with smaller errors, the initial rate of learning is roughly proportional (Kim et al. 2018). Surprisingly, though, the differences in the initial slopes of the learning functions evaporate; for example, clamp sizes of 1. 75° and 15° converge toward a similar asymptote.

These observations led us to recast the basic state-space model, shifting the focus from how error sensitivity constrains the input to the system (B in Equation 2) to an emphasis on how variation in error size constrains the output of the learning process. From this perspective, the update to the sensorimotor map scales for small errors but quickly saturates at the maximum value that the system is capable of changing from one trial to the next. Moreover, the sensitivity to small errors may be modified over time. When initially experienced, the response to a small error may be modest, perhaps reflecting that these errors may be the result of implementation noise. But when observed repeatedly, the system becomes sensitized to that error, recognizing that it likely reflects a change in the environment and thus mandates a corrective adjustment.

Why should implicit recalibration reach an asymptote when presented with clamped visual feedback since the putative SPE signal is never eliminated? One possibility is consonant with the standard state-space model interpretation: The asymptote is reached when the trial-by-trial changes from learning and forgetting are in dynamic opposition. Another possibility is that the asymptote reflects the limits of proprioceptive recalibration (or the system’s tolerance for proprioceptive error). Even though the participant’s subjective experience is that the hand is moving directly to the target, the proprioceptive system may be implicitly responding to a proprioceptive SPE, one that counteracts the effects of the persistent visual SPE.

To date, there has been much less computational development of process models to account for strategy use, at least in comparison to the research on implicit adaptation. Recently, McDougle & Taylor (2019) proposed that, to implement an aiming strategy, participants engage in a mental rotation process, shifting a movement plan that was initially directed to the target location to the aiming location. Consistent with this hypothesis, reaction time increases with the size of the perturbation, mirroring classic findings on mental rotation (Shepard & Metzler 1971). Alternatively, aiming could be performed by choosing to reach toward a memorized or cached location (see Haith & Krakauer 2018). In some ways, this would seem more efficient—why perform a time-consuming, continuous transformation from one target location to another when one can retrieve a memory of the correct solution? However, the memory requirements constitute a cost for caching. If there are eight possible target locations, it would be necessary to remember eight aiming locations, or eight sets of action–outcome relationships, and these locations may be shifting over time (given ongoing adaptation) (Butcher et al. 2017). Empirically, it appears that a memory-based process is used when the number of target locations is small and an algorithmic process (i.e., mental rotation) is used when the number of locations is large (McDougle & Taylor 2019).

4.9. Other Learning Processes

As any skilled athlete will affirm, practice is a necessary component of motor learning. The tennis pro will spend countless hours practicing to get her serve to land in just the right spot. The outcome of each serve provides salient feedback to refine the movement. However, mere repetition can also strengthen a motor memory, even in the absence of feedback. The practice swings of the baseball player as she steps up to bat do not result in any obvious feedback, yet all players engage in this ritual. While the behavior may be cultural, the swings also likely help retrieve and solidify a movement. The strengthening of a movement in the absence of overt feedback is referred to as use-dependent learning (UDL) (Krakauer & Mazzoni 2011), and could be thought of as the behavioral manifestation of Hebbian learning (Verstynen & Sabes 2011).

A striking example of UDL comes from a transcranial magnetic stimulation (TMS) study looking at motor cortex plasticity. At the beginning of the session, the TMS coil was positioned over M1 to elicit adduction of the thumb. The participant was then given the simple task of repeatedly abducting the thumb. Post training, the same M1 stimulation now elicited thumb movements clearly shifted in the direction of abduction (Classen et al. 1998; see also Mawase et al. 2017).

The ideal test of UDL would involve practice in which the participant is unaware of the movement that is being repeated, given that complying with the experimental instructions may be rewarding and recruit processes besides UDL. Diedrichsen et al. (2010b) created this situation with a reaching task in which the goal was to terminate the movement at a particular distance from the start location, independent of the reach angle. Thus, accuracy depended only on movement extent, not direction. Following baseline reaches, the participant’s arm was passively moved the appropriate distance by a robotic device, but, unbeknownst to the participants, the trajectory increasingly deviated to one side over subsequent trials. Following these passive trials, voluntary reaches performed by the participants resembled the deviated trajectory, even though that change had been irrelevant to task performance (Diedrichsen et al. 2010b).

UDL would seem an obvious candidate for a learning process that affects movement execution. Indeed, the TMS changes described above suggest that repetition can have a rapid change in the tuning profiles of neurons within M1. However, a recent paper suggests that a bias to repeat recent movements may reflect constraints in action planning (Marinovic et al. 2017). These biases become diminished when participants are given more time for movement preparation; conversely, preparation for the repeated movement becomes more rapid (Mawaseetal. 2018). Thus, the effects of UDL may arise in processes related to both action selection and movement execution.

The past decade has seen considerable interest in the role of reinforcement learning in the motor domain. In reinforcement learning, the feedback is frequently binary, providing information about the success or failure of an action, or scalar, in terms of providing information about the magnitude of the reward. This stands in contrast to most motor learning tasks, where the feedback is vectorial, providing information about the direction and magnitude of the error: We see that the tennis serve was just outside the service box, not merely that the serve was out.

Can binary feedback be sufficient to learn a visuomotor rotation? Izawa & Shadmehr (2011) provided salient positive feedback in the form of an exploding target for movements that fell within a window corresponding to roughly the magnitude of normal motor variability. This window was originally centered around the target but was gradually rotated, eventually reaching 8° away from the target. Behaviorally, participants were able to track the rotation from the binary feedback. However, learning was much more variable than that observed with standard, vectorial feedback, suggesting an exploratory process (Cashaback et al. 2017, Therrien et al. 2018). Moreover, tests of perceived hand position indicated that, unlike SPE-driven learning, the sensorimotor map was unchanged by binary feedback.

These studies show that reinforcement alone can be an effective means of changing behavior. The more interesting question is: How does reinforcement influence behavior when error-based learning is also relevant? One hypothesis is that reward information has little effect on the rate of learning, but strengthens retention (Galea et al. 2015, Shmuelof et al. 2012a; for a different perspective, see Nikooyan & Ahmed 2015), on the basis of the observation that participants who received rewards during a visuomotor rotation took longer to wash out than those who did not receive rewards. However, Codol and colleagues (Codol et al. 2018, Holland et al. 2018) reported that the maintenance of asymptotic performance during washout was under participants’ explicit control; thus, the effect of reinforcement may be to make strategy use more salient, rather than have a direct effect on an internal model.

Nonetheless, there are some provocative results indicating that reward may also modulate implicit learning processes. If a target jumps mid-reach such that a rotated cursor lands within the target, adaptation is attenuated (Leow et al. 2018). One interpretation of this effect is that having the cursor land in the target results in a reward signal, which moderates the effect of the SPE (Reichenthal et al. 2016). Presumably the “reward” occurs even though the participant is fully aware that the outcome was not the direct result of his movement.

This idea has also been explored in research using clamped visual feedback. In the same way that the implicit recalibration system responds to the cursor as an SPE, missing the target may also produce a TE, even though the task outcome is also outside the participant’s control. Manipulating the size of the target offers one way to test this hypothesis (Kim et al. 2019): A clamp of a fixed size will miss a small target (TE present) but land within a large target (TE absent), with the SPE being the same in the two conditions. As with the target jump manipulation, adaptation is strongly attenuated in the large target condition. This attenuation could come about via the direct modulation of the adaptation system by an intrinsic reward signal, or the operation of a second implicit learning process, one that learns from TE.

5. CONCLUDING REMARKS AND FUTURE DIRECTIONS

This review has covered a broad array of research on sensorimotor control and learning, using reaching movements as a model task. In an interdisciplinary manner, this research has fueled the development of formal models of motor planning and initiation, online control, and sensorimotor learning. These models range in both scope and levels of analysis. For example, technological advances that have allowed for the simultaneous recording from multiple neurons, combined with sophisticated data analysis methods, have opened up new perspectives on motor planning, offering a contrast to the representation-based perspective that had dominated the field. Similarly, simple yet elegant novel behavioral manipulations have proven effective in revealing surprising phenomena that have required an overhaul of the most basic models of motor learning.

We anticipate that the next decade will prove to be just as tumultuous and productive. New tools are emerging that will allow the study of motor control to move beyond the conventional laboratory setting. VR systems could be used to study movement in rich yet well-controlled environments, or to create novel contexts for exploring the flexible and adaptive nature of our motor system (Levin et al. 2015). Apps and other technologies will allow movements to be studied “in the wild, ” creating robust data sets to be mined in the search for general organizational principles that hold across the range of conditions in which we interact with the environment (Mathis et al. 2018). Machine learning algorithms will surely be recruited to plow through the deluge of data that is bound to be produced by these new technologies. The future for our field is surely exciting, with insights from this research inspiring translational advances for robotics, neuroprosthetics, and physical rehabilitation interventions.

Thoughts of our future are also unsettling because of the temptation to let the tools define the questions, with the danger of losing sight of the behavior we are trying to understand (Krakauer et al. 2017). We close this article by outlining a few of the open questions we hope to see answered when the next set of authors come along to review the state of sensorimotor control for this journal.

FUTURE ISSUES.

1. What are the mechanisms operating at different stages of motor planning and implementation, and how do they interact? How do we bring together computational ideas concerned with addressing high-level task requirements (e.g., where and when to move) with lower-level requirements needed to generate the motor commands that activate the appropriate muscles?

2. How does the sensorimotor system deal with variability? Is execution variability always “bad” (noise), something that needs to be minimized? And if variability associated with Planning can be “good, ” supportive of exploitation, how does the system distinguish between different types of variability?

3. How do intrinsic rewards (values) associated with task goals affect action selection andonline control? How do we define and formalize a principled cost function that incorporates the many dimensions that constrain our movements?

4. What is the computational role of the cerebellum in strategy use during sensorimotor learning?

5. Are there unifying principles for understanding sensorimotor learning in a broad context? How do insights obtained in behavioral studies of sensorimotor learning bear on our understanding of more general features of skill learning?