Shape recovery of deformed biomolecular droplets: Dependence on condensate viscoelasticity

Abstract

A theoretical study on the shape dynamics of phase-separated biomolecular droplets is presented, highlighting the importance of condensate viscoelasticity. Previous studies on shape dynamics have modeled biomolecular condensates as purely viscous, but recent data have shown them to be viscoelastic. Here, we present an exact analytical solution for the shape recovery dynamics of deformed biomolecular droplets. The shape recovery of viscous droplets has an exponential time dependence, with the time constant given by the “viscocapillary” ratio, i.e., viscosity over interfacial tension. In contrast, the shape recovery dynamics of viscoelastic droplets is multi-exponential, with shear relaxation yielding additional time constants. During shape recovery, viscoelastic droplets exhibit shear thickening (increase in apparent viscosity) at fast shear relaxation rates but shear thinning (decrease in apparent viscosity) at slow shear relaxation rates. These results highlight the importance of viscoelasticity and expand our understanding of how material properties affect condensate dynamics in general, including aging.

I. INTRODUCTION

Phase-separated biomolecular condensates exhibit different extents of liquidity, which may be crucial for cellular functions and correlated with diseases such as neurodegeneration and cancer.^1–7 Driven by interfacial tension (or capillarity), condensates that are more liquid-like retain a spherical shape and hence appear as micro-sized droplets. The material properties of many condensates also evolve over time and become more solid-like (sometimes referred to as “aging”).^8–13 A simple indication of liquidity is the tendency of deformed droplets to recover their spherical shape. In all the studies so far on the dynamics of such shape changes, biomolecular condensates have been modeled as purely viscous, reporting viscosities that are orders of magnitude higher than that of water.^1,8,14–18 However, recent work has shown that condensates are viscoelastic.^12,19–23 In viscoelastic fluids, shear relaxation is not instantaneous²¹ and its effects, when coupled with viscocapillary effects, can lead to unexpected observations. In this work, we present a theoretical study on the effects of viscoelasticity on the shape recovery dynamics of deformed biomolecular droplets.

Nearly all previous studies on the shape dynamics of biomolecular condensates have dealt with the fusion of droplets when they come into contact.^{1,8,11,14–18,24–28} However, in one study, Hubstenberger et al.¹ reported observations on both droplet fusion and shape recovery of grP-bodies formed in the cytoplasm of Caenorhabditis elegans oocytes. Shape recovery after mechanical stress-induced elongation was faster than droplet fusion by two orders of magnitude, which was suggested as indicating elasticity of these ribonucleoprotein condensates. While theoretical results of viscous fluids have been used for qualitative and quantitative analysis of droplet fusion dynamics^1,14–18,28 and a theoretical model of viscoelastic fluids has been introduced to treat deformation of droplets under external force,^19,20 until now, no theory has been presented for shape recovery of deformed biomolecular droplets.

However, the problem of shape recovery has long received attention in the fluid-dynamics literature. Prosperetti^29,30 presented a full analytical solution to the recovery dynamics of viscous droplets from a small-amplitude deformation. Phenomenological models have also been introduced to propose theoretical results for shape recovery, also known as deformation retraction, of viscoelastic droplets.^31,32 This problem has also been tackled by numerically solving the fluid-dynamics equations.^33–35 There have also been a number of experimental studies on the deformation retraction of polymer blends,^36–39 often indicating the effects of viscoelasticity.

The high viscosities reported in in vitro studies of biomolecular condensates (relative to water) translate into a significant viscosity ratio, η_II/η_I, between the dense droplet phase (indicated by index II; Fig. 1) and the exterior dilute bulk phase (indicated by index I). On the other hand, Caragine et al.²⁴ suggested a case with η_II/η_I ≪ 1. They noted the even higher viscosity of the nucleoplasm surrounding nucleoli, a type of biomolecular condensate specializing in ribosomal biogenesis, than that of droplets formed by a main nucleolar protein.¹⁷ In addition, polymer blends may phase separate to produce dilute-phase “bubbles” in dense coacervates,³⁹ also leading to η_II/η_I ≪ 1. The viscosity ratio is of theoretical interest because in the limiting cases of η_II/η_I = ∞ and 0, one can neglect the fluid dynamics in either the exterior region (i.e., “I”) or interior region (i.e., “II”), significantly simplifying the mathematics. The viscosity ratio may also affect how much viscoelastic droplets and purely viscous droplets differ in shape dynamics.

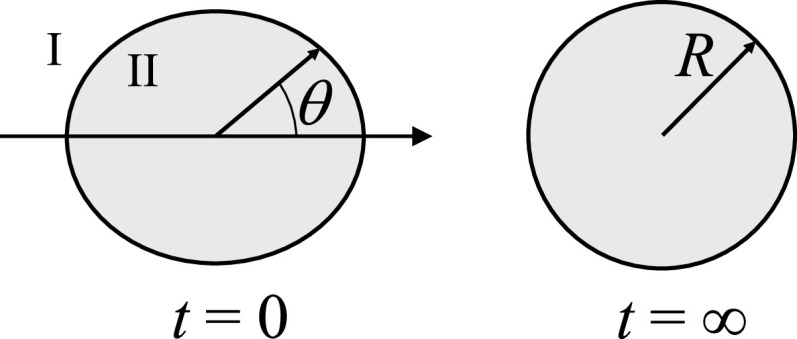
FIG. 1.

Illustration of the shape recovery of a deformed droplet. Left: initial deformation. Right: fully recovered spherical shape. “II” denotes the interior region, i.e., the region inside the droplet, whereas “I” denotes the exterior region.

Here, we develop an analytical solution for the shape recovery dynamics of deformed viscoelastic droplets. This solution is presented in Sec. II. We direct the reader’s focus to Sec. III, where we report shape recovery curves for selected values of viscosities and shear relaxation rates, to illustrate rich effects of viscoelasticity. In particular, during shape recovery, viscoelastic droplets exhibit shear thickening (increase in apparent viscosity) at fast shear relaxation rates but shear thinning (decrease in apparent viscosity) at slow shear relaxation rates. Moreover, our analytical results show that shear relaxation is a new rate-limiting mechanism for shape dynamics, although experimental verification can be challenging. This paper ends with concluding remarks in Sec. IV. We place technical details in Appendixes A–F.

II. THEORY

Our main interest is the shape recovery dynamics of biomolecular droplets formed by phase separation. Below, we first give the results for purely viscous droplets (derivation found in Appendix A) and then generalize the solution to viscoelastic droplets.

We assume that the initial shape deformation is axisymmetric (Fig. 1). At polar angle θ and time t, the radial distance of the interface between the droplet and its surrounding bulk phase can be expressed as

$$r\left(\theta ,t\right)=R+f_l\left(t\right)P_l\left(\cos \theta \right),$$ (1)

where R is the radius of the fully recovered spherical shape, l ≥ 2, and P_l(x) is a Legendre polynomial. As will be apparent below, the solution for viscoelastic droplets is facilitated by working with Laplace transforms, which we denote by a caret. For viscous droplets, we find [Eq. (A42c) in Appendix A] that

$${\widehat{f}}_l\left(s\right)=\frac{f_l\left(0\right)}{s+{\lambda }_l^{\mathrm{D}}},$$ (2)

where s is the counterpart of t in Laplace space,

$${\lambda }_l^{\mathrm{D}}=\frac{l(l+2)(2l+1)}{2(2l^2+4l+3)}\frac{\gamma }{\eta R},$$ (3)

and γ denotes the interfacial tension. The inverse Laplace transform of the foregoing ${\widehat{f}}_l(s)$ is an exponential function of time, with recovery rate ${\lambda }_l^{\mathrm{D}}$, which is inversely proportional to the “viscocapillary” ratio, i.e., viscosity over interfacial tension.

A. Constitutive relation for viscoelastic fluids

In purely viscous or Newtonian fluids, shear relaxation occurs instantaneously, and hence, the stress responds only to the strain rate at the same moment [see Eq. (A3b) in Appendix A]. For later reference, we present this constitutive relation in Laplace space,

$${\widehat{\tilde{\tau }}}_{\mathrm{d}}(s)=\eta \widehat{\dot{\tilde{\epsilon }}}\left(s\right),$$ (4)

where ${\tilde{\mathrm{\tau }}}_{\mathrm{d}}$ is the deviatoric (shape-changing) component of the stress tensor and $\dot{\tilde{\mathrm{\epsilon }}}$ is the strain-rate tensor. In biomolecular condensates and other complex materials, shear relaxation occurs at a finite rate,^{12,20,21,38,39} and consequently, the stress depends on the entire history of the strain rate. Limiting to small strain rates so that the relation between ${\tilde{\mathrm{\tau }}}_{\mathrm{d}}$ and $\dot{\tilde{\mathrm{\epsilon }}}$ remains linear, Eq. (A3b) is generalized to²¹

$${\tilde{\mathrm{\tau }}}_{\mathrm{d}}(t)=\underset{-\infty }{\overset{t}{\int }}d{t}^{\prime }G\left(t-t^{\prime }\right)\dot{\tilde{\mathrm{\epsilon }}}\left(t^{\prime }\right)$$ (5a)

$$={\tilde{\mathrm{\tau }}}_{\mathrm{d}}\left(0\right)+{\int }_0^{t}d{t}^{\prime }G\left(t-t^{\prime }\right)\dot{\tilde{\mathrm{\epsilon }}}\left(t^{\prime }\right).$$ (5b)

The function $G\left(t\right)$ introduced above is the shear relaxation modulus. For our problem at hand, the strain rate starts at t = 0 [i.e., $\dot{\tilde{\mathrm{\epsilon }}}\left(t^{\prime }\right)=0$ for t′ < 0], and hence,

$${\tilde{\mathrm{\tau }}}_{\mathrm{d}}\left(0\right)=0,$$ (5c)

and Eq. (5b) becomes

$${\tilde{\mathrm{\tau }}}_{\mathrm{d}}(t)=\underset{0}{\overset{t}{\int }}d{t}^{\prime }G\left(t-t^{\prime }\right)\dot{\tilde{\mathrm{\epsilon }}}\left(t^{\prime }\right).$$ (5d)

Note that we must also have $G\left(t^{\prime }\right)=0$ for t′ < 0 since otherwise Eq. (5a) would mean that future strain rates [$\dot{\tilde{\mathrm{\epsilon }}}(t^{\prime })$ at t′ > t] would affect the present stress ${\tilde{\mathrm{\tau }}}_{\mathrm{d}}(t)$. Taking the Laplace transform of Eq. (5d), we obtain a simple constitutive relation between ${\widehat{\tilde{\tau }}}_{\mathrm{d}}$ and $\widehat{\dot{\tilde{\epsilon }}}$,

$${\widehat{\tilde{\tau }}}_{\mathrm{d}}(s)=\widehat{G}\left(s\right)\widehat{\dot{\tilde{\epsilon }}}\left(s\right).$$ (5e)

In comparison to Eq. (4) for Newtonian fluids, we see that the only difference is that η is now replaced with $\widehat{G}\left(s\right)$. Therefore, in Laplace space, the Navier–Stokes equations can be generalized to viscoelastic fluids by simply replacing η with $\widehat{G}\left(s\right)$. Correspondingly, the solution for Newtonian fluids can be transformed to the solution for viscoelastic fluids by the same replacement. We will present this solution in Secs. II B--II D. A similar replacement of η, by the Fourier transform of G(t) for viscoelastic fluids, is found in Ref. 20.

It is remarkable that the solution for the shape recovery dynamics of viscoelastic droplets can be easily obtained, in Laplace space anyway, by a substitution of $\widehat{G}\left(s\right)$ for η. Mathematically, this route simplifies the solution enormously and enables easy application to a variety of viscoelasticity models [i.e., different functional forms of $\widehat{G}\left(s\right)$]. For example, Khismatullin and Nadim⁴⁰ derived the normal-mode solution explicitly for the Jeffreys model of viscoelasticity. It can be easily verified that their solution is the same as the counterpart for Newtonian droplets^29,41,42 except with the replacement of η by $\widehat{G}\left(s\right)$. Physically, the replacement of η by $\widehat{G}\left(s\right)$ means that $\widehat{G}\left(s\right)$, the shear relaxation modulus (in Laplace space) of viscoelastic droplets, plays a similar role as the viscosity of Newtonian droplets. Indeed, by definition, Newtonian fluids have a shear relaxation modulus that is constant and equal to the viscosity,

$$\widehat{G}\left(s\right)=\eta \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{N}\mathrm{e}\mathrm{w}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{fl}\mathrm{u}\mathrm{i}\mathrm{d}\mathrm{s}.$$ (6a)

The counterpart in the time domain is a delta function,

$$G\left(t\right)=\eta \delta \left(t\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{N}\mathrm{e}\mathrm{w}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{fl}\mathrm{u}\mathrm{i}\mathrm{d}\mathrm{s},$$ (6b)

which means that shear relaxation occurs instantaneously. For viscoelastic fluids, the value of $\widehat{G}\left(s\right)$ at s = 0 is the zero-shear viscosity, i.e., the viscosity measured at the zero strain rate,

$$\widehat{G}\left(0\right)={\eta }_{\mathrm{z}}.$$ (7)

However, shear relaxation occurs at a finite rate in viscoelastic fluids and $\widehat{G}\left(s\right)$ is no longer a constant. Correspondingly, the shape deformation amplitude $f_l\left(t\right)$ is no longer a single exponential with a time constant dictated by the “viscocapillary” ratio. Rather, additional time constants are introduced by shear relaxation.

We now introduce various models of linear viscoelasticity. In the Maxwell model, shear relaxation is an exponential function of time, with a time constant τ^sr,

$$G\left(t\right)=\frac{\eta }{{\tau }^{\mathrm{s}\mathrm{r}}}{e}^{-t/{\tau }^{\mathrm{s}\mathrm{r}}}\mathrm{f}\mathrm{o}\mathrm{r}t>0.$$ (8)

The Laplace transform is

$$\widehat{G}\left(s\right)=\frac{\eta }{1+{\tau }^{\mathrm{s}\mathrm{r}}s}.$$ (9)

In the limit τ^sr → 0, the Maxwell model reduces to a Newtonian fluid, consistent with the latter’s instantaneous shear relaxation. A linear combination of a Newtonian fluid and the Maxwell model,

$$\widehat{G}\left(s\right)={\eta }_0+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s},$$ (10)

is the Jeffreys model, which can also be seen as the linearized version of the Oldroyd B model. When the Newtonian component of Eq. (10) is also generalized to be Maxwellian, i.e.,

$$\widehat{G}\left(s\right)=\frac{{\eta }_0}{1+{\tau }_0^{\mathrm{s}\mathrm{r}}s}+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s},$$ (11)

we obtain the Burgers model. For the Jeffreys and Burgers models, the zero-shear viscosity is

$${\eta }_{\mathrm{z}}=\widehat{G}\left(0\right)={\eta }_0+{\eta }_1.$$ (12)

We can represent an arbitrary shear relaxation modulus by adding more and more Maxwellian components. However, these more complicated models rarely are useful.

B. Viscoelastic droplets in an ideal-fluid medium

By substituting the shear relaxation modulus $\widehat{G}\left(s\right)$ for the viscosity η in Eq. (3) and using the latter in Eq. (2), we obtain the shape deformation amplitude, ${\widehat{f}}_l\left(s\right)$, for viscoelastic droplets,

$${\widehat{f}}_l\left(s\right)=\frac{f_l(0)}{s+{\lambda }_l^{\mathrm{D}}/\widehat{g}\left(s\right)},$$ (13)

where ${\lambda }_l^{\mathrm{D}}$ is given by Eq. (3) but with η now replaced by η_z, i.e.,

$${\lambda }_l^{\mathrm{D}}=\frac{l(l+2)(2l+1)}{2(2l^2+4l+3)}\frac{\gamma }{{\eta }_{\mathrm{z}}R},$$ (14)

and

$$\widehat{g}\left(s\right)=\frac{\widehat{G}\left(s\right)}{{\eta }_{\mathrm{z}}}.$$ (15)

By definition, $\widehat{g}\left(0\right)=1$. For Newtonian fluids, $\widehat{g}\left(s\right)=1$ for all s. Note that the area under the $f_l\left(t\right)$ vs t curve, given by ${\widehat{f}}_l\left(0\right)$, is

$${\widehat{f}}_l\left(0\right)=\frac{f_l(0)}{{\lambda }_l^{\mathrm{D}}}.$$ (16)

With this result, we can interpret ${\lambda }_l^{\mathrm{D}}$ as the mean recovery rate, in the sense that the exponential function $f_l(0)e^{-{\lambda }_l^{\mathrm{D}}t}$ has the same area as $f_l\left(t\right)$. Equation (16) is derived from Eq. (13) using $\widehat{g}\left(0\right)=1$. Because Eq. (16) holds irrespective of $\widehat{g}\left(s\right)$, the area of the $f_l\left(t\right)$ curve must be conserved when the parameters, in particular the time constants of shear relaxation in $\widehat{g}\left(s\right)$, or even the functional forms of $\widehat{g}\left(s\right)$ are varied.

C. Ideal-fluid bubbles in a viscoelastic medium

Similarly, by substituting the shear relaxation modulus $\widehat{G}\left(s\right)$ for the viscosity η in Eq. (A52c), we obtain the shape deformation amplitude, ${\widehat{f}}_l\left(s\right)$, for ideal-fluid bubbles in a viscoelastic medium,

$${\widehat{f}}_l\left(s\right)=\frac{f_l(0)}{s+{\lambda }_l^{\mathrm{B}}/\widehat{g}\left(s\right)},$$ (17)

where ${\lambda }_l^{\mathrm{B}}$ is given by Eq. (A17) but with η now replaced by η_z,

$${\lambda }_l^{\mathrm{B}}=\frac{(l-1)(l+1)(2l+1)}{2(2l^2+1)}\frac{\gamma }{{\eta }_{\mathrm{z}}R},$$ (18)

and represents the mean recovery rate that corresponds to the area under the $f_l\left(t\right)$ vs t curve.

D. Viscoelastic droplets in a viscous medium and viscous droplets in a viscoelastic medium

For the shape recovery of a deformed viscoelastic droplet in a viscous medium, by substituting ${\widehat{G}}_{\mathrm{I}\mathrm{I}}\left(s\right)$ for the interior viscosity η_II in λ_l that is given by Eq. (A20a) and appears in Eq. (B5), we obtain

$${\widehat{f}}_l\left(s\right)=\frac{f_l\left(0\right)}{s+{\lambda }_l^{\mathrm{I}}/h_l(s)},$$ (19a)

where

$${\lambda }_l^{\mathrm{I}}=\frac{e_l\gamma }{{\eta }_{\mathrm{I}}R},$$ (19b)

$$h_l\left(s\right)=\frac{\left[a_l{\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}{\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)+b_l\right]\left[c_l{\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}{\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)+d_l\right]}{{\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}{\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)+1},$$ (19c)

with a_l, b_l, c_l, d_l, and e_l given by Eqs. (A20b)–(A20f). Furthermore, α_II/I is the viscosity ratio given by Eq. (A20g), but η_II now represents the zero-shear viscosity of the viscoelastic droplet, and

$${\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)=\frac{{\widehat{G}}_{\mathrm{I}\mathrm{I}}\left(s\right)}{{\eta }_{\mathrm{I}\mathrm{I}}}.$$ (19d)

At s = 0, we find that

$${\widehat{f}}_l\left(0\right)=\frac{f_l\left(0\right)}{{\lambda }_l^{\mathrm{I}}/h_l(0)}=\frac{f_l\left(0\right)}{{\lambda }_l},$$ (19e)

where λ_l is given by Eq. (A20a). Equation (19e) means that the area under the $f_l\left(t\right)$ curve is conserved for any ${\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)$, including the one, ${\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)=1$, for Newtonian fluids.

The foregoing results can also apply to the reverse case, i.e., a viscous droplet in a viscoelastic medium, after the following changes: replacing ${\lambda }_l^{\mathrm{I}}$ with ${\lambda }_l^{\mathrm{I}\mathrm{I}}$ and ${\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(s\right)$ with ${\widehat{g}}_{\mathrm{I}}\left(s\right)$ and swapping a_l with b_l and c_l with d_l in Eq. (19c). Finally, the shape recovery dynamics of the most general case, i.e., a viscoelastic droplet in a viscoelastic medium, can be obtained by further modifying λ_l in Eq. (B5). This time, the modification entails substituting both ${\widehat{G}}_{\mathrm{I}\mathrm{I}}\left(s\right)$ for the interior viscosity η_II and ${\widehat{G}}_{\mathrm{I}}\left(s\right)$ for the exterior viscosity η_I in the expression of λ_l given by Eq. (A20a).

III. ILLUSTRATIVE RESULTS AND DISCUSSION

The analytical solution in Sec. II predicts rich dynamic behaviors of deformed droplets during their shape recovery. Here, we present illustrative results, to motivate experimental studies into the effects of viscoelasticity on shape dynamics of biomolecular condensates, and demonstrate the potential importance of the present analytical solution in fitting experimental data and in validating numerical solutions.

A. Comparison between droplet fusion and shape recovery

It is interesting to compare the dynamics of the two kinds of shape changes: fusion of two droplets and recovery of a deformed droplet. The half-length, L_fus(t), of two fusing viscous droplets, initially with equal radius R, in an ideal-fluid medium is approximately given by²⁸

$$L_{\mathrm{f}\mathrm{u}\mathrm{s}}\left(t\right)-L_{\mathrm{f}\mathrm{u}\mathrm{s}}\left(\infty \right)=[L_{\mathrm{f}\mathrm{u}\mathrm{s}}\left(0\right)-L_{\mathrm{f}\mathrm{u}\mathrm{s}}\left(\infty \right)]e^{-{(t/{\tau }_{\mathrm{f}\mathrm{u}\mathrm{s}})}^{\beta }},$$ (20)

where β = 1.5 and

$${\tau }_{\mathrm{f}\mathrm{u}\mathrm{s}}=1.97\frac{\eta R}{\gamma }\equiv 1.97{\tau }^{\mathrm{v}\mathrm{c}}.$$ (21)

The last identity defines the viscocapillary time τ^vc. For the shape recovery of a deformed droplet, the half-length is given by [Eq. (A14)]

$$L_{\mathrm{r}\mathrm{e}\mathrm{c}}\left(t\right)-L_{\mathrm{r}\mathrm{e}\mathrm{c}}\left(\infty \right)=f_l\left(t\right)=\left[L_{\mathrm{r}\mathrm{e}\mathrm{c}}\left(0\right)-L_{\mathrm{r}\mathrm{e}\mathrm{c}}\left(\infty \right)\right]e^{-{\lambda }_l^{\mathrm{D}}t}.$$ (22)

The relaxation rates for l = 2 and 4 are [Eq. (A15)]

$${\lambda }_2^{\mathrm{D}}=\frac{20}{19{\tau }^{\mathrm{v}\mathrm{c}}},$$ (23a)

$${\lambda }_4^D=\frac{36}{17{\tau }^{\mathrm{v}\mathrm{c}}}.$$ (23b)

As shown in Fig. 2, the fusion dynamics is a stretched exponential function of time, occurring more slowly than the shape recovery dynamics of a droplet with a deformation represented by the lowest-order Legendre polynomial (“P2”). As the order of the Legendre polynomial increases, shape recovery becomes even faster. Interestingly, Hubstenberger et al.¹ observed that shape recovery of elongated grP-bodies was much faster than the fusion of grP-bodies. However, Fig. 2 shows that the results predicted for viscous droplets are unlikely to reach the two orders of magnitude difference in timescales, which Hubstenberger et al. suggested as indicating elasticity. Next, we present results for viscoelastic droplets.

FIG. 2.

Comparison of droplet fusion dynamics and shape recovery dynamics. Fusion starts with two equal-sized droplets at contact and ends with a single larger spherical droplet having the same total volume. Deformation recovery is illustrated in Fig. 1; P2 and P4 indicate that the deformation is represented by the second- or fourth-order Legendre polynomial. L denotes the half-length of each system.

B. Shape recovery of viscoelastic droplets

We now examine the time dependence of $f_l\left(t\right)$ for viscoelastic droplets in an ideal fluid. We focus on the Jeffreys model of viscoelasticity. The corresponding results for the Maxwell model and Burgers model are given in Appendixes C and D. These results easily extend to the shape recovery dynamics of bubbles in a viscoelastic medium (Appendix E).

Substituting $\widehat{G}\left(s\right)$ of Eq. (10) for the Jeffreys model into Eq. (13) gives

$${\widehat{f}}_l\left(s\right)=\frac{\left({\eta }_0+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s}\right)f_l(0)}{s\left({\eta }_0+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s}\right)+{\eta }_{\mathrm{z}}{\lambda }_l^{\mathrm{D}}}.$$ (24)

The inverse Laplace transform of Eq. (24) is a sum of two exponentials,

$$f_l\left(t\right)=f_l\left(0\right)\left(A_{l+}{e}^{-{\lambda }_{l+}^{\mathrm{D}}t}+A_{l-}{e}^{-{\lambda }_{l-}^{\mathrm{D}}t}\right),$$ (25a)

as opposed to a single exponential for a Newtonian fluid. The recovery rates and corresponding amplitudes are as follows:

$${\lambda }_{l\pm }^{\mathrm{D}}=\frac{1}{2}\frac{{\eta }_{\mathrm{z}}}{{\eta }_0}\frac{1}{{\tau }_1^{\mathrm{s}\mathrm{r}}}\left[{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}+1\pm \sqrt{{\left({\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}+1\right)}^2-4({\eta }_0/{\eta }_{\mathrm{z}}){\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}\right],$$ (25b)

$$A_{l\pm }=\frac{1}{2}\left[1\pm \frac{{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}-1}{\sqrt{{\left({\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}+1\right)}^2-4({\eta }_0/{\eta }_{\mathrm{z}}){\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}}\right].$$ (25c)

In the limit η₁ → 0, the two recovery rates of Eq. (25b) reduce to ${\lambda }_l^{\mathrm{D}}$ and $1/{\tau }_1^{\mathrm{s}\mathrm{r}}$, and the corresponding amplitudes given by Eq. (25c) reduce to 1 and 0, respectively. Thus, Eq. (25a) properly reduces to the single exponential of Eq. (22) for a Newtonian fluid. In the limit η₀ → 0, the two recovery rates become infinite and ${\lambda }_l^{\mathrm{D}}/(1+{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$, and the corresponding amplitudes are ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}/(1+{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$ and $1/(1+{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$. These results correctly match the counterparts of Maxwell droplets (see Appendix C).

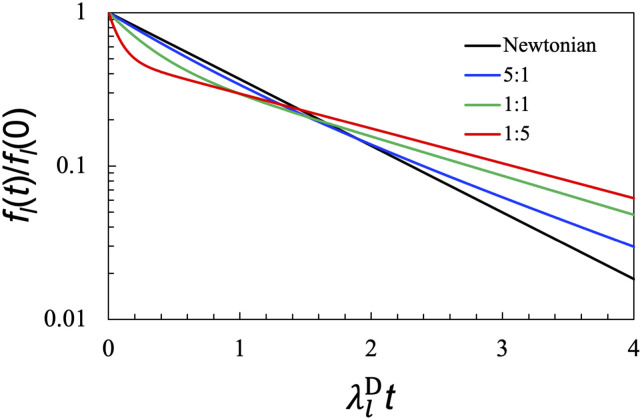
The scaled recovery rates ${\lambda }_{l\pm }^{\mathrm{D}}/{\lambda }_l^{\mathrm{D}}$ and the amplitudes A_l± depend only on two dimensionless parameters: η₀/η_z and ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$. It can be easily shown that ${\lambda }_{l+}^{\mathrm{D}}/{\lambda }_l^{\mathrm{D}}>1$ whereas ${\lambda }_{l-}^{\mathrm{D}}/{\lambda }_l^{\mathrm{D}}<1$ for all parameter values. For a given η₀/η_z, ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ = 1 is a special point, where A_l+/A_l− is 1 and ${\lambda }_{l+}^{\mathrm{D}}/{\lambda }_{l-}^{\mathrm{D}}$ reaches its minimum. At this special ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$, ${\lambda }_{l+}^{\mathrm{D}}/{\lambda }_{l-}^{\mathrm{D}}$ gets closer and closer to 1 as η₀/η_z approaches 1, i.e., when the Newtonian component of the complex shear modulus becomes dominant. In Fig. 3, we compare the shape recovery curves for η₀/η₁ = 5:1, 1:1, and 1:5 while holding ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ at 1. Whereas the curve at η₀/η₁ = 5:1 is close to the counterpart of Newtonian droplets, the curve at η₀/η₁ = 1:5 is clearly non-exponential, with a fast decay followed by a slow decay. The curve at η₀/η₁ = 1:1 is intermediate between those two.

FIG. 3.

Effect of the η₀/η₁ ratio on the shape recovery dynamics of viscoelastic droplets in an ideal fluid. The shear relaxation rate is fixed at ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ = 1, where the two decay components of $f_l\left(t\right)$ have equal amplitudes. The values of η₀/η₁ are shown in the legend. The result for a Newtonian droplet is displayed for reference. The results here are valid for any l.

Recently, we have found that modulating intermolecular interactions, e.g., by adding salt, can tune the η₀/η₁ ratio.²¹ For PGL-3 protein droplets, the Maxwellian component dominates (i.e., η₀/η₁ < 1) at low salt, while the Newtonian component dominates (i.e., η₀/η₁ > 1) at high salt. Qualitatively, we expect the shape recovery curves of PGL-3 droplets to become less non-exponential at increasing salt concentration. Experimental studies of salt effects on the shape recovery dynamics of biomolecular condensates will be of particular interest. Salts also have complex effects on the shear relaxation moduli of polymer blends.⁴³

C. Effect of shear relaxation rate

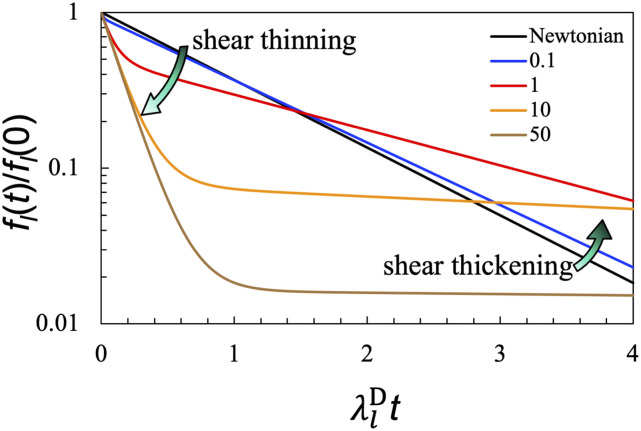
Let us look closely at the effect of ${\tau }_1^{\mathrm{s}\mathrm{r}}$, the shear relaxation rate in the Jeffreys model, on the shape recovery dynamics of viscoelastic droplets in an ideal fluid. In associative polymers, which may serve as a generic model of biomolecular condensates, the main mechanism of shear relaxation is the reconfiguration of polymer networks, and ${\tau }_1^{\mathrm{s}\mathrm{r}}$ represents the time constant for making and breaking of crosslinks between polymer chains.⁴⁴ In Fig. 4, we display shape recovery curves for ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ at 0.1, 1, 10, and 50 while holding η₀/η₁ at 1:5. Each $f_l\left(t\right)$ curve exhibits two successive decays. With increasing ${\tau }_1^{\mathrm{s}\mathrm{r}}$, the amplitude of the first decay becomes larger and that of the second decay becomes smaller, while the recovery rates of both decays become slower. The latter trend is a sign for slowdown in shape recovery by shear relaxation.

FIG. 4.

Effect of the shear relaxation rate on the shape recovery dynamics of viscoelastic droplets in an ideal fluid. The η₀/η₁ ratio is fixed at 1:5, whereas the values of ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ are shown in the legend. The result for a Newtonian droplet is displayed for reference. The results here are valid for any l.

To understand these results more clearly, let us consider two extremes. For extremely fast shear relaxation, i.e., ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}\ll 1$, expanding Eqs. (25b) and (25c) in powers of ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ and keeping terms up to the first power, we find that

$${\lambda }_{l+}^{\mathrm{D}}\approx \frac{{\eta }_{\mathrm{z}}}{{\eta }_0}\frac{1}{{\tau }_1^{\mathrm{s}\mathrm{r}}}+\frac{{\eta }_1}{{\eta }_0}{\lambda }_l^{\mathrm{D}},{\lambda }_{l-}^{\mathrm{D}}\approx {\lambda }_l^{\mathrm{D}},$$ (26)

$$A_{l+}\approx \frac{{\eta }_1}{{\eta }_{\mathrm{z}}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}},A_{l-}\approx 1-\frac{{\eta }_1}{{\eta }_{\mathrm{z}}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}.$$ (27)

As illustrated by the curve at ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ = 0.1 in Fig. 4, the first exponential, $A_{l+}{e}^{-{\lambda }_{l+}^{\mathrm{D}}t}$, has a small amplitude and decays rapidly to 0, and hence, it is less important. The remaining exponential, $A_{l-}{e}^{-{\lambda }_{l-}^{\mathrm{D}}t}$, has an amplitude close to 1 and a recovery rate that is lower than but close to ${\lambda }_l^{\mathrm{D}}$, the Newtonian result. In other words, for ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}<\sim 0.2$, the shape recovery dynamics of viscoelastic droplets is almost a single exponential but with a recovery rate slower than the Newtonian counterpart and thus apparently indicating shear thickening (i.e., increase in apparent viscosity). This slower shape recovery for viscoelastic droplets than for Newtonian droplets can be attributed to a finite rate of shear relaxation.

In the opposite limit where shear relaxation is extremely slow, i.e., ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}\gg 1$, we expand Eqs. (25b) and (25c) in powers of $1/{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ and keep terms up to the first power, finding

$${\lambda }_{l+}^{\mathrm{D}}\approx \frac{{\eta }_{\mathrm{z}}}{{\eta }_0}{\lambda }_l^{\mathrm{D}}+\frac{{\eta }_1}{{\eta }_0}\frac{1}{{\tau }_1^{\mathrm{s}\mathrm{r}}},{\lambda }_{l-}^{\mathrm{D}}\approx \frac{1}{{\tau }_1^{\mathrm{s}\mathrm{r}}},$$ (28)

$$A_{+;l}=1-\frac{{\eta }_1}{{\eta }_{\mathrm{z}}}{({\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}^{-1},A_{-;l}=\frac{{\eta }_1}{{\eta }_{\mathrm{z}}}{({\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}^{-1}.$$ (29)

As illustrated by the curves at ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ = 10 and 50 in Fig. 4, the first exponential has an amplitude that approaches 1 and a recovery rate that approaches $({\eta }_0/{\eta }_{\mathrm{z}}){\lambda }_l^{\mathrm{D}}$, while the second exponential has a very small amplitude but a very slow recovery rate, $1/{\tau }_1^{\mathrm{s}\mathrm{r}}$. The ratio of the areas under the two exponentials is approximately η₀/η₁, and hence, both areas can be significant, but the second, slow exponential may be difficult to detect experimentally due to the small amplitude. The apparent dominance of the first exponential thus gives the impression of fast shape recovery. Note that $({\eta }_0/{\eta }_{\mathrm{z}}){\lambda }_l^{\mathrm{D}}$ is the recovery rate of a Newtonian fluid with viscosity at η₀. In essence, when shear relaxation is very slow, only the Newtonian component of the shear relaxation modulus is active in slowing down shape recovery (i.e., the Maxwell component of the shear relaxation modulus remains dormant on the timescale of the shape recovery). Therefore, during shape recovery, viscoelastic droplets appears to exhibit shear thinning (decrease in apparent viscosity) when shear relaxation is very slow. This apparent shear thinning could explain, at least partially, the shorter than expected timescale of grP-body shape recovery observed by Hubstenberger et al.¹

As noted above, a finite rate of shear relaxation could slow down shape recovery. Naively, one would expect shape recovery to become slower and slower at decreasing shear relaxation rates (i.e., increasing ${\tau }_1^{\mathrm{s}\mathrm{r}}$). Indeed, as noted above, the two recovery rates ${\lambda }_{l+}^{\mathrm{D}}$ and ${\lambda }_{l-}^{\mathrm{D}}$ decrease with increasing ${\tau }_1^{\mathrm{s}\mathrm{r}}$. However, shear relaxation also affects the amplitudes of the two exponentials. Thus, paradoxically, the major exponential (i.e., the one with the larger amplitude) has a recovery rate lower than ${\lambda }_l^{\mathrm{D}}$ when shear relaxation is fast (e.g., ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}<\sim 0.2$), but a recovery rate higher than ${\lambda }_l^{\mathrm{D}}$ when shear relaxation is slow (e.g., ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}>\sim 2$) (Fig. 4). The opposite deviations from ${\lambda }_l^{\mathrm{D}}$ correspond to shear thickening and shear thinning, respectively. Interestingly, associative polymers exhibit shear thickening at moderate steady shear rates and shear thinning at high steady shear rates.⁴⁴ We propose that the shear thickening and thinning phenomena of viscoelastic droplets during shape recovery and of associative polymers under steady shear have a common explanation. Our recent experimental studies that dissected droplet fusion data have presented evidence for shear thickening and shear thinning of biomolecular condensates.^23,28

Of course, we should not forget that there is also a minor exponential, which at increasing ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$ (starting from a value 1) has a time constant that becomes dominated by shear relaxation and less and less dependent on interfacial tension. For extremely slow shear relaxation, the time constant becomes ${\tau }_1^{\mathrm{s}\mathrm{r}}$ itself, thus directly showing that the shear relaxation rate limits shape recovery. However, this new mechanism only accounts for a very small fraction of the total amplitude, thus making experimental verification challenging.

As noted in Subsection III B, the results illustrated in Fig. 4 are also applicable to the shape recovery of bubbles in a viscoelastic medium upon replacing ${\lambda }_l^{\mathrm{D}}$ with ${\lambda }_l^{\mathrm{B}}$. Ali and Prabhu³⁹ recently presented such data where the viscoelastic medium is coacervates formed by potassium poly(styrenesulfonate) and poly(diallyl dimethylammonium bromide). They observed an initial decay followed by a slow second decay, qualitatively in agreement with our prediction. The shear relaxation in their system has ${\tau }_1^{\mathrm{s}\mathrm{r}}$ < 1 s and becomes faster with increasing salt (similar to results found for PGL-3 droplets²¹). In comparison, the time constants of their second decay, corresponding to our $1/{\lambda }_{l-}^{\mathrm{B}}$, are mostly >1 s. Ali and Prabhu analyzed their data essentially by assuming ${\lambda }_{l-}^{\mathrm{B}}={\lambda }_l^{\mathrm{B}}$, i.e., completely neglecting shear relaxation. However, even fast shear relaxation can affect ${\lambda }_{l-}^{\mathrm{B}}$, and hence, its neglect can lead to underestimation of the interfacial tension. For example, at ${\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{B}}$ = 0.1, we predict ${\lambda }_{l-}^{\mathrm{B}}=0.92{\lambda }_l^{\mathrm{B}}$. Ali and Prabhu also reported the time, t_e, for the initial decay to complete. t_e should scale with $1/{\lambda }_{l+}^{\mathrm{B}}$, i.e., the time constant of the initial decay, which we predict to be significantly affected by the shear relaxation rate [see ${\lambda }_{l+}^{\mathrm{D}}$ given by Eq. (26)]. Indeed, Ali and Prabhu reported an ∼10fold decrease in t_e when the salt concentration increased from 1.55 to 1.85M. Over the same range of salt concentration, the time constants of their second decay changed by < twofold, whereas the shear relaxation rates changed substantially, suggesting their major role in determining t_e.

D. Finite viscosity ratio: Newtonian fluids

So far, we have only considered cases where either the exterior or the interior fluid is modeled as ideal. Now, we want to present cases where the viscosity ratio between the two phases is finite so that both interior and the exterior fluid dynamics must be treated at the same time. Both η_I and η_II need to be high for inertial effects to be neglected. As a prelude to cases where a viscoelastic fluid interfaces with a Newtonian fluid, here, we first consider the case where both phases are Newtonian fluids. The shape recovery dynamics is an exponential function [see Eq. (B5)], with the recovery rate λ_l given by Eq. (A20a). For l = 2, the recovery rate is

$${\lambda }_2=\frac{40({\eta }_{\mathrm{I}\mathrm{I}}/{\eta }_{\mathrm{I}}+1)}{(19{\eta }_{\mathrm{I}\mathrm{I}}/{\eta }_{\mathrm{I}}+16)(2{\eta }_{\mathrm{I}\mathrm{I}}/{\eta }_{\mathrm{I}}+3)}\frac{1}{{\tau }_{\mathrm{I}}^{\mathrm{v}\mathrm{c}}},$$ (30a)

where

$${\tau }_{\mathrm{I}}^{\mathrm{v}\mathrm{c}}=\frac{{\eta }_{\mathrm{I}}R}{\gamma }.$$ (30b)

Equation (30a) is identical to the recovery rate widely quoted for droplets approximated as ellipsoids.^{31,32,34,36,39}

Although shapes specified by the second-order Legendre polynomial (“P2”) have been assumed to be equivalent to ellipsoids, e.g., Ref. 45, there are actually noticeable differences between them. As detailed in Appendix F, P2 combined with a small-amplitude fourth-order Legendre polynomial (P4) does an excellent job in reproducing ellipsoidal shapes. A deformation with an ellipsoidal shape thus requires a linear combination of f₂(t) and f₄(t) (see Fig. 2), leading to a bi-exponential decay even when both phases are Newtonian fluids. For the rest of this paper, we will limit to l = 2, focusing attention, instead, on non-exponentiality arising from viscoelasticity.

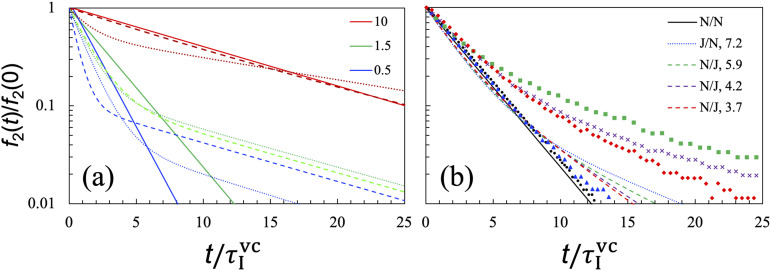
In Fig. 5(a), we present the shape recovery curves for Newtonian droplets in a Newtonian fluid with η_II/η_I at 10, 1.5, and 0.5. This will serve as references for assessing the effect of droplet viscosity in Subsection III E. One can tune η_II/η_I by changing temperature or salt concentration. In cases where the dense phase is inside droplets, η_II/η_I is much higher than 1 while away from the critical point and approaches 1 as the critical point is reached. For complex biomolecular condensates, one can also tune η_II/η_I by varying their macromolecular composition.^16,18,28

FIG. 5.

Shape recovery curves at a finite viscosity ratio between the droplet and bulk phases. (a) Comparison of $f_2\left(t\right)$ for three cases of pairing interior and exterior fluids: Newtonian with Newtonian (solid curves), viscoelastic with Newtonian (dotted curves), and Newtonian with viscoelastic (dashed curves). The viscosity ratios, i.e., η_II/η_I, are shown in the legend. Viscoelasticity is given by the Jeffreys model, with η₀/η₁ = 1:5 and ${\tau }_1^{\mathrm{s}\mathrm{r}}\gamma /{\eta }_{\mathrm{I}}R$ = 10. (b) Comparison of our analytical results (curves) with experimental data of Verhulst et al. (symbols) for five systems, all with η_II/η_I = 1.5. The viscoelasticity was reported as fitting to the Oldroyd B model, with η₀/η₁ ≈ 2:1 and ${\tau }_1^{\mathrm{s}\mathrm{r}}\gamma /{\eta }_{\mathrm{I}}R$ indicated in the legend. Curves and symbols have matching colors for the same systems.

E. Finite viscosity ratio: Viscoelastic fluids

To determine the shape recovery dynamics of viscoelastic droplets in a Newtonian fluid, we obtain f_l(t) of Eq. (19a) by numerical Laplace inversion.⁴⁶ The results are displayed as dotted curves in Fig. 5(a) for Jeffreys droplets with η_II0/η_II1 = 1:5; ${\tau }_{\mathrm{I}\mathrm{I}1}^{\mathrm{s}\mathrm{r}}\gamma /{\eta }_{\mathrm{I}}R$ = 10; and η_II/η_I = 10, 1.5, and 0.5. Similar to the results presented in Figs. 3 and 4 for η_II/η_I = ∞, for each finite η_II/η_I value, the initial decay of f_l(t) for the Jeffreys droplet (“J/N”) is faster than that of the corresponding Newtonian droplet (“N/N”). The J/N curve then slows down and crosses the N/N curve.

It is interesting to compare the shape recovery curves between Jeffreys droplets in a Newtonian fluid (i.e., “J/N”) and Newtonian droplets in a viscoelastic medium (“N/J”). The N/J results are shown as dashed curves in Fig. 5(a). When η_II/η_I > 1, relative to the J/N curves, the corresponding N/J curves move closer to the N/N curves. Conversely, when η_II/η_I < 1, it is the J/N curves that are closer to the N/N curves. At η_II/η_I = 1.5 and 0.5, with ${\tau }_1^{\mathrm{s}\mathrm{r}}\gamma /{\eta }_{\mathrm{I}}R$ = 10, the shear relaxation of the viscoelastic fluids occurs on a timescale that is approximately ten times longer than both the interior and exterior viscocapillary times. Correspondingly, the shape recovery curves at η_II/η_I = 1.5 and 0.5 all have a slow decay with a time constant close to ${\tau }_1^{\mathrm{s}\mathrm{r}}$. Therefore, once again, we observe the scenario where the slow decay is dictated by shear relaxation and independent of interfacial tension.

In Fig. 5(b), we compare our analytical solution with the experimental data of Verhulst et al.³⁸ for N/N, J/N, and N/J systems, all with η_II/η_I = 1.5. For the N/N system, there is good agreement between theory and experiment. For the J/N system, the analytical curve has a significant late slow decay, whereas the experimental curve deviates only slightly from the counterpart for the N/N system. For the N/J systems, both the experimental and analytical curves have a long-time tail and the decay rate of the tail decreases with increasing ${\tau }_1^{\mathrm{s}\mathrm{r}}\gamma /{\eta }_{\mathrm{I}}R$, indicating that this part of the curves is dominated by shear relaxation. However, the analytical solution significantly underestimates the amplitude of the tail. We attribute the underestimation to the fluid-dynamics model adopted here for Newtonian droplets inside a viscoelastic fluid, not our analytical solution. The experimental N/J curves are above the corresponding N/N curve at all times, but the analytical solution of the present fluid-dynamics model predicts that the N/J curves must intersect the N/N curve and all the curves integrate to the same total area. Clearly, the fluid-dynamics model needs to be modified for the N/J systems in order to achieve quantitative agreement with the experimental data. While phenomenological models have achieved partial success in fitting the experimental data,^31,32 we believe that it is more important to identify physical ingredients missing from the fluid-dynamics model and then solve the physical model exactly.

We also compared our analytical solution with the numerical solution of Hooper et al.,³³ who used the Oldroyd B model for viscoelasticity. The analytical and numerical results agree well for Newtonian droplets in a Newtonian fluid. However, for viscoelastic droplets in a Newtonian fluid, the initial decay of the shape deformation of Hooper et al. is faster. Although the analytical solution is limited to linear order (specifically in the extent of shape deformation and in the linearization of the Oldroyd B model), we suspect that the discrepancy is largely due to errors in the numerical solution. The Oldroyd B model is known to be difficult for numerical implementation and to be prone to numerical instability.³⁵ Our own numerical solution using the COMSOL software has shown close agreement with the analytical solution (Naderi, Peng, and Zhou, to be published). The analytical solution thus presents a unique benchmark for testing the accuracy of numerical solutions.

IV. CONCLUDING REMARKS

We have presented an exact analytical solution for the recovery dynamics of biomolecular droplets from small-amplitude deformation. Whereas viscocapillarity sets the timescale for the shape recovery dynamics of viscous droplets, with viscoelasticity, shape recovery becomes multi-exponential. For the Jeffreys model of viscoelasticity featuring a single shear relaxation rate, two exponentials are predicted for the shape recovery dynamics, with time constants shorter and longer, respectively, than the viscocapillary timescale. Shear relaxation inside the droplets affects both the time constants and amplitudes of the exponentials, with one exponential becoming dominant under some conditions. For moderately fast shear relaxation, the dominant exponential is the one with a time constant longer than the viscocapillary timescale, which can be interpreted as arising from an apparent increase in viscosity. Conversely, for very slow shear relaxation, the dominant exponential is the one with a time constant shorter than the viscocapillary timescale, which can be interpreted as arising from an apparent decrease in viscosity. Therefore, during shape recovery, viscoelastic droplets exhibit shear thickening at fast shear relaxation rates but shear thinning at slow shear relaxation rates. Under the latter condition, the time constant of the minor exponential is dictated by shear relaxation, which can thus be seen as a new rate-limiting mechanism for shape dynamics.

It will be interesting to experimentally test the theoretical predictions on the shape recovery dynamics of biomolecular droplets. The experimental data may consist of time-lapse images of droplets after an initial deformation. To analyze the data, one will represent the boundary of a droplet at time t by a sum of Legendre polynomials and determine the expansion coefficients $f_l\left(t\right)$ (cf. Appendix F). One will then fit the time dependence of $f_l\left(t\right)$ to the theoretical results for a model of viscoelasticity [in particular, Eq. (25a)]. One prediction is that the recovery rate depends on the initial shape (see Fig. 2). Initial shapes that are more elongated have components of higher order (i.e., l) Legendre polynomials, which are predicted to have higher recovery rates. This prediction already has support from the data of Hubstenberger et al.,¹ which showed that shape recovery of elongated grP-bodies was much faster than the fusion of grP-bodies. Another theoretical prediction is shear thickening and shear thinning. If the zero-shear viscosity of droplets is known, then experimental data on shape dynamics will be able to tell whether shear thickening or thinning, indeed, occurs. In the most ideal case, the shape recovery data may allow for the discrimination among different models of viscoelasticity.

We anticipate qualitatively similar effects of shear relaxation on droplet fusion dynamics. Indeed, preliminary data from COMSOL calculations on droplet fusion and shape recovery support this contention (Naderi, Peng, and Zhou, to be published). Therefore, in droplet fusion, we can also expect shear thickening for condensates with fast shear relaxation rates but shear thinning for condensates with slow shear relaxation rates. This expectation is confirmed by our recent experimental studies that dissected droplet fusion data of biomolecular condensates.^23,28 It has become a common practice to deduce the interfacial tension by applying the viscocapillary model [Eq. (21)], i.e., by combining the inverse capillary velocity (obtained by, e.g., measuring fusion speed) with zero-shear viscosity (obtained by, e.g., particle tracking). The observation of shear thickening and shear thinning means that interfacial tensions deduced from the viscocapillary model can be in serious error.

There is great interest in condensate aging, especially in its connection with neurodegeneration, but there is little physical understanding of this phenomenon. One possible physical change in biomolecular condensates over time is the slowdown in shear relaxation.¹² Our analytical solution predicts that a slowdown in shear relaxation can lead to a very slow decay in shape dynamics, thereby giving the appearance of stalled or incomplete shape recovery and fusion. The work here thus reveals shear relaxation as a crucial link in understanding condensate aging.

Our analytical solution should prove useful for validating numerical solutions of fluid-dynamics equations for condensate shape changes. Such validation is important, as numerical solutions may be the only option for the theoretical treatment of nonlinear issues such as large-amplitude deformation and nonlinear constitutive relations (e.g., the Oldroyd B model). We do expect that our present solution is still qualitatively and even semi-quantitatively correct when nonlinearity is present, and as such, it will be good for fitting experimental data on shape recovery. Finally, shape recovery and fusion may potentially be modeled by molecular simulations⁴⁵ and our analytical theory can motivate and guide data analysis in such studies.

APPENDIX A: SHAPE RECOVERY OF NEWTONIAN DROPLETS IN A NEWTONIAN MEDIUM

For biomolecular droplets formed by phase separation, η_II ≫ η_I due to significantly higher macromolecular concentrations and extensive intermolecular interactions in the droplet phase. We denote the viscosity of the droplet phase as η, without subscript “II.” The opposite limit, i.e., η_I ≫ η_II, occurs in some other cases. For example, the phase separation of some polymer blends leads to polymer-poor “bubbles” in the coacervate matrix.³⁹ We then neglect η_II and denote the viscosity of the coacervate phase as η, without subscript “I.” We only retain subscripts I and II when considering the full problem where both interior and exterior fluid dynamics are treated.

1. Fluid-dynamics problem

The shape change of a liquid droplet inside an ideal-fluid medium is dictated by the interior fluid dynamics, which we model by the (generalized) Navier–Stokes equations. The first of these equations expresses mass conservation, which for an incompressible fluid has the form

$$\nabla \cdot \mathbf{v}\left(\mathbf{x},t\right)=0,$$ (A1)

where $\mathbf{v}\left(\mathbf{x},t\right)$ is the fluid velocity at position x and time t and ∇ denotes the gradient operator. The second of the Navier–Stokes equations expresses momentum conservation,

$$\varrho \left(\frac{\partial \mathbf{v}}{\partial t}+\mathbf{v}\cdot \nabla \mathbf{v}\right)=\nabla \cdot \tilde{\mathrm{\tau }},$$ (A2)

where ϱ is the fluid density and $\tilde{\mathrm{\tau }}$ is the stress tensor. Closure of this equation requires a constitutive relation for $\tilde{\mathrm{\tau }}$. One contribution to $\tilde{\mathrm{\tau }}$ comes from hydrostatic pressure (p) and is related to volume change; the remaining, deviatoric, contribution comes from fluid viscosity (η) and is related to shape change,

$$\tilde{\mathrm{\tau }}=-p\tilde{\mathrm{I}}+{\tilde{\mathrm{\tau }}}_{\mathrm{d}},$$ (A3a)

where $\tilde{\mathrm{I}}$ is the unit tensor. For purely viscous or Newtonian fluids, the deviatoric contribution is given by

$${\tilde{\mathrm{\tau }}}_{\mathrm{d}}=\eta \dot{\tilde{\mathrm{\epsilon }}},$$ (A3b)

where a dot denotes differentiation with respect to time and

$$\dot{\tilde{\mathrm{\epsilon }}}=\nabla \mathbf{v}+{(\nabla \mathbf{v})}^{\mathrm{T}}$$ (A3c)

is the symmetrized strain-rate tensor, with superscript “T” denoting the transpose. The momentum equation then becomes

$$\varrho \left(\frac{\partial \mathbf{v}}{\partial t}+\mathbf{v}\cdot \nabla \mathbf{v}\right)=-\nabla p+\eta {\nabla }^2\mathbf{v}.$$ (A4a)

At high frictions, the inertial terms on the left-hand side of Eq. (A4a) can be neglected, leading to

$$-\nabla p+\eta {\nabla }^2\mathbf{v}\approx 0.$$ (A4b)

This reduction, similar to the reduction in the Langevin equation to one representing Brownian motion, is justified for biomolecular condensates because of their high viscosity.

To solve Eqs. (A1) and (A4a) [or (A4b)], we have to specify boundary conditions. One is a “kinematic” boundary condition, which expresses the fact that fluid motions lead to changes in the shape of the interface between the droplet and the surrounding bulk phase. If the interface at time t is specified by the condition

$$\mathcal{S}\left(\mathbf{x},t\right)=0\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\mathbf{x}\in \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e},$$ (A5)

then the kinematic boundary condition is

$$\frac{\partial \mathcal{S}}{\partial t}+\mathbf{v}\cdot \nabla \mathcal{S}=0.$$ (A6)

The outward unit normal vector of the interface is given by

$$\mathbf{n}=\frac{\nabla \mathcal{S}}{|\nabla \mathcal{S}|}.$$ (A7)

The remaining boundary conditions express force balance at the interface,

$$\mathbf{n}\cdot \tilde{\mathrm{\tau }}\cdot \mathbf{t}=0,$$ (A8)

$$\mathbf{n}\cdot \tilde{\mathrm{\tau }}\cdot \mathbf{n}=-\gamma \nabla \cdot \mathbf{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{s},$$ (A9)

where t denotes a unit vector along a tangential direction of the interface and γ is the interfacial tension. Note that due to the much higher viscosity inside biomolecular droplets than in the bulk phase, the effect of the velocity field in the bulk phase has been neglected. A constant pressure in the bulk phase can be accounted for by subtracting it from the interior pressure. Therefore, the two force-balance boundary conditions involve only the interior stress tensor.

In the case of ideal-fluid bubbles in a Newtonian-fluid medium, the shape change is dictated by the exterior fluid dynamics. All but one of the above equations still hold when the symbols denote exterior properties. The one exception is a sign change in the boundary condition of Eq. (A9),

$$\mathbf{n}\cdot \tilde{\mathrm{\tau }}\cdot \mathbf{n}=\gamma \nabla \cdot \mathbf{n}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{u}\mathrm{b}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{s}.$$ (A10)

The problem at hand is to find the interface shape function $\mathcal{S}\left(\mathbf{x},t\right)$ at any time t, given the initial shape function $\mathcal{S}\left(\mathbf{x},0\right)$ [and its initial rate $\dot{\mathcal{S}}\left(\mathbf{x},0\right)$ if necessary]. Due to the interfacial tension, a deformed droplet will recover its spherical shape. We refer to this process shape recovery, but terms used in the literature include deformation retraction or relaxation.

2. Solution of Prosperetti

Prosperetti²⁹ solved the shape recovery problem for small-amplitude deformation. That is, the initial shape of the interface between a droplet and the bulk phase (approximated as ideal fluid) was assumed to be a small deformation from a sphere with radius R. Using spherical coordinates (r, θ, ϕ) for the position x (with origin at the center of the reference sphere), the radial distance of the interface at polar angle θ and azimuthal angle ϕ and at time t can be written as (Fig. 1)

$$r\left(\theta ,\varphi ,t\right)=R+f_l\left(t\right)Y_{lm}\left(\theta ,\varphi \right),$$ (A11)

where Y_lm(θ, ϕ) is a spherical harmonic. Because of the orthogonality of spherical harmonics, we can later add up the results for individual spherical harmonics to obtain a complete solution. The amplitude f_l(t) satisfies the following integro-differential equation:

$${\ddot{f}}_l\left(t\right)+b{\dot{f}}_l\left(t\right)-bc\underset{0}{\overset{t}{\int }}d{t}^{\prime }Q\left(t-t^{\prime }\right)\dot{f}(t^{\prime })+{\varpi }_0^2{f}_l\left(t\right)=0,$$ (A12)

where

$$b=\frac{2(l-1)(2l+1)\eta }{\varrho R^2},$$ (A13a)

$$c=\frac{(l-1)(l+1)}{2l+1},$$ (A13b)

$${\varpi }_0^2=\frac{l(l-1)(l+2)\gamma }{\varrho R^3},$$ (A13c)

and for the function $Q\left(t\right)$, only its Laplace transform is known. Denoting the Laplace transform of any function of time, $g\left(t\right)$ as $\widehat{g}(s)$, we have

$$\widehat{Q}(s)=\frac{1}{\frac{w{I}_{l+1/2}(w)}{2I_{l+3/2}(w)}-1}\equiv \frac{1}{\frac{1}{2}{I}_l(w)-1},$$ (A13d)

where $w=R\sqrt{\varrho s/\eta }$ and I_l+1/2(x) are modified Bessel functions of the first kind.

Prosperetti²⁹ considered the long-time asymptotic behavior of f_l(t), where $f_l(t)\approx C(t)e^{-{\nu }_{l}t}$ with C(t) becoming a finite constant as t → ∞, leading to an equation for ν_l that is identical to the classical result of Chandrasekhar⁴¹ and Reid⁴² using normal-mode analysis. This analysis has now been extended to viscoelastic droplets in an ideal fluid.^40,47

Here, our concern is the initial value problem, i.e., the time dependence of f_l(t) starting from t = 0. We are particularly interested in the high-friction regime. In this regime, we neglect the second derivative, ${\ddot{f}}_l(t)$, in Eq. (A12), similar to reducing the Langevin equation to one representing Brownian motion. Furthermore, high friction means w → 0, and hence, we approximate $\widehat{Q}(s)$ as

$$\widehat{Q}\left(s\right)\approx \underset{w\to 0}{\lim }\widehat{Q}\left(s\right)=\frac{2}{2l+1}.$$ (A13e)

This result is independent of s, meaning that $Q\left(t\right)$ is a delta function of time. The solution of Eq. (A12) is an exponential function,

$$f_l\left(t\right)=f_l\left(0\right)e^{-{\lambda }_l^{\mathrm{D}}t},$$ (A14)

with the recovering rate given by

$${\lambda }_l^{\mathrm{D}}=\frac{l(l+2)(2l+1)}{2(2l^2+4l+3)}\frac{\gamma }{\eta R}.$$ (A15)

For ideal-fluid bubbles, Eq. (A12) still holds, but with

$$b=\frac{2(l+2)(2l+1)\eta }{\varrho R^2},$$ (A16a)

$$c=\frac{l(l+2)}{2l+1},$$ (A16b)

$${\varpi }_0^2=\frac{(l-1)(l+1)(l+2)\gamma }{\varrho R^3},$$ (A16c)

$$\widehat{Q}(s)=\frac{1}{\frac{w{K}_{l+1/2}(w)}{2K_{l-1/2}(w)}+1}\equiv \frac{1}{\frac{1}{2}{\mathcal{K}}_l\left(w\right)+1},$$ (A16d)

where K_l+1/2(x) are modified Bessel functions of the second kind. Again, our interest is the high-friction regime, where w → 0 and $\widehat{Q}(s)$ of Eq. (A16d) approaches the same limit as given by Eq. (A13e). The solution for $f_l\left(t\right)$ remains an exponential function, with the recovery rate now given by

$${\lambda }_l^{\mathrm{B}}=\frac{(l-1)(l+1)(2l+1)}{2(2l^2+1)}\frac{\gamma }{\eta R}.$$ (A17)

In Eqs. (A15) and (A17), we have used the superscript “D” to designate shape recovery rates for viscous droplets in an ideal-fluid medium and for ideal-fluid bubbles in a viscous medium, respectively.

Prosperetti³⁰ also solved the full problem where both interior and exterior fluid dynamics are treated, i.e., without invoking η_II ≫ η_I or η_II ≪ η_I. Equation (A12) becomes

$${\ddot{f}}_l\left(t\right)+d^{-1}\underset{0}{\overset{t}{\int }}d{t}^{\prime }\mathfrak{Q}\left(t-t^{\prime }\right){\dot{f}}_l(t^{\prime })+{\varpi }_0^2{f}_l\left(t\right)=0,$$ (A18)

where

$$d=\left[\left(l+1\right){\varrho }_{\mathrm{I}\mathrm{I}}+l{\varrho }_{\mathrm{I}}\right]R^2,$$ (A19a)

$${\varpi }_0^2=\frac{l(l-1)(l+1)(l+2)\gamma }{dR},$$ (A19b)

$$\widehat{\mathfrak{Q}}(s)=\frac{\left\{\begin{array}{c}\hfill \left[\left(2l+1\right){\eta }_{\mathrm{I}\mathrm{I}}{I}_l\left(w_{\mathrm{I}\mathrm{I}}\right)-2l(l+2)({\eta }_{\mathrm{I}\mathrm{I}}-{\eta }_{\mathrm{I}})\right]\hfill \\ \hfill \times \left[\left(2l+1\right){\eta }_{\mathrm{I}}{\mathcal{K}}_l\left(w_{\mathrm{I}}\right)+2(l-1)(l+1)({\eta }_{\mathrm{I}\mathrm{I}}-{\eta }_{\mathrm{I}})\right]\hfill \end{array}\right\}}{{\eta }_{\mathrm{I}\mathrm{I}}{I}_l\left(w_{\mathrm{I}\mathrm{I}}\right)+{\eta }_{\mathrm{I}}{\mathcal{K}}_l\left(w_{\mathrm{I}}\right)-2({\eta }_{\mathrm{I}\mathrm{I}}-{\eta }_{\mathrm{I}})},$$ (A19c)

with subscripts “II” and “I” denoting quantities in the interior and exterior of the droplet. When both η_II and η_I fall in the high-friction regime,

$$\widehat{\mathfrak{Q}}(s)\approx \frac{\left[\left(2l^2+4l+3\right){\eta }_{\mathrm{I}\mathrm{I}}+2l(l+2){\eta }_{\mathrm{I}}\right]\left[2\left(l-1\right)\left(l+1\right){\eta }_{\mathrm{I}\mathrm{I}}+\left(2l^2+1\right){\eta }_{\mathrm{I}}\right]}{(2l+1)({\eta }_{\mathrm{I}\mathrm{I}}+{\eta }_{\mathrm{I}})},$$ (A19d)

and $f_l\left(t\right)$ is an exponential function of time, with the recovery rate given by

$${\lambda }_l=\frac{e_l({\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}+1)}{(a_l{\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}+b_l)(c_l{\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}+d_l)}\frac{\gamma }{{\eta }_{\mathrm{I}}R},$$ (A20a)

where

$$a_l=2l^2+4l+3,$$ (A20b)

$$b_l=2l\left(l+2\right),$$ (A20c)

$$c_l=2\left(l-1\right)\left(l+1\right),$$ (A20d)

$$d_l=2l^2+1,$$ (A20e)

$$e_l=l\left(l-1\right)\left(l+1\right)\left(l+2\right)\left(2l+1\right),$$ (A20f)

$${\alpha }_{\mathrm{I}\mathrm{I}/\mathrm{I}}=\frac{{\eta }_{\mathrm{I}\mathrm{I}}}{{\eta }_{\mathrm{I}}}.$$ (A20g)

One can easily verify that λ_l reduces to ${\lambda }_l^{\mathrm{D}}$ when α_II/I ≫ 1 and to ${\lambda }_l^{\mathrm{B}}$ when α_II/I ≪ 1.

3. New solution

Here, we present a new solution for the shape recovery dynamics in the high-friction regime. This solution easily lends itself to generalization from viscous to viscoelastic fluids. The derivation here for droplets largely follows the solution of a related fluid-dynamics problem.²⁰ We assume that the shape deformation is axisymmetric (Fig. 1). Equation (A11) then reduces to

$$r\left(\theta ,t\right)=R+f_l\left(t\right)P_l\left(\cos \theta \right).$$ (A21)

Note that the lowest l should be 2 since l = 0 corresponds to a change in the droplet radius and thus a violation of volume conservation demanded by fluid incompressibility, and l = 1 corresponds to a translational motion of the entire interface. We will keep terms only up to the first order in f_l(t); to this order, the volume of the droplet is a constant when $f_l\left(t\right)$ changes over time.

The interface shape function can be identified as

$$\mathcal{S}\left(\mathbf{x},t\right)=r-\left[R+f_l\left(t\right)P_l\left(\cos \theta \right)\right].$$ (A22)

The outward normal vector of the interface [Eq. (A7)] can be found as

$$\mathbf{n}={\mathbf{e}}_r-f_l(t)\nabla P_l(\cos \theta )={\mathbf{e}}_r-\frac{f_l(t)}{R}\frac{\partial P_l(\cos \theta )}{\partial \theta }{\mathbf{e}}_{\theta }$$ (A23)

to the first order in f_l(t), where e_r and e_θ are unit vectors along r and θ, respectively. The divergence of n is

$$\begin{array}{ll}\hfill \nabla \cdot \mathbf{n}& =\frac{2}{R}-\frac{2}{R^2}{f}_l(t)P_l(\cos \theta )-\frac{f_l(t)}{R^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial P_l(\cos \theta )}{\partial \theta }\right)\hfill \\ \hfill & =\frac{2}{R}+\frac{\left(l-1\right)\left(l+2\right)}{R^2}{f}_l\left(t\right)P_l\left(\cos \theta \right).\hfill \end{array}$$ (A24)

The fluid velocity v(x, t) is of the same order as f_l(t). Similarly, the pressure should only deviate from the static pressure that balances the interfacial tension of a spherical droplet by an amount, δp(x, t), that is of the same order as f_l(t),

$$p\left(\mathbf{x},t\right)=\frac{2\gamma }{R}+\delta p\left(\mathbf{x},t\right).$$ (A25)

The kinematic boundary condition [Eq. (A6)] yields

$${\dot{f}}_l\left(t\right)P_l\left(\cos \theta \right)=v_r\mathrm{a}\mathrm{t}r=R.$$ (A26)

Subscripts r and θ denote the components of the velocity. The force-balance boundary conditions [Eqs. (A8) and (A9)] lead to

$$\frac{\partial v_r}{\partial \theta }+r\frac{\partial v_{\theta }}{\partial r}-v_{\theta }=0atr=R,$$ (A27)

$$-\delta p+2\eta \frac{\partial v_r}{\partial r}=-\frac{\gamma }{R^2}(l-1)(l+2)f_l(t)P_l(\cos \theta )\mathrm{a}\mathrm{t}r=R.$$ (A28)

The velocity and pressure fields for an axisymmetric problem can be expressed in terms of the stream function Ψ(r, θ, t). For the interior problem considered here for droplets, the stream function has the form⁴⁸

$$\Psi =\left[A\left(t\right)r^{l+3}+B\left(t\right)r^{l+1}\right]Q_l\left(\cos \theta \right),$$ (A29)

where A(t) and B(t) are coefficients to be determined by the boundary conditions and Q_l(x) are related to Legendre polynomials P_l(x) via

$$Q_l\left(x\right)=\underset{-1}{\overset{x}{\int }}d{x}^{\prime }{P}_l\left(x^{\prime }\right)=\frac{P_{l+1}\left(x\right)-P_{l-1}\left(x\right)}{2l+1}.$$ (A30)

The components of the velocity and the pressure are given by

$$v_r=-\frac{1}{r^2}\frac{\partial \Psi }{\partial \cos \theta }=-\left[A\left(t\right)r^{l+1}+B\left(t\right)r^{l-1}\right]P_l\left(\cos \theta \right),$$ (A31)

$$\begin{array}{ll}\hfill v_{\theta }& =-\frac{1}{r\sin \theta }\frac{\partial \Psi }{\partial r}\hfill \\ \hfill & =-\left[A\left(t\right)\left(l+3\right)r^{l+1}+B\left(t\right)\left(l+1\right)r^{l-1}\right]\frac{Q_l\left(\cos \theta \right)}{\sin \theta },\hfill \end{array}$$ (A32)

$$\frac{\delta p}{2\eta }=-A\left(t\right)\left(2+\frac{3}{l}\right)r^l{P}_l\left(\cos \theta \right).$$ (A33)

Substituting Eqs. (A31) and (A32) into Eq. (A27) leads to

$$l(l+2)\overline{A}(t)+(l-1)(l+1)\overline{B}(t)=0,$$ (A34)

where $\overline{A}(t)=A(t)R^l$ and $\overline{B}(t)=B(t)R^{l-2}$. Similarly, using Eqs. (A31) and (A33) in Eq. (A28) leads to

$$\frac{l^2-l-3}{l}\overline{A}\left(t\right)+\left(l-1\right)\overline{B}\left(t\right)=\frac{\gamma }{2\eta R^2}\left(l-1\right)\left(l+2\right)f_l\left(t\right).$$ (A35)

The results for $\overline{A}(t)$ and $\overline{B}(t)$ are

$$\overline{A}\left(t\right)=-\frac{l\left(l-1\right)\left(l+1\right)\left(l+2\right)}{2\left(2l^2+4l+3\right)}\frac{\gamma f_l\left(t\right)}{\eta R^2},$$ (A36a)

$$\overline{B}\left(t\right)=\frac{l^2{\left(l+2\right)}^2}{2\left(2l^2+4l+3\right)}\frac{\gamma f_l\left(t\right)}{\eta R^2}.$$ (A36b)

When these last results are inserted into Eq. (A31), we find that

$$v_r\left(R,\theta ,t\right)=-{\lambda }_l^{\mathrm{D}}{f}_l\left(t\right)P_l\left(\cos \theta \right),$$ (A37)

where ${\lambda }_l^{\mathrm{D}}$ is given by Eq. (A15). Substituting Eq. (A37) into Eq. (A26) yields

$${\dot{f}}_l\left(t\right)+{\lambda }_l^{\mathrm{D}}{f}_l(t)=0.$$ (A38)

The solution of this last equation is the exponential function in Eq. (A14).

In preparation for the generalization to viscoelastic fluids, let us solve the problem again, now using Laplace transforms. The governing equations (A1) and (A4b) and the force-balance boundary conditions [Eqs. (A27) and (A28)] have the same form in Laplace space as they have in the time domain, as does the general form of the stream function [Eq. (A29)]. Therefore, Eqs. (A34) and (A35) take the same form in Laplace space,

$$l(l+2)\widehat{\overline{A}}(s)+(l-1)(l+1)\widehat{\overline{B}}(s)=0,$$ (A39)

$$\frac{l^2-l-3}{l}\widehat{\overline{A}}\left(s\right)+\left(l-1\right)\widehat{\overline{B}}\left(s\right)=\frac{\gamma }{2\eta R^2}\left(l-1\right)\left(l+2\right){\widehat{f}}_l\left(s\right).$$ (A40)

The kinematic boundary condition [Eq. (A26)] now takes the form

$$[s{\widehat{f}}_l\left(s\right)-f_l(0)]P_l\left(\cos \theta \right)={\widehat{v}}_r\mathrm{a}\mathrm{t}r=R.$$ (A41a)

Using Eq. (A31) in the preceding equation, we find that

$$s{\widehat{f}}_l\left(s\right)=f_l\left(0\right)-[\widehat{\overline{A}}\left(s\right)+\widehat{\overline{B}}\left(s\right)]R.$$ (A41b)

Solving Eqs. (A39), (A40), and (A41b), we find that

$$\widehat{\overline{A}}\left(s\right)=-\frac{\frac{\gamma }{R^2}l\left(l-1\right)\left(l+1\right)\left(l+2\right)f_l\left(0\right)}{2\eta s\left(2l^2+4l+3\right)+\frac{\gamma }{R}l\left(l+2\right)\left(2l+1\right)},$$ (A42a)

$$\widehat{\overline{B}}\left(s\right)=\frac{\frac{\gamma }{R^2}{l}^2{\left(l+2\right)}^2{f}_l\left(0\right)}{2s\eta \left(2l^2+4l+3\right)+\frac{\gamma }{R}l\left(l+2\right)\left(2l+1\right)},$$ (A42b)

$${\widehat{f}}_l\left(s\right)=\frac{2\eta \left(2l^2+4l+3\right)f_l\left(0\right)}{2s\eta \left(2l^2+4l+3\right)+\frac{\gamma }{R}l\left(l+2\right)\left(2l+1\right)}=\frac{f_l\left(0\right)}{s+{\lambda }_l^{\mathrm{D}}}.$$ (A42c)

The inverse Laplace transform of the foregoing ${\widehat{f}}_l(s)$ is given by Eq. (A14).

For the exterior problem appropriate for bubbles, the stream function is⁴⁸

$$\Psi =\left[C\left(t\right)r^{-l+2}+D\left(t\right)r^{-l}\right]Q_l\left(\cos \theta \right).$$ (A43)

Analogous to Eqs. (A31)–(A33), we find the velocity and pressure to be

$$v_r=-\left[C\left(t\right)r^{-l}+D\left(t\right)r^{-l-2}\right]P_l\left(\cos \theta \right),$$ (A44)

$$v_{\theta }=\left[\left(l-2\right)C\left(t\right)r^{-l}+lD\left(t\right)r^{-l-2}\right]\frac{Q_l\left(\cos \theta \right)}{\sin \theta },$$ (A45)

$$\frac{p}{2\eta }=-\frac{\gamma }{\eta R}-\frac{2l-1}{l+1}C\left(t\right)r^{-l-1}{P}_l\left(\cos \theta \right).$$ (A46)

The force-balance boundary conditions [Eqs. (A8) and (A10), appropriate for bubbles] lead to

$$\frac{\partial v_r}{\partial \theta }+r\frac{\partial v_{\theta }}{\partial r}-v_{\theta }=0atr=R,$$ (A47)

$$-p+2\eta \frac{\partial v_r}{\partial r}=\frac{2\gamma }{R}+\frac{\gamma }{R^2}(l-1)(l+2)f(t)P_l(\cos \theta )\mathrm{a}\mathrm{t}r=R.$$ (A48)

Substituting Eqs. (A44)–(A46) into Eqs. (A47) and (A48) and expressing the results in Laplace space, we find that

$$(l-1)(l+1)\widehat{\overline{C}}(s)+l(l+2)\widehat{\overline{D}}(s)=0,$$ (A49)

$$\frac{l^2+3l-1}{l+1}\widehat{\overline{C}}\left(s\right)+\left(l+2\right)\widehat{\overline{D}}\left(s\right)=\frac{\gamma }{2\eta R^2}\left(l-1\right)\left(l+2\right){\widehat{f}}_l\left(s\right),$$ (A50)

where $\overline{C}(t)=C(t)R^{-l-1}$ and $\overline{D}(t)=D(t)R^{-l-3}$. Using Eq. (A44) in Eq. (A41b), the kinematic boundary condition in Laplace space, we obtain

$$s{\widehat{f}}_l\left(s\right)=f_l\left(0\right)-[\widehat{\overline{C}}\left(s\right)+\widehat{\overline{D}}\left(s\right)]R.$$ (A51)

Solving the last three equations, we find that

$$\widehat{\overline{C}}\left(s\right)=\frac{\frac{\gamma }{R^2}l\left(l-1\right)\left(l+1\right)\left(l+2\right)f_l\left(0\right)}{2\eta s\left(2l^2+1\right)+\frac{\gamma }{R}\left(l-1\right)\left(l+1\right)\left(2l+1\right)},$$ (A52a)

$$\widehat{\overline{D}}\left(s\right)=-\frac{\frac{\gamma }{R^2}{\left(l-1\right)}^2{\left(l+1\right)}^2{f}_l\left(0\right)}{2\eta s\left(2l^2+1\right)+\frac{\gamma }{R}\left(l-1\right)\left(l+1\right)\left(2l+1\right)},$$ (A52b)

$${\widehat{f}}_l\left(s\right)=\frac{2\eta \left(2l^2+1\right)f_l\left(0\right)}{2\eta s(2l^2+1)+\frac{\gamma }{R}(l-1)(l+1)(2l+1)}=\frac{f_l\left(0\right)}{s+{\lambda }_l^{\mathrm{B}}}.$$ (A52c)

This ${\widehat{f}}_l(s)$ corresponds to an exponential function of time, with the recovery rate ${\lambda }_l^{\mathrm{B}}$ given by Eq. (A17).

APPENDIX B: SOLUTION WHEN BOTH η_I AND η_II ARE FINITE

When both η_I and η_II are finite, we need to consider both the interior and exterior fluid dynamics. The boundary conditions on the interface between the droplet and bulk phases consist of the continuity of the velocity field,

$${\mathbf{v}}_{\mathrm{I}\mathrm{I}}\cdot \mathbf{n}={\mathbf{v}}_{\mathrm{I}}\cdot \mathbf{n},$$ (B1a)

$${\mathbf{v}}_{\mathrm{I}\mathrm{I}}\cdot \mathbf{t}={\mathbf{v}}_{\mathrm{I}}\cdot \mathbf{t},$$ (B1b)

the kinematic equation,

$$\frac{\partial \mathcal{S}}{\partial t}+{\mathbf{v}}_{\mathrm{I}\mathrm{I}}\cdot \nabla \mathcal{S}=0,$$ (B2)

and the force-balance equations,

$$\mathbf{n}\cdot ({\eta }_{\mathrm{I}\mathrm{I}}{\tilde{\mathrm{\epsilon }}}_{\mathrm{I}\mathrm{I}}-{\eta }_{\mathrm{I}}{\tilde{\mathrm{\epsilon }}}_{\mathrm{I}})\cdot \mathbf{t}=0.$$ (B3a)

$$\mathbf{n}\cdot \left({\tilde{\mathbf{\tau }}}_{\mathbf{I}\mathbf{I}}-{\tilde{\mathbf{\tau }}}_{\mathbf{I}}\right)\cdot \mathbf{n}=-\gamma \nabla \cdot \mathbf{n}.$$ (B3b)

The interior velocity and pressure fields are given by Eqs. (A31)–(A33); the exterior counterparts are given by Eqs. (A44)–(A46), except that the term −γ/ηR on the right-hand side of Eq. (A46) should be removed since the effect of this term is already accounted in Eq. (A33) for the interior pressure. Equations (B1a) and (B1b) lead to

$$\widehat{\overline{A}}(s)+\widehat{\overline{B}}(s)=\widehat{\overline{C}}(s)+\widehat{\overline{D}}(s),$$ (B4a)

$$-\left(l+3\right)\widehat{\overline{A}}\left(s\right)-\left(l+1\right)\widehat{\overline{B}}\left(s\right)=\left(l-2\right)\widehat{\overline{C}}\left(s\right)+l\widehat{\overline{D}}\left(s\right).$$ (B4b)

Equation (B3a) leads to

$$\begin{array}{ll}\hfill & {\eta }_{\mathrm{I}\mathrm{I}}\left[l\left(l+2\right)\widehat{\overline{A}}\left(s\right)+\left(l-1\right)\left(l+1\right)\widehat{\overline{B}}\left(s\right)\right]\hfill \\ \hfill & ={\eta }_{\mathrm{I}}\left[\left(l-1\right)\left(l+1\right)\widehat{\overline{C}}\left(s\right)+l\left(l+2\right)\widehat{\overline{D}}\left(s\right)\right].\hfill \end{array}$$ (B4c)

Equation (B3b) leads to

$$\begin{array}{ll}\hfill & {\eta }_{\mathrm{I}\mathrm{I}}\left[\frac{l^2-l-3}{l}\widehat{\overline{A}}\left(s\right)+\left(l-1\right)\widehat{\overline{B}}\left(s\right)\right]\hfill \\ \hfill & +{\eta }_{\mathrm{I}}\left[\frac{l^2+3l-1}{l+1}\widehat{\overline{C}}\left(s\right)+\left(l+2\right)\widehat{\overline{D}}\left(s\right)\right]=\frac{\gamma }{2R^2}\left(l-1\right)\left(l+2\right)\widehat{f}\left(s\right).\hfill \end{array}$$ (B4d)

Finally, Eq. (B2) leads to

$$s{\widehat{f}}_l\left(s\right)=f_l\left(0\right)-[\widehat{\overline{A}}\left(s\right)+\widehat{\overline{B}}\left(s\right)]R,$$ (B4e)

which is the same as Eq. (A41b). Solving Eqs. (B4a)–(B4e), we find that

$${\widehat{f}}_l\left(s\right)=\frac{f_l\left(0\right)}{s+{\lambda }_l},$$ (B5)

where the recovery rate λ_l is given by Eq. (A20a).

APPENDIX C: SHAPE RECOVERY DYNAMICS OF MAXWELL DROPLETS

For the Maxwell model of linear viscoelasticity, substituting $\widehat{G}\left(s\right)$ of Eq. (9) into Eq. (13) would have yielded

$${\widehat{f}}_l\left(s\right)=\frac{f_l(0)}{s+{\lambda }_l^{\mathrm{D}}(1+{\tau }^{\mathrm{s}\mathrm{r}}s)}=\frac{f_l(0)/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}{s+{\lambda }_l^{\mathrm{D}}/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}.$$ (C1)

The inverse Laplace transform is

$$f_l\left(t\right)=\frac{f_l(0)}{1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}{e}^{-{\lambda }_l^{\mathrm{D}}t/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})},$$ (C2)

which is an exponential function of time. The recovery rate, ${\lambda }_l^{\mathrm{D}}/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$, is less than the counterpart for a Newtonian fluid (when τ^sr = 0) by a factor of $1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}$. The apparent zero-time deformation, $f_l(0)/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$, is also less than the nominal value, f_l(0), by the same factor, as required by the conservation of area under the curve [see Eq. (16)]. Hence, evidently, there is a missing amplitude of $f_l\left(0\right)-f_l(0)/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})=[{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})]f_l(0)$.

To find the origin of the missing amplitude, we need to take a step back from Eq. (A42c), which yields Eq. (13) when η is replaced by $\widehat{G}\left(s\right)$, and work with ${\dot{f}}_l\left(t\right)$ instead of f_l(t). Using Eq. (A41b) and Eqs. (A42a) and (A42b) with η replaced by $\widehat{G}\left(s\right)$ of Eq. (9), the Laplace transform of ${\dot{f}}_l\left(t\right)$ is

$$\begin{array}{ll}\hfill s{\widehat{f}}_l\left(s\right)-f_l\left(0\right)& =-[\widehat{\overline{A}}\left(s\right)+\widehat{\overline{B}}\left(s\right)]R\hfill \\ \hfill & =-\frac{{\lambda }_l^{\mathrm{D}}{f}_l\left(0\right)}{\frac{s}{1+{\tau }^{\mathrm{s}\mathrm{r}}s}+{\lambda }_l^{\mathrm{D}}}\hfill \\ \hfill & =-\frac{{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}{f}_l\left(0\right)}{1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}-\frac{f_l\left(0\right)}{1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}\frac{{\lambda }_l^{\mathrm{D}}/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}{s+{\lambda }_l^{\mathrm{D}}/(1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}.\hfill \end{array}$$ (C3)

The inverse Laplace transform is

$${\dot{f}}_l\left(t\right)=-\frac{{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}{f}_l\left(0\right)}{1+{\tau }^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}}\delta \left(t\right)-\frac{f_l(0)}{1+{\tau }^{sr}{\lambda }_l^D}\frac{{\lambda }_l^D}{1+{\tau }^{sr}{\lambda }_l^D}{e}^{-{\lambda }_l^{D}t/(1+{\tau }^{sr}{\lambda }_l^D)}.$$ (C4)

Upon integrating Eq. (C4) over time, the first term, a delta function, leads to an instantaneous drop in the amplitude at t = 0, which is exactly the missing amplitude; the second term yields the result in Eq. (C2), which is applicable for t > 0.

In general, the behavior of f_l(t) near t = 0 is dictated by ${\widehat{f}}_l\left(s\right)$ at s → ∞. If $\widehat{G}\left(\infty \right)$ is a nonzero finite value, then the asymptote of ${\widehat{f}}_l\left(s\right)$ given by Eq. (13) is f_l(0)/s, which upon inverse Laplace transform yields the correct value, f_l(0), for f_l(t) at t = 0. However, this analysis breaks down if $\widehat{G}\left(\infty \right)$ = 0, as is the case for the Maxwell and Burgers models, leading to a missing amplitude. Note that the 0 value of $\widehat{G}\left(\infty \right)$ violates an assumption used for deriving Eq. (13), which is that $\widehat{G}\left(s\right)$ is much greater than the exterior viscosity. The full solution, given by Eq. (19a), that accounts for the exterior viscosity does not suffer a missing amplitude. When ${\widehat{g}}_{\mathrm{I}\mathrm{I}}\left(\infty \right)$ = 0 as in the Maxwell and Burgers models, Eq. (19c) still yields a finite h_l(∞) and therefore Eq. (19a) gives the correct asymptote f_l(0)/s for ${\widehat{f}}_l\left(s\right)$.

APPENDIX D: SHAPE RECOVERY DYNAMICS OF BURGERS DROPLETS

For viscoelastic droplets modeled by the Burgers model, substituting $\widehat{G}\left(s\right)$ of Eq. (11) into Eq. (13) yields

$${\widehat{f}}_l\left(s\right)=\frac{\left(\frac{{\eta }_0}{1+{\tau }_0^{\mathrm{s}\mathrm{r}}s}+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s}\right)f_l(0)}{s\left(\frac{{\eta }_0}{1+{\tau }_0^{\mathrm{s}\mathrm{r}}s}+\frac{{\eta }_1}{1+{\tau }_1^{\mathrm{s}\mathrm{r}}s}\right)+{\eta }_{\mathrm{z}}{\lambda }_l^{\mathrm{D}}}.$$ (D1)

The Burgers model has $\widehat{G}\left(\infty \right)$ = 0, and correspondingly, there is also a missing amplitude, amounting to ${\eta }_{\mathrm{z}}{\tau }_0^{\mathrm{s}\mathrm{r}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}}{f}_l(0)/({\eta }_0{\tau }_1^{\mathrm{s}\mathrm{r}}+{\eta }_1{\tau }_0^{\mathrm{s}\mathrm{r}}+{\eta }_{\mathrm{z}}{\tau }_0^{\mathrm{s}\mathrm{r}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})$, at t = 0. For t > 0, The inverse Laplace transform of Eq. (D1) gives a bi-exponential f_l(t) [see Eq. (25a)]. The two recovery rates and the corresponding amplitudes are

$${\lambda }_{l\pm }^{\mathrm{D}}=\frac{1}{2({\Gamma }_{+}+{\tau }_0^{\mathrm{s}\mathrm{r}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}\left[({\tau }_0^{\mathrm{s}\mathrm{r}}+{\tau }_1^{\mathrm{s}\mathrm{r}}){\lambda }_l^D+1\pm \sqrt{\Delta }\right],$$ (D2)

$$A_{l\pm }=\frac{{\Gamma }_{+}}{2({\Gamma }_{+}+{\tau }_0^{\mathrm{s}\mathrm{r}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})}\left[1\pm \frac{({\Gamma }_{-}/{\Gamma }_{+})({\tau }_1^{\mathrm{s}\mathrm{r}}-{\tau }_0^{\mathrm{s}\mathrm{r}}){\lambda }_l^{\mathrm{D}}-1}{\sqrt{\Delta }}\right],$$ (D3)

where

$$\Delta ={\left[({\tau }_1^{\mathrm{s}\mathrm{r}}-{\tau }_0^{\mathrm{s}\mathrm{r}}){\lambda }_l^{\mathrm{D}}+1\right]}^2-4({\eta }_0/{\eta }_{\mathrm{z}})({\tau }_1^{\mathrm{s}\mathrm{r}}-{\tau }_0^{\mathrm{s}\mathrm{r}}){\lambda }_l^{\mathrm{D}},$$ (D4)

$${\Gamma }_{\pm }=({\eta }_0/{\eta }_{\mathrm{z}}){\tau }_1^{\mathrm{s}\mathrm{r}}\pm ({\eta }_1/{\eta }_{\mathrm{z}}){\tau }_0^{\mathrm{s}\mathrm{r}}.$$ (D5)

Note that

$$A_{l+}+A_{l-}=\frac{{\Gamma }_{+}}{({\Gamma }_{+}+{\tau }_0^{\mathrm{s}\mathrm{r}}{\tau }_1^{\mathrm{s}\mathrm{r}}{\lambda }_l^{\mathrm{D}})},$$ (D6)

which is less than 1 due to the missing amplitude at t = 0.

APPENDIX E: SHAPE RECOVERY DYNAMICS OF IDEAL-FLUID BUBBLES IN A VISCOELASTIC MEDIUM

The results for viscoelastic droplets in an ideal fluid also apply to the shape recovery dynamics of ideal-fluid bubbles in a viscoelastic medium, after replacing ${\lambda }_l^{\mathrm{D}}$ with ${\lambda }_l^{\mathrm{B}}$. The expressions for these two relaxation rates are given in Eqs. (14) and (18), respectively.

APPENDIX F: EFFECT OF INITIAL DEFORMED SHAPE

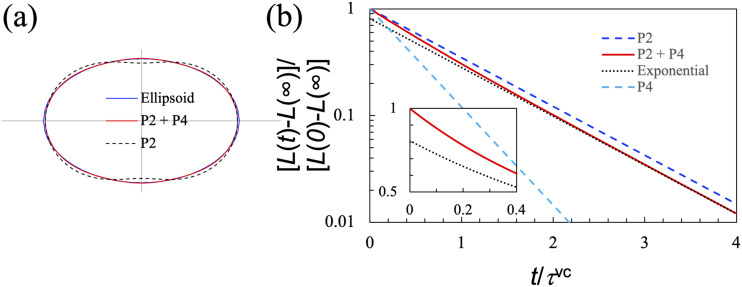
Both Fig. 2 and Eqs. (23a) and (23b) make it clear that the precise shape of the initial deformation affects the recovery dynamics. In particular, an ellipsoid can be approximated well by a combination of the second- and fourth-order Legendre polynomials, as illustrated in Fig. 6(a) for an ellipsoid with a half-length 1.4R and a half-width of 0.87R. In this case, the P2 and P4 amplitudes determined by representing the elliptical cross section by a sum of Legendre polynomials are 0.305 and 0.073, respectively. Recovery dynamics from such an initial ellipsoidal shape can be described by a corresponding linear combination of f₂(t) and f₄(t), leading to a bi-exponential decay [Fig. 6(b)].

FIG. 6.

Effect of initial shape on recovery dynamics. (a) Representation of an ellipse (with major and minor semi-axes at 1.4 and 0.87) by the sum of the first, second (P2), and fourth order (P4) Legendre polynomials. The amplitudes of P2 and P4 are 0.305 and 0.073, respectively. (b) Comparison of the deformation decay curves for P2, P4, and their combination (“P2 + P4”) that represents the ellipse in (a). The dotted curve labeled “exponential” displays the P2 component in the P2 + P4 curve. Inset: difference between the P2 + P4 curve and the P2 component at short times. The ordinate is in linear scale, in contrast to the log scale in the main figure.

AUTHOR DECLARATIONS

Conflict of Interest

The author has no conflicts to disclose.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.