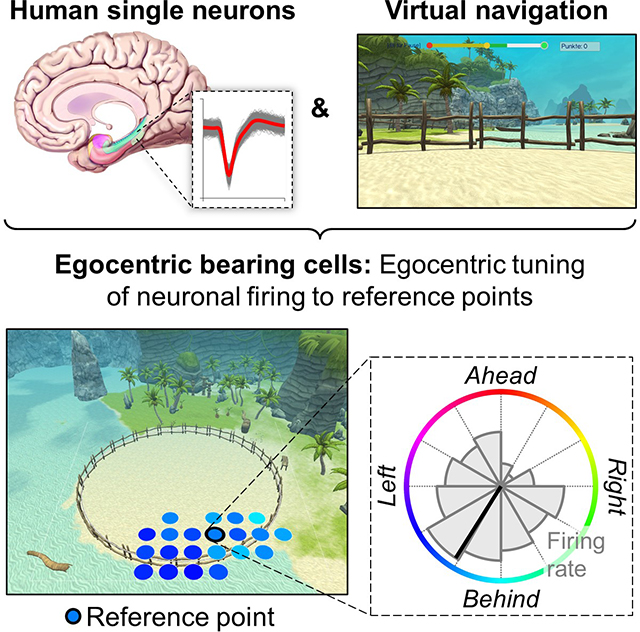
Summary
Spatial navigation and memory rely on neural systems that encode places, distances, and directions in relation to the external world or relative to the navigating organism. Place, grid, and head-direction cells form key units of world-referenced, allocentric cognitive maps, but the neural basis of self-centered, egocentric representations remains poorly understood. Here, we used human single-neuron recordings during virtual spatial navigation tasks to identify neurons providing a neural code for egocentric spatial maps in the human brain. Consistent with previous observations in rodents, these neurons represented egocentric bearings towards reference points positioned throughout the environment. Egocentric bearing cells were abundant in the parahippocampal cortex and supported vectorial representations of egocentric space by also encoding distances towards reference points. Beyond navigation, the observed neurons showed activity increases during spatial and episodic memory recall, suggesting that egocentric bearing cells are not only relevant for navigation but also play a role in human memory.
eTOC Blurb
In this issue of Neuron, Kunz et al. (2021) show that neurons in the human brain encode egocentric bearings and distances towards reference points in spatial environments. These neurons may support human navigation and memory by contributing to the neural basis of cognitive maps that are centered on the subject.
Graphical Abstract
Introduction
Humans and animals navigate and orient themselves by representing information about places, distances, and directions in allocentric reference frames, which are bound to the external world, or in egocentric reference frames, which are centered on the navigating subject (Figure S1) (Ekstrom et al., 2018). Behavioral studies have disentangled the importance of both allocentric and egocentric spatial representations, which complement each other to support efficient spatial behavior in everyday life (Burgess, 2006).
Over the past decades, the neuroscience of spatial navigation has led to a detailed understanding of allocentric neural representations of space (Moser et al., 2017). For example, a place or grid cell may indicate if a subject is in the “northeast” corner of an environment (Hafting et al., 2005; O’Keefe and Dostrovsky, 1971), a head-direction cell may activate whenever navigating “south” (Taube et al., 1990), and a boundary vector/border cell may respond when a boundary is located to the “west” (Lever et al., 2009; Solstad et al., 2008). These single-neuron codes provide the navigating organism with a “cognitive map” that encodes the environment’s structure as well as the subject’s location and orientation in allocentric coordinates (Tolman, 1948).
However, humans and animals experience environments primarily from a first-person perspective, they often remember locations and directions from egocentric viewpoints, and their planning and navigation along routes ultimately requires the paths to be represented in egocentric coordinates. Studies in non-human animals have begun to unravel the neural foundations of mental maps that could support such functions by identifying cells that activate at egocentric directions and distances from spatial boundaries (Alexander et al., 2020; Gofman et al., 2019; Hinman et al., 2019; Wang et al., 2018), the environmental center (LaChance et al., 2019; Wang et al., 2018), objects and landmarks (Deshmukh and Knierim, 2013; Wang et al., 2018), spatial goals (Sarel et al., 2017; Wang et al., 2018), and reference points scattered throughout the environment (Jercog et al., 2019; Wang et al., 2018).
In humans, the single-neuron basis of egocentric spatial representations has remained poorly understood, however. We addressed this gap and hypothesized that neurons in the human medial temporal lobe (MTL) track the instantaneous egocentric relationship between the navigating subject and proximal areas of the environment. Specifically, we tested for human neurons, “egocentric bearing cells” (EBCs), whose activity encodes the subject’s egocentric direction (and distance) towards local reference points, building on prior animal studies (Jercog et al., 2019; LaChance et al., 2019; Sarel et al., 2017; Wang et al., 2018). Such a coding scheme is instrumental for egocentric navigation because it represents the proximal spatial layout relative to a person’s viewpoint, which provides self-centered orientation and allows route planning from a first-person perspective.
Beyond spatial navigation, identifying the neural basis for egocentric cognitive maps also allows for a mechanistic understanding of different types of memory that preserve a subject’s original first-person perspective. We thus tested whether the activity of EBCs supported the processing of spatial information during spatial and episodic memory recall. In this way, our study links the phenomenological description of episodic memories as re-experiences of past personal events from egocentric viewpoints (Conway, 2009; Gardiner, 2001; Tulving, 1972) with the hypothesis that egocentric neural representations of space contribute to the neural substrate of episodic memories (Buzsáki and Moser, 2013; Wang et al., 2020). Overall, our study thus contributes to understanding the neural circuits underlying the first-person perspective in navigation and memory.
Results
Egocentric bearing cells encode egocentric directions towards local reference points
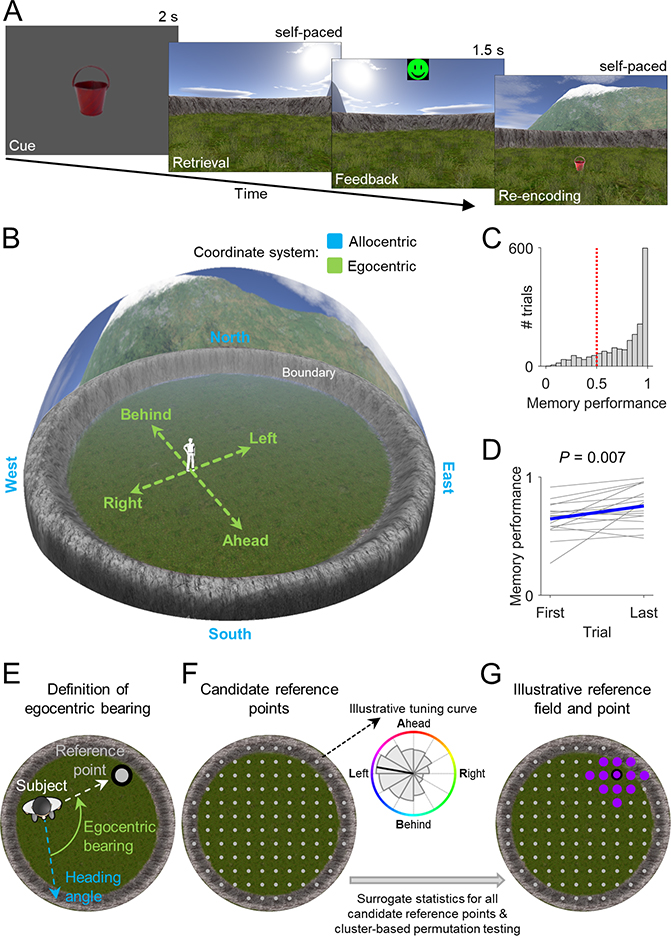
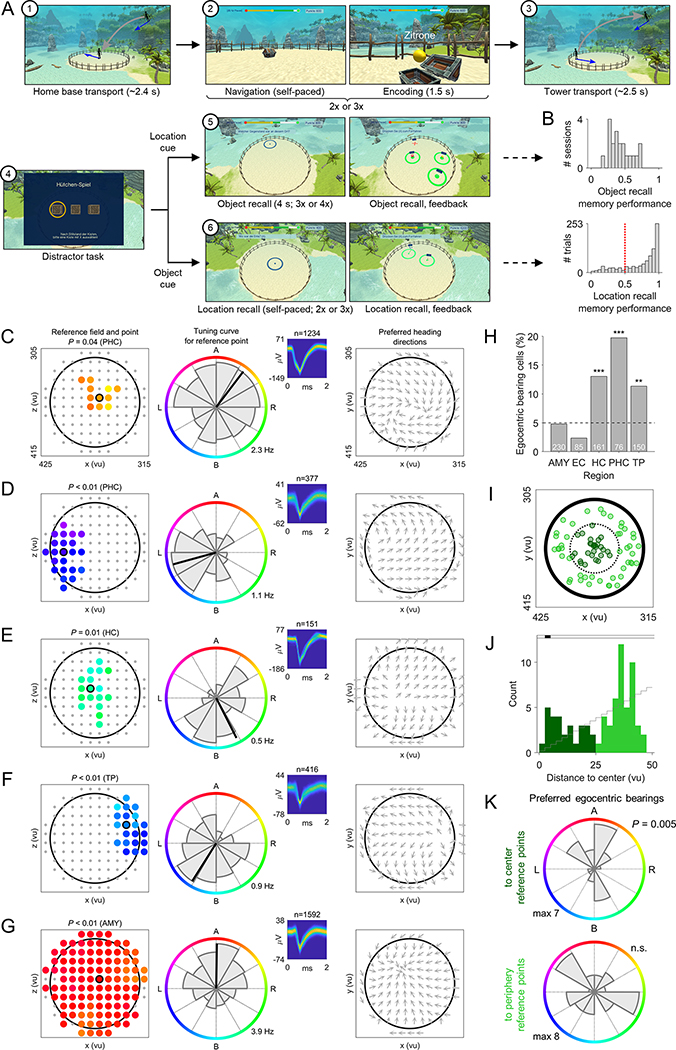
In Study 1, we recorded single-neuron activity from the MTL of 14 epilepsy patients (STAR Methods; Table S1), while they navigated a virtual environment to perform a spatial reference memory task (Kunz et al., 2015, 2019) (Figures 1A and 1B). In this task, patients first learned the spatial locations of 8 different objects during an initial learning period. Afterwards, in each of a series of test trials, patients were cued with one of the 8 objects, tried to remember the object’s associated location, navigated to the remembered location, and pressed a button to mark their response. The patients then received feedback and collected the object from its correct location to re-encode the object–location association. Object locations remained stable throughout each session, which contrasts with Study 2’s hybrid spatial navigation–episodic memory task where the subjects learned unique object–location associations on each trial.
Figure 1. Spatial reference memory task and analysis procedure for identifying egocentric bearing cells.
(A) In each trial, a given object (“cue”) had to be placed at its location (“retrieval”). Patients received feedback depending on response accuracy (“feedback”) and re-encoded the correct object location afterwards (“re-encoding”). (B) Virtual environment. Allocentric and egocentric reference frames are illustrated. (C) Spatial memory performance values across all trials from all patients. Red line, chance level. (D) Change in spatial memory performance between first and last trial. Blue line, mean across subjects. (E) Definition of egocentric bearing. (F) Left, candidate reference points. Right, illustrative tuning curve for one candidate point depicting firing rate as a function of egocentric bearing (coloring) towards this point. Significance of each candidate reference point is tested via surrogate statistics. (G) Cluster-based permutation testing identifies the largest cluster of significant candidate reference points (“reference field”). The “reference point” is the center of mass of the reference field. Coloring, preferred egocentric bearings according to the inset in F.
Throughout the task, we logged the patients’ virtual heading directions and locations to compare them with the simultaneously recorded neuronal activity. Patients contributed a total of 18 sessions (34–167 trials/session; 22–74 min/session) and performed the task well, as spatial memory performance was above chance on 83% of trials (Figure 1C) and increased over the course of the session (t-test, t(17) = 3.051, P = 0.007; Figure 1D). Across all sessions, we recorded from a total of 729 neurons across multiple regions (Figures S2 and S3), including amygdala (242), entorhinal cortex (114), fusiform gyrus (25), hippocampus (146), parahippocampal cortex (65), temporal pole (128) and visual cortex (9).
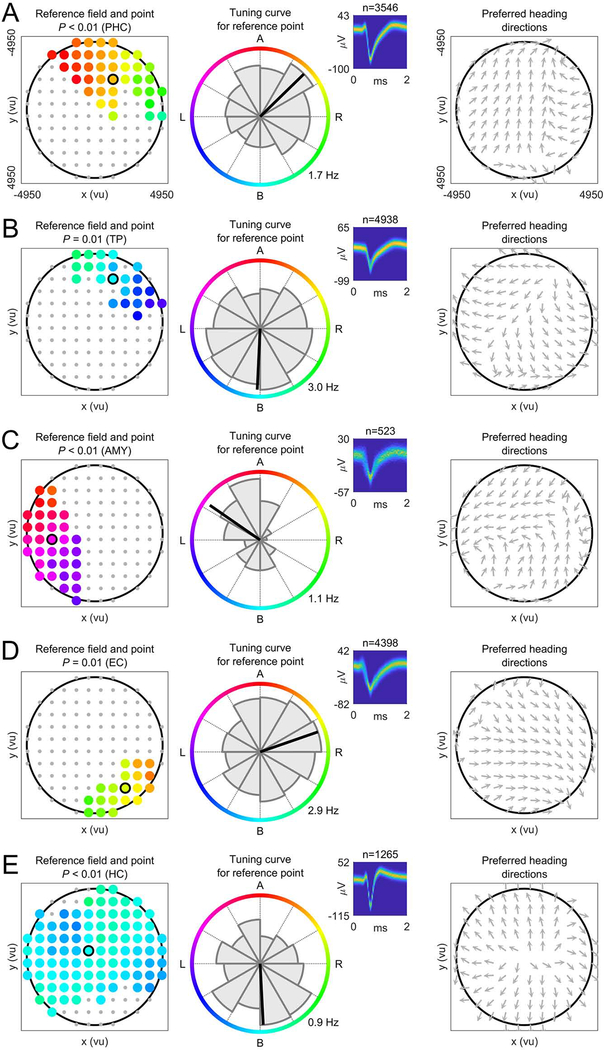
To identify potential human EBCs, we analyzed each neuron’s firing rate as a function of the patient’s egocentric bearing towards local reference points in the virtual environment (Figures 1E and S4) (Jercog et al., 2019; LaChance et al., 2019; Sarel et al., 2017; Wang et al., 2018). Briefly, for each cell we iterated through a grid of candidate reference points (Figure 1F), each time assessing the degree to which the cell’s firing rate throughout navigation varied as a function of the subject’s egocentric bearing towards a given candidate reference point (comparing against surrogate statistics to test for significance). We then identified contiguous clusters of candidate reference points with significant egocentric tuning and measured each cluster’s overall statistical significance using cluster-based permutation testing (Maris and Oostenveld, 2007). The center of mass of the largest significant cluster of significant candidate reference points (“reference field”) defined the reference point (Figure 1G). Our analysis thus resulted in the identification of individual neurons that behaved as EBCs by changing their firing rate to track the subject’s egocentric bearing towards a reference point in the virtual environment (Figure 2; Table S2). For example, the EBC in Figure 2A had its reference point in the “northeast” part of the environment (Figure 2A, left), and the cell’s firing rate increased when this reference point was ~45° to the right of the subject’s current heading (Figure 2A, middle). We further illustrate this cell’s tuning towards its reference point with a vector-field map (Figure 2A, right), showing the cell’s preferred allocentric direction as a function of location (Jercog et al., 2019; Wang et al., 2018).
Figure 2. Egocentric bearing cells encode egocentric directions towards local reference points.
(A to E) Example EBCs. Left column, EBC plot showing the reference field (colored dots) and the reference point (colored dot with black circle). Coloring, preferred egocentric bearing towards each location of the reference field (see colored circle in the middle column). Gray dots, candidate reference points without significant tuning. P-value, significance from cluster-based permutation test. Middle column, tuning curve showing how the cell’s firing rate varies as a function of egocentric bearing towards the reference point (maximum firing rate at bottom right). Colored circle indicates egocentric bearing. Inset, spike shapes as density plot (number above inset indicates spike count); yellow, maximum; blue, 0. Right column, vector-field map showing the cell’s preferred allocentric heading direction across the environment (gray arrows). Large black circles, environmental boundary. A (B; L; R), reference point ahead (behind; to the left; to the right) of the subject. ms, milliseconds; μV, microvolt. AMY, amygdala; EC, entorhinal cortex; HC, hippocampus; PHC, parahippocampal cortex; TP, temporal pole.
In total, we observed 90 EBCs, 12% of all neurons, which is significantly more than expected by chance (binomial test vs. 5% chance, P < 0.001). On average, there were 5.0 ± 1.2 (mean ± SEM) EBCs per recording session. We found at least one EBC in 16 of 18 sessions and in 12 of 14 patients. Some EBCs showed additional firing-rate modulations related to the patients’ allocentric direction and/or location (Figures 3A, S5, and S6), but a significant number of “pure” EBCs remained after excluding those EBCs that were also significantly tuned to allocentric direction and/or place (n = 59; 8%; binomial test, P < 0.001). EBCs were most prevalent in the parahippocampal cortex, where they comprised 28% of all neurons (Figure 3B). This result supports the idea that the functional role of the parahippocampal cortex includes the egocentric representation of space (Weniger and Irle, 2006).
Figure 3. Egocentric bearing cells have reference points positioned throughout the environment, show a range of egocentric bearings, exhibit distance tuning, and their firing rates covary with spatial memory performance.
(A) Overlap between EBCs, direction cells, and place-like cells. (B) Percentage of EBCs across brain regions. Asterisks, significance from binomial tests vs. 5% chance (dashed line). White numbers, total number of cells per region. (C) Spatial distribution of reference points. Dotted line separates center reference points (dark green) from periphery reference points (lime green). (D) Distribution of reference-point distances to the environment center. Black shading, significance at Pcorr. < 0.05 vs. chance (gray stairs). (E) Distribution of preferred egocentric bearings towards reference points in the environment center (left) and towards periphery reference points (right). P-value from Rayleigh test for 2-fold symmetry. (F) Example EBC showing activity linearly correlated with reference-point distance. Gray bars, firing rates; red lines, linear fit. P-values result from the comparison against surrogate statistics. (G) Distance-tuning curves for all EBCs, sorted by peak-firing distance to the reference point. Translucent coloring, absence of significant linear distance tuning. (H) Example EBC with a bearing-distance field, which also exhibited linear distance tuning. Firing-rate map shows firing rate as a function of egocentric bearing and egocentric distance to the reference point. Black line delineates the bearing-distance field. P-value results from the comparison against surrogate statistics. (I) Example EBC with a bearing-distance field, but without linear distance tuning. (J) Additional example EBCs with bearing-distance fields. (K) Relative bearing- and distance-extent of all bearing-distance fields. Inset shows relative 2D extent of all bearing-distance fields. Green, significant bearing-distance fields; gray, unsignificant fields. (L) Summary distribution of all bearing-distance fields. (M) Distribution of memory cells across brain regions. (N) Examples of EBCs that also behaved as memory cells by increasing (left) or decreasing (right) their firing rates in relation to better memory performance. P-values result from the comparison against surrogate statistics. Red lines, linear fit. Firing-rate residuals are displayed since the effect of time/experience was regressed out beforehand. (O) Prevalence of memory cells among egocentric bearing, direction, and place-like cells vs. non-spatial cells. Asterisks, significance from χ2 tests. FG, fusiform gyrus; FR, firing rate; max, maximum; min, minimum. n.s., not significant; *P < 0.05; **P < 0.01; ***P < 0.001.
For EBCs, the computed vector-field maps (e.g., Figure 2A, right) often showed a systematic change in the cell’s preferred allocentric direction across different locations of the environment, which contrasts with the activity of neurons that code for allocentric directions (“direction cells”) because those cells’ vector-field maps consistently represent the same preferred allocentric direction across different locations. For example, one such direction cell activated when a subject was moving “west”, irrespective of its current location (Figure S5A). There were 78 direction cells in our data set (11% of all neurons; binomial test, P < 0.001; Figure S5B), which as a group showed a broad range of preferred allocentric directions, which were not reliably clustered (Rayleigh test, z = 1.705, P = 0.182). To illustrate the different coding schemes of EBCs versus direction cells, we quantified the homogeneity of their vector-field maps and found that direction cells exhibited more similar directional tuning across the environment than EBCs (t-test, t(166) = 6.913, P < 0.001; Figure S5C).
Egocentric bearing cells have reference points positioned throughout the environment and show a range of preferred egocentric bearings
Across the population of EBCs, reference points were positioned in many different locations of the environment, including both the center and the periphery (Figure 3C). Reference points observed in the same session were not closer to each other than expected by chance (permutation test, P = 0.812; Figure S7), suggesting that reference points were similarly broadly distributed across the environment in each experimental session.
Overall, the spatial distribution of reference points overrepresented the environment center: The number of reference points in the central regions of the environment was higher than expected from a uniform distribution of reference points across the environment (binomial tests vs. chance for the 3 innermost bins, all P < 0.001, Bonferroni-corrected; Figure 3D). A similar overrepresentation of the environment center has been observed in rodents (LaChance et al., 2019; Wang et al., 2018), supporting the general notion that the center of an environment has a special role in navigation (Gallistel, 1990).
An EBC’s preferred egocentric bearing depended on the position of its reference point: EBCs with reference points in the center of the environment showed a bimodal distribution of preferred egocentric bearings and tended to represent “ahead” and “behind” bearings (Rayleigh test for 2-fold symmetry, z = 14.215, P < 0.001; Figure 3E). In contrast, EBCs with reference points in the periphery showed a roughly uniform distribution of preferred egocentric bearings (Figure 3E).
Egocentric bearing cells also encode distances to the reference points
We next examined whether EBCs supported full vectorial representations of egocentric space by representing not only egocentric bearing, but also egocentric distance to the reference points. We first tested whether the firing rates of EBCs correlated positively or negatively with the subject’s distance to the reference point (LaChance et al., 2019). 10 of the 90 EBCs showed such a linear relationship between firing rate and distance to the reference point, which is significantly more than expected by chance (binomial test, P = 0.015). Among these 10 cells, we observed examples of both neurons that significantly increased their firing rates when the subject was farther away from the reference point (n = 6) and neurons that significantly increased their firing rates when the subject was closer to the reference point (n = 4) (Figures 3F and 3G).
In a complementary analysis, we computed 2D firing-rate maps that showed the tuning of each EBC’s firing rate as a function of both egocentric bearing and distance to the reference point (Wang et al., 2018). In these firing-rate maps, we then identified “bearing-distance fields” as circumscribed areas of elevated firing. A substantial number of EBCs (n = 32) exhibited significant bearing-distance fields, in which their firing rates represented bearing and distance to the reference point conjunctively (Figures 3H–K). For example, Figure 3J shows the activity of an EBC that responded when the reference point was ahead of the subject and at a distance of ~4,000 virtual units (vu). Across all EBCs, bearing-distance fields covered large parts of the 2D bearing-distance map (Figure 3L), with a greater representation of “ahead” and “behind” bearings and reference-point distances of ~3,000 vu.
These results show that EBCs support full vectorial representations of egocentric space both via linear distance tuning and via conjunctive bearing-distance fields. The combined representation of egocentric bearing and distance may be useful for navigation and orientation because it allows the subject to compute not only the direction to the reference point, but also its exact location.
Firing rates of egocentric bearing cells covary with spatial memory performance during navigation
To address the question whether EBCs were involved in spatial memory, we tested whether EBCs showed firing-rate changes related to spatial memory performance. To this end, we identified neurons whose firing rates correlated with ongoing spatial memory performance (“memory cells”), inspired by the observation that neurons in the monkey hippocampal formation change their firing with learning (Wirth et al., 2003). Memory cells were particularly prevalent in the parahippocampal cortex, entorhinal cortex, and amygdala (Figure 3M) and comprised both positive memory cells, whose firing rates increased with better spatial memory performance, and negative memory cells, which showed the opposite pattern.
A significant number of EBCs fulfilled the criterion for being a memory cell (17 of 90; 19%; binomial test, P < 0.001), including both positive (n = 8) and negative memory by egocentric bearing cells (n = 9; Figure 3N). The percentage of memory cells was higher among EBCs than among non-spatial cells (40 of 523; 8%; χ2 test, χ2(1) = 11.504, P < 0.001; Figure 3O), indicating that EBCs exhibited closer links between their firing rates and spatial memory performance than non-spatial cells. Notably, not only EBCs, but also direction and place-like cells showed significantly increased percentages of memory cells as compared to non-spatial cells (direction cells: 14 of 78; 18%; χ2 test vs. non-spatial cells, χ2(1) = 8.807, P = 0.003; place-like cells: 14 of 85; 16%; χ2 test vs. non-spatial cells, χ2(1) = 7.032, P = 0.008), suggesting a more general link between the activity of spatial cells in the human MTL and spatial memory performance.
Relevance of objects for the activity of egocentric bearing cells
Spatial environments are often populated with objects. These objects can serve as beacons to guide navigation (Chan et al., 2012), their arrangement may define the geometry of the spatial layout (Ekstrom and Isham, 2017), and their presence can result in a distortion of allocentric cognitive maps (Boccara et al., 2019). We thus tested for a relationship between EBCs and neurons coding for such objects, and examined whether reference points were biased towards object locations.
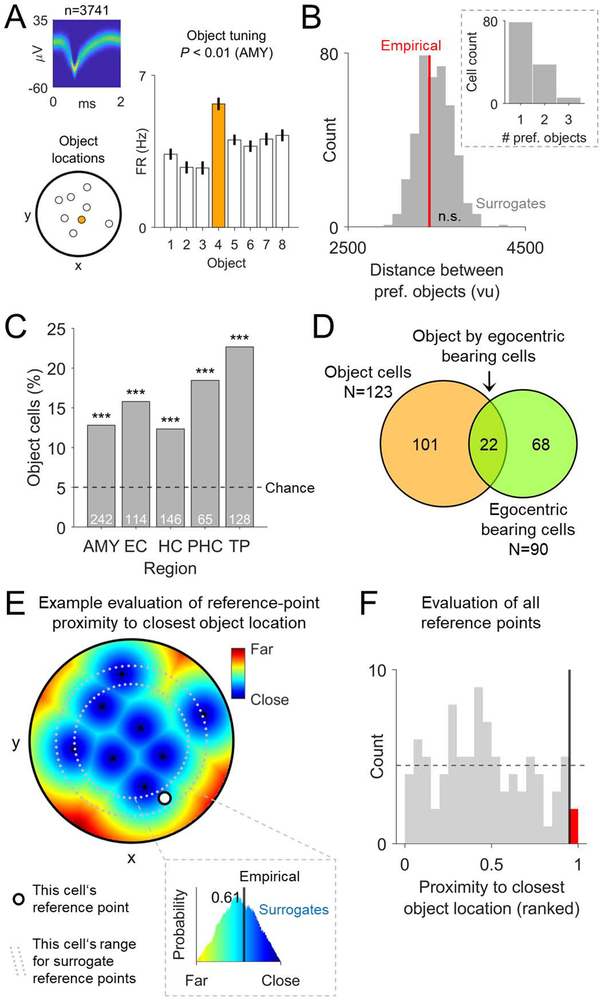
We first identified “object cells”, which changed their firing according to the identity of the objects whose locations the subject was learning and retrieving. For example, Figure 4A shows the activity of an object cell that increased its activity during trials with object #4. Object cells mainly represented non-spatial information about the objects, because—when examining object cells that responded to more than one object (n = 44)—the locations of the preferred objects were not clustered in space (permutation test, P = 0.406; Figure 4B). We observed 123 object cells overall (17% of all neurons; binomial test, P < 0.001; Figure 4C) and found that characteristics of object cells were also common among the identified EBCs (22 object cells among 90 EBCs; binomial test, P < 0.001; Figure 4D). Following theoretical models (Bicanski and Burgess, 2018), these conjunctive object by egocentric bearing cells may constitute a neural interface between spatial and non-spatial task features and may thus provide a neural substrate for pattern completion during memory recall (see below).
Figure 4. Relevance of objects for the activity of egocentric bearing cells.
(A) Example object cell with firing rates that vary as a function of the objects whose locations have to be learned and retrieved throughout the task. Each bar shows the firing rate during trials with a given object. Orange bar depicts the cell’s preferred object. P-value results from the comparison against surrogate statistics. (B) Mean distance between preferred objects of object cells with at least 2 preferred objects. Red line, empirical mean distance between preferred objects; gray bars, histogram of surrogate distances. Inset, number of preferred objects per object cell. (C) Distribution of object cells across brain regions. (D) Overlap between object cells and EBCs. (E) Illustration of the proximity (inverse of the distance) of all arena locations to their closest object location in one example cell. Black dots, object locations; white dot, reference point; gray dotted lines, margin for cell-specific surrogate reference points. Inset shows the rank (here, 0.61) of the empirical proximity between the reference point and its closest object location (black line) relative to the surrogate proximities between surrogate reference points and their closest object locations (colored histogram). (F) Histogram of the proximity of reference points to their closest object location, ranked with respect to the proximity of surrogate reference points to their closest object location, for all EBCs. Vertical black line, 5% alpha level; red bar, number of reference points that are significantly close to their nearest object location. The expected null distribution of the ranked empirical values is a flat histogram (dotted horizontal line). ***P < 0.001.
We then examined whether reference points of EBCs were biased towards object locations. Based on the finding of cells that are egocentrically tuned towards spatial goals or objects (Sarel et al., 2017; Wang et al., 2018) and in view of the possibility that a single environmental cue could determine the location of a reference point, we tested whether reference points were clustered near object locations (Figure 4E). Only 2 of the 90 reference points were significantly close to their nearest object location (binomial test, P = 0.943; Figure 4F). There was also no evidence for significant reference-point shifts towards object locations when we analyzed remembered instead of actual object locations (one significantly close reference point; binomial test, P = 0.990), which could have been the case if EBCs had used the remembered object locations as reference points (Poulter et al., 2020). Further, the allocentric directions towards reference points were not biased towards any of the distal landmarks (χ2 test, χ2(3) = 1.469, P = 0.689). Together, these findings suggest that the locations of reference points were not set by a single environmental cue. Instead, the combined influence of multiple spatial cues may determine the positions of reference points (O’Keefe, 1991), enabling reference points to be present in any part of an environment. This view is compatible with the idea that object locations still have a relevant influence on the locations of reference points and that the absence of reference points near the environmental boundary (Figure 3D) may thus be driven by the absence of objects near the boundary.
Egocentric bearing cells participate in context reinstatement during spatial memory recall
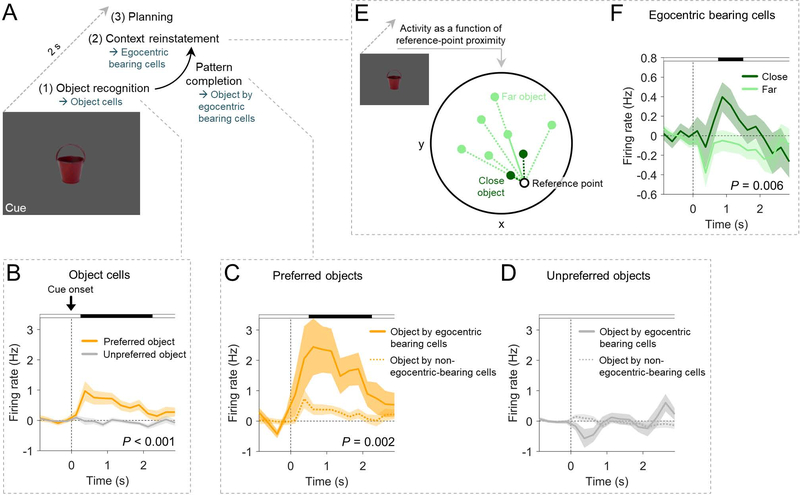
Theoretical models propose that memory recall is often triggered when an individual encounters a sensory cue (Staresina and Wimber, 2019). The cue then induces pattern-completion mechanisms that activate the neural representations underlying a reinstatement of the original spatiotemporal context associated with the cue (Miller et al., 2013). Hence, we hypothesized that object cells and EBCs (which we had identified using the navigation periods) might function in concert to facilitate object recognition and context reinstatement during spatial memory recall (Figure 5A). To test this idea, we analyzed their activity during the cued-recall period of the task, when subjects viewed one of the 8 objects that served as memory cues for the associated locations.
Figure 5. Egocentric bearing cells participate in context reinstatement during spatial memory recall.
(A) Hypothesis on the cognitive processes during memory cues: object recognition (supported by object cells) may trigger pattern completion (involving the activity of conjunctive object by egocentric bearing cells) and context reinstatement (associated with EBC activity). Planning of navigation routes may follow. (B) Firing rates of object cells during cue presentation of trials with the preferred object(s) vs. trials with unpreferred object(s). (C) Firing rates of conjunctive object by egocentric bearing cells during cue presentation of trials with their preferred object(s) as compared to object cells that are not EBCs. (D) Firing rates of conjunctive object by egocentric bearing cells during cue presentation of trials with the unpreferred object(s) as compared to object cells that are not EBCs. (E) Illustration of the separation of cue periods into “close” and “far” depending on whether the location of the cueing object is close to or farther away from the reference point, respectively. (F) Firing rates of EBCs during cue presentation of trials in which the object location is close to the reference point vs. trials in which the object location is farther away from the reference point. Shaded areas, SEM across cells. P-values result from cluster-based permutation tests, which control for multiple comparisons across the entire time windows; black shading at top, time points from the significant cluster. Firing rates in B, C, D, and F are baseline-corrected with respect to a one-second baseline interval before the onset of the cue period.
Examining object-cell activity during the cue period, we found that object cells rapidly increased their firing rates when subjects viewed the cells’ preferred versus unpreferred objects (cluster-based permutation test, P < 0.001; Figure 5B). This result is consistent with a possible involvement of object cells in object recognition. In conjunctive object by egocentric bearing cells (i.e., object cells that also behaved as EBCs), this firing-rate increase during the presentation of preferred objects was particularly pronounced, exceeding the firing-rate increase in the object cells that did not also behave as EBCs (cluster-based permutation test, P = 0.002; Figures 5C and 5D). Following theoretical accounts (Bicanski and Burgess, 2018), such activity in conjunctive object by egocentric bearing cells may relate to pattern completion that facilitates a transition from the cueing object to a reinstatement of the associated spatial context.
We then tested for a potential role of EBCs in reinstating the objects’ spatial contexts. We therefore examined whether the activity of EBCs during cue presentation varied with the location of the presented object relative to the cell’s reference point (Figure 5E). The firing rates of EBCs were greater when the location of the cueing object was close to the reference point (cluster-based permutation test, P = 0.006; Figure 5F), which suggests that EBCs participate in reinstating remembered spatial contexts. Together, object cells and EBCs may thus be involved in the different neural processes of object recognition, pattern completion, and spatial context reinstatement during spatial memory recall.
Egocentric bearing cells in the hybrid spatial navigation–episodic memory task
Episodic memories are past personal experiences of unique events at particular times and places (Tulving, 2002). Egocentric, self-centered neural representations may be relevant for episodic memories (Bicanski and Burgess, 2018; Buzsáki and Moser, 2013; Wang et al., 2018, 2020), because episodic memories are often experienced from the original first-person perspective (Conway, 2009; Tulving, 2002). However, neural evidence for a role of egocentric neural representations in episodic memories has remained elusive.
To probe the role of EBCs in episodic memory, we conducted Study 2 where we recorded single-neuron activity in patients performing a hybrid spatial navigation–episodic memory task (Miller et al., 2018; Tsitsiklis et al., 2020). In this task, subjects formed episodic memories by encountering unique objects at specific times in particular locations on a virtual beach. Later, they were asked to recall those episodes. Specifically, each trial began with a navigation–encoding period (Figure 6A), where patients navigated a virtual beach environment and traveled to 2 or 3 treasure chests at different random locations. When the patients reached a chest, it revealed a unique object whose identity, location, and time they were asked to remember. After the last treasure chest, the patients were passively transported to one of 2 elevated positions, from where they viewed the whole beach. Next, following a distractor task, the memory-recall period began, in which patients were asked to perform 2 types of episodic memory recall: On trials with location-cued object recall, patients were shown a location on the beach and asked to recall the name of the associated object. Conversely, on trials with object-cued location recall, patients were shown the name of an object and asked to indicate the location where it had been located. Subjects then also performed a judgement-of-recency task so that all components of episodic memories (what, where, and when) were probed.
Figure 6. Replication of egocentric bearing cell activity in the hybrid spatial navigation–episodic memory task.
(A) At the beginning of each trial ①, the subject was passively transported to a location on the beach. Figure shows the subject’s movement schematically from the side (gray arrow). Blue arrows, subject’s heading directions. During the navigation–encoding period of each trial ②, the subject navigated towards 2 or 3 treasure chests. Upon arrival, the chest opened and the subject encoded both the object within and the location of the chest. Next, the subject was passively transported ③ to an elevated recall position. During the subsequent distractor task ④ the subject was asked to follow a coin hidden underneath one of 3 moving boxes. Then, during location-cued object recall ⑤, a location on the beach was shown and the subject was asked to recall the associated object. Conversely, during object-cued location recall ⑥, the name of an object was shown, and the subject was asked to recall the associated location. (B) Memory performance for object and location recall. Red dotted line, chance level. (C to G) Example EBCs in the hybrid spatial navigation–episodic memory task. Same depiction as in Figure 2. (H) Distribution of EBCs across brain regions. (I) Spatial distribution of reference points. (J) Distribution of reference-point distances to the environment center. Black shading, statistical significance at Pcorr. < 0.05 vs. chance (gray stairs). (K) Distribution of preferred bearings towards reference points in the environment center and towards periphery reference points. P-value from Rayleigh test for 2-fold symmetry. **P < 0.01; ***P < 0.001.
12 patients completed the hybrid spatial navigation–episodic memory task, contributing a total of 20 sessions (21–40 trials/session; 45–83 min/session). Comparable to previous studies with this task (Miller et al., 2018; Tsitsiklis et al., 2020), patients recalled 44 ± 4% (mean ± SEM) of objects on trials with location-cued object recall and showed above-chance accuracy on 80% of trials with object-cued location recall (Figure 6B). Across all sessions, we recorded from a total of 737 neurons in the amygdala (230), entorhinal cortex (85), fusiform gyrus (26), hippocampus (161), insula (2), parahippocampal cortex (76), temporal pole (150), and visual cortex (7).
We identified EBCs in the navigation–encoding period of this task using the same methods as in the spatial reference memory task and replicated our earlier results by finding 74 EBCs (10% of all neurons; binomial test, P < 0.001; Figures 6C–6G). On average, we found 3.7 ± 0.6 (mean ± SEM) EBCs per session, including at least one EBC in each experimental session. Similar to our findings in the object–location memory task, some EBCs showed additional firing-rate modulations related to allocentric direction or location, but a significant number of “pure” EBCs remained after excluding EBCs that were also direction and/or place-like cells (n = 57; 8%; binomial test, P = 0.001).
The network of EBCs showed similar characteristics as in Study 1: EBCs were most prevalent in the parahippocampal cortex (20%; Figure 6H) and reference points were positioned in all parts of the environment across cells (Figure 6I), with an overrepresentation of the environment center (binomial test vs. chance for the second-innermost bin, P = 0.005, Bonferroni-corrected; Figure 6J). The preferred bearings of EBCs with reference points in the center of the environment showed a bimodal distribution with an overrepresentation of “ahead” and “behind” bearings (Rayleigh test for 2-fold symmetry, z = 5.161, P = 0.005), whereas EBCs with reference points in the periphery showed a roughly uniform distribution of preferred bearings (Figure 6K).
The tuning of egocentric bearing cells persists during passive movement
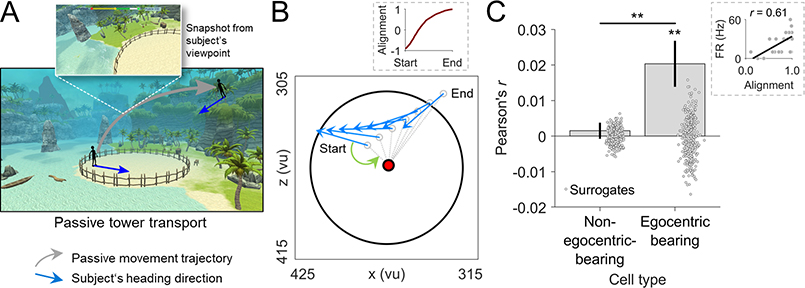
Humans navigate their environments using not only active but also passive movement when they do not move themselves (Chrastil and Warren, 2012). Previous studies in rodents showed that allocentric spatial cell types including place and grid cells considerably change their activity during passive vs. active navigation (Terrazas et al., 2005; Winter et al., 2015). Before turning to the involvement of EBCs in episodic memory recall, we thus asked whether EBCs maintained their tuning during passive movement and found that the egocentric tuning of EBCs persisted during the passive tower transport period (Figure 7)—indicating that active navigation is not a necessary condition for the occurrence of EBCs.
Figure 7. The tuning of egocentric bearing cells persists during passive transport.
(A) Schematic of the tower-transport period. Gray arrow, subject’s movement; blue arrows, subject’s heading directions. (B) Behavioral data from an example tower transport, in which the subject is transported from its location on the beach (Start) to the elevated position (End). Blue arrows, subject’s heading direction at select time points. Red dot, this cell’s reference point. Gray dashed lines, vectors from the subject’s location (unfilled gray dots) to the reference point. Green arrow, egocentric bearing at Start. Height values of the subject’s position are omitted for clarity. Inset, alignment of the current egocentric bearing with the preferred egocentric bearing across the entire transport period (“1” indicates perfect alignment). (C) Mean correlation between firing rates and the alignment of the subject’s current egocentric bearing with the preferred egocentric bearing during passive transport. Point clouds, surrogate means based on shuffled data. Inset, example correlation across time bins from one transport period. *P < 0.05; **P < 0.01.
To assess this effect, we tested whether the firing of EBCs during passive transport increased when the subject’s egocentric bearing towards the cell’s reference point was in alignment with the cell’s preferred egocentric bearing that we had determined during the navigation–encoding periods. We found indeed that stronger alignment with the preferred egocentric bearing correlated with greater firing rates (t-test of correlation values vs. 0, t(73) = 3.141, P = 0.002; permutation test, P < 0.001; Figure 7C). As a control, we confirmed that this phenomenon was not present in non-egocentric-bearing cells (t-test, t(607) = 0.664, P = 0.507; permutation test, P = 0.237) and that it was significantly stronger in EBCs than in non-egocentric-bearing cells (t-test, t(680) = 2.732, P = 0.006). These results indicate that EBCs maintained their tuning during passive movement, potentially helping humans stay oriented when active locomotion is disabled.
Egocentric bearing cells activate during successful episodic memory recall
We finally tested for a role of EBCs in episodic memory. We thus examined whether they activated more strongly during successful as compared to unsuccessful episodic memory recall. As we specifically hypothesized that EBCs would be involved in processing the spatial component of episodic memories, we furthermore predicted that EBCs would activate early during location-cued object recall, when recall began with the presentation of a spatial context cue and proceeded to the subject remembering the corresponding object. Conversely, we expected a late activation of EBCs during object-cued location recall, when the subject’s recall was initiated by a cueing object and then transitioned to reinstating the corresponding spatial context.
To address these issues, we first examined the activity of EBCs during location-cued object recall trials, in which subjects were shown a location on the beach and asked to recall the name of the object they had found at that location during the navigation–encoding period (Figure 8A). During successful recall periods, EBCs showed increased firing shortly after the location cue (cluster-based permutation test for successful recall periods vs. 0, P = 0.043), which was significantly greater than during unsuccessful recalls (cluster-based permutation test for successful vs. unsuccessful recall periods, P = 0.035; Figure 8B). This memory-related firing-rate increase was not present in non-spatial cells (Figure 8C) and was significantly stronger in EBCs than in non-spatial cells (cluster-based permutation test for an interaction between “performance” and “cell type”, P = 0.040; Figure 8D). As not only EBCs but spatial cells in general showed significantly increased firing rates during successful versus unsuccessful recall periods (Figure S8, A to D), our data suggest that EBCs provide a subcomponent of a larger neural network comprising both allocentric and egocentric spatial cell types involved in processing spatial information during episodic memory recall.
Figure 8. Egocentric bearing cells activate during successful episodic memory recall.
(A) Schematic for location-cued object recall. (B and C) Firing rates of EBCs (B) and non-spatial cells (C) during successful vs. unsuccessful object recall. (D) Interaction effect showing a significant difference between the activity of EBCs and non-spatial cells during successful vs. unsuccessful recall periods. (E) Schematic for object-cued location recall. (F and G) Response-locked firing rates of EBCs (F) and non-spatial cells (G) during successful vs. unsuccessful location recall. (H) Interaction effect showing a significant difference between the activity of EBCs and non-spatial cells during successful vs. unsuccessful recall periods. Firing rates in B, C, D, F, G, and H are baseline-corrected with respect to a one-second baseline interval before the onset of the recall period. In B, C, F, and G: black shadings at top, significant clusters of firing-rate differences between successful and unsuccessful recall periods (cluster-based permutation tests, P < 0.05); gray shadings, significant deviations of firing rates from 0 during successful recall periods (cluster-based permutation tests, P < 0.05). In D and H, black shadings indicate significant interaction effects (cluster-based permutation tests, P < 0.05). All cluster-based permutation tests control for multiple comparisons across the entire time window.
We then examined the activity of EBCs during object-cued location recall, in which subjects saw the name of an object and were asked to recall the corresponding location. To indicate their response, subjects moved a target circle across the beach and pressed a button when the remembered location was reached (mean response latency ± SEM, 5.5 ± 0.4 s; Figure 8E). Here, during successful recall, EBCs showed increased firing rates at a later timepoint that preceded the subjects’ response (cluster-based permutation test for successful recall periods vs. 0, P = 0.042). The firing rates during successful recall were significantly greater than during unsuccessful recall (cluster-based permutation test for successful vs. unsuccessful recall periods, P = 0.032; Figure 8F). These effects were not present in non-spatial cells (Figure 8G) and were significantly stronger in EBCs than in non-spatial cells (cluster-based permutation test for an interaction between “performance” and “cell type”, P = 0.006; Figure 8H). Not only EBCs but spatial cells in general showed increased firing rates during successful versus unsuccessful recall periods (Figure S8, E to H), again indicating that EBCs are a subcomponent of a larger neural basis underlying spatial information processing during episodic memory recall.
Together, these results suggest that EBCs participate in successful episodic memory recall. The observation that EBCs activate early when spatial information is the memory cue and that they activate late when spatial information is the memory target may indicate that EBCs are particularly involved in processing the spatial component of episodic memories. We thus speculate that the activity of EBCs during recall helps reinstate the egocentric spatial context of an episodic memory, which may enable the subject to re-experience the subjective, first-person perspective of the original experience.
Discussion
Humans encode, store, and recall information about places, distances, and directions in both allocentric and egocentric reference frames (Ekstrom et al., 2018). Using single-neuron recordings in epilepsy patients performing virtual navigation tasks, we described human egocentric bearing cells, EBCs, whose activity encoded the subject’s egocentric direction towards local reference points in space. A subset of EBCs showed neural activity consistent with a vectorial representation of egocentric space by also encoding the distance to their reference point. EBCs may thus provide a neural code for egocentric spatial maps in the human brain, analogous to how place cells and head-direction cells support allocentric spatial maps. Such an egocentric code provides the subject with self-centered orientation relative to the proximal spatial layout and allows route planning from a first-person perspective. EBCs may thus facilitate egocentric navigation strategies in human behavior.
Our observation of human EBCs builds on prior studies that showed how neurons in rats and bats represent egocentric information (Alexander et al., 2020; Deshmukh and Knierim, 2013; Gofman et al., 2019; Hinman et al., 2019; Jercog et al., 2019; La-Chance et al., 2019; Sarel et al., 2017; Wang et al., 2018; Wilber et al., 2014), how human neurons respond to location-dependent and location-independent views of spatial landmarks (Ekstrom et al., 2003), and how fMRI activity in the human brain changes in response to particular views of spatial scenes (Epstein and Higgins, 2007; Epstein and Kanwisher, 1998; Epstein et al., 2003). Our findings thus contribute to understanding how the brain may support navigation and memory (Table S3).
EBCs showed a broad spatial distribution of reference points across the virtual environment in both tasks. Any part of an environment may thus serve as a reference point, replicating observations in the rodent hippocampal formation (Jercog et al., 2019; Wang et al., 2018). Additionally, we found that the distribution of reference points overrepresented the environment center, which also resembles prior findings in rodents (LaChance et al., 2019; Wang et al., 2018) and underscores the idea that the center of an environment has a distinct role for navigation (Gallistel, 1990). Reference points were not significantly biased towards object locations, which could have been the case if reference points were determined by a single environmental cue (Sarel et al., 2017; Wang et al., 2018). Multiple factors may thus determine the position of reference points, such as the combined influence of object locations, boundaries, and/or distal cues. This enables reference points even in parts of an environment that are devoid of any cues (O’Keefe, 1991), allowing the EBC network to provide the subject with a comprehensive egocentric map of its surrounding environment. The absence of reference points near the environmental boundary (in Study 1) is compatible with this view and may indicate that present or past object locations have a relevant influence on the position of reference points. Future studies could scrutinize the mechanisms by which reference points arise and whether reference points are allocated depending on task demands by experimentally manipulating specific aspects of an environment’s layout.
EBCs were particularly prevalent in the parahippocampal cortex. This region is the human homologue of the rodent postrhinal cortex, where center-bearing cells and egocentric boundary cells have been found in rats (Gofman et al., 2019; LaChance et al., 2019), suggesting that the relevance of this brain region for egocentric spatial representation is conserved across species. Furthermore, the abundance of EBCs in the parahippocampal cortex may be relevant clinically because it helps explain why parahippocampal cortex lesions cause disruptions of performance on navigation and memory tasks that require egocentric reference frames (Ploner et al., 2000; Weniger and Irle, 2006). Due to the parahippocampal cortex lesions, the patients may have had a reduced number of EBCs—as well as fewer center-bearing cells and egocentric boundary cells—which in turn may have accounted for the impaired egocentric navigation and memory performance in these patients. Of note, parahippocampal lesions have also been associated with impaired allocentric navigation, indicating that the human parahippocampal cortex is not only relevant for egocentric but also for allocentric human navigation (Aguirre et al., 1996; Bohbot et al., 1998; Epstein, 2008).
Our results indicate that EBCs are relevant for human memory. First, we found that EBCs activated more strongly during successful than during unsuccessful episodic memory recall, suggesting that egocentric single-neuron codes of space contribute to the neural basis of episodic memory. As EBCs activated early when spatial information cued the episodic memories and late when spatial information had to be recalled, EBCs may be specifically involved in representing spatial aspects of episodic memories. We thus speculate that EBCs contribute to episodic memory by reinstating the egocentric spatial context of the original experience. Relatedly, during spatial memory recall in the spatial reference memory task, EBCs showed increased firing when subjects viewed objects whose associated locations were close to the cells’ reference points. This finding implicates EBCs in memory recollection by participating in a neural cascade that starts with the recognition of a sensory cue and, following pattern completion, leads to a reinstatement of the spatial context associated with the cue (Staresina and Wimber, 2019). Object cells and conjunctive object by egocentric bearing cells may support object recognition and pattern completion in this process, followed by spatial context reinstatement in EBCs. Finally, we also demonstrated that EBCs changed their firing as a function of ongoing spatial memory performance during navigation. EBCs showed increases as well as decreases in their firing rates during periods with good performance, suggesting that both excitatory and inhibitory mechanisms shaped their contribution to spatial memory performance during navigation. Accordingly, EBCs are presumably part of larger neural networks with both positive and negative feedback circuits between the participating ego- and allocentric cell populations that collectively support spatial navigation.
In summary, we identified a neural code for egocentric spatial maps in the human MTL. EBCs appeared to constitute this code’s key unit by encoding egocentric directions between local reference points in the spatial environment and the navigating subject. EBCs may thus provide the subject with an egocentric representation of its proximal environment, allowing the use of egocentric navigation strategies in human spatial behavior. EBCs may furthermore be useful for remembering spatial and episodic memories by helping to process spatial information related to the memories, thus contributing to a vivid recollection of past experiences.
STAR Methods
Resource availability
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Lukas Kunz (drlukaskunz@gmail.com).
Materials availability
Not applicable.
Data and code availability
Data to recreate the figures are available at https://github.com/NeuroLuke/KunzNeuron2021. Raw data are not publicly available because they could compromise research participant privacy, but are available upon request from the lead contact, Lukas Kunz. All custom MATLAB code generated during this study for data analysis is available at https://github.com/NeuroLuke/KunzNeuron2021. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Experimental model and subject details
Human subjects
Across both studies we tested 15 human subjects, who were epilepsy patients undergoing treatment for pharmacologically intractable epilepsy at the Freiburg Epilepsy Center, Freiburg im Breisgau, Germany. Of those, 14 participated in the spatial reference memory task (7 female; age range, 19–51 years; mean age ± SEM, 33.1 ± 3.0 years) and 12 participated in the hybrid spatial navigation–episodic memory task (6 female; age range, 19–51; mean age ± SEM, 35.2 ± 3.3 years). Eleven patients completed both tasks and some patients contributed more than one session per task (Table S1). Informed written consent was obtained from all patients. The studies conformed to the guidelines of the ethics committee of the University Hospital Freiburg, Freiburg im Breisgau, Germany.
Methods details
Neurophysiological recordings
Patients were surgically implanted with intracranial depth electrodes in the medial temporal lobe for diagnostic purposes in order to isolate the epileptic seizure focus for potential subsequent surgical resection. The exact electrode numbers and locations varied across subjects and were determined solely by clinical needs. Neuronal signals were recorded using Behnke-Fried depth electrodes (AD-TECH Medical Instrument Corp., Racine, WI). Each depth electrode contained a bundle of 9 platinum-iridium microelectrodes with a diameter of 40 μm that protruded from the tip of the depth electrode (Fried et al., 1999). The first 8 microelectrodes were used to record action potentials and local field potentials. The ninth microelectrode served as reference. Microelectrode coverage included amygdala, entorhinal cortex, fusiform gyrus, hippocampus, insula, parahippocampal cortex, temporal pole, and visual cortex. We recorded microwire data at 30 kHz using NeuroPort (Blackrock Microsystems, Salt Lake City, UT).
Spike detection and sorting
Neuronal spikes were detected and sorted using Wave_Clus (Chaure et al., 2018). We used default settings with the following exceptions: “template_sdnum” was set to 1.5 to assign unsorted spikes to clusters in a more conservative manner; “min_clus” was set to 60 and “max_clus” was set to 10 in order to avoid over-clustering; and “mintemp” was set to 0.05 to avoid under-clustering. All clusters were visually inspected and judged based on the spike shape and its variance, inter-spike interval (ISI) distribution, and the presence of a plausible refractory period. If necessary, clusters were manually adjusted or excluded. Furthermore, clusters were excluded that exhibited mean firing rates of <0.1 Hz during the analysis time window [following (Ekstrom et al., 2003)]. Spike waveforms are shown as density plots in all figures (Reber et al., 2019).
In the spatial reference memory task, we identified N = 729 clusters (also referred to as “neurons” or “cells” throughout the manuscript) across 18 experimental sessions from all 14 patients. In the hybrid spatial navigation–episodic memory task, we identified N = 737 clusters across 20 experimental sessions from all 12 patients. Neuronal responses from different sessions were treated as statistically independent units. An experienced rater (B.P.S.) assigned the tips of depth electrodes to brain regions based on post-implantation MRI scans in native space so that neurons recorded from the corresponding microelectrodes could be assigned to these regions. We recorded n = 242 (230) neurons from amygdala, n = 114 (85) neurons from entorhinal cortex, n = 25 (26) neurons from fusiform gyrus, n = 146 (161) neurons from hippocampus, n = 0 (2) neurons from the insula, n = 65 (76) neurons from parahippocampal cortex, n = 128 (150) neurons from the temporal pole, and n = 9 (7) from visual cortex (numbers outside brackets refer to the spatial reference memory task; numbers inside brackets refer to the hybrid spatial navigation–episodic memory task). Due to low numbers of neurons in fusiform gyrus, insula, and visual cortex, we excluded these regions from region-specific analyses.
For recording quality assessment (Figure S3), we calculated the number of units recorded on each wire; the ISI refractoriness for each unit; the mean firing rate for each unit; and the waveform peak signal-to-noise ratio (SNR) for each unit. The ISI refractoriness was assessed as the percentage of ISIs with a duration of <3 ms. The waveform peak SNR was determined as: SNR = Apeak/SDnoise, where Apeak is the absolute amplitude of the peak of the mean waveform, and SDnoise is the standard deviation of the raw data trace (filtered between 300 and 3,000 Hz).
Spatial reference memory task
During experimental sessions of Study 1, patients sat in bed and performed a spatial reference memory task on a laptop computer (Figure 1), which was adapted from previous studies (Doeller et al., 2008; Kunz et al., 2015, 2019). The task was developed using Unreal Engine 2 (Epic Games, Cary, North Carolina, USA).
During the task, patients first learned the locations of 8 everyday objects by collecting each object from its location once (this initial learning phase was excluded from all analyses). Afterwards, patients completed variable numbers of test trials (Figure 1A) depending on compliance. Each test trial started with an inter-trial-interval of 3–5 s duration (uniformly distributed). Patients were then shown one of the 8 objects (“cue”; duration of 2 s). During the subsequent retrieval period (“retrieval”; self-paced), patients navigated to the remembered object location and indicated their arrival with a button press. Next, patients received feedback on the accuracy of their response using one of 5 different emoticons (“feedback”; duration of 1.5 s). The retrieved object then appeared in its correct location and patients collected it from there to further improve their associative object–location memories (“re-encoding”; self-paced). The patients could use several different strategies to retrieve the location of the objects: They could encode the object locations in an allocentric reference frame by remembering the object locations as a function of their relationship to the combination of all distal cues. Subjects may have also encoded the object locations in an egocentric reference frame by tracking the location of each object relative to them throughout the task. Other strategies such as beaconing (e.g., a specific object is close to the mountain with the snow-covered peak) may have been employed as well.
Response accuracy was measured as the Euclidean distance between the response location and the correct location (“drop error”). Drop errors were transformed into spatial memory performance values by ranking each drop error within 1 million potential drop errors. Potential drop errors were the distances between the trial-specific correct object location and random locations within the virtual environment. This transformation accounted for the fact that the possible range of drop errors is smaller for object locations in the center of the virtual environment as compared to object locations in the periphery of the virtual environment (Miller et al., 2018): For objects in the environment center, the potential drop errors are in the range between [0, R], whereas they are in the range between [0, 2*R] for objects in the periphery of the arena (where R is the arena radius). Using the transformation procedure, performance values are mapped onto a range between [0, 1], irrespective of whether the associated objects are located in the center or the periphery of the environment. A spatial memory performance value of 1 represents the smallest possible drop error, whereas a spatial memory performance value of 0 represents the largest possible drop error. Chance level is at 0.5, because in that case a given drop error is smaller than 50% of the potential drop errors and larger than the other 50% of potential drop errors. To quantify performance increases within sessions, we computed the change in spatial memory performance between the first and the last trial (averaged across the eight different objects). Similar performance increases were seen when first and second sessions were analyzed separately (paired t-test: first sessions, t(13) = 2.653, P = 0.020; second sessions, t(3) = 6.106, P = 0.009).
The virtual environment comprised a grassy plain with a diameter of ~10,000 virtual units (vu), surrounded by a cylindrical cliff. There were no landmarks within the environment. The background scenery comprised a large and a small mountain, clouds, and the sun (Figures 1A and 1B). All distal landmarks were rendered at infinity and remained stationary throughout the task. Patients navigated the virtual environment using the arrow keys of the laptop computer (forward; turn left; turn right). Instantaneous virtual locations and heading directions (which are identical with viewing directions in our task) were sampled at 50 Hz. We aligned the behavioral data with the electrophysiological data using visual triggers, which were detected by a phototransistor attached to the screen of the laptop computer. The phototransistor signal was recorded together with the electrophysiological data at a temporal resolution of 30 kHz.
Spatial navigation–episodic memory task
During experimental sessions of Study 2, patients sat in bed and performed a computerized hybrid spatial navigation–episodic memory task, which was adapted from previous studies (Miller et al., 2018; Tsitsiklis et al., 2020). The task was developed using Unity3D (Unity Technologies, San Francisco, USA). The virtual environment comprised a beach surrounded by a circular wooden fence with a diameter of 100 vu. There were no landmarks within the environment. Some landmarks (palms and barrels) were close to the wooden fence outside the environment. Half of the beach was adjacent to the sea. The background scenery comprised multiple mountains, palms, and the sky (Figure 6A).
Patients performed up to 40 trials per session. On each trial, patients were placed in a random location on the virtual beach (“passive home base transport”; Figure 6A①). Subjects remained at this location until they initiated the trial with a button press. They then navigated to a number of treasure chests, which appeared successively on the beach (“navigation–encoding period”; Figure 6A②, left). Subjects were encouraged to travel to each chest as quickly as possible in order to receive bonus points for efficient navigation. Upon arrival at a chest, subjects were automatically rotated to directly face the chest, and the chest then opened to reveal an object and the name of this object (Figure 6A②, right). After 1,500 ms, the chest and object vanished. Subjects traveled to 2 or 3 chests during the course of a trial. In a full session with 40 trials, subjects encountered 100 chests.
After traveling to the last chest in a trial, subjects were passively and smoothly moved to one of 2 elevated positions where they had an overhead perspective view of the environment (“passive tower transport”; Figure 6A③). The first elevated position was located at 411/91/409 (x/y/z, where y is height); the second elevated position was located at 327/91/308. Subjects then played a distractor game (Figure 6A④), where they had to track which of 3 constantly moving boxes contained a coin. After the distractor game, the recall period of the trial began. In a given trial, subjects completed either location-cued object recall or object-cued location recall.
During location-cued object recall, n + 1 different locations on the beach were successively indicated with a small blue circle (in random order), where n corresponds to the number of treasure chests opened during the preceding navigation–encoding period. In response to each highlighted location, subjects were given four seconds to say out loud the name of the object that was contained in the treasure chest at that location or “Nichts” (German for “nothing”) for the one location not associated with a treasure chest (Figure 6A⑤, left). Correctness of the response was evaluated using Cortana (Microsoft, Washington, USA). Start and end times of these four-second periods were indicated by a sound.
During object-cued location recall, the names of the objects contained in the n treasure chests from that trial were successively shown to the subjects (in random order). After each presentation, subjects then had to move a small blue target circle (radius of 13 vu) across the beach and to press a button when the circle had reached the remembered location of the associated treasure chest (self-paced; Figure 6A⑥, left).
After being probed for all the locations/objects from a given trial, the subjects then completed a recency judgement task in which they were asked to judge which of 2 objects they had encountered later during the preceding navigation–encoding period (this period was not analyzed in this study). During recall, subjects were thus tested for all components of episodic memory: object, location, and time information. Finally, subjects received feedback (points) on the correctness of their responses—i.e., whether they had correctly recalled the object names during location-cued recall (Figure 6A⑤, right); whether they had correctly recalled the locations during object-cued recall (Figure 6A⑥, right); and whether they had correctly indicated which object they had encountered later during the trial. The next trial started by transporting the subject back onto the beach (“passive home base transport”).
Patients navigated the virtual environment using a game controller (forward; turn left; turn right). Instantaneous virtual locations and heading directions were sampled at 60 Hz. We aligned the behavioral data with the electrophysiological data using triggers, which were sent from the paradigm to the recording system.
To quantify the patients’ episodic memory performance, we calculated 2 different metrics: object-recall performance determined whether an object was correctly recalled in a given location-cued object recall period. For object-cued location recall periods, location-recall performance was quantified as the Euclidean distance between the remembered location and the correct location of the treasure chest in which the cueing object had been encountered during the preceding navigation–encoding period (“drop error”). Using the same rationale and procedure as in the spatial reference memory task, drop errors were ranked within one million potential drop errors to give normalized location-recall performances (see above), with values of 1 representing the best possible response and values of 0 representing the worst possible response (Miller et al., 2018).
Quantification and statistical analysis
General information on statistics
All analyses were carried out in MATLAB 2018b and 2020b using MATLAB toolboxes, custom MATLAB scripts, and FieldTrip (Oostenveld et al., 2011). Unless otherwise indicated, we considered results statistically significant when the corresponding P-value fell below an alpha level of α = 0.05. Analyses were two-sided, unless otherwise specified. Binomial tests evaluated the significance of proportions of neurons relative to a chance level of 5%, unless otherwise specified. Surrogate statistics were generally one-sided to assess whether an empirical test statistic exceeded a distribution of surrogate statistics significantly, unless otherwise specified. Statistics on angular data were carried out using the CircStat toolbox (Berens, 2009). The significance of overlaps between different functional cell types was assessed using χ2 tests.
Information on cell-type identification
At each time point, the participant’s allocentric direction and location was given by the yaw value and the (x/y)-coordinate [or (x/z)-coordinate in the hybrid spatial navigation–episodic memory task] of the virtual character’s position in the virtual environments, respectively. Neuronal spike times were adjusted to the behavioral time axis according to the trigger time stamps. We then downsampled the behavioral data to 10 Hz [following (Jacobs et al., 2010; Miller et al., 2015)] and calculated the neuronal firing rate (Hz) for each sample (i.e., for each 100 ms time bin). Time periods in which the patient remained stationary for >2 s were excluded from the analyses.
To identify different cell types, we employed an ANOVA framework (Ekstrom et al., 2003; Manns et al., 2007; Qasim et al., 2019; Tsitsiklis et al., 2020; Wood et al., 2000), in which we assessed the effects of different factors on firing rates. For example, to identify egocentric bearing cells, we used a three-way ANOVA with factors “direction”, “place”, and “egocentric bearing” (see below). In all ANOVAs (computed via MATLAB’s anovan function), we used Type II sums of squares, which controls for main effects of other factors when determining significance of a given factor. Empirical F-values of a given factor were considered significant, when they exceeded the 95th percentile of 101 surrogate F-values, which we obtained by performing the same ANOVA on circularly shifted firing rates [with the end of the session wrapped to the beginning; following, e.g., (Høydal et al., 2019; Krupic et al., 2012; Omer et al., 2018; Qasim et al., 2019)].
Tuning curves are displayed as the estimated marginal means of a given factor when controlling for the other factors (computed via MATLAB’s multcompare function), inspired by analysis procedures in rodents that identify independent effects of different factors on firing rates (Burgess et al., 2005; Hardcastle et al., 2017).
We note that neuronal tuning strengths in our study were generally lower than in rodents [for similar tuning strengths, see for example (Ekstrom et al., 2003; Jacobs et al., 2010, 2013; Miller et al., 2013; Qasim et al., 2019; Tsitsiklis et al., 2020)]. For example, head-direction cells in rodents often exhibit baseline firing rates of about 0 Hz and increase their firing rates up to about 100 Hz at the preferred head direction (Taube et al., 1990). Directionally sensitive neurons in our study (“direction cells”; e.g., Figure S5A) showed only moderate firing rate increases when subjects moved in the preferred direction (on average, maximum firing rates of the directional tuning curves were 2.8 times as high as the minimum firing rates of the directional tuning curves). Similarly, the response profiles of spatially-modulated neurons (e.g., Figures S6, A to E) were not as clear as in rodent place cells, which is why we call them “place-like cells” in this study.
Different factors may contribute to the reduced selectivity of neuronal responses: In humans, it is not possible to adjust the localization of microelectrodes after implantation and a search for strongly tuned cells is thus not possible. Moreover, patients did not physically navigate the spatial environment, but rather completed a virtual navigation task, potentially associated with broader spatial tuning (Chen et al., 2018). Additionally, neuronal firing in the human brain may be higher-dimensional than in rodents meaning that more internal and external factors (including ongoing thoughts, spontaneous occurrence of memories and ideas, and stimuli in the patient’s room) influence neuronal firing rates. Finally, (subtle) epileptogenic processes may have also affected the sharpness of the neurons’ tuning curves (Shuman et al., 2020).
Egocentric bearing cells
We used the term “egocentric bearing cell” in this study to succinctly describe the egocentric tuning of neurons in the human medial temporal lobe to reference points in the surrounding virtual environment, but we note that similar tuning has been observed in prior rodent studies [e.g., (Wang et al., 2018)].
We identified egocentric bearing cells using a two-step procedure (Figures 1F and 1G). In the first step, separately for each candidate reference point, we analyzed each neuron’s firing rate via a three-way ANOVA with factors “direction”, “place”, and “egocentric bearing” to assess the relevance of “egocentric bearing” while controlling for effects of “direction” and “place”. We calculated egocentric bearings as the angular difference between the subject’s instantaneous heading angle and the concurrent angle of the vector from the subject’s location to the reference point (Figure 1E). Candidate reference points (n = 112) were evenly distributed across the virtual environment (Figure 1F). No candidate reference points were located outside the circular boundary in the spatial reference memory task because the circular cliff was opaque. In the hybrid spatial navigation–episodic memory task, some candidate reference points were positioned slightly outside the circular wooden fence (Figures 6C–6G), because the subjects could look through the wooden fence. The factors “direction” and “egocentric bearing” could take on one of twelve values (angular resolution, 30°). In the spatial reference memory task, the factor “place” could take on one of 100 values representing a 10 × 10 grid overlaid onto the virtual environment. In the hybrid spatial navigation–episodic memory task, the factor “place” could take on one of 36 values representing a 6 × 6 grid overlaid onto the virtual environment, similar to our previous study using the same task (Tsitsiklis et al., 2020). Only factor levels with ≥5 separate observations (for example, 5 temporally distinct visits to location bin i) were included to ensure sufficient behavioral sampling. For the factor “egocentric bearing” we then extracted the raw ANOVA F-value (Fempirical) and the corresponding estimated firing rate map (eFRempirical), which is the tuning curve of the firing rate as a function of “egocentric bearing” while controlling for “direction” and “place” (for examples, see the middle column of Figure 2). Because Fempirical was estimated for all candidate reference points, this analysis resulted in a map of Fempirical values across all candidate reference points. Using the circular-shift procedure described above, we estimated 101 surrogate F-values (Fsurrogate) for each candidate reference point, resulting in 101 Fsurrogate maps across the candidate reference points. A candidate reference point was considered significant, if its Fempirical value exceeded the 95th percentile of its Fsurrogate values (corresponding to P < 0.05). Because we tested for significance in 112 different reference points, we had to control for multiple comparisons (Maris and Oostenveld, 2007). Hence, in the second step, we employed cluster-based permutation testing (Oostenveld et al., 2011) to assess the overall significance of the cell regarding egocentric bearing tuning: contiguous clusters of significant candidate reference points were identified and their percentiles of Fempirical within Fsurrogate were summed up, resulting in a cluster-percentileempirical value (for example, a contiguous cluster of 10 significant candidate reference points, where all candidate reference points had a percentile value of 97%, resulted in a cluster-percentile value of 970%). We considered this cluster-percentileempirical value statistically significant if it exceeded the 95th percentile of surrogate cluster-percentilesurrogate values (corresponding to P < 0.05). Here, cluster-percentilesurrogate values were created by using each of the Fsurrogate maps as a hypothetical Fempirical map once, each time assessing its cluster-percentilesurrogate value by comparing it against all other F maps (both the remaining Fsurrogate maps and the Fempirical map), as described above.
Egocentric bearing cell plots
For each egocentric bearing cell, we show the contiguous cluster of significant candidate reference points (i.e., the “reference field”; e.g., Figure 2A, left): each significant candidate reference point is depicted as a colored, bold dot; non-significant candidate reference points are indicated as gray, small dots. Coloring corresponds to the circular mean of the estimated firing rate map eFRempirical for that candidate reference point (for example, red means that the neuron’s firing rate increased when the subject was moving towards this point; cyan means that the neuron’s firing rate increased when the subject was moving away from this point). We obtained each cell’s reference point by calculating the center of mass of the reference field using MATLAB’s regionprops function.
As an approximate illustration of the cell’s egocentric bearing tuning, we additionally show the cell’s preferred allocentric direction as a function of location (e.g., Figure 2A, right). Here, the location-specific allocentric direction tuning curve is estimated via a two-way ANOVA with factors “direction” and “place”, which takes only data points into account when the subject is in the vicinity of a given location. The 112 candidate reference points (Figure 1F) served as these locations and the arbitrarily chosen vicinity of a location was defined as the location’s coordinate ± 1/3 of the arena diameter. For example, the vector-field map in Figure 2A, right, shows that allocentric direction tuning of this cell varies across different locations, twisting towards a spot in the northeast part of the virtual environment. This vector-field map can thus illustrate the egocentric bearing cell plot. Of note, the vector-field map does not match the egocentric bearing cell plot closely in cases when direction and egocentric bearing explain relevant and independent amounts of variance in the firing rates. This is due to the fact that the egocentric bearing cell plot shows egocentric bearing tuning while accounting for the effects of direction and location (three-way ANOVA with factors “direction”, “place”, and “egocentric bearing”), whereas the vector-field map shows direction tuning while only accounting for the effect of location (two-way ANOVA with factors “direction” and “place”).
Preferred egocentric bearing
For each egocentric bearing cell, we extracted its preferred bearing towards the reference point via the circular mean of the corresponding tuning curve. Tuning curves are displayed as circular histograms, with the length of the wedges depicting firing rates. Bimodality (i.e., 2-fold, 180-degree symmetry) of preferred egocentric bearings was tested by applying a Rayleigh test on the preferred egocentric bearings multiplied by 2.
Control analyses in the spatial reference memory task confirmed that the preferred egocentric bearings of EBCs towards their reference points were stable across time (correlation between the preferred bearings from the first vs. second data half, r(88) = 0.497, P < 0.001), which was also evident when analyzing the full shape of the tuning curves (mean correlation between the egocentric tuning curves from both data halves ± SEM, r = 0.469 ± 0.027; t-test of the correlation values against 0, t(89) = 17.193, P < 0.001).
Effects of tasks
We note that our paradigms may have encouraged the presence of egocentrically tuned neurons needed to solve the tasks (for example, due to the exact spatial layouts of the tasks) and that other tasks may have led to a different prevalence of egocentric versus allocentric single-neuron responses (Ekstrom et al., 2003; Georges-François et al., 1999; Rolls, 1999; Rolls and O’Mara, 1995).
Effects of hemisphere
We observed that egocentric bearing cells were slightly more prevalent in the right than in the left hemisphere: In the spatial reference memory task, 14.4% of all neurons from the right hemisphere were egocentric bearing cells, whereas 9.0% of all neurons from the left hemisphere were egocentric bearing cells (χ2 test, χ2(1) = 4.786, P = 0.029). In the hybrid spatial navigation–episodic memory task, 10.2% of all neurons from the right hemisphere were egocentric bearing cells versus 9.8% of all neurons from the left hemisphere (χ2 test, χ2(1) = 0.025, P = 0.876).
Effects of epileptic processes
To examine whether epileptic processes influenced the prevalence of egocentric bearing cells, we determined the number of egocentric bearing cells when excluding neurons that were recorded on microelectrodes implanted in brain regions potentially involved in the generation of epileptic seizures as defined by clinical criteria. These control analyses revealed 74 egocentric bearing cells among 570 neurons in the spatial reference memory task (13.0%; binomial test vs. 5% chance, P < 0.001) and 63 egocentric bearing cells among 589 neurons in the hybrid spatial navigation–episodic memory task (10.7%; binomial test vs. 5% chance, P < 0.001). These results are similar to our findings when examining all neurons.
Egocentric bearing cells: reference points
To test whether reference points of different egocentric bearing cells recorded during the same session were closer to each other than expected by chance, we calculated the average distance between all reference points from a given session and averaged across sessions afterwards (Dempirical). To create surrogates, reference points were randomly assigned to the different sessions multiple times, each time calculating the average distance between all reference points from a given “surrogate session” and averaging across “surrogate sessions” afterwards (Dsurrogate). We then tested how often Dempirical was smaller than Dsurrogate.
In order to test whether reference points were particularly prevalent in the center of the environment, we estimated the distance of each reference point towards the environment center and binned them into 20 bins. We then tested each bin count against the bin-wise chance level (which is dependent on the ring area of the bin) using binomial tests (including Bonferroni correction for 20 different bins).
To understand whether preferred egocentric bearings varied as a function of whether the reference point was located in the center or the periphery of the environment, we split the egocentric bearing cells into 2 groups depending on whether the center distance of their reference points was within half of the arena radius (center reference points) or outside half of the arena radius (periphery reference points). In the spatial reference memory task, half of the arena radius was 2500 vu; in the hybrid spatial navigation–episodic memory task, half of the arena radius was 25 vu.
To test whether the reference points were significantly close to their nearest object location, we first estimated the Euclidean distance of each reference point towards its closest object location (Dempirical). We then compared Dempirical against surrogate distance values (Dsurrogate) that were obtained by calculating the distance of surrogate reference points towards their nearest object location. Surrogate reference points were created on a cell-specific basis by randomly drawing locations from a circular ring area that had the same distance from the environment center as the corresponding empirical reference point (with a margin of ±450 vu, which is the distance between 2 neighboring candidate reference points; Figure 4E). We used this method for creating surrogate reference points in order to account for the fact that the distances of reference points to the environment center were not randomly distributed but overrepresented small distances (Figure 3D). If Dempirical was smaller than the 5th percentile of Dsurrogate values, the empirical reference point was considered significantly close to its nearest object location. This analysis was performed in relation to both the actual object locations and the remembered object locations. Remembered object locations were calculated as the average response location for a given object.
To examine whether the allocentric directions towards reference points were biased towards the distal landmarks, we counted how often the allocentric directions towards reference points were aligned with specific distal landmarks (small mountain, large mountain, small gap, or large gap). Using a χ2 test, we then tested whether the empirical counts deviated from the distribution of expected counts, which we estimated based on the angular extensions of the landmarks.
Egocentric bearing cells: goal tuning
In the main text, we showed that reference points were not biased towards object locations. This finding implicates that egocentric goal-direction tuning towards the object locations was not a major source of egocentric bearing cell tuning. To provide further evidence for this conclusion, we directly estimated egocentric goal-direction tuning towards the object locations in egocentric bearing cells. Hence, for each egocentric bearing cell and for each object location, we performed a three-way ANOVA with factors “direction”, “place”, and “egocentric goal direction” to estimate the effect of egocentric goal direction on the cell’s firing rate (Fempirical). We then calculated the maximum F statistic across object locations (Fmax-empirical) and compared them to surrogate maximum F statistics (Fmax-surrogate). These Fmax-surrogate statistics were estimated using the identical procedure as for Fmax-empirical with the only difference that object locations were circularly shifted around the center of the environment. For each egocentric bearing cell, we then estimated the rank of Fmax-empirical within the Fmax-surrogate values and compared these ranks against the chance level of 0.5 (chance level is 0.5, because Fmax-empirical is larger than half of the Fmax-surrogate values and smaller than the other half of Fmax-surrogate values in this case). We found that the ranks of Fmax-empirical were not above chance level (one-sample t-test, t(89) = −0.621, P = 0.536), further demonstrating that egocentric goal-direction tuning was not a major source of egocentric bearing cell tuning.
Egocentric bearing cells: distance tuning
Linear distance tuning
To investigate whether egocentric bearing cells linearly encoded the distance towards the reference point, we first analyzed each egocentric bearing cell’s firing rates as a function of direction, place, and egocentric bearing towards the reference point in a three-way ANOVA. The reference point was given by the previously performed egocentric bearing cell analysis. We then extracted the residuals from this ANOVA to correlate them with the distances of the subject to the reference point. We used the ANOVA residuals instead of the original firing rates in order to control for the effects of the other factors (place, direction, and egocentric bearing). We then calculated the Pearson correlation (rempirical) between the distances to the reference point and the residuals. rempirical was compared against surrogate correlation values (rsurrogate), which we obtained using the identical procedure as described for rempirical with the only difference that the firing rates were shifted relative to the navigation data before entering the ANOVA. We considered a cell to exhibit distance tuning (e.g., Figure 3F), if rempirical exceeded the 97.5th percentile of rsurrogate values (positive distance tuning) or if it fell below the 2.5th percentile of rsurrogate values (negative distance tuning). The total number of distance-tuned egocentric bearing cells (with either positive or negative distance tuning) was tested against the chance level of 5% using a binomial test. Since there were no obstacles in the virtual environment, Euclidean distance is identical with path distance in this task.
Conjunctive bearing-distance tuning
To examine whether egocentric bearing cells encoded distances towards reference points by increasing their firing rates at conjunctions of specific egocentric bearings to and particular distances from the reference point, we estimated 2D bearing–distance firing-rate maps (Wang et al., 2018). Firing rates were estimated by dividing the number of spikes by the dwell time in each bearing–distance bin (bearing bin size, 15°; distance bin size, 200 vu; smoothing with a Gaussian kernel of 5-bin size and a SD of 2). We created 1001 surrogate bearing–distance firing-rate maps by circularly shifting the empirical firing rates relative to the behavioral data. We then identified the largest contiguous cluster of bearing–distance bins in which the empirical firing rate exceeded the 95th percentile of surrogate firing rates (clusterempirical) and tested for significance of this cluster using cluster-based permutation testing. During cluster-based permutation testing, we obtained a surrogate cluster for each surrogate firing-rate map (clustersurrogate) by identifying the largest contiguous cluster of bearing–distance bins in which the surrogate firing rates exceeded the 95th percentile of the firing rates from all other surrogate firing-rate maps and the empirical firing-rate map. Empirical clusters (clusterempirical) were considered significant when they exceeded the 95th percentile of all surrogate clusters (clustersurrogate) and we termed them “bearing–distance fields”. To characterize bearing–distance fields, we estimated their extent along the bearing axis (relative to the bearing extent of the entire firing-rate map), their extent along the distance axis (relative to the distance extent of the entire firing-rate map), and their total extent (relative to the total extent of the entire firing-rate map).
Egocentric bearing cells: passive movement
To understand whether egocentric bearing cells maintained their tuning during passive transport, we examined the activity of egocentric bearing cells during the tower-transport period of the hybrid spatial navigation–episodic memory task (Figure 7).
For a given cell and trial, we calculated the egocentric bearing of the subject towards the cell’s reference point for each time point during the transport period (10 Hz temporal resolution) and calculated its alignment with the preferred egocentric bearing that had been estimated in the preceding egocentric bearing cell analysis (on data from the navigation periods). A high alignment value (close or equal to 1) meant that the instantaneous egocentric bearing during passive transport was aligned with the preferred egocentric bearing, whereas a low alignment value (close or equal to −1) meant that the instantaneous egocentric bearing during transport was exactly opposite to the preferred egocentric bearing (e.g., Figure 7B). Specifically, alignment with the preferred egocentric bearing was estimated as: alignmentt = cos(bearingpreferred - headingt), where bearingpreferred is the preferred egocentric bearing (from the navigation period) and headingt is the heading direction of the subject at time t (during the tower-transport period). In each tower-transport period, we then correlated the firing rates of egocentric bearing cells with the corresponding alignment values in order to test whether stronger alignment was associated with higher firing rates. In each cell, we averaged the correlation values across trials afterwards. Across egocentric bearing cells, we then tested whether correlation values were significantly above 0—indicating that there was a general positive association between egocentric bearing cell firing rates and the alignment of the subject’s current egocentric bearing with the preferred egocentric bearing. As a control, we compared the empirical mean correlation value against surrogate means obtained by performing the trial-wise correlations on shuffled data (the firing rates were randomly shuffled with respect to the alignment values on each trial). As another control, we tested for this effect in non-egocentric-bearing cells that had a non-significant reference field.
Direction cells
Rodent head-direction cells (Taube et al., 1990) activate whenever an animal’s head is pointing in a specific global direction that is defined relative to a world-referenced coordinate system (for example, when the head is pointing “north” or “south”). Here, we identified “direction cells” that exhibited firing-rate modulations as a function of the patients’ current heading direction within the virtual environment.
To identify direction cells, we analyzed each neuron’s activity by means of a two-way ANOVA with factors “direction” and “place”. The factor “direction” could take on one of twelve values (angular resolution, 30°). In the spatial reference memory task, the factor “place” could take on one of 100 values representing a 10 × 10 grid overlaid onto the virtual environment. In the hybrid spatial navigation–episodic memory task, the factor “place” could take on one of 36 values representing a 6 × 6 grid overlaid onto the virtual environment, similar to our previous study using the same task (Tsitsiklis et al., 2020). Only factor levels with ≥5 separate observations were included to ensure sufficient behavioral sampling. We then extracted the ANOVA F-value for the factor “direction” (Fempirical) and the estimated firing rate map (eFRempirical), while controlling for the factor “place”. We calculated statistical significance of Fempirical values using surrogate statistics as described above. For each direction cell, we extracted its preferred direction via the circular mean of the directional tuning curve.
To compare the vector-field maps of direction cells with the vector-field maps of egocentric bearing cells, we computed “vector-field strengths” as the Rayleigh vector length of all vectors in the vector-field map (a completely homogeneous vector-field map would result in a Rayleigh vector length of 1; a completely inhomogeneous vector-field map would result in a Rayleigh vector length of 0).
Direction cells vs. egocentric bearing cells
Egocentric bearing cells encode egocentric directions towards local reference points, whereas direction cells encode allocentric directions. However, egocentric direction towards a reference point becomes increasingly similar to allocentric direction with increasing distance of the reference point from the subject.
In the main text, we showed that the homogeneity of vector-field maps differed between egocentric bearing cells and direction cells. We performed additional analyses on the data from the spatial reference memory task to clarify the relationship between egocentric bearing cells and direction cells. First, to provide evidence that egocentric bearing cell tuning did not spuriously arise due to potential collinearities between the factors “direction” and “egocentric bearing” in our three-way ANOVA framework designed to identify egocentric bearing cells, we performed this ANOVA on surrogate data [testing for significance of the tuning curves by comparing against other surrogate data following (Kutter et al., 2018)]. In this way, we empirically estimated the percentage of egocentric bearing cells that may have arisen due to chance (for example, due to interdependencies between the factors “direction” and “egocentric bearing”). As expected, this approach resulted in 4.9% (n = 36) statistically significant outcomes (i.e., false positives) in the spatial reference memory task, confirming the a priori chosen alpha level of α = 0.05.
Second, we performed the egocentric bearing cell analysis using a two-way ANOVA, with factors “place” and “egocentric bearing”, in order to test for the number of egocentric bearing cells when not controlling for allocentric direction in our ANOVA framework. Using this approach, we observed 112 egocentric bearing cells in the spatial reference memory task (15.4%; binomial test vs. 5% chance, P < 0.001; as reported in the main text, we identified 90 egocentric bearing cells when also controlling for allocentric direction). Furthermore, egocentric bearing cell test statistics (i.e., each cell’s cluster-percentileempirical value) were highly similar between both types of ANOVA (Spearman correlation, r(727) = 0.620, P < 0.001) and the overlap between egocentric bearing cells identified via the 2 different analyses was significantly higher than expected by chance (χ2 test, χ2(1) = 165.256, P < 0.001).
Together, these analyses show (i) that egocentric bearing cells exhibit essential differences in their tuning as compared to direction cells; (ii) that egocentric bearing cells do not spuriously arise from potential collinearities between the factors “direction” and “egocentric bearing” in our ANOVA framework; and (iii) that egocentric bearing cells can also be identified in an ANOVA framework with a reduced number of predictors (i.e., with the factors “place” and “egocentric bearing” instead of the factors “direction”, “place”, and “egocentric bearing”).
Place-like cells
We identified place-like cells (Figure S6) using the same procedure as described for direction cells by means of a two-way ANOVA with factors “direction” and “place”. We defined place bins as those spatial bins in which the empirical firing rate exceeded the 95th percentile of surrogate firing rates (Ekstrom et al., 2003).
Memory cells
We identified memory cells (e.g., Figure 3N) as those cells that exhibited a significantly positive or negative partial correlation between their firing rates and spatial memory performance. We used a partial correlation in order to control for the effects of time/experience. Memory-performance values were ranked before computing the partial correlation. Empirical correlation values (rempirical) were compared against surrogate correlation values (rsurrogate) obtained by performing the same analysis based on circularly shifted firing rates. We labeled a neuron as a “memory cell”, if rempirical exceeded the 97.5th percentile of rsurrogate values (positive memory cell) or if it fell below the 2.5th percentile of rsurrogate values (negative memory cell). The number of memory cells (positive and negative memory cells combined) was then tested against 5% chance level using a binomial test.
Object cells
To identify object cells (e.g., Figure 4A), we analyzed each neuron’s activity using a three-way ANOVA with factors “direction”, “place”, and “object”. The factor “object” could take on one of 8 different values (because each patient learned and retrieved the locations of 8 different objects). For all time bins of a given trial, the factor “object” had the same value. The analysis relied on the same time points as the analyses of egocentric bearing cells, direction cells, and place-like cells. Time points during the cue period did not contribute to this analysis. We obtained object cells and preferred objects (i.e., objects for which the cell’s empirical firing rate exceeded the 95th percentile of surrogate firing rates) using surrogate statistics as described above. Preferred objects are indicated as orange bars in Figure 4A. Cells without a preferred object were excluded from the object-cell population.
To examine whether the preferred objects of object cells with ≥2 preferred objects exhibited a specific spatial relationship (i.e., whether they were clustered in space), we estimated the average Euclidean distance between the locations of all preferred objects, separately for each object cell with ≥2 preferred objects, and averaged across cells afterwards (Dempirical). We created surrogate distance values (Dsurrogate) by randomly selecting n object locations per cell, where n corresponds to the number of preferred objects in a given cell. We then determined the percentile of Dempirical within Dsurrogate to test whether Dempirical was smaller than the 5th percentile of Dsurrogate-values (in this case, the locations of preferred objects would be closer to each other than expected by chance; Figure 4B).
Spatial cells and non-spatial cells
Spatial cells were all cells that were either egocentric bearing cells, or direction cells, or place-like cells. Non-spatial cells were all cells that were neither egocentric bearing cells, nor direction cells, nor place-like cells.
Neural activity during spatial memory recall
In order to examine the activity of egocentric bearing cells and object cells during the cue period of the spatial reference memory task (Figure 5), we extracted the cells’ time-resolved firing rates during each cue period (duration of 2 s, with an additional 1 s data segment before the onset and after the offset of the actual cue period; temporal resolution of 4 Hz; no smoothing). Firing rates were baseline-corrected with respect to a 1 s baseline period (−1 to 0 s before the onset of the recall period).
We first examined the effects of the presentation of preferred versus unpreferred objects in object-cells, conjunctive object by egocentric bearing cells, and object by non-egocentric-bearing cells. Object cells and preferred objects had been identified in the preceding object-cell analysis, which was based on data from the retrieval period, feedback period, and re-encoding period (not including the cue periods). For each cell, we calculated one firing-rate time course associated with the presentation of preferred objects (mean across trials in which a preferred object was shown) and one firing-rate time course associated with the presentation of unpreferred objects (mean across all other trials). Afterwards, we used cluster-based permutation testing [10001 permutations; (Maris and Oostenveld, 2007)] to identify a significant cluster of contiguous time points in which recall events exhibited significantly higher firing rates during the presentation of preferred versus unpreferred objects, separately for the different groups of cells.
In egocentric bearing cells, we then examined the effects of the presentation of objects whose associated object locations were close to the reference point (“close” objects) versus the presentation of objects whose associated object locations were farther away from the reference point (“far” objects). Hence, for each egocentric bearing cell, we calculated one firing-rate time course associated with the presentation of “close” objects (those 2 objects whose associated locations were closest to the reference point) and one firing-rate time course associated with the presentation of “far” objects (all other objects). Afterwards, we tested across egocentric bearing cells whether firing rates were higher during trials with “close” objects as compared to trials with “far” objects using cluster-based permutation testing (10001 permutations).
Neural activity during episodic memory recall
To test whether egocentric bearing cells have a role in episodic memory recall, we examined their activity during the recall periods of the hybrid spatial navigation–episodic memory task (Figure 8).
With respect to location-cued object recall, we extracted each cell’s firing rates during each recall event (duration of 4 s, with an additional 1 s data segment before the onset and after the offset of the actual recall period; temporal resolution of 4 Hz; no smoothing). Firing rates were baseline-corrected with respect to a 1 s baseline period (−1 to 0 s before the onset of the recall period). For each cell, we then calculated one firing-rate time course associated with successful object-recall performance (mean across recall events in which the correct object was recalled) and one firing-rate time course associated with unsuccessful object-recall performance (mean across recall events in which the correct object was not recalled). Afterwards, we tested across egocentric bearing cells (and, as a control, across non-spatial cells) whether time-resolved firing rates were significantly increased during successful recall events. To this end, we used cluster-based permutation testing (1001 permutations) to identify a significant cluster of contiguous time points in which successful recall events exhibited firing rates that were (i) significantly above 0 and (ii) significantly higher than during unsuccessful recall events (using two separate analyses). To test whether the contrast between successful and unsuccessful recall events was significantly stronger in egocentric bearing cells than in non-spatial cells, we performed a cluster-based permutation test (1001 permutations) on the firing-rate differences between successful and unsuccessful trials for egocentric bearing cells versus non-spatial cells.
For object-cued location recall, we extracted each cell’s firing rates during each recall event (variable duration, with an additional 1 s data segment before the onset and after the offset of the actual recall period; temporal resolution of 4 Hz; no smoothing). Firing rates were baseline-corrected with respect to a 1 s baseline period (−1 to 0 s before the onset of the recall period). We aligned the firing-rate time courses relative to the response time point and used the data from a time window of −5 to 1 s relative to the response time for further analysis. For each cell, we then calculated one firing-rate time course associated with successful location-recall performance (mean across trials in which location-recall performance was above 0.9) and one firing-rate time course associated with unsuccessful location-recall performance (mean across all other trials). We opted for an absolute performance cutoff of 0.9 to differentiate between successful and unsuccessful recall periods, but similar results were obtained when using a session-specific median split of performance values. Afterwards, we tested across egocentric bearing cells (and, as a control, across non-spatial cells) whether firing rates were significantly increased during successful recall events. Again, we used cluster-based permutation testing (1001 permutations) in order to identify a significant cluster of contiguous time points in which successful recall events exhibited firing rates that were (i) significantly above 0 and (ii) significantly higher than during unsuccessful recall events (using two separate analyses). To test whether the contrast between successful and unsuccessful recall events was significantly stronger in egocentric bearing cells than in non-spatial cells, we performed a cluster-based permutation test (1001 permutations) on the firing-rate differences between successful and unsuccessful trials for egocentric bearing cells versus non-spatial cells.
Supplementary Material
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Data to recreate figures | This paper | https://github.com/NeuroLuke/KunzNeuron2021 |
| Software and algorithms | ||
| MATLAB 2018b and 2020b | MathWorks | RRID: SCR_001622; https://www.mathworks.com |
| Wave_clus 3 spike sorting software | Chaure et al., 2018 | https://github.com/csn-le/wave_clus |
| Custom MATLAB code for data analysis | This paper | https://github.com/NeuroLuke/KunzNeuron2021 |
| Other | ||
| Behnke-Fried depth electrodes | AD-TECH Medical Instrument Corp. | https://adtechmedical.com/depth-electrodes |
Highlights.
Human single-neuron recordings during navigation identify egocentric bearing cells (EBCs)
These EBCs provide a counterpart to allocentric, world-referenced spatial cell types
EBCs encode self-centered bearings and distances towards reference points in space
EBCs play a role in human spatial and episodic memory
Acknowledgements
We are grateful for the patients who participated in this study. We thank the clinical team of the Freiburg Epilepsy Center, Germany, for their continuous support; T. Guth and D. Lachner-Piza for technical assistance; and S. Qasim, M. Peer, and D. Schonhaut for discussions.
LK, AB, ETR, RK, and ASB were supported by the Federal Ministry of Education and Research (BMBF; 01GQ1705A, 01GQ1705B). LK, AB, MT, ASB, and JJ received funding via National Science Foundation (NSF) grant BCS-1724243. LK, AB, and ASB were supported by NIH/NINDS grant U01 NS113198-01. LK received funding via the German Research Foundation (DFG; KU 4060/1-1) and was supported by a travel grant from the Boehringer Ingelheim Fonds (Mainz, Germany). PCR received research grants from the Fraunhofer Society (Munich, Germany) and from the Else Kröner-Fresenius Foundation (Bad Homburg, Germany). BPS was supported by a Wellcome Trust/Royal Society Sir Henry Dale Fellowship (107672/Z/15/Z). NAH received funding via the German Research Foundation (DFG; HE 8302/1-1). RK was supported by the German Research Foundation (DFG; Project-ID 327654276 - SFB 1315). MJK was supported by NIH grants MH055687 and MH061975. JJ was supported by NIH grant MH104606.
Footnotes
Declaration of Interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aguirre GK, Detre JA, Alsop DC, and D’Esposito M (1996). The Parahippocampus Subserves Topographical Learning in Man. Cereb. Cortex 6, 823–829. [DOI] [PubMed] [Google Scholar]
- Alexander AS, Carstensen LC, Hinman JR, Raudies F, William Chapman G, and Hasselmo ME (2020). Egocentric boundary vector tuning of the retrosplenial cortex. Sci. Adv. 6, eaaz2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P (2009). CircStat: A MATLAB Toolbox for Circular Statistics. J. Stat. Softw. 31, 1–21. [Google Scholar]
- Bicanski A, and Burgess N (2018). A neural-level model of spatial memory and imagery. ELife 7, e33752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccara CN, Nardin M, Stella F, O’Neill J, and Csicsvari J (2019). The entorhinal cognitive map is attracted to goals. Science 363, 1443–1447. [DOI] [PubMed] [Google Scholar]
- Bohbot VD, Kalina M, Stepankova K, Spackova N, Petrides M, and Nadel L (1998). Spatial memory deficits in patients with lesions to the right hippocampus and to the right parahippocampal cortex. Neuropsychologia 36, 1217–1238. [DOI] [PubMed] [Google Scholar]
- Burgess N (2006). Spatial memory: how egocentric and allocentric combine. Trends Cogn. Sci. 10, 551–557. [DOI] [PubMed] [Google Scholar]
- Burgess N, Cacucci F, Lever C, and O’Keefe J (2005). Characterizing multiple independent behavioral correlates of cell firing in freely moving animals. Hippocampus 15, 149–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, and Moser EI (2013). Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat. Neurosci. 16, 130–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan E, Baumann O, Bellgrove MA, and Mattingley JB (2012). From objects to landmarks: The function of visual location information in spatial navigation. Front. Psychol. 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaure FJ, Rey HG, and Quian Quiroga R (2018). A novel and fully automatic spike-sorting implementation with variable number of features. J. Neurophysiol. 120, 1859–1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, King JA, Lu Y, Cacucci F, and Burgess N (2018). Spatial cell firing during virtual navigation of open arenas by head-restrained mice. ELife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chrastil ER, and Warren WH (2012). Active and passive contributions to spatial learning. Psychon. Bull. Rev. 19, 1–23. [DOI] [PubMed] [Google Scholar]
- Conway MA (2009). Episodic memories. Neuropsychologia 47, 2305–2313. [DOI] [PubMed] [Google Scholar]
- Deshmukh SS, and Knierim JJ (2013). Influence of local objects on hippocampal representations: Landmark vectors and memory. Hippocampus 23, 253–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doeller CF, King JA, and Burgess N (2008). Parallel striatal and hippocampal systems for landmarks and boundaries in spatial memory. Proc. Natl. Acad. Sci. U. S. A. 105, 5915–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekstrom AD, and Isham EA (2017). Human spatial navigation: representations across dimensions and scales. Curr. Opin. Behav. Sci. 17, 84–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekstrom A, Spiers H, Bohbot V, and Rosenbaum R (2018). Human spatial navigation (Princeton University Press; ). [Google Scholar]
- Ekstrom AD, Kahana MJ, Caplan JB, Fields TA, Isham EA, Newman EL, and Fried I (2003). Cellular networks underlying human spatial navigation. Nature 425, 184–188. [DOI] [PubMed] [Google Scholar]
- Epstein RA (2008). Parahippocampal and retrosplenial contributions to human spatial navigation. Trends Cogn. Sci. 12, 388–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein R, and Kanwisher N (1998). A cortical representation of the local visual environment. Nature 392, 598–601. [DOI] [PubMed] [Google Scholar]
- Epstein RA, and Higgins JS (2007). Differential Parahippocampal and Retrosplenial Involvement in Three Types of Visual Scene Recognition. Cereb. Cortex 17, 1680–1693. [DOI] [PubMed] [Google Scholar]
- Epstein R, Graham KS, and Downing PE (2003). Viewpoint-Specific Scene Representations in Human Parahippocampal Cortex. Neuron 37, 865–876. [DOI] [PubMed] [Google Scholar]
- Fried I, Wilson CL, Maidment NT, Engel J, Behnke E, Fields TA, Macdonald KA, Morrow JW, and Ackerson L (1999). Cerebral microdialysis combined with single-neuron and electroencephalographic recording in neurosurgical patients. J. Neurosurg. 91, 697–705. [DOI] [PubMed] [Google Scholar]
- Gallistel CR (1990). The Organization of Learning.
- Gardiner JM (2001). Episodic memory and autonoetic consciousness: a first–person approach. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 356, 1351–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georges-François P, Rolls ET, and Robertson RG (1999). Spatial View Cells in the Primate Hippocampus: Allocentric View not Head Direction or Eye Position or Place. Cereb. Cortex 9, 197–212. [DOI] [PubMed] [Google Scholar]
- Gofman X, Tocker G, Weiss S, Boccara CN, Lu L, Moser M-B, Moser EI, Morris G, and Derdikman D (2019). Dissociation between Postrhinal Cortex and Downstream Parahippocampal Regions in the Representation of Egocentric Boundaries. Curr. Biol. CB 29, 2751–2757.e4. [DOI] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser M-B, and Moser EI (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806. [DOI] [PubMed] [Google Scholar]
- Hardcastle K, Maheswaranathan N, Ganguli S, and Giocomo LM (2017). A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Chapman GW, and Hasselmo ME (2019). Neuronal representation of environmental boundaries in egocentric coordinates. Nat. Commun. 10, 2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Høydal ØA, Skytøen ER, Andersson SO, Moser M-B, and Moser EI (2019). Object-vector coding in the medial entorhinal cortex. Nature 568, 400–404. [DOI] [PubMed] [Google Scholar]
- Jacobs J, Kahana MJ, Ekstrom AD, Mollison MV, and Fried I (2010). A sense of direction in human entorhinal cortex. Proc. Natl. Acad. Sci. U. S. A. 107, 6487–6492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs J, Weidemann CT, Miller JF, Solway A, Burke JF, Wei X-X, Suthana N, Sperling MR, Sharan AD, Fried I, et al. (2013). Direct recordings of grid-like neuronal activity in human spatial navigation. Nat. Neurosci. 16, 1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jercog PE, Ahmadian Y, Woodruff C, Deb-Sen R, Abbott LF, and Kandel ER (2019). Heading direction with respect to a reference point modulates place-cell activity. Nat. Commun. 10, 2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krupic J, Burgess N, and O’Keefe J (2012). Neural representations of location composed of spatially periodic bands. Science 337, 853–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunz L, Schröder TN, Lee H, Montag C, Lachmann B, Sariyska R, Reuter M, Stirnberg R, Stöcker T, Messing-Floeter PC, et al. (2015). Reduced grid-cell–like representations in adults at genetic risk for Alzheimer’s disease. Science 350, 430–433. [DOI] [PubMed] [Google Scholar]
- Kunz L, Wang L, Lachner-Piza D, Zhang H, Brandt A, Dümpelmann M, Reinacher PC, Coenen VA, Chen D, Wang W-X, et al. (2019). Hippocampal theta phases organize the reactivation of large-scale electrophysiological representations during goal-directed navigation. Sci. Adv. 5, eaav8192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutter EF, Bostroem J, Elger CE, Mormann F, and Nieder A (2018). Single Neurons in the Human Brain Encode Numbers. Neuron 100, 753–761.e4. [DOI] [PubMed] [Google Scholar]
- LaChance PA, Todd TP, and Taube JS (2019). A sense of space in postrhinal cortex. Science 365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lever C, Burton S, Jeewajee A, O’Keefe J, and Burgess N (2009). Boundary vector cells in the subiculum of the hippocampal formation. J. Neurosci. Off. J. Soc. Neurosci. 29, 9771–9777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manns JR, Howard MW, and Eichenbaum H (2007). Gradual Changes in Hippocampal Activity Support Remembering the Order of Events. Neuron 56, 530–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maris E, and Oostenveld R (2007). Nonparametric statistical testing of EEG- and MEG-data. J. Neurosci. Methods 164, 177–190. [DOI] [PubMed] [Google Scholar]
- Miller J, Watrous AJ, Tsitsiklis M, Lee SA, Sheth SA, Schevon CA, Smith EH, Sperling MR, Sharan A, Asadi-Pooya AA, et al. (2018). Lateralized hippocampal oscillations underlie distinct aspects of human spatial memory and navigation. Nat. Commun. 9, 2423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JF, Neufang M, Solway A, Brandt A, Trippel M, Mader I, Hefft S, Merkow M, Polyn SM, Jacobs J, et al. (2013). Neural Activity in Human Hippocampal Formation Reveals the Spatial Context of Retrieved Memories. Science 342, 1111–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JF, Fried I, Suthana N, and Jacobs J (2015). Repeating Spatial Activations in Human Entorhinal Cortex. Curr. Biol. 25, 1080–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moser EI, Moser MB, and McNaughton BL (2017). Spatial representation in the hippocampal formation: A history. Nat. Neurosci. 20. [DOI] [PubMed] [Google Scholar]
- O’Keefe J (1991). An allocentric spatial model for the hippocampal cognitive map. Hippocampus 1, 230–235. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, and Dostrovsky J (1971). The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175. [DOI] [PubMed] [Google Scholar]
- Omer DB, Maimon SR, Las L, and Ulanovsky N (2018). Social place-cells in the bat hippocampus. Science 359, 218–224. [DOI] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, and Schoffelen J-M (2011). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ploner CJ, Gaymard BM, Rivaud-Péchoux S, Baulac M, Clémenceau S, Samson S, and Pierrot-Deseilligny C (2000). Lesions Affecting the Parahippocampal Cortex Yield Spatial Memory Deficits in Humans. Cereb. Cortex 10, 1211–1216. [DOI] [PubMed] [Google Scholar]
- Poulter S, Lee SA, Dachtler J, Wills TJ, and Lever C (2020). Vector trace cells in the subiculum of the hippocampal formation. Nat. Neurosci. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qasim SE, Miller J, Inman CS, Gross RE, Willie JT, Lega B, Lin J-J, Sharan A, Wu C, Sperling MR, et al. (2019). Memory retrieval modulates spatial tuning of single neurons in the human entorhinal cortex. Nat. Neurosci. 433862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reber TP, Bausch M, Mackay S, Boström J, Elger CE, and Mormann F (2019). Representation of abstract semantic knowledge in populations of human single neurons in the medial temporal lobe. PLOS Biol. 17, e3000290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET (1999). Spatial view cells and the representation of place in the primate hippocampus. Hippocampus 9, 467–480. [DOI] [PubMed] [Google Scholar]
- Rolls ET, and O’Mara SM (1995). View-responsive neurons in the primate hippocampal complex. Hippocampus 5, 409–424. [DOI] [PubMed] [Google Scholar]
- Sarel A, Finkelstein A, Las L, and Ulanovsky N (2017). Vectorial representation of spatial goals in the hippocampus of bats. Science 355, 176–180. [DOI] [PubMed] [Google Scholar]
- Shuman T, Aharoni D, Cai DJ, Lee CR, Chavlis S, Page-Harley L, Vetere LM, Feng Y, Yang CY, Mollinedo-Gajate I, et al. (2020). Breakdown of spatial coding and interneuron synchronization in epileptic mice. Nat. Neurosci. 23, 229–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solstad T, Boccara CN, Kropff E, Moser M-B, and Moser EI (2008). Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868. [DOI] [PubMed] [Google Scholar]
- Staresina BP, and Wimber M (2019). A Neural Chronometry of Memory Recall. Trends Cogn. Sci. 23, 1071–1085. [DOI] [PubMed] [Google Scholar]
- Taube JS, Muller RU, and Ranck JB (1990). Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. J. Neurosci. Off. J. Soc. Neurosci. 10, 420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terrazas A, Krause M, Lipa P, Gothard KM, Barnes CA, and McNaughton BL (2005). Self-motion and the hippocampal spatial metric. J. Neurosci. 25, 8085–8096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolman EC (1948). Cognitive maps in rats and men. Psychol. Rev. 55, 189–208. [DOI] [PubMed] [Google Scholar]
- Tsitsiklis M, Miller J, Qasim SE, Inman CS, Gross RE, Willie JT, Smith EH, Sheth SA, Schevon CA, Sperling MR, et al. (2020). Single-Neuron Representations of Spatial Targets in Humans. Curr. Biol. 30, 245–253.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulving E (1972). Episodic and semantic memory. In Organization of Memory., (Oxford, England: Academic Press; ), pp. xiii, 423–xiii, 423. [Google Scholar]
- Tulving E (2002). Episodic Memory: From Mind to Brain. Annu. Rev. Psychol. 53, 1–25. [DOI] [PubMed] [Google Scholar]
- Wang C, Chen X, Lee H, Deshmukh SS, Yoganarasimha D, Savelli F, and Knierim JJ (2018). Egocentric coding of external items in the lateral entorhinal cortex. Science 362, 945–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Chen X, and Knierim JJ (2020). Egocentric and allocentric representations of space in the rodent brain. Curr. Opin. Neurobiol. 60, 12–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weniger G, and Irle E (2006). Posterior parahippocampal gyrus lesions in the human impair egocentric learning in a virtual environment. Eur. J. Neurosci. 24, 2406–2414. [DOI] [PubMed] [Google Scholar]
- Wilber AA, Clark BJ, Forster TC, Tatsuno M, and McNaughton BL (2014). Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. J. Neurosci. 34, 5431–5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter SS, Mehlman ML, Clark BJ, and Taube JS (2015). Passive transport disrupts grid signals in the parahippocampal cortex. Curr. Biol. 25, 2493–2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirth S, Yanike M, Frank LM, Smith AC, Brown EN, and Suzuki WA (2003). Single Neurons in the Monkey Hippocampus and Learning of New Associations. Science 300, 1578–1581. [DOI] [PubMed] [Google Scholar]
- Wood ER, Dudchenko PA, Robitsek RJ, and Eichenbaum H (2000). Hippocampal Neurons Encode Information about Different Types of Memory Episodes Occurring in the Same Location. Neuron 27, 623–633. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data to recreate the figures are available at https://github.com/NeuroLuke/KunzNeuron2021. Raw data are not publicly available because they could compromise research participant privacy, but are available upon request from the lead contact, Lukas Kunz. All custom MATLAB code generated during this study for data analysis is available at https://github.com/NeuroLuke/KunzNeuron2021. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.