Accelerated discovery of 3D printing materials using data-driven multiobjective optimization

Machine learning can aid the discovery of useful 3D printing material formulations.

Abstract

Additive manufacturing has become one of the forefront technologies in fabrication, enabling products impossible to manufacture before. Although many materials exist for additive manufacturing, most suffer from performance trade-offs. Current materials are designed with inefficient human-driven intuition-based methods, leaving them short of optimal solutions. We propose a machine learning approach to accelerating the discovery of additive manufacturing materials with optimal trade-offs in mechanical performance. A multiobjective optimization algorithm automatically guides the experimental design by proposing how to mix primary formulations to create better performing materials. The algorithm is coupled with a semiautonomous fabrication platform to substantially reduce the number of performed experiments and overall time to solution. Without prior knowledge of the primary formulations, the proposed methodology autonomously uncovers 12 optimal formulations and enlarges the discovered performance space 288 times after only 30 experimental iterations. This methodology could be easily generalized to other material design systems and enable automated discovery.

INTRODUCTION

Additive manufacturing is an emerging technique to manufacture objects with complex structures and functions (1, 2). Recently, glass (3), batteries (4–6), high-temperature ceramics (7), and artificial organs (8) have been successfully three-dimensional (3D) printed. Among various polymer printing methods, stereolithography and material jetting 3D printing have shown promising applications such as robotic assemblies (9), prosthetics (10), biologic scaffolds (11), and customized goods (e.g., footwear) (12). However, the development of new 3D printing materials currently relies on domain knowledge of polymer chemistry and extensive experimental trials, constraining the efficiency and scalability of material development. Furthermore, 3D printing materials are typically designed and optimized using one factor at a time (13). This approach often requires testing an excessive number of samples, generating large waste and undesirable environmental impact, while not always finding the most optimal solutions. To make additive manufacturing a more widely adopted manufacturing approach, it is critical to accelerate the development of materials with optimized performance. In addition, to address the challenges of diverse application domains, such as bioengineering and aerospace engineering, material performance needs to be optimized for a specific application.

Different autonomous systems have been recently proposed to accelerate material development and substantially reduce human labor (8, 14–24). For example, Gongora et al. (14) reported an automated 3D printing and testing platform assisted by Bayesian optimization to explore high-compression toughness structures. Rizkin et al. (15) developed a microfluidic reactor to screen zirconocene catalysts combined with a Latin hypercube algorithm for catalytic productivity. A mobile robotic chemist was also developed to search for improved photocatalysts for hydrogen production, driven by a batched Bayesian algorithm (16). Coupled with modern optimization techniques, automated systems can simplify the process of optimizing materials for given performances (17). However, many of these reports focused on single-object optimization. Recently, an autonomous quantum dot synthesis bot was developed (8), which integrated a machine learning–based experiment selection and flow chemistry to explore multiobjective performance. However, the whole process was conducted in liquid, which may not be able to cover other more complex formulation-processing-property relationships. Regardless of this progress, it should be noticed that the cost and time per experiment are often high, material supply might be limited, and collecting large amounts of data is impractical. Thus, data-efficient optimization algorithms are preferred. In addition, for many real-world applications, multiple performance criteria should be met. Satisfying multiple objectives simultaneously increases the complexity of performance space search and the ability to find an optimal solution. In this scenario, a multiobjective optimization approach that guides the sampling of design space can be used to efficiently reduce the number of performed experiments (25).

In this work, we propose a semiautomated data-driven workflow (summarized in Fig. 1) for finding new photocurable inks for additive manufacturing. The semiautomated pipeline is developed to be cost-effective and efficient for finding 3D printing materials; however, a completely autonomous system is possible with certain robotic manipulators (14, 16). The aim of the workflow is to find a set of best composite formulations composed of six primary formulations of photocurable inks to improve the mechanical properties beyond the performance levels of primary formulations designed by hand. These composite formulations are automatically optimized for multiple performance objectives with a limited amount of experiments performed.

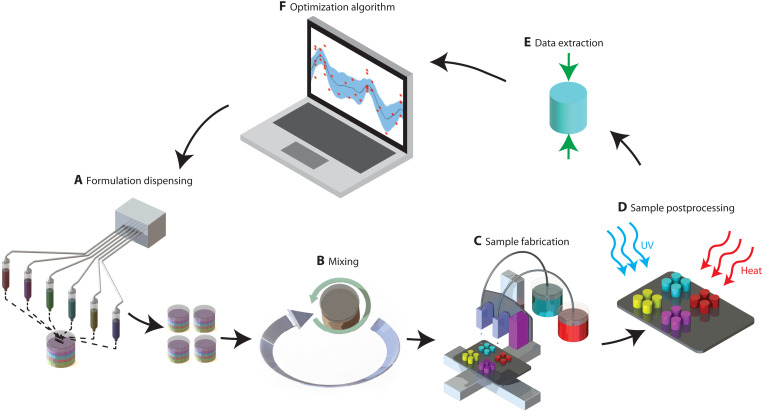
Fig. 1. Schematic workflow of the accelerated material discovery system.

(A) Primary ink dispenser for dispensing desired formulations. (B) Speed mixer for formulation homogenization. (C) Jet valve 3D printer for sample fabrication. (D) Sample postprocessing with ultraviolet (UV) curing and heating. (E) Compression test for performance data extraction. (F) Bayesian optimization algorithm for formulation and performance evaluation, as well as suggestion for which new formulations to test.

The proposed workflow starts by dispensing the primary formulations on demand in a specific ratio (Fig. 1A) and then thoroughly mixing them (Fig. 1B) to prepare a composite formulation. Each composite formulation is then transferred into a jet valve 3D printer for sample fabrication (Fig. 1C and fig. S2), followed by postprocessing (Fig. 1D) to complete the sample preparation. The samples are then tested to extract their multiple quantitative mechanical performance parameters (i.e., toughness, compression modulus, and maximum compression strength) (Fig. 1E and fig. S4). To minimize the resources spent on testing different formulations and rapidly find better performance designs, we use a data-driven approach based on Bayesian optimization (Fig. 1F). This optimization approach automatically learns from prior experiments to inform future decisions on which formulations to test next. A key insight in decision-making lies in balancing between exploiting the most promising formulations and exploring the uncertain regions of the design space. We iterate through the workflow until the experimental budget is reached.

We demonstrate the rapid performance space improvement and discovery of 12 3D printing materials with optimal trade-offs after only 30 algorithm iterations. Our method can be easily generalized to other formulation design problems, such as optimization of tough hydrogels (26), surgical sealants (27), or nanocomposite coatings (28).

RESULTS

Base ingredients and material formulations

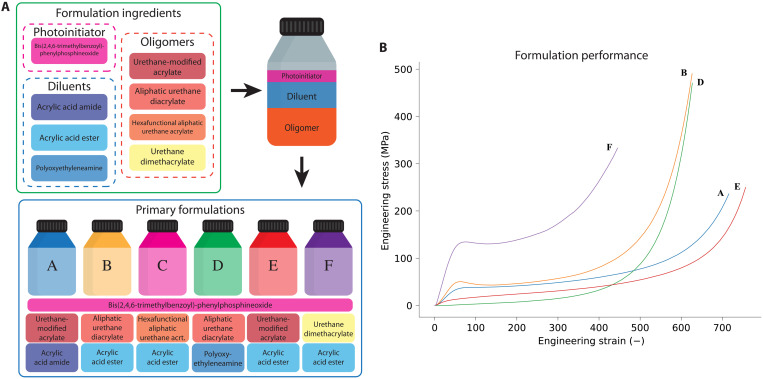
We begin by generating a set of photocurable primary formulations that are compatible with each other to mix and have diverse mechanical properties. As key materials for 3D printing, photocurable monomers and oligomers are widely used in light- and ink-based printing (29, 30). Thus, the development of photopolymers’ formulation libraries would be a substantial step to meet customized printing requirements. Instead of developing printing materials from scratch, we start by identifying eight commercially available formulation ingredients (one photoinitiator, three diluents, and four oligomers), as illustrated in Fig. 2 (details can be found in Materials and Methods). Then, six primary formulations (A to F) are made up of the eight formulation ingredients in the library. To ensure that all possible combinations of formulation ingredients are 3D printable, the primaries are designed to be within a printable regime of viscosities. Surfactant is also added to adjust the surface tension, increasing compatibility with the printer. The photoinitiator is set as a constant across all formulation primaries to avoid its influence on sample performance. Primary formulations are preselected for their ease of printability, print viscosity, and uniqueness of mechanical properties and chemical composition compared to others in the initial screening. However, the selection of materials can be easily expanded depending on the printing method and specific application.

Fig. 2. Primary formulations A, B, C, D, E, and F used in our system.

(A) Primary formulations are made up of eight formulation ingredients (one photoinitiator, three diluents, and four oligomers). (B) Primary formulation performance. The primary formulations are designed to cover a broad range of mechanical properties. Formulation C was too brittle to postprocess and test.

A composite formulation is created by mixing the six primary formulations in a desired ratio. These primary formulations are automatically dispensed by a six-channel syringe pump system (details can be found in Materials and Methods) and subsequently homogenized in a dual asymmetric centrifuge mixer. These two steps reduce the time and variation for sample preparation, resulting in a set of inks with different formulations that are suggested by the optimization algorithm.

Jet valve 3D printing

To increase the variety of inks that can be printed and to reduce the printing setup time, we use a 3D printing process based on the jet valve dispensing technique. When compared to other types of 3D printing techniques, jet valve has the ability to dispense inks with a larger variety of fluid properties (31). Furthermore, jet valve dispensing requires less tuning of process parameters to attain reliable printing. These traits increased ink variety that could be tested and reduced the time for sample fabrication and data collection. To reduce unnecessary variations in geometry and degree of polymerization caused by 3D printing, samples are postprocessed via ultraviolet (UV) curing and heating to ensure complete reaction of components and are flattened via a machining process to eliminate variations in cylinder height (details can be found in Materials and Methods).

Because of the layer-by-layer fashion of 3D printing, processing introduces a number of features, such as layer-to-layer adhesion and uniform curing throughout the thickness, which can affect the resulting mechanical properties of the printed material (32). Hence, testing 3D printed composite formulations rather than casting bulk material ensures that the processing effects on mechanical performance are included in the optimization. Fine-tuning process parameters while optimizing the chemical composition of the formulations may also lead to other optimal solutions. In an extended optimization scheme, 3D printing parameters could also explicitly be included for optimization but are not in this work. Last, to extract the performance data from each formulation, the 3D printed and postprocessed samples are compression-tested using a universal tester.

Multiobjective optimization with batch evaluations

Composite formulations with high degrees of primary C (consisting of hexafunctional aliphatic urethane acrylate, expectedly yielding the highest possible cross-linking density in cured materials by weight and acrylic acid ester) turned out to be too brittle to flatten for compression testing. Therefore, we imposed a maximum fraction of 50% of C in a formulation, leading to the following constraints on the formulation design: (i) a, b, d, e, f ∈ [0,1]; (ii) c ∈ [0,0.5]; and (iii) a + b + c + d + e + f = 1, where a, b, c, d, e, and f refer to the amounts of each of six primaries, scaled to be between 0 and 1 in the ratio of the sample weight. We further use a to f as variables in our optimization system (indicated in Fig. 3).

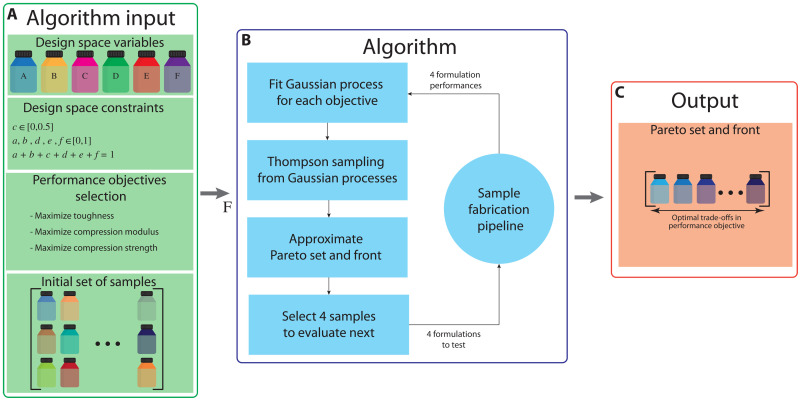
Fig. 3. Overview of the optimization algorithm used to find optimal 3D printing material formulations.

(A) The information needed for input that are the variables within the design space, design space constraints, performance objectives the algorithm is trying to attain, and an initial set of data that is used by the algorithm to build an initial model. (B) An overview of the iterative steps taken by the algorithm to suggest new formulations that may have higher performance. (C) The output from the algorithm after it has finished optimization.

The goal of the optimization algorithm is to navigate the 6D design space of primary formulation ratios a to f and quickly uncover the best performance designs with respect to three objectives: toughness, compression modulus, and maximum strength. These performance objectives are chosen because they are mechanical properties that are important for designing and selecting structural materials in engineering applications (33). Typically, all three of these material properties need to be maximized for many engineering applications. However, these objectives can often be conflicting (34); hence, there is no single optimal solution, but rather a set of best performance designs with different trade-offs. Depending on the application, the higher performance of one of these properties can be more important than others. The set of such solutions is formally called the Pareto set, and their corresponding values in the performance space are called the Pareto front. A point is considered to be Pareto optimal if improvements in one objective can only be achieved if at least one other objective value is decreased. The quality of the Pareto front is measured with a hypervolume indicator, i.e., a volume of the region of the performance space dominated by the points on the Pareto front (see fig. S5). Here, our goal is to find the Pareto front with the largest possible hypervolume indicator.

The design space is a 6D space with five parameters that can take real values between 0 and 1, and the sixth parameter varies between 0 and 0.5 (due to the limitation imposed on C; a detailed description of the design space is available in Materials and Methods). Randomly or intuitively sampling this design space may take months or years to gain enough knowledge of the samples’ performance and uncover optimal regions of the space. To make the optimization more time- and cost-efficient, we use a data-driven approach. The approach learns to predict the performance of untested samples and guides the sampling of the design space to quickly find better performance designs. More specifically, we follow the Bayesian optimization strategy that has proven effective for applications with black-box objective functions and a limited budget of tested samples (35). Our approach adapts the algorithm proposed by Bradford et al. (25) that solves a multiobjective Bayesian optimization problem, as we aim to optimize three objectives simultaneously. The optimization algorithm consists of four main parts, summarized in Fig. 3. More details on the algorithm are available in Materials and Methods. To further reduce the experimental time, in each algorithm iteration, we evaluate a batch of four different samples in parallel.

Discovered materials with optimal trade-offs

To test the proposed material development workflow, we conduct 30 algorithm iterations in total, as our budget is fixed to 120 samples in addition to the initial dataset. In each algorithm iteration, to reduce time, four samples are tested in parallel, giving a total of 120 tested samples during the optimization. After testing a total of 150 samples (30 initial samples and 120 proposed by the algorithm), the system was able to identify a set of 12 formulations that had optimal trade-offs in the three mechanical properties of compression modulus, maximum compression strength, and toughness, as shown in Fig. 4. The Pareto set includes formulations that increase the maximum compression strength by 70.8% and toughness by 50.8% over the performance of the initial six primaries. With the increasing number of samples, it is noticeable that the Gaussian process (GP) model gains its prediction capability, showing a lower relative error from iteration 2 to iteration 30 (fig. S7). In circumstances where only sparse data are available for model training, the model’s prediction capability is relatively low and is not recommended for prediction; however, these models are still helpful for optimization problems.

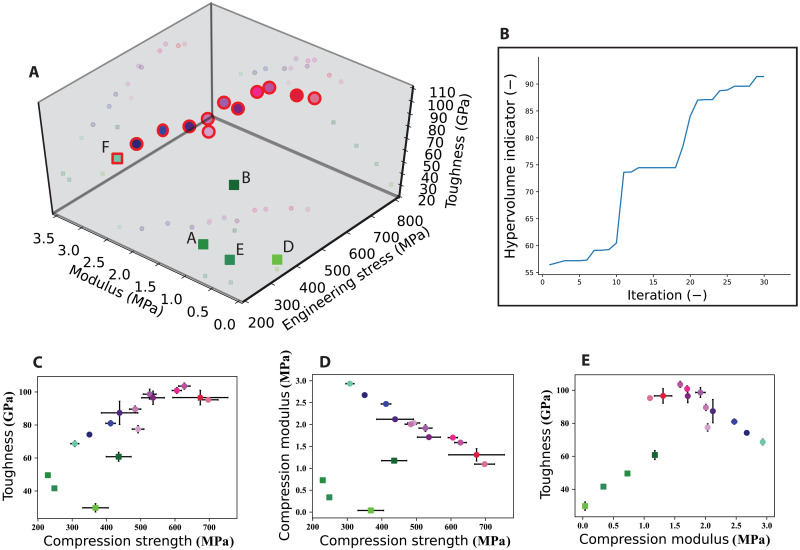
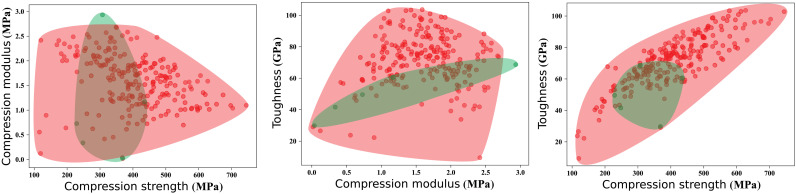
Fig. 4. Performance results.

(A) 3D plot of the performance space, including the performance of five primary formulations A, B, D, E, and F in green squares, and the points on the Pareto front obtained after 30 algorithm iterations, circled in red. Primary C is missing as it is too brittle to test in a pure form. Note that primary ink F lies on the Pareto front. (B) Hypervolume improvement plot. Hypervolume indicator shows the actual improvement of the Pareto front over iterations of the optimization. (C to E) Corresponding 2D plots of pairs of performance objectives.

The optimization found the final points on the Pareto set at iterations 0 (as the primary formulation F is Pareto optimal), 10, 18, 20 (two points), 21, 23, 24, 25, 27, 28, and 30. The formulations with the highest performance compression strength and toughness are found at iterations 28 and 23, respectively. Furthermore, the hypervolume did not attain a steady-state value before the budget was reached. By further optimizing, more formulations could be attained. After 30 iterations, the optimization algorithm increased the hypervolume indicator of the performance space by a factor of 1.65, while our pipeline gave an overall improvement by a factor of 3.25 (see Fig. 4B). The hypervolume of the formulation primaries, initial dataset, and final Pareto front are 2.86 × 10⁷, 5.64 × 10⁷, and 9.32 × 10⁷, respectively. This improvement means that by further optimizing the current set of formulation primaries, a much broader set of performance parameters can be attained. The formulations in the Pareto set vary in compression strength from 308 to 697 MPa. The highest compression strength of the initial six primary formulations was 435 MPa of primary B. Compression modulus of optimal solutions spans from 1.1 to 2.93 MPa. The optimization yielded no composite formulation with a higher compression modulus than primary F; hence, the pure primary F formulation lies on the final Pareto set. Pareto set toughness varies from 68.6 GPa of pure primary F to 103.6 GPa.

Aside from finding the set of optimal solutions, our algorithm that guides the design search also rapidly expands the span of the discovered performance space (see Fig. 5). The algorithm encourages exploration of unknown regions of the performance space and finds materials with a larger variability in properties. When monitoring the compression strength and compression modulus performance of primary formulations and all evaluated samples, the performance space is enlarged by 250%. The enlargement in compression strength and toughness is larger and rises by 399%. In the view of compression modulus and toughness, the performance space is improved by 584%. The convex hull, a measure of the performance space volume enclosed inside all tested samples, increased 288 times from the performance space volume of the initial five primary formulations. This improvement could be important for applications where a specific property range is required and cannot be easily found manually.

Fig. 5. Performance space coverage.

For each pair of performance objectives, initial coverage of the performance space is shown in green (spanned by the primary formulations), and the coverage after 30 algorithm iterations is shown in red.

DISCUSSION

The discovered formulations in the Pareto set are useful materials in the design of compliant structures where material with an application-tailored modulus must be selected to attain the desired outcome (36, 37). Compliant and metamaterial mechanisms that require an actuation force can be tailored by changing the modulus of the materials. To increase the required actuation force, higher modulus materials can be used. Tunable toughness properties are also important for aerospace, packaging, and medical applications to reduce mechanical failure and ensure design usability.

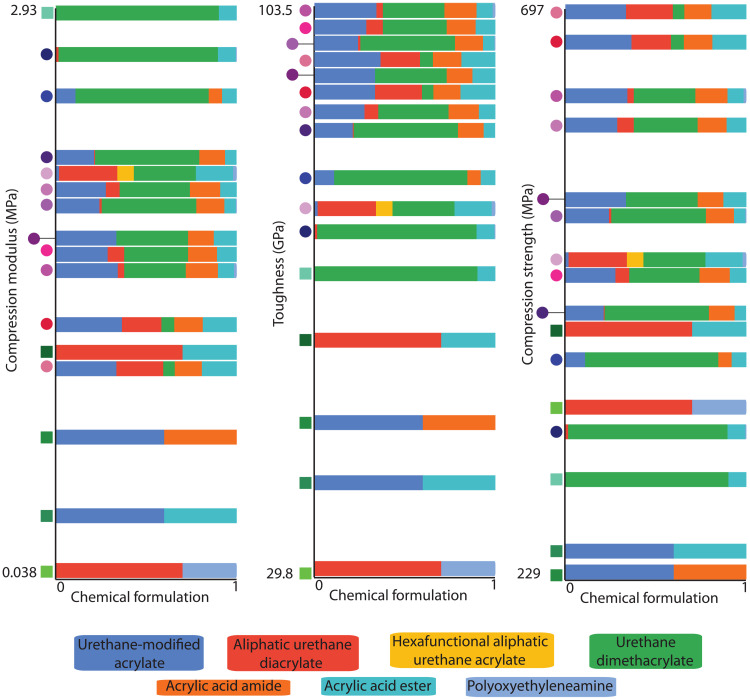
The dataset produced by the optimization also provides interesting observations about the chemical composition’s effect on the resulting mechanical performance of the material, discussed below and graphically presented in Fig. 6. Urethane dimethacrylate (UDMA), the main component in base mixture F, is seen to have a large contribution to materials with a high modulus. This contribution is likely due to its high conversion rate and tendency to form hydrogen bonds (38). In addition, we see the tendency of the optimization engine to minimize the contribution of hexafunctional aliphatic urethane acrylate, a highly cross-link reagent that leans toward brittle prints. High toughness performance is attained by having formulations with oligomers of urethane-modified acrylate in the amount of 24 to 37%, aliphatic urethane diacrylate in the amount up to 26%, and UDMA in the amount up to 40%. High toughness formulations also have diluents acrylic acid amide and acrylic acid ester in the range of 14 to 18% and 1 to 19%, respectively. The highest performance compression strength composite formulations included oligomers, urethane-modified acrylate at 34%, aliphatic urethane diarylate at 26%, and UDMA at 6%. They also include diluents, acrylic acid amide at 15% and acrylic acid ester at 19%.

Fig. 6. Pareto optimal compositions.

Comparison of Pareto optimal (circle) performance characteristics with initial primary formulations (green squares) shows the relationship between performance and formulation ingredients. Base formulation ingredient compositions are indicated via the bar graphs in the chart. Note that the highest compression modulus point is both the primary formulation point (green square) and Pareto optimal.

The system presented in this paper provides an automation-ready pipeline for improving the performance characteristics of a mixed polymer system. The process is designed for automation with the initial base compositions having a much lower viscosity range to handle than starting from pure polymers. In addition, automated equipment exists at all steps of the pipeline, from mixing to sample machining; every step of the process can be fully automated. This provides a template for a process that can be adapted to various optimizations, such as coatings or molding, via alteration of the base materials used in the experiments.

While this study presents many advances in multiobjective optimization for 3D printing, it is not without limitation. When defining the design space, base compositions were limited to human-chosen inks that were known to print. This provides an improvement in efficiency as all possible combinations are printable; however, it may miss some combinations that lie outside of the combination of base inks. Similarly, an improvement could be made to the initial choosing of base compositions via an algorithmic selection mechanic or an expansion to compose using individual chemicals instead of base compositions. The selection of jet valve dispensing as the printing process allows for a large range of materials to be considered and, however, prevents the direct application of the results to commercial printing processes. The same study could be performed on a commercial printing platform to develop application-ready inks.

In summary, the material discovery system described here provides a new way of optimizing photopolymer formulations for additive manufacturing. Using this system allowed us to find a set of 3D printing material formulations with optimal trade-offs in the mechanical properties of compression modulus, compression strength, and toughness. Although this study focuses on the optimization formulations for 3D printing photopolymers, this system can be applied to optimizing materials for other performance objectives, as well as optimizing materials for other manufacturing processes. Our material discovery system lays a foundation for a new tool for material engineers and polymer chemists to find and optimize material formulations for a variety of performance objectives and applications.

MATERIALS AND METHODS

Materials

Modified urethane diacrylate, aliphatic urethane diacrylate, and polyoxyethyleneamine as well as bis(2,4,6-trimethylbenzoyl)-phenylphosphineoxide are provided by BASF. Aliphatic urethane hexaacrylate is acquired from Sartometer. Acrylic acid amide and acrylic acid ester are provided by Rahn AG. Tween 20 (polysorbate 20) and UDMA are purchased from Sigma-Aldrich.

Making 3D printable primary inks

Both viscosity and surface tension limit the compatibility of potential formulations with mixing equipment. Using a jet valve–based 3D printing technology also encounters limitations on both viscosity and surface tension. Lower limitations are imposed by the tendency of the ink to leak from the valve or spread substantially upon contacting the print platform, yielding low print quality. An upper bound on these properties is formed by the inability of the ink to properly separate from the printhead, preventing droplets from forming and causing the printhead to clog. Studies are performed to ensure that the rheology of the inks remains stable while mixing across the design space.

Formulation ink compositions

Six primary formulations are composed to form the basis for the design space. The primary formulations consist of four main components, oligomer, a reactive diluent, photoinitiator, and surfactant. The primary formulations A to F are given in table S2. The oligomer is the main component of each primary ink, transferring most physical properties to the final printed sample. The reactive diluent serves to reduce the viscosity of the ink to bring it to a printable level. The diluent also factors into the final material properties, as it becomes integrated into the final material structure. The photoinitiator component turns UV light into free radicals to polymerize the material and cross-link the oligomer and reactive diluent together. Surfactant components are added to reduce the surface tension, which aids in droplet formation during the printing process.

Handling and experimental cost

The sample fabrication pipeline operates in a semiautomated manner, where many of the steps can be completed without human input. The dispensing, mixing, 3D printing, postprocessing, and testing steps can be completed without human input. Labor is needed to transfer materials between different steps of the sample fabrication pipeline.

The advantage of using the sample fabrication pipeline is to produce and test formulations at a minimal cost. To do this, the sample fabrication pipeline design has been optimized. The duration of each step of the sample fabrication pipeline is listed in table S1.

Dispensing

Dispensing of the primary formulation is performed using a custom syringe pump–based system. Using a positive displacement syringe pump system gives a viscosity and surface tension agnostic method to dispense precise material amounts. The system was constructed using stepper motors driving linear rails to compress 100-ml glass syringes. Syringe outputs are all routed to a manifold that directs the primary formulations into a single mixing cup. The system is controlled using a microcontroller (Arduino Mega 2560, Turin, Italy) with six-axis stepper control software (GRBL, open-source software). This software synchronizes all of the movement commands, so primary formulations can be simultaneously dispensed at varying speeds. To dispense a specific primary formulation, the displacement of each syringe is calculated to be proportional to the primary formulation’s contribution to the composite formulation. This six-axis command is then issued to the controller. Gathering only the steady-state flow from the dispenser allows for differences in the surface tension and viscosity of the different primary formulations to be circumvented.

Mixing

Mixing components together takes a substantial amount of the total time used for preparing formulations for 3D printing. The mixing process is designed to mitigate the amount of time it takes to mix a formulation during processing while ensuring that each formulation was homogenous. To reduce the mixing time down to a more acceptable range, a SpeedMixer (FlackTek, Landrum, SC, USA) is used to mix the components together and is shown in fig. S1. This instrument is a dual-axis centrifuge, causing materials within the mixing vessel to flow into themselves, rapidly mixing them together (39, 40). To ensure that each formulation reaches a homogenous solution, the overall mixing time is 64.7 s (30 s of mixing and 34.7 s of handling) at 3000 rpm for each formulation mixed.

3D printing

To print 3D printing inks with a wide variety of fluid properties, we designed a hardware setup based on a piezo-actuated jet valve. The jetting head consists of a nozzle with a diameter of 300 μm, a spring-loaded needle valve, a pressurized ink reservoir, a valve body, and a piezoelectric actuator as shown in fig. S2. To create a droplet, first, the piezoelectric actuator releases the force holding the needle valve in the closed position. The spring forces the needle valve into its open state. The pressurized ink is forced through the nozzle opening dispensing fluid. Last, the piezoelectric actuator closes the needle valve into the closed position, cutting off the flow of ink. The amount of formulation that is dispensed is a function of the opening time of the nozzle, the backpressure of the ink, and the ink’s fluid properties.

The jet valve 3D printer is composed of two jet valve dispensers (PICO Pμlse from Nordson EFD, Providence, RI, USA), a 365-nm UV light-emitting diode (LED) (Phoseon Technology, Hillsboro, OR, USA), a Cartesian robot (Hiwin Mikrosystems, Taichung, Taiwan), a gantry, a build platform, and a controller. The jet valve dispensers are used to dispense two materials in parallel. The UV LED is used to cure the ink after it is dispensed by the dispensers (41). The Cartesian robot is used to change the position of the jet valve dispensers and UV LED with respect to the build platform. The movement of the Cartesian robot and the actuation of the dispensers and UV LED are controlled by a G-code file that is interpreted by the controller (42).

The controller uses the same g-code file for each formulation. To create a layer of the 3D printed sample, the dispenser follows a vector path and deposits droplets of ink to create a continuous line of material. It follows a vector path until an entire layer of material is deposited. After the layer is finished, the UV LED is turned on and rasters over the entire deposited layer to cure the ink. After curing, the dispensers and UV LED are incremented upward by the thickness of one layer, and the process repeats until the prescribed 3D object has been dispensed.

G-code instructions are produced using slicing software (Slic3r, open-source software), which generates printing instructions for a fused deposition modeling process. This code is then postprocessed further to insert UV LED steps at the end of layers and to change dispensing instructions to communicate properly with the jet valve dispensers. Four 8 mm by 8 mm cylinders in a grid array are imported into the slicing software. Droplet spacing of 0.5 mm was selected to ensure that no voids were present between droplets. The exact g-code print instructions were used for each sample printed, ensuring that droplet spacing, UV curing, and printing path were constant across all samples.

To ensure that the droplet mass was constant across all samples, adjustment of printhead parameters was needed to ensure printability and consistency in droplet mass across ink formulations. The temperature of the printhead was kept at a steady 60°C for all prints, and the close voltage of the valve was also kept at the maximum possible value. Values for syringe pressure, valve opening percentage, and valve opening time were adjusted per print to normalize the mass of an individual droplet. Changing these dispensing parameters result in changes in droplet diameter as shown in fig. S3. As valve opening percentage, syringe pressure, and valve opening time increase, the size of the droplet increases. These parameters must be over a threshold that ensures that a droplet is jetted properly. If jetting parameters are set too high, then splashing can occur when the formulation hits the substrate. Jetting parameters were selected manually for each formulation.

Postprocessing of printed samples

To ensure consistency across all printed samples with different formulations, we use a postcuring step after printing to complete the polymerization process. This accounts for any reaction rate–based differences in the printing process due to differing ink compositions, which could be accounted for in printing process optimization. Typically, 1 hour of baking at 60°C and flooding in 365/405-nm UV light in a postcuring oven (Wicked Engineering, East Windsor, CT, USA) is used to complete polymerization. Further, to remove variations in the height of the compression samples caused by printing and postprocessing (43), the samples are flattened with a machining process.

Mechanical performance testing of printed samples

Physical characteristics of maximum stress, maximum toughness, and modulus are chosen for the performance space. ASTM D638 standard was initially chosen for measuring these properties, using the smallest possible dog bone (standard V) allowed in the documentation. This provided for a dog bone of 63.5 mm by 9.5 mm and an overall volume of approximately 1580 mm³. While useful for initial testing and verification of our method against material data, these samples require precise positioning in a universal testing system (Instron, 68SC-1) taking approximately 3 min per replicate and 12 min per sample to complete testing.

An alternative testing methodology is desired to increase throughput and reduce material requirements. Compression testing (44) circumvents the precision positioning step required in tensile testing, reducing testing time. In addition, the sample size has been shrunk to 8 mm in diameter, with an overall volume of approximately 400 mm³. This allows for more samples to be printed on each print platform, reducing printing time and reducing the amount of raw materials to complete optimization.

Compression testing is completed on the Instron 5984 Universal Tester. Multiple compression rates were tested on these instruments, finding a maximum compression rate of 3 mm/min while maintaining consistency in testing data. In addition to optimizing the rate of compression, a machining step was added to the process to remove inconsistencies on the top of the printed samples. These inconsistencies arise from differences in surface tensions between inks, resulting in differing degrees of doming between prints. By roughly machining the printed samples while still attached to the print platform, consistent surfaces on the top and bottom can be achieved in an automation-friendly format in less than 2 min per composition. These samples are then measured in both diameter and height via a caliper to account for dimensional differences. All the samples are measured three times to obtain a reliable result. Mechanical properties are then computed from the stress-strain curve of each sample, averaged, and inputted to the optimization algorithm.

Performance data analysis

To complement the highly automated process of manufacturing samples, an analysis pipeline is also introduced, which, without any human intervention, is able to produce performance parameters from raw stress-strain data as shown in fig. S4. Initial data were first transformed into engineering stress by dividing the measured force by the surface area of the sample. Engineering strain was normalized by dividing the displacement of the tester by the original height of the sample. Once converted to engineering values, the stress-strain data are then trimmed, allowing for excess data in the initial loading cycle of the tester to be removed along with data after the failure point of the sample. The initial loading segment is trimmed via careful monitoring of the slope of the stress-strain data, looking for the slope to increase to at least 0.1, all data before this point is discarded as noise in initial loading. To find the failure point, the second derivative of the engineering data was rank-ordered and filtered for points with at least three consecutive negative slopes following. Additional filtering on this list of potential failure points was applied, removing points that occurred within the first 30% of the data series. These two methodologies were developed using initial datasets, comparing against how a human mechanical engineer would process the stress-strain data.

Once the initial data were preprocessed, transformation into performance parameters could occur. The modulus was determined by calculating a linear fit on the engineering stress-strain data for all points less than 100 MPa with a sliding window of 20 data points. The median modulus is then calculated from these values, and a filter for all moduli within 60% of the median is applied. Using the values within 60% deviation from the median, a final linear fit is applied across the entire range and classified as the modulus for the sample. Similar to the trimming of the stress-strain data, these calculated values are compared to human calculated values from a mechanical engineer for the initial dataset. The maximal values for both engineering stress and strain are taken from the trimmed data and used for performance values.

Design space and initial samples

The design space is 6D, where five parameters can take real continuous values from 0 to 1, and one parameter is constrained from 0 to 0.5. To simplify the fabrication, we limit the parameters to values with two decimals due to resolution limitations in dispensing. In that case, five parameters can take 101 different values, and the sixth parameter can take 51 different values. Furthermore, these parameters need to sum up to 1 because each of the parameters represents a part in the ratio of the resulting formulation. All valid combinations of these parameters then lie on a standard five simplex, a 5D polytope that is a convex hull of its six vertices. The total number of possible designs is 82,622,991.

The set of 25 initial samples is generated to uniformly cover the design. We get uniformly distributed points on the standard simplex by generating a random vector of five values from the symmetric Dirichlet distribution.

Multiobjective optimization algorithm

We start by evaluating 25 randomly generated samples that try to cover the design space as uniformly as possible and five primary formulations, having 30 initial samples in total. The first part of the algorithm fits a GP for each objective independently. The GPs are trained on the evaluated data points and are used as a surrogate model for black-box objective functions. The Thompson sampling of the GPs is then used to balance the trade-offs of exploiting the best performance regions and exploring unseen regions of the design space (45). The third part of the algorithm solves a multiobjective optimization problem on the previously sampled functions. This part extracts a predicted Pareto front and Pareto set. The final stage of the algorithm proposes which samples to evaluate in the next iteration. To further reduce the experimental time, we propose a batch of four samples to be evaluated in parallel. Four samples with the largest expected hypervolume improvement from the predicted Pareto front are chosen. We then evaluate the proposed samples, add them to the currently available dataset, and iterate through the algorithm.

Algorithm parameters

More details on each part of the algorithm and general hyperparameters can be found by Bradford et al. (25). Here, we list hyperparameters and algorithm alterations used in our implementation.

In each iteration of the algorithm, a GP is fitted for each objective independently. To train the hyperparameters of GP, the maximum a posteriori estimate is used, as proposed by Bradford et al. (25). We use a Matérn kernel 5/2, as it can support the most general and complex function types.

To solve the multiobjective optimization problem on objective functions extracted with Thompson sampling from GPs, a standard NSGA-II solver (46) is used. In each iteration, we use a population size of 100 and a total number of 100 generations. Handling the linear equality constraint a + b + c + d + e + f = 1 is performed by adding two inequality constraints to the solver, a + b + c + d + e + f − 1 0 and a + b + c + d + e + f − 1 0, making sure that mutation points that do not satisfy these constraints are not proposed.

To monitor the hypervolume improvement over iterations, we use a fixed reference point [1.36 × 10², 0.0378, 2.22 × 10⁴] throughout the performance space. This point is chosen because it has a minimal value for each of the three objectives of evaluated points in the initial dataset.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S7

Tables S1 to S4