Modeling zebrafish geotaxis as a feedback control process

Abstract

Developing mathematical models of the feedback control process underlying animal behavior is of critical importance to understand their interactions with the environment and emotional responses. For instance, fish geotaxis (the tendency to swim at the bottom of the tank) is known to be a highly sensitive measure of anxiety, but how and why animals tend to display such a complex response is yet to be fully clarified. Leveraging the theory of stochastic differential equations, we develop a data-driven model of geotaxis in the form of a feedback control loop where fish use information about the hydrostatic pressure to dive towards the bottom of the tank. The proposed framework extends open-loop models by incorporating a simple, yet effective, control mechanism to explain geotaxis. We focus on the zebrafish animal model, which is a species of choice in the study of anxiety disorders. We calibrate the model using available experimental data on acute ethanol treatment of adult zebrafish, and demonstrate its effectiveness across a wide range of comparisons between theoretical predictions and empirical observations.

I. Introduction

How the brain elaborates and integrates sensory information that is ultimately used to produce specific locomotory patterns is of crucial importance to understand the neural basis of behavior [1], [2]. This process can be seen as a feedback control system, whereby animals feed back information gathered from their surroundings and transform it into locomotion. Uncovering such a feedback process can help understand how animals interact with their environment and provide insight into their emotional responses.

Zebrafish (Danio rerio) –a freshwater species with a high genetic homology to humans [3]– has been employed as a model organism for hypothesis testing that can be informative of related human health [4]. In particular, experiments with zebrafish could help clarify the underpinnings of anxiety disorders in humans, which is an emotional state mainly characterized by troubling feelings, worrying, and physical changes such as increase hearth rate or blood pressure [5].

Zebrafish possess a complex anxiety-related behavioral phenotype, ranging from freezing, which involves complete cessation of movement, except for eyes and gills, to geotaxis, that is, the preference to swim at the bottom of the tank. Geotaxis is a very sensitive indicator of anxiety in zebrafish [6] and can be quantified by measuring the distance travelled by the subject at the bottom of the tank, or the frequency and duration of its visits to the bottom of the tank. Within the existing literature, it has been shown that treating fish with anxiogenic drugs can exacerbate their geotactic response. Contrarily, anxiolytic treatments reduce geotaxis, which is similar to the habituation time of a fish in a new environment (novel tank test) [7], [8].

Despite its extensive use as metric of anxiety in experimental assays, the mechanisms underlying this complex anxiety-related behavior are yet to be fully understood. Mathematical models of zebrafish locomotion, based on the theory of stochastic differential equations (SDEs), have been shown to be a promising approach to understand the mechanism underlying single [9]–[12] and collective [13]–[18] behavior. However, to the best of our knowledge, there are not existing models that can capture the dynamics of geotaxis. Particularly important is the study of time effects in geotaxis, which could be indicative of habituation to a new environment or absorption of the administered drug [19].

In this paper, we developed a data-driven model of zebrafish geotaxis consisting of a feedback control loop where fish use information of hydrostatic pressure (proportional to the vertical position along the water column) and its heading angle to dive towards the bottom of the tank. In particular, we extended the open loop zebrafish model in [12] to account for geotaxis. The model consists of a set of coupled SDEs describing the time evolution of speed and turn rate that can reproduce the fish motion on the front plane. We incorporated a bias along the gravity vector as a feedback term acting on the turn rate dynamics. This simple, yet effective, control mechanism enables the fish to adjust its turning maneuvers in real time and perform geotaxis.

The model was calibrated using data on acute ethanol treatment of adult zebrafish from our previous experiment [19]. The efficacy of the proposed model was validated by comparing the average scoring of three different metrics; namely, distance from the bottom, speed, and absolute turn rate on real and synthetic data. The comparison suggests that the model can not only predict swimming at the bottom of the tank, but also time effects during geotaxis. The main contribution of this paper is to extend the current literature on mathematical modeling of zebrafish behavior to closed-loop systems, by specifically developing a data-driven model of geotaxis. From a behavioral neuroscience perspective, this effort constitutes an additional step toward in-silico experiments on anxiety response of zebrafish, which could benefit animal research and welfare.

This paper is organized as follows: the description of the experiment, data acquisition, and processing are given in Section II. The geotaxis model is presented in Section III. In Section IV, we illustrate the model calibration process and demonstrate the effectiveness of our model by comparing theoretical predictions with experiments. Finally, concluding remarks and suggestions for future work are summarized in Section V.

II. Experiments, data collection, and processing

We use data of the experimental condition from [19], where adult subjects were administered acute treatment of ethanol 1.00%. The data set consists of video-recordings of fifteen individual zebrafish swimming in a tank of 29 × 14 × 8.5 cm (length × height × width). The water depth was kept at 13 cm and the video recordings were obtained at 30 frames/s. The experiment was approved by the NYU Washington Square Campus University Animal Welfare Committee (UAWC) under IACUC protocol 13–1424. All videos of the experiments were processed in MATLAB (2019b) using a multi-target tracking system [20] that outputs time series of the centroid positions on the front plane ${\left\{x\left(k{\delta }_t\right)\right\}}_{k=0}^{n-1}$, ${\left\{y\left(k{\delta }_t\right)\right\}}_{k=0}^{n-1}$ and their respective velocities ${\left\{v_x\left(k{\delta }_t\right)\right\}}_{k=0}^{n-1}$, ${\left\{v_y\left(k{\delta }_t\right)\right\}}_{k=0}^{n-1}$, as depicted in Fig. 1. n = 10, 800 is the total number of samples, with sampling rate δ_t := 1/30 s, corresponding to the total experimental time of 6 min (360 s). The centroid coordinates belong to the intervals x ∈ [−x_max, x_max] and y ∈ [−y_max, y_max], with x_max and y_max being the maximum length and height of the test section (2x_max × 2y_max) = (29 cm × 13 cm).

Fig. 1.

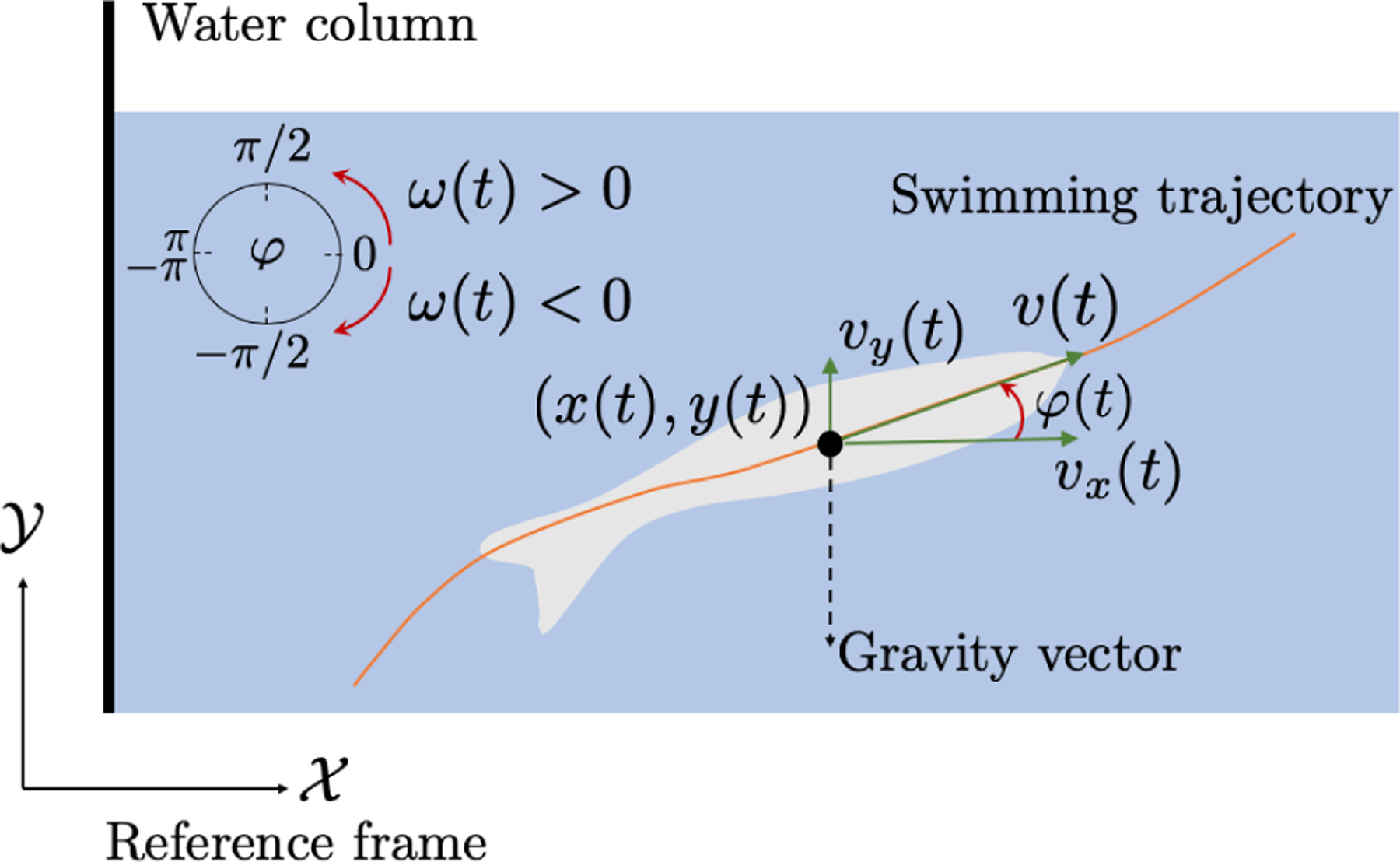
Illustration of a zebrafish swimming trajectory. The tracking software identifies the centroid (x(t), y(t)) for each frame providing a time series of positions along with estimates of the velocity components υ_x(t) and υ_y(t). Swimming trajectories are further utilized for estimating the turn rate ω(t) and heading angle φ(t) of the fish.

All time series were processed using a Daubechies wavelet filter [21] to attenuate noise introduced during tracking. Using the filtered outputs we calculate the fish speed υ(t) and the turn rate ω(t). The speed was computed as a function of the velocity components along the $(\mathcal{X},\mathcal{Y})$ axes (see Fig. 1), $v(t):=\sqrt{v_x^2(t)+v_y^2(t)}$. For calculating the turn rate, we considered the fish speed to be constant between two consecutive centroid positions, then, their difference $\tilde{x}\left(k{\delta }_t\right):=x\left((k+1){\delta }_t\right)-x\left(k{\delta }_t\right)$ and $\tilde{y}\left(k{\delta }_t\right):=y\left((k+1){\delta }_t\right)-y\left(k{\delta }_t\right)$ should satisfy $\tilde{x}\left(k{\delta }_t\right)={\delta }_{t}v\left(k{\delta }_t\right)\text{cos}\left(\phi \left(k{\delta }_t\right)\right)$ and $\tilde{y}\left(k{\delta }_t\right)={\delta }_{t}v\left(k{\delta }_t\right)\text{sin}\left(\phi \left(k{\delta }_t\right)\right)$ where φ(kδ_t) is the heading angle, as shown in Fig. 1. The turn rate was estimated by ω(kδ_t) = δ_φ(kδ_t)/δ_t, where δ_φ(kδ_t) is the turn angle increment between the V₁ vector from the origin to $(\tilde{x}\left(k{\delta }_t\right),\tilde{y}\left(k{\delta }_t\right))$ and V₂ vector from the origin to $\left(\tilde{x}\right(\left(k+1\right){\delta }_t),\tilde{y}\left((k+1){\delta }_t\right))$. To quantify geotaxis, we measure the tendency of the fish to swim at the bottom of the tank in terms of the normalized distance from the bottom of the tank D(t) = |y_max + y(t)|/(2y_max).

In order to assess time variations during geotaxis, we split the 6 min time series of all trials into three time windows of 2 min each. We selected 2 min as the time window to provide enough data points for calibrating the proposed mathematical model. We calculated the time average of the distance from the bottom $\overline{D}=\langle D(t)\rangle$ over each time window. Results are shown in Table I.

Table I.

Average distance from the bottom $\overline{D}$

	Fish identity (ID)		Time window
		1	2	3
	1	0.2062	0.6484	0.7252
	2	0.1169	0.4352	0.7742
	3	-	0.9547	0.9498
	4	0.0664	0.0604	0.1366
$\overline{D}$ ∈ [0, 1]	5	0.1298	0.1009	0.1176
	6	0.5005	0.5809	0.7056
$\overline{D}$ = 1: Top	7	0.1636	0.271	0.2754
	8	0.4591	0.6769	0.7573
$\overline{D}$ = 0: Bottom	9	0.0767	0.0921	0.1323
	10	0.0978	0.5482	0.8201
	11	0.1438	0.0942	0.1074
	12	0.0878	0.0806	0.0806
	13	0.1539	0.2324	0.3599
	14	-	0.6501	0.659
	15	0.1241	0.2783	0.3666
	mean	0.2650	0.3802	0.4645
	std	0.1335	0.2724	0.3029

Using the interquartile range rule [22], we identified two outliers on the first time window and neglected from the analysis. We compared the average distance to the bottom $\overline{D}$ across the three time windows using one-way analysis of variance (ANOVA) with time window as the independent variable [22]. We found a significant statistical effect of time on the tendency of the fish to swim at the bottom of the tank (F (2, 13) = 4.339; p-value< 0.05). Post hoc analysis indicated a significant difference between the first and third time windows. This suggests that, due to the concurrent habituation to the tank and ethanol absorption, geotaxis decreases over time.

III. Data-driven modeling of geotaxis

Exemplary fish swimming trajectories of subject four are shown in Figs. 2(a)–2(c) for three different time windows of 2 min each. We also plot the respective heat maps by dividing the tank in 9 × 4 rectangles of approximately 3.22 cm × 3.25 cm each, corresponding to a grid of approximately 1 Body Length (BL) in size (3 cm). These diagrams indicate the preference of staying in a particular box of the grid (encapsulated by the probability p_i).

Fig. 2.

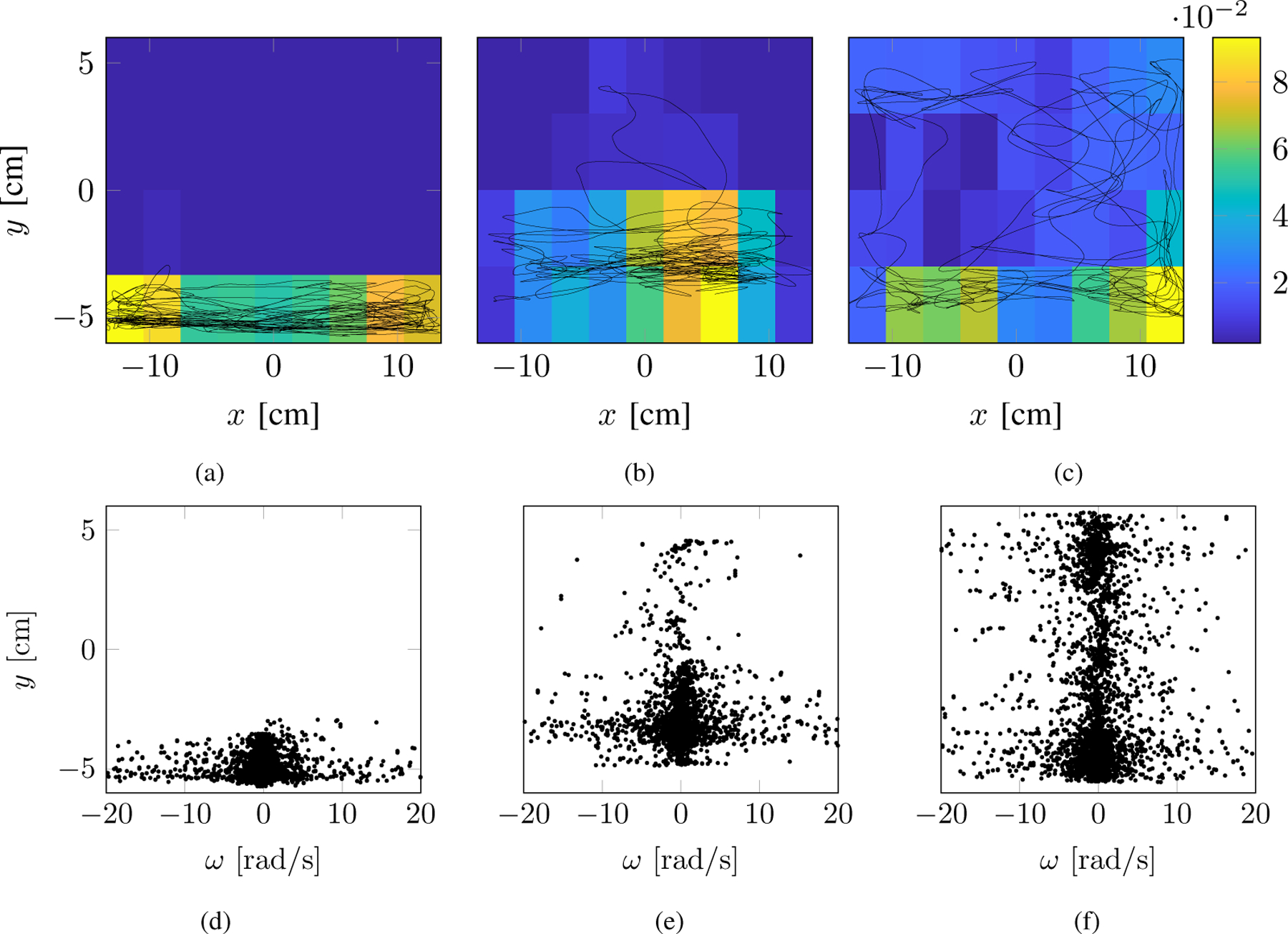
Example of geotactic behavior (ID= 15). The first, second, and third columns correspond to the three time windows. Top panels are the swimming trajectories (x(t), y(t)) along with their heat maps representing the frequency of positions in the tank. Blue colors indicate lower preference, while yellow colors identify a higher one. Bottom panels are the turn rate ω(t) along the water column position y(t).

We note that for the initial time window (first two minutes) the animal tends to swim at the bottom of the tank and explores less its surroundings when compared with the second and third time windows, where the fish occupies a larger area. In fact, its spatial entropy (defined as $-{\sum }_{i=1}^{36}{p}_i{\text{log}}_2\left(p_i\right)$) is initially 3.153 bits and its activity is mostly concentrated at the lower left corner of the tank, while for the second and third time windows the spatial entropy increases to 4.021 and 4.645 bits, respectively. We document a similar phenomenon on the plots of turn rate along the water column in Figs. 2(d)–2(e). In particular, the turn rate is mostly concentrated at the bottom of the tank for the initial time windows, while it becomes more scattered across the tank for the final window.

In the following, we show that this geotactic response can be captured by adding a time-dependent bias along the gravity vector to the turn rate dynamics of the open-loop model proposed in [11].

A. Zebrafish kinematics

We start with the equations of motion for the fish position (x(t), y(t)) and its heading angle φ(t), in the form of the following set of ordinary differential equations [12]:

$$\frac{\text{d}x(t)}{\text{d}t}=v(t)\text{cos}(\phi (t)),\frac{\text{d}y(t)}{\text{d}t}=v(t)\text{sin}(\phi (t)),$$ (1a)

$$\frac{\text{d}\phi (t)}{\text{d}t}=\omega (t).$$ (1b)

B. Modeling the time evolution of speed and turn rate

To describe the time-evolution of speed and turn rate we use a set of SDEs [11], [14], [17]. In particular, in [12] it was shown that the speed can be captured by the following logistic model:

$$\text{d}v(t)=\left[\eta v(t)-g(\omega (t))v^2(t)\right]\text{d}t+{\sigma }_{v}v(t)\text{d}{W}_v(t),$$ (2a)

$$g(\omega (t))=\frac{1}{{\text{std}}_{\omega }\text{BL}}\left|\omega (t)\right|,$$ (2b)

where η[s⁻¹] and σ_υ[s^−1/2] are positive parameters. The former represents the linear rate of growth of the speed, while the latter, is the strength of the added noise W_υ(t), which is a standard Wiener process. The nonlinear function g(ω(t)) [cm⁻¹] regulates the increase or decrease of the speed according to the turn rate ω(t). This function captures the typical relationship between speed and turn rate [12], that is, for higher turn rate activity the fish should decrease speed while for lower turn rates it should increase the speed. Moreover, std_ω = std[ω(t)] is a constant representing the standard deviation of the experimental turn rate.

The time evolution of turn rate can be described by the jump persistent turning walker [11], which consists of a mean reverting jump diffusion process given by

$$\text{d}\omega (t)=\alpha \left({\omega }^{*}(t)-\omega (t)\right)\text{d}t+\sigma \text{d}{W}_{\omega }(t)+\text{d}J(t),$$ (3)

where α [s⁻¹] is the relaxation rate associated with a fish ability to resume straight swimming, and σ [rad s^−3/2] is a positive parameter weighting the added noise W_ω(t), which is a standard Wiener process. The term J(t) is a compound Poisson process describing sudden turning maneuvers of intensity γ [rad s⁻¹] and frequency λ [s⁻¹]. This term accounts for sudden U, or C-turns which are typical of zebrafish swimming style [11]. Here, $J(t)={\sum }_{j=1}^{N(t)}{X}_j\left(t\right)$, where X_j(t) are independent and identically distributed Gaussian random variables with zero mean and variance γ². The intensity and frequency of sudden turns is governed by the the stochastic counting process N(t), whose increments N(t″) − N(t′) are Poisson random variables λ(t″ − t′) for any t′, t″ ∈ t with t″ > t′.

The term ω*(t) is given by

$${\omega }^{*}(t)={\omega }_{\text{W}}(t)+{\omega }_{\text{G}}(t),$$ (4)

where ω_W(t) describes the interaction with the walls while ω_G(t) encapsulates the geotactic contribution. Similar to [17], we consider the interaction with walls to be given by

$${\omega }_{\text{W}}(t)=\frac{K_w}{a_{w}d(t)+1}\text{sgn}(\varphi (t)),$$ (5)

where sgn(·) is the sign function, K_w [rad s⁻¹] and a_w [cm⁻¹] are both positive parameters, d(t) is the distance from the wall, and ϕ(t) is the projected angle to collision (for mode details on the wall interaction term see [12], Fig. 5). In our numerical simulations we found that selecting K_w = 15 rad s⁻¹ and a_w = 10 cm⁻¹ reproduces realistic turns.

Fig. 5.

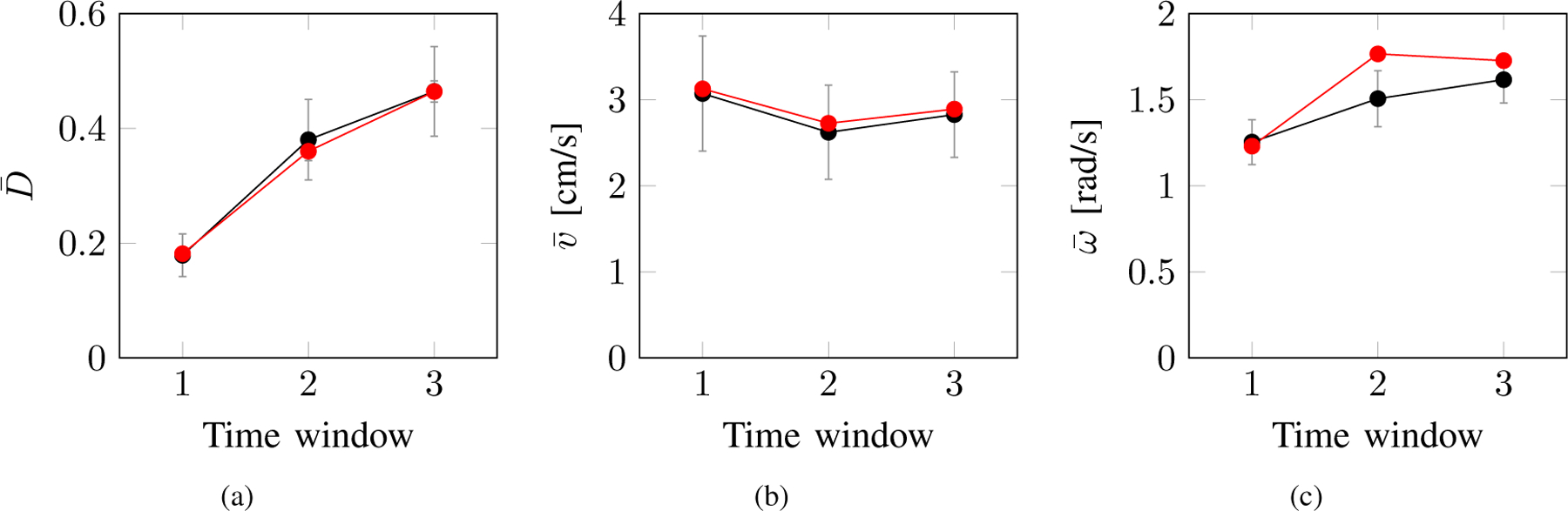
Comparison of the average scoring of three different behavioral metrics for experimental (red) and numerical (black) data. (a) Distance from the bottom, (b) speed, and (c) absolute turn rate. Vertical lines represent standard error of the means (SEM).

C. Modeling the geotactic control process

From the example shown in Fig. 2, we identify two main characteristics of a typical geotactic fish; namely,

• the animal has a natural bias along the gravity vector

• while the bias might be initially strong, it can decrease over time.

Based on these observations, we consider the geotaxis term ω_G(t) to be a bias along the gravity vector whose strength varies over time.

We propose the geotactic bias ω_G(t) to be given by

$${\omega }_{\text{G}}(t)=-A{h}^2(t)\text{cos}(\phi ),$$ (6)

where A [rad cm⁻² s⁻¹] is a positive constant representing the strength of the geotactic term and h(t) := y(t) − y_max is the height or position of the animal along the water column.

This simple turning mechanism is illustrated in Fig. 3 and affords zebrafish the ability to direct its heading towards the bottom of the tank. This mechanism was observed in diving maneuvers from geotactic zebrafish in which turning instances (clockwise or counterclockwise) could be approximated by the function −cos(φ).

Fig. 3.

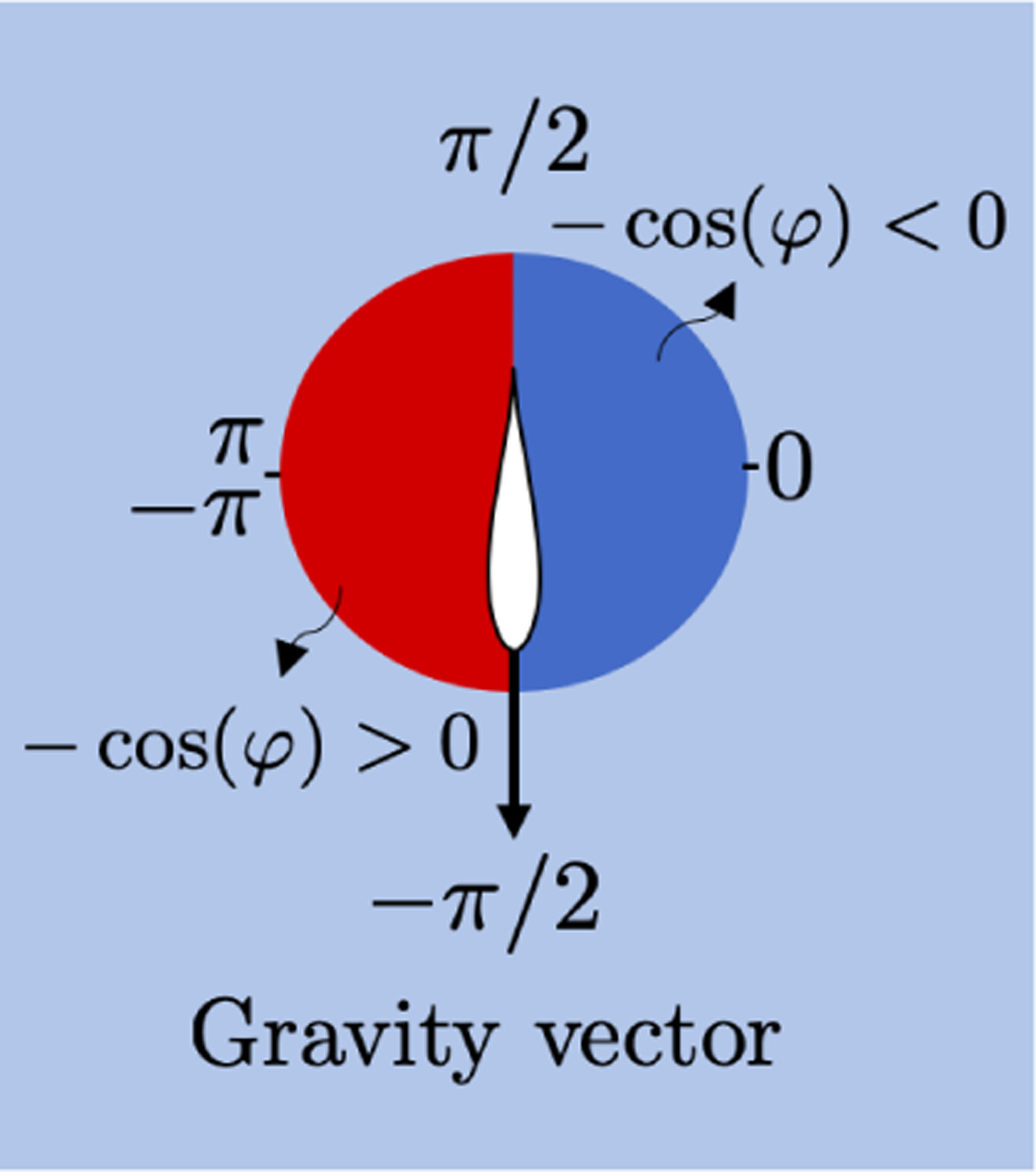
Illustration of the geotactic bias mechanism. For heading angles inside the blue region the fish tends to turn clockwise, while inside the red region, turning tends to be counterclockwise.

The resulting system of equations can be viewed as a feedback control system (see Fig. 4) with the geotaxis bias being the control action driving the heading towards the reference value −π/2. The geotaxis control depends also on the position h(t). This term is introduced to account for a decaying swimming activity along the water column. That is, lower swimming activity at the top and higher activity at the bottom, as reported in Figs. 2(d) and 2(e). The model requires the fish to be able to appraise its global position h(t) in the tank. This is made possible by the lateral line and vestibular systems that can help estimate pressure changes [23], proportional to h(t), thereby closing the loop.

Fig. 4.

Illustration of the feedback control process of geotaxis.

IV. Model calibration and validation

Here, we first present the method for calibrating our mathematical model using the time series of speed and turn rate. Then, we validate the model by comparing real versus in-silico experiments.

A. Maximum likelihood estimation

Since the zebrafish geotactic response is time-dependent, as illustrated in the example in Fig. 1, we split the time series of speed and turn rate, into three time windows of 2 min each. Then, for each time window we obtained estimates of the model parameters.

Following [11], we used the maximum likelihood method to estimate the set of parameters Θ₁ = [η, σ_υ]^T and Θ₂ = [α, σ, γ, λ]^T by solving the following two independent optimization problems:

$${\widehat{\Theta }}_1=\text{arg}\underset{{\Theta }_1}{\text{min}}\left[-\sum _{r=0}^{\tilde{n}}\text{log}{\ell }_v\left({\Theta }_1,\omega \left(r{\delta }_t\right),\tilde{v}\left(r{\delta }_t\right)\right)\right],$$ (7)

and

$${\widehat{\Theta }}_2=\text{arg}\underset{{\Theta }_2}{\text{min}}\left[-\sum _{r=0}^{\tilde{n}}\text{log}{\ell }_{\omega }\left({\Theta }_2,\omega \left(r{\delta }_t\right)\right)\right],$$ (8)

where the time series of speed and turn rate were truncated to only include instances away from the wall (more than 1 BL). Here, ñ < n identifies the length of these truncated time series, for which we used the same notation as the original ones with an abuse of notation. The functions ℓ_v(Θ₁, ω(rδ_t), v(rδ_t)) and ℓ_ω(Θ₂, ω(rδ_t)) are the likelihood functions obtained from discretizing Eqs. (2a),(2b), and (3). These quantities are given by [12]

$${\ell }_v\left({\Theta }_1,\omega \left(r{\delta }_t\right),v\left(r{\delta }_t\right)\right)=f\left(q\left(r{\delta }_t\right),0,\sqrt{{\sigma }_v^2{\delta }_t}\right),$$ (9)

and [11]

$${\ell }_{\omega }\left({\Theta }_2,\omega \left(r{\delta }_t\right)\right)=\lambda {\delta }_{t}f\left(\zeta \left(r{\delta }_t\right),0,\sqrt{s\left(r{\delta }_t\right)+{\gamma }^2}\right)+\left(1-\lambda {\delta }_t\right)f\left(\zeta \left(r{\delta }_t\right),0,\sqrt{s\left(r{\delta }_t\right)}\right),$$ (10)

where f(·, m₁, m₂) is the Gaussian distribution with mean m₁ and variance $m_2^2,\zeta \left(r{\delta }_t\right)=\omega \left((r+1){\delta }_t\right)-s\left(r{\delta }_t\right)$, $s\left(r{\delta }_t\right)={\sigma }^2/2\alpha \left(1-\text{exp}\left(-2\alpha {\delta }_t\right)\right)$, and

$$q\left(r{\delta }_t\right)=-\eta {\delta }_t+1+\frac{v\left(r{\delta }_t\right)\left|\omega \left(r{\delta }_t\right){\delta }_t\right|}{{\text{BL}\text{std}}_{\omega }}+\frac{v\left((r+1){\delta }_t\right)}{v\left(r{\delta }_t\right)}.$$ (11)

We used the optimization toolbox of MATLAB (2019b) for solving the optimization problems in Eqs. (7) and (8). An initial guess of the parameters α and σ is given by the Vasicek calibration method [24], while all the other initial parameter guess are set to zero. The average calibrated parameters $\left[{\widehat{\Theta }}_1^{\top },{\widehat{\Theta }}_2^{\top }\right]$ for all fish across each time window, neglecting divergent points, were given by [0.577 s⁻¹, 0.379 s^−1/2, 5.435 s⁻¹, 2.682 rad s^−3/2, 4.868 rad s⁻¹, 0.876 s⁻¹], [3.040 s⁻¹, 3.567 s^−1/2, 5.694 s⁻¹, 0.998 rad s^−3/2, 0.308 rad s⁻¹, 0.325 s⁻¹], and [3.694 s⁻¹, 4.322 s^−1/2, 5.706 s⁻¹, 0.825 rad s^−3/2, 0.422 rad s⁻¹, 0.327 s⁻¹], respectively.

To calibrate the geotactic gain A, we plotted the time average of the distance to the bottom $\overline{D}$ for different values A. We split the process into three main steps: (i) we carried out 50 simulations of our model using the average calibrated parameters and varying A on the interval [0,0.1] rad cm⁻² s⁻¹. To solve the system of SDEs, we used the use the Euler-Maruyama method [25] with a time step of 1/30 s, matching the sampling of the experimental time series. (ii) Next, we computed $\overline{D}$ for all simulated trajectories and plotted against A. We found a decaying exponential trend $\overline{D}~0.269\text{exp}(-38.282A)+0.192$ that was fitted with standard regression in MATLAB (2019b). (iii) Finally, using this exponential function, we obtained the values of A according to the experimental value of $\overline{D}$ in Table I from the first to the third time window, yielding A = 0.1, 0.01, and 0 rad cm⁻² s⁻¹, respectively.

B. Model validation

To validate our model, we compared the average of three metrics: average distance from the bottom $\overline{D}$, average speed $\overline{v}=\langle v(t)\rangle$, and average absolute turn rate $\overline{\omega }=\langle \left|\omega (t)\right|\rangle$ between experimental and numerical data for the three different time windows. Our simulations consist in solving the closed-loop system in Eqs. (1), (3), (5), (6) for each of the three time windows of 2 min, yielding a total of 6 min of simulation time. During each time window, we used the corresponding set of calibrated parameters found in the previous section. At the beginning of the simulations, all initial conditions were randomly chosen, while for the second and third windows the initial conditions correspond to the final values obtained from the simulation in the previous time window.

The results are shown in Fig. 5. Therein, we notice a remarkable agreement between numerical and experimental results. Not only does our model capture the tendency to swim at the bottom of the tank, but also it predicts its time evolution, whereby fish tends to reduce geotaxis as time progresses [6]. This time-dependent behavior was also observed in independent experiments, where the initial strong geotactic activity is associated with a defensive mechanism that gradually vanishes as the fish habituates to the novel environment or the effect of the pharmacological manipulation decays [26], [27].

V. Conclusions

In this paper, we developed a data-driven mathematical model of geotaxis in adult zebrafish. We extended previous zebrafish models by incorporating a feedback control loop that adjusts the turn rate of the fish according to the position along the water column and its heading angle. This simple, yet effective, control mechanism allows the fish to dive and perform geotaxis. Our model was calibrated using a set of real data, and its effectiveness was tested by comparing the average scoring of three different behavioral metrics evaluated with real and synthetic data. Our results demonstrate that the proposed feedback mechanism can reproduce the geotactic response of real experiments and their time evolution.

This study complements our previous work [12] that examined freezing response through open-loop hybrid dynamics, by making a, critical step toward the ability to study anxiety-related disorders through in-silico experiments. Future work should seek to integrate these efforts toward a comprehensive three-dimensional model, that could capture freezing and geotaxis, for the investigation of the effect of different pharmacological manipulations on behavior.