Summary:
Longitudinal biomarkers are widely used in biomedical and translational researches to monitor the progressions of diseases. Methods have been proposed to jointly model longitudinal data and survival data, but its causal mechanism is yet to be investigated rigorously. Understanding how much of the total treatment effect is through the biomarker is important in understanding the treatment mechanism and evaluating the biomarker. In this work, we propose a causal mediation analysis method to compute the direct and indirect effects, when a joint modeling approach is used to take the longitudinal biomarker as the mediator and the survival endpoint as the outcome. Such a joint modeling approach allows us to relax the commonly used “sequential ignorability” assumption. We demonstrate how to evaluate longitudinally measured biomarkers using our method with two case studies, an AIDS study and a liver cirrhosis study.
Keywords: causal inference, joint modeling, longitudinal data, mediation analysis, survival data
1. Introduction
There is a need for biomedical and translational researches to discover biological surrogates, namely biomarkers, to monitor the progressions of diseases. For example, in HIV studies, researchers are trying to establish biomarkers from short-term laboratory tests, such as CD4+ counts, CD4/CD8 ratio and viral loads, as surrogates for the long-term disease progressions, so the long-term treatment benefits can be revealed in a more timely manner (Tsoukas and Bernard, 1994; Hughes et al., 1998). The key to establishing the validity of such biomarkers is to quantify the correlation between a candidate biomarker and its corresponding endpoint of interest, which is usually a time to event variable, such as death or development of a new symptom. For single-time measured biomarkers, various criteria have been proposed to evaluate the validity (Lange and Hansen, 2011; Martinussen et al., 2011; Zheng and Zhou, 2017; Huang and Yang, 2017; Luo and Geng, 2016). However, many candidate biomarkers, such as CD4 counts for HIV, hemoglobin levels for end-stage renal disease, and a prostate-specific antigen for prostate cancer, are measured longitudinally. Understanding the role of such biomarkers in the causal pathway from treatment to disease outcome is important for future treatment design. However, methods to investigate such a mechanism are limited.
There are three most commonly encountered causal mechanisms between the biomarker and the survival outcome after adjusting for all the measured variables: (1) the biomarker is a “cause” for the outcome without unmeasured confounding; (2) the association between the biomarker and the outcome is purely from unmeasured confounding; or (3) the biomarker is a “cause” for the outcome, but the association is partly confounded by unmeasured variables (Figure 1). Previously, under the context of surrogate evaluation, the estimation of the proportion of treatment effect through the biomarker surrogate for survival outcomes have been studied (Wang and Taylor, 2002; Taylor et al., 2005; Parast et al., 2017; Wang et al., 2020); and Liu et al. (2018) proposed a method to qualitatively identify the causal mechanism between the longitudinal biomarker and the survival outcome. However, there remains a gap to quantify how much of the treatment effect is through changing the biomarker under each of the three causal mechanisms above. This quantification is often meaningful in evaluating the quality of the biomarker and in understanding the mechanism of the treatment. Take the HIV study as an example, if we could quantify how much of the treatment effect is through the change of CD4+ counts, CD4/CD8 ratio and/or viral loads, we are able to use this information to choose the most effective biomarker. In addition, we gain a better knowledge of the treatment mechanism.
Figure 1.
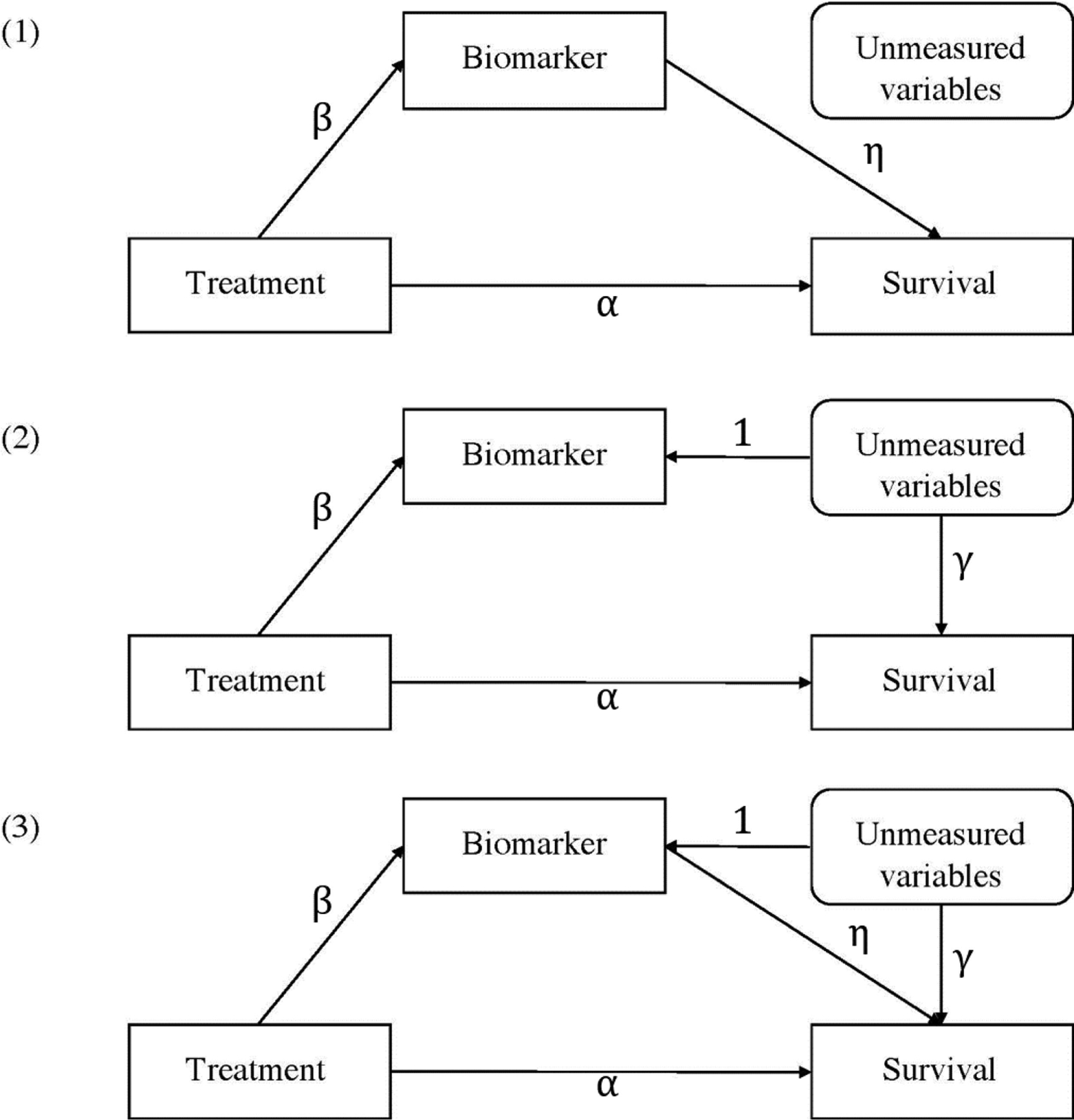
Directed acyclic graph for commonly encountered causal mechanisms between the biomarker and the survival outcome.
In causal mediation analysis, natural direct effect (NDE) and natural indirect effect (NIE) are important quantities to decompose the total treatment effect (TE). First, NDE and NIE provide information on the mechanism of the treatment; second, for the biomarker development case, NIE can be used to quantify the mediation effect of the biomarker as a measure of the utility of the biomarker. So far there is limited research on the causality in the joint analysis of longitudinal and survival data. Ibrahim et al. (2010) gave a brief introduction to the causality in the joint models of longitudinal and survival data without calculating NDE and NIE. Zheng and van der Laan (2017) provided a flexible nonparametric estimation of the NDE and NIE for the longitudinal exposure/mediator with the survival outcome under the “sequential ignorability” (SI) assumption. In the survival setting with a time-varying exposure or mediator, the interventional direct effect (IDE) and the interventional indirect effect (IIE) are used to generalize the definition of the NDE and NIE. Lin et al. (2017) proposed a method with a SAS Macro to estimate the IDE and IIE using g-formula under SI assumption. Didelez (2019) discussed the problem of defining the causal mediation effect when the longitudinal biomarker is only well defined up to the event time and provided a solution to the problem by decomposing the treatment hypothetically into two components. All these methods depend on the stringent SI assumption, which indicates that (i) conditioning on observed covariates, there is no confounding between the treatment and mediator process; (ii) conditioning on observed covariates and the treatment, there is no confounding between the mediator process and the outcome of interest.
In this paper, we first provide estimators for NDE and NIE when the longitudinal biomarker and the survival outcome are jointly modeled under the SI assumption; then we provide estimators for NDE and NIE with a weaker assumption that allows confounding in the form of shared random effects between the mediator and outcome, which relaxes part (ii) of the SI assumption. Depending on whether the shared latent variable (unmeasured confounding) is continuous or categorical, shared random-effects models and shared latent class models have been proposed (Wulfsohn and Tsiatis, 1997; Liu et al., 2007, 2008; Liu and Huang, 2009; Tsiatis and Davidian, 2004; Lin et al., 2002; Proust-Lima and Taylor, 2009; Liu et al., 2015). We focus our method on the shared random-effects model. The extension to the shared latent class model will be straightforward following similar derivations. There is no closed-form solution to our defined NDE and NIE. To tackle the computational difficulty, we proposed a Monte-Carlo method for numerical integration. We studied the finite sample performance of the NDE and NIE estimators and the sensitivity to model misspecification with simulations. We also demonstrated the application of NDE and NIE in understanding the mediation effect in two clinical trial examples. Our first example, the CPCRA study, is a comparative trial of didanosine and zalcitabine in HIV patients. In this study, the CD4 counts are longitudinally measured, enabling us to study its mediation effect. With this study, we illustrate how to quantify the mediation effect of longitudinally measured CD4 counts on the treatment of HIV in the survival study. Our second example, the prothrombin study, is a clinical trial on the treatment effect of prednisone in patients with liver cirrhosis. In this study, the prothrombin index (PI) is longitudinally measured, allowing us to study its mediation effect. We illustrate how to infer about the mediation effect using the NDE and NIE we proposed for both examples.
The rest of this paper is organized as follows. In Section 2, we define our notations and present the formula for calculating the NDE and NIE followed by a discussion of the numerical computation approach. In Section 3, we present simulation studies to explore the finite sample performance of our proposed method. In Section 4, we apply our method to two clinical trials: an AIDS study and a liver cirrhosis study. In Section 5, we summarize our findings and discuss the potential extensions.
2. Method
We consider a potential outcome framework. We denote the treatment of individual i with Zi ∈ {0, 1}, where Zi = 1 represents being assigned to the treatment group and Zi = 0 represents being assigned to the control group. Under the stable unit treatment value assumption (SUTVA), we define the time-varying potential mediator for individual i at time u with treatment z as , and the corresponding biomarker mediator process , where τ is the largest possible follow-up time, and is the set of all possible biomarker mediator processes. Define the potential time to event with treatment z and biomarker mediator process , and the corresponding potential censoring time as . As noted in Didelez (2019), the counterfactual biomarker definition can be problematic and cause identification issues if we allow the survival status to affect the biomarker value. Here we define and model the biomarker process as the potential mediator process if the individual is alive and under certain treatment. Also, we adopt the consistency assumption which links the potential outcomes to the observed outcomes. So we have potentially observable mediator , time to event and censoring time , where . For our data examples, we cannot measure the mediator continuously and Mi(u) are only observed at . The first part of the SUTVA assumption, namely no-multiple-versions-of-treatment, requires the potential outcomes for each patient under each treatment level can only take a single value. This assumption is reasonable because for each level of Z, the treatment is clearly defined and no subcategories are involved. The second part of the SUTVA assumption, i.e., no interference between individuals, is also likely to hold because the outcome is not infectious disease and one individual’s treatment assignment is unlikely to affect the outcome of other individuals. The consistency assumption requires no measurement error in the biomarker process and this assumption is reasonable given the magnitude of the measurement error for the two biomarkers in our examples is relatively small comparing to the biomarkers’ variation over time (Young et al., 2005; Croquet et al., 2002). Due to censoring, we observe the follow-up time and the event indicator Δi = I(Ti ⩽ Ci). We denote the observed baseline covariates for individual i as Xi ∈ Rp. With survival outcome, the TE of Z on T, as well as the NDE and the NIE can be defined on different scales; for example, the survival function, the cumulative hazard, or the hazard function. We will discuss the estimation of the NDE and NIE on the scale of survival probability as defined in Equations (1)and (2) under different assumptions:
| (1) |
| (2) |
2.1. Sequential Ignorability
We first consider the setting under the strong SI assumption. SI assumes that
| (3) |
| (4) |
Under the SI assumption, the NDE and NIE as defined in equations (1) and (2) can be written as
where S(·) is the survival function and FX(·) and are distribution functions. If we are interested in the calculation of NDE and NIE within a specific subgroup X = x, then we do not need the outer integration over x.
To estimate the NDE and NIE, we first model the longitudinally measured potential mediator with a linear mixed model:
| (5) |
where is linearly associated with the treatment indicator z with coefficient β1, some other known covariates Xi with coefficient β2, the time u with coefficient β3, the interaction between treatment and time with coefficient β4, and a random intercept ai0 and a random slope ai1. The residual term ei(u) is the individual specific biomarker fluctuation over time plus measurement error (if any), which is assumed to be independent of z, Xi and ais, but can be dependent on u.
To estimate S(·), we use a Cox model, , where is the potential hazard for individual i, when Zi = z and at time t, and λ0(t) is the baseline hazard. In this model, we assume that depends on only through the term m(t)η. If we would like to consider interactions between the treatment and mediator, we can modify the survival model as .
Next, can be estimated with the distribution assumption of ei(u). For example, in (5), we assume , and is independent of ei(u). Then we obtain that follows a Gaussian process conditioning on Z and X.
2.2. Confounding via Shared Random Effect
Usually, the randomized trial can only guarantee that Z is randomized. However, (4) requires that the biomarker mediator can also be treated as being randomized conditional on Z. Therefore the second part of the SI assumption is too strong and hard to satisfy. To weaken this assumption and make it more plausible, we relax the second part of SI (4) that we only require to be independent with (,) if we condition on Z and X, as well as the unobserved latent shared random effect a, i.e. we assume
| (6) |
where a is the shared random effects which represents the individual heterogeneity. Under such assumption, we have the following expressions for the NDE and NIE:
| (7) |
| (8) |
If we are interested in the effects within a specific subgroup X = x, we can simply ignore the outer integration over x.
To consistently estimate the NDE and NIE, we first model as in (5). We can estimate Fa and by further assuming ai ~ N(0, Σa) and ei(t) is white noise with scale σ2. Next, along the lines of Liu et al. (2018), to estimate S(·), we model the hazard for the counterfactual survival time when individual i is assigned to a treatment level z and is assigned a mediator level , , as
| (Model 1) |
which will lead to the derived survival function for observed data as , where compared with the previous section, we added the shared latent variable. Since we cannot observe Mi(u) continuously, we approximate the integration in likelihood computation by , where is the last value carry forward imputation of Mi(u) based on the observation at discrete time points . If we assume interactions between the shared latent effect and mediator, we can model as
| (Model 2) |
and .
2.3. Numerical integration to estimate the NDE and NIE
Since is with infinite dimensions, there is no closed form for the defined integrations for the NDE’s and NIE’s in the previous section. We can use a Monte-Carlo method to numerically compute this integration. We choose K points 0 = t0 < ⋯ < tK = t and denote t = (t1, ⋯ , tK) and m = (m1, ⋯ , mK) where mj = m(tj). These time points are different from the actual measurement time points, and K usually needs to be much larger than the number of measurements per individual to make the approximation accurate. Then we can estimate the NDE and NIE by plugging in the specific form of survival function and normal density of the mediator process where the integrations can be computed numerically (details shown in the Web Appendix A). The confidence interval can be computed via Bootstrap. Also, the Monte Carlo error can be evaluated by varying the number of nodes used for the integration as well as the number of time points K. When the computational resource is limited, we can sample parameters from the asymptotic variance-covariance matrix of the estimated parameters and compute the corresponding NIE and NDE distribution correspondingly. This approach is used in our simulation studies.
3. Simulation
Although the finite sample performance of the joint modeling fitting approach we used has been studied through extensive simulation (Wulfsohn and Tsiatis, 1997; Liu et al., 2007), it is unknown whether using the fitted parameters to calculate the NDE and NIE as we proposed yields good results. In this section, we perform simulation studies to evaluate the performance of our proposed estimator for NDE and NIE and their robustness to the misspecification of the model. The details on the simulation setting can be found on the Web Appendix B.
Table 1 shows the simulation reuslts. When the random effect follows normal distribution N(0, 1) and the joint model assumed is correctly specified (settings I and II), the fitting for both NIE and NDE perform well with small bias and approximate correct coverage rate when our model is correctly specified. Slight low coverage was observed for NIE when there is interaction which might reflect the insufficient sample size for the asymptotic normality to work well. When the random effect is misspecified (settings III) and there is interaction that are not included in the specified model (setting IV). From the results, we see our estimator is robust to the misspecification of the random effect distribution but is a little sensitive to the misspecification of the fixed effect form. This suggests the need of the goodness of fit test evaluation in real data analysis to determine the correct fixed effect model and avoid using an oversimplified model when sample size allows.
Table 1.
Bias, standard deviation (SD), median estimated standard error (MeSE), and coverage rate for 95% nominal confidence interval (CR) from four simulation settings.
| Setting | Time | Effect | Bias | SD | MeSE | CR |
|---|---|---|---|---|---|---|
| I | 2 | NDE | −0.005 | 0.051 | 0.046 | 94.0% |
| NIE | 0.000 | 0.044 | 0.041 | 93.5% | ||
| 4 | NDE | −0.004 | 0.055 | 0.051 | 95.0% | |
| NIE | 0.001 | 0.037 | 0.033 | 92.5% | ||
| 6 | NDE | −0.003 | 0.051 | 0.049 | 97.0% | |
| NIE | 0.003 | 0.028 | 0.026 | 92.0% | ||
| 8 | NDE | −0.001 | 0.045 | 0.046 | 98.0% | |
| NIE | 0.003 | 0.023 | 0.023 | 93.0% | ||
| II | 2 | NDE | 0.001 | 0.049 | 0.050 | 96.0% |
| NIE | −0.003 | 0.035 | 0.032 | 91.0% | ||
| 4 | NDE | 0.000 | 0.052 | 0.053 | 95.5% | |
| NIE | −0.002 | 0.031 | 0.028 | 90.0% | ||
| 6 | NDE | 0.000 | 0.048 | 0.050 | 95.5% | |
| NIE | −0.001 | 0.025 | 0.024 | 89.5% | ||
| 8 | NDE | 0.000 | 0.043 | 0.046 | 96.5% | |
| NIE | −0.001 | 0.021 | 0.023 | 90.5% | ||
| III | 2 | NDE | 0.010 | 0.053 | 0.048 | 92.5% |
| NIE | −0.002 | 0.047 | 0.042 | 90.0% | ||
| 4 | NDE | 0.006 | 0.056 | 0.053 | 93.5% | |
| NIE | −0.005 | 0.037 | 0.034 | 93.5% | ||
| 6 | NDE | −0.003 | 0.052 | 0.050 | 92.5% | |
| NIE | −0.005 | 0.028 | 0.027 | 95.5% | ||
| 8 | NDE | −0.011 | 0.046 | 0.045 | 93.5% | |
| NIE | −0.004 | 0.022 | 0.023 | 96.5% | ||
| IV | 2 | NDE | 0.034 | 0.063 | 0.054 | 87.0% |
| NIE | −0.010 | 0.057 | 0.045 | 86.5% | ||
| 4 | NDE | 0.019 | 0.070 | 0.062 | 89.0% | |
| NIE | 0.010 | 0.053 | 0.042 | 84.5% | ||
| 6 | NDE | 0.001 | 0.065 | 0.059 | 90.5% | |
| NIE | 0.016 | 0.041 | 0.035 | 79.0% | ||
| 8 | NDE | −0.012 | 0.056 | 0.052 | 94.0% | |
| NIE | 0.017 | 0.031 | 0.029 | 79.5% |
4. Real data analysis
4.1. CPCRA Study
We apply our method to the Terry Beirn CPCRA study. The study evenly randomize 467 patients who previously received zidovudine and had 300 or fewer CD4 cells per cubic millimeter into two groups to receive either didanosine (ddI, n=230) or zalcitabine (ddC, n=237). The primary outcome of interest is the overall survival. There are 100 and 88 deaths in the ddI and ddC groups respectively during the follow-up period (median 13 months; range 1–21 months). The biomarker of interest in this study is the CD4 counts, which is measured longitudinally at baseline and approximately every two months up to twenty months. Since the original CD4 measures are highly skewed and there are about 2.3% of measures being zeros, we use log(CD4+1) as the biomarker mediator M in our model. Five baseline covariates are included in both the biomarker and the survival models as X including: (1) treatment (1: ddC; 0: ddI), (2) gender (1: female; 0: male), (3) previous opportunistic infection (1: AIDS diagnosis at baseline; 0: no AIDS diagnosis), (4) stratum (1: AZT intolerance; 0: AZT failure), and (5) baseline hemoglobin (centered at mean = 12).
Although the total effect of the ddI and ddC is non-significant (p = 0.15), this may be due to a lack of power or the cancellation between the direct and indirect effects. Therefore we further estimate NDE and NIE separately to see how the treatment affects the outcome and CD4. In Model 1, we assume there is no interaction between the random effects a and the biomarker mediator M(t); while in Model 2, we consider the interaction between the random intercept a0 and random slope a1 and the biomarker mediator M(t). We model the baseline hazard as a piecewise constant function with ten pieces, with the endpoints of the pieces being every 10th percentiles of the death time. To see the impact of SI assumption on the estimation of NDE and NIE, we also fit the longitudinal model and survival model separately and calculate the NIE and NDE from that fitting (we call this model the separate model).
The estimates for the parameters involved in the biomarker model (5) and the survival model (Model 1) or (Model 2) are shown in Table 2. The fitting of the biomarker model shows that the treatment does not have a statistically significant effect on the biomarker for both the main effect and the interaction effect, suggesting that there is no evidence showing ddC’s effect on CD4 compared with ddI. The fitting for the survival model shows that there is neither statistically significant treatment effect (p = 0.17 in Model 1 and p = 0.14 in Model 2) nor biomarker effect (p = 0.06 in Model 1 and p = 0.12 in Model 2) on survival after adjustment for the observed covariates and shared latent effects. This shows that neither ddC nor CD4 has an evident direct effect on the outcome. For this study, Model 1 is more appropriate than Model 2, since there is no evidence that the interactions exist (p = 0.29 and p = 0.33). Also, the significant effect of the shared latent effect suggests the violation of the SI assumption. The estimated NIE and NDE (solid line in Figure 2) with the 95% pointwise confidence intervals (dashed lines in Figure 2) from the two joint models as well as the separate models are presented. Also, we compare the summation of the estimated NDE and NIE with the estimated TE. The fittings of Models 1 and 2 are similar, while the separate model provides very different results, where the NDE is overestimated with some significance shown at early time points; and the NIE estimation changes direction (from positive to negative). This shows the potential confounding effect of the shared random effect. This is in accordance with the test results that there is no significant interaction between the latent random effect a and the biomarker mediator M(t). According to our result, although there is a relatively higher magnitude in NDE compared to NIE, both values are not significantly different from 0 except for Model 2 at the larger time points where we observe a marginal significant NDE. Therefore there is no evidence to support that the biomarker mediates the effect of treatment on the survival outcome. These results indicate that the observed association between CD4 and the outcome is statistically insignificant after adjusting for the latent random effect. This finding is consistent with the previous qualitative finding from Liu et al. (2018) that the association between CD4 and outcome is purely due to time-independent unmeasured confounding (modeled as the latent random effect here). Also we notice that the sum of estimated NDE and NIE are close to the estimated TE as expected. This study suggests that (1) there is no evidence to support CD4 as a good mediator for the treatment effect of ddC, and (2) the association between CD4 and the outcome might be purely from unmeasured confounding, therefore it might not be a desirable target to intervene on. This result might be due to the limitation of the data that the patients selected all had relatively low CD4 (300 or fewer CD4 cells per cubic millimeter). Thus, the change of CD4 is relatively small during the trial, and most of the associations of low CD4 and high death risk is explaind by the baseline shared random effect which might attribute to health status. In addition, the correlation between the shared random effect and CD4 would likely cause some variance inflation. These might lead to the insufficient power to detect the CD4 effect for the outcome and thus only marginal significant result is found (p = 0.06).
Table 2.
Results from the CPCRA study
| Model 1 | Model 2 | |||||
|---|---|---|---|---|---|---|
| Variable | Est | SE | p-value | Est | SE | p-value |
| Longitudinal | ||||||
| Intercept | 4.07 | 0.18 | <0.0001 | 4.06 | 0.18 | <0.0001 |
| Treatment | −0.08 | 0.11 | 0.47 | −0.08 | 0.11 | 0.49 |
| Year | −0.79 | 0.10 | <0.0001 | −0.77 | 0.11 | <0.0001 |
| Gender | 0.24 | 0.19 | 0.20 | 0.25 | 0.19 | 0.19 |
| PrevOI | −0.95 | 0.14 | <0.0001 | −0.94 | 0.14 | <0.0001 |
| Stratum | 0.12 | 0.13 | 0.38 | 0.13 | 0.13 | 0.34 |
| HgB | 0.23 | 0.03 | <0.0001 | 0.24 | 0.03 | <0.0001 |
| Treatment × Year | −0.09 | 0.12 | 0.45 | −0.10 | 0.12 | 0.43 |
| Random Effect: Intercept | 1.21 | 0.09 | <0.0001 | 1.22 | 0.09 | <0.0001 |
| Random Effect: Slope | 0.67 | 0.11 | <0.0001 | 0.66 | 0.11 | <0.0001 |
| Random Effect Covariance | −0.03 | 0.07 | 0.73 | −0.02 | 0.07 | 0.77 |
| 0.30 | 0.01 | <0.0001 | 0.30 | 0.01 | <0.0001 | |
| Survival | ||||||
| Treatment | −0.26 | 0.19 | 0.17 | −0.28 | 0.18 | 0.14 |
| CD4 | 0.36 | 0.19 | 0.06 | 0.32 | 0.21 | 0.12 |
| Shared Effect Intercept | −0.92 | 0.24 | 0.0001 | −0.71 | 0.31 | 0.02 |
| Shared Effect Slope | −0.75 | 0.30 | 0.01 | −0.90 | 0.39 | 0.02 |
| CD4×Shared Effect Intercept | NA | NA | NA | −0.06 | 0.06 | 0.29 |
| CD4×Shared Effect Slope | NA | NA | NA | 0.09 | 0.09 | 0.33 |
| Gender | −0.19 | 0.32 | 0.55 | −0.16 | 0.31 | 0.62 |
| PrevOI | 1.47 | 0.36 | <0.0001 | 1.37 | 0.35 | 0.0001 |
| Stratum | −0.18 | 0.21 | 0.41 | −0.20 | 0.21 | 0.34 |
| HgB | −0.50 | 0.08 | <0.0001 | −0.49 | 0.09 | <0.0001 |
Figure 2.
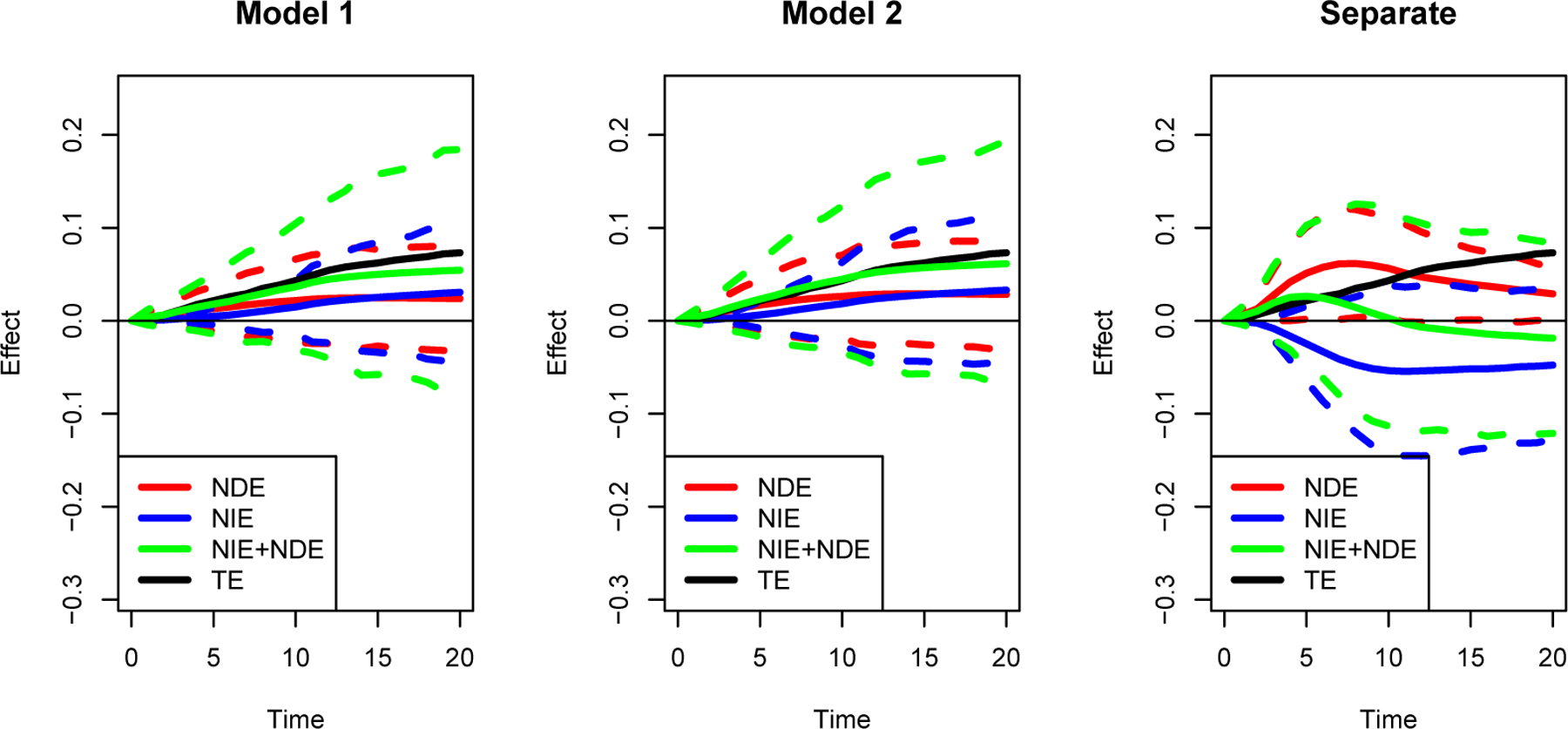
Estimation (solid lines) with bootstrapped 95% point-wise confidence intervals (dash lines) of the natural direct effect (NDE) and natural indirect effects (NIE) of treatment on overall survival probability for CPCRA study.
4.2. Prothrombin
The second data example to illustrate our method comes from a clinical trial to study the effect of prednisone on liver cirrhosis. In this study, 488 patients are followed longitudinally with an average of 6.1 measurements of the biomarker of interest (prothrombin index, PI) per individual. A low PI is usually considered as an indication of the high risk of serious liver damage or cirrhosis. The primary outcome is overall survival. In the follow-up period, 292 events (death) were observed, leading to a censoring rate of 0.40. The question of interest is how the prednisone treatment effect is mediated through the change of PI on the risk of death.
We fit models with and without including the interaction terms between the mediator and the latent random effects. In Model 1, we assume there is no interaction between the latent random effects and the biomarker mediator M(t); while in Model 2, we consider the interaction between the latent random effects and the biomarker mediator M(t). The baseline hazard is modeled as a piecewise constant function with ten pieces, separated at every 10th quantile of the death time. The estimated covariance between the random intercept and random slope is close to zero. For the estimation efficiency, we perform the analysis assuming Σa to be a diagonal matrix. Similar as in Section 4.1, we also fit the longitudinal model and survival model separately and calculate the NIE and NDE from that fitting (we call this model the separate model).
The estimates for the parameters involved in the biomarker model (5) and the survival model (Model 1) or (Model 2) are shown in Table 3. The fitting of the biomarker model shows that the treatment has a significant main effect on the biomarker (p = 0.0001 in both Models 1 and 2) and the interaction between treatment and time is not statistically significant. The fitting for the survival model shows that there is no significant treatment effect on survival (p = 0.37 in Model 1 and p = 0.38 in Model 2) after adjusting for the mediator, but there is a significant main effect of the biomarker on the survival outcome (p < 0.0001 in both Model 1 and 2). These results indicate that there is strong evidence that the prednisone treatment effect is purely mediated through the change of PI. From Table 3, we can see that there is a statistically significant interaction between the biomarker (PI) and the latent random slope on the survival outcome with p < 0.0001. Therefore, in this case, Model 2 is more appropriate than Model 1. Also, the significant shared effect in the survival model suggests the failure of SI assumption. The estimated NIE and NDE with the 95% point-wise confidence intervals for these models are shown in Figure 3. Also, the sum of estimated NDE and NIE are plotted in comparison with estiamated TE. We can see strong NIE through PI from both models, and the model with interaction (Model 2) shows a stronger estimated NIE. The fitting from the separate model is very similar to the result from Model 1, which is consistent with the fact that the coefficients of random effects are not significant in the survival part of Model 1. The interaction term is statistically significant; this suggests that the model misspecification potentially bias the estimation of NIE. In this data example, failing to model the interactions between the mediator and the latent random effects leads to an underestimation of the mediation effect of PI. After removing the effect through PI, we notice that the direct effect is not statistically significant from 0, which suggests we cannot reject the null hypothesis that all treatment effects are mediated through PI. This finding suggests that the working mechanism of the treatment is likely through PI, which opens the potential opportunity in developing new treatments of liver cirrhosis through regulating PI. We notice that the sum of estimated NDE and NIE is slightly larger than to the estimated TE as expected, but the difference is not significant. The difference might be mitigated if more observed covariates are made available and added into the model, as in the CPCRA Study.
Table 3.
Results from the prothrombin data.
| Model 1 | Model 2 | |||||
|---|---|---|---|---|---|---|
| Variable | Est | SE | p-value | Est | SE | p-value |
| Longitudinal | ||||||
| Intercept | 76.9 | 1.3 | <0.0001 | 76.9 | 1.3 | <0.0001 |
| Treatment | −7.3 | 1.9 | 0.0001 | −7.3 | 1.9 | 0.0001 |
| Time | 0.73 | 0.5 | 0.15 | 0.77 | 0.4 | 0.08 |
| Treatment × Time | 0.38 | 0.6 | 0.52 | 0.4 | 0.5 | 0.43 |
| Shared Effect Intercept | 337.2 | 27.5 | <0.0001 | 337.2 | 26.8 | <0.001 |
| Shared Effect Slope | 12.9 | 2.4 | <0.0001 | 12.9 | 2.3 | <0.001 |
| 301.1 | 9.2 | <0.0001 | 301.1 | 9.2 | <0.001 | |
| Survival | ||||||
| Treatment | −0.11 | 0.1 | 0.37 | −0.13 | 0.1 | 0.38 |
| PI | −0.034 | 0.004 | <0.0001 | −0.040 | 0.005 | <0.0001 |
| Shared Effect Intercept | 0.009 | 0.006 | 0.88 | −0.004 | 0.02 | 0.78 |
| Shared Effect Slope | −0.054 | 0.04 | 0.14 | −0.78 | 0.1 | <0.0001 |
| PI×Shared Effect Intercept | NA | NA | NA | 0.0002 | 0.0002 | 0.41 |
| PI×Shared Effect Slope | NA | NA | NA | 0.010 | 0.0001 | <0.0001 |
Figure 3.
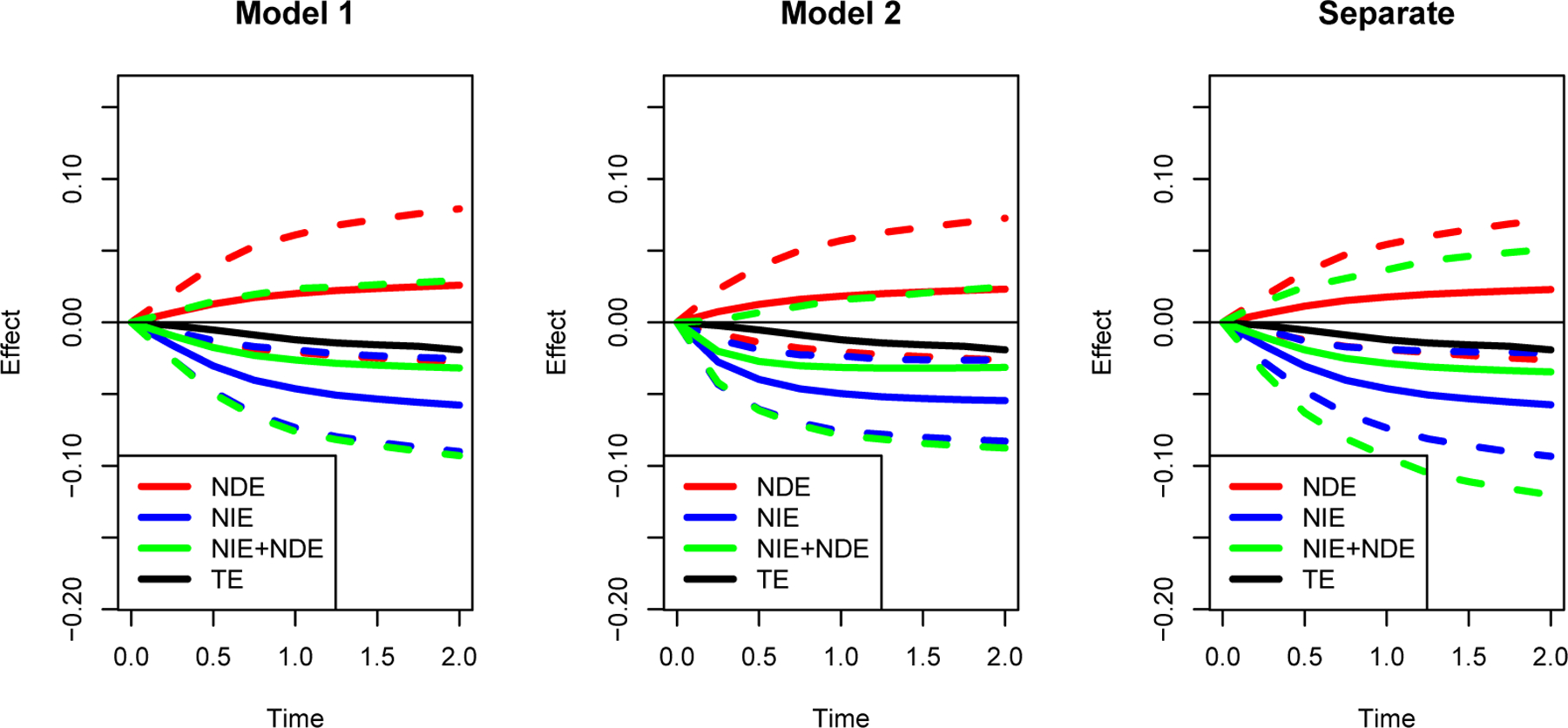
Estimation (solid lines) with bootstrapped 95% point-wise confidence intervals (dash lines) of the natural direct effect (NDE) and natural indirect effects (NIE) of treatment on overall survival probability for prothrombin data.
5. Discussion
In this work, we illustrate how to quantify the relationship between a longitudinal biomarker and a time to event outcome through joint modeling in the potential outcome framework, either under the assumption of sequential ignorability, or allowing confounding between the mediator and the latent shared random effect. This method can provide very important information for practitioners. For example, it can be used to evaluate the performance of a biomarker as a surrogate for the treatment, to understand the working mechanism of a treatment, or to identify a possible target for curing a certain disease.
In real data applications, the performance of the estimation of NDE and NIE depends on the selection of an appropriate joint model. Therefore, before applying our method, we recommend the practitioners to do model selection using some traditional model building techniques, such as AIC, BIC, or test for higher-order terms. We note a different formulation in the joint model by using ai0+ai1t to characterize the “unmeasured variables” in the bottom plot of Figure 1. In an earlier paper on joint model (Liu and Huang, 2009), we found that it has a poorer fit (though the difference is small) for the CD4 data than using (ai0, ai1)⊤ for the CD4 datasest. It is of interest to consider this formulation in other application studies.
Our method for computing NDE and NIE allows the relaxation of the sequential ignorability assumption by including confounding of latent shared random effects. This relaxation is very meaningful in practical uses. For clinical trials, although the treatment and control groups are randomized, it is very difficult, or unrealistic to also randomize the biomarker simultaneously given the limited sample size and the longitudinal feature of the biomarker.
Although the joint model presented in this paper is not new, it is only used as an example to demonstrate our novel way to handle the unmeasured confounders. When either the biomarker model is nonlinear or the proportional hazards model does not hold, our proposed framework of using shared random effects to model baseline unmeasured confounding and the general integration formula for NIE and NDE (Equations 7 and 8) can still be applied in principle. But the specific formula for the survival function, the distribution of random effect a and the distribution of FM|Z,a,X need to be modified and the fitting of parameters in those alternative models require advanced joint modeling methods. For example, if the mediator is not continuous but categorical, a latent class model can be used. Similarly, the Cox model can be replaced with other survival regression models if the corresponding joint modeling approach is available, for example, Cox model with time dependent coefficients or accelerated failure time model. Future work will be needed to allow the existence of multiple biomarker processes and to evaluate their relative strength as mediators.
The main idea of this method is to use a mixed effects model to estimate the unmeasured confounders. A similar idea that has shown success in learning unmeasured confounders from the observational study. Instead of specifically using measurement at different times, unmeasured confounders are estimated using factor analysis when there are more than one exposures of interest that are affected by these unmeasured confounders (Wang and Blei, 2019). One key assumption we make behind this idea is that the unmeasured confounders are time-independent. We also require that the unmeasured confounders affect more than a single time biomarker process for identifiability. Therefore in real data applications, we must keep in mind that potential unmeasured confounding with only instant effects are not taken care of with this method. Alternatively, we can try to find an instrumental variable to help identify such effects by extending the mediation method in the setting of single-time mediator and survival outcome (Zheng and Zhou, 2017) to longitudinal mediator setting.
One limitation for our analysis is that we treat CD4 and PI biomarker processes as external and assume their values are not affected by death, which is a common assumption in the joint model framework. Though this technical assumption is not entirely realistic philosophically, mathematically it leads to the correct estimation of regression parameters given that the observed likelihood does not depend on the biomarker process after death. The calculation of usual NDE and NIE does depend on the model of biomarker process after death and is not identifiable as mentioned in Didelez (2019), which leads us to redefine the NDE and NIE based on a hypothetical biomarker rather than the true biomarker as a remedy. It is worthy of future study to explore additional model assumptions that will allow us to estimate the usual NDE and NIE.
The consistency assumption might be violated when the potential measurement error issue exists for the biomarker process. In general, the term ei(u) contains both the biomarker variability over time as well as the measurement error and these two parts are not identifiable nonparametrically without replicate measures at the same time points. In our example, the measurement of CD4 and PI is relatively mature which might result in relative small measurement error. But for biomarker process that are less accurately measured, we might need the information from replicate measurements for the magnitude of the error. Mediation analysis with measurement error has been studied for non-time-to-event outcome (Valeri et al., 2014; Valeri and TJ, 2014; Loh et al., 2020). In the joint modeling setting, instead of considering the effect of the observed error-prone biomarker on the outcome, the effect of the underlying true biomarker needs to be modeled. The extension of our proposed method to such models with measurement error in biomarker is worth future research. Given that the biomarker is not measured at each time continuously, we note that the last value carried forward imputation is a common and simple approach to handle time dependent covariates in survival analysis.. Better imputation approach and smoothing technique might worth exploring in future research.
Supplementary Material
Acknowledgements
This research is partly supported by National Heart, Lung, and Blood Institute under grant R01 HL136942, National Institute on Aging grant R21 AG063370, and Washington University Institute of Clinical and Translational Sciences grant UL1TR002345 from the National Center for Advancing Translational Sciences (NCATS).
Footnotes
Data Availability Statement
The data that support the findings in this paper are openly available in the JM package in R CRAN at https://CRAN.R-project.org/package=JM, Rizopoulos (2018).
Supporting Information
The Web Appendix referenced in section 2.3 and section 3 are available with this paper at the Biometrics website on Wiley Online Library. Data supporting the finding of this paper, aids and prothro, are publicly available as described in the data availability statement. The SAS and R codes for the analysis of this paper are available at https://github.com/zzhengccheng/Joint_Modeling_Mediation_Public.
Contributor Information
Cheng Zheng, Department of Biostatistics, University of Nebraska Medical Center, Omaha, Nebraska, U.S.A..
Lei Liu, Division of Biostatistics, Washington University in St. Louis, St. Louis, Missouri, U.S.A..
References
- Croquet V, Vuillemin E, Ternisien C, Pilette C, Oberti F, Gallois Y, Trossaert M, Rousselet M, Chappard D, and Cales P (2002). Prothrombin index is an indirect marker of severe liver fibrosis. European Journal of Gastroenterology & Hepatology, 14:1133–1141. [DOI] [PubMed] [Google Scholar]
- Didelez V (2019). Defining causal mediation with a longitudinal mediator and a survival outcome. Lifetime Data Analysis, 25:593–610. [DOI] [PubMed] [Google Scholar]
- Huang Y and Yang H (2017). Causal mediation analysis of survival outcome with multiple mediators. Epidemiology, 28:370–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes M, Daniels M, Fischl M, Kim S, and Schooley R (1998). Cd4 cell count as a surrogate endpoint in hiv clinical trials: a meta-analysis of studies of the aids clinical trials group. AIDS, 12:1823–1832. [DOI] [PubMed] [Google Scholar]
- Ibrahim J, Chu H, and Chen L (2010). Basic concepts and methods for joint models of longitudinal and survival data. J Clin Oncol, 28:2796–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange T and Hansen J (2011). Direct and indirect effects in a survival context. Epidemiology, 22:575–581. [DOI] [PubMed] [Google Scholar]
- Lin H, Turnbull B, McCulloch C, and Slate E (2002). Latent class models for joint analysis of longitudinal biomarker and event process data: application to longitudinal prostate-specific antigen readings and prostate cancer. J Am Stat Assoc, 97:53–65. [Google Scholar]
- Lin S, Young J, Logan R, and VanderWeele T (2017). Mediation analysis for a survival outcome with time-varying exposures, mediators, and confounders. Statist Med, 36:4153–4166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L and Huang X (2009). Joint analysis of correlated repeated measures and recurrent events processes in the presence of a dependent terminal event. JR Stat Soc Ser C Appl Stat, 58:65–81. [Google Scholar]
- Liu L, Ma J, and O’Quigley J (2008). Joint analysis of multi-level repeated measures data and survival: an application to the end stage renal disease. Statist Med, 27:5679–5691. [DOI] [PubMed] [Google Scholar]
- Liu L, Wolfe R, and Kalbfleisch J (2007). A shared random effects model for censored medical costs and mortality. Statist Med, 26:139–155. [DOI] [PubMed] [Google Scholar]
- Liu L, Zheng C, and Kang J (2018). Exploring causality mechanism in the joint analysis of longitudinal and survival data. Statistics in Medicine, 37:3733–3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Liu L, and Zhou J (2015). A joint latent class model of survival and longitudinal data. Comput Stat Data Anal, 91:40–50. [Google Scholar]
- Loh W, Moerkerke B, Loeys T, Poppe L, Crombez G, and Vansteelandt S (2020). Estimation of controlled direct effects in longitudinal mediation analyses with latent variables in randomized studies. Multivariate Behavioral Research, 55:763–785. [DOI] [PubMed] [Google Scholar]
- Luo P and Geng Z (2016). Causal mediation analysis for survival outcome with unobserved mediator-outcome confounders. Comput Stat Data Anal, 93:336–347. [Google Scholar]
- Martinussen T, Vansteelandt S, Gerster M, and von Bornemann Hjelmborg J (2011). Estimation of direct effects for survival data by using the aalen additive hazards model. J R Stat Soc Ser B, 73:773–788. [Google Scholar]
- Parast L, Cai T, and Tian L (2017). Evaluating surrogate marker information using censored data. Statistics in Medicine, 36:1767–1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proust-Lima C and Taylor J (2009). Development and validation of a dynamic prognostic tool for prostate cancer recurrence using repeated measures of post treatment psa: a joint modeling approach. Biostatistics, 10:535–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizopoulos D (2018). JM: Joint modeling of longitudinal and survival data. R package version 1. 4–8. [Google Scholar]
- Taylor J, Wang Y, and Thiebaut R (2005). Counterfactual links to the proportion of treatment effect explained by a surrogate marker. Biometrics, 61:1102–1111. [DOI] [PubMed] [Google Scholar]
- Tsiatis A and Davidian M (2004). Joint modeling of longitudinal and time-to-event data: an overview. Stat Sin, 14:809–834. [Google Scholar]
- Tsoukas C and Bernard N (1994). Markers predicting progression of human immunodeficiency virus-related disease. Clinical Microbiology Reviews, 7:14–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeri L and TJ V (2014). The estimation of direct and indirect causal effects in the presence of misclassified binary mediator. Biostatistics, 15:498–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeri L, X L, and TJ V (2014). Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model. Statistics in medicine, 33:4875–4890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Parast L, Tian L, and Cai T (2020). Model-free approach to quantifying the proportion of treatment effect explained by a surrogate marker. Biometrika, 107:107–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y and Blei D (2019). The blessing of multiple causes. J Am Stat Assoc, 114:1574–1596. [Google Scholar]
- Wang Y and Taylor J (2002). A measure of the proportion of treatment effect explained by a surrogate marker. Biometrics, 58:803–812. [DOI] [PubMed] [Google Scholar]
- Wulfsohn M and Tsiatis A (1997). A joint model for survival and longitudinal data measured with error. Biometrics, 53:330–339. [PubMed] [Google Scholar]
- Young B, Ng O, Lye D, and Leo Y (2005). Derivation and validation of an accurate estimation of cd4 counts from the absolute lymphocyte count in virologically suppressed and immunologically reconstituted hiv infected adults. BMC Infect Dis, 15:330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C and Zhou X (2017). Causal mediation analysis on failure time outcome without sequential ignorability. Lifetime Data Anal, 23:533–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W and van der Laan M (2017). Longitudinal mediation analysis with time-varying mediator and exposures, with application to survival outcomes. J Causal Inference, 5(2). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


